Multi-attribute group decision making based on p, q-quasirung orthopair fuzzy Yager prioritized weighted geometric aggregation operator of p, q-quasirung orthopair fuzzy numbers

Abstract

In this paper, we propose a novel multi-attribute group decision making (MAGDM) approach under the p, q-quasirung orthopair fuzzy number (p, q-QOFN) environment. For this, we propose new multiplication operation and scalar power operation for p, q-QOFNs based on Yager’s norm. Then, by using the proposed multiplication operation and scalar power operation of p, q-QOFNs and the concept of prioritized geometric aggregation operator (AO), we propose the p, q-quasirung orthopair fuzzy Yager prioritized weighted geometric (p, q-QOFYPWG) AO for aggregating p, q-QOFNs. We also prove the different properties of the proposed p, q-QOFYPWG AO of p, q-QOFNs. However, based on the proposed p, q-QOFYPWG AO, we propose a new MAGDM approach in the context of p, q-QOFNs environment. Afterwards, we utilize the proposed MAGDM approach to solve the different MAGDM problems, and compare the preference orders (POs) obtained from the proposed MAGDM approach to POs obtained from other existing MAGDM approaches. The proposed MAGDM approach can overcome the shortcomings of the existing MAGDM approaches, where they cannot distinguish the POs of the alternatives in some cases. The proposed MAGDM approach provides a very useful approach to deal with MAGDM problems in the p, q-QOFNs environment.

1 Introduction

Multi-attribute group decision making (MAGDM) is the cognitive process of choosing a particular action from the several available alternatives. It is essential in everyday life, business, and governance because it enables individuals and organizations to manage challenges, make decisions, and achieve goals. Usually, effective MAGDM involves the assessment of possible choices on the basis of some criteria, goals, and constraints. Hence, it is evident that efficient MAGDM is crucial due to the necessity of successfully managing resources and addressing changes and objectives in situations where uncertainty is involved. It originates from incomplete, vague, or estimative information, which prevents reasonable foresight into its effects. To deal with such uncertainties, Zadeh (1965) introduced the theory of fuzzy sets (FSs) in 1965, where a variable can have membership grade (MG) instead of true or false values. Later, Atanassov (1986) defined the extension of the FS known as intuitionistic fuzzy sets (IFSs) that include the non-membership grade (NMG) with the MG. Following this, Yager (2013) generalized the IFSs to Pythagorean fuzzy sets (PFSs) to solve the uncertainties of the environment more effectively, and PFS provides more flexibility to decision making experts (DMExs). However, in certain instances, PFS may not adequately capture the evaluations of the DMExs. Therefore, Yager (2016) expanded on the ideas of IFS and PFS by creating the q-rung orthopair fuzzy set (q-ROFS) $\langle \zeta _{\mathfrak {T}}, \varrho _{\mathfrak {T}}\rangle$ which satisfy the condition: $0\le \zeta _{\mathfrak {T}}\le 1$, $0\le \varrho _{\mathfrak {T}}\le 1$, $0\le \zeta _{\mathfrak {T}}^q + \varrho _{\mathfrak {T}}^q \le 1$ and $q\ge 1$, which provides more range to express the information comparative to IFSs and PFSs. Many researchers have widely utilized the IFSs, PFSs and q-ROFS in various decision-making scenarios (Liu and Chen 2017; Chen et al. 2016; Chen and Niou 2011; Hussain et al. 2023; Alcantud 2023; Salimian and Mousavi 2022; Dutta and Borah 2022; Gao et al. 2021; Zhang et al. 2020; Çalı and Balaman 2019; Kumar and Chen 2022a; Xu and Wang 2012; Chen et al. 2014; Zhang et al. 2015; Kumar and Chen 2023; Garg 2021; Rahman and Ali 2020; Akram et al. 2020; Khan et al. 2019; Liu et al. 2024; Kumar and Chen 2022b; Zhang and Chen 2022; Garg and Chen 2020; Garg 2020; Liu et al. 2018; Pinar and Boran 2020; Wang et al. 2020; Zhong et al. 2019). Zhang et al. (2020) defined the MAGDM approach based on the multiplicative preference relations in the context of intuitionistic fuzzy numbers (IFNs). Kumar and Chen (2022a) proposed the advanced Heronian mean aggregation operator (AO) and MAGDM approach based on the proposed AO in the IFNs environment. Akram et al. (2020) proposed the MAGDM approach for the Pythagoran fuzzy numbers (PFNs) environment by using the ELECTRE technique. Kumar and Chen (2023) proposed the entropy measure of PFSs and AO for aggregation PFNs for MAGDM approach. Garg (2020) developed the AOs based on trigonometric functions and MAGDM approach based on the proposed AOs under the q-rung orthopair fuzzy numbers (q-ROFNs) environment. Liu et al. (2024) developed the AOs based on the Aczel-Alsina norm and power Heronian mean for MAGDM in the context of q-ROFNs.

In a q-ROFS, DMExs must assign equal values of q for both MG and NMG, a constraint that can significantly impact the overall decision-making process. To overcome this limitation, Seikh and Mandal (2022) introduced p, q-quasirung orthopair fuzzy set (p, q-QOFS) and introduced the p, q-quasirung orthopair fuzzy number (p, q-QOFN), where a p, q-QOFS $\mathfrak {R}$ in the universal set Y is defined as $\mathfrak {R}= \{\langle y,\zeta _{\mathfrak {R}}(y), \varrho _{\mathfrak {R}}(y) \rangle \mid y \in Y\}$, which satisfy the condition: $0\le \zeta _{\mathfrak {R}}(y)\le 1$, $0\le \varrho _{\mathfrak {R}}(y)\le 1$, $0\le \zeta _{\mathfrak {R}}^p + \varrho _{\mathfrak {R}}^q \le 1$, $p\ge 1$ and $q\ge 1$. The p, q-QOFS allows for a nuanced representation of uncertainty, which can be finely tuned by adjusting p and q. The p, q-QOFS becomes an IFS when $p=q=1$ and becomes a PFS when $p=q=2$. Similarly, when $p=q$, p, q-QOFS is converted into q-ROFS. In last 3 years, researchers have used p, q-QOFSs widely to develop the different MAGDM method (Seikh and Mandal 2022; Rahim et al. 2023b, a, 2024b, a, c; Ahmad et al. 2024). Seikh and Mandal (2022) proposed the AOs for aggregating the p, q-QOFNs and MAGDM approach by using the proposed AOs to solve the problem of suitable site selection for electric vehicle charging. Rahim et al. (2023b) presented AOs based on confidence level technique and MAGDM approach by using the proposed AOs for the p, q-QOFNs environment. Rahim et al. (2023a) proposed the AOs based on sine trigonometric function for aggregating p, q-QOFNs and MAGDM approach based on the proposed AOs under the p, q-QOFNs environment. Rahim et al. (2024a) proposed the cosine similarity measure and distance measures for p, q-QOFSs and its application in MAGDM. Rahim et al. (2024c) introduced Dombi AOs for aggregating the p, q-QOFNs and MAGDM method based on the proposed AOs in the context of p, q-QOFNs. Ahmad et al. (2024) developed AOs based on the Hamacher norm and MAGDM approach based on proposed AOs in p, q-QOFNs environment. Rahim et al. (2024b) proposed the MAGDM approach based on the COPRAS technique for the p, q-QOFNs environment and its application in green supplier selection.

In this paper, we find that Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022), Ahmad et al.’s MAGDM approach (Ahmad et al. 2024), Garg’s MAGDM approach (Garg 2020), and Rahim et al.’s MAGDM approach (Rahim et al. 2023a) have the shortcomings, where they cannot distinguish the preference orders (POs) of the alternatives in some cases. Therefore, in order to overcome the shortcomings of Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022), Ahmad et al.’s MAGDM approach (Ahmad et al. 2024), Garg’s MAGDM approach (Garg 2020), and Rahim et al.’s MAGDM approach (Rahim et al. 2023a), it is necessary to propose a new MAGDM approach under the p, q-QOFNs environment.

In this paper, we propose new operations for p, q-QOFNs based on Yager’s norm (Yager 1994), namely, multiplication operation and scalar power operation. However, by using the proposed multiplication operation and scalar power operation, we propose the p, q-quasirung orthopair fuzzy Yager prioritized weighted geometric (p, q-QOFYPWG) AO for aggregating the p, q-QOFNs. We also prove the various properties of proposed p, q-QOFYPWG AO of p, q-QOFNs. Furthermore, by utilizing the p, q-QOFYPWG AO, we propose a novel MAGDM approach under the p, q-QOFNs environment. Afterwards, we solve a few MAGDM problems by using the proposed MAGDM approach and compare the preference orders (POs) obtained from the proposed MAGDM approach with POs obtained from other existing MAGDM approaches. The proposed MAGDM approach can overcome the shortcomings of Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022), Ahmad et al.’s MAGDM approach (Ahmad et al. 2024), Garg’s MAGDM approach (Garg 2020) and Rahim et al.’s MAGDM approach (Rahim et al. 2023a), where they cannot distinguish the POs of the alternatives in some cases.

The remaining part of this paper is organized as follows: Sect. 2 contains the elementary concepts relevant to this paper. In Sect. 3, we propose the multiplication operation and scalar power operation for p, q-QOFNs using Yager’s norm. Section 4 propose the p, q-QOFYPWG AO based on the proposed operational laws of p, q-QOFNs. In Sect. 5, we propose a new MAGDM approach in the p, q-QOF environment. Finally, Sect. 6 provides conclusion of the paper.

2 Preliminaries

This section presents the basic information related to this article.

Definition 1

(Yager 2016) A q-ROFS $\mathfrak {T}$ in the universe of discourse Y is defined as:

$$\begin{aligned} \mathfrak {T}= \{\langle y,\zeta _{\mathfrak {T}}(y), \varrho _{\mathfrak {T}}(y) \rangle \mid y \in Y\}, \end{aligned}$$

(1)

where $\zeta _{\mathfrak {T}}(y):Y \rightarrow [0,1]$ denotes the MG and $\varrho _{\mathfrak {T}}(y):Y \rightarrow [0,1]$ denotes the NMG of $y\in Y$, respectively, where $0\le \zeta _{\mathfrak {T}}(y)\le 1$, $0\le \varrho _{\mathfrak {T}}(y)\le 1$, $0 \le (\zeta _{\mathfrak {T}}(y))^q+(\varrho _{\mathfrak {T}}(y))^q \le 1$ and $q\ge 1$. The hesitancy degree of an element $y \in Y$ is $(\pi _{\mathfrak {T}}(y))=(1-(\zeta _{\mathfrak {T}}(y))^q-(\varrho _{\mathfrak {T}}(y))^q)^{\frac{1}{q}}$.

Usually, the pair $\langle \zeta _\mathfrak {T}(y), \varrho _\mathfrak {T}(y) \rangle$ in the q-ROFSs $\mathfrak {T}= \{\langle y,\zeta _{\mathfrak {T}}(y), \varrho _{\mathfrak {T}}(y) \rangle \mid y \in Y\}$ called the q-ROFN.

Definition 2

(Yager 2016) Let $\mathfrak {T}_{1}=\langle \zeta _{1}, \varrho _{1} \rangle$, $\mathfrak {T}_{2}=\langle \zeta _{2}, \varrho _{2} \rangle$ and $\mathfrak {T}=\langle \zeta , \varrho \rangle$ be three q-ROFNs, $\kappa >0$. Then

• (i) $\mathfrak {T}_{1}\oplus \mathfrak {T}_{2}=\left\langle \root q \of {\zeta ^q_{1}+{\zeta ^q_{2}}-\zeta _{1}^q\zeta _{2}^q},\varrho _{1}\varrho _{2} \right\rangle$;

• (ii) $\mathfrak {T}_{1}\otimes \mathfrak {T}_{2}=\left\langle \zeta _{1}\zeta _{2},\root q \of {{\varrho ^q_{1}}+{\varrho ^q_{2}}-\varrho _{1}^q \varrho _{2}^q} \right\rangle$;

• (iii) $\kappa \mathfrak {T}=\left\langle \root q \of {1-(1-\zeta ^q)^{\kappa }},\varrho ^{\kappa } \right\rangle$;

• (iv) $\mathfrak {T}^{\kappa }=\left\langle \zeta ^{\kappa },\root q \of {1-(1-\varrho ^q)^{\kappa }}\right\rangle$.

Definition 3

(Seikh and Mandal 2022) A p, q-QOFS $\mathfrak {R}$ in finite universe of discourse Y is defined as:

$$\begin{aligned} \mathfrak {R}= \{\langle y,\zeta _{\mathfrak {R}}(y), \varrho _{\mathfrak {R}}(y) \rangle \mid y \in Y\}, \end{aligned}$$

(2)

where $\zeta _{\mathfrak {R}}(y)$ denotes the MG and $\varrho _{\mathfrak {R}}(y)$ denotes the NMG of $y\in Y$, respectively, where $0\le \zeta _{\mathfrak {R}}(y)\le 1$, $0\le \varrho _{\mathfrak {R}}(y)\le 1$, $0 \le (\zeta _{\mathfrak {R}}(y))^p+(\varrho _{\mathfrak {R}}(y))^q \le 1$, $p\ge 1$ and $q\ge 1$. The hesitancy degree of an element $y \in Y$ is $(\pi _{\mathfrak {R}}(y))^l=1-(\zeta _{\mathfrak {R}}(y))^p-(\varrho _{\mathfrak {R}}(y))^q$, where l is the least common multiple (LCM) of p and q.

In (Seikh and Mandal 2022), Seikh and Mandal called the pair $\langle \zeta _\mathfrak {R}, \varrho _\mathfrak {R} \rangle$ in the p, q-QOFS $\mathfrak {R}= \{\langle y,\zeta _{\mathfrak {R}}(y), \varrho _{\mathfrak {R}}(y) \rangle \mid y \in Y\}$ a p, q-QOFN.

Remark 1

Let us consider a case where we need to determine the minimum values of p and q, both greater than or equal to 1, for a given orthopair $\langle \zeta _\mathfrak {R}, \varrho _\mathfrak {R} \rangle$, such that $\zeta ^p_{\mathfrak {R}}+\varrho ^q_\mathfrak {R} \le 1$. Iterative computing approaches can provide unique solutions to issues that lack a closed-form solution. The minimal values of p and q that satisfy $\zeta ^p_\mathfrak {R}+\varrho ^q_\mathfrak {R} \le 1$ are referred to as the p, q-niche of $\langle \zeta _\mathfrak {R}, \varrho _\mathfrak {R} \rangle$. Note that if $\hat{p},\hat{q}$ is the p, q-niche of $\langle \zeta _\mathfrak {R}, \varrho _\mathfrak {R} \rangle$, then $\langle \zeta _\mathfrak {R}, \varrho _\mathfrak {R} \rangle$ is valid for all $p \ge \hat{p}$ and $q \ge \hat{q}$.

Let $Z=\{z_1,z_2,\ldots , z_n\}$ be some provided data and $\digamma$ be a fuzzy concept. Assume an expert presents his preference as an orthopair $\langle \zeta _\mathfrak {R}(z_{j}), \varrho _\mathfrak {R}(z_{j}) \rangle$ for each $z_{j}\in Z$. Now the problem is to accurately portray the information by estimating the proper values of p and q. We may now proceed as follows:

• (i) Determine the p, q-niche for each orthopair $\langle \zeta _\mathfrak {R}(z_{j}), \varrho _\mathfrak {R}(z_{j}) \rangle$, say $p_j,q_j$.

• (ii) Determine the $p^{*}$ and $q^{*}$ niches where $p^* = \max _{j}\{p_{j}\}$ and $q^* = \max _{j}\{q_{j}\}$.

• (iii) Then we may denote E as $p^{*},q^{*}$-QOFS.

Definition 4

(Seikh and Mandal 2022) Let $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1} \rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2} \rangle$ and $\mathfrak {R}=\langle \zeta , \varrho \rangle$ be three p, q-QOFNs. Then,

• (i) $\mathfrak {R}_{1}\oplus \mathfrak {R}_{2}=\left\langle \root p \of {{\zeta ^p_{1}}+{\zeta ^p_{2}}-\zeta _{1}^p\zeta _{2}^p},\varrho _{1}\varrho _{2}\right\rangle$.

• (ii) $\mathfrak {R}_{1}\oplus \mathfrak {R}_{2}=\left\langle \zeta _{1}\zeta _{2},\root q \of {{\varrho ^q_{1}}+{\varrho ^q_{2}}-\varrho _{1}^q \varrho _{2}^q} \right\rangle$.

• (iii) $\kappa \mathfrak {R}=\left\langle \root p \of {1-(1-\zeta ^p)^{\kappa }},\varrho ^{\kappa } \right\rangle$, where $\kappa >0$.

• (iv) $\mathfrak {R}^{\kappa }=\left\langle \zeta ^{\kappa },\root q \of {1-(1-\varrho ^q)^{\kappa }} \right\rangle$, where $\kappa >0$.

Definition 5

(Seikh and Mandal 2022) Let $\mathfrak {R}=\langle \zeta , \varrho \rangle$ be a p, q-QOFN. The score function $S(\mathfrak {R})$ of $\mathfrak {R}$ is defined as follows:

$$\begin{aligned} S(\mathfrak {R})= \frac{1+\zeta ^p-\varrho ^q}{2}, \end{aligned}$$

(3)

where $S(\mathfrak {R}) \in [0,1]$, $p\ge 1$ and $q\ge 1$.

Definition 6

(Seikh and Mandal 2022) Let $\mathfrak {R}=\langle \zeta , \varrho \rangle$ be a p, q-QOFN. The accuracy function ${A}(\mathfrak {R})$ of $\mathfrak {R}$ is defined as follows:

$$\begin{aligned} {A}(\mathfrak {R})= \zeta ^p+\varrho ^q, \end{aligned}$$

(4)

where ${A}(\mathfrak {R}) \in [0,1]$, $p\ge 1$ and $q\ge 1$.

Definition 7

(Seikh and Mandal 2022) Let $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1} \rangle$ and $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2} \rangle$ be two p, q-QOFN. Then,

• (i) If $S(\mathfrak {R}_{1})>S(\mathfrak {R}_{2})$ then $\mathfrak {R}_{1}\succ \mathfrak {R}_{2}$.

• (ii) If $S(\mathfrak {R}_{1})<S(\mathfrak {R}_{2})$ then $\mathfrak {R}_{1}\prec \mathfrak {R}_{2}$.

• (iii) If $S(\mathfrak {R}_{1})=S(\mathfrak {R}_{2})$ and,

• (a) If ${A}(\mathfrak {R}_{1})>({A}\mathfrak {R}_{2})$ then $\mathfrak {R}_{1}\succ \mathfrak {R}_{2}$.

• (b) If ${A}(\mathfrak {R}_{1})<{A}(\mathfrak {R}_{2})$ then $\mathfrak {R}_{1}\prec \mathfrak {R}_{2}$.

• (c) If ${A}(\mathfrak {R}_{1})={A}(\mathfrak {R}_{2})$ then $\mathfrak {R}_{1}\sim \mathfrak {R}_{2}$.

Definition 8

(Yager 1994) Let $\alpha$ and $\beta$ be two real numbers and $\lambda > 0$. The Yager’s t-norm $Y_{TN}$ and t-conorm $Y_{TCN}$ are defined as follows:

$$\begin{aligned} Y_{TN}(\alpha ,\beta )=1-\min (1,((1-\alpha )^{\lambda }+(1-\beta )^{\lambda })^{\frac{1}{\lambda }}), \\ Y_{TCN}(\alpha ,\beta )=\min (1,(\alpha ^{\lambda }+\beta ^{\lambda })^{\frac{1}{\lambda }}). \end{aligned}$$

Definition 9

(Yager 2008) Let H be any alternative and let $\Phi _{1},\Phi _{2},\ldots ,$ and $\Phi _{n}$ be attributes with the linear priority order $\Phi _{1}\succ \Phi _{2}\succ \ldots \succ \Phi _{n}$. If attribute $\Phi _{e}$ has a higher priority order than attribute $\Phi _{h}$ then $e<h$, where $e,h=1,2,\ldots ,n$ and $e\ne h$. Let $\Phi _{h}(H)$ represents the performance of the alternative H with respect to the attribute $\Phi _{h}$, where $\Phi _{h}(H) \in [0,1]$. The prioritized geometric (PG) AO of $\Phi _{1}(H),\Phi _{2}(H),\ldots ,$ and $\Phi _{n}(H)$ is defined as follows:

$$\begin{aligned} PG(\Phi _{1}(H),\Phi _{2}(H),\ldots ,\Phi _{n}(H))= \prod _{h=1}^{n} (\Phi _{h}(H))^{\frac{T_{h}}{\sum _{i=1}^{n}T_{i}}},\nonumber \\ \end{aligned}$$

(5)

where $T_{1}=1$, $T_{h}=\prod _{k=1}^{h-1}\Phi _{k}(H)$ and $h=2,3,\ldots ,n$.

3 The proposed p, q- quasirung orthopair fuzzy operations based on Yager’s norm

In this section, we propose new multiplication operation and scalar power operation for p, q-QOFNs based on Yager’s t-NM $Y_{TN}$ and t-CNM $Y_{TCN}$ defined in Definition 8.

Definition 10

Let $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1} \rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2} \rangle$ and $\mathfrak {R}=\langle \zeta , \varrho \rangle$ be three p, q-QOFNs. The proposed multiplication operation and proposed scalar power operation for p, q-QOFNs $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1} \rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2} \rangle$ and $\mathfrak {R}=\langle \zeta , \varrho \rangle$ based on the Yager’s norm are defined as follows:

• (i) Multiplication operation:

  $$\begin{aligned} & \mathfrak {R}_{1}\otimes \mathfrak {R}_{2}\nonumber \\ & =\left\langle \root p \of {1-\min (1,((1-\zeta _{1}^{p})^\lambda +(1-\zeta _{2}^{p})^\lambda )^{\frac{1}{\lambda }})},\right. \nonumber \\ & \left. \root q \of {\min (1,(\varrho _{1}^{q\lambda }+\varrho _{2}^{q\lambda })^{\frac{1}{\lambda }})}\right\rangle , \end{aligned}$$

  (6)

  where $p\ge 1$, $q\ge 1$ and $\lambda >0$.

• (ii) Scalar power operation:

  $$\begin{aligned} \mathfrak {R}^{\kappa }= & \left\langle \root p \of {1-\min (1,(\kappa (1-\zeta ^{p})^\lambda )^{\frac{1}{\lambda }})},\right. \nonumber \\ & \left. \root q \of {\min (1,(\kappa \varrho ^{q\lambda })^{\frac{1}{\lambda }})} \right\rangle , \end{aligned}$$

  (7)

  where $p\ge 1$, $q\ge 1$, $\kappa >0$ and $\lambda >0$.

Example 1

Let $\mathfrak {R}_{1}=\langle 0.7, 0.6 \rangle$ and $\mathfrak {R}_{2}=\langle 0.8,0.4 \rangle$ be two p, q-QOFNs. Then,

• (i) By using Eq. (6), for $p=3$, $q=3$, and $\lambda =3$, we obtain

  $$\begin{aligned} \mathfrak {R}_{1}\otimes \mathfrak {R}_{2}= & \left\langle \root p \of {1-\min (1,((1-\zeta _{1}^{p})^\lambda +(1-\zeta _{2}^{p})^\lambda )^{\frac{1}{\lambda }})}, \right. \\ & \left. \root q \of {\min (1,(\varrho _{1}^{q\lambda }+\varrho _{2}^{q\lambda })^{\frac{1}{\lambda }})}\right\rangle \\= & \left\langle \root 3 \of {1-\min (1,((1-0.7^{3})^3 +(1-0.8^{3})^3)^{\frac{1}{3}})}, \right. \\ & \left. \root 3 \of {\min (1,(0.6^{9}+0.4^{9})^{\frac{1}{3}})}\right\rangle \\= & \langle 0.64, 0.60 \rangle . \end{aligned}$$

• (ii) By using Eq. (7), for $p=3$, $q=3,\lambda =3$, and $\kappa =2$, we obtain

  $$\begin{aligned} {\mathfrak {R}_{1}}^2= & \left\langle \root p \of {1-\min (1,(\kappa (1-\zeta ^{p}_{1})^\lambda )^{\frac{1}{\lambda }})}, \right. \\ & \left. \root q \of {\min (1,(\kappa \varrho ^{q\lambda }_{1})^{\frac{1}{\lambda }})} \right\rangle \\= & \left\langle \root 3 \of {1-\min (1,(2 (1-0.7^{3})^3)^{\frac{1}{3}})}, \right. \\ & \left. \root 3 \of {\min (1,(2(0.6)^{9})^{\frac{1}{3}})} \right\rangle \\= & \langle 0.56, 0.65 \rangle . \end{aligned}$$

Theorem 1

Let $\mathfrak {R}_{1}$, $\mathfrak {R}_{2}$ and $\mathfrak {R}$ be three p, q-QOFNs. The proposed multiplication operation and scalar power operation, defined in Definition 10, satisfy the following properties:

• (i) $\mathfrak {R}_{1}\otimes \mathfrak {R}_{2}=\mathfrak {R}_{2}\otimes \mathfrak {R}_{1}$,

• (ii) $(\mathfrak {R}_{1}\otimes \mathfrak {R}_{2})^{\kappa }=\mathfrak {R}_{1}^{\kappa }\otimes \mathfrak {R}_{2}^{\kappa }$,

• (iii) $\mathfrak {R}^{\kappa _{1}}\otimes R ^{\kappa _{2}}= \mathfrak {R}^{(\kappa _{1}+\kappa _{2})}$,

where $\kappa >0$, $\kappa _{1}>0$ and $\kappa _{2}>0$.

Proof

Let $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1} \rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2} \rangle$ and $\mathfrak {R}=\langle \zeta , \varrho \rangle$ be three p, q-QOFNs. Then,

• (i) By using Eq. (6), we have

  $$\begin{aligned} \mathfrak {R}_{1}\otimes \mathfrak {R}_{2}= & \left\langle \root p \of {1-\min (1,((1-\zeta _{1}^{p})^\lambda +(1-\zeta _{2}^{p})^\lambda )^{\frac{1}{\lambda }})},\right. \\ & \left. \root q \of {\min (1,(\varrho _{1}^{q\lambda }+\varrho _{2}^{q\lambda })^{\frac{1}{\lambda }})}\right\rangle \\= & \left\langle \root p \of {1-\min (1,((1-\zeta _{2}^{p})^\lambda +(1-\zeta _{1}^{p})^\lambda )^{\frac{1}{\lambda }})}, \right. \\ & \left. \root q \of {\min (1,(\varrho _{2}^{q\lambda }+\varrho _{1}^{q\lambda })^{\frac{1}{\lambda }})}\right\rangle \\= & \mathfrak {R}_{2}\otimes \mathfrak {R}_{1}, \end{aligned}$$

  where $p\ge 1$, $q\ge 1$ and $\lambda >0$.

• (ii) By using Eq. (6) and (7), we have

  $$\begin{aligned} (\mathfrak {R}_{1}\otimes \mathfrak {R}_{2})^{\kappa }= & \left\langle \root p \of {1-\min (1,((1-\zeta _{1}^{p})^\lambda +(1-\zeta _{2}^{p})^\lambda )^{\frac{1}{\lambda }})},\right. \\ & \left. \root q \of {\min (1,(\varrho _{1}^{q\lambda }+\varrho _{2}^{q\lambda })^{\frac{1}{\lambda }})}\right\rangle ^ {\kappa }\\= & \left\langle \root p \of {1-\min (1,(\kappa ((1-\zeta _{1}^{p})^\lambda +(1-\zeta _{2}^{p})^\lambda ))^{\frac{1}{\lambda }})},\right. \\ & \left. \root q \of {\min (1,\kappa ((\varrho _{1}^{q\lambda }+\varrho _{2}^{q\lambda })^{\frac{1}{\lambda }}))}\right\rangle \\= & \left\langle \root p \of {1-\min (1,(\kappa (1-\zeta _{1}^{p})^\lambda +\kappa (1-\zeta _{2}^{p})^\lambda )^{\frac{1}{\lambda }})}, \right. \\ & \left. \root q \of {\min (1,(\kappa \varrho _{1}^{q\lambda }+\kappa \varrho _{2}^{q\lambda })^{\frac{1}{\lambda }})}\right\rangle \\= & \mathfrak {R}_{1}^{\kappa }\otimes \mathfrak {R}_{2}^{\kappa }, \end{aligned}$$

  where $p\ge 1$, $q\ge 1$, $\lambda >0$ and $\kappa >0$.

• (iii) By using Eq. (6) and (7), we have

  $$\begin{aligned} \mathfrak {R}^{\kappa _{1}}\otimes \mathfrak {R}^{\kappa _{2}}= & \left\langle \root p \of {1-\min (1,(\kappa _{1}(1-\zeta ^{p})^\lambda +\kappa _{2}(1-\zeta ^{p})^\lambda )^{\frac{1}{\lambda }})},\right. \\ & \left. \root q \of {\min (1,(\kappa _{1}\varrho ^{q\lambda }+\kappa _{2} \varrho ^{q\lambda })^{\frac{1}{\lambda }})}\right\rangle \\= & \left\langle \root p \of {1-\min (1,((\kappa _{1} +\kappa _{2})(1-\zeta ^{p})^\lambda )^{\frac{1}{\lambda }})}, \right. \\ & \left. \root q \of {\min (1,(\kappa _{1}+\kappa _{2}) \varrho ^{q\lambda })^{\frac{1}{\lambda }})}\right\rangle \\= & \mathfrak {R}^{(\kappa _{1}+\kappa _{2})}, \end{aligned}$$

  where $p\ge 1$, $q\ge 1$, $\lambda >0$, $\kappa _1>0$ and $\kappa _2>0$.

$\square$

4 The proposed p, q- quasirung orthopair fuzzy Yager prioritized weighted geometric aggregation operator of p, q-QOFNs

In this section, we propose the p, q-quasirung orthopair fuzzy Yager prioritized weighted geometric (p, q-QOFYPWG) AO for p, q-QOFNs based on the proposed multiplication operation, scalar power operation and the prioritized geometric AO given in Definition 9.

Definition 11

Let $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1}\rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2}\rangle$, $\ldots$, and $\mathfrak {R}_{n}=\langle \zeta _{n}, \varrho _{n}\rangle$ be n p, q-QOFNs. The proposed p, q-QOFYPWG AO for aggregating the p, q-QOFNs $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1}\rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2}\rangle$, $\ldots$, and $\mathfrak {R}_{n}=\langle \zeta _{n}, \varrho _{n}\rangle$ is defined as:

$$\begin{aligned} & p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n})=\nonumber \\ & \quad \otimes _{h=1}^{n}\mathfrak {R}_{h}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}, \end{aligned}$$

(8)

where $p\ge 1$, $q\ge 1$, $\lambda >0$, $w_{h}$ represents the weight of p, q-QOFN $\mathfrak {R}_{h}$, $w_{h} \ge 0$, $h=1,2,\ldots , n$, $\sum _{h=1}^{n}w_{h}=1$, $T_{1}=1$, $T_{h}=\prod _{e=1}^{h-1}S(\mathfrak {R}_{e})$, $h=2, 3, \ldots ,n$, and $S(\mathfrak {R}_{e})$ is the score value of the p, q-QOFN $\mathfrak {R}_{e}=\langle \zeta _{e}, \varrho _{e} \rangle$ calculated by Eq. (3), $S(\mathfrak {R}_{e})=\frac{1+\zeta ^p_{{e}}-\varrho ^q_{e}}{2}$ and $e=1,2,\ldots ,h-1$.

Theorem 2

Let $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1}\rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2}\rangle$, $\ldots$, and $\mathfrak {R}_{n}=\langle \zeta _{n}, \varrho _{n}\rangle$ be n p, q-QOFNs. The aggregated value of p, q-QOFNs $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1} \rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2} \rangle$,, $\ldots$, and $\mathfrak {R}_{n}=\langle \zeta _{n}, \varrho _{n} \rangle$ by using the proposed p, q-QOFYPWG AO is a p, q-QOFN and given as follows:

$$\begin{aligned} & p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n})\nonumber \\ & \quad =\left\langle \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{n}\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}(1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\right. \nonumber \\ & \qquad \left. \root q \of {\min \left\{ 1,\left( \sum _{h=1}^{n}\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}} (\varrho _{h}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \right\rangle , \end{aligned}$$

(9)

where $p\ge 1$, $q\ge 1$, $\lambda >0$, $w_{h}$ represents the weight of p, q-QOFN $\mathfrak {R}_{h}$, $w_{h}\ge 0$, $h=1,2,\ldots , n$, $\sum _{h=1}^{n}w_{h}=1$, $T_{1}=1$, $T_{h}=\prod _{e=1}^{h-1}S(\mathfrak {R}_{e})$, $h=2, 3, \ldots ,n$, and $S(\mathfrak {R}_{e})$ is the score value of the p, q-QOFN $\mathfrak {R}_{e}=\langle \zeta _{e}, \varrho _{e} \rangle$ calculated by Eq. (3), $S(\mathfrak {R}_{e})=\frac{1+\zeta ^p_{e}-\varrho ^q_{e}}{2}$ and $e=1,2,\ldots ,h-1$.

Proof

Let $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1}\rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2}\rangle$, $\ldots$, and $\mathfrak {R}_{n}=\langle \zeta _{n}, \varrho _{n}\rangle$ be p, q-QOFNs and let $u_{h}=\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}$. To prove this theorem, we use the mathematical induction approach, as illustrated below:

• (i) Take $h=2$, then by using Eq. (7), we obtain

  $$\begin{aligned} {\mathfrak {R}_1}^{u_{1}}= & \left\langle \root p \of {1-\min \left\{ 1,\left( u_{1} (1-\zeta _{1}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} }, \right. \\ & \left. \root q \of {\min \left\{ 1,\left( u_{1}(\varrho _{1}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \right\rangle ,\\ {\mathfrak {R}_2}^{u_{2}}= & \left\langle \root p \of {1-\min \left\{ 1,\left( u_{2} (1-\zeta _{2}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} }, \right. \\ & \left. \root q \of {\min \left\{ 1,\left( u_{2}(\varrho _{2}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \right\rangle . \end{aligned}$$

  Then, by using Eq. (6), we obtain

  $$\begin{aligned} & p, q-QOFYPWG(\mathfrak {R}_1,\mathfrak {R}_2)={\mathfrak {R}_1}^{u_{1}}\otimes {\mathfrak {R}_2}^{u_{2}}\\ & \quad = \left\langle \root p \of {1-\min \left\{ 1,\left( u_{1} (1-\zeta _{1}^{p})^{\lambda }+u_{2} (1-\zeta _{2}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} }\right. ,\\ & \qquad \left. \root q \of {\min \left\{ 1,\left( u_{1}(\varrho _{1}^{q})^{\lambda }+u_{2}(\varrho _{2}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \right\rangle \\ & \quad =\left\langle \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{2}u_{h} (1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\right. \\ & \qquad \left. \root q \of {\min \left\{ 1,\left( \sum _{h=1}^{2}u_{h}(\varrho _{h}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} }\right\rangle . \end{aligned}$$

  Hence, the result given in Eq. (9) is valid for $h=2$.

• (ii) Suppose the result given in Eq. (9) is valid for $h=n$, where

  $$\begin{aligned} & p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n})\\ & \quad =\left\langle \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{n}u_h (1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\right. \\ & \quad \left. \root q \of {\min \left\{ 1,\left( \sum _{h=1}^{n}u_h(\varrho _{h}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \right\rangle . \end{aligned}$$

• (iii) Now, take $h=n+1$, we get

  $$\begin{aligned} & p, q-QOFYPWG(\mathfrak {R}_1,\mathfrak {R}_2,\ldots \mathfrak {R}_{n+1})\\ & \quad =\left( \otimes _{h=1}^{n}{\mathfrak {R}_h}^{u_{h}}\right) \otimes {\mathfrak {R}_{n+1}}^{u_{n+1}}\\ & \quad = \left\langle \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{n}u_{h} (1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\right. \\ & \quad \left. \root q \of {\min \left\{ 1,\left( \sum _{h=1}^{n}u_{h}(\varrho _{h}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} }\right\rangle \\ & \quad \otimes \left\langle \root p \of {1-\min \left\{ 1,\left( u_{n+1} (1-\zeta _{{n+1}}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\right. \\ & \quad \left. \root q \of {\min \left\{ 1,\left( u_{n+1}(\varrho _{{n+1}}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \right\rangle \\ & \quad =\left\langle \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{n+1}u_h (1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\right. \\ & \quad \left. \root q \of {\min \left\{ 1,\left( \sum _{h=1}^{n+1}u_h(\varrho _{h}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \right\rangle . \end{aligned}$$

  Hence, the result given in Eq. (9) is valid for $h=n+1$. Thus, the result is true for all natural numbers. Now, we shall prove that the result given in Eq. (9) is a p, q-QOFN. Let

  $$\begin{aligned} \delta= & \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{n}\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}} (1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} }\\= & \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{n}u_h (1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\\ \gamma= & \root q \of {\min \left\{ 1,\left( \sum _{h=1}^{n}\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}(\varrho _{h}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \\= & \root q \of {\min \left\{ 1,\left( \sum _{h=1}^{n}u_h(\varrho _{h}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} }. \end{aligned}$$

  Now, we will show that

  • (a) $0\le \delta \le 1$ and $0\le \gamma \le 1$,

  • (b) $0\le \delta ^p+\gamma ^q\le 1$.

  First, we prove that $0\le \delta \le 1$. Because $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1}\rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2}\rangle$, $\ldots$, and $\mathfrak {R}_{n}=\langle \zeta _{n}, \varrho _{n}\rangle$ are the p, q-QOFNs, we get $0\le \zeta _h \le 1$, $0\le \varrho _h \le 1$ and $0\le \zeta _h^p +\varrho _h^q \le 1$, for all $h=1,2,\ldots ,n$, $p\ge 1$ and $q\ge 1$. Therefore, we get $0 \le {\zeta _{h} }^p\le 1$. Because $\lambda >0$, we get $0 \le (1-\zeta _{h}^p)^\lambda \le 1$. Now, let $u_{h}=\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}$, since $w_h \ge 0$, $S(\mathfrak {R}_h)\in [0,1], T_1=1$ and $T_k=\prod _{e=1}^{k-1}S(\mathfrak {R}_e)$ $\implies T_h\in [0,1]$ and $w_{h}T_{h}\in [0,1]$. Therefore, we get $0 \le \frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}} \le 1$ $\implies 0 \le u_h \le 1$. Thus, we get $0 \le \left( \sum _{h=1}^{n}u_{h} (1-\zeta _{\mathfrak {R}_{h}}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\le 1$ and $0 \le 1-\min \left\{ 1,\left( \sum _{h=1}^{n}u_h (1-\zeta _{\mathfrak {R}_{h}}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} \le 1$. It implies that $0 \le \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{n}u_h (1-\zeta _{\mathfrak {R}_{h}}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} }\le 1$. Hence $0 \le \delta \le 1$. Similarly, we can show that $0\le \gamma \le 1$. Now, we prove that $0 \le \delta ^p+\gamma ^q\le 1$. Since, $0\le \zeta _{h}\le 1$, $0\le \varrho _{h} \le 1$ and $0\le \zeta _{h}^p+\varrho _{h}^q \le 1$, then we have,

  $$\begin{aligned} & \varrho _{h}^q \le 1-\zeta _{h}^p.\\ & \quad \implies \sum _{h=1}^{n}u_{h}\varrho _{h}^{q\lambda }\le \sum _{h=1}^{n}u_{h}(1-\zeta _{h}^{p})^{\lambda } \\ & \quad \implies \min \left\{ 1,\sum _{h=1}^{n}u_{h}(\varrho _{h}^{q\lambda })^{\frac{1}{\lambda }}\right\} \le \min \left\{ 1,\left( \sum _{h=1}^{n}\delta _{h}(1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} \\ & \quad \implies \min \left\{ 1,\sum _{h=1}^{n}u_{h}(\varrho _{h}^{q\lambda })^{\frac{1}{\lambda }}\right\} \\ & \qquad - \min \left\{ 1,\left( \sum _{h=1}^{n}u_{h}(1-\zeta _{h}^{p})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} \le 0\\ & \quad \implies 1-\min \left\{ 1,\sum _{h=1}^{n}u_{h}(1-\zeta _{h}^{p\lambda })^{\frac{1}{\lambda }}\right\} + \min \left\{ 1,\left( \sum _{h=1}^{n}u_{h}(\varrho _{h}^{q})^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} \le 1\\ & \quad \implies \delta ^p+\gamma ^q\le 1.\\ \end{aligned}$$

  Because $\delta \ge 0$, $\gamma \ge 0$, $p\ge 1$ and $q\ge 1$, we get $\delta ^p\ge 0$, $\gamma ^q\ge 0$ and $\delta ^p+\gamma ^q\ge 0$. Hence, $0 \le \delta ^p+\gamma ^q\le 1$.

$\square$

Example 2

Let $\mathfrak {R}_{1}=\langle 0.6,0.8 \rangle$, $\mathfrak {R}_{2}=\langle 0.4,0.6 \rangle$ and $\mathfrak {R}_{3}=\langle 0.5,0.5 \rangle$ be three p, q-QOFNs with weights $w_{1}=0.3, w_{2}=0.4$ and $w_{3}=0.3$, respectively. First, we calculate the values of $T_{1}=1$, $T_{2}=S(\mathfrak {R}_{1})=\frac{1+\zeta ^p_{1}-\varrho ^q_{1}}{2}=\frac{1+0.6^{3}-0.8^{1}}{2}=0.2080$ and $T_{3}=S(\mathfrak {R}_{1})\times S(\mathfrak {R}_{2})=0.2080 \times 0.2320=0.0483$. By using the proposed p, q-QOFYPWG AO of p, q-QOFNs shown in Eq. (8), we aggregate the p, q-QOFNs $\mathfrak {R}_{1},\mathfrak {R}_{2}$ and $\mathfrak {R}_{3}$, where $p=3$, $q=1$, $\lambda =2$ and

$$\begin{aligned} p, q-QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\mathfrak {R}_{3}) & =\left\langle \root p \of {1-\min \left\{ 1, \left( \begin{aligned} \frac{0.3\times 1}{0.3\times 1+0.4\times 0.2080+0.3\times 0.0483}(1-0.6^{3})^{2}+\\ \frac{0.4\times 0.2080}{0.3\times 1+0.4\times 0.2080+0.3\times 0.0483}(1-0.4^{3})^{2}+\\ \frac{0.3\times 0.0483}{0.3\times 1+0.4\times 0.2080+0.3\times 0.0483}(1-0.5^{3})^{2} \end{aligned} \right) ^{\frac{1}{2}}\right\} } \right. ,\\ & \qquad \left. \root q \of {\min \left\{ 1, \left( \begin{aligned} \frac{0.3\times 1}{0.3\times 1+0.4\times 0.2080+0.3\times 0.0483}(0.8^{1})^{2}+\\ \frac{0.4\times 0.2080}{0.3\times 1+0.4\times 0.2080+0.3\times 0.0483}(0.6^{1})^{2}+\\ \frac{0.3\times 0.0483}{0.3\times 1+0.4\times 0.2080+0.3\times 0.0483}(0.5^{1})^{2} \end{aligned} \right) ^{\frac{1}{2}}\right\} } \right\rangle \\ & =\langle 0.5631, 0.7531 \rangle . \end{aligned}$$

In the following, we present some characteristics of the proposed p, q-QOFYPWG AO of p, q-QOFNs.

Property 1

(Idempotency) Let $\mathfrak {R}_{1}=\langle \zeta _{1}, \varrho _{1}\rangle$, $\mathfrak {R}_{2}=\langle \zeta _{2}, \varrho _{2}\rangle$, $\ldots$, and $\mathfrak {R}_{n}=\langle \zeta _{n}, \varrho _{n}\rangle$ be n p, q-QOFNs with weights $w_{1}$, $w_{2}$,$\ldots$ and $w_{n}$, respectively, where $w_{h}\ge 0$, $\sum _{h=1}^{n}w_{h}=1$ and $h=1,2,\ldots ,n$. If $\mathfrak {R}_{1}=\mathfrak {R}_{2}=\ldots =\mathfrak {R}_{n}=\mathfrak {R}$, then

$$\begin{aligned} p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n})= \mathfrak {R}. \end{aligned}$$

Proof

Since the weights of the p, q-QOFNs $\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots , \mathfrak {R}_{n}$ are $w_{1},w_{2},\ldots ,w_{n}$, respectively, where $w_{h}\ge 0$ and $\sum _{h=1}^{n}w_{h}=1$, if $\mathfrak {R}_{1}=\mathfrak {R}_{2},\ldots ,= \mathfrak {R}_{n}=\mathfrak {R}$, then by using Eq.(8), we get

$$\begin{aligned} & p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n})\\ & =\otimes _{h=1}^{n}\mathfrak {R}_{h}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\ & = \otimes _{h=1}^{n}\mathfrak {R}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\ & =\mathfrak {R}^{\frac{\sum _{h=1}^{n}w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\ & =\mathfrak {R}. \end{aligned}$$

$\square$

Property 2

(Boundedness) Let $\mathfrak {R}_{1}, \mathfrak {R}_{2},\ldots ,$ and $\mathfrak {R}_{n}$ be p, q-QOFNs, $\mathfrak {R}^{-}=\min \{\mathfrak {R}_{1}, \mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}\}$ and $\mathfrak {R}^{+}=\max \{\mathfrak {R}_{1}, \mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}\}$. Then,

$$\begin{aligned} \mathfrak {R}^{-} \le p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}) \le \mathfrak {R}^{+}. \end{aligned}$$

Proof

Since $\mathfrak {R}^{-}=\min \{\mathfrak {R}_{1}, \mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}\}$ and $\mathfrak {R}^{+}=\max \{\mathfrak {R}_{1}, \mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}\}$, therefore by using Eq. (8), we obtain

$$\begin{aligned} & p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n})\\ & \quad = \otimes _{h=1}^{n}\mathfrak {R}_{h}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\ & \quad \le \otimes _{h=1}^{n}{\mathfrak {R}^{+}}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\ & \quad = {\mathfrak {R}^{+}}^{ \frac{\sum _{h=1}^{n}w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\ & \quad =\mathfrak {R}^{+}. \end{aligned}$$

Similarly,

$$\begin{aligned} p, q- & QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n})\\= & \otimes _{h=1}^{n}\mathfrak {R}_{h}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\\ge & \otimes _{h=1}^{n}{\mathfrak {R}^{-}}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\= & {\mathfrak {R}^{-}}^{\frac{\sum _{h=1}^{n}w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}\\= & \mathfrak {R}^{-}. \end{aligned}$$

Thus, we get $\mathfrak {R}^{-} \le p, q-QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}) \le \mathfrak {R}^{+}.$ $\square$

Property 3

(Monotonicity) Let $\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}$ and $\dot{\mathfrak {R}_{1}},\dot{\mathfrak {R}_{2}},\ldots ,\dot{\mathfrak {R}_{n}}$ be two families of p, q-QOFNs. If $\mathfrak {R}_{h} \le \dot{\mathfrak {R}_{h}}$, where $h=1,2,\ldots ,n$, then

$$\begin{aligned} & p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}) \\ & \quad \le p, q - QOFYPWG(\dot{\mathfrak {R}_{1}},\dot{\mathfrak {R}_{2}},\ldots ,\dot{\mathfrak {R}_{n}}). \end{aligned}$$

Proof

By using Eq. (8), we obtain

$$\begin{aligned} & p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n})=\\ & \quad \otimes _{h=1}^{n}\mathfrak {R}_{h}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}},\\ & p, q - QOFYPWG(\dot{\mathfrak {R}_{1}},\dot{\mathfrak {R}_{2}},\ldots ,\dot{\mathfrak {R}_{n}})=\\ & \quad \otimes _{h=1}^{n}{\dot{\mathfrak {R}_{h}}}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}. \end{aligned}$$

Since $\mathfrak {R}_{h} \le \dot{\mathfrak {R}_{h}}$, $\forall h=1,2,\ldots , n,$ we obtain $\otimes _{h=1}^{n}\mathfrak {R}_{h}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}} \le \otimes _{h=1}^{n}{\dot{\mathfrak {R}_{h}}}^{\frac{w_{h}T_{h}}{\sum _{h=1}^{n}w_{h}T_{h}}}$. Thus, we get $p, q - QOFYPWG(\mathfrak {R}_{1},\mathfrak {R}_{2},\ldots ,\mathfrak {R}_{n}) \le p, q - QOFYPWG(\dot{\mathfrak {R}_{1}},\dot{\mathfrak {R}_{2}},\ldots ,\dot{\mathfrak {R}_{n}})$. $\square$

5 The proposed MAGDM approach based on the proposed p, q-QOFYPWG AO of p, q-QOFNs

In this section, we propose a novel MAGDM approach based on the proposed p, q-QOFYPWG AO under the p, q-QOFNs environment. Let $H_{1},H_{2},\ldots ,$ and $H_{m}$ are m alternatives and let $\Phi _{1},\Phi _{2},\ldots ,$ and $\Phi _{n}$ are n attributes. Let $\Psi _{1},\Psi _{2},\ldots ,\Psi _{y}$ be the decision making experts (DMExs) with respective weights $\varpi _{1},\varpi _{2},\ldots ,\varpi _{y}$, respectively, where $\varpi _{j}\ge 0$, $j=1,2,\ldots ,y$ and $\sum _{j=1}^{y}\varpi _{j}= 1$. Each DMEx $\Psi _{j}$ assesses the attribute $\Phi _{h}$ of the alternative $H_{e}$ by utilizing p, q-QOFN $\tilde{\mathfrak {R}}^{j}_{eh}=\langle \tilde{\zeta }^{j}_{eh}, \tilde{\varrho }^{j}_{eh} \rangle$ to construct the decision matrix (DMx) $\tilde{L}^{j}=(\tilde{\mathfrak {R}}^{j}_{eh})_{m\times n}$, shown as follows:

The proposed MAGDM approach involves the following steps:

• Step 1: Convert the DMXs $\tilde{L}^1 = ({\tilde{\mathfrak {R}}^1_{eh}})_{m\times n} = (\langle {\tilde{\zeta }^1_{eh}},{\tilde{\varrho }^1_{eh}} \rangle )_{m\times n}, \tilde{L}^2 = ({\tilde{\mathfrak {R}}^2_{eh}})_{m\times n} = (\langle {\tilde{\zeta }^2_{eh}},{\tilde{\varrho }^2_{eh}} \rangle )_{m\times n}, \ldots$, $\tilde{L}^y = ({\tilde{\mathfrak {R}}^y_{eh}})_{m\times n} = (\langle {\tilde{\zeta }^y_{eh}}, {\tilde{\varrho }^y_{eh}} \rangle )_{m\times n}$, into normalized DMxs (NDMxs) ${L}^1 = ({\mathfrak {R}^1_{eh}})_{m\times n} = (\langle {{\zeta }^1_{eh}},{{\varrho }^1_{eh}} \rangle )_{m\times n}, {L}^2 = ({{\mathfrak {R}}^2_{eh}})_{m\times n} = (\langle {{\zeta }^2_{eh}},{{\varrho }^2_{eh}} \rangle )_{m\times n}, \ldots$, ${L}^y = ({{\mathfrak {R}}^y_{eh}})_{m\times n} = (\langle {{\zeta }^y_{eh}}, {{\varrho }^y_{eh}} \rangle )_{m\times n}$ as follows:

  $$\begin{aligned} {\mathfrak {R}^j_{eh}}= & {\left\{ \begin{array}{ll} \langle {\tilde{\zeta }^j_{eh}}, {\tilde{\varrho }^j_{eh}} \rangle :& \text { for benefit type attribute} \\ \langle {\tilde{\varrho }^j_{eh}}, {\tilde{\zeta }^j_{eh}}\rangle :& \text { for cost type attribute} \end{array}\right. }, \end{aligned}$$

  (10)

  where $e = 1, 2, \ldots , m, h = 1, 2, \ldots , n$ and $j = 1, 2, \ldots , y$.

• Step 2: Compute the values $T^1_{eh},T^2_{eh}, \ldots$, and $T^y_{eh}$ of p, q-QOFNs $\mathfrak {R}^1_{eh},\mathfrak {R}^2_{eh},\ldots$, and $\mathfrak {R}^y_{eh}$ appeared in NDMxs ${L}^1 = ({\mathfrak {R}^1_{eh}})_{m\times n} = (\langle {{\zeta }^1_{eh}},{{\varrho }^1_{eh}} \rangle )_{m\times n}, {L}^2 = ({{\mathfrak {R}}^2_{eh}})_{m\times n} = (\langle {{\zeta }^2_{eh}},{{\varrho }^2_{eh}} \rangle )_{m\times n}, \ldots$, and ${L}^y = ({{\mathfrak {R}}^y_{eh}})_{m\times n} = (\langle {{\zeta }^y_{eh}}, {{\varrho }^y_{eh}} \rangle )_{m\times n}$, respectively, to construct the matrices $T^{1}=(T^{1}_{eh})_{m\times n}$, $T^{2}=(T^{2}_{eh})_{m\times n}$, $\ldots$, and $T^{y}=(T^{y}_{eh})_{m\times n}$, as follows:

  $$\begin{aligned} {T^j_{eh}}= & {\left\{ \begin{array}{ll} 1:& \text {if} j=1 \\ \prod _{a=1}^{j-1}S(\mathfrak {R}^{a}_{eh}):& \text {if} j=2,3, \ldots , y \end{array}\right. }, \end{aligned}$$

  (11)

  where $S(\mathfrak {R}^{a}_{eh})=\frac{1+(\zeta ^a_{eh})^p-(\varrho ^a_{eh})^q}{2}$ is the score value of the p, q-QOFN $\mathfrak {R}^a_{eh}$ which is obtained by Eq. (3), $p\ge 1$, $q\ge 1$, $e = 1, 2, \ldots , m, h = 1, 2, \ldots , n$ and $a = 1, 2, \ldots , y-1$.

• Step 3: Based on the obtained matrices $T^{1}=(T^{1}_{eh})_{m\times n}$, $T^{2}=(T^{2}_{eh})_{m\times n}$ and $T^{y}=(T^{y}_{eh})_{m\times n}$ and the weights $\varpi _{1},\varpi _{2},\ldots ,\varpi _{y}$ of the DMExs $\Psi _{1},\Psi _{2},\ldots ,\Psi _{y}$, respectively, we compute the weights $\varsigma ^{1}_{eh},\varsigma ^{2}_{eh},\ldots$, and $\varsigma ^{y}_{eh}$ of p, q-QOFNs $\mathfrak {R}^1_{eh},\mathfrak {R}^2_{eh},\ldots$, and $\mathfrak {R}^y_{eh}$, respectively, to construct the weighted matrices $W^{1}=(\varsigma ^{1}_{eh})_{m\times n}$, $W^{2}=(\varsigma ^{2}_{eh})_{m\times n}, \ldots ,$ and $W^{y}=(\varsigma ^{y}_{eh})_{m\times n}$, shown as follows:

  $$\begin{aligned} \varsigma ^{j}_{eh}=\frac{\varpi _{j}T^{j}_{eh}}{\sum _{j=1}^{y}\varpi _{j}T^{j}_{eh}}, \end{aligned}$$

  (12)

  where $e = 1, 2, \ldots , m$, $h = 1, 2, \ldots , n$ and $j = 1, 2, \ldots , y$.

• Step 4: Based on the obtained weights $\varsigma ^{1}_{eh},\varsigma ^{2}_{eh},\ldots$, and $\varsigma ^{y}_{eh}$ of p, q-QOFNs $\mathfrak {R}^1_{eh},\mathfrak {R}^2_{eh},\ldots$, and $\mathfrak {R}^y_{eh}$, respectively, and proposed p, q-QOFYPWG AO shown in Eq. (8), we aggregate the p, q-QOFNs $\mathfrak {R}^1_{eh},\mathfrak {R}^2_{eh},\ldots$, and $\mathfrak {R}^y_{eh}$ that appeared in NDMxs ${L}^1 = ({\mathfrak {R}^1_{eh}})_{m\times n}, {L}^2 = ({{\mathfrak {R}}^2_{eh}})_{m\times n}, \ldots$, ${L}^y = ({{\mathfrak {R}}^y_{eh}})_{m\times n}$ respectively, to get the aggregated p, q-QOFN $\mathfrak {R}_{eh}=\langle \zeta _{eh}, \varrho _{eh} \rangle$ for constructing the collective DMx (CDMx) ${L}=({{\mathfrak {R}}_{eh}})_{m\times n}$, shown as follows:

  $$\begin{aligned} \mathfrak {R}_{eh}= & p, q-QOFYPWG(\mathfrak {R}^1_{eh},\mathfrak {R}^2_{eh},\ldots ,\mathfrak {R}^y_{eh})\nonumber \\= & \left\langle \root p \of {1-\min \left\{ 1,\left( \sum _{j=1}^{y}\varsigma ^{j}_{eh}\left( 1-\left( \zeta ^{j}_{eh}\right) ^{p}\right) ^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\right. \nonumber \\ & \left. \root q \of {\min \left\{ 1,\left( \sum _{j=1}^{y}\varsigma ^{j}_{eh} \left( \varrho ^{j}_{eh}\right) ^{q\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \right\rangle , \end{aligned}$$

  (13)

  where $e = 1, 2, \ldots , m, h = 1, 2, \ldots , n$, $p\ge 1$, $q\ge 1$, and $\lambda \in (0,\infty )$.

• Step 5: Calculate the value $T_{eh}$ of the p, q-QOFNs $\mathfrak {R}_{eh}$ appeared in CDMx ${L}=({{\mathfrak {R}}_{eh}})_{m\times n}$ to construct the matrix $T=(T_{eh})_{m \times n}$, where

  $$\begin{aligned} {T_{eh}}= & {\left\{ \begin{array}{ll} 1:& \text {if}\, t=1, \\ \prod _{t=1}^{h-1}S(\mathfrak {R}_{et}):& \text {if}\, h=2,3, \ldots , n, \end{array}\right. } \end{aligned}$$

  (14)

  $S(\mathfrak {R}_{et})$ is the score value of the p, q-QOFN $\mathfrak {R}_{et}$ obtained by using Eq. (3), $e = 1, 2, \ldots , m; h=1,2,\ldots ,n; t = 1, 2, \ldots , n-1$.

• Step 6: Compute the entropy $E_h$ of the attribute $\Phi _h$ by using the p, q-QOFN $\mathfrak {R}_{1\,h}$, $\mathfrak {R}_{2\,h}$, $\ldots$, $\mathfrak {R}_{mh}$ appeared in $h^{th}$ column of CDMx ${L}=({{\mathfrak {R}}_{eh}})_{m\times n}$, shown as follows:

  $$\begin{aligned} E_h = {\frac{1}{m}}\sum _{e=1}^{m}\tan \left( \frac{\pi }{4}-\frac{|(\zeta _{eh})^p-(\varrho _{eh})^q|(1-(\pi _{eh})^l)}{4} \pi \right) ,\nonumber \\ \end{aligned}$$

  (15)

  where $e=1,2,\ldots ,m$, $h=1,2,\ldots ,n$, $(\pi _{eh})^l=1-(\zeta _{eh})^p-(\varrho _{eh})^q$, l is the LCM of p and q. Now by using the above entropy, we compute the weights $w_1$, $w_2$, $\ldots$, $w_n$ of the attributes $\Phi _{1},\Phi _{2},\ldots ,\Phi _{n}$, respectively, as follows:

  $$\begin{aligned} w_h=\frac{1-E_h}{n-\sum _{h=1}^{n}E_h}, \end{aligned}$$

  (16)

  where $w_{h}\ge 0$, $h=1,2,\ldots ,n$ and $\sum _{h=1}^{n}w_{h}= 1$.

• Step 7: By utilizing the obtained weights $w_1,w_2,\ldots ,w_n$ and obtained matrix $T=(T_{eh})_{m \times n}$, we calculate the weights $\varsigma _{e1},\varsigma _{e2},\ldots$, and $\varsigma _{en}$ of p, q-QOFNs $\mathfrak {R}_{e1},\mathfrak {R}_{e2},\ldots ,$ and $\mathfrak {R}_{en}$, respectively, to construct the weighted matrix $W=(\varsigma _{eh})_{m\times n}$, where

  $$\begin{aligned} \varsigma _{eh}=\frac{w_{h}T_{eh}}{\sum _{h=1}^{n}w_{h}T_{eh}}, \end{aligned}$$

  (17)

  $e = 1, 2, \ldots , m$ and $h = 1, 2, \ldots , n$.

• Step 8: Based on the proposed p, q-QOFYPWG AO given in Eq. (8), we aggregate the p, q-QOFNs $\mathfrak {R}_{e1},\mathfrak {R}_{e2},\ldots ,$ and $\mathfrak {R}_{en}$ which appeared in the $h^{th}$ row of the CDMx ${L}=({{\mathfrak {R}}_{eh}})_{m\times n}$ to obtain the overall p, q-QOFN $\mathfrak {R}_{e}= \langle \zeta _{e}, \varrho _{e} \rangle$ of alternatives $H_{e}$, shown as follows:

  $$\begin{aligned} \mathfrak {R}_{e}= & p, q-QOFYPWG(\mathfrak {R}_{e1},\mathfrak {R}_{e2},\ldots ,\mathfrak {R}_{en})\nonumber \\= & \Bigg \langle \root p \of {1-\min \left\{ 1,\left( \sum _{h=1}^{n}\varsigma _{eh}\left( 1-(\zeta _{eh})^{p}\right) ^{\lambda }\right) ^{\frac{1}{\lambda }}\right\} },\nonumber \\ & \root q \of {\min \left\{ 1,\left( \sum _{h=1}^{n}\varsigma _{eh} \left( \varrho _{eh}\right) ^{q\lambda }\right) ^{\frac{1}{\lambda }}\right\} } \Bigg \rangle , \end{aligned}$$

  (18)

  where, $e=1,2,\ldots ,m$, $p,q\ge 1$ and $\lambda \in (0,\infty ).$

• Step 9: By using the Eq.(3), we calculate the score values $S(\mathfrak {R}_{1})$, $S(\mathfrak {R}_{2})$, $\ldots$, and $S(\mathfrak {R}_{m})$ of the overall p, q-QOFNs $\mathfrak {R}_{1}= \langle \zeta _{1}, \varrho _{1} \rangle$, $\mathfrak {R}_{2}= \langle \zeta _{2}, \varrho _{2} \rangle$, $\ldots$, $\mathfrak {R}_{m}= \langle \zeta _{m}, \varrho _{m} \rangle$ of the alternative $H_{1}$, $H_{2}$, ..., and $H_{m}$, respectively, shown as follows:

  $$\begin{aligned} S(\mathfrak {R}_{e})=\frac{1+(\zeta _{e})^p-(\varrho _{e})^q}{2}, \end{aligned}$$

  (19)

  where $S(\mathfrak {R}_{e})\in [0,1]$ and $e=1,2,\ldots ,m$.

• Step 10: If $S(\mathfrak {R}_{a})>S(\mathfrak {R}_{b})$, then based on Definition 7, the preference order (PO) between the alternatives $\mathfrak {R}_a$ and $\mathfrak {R}_b$ is $``\mathfrak {R}_a\succ \mathfrak {R}_b",$ where $a=1,2,\ldots ,m$, $b=1,2,\ldots ,m$ and $a\ne b$. If $S(\mathfrak {R}_{a})=S(\mathfrak {R}_{b})$, then, by using Eq.(4), we compute the accuracy values $A(\mathfrak {R}_{a})=(\zeta _{a})^p+(\varrho _{a})^q$ and $A(\mathfrak {R}_{b})=(\zeta _{b})^p+(\varrho _{b})^q$ of the overall p, q-QOFNs $\mathfrak {R}_{a}= \langle \zeta _{a}, \varrho _{a} \rangle$ and $\mathfrak {R}_{b}= \langle \zeta _{b}, \varrho _{b} \rangle$, respectively. If $A(\mathfrak {R}_{a})>A(\mathfrak {R}_{b})$, then according to Definition 7, the PO between the alternatives $\mathfrak {R}_a$ and $\mathfrak {R}_b$ is $``\mathfrak {R}_a\succ \mathfrak {R}_b"$. If $S(\mathfrak {R}_{a})=S(\mathfrak {R}_{b})$ and $A(\mathfrak {R}_{a})=A(\mathfrak {R}_{b})$, then alternatives $\mathfrak {R}_a$ and $\mathfrak {R}_b$ have the same PO, where $a\ne b$. Thus, we get the PO of the alternatives $\mathfrak {R}_1,\mathfrak {R}_2,\ldots ,$ and $\mathfrak {R}_e$ and select the best choice.

Example 3

(Garg 2020) The government wants to prevent urban migration by selecting an ideal company for creating economic opportunities in rural areas of Jharkhand. Let the four attributes outlined by the government for selecting companies are: $\Phi _{1}$ (“Focusing on technical capability”), $\Phi _{2}$ (“Financial status”), $\Phi _{3}$ (“Company background”) and $\Phi _{4}$ (“References from previous projects”). Let the five companies $H_{1},H_{2},H_{3},H_{4}$ and $H_{5}$ as alternatives have shown keen interest in the project. Three DMExs $\Psi _{1},\Psi _{2}$ and $\Psi _{3}$ evaluate the companies $H_{1},H_{2},H_{3},H_{4}$ and $H_{5}$ towards the attributes $\Phi _{1}$, $\Phi _{2}$, $\Phi _{3}$ and $\Phi _{4}$. The weights of the DMExs $\Psi _{1},\Psi _{2}$ and $\Psi _{3}$ are $\varpi _{1}=0.35, \varpi _{2}=0.40$ and $\varpi _{3}=0.25$, respectively. Each DMEx $\Psi _{j}$ assesses the attribute $\Phi _{h}$ of the alternative $H_{e}$ by utilizing p, q-QOFN $\tilde{\mathfrak {R}}^{j}_{eh}=\langle \tilde{\zeta }^{j}_{eh}, \tilde{\varrho }^{j}_{eh} \rangle$, where $j=1,2,3$, $e=1,2,3,4,5$ and $h=1,2,3,4$, to construct the DMx $\tilde{L}^{j}=(\tilde{\mathfrak {R}}^{j}_{eh})_{5\times 4}$, shown as follows:

In the following, we utilize the proposed MAGDM approach to solve this MAGDM problem.

• Step 1: Since all the attributes $\Phi _{1}$, $\Phi _{2}$,$\Phi _{3}$ and $\Phi _{4}$ are benefit type, by using Eq. (10), we get NDMxs ${L}^1 = (\tilde{\mathfrak {R}}_{eh}^1)_{5 \times 4} =({\mathfrak {R}}_{eh}^1)_{5 \times 4} = (\langle {{\zeta }_{eh}^1}, {{\varrho }_{eh}^1}\rangle )_{5\times 4}$, ${L}^2 = (\tilde{\mathfrak {R}}_{eh}^2)_{5 \times 4} =({\mathfrak {R}}_{eh}^2)_{5 \times 4} = (\langle {{\zeta }_{eh}^2},{{\varrho }_{eh}^2}\rangle )_{5\times 4}$ and ${L}^3 = (\tilde{\mathfrak {R}}_{eh}^3)_{5 \times 4} =({\mathfrak {R}}_{eh}^3)_{5 \times 4} = (\langle {{\zeta }_{eh}^3},{{\varrho }_{eh}^3}\rangle )_{5\times 4}$.

• Step 2: By using Eq. (11), we calculate the values of $T^{1}_{eh},T^{2}_{eh}$ and $T^{3}_{eh}$ of p, q-QOFNs $\mathfrak {R}^{1}_{eh},\mathfrak {R}^{2}_{eh}$ and $\mathfrak {R}^{3}_{eh}$ of the NDMx ${L}^1 =({\mathfrak {R}}_{eh}^1)_{5 \times 4}$, ${L}^2 =({\mathfrak {R}}_{eh}^2)_{5 \times 4}$, and ${L}^3 =({\mathfrak {R}}_{eh}^3)_{5 \times 4}$, respectively, to obtain the matrices $T^{1}=(T^{1}_{eh})_{5\times 4}$, $T^{2}=(T^{2}_{eh})_{5\times 4}$ and $T^{3}=(T^{3}_{eh})_{5\times 4}$, where, $p=1$, $q=4$, $\lambda =1$,

  
  
  

• Step 3: By using Eq. (12), the obtained matrices $T^{1}, T^{2}$ and $T^{3}$ and the weights $\varpi _{1}=0.35, \varpi _{2}=0.40$ and $\varpi _{3}=0.25$ of the DMExs $\Psi ^1,\Psi ^2$ and $\Psi ^3$, respectively, we calculate the weights $\varsigma ^{1}_{eh}, \varsigma ^{2}_{eh}$ and $\varsigma ^{3}_{eh}$ of p, q-QOFNs $\mathfrak {R}^{1}_{eh},\mathfrak {R}^{2}_{eh}$ and $\mathfrak {R}^{3}_{eh}$, respectively, to construct the weighted matrices $W^{1}=(\varsigma ^{1}_{eh})_{5\times 4}$, $W^{2}=(\varsigma ^{2}_{eh})_{5\times 4}$ and $W^{3}=(\varsigma ^{3}_{eh})_{5\times 4}$, where $p=1$, $q=4$, $e=1,2,3,4,5$ and $h=1,2,3,4$,

  
  
  

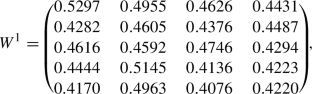
• Step 4: By using Eq. (13), we obtain the aggregated p, q-QOFN $\mathfrak {R}_{eh}=\langle {{\zeta }_{eh}},{{\varrho }_{eh}}\rangle$ by aggregating the p, q-QOFNs $\mathfrak {R}^{1}_{eh}=\langle {{\zeta }_{eh}^1},{{\varrho }_{eh}^1}\rangle$, $\mathfrak {R}^{2}_{eh}=\langle {{\zeta }_{eh}^2},{{\varrho }_{eh}^2}\rangle$ and $\mathfrak {R}^{3}_{eh}=\langle {{\zeta }_{eh}^3},{{\varrho }_{eh}^3}\rangle$ that appeared in the NDMxs $L^{1}=(\mathfrak {R}^{1}_{eh})_{5\times 4}$, $L^{2}=(\mathfrak {R}^{2}_{eh})_{5\times 4}$ and $L^{3}=(\mathfrak {R}^{3}_{eh})_{5\times 4}$, respectively, to construct the CDMx $L=(\mathfrak {R}_{eh})_{5\times 4}=\langle \zeta _{eh}, \varrho _{eh} \rangle _{5\times 4}$, where $\lambda =1$, $p=1$ and $q=4$,

  

• Step 5: By using Eq. (14), we calculate the value $T_{eh}$ of the aggregated p, q-QOFN $\mathfrak {R}_{eh}$, to get the matrix $T=(T_{eh})_{5\times 4}$, where $e=1,2,3,4,5$ and $h=1,2,3,4$,

  

• Step 6: By using Eq. (15), we calculate the entropies $E_1$, $E_2$, $E_3$ and $E_4$ of the attributes $\Phi _1$, $\Phi _2$, $\Phi _3$ and $\Phi _4$, respectively, where $E_1= 0.6890$, $E_2= 0.7785$, $E_3=0.6444$ and $E_4=0.6428$. Then, by using Eq. (16), we calculate the weights $w_1$, $w_2$, $w_3$, $w_4$ of the attributes $\Phi _1$, $\Phi _2$, $\Phi _3$ and $\Phi _4$, respectively, where $w_{1}= 0.2497,w_{2}= 0.1779,w_{3}=0.2855$ and $w_{4}=0.2869$.

• Step 7: By using Eq. (17), the obtained matrix T and the weights $w_{1}= 0.2497,w_{2}= 0.1779,w_{3}=0.2855$ and $w_{4}=0.2869$ of the attributes $\Phi _{1}, \Phi _{2}, \Phi _{3}$ and $\Phi _{4}$, respectively, we calculate the weight $\varsigma _{eh}$ of p, q-QOFN $R_{eh}$, to construct the weighted matrix $W=(\varsigma _{eh})_{5 \times 4}$, where $e=1,2,3,4,5$, $h=1,2,3,4$,

  

• Step 8: By using Eq. (18) and obtained weight matrix $W=(\varsigma _{eh})_{5 \times 4}$, we obtain the overall aggregated p, q-QOFN $\mathfrak {R}_{e}=\langle \zeta _{e}, \varrho _{e} \rangle$ of the alternative $H_{e}$, where $e=1,2,3,4,5$, $\zeta _{1} = 0.3304$, $\varrho _{1} = 0.5466$, $\zeta _{2} = 0.5194$, $\varrho _{2} = 0.2573$, $\zeta _{3} = 0.4835$, $\varrho _{3} = 0.3177$,$\zeta _{4} = 0.4535$, $\varrho _{4} = 0.4286$, $\zeta _{5} = 0.5731$, $\varrho _{5} = 0.3172$, $\mathfrak {R}_{1}= \langle 0.3304, 0.5466 \rangle$, $\mathfrak {R}_{2}= \langle 0.5194, 0.2573 \rangle$, $\mathfrak {R}_{3}= \langle 0.4835, 0.3177 \rangle$, $\mathfrak {R}_{4}= \langle 0.4535, 0.4286 \rangle$ and $\mathfrak {R}_{5}= \langle 0.5731,0.3172 \rangle$.

• Step 9: By using Eq. (19), we calculate the score values $S(\mathfrak {R}_{1})$,$S(\mathfrak {R}_{2})$, $S(\mathfrak {R}_{3})$, $S(\mathfrak {R}_{4})$ and $S(\mathfrak {R}_{5})$ of the overall aggregated p, q-QOFNs $\mathfrak {R}_{1}= \langle 0.3304, 0.5466 \rangle$, $\mathfrak {R}_{2}= \langle 0.5194, 0.2573 \rangle$, $\mathfrak {R}_{3}= \langle 0.4835, 0.3177 \rangle$, $\mathfrak {R}_{4}= \langle 0.4535, 0.4286 \rangle$ and $\mathfrak {R}_{5}= \langle 0.5731, 0.3172 \rangle$, respectively, where $S(\mathfrak {R}_{1})=0.6206$,$S(\mathfrak {R}_{2})=0.7575$, $S(\mathfrak {R}_{3})=0.7366$, $S(\mathfrak {R}_{4})=0.7099$ and $S(\mathfrak {R}_{5})=0.7815$.

• Step 10: Because $S(\mathfrak {R}_{5})>S(\mathfrak {R}_{2})>S(\mathfrak {R}_{3})>S(\mathfrak {R}_{4})>S(\mathfrak {R}_{1})$, where $S(\mathfrak {R}_{1})=0.6206$,$S(\mathfrak {R}_{2})=0.7575$, $S(\mathfrak {R}_{3})=0.7366$, $S(\mathfrak {R}_{4})=0.7099$ and $S(\mathfrak {R}_{5})=0.7815$, the PO of the alternatives $H_{1}, H_{2}, H_{3}, H_{4}$ and $H_{5}$ is $``H_{5}\succ H_{2}\succ H_{3}\succ H_{4}\succ H_{1}"$. Thus, $H_{5}$ is the best alternative.

Table 1 presents a comparison of the POs of the alternatives $H_{1}, H_{2}, H_{3}, H_{4}$ and $H_{5}$ obtained by various MAGDM approaches for Example 3. From Table 1, it is clear that Garg’s MAGDM approach (Garg 2020), Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022), Rahim et al.’s MAGDM approach (Rahim et al. 2023a), Ahmad et al.’s MAGDM approach (Ahmad et al. 2024) and the proposed MAGDM approach obtain the same PO $``H_{5}\succ H_{2}\succ H_{3}\succ H_{4}\succ H_{1}"$ of the alternatives $H_{1}, H_{2}, H_{3}, H_{4}$ and $H_{5}$.

Table 1 A comparison of the POs of alternatives obtained by several MAGDM approaches for Example 3

Example 4

Let $H_{1}, H_{2}, H_{3}$ and $H_{4}$ be four alternatives and $\Phi _{1}$, $\Phi _{2}$, $\Phi _{3}$ and $\Phi _{4}$ be four attributes. The weights of the DMExs $\Psi _{1},\Psi _{2}$ and $\Psi _{3}$ are $\varpi _{1}=0.40, \varpi _{2}=0.20$ and $\varpi _{3}=0.40$, respectively. Each DMEx $\Psi _{j}$ assesses the attribute $\Phi _{h}$ of the alternative $H_{e}$ by utilizing p, q-QOFN $\tilde{\mathfrak {R}}^{j}_{eh}=\langle \tilde{\zeta }^{j}_{eh}, \tilde{\varrho }^{j}_{eh} \rangle$, where $j=1,2,3$, $e=1,2,3,4$ and $h=1,2,3,4$, to construct the DMx $\tilde{L}^{j}=(\tilde{\mathfrak {R}}^{j}_{eh})_{4\times 4}$, shown as follows:

In the following, we utilize the proposed MAGDM approach to solve this MAGDM problem.

• Step 1: Since all the attributes $\Phi _{1}$, $\Phi _{2}$, $\Phi _{3}$ and $\Phi _{4}$ are benefit type, by using Eq. (10), we get NDMxs ${L}^1 = (\tilde{\mathfrak {R}}_{eh}^1)_{4 \times 4} =({\mathfrak {R}}_{eh}^1)_{4 \times 4} = (\langle {{\zeta }_{eh}^1}, {{\varrho }_{eh}^1}\rangle )_{4\times 4}$, ${L}^2 = (\tilde{\mathfrak {R}}_{eh}^2)_{4 \times 4} =({\mathfrak {R}}_{eh}^2)_{4 \times 4} = (\langle {{\zeta }_{eh}^2},{{\varrho }_{eh}^2}\rangle )_{4\times 4}$ and ${L}^3 = (\tilde{\mathfrak {R}}_{eh}^3)_{4 \times 4} =({\mathfrak {R}}_{eh}^3)_{4 \times 4} = (\langle {{\zeta }_{eh}^3},{{\varrho }_{eh}^3}\rangle )_{4\times 4}$.

• Step 2: By using Eq. (11), we calculate the values of $T^{1}_{eh}, T^{2}_{eh}$ and $T^{3}_{eh}$ of p, q-QOFNs $\mathfrak {R}^{1}_{eh}, \mathfrak {R}^{2}_{eh}$ and $\mathfrak {R}^{3}_{eh}$ of the NDMx $L^1=(\mathfrak {R}^1_{eh})_{4\times 4}$, $L^2=(\mathfrak {R}^2_{eh})_{4\times 4}$ and $L^3=(\mathfrak {R}^3_{eh})_{4\times 4}$, respectively, to obtain the matrices $T^{1}=(T^{1}_{eh})_{4\times 4}$, $T^{2}=(T^{2}_{eh})_{4\times 4}$ and $T^{3}=(T^{3}_{eh})_{4\times 4}$, where $p=3$, $q=3$, $\lambda =1$,

  
  
  

• Step 3: By using Eq. (12), the obtained matrices $T^{1}, T^{2}$ and $T^{3}$ and the weights $\varpi _{1}=0.40, \varpi _{2}=0.20$ and $\varpi _{3}=0.40$ of the DMExs $\Psi ^1, \Psi ^2$ and $\Psi ^3$, respectively, we calculate the weights $\varsigma ^{1}_{eh}, \varsigma ^{2}_{eh}$ and $\varsigma ^{3}_{eh}$ of p, q-QOFNs $\mathfrak {R}^{1}_{eh}, \mathfrak {R}^{2}_{eh}$ and $\mathfrak {R}^{3}_{eh}$, respectively, to construct the weighted matrices $W^{1}=(\varsigma ^{1}_{eh})_{4\times 4}$, $W^{2}=(\varsigma ^{2}_{eh})_{4\times 4}$ and $W^{3}=(\varsigma ^{3}_{eh})_{4\times 4}$, where $p=3,q=3, e=1,2,3,4$ and $h=1,2,3,4$,

  
  
  

• Step 4: By using Eq. (13), we obtain the aggregated p, q-QOFN $\mathfrak {R}_{eh}=\langle {{\zeta }_{eh}},{{\varrho }_{eh}}\rangle$ by aggregating the p, q-QOFNs $\mathfrak {R}^{1}_{eh}=\langle {{\zeta }_{eh}^1},{{\varrho }_{eh}^1}\rangle$, $\mathfrak {R}^{2}_{eh}=\langle {{\zeta }_{eh}^2},{{\varrho }_{eh}^2}\rangle$ and $\mathfrak {R}^{3}_{eh}=\langle {{\zeta }_{eh}^3},{{\varrho }_{eh}^3}\rangle$ that appeared in the NDMxs $L^{1}=(\mathfrak {R}^{1}_{eh})_{4\times 4}$, $L^{2}=(\mathfrak {R}^{2}_{eh})_{4\times 4}$ and $L^{3}=(\mathfrak {R}^{3}_{eh})_{4\times 4}$, respectively, to construct the CDMx $L=(\mathfrak {R}_{eh})_{4\times 4}=\langle \zeta _{eh}, \varrho _{eh} \rangle _{4\times 4}$, where $\lambda =1, p=3$ and $q=3$,

  

• Step 5: By using Eq. (14), we calculate the value $T_{eh}$ of the aggregated p, q-QOFN $\mathfrak {R}_{eh}$, to get the matrix $T=(T_{eh})_{4\times 4}$, where $e=1,2,3,4$ and $h=1,2,3,4$,

  

• Step 6: By using Eq. (15), we calculate the entropies $E_1$, $E_2$, $E_3$ and $E_4$ of the attributes $\Phi _1$, $\Phi _2$, $\Phi _3$ and $\Phi _4$, respectively, where $E_1= 0.9336$, $E_2= 0.9868$, $E_3=0.9480$ and $E_4=0.9614$. Then, by using Eq. (16), we calculate the weights $w_1$, $w_2$, $w_3$, $w_4$ of the attributes $\Phi _1$, $\Phi _2$, $\Phi _3$ and $\Phi _4$, respectively, where $w_{1}= 0.3902,w_{2}= 0.0775,w_{3}=0.3054$ and $w_{4}=0.2268$.

• Step 7: By using Eq. (17), the obtained matrix T and the weights $w_{1}= 0.3902,w_{2}= 0.0775,w_{3}=0.3054$ and $w_{4}=0.2268$ of the attributes $\Phi _{1}, \Phi _{2}, \Phi _{3}$ and $\Phi _{4}$, respectively, we calculate the weight $\varsigma _{eh}$ of p, q-QOFN $R_{eh}$, to construct the weighted matrix $W=(\varsigma _{eh})_{4 \times 4}$, where $e=1,2,3,4$, $h=1,2,3,4$,

  

• Step 8: By using Eq. (18) and obtained weight matrix $W=(\varsigma _{eh})_{4 \times 4}$, we obtain the overall aggregated p, q-QOFN $\mathfrak {R}_{e}=\langle \zeta _{e}, \varrho _{e} \rangle$ of the alternative $H_{e}$, where $e=1,2,3,4$, $\zeta _{1} = 0.4830$, $\varrho _{1} = 0.4381$, $\zeta _{2} = 0.2770$, $\varrho _{2} = 0.6639$, $\zeta _{3} = 0.3985$, $\varrho _{3} = 0.3443$,$\zeta _{4} = 0.6231$, $\varrho _{4} = 0.2617$, $\mathfrak {R}_{1}= \langle 0.4830, 0.4381 \rangle$, $\mathfrak {R}_{2}= \langle 0.2770, 0.6639 \rangle$, $\mathfrak {R}_{3}= \langle 0.3985, 0.3443 \rangle$ and $\mathfrak {R}_{4}= \langle 0.6231, 0.2617 \rangle$.

• Step 9: By using Eq. (19), we calculate the score values $S(\mathfrak {R}_{1})$, $S(\mathfrak {R}_{2})$, $S(\mathfrak {R}_{3})$ and $S(\mathfrak {R}_{4})$ of the overall aggregated p, q-QOFNs $\mathfrak {R}_{1}= \langle 0.4830, 0.4381 \rangle$, $\mathfrak {R}_{2}= \langle 0.2770, 0.6639 \rangle$, $\mathfrak {R}_{3}= \langle 0.3985, 0.3443 \rangle$ and $\mathfrak {R}_{4}= \langle 0.6231, 0.2617 \rangle$, respectively, where $S(\mathfrak {R}_{1})=0.5143$,$S(\mathfrak {R}_{2})=0.3643$, $S(\mathfrak {R}_{3})=0.5112$ and $S(\mathfrak {R}_{4})=0.6120$.

• Step 10: Because $S(\mathfrak {R}_{4})>S(\mathfrak {R}_{1})>S(\mathfrak {R}_{3})>S(\mathfrak {R}_{2})$, where $S(\mathfrak {R}_{1})=0.5143$,$S(\mathfrak {R}_{2})=0.3643$, $S(\mathfrak {R}_{3})=0.5112$ and $S(\mathfrak {R}_{4})=0.6120$, the PO of the alternatives $H_{1}, H_{2}, H_{3}$ and $H_{4}$ is $``H_{4}\succ H_{1}\succ H_{3}\succ H_{2}"$. Thus, $H_{4}$ is the best alternative.

Table 2 presents a comparison of the POs of the alternatives $H_{1}, H_{2}, H_{3}$ and $H_{4}$ obtained by various MAGDM approaches for Example 4. From Table 2, it is clear that Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022) and Ahmad et al.’s MAGDM approach (Ahmad et al. 2024) cannot handle this MAGDM problem because it get the indeterminant form in the intermediate steps while solving this MAGDM problem. However, Garg’s MAGDM approach (Garg 2020), Rahim et al.’s MAGDM approach (Rahim et al. 2023a) and the proposed MAGDM approach obtain the same PO $``H_{4}\succ H_{1}\succ H_{3}\succ H_{2}"$ for the alternatives $H_{1}, H_{2}, H_{3}$ and $H_{4}$. Therefore, the proposed MAGDM approach can overcome the shortcomings of Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022) and Ahmad et al.’s MAGDM approach (Ahmad et al. 2024) in this case.

Table 2 A comparison of the POs of alternatives obtained by several MAGDM approaches for Example 4

Example 5

Let $H_{1}, H_{2}, H_{3}$ and $H_{4}$ be four alternatives and $\Phi _{1}$, $\Phi _{2}$, $\Phi _{3}$ and $\Phi _{4}$ be four attributes. The weights of the DMExs $\Psi _{1}, \Psi _{2}$ and $\Psi _{3}$ are $\varpi _{1}=0.40, \varpi _{2}=0.40$ and $\varpi _{3}=0.20$, respectively. Each DMEx $\Psi _{j}$ assesses the attribute $\Phi _{h}$ of the alternative $H_{e}$ by utilizing p, q-QOFN $\tilde{\mathfrak {R}}^{j}_{eh}=\langle \tilde{\zeta }^{j}_{eh}, \tilde{\varrho }^{j}_{eh} \rangle$, where $j=1,2,3$, $e=1,2,3,4$ and $h=1,2,3,4$, to construct the DMx $\tilde{L}^{j}=(\tilde{\mathfrak {R}}^{j}_{eh})_{4\times 4}$, shown as follows:

Table 3 A comparison of the POs of alternatives obtained by several MAGDM approaches for Example 5

In the following, we utilize the proposed MAGDM approach to solve this MAGDM problem.

• Step 1: Since all the attributes $\Phi _{1}$, $\Phi _{2}$, $\Phi _{3}$ and $\Phi _{4}$ are benefit type, by using Eq. (10), we get NDMxs ${L}^1 = (\tilde{\mathfrak {R}}_{eh}^1)_{4 \times 4} =({\mathfrak {R}}_{eh}^1)_{4 \times 4} = (\langle {{\zeta }_{eh}^1}, {{\varrho }_{eh}^1}\rangle )_{4\times 4}$, ${L}^2 = (\tilde{\mathfrak {R}}_{eh}^2)_{4 \times 4} =({\mathfrak {R}}_{eh}^2)_{4 \times 4} = (\langle {{\zeta }_{eh}^2},{{\varrho }_{eh}^2}\rangle )_{4\times 4}$ and ${L}^3 = (\tilde{\mathfrak {R}}_{eh}^3)_{4 \times 4} =({\mathfrak {R}}_{eh}^3)_{4 \times 4} = (\langle {{\zeta }_{eh}^3},{{\varrho }_{eh}^3}\rangle )_{4\times 4}$.

• Step 2: By using Eq. (11), we calculate the values of $T^{1}_{eh}, T^{2}_{eh}$ and $T^{3}_{eh}$ of p, q-QOFNs $\mathfrak {R}^{1}_{eh}, \mathfrak {R}^{2}_{eh}$ and $\mathfrak {R}^{3}_{eh}$ of the NDMx ${L}^1 =({\mathfrak {R}}_{eh}^1)_{4 \times 4}$, ${L}^2 =({\mathfrak {R}}_{eh}^2)_{4 \times 4}$ and ${L}^3 =({\mathfrak {R}}_{eh}^3)_{4 \times 4}$ respectively, to obtain the matrices $T^{1}=(T^{1}_{eh})_{4\times 4}$, $T^{2}=(T^{2}_{eh})_{4\times 4}$ and $T^{3}=(T^{3}_{eh})_{4\times 4}$, where $p=3$, $q=3$, $\lambda =1$,

  
  
  

• Step 3: By using Eq. (12), the obtained matrices $T^{1}, T^{2}$ and $T^{3}$ and the weights $\varpi _{1}=0.40, \varpi _{2}=0.40$ and $\varpi _{3}=0.20$ of the DMExs $\Psi ^1,\Psi ^2$ and $\Psi ^3$, respectively, we calculate the weights $\varsigma ^{1}_{eh}, \varsigma ^{2}_{eh}$ and $\varsigma ^{3}_{eh}$ of p, q-QOFNs $\mathfrak {R}^{1}_{eh},\mathfrak {R}^{2}_{eh}$ and $\mathfrak {R}^{3}_{eh}$, respectively, to construct the weighted matrices $W^{1}=(\varsigma ^{1}_{eh})_{4\times 4}$, $W^{2}=(\varsigma ^{2}_{eh})_{4\times 4}$ and $W^{3}=(\varsigma ^{3}_{eh})_{4\times 4}$, where $p=3,q=3, e=1,2,3,4$ and $h=1,2,3,4$,

  
  
  

• Step 4: By using Eq. (13), we obtain the aggregated p, q-QOFN $\mathfrak {R}_{eh}=\langle {{\zeta }_{eh}},{{\varrho }_{eh}}\rangle$ by aggregating the p, q-QOFNs $\mathfrak {R}^{1}_{eh}=\langle {{\zeta }_{eh}^1},{{\varrho }_{eh}^1}\rangle$, $\mathfrak {R}^{2}_{eh}=\langle {{\zeta }_{eh}^2},{{\varrho }_{eh}^2}\rangle$ and $\mathfrak {R}^{3}_{eh}=\langle {{\zeta }_{eh}^3},{{\varrho }_{eh}^3}\rangle$ that appeared in the NDMxs $L^{1}=(\mathfrak {R}^{1}_{eh})_{4\times 4}$, $L^{2}=(\mathfrak {R}^{2}_{eh})_{4\times 4}$ and $L^{3}=(\mathfrak {R}^{3}_{eh})_{4\times 4}$, respectively, to construct the CDMx $L=(\mathfrak {R}_{eh})_{4\times 4}=\langle \zeta _{eh}, \varrho _{eh} \rangle _{4\times 4}$, where $\lambda =1, p=3$ and $q=3$,

  

• Step 5: By using Eq. (14), we calculate the value $T_{eh}$ of the aggregated p, q-QOFN $\mathfrak {R}_{eh}$, to get the matrix $T=(T_{eh})_{4\times 4}$, where $e=1,2,3,4$ and $h=1,2,3,4$,

  

• Step 6: By using Eq. (15), we calculate the entropies $E_1$, $E_2$, $E_3$ and $E_4$ of the attributes $\Phi _1$, $\Phi _2$, $\Phi _3$ and $\Phi _4$, respectively, where $E_1= 0.7313$, $E_2= 0.9963$, $E_3=0.9781$ and $E_4=0.9634$. Then, by using Eq. (16), we calculate the weights $w_1$, $w_2$, $w_3$, $w_4$ of the attributes $\Phi _1$, $\Phi _2$, $\Phi _3$ and $\Phi _4$, respectively, where $w_{1}= 0.8119,w_{2}= 0.0113,w_{3}=0.0662$ and $w_{4}=0.1106$.

• Step 7: By using Eq. (17), the obtained matrix T and the weights $w_{1}= 0.8119,w_{2}= 0.0113,w_{3}=0.0662$ and $w_{4}=0.1106$ of the attributes $\Phi _{1}, \Phi _{2}, \Phi _{3}$ and $\Phi _{4}$, respectively, we calculate the weight $\varsigma _{eh}$ of p, q-QOFN $\mathfrak {R}_{eh}$, to construct the weighted matrix $W=(\varsigma _{eh})_{4 \times 4}$, where $e=1,2,3,4$ and $h=1,2,3,4$,

  

• Step 8: By using Eq. (18) and obtained weight matrix $W=(\varsigma _{eh})_{4 \times 4}$, we obtain the overall aggregated p, q-QOFN $\mathfrak {R}_{e}=\langle \zeta _{e}, \varrho _{e} \rangle$, of the alternative $H_{e}$, where $e=1,2,3,4$, $\zeta _{1} = 0.3722$, $\varrho _{1} = 0.3619$, $\zeta _{2} = 0.1249$, $\varrho _{2} = 0.5336$, $\zeta _{3} = 0$, $\varrho _{3} = 1$,$\zeta _{4} = 0.5399$, $\varrho _{4} = 0.1361$, $\mathfrak {R}_{1}= \langle 0.3722, 0.3619 \rangle$, $\mathfrak {R}_{2}= \langle 0.1249, 0.5336 \rangle$, $\mathfrak {R}_{3}= \langle 0, 1 \rangle$ and $\mathfrak {R}_{4}= \langle 0.5399, 0.1361 \rangle$.

• Step 9: By using Eq. (19), we calculate the score values $S(\mathfrak {R}_{1})$,$S(\mathfrak {R}_{2})$, $S(\mathfrak {R}_{3})$ and $S(\mathfrak {R}_{4})$ of the overall aggregated p, q-QOFNs $\mathfrak {R}_{1}= \langle 0.3722, 0.3619 \rangle$, $\mathfrak {R}_{2}= \langle 0.1249, 0.5336 \rangle$, $\mathfrak {R}_{3}= \langle 0, 1 \rangle$ and $\mathfrak {R}_{4}= \langle 0.5399, 0.1361 \rangle$, respectively, where $S(\mathfrak {R}_{1})=0.5021$,$S(\mathfrak {R}_{2})=0.4250$, $S(\mathfrak {R}_{3})=0$ and $S(\mathfrak {R}_{4})=0.5774$.

• Step 10: Because $S(\mathfrak {R}_{4})>S(\mathfrak {R}_{1})>S(\mathfrak {R}_{2})>S(\mathfrak {R}_{3})$, where $S(\mathfrak {R}_{1})=0.5021$,$S(\mathfrak {R}_{2})=0.4250$, $S(\mathfrak {R}_{3})=0$ and $S(\mathfrak {R}_{4})=0.5774$, the PO of the alternatives $H_{1}, H_{2}, H_{3}$ and $H_{4}$ is $``H_{4}\succ H_{1}\succ H_{2}\succ H_{3}"$. Thus, $H_{4}$ is the best alternative.

Table 3 presents a comparison of the POs of the alternatives $H_{1},H_{2},H_{3}$ and $H_{4}$ obtained by various MAGDM approaches for Example 5. From Table 3, it is clear that Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022) cannot handle this MAGDM problem because it get the indeterminant form in the intermediate steps while solving this MAGDM problem. However, Garg’s MAGDM approach (Garg 2020) obtain the PO $``H_{1}= H_{4}\succ H_{2}\succ H_{3}"$ the alternatives $H_{1}, H_{2}, H_{3}$ and $H_{4}$, where it cannot distinguish the PO between the alternatives $H_1$ and $H_4$ in this particular case. While, Rahim et al.’s MAGDM approach (Rahim et al. 2023a) obtain the PO $``H_{1}= H_{2}= H_{4}\succ H_{3}"$ for the alternatives $H_{1}, H_{2}, H_{3}$, and $H_{4}$, where it cannot distinguish the PO among the alternatives $H_1$, $H_2$ and $H_4$ in this particular case. Moreover, Ahmad et al.’s MAGDM approach (Ahmad et al. 2024) and the proposed MAGDM approaches obtain the same PO $``H_{4}\succ H_{1}\succ H_{2}\succ H_{3}"$ of the alternatives $H_{1},H_{2},H_{3}$, and $H_{4}$. Therefore, the proposed MAGDM approach can overcome the shortcomings of Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022), Garg’s MAGDM approach (Garg 2020) and Rahim et al.’s MAGDM approach (Rahim et al. 2023a) in this case.

6 Conclusion

In this paper, we have proposed new multiplication operation and scalar power operation for p, q-quasirung orthopair fuzzy numbers (p, q-QOFNs) based on Yager’s norm. Then, by using the proposed multiplication operation and scalar power operation of p, q-QOFNs and the concept of prioritized geometric aggregation operator (AO), we have proposed the p, q-quasirung orthopair fuzzy Yager prioritized weighted geometric (p, q-QOFYPWG) AO for aggregating p, q-QOFNs. We have also proved several properties of the proposed p, q-QOFYPWG AO of p, q-QOFNs. However, based on the proposed p, q-QOFYPWG AO, we have proposed a new MAGDM approach under the p, q-QOFNs environment. Afterwards, we have utilized the proposed MAGDM approach to solve different numerical MAGDM problems and compare the preference orders (POs) obtained from the proposed MAGDM method with POs obtained from Garg’s MAGDM approach (Garg 2020), Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022), Rahim et al.’s MAGDM approach (Rahim et al. 2023a) and Ahmad et al.’s MAGDM approach (Ahmad et al. 2024). From Example 3, Example 4 and Example 5, it is clear that the proposed MAGDM method can overcome the shortcomings of Garg’s MAGDM approach (Garg 2020), Seikh and Mandal’s MAGDM approach (Seikh and Mandal 2022), Rahim et al.’s MAGDM approach (Rahim et al. 2023a) and Ahmad et al.’s MAGDM approach (Ahmad et al. 2024), where they can not distinguish between the POs of available alternatives. The proposed MAGDM approach offers a useful approach to deal with MAGDM problems in the p, q-QOFNs environment.