Abstract
Supplier selection and evaluation is a crucial decision-making issue to establish an effective supply chain. Higher-order fuzzy decision-making methods have become powerful tools to support decision-makers in solving their problems effectively by reflecting uncertainty in calculations better than crisp sets in the last 3 decades. The q-rung orthopair fuzzy (q-ROF) sets which are the general form of both intuitionistic and Pythagorean fuzzy sets, have been recently introduced to provide decision-makers more freedom of expression than other fuzzy sets. In this paper, we introduce q-ROF TOPSIS and q-ROF ELECTRE as two separate methods and new approaches for group decision making to select the best supplier. As the existing distance measures in q-rung orthopair fuzzy environment have some drawbacks and generate counter-intuitive results, we propose a new distance measure along with its proofs to use in both q-ROF TOPSIS and q-ROF ELECTRE methods. Moreover, a comparison study is conducted to illustrate the superiority of the proposed distance measure. Subsequently, a comprehensive case study is performed with q-ROF TOPSIS and q-ROF ELECTRE methods separately to choose the best supplier for a construction company by rating the importance of criteria and alternatives under q-ROF environment. Finally, a comparison and parameter analysis are performed among the proposed q-ROF TOPSIS and q-ROF ELECTRE methods and existing q-ROF decision-making methods to demonstrate the effectiveness of our proposed methods.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Supply chain management (SCM) supports companies about their improvements for their business planning and actions. The success of those companies depends to some extent on the proper functioning of the supply activity. Every business that wants to achieve its targets has to manage the procurement process effectively. The evaluation of suppliers is one of the most critical parts of procurement management.
The earliest studies on supplier selection were proposed by Dickson [10], which focused on the supplier selection criteria by meeting the purchasing manager of 273 enterprises. It was observed that 23 criteria ultimately impacted supplier selection. Weber et al. [43] analyzed 74 studies on supplier selection between 1966 and 1990 and concluded that price, delivery time, and product quality are very important criteria for supplier selection. Vonderembse and Tracey [38] proposed that selecting the criteria affected the performance of the enterprise. Wilson [45] dealt with the relative change in the supplier selection criteria during the last decades of the twentieth century. Shen and Yu [32] studied strategic vendor selection. In the last decades, the studies have concentrated on supplier selection methods. Weber et al. [43] classified these methods in three categories as linear weighting, statistical/probability approaches, and mathematical programming models. The parameters of the supplier selection or evaluation vary according to the type of product, its quantity, and its supplier, which might be thought of as a single or multiple supplier.
A large number of supplier selection criteria might be taken into consideration when purchasing new products from known suppliers or products or services from unknown suppliers, which requires decision-making at a high level of uncertainty. This uncertainty is modelled by the fuzzy set theory (FST) as supplier selection and evaluation are often considered multiple criteria decision-making problems that are expected to be solved without exact information. In the last 3 decades, FST has become a powerful tool to solve decision-making problems effectively, in which the available information is vague or imprecise [25]. The FST offers a mathematical way to model uncertainty preferences by adjusting the weights of performance criteria. Chen et al. [5] integrated TOPSIS method and fuzzy set to find the best supplier to a manufacturing company. Haq and Kannan [18] introduced a fuzzy AHP method to evaluate alternative suppliers for the rubber industry. Chou and Chang [8] suggested an approach of fuzzy simple multi-criteria rating method to select the most appropriate supplier in the strategic view of supply chain management. Sanayei et al. [31] proposed integrated fuzzy sets theory and VIKOR method to handle the selection process of supplier for an automobile part manufacturing company. Dengfeng and Chuntian [9] suggested TOPSIS method based on the integration of Dempster Shafer theory and fuzzy set for appropriate supplier selection. Rezaei et al. [30] used the fuzzy AHP method and conjunctive screening method to select the most suitable supplier on airline retail industry. Beikkhakhian et al. [2] suggested a method based on fuzzy AHP-TOPSIS and interpretive structural modelling to evaluate suppliers. Simic et al. [33] categorized the supplier assessment and selection methods as individual fuzzy and integrated fuzzy approaches. Rashidi and Cullinane [29] compared the performance of fuzzy data envelope analysis and fuzzy TOPSIS method in supplier selection.
Miscellaneous decision-making models and techniques like mathematics, statistics and artificial intelligence are used with fuzzy methods. After Zadeh’s [56] proposal of the FST, which deals with vagueness and ambiguity, many other fuzzy set theories have been proposed. For instance, the intuitionistic fuzzy set (IFS) theory, introduced by Atanassov [1], is an advanced version of Zadeh’s fuzzy sets but has two additional parameters that are non-membership degree and hesitation (indeterminacy) degree besides the membership degree. Some studies have used higher-order fuzzy sets [47]. Xu and Zhao [49] studied and analyzed the intuitionistic fuzzy decision-making methods, involving the determination of attribute weights, the aggregation of intuitionistic fuzzy information and the ranking of alternatives. Gupta et al. [17] studied on an 8 step MADM method under incomplete weight information on intuitionistic fuzzy and extended to interval-valued intuitionistic fuzzy (IVIF) information. Feng et al. [13] proposed an algorithm for solving MADM problems using generalized intuitionistic fuzzy soft sets. Feng et al. [14] introduced many new lexicographic orders tools for comparing intuitionistic fuzzy values with the aid of the membership function, non-membership function, score function, accuracy function, and expectation score function.
In the last 10 years, supplier selection problem has been handled with methods in higher order fuzzy environment. Boran et al. [4] proposed an intuitionistic fuzzy (IF) multiple criteria group decision making with the TOPSIS method for supplier selection problem. Memari et al. [26] used an intuitionistic fuzzy TOPSIS method for selecting the suitable supplier considering thirty criteria on the spare parts manufacturer of the automotive sector. Yu et al. [55] extended the TOPSIS method to the interval-valued Pythagorean fuzzy environment for group decision-making problems in supplier selection.
The degree of information (similarity or distance) measure on the higher-order fuzzy sets has been applied in decision-making problems [47]. One of the early studies of information measures was proposed by Szmidt and Kacprzyk [34] enhanced the Hamming Distance and the Euclidian Distance to IFS. Wang and Xin [42] had some criticism on the studies of Szmidt and Kacprzyk [34] that they were not effective enough. Grzegorzewski [16], Chen [7], Hung and Yang [20] studied on extending some distance measures such as the Hamming, the Euclidean or Hausdorff distances to IFSs and developed new similarity measures. Li et al. [22], Liang and Shi [23] studied on suggestions or criticisms for some new similarity measures for IFSs. Xu and Chen [48] studied on the Hamming, Euclidean, and the Hausdorff weighted distance measures. Xu and Yager [50], Verma and Sharma [36] introduce a divergence (relative information) measure, a kind of a discrimination measure for IFS, Boran and Akay [3] also proposed some distance measures for IFS. Verma and Sharma [37] proposed also a measure to determine the inaccuracy between two ‘intuitionistic fuzzy sets’.
After IFS, Pythagorean fuzzy sets (PFS) proposed by Yager [51], which are general forms of the IFS, simply the square sum of membership degree and non-membership degree is less than or equal to one. Consequently, with Pythagorean fuzzy numbers (PFNs) membership degree and non-membership degree have been expanded when compared to IF numbers (IFNs), such as the sum of these degrees in PFNs might be bigger than 1. For example, while the membership degree is (0.8), the non-membership might be (0.6), because \((0. 8 )^{2} + (0. 6 )^{2} \, \le { 1}\), but it is not possible in IFS as \((0. 8+ 0. 6 ) > { 1}\). PFS can solve the problems which give decision-maker larger area of deciding that the IFS cannot do, once considering some practical issues. Zhang and Xu [57] suggested a distance measure of PFNs extended from that of IFNs. Li and Zeng [21] proposed distance measures of PFN with four parameters, which are a membership and non-membership degree, strength, and direction of commitment. Verma and Merigó [35] proposed a generalized hybrid trigonometric similarity measure based on cosine and cotangent functions and applied it to MCDM problems with Pythagorean fuzzy information.
After the introduction of PFS, Yager [52] proposed the q-rung orthopair fuzzy sets (q-ROFs), in which the sum of the qth powers of the (membership and non-membership) degrees is restricted to one [53]. The more the rung q increases, the more acceptable space of orthopairs increases; hence, more orthopairs satisfy the limitations. As a result, q-ROF numbers give us the flexibility to mean a broader scope of fuzzy information. Namely, with the q parameter, we can express a more comprehensive information range; therefore, q-ROFs are more convenient for the vagueness. As q-ROFs application range is more comprehensive than previous fuzzy sets, in accordance with the change of the q parameter (q ≥ 1) shows us that q-ROF is broader, more flexible and appropriate for the complicated and unclear environment than PFS and IFS [39]. So, the larger a q level is determined, the more flexibility might be depicted.
Although q-ROFs provide the flexibility to express a wider information range, there is not enough study concerning distance measures and decision-making methods with q-ROF numbers. Peng and Liu [28] studied the systematic transformation for information measures (distance measure, entropy, inclusion measure and similarity measure) for q-ROFSs, presented new relations for information measures and used these new ideas on clustering, medical diagnosis and pattern recognition. Du [11] studied on Minkowski-type distance measures (Euclid, Hamming, and Chebyshev) for generalized orthopair fuzzy sets. Wang et al. [40] proposed some cosine similarity measures. However, the measures proposed by Du [11] and Wang et al. [40] both have counter-intuitive problems. Liu and Wang [24] proposed two decision-making methods based on q-ROF aggregation operators; however, they have some drawbacks. Therefore, it is obvious that a decision-making method and a distance measure between q-ROF numbers are required.
The originalities of this paper are threefold. Firstly, this paper introduces a novel distance measure between q-ROF numbers. A distance measure on q-ROFs is represented and proved. As mentioned above, existing distance measures have some drawbacks. When compared with existing IFS and q-ROF distance measures, it is illustrated that the proposed distance measure has no drawbacks and counter-intuitive results. Secondly, we proposed two new q-ROF multiple criteria group decision-making methods by extending TOPSIS and ELECTRE to q-ROF ELECTRE methods to q-ROF environment using the proposed novel distance measure. To the best of our knowledge, it is the first time that ELECTRE method is extended to q-ROF environment. We compared q-ROF TOPSIS and q-ROF ELECTRE with other existing q-ROF decision-making methods and proposed obtained better results. The advantage of q-ROF ELECTRE method is it’s being parametric concerning uncertainty. Thirdly, when investigating supplier selection problem, it is the first time that q-ROF TOPSIS and q-ROF ELECTRE methods are used in supplier selection problem.
The rest of the paper is arranged as follows. We explain the fuzzy sets from Zadeh’s classical ones to q-rung orthopair fuzzy sets of Yager in Sect. 2. The new distance measure, it’s proof, interpretation and comparison with other measures are introduced in Sect. 3. q-ROF TOPSIS and q-ROF ELECTRE methods are explained in Sect. 4. The application of the proposed distance measure to supplier selection integrated with the proposed methods are presented in Sect. 5 as a numerical example. We made a conclusion in Sect. 6.
2 Preliminaries
In this section, we make an introduction for the concept of fuzzy sets beginning with Zadeh’s classical ones to q-ROFs which are related to our model of a different distance measure.
Definition 1
[56] A fuzzy set A in the universe of discourse \(X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}\) is a set of ordered pairs:
where \(\mu_{A} (x){\kern 1pt} {\kern 1pt} :{\kern 1pt} {\kern 1pt} {\kern 1pt} X \to \left[ {0,1} \right]\) is the membership degree.
Definition 2
[1] An intuitionistic fuzzy set A in X can be defined as:
where the functions \(\mu_{A} (x){\kern 1pt} {\kern 1pt} :{\kern 1pt} {\kern 1pt} {\kern 1pt} X \to \left[ {0,1} \right]\) and \(v_{A} (x){\kern 1pt} {\kern 1pt} :{\kern 1pt} {\kern 1pt} {\kern 1pt} X \to \left[ {0,1} \right]\) define membership degree and non-membership degree of x, respectively, such that:
The hesitation degree of the IFS is:
which shows the hesitation degree of x belonging to A or not. It’s also true that:
While the minority of \(\pi_{A} (x)\) shows the precision of our knowledge about x, the greatness of it shows the vagueness.
Definition 3
Yager [51] introduced Pythagorean fuzzy sets membership degree couple of values (a, b) such that a, b ∈ [0, 1] as follows:
Here, a = AY (x), membership degree of x in A, and b = AN (x) the non-membership degree of x in A. We also see that for this pair a2 + b2= r2, in which r is the radius.
Definition 4
As Yager [52] proposed, a qth rung orthopair fuzzy subset A of X has given below:
where \(\mu_{A} :X \to \left[ {0,1} \right]\) indicates membership degree and \(v_{A} :X \to \left[ {0,1} \right]\) indicates non-membership degree of \(x \in X\) to the set A with below condition:
The degree of hesitancy can be defined as \(\pi_{A} (x) = \left( {1 - (\mu_{A} (x))^{q} - (v_{A} (x))^{q} } \right)^{1/q}\). Yager [52], as presented in Fig. 1, proposed that Atanassov’s IFSs are q-ROFs with q = 1, and PFS are q-ROFs with q = 2.
Definition 5
[39, 41, 44] Let \(A = (\mu (x),v(x))\) be a q-ROF number, the score function and the accuracy function of A are respectively given below:
Definition 6
[24] Suppose \(\alpha_{k} = \left\langle {\mu_{k} (x),v_{k} (x)} \right\rangle ,(k = 1,2, \ldots ,n)\) is a collection of q-ROFNs, then the q-rung orthopair fuzzy weighted averaging operator (q-ROFWA) is given as follows:
Definition 7
[24] Similarly as q-ROFWA, Suppose \(\alpha_{k} = \left\langle {\mu_{k} (x),v_{k} (x)} \right\rangle ,(k = 1,2, \ldots ,n)\) is a collection of q-ROFNs, then the q-rung orthopair fuzzy weighted geometric operator (q-ROFWG) is presented as follows:
In Definitions 6 and 7, \(\lambda = (\lambda_{1} ,\lambda_{2} ,\lambda_{3,} \ldots ,\lambda_{n} )^{T}\) is a weight vector of \((\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{l} )\), such that \(0 \le \lambda_{k} \le 1\) and \(\sum\nolimits_{k = 1}^{l} {\lambda_{k} = 1}\).
Definition 8
A mapping \(D:qROF(X){\kern 1pt} {\kern 1pt} \times qROF(X) \to \left[ {0,1} \right]\), \(D\left( {A,B} \right)\) is a distance between \(A \in qROF\left( X \right)\) and \(B \in qROF\left( X \right)\) if \(D\left( {A,B} \right)\) satisfies:
-
(A1)
\(0 \le D\left( {A,B} \right) \le 1\)
-
(A2)
\(D\left( {A,B} \right) = 0\) if and only if \(A = B\)
-
(A3)
\(D\left( {A,B} \right) = D\left( {B,A} \right)\)
-
(A4)
If \(A \subseteq B \subseteq C\) then \(D(A,C) \ge D(A,B)\)
3 A novel distance measure between q-rung orthopair fuzzy sets
A new distance measure between q-ROFs with its proofs and the interpretation of the proposed novel distance measure is given in this section. Moreover, the comparison of the proposed distance measure with the existing distance measures is performed to illustrate the superiority of the proposed distance measure.
3.1 Proposal and the proof of the novel distance measure
Let A and B be two q-ROFs in X where \(X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}\). The proposed novel distance measure is defined as follows:
where p = 1,2,…,n and
Here, \(p\) is the \(L_{p}\) norm, and k is a parameter of uncertainty, are explained in detail in Sect. 3.2.
Theorem 1
\(D\left( {A,B} \right)\)is the distance between two q-ROFs\(A\)and\(B\)in\(X\).
Proof
A(1) Let \(A\) and \(B\) be two q-ROFs.
It is known that \(0 \le \mu_{A} (x_{i} ) \le 1\), \(0 \le \mu_{B} \le 1\) and \(k \in \left[ {\frac{1}{3},\frac{1}{2}} \right]\) then
It is easy to see that:
Since \(0 \le v_{A} (x_{i} ) \le 1\) and \(0 \le v_{B} (x_{i} ) \le 1\) then \(0 \le v_{A}^{q} (x_{i} ) \le 1\) and \(0 \le v_{B}^{q} (x_{i} ) \le 1\) are also true. Moreover, based on \(0 \le 1 - v_{A}^{q} (x_{i} ) \le 1\) and \(0 \le 1 - v_{B}^{q} (x_{i} ) \le 1\), \(0 \le \sqrt[q]{{(1 - v_{A}^{q} (x_{i} ))}} \le 1\) and \(0 \le \sqrt[q]{{(1 - v_{B}^{q} (x_{i} ))}} \le 1\) are obtained. Consequently, we get: \(- 1 \le \sqrt[q]{{1 - v_{A}^{q} (x_{i} )}} - \sqrt[q]{{1 - v_{B}^{q} (x_{i} )}} \le 1\) and product this inequation with k we get Eq. (16) as follows:
So, with the Eqs. (15) and (16) we can have the following inequality:
Hence, \(- 1 \le \left( {(1 - k)(\mu_{A} (x_{i} ) - \mu_{B} (x_{i} )) + k\left( {\sqrt[q]{{1 - v_{A}^{q} (x_{i} )}} - \sqrt[q]{{1 - v_{B}^{q} (x_{i} )}}} \right)} \right) \le 1\) because of the absolute value it becomes:
Second part of the formula indicated below is also similar with the first part,
As \(0 \le v_{A} (x_{i} ) \le 1\), \(0 \le v_{B} \le 1\) and \(k \in \left[ {\frac{1}{3},\frac{1}{2}} \right]\) then \(- 1 \le v_{A} (x_{i} ) - v_{B} (x_{i} ) \le 1\), \(1 - k > 0\), therefore, Eq. (20) is obtained as follows:
If \(0 \le \mu_{A} (x_{i} ) \le 1\) and \(0 \le \mu_{B} (x_{i} ) \le 1\), then \(0 \le \mu_{A}^{q} (x_{i} ) \le 1\) and \(0 \le \mu_{B}^{q} (x_{i} ) \le 1\) are also true. Furthermore, based on \(0 \le 1 - \mu_{A}^{q} (x_{i} ) \le 1\) and \(0 \le 1 - \mu_{B}^{q} (x_{i} ) \le 1\) the following inequalities are obtained \(0 \le \sqrt[q]{{(1 - \mu_{A}^{q} (x_{i} ))}} \le 1\) and \(0 \le \sqrt[q]{{(1 - \mu_{B}^{q} (x_{i} ))}} \le 1\).
Consequently, \(- 1 \le \sqrt[q]{{1 - \mu_{A}^{q} (x_{i} )}} - \sqrt[q]{{1 - \mu_{B}^{q} (x_{i} )}} \le 1\) and product this inequality with k we get Eq. (21) as follows:
Integrating Eqs. (20) and (21), the following inequality is held:
and it becomes:
Finally, from Eqs. (18) and (23), Eq. (24) is obtained as follows:
Therefore, the distance between A and B we have the inequality of \(1 \ge D(A,B) \ge 0\).
A(2) Let A and B be two q-ROFs then \(\mu_{A} (x_{i} ) = \mu_{B} (x_{i} )\), \(v_{A} (x_{i} ) = v_{B} (x_{i} )\) and \(\mu_{A} (x_{i} ) - \mu_{B} (x_{i} ) = 0\), \(v_{A} (x_{i} ) - v_{B} (x_{i} ) = 0\). Thus, D(A, B) is equal to zero.
A(3) Let A and B be two q-ROFs then the first part of the formula is as follows:
Based on the absolute value, Eq. (26) is expressed as follows:
The second part is also similar:
Based on the absolute value, Eq. (28) is expressed as follows:
Thus we can conclude that D(A, B) is equal to D(B, A).
A(4) Let A, B, and C be three q-ROFs, the formula of the distance measure between A, B and A, C are respectively given below:
If \(A \subseteq B \subseteq C\) then \(\mu_{C} (x_{i} ) \ge \mu_{B} (x_{i} ) \ge \mu_{A} (x_{i} )\) and \(v_{A} (x_{i} ) \ge v_{B} (x_{i} ) \ge v_{C} (x_{i} )\) and \(k \in \left[ {\frac{1}{3},\frac{1}{2}} \right]\) so \(1 \ge \mu_{C} (x_{i} ) \ge \mu_{B} (x_{i} ) \ge \mu_{A} (x_{i} ) \ge 0\), \(1 \ge v_{A} (x_{i} ) \ge v_{B} (x_{i} ) \ge v_{C} (x_{i} ) \ge 0\) and \(1 > 1 - k > 0\) are held.
Moreover, \(\left| {\mu_{C} (x_{i} ) - \mu_{A} (x_{i} )} \right| \ge \left| {\mu_{B} (x_{i} ) - \mu_{A} (x_{i} )} \right|\) is held and Eq. (31) is obtained as follows:
If \(v_{A} (x_{i} ) \ge v_{B} (x_{i} ) \ge v_{C} (x_{i} )\) then \(v_{A}^{q} (x_{i} ) \ge v_{B}^{q} (x_{i} ) \ge v_{C}^{q} (x_{i} )\) and \(1 - v_{A}^{q} (x_{i} ) \le 1 - v_{B}^{q} (x_{i} ) \le 1 - v_{C}^{q} (x_{i} )\). Inequality given in Eqs. (32) and (33) are easily held as follows:
Consequently, with Eqs. (31) and (33) we obtain Eq. (34) as follows:
For the second part of the formula, as \(|v_{C} (x_{i} ) - v_{A} (x_{i} )| \ge |v_{B} (x_{i} ) - v_{A} (x_{i} )|\) and \(1 > 1 - k > 0\) Eq. (35) is held:
If \(\mu_{A} (x_{i} ) \ge \mu_{B} (x_{i} ) \ge \mu_{c} (x_{i} )\) then \(\mu_{A}^{q} (x_{i} ) \ge \mu_{B}^{q} (x_{i} ) \ge \mu_{C}^{q} (x_{i} )\) and \(1 - \mu_{A}^{q} (x_{i} ) \le 1 - \mu_{B}^{q} (x_{i} ) \le 1 - \mu_{C}^{q} (x_{i} )\) Moreover, it is easy to see that \(\sqrt[q]{{(1 - \mu_{A}^{q} (x_{i} ))}} \le \sqrt[q]{{(1 - \mu_{B}^{q} (x_{i} ))}} \le \sqrt[q]{{(1 - \mu_{C}^{q} (x_{i} ))}}\). Therefore, the following inequality is determined as follows:
Consequently, with Eqs. (35) and (36) we obtain Eq. (37) as follows:
Finally, with the Eqs. (34) and (37), it is easy to say that \(D(A,C) \ge D(A,B)\). Similarly, \(D(A,C) \ge D(B,C)\) is also held. As the conditions (A1)–(A4) are satisfied, \(D\left( {A,B} \right)\) is a distance measure between q-ROFs A and B.
Theorem 2
\(D_{w} \left( {A,B} \right)\)is a weighted distance measure between two q-ROFs\(A\)and\(B\)in\(X\).
where p = 1,2,…,n and\(k = {{\left( {\frac{1}{2}q^{2} + \frac{3}{2}q - \frac{1}{3}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{1}{2}q^{2} + \frac{3}{2}q - \frac{1}{3}} \right)} {\left( {q^{2} + 3q + 1} \right)}}} \right. \kern-0pt} {\left( {q^{2} + 3q + 1} \right)}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k \in \left[ {\frac{1}{3},\frac{1}{2}} \right]\)also, \(w_{i}\)is the weights of the features\(\left( {x_{i} } \right)\)\(w_{i} \in \left[ {0,1} \right]\)and\(\sum\nolimits_{i = 1}^{n} {w_{i} = 1}\)
Proof
A(1) If we obtain the product of Eq. (18) with \(w_{i}\), then we can easily have:
The following inequality, based on Eq. (39), can be written as:
So, it’s easy to see that \(\sum\nolimits_{i = 1}^{n} {w_{i} }\) is equal to 1 since \(\sum\nolimits_{i = 1}^{n} {w_{i} = 1}\). Equivalently, if we product Eq. (23) with \(w_{i}\), we have:
The following inequality, based on Eq. (41), can be written as:
So, it’s easy to see that \(\sum\nolimits_{i = 1}^{n} {w_{i} }\) is equal to 1 in since \(\sum\nolimits_{i = 1}^{n} {w_{i} = 1}\). Finally, we obtain the following inequality using Eqs. (40) and (42) that:
Thus, \(0 \le D_{w} \left( {A,B} \right) \le 1\).
A(2) Let A and B be two q-ROFs then \(\mu_{A} (x_{i} ) = \mu_{B} (x_{i} )\), \(v_{A} (x_{i} ) = v_{B} (x_{i} )\) and \(\mu_{A} (x_{i} ) - \mu_{B} (x_{i} ) = 0\), \(v_{A} (x_{i} ) - v_{B} (x_{i} ) = 0\). Therefore, the weighted distance measure \(D_{w} \left( {A,B} \right)\) is equal to zero.
A(3) If we product both sides defined in Eqs. (26) and (28) with \(w_{i}\) we have Eqs. (44) and (45) as follows:
Thus, \(D_{w} \left( {A,B} \right) = D_{w} \left( {B,A} \right)\).
A(4) If we product Eqs. (34) and (37) with \(w_{i}\), we have
Since all \(w_{i} \ge 0\), consequently, we obtain the following inequality \(D_{w} \left( {A,C} \right) \ge D_{w} \left( {A,B} \right)\). Similarly, \(D_{w} \left( {A,C} \right) \ge D_{w} \left( {B,C} \right)\) is also held. So, finally, we conclude that \(D_{w} \left( {A,B} \right)\) is a distance measure between q-ROFs A and B since \(D_{w} \left( {A,B} \right)\) satisfies (A1)–(A4).
3.2 Interpretation of the novel distance measure
Under this sub-section, we interpret the proposed distance measure and analyze the usage of parameter k defined in the formula.
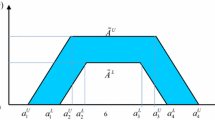
Let \(\left( {\mu_{A} (x),v_{A} (x)} \right)\) and \(\left( {\mu_{B} (x),v_{B} (x)} \right)\) be two q-ROFNs. The basic formula of distance measure is:
As can be easily seen in Fig. 2:
where
The parameter k is related to the shape of the area construed by order of q. If q = 1 then q-ROFs is IFS and the area of ROP becomes a triangle. Then the parameter k is equal to \(\frac{1}{3}\) using the formula. When q = 2, q-ROFs is Pythagorean fuzzy set, and the area of ROP becomes a quarter circle. Consequently, parameter k is equal to 0.424242 using the formula. For q = ∞, the area of ROPS becomes a rectangle, and then the parameter k is equal to \(\frac{1}{2}\) since \(\mathop {\lim }\nolimits_{q \to \infty } \left\{ {\left( {\frac{1}{2}q^{2} + \frac{3}{2}q - \frac{1}{3}} \right)/(q^{2} + 3q + 1)} \right\} = \frac{1}{2}\). Actually, the formula for k gives the centre of gravity of different shapes that are constructed by different qth order.
It is observed that the hesitation degree (π) in a q-ROF set is bigger than in PFS and IFS as the q increases. In order to solve this problem, the hesitation degree is distributed to the membership \((\mu )\) and non-membership \((v)\) degrees in the abovementioned distance measure. Based on this idea, we get the following equation as follows:
Then we can simplify the first part of the equation as below:
We can use the same method for the second part:
Therefore with the abovementioned Eqs. (51) and (52), we can easily get the simplified distance measure as below:
where p = 1,2,3,…,n and
3.3 A comparison of the similarity measures
In this subsection, a comparison between our proposed distance measure and existing measures in the literature (Table 1) is conducted. Most of the distance measures are proposed for IFS; however, we also take into consideration the study of Du [11] for Minkowski-type distance measures for generalized orthopair fuzzy sets.
3.3.1 IFS similarity measures
In order to use the same term, we convert our proposed distance measure to similarity measure [S(A, B)] using the below formula:
Table 2 presents a comparison of the similarity measures with counter-intuitive examples (p = 1 in SHB, \(S_{e}^{p}\), \(S_{s}^{p}\), \(S_{h}^{p}\)). It is obvious that the second axiom (A2) is not satisfied by SC (A, B), SDC (A, B), CIFS (A, B) since SC (A, B) = SDC (A, B) = CIFS (A, B) = 1 when A = (0.3,0.3) and B = (0.4, 0.4). In a similar way (A2) is not satisfied by SC (A, B), SDC (A, B) when A = (0.5, 0.5), B = (0, 0) and A = (0.4, 0.2), B = (0.5, 0.3). Some similarity measures do not distinguish positive difference from negative difference, SH (A, B) = SH (C, D) = 0.9 when A = (0.3, 0.3), B = (0.4, 0.4), C = (0.3, 0.4) and D = (0.4, 0.3). The same counter-intuitivity might be seen in SO, SHB, \(S_{e}^{p}\), \(S_{h}^{p}\), \(S_{HY}^{1}\), \(S_{HY}^{2}\) and \(S_{HY}^{3}\). Another counter-intuitive problem occurs when \(A = (1,0)\), \(B = (0,0)\), \(C = (0.5,0.5)\) so both \(S_{H} (A,B)\) and \(S_{H} (C,B)\) are equal to 0.5. It also occurs for SHB, \(S_{e}^{p}\) and CIFS. Likewise SL (A, B) = SL (A, C) = 0.95 when A = (0.4, 0.2), B = (0.5, 0.3), C = (0.5, 0.2).
Another problem occurs when we take A = (0.4, 0.2), B = (0.5, 0.3), C = (0.5, 0.2). We expect the similarity between A and B should be equal or greater than the similarity between A and C, since \(C \ge B \ge A\) according to score function and accuracy function. However, it does not occur when SH, SO, SHB, \(S_{e}^{p}\) and \(S_{h}^{p}\) are used.
3.3.2 Comparison of existing q-ROF similarity measures
There are a few similarity measures related to q-ROF numbers. Du [11] mentioned as Minkowski-type similarity measures Hamming (SHamming) and Euclid (SEuclid). Wang et al. [40] proposed two similarity measures based on cosine measures. In the comparison study, the value of q is equal to 3 for all similarity measures, and the value of p is equal to 1 in the proposed distance measure.
When the results of the Hamming (SHamming) are examined, it is observed that many counter-intuitive results exist. It is easy to see that Hamming similarity measure does not satisfy the fourth axiom (A4) in the first four cases presented in Table 3. For example, in the first case, q-ROF numbers are A = (0, 0.5), B = (0.5, 0.6) and C = (0.4, 0.2) and it is expected that S(A, C) > S(A, B) and S(A, C) > S(B, C) since C > B > A, according to their score function. Therefore, S(A, C) should be smaller or equal to both S(A, B) and S(B, C) according to the fourth axiom (A4). However, SHamming (A, C) has the greatest value among the three values. Similar counter-intuitive results occur in the second, third and fourth cases in which C > B > A; however, SHamming (A, C) is greater than SHamming (A, B) and SHamming (B, C). Last but not least, Hamming similarity measure does not distinguish positive difference from negative difference, as it is seen in fifth and sixth groups when in fifth group A = (0.3, 0.3), B = (0.4, 0.4) and in the sixth group A = (0.3, 0.4) and B = (0.4, 0.3) and their both results are equal as S(A, B) = 0.963.
Euclid distance also does not satisfy the fourth axiom (A4). As it is seen in Table 4, in the first case, A = (0.1, 0.9), B = (0.1, 0.6), C = (0.7, 0.8) and C > B > A according to their score function. SEuclid (A, C) should be the smallest value; however, SEuclid (A, C) is greater than both SEuclid (A, B) and SEuclid (B, C). Therefore, Euclid distance does not satisfy the fourth axiom (A4). Similarly, in the second, third and fourth cases C > B > A, SEuclid (A, C) is the greatest among three similarities and therefore, the first four cases do not satisfy the fourth axiom (A4). Euclid similarity measure does not distinguish positive difference from negative difference like Hamming measure. For example, in the fifth and the sixth groups respectively A = (0.3, 0.3), B = (0.4, 0.4) and A = (0.3, 0.4), B = (0.4, 0.3). Even they are all different numbers, their similarity results are equal as SEuclid (A, B) = 0.963.
Wang et al. [40] proposed two q-ROF cosine similarity measures called q-ROFC1 and q-ROFC2 which have many counter-intuitive results. For example, the “division by zero” problem occurs in both S1q-ROFC and S2q-ROFC as indicated in the sixth case presented in Table 5. Another problem is observed both in S1q-ROFC and S2q-ROFC , in the fourth and fifth cases in which C > B > A according to their score and accuracy function. Therefore S(A, C) should be smaller or equal to both S(A, B) and S(B, C) considering the fourth axiom (A4). However, in the fourth cases where A = (0.7, 0.8), B = (0.1, 0.2), C = (0.8, 0.2), as C > B > A, both similarity measures S1q-ROFC and S2q-ROFC do not satisfy the fourth axiom (A4) as S(A,C) has the greatest value among all. The same problem occurs in the fifth case in both similarity measures of S1q-ROFC and S2q-ROFC .
Moreover, the S1q-ROFC does not distinguish similarity in the first three cases presented in Table 5. In the second and third cases, S1q-ROFC is equal to one, means that two q-ROF numbers are the same numbers, which is unreasonable. This result violates the second axiom (A2), which requires “\(S\left( {A,B} \right) = 1\) if and only if \(A = B\)”. For example, the numbers given as A = (0.2, 0.1), B = (0.8, 0.4), C = (0.4, 0.2) in the second case and A = (0.4, 0), B = (0.8, 0), C = (0.5, 0) in the third case are different q-ROF numbers. Another counter-intuitive result is seen in the first case as the numbers are A = (0.8, 0), B = (0, 0.3), C = (0.9, 0) the similarity measures are S(A, B) = S(B, C) = 0 which is also an unreasonable result. Therefore, it is obvious that all existing q-ROF similarity measures have many counter-intuitive results which can be easily seen in Tables 3, 4 and 5. Finally, our proposed q-ROF distance measure has no counter-intuitive situation.
4 Application of novel distance measure for proposed models
In this section, we propose two new and separate q-ROF MCDM methods which are q-ROF TOPSIS and q-ROF ELECTRE methods. We used our novel distance measure in both proposed methods.
4.1 Application of q-ROF TOPSIS method
Let \({\text{A }} = \, \left\{ {A_{1} ,A_{2} ,A_{3} , { } \ldots ,{\text{A}}_{m} } \right\}\) be a set of alternatives and \({\text{X }} = \, \left\{ {X_{1} ,X_{2} ,X_{3} , { } \ldots \, ,{\text{X}}_{n} } \right\}\) be a set of criteria, the steps of the TOPSIS method for q-Rung Orthopair Fuzzy Sets are given below [4]:
Step 1. Determine the weights of decision-makers (DMs).
The ranking of DMs is declared as linguistic terms are expressed in q-rung orthopair fuzzy numbers. Let \(D_{k} = \left[ {\mu_{k} (x),v_{k} (x),\pi_{k} (x)} \right]\) be a q-ROF number to evaluate the performance of kth of the l decision-maker. The score function [41, 44] of the q-ROF number introduced in Eq. (9) can be used to rate the kth decision-maker as follows:
and \(\sum\nolimits_{k = 1}^{l} {\lambda_{k} } = 1.\)
Step 2. Aggregate the ratings of alternatives based on DMs opinions.
At the beginning DMs rate the alternatives with the linguistic terms. Then, these terms converted to a q-ROF number. Suppose \(\alpha_{k} = \left\langle {\mu_{k} (x),v_{k} (x)} \right\rangle (k = 1,2,3, \ldots ,l)\) is a collection of q-ROF numbers are aggregated with DM weights (\(\lambda_{k}\)) with q-ROFWA operator proposed by [Liu and Wang [24]] indicated as follows:
The aggregated q-ROF decision matrix (R) can be described as follows:
\({\text{R}} = ( {\text{r}}_{ij} )_{mxn} ,\) where \(\left( {\mu_{{A_{i} }} (x_{j} ),v_{{A_{i} }} (x_{j} ),\pi_{{A_{i} }} (x_{j} )} \right)\), \(( {\text{i = 1, 2, }} \ldots {\text{ , m; j = 1, 2, }} \ldots , {\text{ n)}} .\)
Step 3. Determine the importance weights of the evaluation criteria.
The criteria might have different importance degrees. W indicates an importance degree. To obtain W, we get the ratings of all DMs individually in linguistic terms, convert them into q-ROF numbers and calculate their score functions with below formula of Eq. (57):
Step 4. Build an aggregated weighted q-ROF decision matrix.
After q-ROF decision matrix is implemented with the weights, the aggregated weighted q-ROF decision matrix (R′) is built as follows [24]:
\(r_{ij}^{\prime } = (\mu_{ij}^{\prime } ,v_{ij}^{\prime } ,\pi_{ij}^{\prime } ) = \left( {\mu_{{A_{i} W}} (x_{j} ),v_{{A_{i} W}} (x_{j} ),\pi_{{A_{i} W}} (x_{j} )} \right)\) is an element of the aggregated weighted q-ROF decision matrix where \(( {\text{i = 1,2,3, }} \ldots , {\text{m; j = 1,2,3, }} \ldots , {\text{ n)}} .\)
Step 5. Defining the q-ROF Positive Ideal Solution (q-ROFPIS, A*), and the q-ROF Negative Ideal Solution (q-ROFNIS, \(A^{ - }\)):
When q-ROFPIS allows maximizing the benefit and minimizing the cost, contrarily, q-ROFNIS minimizes the benefit and maximizes the cost attributes. Let \(J_{1} {\text{and}} J_{2}\) respectively, be benefit and cost criteria. A* is q-ROFPIS and \(A^{ - }\) is q-ROFNIS. So, A* and \(A^{ - }\) can be obtained as:
Step 6. Calculate the separation measures to the positive and negative ideal solutions.
In order to calculate separation between alternatives on q-ROFs, the new distance measure that we suggested in Sect. 3 is used for q-ROF numbers. The separation measures, \({\text{S}}_{\text{i}}^{*}\) and \(S_{i}^{ - }\), of each alternative from q-ROFPIS and q-ROFNIS are calculated in Eq. (64):
where p = 1, 2, …,n and
Step 7. Calculate the relative closeness coefficient (\(C_{i*}\)).
\(C_{i*}\) is calculated for the q-ROF ideal solution as follows:
Step 8. Rank the alternatives.
After the relative closeness coefficients are determined, to make the decision, we can rank the alternatives using a descending order of \(C_{i*}\)’s.
4.2 Application of q-ROF ELECTRE method
Q-ROF ELECTRE method has eight steps which are presented as follows [46].
Step 1. Determine the q-ROF ELECTRE decision matrix.
As we did in TOPSIS Step 2 DMs rate the alternatives with the linguistic terms, and they converted to a q-ROF number given as in step 2 of TOPSIS method. The aggregated q-ROF decision matrix can be described as follows:
\({\text{R}} = ({\text{r}}_{ij} )_{mxn} ,\) where \(\left( {\mu_{{A_{i} }} (x_{j} ),v_{{A_{i} }} (x_{j} ),\pi_{{A_{i} }} (x_{j} )} \right)\), \(( {\text{i = 1, 2, }} \ldots {\text{ , m; j = 1, 2, }} \ldots , {\text{ n)}} .\)
The attributes have subjective importance, W, like q-ROF TOPSIS, the sum of the weight of attributes \(x_{1}\) to \(x_{n}\) is equal to 1.
Step 2. Determine the sets of concordance and discordance.
Concordance sets show the preferences in each pair of the alternatives like Alternate k to Alternate l and can be classified as strong, moderate and weak concordance sets.
The strong concordance set \({\text{C}}_{kl} {\text{ of A}}_{k} {\text{ and A}}_{l}\) is composed of the criteria in which \({\text{A}}_{k}\) is better than \({\text{A}}_{l}\) and can be formulated as
The moderate concordance set \({\text{C}}_{kl}^{\prime }\) is:
The weak concordance set \({\text{C}}_{kl}^{\prime \prime }\) is:
On the contrary of concordance sets, discordance set \({\text{D}}_{kl}\) shows the criteria for which Alternative k is not preferred to Alternative l. So, the strong discordance set \({\text{D}}_{kl}\) can be formulated as:
The moderate discordance set \({\text{D}}_{kl}^{\prime }\) can be formulated as:
Finally, the weak discordance set \({\text{D}}_{kl}^{\prime \prime }\) can be formulated as:
The decision-makers give the weight of these sets according to their importance. The weights of \({\text{C}}_{kl} , {\text{ C}}_{kl}^{\prime } , {\text{ C}}_{kl}^{\prime \prime } {\text{ and D}}_{kl} ,{\text{D}}_{kl}^{\prime } , {\text{ D}}_{kl}^{\prime \prime }\) are \({\text{W}}_{C} , {\text{ W}}_{{C^{\prime } }} , {\text{ W}}_{{C^{\prime \prime } }} , {\text{W}}_{D} , {\text{ W}}_{{D^{\prime } }} {\text{ and W}}_{{D^{\prime \prime } }}\) respectively.
Step 3. Calculate the concordance matrix.
The concordance set is calculated based on concordance index, which is equal to the sum of the weights related to the criteria in the concordance set. The concordance index might be calculated as follows:
where \({\text{W}}_{j}\) is the weight of attributes defined in Step 1 and \({\text{W}}_{C} , {\text{ W}}_{{C^{'} }} , {\text{ W}}_{{C^{''} }}\) are weights which are defined in Step 2.
Step 4. Calculate the discordance matrix.
The discordance index \({\text{d}}_{kl}\) is formulated as:
For \(dis(X_{kj} ,X_{lj} )\) distance measure which was proposed in Sect. 4 is used.
Step 5. Calculate the concordance dominance matrix.
The concordance dominance matrix is obtained based on the threshold value of the concordance index, which is the average value of the matrix. When the concordance index \({\text{C}}_{kl}\) exceeds the threshold value \(\bar{c}\), as an example, \(c_{kl} \, \ge \bar{c}\), and
Based on \(\bar{c}\), the concordance dominance matrix F might be constructed, the elements of which can be defined as:
Then each element of 1 in matrix F shows the dominance of one alternative to another.
Step 6. Calculate the discordance dominance matrix.
Similar to the previous matrix it is determined by a threshold value \(\bar{d}\) and the elements of \(g_{kl}\) of the discordance dominance matrix G is defined as:
Step 7. Calculate the aggregate dominance matrix.
In this step, the intersection of both concordance and discordance dominance matrices is determined as an aggregate dominance matrix, E, its elements defined \(e_{kl}\) by the formula of:
Step 8. Eliminate the less favorable alternatives.
In matrix E, \(e_{kl} = 1\) implies that \(A_{k} {\text{ is preferred to }}A_{l}\) by utilizing both concordance and discordance dominance matrices values; however, \(A_{k}\) might be dominated by the other alternatives. If any column of the matrix E has at least one value of 1, it is “ELECTREcally” dominated by the related row(s). Therefore; we eliminate any column(s) which has the value of 1.
4.3 Using q-ROF TOPSIS for ranking the alternatives
If ELECTRE method cannot rank all the alternatives as required, we may use some of the steps of q-ROF TOPSIS to rank the alternatives. It is better to integrate TOPSIS index to our q-ROF ELECTRE with below steps starting from Step 5.
Step 5b. Calculate concordance dominance matrix using positive ideal solution of TOPSIS.
As \(c^{*}\) is the biggest value in the matrix, we calculate:
Then the concordance dominance matrix \(C^{'}\) is constructed.
Step 6b. Calculate discordance dominance matrix like in Step 5b.
As \(d^{*}\) is the biggest value we calculate:
Then the concordance dominance matrix \(D^{\prime }\) is obtained.
Step 7b. Calculate the aggregate dominance matrix U.
The aggregate dominance matrix U is constructed based on Eqs. (80) and (81) as follows:
Any element (\(u_{kl}\)) of U is defined as:
Step 8b. Determine the best option.
The average value of \(u_{kl}\) is computed in Eq. (82) as follows:
The best alternative \(A^{*}\) can be determined by Eq. (83) as follows:
Then the alternatives are ranked in descending order of \(A_{j}\)’s.
5 A numerical example for supplier selection
In this section, a numerical example is given to illustrate the application of the proposed models both q-ROF TOPSIS and q-ROF ELECTRE, and then compare the result of the proposed models with the existing models in the literature. Furthermore, the effect of parameters p and q in both methods is dealt with in this section.
5.1 Numerical example with q-ROF TOPSIS
A construction company intends to select the best supplier for construction materials like concrete, marble, ceramics, and installation of these materials to its structures. After pre-evaluation, eight suppliers qualified for the final evaluation. So, three DMs have been selected as an expert to evaluate these eight suppliers. Ten evaluation criteria are determined under three criteria groups of [15] economic, environmental, and social criteria are listed in Table 6 (The value of q is equal to 3):
Step 1. Determine the weights of DMs
The multiple criteria group decision making importance degrees of DMs were shown in Table 7. Linguistic terms used for the ratings of the DMs and criteria are given in Table 8. DMs weighting formula introduced in Eq. (55) is calculated as follows:
Step 2. Aggregate the ratings of alternatives based on DMs opinions.
Three DMs evaluate eight suppliers concerning ten criteria. Linguistic terms of DMs evaluation are converted to q-ROF numbers according to Table 8. The ratings of the alternatives both in linguistic terms are shown in Table 9.
These ratings, which are q-ROF numbers, are aggregated with DM weights (\(\lambda_{k}\)) with q-ROFWA operator proposed by Liu and Wang [24] indicated in Eq. (55). Consequently, we might obtain an aggregated q-ROF decision matrix (RTOPSIS), which is shown below.
Step 3. Determine the importance weights of the evaluation criteria.
Ratings of all DMs individually in linguistic terms are converted into q-ROF numbers and calculate their score functions with the Eq. (57). After the criteria group weights are determined, each of the ten individual criteria weights are calculated with the same procedure. All calculations for the weights of criteria are shown in Tables 10, 11 and 12.
Step 4. Construct an aggregated weighted q-rung orthopair fuzzy decision matrix.
After the weights of criteria (W) and the aggregated q-ROF decision matrix are implemented, the aggregated weighted q-ROF decision matrix (R′) is built with Eqs. (57) and (58) and indicated above.
Step 5. Defining the q-ROF Positive–Negative Ideal Solutions
All criteria other than C4 (Cost) and C7 (Water/Energy Consumption) are benefit criteria. Then the q-ROF positive-ideal solution A* and the q-ROF negative-ideal solution \(A^{ - }\) were obtained with the Eqs. (59)–(63) and presented as follows:
Step 6. Calculate the separation measures to the positive and negative ideal solutions.
In order to calculate separation between alternatives on q-rung orthopair fuzzy set, a novel distance measure which is proposed in Sect. 3 is used and below distances are calculated.
The separation measures, \({\text{S}}_{\text{i}}^{*}\) and \(S_{i}^{ - }\), are calculated according to Eq. (64) with p = 1 and shown in Table 13.
Step 7. Calculate the relative closeness coefficient (\(C_{i*}\)).
\(C_{i*}\) is calculated with the formula presented in Eq. (65) and shown in Table 13.
Step 8. Rank the alternatives.
After the separation measures \({\text{S}}_{\text{i}}^{*}\) and \(S_{i}^{ - }\) finally, the relative closeness coefficients are determined, we might rank the alternatives due to the descending order of \(C_{i*}\)’s. Ranks, from best to worst suppliers are respectively, A1 > A6 > A3 > A8 > A2 > A7 > A4 > A5.
5.2 Numerical example with q-ROF ELECTRE
Same case study problem is solved by the q-ROF ELECTRE method. We have used the same DM’s evaluation and weights which are given for q-ROF TOPSIS method in the previous section.
Step 1. The q-ROF decision matrix (RELECTRE) was calculated in the previous section is used after cost criteria converted to benefit criteria:
The weights of criteria given by the decision-makers are:
Step 2. Calculate the concordance and discordance sets.
The DM’s give the relative weight for strong, moderate and weak concordance and discordance sets as below:
Therefore, we can determine the strong concordance set (Ckl):
In the strong concordance set, Alternative 4 is preferred to Alternative 2 strongly regarding 2nd and 6th criteria values considering \(C_{42} = \left\{ {2,6} \right\}\). We can determine the moderate (\(C_{kl}^{\prime }\)) and weak (\(C_{kl}^{\prime \prime }\)) concordance sets as below:
The strong discordance set (\(D_{kl}\)) is obtained as follows:
The medium (\(D_{kl}^{\prime }\)) and weak (\(D_{kl}^{\prime \prime }\)) discordance sets are determined as follows:
Step 3. Calculate the concordance matrix.
The concordance matrix is constructed as follows:
To illustrate how the value in the concordance matrix, c38 is computed as follows:
Step 4. Calculate the discordance matrix.
The discordance matrix is constructed as follows:
To illustrate how the value in the concordance matrix is determined, d13 is computed as follows:
Step 5. Calculate the concordance dominance matrix (F).
The average value for concordance index is computed as follows:
The concordance dominance matrix is constructed as follows:
Step 6. Calculate the discordance dominance matrix (G).
The average value for discordance index is computed as follows:
The discordance dominance matrix is constructed as follows:
Step 7. Determine the aggregate dominance matrix (E).
The aggregate dominance matrix is obtained as follows:
Step 8. Eliminate the less favourable alternatives:
In matrix E, the overranking relationships are obtained and illustrated in Fig. 3 as follows:
As the ranking is not certain, q-ROF TOPSIS ranking process is used.
Step 5b. Calculate concordance outranking matrix.
The concordance outranking matrix is obtained as follows:
which is \(c^{*} = 0.733\).
Step 6b. Calculate discordance outranking matrix.
The discordance outranking matrix is determined as follows:
which is \(d^{*} = 1\).
In Step 7b. Calculate the aggregate outranking matrix.
The aggregate outranking matrix is obtained as follows:
Step 8b. Determine the best alternative.
The values of the alternatives are: \(\bar{u}_{1} = 0.536 , { }\bar{u}_{2} = 0. 1 9 1 ,\)\(\, \bar{u}_{3} = 0.643 , { }\bar{u}_{4} = 0.202 , { }\bar{u}_{5} = 0 , { }\)\(\bar{u}_{6} = 0. 5 0 4 , { }\)\(\bar{u}_{7} = 0. 0 7 6 , { }\bar{u}_{8} = 0.518. \,\) The optimal ranking is \(A_{3} \succ A_{1} \succ A_{8} \succ A_{6} \succ A_{4} \succ A_{2} \succ A_{7} \succ A_{5}\).
5.3 Comparison of proposed methods with the existing ones
5.3.1 Existing methods
Liu and Wang [24] proposed two decision-making methods based on q-ROF aggregation operators, which are q-ROFWA and q-ROFWG operators (Definition 6 and 7, respectively). In both decision-making methods, the steps are the same except the part aggregate operators are used. The steps are briefly introduced as follows.
Step 1. Normalize the aggregated weighted q-ROF decision matrix defined in q-ROF TOPSIS at Step 4. As two different types of criteria, cost, and benefit exist, it is needed to convert cost type of criteria to benefit one using the following equation as:
Step 2. Aggregate all criteria values to the comprehensive value by q-ROFWA (first method) or q-ROFWG (second method) operators as follows:
Step 3. Calculate the score function and accuracy function defined in Eqs. (9) and Eq. (10), respectively.
Step 4. Rank all the alternatives. The bigger \(z_{i}\) (q-ROFN), the better the alternative is.
The methods proposed by Liu and Wang [24] have been applied to our supplier selection problem in the following steps:
Step 1. To normalize the aggregated weighted q-ROF decision matrix.
As the fourth and seventh criteria are cost criteria in our supplier selection problem, they are converted to benefit criteria using Eq. (66).
Step 2. Aggregated all criteria values by q-ROFWA (1st method) and q-ROFWG (2nd method) operators.
\(z_{i}\) (q-ROFNs) for each alternative have been obtained using Eq. (67) and Eq. (68) and shown in Table 14.
Step 3. Calculate the score function and accuracy function
The score function and accuracy function of each alternative have been calculated and presented in Table 15.
Step 4. Rank all the alternatives according to accuracy function and compare with our proposed q-ROF TOPSIS method.
The ranking of alternatives in three different methods have been shown and compared in Table 16.
It can be easily observed that the result of the q-ROFWA method is close to our proposed method. Four of the eight rankings of the q-ROFWA method are the same as the proposed method. On the other hand, when we look at the results of the q-ROFWG method, only the first two rankings are similar (A1 and A6) but in a different order with our proposed method. As q-ROF TOPSIS has considered both q-ROFPIS and q-ROFNIS, it is a compelling method for multiple criteria decision making compared with the q-ROFWA and the q-ROFWG methods.
5.4 Effects of the parameters p and q
5.4.1 The q-ROF TOPSIS method
To analyze the effects of parameters p and q in our q-ROF TOPSIS method, a test is performed using our case study by taking different values of these parameters; for p = (1, 2, 3, 4) and q = (2, 3, 4, 5, 6, 7, 8, 9, 10). The effects of parameters p and q on the closeness coefficient of alternatives and ranking orders are presented in Fig. 4a–d.
In Fig. 4a (where p = 1) increasing q values does not have a great effect on the \(C_{i*}\) values and even the rankings of the alternatives at all. Only \(C_{i*}\) values of A7 decrease when q value increases. In Fig. 4b, c, after q > 2, \(C_{i*}\) values of A2, A3, A4, A6, and A8 are suddenly increasing, \(C_{i*}\) value of A5 is slowly increasing, \(C_{i*}\) value of A1 keeps stable and Ci* value of A7 decreases. In Fig. 4d, \(C_{i*}\) values of A2, A6, and A8 are suddenly increasing, \(C_{i*}\) value of A3, A4, A5 are slowly increasing, \(C_{i*}\) value of A1 keeps stable and \(C_{i*}\) value of A7 decreases when q > 2.
It is easy to see that when all figures are analyzed, A7 is the only option that shows an absolute decline in rankings while q and p parameters are increasing. When we focus on A7 and check the aggregated q-ROF decision matrix µ values (in Sect. 5.1, step 2), we observe that the ratings of A7 have an unstable character which changes more sharply than the other alternatives, namely; in five of the ten criteria A7 has the lowest rating (1st, 5th, and 8–10th), whereas in three of ten criteria (2nd, 3rd, and 6th) it has the best ratings. When q value increases, A7 is far away q-ROFPIS and close to q-ROFNIS and; therefore, \(C_{i*}\) value of A7 decreases; on the other hand, \(C_{i*}\) value of other alternatives increases. Moreover, \(C_{i*}\) value of alternatives except for A7 increases when p value increases since the distance measure between alternatives and PIS and NIS converge to zero. Finally, we may infer that the increase in the value of parameters q or p has a negative effect on unstable rankings. Increase in p value makes the differences between rankings of the alternatives more apparent than the increase in the q value does. The increase of both p and q values not changing the rankings supports our models’ validity. In nearly all cases except for one (p = 4 and q = 10), A1 is the best alternative and A5 is the worst alternative in all situations. So, q-ROF TOPSIS method is more stable when the value of p is equal to one.
The effect of parameter q for the q-ROF TOPSIS method is also analyzed by using Hamming and Euclid distance measures to demonstrate the stability of our proposed distance measure. A test is conducted using our case study by taking values of q (q = 2, 3, 4, 5, 6, 7, 8, 9, 10) for q-ROF TOPSIS using Hamming and Euclid distance measures. The effects are presented in Fig. 5. It can be easily observed that our proposed distance measure is more stable (Fig. 4) because only one alternative (Alt7) ranking is changed for the reasons explained before. However, in Hamming distance (Fig. 5a) ranking of 5 alternatives and in Euclid distance (Fig. 5b) ranking of 6 alternatives changes during the parameter range of q = (2–10).
5.4.2 The q-ROF ELECTRE method
A parameter analyses is made with q (2, 3, 4, 5, 6, 7, 8, 9, 10) and p (1, 2, 3) values. It can be easily seen from Fig. 6 that q-ROF ELECTRE method is more stable than other q-ROF methods since it is not affected by p and q parameters. From 8 alternatives, rankings of only 1 or maximum 2 alternatives are affected, and others remain almost in the same values.
The effect of Hamming and Euclid distance measures in q-ROF ELECTRE is also examined to demonstrate the stability of our proposed distance measure. A test is conducted using Hamming and Euclid distance measures. The effects are presented in Fig. 7. It can be easily observed that rankings which are calculated by our proposed distance measure are close with the rankings of the other two measures.
5.4.3 Existing methods
The effects of the parameter q in the q-ROFWA and the q-ROFWG methods are also analyzed. A test is conducted using our case study by taking different values of q (q = 2, 3, 4, 5, 6, 7, 8, 9, 10). The effects of parameters q on score and accuracy function and ranking orders are presented in Fig. 8a–d. It is easy to see that the score function in both methods converges to 0.5 and the accuracy function in both methods converges to 0 when the value of q increases. Consequently, it’s clear that both methods do not have the capability to differentiate alternatives.
6 Conclusion
Q rung orthopair fuzzy sets (q-ROFs) provides decision-makers more freedom of expression than other fuzzy sets; however, there are very few decision-making methods and distance measures using q-rung orthopair fuzzy sets. To fill this gap, in this paper, first, we proposed a new distance measure between q-ROFs along with proofs. We compared our measure with existing IFS and q-ROF distance measures and proved that ours has no counter-intuitive situation. On the other hand, we observe a drawback that the hesitation degree (π) in a q-ROF set is bigger than in PFS and IFS as the q increases. As a solution, we distributed this hesitation to membership \((\mu )\) and non-membership \((v)\) degrees in the proposed distance measure.
Secondly, we introduced two separate q-ROF multiple criteria group decision-making methods by extending the TOPSIS and ELECTRE methods to “q-ROF TOPSIS” and “q-ROF ELECTRE” methods with the help of our novel distance measure. We compared these two methods with the other existing q-ROF decision-making methods by a comprehensive case study consisting of ten criteria and eight alternatives and then, we have got better results. The advantage of our methods is their being parametric concerning uncertainty. Our observation with the change of the p and q parameters shows us that q-ROF TOPSIS and q-ROF ELECTRE methods crystallize the differences between alternatives and make the results more apparent than the other existing methods and eventually, by differentiating the alternatives they facilitate the decision-making process. Besides these benefits, q-ROF ELECTRE has also an advantage of giving stable results in which the rankings of alternatives are not affected by parameter changes. In further research, our proposed distance measure might be extended to other q-ROF MCDM methods.
References
Atanassov KT (1996) An equality between intuitionistic fuzzy sets. Fuzzy Sets Syst 79:257–258. https://doi.org/10.1016/0165-0114(95)00173-5
Beikkhakhian Y, Javanmardi M, Karbasian M, Khayambashi B (2015) The application of ISM model in evaluating agile suppliers selection criteria and ranking suppliers using fuzzy TOPSIS-AHP methods. Expert Syst Appl. https://doi.org/10.1016/j.eswa.2015.02.035
Boran FE, Akay D (2014) A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition. Inf Sci 255:45–57. https://doi.org/10.1016/j.ins.2013.08.013
Boran FE, Genc S, Kurt M, Akay D (2009) A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst Appl 36:11363–11368. https://doi.org/10.1016/j.eswa.2009.03.039
Chen CT, Lin CT, Huang SF (2006) A fuzzy approach for supplier evaluation and selection in supply chain management. Int J Prod Econ 102:289–301. https://doi.org/10.1016/j.ijpe.2005.03.009
Chen S-M (1995) Measures of similarity between vague sets. Fuzzy Sets Syst 74:217–223
Chen T-Y (2007) A note on distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff metric. Fuzzy Sets Syst 158:2523–2525. https://doi.org/10.1016/j.fss.2007.04.024
Chou S-Y, Chang Y-H (2008) A decision support system for supplier selection based on a strategy-aligned fuzzy SMART approach. Expert Syst Appl 34:2241–2253. https://doi.org/10.1016/j.eswa.2007.03.001
Dengfeng L, Chuntian C (2002) New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recogn Lett 23:221–225
Dickson GW (1966) An analysis of vendor selection systems and decisions. J Purch 2:5–17. https://doi.org/10.1111/j.1745-493X.1966.tb00818.x
Du WS (2018) Minkowski-type distance measures for generalized orthopair fuzzy sets. Int J Intell Syst 33:802–817
Fan L, Zhangyan X (2001) Similarity measures between vague sets. J Softw 12:922–927
Feng F, Fujita H, Ali MI, Yager RR, Liu X (2018) Another view on generalized intuitionistic fuzzy soft sets and related multiattribute decision making methods. IEEE Trans Fuzzy Syst 27:474–488
Feng F, Liang M, Fujita H, Yager RR, Liu X (2019) Lexicographic orders of intuitionistic fuzzy values and their relationships. Mathematics 7:166
Ghoushchi SJ, Milan MD, Rezaee MJ (2018) Evaluation and selection of sustainable suppliers in supply chain using new GP-DEA model with imprecise data. J Ind Eng Int 14:613–625. https://doi.org/10.1007/s40092-017-0246-2
Grzegorzewski P (2004) Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff metric. Fuzzy Sets Syst 148:319–328. https://doi.org/10.1016/j.fss.2003.08.005
Gupta P, Lin C-T, Mehlawat MK, Grover N, Man Systems C (2015) A new method for intuitionistic fuzzy multiattribute decision making. IEEE Trans Syst Man Cybern Syst 46:1167–1179
Haq AN, Kannan G (2006) Fuzzy analytical hierarchy process for evaluating and selecting a vendor in a supply chain model. Int J Adv Manuf Technol 29:826–835. https://doi.org/10.1007/s00170-005-2562-8
Hong DH, Kim C (1999) A note on similarity measures between vague sets and between elements. Inf Sci 115:83–96
Hung W-L, Yang M-S (2004) Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance. Pattern Recogn Lett 25:1603–1611. https://doi.org/10.1016/j.patrec.2004.06.006
Li D, Zeng W (2018) Distance measure of Pythagorean fuzzy sets. Int J Intell Syst 33:348–361. https://doi.org/10.1002/int.21934
Li Y, Zhongxian C, Degin Y (2002) Similarity measures between vague sets and vague entropy. J Comput Sci 29:129–132
Liang Z, Shi P (2003) Similarity measures on intuitionistic fuzzy sets. Pattern Recogn Lett 24:2687–2693. https://doi.org/10.1016/S0167-8655(03)00111-9
Liu PD, Wang P (2018) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J Intell Syst 33:259–280. https://doi.org/10.1002/int.21927
Mardani A, Nilashi M, Zavadskas EK, Awang SR, Zare H, Jamal NM (2018) Decision making methods based on fuzzy aggregation operators: 3 decades review from 1986 to 2017. Int J Inf Technol Decis Mak 17:391–466. https://doi.org/10.1142/S021962201830001x
Memari A, Dargi A, Jokar MRA, Ahmad R, Rahim ARA (2019) Sustainable supplier selection: a multi-criteria intuitionistic fuzzy TOPSIS method. J Manuf Syst 50:9–24. https://doi.org/10.1016/j.jmsy.2018.11.002
Mitchell HB (2003) On the Dengfeng–Chuntian similarity measure and its application to pattern recognition. Pattern Recogn Lett 24:3101–3104
Peng X, Liu L (2019) Information measures for q-rung orthopair fuzzy sets. Int J Intell Syst 34:1795–1834
Rashidi K, Cullinane K (2019) A comparison of fuzzy DEA and fuzzy TOPSIS in sustainable supplier selection: implications for sourcing strategy. Expert Syst Appl 121:266–281. https://doi.org/10.1016/j.eswa.2018.12.025
Rezaei J, Fahim PB, Tavasszy L (2014) Supplier selection in the airline retail industry using a funnel methodology: conjunctive screening method and fuzzy AHP. Expert Syst Appl 41:8165–8179. https://doi.org/10.1016/j.eswa.2014.07.005
Sanayei A, Mousavi SF, Yazdankhah A (2010) Group decision making process for supplier selection with VIKOR under fuzzy environment. Expert Syst Appl 37:24–30. https://doi.org/10.1016/j.eswa.2009.04.063
Shen C-Y, Yu K-T (2013) Strategic vender selection criteria. Procedia Comput Sci 17:350–356. https://doi.org/10.1016/j.procs.2013.05.045
Simic D, Kovacevic I, Svircevic V, Simic S (2017) 50 years of fuzzy set theory and models for supplier assessment and selection: a literature review. J Appl Log 24:85–96. https://doi.org/10.1016/j.jal.2016.11.016
Szmidt E, Kacprzyk J (2000) Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst 114:505–518. https://doi.org/10.1016/S0165-0114(98)00244-9
Verma R, Merigó JM (2019) On generalized similarity measures for Pythagorean fuzzy sets and their applications to multiple attribute decision-making. Int J Intell Syst 34:2556–2583
Verma R, Sharma BD (2012) On generalized intuitionistic fuzzy divergence (relative information) and their properties. J Uncertain Syst 6:308–320
Verma R, Sharma BD (2014) A new measure of inaccuracy with its application to multi-criteria decision making under intuitionistic fuzzy environment. J Intell Fuzzy Syst 27:1811–1824
Vonderembse MA, Tracey M (1999) The impact of supplier selection criteria and supplier involvement on manufacturing performance. J Supply Chain Manag 35:33–39. https://doi.org/10.1111/j.1745-493X.1999.tb00060.x
Wang H, Ju Y, Liu P (2019) Multi-attribute group decision-making methods based on q-rung orthopair fuzzy linguistic sets. Int J Intell Syst. https://doi.org/10.1002/int.22089
Wang P, Wang J, Wei G, Wei C (2019) Similarity measures of q-rung orthopair fuzzy sets based on cosine function and their applications. Mathematics 7:340
Wang R, Li Y (2018) A novel approach for green supplier selection under a q-rung orthopair fuzzy environment. Symmetry 10:687. https://doi.org/10.3390/sym10120687
Wang WQ, Xin XL (2005) Distance measure between intuitionistic fuzzy sets. Pattern Recogn Lett 26:2063–2069. https://doi.org/10.1016/j.patrec.2005.03.018
Weber CA, Current JR, Benton WC (1991) Vendor selection criteria and methods. Eur J Oper Res 50:2–18. https://doi.org/10.1016/0377-2217(91)90033-R
Wei G, Gao H, Wei Y (2018) Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making. Int J Intell Syst 33:1426–1458. https://doi.org/10.1002/int.21985
Wilson EJ (1994) The relative importance of supplier selection criteria: a review and update. Int J Purch Mater Manag 30:34–41. https://doi.org/10.1111/j.1745-493X.1994.tb00195.x
Wu MC, Chen TY (2011) The ELECTRE multicriteria analysis approach based on Atanassov’s intuitionistic fuzzy sets. Expert Syst Appl 38:12318–12327. https://doi.org/10.1016/j.eswa.2011.04.010
Xia MM, Xu ZS (2010) Some new similarity measures for intuitionistic fuzzy values and their application in group decision making. J Syst Sci Syst Eng 19:430–452. https://doi.org/10.1007/s11518-010-5151-9
Xu Z, Chen J (2008) An overview of distance and similarity measures of intuitionistic fuzzy sets. Int J Uncertain Fuzziness Knowl Based Syst 16:529–555. https://doi.org/10.1142/S0218488508005406
Xu Z, Zhao N (2016) Information fusion for intuitionistic fuzzy decision making: an overview. Inf Fusion 28:10–23
Xu ZS, Yager RR (2009) Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group. Fuzzy Optim Decis Mak 8:123–139. https://doi.org/10.1007/s10700-009-9056-3
Yager RR (2014) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22:958–965. https://doi.org/10.1109/Tfuzz.2013.2278989
Yager RR (2017) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25:1222–1230. https://doi.org/10.1109/Tfuzz.2016.2604005
Yager RR, Alajlan N (2017) Approximate reasoning with generalized orthopair fuzzy sets. Inf Fusion 38:65–73. https://doi.org/10.1016/j.inffus.2017.02.005
Ye J (2011) Cosine similarity measures for intuitionistic fuzzy sets and their applications. Math Comput Model 53:91–97
Yu C, Shao Y, Wang K, Zhang L (2019) A group decision making sustainable supplier selection approach using extended TOPSIS under interval-valued Pythagorean fuzzy environment. Expert Syst Appl 121:1–17. https://doi.org/10.1016/j.eswa.2018.12.010
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353. https://doi.org/10.1016/S0019-9958(65)90241-X
Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29:1061–1078. https://doi.org/10.1002/int.21676
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Pinar, A., Boran, F.E. A q-rung orthopair fuzzy multi-criteria group decision making method for supplier selection based on a novel distance measure. Int. J. Mach. Learn. & Cyber. 11, 1749–1780 (2020). https://doi.org/10.1007/s13042-020-01070-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-020-01070-1