A decision-making mechanism for multi-attribute group decision-making using 2-tuple linguistic T-spherical fuzzy maximizing deviation method

Abstract

Hospital performance evaluation is vital for effective hospital management as it provides valuable information about a hospital’s condition and enables adaptable implementation based on various attributes. In this research, a multi-attribute group decision-making (MAGDM) method using a 2-tuple linguistic T-spherical fuzzy set (2TLT-SFS) is proposed in the context of the cognitive information presented in the hospital evaluation process. The T-spherical fuzzy set is the most advanced generalization of the q-rung orthopair fuzzy set (q-ROFS) which is capable of handling the uncertainty, fuzziness and ambiguity in terms of four parameters: positivity (yes), negativity (no), impartiality (abstain), and denial (non-acceptance). The 2-tuple linguistic terminology is used to measure the validity of ambiguous data. We propose the 2TLT-SF Hamy mean (2TLT-SFHM) operator, 2TLT-SF weighted Hamy mean (2TLT-SFWHM) operator, 2TLT-SF dual Hamy mean (2TLT-SFDHM) operator and 2TLT-SF weighted dual Hamy mean (2TLT-SFWDHM) operator by combining the 2TLT-SFS and HM operator. Then, based on the proposed maximizing deviation method, a new optimization model is built that is able to exploit expert preference to find the best objective weights among attributes. Next, we extend the TOPSIS (technique for establishing order preference by similarity to the ideal solution) method to the 2TLT-SF-TOPSIS version which not only accounts for human cognition’s inherent uncertainty but also allows experts a wider context to express their decision. Finally, we give a case study about the selection of key performance indicators for hospital performance evaluation to support our proposed method. The findings from parameter analysis and comparative analysis demonstrate the method’s efficacy and reliability. The outcomes demonstrate that our approach successfully handles the assessment and choice of key performance indicators for hospital performance evaluation and captures the relationship between any number of attributes.

1 Introduction

People are increasingly seeking quality medical resources as the US economy continues to grow quickly. In this scenario, prestigious hospitals are overloaded with patients, registration is challenging, primary healthcare facilities are understaffed and wasting medical resources. Therefore, it is essential to use cutting-edge hospital administration technologies to raise the general medical standards of public hospitals. Hospital performance evaluation (HPE) is an effective technique used by hospital managers to assess and supervise hospital activities (Mohammadkarim et al. 2011). Hospitals can analyze their strengths and weaknesses to improve medical standards based on key performance indicators (KPIs) for the HPE. KPIs for HPE will serve as a kind of feedback for US medical reform. It is a guideline to improve the performance of hospital/medical departments if the performances of a hospital in different periods are different. There are diverse KPIs that should be considered in HPE, for example, hospital equipment, service attitude, medication and pharmaceutical, hospital sanitation, and environment. In this regard, it is difficult to select the best hospital that outperforms the competition in every way. Although several models have been developed to assess hospital performance but the majority of them either have limited application or assess performance in various ways. Few hospital performance assessment systems contain a balanced review of the inputs, processes, and outputs. Some of these models have a stronger emphasis on structural components or inputs, while others are more concerned with process evaluation and some of them with results. As a result, different studies have utilized different models. The identification of performance evaluation objectives, the assessment of various aspects of hospital performance, and the involvement of stakeholders in the design and development of the performance evaluation system are some of the difficulties in the design of a hospital performance evaluation system (Taslimi and Zayandeh 2013). Hospitals are large users of health system expenditures and resources; therefore, it is not surprising that scholars and policymakers pay particular attention to them (Sadeghifar et al. 2011).

Multi-attribute decision-making (MADM) is a crucial part of decision sciences that can provide ranking results for finite alternatives based on the attribute values of various alternatives. MAGDM, also known as multiple criteria group decision making (MCGDM), has become a popular study topic in recent years due to the ambiguity and fuzziness of human thought and objective matter (Akram and Bibi 2023; Akram et al. 2023; Alahmadi et al. 2023; Chang et al. 2014; Kumar and Chen 2022a, b; Liu et al. 2020a, b; Salsabeela et al. 2023). In general, the development of enterprises and social decision-making (DM) has been linked to the issue of MADM in recent years which has been widely used in a variety of fields (Akram et al. 2021; Garg et al. 2021; Liu et al. 2022; Naz et al. 2022a, b, c, d, e). A significant difficulty in the real-world DM process is expressing attribute values more efficiently and accurately. It is not enough to express the attribute values of alternatives with exact values due to the fuzziness of DM environments and the complexity of DM problems. Zadeh (1965) was the first to propose the fuzzy set theory which is the most effective DM environment for dealing with imprecise, vague, or incomplete information. As a generalization of the concept of a fuzzy set (FS), Atanassov (1999) introduced the concept of an intuitionistic fuzzy set (IFS) characterized by a membership degree (MD) and a non-membership degree (NMD) whose sum of MD and NMD is less than or equal to 1. Pythagorean fuzzy set (PFS) (Yager 2013) has recently emerged as a helpful and effective tool for representing uncertainty in MAGDM problems (Zeb et al. 2019). The sum of squares of MD and NMD is less than or equal to 1, a feature of the PFS that makes it more generic than the IFS. Yager (2016) proposed the q-ROFS based on IFS and PFS in which the sum of the qth power of the MD and the qth power of the NMD is limited to one. All of the aforementioned sets, nevertheless, contain duplet forms (such as MD and NMD), which makes it challenging for them to account for the various degrees of abstinence and refusal.

To resolve the limitations of the above-mentioned sets, Mahmood et al. (2019) presented the T-SFS, a generalization of the q-ROFS with a high capacity to cope with uncertainty. The T-SFS is constructed by three different functions known as MD, abstention degree (AD), and NMD, with the condition that the total of the three degrees’ qth powers does not exceed 1. T-SFS has a variety of structures, but they are comparable to q-ROFS as it has a better ability to solve MAGDM scenarios than q-ROFS, when there is ambiguity as illustrated in the prior discussion. T-SF Hamacher aggregation operators (AOs) were developed by Ullah et al. (2020) to evaluate investment performance. Guleria and Bajaj (2020) developed two algorithms for solving supply chain management and service center evaluation problems using the T-SF graph concept. Ullah et al. (2018) developed T-SFSs similarity measures and utilized them for pattern recognition. Quek et al. (2019) introduced generalized T-SF weighted AOs. Vagueness and imprecision might make it difficult for experts to express their opinions clearly while maintaining a steady and accurate DM process. In general, experts involved in these issues employ linguistic descriptors to deal with imprecision.

There have been many breakthroughs in research on linguistic MAGDM issues, since Zadeh (1975) proposed the notion of linguistic variables (LVs), specifically to solve linguistic MAGDM concerns. In many domains and applications, the fuzzy linguistic approach has provided excellent results. In recent literature, various scholars have investigated the difficulties of group DM in which both attribute and decision expert weights are expressed as linguistic terms. They defined linguistic assessment operational principles, established a few new operators and proposed an MAGDM-based method that focuses on actual linguistic knowledge. Herrera and Martinez (2000a); Herrera and Martínez (2000b) proposed 2TL computational model, 2TL AOs, and DM methodologies. Wang (2009) proposed the evaluation model for selecting an appropriate agile manufacturing system. Novel 2TLPF Heronian mean AOs were examined by Deng et al. (2019) by combining the generalized and geometric Heronian mean AOs with their weighted forms in the context of 2TLPFNs. Ju et al. (2020) proposed the q-ROFTL weighted averaging and weighted geometric operators. They also demonstrated the q-ROFTL Muirhead mean and dual Muirhead mean operators. The complex q-ROFTL Maclaurin symmetric mean (MSM) and the complex q-ROFTL dual MSM operators were introduced by Rong et al. (2020) along with other appealing aspects of the proposed operators. Wang et al. (2021) proposed the interval 2TLIF numbers to more accurately depict the fuzziness of human thoughts and to prevent information loss/distortion during information aggregation phases. The payoffs of the matrix game were represented by Verma and Aggarwal (2021) using 2TIFL values.

Many different types of studies have been conducted to become aware of the correlation between arguments which is an important feature of aggregated data. The HM (Hara et al. 1998) and DHM (Wu et al. 2018) operators are well-known for depicting interrelationships between any number of parameters assigned via variable vector. One of the most all-encompassing, adaptive, and prevalent notions is the HM operator which is utilized by certain academics to operate problematic and contradicting data in a variety of settings to determine the relationship between various properties. As a result, the HM and DHM operators can provide a reliable and adaptable technique for solving information fusion challenges in MAGDM problems. Liang (2020) also initiated the HM operators for IFSs. Li et al. (2018a, 2018b) proposed the Dombi HM operators for IFSs. Wu et al. (2019) initiated and developed the Dombi HM operators for interval-valued IFSs. Li et al. (2018a) investigated the HM operators for PFS. Wang et al. (2019) investigated the HM operators under the q-ROFSs.

Various methods such as PROMETHEE (Chen et al. 2015), MULTIMOORA (Gou et al. 2017), VIKOR (Opricovic and Tzeng 2004), and KEMIRA (Krylovas et al. 2014) have been proposed in recent years to handle MAGDM problems. Attribute weighting and alternative ranking were the two steps of MAGDM. There are multiple approaches for calculating the weights of various attributes. Some of these strategies are based on data, while others are based on the expertise and understanding of the designers or engineers. The maximizing deviation method is one of the most frequently utilized methods for weighing attributes based on expert judgements.Furthermore, TOPSIS is an alternate ranking method for determining the best alternative with the least and largest distances from the positive ideal solution (PIS) and negative ideal solution (NIS), respectively. This method is slightly less difficult than previous weight-measurement methods. Various MAGDM breakthroughs have been integrated into studies throughout the years, which have been developed by previous studies to tackle increasingly tough decision dilemmas in our daily lives. The following are essential components of every evaluation: (a) alternatives; (b) attributes; (c) relative relevance (importance/value) of each attribute; (d) measurement of the quality of the alternatives with the attribute; and (e) means of distinguishing between distinct alternatives. The goal of the MAGDM strategy is to choose the best alternative among several reasonable alternatives, all subject to varying degrees of competitiveness. Hwang and Yoon (1981a, 1981b) strategy for establishing the TOPSIS method is one of the most effective and desirable DM techniques. Many researchers extended this method with different operators. Liang and Xu (2017) extended the TOPSIS method to a hesitant Pythagorean fuzzy environment. There is considerable literature devoted to the study and application of TOPSIS theory to a wide range of MAGDM problems. As the limitations of classical data in real applications became apparent, some specialists began to design a new TOPSIS method in a variety of contexts (fuzzy environment, IF environment, PF environment, and so on). Few researchers have extended the TOPSIS method in diverse contexts.

TOPSIS is a valuable tool, since it determines the distance between each alternative to the PIS and NIS. Furthermore, the TOPSIS method has numerous advantages, including: (1) the computing results are consistent; (2) calculating equations is not difficult; (3) the model can be used in conjunction with other methodologies. As a consequence, we may conclude that the TOPSIS framework is an important tool in today’s DM context. According to the aforementioned study, there is no published information concerning the 2TLT-SF-TOPSIS method based on HM operators. The goal of this research is to utilize the concept of 2TLT-SFS. Furthermore, because information AOs are important in DM techniques, we propose that the HM AOs can be used in a 2TLT-SF environment to better reflect the assessed values than other methods. The following are some of the objectives and novelties of this study article that are unique:

• The 2TLT-SFS is utilized for communicating data complexity. The 2TLT-SFS combines the benefits of both the 2TL terms and T-SFSs which also increases the T-SFS’s effectiveness.

• To cope with group DM problems in which the attributes have interrelationships, we design a family of HM AOs of 2TLT-SFS, such as the 2TLT-SFHM operator, the 2TLT-SFWHM operator, the 2TLT-SFDHM operator, and the 2TLT-SFWDHM operator.

• Certain theorems, properties, and formal definitions of the suggested information AOs are discussed under the current circumstances.

• In this paper, we propose a new maximizing deviation method for objectively determining attribute weights under 2TLT-SF environment.

• To rank the alternatives, the 2TLT-SF-TOPSIS method is proposed which is based on the 2TLT-SFWHM and 2TLT-SFWDHM operators. The evaluation preferences of experts are fused using a unique MAGDM model.

• To present the usefulness and effectiveness of the proposed method, we give an illustrative example of the selection of KPIs for HPE.

To the best of our knowledge, the above-mentioned discussions have never been done before, which adds to the distinctiveness of our research work. The following is the structure of the paper: Sect. 2 covers various key ideas, including the 2TL representation model, a description of T-SFS, the HM operator, and the dual HM operator. It also introduces the notion of 2TLT-SFSs, as well as its operational laws. The 2TLT-SFHM, 2TLT-SFDHM, 2TLT-SFWHM, and 2TLT-SFWDHM aggregation operators with the optimal properties are developed in Sect. 3. In Sect. 4, a MAGDM strategy is constructed using the 2TLT-SFWHM and 2TLT-SFWDHM operators in the 2TLT-SF environment. Section 5 provides a numerical example, parameter influence, comparison analysis, and benefits to illustrate the usefulness and superiority of the established method. Finally, Sect. 6 summarizes the research study and suggests future directions.

2 Preliminaries

Definition 1

(Herrera and Martinez 2000a, b) Let $S=\{s_{\jmath }|\jmath =0, 1, \ldots , \tau \}$ be a linguistic term set (LTS) and $\varrho \in [0, \tau ]$ be a numeric value expressing the linguistic symbolic aggregation result. The function $\Delta$ for obtaining the 2-tuple linguistic information comparable to $\varrho$ is thus defined as follows:

$$\begin{aligned} \Delta :[0, \tau ]\rightarrow S\times [-0.5,0.5), \end{aligned}$$

$$\begin{aligned} \Delta (\varrho )={\left\{ \begin{array}{ll} s_{\jmath }, \jmath =\text {round}(\varrho )\\ \upsilon = \varrho -\jmath ,~\upsilon \in [-0.5, 0.5), \end{array}\right. } \end{aligned}$$

(1)

where round (.) is the usual round operation and $s_{\jmath }$ has the closest index label to $\varrho$.

Definition 2

(Herrera and Martinez 2000a, b) Let $S=\{s_{\jmath }|\jmath =0, 1, \ldots , \tau \}$ be a LTS and $(s_{\jmath },\upsilon _{\jmath })$ be a 2-tuple, there exists a function $\Delta ^{-1}$ that restore the 2-tuple to its equivalent numerical value $\varrho \in [0, \tau ]\subset R,$ where

$$\begin{aligned} \Delta ^{-1}: S\times [-0.5, 0.5)\rightarrow [0, \tau ],\nonumber \\ \Delta ^{-1}(s_{\jmath }, \upsilon )= \jmath +\upsilon =\varrho . \end{aligned}$$

(2)

Mahmood et al. (2019) defined the T-spherical fuzzy set as an extension of q-ROFS and SFS (spherical fuzzy set) as follows:

Definition 3

(Mahmood et al. 2019) For any universal set L, a T-SFS is of the form

$$\begin{aligned} T=\{\langle \lambda , (p(\lambda ),h(\lambda ),r(\lambda ))\rangle |\lambda \in L\}, \end{aligned}$$

where $p,h,r: L\rightarrow [0,1]$ represent the MD, AD and NMD, respectively, with the condition $0 \le (p(\lambda ))^q+(h(\lambda ))^q+(r(\lambda ))^q\le 1$ for positive number $q\ge 1$ and $\pi (\lambda )= \root q \of {1-((p(\lambda ))^q +(h(\lambda ))^q +(r(\lambda ))^q)}$ is known as the degree of refusal of $\lambda$ in T. To express information conveniently, the triplet (p, h, r) is known as a T-SFN.

A T-SFN is a generalized form of existing fuzzy framework and it reduces to:

• (i) Spherical fuzzy number; by taking q as 2.

• (ii) Picture fuzzy number; by taking q as 1.

• (iii) q-Rung orthopair fuzzy number; by taking h as zero.

• (iv) Pythagorean fuzzy number; by taking h as zero and q as 2.

• (v) Intuitionistic fuzzy number; by taking h as zero and q as 1.

• (vi) Fuzzy number; by taking h and r as zero and q as 1.

Inspired by the ideas of 2TL terms and T-SF sets, Naz et al. (2022a) proposed the new concept of 2TLT-SFSs by combining both the advantages of 2TL terms and T-SFSs. The newly proposed set has flexibility due to the qth power of MD, AD and NMD. The mathematical representation of 2TLT-SFS is described as follows:

Definition 4

(Naz et al. 2022a) A 2TLT-SFS F in L

$$\begin{aligned} F=\{\langle \lambda ,(({s_{p}(\lambda )},\wp (\lambda )),(s_{h}(\lambda ), \eta (\lambda )),(s_{r}(\lambda ),\zeta (\lambda )))\rangle \mid \lambda \in L\}, \end{aligned}$$

(3)

where $({s_{p}(\lambda )},\wp (\lambda )),(s_{h}(\lambda ),\eta (\lambda )),$ and $(s_{r}(\lambda ),\zeta (\lambda ))$ represent the positive, neutral and negative membership degrees, respectively, with the conditions $s_{p}(\lambda ), s_{h}(\lambda ), s_{r}(\lambda ) \in F$, $\wp (\lambda ), \eta (\lambda ), \zeta (\lambda )\in [-0.5,0.5),$ $0\le \Delta ^{-1}({s_{p}(\lambda )},\wp (\lambda ))\le \tau$, $0\le \Delta ^{-1}({s_{h}(\lambda )},\eta (\lambda ))\le \tau$, $0\le \Delta ^{-1}({s_{r}(\lambda )},\zeta (\lambda ))\le \tau$ and $0\le (\Delta ^{-1}({s_{p}(\lambda )},\wp (\lambda )))^q+ (\Delta ^{-1}({s_{h}(\lambda )},\eta (\lambda )))^q+ (\Delta ^{-1}({s_{r}(\lambda )},\zeta (\lambda )))^q\le \tau ^q$. For convenience, we say $F=(({s_{{p}}},\wp ),({s_{{h}}},\eta ),({s_{{r}}},\zeta ))$, is a 2TLT-SFN.

To compare any two 2TLT-SFNs, their score function and accuracy function are defined as follows:

Definition 5

(Naz et al. 2022a) Let $F=(({s_{p}},\wp ),({s_{h}},\eta ),(s_{r},\zeta ))$ be a 2TLT-SFN. Then, the score function $\digamma$ can be represented as

$$\begin{aligned} {\textstyle \digamma (F)=\Delta \left( \frac{\tau }{2} \left( 1+\left( \frac{\Delta ^{-1}({s_{p}},\wp )}{\tau }\right) ^{q}- \left( \frac{\Delta ^{-1}({s_{r}},\zeta )}{\tau }\right) ^{q}\right) \right) ,~\digamma (F)\in [0, \tau ]}, \end{aligned}$$

(4)

and its accuracy function $\beth$ is defined as

$$\begin{aligned} {\textstyle \beth (F)=\Delta \left( \tau \left( \left( \frac{\Delta ^{-1}({s_{p}},\wp )}{\tau }\right) ^{q} +\left( \frac{\Delta ^{-1}({s_{r}},\zeta )}{\tau }\right) ^{q}\right) \right) ,~\beth (F)\in [0,\tau ]}. \end{aligned}$$

(5)

Here, we will put forward the novel operational laws based on the 2TLT-SFNs, such as addition, multiplication, scalar multiplication and power rule.

Definition 6

(Naz et al. 2022a) Let $F=((s_{p},\wp ),(s_{h},\eta ),(s_{r},\zeta )),$ $F_1=((s_{p_{1}},\wp _{1}),(s_{h_{1}},\eta _{1}),(s_{r_{1}},\zeta _{1}))$ and

$F_2=((s_{p_{2}},\wp _{2}),(s_{h_{2}},\eta _{2}),(s_{r_{2}},\zeta _{2}))$ be three 2TLT-SFNs, $q\ge 1$, then

• 1.
  $$F_{1}\oplus F_{2}={\left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{p_{1}},\wp _{1})}{\tau }\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{p_{2}},\wp _{2})}{\tau }\right) ^{q}\right) }\right) ,\\ \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{h_{1}},\eta _{1})}{\tau }\right) \left( \frac{\Delta ^{-1}(s_{h_{2}},\eta _{2})}{\tau }\right) \right) , \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{r_{1}},\zeta _{1})}{\tau }\right) \left( \frac{\Delta ^{-1}(s_{r_{2}},\zeta _{2})}{\tau }\right) \right) \end{array}\right) };$$
• 2.
  $$F_{1}\otimes F_{2}={\left( \begin{array}{l} \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{p_{1}},\wp _{1})}{\tau }\right) \left( \frac{\Delta ^{-1}(s_{p_{2}},\wp _{2})}{\tau }\right) \right) ,\\ \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{h_{1}},\eta _{1})}{\tau }\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{h_{2}}, \eta _{2})}{\tau }\right) ^{q}\right) }\right) ,\\ \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{r_{1}},\zeta _{1})}{\tau }\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{r_{2}}, \zeta _{2})}{\tau }\right) ^{q}\right) }\right) \end{array}\right) };$$

• 3. $\omega F={\left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{p},\wp )}{\tau }\right) ^{q}\right) ^{\omega }}\right) , \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{h},\eta )}{\tau }\right) ^{\omega }\right) , \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{r},\zeta )}{\tau }\right) ^{\omega }\right) \end{array}\right) },~ \omega >0;$

• 4. $F^{\omega }={\left( \begin{array}{l} \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{p},\wp )}{\tau }\right) ^{\omega }\right) , \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{h},\eta )}{\tau }\right) ^{q}\right) ^{\omega }}\right) , \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{r},\zeta )}{\tau }\right) ^{q}\right) ^{\omega }}\right) \end{array}\right) },~ \omega >0.$

Definition 7

(Naz et al. 2022a) Let $F_{1}=(({s_{{p}_1}},{\wp _1}),({s_{{h}_1}},{\eta _1}),({s_{{r}_1}},{\zeta _1}))$ and $F_{2}=(({s_{{p}_2}},{\wp _2}),({s_{{h}_2}},{\eta _2}),({s_{{r}_2}},{\zeta _2}))$ be two 2TLT-SFNs, then these two 2TLT-SFNs can be compared according to the following rules:

• (1) If $\digamma (F_{1})>\digamma (F_{2})$, then $F_{1}>F_{2}$;

• (2) If $\digamma (F_{1})=\digamma (F_{2})$, then

  • If $\beth (F_{1})>\beth (F_{2})$, then $F_{1}> F_{2}$;

  • If $\beth (F_{1})=\beth (F_{2})$, then $F_{1} \sim F_{2}$.

3 The 2TLT-SF Hamy mean aggregation operators

Hara et al. (1998) proposed the concept of Hamy mean aggregation operator. In this section, the 2TLT-SFHM, 2TLT-SFWHM, 2TLT-SFDHM and 2TLT-SFWDHM operators are proposed for aggregating the 2TLT-SFNs by extending the HM AOs to the 2TLT-SF environment. Since 2TLT-SFS is a useful technique for expressing ambiguous data in a real-world DM context. Core properties of AOs are idempotency, monotonicity and boundedness.

Here, we introduce the new concept of the 2TLT-SFHM operators for aggregating 2TLT-SFNs, and examine its distinctive and preferred properties by generalizing the HM operator with 2TLT-SFS.

Definition 8

Let $F_\jmath =\left( (s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )\right) (\jmath =1,2,\ldots ,n)$ be a collection of 2TLT-SFNs. The 2TLT-SFHM operator is a mapping $T^{n}\rightarrow T$, such that

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})=\frac{\oplus _{1\le \imath _{1}<\ldots <\imath _{z}\le n}\left( \otimes ^{z}_{\jmath =1}F_{\imath _{\jmath }}\right) ^{\frac{1}{z}}}{C^{z}_{n}}. \end{aligned}$$

(6)

Theorem 1

Utilizing the 2TLT-SFHM operator, the aggregated value is also a 2TLT-SFN, where

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})\nonumber \\{} & {} = \left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n}\left( 1-\left( \prod \limits ^{z}_{\jmath =1} \frac{\Delta ^{-1}(s_{p_\jmath },\wp _\jmath )}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1}(s_{h_\jmath }, \eta _\jmath )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z}\le n} \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1}(s_{r_\jmath }, \zeta _\jmath )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) \end{array} \right) . \end{aligned}$$

(7)

Proof

By utilizing Definition 6, we get

$$\begin{aligned} \otimes ^{z}_{\jmath =1}F_{\imath _{\jmath }}= & {} \left( \begin{array}{l} \Delta \left( \tau \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{p_\jmath },\wp _\jmath )}{\tau }\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1}(s_{h_\jmath }, \eta _\jmath )}{\tau }\right) ^{q}\right) }\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{q}\right) }\right) \end{array} \right) . \end{aligned}$$

Thus,

$$\begin{aligned} \left( \otimes ^{z}_{\jmath =1}F_{\imath _{\jmath }}\right) ^{\frac{1}{z}}= & {} \left( \begin{array}{l} \Delta \left( \tau \left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1} (s_{p_\jmath },\wp _\jmath )}{\tau }\right) ^{\frac{1}{z}}\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{h_\jmath },\eta _\jmath )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) \end{array}\right) . \end{aligned}$$

Therefore

$$\begin{aligned} \oplus _{1\le \imath _{1}<\ldots<\imath _{z}\le n}\left( \otimes ^{z}_{\jmath =1} F_{\imath _{\jmath }}\right) ^{\frac{1}{z}}= & {} \left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1} (s_{p_\jmath },\wp _\jmath )}{\tau }\right) ^{\frac{q}{z}}\right) }\right) ,\\ \Delta \left( \tau \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{h_\jmath },\eta _\jmath )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ,\\ \Delta \left( \tau \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z}\le n} \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) \end{array} \right) . \end{aligned}$$

Furthermore

$$\begin{aligned} \text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})= & {} \left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{p_\jmath },\wp _\jmath )}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{h_\jmath },\eta _\jmath )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z}\le n} \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) \end{array} \right) . \end{aligned}$$

$\square$

The desirable properties of the 2TLT-SFHM operator, such as idempotency, monotonicity and boundedness, are also described below.

Property 1

(Idempotency). If all $F_\jmath =\left( (s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )\right) (\jmath =1,2,\ldots ,n)$ are equal, for all $\jmath$, then $\begin{aligned}{} & {} \text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})=F. \end{aligned}$

Proof

$$\begin{aligned} \text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})= & {} \left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{p},\wp )}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z} \le n}\root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1- \left( \frac{\Delta ^{-1}(s_{h},\eta )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z} \le n}\root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{r},\zeta )}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) \end{array}\right) \\= & {} \left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\left( \left( 1-\left( \left( \frac{\Delta ^{-1}(s_{p},\wp )}{\tau }\right) ^{z}\right) ^{\frac{q}{z}}\right) ^{C^{z}_{n}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ \Delta \left( \tau \left( \root q \of {1-\left( \left( 1-\left( \frac{\Delta ^{-1}(s_{h},\eta )}{\tau }\right) ^{q}\right) ^{z}\right) ^ {\frac{1}{z}}}\right) ^{C^{z}_{n}}\right) ^{\frac{1}{C^{z}_{n}}},\\ \Delta \left( \tau \left( \root q \of {1-\left( \left( 1-\left( \frac{\Delta ^{-1}(s_{r},\zeta )}{\tau }\right) ^{q}\right) ^{z}\right) ^ {\frac{1}{z}}}\right) ^{C^{z}_{n}}\right) ^{\frac{1}{C^{z}_{n}}} \end{array}\right) \\= & {} ((s_{p},\wp ),(s_{h},\eta ),(s_{r},\zeta ))=F. \end{aligned}$$

$\square$

Property 2

(Monotonicity). Let $F_\jmath =\left( (s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )\right)$ and $F'_\jmath =\left( (s'_{p_\jmath },\wp '_\jmath ),(s'_{h_\jmath }, \eta '_\jmath ),(s'_{r_\jmath },\zeta '_\jmath )\right) (\jmath =1,2,\ldots ,n)$ be two sets of 2TLT-SFNs, if $F_{\jmath }\le F'_{\jmath }$, for all $\jmath$, then $\begin{aligned} \text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n}) \le \text {2TL}T\text {-SFHM}^{(z)}(F'_{1},F'_{2},\ldots ,F'_{n}). \end{aligned}$

Proof

Let $F_\jmath =\left( (s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )\right)$ and $F'_\jmath =\left( (s'_{p_\jmath },\wp '_\jmath ),(s'_{h_\jmath }, \eta '_\jmath ),(s'_{r_\jmath },\zeta '_\jmath )\right) (\jmath =1,2,\ldots ,n)$ be two sets of 2TLT-SFNs, let

$$\begin{aligned} (s_{p},\wp )= & {} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n}\left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{p_{\jmath }}, \wp _{\jmath })}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ (s_{h},\eta )= & {} \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n}\root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) ,\\ (s_{r},\zeta )= & {} \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z}\le n}\root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{r_{\jmath }},\zeta _{\jmath })}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) , \end{aligned}$$

given that $(s_{p_{\jmath }},\wp _{\jmath })\le (s'_{p_{\jmath }},\wp '_{\jmath })$; then

$$\begin{aligned} \left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{p_{\jmath }}, \wp _{\jmath })}{\tau }\right) ^{\frac{q}{z}}\le \left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s'_{p_{\jmath }}, \wp '_{\jmath })}{\tau }\right) ^{\frac{q}{z}}. \end{aligned}$$

Moreover

$$\begin{aligned} \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z} \le n}\left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{p_{\jmath }},\wp _{\jmath })}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}} \ge \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z} \le n}\left( 1-\left( \prod \limits ^{z} _{\jmath =1}\frac{\Delta ^{-1}(s'_{p_{\jmath }},\wp '_{\jmath })}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}. \end{aligned}$$

Furthermore

$$\begin{aligned} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n}\left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{p_{\jmath }}, \wp _{\jmath })}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) \le \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots <\imath _{z}\le n}\left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s'_{p_{\jmath }}, \wp '_{\jmath })}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) \end{aligned}$$

Therefore, $(s_{p},\wp ) \le (s'_{p},\wp ')$. Similarly, we can show that $(s_{h},\eta ) \ge (s'_{h},\eta ')$ and $(s_{r},\zeta ) \ge (s'_{r},\zeta ')$.

Hence, $\text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})\le \text {2TL}T\text {-SFHM}^{(z)}(F'_{1},F'_{2},\ldots ,F'_{n}).$ $\square$

Property 3

(Boundedness). Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )) (\jmath =1,2,\ldots ,n)$ be a collection of 2TLT-SFNs and let $F^{-}=\min \limits _{\jmath }((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{h_\jmath },\eta _\jmath ))$ and $F^{+}=\max \limits _{\jmath }((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{h_\jmath },\eta _\jmath ))$; then $\begin{aligned}{} & {} F^{-}\le \text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})\le F^{+}. \end{aligned}$. From Property 1,

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFHM}^{(z)}(F^{-}_{1},F^{-}_{2},\ldots ,F^{-}_{n})= F^{-},\, \text {2TL}T\text {-SFHM}^{(z)}(F^{+}_{1},F^{+}_{2},\ldots ,F^{+}_{n})= F^{+}. \end{aligned}$$

From Property 2,

$$\begin{aligned}{} & {} F^{-}\le \text {2TL}T\text {-SFHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})\le F^{+}. \end{aligned}$$

3.1 2TLT-SFWHM aggregation operator

The 2TLT-SFHM AO does not show the weighting values of attributes in Theorem 1. To solve MAGDM issues, attribute weights, expert weights and attribute evaluation values are all crucial components. To overcome the constraints of the 2TLT-SFHM operator, we shall introduce the 2TLT-SFWHM operator with certain preferred properties.

Definition 9

Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )) (\jmath =1,2,\ldots ,n)$ be a collection of 2TLT-SFNs with weight vector $\xi _{\jmath }=(\xi _{1},\xi _{2},\ldots ,\xi _{n})^{T}$, thereby satisfying $\xi _{\jmath } \in [0, 1]$ and $\sum \nolimits ^{n}_{\jmath =1}\xi _{\jmath }=1$. The 2TLT-SFWHM operator is a mapping $T^{n}\rightarrow T$, such that

$$\begin{aligned}{} & {} \text {2TL}T\text {-FWHM}^{(z)}_{\xi }(F_{1},F_{2},\ldots ,F_{n}) =\frac{\oplus _{1\le \imath _{1}<\ldots <\imath _{z}\le n}\left( \otimes ^{z}_{\jmath =1} (F_{\imath _{\jmath }})^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}{C^{z}_{n}}. \end{aligned}$$

(8)

Theorem 2

Using the 2TLT-SFWHM operator, the aggregated value is also a 2TLT-SFN, where

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFWHM}^{(z)}_{\xi }(F_{1},F_{2},\ldots ,F_{n})\nonumber \\{} & {} = \left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \left( 1-\left( \prod \limits ^{z}_{\jmath =1}\left( \frac{\Delta ^{-1}(s_{p_{\jmath }}, \wp _{\jmath })}{\tau }\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \root q \of {1-\left( \prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z}\le n} \root q \of {1-\left( \prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1}(s_{r_\jmath }, \zeta _\jmath )}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) \end{array} \right) . \end{aligned}$$

(9)

Proof

By utilizing Definition 6, we get

$$\begin{aligned} (F_{\imath _{\jmath }})^{\xi _{\imath _{\jmath }}}= & {} \left( \begin{array}{l} \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{p_{\jmath }}, \wp _{\jmath })}{\tau }\right) ^{\xi _{\imath _{\jmath }}}\right) ,\\ \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1} (s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}}\right) ,\\ \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1} (s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}}\right) \end{array} \right) . \end{aligned}$$

Then,

$$\begin{aligned} \otimes ^{z}_{\jmath =1}(F_{\imath _{\jmath }})^{\xi _{\imath _{\jmath }}}= & {} \left( \begin{array}{l} \Delta \left( \tau \prod \limits ^{z}_{\jmath =1} \left( \frac{\Delta ^{-1}(s_{p_{\jmath }},\wp _{\jmath })}{\tau }\right) ^{\xi _{\imath _{\jmath }}}\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits ^{z}_{\jmath =1} \left( 1-\left( \frac{\Delta ^{-1}(s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{q} \right) ^{\xi _{\imath _{\jmath }}}}\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits ^{z}_{\jmath =1} \left( 1-\left( \frac{\Delta ^{-1}(s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}}\right) \end{array} \right) . \end{aligned}$$

Thus,

$$\begin{aligned} \left( \otimes ^{z}_{\jmath =1}\left( F_{\imath _{\jmath }} \right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}= & {} \left( \begin{array}{l} \Delta \left( \tau \left( \prod \limits ^{z}_{\jmath =1} \left( \frac{\Delta ^{-1}(s_{p_{\jmath } },\wp _{\jmath })}{\tau }\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}\right) ,\\ \Delta \left( \tau \root q \of {1-\left( \prod \limits ^{z}_{\jmath =1} \left( 1-\left( \frac{\Delta ^{-1}(s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{q} \right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}\right) ,\\ \Delta \left( \tau \root q \of {1-\left( \prod \limits ^{z} _{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1}(s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{q} \right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}\right) \end{array}\right) . \end{aligned}$$

Therefore

$$\begin{aligned}{} & {} \oplus _{1\le \imath _{1}<\ldots<\imath _{z}\le n}\left( \otimes ^{z}_{\jmath =1}\left( F_{\imath _{x}} \right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}\\{} & {} = \left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \left( 1-\left( \prod \limits ^{z}_{\jmath =1}\left( \frac{\Delta ^{-1}(s_{p_{\jmath }}, \wp _{\jmath })}{\tau }\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{q}{z}}\right) }\right) ,\\ \Delta \left( \tau \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \root q \of {1-\left( \prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}\right) ,\\ \Delta \left( \tau \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z}\le n} \root q \of {1-\left( \prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}\right) \end{array} \right) . \end{aligned}$$

Furthermore

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFWHM}^{(z)}_{\xi }(F_{1},F_{2},\ldots ,F_{n})\\{} & {} = \left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots< \imath _{z}\le n}\left( 1-\left( \prod \limits ^{z}_{\jmath =1} \left( \frac{\Delta ^{-1}(s_{p_{\jmath }},\wp _{\jmath })}{\tau }\right) ^{\xi _{\imath _{\jmath }}} \right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \root q \of {1-\left( \prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) ,\\ \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots <\imath _{z} \le n}\root q \of {1-\left( \prod \limits ^{z} _{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1}(s_{r_\jmath },\zeta _\jmath )}{\tau } \right) ^{q}\right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) \end{array} \right) . \end{aligned}$$

$\square$

Property 4

(Monotonicity). Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$ and $F'_{\jmath }=((s'_{p_\jmath },\wp '_\jmath ),(s'_{h_\jmath }, \eta '_\jmath ),(s'_{r_\jmath },\zeta '_\jmath )) (\jmath =1,2,\ldots ,n)$ be two sets of 2TLT-SFNs, if $F_{\jmath }\le F'_{\jmath }$, for all $\jmath$, then

$$\begin{aligned} \text {2TL}T\text {-SFWHM}^{(z)}_{\xi }(F_{1},F_{2},\ldots ,F_{n})\le \text {2TL}T\text {-SFWHM}^{(z)}_{\xi }(F'_{1},F'_{2},\ldots ,F'_{n}). \end{aligned}$$

Property 5

(Boundedness). Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )) (\jmath =1,2,\ldots ,n)$ be a collection of 2TLT-SFNs and let $F^{-}=\min _{\jmath }((s_{p_{\jmath } },\wp _{\jmath }),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$ and $F^{+}=\max _{\jmath }((s_{p_{\jmath }},\wp _{\jmath }),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$; then

$$\begin{aligned}{} & {} F^{-}\le \text {2TL}T\text {-SFWHM}^{(z)}_{\xi }(F_{1},F_{2},\ldots ,F_{n})\le F^{+}. \end{aligned}$$

Idempotency is obviously not a property of the 2TLT-SFWHM operator.

3.2 2TLT-SFDHM aggregation operator

In this subsection, we will augment the DHM operator with 2TLT-SFS to propose the 2TLT-SFDHM operator for aggregating 2TLT-SFNs and also examine its desirable properties.

Definition 10

Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )) (\jmath =1,2,\ldots ,n)$ be a collection of 2TLT-SFNs. The 2TLT-SFDHM operator is a mapping $T^{n}\rightarrow T$, such that

$$\begin{aligned} \text {2TL}T\text {-SFDHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n}) =\left( \otimes _{1\le \imath _{1}<\ldots <\imath _{z}\le n}\left( \frac{\oplus ^{z}_{\jmath =1}F_{\imath _{\jmath }}}{z}\right) \right) ^{\frac{1}{C^{z}_{n}}}. \end{aligned}$$

(10)

Theorem 3

The aggregated value by utilizing 2TLT-SFDHM operator is also a 2TLT-SFN, where

$$\begin{aligned} \nonumber{} & {} \text {2TL}T\text {-SFDHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})\\{} & {} = \left( \begin{array}{l} \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \root q \of {1-\prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1}(s_{p_{\jmath }}, \wp _{\jmath })}{\tau }\right) ^{q}\right) ^{\frac{1}{z}}}\right) ^{\frac{1}{C^{z}_{n}}}\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}<n} \left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{\frac{q}{z} }\right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}<n} \left( 1-\left( \prod \limits ^{z}_{\jmath =1}\frac{\Delta ^{-1}(s_{r_\jmath },\zeta _\jmath )}{\tau }\right) ^{\frac{q}{z}}\right) ^{\frac{1}{C^{z}_{n}}}}\right) \end{array}\right) . \end{aligned}$$

(11)

Property 6

(Idempotency). If all $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )) (\jmath =1,2,\ldots ,n)$ are equal, for all $\jmath$, then

$$\begin{aligned} \text {2TL}T\text {-SFDHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})=F. \end{aligned}$$

Property 7

(Monotonicity). Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$ and $F'_{\jmath }=((s'_{p_\jmath },\wp '_\jmath ),(s'_{h_\jmath }, \eta '_\jmath ),(s'_{r_\jmath },\zeta '_\jmath )) (\jmath =1,2,\ldots ,n)$ be two sets of 2TLT-SFNs, if $F_{\jmath }\le F'_{\jmath }$, for all $\jmath$, then

$$\begin{aligned} \text {2TL}T\text {-SFDHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})\le \text {2TL}T\text {-SFDHM}^{(z)}(F'_{1},F'_{2},\ldots ,F'_{n}). \end{aligned}$$

Property 8

(Boundedness). Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )) (\jmath =1,2,\ldots ,n)$ be a collection of 2TLT-SFNs and let $F^{-}=\min _{\jmath }((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$ and $F^{+}=\max _{\jmath }((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$; then $\begin{aligned} F^{-}\le \text {2TL}T\text {-SFDHM}^{(z)}(F_{1},F_{2},\ldots ,F_{n})\le F^{+}. \end{aligned}$

3.3 2TLT-SFWDHM aggregation operator

The value of the aggregated arguments is not taken into account by the 2TLT-SFDHM operator, as demonstrated in Theorem 3. However, in many real-life situations, particularly in MAGDM, attribute weights play an important role in the aggregation process. The 2TLT-SFDHM operator does not consider the attribute values. The 2TLT-SFWDHM operator is proposed to overcome the constraints of 2TLT-SFDHM.

Definition 11

Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )) (\jmath =1,2,\ldots ,n)$ be a collection of 2TLT-SFNs with weight vector $\xi _{\jmath }=(\xi _{1},\xi _{2},\ldots ,\xi _{n})^{T}$, thereby satisfying $\xi _{\jmath } \in [0, 1]$ and $\sum \limits ^{n}_{\jmath =1}\xi _{\jmath }=1$. The 2TLT-SFWDHM operator is a mapping $T^{n}\rightarrow T$, such that

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFWDHM}^{(z)}_{\xi }(F_{1},F_{2},\ldots ,F_{n}) =\left( \otimes _{1\le \imath _{1}<\ldots <\imath _{z}\le n} \left( \frac{\oplus ^{z}_{\jmath =1}\xi _{\imath _{\jmath }} F_{\imath _{\jmath }}}{z}\right) \right) ^{\frac{1}{C^{z}_{n}}}. \end{aligned}$$

(12)

Theorem 4

Using the 2TLT-SFWDHM operator, the aggregated value is also a 2TLT-SFN, where

$$\begin{aligned} \nonumber{} & {} \text {2TL}T\text {-SFWDHM}_{\xi }^{(z)}(F_{1},F_{2},\ldots ,F_{n})\\ {}{} & {} = \left( \begin{array}{l} \Delta \left( \tau \left( \prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}\le n} \root q \of {1-\left( \prod \limits ^{z}_{\jmath =1}\left( 1-\left( \frac{\Delta ^{-1} (s_{p_{\jmath }},\wp _{\jmath })}{\tau }\right) ^{q}\right) ^{\xi _{\imath _{\jmath } }}\right) ^{\frac{1}{z}}} \right) ^{\frac{1}{C^{z}_{n}}}\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}<n}\left( 1-\left( \prod \limits ^{z} _{\jmath =1}\left( \frac{\Delta ^{-1}(s_{h_{\jmath }},\eta _{\jmath })}{\tau }\right) ^{\xi _{\imath _{\jmath } }}\right) ^{\frac{q}{z}} \right) ^{\frac{1}{C^{z}_{n}}}}\right) ,\\ \Delta \left( \tau \root q \of {1-\prod \limits _{1\le \imath _{1}<\ldots<\imath _{z}<n} \left( 1-\left( \prod \limits ^{z}_{\jmath =1} \left( \frac{\Delta ^{-1}(s_{r_\jmath },\zeta _\jmath )}{\tau } \right) ^{\xi _{\imath _{\jmath }}}\right) ^{\frac{q}{z}} \right) ^{\frac{1}{C^{z}_{n}}}}\right) \end{array}\right) . \end{aligned}$$

(13)

Property 9

(Monotonicity). Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$ and $F'_{\jmath }=((s'_{p_\jmath },\wp '_\jmath ),(s'_{h_\jmath }, \eta '_\jmath ),(s'_{r_\jmath },\zeta '_\jmath )),(\jmath =1,2,\ldots ,n)$ be two sets of 2TLT-SFNs, if $F_{\jmath }\le F'_{\jmath }$, for all $\jmath$, then

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFWDHM}_{\xi }^{(z)}(F_{1},F_{2},\ldots ,F_{n})\le \text {2TL}T\text {-SFWDHM}_{\xi }^{(z)}(F'_{1},F'_{2},\ldots ,F'_{n}). \end{aligned}$$

Property 10

(Boundedness). Let $F_{\jmath }=((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath )) (\jmath =1,2,\ldots ,n)$ be a collection of 2TLT-SFNs and let $F^{-}=\min _{\jmath }((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$ and $F^{+}=\max _{\jmath }((s_{p_\jmath },\wp _\jmath ),(s_{h_\jmath }, \eta _\jmath ),(s_{r_\jmath },\zeta _\jmath ))$; then

$$\begin{aligned} F^{-}\le \text {2TL}T\text {-SFWDHM}_{\xi }^{(z)}(F_{1},F_{2},\ldots ,F_{n})\le F^{+}. \end{aligned}$$

Idempotency is obviously not a property of the 2TLT-SFWDHM operator.

4 The proposed methodology

red This section gives a framework for calculating attributes weight and the ranking results with completely unknown weight information and incomplete weight information on attributes weight for all the alternatives under the 2TLT-SF environment.

Consider an MAGDM issue where there is a set of e alternatives $\Xi = \{\Xi _1, \Xi _2,\ldots , \Xi _e\}$, a set of n attributes $l = \{l_1, l_2,\ldots , l_n\}$ and a set of t experts $\Re = \{\Re _1,\Re _2,\ldots ,\Re _t\}$ and let $\xi = (\xi _1, \xi _2, \ldots , \xi _n)$ and $\xi ' = (\xi '_1, \xi '_2, \ldots , \xi '_t)$ be the weighting vectors of the attributes and the experts satisfying $\xi _{{\jmath }}\in [0, 1]$, $\xi '_{\ell }\in [0, 1]$, $\sum \nolimits _{{\jmath }=1}^n \xi _{{\jmath }}=1$ and $\sum \nolimits _{\ell =1}^{t} \xi '_{\ell }=1$, respectively. For attributes $l_{\jmath } ({\jmath } = 1, 2,\ldots , n)$, the evaluation values of each alternative $\Xi _{\imath } ({\imath } = 1, 2,\ldots , e)$ given by each decision maker $\Re _{\ell } ({\ell } = 1, 2, \ldots , t)$ are expressed in the form of the 2TLT-SF decision matrices $F^{(t)}= (F_{\imath \jmath }^{(t)})_{e \times n}$.

4.1 Computation of optimal weights using maximizing deviation method

Case I: Completely unknown information on attribute weights

We build an optimization model based on the maximizing deviation method to find the best relative weight for attribute $l_\jmath \in l$ in a 2TLT-SF environment. The deviation of the alternative $\Xi _\imath$ to all other alternatives for each attribute $l_\jmath$ can be expressed as:

$$\begin{aligned} D_{\imath \jmath }\left( \xi ^*\right) = \sum \limits _{k=1}^n \left( \xi _\jmath ^*\right) d\left( F_{\imath \jmath },F_{k\jmath }\right) , ~~\imath =1,2,\ldots ,e~, ~~ \jmath =1,2,\ldots ,n \end{aligned}$$

(14)

where

$$\begin{aligned} d(F_{\imath {\jmath }}, F_{k{\jmath }}) =\Delta \left( \frac{\tau }{2} \left( \begin{array}{l} \left| \left( \frac{\Delta ^{-1}\left( s_{p_{\imath {\jmath }}},\wp _{\imath {\jmath }}\right) }{\tau } \right) ^q -\left( \frac{\Delta ^{-1}\left( s_{p_{k{\jmath }}},\wp _{k{\jmath }}\right) }{\tau }\right) ^q \right| ^q+\\ \left| \left( \frac{\Delta ^{-1}\left( s_{h_{\imath \jmath }},\eta _{\imath \jmath }\right) }{\tau }\right) ^q - \left( \frac{\Delta ^{-1}\left( s_{h_{k\jmath }},\eta _{k\jmath }\right) }{\tau }\right) ^q \right| ^q +\\ \left| \left( \frac{\Delta ^{-1}\left( s_{r_{\imath {\jmath }}},\zeta _{\imath {\jmath }}\right) }{\tau } \right) ^q -\left( \frac{\Delta ^{-1}\left( s_{r_{k{\jmath }}},\zeta _{k{\jmath }}\right) }{\tau }\right) ^q \right| ^q \end{array}\right) \right) ^{\frac{1}{q}} \end{aligned}$$

(15)

denotes the 2TLT-SF Euclidean distance between the 2TLT-SFNs $F_{\imath {\jmath }}, F_{k{\jmath }}$.

Let

$$\begin{aligned} D_\jmath (\xi ^*) = \sum \limits _{\imath =1}^e D_{\imath \jmath }\left( \xi ^*\right) =\sum \limits _{\imath =1}^e \sum \limits _{k=1}^e \left( \xi _\jmath ^*\right) d(F_{\imath {\jmath }}, F_{k{\jmath }}),~~\jmath =1,2,\ldots ,n. \end{aligned}$$

(16)

$D_\jmath (\xi ^*)$ represents the deviation value of all alternatives to other alternatives for the attribute $l_\jmath \in l$.

$$\begin{aligned} (M-1){\left\{ \begin{array}{ll}\begin{array}{ll} \max D(\xi ^*)=\sum \limits _{\jmath =1}^n\sum \limits _{\imath =1}^e\sum \limits _{k=1}^e(\xi _\jmath ^*)d(F_{\imath {\jmath }}, F_{k{\jmath }})\\ s.t.~\xi _{\jmath }^*\ge 0, \jmath =1,2,\ldots ,n,~\sum \limits _{\jmath =1}^{n}{{\xi }_{\jmath }^*}^{2}=1. \end{array} \end{array}\right. } \end{aligned}$$

To solve the above model, we consider

$$\begin{aligned} L(\xi ^*,\gimel ) =\sum \limits _{\jmath =1}^n\sum \limits _{\imath =1}^e\sum \limits _{k=1}^e(\xi _\jmath ^*)d(F_{\imath {\jmath }}, F_{k{\jmath }})+ \frac{\gimel }{2}\left( \sum \limits _{\jmath =1}^{n}{\xi _{\jmath }^*}^2 -1\right) \end{aligned}$$

(17)

which represents the Lagrange function of the constrained optimization problem (M-1), where $\gimel$ is a real number denoting the Lagrange multiplier variable. Then, the partial derivatives of L are computed as:

$$\begin{aligned}{} & {} \frac{\partial L}{\partial \xi _\jmath ^*}= \sum \limits _{\imath =1}^e\sum \limits _{k=1}^ed(F_{\imath {\jmath }}, F_{k{\jmath }}) + \gimel \xi _\jmath ^* = 0. \end{aligned}$$

(18)

$$\begin{aligned}{} & {} \frac{\partial L}{\partial \gimel }=\frac{1}{2}\left( \sum \limits _{\jmath =1}^{n} {\xi _{\jmath }^*}^2 -1\right) =0. \end{aligned}$$

(19)

It follows Eq. (18)

$$\begin{aligned} \xi _\jmath ^* = \frac{-\sum \nolimits _{\imath =1}^e\sum \nolimits _{k=1}^ed(F_{\imath {\jmath }}, F_{k{\jmath }})}{\gimel },~~\jmath =1,2,\ldots ,n. \end{aligned}$$

(20)

Putting Eq. (20) into (19)

$$\begin{aligned} \gimel = -\sqrt{\sum \nolimits _{\jmath =1}^n\left( \sum \nolimits _{\imath =1}^e\sum \nolimits _{k=1}^ed(F_{\imath {\jmath }}, F_{k{\jmath }})\right) ^2}. \end{aligned}$$

(21)

Obviously, $\gimel < 0,\sum \nolimits _{\imath =1}^{e}\sum \nolimits _{k=1}^{e}d(F_{\imath {\jmath }}, F_{k{\jmath }})$ denotes the sum of all the alternatives’ deviations from the $\jmath$th attribute and

$\sqrt{\sum \nolimits _{\jmath =1}^{n}\left( \sum \nolimits _{\imath =1}^e\sum \nolimits _{k=1}^ed(F_{\imath {\jmath }}, F_{k{\jmath }}) \right) ^2}$ denotes the sum of all of the alternatives’ deviations with respect to all the attributes.

Then utilizing Eq. (20) and (21)

$$\begin{aligned} \xi _\jmath ^* = \frac{\sum \nolimits _{\imath =1}^{e}\sum \limits _{k=1}^{e}d(F_{\imath {\jmath }}, F_{k{\jmath }})}{\sqrt{\sum \limits _{\jmath =1}^n\left( \sum \nolimits _{\imath =1}^e\sum \nolimits _{k=1}^ed(F_{\imath {\jmath }}, F_{k{\jmath }})\right) ^2}}. \end{aligned}$$

(22)

For the sake of simplicity,

$$\begin{aligned} \chi _\jmath = \sum \nolimits _{\imath =1}^{e}\sum \nolimits _{k=1}^{e}d(F_{\imath {\jmath }}, F_{k{\jmath }}), ~~\jmath =1,2,\ldots ,n \end{aligned}$$

(23)

then Eq. (22) becomes:

$$\begin{aligned} \xi _\jmath ^* = \frac{\chi _\jmath }{\sqrt{\sum \nolimits _{\jmath =1}^n \chi _{\jmath }^2}}, ~~~~\jmath =1,2,\ldots ,n. \end{aligned}$$

(24)

It is simple to verify that $\xi _\jmath ^*(\jmath = 1, 2,\ldots ,n)$ are positive and satisfy the constrained conditions in the model (M-1) and that the solution is unique using Eq. (24).

Normalize $\xi _\jmath ^* (\jmath = 1, 2,\ldots , n)$ to make the sum of $\xi _\jmath ^*$ into a unit, we have

$$\begin{aligned} \xi _{\jmath } = \frac{{\xi _\jmath }^*}{\sum \nolimits _{\jmath =1}^{n}\xi _\jmath ^*} = \frac{\chi _\jmath }{\sum \nolimits _{\jmath =1}^{n}\chi _\jmath }, ~~~\jmath =1,2,\ldots ,n. \end{aligned}$$

(25)

Case II: Partly known information on attribute weights

In some cases, the weight vector information is only partially known rather than completely known. In these cases, based on the set of known weights information $\aleph$, the constrained optimization model can be designed as follows:

$$\begin{aligned} (M-2){\left\{ \begin{array}{ll}\begin{array}{ll} \max D(\xi )=\sum \limits _{\jmath =1}^{n}\sum \limits _{\imath =1}^{e}\sum \limits _{k=1}^{e}\xi _{\jmath } d(F_{\imath {\jmath }}, F_{k{\jmath }})\\ s.t.~~ \xi \in \aleph , ~\xi _{\jmath }\ge 0, \jmath =1,2,\ldots ,n,~\sum \limits _{\jmath =1}^{n}\xi _{\jmath }=1 \end{array} \end{array}\right. } \end{aligned}$$

where $\aleph$ also refers to a collection of restriction constraints that the weight value $\xi _\jmath ^*$ should satisfy in order to fulfil the requirements in real-world scenarios. A linear programming model $(M-2)$ is used. We acquire the best answer $\xi = (\xi _1, \xi _2,\ldots , \xi _n)^T$ by solving this model, which can be used as the weight vector for the attributes.

4.2 Basic description of the MAGDM algorithm

TOPSIS (Xu and Zhang 2013), TODIqM (Wei et al. 2015), VIKOR (Opricovic and Tzeng 2004), MULTIMOORA (Gou et al. 2017) and the minimum deviation method (Zhao et al. 2017) are few of the recently developed MAGDM methods. TOPSIS is a well-known and simple method for assisting an expert in selecting the best alternative based on the minimum distance from the PIS and the maximum distance from the NIS. This study employs the TOPSIS method developed by Hwang and Yoon (1981a, 1981b) red We develop a 2TLT-SF-TOPSIS method to successfully manipulate the aforementioned MAGDM problem with 2TLT-SFNs, which is based on the idea that the best alternative should be at the shortest distance from the 2TLT-SF-PIS and the farthest distance from the 2TLT-SF-NIS.

4.3 Calculation steps of the MAGDM algorithm

In general, after obtaining the attribute weight values based on the maximizing deviation method, as per the literature, we should use a specific type of operator to aggregate the provided decision information to obtain the overall preference value of each alternative, rank the alternatives, and choose the most desirable one(s). However, the complexity of the aggregation process used by 2TLT-SF aggregation operators leads in the loss of too much information, which demonstrates a lack of accuracy in the findings. Consequently, to address this drawback, in this subsection, an MAGDM issue is described with the elements indicating the value of all alternatives relative to each attribute under the 2TLT-SF environment. The detailed algorithm of the 2TLT-SF-TOPSIS method as shown in Fig. 1 is explained in the following:

Step 1.:

Utilize 2TLT-SFWHM operator or 2TLT-SFWDHM operator from Eqs. (9) or (13) to fuse 2TLT-SF decision matrices $F^{(t)}= (F_{\imath \jmath }^{(t)})_{e \times n}$ into a collective one $F= (F_{\imath \jmath })_{e \times n}$.

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFWHM}^{(z)}_{\xi '}(F_{1},F_{2},\ldots ,F_{n}) =\frac{\oplus _{1\le \imath _{1}<\ldots <\imath _{z}\le n}\left( \otimes ^{z}_{\jmath =1}(F_{\imath _{\jmath }})^{\xi '_{\imath _{\jmath }}}\right) ^{\frac{1}{z}}}{C^{z}_{n}}, \end{aligned}$$

(26)

$$\begin{aligned}{} & {} \text {2TL}T\text {-SFWDHM}^{(z)}_{\xi }(F_{1},F_{2},\ldots ,F_{n})=\left( \otimes _{1\le \imath _{1}<\ldots <\imath _{z}\le n}\left( \frac{\oplus ^{z}_{\jmath =1}\xi _{\imath _{\jmath }}F_{\imath _{\jmath }}}{z}\right) \right) ^{\frac{1}{C^{z}_{n}}}. \end{aligned}$$

(27)

Step 2.:

Obtain the attributes weights $\xi _\jmath = (\xi _1, \xi _2, \ldots , \xi _n)^T$ by maximizing deviation using Eq. (25) (if the attribute weights are completely unknown) or model $(M-2)$ (if the attribute weights are partially known).

Step 3.:

The weighted aggregated 2TLT-SF decision matrix $\left( F'_{\imath \jmath }\right) _{e\times n}$ can be constructed using the multiplication operator.

$$\begin{aligned}{} & {} F'_{\imath \jmath }= \xi _\jmath \otimes F_{\imath \jmath } \end{aligned}$$

(28)

where $F'_{\imath \jmath } =\left( \left( s_{p \xi _{\imath \jmath }},\wp _{\imath \jmath }\right) ,\left( s_{h \xi _{\imath \jmath }},\eta _{\imath \jmath }\right) ,\left( s_{r \xi _{\imath \jmath }},\zeta _{\imath \jmath }\right) \right).$

Step 4.:

Calculate the PIS $(F^+)$ and the NIS $(F^-)$ using 2TLT-SFNs’ score and accuracy functions (if the score functions are equal, the accuracy functions are used to rank the 2TLT-SFNs).

$$\begin{aligned}{} & {} F^+ = \{ \lambda , \max _\imath (F'_{\imath \jmath }) | \jmath =1,2,\ldots ,n\} = \left[ F{_\jmath }^+\right] _{1\times n}. \end{aligned}$$

(29)

$$\begin{aligned}{} & {} F^- = \{ \lambda , \min _\imath (F'_{\imath \jmath }) | \jmath =1,2,\ldots ,n\} = \left[ F{_\jmath }^-\right] _{1\times n}. \end{aligned}$$

(30)

Step 5.:

To determine the distances of each alternative from both the 2TLT-SF-PIS and the 2TLT-SF-NIS, we start by defining a separation measure. To accomplish this, use the following normalized Euclidean distance between two 2TLT-SFNs:

$$\begin{aligned} d_{\imath }^+= & {} \sum _{\jmath =1}^n d(F_{\imath \jmath }, F^+) \xi _\jmath , \end{aligned}$$

(31)

$$\begin{aligned} d_{\imath }^+= & {} \Delta \left( \frac{\tau }{2} \left( \begin{array}{l} \left| \left( \frac{\Delta ^{-1}\left( s_{p_{\imath {\jmath }}},\wp _{\imath {\jmath }}\right) }{\tau }\right) ^q -\left( \frac{\Delta ^{-1}\left( s_{p_{k{\jmath }}},\wp _{k{\jmath }}\right) }{\tau }^+\right) ^q \right| ^q+\\ \left| \left( \frac{\Delta ^{-1}\left( s_{h_{\imath \jmath }},\eta _{\imath \jmath }\right) }{\tau }\right) ^q -\left( \frac{\Delta ^{-1}\left( s_{h_{k\jmath }},\eta _{k\jmath }\right) }{\tau }^+\right) ^q \right| ^q +\\ \left| \left( \frac{\Delta ^{-1}\left( s_{r_{\imath {\jmath }}},\zeta _{\imath {\jmath }}\right) }{\tau }\right) ^q -\left( \frac{\Delta ^{-1}\left( s_{r_{k{\jmath }}},\zeta _{k{\jmath }}\right) }{\tau }^+\right) ^q \right| ^q \end{array}\right) \right) ^{\frac{1}{q}} \end{aligned}$$

(32)

$$\begin{aligned} d_{\imath }^-= & {} \sum _{\jmath =1}^n d(F_{\imath \jmath }, F^-) \xi _\jmath \end{aligned}$$

(33)

$$\begin{aligned} d_{\imath }^+= & {} \Delta \left( \frac{\tau }{2} \left( \begin{array}{l} \left| \left( \frac{\Delta ^{-1}\left( s_{p_{\imath {\jmath }}},\wp _{\imath {\jmath }}\right) }{\tau }\right) ^q -\left( \frac{\Delta ^{-1}\left( s_{p_{k{\jmath }}},\wp _{k{\jmath }}\right) }{\tau }^-\right) ^q \right| ^q+\\ \left| \left( \frac{\Delta ^{-1}\left( s_{h_{\imath \jmath }},\eta _{\imath \jmath }\right) }{\tau }\right) ^q -\left( \frac{\Delta ^{-1}\left( s_{h_{k\jmath }},\eta _{k\jmath }\right) }{\tau }^-\right) ^q \right| ^q +\\ \left| \left( \frac{\Delta ^{-1}\left( s_{r_{\imath {\jmath }}},\zeta _{\imath {\jmath }}\right) }{\tau }\right) ^q -\left( \frac{\Delta ^{-1}\left( s_{r_{k{\jmath }}},\zeta _{k{\jmath }}\right) }{\tau }^-\right) ^q \right| ^q \end{array}\right) \right) ^{\frac{1}{q}} \end{aligned}$$

(34)

Step 6.:

The formula for calculating the relative closeness (RC) coefficient of an alternative $\Xi _\imath$ relative to 2TLT-SF-PIS is:

$$\begin{aligned} RC_{\imath } = \frac{d_{\imath }^-}{d_{\imath }^+ + d_{\imath }^-},~~~~ \imath = 1,2,\ldots ,e \end{aligned}$$

(35)

Step 7.:

The RC coefficient can be used to determine the preferred ranking of alternatives and the optimal alternative. On the other hand, Hadi-Vencheh and Mirjaberi (2014) claimed that in some cases, RC may be unable to produce an optimal alternative that is both closest to the PIS and farthest from the NIS at the same time. They devised the revised closeness index ($\Psi _{\imath }$) to address this shortcoming:

$$\begin{aligned} \Psi _{\imath } = \frac{d_{\imath }^-}{d_{{\imath }\max }^-} - \frac{d_{\imath }^+}{d_{{\imath }\min }^+},~~~~ {\imath }= 1,2,\ldots ,e \end{aligned}$$

(36)

Fig. 1

Scheme of the developed approach for MAGDM

5 Literal depiction

5.1 The selection of key performance indicators (KPIs) for HPE

A framework of KPIs for HPE is built through a literature review and interviews with people involved in HPE, such as doctors, patients, medical officers, and clinical experts, and is based on previous studies. The framework, which consists of five main attributes and 20 sub attributes, as well as the reasons for including these main attributes in the KPI framework are described below. Hospital equipment main attribute has been created to determine how advanced the hospital’s equipment are. It is critical to use high-tech clinical equipment to provide high-quality health-care services. Additional diagnostic and therapeutic procedures will be made feasible by advanced hospital equipment due to high clinical quality. As a result, hospital equipment has a substantial impact on hospital performance, which is why these attributes are included in our framework. The service attitude contains an attribute for describing the performance of hospital support services. Patient satisfaction is considerably affected by the attitude of hospital support services. According to a multi-site study of medical-surgical units in 146 hospitals across the United States, a favorable attitude towards support services helps patients stay in a good mood, which helps patients and medical staff communicate more effectively As a result, we included an attribute for this essential factor in our KPI system. The pharmacy and medical treatment dimensions include an attribute that describes the hospital’s ability to treat patients and shows the hospital’s dependability. Good treatment outcomes, comprehensive medication instructions, and extensive patient information provided by doctors can bring physical and psychological relief to patients, as well as inspire trust in the hospital. As a result, in light of the importance of pharmacy and medical treatment, we have included attributes in our KPI framework. The traits relating to the abilities and knowledge of the hospital’s medical professionals are defined by the professional capability. When evaluating hospital performance, professional skill plays a crucial role in patient satisfaction. It should be included in the KPI framework, since patients who view medical professionals as competent will feel cared for and give the hospital a positive rating. As a result, we should include these requirements in our KPI framework for these main attributes. The hospital sanitation and environment component includes attributes for assessing the hospital’s ventilation, sanitation and cleanliness. The relevance of hospital sanitation and environment is demonstrated through a proposed tool for measuring patient perceptions of hospital performance. In hospitals, infections can occur if sanitation standards are poor, putting patients’ health at risk and lowering their hospital ratings. We incorporate this essential attribute into our KPI system.

Fig. 2

Model of literal depiction

5.2 The application of 2TLT-SF-TOPSIS

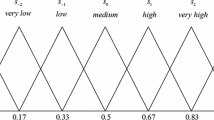
This study offers a numerical example of measuring hospital performance by 2TLT-SF-TOPSIS method and the KPI framework. In this study, seven hospitals $\Xi = \{ \Xi _1, \Xi _2, \ldots , \Xi _7 \}$ needed to be evaluated. An expert shows the evaluation values for 2TLT-SFNs based on 20 attributes, as shown in Fig. 2. Suppose, seven hospitals are evaluated by four experts $\Re = \{\Re _1,\Re _2,\Re _3,\Re _4\}$ (doctor, patient, medical officer and clinical expert) with weighting vector $\xi ' = (0.2,0.4,0.3,0.1)^T$ for choosing the best hospital. Based on the LTS S = ($s_0=$ Extremely critical, $s_1=$ Highly important, $s_2=$ very important, $s_3=$ important, $s_4=$ moderately important, $s_5=$ less important, $s_6=$ un-important, $s_7=$ absolutely un-important, $s_8=$ extremely un-important) four experts provide their opinions. Each decision expert has an opinion on the selection of the best hospital based on their experience. These hospitals are:

• Hospital A $(\Xi _1)$.

• Hospital B $(\Xi _2)$.

• Hospital C $(\Xi _3)$.

• Hospital D $(\Xi _4)$.

• Hospital E $(\Xi _5)$.

• Hospital F $(\Xi _6)$.

• Hospital G $(\Xi _7)$.

Decision matrices after evaluating each hospital’s capacity using the 2TLT-SFNs for selecting the best hospital are listed in Tables 1, 2, 3, 4 based on the experts’ suggestions.

Table 1 2TLT-SF decision matrix provided by doctor

Table 2 2TLT-SF decision matrix provided by patient

Table 3 2TLT-SF decision matrix provided by medical officer

Table 4 2TLT-SF decision matrix provided by clinical expert

5.3 Decision-making procedure based on the 2TLT-SFWHM operator

We now apply the developed method to choose the best KPI for HPE, which includes the following two cases:

Table 5 Fused matrix of 2TLT-SFNs based on weighted Hamy mean operator

Table 6 Weighted aggregated decision matrix of 2TLT-SFNs

Table 7 Separation measures of alternatives

Case I: The following stages are included in the MAGDM approach for choosing the appropriate KPI for HPE if the attribute weights information is unknown:

Step 1.:

Utilize Eq. (26) to fuse decision matrices into a collective one based on 2TLT-SFWHM operator by taking $q=4$ and $z=3$, as shown in Table 5.

Step 2.:

Obtain optimal weight vector using Eq. (25).

$$\begin{aligned} \xi =\left( 0.1485, 0.0857, 0.1660, 0.1807, 0.4191\right) ^{T}. \end{aligned}$$

Step 3.:

Calculate the weighted aggregated decision matrix of 2TLT-SFNs utilizing Eq. (28), as shown in Table 6.

Step 4.:

Utilize Eqs. (29) and (30) to calculate the 2TLT-SF-PIS and the 2TLT-SF-NIS, respectively, as follows:

$$\begin{aligned} F^+= & {} \{\{(s_4,0.4399),(s_6,-0.1614),(s_6,0.4929)\},\{(s_4,0.4603),(s_7,-0.3296),(s_7,-0.1098)\},\\{} & {} \{(s_5,-0.0580),(s_6,-0.3213),(s_6,-0.1335)\},\{(s_6,0.1519),(s_5,0.3213),(s_6,-0.4558)\},\\{} & {} \{(s_6,0.1266),(s_4,0.4264),(s_3,0.1648)\}\}\\ F^-= & {} \{\{(s_3,0.4291),(s_6,0.1826),(s_7,0.2310)\},\{(s_3,0.1494),(s_7,0.0055),(s_8,-0.3766)\},\\{} & {} \{(s_3,-0.2877),(s_6,-0.1954),(s_8,-0.2025)\},\{(s_4,0.0432),(s_6,0.2055),(s_7,-0.0276)\},\\{} & {} \{(s_2,0.4625),(s_3,0.3505),(s_8,-0.3662)\}\} \end{aligned}$$

Step 5.:

Utilize Eq. (32)and (34) to calculate the separation measures $d_\imath ^+$ and $d_\imath ^-$ of each alternative $\Xi _{\imath }$ from the 2TLT-SF-PIS and the 2TLT-SF-NIS, respectively, as shown in Table 7.

Step 6.:

Utilize Eq. (35) to calculate the $RC_{\imath }$ coefficient of each alternative $\Xi _{\imath }$ relative to the 2TLT-SF-PIS $F^+$.

$$\begin{aligned} RC_1= 0.7153,~RC_2= 0.6424,~RC_3= 0.5096,~RC_4= 0.3534,~RC_5= 0.6358,~RC_6= 0.3582,~RC_7= 0.6030. \end{aligned}$$

Step 7.:

Utilize Eq. (36) to calculate the revised closeness index $\Psi _{\imath }~({\imath }= 1,2,\ldots ,e)$ and rank the alternatives in the descending order of $\Psi _{\imath }$, as shown in Table 8.

Table 8 Revised closeness index for alternatives and ranking

Case II: The weights of attributes are partly known and the information of known weights is as follows:

Table 9 Weighted aggregated matrix of 2TLT-SFNs

Table 10 Separation measures of alternatives

$\aleph = \{0.15 \le \xi _1 \le 0.2,0.16 \le \xi _2 \le 0.18,0.3 \le \xi _3 \le 0.35,0.2 \le \xi _4 \le 0.45, 0.09 \le \xi _5 \le 0.23, \sum \nolimits _{\jmath =1}^5 \xi _\jmath = 1\}$

Step 1.:

Utilize Eq. (26) to fuse decision matrices into a collective one based on 2TLT-SFWHM operator by taking $q=4$ and $z=3$, as shown in Table 5.

Step 2.:

Utilize the model (M-2) to construct the single-objective model as follows:

$(M-2)\left\{ \begin{array}{ll} \max D(\xi )= 3.1240\xi _{1}+4.2952\xi _{2}+7.9312\xi _{3}+4.1606\xi _{4}+8.2658\xi _{5}\\ s.t.~~\xi \in \Im , \xi _{\jmath }\ge 0, \jmath =1,2,3,4,5,~\sum \limits _{\jmath =1}^{5}\xi _{\jmath }=1 \end{array} \right.$

By solving this model obtain the optimal weight vector as follows:

$$\begin{aligned} \xi = \left( 0.1500,0.1600,0.3000,0.2000,0.1900\right) ^{T}. \end{aligned}$$

Step 3.:

Calculate the weighted aggregated decision matrix of 2TLT-SFNs utilizing Eq. (28), as shown in Table 9.

Step 4.:

Utilize Eqs. (29) and (30) to calculate the 2TLT-SF-PIS and the 2TLT-SF-NIS, respectively, as follows:

$$\begin{aligned} F^+= & {} \{\{(s_4,0.4506 ),(s_6,-0.1799),(s_6,0.4792 )\},\{(s_5,0.1580),(s_6,-0.3021),(s_6,0.0534)\},\\{} & {} \{(s_6,-0.3570),(s_4,0.3062),(s_5,-0.4329)\},\{(s_6,-0.0270),(s_5,0.0945),(s_5,0.3313)\},\\{} & {} \{(s_5,0.1665),(s_6,-0.4483),(s_5,-0.2542)\}\}\\ F^-= & {} \{\{(s_3, 0.4376),(s_6,0.1666),(s_7,0.2237)\},\{(s_4,-0.3283),(s_6,0.2439),(s_7,0.3112)\},\\{} & {} \{(s_3,0.1406),(s_4,0.4804),(s_8,-0.3622)\},\{(s_4,0.1433),(s_6,0.0394 ),(s_7,-0.1292)\},\\{} & {} \{(s_2,0.0219),(s_5,-0.3918),(s_8,-0.1681)\}\} \end{aligned}$$

Step 5.:

Utilize Eqs. (32) and (34) to calculate the separation measures $d_\imath ^+$ and $d_\imath ^-$ of each alternative $\Xi _{\imath }$ from the 2TLT-SF-PIS and the 2TLT-SF-NIS, respectively, as shown in Table 10.

Step 6.:

Utilize Eq. (35) to calculate the $RC_{\imath }$ coefficient of each alternative $\Xi _{\imath }$ relative to the 2TLT-SF-PIS $F^+$.

$$\begin{aligned} RC_1= 0.7176,~RC_2= 0.6119,~RC_3=0.4844,~RC_4= 0.4136,~RC_5= 0.5855,~RC_6= 0.2665,~RC_7= 0.5908. \end{aligned}$$

Step 7.:

Utilize Eq. (36) to calculate the revised closeness index $\Psi _{\imath }~({\imath }= 1,2,\ldots ,e)$ and rank the alternatives in the descending order of $\Psi (\Xi _{\imath })$, as shown in Table 11.

Table 11 Revised closeness index of alternatives and ranking

Table 12 Fused matrix of 2TLT-SFNs utilizing weighted dual Hamy mean

5.4 Decision-making procedure based on the 2TLT-SFWDHM operator

Case I: The phases of the MAGDM technique to select the best KPI for HPE are as follows: The following stages are included in the MAGDM approach for choosing the appropriate KPI for HPE if the attribute weights information is unknown:

Step 1.:

Utilize Eq. (27) to fuse decision matrices into a collective one based on 2TLT-SFWDHM operator by taking $q=4$ and $z=3$, as shown in Table 12.

Step 2.:

Obtain optimal weight vector using Eq. (25).

$$\begin{aligned} \xi =\left( 0.1485, 0.0857, 0.1660, 0.1807, 0.4191\right) ^{T}. \end{aligned}$$

Step 3.:

Calculate the weighted aggregated decision matrix of 2TLT-SFNs utilizing Eq. (28), as shown in Table 13.

Step 4.:

Utilize Eqs. (29) and (30) to calculate the 2TLT-SF-PIS and the 2TLT-SF-NIS, respectively, as follows:

$$\begin{aligned} F^+\,=\, & {} \{\{(s_7,0.0955 ),(s_3,0.1649),(s_4,-0.3549 )\},\{(s_8,-0.2778),(s_2,0.4437),(s_3,0.1036)\},\\{} & {} \{(s_7,0.2350),(s_3,0.3056),(s_4,-0.4004)\},\{(s_8,-0.1810),(s_2,0.3707),(s_2,0.4939)\},\\{} & {} \{(s_6,0.3140),(s_4,0.2706),(s_4,0.0028)\}\} \end{aligned}$$

$$\begin{aligned} F^-\,=\, & {} \{\{(s_6, 0.0969),(s_4,-0.3528),(s_5,-0.2010)\},\{(s_7,0.0055),(s_3,0.1494),(s_5,-0.3844)\},\\{} & {} \{(s_6,0.3694),(s_4,-0.4501),(s_4,0.1681)\},\{(s_6,0.0418),(s_4,-0.3521 ),(s_5,-0.0294)\},\\{} & {} \{(s_3,-0.1446),(s_3,-0.3523),(s_7,-0.3937)\}\} \end{aligned}$$

Step 5.:

Utilize Eq. (32) and (34) to calculate the separation measures $d_\imath ^+$ and $d_\imath ^-$ of each alternative $\Xi _{\imath }$ from the 2TLT-SF-PIS and the 2TLT-S-NIS, respectively, as shown in Table 14.

Step 6.:

Utilize Eq. (35) to calculate the $RC_{\imath }$ coefficient of each alternative $\Xi _{\imath }$ relative to the 2TLT-SF-PIS $F^+$.

$$\begin{aligned} RC_1= 0.4604,~RC_2= 0.7502,~RC_3=0.3083,~RC_4= 0.3462,~RC_5= 0.5123,~RC_6= 0.2412,~RC_7= 0.4922. \end{aligned}$$

Step 7.:

Utilize Eq. (36) to calculate revised closeness index $\Psi _{\imath }~({\imath }= 1,2,\ldots ,e)$ and rank the alternatives in the descending order of $\Psi _{\imath }$, as shown in Table 15.

Table 13 Weighted aggregated matrix of 2TLT-SFNs

Table 14 Separation measures of alternatives

Table 15 Revised closeness index of alternatives and ranking

Case II: The weights of attributes are partly known and the information of known weights is as follows:

$\aleph = \{0.15 \le \xi _1 \le 0.2,0.16 \le \xi _2 \le 0.18,0.3 \le \xi _3 \le 0.35,0.2 \le \xi _4 \le 0.45, 0.09 \le \xi _5 \le 0.23, \sum \nolimits _{{\jmath }=1}^5 \xi _{\jmath } = 1 \}$

Step 1.:

Utilize Eq. (27) to fuse decision matrices into a collective one based on 2TLT-SFWDHM operator by taking $q=4$ and $z=3$, as shown in Table 12.

Step 2.:

Utilize the model (M-2) to construct the single-objective model as follows:

$(M-2)\left\{ \begin{array}{ll} \max D(\xi )= 3.1240\xi _{1}+4.2952\xi _{2}+7.9312\xi _{3}+4.1606\xi _{4}+8.2658\xi _{5}\\ s.t.~~\xi \in \Im , \xi _{\jmath }\ge 0, \jmath =1,2,3,4,5,~\sum \limits _{\jmath =1}^{5}\xi _{\jmath }=1 \end{array} \right.$

By solving this model obtain the optimal weight vector as follows:

$$\begin{aligned} \xi = \left( 0.1500,0.1600,0.3000,0.2000,0.1900\right) ^{T}. \end{aligned}$$

Step 3.:

Calculate the weighted aggregated decision matrix of 2TLT-SFNs utilizing Eq. (28), as shown in Table 16.

Step 4.:

Utilize Eqs. (29) and (30) to calculate the 2TLT-SF-PIS and the 2TLT-SF-NIS, respectively, as follows:

$$\begin{aligned} F^+\,=\, & {} \{\{(s_7,0.0869),(s_3,0.1728),(s_4,-0.3459)\},\{(s_7,0.4892),(s_3,-0.1462),(s_4,-0.3811)\},\\{} & {} \{(s_7,-0.3288),(s_4,-0.1786),(s_4,0.1561)\},\{(s_8,-0.2001),(s_2,0.4314),(s_3,-0.4423)\},\\{} & {} \{(s_7,0.1861),(s_4,-0.4756),(s_3,0.2986)\}\}\\ F^-\,=\, & {} \{\{(s_6,0.0802),(s_4,0.3438),(s_5,-0.0095)\},\{(s_6,0.2439),(s_4,-0.3283),(s_5,0.3290)\},\\{} & {} \{(s_5,0.2989),(s_4,0.0997),(s_5,-0.2038)\},\{(s_6,-0.1367),(s_4,-0.2606),(s_5,0.0877)\},\\{} & {} \{(s_5,0.0148),(s_2,0.1744),(s_6,-0.3607)\}\} \end{aligned}$$

Step 5.:

Utilize Eq. (32) and (34) to calculate the separation measures $d_\imath ^+$ and $d_\imath ^-$ of each alternative $\Xi _{\imath }$ from the 2TLT-SF-PIS and the 2TLT-SF-NIS, respectively, as shown in Table 17:

Step 6.:

Utilize Eq. (35) to calculate the $RC_{\imath }$ coefficient of each alternative $\Xi _{\imath }$ relative to the 2TLT-SF-PIS $F^+$.

$$\begin{aligned} RC_1= 0.4442,~RC_2= 0.7210,~RC_3= 0.3209,~RC_4= 0.3417,~RC_5= 0.5307,~RC_6= 0.2419,~RC_7= 0.4764. \end{aligned}$$

Step 7.:

Utilize Eq. (36) to calculate the revised closeness index $\Psi _{\imath }~({\imath }= 1,2,\ldots ,e)$ and rank the alternatives in the descending order of $\Psi (\Xi _{\imath })$, as shown in Table 18.

Table 16 Weighted aggregated matrix of 2TLT-SFNs

Table 17 Separation measures of alternatives

Table 18 Revised closeness index of alternatives and ranking results

5.5 Sensitive analysis

A sensitivity analysis has been performed in this section to examine the impact of various conditions on hospitals’ rankings. We investigated seven distinct scenarios based on various parameters. While aggregating data, it’s worth noting that the 2TLT-SFWHM operator’s parameters z and q play a crucial role in determining the results, and the variation of these parameters also effects the ranking results. The variation of parameters z and q enables decision makers to extend their decision assessment space based on the 2TLT-SFWHM and 2TLT-SFWDHM operators as well as the influence of parameters on the ranking results is analyzed to check the validity and effectiveness of the proposed approach. We deal with the variation of these two factors to determine how they effect the results: (1) Let $z=1,2,3,4$ and $q=4$, the influence of z and q on the ranking results is investigated. (2) Let $z=3$ and $q = 1,3,5,7,9,11,13,15,17,19$, the influence of z and q on the ranking results is investigated.

To reflect the influence of the different values of the parameter z by utilizing the 2TLT-SFWHM operator, we perform a sensitivity analysis by varying the values of parameter z (Suppose $q=4$). By changing parameter z values from 1 to 4, we can obtain the changed ranking results of alternatives, which are listed in Table 19. The influence of different values of the parameter z by utilizing the 2TLT-SFWDHM operator is shown in Table 20.

We can also see that the alternatives are ranked in order of importance when $q = 1,3,5,7,9,11,13,15,17,19$ by utilizing 2TLT-SFWHM and 2TLT-SFWDHM operator, as shown in Tables 21 and 22 (Suppose z = 3), respectively. From the above discussion, it is noted that for different values of the parameter the optimal alternative remains the same. However, there is a slight difference in the ranking of the remaining alternatives. The summary of the results shows that the maximum revised closeness index value corresponds to alternative $\Xi _{1}$ or $\Xi _{2}$.

Table 19 Closeness index $(\Psi _{\imath })$ and ranking results by 2TLT-SFWHM operator ($q = 4$)

Table 20 Closeness index $(\Psi _{\imath })$ and ranking results by 2TLT-SFWDHM operator ($q = 4$)

Table 21 Closeness index $(\Psi _{\imath })$ and ranking results by 2TLT-SFWHM operator ($z = 3$)

Table 22 Closeness index $(\Psi _{\imath })$ and ranking result by 2TLT-SFWDHM operator ($z = 3$)

5.6 Comparative analysis

Here, we perform a comparative analysis of the suggested methodology with other methods to demonstrate the acceptability and effectiveness of the 2TLT-SF-TOPSIS method. We adapt the EDAS, CODAS and MABAC methods for the 2TLT-SF environment and analyze them with our suggested method. For the selection of KPIs for the HPE, we carefully calculate the decision results using these methodologies. Tables 23 and 24 illustrate the ranking results obtained by the various methods based on 2TLT-SFWHM and 2TLT-SFWDHM operators, respectively. Due to the fundamental behaviour of the multiple aggregation methods, there are some variations in the ranking results of alternatives. However, although the revised closeness index used to compare the alternatives differs, the final rankings of the KPIs for HPE are the same.From the decision results, it can be observed that the best alternative according to all methods is $\Xi _{1}$ or $\Xi _{2}$. Our suggested approach is better than existing approaches, because it not only captures the relationships between the several input arguments but also gives experts the flexibility to represent their fuzzy knowledge in a broad area. Moreover, the proposed method allows experts to select their risk preferences based on the variation of parameters.

Table 23 Ranking results utilizing different methods based on WHM operator

Table 24 Ranking results utilizing different methods based on WDHM operator

Now, we compare the effects of different sets on our proposed method. Our method is based on 2TLT-SFS which has the effect of both 2TL term and T-SFS. The 2TLT-SFS can provide more useful information and can be applied in a wider range of DM circumstances. When we compare it with the picture fuzzy set and spherical fuzzy set there is a minor change in the ranking results of alternatives but the best alternative is ${\Xi _1}$ and ${\Xi _2}$ same as in 2TLT-SFS which is shown in Tables 25 and 26.

Table 25 Ranking results utilizing different sets based on WHM operator

Table 26 Ranking results utilizing different sets based on WDHM operator

6 Conclusions and future work

TOPSIS is a classical MAGDM methodology that uses crisp information to rank the preference orders of feasible alternatives and allocate the optimal choice. In the DM process, the collective opinion of a group of experts boosts the credibility of the results. Many real-world MAGDM problems occur in a complex environment and are frequently based on imprecise data and uncertainty. The 2TLT-SFS is appropriate for dealing with the ambiguity of decision makers’ judgment over alternatives concerning attributes. This paper introduced a novel theory on 2TLT-SFS as well as the principles of the theory, which included arithmetic operations and AOs. We proposed a DM methodology known as the maximizing deviation method using 2TLT-SFS to determine the attribute’s optimal relative weights. A MAGDM method, namely, 2TLT-SF-TOPSIS, based on the novel theory has been developed. The developed 2TLT-SF-TOPSIS method considers normalized Euclidean distances and calculates the closeness ratios to ideal solutions based on these distances. We have used the suggested approach to solve a real-world issue involving hospital performance evaluation. In this paper, we have concluded that hospital A ($\digamma _1$) and hospital B ($\digamma _2$) are the best among seven hospitals based on the KPIs for HPE. The comparative analysis shows that the 2TLT-SF-TOPSIS method is successful and practicable when compared to other methods. Our method appears to be simple, has less information loss, and can be easily applied to other organizational DM problems in a 2TLT-SF environment. We have evolved to the conclusion that the established technique is a more precise, general, and flexible, since it offers DMs greater latitude to assess the alternatives using linguistic criteria. In the future, our established method can be successfully applied to any group DM problem, such as industrial engineering, medical sciences, company management, and so forth.