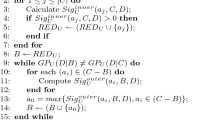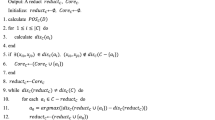1 Introduction

Rough set theory [1], as one of the effective tools to handle uncertainty requiring no preliminary or additional information about data, has been applied successfully in various applications, such as machine learning [2,3,4], rule mining [5], forecast [6], decision supporting [7,8,9], knowledge engineering [10, 11], disease diagnosis [12,13,14], genetic engineering [15, 16], uncertainty modelling [17,18,19,20,21], and other applications [22,23,24,25].

Attribute reduction, also called attribute selection or feature selection, as one of the most important core applications of rough sets, can select a few attributes with high importance from all attributes of information systems for many practical applications. Selected attributes are retained and unselected attributes are removed, the process of which is treated as a pre-processing stage of data analysis without decreasing the accuracy of classification. Many researchers have deeply studied non-incremental attribute reduction, also called classic attribute reduction or static attribute reduction, and have obtained many achievements. In general, non-incremental attribute reduction approaches can be divided into four categories: methods based on positive domain [26, 27], methods based on discernibility matrix [28,29,30,31,32], methods based on information entropy [15, 33, 34] and other attribute reduction methods [35,36,37,38,39,40,41]. For example, Fan et al. [26] presented systematic acceleration policies that can reduce the computational domain and optimize the computation of the positive region. Ni et al. [27] presented a novel accelerator based on the positive region for attribute reduction. Konecny [30] studied the problem of attribute reduction by using discernibility matrix in various extensions of formal concept analysis. Wang et al. [31] proposed a new feature evaluation function for feature selection by using discernibility matrix. Dai and Tian [33] defined the concepts of knowledge information entropy, knowledge rough entropy, knowledge granulation and knowledge granularity measure in set-valued information systems and studied relationship between these concepts. Wang et al. [34] developed an information entropy based attribute reduction algorithm for data sets with dynamically varying data values. Dai et al. [36] put forward two new attribute reduction algorithms based on quick neighbor inconsistent pairs, which can reduce the time for finding a reduct. Wang et al. [40] introduced distance measures into fuzzy rough sets by constructing a fuzzy rough set model based on distance measure with a fixed parameter and proposed a greedy convergent algorithm for attribute reduction. Dai et al. [37] proposed two attribute selection algorithms from the viewpoint of the object pair which can ignore the object pairs that were already discerned by the selected attribute subsets and needed only to deal with part of object pairs instead of the whole object pairs from the discourse.

Unlike non-incremental reduction which needs to be calculated from scratch, incremental reduction approaches can use the previous reduction results which have been obtained from the original decision system, to get new reduct of the changed decision system. This advantage of incremental reduction approaches greatly satisfies current situation that data sets usually vary with time, which has aroused the interest of researchers. There are several useful findings that can handle three conditions: variation of object sets [42,43,44,45,46,47], variation of attribute sets [48] and variation of attribute values [49, 50]. For example, Yang et al. [46] presented an efficient incremental algorithm which includes active sample selection process and incremental attribute reduction process for dynamic data sets with increasing samples. Ma et al. [44] introduced a compressed binary discernibility matrix and developed an incremental attribute reduction algorithm for group dynamic data considering both situations of single dynamic object and group dynamic objects. Jing et al. [48]considered the variation of attribute sets in complete decision systems and presented the corresponding incremental algorithms for attribute reduction. Wei et al. [50] proposed a discernibility matrix based incremental attribute reduction algorithm which can obtain all the reducts of dynamic data. There are a few algorithms that can deal with more complex situations, for example, Jing et al. [51] developed incremental methods to update reducts when attributes and objects of the decision system increased simultaneously. Yang et al. [52] presented a unified incremental reduction algorithm to deal with three kinds of variations of decision systems, such as adding an object, deleting an object and modifying the object’s value.

Although researches on incremental attribute reduction can obtain reducts effectively and efficiently, they are based on the equivalence relation that could not be applied directly to incomplete decision systems with missing attribute values. To our best knowledge, a few achievements of the research on attribute reduction for incomplete decision systems have been obtained but not sufficient. Shu et al. [53, 54] focused on positive region-based incremental mechanisms for attribute reduction algorithms to get new attribute reducts when attribute values varied, attribute set varied and object set varied. Xie and Qin [55] introduced inconsistency degree to update reduct incrementally for dynamic incomplete decision and proved that the attribute reduction based on the inconsistency degree was equivalent to that based on the positive region. Luo et al. [56] proposed a model of dynamic probabilistic rough sets with incomplete data and presented incremental updating strategies and algorithms when adding and removing objects, respectively. Attribute reduction methods listed above obtain reducts for incomplete decision systems from the perspective of positive domain, information entropy or discrimination matrix. Zhang and Dai [57] proposed knowledge granularity based incremental attribute reduction methods from the perspective of granular computing for incomplete decision systems with objects varying and obtained satisfactory effects. However, they only considered the situation that objects varied one by one. Therefore, we investigate incremental mechanisms of knowledge granularity to get the reducts efficiently when multiple objects are added to or removed from incomplete decision systems simultaneously in this paper.

The remainder of the paper is organized as follows. Section 2 reviews basic concepts in rough set theory and knowledge granulation related concepts for incomplete decision systems. Section 3 investigates incremental mechanisms to calculate knowledge granularity for the cases of adding and deleting multiple objects respectively at a time and corresponding reduction algorithms for incomplete decision systems. Experiments and comparisons on practical data sets have been conducted in Sect 4. Section 5 presents conclusions and points out our further research direction.

2 Preliminary knowledge

In this section, we review some basic concepts in rough set theory [1, 58], definitions of knowledge granulation, relative knowledge granularity, inner significance and outer significance respectively for incomplete decision systems, which can be found in [33, 48, 59].

2.1 Basic concepts in rough set theory

An information system is a quadruple \(IIS = \left\langle {U,A,V,f} \right\rangle\), where U denotes a non-empty finite set of objects, which is called the universe; A denotes a non-empty finite set of condition attributes; V is the union of attribute domains, \(V=\bigcup _{a\in A}V_a\), where \(V_a\) is the value set of attribute a, called the domain of a; \(f:U\times A\rightarrow V\) is an information function which assigns particular values from domains of attribute to objects such as \(a\in A\), \(x\in U\), \(f(a,x)\in V_a\), where f(a, x) denotes the value of attribute a for object x. Each attribute subset \(B \subseteq A\) determines a binary indiscernible relation as follows:

$$\begin{aligned} IND(B) = \left\{ {\left( {{u_i},{u_j}} \right) \in {U^2}|\forall a \in B,a\left( {{u_i}} \right) = a\left( {{u_j}} \right) } \right\} \end{aligned}$$
(1)

By the relation IND(B), we obtain the partition of U denoted by U/IND(B) or U/B. For \(B \subseteq A\) and \(X \subseteq U\), the lower approximation and the upper approximation of X can be defined as follows:

$$\begin{aligned} {\underline{B}} X&= \left\{ {{u_i} \in U|\left[ {{u_i}} \right] _B \subseteq X} \right\} \\ {\overline{B}} X&= \left\{ {{u_i} \in U|\left[ {{u_i}} \right] _B \cap X \ne \emptyset } \right\} , \end{aligned}$$

where \({\underline{B}} X\) is a set of objects that belong to X with certainty, while \({{\overline{B}}} X\) is a set of objects that possibly belong to X.

A decision system is a quadruple \(DS =\langle U,C \cup D,V,f \rangle\), where D is the decision attribute set, C is the condition attribute set, and \(C \cap D= \emptyset\); V is the union of attribute domain, i.e., \(V=V_C\cup V_D\). In general, we assume that \(D=\{d\}\). If there exists an \(a \in A\), \(x \in U\) such that \(f\left( {a,x} \right)\) is equal to a missing value, then the decision system is called an incomplete decision system (IDS). Thus, an incomplete decision system can be denoted as: \(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\), where \(* \in V_C, *\notin V_D\).

Definition 1

[58] Let IDS = \(\left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete decision system, \(\forall B \subseteq C\), the binary tolerance relations between objects that are possibly indiscernible in terms of values of attributes in B is defined as

$$\begin{aligned} T(B)&= \{(x,y)|\forall a \in B,f(a,x) = f(a,y)\\&\quad \vee f(a,x) = * \vee f(a,y) = *\} \end{aligned}$$
(2)

T(B) is reflexive and symmetric, but not necessarily transitive.

Definition 2

[58] Let IDS = \(\left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete decision system, \(x \in U\) and \(B \subseteq C\), the tolerance class of the object x with respect to attribute set B is defined by:

$$\begin{aligned} T_B(x) = \left\{ {y|\left( {x,y} \right) \in T(B)} \right\} \end{aligned}$$
(3)

2.2 Knowledge granulation in incomplete decision systems

Definition 3

[33] Let \(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete decision system, \(B \subseteq C\). \(T_B(u_i)\) is the tolerance class of object \(u_i\) with respect to B. The knowledge granularity of B on U is defined as follows:

$$\begin{aligned} GK_U(B)=\displaystyle {\frac{1}{|U|^2} \sum _{i=1}^{|U|}} {|T_B(u_i)|} \end{aligned}$$
(4)

where |U| stands for the number of objects in U.

Table 1 Incomplete decision system 1
Full size table

Example 1

Example for computing of the knowledge granularity.

Table 1 shows an incomplete decision system \(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\), where \(U=\{ {u_1},{u_2},{u_3},{u_4},{u_5}\}\), \(C = \{ {a_1},{a_2},{a_3},{a_4},{a_5}\}\) and \(D=\{d\}\). According to Definition 2, we have \(T_C(u_1)=\{u_1\}\), \(T_C(u_2)=\{u_2,u_4\}\), \(T_C(u_3)=\{u_3,u_4\}\), \(T_C(u_4)=\{u_2,u_3,u_4\}\), \(T_C(u_5)=\{u_5\}\). According to Definition 3, we have \(GK_U(C)=\frac{1}{5^2}(1+2+2+3+1)=\frac{9}{25}\). Similarly, we can get \(GK_U(C\cup D)=\frac{5}{25}\).

Let \(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete system, \(P,Q\subseteq C\). If \(P\subseteq Q\), then \(GK_U(P)\ge GK_U(Q)\) [57]. Thus, the measure of knowledge granularity has the monotonicity with respect to attributes and is reasonable for the uncertainty measure in rough set theory.

Definition 4

[48] Let IDS = \(\left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete decision system, \(B \subseteq C\). T(B) and \(T(B\cup D)\) are the tolerance relations for attribute set B and \(B\cup D\), respectively. The knowledge granularity of B relative to D on U is defined as follows:

$$\begin{aligned} GK_U(D|B)=GK_U(B)-GK_U(B\cup D) \end{aligned}$$
(5)

Definition 5

[48] Let IDS = \(\left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete decision system, \(B \subseteq C\) and \(a \in B\). \(T_B\), \(T_{B-\{a\}}\), \(T_{B\cup D}\) and \(T_{{(B-\{a\})}\cup D}\) are the tolerance relations for B, \(B-\{a\}\), \(B\cup D\) and \((B-\{a\})\cup D\), respectively. The significance measure (inner significance) of a in B on U is defined as follows:

$$\begin{aligned} Sig^{inner}_U(a,B,D)= GK_U(D|(B-\{a\}))-GK_U(D|B) \end{aligned}$$
(6)

Definition 6

[59] Let IDS = \(\left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete decision system, the core of IDS is defined as follows:

$$\begin{aligned} {Core}_C= \{a\in C|{Sig}^{inner}_U(a,C,D)>0\} \end{aligned}$$
(7)

If \(\forall a\in C, {Sig}^{inner}_U(a,C,D)=0\), then \({Core}_C= \emptyset\).

Where a denotes any one attribute in C.

Example 2

(Continued from Example 1) According to Definition 4, we have \(GK_U(D|C)=\frac{9}{25}- \frac{5}{25}=\frac{4}{25}\). Similarly, we can get \(GK_U(D|C-\{a_1\})=\frac{4}{25}\), \(GK_U(D|C-\{a_2\})=\frac{6}{25}\), \(GK_U(D|C-\{a_3\})=\frac{4}{25}\), \(GK_U(D|C-\{a_4\})=\frac{4}{25}\) and \(GK_U(D|C-\{a_5\})=\frac{4}{25}\). Then according to Definition 5, we can get \(Sig^{inner}_U(a_1,C,D)=\frac{4}{25}-\frac{4}{25}=0\), \(Sig^{inner}_U(a_2,C,D)=\frac{6}{25}-\frac{4}{25}=\frac{2}{25}\), \(Sig^{inner}_U(a_3,C,D)=\frac{4}{25}-\frac{4}{25}=0\), \(Sig^{inner}_U(a_4,C,D)=\frac{4}{25}-\frac{4}{25}=0\), \(Sig^{inner}_U(a_5,C,D)=\frac{4}{25}-\frac{4}{25}=0\). Then, we have \({Core}_C=\{a_2\}.\)

Definition 7

[48] Let IDS = \(\left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete decision system, \(B\subseteq C\). \(T_B\), \(T_{B\cup D}\), \(T_{B\cup \{a\}}\) and \(T_{{(B\cup \{a\})}\cup D}\) are the tolerance relations for B, \(B\cup D\), \(B\cup \{a\}\) and \({(B\cup \{a\})}\cup D\), respectively. Then \(\forall a \in (C - B )\), the significance measure (outer significance) of a in B on U is defined as follows:

$$\begin{aligned} Sig^{outer}_U(a,B,D)= GK_U(D|B)-GK_U(D|(B\cup \{a\})) \end{aligned}$$
(8)

Definition 8

[48] Let IDS = \(\left\langle {U,C \cup D,V,f} \right\rangle\) be an incomplete decision system, \(B\subseteq C\). B is a relative reduct based on the knowledge granularity of IDS if

  1. (1)

    \(GK_U(D|B)= GK_U(D|C)\)

  2. (2)

    \(\forall a\in B, GK_U(D|(B-\{a\})) \ne GK_U(D|B)\).

3 Incremental attribute reduction for incomplete decision systems when multiple objects arrive simultaneously

Incremental attribute reduction algorithms for incomplete decision systems which objects are added to and deleted from one by one were discussed in [57]. After investigating the incremental mechanisms to compute knowledge granularity for incomplete decision systems when multiple objects are added at a time and multiple objects are deleted at a time, this section introduces two incremental attribute reduction algorithms based on knowledge granularity for the addition of multiple objects and the deletion of multiple objects respectively.

3.1 An incremental mechanism to calculate knowledge granularity for IDS when adding multiple objects

This section investigates the changes of knowledge granularity, relative knowledge granularity, inner significance and outer significance, and then introduces the incremental mechanisms for calculating knowledge granularity when multiple objects are added to an incomplete decision system at a time.

Proposition 1

Let\(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\)be an incomplete decision system. \(U=\{u_1,u_2,\ldots ,u_n\}\)denotes a non-empty finite set containingnobjects. \(U'=\{u_1',u_2', \ldots ,u_s'\}\)denotes the incremental object set containingsobjects that will be added to IDS, and\(T^{U^+}_C\)is the tolerance relation on\(U^+=U\cup U'\). The knowledge granularity of C on\(U^+\)is

$$\begin{aligned} GK_{U^+}(C)=\displaystyle {\frac{1}{(n+s)^2}( n^2GK_{U}(C) + 2\sum _{j=1}^{s} {|T^{U}_C(u_j')|}}+\displaystyle {\sum _{j=1}^{s} {|T^{U'}_C(u_j')|)}} \end{aligned}$$
(9)

where\(T^{U}_C(u_j') = \left\{ {u_i|\left( {u_j',u_i} \right) \in T^{U^+}_C, 1\le i\le n, 1\le j\le s} \right\}\)and\(T^{U'}_C(u_j') = \left\{ {u_i'|\left( {u_j',u_i'} \right) \in T^{U^+}_C, 1\le i\le s, 1\le j\le s} \right\}\).

Proof

When \(u_j'(1\le j\le s)\) is adding to U, the tolerance class of \(u_i(1\le i\le n)\) on \(U^+\) is

$$\begin{aligned} T^{U^+}_C(u_i) = \left\{ \begin{array}{l} T^{U}_C(u_i)\cup \{u_j'\},\;(u_i,u_j')\in T^{U^+}_C\;\\ T^{U}_C(u_i),\;(u_i,u_j')\notin T^{U^+}_C\; \end{array} \right. \end{aligned}$$

We can get

$$\begin{aligned} T^{U^+}_C(u_i) = T^{U}_C(u_i) \cup T^{U'}_C(u_i), 1\le i\le n \end{aligned}$$

and

$$\begin{aligned} T^{U^+}_C(u_j') = T^{U}_C(u_j') \cup T^{U'}_C(u_j'), 1\le j\le s. \end{aligned}$$

Then we have

$$\begin{aligned} |T^{U^+}_C(u_i)| = |T^{U}_C(u_i)| + |T^{U'}_C(u_i)|, 1\le i\le n \end{aligned}$$

and

$$\begin{aligned} |T^{U^+}_C(u_j')| = |T^{U}_C(u_j')| + |T^{U'}_C(u_j')|, 1\le j\le s. \end{aligned}$$

If \(u_j' \in T^{U'}_C(u_i)\) then \(u_i \in T^{U}_C(u_j'),1\le i\le n,1\le j\le s\) and vice versa, because tolerance relation is symmetric. Obviously, we can get \({\sum _{i=1}^{|U|}|T^{U'}_C(u_i)|} = {\sum _{j=1}^{|U'|}|T^{U}_C(u_j')|}\). According to Definition 3, the knowledge granularity of C on \(U^+\) is described as following:

$$\begin{aligned}&GK_{U^+}(C)\\&\quad =\displaystyle {\frac{1}{|U^+|^2} \sum _{i=1}^{|U^+|} {|T^{U^+}_C(u_i)|}}\\&\quad =\displaystyle {\frac{1}{|U^+|^2}\left( \sum _{i=1}^{|U|} {|T^{U^+}_C(u_i)|}+\sum _{j=1}^{|U'|} {|T^{U^+}_C(u_j')|}\right) }\\&\quad =\displaystyle {\frac{1}{|U^+|^2}\left( \sum _{i=1}^{|U|} {|T^{U}_C(u_i)|}+\sum _{i=1}^{|U|} {|T^{U'}_C(u_i)|} + \sum _{j=1}^{|U'|} {|T^{U}_C(u_j')|}\right. }\\&\qquad +\displaystyle \left. {\sum _{j=1}^{|U'|} {|T^{U'}_C(u_j')|}}\right) \\&\quad =\displaystyle {\frac{1}{(n+s)^2}( n^2GK_{U}(C) + 2\sum _{j=1}^{s} {|T^{U}_C(u_j')|} + \sum _{j=1}^{s} {|T^{U'}_C(u_j')|})}\\ \end{aligned}$$

\(\square\)

If \(U'=\{u_1'\}\), that denotes adding objects one by one to the original object set U, then Eq. (9) can be written as \(\displaystyle {\frac{1}{(n+1)^2}( n^2GK_{U}(C) + 2|T^{U}_C(u_1')| + |T^{U'}_C(u_1')|)}\). From \(T^{U}_C(u_1')=T^{U^+}_C(u_1')-\{u_1'\}\) and \(u_1' \in T^{U^+}_C(u_1')\), we get \(|T^{U}_C(u_1')|=|T^{U^+}_C(u_1')|-1\). Since \(T^{U'}_C(u_1')=\{u_1'\}\), we have \(|T^{U'}_C(u_1')|=1\). Then we get \(2|T^{U}_C(u_1')| + |T^{U'}_C(u_1')|= 2(|T^{U^+}_C(u_1')|-1)+1=2|T^{U^+}_C(u_1')|-1\). Therefore, Eq. (9) degenerates into Eq. (9) in [57]. In other words, the case of incrementally getting the knowledge granularity under the circumstance of adding objects one by one is a special case of adding multiple objects at a time.

Table 2 Incremental data set to the incomplete decision system 1 in Table 1
Full size table

Example 3

(Continued from Example 1) Table 2 shows an incremental data set \(U'=\{ {u_1'},{u_2'},{u_3'},{u_4'}\}\). According to Definition 2, we have \(T^{U}_C(u_1')=\{u_1\}\), \(T^{U}_C(u_2')= \{u_1\}\), \(T^{U}_C(u_3')=\{u_2,u_3,u_4,u_5\}\), \(T^{U}_C(u_4')= \emptyset\), \(T^{U'}_C(u_1')=\{u_1',u_2'\}\), \(T^{U'}_C(u_2')=\{u_1',u_2'\}\), \(T^{U'}_C(u_3')=\{u_3'\}\), \(T^{U'}_C(u_4')=\{u_4'\}\). According to Example 1, we have \(GK_U(C)=\frac{9}{25}\). Then, we can get \(GK_{U^+}(C)=\frac{1}{(5+4)^2}( 5^2\times \frac{9}{25} + 2(1+1+4+0)+(2+2+1+1))=\frac{27}{81}\).

Proposition 2

Let\(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\)be an incomplete decision system. \(U'=\{u_1',u_2', \ldots ,u_s'\}\)is the incremental object set. \(T^{U}_C(u_j')\)and\(T^{U}_{C\cup D}(u_j')\)are the tolerance classes of\(u_j'\)with respect to attribute setsCand\(C\cup D\)onU, respectively. \(T^{U'}_C(u_j')\)and\(T^{U'}_{C\cup D}(u_j')\)are the tolerance classes of\(u_j'\)with respect to attribute setsCand\(C\cup D\)on\(U'\), respectively. The knowledge granularity of C relative to D on\(U^+\)is

$$\begin{aligned}&GK_{U^+}(D|C)=\displaystyle {\frac{1}{(n+s)^2}(n^2GK_U(D|C)}\\&\qquad +\displaystyle {2\sum _{j=1}^{s} {(|T^{U}_C(u_j')|}-|T^{U}_{C\cup D}(u_j')|)}\\&\qquad +\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_C(u_j')|-|T^{U'}_{C\cup D}(u_j')|)})} \end{aligned}$$
(10)

where |.| denotes the cardinality of a set.

Proof

According to Definition 4 and Proposition 1, we have

$$\begin{aligned}&GK_{U^+}(D|C)\\&\quad =GK_{U^+}(C)-GK_{U^+}(C\cup D)\\&\quad =\displaystyle {\frac{1}{(n+s)^2}( n^2GK_{U}(C) + 2\sum _{j=1}^{s} {|T^{U}_C(u_j')|} }\\&\qquad + \displaystyle {\sum _{j=1}^{s} {|T^{U'}_C(u_j')|})-\frac{1}{(n+s)^2}( n^2GK_{U}(C\cup D) }\\&\qquad + \displaystyle {2\sum _{j=1}^{s} {|T^{U}_{C\cup D}(u_j')|} + \sum _{j=1}^{s} {|T^{U'}_{C\cup D}(u_j')|})}\\&\quad =\displaystyle {\frac{1}{(n+s)^2}(n^2GK_U(D|C)+2\sum _{j=1}^{s} {(|T^{U}_C(u_j')|}}\\&\qquad -|T^{U}_{C\cup D}(u_j')|)+\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_C(u_j')|-|T^{U'}_{C\cup D}(u_j')|)})} \end{aligned}$$

\(\square\)

If \(U'=\{u_1'\}\), that denotes adding objects one by one to the original object set U, then Eq. (10) can be written as

$$\begin{aligned}&\displaystyle {\frac{1}{(n+1)^2}(n^2GK_U(D|C)+2(|T^{U}_C(u_1')|-|T^{U}_{C\cup D}(u_1')|)} \\&\quad+(|T^{U'}_C(u_1')|-|T^{U'}_{C\cup D}(u_1')|)). \end{aligned}$$

From \(T^{U}_C(u_1')=T^{U^+}_C(u_1')-\{u_1'\}\) and \(u_1' \in T^{U^+}_C(u_1')\), we get \(|T^{U}_C(u_1')|=|T^{U^+}_C(u_1')|-1\). Similarly, \(|T^{U}_{C\cup D}(u_1')|=|T^{U^+}_{C\cup D}(u_1')|-1\). Since \(T^{U'}_C(u_1')=\{u_1'\}\), we have \(|T^{U'}_C(u_1')| =1\). Similarly, \(|T^{U'}_{C\cup D}(u_1')|)|=1\). Finally, Eq. (10) can be written as \(\displaystyle {\frac{1}{(n+1)^2}(n^2GK_U(D|C)+2(|T^{U^+}_C(u_1')|-|T^{U^+}_{C\cup D}(u_1')|))}\). Therefore, Eq. (10) can degenerate into Eq. (10) in [57]. In other words, the case of incrementally getting the relative knowledge granularity under the circumstance of adding objects one by one is a special case of adding multiple objects at a time.

Example 4

(Continued from Example 3) According to Definition 2, we have \(T^{U}_{C\cup D}(u_1')=\{u_1\}\), \(T^{U}_{C\cup D}(u_2')= \emptyset\), \(T^{U}_{C\cup D}(u_3')=\{u_2,u_3\}\), \(T^{U}_{C\cup D}(u_4')= \emptyset\), \(T^{U'}_{C\cup D}(u_1')=\{u_1'\}\), \(T^{U'}_{C\cup D}(u_2')=\{u_2'\}\), \(T^{U'}_{C\cup D}(u_3')=\{u_3'\}\), \(T^{U'}_{C\cup D}(u_4')=\{u_4'\}\). According to Example 2, we have \(GK_U(D|C)=\frac{4}{25}\). Then, we get \(GK_{U^+}(D|C)= \frac{1}{(5+4)^2}( 5^2\times \frac{4}{25} + 2(1-1+1-0+4-2+0-0)+(2-1+2-1+1-1+1-1))=\frac{12}{81}\).

Proposition 3

Let\(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\)be an incomplete decision system. \(U'=\{u_1',u_2', \ldots ,u_s'\}\)is the incremental object set. \(T^{U}_C(u_j')\), \(T^{U}_{C\cup D}(u_j')\), \(T^{U}_{C-\{a\}}(u_j')\)and\(T^{U}_{(C-\{a\})\cup D}(u_j')\)are the tolerance classes of\(u_j'\)with respect to attribute setsC, \(C\cup D\), \(C-\{a\}\)and\((C-\{a\})\cup D\)onU, respectively. \(T^{U'}_C(u_j')\), \(T^{U'}_{C\cup D}(u_j')\), \(T^{U'}_{C-\{a\}}(u_j')\)and\(T^{U'}_{(C-\{a\})\cup D}(u_j')\)are the tolerance classes of\(u_j'\)with respect to attribute setsC, \(C\cup D\), \(C-\{a\}\)and\((C-\{a\})\cup D\)on\(U'\), respectively. Then\(\forall a\in C\), the inner significance ofainCon\(U^+\)is

$$\begin{aligned}&Sig^{inner}_{U^+}(a,C,D)=\displaystyle {\frac{1}{{(n+s)}^2}(n^2Sig^{inner}_U(a,C,D)}\\&\qquad +\displaystyle {2\sum _{j=1}^{s}(|T^{U}_{C-\{a\}}(u_j')|-|T^{U}_{(C-\{a\})\cup D}(u_j')|}\\&\qquad -|T^{U}_C(u_j')|+|T^{U}_{C\cup D}(u_j')|)+\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_{C-\{a\}}(u_j')|}}\\&\qquad -|T^{U'}_{(C-\{a\})\cup D}(u_j')|-|T^{U'}_C(u_j')|+|T^{U'}_{C\cup D}(u_j')|))\\ \end{aligned}$$
(11)

Proof

According to Definition 5 and Proposition 2, we can get

$$\begin{aligned}&Sig^{inner}_{U^+}(a,C,D)\\&\quad =GK_{U^+}(D|C-\{a\})-GK_{U^+}(D|C)\\&\quad =\displaystyle {\frac{1}{(n+s)^2}(n^2GK_U(D|C-\{a\})}\\&\qquad +\displaystyle {2\sum _{j=1}^{s} (|T^{U}_{C-\{a\}}(u_j')|-|T^{U}_{(C-\{a\})\cup D}(u_j')|)}\\&\qquad +\displaystyle {\sum _{j=1}^{s} (|T^{U'}_{C-\{a\}}(u_j')|-|T^{U'}_{(C-\{a\})\cup D}(u_j')|))}\\&\qquad -\displaystyle {\frac{1}{(n+s)^2}(n^2GK_U(D|C)+2\sum _{j=1}^{s} {(|T^{U}_C(u_j')|}}\\&\qquad -|T^{U}_{C\cup D}(u_j')|)+\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_C(u_j')|-|T^{U'}_{C\cup D}(u_j')|)})}\\&\quad =\displaystyle {\frac{1}{{(n+s)}^2}(n^2Sig^{inner}_U(a,C,D)+2\sum _{j=1}^{s} {(|T^{U}_{C-\{a\}}(u_j')|}}\\&\qquad -|T^{U}_{(C-\{a\})\cup D}(u_j')|-|T^{U}_C(u_j')|+|T^{U}_{C\cup D}(u_j')|)\\&\qquad +\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_{C-\{a\}}(u_j')|-|T^{U'}_{(C-\{a\})\cup D}(u_j')|}}\\&\qquad -|T^{U'}_C(u_j')|+|T^{U'}_{C\cup D}(u_j')|))\\ \end{aligned}$$

\(\square\)

Similarly, if \(U'=\{u_1'\}\), then Eq. (11) can be written as

$$\begin{aligned}&\displaystyle {\frac{1}{{(n+s)}^2}(n^2Sig^{inner}_U(a,C,D)+2{(|T^{U}_{C-\{a\}}(u_1')|}}\\&\quad -|T^{U}_{(C-\{a\})\cup D}(u_1')|-|T^{U}_C(u_1')|+|T^{U}_{C\cup D}(u_1')|)).\\ \end{aligned}$$

From \(T^{U}_C(u_1')=T^{U^+}_C(u_1')-\{u_1'\}\) and \(u_1' \in T^{U^+}_C(u_1')\), we get \(|T^{U}_C(u_1')|=|T^{U^+}_C(u_1')|-1\). Similarly,\(|T^{U}_{C\cup D}(u_1')|=|T^{U^+}_{C\cup D}(u_1')|-1\), \(|T^{U}_{C-\{a\}}(u_1')|=|T^{U^+}_{C-\{a\}}(u_1')|-1\) and \(|T^{U}_{(C-\{a\})\cup D}(u_1')|=|T^{U^+}_{(C-\{a\})\cup D}(u_1')|-1\) . Since \(T^{U'}_C(u_1')=\{u_1'\}\), we have \(|T^{U'}_C(u_1')|=1\). Similarly, \(|T^{U'}_{C\cup D}(u_1')|)|=1\), \(|T^{U'}_{C-\{a\}}(u_j')|=1\) and \(|T^{U'}_{(C-\{a\})\cup D}(u_j')|=1\). Finally, Eq. (11) can be written as

$$\begin{aligned}&\displaystyle {\frac{1}{{(n+s)}^2}(n^2Sig^{inner}_U(a,C,D)+2{(|T^{U^+}_{C-\{a\}}(u_1')|}-|T^{U^+}_C(u_1')|}\\&\quad -|T^{U^+}_{(C-\{a\})\cup D}(u_1')|+|T^{U^+}_{C\cup D}(u_1')|)).\\ \end{aligned}$$

Therefore, Eq. (11) degenerates into Eq. (11) in [57]. In other words, the case of incrementally getting the inner significance under the circumstance of adding objects one by one is a special case of adding multiple objects at a time.

Proposition 4

Let\(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\)be an incomplete decision system. \(U'=\{u_1',u_2', \ldots ,u_s'\}\)is the incremental object set. \(T^U_B(u_j')\), \(T^U_{B\cup D}(u_j')\), \(T^U_{B\cup \{a\}}(u_j')\)and\(T^U_{B\cup \{a\}\cup D}(u_j')\)are the tolerance classes of\(u_j'\)with respect to attribute setsB, \(B\cup D\), \(B\cup \{a\}\)and\(B\cup \{a\}\cup D\)onU, respectively.\(T^{U'}_B(u_j')\), \(T^{U'}_{B\cup D}(u_j')\), \(T^{U'}_{B\cup \{a\}}(u_j')\)and\(T^{U'}_{B\cup \{a\}\cup D}(u_j')\)are the tolerance classes of\(u_j'\)with respect to attribute setsB, \(B\cup D\), \(B\cup \{a\}\)and\(B\cup \{a\}\cup D\)on\(U'\), respectively. Then\(\forall a\in (C-B)\), the outer significance ofainBon\(U^+\)is

$$\begin{aligned}&Sig_{U^+}^{outer}(a,B,D)=\displaystyle { \frac{1}{{(n+s)}^2} (n^2Sig^{outer}_U(a,B,D)}\\&\qquad +\displaystyle {2\sum _{j=1}^{s} {(|T^{U}_{B}(u_j')|-|T^{U}_{B\cup D}(u_j')|-|T^{U}_{B\cup \{a\}}(u_j')|}}\\&\qquad +|T^{U}_{{B\cup \{a\}}\cup D}(u_j')|)+\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_{B}(u_j')|-|T^{U'}_{B\cup D}(u_j')|}}\\&\qquad -|T^{U'}_{B\cup \{a\}}(u_j')|+|T^{U'}_{{B\cup \{a\}}\cup D}(u_j')|)) \end{aligned}$$
(12)

Proof

According to Definition 7 and Proposition 2, we can get

$$\begin{aligned}&Sig^{outer}_{U^+}(a,B,D)\\&\quad =GK_{U^+}(D|B) - GK_{U^+}(D|(B\cup \{a\}))\\&\quad =\displaystyle {\frac{1}{(n+s)^2}(n^2GK_U(D|B)+2\sum _{j=1}^{s} {(|T^{U}_B(u_j')|}}\\&\qquad -|T^{U}_{B\cup D}(u_j')|)+\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_B(u_j')|-|T^{U'}_{B\cup D}(u_j')|)})}\\&\qquad -\displaystyle {\frac{1}{(n+s)^2}(n^2GK_U(D|B\cup \{a\})}\\&\qquad +\displaystyle {2\sum _{j=1}^{s} {(|T^{U}_{B\cup \{a\}}(u_j')|}-|T^{U}_{{B\cup \{a\}}\cup D}(u_j')|)}\\&\qquad +\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_{B\cup \{a\}}(u_j')|-|T^{U'}_{{B\cup \{a\}}\cup D}(u_j')|)})}\\&\quad =\displaystyle {\frac{1}{{(n+s)}^2} (n^2Sig^{outer}_U(a,B,D)+2\sum _{j=1}^{s} {(|T^{U}_{B}(u_j')|}}\\&\qquad -|T^{U}_{B\cup D}(u_j')|-|T^{U}_{B\cup \{a\}}(u_j')|+|T^{U}_{{B\cup \{a\}}\cup D}(u_j')|)\\&\qquad +\displaystyle {\sum _{j=1}^{s} {(|T^{U'}_{B}(u_j')|-|T^{U'}_{B\cup D}(u_j')|}-|T^{U'}_{B\cup \{a\}}(u_j')|}\\&\qquad +|T^{U'}_{{B\cup \{a\}}\cup D}(u_j')|))\\ \end{aligned}$$

\(\square\)

Similarly, if \(U'=\{u_1'\}\), then Eq. (12) can be written as

$$\begin{aligned}&\displaystyle {\frac{1}{{(n+1)}^2} (n^2Sig^{outer}_U(a,B,D)+2(|T^{U^+}_{B}(u_j')|-|T^{U^+}_{B\cup D}(u_j')|}\\&-|T^{U^+}_{B\cup \{a\}}(u_j')|+|T^{U^+}_{{B\cup \{a\}}\cup D}(u_j')|). \end{aligned}$$

Therefore, the case of incrementally getting the outer significance under the circumstance of adding objects one by one is a special case of adding multiple objects at a time.

3.2 An incremental reduction algorithm for IDS when adding multiple objects

The traditional heuristic attribute reduction algorithm based on knowledge granularity for decision systems (THA) was discussed in detail in [57]. Based on the incremental mechanisms of knowledge granularity above, this subsection introduces an incremental attribute reduction algorithm (see Algorithm 1) using knowledge granularity when adding multiple objects to the decision system. At last, a brief comparison of time complexity between incremental reduction algorithm and traditional heuristic reduction algorithm is given.

figure a

In Algorithm 1, \(U^+\) denotes the object set of the new decision system after adding the incremental object set \(U'\) to the original object set U. The detailed execution process of Algorithm 1 is as follows. In Step 1, the reduct \(RED_U\) on U is assigned to B. In Step 2, \(\sum _{j=1}^{|U'|} {|T^{U}_B(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U}_{B\cup D}(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U'}_B(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U'}_{B\cup D}(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U}_C(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U}_{C\cup D}(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U'}_C(u_j')|}\) and \(\sum _{j=1}^{|U'|} {|T^{U'}_{C\cup D}(u_j')|}\) are calculated respectively. In Step 3, the knowledge granularity of B relative to D on \(U^+\)(\(GK_{U^+}(D|B)\)) and the knowledge granularity of C relative to D on \(U^+\)(\(GK_{U^+}(D|C)\)) are calculated respectively according to Proposition 2. In Step 4, \(GK_{U^+}(D|B)\) is compared with \(GK_{U^+}(D|C)\), if they are equal, then the algorithm flow skips to Step 19, which indicates that the reducts of \(U^+\) and U are identical. Otherwise, the loop consisting of Steps 7–13 executes. Steps 8–10 constitute a loop to calculate the outer significance of an certain \(a_i \in (C-B)\) which is \(Sig^{outer}_{U^+}(a_i,B,D)\) according to Proposition 4. In Step 11, \(a_0\) is used to store the attribute that has the maximum value of outer significance. In Step 12, \(a_0\) is added to B. Steps 14–18 are actually used to delete attributes that satisfy the second condition in Definition 8 through a loop with |B| times. In Step 15, \(GK_{U^+}(D|(B-\{a\}))\) is compared with \(GK_{U^+}(D|C)\), if they are equal, then \(a_i\) is deleted from B, which indicates that \(a_i\) is redundant and can not be in the reduct of \(U^+\). In Step 19, B is assigned to \(RED_{U^+}\). In Step 20, \(RED_{U^+}\) is returned as the result of Algorithm 1.

The time complexity of Algorithm 1 is \(O(|U'||U||B| (|C|-|B|))\). According to Definition 2, the time complexity of computing \(T^{U}_B(u_j')\) is O(|U||B|). Then the time complexity of computing \(\sum _{j=1}^{|U'|} {|T^{U}_B(u_j')|}\) is \(O(|U'| |U||B|)\). Similarly, we get the time complexity of computing \(\sum _{j=1}^{|U'|} {|T^{U'}_B(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U}_C(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U'}_C(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U}_{B\cup D}(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U'}_{B\cup D}(u_j')|}\), \(\sum _{j=1}^{|U'|} {|T^{U}_{C\cup D}(u_j')|}\) and \(\sum _{j=1}^{|U'|} {|T^{U'}_{C\cup D}(u_j')|}\) in Step 2 respectively. According to Proposition 2, the time complexity of Steps 2–3 is \(O(|U'||U||B|+|U'||U|(|B|+1)+|U'|^2|B|+|U'|^2(|B|+1)+ |U'||U||C|+|U'||U|(|C|+1)+|U'|^2|C|+|U'|^2(|C|+1))\approx O(|U'||U||C|)\). According to Proposition 4, the time complexity of computing \(Sig^{outer}_{U^+}(a_i,B,D)\) is \(O(|U'||U||B|)\). Then the time complexity of Steps 7–13 is \(O(|U'||U||B|(|C|-|B|))\). Similarly, the time complexity of Steps 14–18 is \(O(|U'||U||B|^2)\). Hence, the time complexity of Algorithm 1 is \(O(|U'||U||C|+|U'||U||B| (|C|-|B|)+|U'||U||B|^2)\approx O(|U'||U||B|(|C|-|B|))\).

Two algorithms for comparison with algorithm KGIRA-M were introduced in [57]. One is the non-incremental algorithm called algorithm THA which is converted as algorithm THA-M in this paper to be suitable for incomplete decision systems under the situation of adding multiple objects at a time. Another is incremental algorithm called algorithm KGIRA which is called as algorithm KGIRA-S in this paper for incomplete decision systems under the situation of adding one object at a time. Since the number of objects is \(|U^+|\) after adding the incremental object set \(U'\) to the original object set U, the time complexity of THA-M is actually \(O(|U^+|^2|C|^2)\). Because \(|U'| \le |U^+|\), \(|U| \le |U^+|\) and \(|B| \le |C|\) , \(O(|U'||U||B|(|C|-|B|\) is much lower than \(O(|U^+|^2|C|^2)\). Hence, the time complexity of algorithm KGIRA-M is much smaller than that of algorithm THA-M. Since the number of objects is \(|U^+|\) after adding the object set \(U'\) to the original object set U, the time complexity of KGIRA-S is \(O(|U'||U||C|^2)\). Because \(|B| \le |C|\), \(O(|U'||U||B|(|C|-|B|))\) is lower than \(O(|U'||U||C|^2)\). Hence, the time complexity of algorithm KGIRA-M is smaller than that of algorithm KGIRA-S. Since \(|U'| \ll |U^+|\) and \(|U|<|U^+|\) , we can draw the conclusion that the time complexity of KGIRA-S is also much smaller than that of algorithm THA-M.

3.3 An incremental mechanism to calculate knowledge granularity for IDS when deleting multiple objects

For the sake of convenience, let \(U=\{u_1,u_2,\ldots ,u_n\}\) be the original object set in the incomplete decision system \(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\). \(U''=\{u_1'',u_2'',\ldots ,u_t''\}\subset U\) denotes the object set whose objects will be deleted from U. For simplicity, \(U^-\) denotes \(U-U''\) in the following.

Proposition 5

Let\(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\)be an incomplete decision system. \(T^{U^-}_C(u_j'')\)and\(T^{U''}_C(u_j'')\)are the tolerance classes of\(u_j''\)with respect to attribute setCon\(U^-\)and\(U''\), respectively. The knowledge granularity of C on\(U^-\)is

$$\begin{aligned} GK_{U^-}(C)=\displaystyle {\frac{1}{(n-t)^2}( n^2GK_{U}(C)-2\sum _{j=1}^{t}|T^{U^-}_C(u_j'')|}-\displaystyle {\sum _{j=1}^{t}|T^{U''}_C(u_j'')|)} \end{aligned}$$
(13)

Proof

When \(u_j''(1\le j\le t)\) is deleted from U, the tolerance class of \(u_i(1\le i\le n-t)\) on \(U^-\) is

$$\begin{aligned} T^{U^-}_C(u_i) = \left\{ \begin{array}{l} T^{U}_C(u_i) - \{u_j''\},\;(u_i,u_j'')\in T^{U}_C\;\\ T^{U}_C(u_i),\;(u_i,u_j'')\notin T^{U}_C\; \end{array} \right. \end{aligned}$$

Then we can get

$$\begin{aligned} T^{U^-}_C(u_i) = T^{U}_C(u_i) - T^{U''}_C(u_i), \quad 1\le i\le n-t \end{aligned}$$

and

$$\begin{aligned} T^{U^-}_C(u_j'') = T^{U}_C(u_j'') - T^{U''}_C(u_j''), \quad 1\le j\le t. \end{aligned}$$

Since \(T^{U''}_C(u_i)\subset T^{U}_C(u_i)\), we can get

$$\begin{aligned} |T^{U^-}_C(u_i)| = |T^{U}_C(u_i)| - |T^{U''}_C(u_i)|,\quad 1\le i\le n-t. \end{aligned}$$

Similarly, we can get

$$\begin{aligned} |T^{U^-}_C(u_j')| = |T^{U}_C(u_j'')| - |T^{U''}_C(u_j'')|, \quad 1\le j\le t. \end{aligned}$$

If \(u_j'' \in T^{U''}_C(u_i)\) then \(u_i \in T^{U^-}_C(u_j''),1\le i\le n-t,1\le j\le t\) and vice versa, because tolerance relation is symmetric. Obviously, we can get \({\sum _{i=1}^{|U^-|}|T^{U''}_C(u_i)|}={\sum _{j=1}^{|U''|}|T^{U^-}_C(u_j'')|}\). According to Definition 3, the knowledge granularity of C on \(U^-\) is described as follows:

$$\begin{aligned}&GK_{U^-}(C)\\&\quad =\displaystyle {\frac{1}{|U^-|^2} \sum _{i=1}^{|U^-|} {|T^{U^-}_C(u_i)|}}\\&\quad =\displaystyle {\frac{1}{|U^-|^2}\left( \sum _{i=1}^{|U|} {|T^{U}_C(u_i)|}-\sum _{i=1}^{|U^-|}|T^{U''}_C(u_i)|\right. }\\&\qquad -\displaystyle {\left. \sum _{j=1}^{|U''|}|T^{U^-}_C(u_j'')|-\sum _{j=1}^{|U''|}|T^{U''}_C(u_j'')|\right) }\\&\quad =\displaystyle {\frac{1}{(n-t)^2}( n^2GK_{U}(C)-2\sum _{j=1}^{t}|T^{U^-}_C(u_j'')|}\\&\qquad -\displaystyle {\sum _{j=1}^{t}|T^{U''}_C(u_j'')|)} \end{aligned}$$

\(\square\)

If \(U''=\{u_1''\}\), which denotes deleting objects one by one from the original object set U, then Eq. (13) can be written as \(\displaystyle {\frac{1}{(n-1)^2}( n^2GK_{U}(C)-2|T^{U^-}_C(u_1'')|-|T^{U''}_C(u_1'')|)}\). Because \(T^{U}_C(u_1'')=T^{U^-}_C(u_1'') \cup \{u_1''\}\) and \(u_1'' \notin T^{U^-}_C(u_1'')\), we have \(|T^{U^-}_C(u_1'')|=|T^{U}_C(u_1'')|-1\). Then Eq. (13) can be written as \(\displaystyle {\frac{1}{(n-1)^2}( n^2GK_{U}(C)-(2|T^{U}_C(u_1'')|-1))}\). Therefore, Eq. (13) degenerates into Eq. (13) in [57]. In other words, the case of incrementally getting the relative knowledge granularity under the circumstance of deleting objects one by one is a special case of deleting multiple objects at a time.

Proposition 6

Let\(IDS = \left\langle {U,C \cup D,V,f} \right\rangle\)be an incomplete decision system. \(u_n\)is the diminishing object. \(T_C(u_n)\)and\(T_{C\cup D}(u_n)\)are the tolerance classes of\(u_n\)with respect to attribute setsCand\(C\cup D\)onU, respectively. The knowledge granularity of C relative to D on\(U^-\)is

$$\begin{aligned} GK_{U^-}(D|C)= \displaystyle {\frac{1}{(n-t)^2}( n^2GK_U(D|C)-2\sum _{j=1}^{t}(|T^{U^-}_C(u_j'')|} -|T^{U^-}_{C\cup D}(u_j'')|)-\displaystyle {\sum _{j=1}^{t}(|T^{U''}_C(u_j'')|-|T^{U''}_{C\cup D}(u_j'')|))} \end{aligned}$$
(14)

Proof

According to Definition 4 and Proposition 5, we have

$$\begin{aligned}&GK_{U^-}(D|C)\\&\quad =GK_{U^-}(C)-GK_{U^-}(C\cup D)\\&\quad =\displaystyle {\frac{1}{(n-t)^2}( n^2GK_{U}(C)-2\sum _{j=1}^{|U''|}|T^{U^-}_C(u_j'')|}\\&\qquad -\displaystyle {\sum _{j=1}^{|U''|}|T^{U''}_C(u_j'')|)-\frac{1}{(n-t)^2}( n^2GK_{U}(C\cup D)}\\&\qquad -\displaystyle {2\sum _{j=1}^{|U''|}|T^{U^-}_{C\cup D}(u_j'')|-\sum _{j=1}^{|U''|}|T^{U''}_{C\cup D}(u_j'')|)}\\&\quad =\displaystyle {\frac{1}{(n-t)^2}( n^2GK_U(D|C)-2\sum _{j=1}^{t}(|T^{U^-}_C(u_j'')|}\\&\qquad -|T^{U^-}_{C\cup D}(u_j'')|)-\displaystyle {\sum _{j=1}^{t}(|T^{U''}_C(u_j'')|-|T^{U''}_{C\cup D}(u_j'')|))}\\ \end{aligned}$$

\(\square\)

If \(U''=\{u_1''\}\), then Eq. (14) can be written as

$$\begin{aligned}&\displaystyle {\frac{1}{(n-1)^2}( n^2GK_U(D|C)-2(|T^{U^-}_C(u_1'')|-|T^{U^-}_{C\cup D}(u_1'')|)-}\\&(|T^{U''}_C(u_1'')|-|T^{U''}_{C\cup D}(u_1'')|)). \end{aligned}$$

Since \(T^{U}_C(u_1'')=T^{U^-}_C(u_1'') \cup \{u_1''\}\) and \(u_1'' \notin T^{U^-}_C(u_1'')\), we get \(|T^{U^-}_C(u_1'')|=|T^{U}_C(u_1'')|-1\). Similarly, \(|T^{U^-}_{C\cup D}(u_1'')|=|T^{U}_{C\cup D}(u_1'')|-1\). Since \(T^{U''}_C(u_1'')=\{u_1''\}\), we have \(|T^{U''}_C(u_1'')| =1\). Similarly, \(|T^{U''}_{C\cup D}(u_1'')|=1\). Then Eq. (14) can be written as \(\displaystyle {\frac{1}{(n-1)^2}( n^2GK_{U}(C)-2(|T^{U}_C(u_1'')|-|T^{U}_{C\cup D}(u_1'')|))}\).

Therefore, Eq. (14) degenerates into Eq. (14) in [57]. In other words, the case of incrementally getting the relative knowledge granularity under the circumstance of deleting objects one by one is a special case of deleting multiple objects at a time. To sum up, all situations of handling objects one by one in [57] are special cases of those of handling multiple objects at a time for getting new reducts in this paper.

3.4 An incremental reduction algorithm for IDS when deleting multiple objects

Based on the incremental mechanisms of knowledge granularity above, this subsection introduces an incremental attribute reduction algorithm (see Algorithm 2) when deleting multiple objects from an incomplete decision system.

figure b

In Algorithm 2, \(U^-\) denotes the object set of the new decision system after deleting objects in \(U''\) from the original object set U. The detailed execution process of Algorithm 2 is as follows. In Step 1, the reduct \(RED_U\) on U is assigned to B. In Step 2, \(\sum _{j=1}^{|U''|}|T^{U^-}_{C\cup D}(u_j'')|\), \(\sum _{j=1}^{|U''|}|T^{U^-}_C(u_j'')|\), \(\sum _{j=1}^{|U''|}|T^{U''}_{C\cup D}(u_j'')|\) and \(\sum _{j=1}^{|U''|}(|T^{U''}_C(u_j'')|\) are calculated respectively. In Step 3, the knowledge granularity of C relative to D on \(U^-\)(\(GP_{U^-}(D|C)\)) is calculated according to Proposition 6. Steps 4–8 are actually used to delete attributes that satisfies the second condition in Definition 8 through a loop with |B| times. In Step 5, \(GP_{U^-}(D|(B-\{a_i\}))\) is compared with \(GP_{U^-}(D|(B-\{a_i\}))\). If \(GP_{U^-}(D|(B-\{a_i\}))\) is equal to \(GP_{U^-}(D|C)\), then \(a_i\) is deleted from B, which indicates \(a_i\) is redundant and can not be in the reduct of \(U^-\). In Step 9, B is assigned to \(RED_{U^-}\). In Step 10, \(RED_{U^-}\) is returned as the result of Algorithm 2.

The time complexity of Algorithm 2 is \(O(|U''||U^-| |B|^2)\). According to Definitions 1 and 2, the time complexity of computing \(\sum _{j=1}^{|U''|}|T^{U^-}_C(u_j'')|\) is \(O(|U''| |U^-||C|)\), the time complexity of computing \(\sum _{j=1}^{|U''|}|T^{U^-}_{C\cup D}(u_j'')|\) is \(O(|U''||U^-|(|C|+1))\), the time complexity of computing \(\sum _{j=1}^{|U''|}(|T^{U''}_C(u_j'')|\) is \(O(|U''|^2|C|)\) and the time complexity of computing \(\sum _{j=1}^{|U''|}|T^{U''}_{C\cup D}(u_j'')|\) is \(O(|U''|^2(|C|+1))\). Then according to Proposition 6, the time complexity of Steps 2–3 is \(O(|U''||U^-||C|+|U''||U^-|(|C|+1)+|U''|^2|C|+|U''|^2(|C|+1))\approx O(|U''| |U^-||C|)\). In Step 5, the time complexity of computing \(GP_{U^-}(D|(B-\{a_i\}))\) is similar to that of \(GP_{U^-}(D|C)\). Since \(|U''|\ll |U^-|\), the time complexity of Steps 4–8 is \(O(|B|(|U''||U^-||B|+|U''||U^-|(|B|+1)+|U''|^2|B|+|U''|^2(|B|+1)))\approx O(|U''||U^-||B|^2)\). In general, if a reduct obtained is of practical value, \(|C|\le |B|^2\) should be satisfied. Hence, the time complexity of Algorithm 2 is \(O(|U''||U^-||C|+|U''||U^-||B|^2)\approx O(|U''||U^-||B|^2)\).

Two algorithms for comparison with algorithm KGIRD-M were introduced in [57]. One is the non-incremental algorithm called algorithm THA which is converted as algorithm THD-M in this paper to be suitable for incomplete decision systems under the situation of deleting multiple objects at a time. Another is the incremental algorithm called algorithm KGIRD which is called as algorithm KGIRD-S in this paper for incomplete decision systems under the situation of deleting one object at a time. Since the number of objects is \(|U^-|\), the time complexity of THD-M is actually \(O(|U^-|^2|C|^2)\) when deleting the object set \(U''\) from the original object set U. Because \(|B| \le |C|\) and \(|U''| \le |U^-|\), \(O(|U''||U^-||B|^2)\) is lower than \(O(|U^-|^2|C|^2)\). Hence, the time complexity of algorithm KGIRD-M is much smaller than that of algorithm THD-M. Since the number of objects is \(|U^-|\) after deleting the object set \(U''\) from the original object set U, the time complexity of KGIRD-S is \(O(|U''||U^-||C|^2)\). Because \(|B| \le |C|\), \(O(|U''||U^-||B|^2)\) is lower than \(O(|U''||U^-||C|^2)\). Hence, the time complexity of algorithm KGIRD-M is smaller than that of algorithm KGIRD-S. Since \(|U''| \ll |U^-|\), we can draw the conclusion that the time complexity of KGIRD-S is also much smaller than that of algorithm THD-M.

4 Empirical experiments

4.1 A description of data sets and experimental environment

The proposed incremental attribute reduction algorithms are tested on data sets available from the University of California Irvine (UCI) Repository of Machine Learning Database (http://archive.ics.uci.edu/ml) and the Kent Ridge Biomedical Data Set Repository (http://leo.ugr.es/elvira/DBCRepository/). In order to get incomplete decision systems from complete data sets, \(5\%\) of the attribute values randomly selected from each complete data set are deleted. The characteristics of the data sets are summarized in Table 3.

Table 3 A description of data sets
Full size table

The proposed algorithms and comparative algorithms are implemented in Eclipse IDE for Java Developers with Neon.3 Release (4.6.3) version using JDK \(1.8.0\_111\) version and they have been carried out on a personal computer with the following specification: Intel Core i3-3120M 2.5GHz CPU, 4.0 GB of memory and 64-bit Win7.

4.2 Performance comparison on computational time

In the comparative experiments under the condition that objects are added to decision systems, each original data set is divided into ten parts averagely according to the number of objects. Two parts of each original data set is set as the basic data set and the rest are set as the incremental data set which is going to be added to the basic data set in subsequent steps. In algorithm KGIRA-S, objects in incremental data set are added to basic data set one by one. Once all objects in one part of the original data set are added to the basic data set, the spent time is recorded, until all parts in the incremental data set are added to the basic data set. In algorithms KGIRA-M and THA-M, one part in the incremental data set is added to the basic data set at a time which makes a note of the time. In each sub-figure of Fig. 1, the x-axis represents the percentage of the number of objects in the basic data set to that of objects in the original data set and the y-axis represents the value of computational time. Asterisk marked lines denote the computational time of algorithm KGIRA-M, circle marked lines denote the computational time of algorithm KGIRA-S and plus marked lines denote the computational time of algorithm THA-M.

Fig. 1
figure 1

Comparisons for computational time of different algorithms for adding objects

Full size image

From Fig. 1, for each data set, the computational time of three algorithms increases with the number of objects which are added to the basic data set. The computational time of algorithms KGIRA-M and KGIRA-S is much shorter than that of the algorithm THA-M, which illustrates that incremental algorithms are more efficient than the non-incremental algorithm. Moreover, the computational time of algorithm KGIRA-M is shorter than that of algorithm KGIRA-S, which shows that processing multiple objects at a time is more efficient than processing one object at a time by the incremental approaches. It is clearly that the proposed algorithm KGIRA-M has the highest efficiency among the three comparative algorithms.

In the comparative experiments of deleting objects from the original data set, each original data set is set as basic data set and divided into ten parts (Part 1, Part2, ..., Part10) averagely according to the number of objects. In algorithm KGIRD-S, objects are deleted from the basic data set until eight parts (Part 1, Part2, ..., Part8) of the original data set are removed. In each part to be removed, objects are deleted one by one. Once one part is deleted from the basic data set, the accumulative computing time is recorded. In algorithms KGIRD-M and THD-M, objects from one part of the basic data set are deleted at a time which makes a note of the time. The x-axis represents the percentage of the number of objects retained to that of objects in the original data set and the y-axis represents the value of computational time. The accumulative time is recorded for all algorithms. Asterisk marked lines denote computational time of algorithm KGIRD-M, circle marked lines denote computational time of algorithm KGIRD-S and plus marked lines denote computational time of algorithm THD-M.

Fig. 2
figure 2

Comparisons for computational time of different algorithms for deleting objects

Full size image

From Fig. 2, for each data set, the computational time of three algorithms increases when the number of objects deleted from decision system increases. The computational time of algorithms KGIRD-M and KGIRD-S is much smaller than that of the algorithm THD-M, which illustrates that incremental algorithms are more efficient than the non-incremental algorithm. Moreover, the computational time of algorithm KGIRD-M is smaller than that of the algorithm KGIRD-S, which shows that processing multiple objects at a time is more efficient than processing one object at a time by the incremental approaches. It should be noted that the computational time of algorithm KGIRD-M and algorithm KGIRD-S looks close for the data sets LSVT voice, Colon, and AMLALL. This is because the computational time of algorithm KGIRD-M is close to that of algorithm KGIRD-S relative to the computational time of algorithm THD-M. In fact, the computational time of algorithm KGIRD-S is several times that of algorithm KGIRD-M on the same data set. For example, on the data set AMLALL, the computational time of algorithm KGIRD-S is nearly four times that of algorithm KGIRD-M. It is clearly that the proposed algorithm KGIRD-M has the highest efficiency among the three comparative algorithms.

4.3 Performance comparison on reduct size

In general, the number of attributes in a reduct, also called the size of the reduct(SR), is an important reference index to evaluate the effects of attribute reduction algorithms. The efficiency of data processing increases with SR decreasing, because the number of attributes participating in the calculation decreases with SR decreasing. In Table 4, the reduct for each data set is obtained from the data set with all of the objects. We can find that reducts obtained by algorithm KGIRA-M or KGIRA-S are not the same as those obtained by algorithm THA-M. Moreover, SR obtained by algorithm KGIRA-M or KGIRA-S is a little more than that obtained by algorithm THA-M on most of data sets. It is because that algorithms KGIRA-M and KGIRA-S get reducts through the previous results. However, SR obtained by algorithm KGIRA-M is less than that obtained by algorithm KGIRA-S on most of data sets, because algorithm KGIRA-M gets reducts based on the previous results in a way that multiple objects are processed at a time rather than one by one.

Table 4 Comparisons for reducts of different algorithms for adding objects
Full size table

In Table 5, the reduct for each data set is obtained from the data set with remained objects. We can find that reducts obtained by algorithms KGIRD-M and KGIRD-S are obviously different from those obtained by algorithm THD-M. Furthermore, SR obtained by algorithm KGIRA-M or KGIRA-S is a little more than that obtained by algorithm THD-M. It is because, on the one hand, algorithms KGIRD-M and KGIRD-S get the reducts based on the previous results while algorithm THD-M computes the results from the beginning, on the other hand, results of attribute reduction for decision systems are not unique. However, reducts obtained by algorithm KGIRD-M are the same as those obtained by algorithm KGIRD-S on most data sets.

Table 5 Comparisons for reducts of different algorithms for deleting objects
Full size table

4.4 Performance comparison on classification accuracy

In Table 6, the classification accuracy is calculated by Naive Bayes Classifier (NB) and Decision Tree algorithm (REPTree) with fivefold cross-validation from the reducts of algorithms KGIRA-M, KGIRA-S and THA-M. From Table 6, it is clear that the average classification accuracy of the reducts found by incremental algorithms is better than that by non-incremental algorithm. Furthermore, the average classification accuracy of the reducts found by algorithm KGIRA-M is higher than that by algorithm KGIRA-S. The experimental results show that the proposed algorithm KGIRA-M can discover a better attribute reduct compared with algorithm KGIRA-S and THA-M from the viewpoint of classification performance. Moreover, algorithm KGIRA-M can discover a feasible attribute reduct with the shortest computational time compared with algorithms KGIRA-S and THA-M.

Table 6 Comparison on classification accuracy of different algorithms for adding objects
Full size table

In Table 7, the classification performance is calculated on the reducts obtained by algorithms KGIRD-M, KGIRD-S and THD-M. The results of classification accuracy are calculated by Naive Bayes Classifier (NB) and Decision Tree algorithm(REPTree) with fivefold cross-validation. From Table 7, it is clear that the average classification accuracy of the reducts found by incremental algorithm KGIRD-M is slightly higher than that by algorithms KGIRD-S and THD-M. The experimental results show that the incremental algorithm KGIRD-M can discover a satisfactory attribute reduct from the viewpoint of classification performance. Moreover, algorithm KGIRD-M can discover a feasible attribute reduct with the shortest computational time compared with algorithms KGIRD-S and THD-M.

Table 7 Comparison on classification accuracy of different algorithms for deleting objects
Full size table

5 Conclusion

In this paper, we exploit deeper insights into incremental mechanisms for the attribute reduction process from granulation perspective. By introducing the granulation measure into incomplete decision systems, we propose two incremental attribute reduction approaches based on knowledge granularity under the situations of adding multiple objects and deleting multiple objects at a time, respectively. Compared with existing methods, our incremental attribute reduction approaches can deal with variation of object sets in incomplete decision systems effectively.

Attribute reduction for other variations of incomplete decision systems is not concerned, and we plan to study knowledge granularity based incremental attribute reduction solutions for incomplete decision systems under the situation of variation of attribute sets or attribute values.