Abstract
In this paper, we study interval-valued fuzzy probabilistic rough sets (IVF-PRSs) based on multiple interval-valued fuzzy preference relations (IVFPRs) and consistency matrices, i.e., the multi-granulation interval-valued fuzzy preference relation probabilistic rough sets (MG-IVFPR-PRSs). First, in the proposed study, we convert IVFPRs into fuzzy preference relations (FPRs), and then construct the consistency matrix, the collective consistency matrix, the weighted collective preference relations, and the group collective preference relation (GCPR). Using this GCPR, four types of MG-IVFPR-PRSs are founded in terms of different constraints on parameter. Finally, to find a suitable way of explaining and determining these parameters in each model, three-way decisions are studied based on Bayesian minimum-risk procedure, i.e., the multi-granulation interval-valued fuzzy preference relation decision-theoretic rough set approach. An example is included to show the feasibility and potential of the theoretic results obtained.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The idea of rough set theory was basically proposed by Pawlak in (1982). A key notion of that theory is the approximation of a subset of objects by a pair of definable sets called lower and upper approximations. It is characterized by a zero tolerance of errors; that is, an object in the lower approximation which certainly belongs to set and an object in the complement of the upper approximation which certainly does not belongs to the set. For that reason, many different generalizations of rough sets are proposed. By introducing certain levels of errors, probabilistic rough sets (PRSs) (Yao 2008) are quantitative generalization of rough sets. Although several specific models of PRSs had been considered by some studies (Yao 1998, 2003; Ma and Sun 2012; Ziarko 2005, 2008; Wang and Xu 2002; Yao et al. 2008; Pawlak et al. 1988; Polkowski 1996), a more general model, called decision-theoretic rough set (DTRS) model, was proposed by Yao and Wong (1992) and Yao (2009). With the aid of Bayesian minimum-risk decision procedure, DTRS model offers mathematical way to interpret and determine the required thresholds in PRS. This model is fulfilled by splitting the approximated set into three regions, conducted by the idea of 3WDs (Yao 2010). The 3WDs consists of three different kinds of rules—positive rules (corresponding to positive region), negative rules (corresponding to the negative region), and boundary rules (corresponding to boundary region). In DTRS model, based on Bayesian minimum risk, conditional probability and loss function play an important role in determining thresholds from the given cost function. Different thresholds for different PRSs can be deduced from appropriate cost functions.
However, the PRSs and DTRS model cannot deal with numerical data directly. For that reason, many studies usually adopted in real applications, which define all types of relations rather than equivalence relations, e.g., tolerance relations (Liang et al. 2012), similarity measures (Liu et al. 2016), dominance relations (Du and Hu 2016), covering (Wang et al. 2015), inclusion measures (Zhang et al. 2016), fuzzy relations (Wei and Zhang 2004; Sun et al. 2014; Yang et al. 2013), intuitionistic fuzzy relations (Liang and Liu 2015; Zhang et al. 2017), and bipolar-valued fuzzy relations (Mandal and Ranadive 2017). They can be used to measure and represent various real values.
To handling all types of real data, Zadeh (1965) introduced fuzzy sets. The remarkable applications of fuzzy sets are done in Horng et al. (2005), Chen and Kao (2013), Chen and Hong (2014), Chen (1996), Chen and Chen (2011), and Chen et al. (2009). However, it is well known that interval-valued fuzzy set (IVFS) is more effective than fuzzy set for imprecise evaluation (Chen and Horng 1996; Chen 1997; Chen et al. 1997; Chen and Hsiao 2000; Chen and Chen 2008, 2009; Wei and Chen 2009; Chen and Wang 2009; Chen and Sanguansat 2011; Mendel et al. 2006; Chen and Lee 2010; Lee and Chen 2008). Thus, studies on combination of IVFS and rough set theory have been considered to be significant approach to rough set theory. Liang and Liu 2014 combined IVFS and DTRS, and then study on 3WDs with interval-valued decision-theoretic rough sets (IVDTRS). Zhao and Hu (2015, 2016) study interval-valued fuzzy decision-theoretic rough set (IVF-DTRS) approaches based on fuzzy probability measure and IVF-PRSs and their corresponding 3WDs.
Granular computing (Pedrycz and Chen 2011, 2015a, b) is an emerging computing paradigm of information processing. It concerns the processing of complex information entities called granules, which arise in the process of data abstraction and derivation of knowledge from information or data. Therefore, in the viewpoint of granular computing, Qian et al. (2010b) generalized Pawlak rough set model to a multi-granulation rough set (MGRS) model using multiple equivalence relations instead of single equivalence relation. In the MGRS model, two basic models are mainly proposed, such as optimistic and pessimistic MGRS (Qian et al. 2010b). Since then, MGRSs have been developed quickly (Qian et al. 2010a; Liu et al. 2014; Lin et al. 2012; Xu et al. 2011, 2012, 2013, 2014). The combination of MGRSs and DTRSs is an important topic among these developments (Lv et al. 2013; Feng and Mi 2016; Qian et al. 2014).
However, preference analysis is a class of important issues in group decision-making for pairwisely comparing alternatives. The decision makers are expressed his/her opinions as preference relations. Then, they are used to deriving the weights of alternatives, and thus, the best alternative is chosen. Based on fuzzy set theory (Zadeh 1965), the preference degree of the alternative \(x_{i}\) over the alternative \(x_{j}\) can be expressed as \(r_{ij}\in [0,1]\). Then, a fuzzy binary relation on \(U=\{x_{1},x_{2},\ldots , x_{n}\}\) is defined and a preference matrix \(R(x_{i},x_{j})=(r_{ij})_{n \times n}\) with the entries \(r_{ij}\) is given. The preference matrix is called an FPR (Tanio 1984; Chen and Niou 2011), where \(r_{ij}\in [0,1]\) and \(r_{ii}=0.5\), since the preference value is exact real numbers. However, owing to the complexity and uncertainty of the real-world decision-making problems, it is difficult to provide precise preference value to evaluate the judgments. For that reason, it is popular to study decision-making models and their applications, where the judgments of decision makers are expressed as interval-valued comparison matrix (Xu 2011; Chen et al. 2015; Liu et al. 2018).
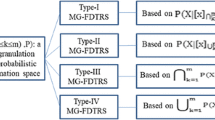
On the basis of above-mentioned analysis, IVF-PRSs considered the incomplete available information and the possible existence of random available information of the objects, while it cannot consider multi-granulation and preference analysis. In group decision-making problem using IVFPRs, the decision results are obtained pairwise comparing the objects according to derive its weights, while it cannot consider the incomplete available information and the possible existence of random available information of the objects. Therefore, the motivation of this paper is to study IVF-PRSs based on multiple IVFPRs and consistency matrices, i.e., MG-IVFPR-PRSs. In fact, the consistency matrices are constructed to avoid the self-contradiction of the objects. Based on MG-IVFPR-PRSs, we develop a new approach for group decision-making which is considered the incomplete available information, the possible existence of random available information, and preference analysis. First, a multi-granulation interval-valued fuzzy preference relation probabilistic approximation space (MG-IVFPR-PAS) is defined using m IVFPRs. Then, we aggregate the m IVFPRs given by m experts and construct the group collective preference relation (GCPR) according to the method as given in Chen et al. (2015). Second, we investigate four types of MG-IVFPR-PRSs within the frameworks of MG-IVFPR-PAS and GCPR in terms of different constraints on parameters. Third, Bayesian decision procedure within the MG-IVFPR-PRS, i.e., the MG-IVFPR-DTRS approach is studied. Finally, we develop a new approach for group decision-making using MG-IVFPR-PRSs and their corresponding 3WDs. What we want to do is shown in Fig. 1.
The paper is organized as follows: in Sect. 2, some basic concepts about fuzzy probability and FPRs are briefly represented. Section 3 is devoted to MG-FPR-PRS models as well as associated 3WDs in the framework of MG-IVFPR-PAS. In Sect. 4, we propose a new approach for group decision-making based on MG-IVFPR-PRSs including practical applications. Section 5 concludes the paper.
2 Preliminaries
In this section, we will review some basic concepts such as interval-valued fuzzy sets, interval-valued fuzzy probability, and interval-valued fuzzy preference relations, which have been addressed in Zadeh (1965, 1968), Zhao and Hu (2015, 2016), Tanio (1984), Lee (2012), and Chen et al. (2014).
2.1 Fuzzy sets and probability theory
Let U be a universe of discourse. A fuzzy set A is a mapping from U into [0, 1], i.e., \(A : U \rightarrow [0, 1], x \mapsto A(x)\in [0, 1],~ \forall x\in U\). The family of all fuzzy sets on U is denoted by F(U). Given a fuzzy set \(A \in F(U)\) and \(\alpha \in [0, 1]\), the \(\alpha\)-cut set of A is defined as \(A_{\alpha } = \{x \in U : A(x) \ge \alpha \}\), which is a classical subset of U.
Definition 1
(Zadeh 1968) Let \((U, \texttt {A}, P)\) be a probability space in which U is a sample space of events, \(\texttt {A}\) is a \(\sigma\)-algebra of events (i.e., the measurable subsets of U), and P is a probability measure defined on \(\texttt {A}\). For a fuzzy set \(A \in F(U)\), if \(A \in \zeta (\texttt {A})= \{A \in F(U) : A_{\alpha } \in \texttt {A}, \alpha \in [0,1] \}\), then A is a fuzzy event on U. The probability of fuzzy event A (called the fuzzy probability of A) is \(P(A) = \int _{U}A(x) dP\).
If \(U = \{x_{1}, x_{2}, \ldots , x_{n} \}\), and \(p_{i}= P(\{x_{i}\})\)\((i = 1, 2, \ldots , n)\), then
Definition 2
(Zadeh 1968) Let \((U, \texttt {A}, P)\) be a probability space and A, B be two fuzzy events on U. If \(P(B) \ne 0\), then the conditional probability of A given B (called fuzzy conditional probability) is defined as \(P(A\mid B) = \dfrac{P(AB)}{P(B)}\).
If \(U = \{x_{1}, x_{2}, \ldots , x_{n} \}\), and \(p_{i}= P(\{x_{i}\})\)\((i = 1, 2, \ldots , n)\), then
for all fuzzy events \(A, B \in \zeta (\texttt {A})\).
Proposition 1
(Zhao and Hu 2016) Let (U, \(\texttt {A}\), P) be a probability space andA, B, Cbe three fuzzy events onU. If\(P(A) \ne 0\), then the following conclusions hold.
-
(1)
\(P(\emptyset \mid A) = 0, P(U \mid A) = 1\);
-
(2)
If \(B\subseteq C\), then \(P(B) \le P(C)\) and \(P(B\mid A) \le P(C \mid A)\);
-
(3)
\(P(B\mid A) + P(B^{c}\mid A) = 1\).
2.2 Interval-valued fuzzy sets and probability theory
Let \(\mathbf I _{\mathbb {R}^{+}} = \{[a^{-},a^{+}] : 0 \le a^{-} \le a^{+}, a^{-},a^{+} \in \mathbb {R}^{+}\}\) be the family of all positive interval numbers. We denote by \(\tilde{a}=[a,a]\) the degenerate interval numbers. The arithmetic operation of interval numbers is defined as follows: for all \([a^{-},a^{+}], [b^{-},b^{+}] \in \mathbf I _{\mathbb {R}^{+}}\),
and if \(b^{-}\ne 0\), the division is defined as follows:
For simplicity, symbol \(\otimes\) is omitted in the sequel.
If \(0 \le a^{-} \le a^{+} \le 1\), it is defined that \(\overline{1} - [a^{-},a^{+}] = [1 - a^{+}, 1 - a^{-}]\).
The order relation on \(\mathbf I _{\mathbb {R}^{+}}\) is defined as: for all \([a^{-},a^{+}], [b^{-},b^{+}] \in \mathbf I _{\mathbb {R}^{+}}\),
Obviously, the order on \(\mathbf I _{\mathbb {R}^{+}}\) is partial. The strict order of interval numbers is defined as: \([a^{-},a^{+}] < [b^{-},b^{+}]\) if and only if \(a^{-} < b^{-}\), \(a^{+} \le b^{+}\) or \(a^{-} \le b^{-}\), \(a^{+} < b^{+}\).
Based on the order relation defined in (6) for positive interval numbers, the corresponding join, \(\vee\), and meet, \(\wedge\), are defined, respectively, as follows: for all \([a^{-},a^{+}], [b^{-},b^{+}] \in \mathbf I _{\mathbb {R}^{+}}.\)
Let \(\mathbf I _{[0,1]} = \{[a^{-},a^{+}] : 0 \le a^{-} \le a^{+} \le 1\}\) be the set of all interval numbers on [0, 1]. Let U be a universe of discourse. An interval-valued fuzzy set (IVFS) on U is a mapping that assigns each object in U a unique interval value from \(\mathbf I _{[0,1]}\), that is
Let \(\mathcal {A}(x) = [a^{-},a^{+}] \triangleq [A^{-}(x),A^{+}(x)]\) for each \(x \in U\). Then, two fuzzy sets \(A^{-}\) and \(A^{+}\) on U, called lower and upper fuzzy sets of \(\mathcal {A}\), are derived with \(A^{-}\subseteq A^{+}\). Subsequently, an IVFS \(\mathcal {A}\) is always denoted by \([A^{-},A^{+}]\). Let \({F}_\mathbf{I _{[0,1]}}(U)\) be the family of all IVFSs on U. The operators for IVFSs are defined through respective operations on lower and upper fuzzy sets. For all IVFSs \(\mathcal {A}, \mathcal {B} \in {F}_\mathbf{I _{[0,1]}}(U)\) and each \(x \in U\),
The order of IVFSs is defined as: for all \(\mathcal {A}, \mathcal {B} \in {F}_\mathbf{I _{[0,1]}}(U)\), \(\mathcal {A} \subseteq \mathcal {B} \Leftrightarrow A^{-}(x) \le B^{-}(x), A^{+}(x) \le B^{+}(x)\), \(\forall x \in U\).
Definition 3
(Zadeh 1968) Let \((U, \texttt {A}, P)\) be a probability space in which U is a sample space of events, \(\texttt {A}\) is a \(\sigma\)-algebra of events (i.e., the measurable subsets of U), and P is a probability measure defined on \(\texttt {A}\). For an IVFS \(\mathcal {A}\) on U, if
where \((A^{-})_{\alpha }\) and \((A^{+})_{\alpha }\) are \(\alpha\)-cut sets of lower and upper fuzzy sets of \(\mathcal {A}\), respectively, and then, \(\mathcal {A}\) is an interval-valued fuzzy event on U. The probability of an interval-valued fuzzy event \(\mathcal {A}\) (called the interval-valued fuzzy probability of \(\mathcal {A}\)) is
where \(\mathcal {A} = [A^{-}, A^{+}]\).
If \(U = \{x_{1}, x_{2}, \ldots , x_{n} \}\), and \(p_{i}= P(\{x_{i}\})\)\((i = 1, 2, \ldots , n)\), then Definition 1 that
for each interval-valued fuzzy event \(\mathcal {A} = [A^{-}\), \(A^{+}] \in {F}_\mathbf{I _{[0,1]}}(U).\)
Definition 4
(Zhao and Hu 2015) Let \((U, \texttt {A}, P)\) be a probability space and \(\mathcal {A} = [A^{-}, A^{+}]\), \(\mathcal {B} = [B^{-}, B^{+}]\) be two interval-valued fuzzy events on U with \(P(B^{-}) \ne 0\). The conditional probability of \(\mathcal {A}\) given \(\mathcal {B}\) (called interval-valued fuzzy conditional probability) is defined by
Proposition 2
(Zhao and Hu 2015) Let (U, \(\texttt {A}\), P) be a probability space and\(\mathcal {A} = [A^{-}, A^{+}]\), \(\mathcal {B} = [B^{-}, B^{+}]\)be two interval-valued fuzzy events onUwith\(P(B^{-}) \ne 0\), the following holds:
If \(U = \{x_{1}, x_{2}, \ldots , x_{n} \}\), and \(p_{i}= P(\{x_{i}\})\)\((i = 1, 2, \ldots , n)\), then
Proposition 3
(Zhao and Hu 2016) Let (U, \(\texttt {A}\), P) be a probability space and\(\mathcal {A} = [A^{-}, A^{+}]\), \(\mathcal {B} = [B^{-}, B^{+}]\)and\(\mathcal {C} = [C^{-}, C^{+}]\)be three interval-valued fuzzy events onU. If\(P(A^{-}) \ne 0\), then the following conclusions hold.
-
(1)
\(P(\emptyset \mid \mathcal {A}) = \tilde{0}, P(U \mid \mathcal {A}) = \tilde{1}\) ; and
-
(2)
If \(\mathcal {B}\subseteq \mathcal {C}\), then\(P(\mathcal {B}\mid \mathcal {A}) \le P(\mathcal {C} \mid \mathcal {A})\).
According to Propositions 1 and 2 that
2.3 Fuzzy and interval-valued fuzzy preference relations
Definition 5
(Tanio 1984) Let R be a fuzzy preference relation (FPR) for the set \(U = \{x_{1}\), \(x_{2}\), \(\cdots\), \(x_{n}\}\), shown as follows:

where \(r_{ij}\) denotes the degree of preference of alternative \(x_{i}\) over alternative \(x_{j}\), \(r_{ij} \in [0,1]\), \(r_{ii}=0.5\), \(1\le i \le n\) and \(1\le j \le n\). Especially,
\(r_{ij}=0.5\) indicates that there is no difference between alternative \(x_{i}\) and alternative \(x_{j}\);
\(r_{ij}>0.5\) indicates that alternative \(x_{i}\) is better than alternative \(x_{j}\);
\(r_{ij}<0.5\) indicates that alternative \(x_{j}\) is better than alternative \(x_{i}\);
\(r_{ij}=1\) indicates that alternative \(x_{i}\) is absolutely better than alternative \(x_{j}\);
\(r_{ij}=0\) indicates that alternative \(x_{j}\) is absolutely better than alternative \(x_{i}\);
where \(1\le i \le n\) and \(1\le j \le n\).
Definition 6
(Lee 2012) Given a fuzzy preference relation \(R=(r_{ij})_{n \times n}\), where \(r_{ij}\) denotes the fuzzy preference value (FPV) for alternative \(x_{i}\) over alternative \(x_{j}\), \(r_{ij} + r_{ji} = 1\), \(r_{ii}=0.5\), \(1\le i \le n\) and \(1\le j \le n\). The consistency matrix \(\overline{R} = (\overline{r}_{ik})_{n \times n}\) is constructed based on the FPR R, shown as follows:
The consistency matrix \(\overline{R} = (\overline{r}_{ik})_{n \times n}\) has the following properties (Lee 2012):
-
(1)
\(\overline{r}_{ik} + \overline{r}_{ki} = 1\),
-
(2)
\(\overline{r}_{ii}=0.5\),
-
(3)
\(\overline{r}_{ik} = \overline{r}_{ij} + \overline{r}_{jk} - 0.5\),
-
(4)
\(r_{ik} \le r_{is}\) for all \(i \in \{1,2,\ldots ,n\}\), where \(k \in \{1,2,\ldots ,n\}\) and \(s \in \{1,2,\ldots ,n\}\).
Definition 7
(Chen et al. 2014) Let \(\overline{R} =\)\((\overline{r}_{ik})_{n \times n}\) be a consistency matrix constructed by a FPR \(R=(r_{ij})_{n \times n}\) given by an expert. The consistency degree d between R and \(\overline{R}\) is defined as follows:
where \(d \in [0,1]\), \(r_{ij}\) denotes the FPV in the FPR R for alternative \(x_{i}\) over alternative \(x_{j}\), and \(\overline{r}_{ij}\) denote an FPV in the consistency matrix \(\overline{R}\) for alternative \(x_{i}\) over alternative \(x_{j}\), \(1\le i \le n\), and \(1\le j \le n\). The larger the value of d, the more consistent the FPR given by the expert. If the value of d is close to one, then the information of the FPR given by the expert is more consistent.
Definition 8
(Xu 2011) Let \(\mathcal {R}\) be an interval-valued fuzzy preference relation (IVFPR) for the set \(U = \{x_{1}, x_{2}, \ldots , x_{n}\}\), shown as follows:

where \(\nabla_{ij} = [r_{ij}^{-}, r_{ij}^{+}]\) denotes an interval-valued fuzzy preference value (IVFPV) for alternative \(x_{i}\) over alternative \(x_{j}\). Then, \(0 \le r_{ij}^{-} \le r_{ij}^{+} \le 1\), \(\nabla_{ji} = \tilde{1} - \nabla_{ij} = [1 - r_{ij}^{+}, 1 - r_{ij}^{-}]\), \(r_{ii}^{+}= r_{ii}^{-} = 0.5\), \(1\le i \le n\) and \(1\le j \le n\).
3 Multi-granulation interval-valued fuzzy preference relation probabilistic rough sets
This section proposes the model of multi-granulation interval-valued fuzzy preference relation probabilistic rough sets (MG-IVFPR-PRSs), within the framework of multi-granulation interval-valued fuzzy preference relation probabilistic approximation space.
Definition 9
Let \(U = \{x_{1}, x_{2}, \ldots , x_{n}\}\) be a non-empty finite universe. \(\mathcal {R}^{q} (1 \le q \le m)\) be m IVFPRs for the set U. P be a probability measure defined on the \(\sigma\)-algebra formed by the image of element \(x_{i} \in U (1 \le i \le n)\). Then, we call \((U, \mathcal {R}^{q}(1 \le k \le m), P)\) a multi-granulation interval-valued fuzzy preference relation probabilistic approximation space (MG-IVFPR-PAS).
For aggregating the m IVFPRs \(R^{q} (1 \le q \le m)\) given by m experts \(e_{q}(1 \le q \le m)\), we adopt the following algorithm as given in Chen et al. (2015).
Algorithm 1 Assume that there are m IVFPRs \(\mathcal {R}^{1}\), \(\mathcal {R}^{2}\), \(\ldots\), \(\mathcal {R}^{m}\) given by m experts \(e_{1}\), \(e_{2}\), \(\ldots\), \(e_{m}\), respectively. Assume that the IVFPR \(\mathcal {R}^{q}\) given by expert \(e_{q}\) for alternative \(x_{i}\) over alternative \(x_{j}\) is shown as follows:

where \(\nabla^{q}_{ij}\) is an IVFPV, \(\nabla^{q}_{ij} = [{r_{ij}^{-}}^{q}, {r_{ij}^{+}}^{q}]\), \(0 \le {r_{ij}^{-}}^{q} \le {r_{ij}^{+}}^{q} \le 1\), \(\nabla_{ji}^{q} = \tilde{1} - \nabla_{ij}^{q} = [1 - {r_{ij}^{+}}^{q}, 1 - {r_{ij}^{-}}^{q}]\), \({\nabla_{ii}^{+}}^{q} = {\nabla_{ii}^{-}}^{q} = 0.5\), \(1\le i \le n\), \(1\le j \le n\), and \(1\le q \le m\).
Step 1: For the IVFPRs given by expert \(e_{q}\), construct the FPR \(R^{q} = (r_{ij}^{q})_{n \times n}\) for expert \(e_{q}\), construct the consistency matrix \(\overline{R}^{q}=(\overline{r}^{q}_{ij})_{n \times n}\) for each expert \(e_{q}\), construct the collective consistency matrix \(\overline{R}^{*}\)\(=(\overline{r}^{*}_{ij})_{n \times n}\), and calculate the consistency degree \(d_{q}\) of expert \(e_{q}\), where
where \(1\le i \le n\), \(1\le j \le n\), \(1\le q \le m\) and \(\theta \in [0,1]\). In Eq. (16), we let \(r_{ij}^{q} = \frac{1}{2} ({r_{ij}^{-}}^{q} + {r_{ij}^{+}}^{q})\), where \(r_{ij}^{q} \in [0,1]\), \(1\le i \le n\), \(1\le j \le n\) and \(1\le q \le m\), such that we can transform the IVFPR \(\mathcal {R}^{q}(x_{i}, x_{j}) = (\nabla^{q}_{ij})_{n \times n}\) given by expert \(e_{q}\) into the FPR \(R^{q} = (r_{ij}^{q})_{n \times n}\), where \(r_{ij}^{q} \in [0,1]\), \(1\le i \le n\), \(1\le j \le n\), \(1\le q \le m\) and m is the number of decision makers. In Eq. (17), we adopt Eq. (12) to construct the consistency matrix \(\overline{R}^{q}=(\overline{r}^{q}_{ij})_{n \times n}\) for expert \(e_{q}\), where \(\overline{r}^{q}_{ij} \in [0,1]\), \(1\le i \le n\), \(1\le j \le n\)\(1\le q \le m\), and m is the number of decision makers. In Eq. (18), we adopt Eq. (13) to calculate the consistency degree \(d_{q}\) for expert \(e_{q}\), where \(d_{q} \in [0,1]\), \(1\le q \le m\), and m is the number of decision makers. In Eq. (19), we let \(\overline{r}^{*}_{ij} = \frac{1}{m}\sum _{q=1}^{m}\overline{r}^{q}_{ij}\) to construct the collective consistency matrix \(\overline{R}^{*}=(\overline{r}^{*}_{ij})_{n \times n}\) for all experts, where \(\overline{r}^{q}_{ij} \in [0,1]\), \(1\le i \le n\), \(1\le j \le n\), \(1\le q \le m\), and m is the number of decision makers.
Step 2: Calculate the weight \(\lambda _{q}\) of expert \(e_{q}\) based on the obtained consistency degrees of the experts, shown as follows:
where \(d_{q}\) is the consensus degree of expert \(e_{q}\) and \(1\le q \le m\).
Step 3: Construct the weighted collective preference relation \(\mathcal {R}^{*} = (\nabla^{*}_{ij})_{n \times n}\) for all experts, shown as follows:
where \(1\le i \le n\), \(1\le j \le n\) and \(1\le q \le m\).
Step 4: Construct the group collective preference relation (GCPR) \(\widehat{\mathcal {R}} = (\widehat{\nabla}_{ij})_{n \times n}\) for all experts, shown as follows:
where \(1\le i \le n\), \(1\le j \le n\), and \(1\le q \le m\). Equation (22) shows that the GCPR is also IVFS, so we denote \(\widehat{\mathcal {R}} = [\widehat{\mathcal {R}}^{-}, \widehat{\mathcal {R}}^{+}]\).
Definition 10
Let \(\mathcal {R}^{q} (1 \le q \le m)\) be m IVFPRs for the set U given by the experts \(e_{q} (1 \le q \le m)\), respectively. Let \(\widehat{\mathcal {R}}\) be the GCPR constructed by m IVFPRs \(\mathcal {R}^{q} (1 \le q \le m)\). Then, for each \(x_{i} \in U (1 \le i \le n)\), the IVFS \([x_{i}]_{\widehat{\mathcal {R}}}\) is defined as
for all \(x_{j} \in U (1 \le j \le n)\). In Eq. (23), we adopt Algorithm 3 to calculate the fuzzy set \([x_{i}]_{\widehat{\mathcal {R}}}(1 \le i \le n)\).
3.1 MG-IVFPR-PRSs based on interval-valued fuzzy probability
The aim of proposing MG-IVFPR-PRSs is to characterize fuzzy events in terms of the available knowledge represented by m IVFPRs given by the m experts.
Definition 11
Let \((U, \mathcal {R}^{q}(1 \le k \le m), P)\) be a MG-IVFPR-PAS, \(\widehat{\mathcal {R}}\) be the GCPR constructed by m IVFPRs \(\mathcal {R}^{q} (1 \le q \le m)\), and \(\mathcal {A} = [A^{-}, A^{+}] (\in {F}_{\mathbf{I} _{[0,1]}}(U))\) be a interval-valued fuzzy event. For a pair of parameters \([\alpha ^{-}, \alpha ^{+}]\) and \([\beta ^{-}, \beta ^{+}]\) with \(\tilde{0} \le [\beta ^{-}, \beta ^{+}]< P(\mathcal {A}) < [\alpha ^{-}, \alpha ^{+}] \le \tilde{1}\), the \([\alpha ^{-}, \alpha ^{+}]\)-multi-granulation interval-valued fuzzy preference relation probabilistic lower approximation and \([\beta ^{-}, \beta ^{+}]\)-multi-granulation interval-valued fuzzy preference relation probabilistic upper approximation of \(\mathcal {A}\) are defined, respectively, as follows:
The pair \((\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-}, \alpha ^{+}]}(\mathcal {A}), \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}(\mathcal {A}))\) is called \(([\alpha ^{-}, \alpha ^{+}], [\beta ^{-}, \beta ^{+}])\)-multi-granulation interval-valued fuzzy preference relation probabilistic rough set (\(([\alpha ^{-}, \alpha ^{+}], [\beta ^{-}, \beta ^{+}])\)-MG-IVFPR-PRS) of \(\mathcal {A}\). The positive, negative, and boundary regions of \(\mathcal {A}\) are defined, respectively, as follows:
Remark 1
If \(U = \{x_{1}, x_{2}, \ldots , x_{n} \},\) and \(P(x_{i})\)\(=\)\(p_{i}(i = 1, 2, \ldots , n)\), then we have
where
Proposition 4
Let\((U, \mathcal {R}^{q}(1 \le k \le m), P)\)be a MG-IVFPR-PAS,\(\widehat{\mathcal {R}}\)be the GCPR constructed bymIVFPRs\(\mathcal {R}^{q} (1 \le q \le m)\)and\(\mathcal {A}, \mathcal {B} \in {F}_{I _{[0,1]}}(U)\)with\(P(\mathcal {A}) \ne \tilde{0}\). The following properties hold.
-
(1)
If\(\tilde{0} \le [\beta ^{-}, \beta ^{+}]< P(\mathcal {A}) < [\alpha ^{-},\alpha ^{+}] \le \tilde{1}\), then\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}(\mathcal {A}) \subseteq \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}(\mathcal {A})\).
-
(2)
\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}(\emptyset )= \emptyset,\) \(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}(U) = U\) for all \(\tilde{0} < [\alpha ^{-},\alpha ^{+}] \le \tilde{1}\) and \(\tilde{0} \le [\beta ^{-}, \beta ^{+}] < \tilde{1}.\)
-
(3)
If\(\mathcal {A} \subseteq \mathcal {B}\)and\([\beta ^{-}, \beta ^{+}] < P(\mathcal {A})\wedge P(\mathcal {B}),\)\(P(\mathcal {A})\vee P(\mathcal {B}) < [\alpha ^{-},\alpha ^{+}]\), then\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}\)\((\mathcal {A})\)\(\subseteq\)\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}\)\((\mathcal {B})\)and\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}\)\((\mathcal {A})\)\(\subseteq\)\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}\)\((\mathcal {B})\).
-
(4)
If\(P(\mathcal {A}) < [\alpha _{1}^{-},\alpha _{1}^{+}] \le [\alpha _{2}^{-},\alpha _{2}^{+}] \le \tilde{1}\)and\(\tilde{0} \le [\beta _{1}^{-},\beta _{1}^{+}] \le [\beta _{2}^{-},\beta _{2}^{+}] < P(\mathcal {A})\), then\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{2}^{-},\alpha _{2}^{+}]}(\mathcal {A}) \subseteq \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{1}^{-},\alpha _{1}^{+}]}(\mathcal {A})\)and\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta _{2}^{-},\beta _{2}^{+}]}\)\((\mathcal {A})\)\(\subseteq\)\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta _{1}^{-},\beta _{1}^{+}]}\)\((\mathcal {A})\).
Proof
-
(1)
If \(x \in \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}(\mathcal {A})\), \(\forall x \in U\), then \(P(\mathcal {A} \mid [x]_{\widehat{\mathcal {R}}}) \ge [\alpha ^{-}, \alpha ^{+}]>[\beta ^{-}, \beta ^{+}]\). It shows that \(x \in \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}(\mathcal {A})\). Therefore, we prove: \(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}\)\((\mathcal {A}) \subseteq \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}(\mathcal {A})\).
-
(2)
From Proposition 3(1), we have
$$\begin{aligned}&\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}(\emptyset )\\&\quad = \{x \in U: P(\emptyset \mid [x]_{\widehat{\mathcal {R}}}) \ge [\alpha ^{-},\alpha ^{+}] \}\\&\quad = \{x \in U: \tilde{0} \ge [\alpha ^{-},\alpha ^{+}] \}\\&\quad = \emptyset , \end{aligned}$$$$\begin{aligned}&\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-},\beta ^{+}]}(U)\\&\quad = \{x \in U: P(U \mid [x]_{\widehat{\mathcal {R}}})> [\beta ^{-},\beta ^{+}] \}\\&\quad = \{x \in U: \tilde{1} \ge [\alpha ^{-},\alpha ^{+}] \}\\&\quad = U. \end{aligned}$$ -
(3)
If \(x \in \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}(\mathcal {A})\), \(\forall x \in U\), then \(P(\mathcal {A} \mid [x]_{\widehat{\mathcal {R}}}) \ge [\alpha ^{-}, \alpha ^{+}]\). Since \(\mathcal {A} \subseteq \mathcal {B}\), then from Proposition 3(2), we have \(P(\mathcal {A} \mid [x]_{\widehat{\mathcal {R}}}) \le P(\mathcal {B} \mid [x]_{\widehat{\mathcal {R}}})\). Therefore, we have \(P(\mathcal {B} \mid [x]_{\widehat{\mathcal {R}}}) \ge [\alpha ^{-}, \alpha ^{+}]\). It shows that \(x \in \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}(\mathcal {B})\). Therefore, we prove \(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}\)\((\mathcal {A})\)\(\subseteq\)\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}]}\)\((\mathcal {B})\). Similarly, we can prove \(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}\)\((\mathcal {A})\)\(\subseteq\)\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta ^{-}, \beta ^{+}]}\)\((\mathcal {B})\).
-
(4)
If \(x \in \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{2}^{-},\alpha _{2}^{+}]}(\mathcal {A})\), \(\forall x \in U\), then \(P(\mathcal {A} \mid [x]_{\widehat{\mathcal {R}}}) \ge [\alpha _{2}^{-},\alpha _{2}^{+}] \ge [\alpha _{1}^{-},\alpha _{1}^{+}]\). It shows that \(x \in \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{1}^{-},\alpha _{1}^{+}]}(\mathcal {A})\). Therefore, we can prove \(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{2}^{-},\alpha _{2}^{+}]}\)\((\mathcal {A}) \subseteq \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{1}^{-},\alpha _{1}^{+}]}(\mathcal {A})\). Similarly, we can prove and \(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta _{2}^{-},\beta _{2}^{+}]}\)\((\mathcal {A})\)\(\subseteq\)\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\beta _{1}^{-},\beta _{1}^{+}]}\)\((\mathcal {A})\).
A special case of \(([\alpha ^{-},\alpha ^{+}], [\beta ^{-},\beta ^{+}])\)-MG-IVFPR-PRS with \([\beta ^{-},\beta ^{+}] = \tilde{1} - [\alpha ^{-},\alpha ^{+}]< P(\mathcal {A}) < [\alpha ^{-},\alpha ^{+}]\) is referred to as symmetric MG-IVFPR-PRS. One of the advantages is that only one parameter needs to be decided. This would deduce the cost in evaluation of values of parameters.
Definition 12
Let \((U, \mathcal {R}^{q}(1 \le k \le m), P)\) be a MG-IVFPR-PAS, \(\widehat{\mathcal {R}}\) be the GCPR constructed by m IVFPRs \(\mathcal {R}^{q} (1 \le q \le m)\) and \(\mathcal {A} = [A^{-}, A^{+}] (\in {F}_{I _{[0,1]}}(U))\) be a interval-valued fuzzy event. For \(\tilde{0.5} < [\alpha ^{-},\alpha ^{+}] \le \tilde{1}\), the \([\alpha ^{-},\alpha ^{+}]\)-multi-granulation interval-valued fuzzy preference relation probabilistic lower and upper approximations of \(\mathcal {A}\) are defined, respectively, as follows:
The pair \((\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-}, \alpha ^{+}]}(\mathcal {A}), \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-}, \alpha ^{+}]}(\mathcal {A}))\), is called \([\alpha ^{-}, \alpha ^{+}]\)-multi-granulation interval-valued fuzzy preference relation probabilistic rough set (\([\alpha ^{-}\), \(\alpha ^{+}]\)-MG-IVFPR-PRS) of \(\mathcal {A}\). The positive, negative and boundary regions of \(\mathcal {A}\) are defined, respectively, as follows:
From Definition 12, the following assertions are clear.
Proposition 5
Let\((U, \mathcal {R}^{q}(1 \le k \le m), P)\)be a MG-IVFPR-PAS,\(\widehat{\mathcal {R}}\)be the GCPR constructed bymIVFPRs\(\mathcal {R}^{q} (1 \le q \le m)\)and\(\mathcal {A}, \mathcal {B} \in {F}_{I _{[0,1]}}(U)\)with\(\tilde{0.5} < [\alpha ^{-},\alpha ^{+}] \le \tilde{1}\). The following properties hold.
-
(1)
\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(\mathcal {A}) \subseteq \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(\mathcal {A})\).
-
(2)
\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(\emptyset ) =\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(\emptyset ) = \emptyset\), \(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(U) =\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(U) = U.\)
-
(3)
If\(\mathcal {A} \subseteq \mathcal {B}\), then\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(\mathcal {A}) \subseteq \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(\mathcal {B})\)and\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(\mathcal {A}) \subseteq \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha ^{-},\alpha ^{+}] }(\mathcal {B})\).
-
(4)
If\(\tilde{0.5} < [\alpha _{1}^{-},\alpha _{1}^{+}] \le [\alpha _{2}^{-},\alpha _{2}^{+}] \le \tilde{1}\), then\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{2}^{-},\alpha _{2}^{+}]}(\mathcal {A}) \subseteq \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{1}^{-},\alpha _{1}^{+}]}(\mathcal {A})\)and\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{1}^{-},\alpha _{1}^{+}]}(\mathcal {A}) \subseteq \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{[\alpha _{2}^{-},\alpha _{2}^{+}]}(\mathcal {A})\).
The above two kinds of MG-IVFPR-PRSs, \(([\alpha ^{-},\alpha ^{+}], [\beta ^{-},\beta ^{+}])\)-MG-IVFPR-PRS and \([\alpha ^{-}\), \(\alpha ^{+}]\)-MG-IVFPR-PRS are parameter-related, i.e., all needs to evaluate values of parameters when applying them. In the following, we introduce another two kinds of MG-IVFPR-PRSs, their parameter free, i.e., which do not have undetermined parameter.
Definition 13
Let \((U, \mathcal {R}^{q}(1 \le k \le m), P)\) be a MG-IVFPR-PAS, \(\widehat{\mathcal {R}}\) be the GCPR constructed by m IVFPRs \(\mathcal {R}^{q} (1 \le q \le m)\), and \(\mathcal {A} = [A^{-}, A^{+}] (\in {F}_{\mathbf{I} _{[0,1]}}(U))\) be a interval-valued fuzzy event. The \(\tilde{0.5}\)-multi-granulation interval-valued fuzzy preference relation probabilistic lower and upper approximations of \(\mathcal {A}\) are defined, respectively, as follows:
The pair \((\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\mathcal {A}), \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\mathcal {A}))\) is called \(\tilde{0.5}\)-multi-granulation interval-valued fuzzy preference relation probabilistic rough set (\(\tilde{0.5}\)-MG-IVFPR-PRS) of \(\mathcal {A}\). The positive, negative, and boundary regions of \(\mathcal {A}\) are defined, respectively, as follows:
From Definition 13, the following assertions are clear.
Proposition 6
Let\((U, \mathcal {R}^{q}(1 \le k \le m), P)\)be a MG-IVFPR-PAS,\(\widehat{\mathcal {R}}\)be the GCPR constructed bymIVFPRs\(\mathcal {R}^{q} (1 \le q \le m)\)and\(\mathcal {A}, \mathcal {B} \in {F}_{I _{[0,1]}}(U)\). The following properties hold.
-
(1)
\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\mathcal {A}) \subseteq \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\mathcal {A})\).
-
(2)
\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\emptyset ) =\overline{\text {Apr}}_{\tilde{R}}^{\tilde{0.5}}(\emptyset )= \emptyset\); \(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(U) =\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(U) = U.\)
-
(3)
If\(\mathcal {A} \subseteq \mathcal {B}\), then\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\mathcal {A}) \subseteq \underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\mathcal {B} )\)and\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\mathcal {A}) \subseteq \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{\tilde{0.5}}(\mathcal {B} ).\)
Definition 14
Let \((U, \mathcal {R}^{q}(1 \le k \le m), P)\) be a MG-IVFPR-PAS, \(\widehat{\mathcal {R}}\) be the GCPR constructed by m IVFPRs \(\mathcal {R}^{q} (1 \le q \le m)\) and \(\mathcal {A} = [A^{-}, A^{+}] (\in {F}_{I _{[0,1]}}(U))\) be a interval-valued fuzzy event. The Bayesian multi-granulation interval-valued fuzzy preference relation probabilistic lower and upper approximations of \(\mathcal {A}\) are defined, respectively, as follows:
The pair \((\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{P(\mathcal {A})}(\mathcal {A}), \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{P(\mathcal {A})}(\mathcal {A}))\), is called Bayesian multi-granulation interval-valued fuzzy preference relation probabilistic rough set (B-MG-IVFPR-PRS) of \(\mathcal {A}\). The positive, negative, and boundary regions of \(\mathcal {A}\) are defined, respectively, as follows:
From Definition 14, the following assertions are clear.
Proposition 7
Let\((U, \mathcal {R}^{q}(1 \le k \le m), P)\)be a MG-IVFPR-PAS,\(\widehat{\mathcal {R}}\)be the GCPR constructed bymIVFPRs\(\mathcal {R}^{q} (1 \le q \le m)\)and\(\mathcal {A} \in {F}_{I _{[0,1]}}(U)\). The following properties hold.
-
(1)
\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{P(\mathcal {A})}(\mathcal {A}) \subseteq \overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{P(\mathcal {A})}(\mathcal {A})\).
-
(2)
\(\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{P(\mathcal {A})}(\emptyset ) =\underline{\text {Apr}}_{\widehat{\mathcal {R}}}^{P(\mathcal {A})}(U) = \emptyset ,\)\(\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{P(\mathcal {A})}(\emptyset ) =\overline{\text {Apr}}_{\widehat{\mathcal {R}}}^{P(\mathcal {A})}(U) = U\).
3.2 Bayesian decision procedure within MG-IVFPR-PAS
We mainly discuss, in this section, DTRS approach for IVFSs in the framework of MG-IVFPR-PAS, i.e., the MG-IVFPR-DTRS approach.
Let \((U, \mathcal {R}^{q}(1 \le k \le m), P)\) be a MG-IVFPR-PAS, \(\widehat{\mathcal {R}}\) be the GCPR constructed by m IVFPRs \(\mathcal {R}^{q} (1 \le q \le m)\). The Bayesian decision procedure adopts two states and three actions to describe the decision process. The set of states is given by \(\Omega = \{\mathcal {A}, \mathcal {A}^{c}\}\), where \(\mathcal {A}\) is an IVFS. The set of actions is \(\{a_{P}, a_{N}, a_{B}\}\), where \(a_{P}\), \(a_{N}\), and \(a_{B}\) represent the three actions in classifying an object, namely, deciding POS\((\mathcal {A})\), deciding NEG\((\mathcal {A})\), and deciding BND\((\mathcal {A})\), respectively. The interval-valued loss function \(\lambda\) is given by a \(3 \times 2\) interval-valued matrix shown in Table 1.
The expected losses of taking the individual actions for element x are computed (expressed) as follows:
Note that, for example, due to the interval values of \(\lambda _{PP}\) and \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), the product of Eq. (27) is defined by formula (4) and the addition operator, \(\oplus\), is defined by formula (3). For each element \(x_{i} \in U (1\le i \le n)\), the IVFS \([x_{i}]_{\widehat{\mathcal {R}}}\) is adopted as the description of \(x_{i} (1\le i \le n)\) and defined in Definition 3.3. The Bayesian decision procedure leads to the following three minimum-risk decision rules:
-
(P1)
If \(\mathcal {L}_{P} \le \mathcal {L}_{B}\) and \(\mathcal {L}_{P} \le \mathcal {L}_{N}\), then decide \(x_{i} \in \text {POS}(\mathcal {A})\).
-
(N1)
If \(\mathcal {L}_{N} \le \mathcal {L}_{P}\) and \(\mathcal {L}_{N} \le \mathcal {L}_{B}\), then decide \(x_{i} \in \text {NEG}(\mathcal {A})\).
-
(B1)
For remaining elements \(x_{i} \in U (1\le i \le n)\) satisfying neither (P1) nor (N1), decide \(x_{i} \in \text {BND}(\mathcal {A})\).
Since the equation \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}}) + P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\(= \tilde{1}\) does not hold in general. Therefore, to simplify the following discussion, we denote
Then, by Proposition 2 and Remark 1, we have
As a result, the losses for taking actions \(a_{P}\), \(a_{B}\) and \(a_{N}\) can be expressed as
From Eqs. (32)–(34), we have the following equivalences:
-
(1)
\(\mathcal {L}(a_{P} \mid [x_{i}]_{\widehat{\mathcal {R}}}) \le \mathcal {L}(a_{B} \mid [x_{i}]_{\widehat{\mathcal {R}}})\Leftrightarrow (\lambda _{BP}^{-}-\lambda _{PP}^{-})(P_{1}\wedge p_{2}) \ge (\lambda _{PN}^{-}-\lambda _{BN}^{-}) (1 - p_{3}\vee p_{4})\), \((\lambda _{BP}^{+}-\lambda _{PP}^{+})(P_{1}\vee p_{2}) \ge (\lambda _{PN}^{-}-\lambda _{BN}^{-}) (1 - p_{3}\wedge p_{4})\);
-
(2)
\(\mathcal {L}(a_{P} \mid [x_{i}]_{\widehat{\mathcal {R}}}) \le \mathcal {L}(a_{N} \mid [x_{i}]_{\widehat{\mathcal {R}}})\Leftrightarrow (\lambda _{NP}^{-}-\lambda _{PP}^{-})(P_{1}\wedge p_{2}) \ge (\lambda _{PN}^{-}-\lambda _{NN}^{-}) (1 - p_{3}\vee p_{4})\), \((\lambda _{NP}^{+}-\lambda _{PP}^{+})(P_{1}\vee p_{2}) \ge (\lambda _{PN}^{-}-\lambda _{NN}^{-}) (1 - p_{3}\wedge p_{4})\);
-
(3)
\(\mathcal {L}(a_{N} \mid [x_{i}]_{\widehat{\mathcal {R}}}) \le \mathcal {L}(a_{P} \mid [x_{i}]_{\widehat{\mathcal {R}}})\Leftrightarrow (\lambda _{NP}^{-}-\lambda _{PP}^{-})(P_{1}\wedge p_{2}) \ge (\lambda _{PN}^{-}-\lambda _{NN}^{-}) (1 - p_{3}\vee p_{4}),\) \((\lambda _{NP}^{+}-\lambda _{PP}^{+})(P_{1}\vee p_{2}) \ge (\lambda _{PN}^{-}-\lambda _{NN}^{-}) (1 - p_{3}\wedge p_{4});\)
-
(4)
\(\mathcal {L}(a_{N} \mid [x_{i}]_{\widehat{\mathcal {R}}}) \le \mathcal {L}(a_{B} \mid [x_{i}]_{\widehat{\mathcal {R}}})\Leftrightarrow (\lambda _{NP}^{-}-\lambda _{BP}^{-})(P_{1}\wedge p_{2}) \ge (\lambda _{BN}^{-}-\lambda _{NN}^{-}) (1 - p_{3}\vee p_{4}),\) \((\lambda _{NP}^{+}-\lambda _{BP}^{+})(P_{1}\vee p_{2}) \ge (\lambda _{BN}^{-}-\lambda _{NN}^{-}) (1 - p_{3}\wedge p_{4}).\)
Consider a special kind of loss function:
That is, the loss of classifying an object \(x_{i}\) in state \(\mathcal {A}\) into the positive region POS\((\mathcal {A})\) is less than or equal to the loss of classifying \(x_{i}(1 \le i \le n)\) into the boundary region BND\((\mathcal {A})\), and both of these losses are less than the loss of classifying \(x_{i}(1 \le i \le n)\) into the negative region NEG\((\mathcal {A})\). The reverse order of losses is used for classifying an object that does not in state \(\mathcal {A}\).
From Eq. (35) that
Denote parameters
Then, we have the following:
According to condition (35), decision rules (P1)–(N1) can be equivalently rewritten as follows based on aforementioned analyses:
-
(P2)
If \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\ge [\alpha ^{-},\alpha ^{+}] P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) and \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\ge [\gamma ^{-},\gamma ^{+}] P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), then decide \(x_{i} \in \text {POS}(\mathcal {A})\);
-
(N2)
If \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\le [\gamma ^{-},\gamma ^{+}] P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) and \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\le [\beta ^{-},\beta ^{+}] P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), then decide \(x_{i} \in \text {NEG}(\mathcal {A})\);
-
(B2)
For remaining elements \(x_{i} \in U (1\le i \le n)\) satisfying neither (P2) nor (N2), decide \(x_{i} \in \text {BND}(\mathcal {A})\).
If the loss function still satisfies the following conditions:
then it follows that \(\alpha ^{*}>\gamma ^{*}>\beta ^{*}\). For the same time, we have
Thus, the decision rules (P2)–(N2) can be obtained under conditions (35) and (39):
-
(P3)
If \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\ge [\alpha ^{-},\alpha ^{+}] P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), then decide \(x_{i} \in \text {POS}(\mathcal {A})\);
-
(N3)
If \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\le [\beta ^{-},\beta ^{+}] P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), then decide \(x_{i} \in \text {NEG}(\mathcal {A})\);
-
(B3)
For remaining elements \(x_{i} \in U (1\le i \le n)\) satisfying neither (P3) nor (N3), decide \(x_{i} \in \text {BND}(\mathcal {A})\).
Let us consider another condition of loss function:
If the loss function satisfies conditions (35) and (40), it then follows that \(\alpha ^{*} = \gamma ^{*} = \beta ^{*}\). Thus, we have
When the losses of classifying \(x_{i}\) into \(\text {POS}(\mathcal {A})\) and \(\text {BND}(\mathcal {A})\) are the same, we decide \(x_{i} \in \text {BND}(\mathcal {A})\). Similarly, when the losses of classifying \(x_{i}\) into \(\text {NEG}(\mathcal {A})\) and BND\((\mathcal {A})\) are the same, we decide \(x_{i} \in \text {BND}\)\((\mathcal {A})\). According to this tie-breaking criteria and the equivalences (41) and (42), the following simplified and equivalent forms of decision rules (P2)–(N2) are obtained:
-
(P4)
If \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})> [\alpha ^{-},\alpha ^{+}]\), then decide \(x_{i} \in \text {POS}(\mathcal {A})\);
-
(N4)
If \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})< [\alpha ^{-},\alpha ^{+}]\), then decide \(x_{i} \in \text {NEG}(\mathcal {A})\);
-
(B4)
For remaining elements \(x_{i} \in U (1\le i \le n)\) satisfying neither (P4) nor (N4), decide \(x_{i} \in \text {BND}(\mathcal {A})\).
Remark 2
Since the order relation defined in Eq. (6) is partial. Therefore, the situation in some cases must be arise two intervals cannot compare directly. In this cases, we adopt the comparing methods as given in Liang and Liu (2014). The method is described as follows:
Let \([a^{-},a^{+}], [b^{-},b^{+}] \in \mathbf I _{\mathbb {R}^{+}}\) and \(\theta \in [0,1]\) is constant. If \(M_{\theta }( [a^{-},a^{+}]) \le M_{\theta }([b^{-},b^{+}])\), then \([a^{-},a^{+}] \le [b^{-},b^{+}]\), and vice versa, where \(M_{\theta }([a^{-},a^{+}]) = (1 - \theta ) a^{-} + \theta a^{+}\) and \(M_{\theta }([b^{-},b^{+}]\)\()= (1 - \theta ) b^{-} + \theta b^{+}\). Where \(M_{\theta }\) is a transformed outcome and \(\theta\) reflects the risk attitude of decision maker.
The above compare method is applied only for those situations when the two intervals cannot be compare directly.
4 An approach to group decision-making based on MG-IVFPR-PRS
Based on the MG-IVFPR-PRS model in Sect. 3, it is requisite to consider their applications in group decision-making problems. In what follows, we give the algorithm to solve the group decision-making problem with MG-IVFPR-PRS.
4.1 An algorithm
With the help of the results in Sect. 3, we design the algorithm of group decision-making based on the MG-IVFPR-PRS model and their corresponding 3WDs. The key steps are elaborated as follows:
Step 1: Suppose that a group decision-making problem has a set of alternatives \(U =\{x_{1},x_{2},\ldots,x_{n}\}.\) Assume that there are m decision makers \(e_{1},e_{2},\ldots,e_{m}\) provides m IVFPRs \(\mathcal {R}^{1}, \mathcal {R}^{2},\ldots,\mathcal {R}^{m}\) to evaluate his/her judgments on U.
Step 2: Using Algorithm 1, to construct GCPR \(\widehat{\mathcal {R}}\) for all decision makers.
Step 3: Presenting the values of \(\mathcal {A}\) is the incomplete available information of all the characteristic factors \(x_{i}(i=1,2,\ldots ,n)\).
Step 4: Presenting the values of \(P(x_{i})=p_{i}(i=1,2,\ldots ,n)\) is the possible existence of random available information of all of \(x_{i}(i=1,2,\ldots ,n)\).
Step 5: Based on Eq. (24), computing the conditional probability \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\).
Step 6: Based on Eq. (36), computing the conditional probability \(P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\).
Step 7: Presenting the values of loss function \(\lambda _{\Delta \nabla }\)\((\Delta =P,B,N; \nabla =P,N)\) according to Table 1.
Step 8: If the values of loss functions satisfy the conditions (35) and (39), then go to Step 9. Otherwise, we need to assign a new values of loss functions and go to Step 5.
Step 9: Based on Eqs. (36)–(38), calculate the thresholds \([\alpha ^{-},\alpha ^{+}]\), \([\gamma ^{-},\gamma ^{+}]\) and \([\beta ^{-},\beta ^{+}]\).
Step 10: Using Eq. (4), computing \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\) and \([\beta ^{-},\beta ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\).
Step 11: If \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\) compare directly \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\) and \([\beta ^{-},\beta ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\), then go to Step 13. Otherwise, go to Step 12.
Step 12: Based on Remark 2, transform \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\), \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\) and \([\beta ^{-},\beta ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,\ldots ,n)\) to \(M_{\theta }(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}}))\)\((i=1,2,\ldots ,n)\), \(M_{\theta }([\alpha ^{-},\alpha ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}}))\)\((i=1,2,\ldots ,n)\) and \(M_{\theta }([\beta ^{-},\beta ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}}))\)\((i=1,2,\ldots ,n)\) with a certain value of \(\theta \in [0,1]\). Then, go to Step 12.
Step 13: Making the decision according to the decision rules (P2)–(N2).
4.2 An illustrative example
In this subsection, we apply the propose algorithm to a real group decision-making. This example is about quick decision-making based on a real investment context, under MG-IVFPR-PRS environment. Furthermore, analysis is done to provide to show the feasibility and reasonableness of the proposed models.
4.2.1 Problem description
The various types of mutual funds (MFs) of different companies listed in the Growth Enterprise Market board of the India Stock Exchange are a popular investment source to an investor as a long-term investment. However, the sufficient knowledge about the various types of MFs of different companies is always not possible for every investor. Our proposed models are effective for those investors. Suppose an investor plans to invest his/her money in MFs of different companies, with the aim of high returns, while he/she has no sufficient knowledge about all MFs. He/she chooses initially five MFs according to the past performances, while he/she invests his/her money to the best options out of these five MFs. For this, he/she decides to take advice’s from three stock market brokers in India. For making reasonable options, we have the following decision analysis.
4.2.2 Decision analysis
We use the algorithm in Sect. 4.1 of decision analysis based on MG-IVFPR-PRSs for group decision-making.
Step 1: Suppose \(U = \{x_{1},x_{2},x_{3},x_{4},x_{5}\}\) be the five MFs and \(E=\{e_{1},e_{2},e_{3}\}\) be the three brokers. Assume that these three brokers provide his/her judgments using IVFPRs, which represent in Eqs. (43)–(45).



Step 2: Using Algorithm 1, to construct GCPR \(\widehat{\mathcal {R}}\) for all brokers, which represent in Eq. (46).

Step 3: Let IVFS
be the quantitative description of all the characteristic factors \(x_{i}(i=1,2,3,4,5)\) according to the available inaccurate and insufficient information.
Step 4: Let \(\{0.15, 0.13, 0.24, 0.18, 0.3\}\) be the possible existence of random available information of \(x_{i}(i=1,2,3,4,5).\)
Step 5: Using Eq. (24), we compute the conditional probability \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,3,4,5)\) as follows:
Step 6: Using Eq. (36), we compute the conditional probability \(P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,3,4,5)\) as follows:
Step 7: Suppose that the loss function is given as follows: \(\lambda _{PP}=[1,2]\), \(\lambda _{BP}=[3,5]\), \(\lambda _{NP}=[5,8]\), \(\lambda _{NN}=[0,1]\), \(\lambda _{BN}=[5,7.6]\), and \(\lambda _{PN}=[11,15.1]\).
Step 8: Since the given loss functions satisfy the conditions (35) and (39).
Step 9: Based on Eqs. (36)–(38), we compute the thresholds values: \([\alpha ^{-},\alpha ^{+}] = [3\), 2.5], \([\gamma ^{-},\gamma ^{+}]=[2.75,2.35]\), and \([\beta ^{-},\beta ^{+}]=[2.5,2.2]\).
Step 10: Based on Eq. (4), we compute \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,3,4,5)\) and \([\beta ^{-},\beta ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\)\((i=1,2,3,4,5)\) as follows:
and
Step 11: Since \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) cannot be compared directly \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) and \([\beta ^{-},\beta ^{+}]P(\mathcal {A}^{c} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) for all \((i=1,2,3,4,5)\). Then, go to Step 12.
Step 12: Based on Remark 2, we transform \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), and \([\beta ^{-},\beta ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) with different values of \(\theta\). The results are shown in Figs. 2, 3, and 4.
Step 13: According to the decision rules (P2)–(N2), the decision results are shown in Table 2 with different values of \(\theta\).
From Table 2, we can see that the smaller value of \(\theta\), the decision results may be different for the higher value of \(\theta\). However, the decision results are unchanged from certain stage with the increasing of \(\theta\). For clarity, we display the decision results in Fig. 8. In this paper, we suggest that an appropriate value of \(\theta\) is between 0.5 and 1 due to the fact that it can get an appropriate decision results.
4.2.3 The influences of the parameter \(\theta\)
During the decision analysis of group decision-making based on MG-IVFPR-PRSs, it involves the parameter \(\theta\). In what follows, we successively analyze this parameter to the selection of MFs in details.
-
1.
The transform outcomes values of \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), and \([\beta ^{-},\beta ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) with different values of \(\theta\). Based on Remark 2, the transform outcomes of \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), and \([\beta ^{-},\beta ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) with different values of \(\theta\) are further discussed in Figs. 5, 6, and 7. With regard to the results of Figs. 5, 6, and 7, we find that the transform outcomes of \(P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\), and \([\beta ^{-},\beta ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) are increasing with the increasing of \(\theta\).
-
2.
The decision rules with different values of \(\theta\) Continuing the discussion of Figs. 5, 6, and 7, we deduce the decision rules with different values of \(\theta\). On the basis of the condition \([\alpha ^{-},\alpha ^{+}]> [\beta ^{-},\beta ^{+}]> [\gamma ^{-},\gamma ^{+}]\), we generate decision rules (P2)–(N2), i.e., POS\((\mathcal {A})\), NEG\((\mathcal {A})\) and BND\((\mathcal {A})\). With respect to (P2)–(N2), the three decision regions rely on the values of \([\alpha ^{-},\alpha ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\) and \([\beta ^{-},\beta ^{+}]P(\mathcal {A} \mid [x_{i}]_{\widehat{\mathcal {R}}})\). Hence, the decision rules with different values of \(\theta\) are described in Fig. 8.
4.3 Comparisons of the proposed model and other existing models in group decision-making problems
-
1.
Comparison with IVF-PRS model The IVF-PRS model in Zhao and Hu (2016) is established based on single interval-valued fuzzy relation (IVFR), so the model in Zhao and Hu (2016) cannot deal with group decision-making problems with preference analysis. The MG-IVFPR-PRS model proposed in the present paper is based on multiple IVFPRs, which can deal group decision-making problems with preference analysis. Hence, the application domain of the MG-IVFPR-PRS model is wider than that of the IVF-PRS model in Zhao and Hu (2016).
-
2.
Comparison with IVF-DTRS approach The interval-valued decision-theoretic rough set approach in Liang and Liu (2014) is established based on single classical equivalence relation and consider that only the loss function is interval-valued. The IVF-DTRS approach in Zhao and Hu (2016) is established based on single IVFR and also consider that the loss function is interval-valued. However, these approaches cannot be dealt with group decision-making with preference analysis. Our proposed approaches can do it.
-
3.
Comparison with group decision-making method based on IVFPRs The method for group decision-making in Chen et al. (2015) is established on IVFPRs and consistency matrices. Using this model, the decision results are obtained only on the basis of experts’ suggestions which cannot consider the incomplete available information and the existence of random available information. However, we cannot avoid it for obtaining more accurate decision results. If we consider these two types available information, the obtained decision results may be different. For instance, if we obtain the decision results to propose example, using the method in Chen et al. (2015), the best option is \(x_{1}\) and the worst option is \(x_{4}\). However, if we use the method proposed in the present paper, the best option is \(x_{1}\) (positive region) and the worst option is \(x_{3}\) (negative region).
5 Conclusion
This paper investigates MG-IVFPR-PRS models within the frameworks of MG-IVFPR-PAS and GCPR. Using this model, we have presented an approach for group decision-making, which is basis of the experts’ suggestions, the incomplete available information, and the existence of random available information of the objects. The proposed method provides us with a useful way for group decision-making using MG-IVFPR-PRS model based on IVFPRs and consistency matrices.
In this paper, we cannot consider the mathematical way to find the optimal value of the parameter \(\theta\); however, it plays important role for the decision analysis of group decision-making based on MG-IVFPR-PRSs. To address this issue, we use optimization techniques as given by Tsai et al. (2008, 2012), Chen and Huang (2003), Chen and Chung (2006) and Chen and Chien (2011) in our future concerns.
References
Chen SM (1996) A fuzzy reasoning approach for rule-based systems based on fuzzy logics. IEEE Trans Systems Man Cybern Part B Cybern 26(5):769–778
Chen SM (1997) Interval-valued fuzzy hypergraph and fuzzy partition. IEEE Trans Systems Man Cybern Part B Cybern 27(4):725–733
Chen SJ, Chen SM (2008) Fuzzy risk analysis based on measures of similarity between interval-valued fuzzy numbers. Comput Math Appl 55:1670–1685
Chen SM, Chen JH (2009) Fuzzy risk analysis based on similarity measures between interval-valued fuzzy numbers and interval-valued fuzzy number arithmetic operators. Expert Syst Appl 36(3):6309–6317
Chen SM, Chen CD (2011) Handling forecasting problems based on high-order fuzzy logical relationships. Expert Syst Appl 38(4):3857–3864
Chen SM, Chien CY (2011) Parallelized genetic ant colony systems for solving the traveling salesman problem. Expert Syst Appl 38(4):3873–3883
Chen SM, Chung NY (2006) Forecasting enrollments of students using fuzzy time series and genetic algorithms. Int J Inf Manag Sci 17(3):1–17
Chen SM, Hong JA (2014) Multicriteria linguistic decision making based on hesitant fuzzy linguistic term sets and the aggregation of fuzzy sets. Inf Sci 286:63–74
Chen SM, Horng YJ (1996) Finding inheritance hierarchies in interval-valued fuzzy concept-networks. Fuzzy Sets Syst 84:75–83
Chen SM, Hsiao WH (2000) Bidirectional approximate reasoning for rule-based systems using interval-valued fuzzy sets. Fuzzy Sets Syst 113:185–203
Chen SM, Huang CM (2003) Generating weighted fuzzy rules from relational database systems for estimating values using genetic algorithms. IEEE Trans Fuzzy Syst 11(4):495–506
Chen SM, Kao PY (2013) Taiex forecasting based on fuzzy time series, particle swarm optimization techniques and support vector machines. Inf Sci 247:62–71
Chen SM, Lee LW (2010) Fuzzy multiple criteria hierarchical group decision-making based on interval type-2 fuzzy sets. IEEE Trans Syst Man Cybern Part A Syst Hum 40(5):1120–1128
Chen SM, Niou SJ (2011) Fuzzy multiple attributes group decision-making based on fuzzy preference relations. Expert Syst Appl 38(4):3865–3872
Chen SM, Sanguansat K (2011) Analyzing fuzzy risk based on similarity measures between interval-valued fuzzy numbers. Expert Syst Appl 38(7):8612–8621
Chen SM, Wang HY (2009) Evaluating students’ answerscripts based on interval-valued fuzzy grade sheets. Expert Syst Appl 36(6):9839–9846
Chen SM, Hsiao WH, Jong WT (1997) Bidirectional approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets Syst 91:339–353
Chen SM, Wang NY, Pan JS (2009) Forecasting enrollments using automatic clustering techniques and fuzzy logical relationships. Expert Syst Appl 36(8):11,070–11,076
Chen SM, Lin TE, Lee LW (2014) Group decision making using incomplete fuzzy preference relations based on the additive consistency and the order consistency. Inf Sci 259:1–15
Chen SM, Cheng SH, Lin TE (2015) Group decision making systems using group recommendations based on interval fuzzy preference relations and consistency matrices. Inf Sci 298:555–567
Du WS, Hu BQ (2016) Dominance-based rough set approach to incomplete ordered information systems. Inf Sci 346:106–129
Feng T, Mi JS (2016) Variable precision multigranulation decision-theoretic fuzzy rough sets. Knowl Based Syst 91:93–101
Horng YJ, Chen SM, Chang YC, Lee CH (2005) A new method for fuzzy information retrieval based on fuzzy hierarchical clustering and fuzzy inference techniques. IEEE Trans Fuzzy Syst 13(2):216–228
Lee LW, Chen SM (2008) Fuzzy multiple attributes group decision-making based on the extension of TOPSIS method and interval type-2 fuzzy sets. In: Proceedings of the 2008 international conference on machine learning and cybernetics, Kunming, China, vol 6, pp 3260–3265
Lee LW (2012) Group decision making with incomplete fuzzy preference relations based on the additive consistency and the order consistency. Expert Syst Appl 39(14):11,666–11,676
Liang D, Liu D (2014) Systematic studies on three-way decisions with interval-valued decision-theoretic rough sets. Inf Sci 276:186–203
Liang DC, Liu D (2015) Deriving three-way decisions from intuitionistic fuzzy decision-theoretic rough sets. Inf Sci 300:28–48
Liang JY, Li R, Qian YH (2012) Distance: a more comprehensible perspective for measures in rough set theory. Knowl Based Syst 27:126–136
Lin G, Qian Y, Liang J (2012) Nmgrs: neighborhood-based multigranulation rough sets. Int J Approx Reason 53:1404–1418
Liu C, Miao D, Qian J (2014) On multi-granulation covering rough sets. Int J Approx Reason 55:1404–1418
Liu D, Liang DC, Wang CC (2016) A novel three-way decision model based on incomplete information system. Knowl Based Syst 91:32–45
Liu F, Peng YN, Yu Q, Zhao H (2018) A decision-making model based on interval additive reciprocal matrices with additive approximation-consistency. Inf Sci 422:161–176
Lv Y, Chen Q, Wu L (2013) Multi-granulation probabilistic rough set model. Int Conf Fuzzy Syst Knowl Discov 10:146–151
Ma W, Sun B (2012) Probabilistic rough set over two universes and rough entropy. Int J Approx Reason 53:608–619
Mandal P, Ranadive AS (2017) Multi-granulation bipolar-valued fuzzy probabilistic rough sets and their corresponding three-way decisions over two universes. Soft Comput. https://doi.org/10.1007/s00500-017-2765-6
Mendel JM, John RI, Liu F (2006) Interval type-2 fuzzy logic systems made simple. IEEE Trans Fuzzy Syst 14(6):808–821
Pawlak Z (1982) Rough sets. Int J Comput Inform Sci 11:341–356
Pawlak Z, Wong SKW, Ziarko W (1988) Rough sets: probabilistic versus deterministic approach. Int J Man Mach Stud 29:81–95
Pedrycz W, Chen SM (2011) Granular computing and intelligent systems: design with information granules of high order and high type. Springer, Heidelberg
Pedrycz W, Chen SM (2015a) Granular computing and decision-making: interactive and iterative approaches. Springer, Heidelberg
Pedrycz W, Chen SM (2015b) Information granularity, big data, and computational intelligence. Springer, Heidelberg
Polkowski L (1996) Rough mereology: a new paradigm for approximate reasoning. Int J Approx Reason 15:333–365
Qian Y, Liang J, Dang C (2010a) Incomplete multigranulation rough set. IEEE Trans Syst Man Cybern 20:420–431
Qian YH, Liang JY, Yao YY, Dang CY (2010b) MGRS: a multigranulation rough set. Inf Sci 180:949–970
Qian YH, Zhang H, Sang YL, Liang JY (2014) Multigranulation decision-theoretic rough sets. Int J Approx Reason 55:225–237
Sun B, Ma W, Zhao H (2014) Decision-theoretic rough fuzzy set model and application. Inf Sci 283:180–196
Tanio T (1984) Fuzzy preference orderings in group decision making. Fuzzy Sets Syst 12:117–131
Tsai PW, Pan JS, Chen SM, Liao BY, Hao SP (2008) Parallel cat swarm optimization. In: Proceedings of the 2008 international conference on machine learning and cybernetics, Kunming, China, vol 6, pp 3328–3333
Tsai PW, Pan JS, Chen SM, Liao BY (2012) Enhanced parallel cat swarm optimization based on the taguchi method. Expert Syst Appl 39(7):6309–6319
Wang JY, Xu LM (2002) Probabilistic rough set model. Comput Sci 29(8):76–78
Wang ZH, Wang H, Feng QR, Shu L (2015) The approximation number function and the characterization of covering approximation space. Inf Sci 305:196–207
Wei SH, Chen SM (2009) Fuzzy risk analysis based on interval-valued fuzzy numbers. Expert Syst Appl 16(2):2285–2299
Wei L, Zhang WX (2004) Probabilistic rough sets characterized by fuzzy sets. Int J Uncertain Fuzziness Knowl Based Syst 12:47–60
Xu Z (2011) Consistency of interval fuzzy preference relations in group decision making. Appl Soft Comput 11(5):3898–3909
Xu W, Wang Q, Zhang X (2011) Multi-granulation fuzzy rough sets in a fuzzy tolerance approximation space. Int J Gen Syst 13:246–259
Xu W, Wang Q, Zhang X (2012) A generalized multi-granulation rough set approach. Lect Notes Bioinf 1(6840):681–689
Xu W, Wang Q, Zhang X (2013) Multi-granulation rough sets based on tolerance relations. Soft Comput 17:1241–1252
Xu W, Wang Q, Luo S (2014) Multi-granulation fuzzy rough sets. J Intell Fuzzy Syst 26:1323–1340
Yang HL, Liao X, Wang S, Wang J (2013) Fuzzy probabilistic rough set model on two universes and its applications. Int J Approx Reason 54:1410–1420
Yao YY (1998) Relational interpretations of neighborhood operators and rough set approximation. Inf Sci 111:239–259
Yao YY (2003) Probabilistic approaches to rough sets. Expert Syst 20:287–297
Yao YY (2008) Probabilistic rough set approximations. Int J Approx Reason 49:255–271
Yao YY (2009) Three-way decision: an interpretation of rules in rough set theory. Lect Notes Comput Sci 5589:642–649
Yao YY (2010) Three-way decisions with probabilistic rough sets. Inf Sci 180:341–353
Yao YY, Wong SKM (1992) A decision theoretic framework for approximating concepts. Int J Man Mach Stud 37:793–809
Yao JT, Yao YY, Ziarko W (2008) Probabilistic rough sets: approximations, decision-makings, and applications. Int J Approx Reason 49:253–254
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–358
Zadeh LA (1968) Probability measures of fuzzy events. J Math Anal Appl 23:421–427
Zhang HY, Yang SY, Ma JM (2016) Ranking interval sets based on inclusion measures and applications to three-way decisions. Knowl Based Syst 91:62–70
Zhang XX, Chen DG, Tsang ECC (2017) Generalized dominance rough set models for the dominance intuitionistic fuzzy information systems. Inf Sci 378:1–25
Zhao XR, Hu BQ (2015) Fuzzy and interval-valued decision-theoretic rough set approaches based on the fuzzy probability measure. Inf Sci 298:534–554
Zhao XR, Hu BQ (2016) Fuzzy probabilistic rough sets and their corresponding three-way decisions. Knowl Based Syst 91:126–142
Ziarko W (2005) Probabilistic rough sets. Lect Notes Comput Sci 3641:283–293
Ziarko W (2008) Probabilistic approach to rough sets. Int J Approx Reason 49:272–284
Acknowledgements
The authors would like to thank the Editor-in-Chief and reviewers for their thoughtful comments and valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Prasenjit Mandal and A. S. Ranadive declare that there is no conflict of interest.
Ethical approval
This article does not contain any study performed on humans or animals by the authors.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Rights and permissions
About this article
Cite this article
Mandal, P., Ranadive, A.S. Multi-granulation interval-valued fuzzy probabilistic rough sets and their corresponding three-way decisions based on interval-valued fuzzy preference relations. Granul. Comput. 4, 89–108 (2019). https://doi.org/10.1007/s41066-018-0090-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41066-018-0090-9