1 Introduction

Fuzzy set theory [1], initially proposed by Zadeh in 1965, extends classical set theory to express fuzzy concepts. It involves representing the object under investigation and its corresponding fuzzy concept as a fuzzy set, establishing a suitable membership function, and analyzing the fuzzy object through relevant operations and transformations of the fuzzy set. Fuzzy set theory provides a mathematical framework and methodology for studying and dealing with imprecise phenomena. Since the concept of fuzziness has found the description way of fuzzy sets, the methods of fuzzy mathematics can also be described to evaluate, reasoning, make decisions and control. For example, fuzzy clustering analysis [2], fuzzy pattern recognition [3, 4], fuzzy comprehensive evaluation [5], fuzzy decision-making [6] and fuzzy prediction [7], fuzzy control [8], fuzzy information processing [9,10,11], and others. These methods constitute a fuzzy system theory and a rudiment of speculative mathematics. It has made concrete research achievements in medical diagnosis [12], meteorological prediction [13], economic management [15, 16], aerospace control [8, 14], remote sensing [17] and other fields. It has proven its utility and effectiveness in practical applications.

As a special data type different from the classical single value, the interval value is a common data type in fields such as approximate reasoning, signal processing, and control. While traditional datasets in machine learning and data mining represent a single real value, which is used to represent just one exact value, while each value in interval-valued data is expressed as an interval, which is denoted as a range. This unique representation offers several advantages and practical significance. For instance, when dealing with measurement errors that are sometimes unavoidable, interval values can be employed, and then the results can be expressed as interval values. Furthermore, interval values are also particularly useful for continuous attributes where other data types cannot meet the same requirement simultaneously. Let us take the temperature as another example. Consider the example of temperature. On a certain day in September, the temperature in city A ranges from \(10 ^{\circ }C\) to \(16 ^{\circ }C\). Representing this using a real value cannot directly express that, so we always use an average temperature as a substitute. In that case, we can say that the average temperature is \(13 ^{\circ }C\). On the other hand, we can also use an interval value to precisely express the variation range, which is expressed as \([10 ^{\circ }C, 16 ^{\circ }C]\), and it can reflect the facts better than the average temperature \(13 ^{\circ }C\). Clearly, an interval value conveys more information than a single value, which highlights the necessity of studying interval-valued data. This is one of the reasons why it is necessary to study interval-valued data.

Rough set theory, originally proposed by Pawlak [18], is built on the basis of the classification mechanism and is classified as an equivalence relation within a specific universe. A concept is presented by a subset of a universe of objects and is approximated by a pair of definable concepts of a logical language. The fundamental idea behind rough set theory is to utilize known knowledge from a knowledge base to approximate the inaccurate and uncertain knowledge. Since both rough set and fuzzy set are important tools to deal with the uncertainty in the complex system, more and more scholars have paid attention to the research of combining these two methods, leading to remarkable results. Among these studies, Dubois and Prade [19] first proposed the fuzzy rough set model. In Dubois’s fuzzy rough set model, the membership functions for upper and lower approximations are obtained firstly, which means that the upper and lower approximations are fuzzy sets. Due to its distinctive advantages in dealing with complex systems, significant research efforts have been dedicated to advancing the fuzzy rough set model [20,21,22,23]. Notably, after introducing the conditional probability that can reflect the relative quantitative information into the upper and lower approximations of fuzzy rough sets to improve the fault tolerance of the model, the applicability of the model are further upgraded [24,25,26].

Pawlak rough set and its corresponding generalization forms are composed of a series of classes, which can be considered as information granules. To effectively leverage information granules in the design and analysis of intelligent systems, we need to make information granules more explicit. Yao was the first to establish the relationship between approximation and information granulation [27]. Peters et al. addressed a measurement of information granule using the rough set framework [28]. In particular, Rasiowa introduced approximation methods in the basis of many indiscernibility relations, and they are used to specify approximations [29]. Qian et al. expanded the concept of granularity from single to multi-granularity [30]. Subsequently, scientists further extended the multi-granularity case to different environments and provided significant outcomes [31,32,33]. However, it becomes apparent that while these methods can partially solve the problem of rough modeling in single-valued fuzzy systems, they appear to be inadequate when confronted with the more prevalently presence of interval-valued fuzzy data [34,35,36,37,38,39,40,41,42], these methods seem to be rather powerless. Accordingly, an effective and appropriate rough fuzzy method suitable for interval-valued data is urgently needed to deal with the rough fuzzy modeling problem of interval-valued fuzzy systems.

Interval values are commonly encountered in various real-world scenarios and domains. They are used to represent uncertainties, imprecisions, or variations in measurements or observations. By focusing on interval values, the research acknowledges and addresses the practical relevance and applicability of the findings to real-world problems. Interval values inherently encapsulate uncertainty. By explicitly dealing with uncertainty through interval representations, researchers can quantitatively assess the degree of uncertainty and make informed decisions that account for the range of possible outcomes. This is especially important in situations where decision-making under uncertainty is crucial. Interval values can effectively handle situations where data variability exists. In many cases, measurements or observations may not be precise and can vary within a certain range. Interval values allow for direct comparisons between data points or entities. By employing the fuzzy similarity relation derived from the diversity function, the research can quantitatively assess the degree of similarity or dissimilarity between interval-valued data. This facilitates comparative analysis and aids in identifying patterns, trends, or relationships that may not be apparent when using single-point estimates. Interval-valued fuzzy decision systems have gained significant attention in the field of decision analysis due to their ability to handle uncertain and imprecise information. However, despite their potential, the existing research on interval-valued fuzzy decision systems has certain limitations that hinder their full utilization and applicability. This study explores the construction method of multi-granularity probabilistic rough set models by introducing a novel fuzzy similarity relation in interval-valued fuzzy decision systems, and verifies the effectiveness and practicality through application case studies. These innovative points provide new methods and tools for dealing with interval-valued fuzzy decision systems, which help to handle uncertainty and conduct decision reasoning in practical problems. The main contributions of this article could be summarized into three aspects.

  1. (1)

    Introduction of fuzzy similarity relation based on diversity function. The paper introduces a novel fuzzy similarity function based on a diversity function for handling data in interval-valued fuzzy decision systems. This similarity relation provides a viable foundation for constructing probabilistic rough fuzzy sets and multi-granularity probabilistic rough fuzzy set models.

  2. (2)

    Construction of probabilistic rough fuzzy sets and multi-granularity probabilistic rough fuzzy sets. The paper proposes three kinds of multi-granularity probabilistic rough fuzzy sets to address interval-valued fuzzy data and derives decision rules from these models. The introduction of these models enables more effective uncertainty modeling and decision reasoning in interval-valued fuzzy decision systems.

  3. (3)

    Application case study. To elucidate the concepts of interval-valued probabilistic rough fuzzy sets and multi-granularity probabilistic rough fuzzy sets, the paper conducts a case study. This study is highly valuable for the practical application of these theories, aiding users in better understanding and applying the proposed methods.

This paper is organized as follows. Sect. 2 provides an introduction to the basic concepts of fuzzy sets and interval-valued fuzzy decision systems. In Sect. 3, we present the process of constructing the fuzzy similarity relation for interval-valued data. This involves defining the possible degree between any two interval values and introducing the diversity function between two objects. Then the fuzzy similarity relation is formulated. In Sect. 4, we mainly study the probabilistic rough fuzzy approximations with single granularity for interval-valued fuzzy systems. Then the corresponding properties are also provided. Moving on to Sect. 5, we introduce the probabilistic rough fuzzy set models for interval-valued fuzzy systems, considering three different types of of multi-granularity, namely, mean multi-granularity, optimistic multi-granularity and pessimistic multi-granularity. Moreover, the corresponding decision rules for these special multi-granularity models are derived. In Sect. 6, we provide an illustrative example that showcases the application of the proposed methods in a multi-granularity space formed by three experts. Finally, Sect. 7 draws the main conclusions and puts forward further directions for future research.

2 Related Fundamental Works

The class of all subsets of a non-empty set U is denoted by \({\mathcal {P}}(U)\), and the class of all fuzzy subsets of U is denoted by \({\mathcal {F}}(U)\). A fuzzy subset of U is defined as a membership function assigning to each element x of U a certain degree of membership. The value \(X(x)\in [0,1]\) is referred to as the membership degree of x to the fuzzy set X. A set composed of fuzzy sets \(\{X_{1}, X_{2}, \cdots , X_{r}\}\) is called a fuzzy partition of U if they satisfy \(\forall x\in U,\sum \nolimits _{i=1}^{r}X_{i}(x)= 1\).

For fuzzy sets \(X_{1}, X_{2}\in U\), the basic operations on fuzzy set are described as follows.

  1. (1)

    \(X_{1}\subseteq X_{2}\), if \(\forall x\in U\), \(X_{1}(x)\le X_{2}(x)\).

  2. (2)

    \(X_{1}= X_{2}\), if \(X_{1}\subseteq X_{2}\) and \(X_{2}\subseteq X_{1}\).

  3. (3)

    \((X_{1}\cup X_{2})(x) =\max \{X_{1}(x), X_{2}(x)\}\).

  4. (4)

    \((X_{1}\cap X_{2})(x) =\min \{X_{1}(x), X_{2}(x)\}\).

The complement and the cardinality of fuzzy set X are expressed as follows.

  1. (1)

    \(\lnot X(x) =1-X(x)\).

  2. (2)

    \(|X|=\sum \limits _{x\in U} X(x)\).

An interval value is denoted as \(u=[u^{-}, u^{+}]\), in which \(u^{-}, u^{+}\in {\textbf{R}}\) and \(u^{-}< u^{+}\) always holds. \(u^{-}\) is the lower boundary of interval value u, and b is the upper boundary of u. For two interval values \(u=[u^{-}, u^{+}]\) and \(v=[v^{-}, v^{+}]\), \(u=v\) holds iff \(u^{-}=v^{-}\) and \(u^{+}=v^{+}\). An interval value can be viewed as a collection of continuous values and can be visualized as a region on the real number line. Furthermore, we define the set of all interval values as \(\mathbb{I}\mathbb{V}=\{u| u=[u^{-}, u^{+}], u^{-}, u^{+}\in {\textbf{R}}\}\). This set comprises all interval values u where \(u^{-}\) and \(u^{+}\) are real numbers.

An information system is defined as (U, AT, V, f), in which \(U=\{x_{1}, x_{2}, \cdot \cdot \cdot , x_{n}\}\) is non-empty finite set of objects; \(AT=\{a_{1}, a_{2}, \cdot \cdot \cdot , a_{m}\}\) is a non-empty finite set of attributes or features, \(V=\bigcup \limits _{a_{l}\in AT}V_{a_{l}}\), where \(V_{a_{l}}\) is the domain of conditional attributes \(a_{l}\), and \(V_{a_{l}}\in \mathbb{I}\mathbb{V}\); and \(f: U\times AT\rightarrow V\) is a mapping from \(U\times AT\) to V.

For an information system (U, AT, V, f), if \(\forall x\in U, a_{l}\in AT\), \(f(x,a_{l})\in V_{a_{l}}\), then (U, AT, V, f) is called an interval-valued information system (IV-IS). When (U, AT, V, f) is accompanied by fuzzy decision D, we call it interval-valued fuzzy decision system (IV-FDS). Generally, we use \((U,AT\cup D,V,f)\) to represent an IV-FDS.

3 Fuzzy Similarity Relation for Interval-Valued Data

In this section, we introduce the diversity function for an attribute set in interval-valued information systems. Let us first show an interval-valued information system depicted in Table 1.

Table 1 Interval-valued information system
Full size table

Definition 3.1

For two interval values \(u_{1}=[u_{1}^{-}, u_{1}^{+}]\) and \(u_{2}=[v_{2}^{-}, v_{2}^{+}]\), the possible degree of interval value \(u_{1}\) greater than \(u_{2}\) is defined as

$$\begin{aligned}\begin{aligned} P(u_{1},u_{2})=\min \left\{ 1, \max \left\{ \frac{u_{1}^{+}-u_{2}^{-}}{(u_{1}^{+}-u_{1}^{-})+(u_{2}^{+}-u_{2}^{-})}, 0\right\} \right\} . \end{aligned}\end{aligned}$$

From the above definition, \(P(u_{1},u_{2})\) is the probability of interval value \(u_{1}\) greater than \(u_{2}\), and \(P(u_{2},u_{1})\) is the probability of interval value \(u_{2}\) greater than interval value \(u_{1}\). So the formula \(|P(u_{1},u_{2})-P(u_{2},u_{1})|\) can be viewed as diversity degree between \(u_{1}\) and \(u_{2}\).

Definition 3.2

Let (U, AT, V, f) be an interval-valued information system, \(x_{i}\) and \(x_{j}\) are two objects in U. For a subset \(B\subseteq AT\), the diversity function between two objects \(x_{i}\) and \(x_{j}\) on attribute set B is defined as

$$\begin{aligned}\begin{aligned}&d(x_{i}, x_{j}) = \\&\sum \limits _{l =1}^{m}\left| P\left( f(x_{i}, a_{l}), f(x_{j}, a_{l})\right) - P\left( f(x_{j}, a_{l}), f(x_{i}, a_{l})\right) \right| , \end{aligned}\end{aligned}$$

where \(f(x_{i}, a_{l})= [u_{i,l}^{-},u_{i,l}^{+}]\) is the interval value of \(x_{i}\) on \(a_{l}\) and \(m=|B|\).

The diversity function can be mathematically expressed using the specific expression: \(d(x_{i} ,x_{j} ) = \sum\nolimits_{{l = 1}}^{m} {\left| {P\left( {[u_{{i,l}}^{ - } ,u_{{i,l}}^{ + } ],[u_{{j,l}}^{ - } ,u_{{j,l}}^{ + } ]} \right) - P\left( {[u_{{j,l}}^{ - } ,u_{{j,l}}^{ + } ],[u_{{i,l}}^{ - } ,u_{{i,l}}^{ + } ]} \right)} \right|}\) in the IV-IS.

Definition 3.3

Let (U, AT, V, f) be an interval-valued information system and \(B\subseteq AT\), the diversity matrix of B is defined by

$$\begin{aligned} D_{B}= \begin{pmatrix} d(x_{1}, x_{1}) &{} d(x_{1}, x_{2}) &{} \cdots &{} d(x_{1}, x_{n})\\ d(x_{2}, x_{1}) &{} d(x_{2}, x_{2}) &{} \cdots &{} d(x_{2}, x_{n})\\ \vdots &{} \vdots &{} d(x_{i}, x_{j}) &{} \vdots \\ d(x_{n}, x_{1}) &{} d(x_{n}, x_{2}) &{} \cdots &{} d(x_{n}, x_{n}) \end{pmatrix}, \end{aligned}$$

where \(d(x_{i}, x_{j})\) is the diversity function between two objects \(x_{i}\) and \(x_{j}\) on B.

Definition 3.4

Let \(I = (U, AT, V, f)\) be an interval-valued information system and \(B\subseteq AT\). \(D_{AT}\) and \(D_{B}\) are two diversity matrices on AT and B. The \(D^{'}_{B}\) is normalized as

$$\begin{aligned} D^{'}_{B} = \frac{D_{B}}{\max (D_{AT})}, \end{aligned}$$

the \(\max (D_{AT})\) represents for the maximal value of elements of diversity matrix \(D_{AT}\).

Definition 3.5

Let \(I = (U, AT, V, f)\) be an interval-valued information system and a subset \(B\subseteq AT\). Suppose \(D^{'}_{B}\) is a normalized diversity matrix on B. The element \(d(x_{i}, x_{j})\) of \(D^{'}_{B}\) is the normalized diversity between two objects \(x_{i}\) and \(x_{j}\) on B. Then \(R_{B}\) is a fuzzy relation on B, denoted by the relation matrix \(S_{R_{B}}\) as follows.

$$\begin{aligned}\begin{aligned}&S_{R_{B}}=\\&\begin{pmatrix} R_{B}(x_{1}, x_{1}) &{} R_{B}(x_{1}, x_{2}) &{} \cdots &{} R_{B}(x_{1}, x_{n})\\ R_{B}(x_{2}, x_{1}) &{} R_{B}(x_{2}, x_{2}) &{} \cdots &{} R_{B}(x_{2}, x_{n})\\ \vdots &{} \vdots &{} R_{B}(x_{i}, x_{j}) &{} \vdots \\ R_{B}(x_{n}, x_{1}) &{} R_{B}(x_{n}, x_{2}) &{} \cdots &{} R_{B}(x_{n}, x_{n}) \end{pmatrix}, \end{aligned} \end{aligned}$$

where \(R_{B}(x_{i}, x_{j})=1- d(x_{i}, x_{j})\).

It could be easily verified that fuzzy relation \(R_{B}\) satisfies

  1. (1)

    Reflexive: \(\forall x_{i}\in U, R_{B}(x_{i},x_{i})= 1\);

  2. (2)

    Symmetry: \(\forall x_{i}, x_{j}\in U, R_{B}(x_{i},x_{j})= R_{B}(x_{j},x_{i})\).

These properties indicate that \(R_{B}\) is a fuzzy similarity relation. Then \(R_{B}(x_{i}, x_{j})\) denotes the similarity degree between \(x_{i}\) and \(x_{j}\) on B.

The fuzzy similarity relation induces fuzzy similarity classes, which form a fuzzy covering of the domain. Let us focus on the following concepts about fuzzy covering and fuzzy similarity classes.

Definition 3.6

Let (U, AT, V, f) be an interval-valued information system, \(R_{B}\) is a fuzzy similarity relation on \(B\subseteq AT\). A fuzzy covering induced by \(R_{B}\) is defined by

$$\begin{aligned} U/R_{B}=\{[x_{i}]_{R_{B}}| x_{i}\in U\}, \end{aligned}$$

where

$$\begin{aligned}{}[x_{i}]_{R_{B}}=\sum \limits _{x_{j}\in U}\frac{R_{B}(x_{i}, x_{j})}{x_{j}} \end{aligned}$$

is the fuzzy similarity class belonging to \(x_{i}\), and the symbol “\(\sum\)" denotes a union of elements.

The cardinality of \([x_{i}]_{R_{B}}\) is derived as

$$\begin{aligned} |[x_{i}]_{R_{B}}|=\sum \limits _{x_{j}\in U}R_{B}(x_{i}, x_{j}). \end{aligned}$$

Example 1

Table 2 is an interval-valued information system from the reference, where the object set \(U=\{x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7},x_{8},x_{9},x_{10}\}\), and the attribute set \(AT=\{a_{1},a_{2},a_{3},a_{4},a_{5}\}\).

Table 2 An interval-valued information system
Full size table

The diversity matrix of the attribute set \(AT=\{a_{1},a_{2},a_{3},a_{4},a_{5}\}\) is formed as

$$\begin{aligned}\begin{aligned}&D(AT)=\\&\begin{pmatrix} 0 &{}5.00 &{}5.00 &{}5.00 &{}3.42 &{}5.00 &{}2.58 &{}1.63 &{}2.07 &{}3.03 \\ 5.00 &{}0 &{}4.50 &{}4.78 &{}3.50 &{}4.46 &{}4.33 &{}4.42 &{}4.92 &{}3.20 \\ 5.00 &{}4.50 &{}0 &{}3.69 &{}5.00 &{}2.60 &{}5.00 &{}5.00 &{}5.00 &{}5.00 \\ 5.00 &{}4.78 &{}3.69 &{}0 &{}5.00 &{}2.34 &{}5.00 &{}5.00 &{}5.00 &{}5.00 \\ 3.42 &{}3.50 &{}5.00 &{}5.00 &{}0 &{}5.00 &{}2.85 &{}3.60 &{}2.36 &{}1.75 \\ 5.00 &{}4.46 &{}2.60 &{}2.34 &{}5.00 &{}0 &{}5.00 &{}5.00 &{}5.00 &{}4.96 \\ 2.58 &{}4.33 &{}5.00 &{}5.00 &{}2.84 &{}5.00 &{}0 &{}3.16 &{}2.76 &{}2.45 \\ 1.63 &{}4.42 &{}5.00 &{}5.00 &{}3.60 &{}5.00 &{}3.16 &{}0 &{}3.37 &{}2.67 \\ 2.07 &{}4.92 &{}5.00 &{}5.00 &{}2.36 &{}5.00 &{}2.76 &{}3.37 &{}0 &{}2.99 \\ 3.03 &{}3.20 &{}5.00 &{}5.00 &{}1.75 &{}4.96 &{}2.45 &{}2.67 &{}2.99 &{}0 \end{pmatrix}. \end{aligned}\end{aligned}$$

We can easily obtain that \(max(D(AT))=5.00\), from Definition 3.4, the above diversity matrix is normalized as follows.

$$\begin{aligned}\begin{aligned}&D(AT^{'})=\\&\begin{pmatrix} 0 &{}1.00 &{}1.00 &{}1.00 &{}0.68 &{}1.00 &{}0.52 &{}0.33 &{}0.41 &{}0.61 \\ 1.00 &{}0 &{}0.90 &{}0.96 &{}0.70 &{}0.89 &{}0.87 &{}0.88 &{}0.98 &{}0.64 \\ 1.00 &{}0.90 &{}0 &{}0.74 &{}1.00 &{}0.52 &{}1.00 &{}1.00 &{}1.00 &{}1.00 \\ 1.00 &{}0.96 &{}0.74 &{}0 &{}1.00 &{}0.47 &{}1.00 &{}1.00 &{}1.00 &{}1.00 \\ 0.68 &{}0.70 &{}1.00 &{}1.00 &{}0 &{}1.00 &{}0.57 &{}0.72 &{}0.47 &{}0.35 \\ 1.00 &{}0.89 &{}0.52 &{}0.47 &{}1.00 &{}0 &{}1.00 &{}1.00 &{}1.00 &{}0.99 \\ 0.52 &{}0.87 &{}1.00 &{}1.00 &{}0.57 &{}1.00 &{}0 &{}0.63 &{}0.55 &{}0.49 \\ 0.33 &{}0.88 &{}1.00 &{}1.00 &{}0.72 &{}1.00 &{}0.63 &{}0 &{}0.67 &{}0.53 \\ 0.41 &{}0.98 &{}1.00 &{}1.00 &{}0.47 &{}1.00 &{}0.55 &{}0.67 &{}0 &{}0.60 \\ 0.61 &{}0.64 &{}1.00 &{}1.00 &{}0.35 &{}0.99 &{}0.49 &{}0.53 &{}0.60 &{}0 \end{pmatrix}. \end{aligned}\end{aligned}$$

Based on the fuzzy similarity relation matrix defined in Definition 3.5, we obtain that

$$\begin{aligned}\begin{aligned}&S_{R_{AT}}=\\&\begin{pmatrix} 1.00 &{}0 &{}0 &{}0 &{}0.32 &{}0 &{}0.48 &{}0.67 &{}0.59 &{}0.39 \\ 0 &{}1.00 &{}0.10 &{}0.04 &{}0.30 &{}0.11 &{}0.13 &{}0.12 &{}0.02 &{}0.36 \\ 0 &{}0.10 &{}1.00 &{}0.26 &{}0 &{}0.48 &{}0 &{}0 &{}0 &{}0 \\ 0 &{}0.04 &{}0.26 &{}1.00 &{}0 &{}0.53 &{}0 &{}0 &{}0 &{}0 \\ 0.31 &{}0.30 &{}0 &{}0 &{}1.00 &{}0 &{}0.43 &{}0.28 &{}0.53 &{}0.65 \\ 0 &{}0.11 &{}0.48 &{}0.53 &{}0 &{}1.00 &{}0 &{}0 &{}0 &{}0.01 \\ 0.48 &{}0.13 &{}0 &{}0 &{}0.43 &{}0 &{}1.00 &{}0.37 &{}0.45 &{}0.51 \\ 0.67 &{}0.12 &{}0 &{}0 &{}0.28 &{}0 &{}0.37 &{}1.00 &{}0.33 &{}0.47 \\ 0.59 &{}0.02 &{}0 &{}0 &{}0.53 &{}0 &{}0.45 &{}0.33 &{}1.00 &{}0.40 \\ 0.39 &{}0.36 &{}0 &{}0 &{}0.65 &{}0.01 &{}0.51 &{}0.47 &{}0.40 &{}1.00 \end{pmatrix}. \end{aligned}\end{aligned}$$

then the similarity classes with regard to the fussy similarity relation \(R_{AT}\) are listed as follows.

\([x_{1}]_{AT} = \{\frac{1}{x_{1}}+ \frac{0.32}{x_{5}}+ \frac{0.48}{x_{7}}+ \frac{0.67}{x_{8}}+ \frac{0.59}{x_{9}}+ \frac{0.39}{x_{10}}\},\)

\([x_{2}]_{AT} = \{\frac{1}{x_{2}}+ \frac{0.10}{x_{3}}+ \frac{0.04}{x_{4}}+ \frac{0.30}{x_{5}}+ \frac{0.11}{x_{6}}+ \frac{0.13}{x_{7}}+ \frac{0.12}{x_{8}}+ \frac{0.02}{x_{9}}+ \frac{0.36}{x_{10}}\},\)

\([x_{3}]_{AT} = \{\frac{0.10}{x_{2}}+ \frac{1}{x_{3}}+ \frac{0.26}{x_{4}}+ \frac{0.48}{x_{6}}\},\)

\([x_{4}]_{AT} = \{\frac{0.04}{x_{2}}+ \frac{0.26}{x_{3}}+ \frac{1}{x_{4}}+ \frac{0.53}{x_{6}}\},\)

\([x_{5}]_{AT} = \{\frac{0.31}{x_{1}}+ \frac{0.30}{x_{2}}+ \frac{1}{x_{5}}+ \frac{0.43}{x_{7}}+ \frac{0.28}{x_{8}}+ \frac{0.53}{x_{9}}+ \frac{0.65}{x_{10}}\},\)

\([x_{6}]_{AT} = \{\frac{0.11}{x_{2}}+ \frac{0.48}{x_{3}}+ \frac{0.53}{x_{4}}+ \frac{1}{x_{6}}+ \frac{0.01}{x_{10}}\},\)

\([x_{7}]_{AT} = \{\frac{0.48}{x_{1}}+ \frac{0.13}{x_{2}}+ \frac{0.43}{x_{5}}+ \frac{1}{x_{7}}+ \frac{0.37}{x_{8}}+ \frac{0.45}{x_{9}}+ \frac{0.51}{x_{10}}\},\)

\([x_{8}]_{AT} = \{\frac{0.67}{x_{1}}+ \frac{0.12}{x_{2}}+ \frac{0.28}{x_{5}}+ \frac{0.37}{x_{7}}+ \frac{1}{x_{8}}+ \frac{0.33}{x_{9}}+ \frac{0.47}{x_{10}}\},\)

\([x_{9}]_{AT} = \{\frac{0.59}{x_{1}}+ \frac{0.02}{x_{2}}+ \frac{0.53}{x_{5}}+ \frac{0.45}{x_{7}}+ \frac{0.33}{x_{8}}+ \frac{1}{x_{9}}+ \frac{0.40}{x_{10}}\},\)

\([x_{10}]_{AT} = \{\frac{0.39}{x_{1}}+ \frac{0.36}{x_{2}}+ \frac{0.65}{x_{5}}+ \frac{0.01}{x_{6}}+ \frac{0.51}{x_{7}}+ \frac{0.47}{x_{8}}+ \frac{0.40}{x_{9}}+ \frac{1}{x_{10}}\}.\)

4 Probabilistic Rough Fuzzy Approximations for Interval-Valued Fuzzy Systems

In this section, we consider the interval-valued probabilistic rough fuzzy set (IV-PRFS) approach.

Definition 4.1

(IV-PRFS) Let \((U, AT\cup D, V, f)\) be an IV-FDS, \(R_{B}\) is a fuzzy similarity relation on \(B\subseteq AT\). For \(X\in {\mathcal {F}}(U)\) and \(0\le \beta <\alpha \le 1\), the interval-valued probabilistic rough fuzzy lower and upper approximation operators of X based on parameters \(\alpha\) and \(\beta\) with respect to \(R_{B}\) are defined as

$$\begin{aligned}\begin{aligned}&\underline{R_{B}^{(\alpha ,\beta )}}(X)=\left\{ x\in U|P(X|[x]_{R_{B}})\ge \alpha \right\} ;\\&\overline{R_{B}^{(\alpha ,\beta )}}(X)=\left\{ x\in U|P(X|[x]_{R_{B}})> \beta \right\} , \end{aligned}\end{aligned}$$

where \(P(X|[x]_{R_{B}})=\frac{|[x]_{R_{B}}\cap X|}{|[x]_{R_{B}}|}\) is the conditional probability determined by the rough membership function. From the presented two approximation operators, an IV-PRFS model could be determined if \(\underline{R_{B}^{(\alpha ,\beta )}}(X) \ne \overline{R_{B}^{(\alpha ,\beta )}}(X)\), denoted by \((\underline{R_{B}^{(\alpha ,\beta )}}(X), \overline{R_{B}^{(\alpha ,\beta )}}(X))\). Otherwise, we say that X is the interval-valued probabilistic definable fuzzy set.

The thresholds \(\alpha\) and \(\beta\) are parameters derived from the losses of the Bayesian decision procedure. The loss function represents standard threshold values that have a practical and intuitive interpretation. In real-world applications, the loss or cost can be easily interpreted and measured. Therefore, the thresholds \(\alpha\) and \(\beta\) have concrete and tangible meanings in the context of the specific application.

Usually, the approximated target concept X is the fuzzy decision D in the interval-valued fuzzy decision system. The approximations defined above constitute a method to approximately describe a fuzzy set X using interval-valued probabilistic rough fuzzy approximations. Three decision regions of X for B in IV-PRFS model are then expressed as follows.

$$\begin{aligned}\begin{aligned} Pos(X)&\ =\underline{R_{B}^{(\alpha , \beta )}}(X) \\&\ = \left\{ x\in U|P(X|[x]_{R_{B}})\ge \alpha \right\} ,\\ Neg(X)&\ = U- \overline{R_{B}^{(\alpha , \beta )}}(X)\\&\ = \left\{ x\in U|P(X|[x]_{R_{B}})\le \beta \right\} ,\\ Bnd(X)&\ = \overline{R_{B}^{(\alpha , \beta )}}(X)- \underline{R_{B}^{(\alpha , \beta )}}(X)\\&\ = \left\{ x\in U|\beta<P(X|[x]_{R_{B}})< \alpha \right\} , \end{aligned}\end{aligned}$$

where Pos(X) represents positive region, Neg(X) represents negative region, and Bnd(X) represents boundary region.

It should be noted that the set type of the upper and lower approximations obtained by constructing IV-PRFS model to approximate the arbitrary \({\widetilde{X}}\) is longer a fuzzy set, but classical set. It means that we use two classical sets (upper and lower approximations) to approximate a given fuzzy set.

Theorem 4.1

Let (U, AT, V, f) be an interval-valued information system, \(B\subseteq AT\). For \(X\in {\mathcal {F}}(U)\) and \(0\le \beta _{1}\le \beta _{2}<\alpha _{2}\le \alpha _{1}\le 1\), then

  1. (1)

    \(\underline{R_{B}^{(\alpha _{1}, \beta _{1})}}(X)\subseteq \underline{R_{B}^{(\alpha _{2}, \beta _{2})}}(X);\)

  2. (2)

    \(\overline{R_{B}^{(\alpha _{1}, \beta _{1})}}(X)\supseteq \overline{R_{B}^{(\alpha _{2}, \beta _{2})}}(X).\)

Proof

  1. (1)

    From the lower approximation defined in Definition 4.1,

    $$\begin{aligned}\begin{aligned}&x\in \underline{R_{B}^{(\alpha _{1}, \beta _{1})}}(X) \\&\Rightarrow P(X|[x]_{R_{B}})> \alpha _{1}\ge \alpha _{2} \\&\Rightarrow x\in \underline{R_{B}^{(\alpha _{2}, \beta _{2})}}(X). \end{aligned}\end{aligned}$$
  2. (2)

    From the upper approximation defined in Definition 4.1,

    $$\begin{aligned}\begin{aligned}&x\in \overline{R_{B}^{(\alpha _{2}, \beta _{2})}}(X)\\&\Rightarrow (X|[x]_{R_{B}})> \beta _{2}\ge \beta _{1}\\&\Rightarrow x\in \overline{R_{B}^{(\alpha _{1}, \beta _{1})}}(X). \end{aligned}\end{aligned}$$

\(\square\)

In the following Theorem 4.2 and Theorem 4.3, we provide the important monotonicity of the DP-RFS model.

Theorem 4.2

Let (U, AT, V, f) be an interval-valued information system, \(B\subseteq AT\). For \(X_{1}, X_{2}\in {\mathcal {F}}(U)\) and \(X_{1}\subseteq X_{2}\), \(0\le \beta <\alpha \le 1\), then

  1. (1)

    \(\underline{R_{B}^{(\alpha , \beta )}}(X_{1})\subseteq \underline{R_{B}^{(\alpha , \beta )}}(X_{2});\)

  2. (2)

    \(\overline{R_{B}^{(\alpha , \beta )}}(X_{1})\subseteq \overline{R_{B}^{(\alpha , \beta )}}(X_{2}).\)

Proof

As \(X_{1}\subseteq X_{2}\), \(\forall x\in U\), it follows that \(|[x]_{R_{B}}\cap X_{1}|\le |[x]_{R_{B}}\cap X_{2}|\), which means \(\frac{|[x]_{R_{B}}\cap X_{1}|}{|[x]_{R_{B}}|}\le \frac{|[x]_{R_{B}}\cap X_{2}|}{|[x]_{R_{B}}|}\).

  1. (1)

    If \(x\in \underline{R_{B}^{(\alpha , \beta )}}(X_{1})\), then \(\frac{|[x]_{R_{B}}\cap X_{1}|}{|[x]_{R_{B}}|}\ge \alpha\), so \(\frac{|[x]_{R_{B}}\cap X_{2}|}{|[x]_{R_{B}}|}\ge \alpha\), we obtain that \(x\in \underline{R_{B}^{(\alpha , \beta )}}(X_{2})\).

  2. (2)

    If \(x\in \overline{R_{B}^{(\alpha , \beta )}}(X_{1})\), then \(\frac{|[x]_{R_{B}}\cap X_{1}|}{|[x]_{R_{B}}|}\ge \beta\), so \(\frac{|[x]_{R_{B}}\cap X_{2}|}{|[x]_{R_{B}}|}\ge \beta\), we obtain that \(x\in \overline{R_{B}^{(\alpha , \beta )}}(X_{2})\).

\(\square\)

Theorem 4.3

Let (U, AT, V, f) be an interval-valued information system, \(B_{1}\subseteq B_{2}\subseteq AT\). For \(X\in {\mathcal {F}}(U)\) and \(0\le \beta <\alpha \le 1\), then

  1. (1)

    \(\underline{R_{B_{1}}^{(\alpha , \beta )}}(X)\subseteq \underline{R_{B_{2}}^{(\alpha , \beta )}}(X);\)

  2. (2)

    \(\overline{R_{B_{1}}^{(\alpha , \beta )}}(X)\subseteq \overline{R_{B_{2}}^{(\alpha , \beta )}}(X).\)

Proof

Because \(B_{1}\subseteq B_{2}\), according to Definition 4.2 and Definition 4.3, \(D_{B_{1}}\le D_{B_{2}}\). From Definition 3.5, \(S_{R_{B_{1}}}\ge S_{R_{B_{2}}}\). So this theorem could be easily derived. \(\square\)

In the following, an example is employed to introduce the IV-PRFS.

Example 2

(Continuation of Example 1.) Consider the decision fuzzy set \(D=\{\frac{0.42}{x_{1}}+\frac{0.72}{x_{2}}+\frac{0.00}{x_{3}}+\frac{0.30}{x_{4}}+\frac{0.15}{x_{5}}+\frac{0.09}{x_{6}}+\frac{0.19}{x_{7}}+\frac{0.35}{x_{8}}+\frac{0.40}{x_{9}}+\frac{0.54}{x_{10}}\}\), which represents the initial diagnosis of each patient suffering from a cold. The two parameters are set as \(\alpha =0.6\) and \(\beta = 0.3\). The cardinality of intersection between \([x_{i}]_{AT}\) (\(i=1,2,,\cdots , 10\)) and D are calculated as

$$\begin{aligned} |[x_{1}]_{R_{AT}}\cap D| = 2.34, |[x_{2}]_{R_{AT}}\cap D| = 1.90, \\ |[x_{3}]_{R_{AT}}\cap D| = 0.00, |[x_{4}]_{R_{AT}}\cap D| = 0.91, \\ |[x_{5}]_{R_{AT}}\cap D| = 1.03, |[x_{6}]_{R_{AT}}\cap D| = 0.38, \\ |[x_{7}]_{R_{AT}}\cap D| = 1.25, |[x_{8}]_{R_{AT}}\cap D| = 2.11, \\ |[x_{9}]_{R_{AT}}\cap D| = 2.33, |[x_{10}]_{R_{AT}}\cap D| = 3.21. \end{aligned}$$

The cardinality of \([x_{i}]_{AT}\) (\(i=1,2,,\cdots , 10\)) are shown as

$$\begin{aligned} |[x_{1}]_{R_{AT}}| = 3.45,\ |[x_{2}]_{R_{AT}}| = 2.18, \\ |[x_{3}]_{R_{AT}}| = 1.84,\ |[x_{4}]_{R_{AT}}| = 1.84, \\ |[x_{5}]_{R_{AT}}| = 3.50,\ |[x_{6}]_{R_{AT}}| = 2.13, \\ |[x_{7}]_{R_{AT}}| = 3.37,\ |[x_{8}]_{R_{AT}}| = 3.23, \\ |[x_{9}]_{R_{AT}}| = 3.51,\ |[x_{10}]_{R_{AT}}| = 3.79. \end{aligned}$$

The interval-valued probabilistic rough fuzzy lower and upper approximations of X based on \(\alpha =0.6\) and \(\beta = 0.3\) with respect to the attribute set AT are obtained as follows.

$$\begin{aligned}\begin{aligned}&\underline{R_{B}^{(\alpha ,\beta )}}(D)= \{x_{2}, x_{5}, x_{7}, x_{8}, x_{10}\};\\&\overline{R_{B}^{(\alpha ,\beta )}}(D)= \{x_{1}, x_{2}, x_{5}, x_{7}, x_{8},x_{9}, x_{10}\}. \end{aligned}\end{aligned}$$

The three-way decision regions are

\(Pos_{B}(D) = \{x_{2}, x_{5}, x_{7}, x_{8}, x_{10}\};\)

\(Neg_{B}(D) = \{x_{3}, x_{4}, x_{6}\};\)

\(Bnd_{B}(D) = \{x_{1}, x_{9}\}.\)

From the above three-way decision regions, the decision rules of acceptance, rejection and postponement could be derived.

5 Multi-Granularity Probabilistic Rough Fuzzy Approximations for IV-FDSs

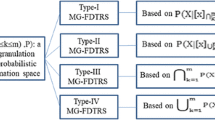
In the subsequent sections, we examine two types of interval-valued multi-granularity probabilistic rough fuzzy set (IV-MG-PRFS) models. Each model is tailored to a specific application context, and the choice between the two models should be based on the specific requirements of the application. We begin by introducing the first type of IV-MG-PRFS, known as the interval-valued mean multi-granularity probabilistic rough fuzzy set (IV-MMG-PRFS).

Definition 5.1

let \((U, AT\cup D, V, f)\) be an IV-FDS, \(R_{B_{1}}, R_{B_{2}}, \cdots , R_{B_{m}}\) are fuzzy similarity relation on \(B_{1}, B_{2}, \cdots , B_{m}\subseteq AT\). \(\forall X\in {\mathcal {F}}(U)\) and \(0\le \beta <\alpha \le 1\).

The interval-valued mean multi-granularity probabilistic rough fuzzy lower and upper approximations are denoted by

$$\begin{aligned}\begin{aligned}&\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)=\left\{ x\in U|\frac{\sum \limits _{i=1}^{m}P(X|[x]_{R_{B_{i}}})}{m}\ge \alpha \right\} \\&\overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)=\left\{ x\in U|\frac{\sum \limits _{i=1}^{m}P(X|[x]_{R_{B_{i}}})}{m}> \beta \right\} . \end{aligned} \end{aligned}$$

If \(\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)\ne \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)\), the IV-MMG-PRFS model could be determined, denoted by \(\left( \underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X), \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)\right)\).

It is easy to verify that \(\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)\subseteq \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)\) always holds. Then three decision regions of X in IV-MMG-PRFS model are then expressed, namely

$$\begin{aligned}\begin{aligned}&Pos_{M}(X) =\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X) \\&Neg_{M}(X) = U- \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)\\&Bnd_{M}(X) = \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X)- \underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(X) \end{aligned} \end{aligned}$$

where \(Pos_{M}(X)\) represents interval-valued mean multi-granularity probabilistic positive region, \(Neg_{M}(X)\) represents interval-valued mean multi-granularity probabilistic negative region, and \(Bnd_{M}(X)\) represents interval-valued mean multi-granularity probabilistic boundary region. Based on these regions, we obtain the IF-THEN decision rules:

(P):

If \(\sum \limits _{i=1}^{m}P(X|[x]_{R_{B_{i}}})/m\ge \alpha\), then decide \(Pos_{M}(X)\).

(N):

If \(\sum \limits _{i=1}^{m}P(X|[x]_{R_{B_{i}}})/m\le \beta\), then decide \(Neg_{M}(X)\).

(B):

If \(\beta<\sum \limits _{i=1}^{m}P(X|[x]_{R_{B_{i}}})/m< \alpha\), then decide \(Bnd_{M}(X)\).

Definition 5.2

Let \((U, AT\cup D, V, f)\) be an IV-FDS, \(R_{B_{1}}, R_{B_{2}}, \cdots , R_{B_{m}}\) are fuzzy similarity relation on \(B_{1}, B_{2}, \cdots , B_{m}\subseteq AT\). \(\forall X\in {\mathcal {F}}(U)\) and \(0\le \beta <\alpha \le 1\). The interval-valued optimistic multi-granularity probabilistic rough fuzzy lower and upper approximations are denoted by

$$\begin{aligned}\begin{aligned}&\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)=\left\{ x\in U|\bigvee _{i=1}^{m}(P(X|[x]_{R_{B_{i}}})\ge \alpha )\right\} \\&\overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)=\left\{ x\in U|\bigwedge _{i=1}^{m}(P(X|[x]_{R_{B_{i}}})> \beta )\right\} . \end{aligned} \end{aligned}$$

If \(\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\ne \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\), the IV-OMG-PRFS model could be determined, denoted by \(\left( \underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X), \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\right)\).

It should be noted that there is no inclusion relation between \(\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\) and \(\overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\), positive region, negative region upper and lower boundary regions are naturally proposed. We form the following decision regions of X in IV-OMG-PRFS model, namely

$$\begin{aligned}\begin{aligned}&Pos_{O}(X) =\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\cap \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X) \\&Neg_{O}(X) = U- (\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\cup \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X))\\&Ubn_{O}(X) = \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)- \underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\\&Lbn_{O}(X) = \underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)- \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(X)\\ \end{aligned} \end{aligned}$$

where \(Pos_{O}(X)\) represents interval-valued optimistic multi-granularity probabilistic positive region, \(Neg_{O}(X)\) represents interval-valued optimistic multi-granularity probabilistic negative region, \(Ubn_{O}(X)\) represents interval-valued optimistic multi-granularity probabilistic upper boundary region, and \(Lbn_{O}(X)\) represents interval-valued optimistic multi-granularity probabilistic lower boundary region. The interval-valued optimistic multi-granularity probabilistic boundary region is the union of upper boundary region and lower boundary region, which means \(Bnd_{O}(X)= Ubn_{O}(X) \cup Lbn_{O}(X).\) Based on these regions, we obtain the IF-THEN decision rules:

(P):

If \(\forall i\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{i}}})> \beta\), and \(\exists j\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{j}}})\ge \alpha\), then decide \(Pos_{O}(X)\).

(N):

If \(\forall i\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{i}}})< \alpha\), and \(\exists j\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{j}}})\le \beta\), then decide \(Neg_{O}(X)\).

(U):

If \(\forall i\in \{1,2,\cdots , m\}\), s.t. \(\beta<P(X|[x]_{R_{B_{i}}})< \alpha\), then decide \(Ubn_{O}(X)\).

(L):

If \(\exists i\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{i}}})\ge \alpha\), and \(\exists j\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{j}}})< \beta\), then decide \(Lbn_{O}(X)\).

Definition 5.3

Let \((U, AT\cup D, V, f)\) be an IV-FDS, \(R_{B_{1}}, R_{B_{2}}, \cdots , R_{B_{m}}\) are fuzzy similarity relation on \(B_{1}, B_{2}, \cdots , B_{m}\subseteq AT\). \(\forall X\in {\mathcal {F}}(U)\) and \(0\le \beta <\alpha \le 1\). The interval-valued pessimistic multi-granularity probabilistic rough fuzzy lower and upper approximations are denoted by

$$\begin{aligned}\begin{aligned}&\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X)=\left\{ x\in U|\bigwedge _{i=1}^{m}(P(X|[x]_{R_{B_{i}}})\ge \alpha )\right\} \\&\overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X)=\left\{ x\in U|\bigvee _{i=1}^{m}(P(X|[x]_{R_{B_{i}}})> \beta )\right\} . \end{aligned} \end{aligned}$$

The IV-PMG-PRFS model could be determined based on the above two operators, denoted by \(\left( \underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X), \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X)\right)\).

It is easy to verify that \(\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X)\subseteq \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X)\) always holds. Then three decision regions of X in IV-PMG-PRFS model are then expressed, namely

$$\begin{aligned}\begin{aligned}&Pos_{P}(X) =\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X) \\&Neg_{P}(X) = U- \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X)\\&Bnd_{P}(X) = \overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X)- \underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(X) \end{aligned} \end{aligned}$$

where \(Pos_{P}(X)\) represents interval-valued pessimistic multi-granularity probabilistic positive region, \(Neg_{P}(X)\) represents interval-valued pessimistic multi-granularity probabilistic negative region, and \(Bnd_{P}(X)\) represents interval-valued pessimistic multi-granularity probabilistic boundary region. Based on these regions, we obtain the IF-THEN decision rules:

(P):

If \(\forall i\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{i}}})> \alpha\), then decide \(Pos_{P}(X)\).

(N):

If \(\forall i\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{i}}})\le \beta\), then decide \(Neg_{P}(X)\).

(B):

If \(\exists i\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{i}}})< \alpha\), and \(\exists j\in \{1,2,\cdots , m\}\), s.t. \(P(X|[x]_{R_{B_{i}}})> \beta\) then decide \(Bnd_{P}(X)\).

6 Illustrative Case Study

Based on the presented three kinds of multi-granularity probabilistic rough fuzzy set models for interval-valued fuzzy systems, we can make more comprehensive decisions and evaluations when dealing with multi-source decision fusion in the actual decision processes. There are many practical examples of multi-source decision fusion involving interval-valued fuzzy systems in the actual decision processes. Let us give several examples as follows. (1) Medical diagnosis. In the field of medicine, utilizing multi-granularity decision fusion with interval-valued fuzzy systems can assist in the accurate patient diagnosis. By integrating data from different medical tests or diagnostic tools, such as results from various laboratory tests or expert opinions, a more comprehensive and reliable diagnosis can be obtained. (2) Financial investment decision-making. In the financial domain, employing multi-granularity decision fusion with interval-valued fuzzy systems can aid investors in making informed investment decisions. By integrating information from different financial indicators, market prediction models, or expert judgments, risks can be minimized, and the accuracy of evaluating investment projects can be improved. (3) Engineering project decision-making. In the engineering field, employing multi-granularity decision fusion with interval-valued fuzzy systems can assist engineers in making complex project decisions. By fusing knowledge and experience from various domains, such as structural design, environmental assessment, and cost estimation, multiple factors can be considered comprehensively, reducing decision uncertainty. These examples illustrate the application of multi-granularity decision fusion with interval-valued fuzzy systems in real-world decision processes. By integrating data and decisions from diverse sources, more accurate, comprehensive, and reliable decision support can be provided.

Example 3

To make the presented models more comprehensible, we provide a real world application background to Table 2, where U is a universe which consists of ten patients with the clinical features degree; the attributes \(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\) are Cough, Rhinorrhoea, Myodynia, Diarrhea, Nausea, respectively. In the early stage of Virus Flu outbreak, due to its similar condition with traditional pneumonia, but with many different performance characteristics, multiple experts may be required to diagnose the same patient, and different experts may have different considerations for the selected characteristics. In this case, each expert’s diagnosis of patients can be regarded as a single granularity decision.

For the Doctor \(M_{1}\), he (or she) believe that among the 5 clinical features, \(B_{1}=\{a_{1}, a_{2}, a_{3}\}\) need to be considered. For the Doctor \(M_{2}\), he (or she) believes that among the 5 clinical features, \(B_{2}=\{a_{1}, a_{3}, a_{5}\}\) need to be considered. For the Doctor \(M_{3}\), he (or she) believes that among the 5 clinical features, \(B_{3}=\{a_{3}, a_{4}, a_{5}\}\) need to be considered. Next we will make sure the patients who need to obtain treatments, who need not to obtain treatments and who need a further observation. We consider the two parameters \(\alpha =0.6, \beta =0.5\), which will be considered in this case study. We can get the conditional probability as follows. The calculated statistical results of the upper and lower approximations for Doctor \(M_{1}\), Doctor \(M_{2}\) and Doctor \(M_{3}\) are listed in Table 3.

Table 3 Statistical results for three Doctors
Full size table

According to the results displayed in Table 3, we can obtain the multi-granularity probabilistic rough fuzzy approximations for interval-valued fuzzy decision systems.

In order to facilitate the comparisons, we first calculate the lower and upper approximations of D regard to \(B_{1}\) in IV-PRFS as

$$\begin{aligned}\begin{aligned}&\underline{R_{B_{1}}^{(\alpha ,\beta )}}(D)= \{x_{1}, x_{2}, x_{7}\};\\&\overline{R_{B_{1}}^{(\alpha ,\beta )}}(D)= \{x_{1}, x_{2}, x_{5}, x_{7}, x_{8}, x_{9}, x_{10}\}. \end{aligned}\end{aligned}$$

The three-way decision regions are

\(Pos_{B_{1}}(D) = \{x_{1}, x_{2}, x_{7}\};\)

\(Neg_{B_{1}}(D) = \{x_{3}, x_{4}, x_{6}\};\)

\(Bnd_{B_{1}}(D) = \{x_{5}, x_{8}, x_{9}, x_{10}\}.\)

The lower and upper approximations of D regard to \(B_{2}\) in IV-PRFS are

$$\begin{aligned}\begin{aligned}&\underline{R_{B_{2}}^{(\alpha ,\beta )}}(D)= \{x_{2}, x_{5}, x_{7}, x_{8}, x_{10}\};\\&\overline{R_{B_{2}}^{(\alpha ,\beta )}}(D)= \{x_{2}, x_{5}, x_{7}, x_{8}, x_{9}, x_{10}\}. \end{aligned}\end{aligned}$$

The three-way decision regions are

\(Pos_{B_{2}}(D) = \{x_{2}, x_{5}, x_{7}, x_{8}, x_{10}\};\)

\(Neg_{B_{2}}(D) = \{x_{1}, x_{3}, x_{4}, x_{6}\};\)

\(Bnd_{B_{2}}(D) = \{x_{9}\}.\)

The lower and upper approximations of D regard to \(B_{3}\) in IV-PRFS are

$$\begin{aligned}\begin{aligned}&\underline{R_{B_{3}}^{(\alpha ,\beta )}}(D)= \{x_{2}, x_{5}, x_{10}\};\\&\overline{R_{B_{3}}^{(\alpha ,\beta )}}(D)= \{x_{2}, x_{5}, x_{7}, x_{8}, x_{9}, x_{10}\}. \end{aligned}\end{aligned}$$

The three-way decision regions are

\(Pos_{B_{3}}(D) = \{x_{2}, x_{5}, x_{10}\};\)

\(Neg_{B_{3}}(D) = \{x_{1}, x_{3}, x_{4}, x_{6}\};\)

\(Bnd_{B_{3}}(D) = \{x_{7}, x_{8}, x_{9}\}.\)

The lower and upper approximations of D for IV-MMG-PRFS model as shown as

$$\begin{aligned}\begin{aligned}&\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(D)=\{x_{2}, x_{5}, x_{8}, x_{10}\};\\&\overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{M}(D)=\{x_{1}, x_{2}, x_{5}, x_{7}, x_{8}, x_{9}, x_{10}\}. \end{aligned}\end{aligned}$$

Then three decision regions of D in IV-MMG-PRFS model are then expressed, namely

\(Pos_{M}(D) = \{x_{2}, x_{5}, x_{8}, x_{10}\};\)

\(Neg_{M}(D) = \{x_{3}, x_{4}, x_{6}\};\)

\(Bnd_{M}(D) = \{x_{1}, x_{7}, x_{9}\}\)

The lower and upper approximations of D for IV-OMG-PRFS model as shown as

$$\begin{aligned}\begin{aligned}&\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(D)=\{x_{1}, x_{2}, x_{5}, x_{7}, x_{8}, x_{10}\};\\&\overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{O}(D)=\{x_{2}, x_{5}, x_{7}, x_{8}, x_{9},x_{10}\}. \end{aligned}\end{aligned}$$

Then four decision regions of D in IV-OMG-PRFS model are then expressed, namely

\(Pos_{O}(D) = \{x_{2}, x_{5}, x_{7}, x_{8}, x_{10}\};\)

\(Neg_{O}(D) = \{x_{3}, x_{4}, x_{6}\};\)

\(Ubn_{O}(D) = \{x_{9}\};\)

\(Lbn_{O}(D) = \{x_{1}\}.\)

The lower and upper approximations of D for IV-PMG-PRFS model as shown as

$$\begin{aligned}\begin{aligned}&\underline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(D)=\{x_{2}\};\\&\overline{R_{\sum \limits _{i=1}^{m}B_{i}}^{(\alpha , \beta )}}^{P}(D)=\{x_{1}, x_{2}, x_{5}, x_{7}, x_{8}, x_{9}, x_{10}\}. \end{aligned}\end{aligned}$$

Then three decision regions of D in IV-PMG-PRFS model are then expressed, namely

\(Pos_{P}(D) = \{x_{2}\};\)

\(Neg_{P}(D) = \{x_{3}, x_{4}, x_{6}\};\)

\(Bnd_{P}(D) = \{x_{1}, x_{5}, x_{7}, x_{8}, x_{9}, x_{10}\}.\)

The upper and lower approximations of D in different types of interval-valued single granularity and multi-granularity rough fuzzy sets are concluded in Table 4. With regard to this example of medical diagnosis from three Doctors, we can make more comprehensive and objective decisions to decide whether patients need the remedies using three types of IV-MG-PRFS in interval-valued fuzzy decision systems. The related decision regions of the patients in different models are displayed and compared in Table 5 and Fig. 1.

Table 4 Approximations in different models
Full size table
Table 5 Decision regions in different models
Full size table
Fig. 1
figure 1

Decision regions in different models

Full size image

Here, let us take the patient \(x_{8}\) for example. The results in Table 4 indicate that different models can be used to generate different decision regions, and the patient \(x_{8}\) belonging to different decision regions formed by the different models illustrate this effect.

In the actual decision-making circumstance, we have three IV-MG-PRFS models to be selected. Which model should be selected is based on the actual situation. What one ought to do is to choose a model from these models firstly. Then the decision regions of the selected model could be derived accordingly. If different types of models were selected, the decision rules might be totally different.

As it is impractical to decide whether \(x_{8}\) needs to receive the treatment based on the membership degree \(D(x_{8})=0.35\) of the initial diagnosis D, the doctors needs to make decisions based on some more methods. There are many generalized rough set methods available, including the IV-MG-PRFS models. When we consider the multi-granularity circumstances, the mean multi-granularity, optimistic multi-granularity, and pessimistic multi-granularity could be generated. Whether \(x_{8}\) needs to receive treatment depends on which model the doctors have chosen. We can clearly explain the decisions made on \(x_{8}\) as follows. If the IV-MMG-PRFS model is selected, \(x_{8}\in Pos_{M}(D)\), then \(x_{8}\) needs to receive treatment. If the IV-OMG-PRFS model is selected, \(x_{8}\in Pos_{O}(D)\), then \(x_{8}\) needs to receive treatment. If the IV-PMG-PRFS model is selected, \(x_{8}\in Bnd_{P}(D)\), then \(x_{8}\) needs to be observed to make decisions whether he (or she) needs to receive treatment.

7 Conclusions

Multi-granularity fusion refers to the integration of information gathered from various investigations and analyses using appropriate methods. It aims to evaluate and unify the information, ultimately achieving a consolidated and enhanced understanding compared to individual data sources. Researchers have increasingly focused on studying multi-granularity fusion to address the challenge of integrating information from different levels of granularity. In the context of multi-granularity information fusion, the field of multi-granularity granular computing plays a crucial role. It not only extracts the core aspects of problem-solving from complex multi-source data through multiple perspectives but also provides flexibility in scaling and splitting problems using different granularities. This concept aligns well with the requirements of processing large-scale complex data. However, traditional multi-granularity granular computing approaches have limitations when it comes to handling quantitative information. They often overlook the distinctions and relationships between relative and absolute measures, focusing solely on relative quantification through quantitative descriptions. In reality, it is important to consider the influence of quantitative information on the decision-making process simultaneously. The main objective of this paper is to explore multi-granularity probabilistic rough fuzzy set (MG-PRFS) models in interval-valued fuzzy decision systems. The aim is to develop decision-making rule analyses based on the fusion of multi-granularity quantitative computing in interval-valued fuzzy decision systems. The paper introduces new concepts and models, supported by real-life case studies, and discusses the decision regions of decision classes in different models. It presents a framework for the IV-MG-PRFS model. In future work, it would be valuable to investigate uncertainty measurement and explore the underlying properties of the proposed models in terms of decision rules.