The effect of cohesion heterogeneity and anisotropy in c–φ soils on the static and seismic bearing capacity of shallow foundations

Abstract

This research aimed to assess the influence of the cohesion heterogeneity and anisotropy on the ultimate seismic and static bearing capacity, (q_ult), of a strip footing resting on c–φ soils. Most investigations have used complicated methods that were only related to the static loading condition. Herein, a simple innovative method was proposed to compute the q_ult of the strip footing via the method of limit equilibrium, by combining it with the approach of pseudo-static seismic loading and using the simplified Coulomb failure mechanism. Cohesion was assumed to be anisotropic and heterogeneous, and the anisotropy of the friction angle was neglected. A single equivalent coefficient, N_c(eq), was used to determine the ultimate bearing capacity. The optimal N_c(eq) was estimated using the algorithm of particle swarm optimization (PSO), and the findings were compared to those of earlier studies. The impact of the heterogeneous coefficient (υ) and anisotropy ratio (K) on the seismic and static N_c(eq) was also assessed. Overall, raising υ and reducing K increased the static and seismic N_c(eq). Moreover, the failure zone depth declined by increasing υ and K, while the failure zone horizontal extension decreased by raising υ and reducing K. The findings indicated the suitability of the proposed approach as an innovative method for assessing the q_ult of foundations placed on c–φ soils with cohesion heterogeneity and anisotropy.

Introduction

The ultimate bearing capacity, (q_ult), of shallow foundations on isotropic and homogeneous soils has been an interesting research topic. A comprehensive theory was first proposed by Terzaghi [1], who presented non-dimensional bearing capacity factors to evaluate the q_ult which only depended on the friction angle. Based on Terzaghi's equation, Meyerhof [2, 3], Hansen [4], and Vesic [5] presented bearing capacity equations. Numerous studies have focused on the seismic q_ult of foundations placed on isotropic and homogeneous soils. Various solution techniques, e.g., limit equilibrium, the method of slices, upper bound limit analysis, and the stress characteristics method, have also been used for this purpose. Some relevant studies include those by Budhu and Al-Karni [6], Richards Jr et al. [7], Dormieux and Pecker [8], Soubra [8,9,10], Kumar and Mohan Rao [11], Choudhury and Rao [12], and Ghosh and Debnath [13].

Natural soil deposits are heterogeneous and anisotropic in terms of cohesion [14,15,16,17]. As a fundamental property of materials, anisotropy has a substantial influence on the q_ult. Most soils are anisotropic due to particles' orientation and anisotropic settlement [18]. Casagrande [15] proposed two kinds of anisotropy, inherent and induced, and elucidated the difference between them. Cohesion varies with failure plane orientation because of soil anisotropy. In bearing capacity, besides any presumed failure surface, the direction of principal stresses changes from one point to another. Employing the cohesion values of each orientation of the failure surface can, thus, provide more accurate findings.

Several studies have assessed the bearing capacity of foundations on clay by assuming the anisotropy and heterogeneity of clays. For instance, Skempton [19] examined the q_ult of foundations rested on heterogeneous clay via empirical formulas. Raymond [20] also studied the q_ult of a surface foundation resting on a frictionless soil by considering the circular mechanism failure and presuming a linear strength variation with depth. By assuming the cylindrical failure surface, Sreenivasulu and Ranganatham [21] explored the q_ult of foundations on heterogeneous and anisotropic clay. Menzies [22] adopted the limit equilibrium approach, considered a mechanism of circular failure, and provided a correction coefficient for the influence of cohesion anisotropy on the q_ult. Reddy and Srinivasan [23, 24] also assumed a mechanism of circular failure and studied the q_ult of foundations over heterogeneous and anisotropic clay. The impact of anisotropy and heterogeneity on the q_ult of c–φ soils, including the φ = 0 conditions of soils, was investigated by Reddy and Sriniuasan [25] via the upper bound theory and the mechanism of circular failure. Moreover, Chen [26] assessed the q_ult of a foundation placed on heterogeneous and anisotropic clay based on upper bound analysis by considering a mechanism of circular failure. Although the mechanism of circular failure facilitates the mathematical analysis, it cannot yield the best result. Davis and Christian [27] adopted the slip-line approach and proposed a correction factor based on the soil strength parameters to calculate the q_ult on anisotropic clays. Davis and Booker [28] also employed the characteristic line method and explored the influence of heterogeneous clay on the q_ult. By performing the upper bound limit analysis, Salencon [29] studied the q_ult of a strip foundation on clay while assuming a linear change of cohesion with depth. Furthermore, Reddy and Rao [30] analyzed the q_ult of the strip foundation resting on heterogeneous and anisotropic clays using limit analysis by considering a mechanism of failure similar to a Prandtl-type one but with different wedge angles. By employing the finite-element method, Gourvenec and Randolph [31] studied the q_ult of circular and strip foundations on heterogeneous clays. Al-Shamrani [32] also applied the upper bound approach to present the bearing capacity factors of smooth and rough foundations on clays. Al-Shamrani and Moghal [33] proposed a method based on the kinematical procedure of limit analysis to assess the q_ult of a strip foundation on anisotropic clay. Yang and Du [34] used the method of discrete element to investigate the influence of heterogeneous and anisotropic soil on the q_ult of a foundation in the framework of the upper bound theory. Moreover, Izadi et al. [35] assessed the impact of the heterogeneity of cohesion on the ${q}_{ult}$ by employing the method of limit equilibrium. All these studies demonstrate that heterogeneity and anisotropy markedly affect the q_ult of foundations on clay.

Several studies have also assessed the impact of anisotropy and heterogeneity on the q_ult of footings placed on c–φ soils. Meyerhof [36], for instance, studied the q_ult of soils with anisotropy in the friction angle. To this end, Meyerhof considered two extreme values of φ for the outer zones and the equivalent φ for the radial shear zone. Reddy and Rao [37] investigated the q_ult of anisotropic and heterogeneous (c–φ) soil via the upper bound approach and graphically reported the results. Nakase [38] also provided a complete set of bearing capacity factors for rectangular footings on clays with cohesion linearly rising with depth. To this end, a combination of the slip circle solution for the rectangular footing and the exact plasticity solution for the continuous footing was employed. Pakdel et al. [18] examined the influence of friction angle anisotropy on the q_ult of foundations resting on a frictional soil. They adopted the approaches of pseudo-dynamic and pseudo-static seismic loading for this purpose and concluded that in both approaches, the q_ult rises with a reduction in anisotropy.

Based on the literature review, there is a dearth of studies into the impact of cohesion heterogeneity and anisotropy on the q_ult of foundations resting on c–φ soils. The majority of employed approaches are also complicated and related to the static loading condition. Accordingly, it is necessary to use a simple method with fewer and more understandable mathematical calculations. The dearth of documented solutions for the seismic bearing capacity of shallow foundations resting on c-phi soils with anisotropy and cohesion heterogeneity motivated more rigorous approaches to consider inherent soil properties.

For this purpose, the current study aimed to evaluate the impact of the cohesion heterogeneity and anisotropy on the seismic q_ult of foundations placed on c–φ soil using a simple technique. The method of limit equilibrium combined with the pseudo-static approach and the simplified Coulomb failure mechanism were adopted for this purpose. The mechanism of two-wedge failure suggested by Richards Jr et al. [7] was also employed. This mechanism defines an active failure zone under the footing and a passive failure zone adjacent to the active zone.

Although the pseudo-dynamic seismic loading method provides more accurate results than the pseudo-static seismic loading method in seismic conditions, the pseudo-static seismic loading method has easier calculations and is more understandable for users. In addition, the pseudo-static seismic loading method to determine the seismic bearing capacity has been used and confirmed by various researchers [13, 39, 40].

Herein, only the effect of cohesion heterogeneity and anisotropy on bearing capacity was studied, while the effect of friction angle anisotropy was ignored. The Mohr–Coulomb’s failure criterion expresses that the strength of the soil can be described by two parameters: friction angle φ and cohesion c. As for mechanical anisotropy, different studies, e.g., those by Duncan and Seed [41] and Mayne [42], concluded that φ shows merely a modest anisotropy and is independent from the load direction. Nevertheless, cohesion was highly dependent on the stress paths and the type of the test performed to measure the shear strength parameters. Therefore, as this study aimed only to investigate the effect of cohesion heterogeneity and anisotropy on the seismic q_ult of foundations, the friction angle was assumed to be constant in all directions and points of the soil.

The bearing capacity factor was introduced as an equivalent coefficient, i.e., N_c(eq). Comprehensive comparisons were also made with the published findings. This study used the algorithm of particle swarm optimization (PSO) and MATLAB Mathworks for optimization.

Cohesion heterogeneity and anisotropy

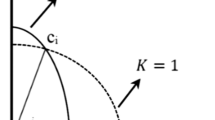
The varying pattern of cohesion anisotropy as reported by Casagrande [15], Livneh and Komornik [16], Chen [26], and Livneh and Greenstein [43] is depicted in Fig. 1. The change of cohesion with the inclination angle (i) is obtained from:

$$c_{{\text{i}}} = c_{{\text{h}}} + \left( {c_{{\text{h}}} - c_{{\text{v}}} } \right)\sin^{2} i = c_{{\text{h}}} \left( {1 + \left( {K - 1} \right)\sin^{2} i} \right)$$

(1)

where i denotes the angle between the maximum principal stress and the horizontal plane, c_i is the cohesion relating to inclination i, c_h and c_v represent the cohesion along the horizontal and vertical axes, respectively, and K indicates the anisotropy coefficient of cohesion or the ratio of c_v/c_h.

Fig. 1

Anisotropy of the cohesion

The soil is isotropic if K = 1. According to Lo [44], values of K vary in the range of 0.77–1.7; however, Reddy and Rao [30] reported this range to be 0.8–2, and Davis and Christian [27] reported it as 0.75–1.56. Note that although c is anisotropic, the anisotropy of the friction angle (ϕ) is not evident. As such, when discussing the anisotropy of soil in the current research, the anisotropy of the friction angle of the soil was neglected. Figure 2 displays the varying pattern of cohesion heterogeneity.

Fig. 2

Variation of cohesion with depth

The change in cohesion with depth is assumed to be linear. Cohesion at depth h from the surface is defined by:

$$c_{{\text{h}}} = c_{{{\text{h}}0}} + h$$

(2)

where ${c}_{\mathrm{h}0}$ indicates the horizontal cohesion at h = 0, and λ denotes the rate of cohesion growth with depth, which is suggested to fall in the 0.6–3 kPa/m range by Tani and Craig [45] and to 5 kPa/m by Wood [46].

Model definition

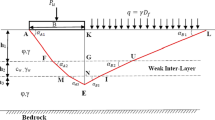
A foundation with the width of B₀ was considered on the (c–φ) soil (Fig. 3). The ultimate bearing capacity was computed via the following formula:

$$q_{{{\text{ult}}}} = c_{{\text{v}}} N_{{{\text{c}}\left( {{\text{eq}}} \right)}}$$

(3)

where ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ represents the equivalent single bearing capacity coefficient to jointly consider the contributions of cohesion, surcharge, and unit weight.

Fig. 3

Failure mechanism and wedges assumed in the present analysis

The failure mechanism is illustrated in Fig. 3. Here, D_f, P_U, and γ represent the footing depth, the vertical load on the footing, and the unit weight of the soil, respectively. Based on Fig. 3, it is assumed that the virtual surface of KE is a vertical retaining wall. In the failure stage, the active pressure caused by the weight of the AKE wedge and the q_ult is applied on this retaining wall from the left side, and the passive pressure caused by surcharge $(q=\gamma {D}_{\mathrm{f}})$ and the weight of the KBE wedge is applied to the right side. Active and passive forces must be equal on the virtual retaining wall to achieve equilibrium. The details of the calculations are given below.

Method of analysis

The assumptions for the analytical solution are as follows: (I) A uniform surcharge is assumed to account for the weight of the soil above the base of the footing; (II) all the parameters in the soil, except for the cohesion coefficient, are isotropic and homogeneous; (III) the failure mechanism includes an active and a passive wedge; and (IV) the soil is either completely dry or completely saturated. Note that the failure path considered herein, AE and EB, as a predetermined failure path, are the limitations of this study.

To compute the ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$, the geometry of the failure wedge is illustrated in Fig. 4. In this figure, φ shows the soil friction angle, α_A and α_B represent the slip surface angle in the active and passive zones, respectively, δ indicates the interface friction angle along the surface between the passive and active zones, and k_h and k_v denote the horizontal and vertical earthquake acceleration coefficients, respectively.

Fig. 4

Free body diagrams of the active and passive wedges

P_a is an active lateral force, and P_p is passive force. The ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ is calculated by equating forces on the passive and active zones and utilizing the method of limit equilibrium. P_a is computed from Eqs. (4)–(7) by considering the active zone (Fig. 4a).

$$\sum H = 0 \Rightarrow R_{A} \sin \left( {\alpha_{{\text{A}}} - \varphi } \right) - C_{{{\text{AE}}}} \cos \alpha_{{\text{A}}} - P_{{\text{a}}} \cos \delta + \left( {P_{U} + W_{A} } \right)k_{{\text{h}}} = 0$$

(4)

$$\sum V = 0 \Rightarrow R_{A} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right) + C_{{{\text{AE}}}} \sin \alpha_{{\text{A}}} + C_{{{\text{KE}}}} - \left( {P_{u} + W_{A} } \right)\left( {1 \pm k_{{\text{v}}} } \right) + P_{{\text{a}}} \sin \delta = 0$$

(5)

$$W_{A} = \frac{1}{2}B^{2} \gamma \tan \alpha_{{\text{A}}}$$

(6)

$$\begin{aligned} P_{{\text{a}}} = & \left( {P_{u} + W_{A} } \right)\left( {\frac{{\left( {1 \pm k_{{\text{v}}} } \right)\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + k_{{\text{h}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) \\ \; - c_{{\text{h}}} \left( {1 + \left( {K - 1} \right)\sin^{2} \alpha_{{\text{A}}} } \right)h\left( {\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + \cot \alpha_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) \\ \; - \lambda h^{2} \left( {\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + 0.5\cot \alpha_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) - Kc_{{\text{h}}} h\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}} \\ \end{aligned}$$

(7)

P_p is calculated from Eqs. (8)–(12) by considering the passive zone (Fig. 4b).

$$\sum H = 0 \Rightarrow P_{{\text{p}}} \cos \delta - R_{B} \sin \left( {\alpha_{B} + \varphi } \right) - C_{{{\text{UE}}}} \cos \alpha_{B} + \left( {P + W_{B} } \right)k_{{\text{h}}} = 0$$

(8)

$$\sum V = 0 \Rightarrow R_{B} \cos \left( {\alpha_{B} + \varphi } \right) - \left( {P + W_{B} } \right)\left( {1 \pm k_{{\text{v}}} } \right) - P_{{\text{p}}} \sin \delta - C_{{{\text{UE}}}} \sin \alpha_{B} - C_{{{\text{KE}}}} = 0$$

(9)

$$W_{A} = \frac{1}{2}B\gamma \tan^{2} \alpha_{A} \cot \alpha_{B}$$

(10)

$$P = \gamma D_{f} \left( {B\tan \alpha_{A} \cot \alpha_{B} } \right)$$

(11)

$$\begin{aligned} P_{p} = & \left( {P + W_{B} } \right)\left( {\frac{{\left( {1 \pm k_{v} } \right)\sin \left( {\alpha_{B} + \varphi } \right) - k_{h} \cos \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}}} \right) \\ \; + c_{h} \left( {1 + \left( {K - 1} \right)sin^{2} \alpha_{B} } \right)h\left( {\frac{{\sin \left( {\alpha_{B} + \varphi } \right) + cot\alpha_{B} \cos \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}}} \right) \\ \, + \lambda h^{2} \left( {\frac{{\sin \left( {\alpha_{B} + \varphi } \right) + 0.5cot\alpha_{B} \cos \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}}} \right) + Kc_{h} h\frac{{\sin \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}} \\ \end{aligned}$$

(12)

Given that the two wedges are in equilibrium, P_p and P_a are equal. Thus, by equating P_p and P_a, the ${N}_{c\left(eq\right)}$ can be calculated as follows:

$$N_{{{\text{c}}\left( {{\text{eq}}} \right)}} = G\left( {\frac{b}{a} + \frac{d}{a}} \right) + \left( \frac{f}{a} \right) + \frac{e}{a}$$

(13)

$$G = \left( {\frac{\gamma B}{{c_{{\text{h}}} }}} \right)$$

(14)

$$\upsilon = \left( {\frac{B}{{c_{{\text{h}}} }}} \right)$$

(15)

where υ is the heterogeneous coefficient of cohesion.

The equations for b, e, a, d, and f are presented in Appendix 1.

Equations (13), (14), and (15) show that the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ depends on B₀, c, c_v, φ, c_h,, k_h, α_B, υ, k_v, K, α_A, and λ. Here, all the parameters except α_A and α_B are constant. To determine the optimal value of${N}_{c\left(eq\right)}$, the optimization procedure is conducted in terms of α_A and α_B. Figure 5 displays the flowchart of calculating the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ using limit equilibrium.

Fig. 5

Flowchart of the limit equilibrium method to estimate the bearing capacity of foundations

Particle swarm optimization (PSO)

PSO is a stochastic population-based optimization technique established and developed by Kennedy and Eberhart [47]. This technique is influenced by the social behavior of bird flocking. The assumptions of this technique are as follows: (1) Consider a flock of birds randomly seeking food in a given region. (2) The searched region contains a single piece of food. (3) Although none of the birds are aware of the food's precise location, they are aware of its distance in each iteration. (4) Following the bird closest to the food is a successful strategy. PSO employs this scenario and applies it to solve optimization problems in MATLAB Mathworks.

The PSO algorithm is appropriate for solving low-dimensional problems such as that discussed in the current study. Candidate particles or prospective solutions fly over the subject search area in PSO to ensure that they find the best possible position. This optimal position is often described by the fitness function's optimum value. The position and velocity of a particle in the search space are denoted by X and V, respectively. The ith particle can be construed as Xi = (x_i1; x_i2; x_i3;…; x_id), and the velocity of the ith particle is defined by Vi = (v_i1; v_i2; v_i3;…; v_id). In addition, d indicates the problem's dimension. Here, Pi = (p_i1; p_i2; p_i3;…; p_id) and Pg = (p_g1, p_g2, p_g3…p_gd) represent the best prior particle of the ith particle and the index of the best particle in the examined population, respectively. Each particle’s position and velocity can be estimated using Eqs. (16) and (17):

$$X_{{{\text{id}}}} = X_{{{\text{id}}}} + V_{{{\text{id}}}} { }$$

(16)

$$V_{{{\text{id}}}} =\; \omega \times V_{{{\text{id}}}} + c_{1} \times {\text{rand}} \times \left( {P_{{{\text{id}}}} - X_{{{\text{id}}}} } \right) + c_{1} \times {\text{rand}} \times \left( {P_{{{\text{gd}}}} - X_{{{\text{id}}}} } \right)$$

(17)

Here, c₁ and c₂ are the acceleration coefficient or position constants, rand is a random number between 0 and 1, and $\omega$ denotes the inertia weight coefficient determined using the following equation:

$$\omega \left( {gn} \right) = \omega_{{{\text{max}}}} - \left[ {\frac{{\left( {\omega_{{{\text{max}}}} - \omega_{{{\text{min}}}} } \right)}}{NI}} \right]*gn$$

(18)

where gn stands for generation.

Debnath and Ghosh [39, 40], Haghsheno et al. [48], and Haghsheno and Arabani [49] have confirmed the efficiency of PSO for calculating q_ult.

Results of solution, comparisons, and discussions

To validate the solution, the findings of this investigation are compared with the literature. In this comparison, the solutions reported by Reedy and Srinivasan [25] and Peck et al. [50] are based on the method of limit equilibrium, whereas those proposed by Livneh and Greenstein [43], Davis and Booker [28] and Davis and Christian [27] are based on the slip-line method. Salencon [29], Reddy and Rao [30] Reddy and Srinivasan [25], Al-Shamrani [32] and Yang and Du [34] have also applied upper bound limit analysis for this purpose. Finally, the solution of Al-Shamrani and Moghal [33] was achieved via the kinematic procedure of limit analysis. First, the results of this investigation are compared to those of prior research on homogeneous and anisotropic soil, as well as heterogeneous and isotropic soil for the case of φ = 0. Table 1 compares the values of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ obtained from this research with those in the prior investigations for soil in the case of φ = 0. In this table, it is assumed that the soil is homogeneous and anisotropic. For the homogeneous and isotropic case (υ = 0 and K = 1), ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ = 5.656 is calculated in this paper (Table 1).

Table 1 Bearing capacity coefficient for footing on anisotropic soil for the case of φ = 0 irrespective of the inhomogeneity

The value of ${N}_{c\left(eq\right)}$ is slightly higher than the value derived by the failure mechanism of Prandtl-type (N_c=5.14) by about 10%. Based on Table 1, regardless of soil heterogeneity, the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ is slightly larger than the results of Reddy and Srinivasan [25], Reddy and Rao [30], and Davis and Christian [27]. As for the values reported by Reddy and Srinivasan [25], the discrepancy between the two results is about 0.6% and 1% for K = 0.8 and K = 2, respectively. As for the results of the solution given by Davis and Christian [27], the difference between the two results declines from 8.3% at K = 0.8 to 2.2% at K = 2. Finally, as for the results of Reddy and Rao [30], the difference between the two results is 4% for K = 0.8 and rises to reach 20.5% for K = 2. Also, based on Table 1, it is evident that the current solution underrepresented bearing capacity coefficient compared to those reported by Al-Shamrani and Moghal [33] and Yang and Du [34]. Compared to the results of Al-Shamrani and Moghal [33], the difference between the two results is about 0.50% and 5.2% for K = 0.8 and K = 2, respectively. Besides, compared to the result obtained from Yang and Du [34], the difference between the two results is 1.6–7.70% for K = 0.8 and K = 2, respectively. For practical applications, these differences are acceptable and do not significantly affect the predicted bearing capacity coefficient much more than the parameters of shear strength. Therefore, according to Table 1, it can be concluded that the values of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ acquired from the current study have a negligible difference with those provided by Al-Shamrani and Moghal [33] and Reddy and Srinivasan [25]. The important point concluded from Table 1 is that by ignoring anisotropy and assuming that cohesion is equal in all directions, the obtained bearing capacity is significantly on the unsafe side for K values of greater than 1 and conservative for K values of smaller than 1. This means that the degree of vulnerability and conservatism increases when K is much more or much less than 1. The values of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ for heterogeneous and isotropic soil for the case of φ = 0 are presented in Table 2.

Table 2 Bearing capacity coefficient for footing on isotropic and heterogeneous soil for the case of φ = 0

As can be seen, the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ rises with the increment in υ, suggesting that the influence of heterogeneity on ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ becomes more considerable with rising υ in all estimates. Table 2 shows that the values of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ derived from the current study are greater by no more than 10% than the values provided by Salencon [29] for any value of υ. When υ = 0, the present results are slightly smaller than Al-Shamrani [32] and Yang and Du [34], about less than 0.1% and 1%, respectively. However, the differences become 15.2% and 60.4%, respectively, when υ = 10. Furthermore, the current solution overestimated that of Davis and Booker (1973), with the deviation being 9.1% for υ = 0 and it constantly increases to reach about 21.8% for υ = 10. It is clear from Table 2 that the present solution overestimates the results of Livneh and Greenstein [43], Peck et al. [50], Reddy and Rao [30], and Reddy and Srinivasan [25] by 9%, 9%, 9%, and 2.4%, respectively, at υ = 0. When υ = 10, the present results are smaller than those of Livneh and Greenstein [43], Peck et al. [50], Reddy and Rao [30], and Reddy and Srinivasan [25] by 56.7%, 87.9%, 23.3%, and 28.4%, respectively. Moreover, the effect of heterogeneity on the value of ${N}_{c\left(eq\right)}$ obtained by current study is less than that of Reddy and Srinivasan [25] for 0.5 < υ < 10 and the difference between the two solutions range from about 1–28.5%, for υ = 0.5 and υ = 10. So, according to Table 2, it can be concluded that the findings of the present research for heterogeneous and isotropic soil (φ = 0) have an acceptable agreement with the findings of the upper bound theory, especially the results provided by Salencon [29] and Al-Shamrani [32], and the discrepancy between the two solutions is considered sensible for practical purposes. From a practical point of view, it is crucial for the bearing capacity coefficient of the solution from the limit equilibrium method to be equal to the upper bound theory; this is because the limit equilibrium method is widely used by engineers, while the upper bound theory is often neglected as a method that yields unsafe solutions (Michalowski 1994). One of the conceivable explanations behind the difference between the present result and the results provided by Livneh and Greenstein [43], Davis and Booker [28] and Davis and Christian [27], Salencon [29], Reddy and Rao [30], Reddy and Srinivasan [25], Al-Shamrani [32] and Yang and Du [34], Al-Shamrani and Moghal [33] can be due to the use of different methods and different failure mechanisms, but the discrepancy between the findings of current solution and those of Reedy and Srinivasan [25] and Peck et al. [50] can be attributed to the different assumed failure mechanisms, not to the method of analysis.

The curves in Fig. 6 indicate the impact of the anisotropy and heterogeneity of cohesion on the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ of foundation placed on soil (φ = 0) for the case that K is 0.8–2 and υ is 0–10.

Fig. 6

Comparisons of the value of the bearing capacity factor for heterogeneous soil for the case of φ = 0

According to Fig. 6, the value of N_c(eq) reduces with an increment in K and decreases with a decrease in υ. For a constant K, the increase in υ actually means a rise in λ. Therefore, it can be argued that with an increase in λ, the bearing capacity also rises. Moreover, the effect of λ on the bearing capacity increases with a decline of K. It is seen that the effect of anisotropy on the value of ${N}_{c\left(eq\right)}$ becomes more noticeable with an increase in υ.

Table 3 compares the values of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ for isotropic and homogeneous (c–φ) soils derived from the current research with those of the previous studies for G = 0, K = 1, and υ = 0. Here, G = 0 means ignoring the weight of the soil and depth of footing below the ground surface. In the current analysis, Delta (δ) is a quite effective parameter. Consequently, the results were evaluated for five cases, namely δ = 0, δ = φ/2, δ = 2φ/3, δ = 3φ/4, and δ = φ.

Table 3 Comparison of the value of the bearing capacity coefficient for G = 0, K = 1 and υ = 0

As can be seen from the table, the values of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ provided by the current research are close to those of other results for the case δ = 0.5φ. As can be seen, the present result overestimates the results of Salnecon (1974), Chen (1975), Reddy and Rao [37], and Meyerhof [36] by 7.7%, 7.8%, 7.8%, and 12.4% at δ = 0.5φ and φ = 10, respectively, while being smaller than the result of Reedy and Srinivasan [25]. By increasing the φ to 30°, the difference in the present results with others greatly declines and reaches about 0–2.5%. In general, the discrepancies in the results can be due to the differences in the analysis method, optimization approaches, and embedded assumptions. Figure 7 compares the value of anisotropic and homogeneity bearing capacity coefficient for c–φ soils obtained from the current research with those of Reddy and Srinivasan [25] and Reddy and Rao [37] for G = 0, δ = φ/2, and δ = 2φ/3. As can be seen from Fig. 7, the value of ${N}_{c\left(eq\right)}$ increases with a decrease in K. Moreover, the values of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ in the current research are very close to the results of these researchers at δ = φ/2.

Fig. 7

Comparison of values of N_c(eq) value for G = 0, a υ = 0, b υ = 0.4, and c υ = 1.2

By considering the weight of the soil and depth of foundation below ground surface, G > 0, Fig. 8 compares the results provided by the current study with those of Reddy and Srinivasan [25] and Reddy and Rao [37]. According to Fig. 8, four cases are examined:

• i. K = 0.8 and δ = 0.5φ: For φ = 10°, the present results are a little more than those of Reddy and Srinivasan [25] and Reddy and Rao [37], with the maximum deviation 3.8% and 2.6%, respectively. When φ = 20°, the difference between the current results and the results of Reddy and Srinivasan [25] is very small (i.e., 0.8%). However, by increasing ϕ to 30°, the result provided by Reddy and Srinivasan [25] is greater than those of the present study by 12.8% for υ = 0 and consistently decrease to reach about 0% for υ = 1.6. The results of Reddy and Rao [37] for φ = 20° and 30° are more than the present results by 9% and 12.8%, respectively.

• ii. K = 0.8 and δ = 2φ/3: Fig. 8 shows that the current solution overestimated that of Reddy and Rao [37] by 5.1%, 4.4%, and 1.5% for φ = 10, φ = 20°, and φ = 30°, respectively. Moreover, the present findings are more than the results provided by Reddy and Srinivasan [25] about 6.5% and 9.5% for φ = 10° and φ = 20°, respectively. For φ = 30°, this difference for the present result and that of Reddy and Srinivasan [25] is 6% for υ = 0.4 and increases up to 21% for υ = 1.6.

• iii. K = 2 and δ = 0.5φ: Fig. 8 illustrates that the ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ obtained in this study is less than those of Reddy and Srinivasan [25] and Reddy and Rao [37]. When υ = 0, the difference between the findings of this research and those of Reddy and Srinivasan [25] for φ = 10°, 20°, and 30° is about 0.1%, 0.8%, and 7.5%, respectively. By increasing υ to 1.6, the difference increases by 9.2%, 2.3%, and 15%, respectively. The difference between the results provided by Reddy and Rao [37] and the present study is about 0.5%, 5.3%, and 16.4% for φ = 10°, 20°, and 30°, respectively. Moreover, when υ = 1.6, the difference becomes 10.7%, 14.9%, and 23.7%, respectively.

• iv. K = 2 and δ = 2φ/3: According to Fig. 8, when φ = 10° and υ is in the low range (0 < υ < 0.4), the values of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ obtained by the current research are more than those of Reddy and Srinivasan [25] and Reddy and Reddy and Rao [37] by 3% and 1.5%, respectively. In comparison, for 0.8 < υ < 1.6, the results provided by Reddy and Srinivasan [25] and Reddy and Rao [37] are more than those reported in the present result by 6.8% and 8.4%, respectively. By increasing friction angle to 20°, the results of this study increase more than those of Reddy and Srinivasan [25] by 7.5% for υ = 0 and 5.5% for υ = 1.6. Besides, when φ = 30°, this difference reaches a maximum of 10.9%. When φ = 20° and 30°, the results obtained from Reddy and Rao [37] are more than that of the current results. When, υ = 0, the difference between the two results is 0.1% and when υ reaches 1.6, the difference becomes no more than 8.8%.

Fig. 8

Comparison of values of N_c(eq) value for G/K = 4 and a φ = 10°, b φ = 20°, and c φ = 30°

Therefore, according to Fig. 8 and aforementioned explanations, when the impact of anisotropy and heterogeneity on the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ of c–φ soils are examined for ϕ = 10–20°, it is better to use the δ = 0.5φ. By increasing the friction angle to 30°, the results obtained using the δ = 0.5φ are conservative. Given the difference between the results of this research and the results of Reddy and Srinivasan [25] and Reddy and Rao [37], it can be concluded that the solution proposed in this research yields acceptable results.

In general, based on the explanations provided based on Tables 1, 2, and 3 and Figs. 7 and 8, and the comparison of the results of this and other studies conducted in three conditions (soil (φ = 0) with cohesion homogeneity and anisotropy, soil (φ = 0) with cohesion heterogeneity and isotropy, and (c–φ) soil with cohesion heterogeneity and anisotropy), it can be concluded that the method and failure mechanism used in this study provide a reliable method for calculating the bearing capacity of shallow foundations located on all three conditions.

Parametric Study

The isotropic and homogeneous ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ for the static and seismic conditions are presented in Tables 4 and 5, respectively. It is clear from these Tables that as G grows, so does the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$. This is because the soil weight rather than the cohesion is the main source of the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ [26]. Tables 6, 7, and 8 give the ratio of the anisotropic and heterogeneous ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ to the isotropic and homogeneous ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ in order to study the effect of υ and K on the static and seismic ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$.

Table 4 Isotropic and homogeneous N_c(eq) for static condition,

Table 5 Isotropic and homogeneous N_c(eq) for seismic condition,

Table 6 Anisotropic and heterogeneous versus isotropic and homogeneous bearing capacity coefficient for static condition

Table 7 Anisotropic and heterogeneous versus isotropic and homogeneous bearing capacity coefficient for seismic condition and φ = 0

Table 8 Anisotropic and heterogeneous versus isotropic and homogeneous bearing capacity coefficient for seismic condition, φ = 10 and δ = 0.5φ

The anisotropic and homogeneous ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ are obtained by using the values of Tables 4 or 5 and multiplying them by the values of Tables 6 or 7 and 8. It is noteworthy that Tables 7 and 8 are presented for φ = 0° and 10° and the results for other friction angles, φ = 20° and 30°, are presented in Tables 10, 11 and 12 in Appendix 2. Ranges of various parameters are as follows:

$$\varphi = 0$$

$$\varphi = 10,\; {\text{and}}\; 20 \leftrightarrow \delta = 0.5\varphi$$

$$\varphi = 30 \leftrightarrow \delta = 0.5\varphi , \;{\text{and}}\; 2\varphi /3$$

$$\upsilon = 0, 0.5, 1, \;{\text{and}}\; 2\quad G = 0.5,\; {\text{and}}\; 2\quad K = 0.8,1,\; {\text{and}}\; 2 \quad \frac{{D_{f} }}{B} = 0.5$$

$$k_{h} = 0.1, 0.2,\;{\text{and}}\; 0.3\quad k_{v} = 0, 0.5\,k_{h} ,\; {\text{and}} \;k_{h}$$

According to Table 6, the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ increases with increasing υ and decreasing K. Comparing the results for K = 0.8 with K = 1 and 2 reveals that the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ obtained by K = 0.8 is about 12–35% more than K = 1 and 61–133% more than K = 2. Hence, this discrepancy demonstrates that K significantly affects the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$.

Furthermore, Table 6 shows that the effect of heterogeneity and anisotropy on the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ rises with an enhancement in the friction angle.

The same result can be obtained by comparing the results of Tables 7 and 8 for seismic conditions. Similar to the static condition, a rise in υ and a reduction in K have increased the seismic bearing capacity.

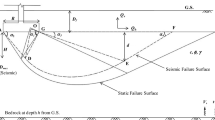
Table 9 displays the failure zone depth (h) and the active and passive wedge angles for the soils in the case of φ = 0 in the one case of the seismic condition (k_h = 0.1 and k_v = 0.5k_h) and compares them with the findings of Izadi et al. [35]. Table 9 indicates the complete matching of the results of the two studies. According to Table 9, failure zone depth reduces with an enhancement in υ. This result is consistent with physical principles because, by an increase in this coefficient, failure occurs in the weaker upper portion [32]. From Table 9, it is clear that the angle of active wedge has a descending trend by raising the value of υ. The angle of passive wedge is constant for isotropic and heterogeneous soil. In comparison, when K = 0.8 and 2, the passive wedge angle changes with increasing ν are less than 6%. According to the above explanations and the calculations of the failure zone depth presented in Table 9 for B = 2, it can be found that the passive vertex comes closer to the edge of the footing. In other words, the mechanism of narrow failure is formed below the foundation.

Table 9 Active and passive angle variations and calculates the depth of failure zone for soils in the case of φ = 0

Figure 9 depicts the variation of the active and passive angles, the failure zone depth, and the horizontal extension of the failure zone with υ for different K values. Here, it is presumed that φ = 10°, G = 2, B = 2, D_f/B = 0.5, k_h = 0.1, and k_V= 0.5 k_h. Note that if the soil is partially saturated, all the equations used will change, and thus, all the values of h, L α_A, and α_B will differ from what was determined in this study. This issue was studied by Nouzari et al. [51].

Fig. 9

The variation of a the active and passive angles and b the depth of failure zone c the horizontal extension of failure zone for (c–φ) soils with heterogeneous coefficient for various anisotropy ratio

To clarify the impact of υ on the passive and active angles, the values of υ are considered from 0 to 20. The active angles decrease as υ and K increase, as seen in Fig. 9a. The passive angles also decrease with increasing K but its changes with the increase in υ are very slight for each anisotropy ratio. For example, for K = 0.8, it increases with a very gentle gradient while for K = 1 and 2, it decreases with a very gentle gradient.

Figure 9b demonstrates that an increment in υ and K causes a decrease in the failure zone depth. It means that in c–φ soil similar clay soils, a shallower failure zone occurs by rising the values of υ and K. With an increment in υ, the increase rate in the failure zone depth becomes gradually smaller. Moreover, between υ and K, the former has a higher impact on the failure zone depth. From Fig. 9b, it is inferred that as the value of υ obtains larger, the impact of K on the failure zone depth almost vanishes, especially for υ > 10. Figure 9c indicates that the horizontal extension of the failure zone, L (shown in Fig. 10), decreases with an increase in υ and a decrease in K. In order to better comprehend the influence of υ and K on the position of the failure surface, Fig. 10 depicts the failure surfaces for two heterogeneous and anisotropic conditions.

Fig. 10

Schematic demonstration of failure mechanism for different values of a anisotropy ratio and b heterogeneous coefficient

Based on Fig. 10, with an increase in υ, the horizontal extension of the failure zone and the depth of the failure zone decrease. Since the results showed that increasing υ raises ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$, it can be concluded that due to increasing ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$, the horizontal extension of the failure zone and the depth of the failure zone decrease.

Future research directions

The pseudo-static seismic loading method and Coulomb's simple failure mechanism for homogenous and isotropic soil under seismic loading conditions were used and confirmed in the previous studies. The effect of cohesion heterogeneity and anisotropy on the soil's bearing capacity (c–φ) in static conditions was also investigated in previous research. Herein, using the pseudo-static seismic loading method and Coleman's simple failure mechanism, the effect of cohesion heterogeneity and anisotropy on static and seismic bearing capacity was evaluated, compared with the results of previous investigations, and confirmed. However, for more certainty, it is recommended that studies use laboratory and field tests to validate these results and those of previous research. It is also suggested that future studies evaluate the effect of cohesion heterogeneity and anisotropy using pseudo-dynamic seismic loading, which can provide better results for seismic conditions. Investigating the effect of earthquake acceleration coefficients on the bearing capacity of soil (c–φ) with cohesion heterogeneity and anisotropy using methods such as limit analysis and slip-line can enable a more accurate investigation and comparison of the results. Furthermore, investigating the effects of the combination of friction angle anisotropy and cohesion heterogeneity and anisotropy on the bearing capacity of foundations is an important topic for future research. A similar simple model should also be proposed for the bearing capacity of foundations for partially saturated soils using the method and model used in this research.

Conclusions

This study presented an innovative way to examine the impact of the anisotropy and heterogeneity of cohesion on the ultimate bearing capacity of a footing placed on (c–φ) soils. The main results of this research are as follows:

• Employing the method of limit equilibrium, combining it with the pseudo-static seismic loading condition, and using the simplified Coulomb failure mechanism can yield an efficient method to determine the effect of cohesion heterogeneity and anisotropy on the q_ult.

• When the soil is homogeneous and anisotropic for the case of φ = 0, the results of the current investigation are close to those of Reddy and Srinivasan [25] and Al-Shamrani and Moghal [33] with a difference of less than 1% and 5.5%, respectively.

• When the soil is heterogeneous and isotropic for the case of φ = 0, the current results are close to those of Salencon [29] and Al-Shamrani [32] with a difference of less than 10% and 15.2%, respectively.

• The delta (δ) is highly influential on the anisotropic and heterogeneous ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$.

• The value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ for isotropic and homogeneous (c–φ) soils obtained from the current study is very close to the results of Reddy and Srinivasan [25] and Reddy and Rao [37] in δ = φ/2.

• When the soil is heterogeneous and anisotropic, the friction angle is 10 and 20° and δ = φ/2, the current results are close to those of Reddy and Srinivasan [25] and Reddy and Rao [37]. Therefore, these situations were recognized as the best scenario. Furthermore, by increasing the friction angle to 30°, the present results become more conservative than those of other studies.

• Under static and seismic conditions, increasing υ and decreasing K enhance the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$. Furthermore, when seismic stress is applied, the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ declines.

• With increasing the friction angle, the impact of υ and K on the value of ${N}_{\mathrm{c}\left(\mathrm{eq}\right)}$ rises.

• The failure zone depth and the horizontal extension of the failure zone are reduced with an increment in υ and K .

Appendices

Appendix 1: Analytical Functions of Eq. (13)

$$a = \left( {\frac{{\left( {1 - k_{{\text{v}}} } \right)\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + k_{{\text{h}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right)$$

(19)

$$d = \left( \frac{1}{K} \right)\left( {\frac{{D_{f} }}{B}} \right)\left( {\tan \alpha_{A} \cot \alpha_{B} } \right)\left( {\frac{{\left( {1 - K_{v} } \right)\sin \left( {\alpha_{B} + \varphi } \right) - K_{h} \cos \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}}} \right)$$

(20)

$$b = \left( \frac{1}{K} \right)\left[ \begin{gathered} \left( {\frac{1}{2}\tan^{2} \alpha_{{\text{A}}} \cot \alpha_{B} } \right)\left( {\frac{{\left( {1 - K_{{\text{v}}} } \right)\sin \left( {\alpha_{B} + \varphi } \right) - K_{{\text{h}}} \cos \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}}} \right) \hfill \\ - \left( {\frac{1}{2}\tan \alpha_{{\text{A}}} } \right)\left( {\frac{{\left( {1 - k_{{\text{v}}} } \right)\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + k_{{\text{h}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) \hfill \\ \end{gathered} \right]$$

(21)

$$\begin{aligned} e = & \frac{1}{K}\left( {1 + \left( {K - 1} \right)sin^{2} \alpha_{B} } \right)\left( \frac{h}{B} \right)\left( {\frac{{\sin \left( {\alpha_{B} + \varphi } \right) + cot\alpha_{B} \cos \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}}} \right) + \left( \frac{h}{B} \right)\frac{{\sin \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}} \\ \; + \frac{1}{K}\left( {1 + \left( {K - 1} \right)\sin^{2} \alpha_{{\text{A}}} } \right)\left( \frac{h}{B} \right)\left( {\frac{{\sin \left( {\alpha_{A} - \varphi } \right) + \cot \alpha_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) \\ \; + \left( \frac{h}{B} \right)\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}} \\ \end{aligned}$$

(22)

$$f = \left( \frac{1}{K} \right)\left( \frac{h}{B} \right)^{2} \left[ \begin{gathered} \left( {\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + 0.5\cot \alpha_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) \hfill \\ + \left( {\frac{{\sin \left( {\alpha_{B} + \varphi } \right) + 0.5\cot \alpha_{B} \cos \left( {\alpha_{B} + \varphi } \right)}}{{\cos \left( {\alpha_{B} + \varphi + \delta } \right)}}} \right) \hfill \\ \end{gathered} \right]$$

(23)

Appendix 2: Tables to determine the effect of nonhomogeneous coefficient and anisotropy ratio on static and seismic bearing capacity coefficient

See Tables 10

Table 10 Anisotropic and heterogeneous versus isotropic and homogeneous bearing capacity coefficient for seismic condition, φ = 20° and δ = 0.5φ

, 11

Table 11 Anisotropic and heterogeneous versus isotropic and homogeneous bearing capacity coefficient for seismic condition, φ = 30° and δ = 0.5φ

and 12.

Table 12 Anisotropic and heterogeneous versus isotropic and homogeneous bearing capacity coefficient for seismic condition, φ = 30° and δ = 2φ/3