Seismic Bearing Capacity of Shallow Foundations Placed on an Anisotropic and Nonhomogeneous Inclined Ground

Abstract

In the present study, the limit equilibrium method combined with the pseudo-static seismic loading approach and applying the simplified Coulomb failure mechanism were employed for calculating the bearing capacity of nonhomogeneous and anisotropic soils on slopes. It was assumed that the cohesion coefficient was nonhomogeneous and anisotropic and anisotropy effect was ignored for the friction angle. For estimating optimal bearing capacity values, the particle swarm optimization algorithm was used. Comparing the results of previous researchers with those of the present study for isotropic and homogeneous soils indicated that the present solution provided acceptable values for the bearing capacity of shallow foundations. The effect of anisotropy ratio and the nonhomogeneous coefficient on the seismic bearing capacity was evaluated and found that decreasing the anisotropy ratio and increasing the nonhomogeneous coefficient cause an increase in the seismic bearing capacity. Furthermore, the results showed that the depth of the failure zone decreases with increasing the nonhomogeneous coefficient, the anisotropy ratio, and the seismic acceleration coefficient, while the depth of the failure zone increases with an increase in the slope inclination.

Introduction

The ultimate bearing capacity of a shallow foundation is a very important concept that every civil engineer faces when designing the structures. Many investigators have studied the static and seismic bearing capacity of shallow foundation rested on the horizontal ground [1,2,3,4,5,6,7,8,9,10]. Because some structures are built near the slope or on the slope, many authors [11,12,13] evaluated the behavior of shallow foundations near or on slopes under static conditions. Some researchers have analyzed the seismic bearing capacity of shallow strip footings near the slope or on the slope using the pseudo-static approach combined with different solution techniques such as limit equilibrium method [14,15,16,17,18,19,20,21,22], the method of stress characteristics [23,24,25,26], the lower bound [27,28,29,30,31,32], and the upper bound [33,34,35,36,37,38,39]. The studies indicated that the seismic bearing capacity of a shallow foundation located near the slope was significantly affected by the slope angle, the seismic acceleration coefficient, the distance between the shallow foundation edge, and the edge of the slope. Also, they have shown that the bearing capacity of a footing decreases with an increase in the horizontal seismic acceleration coefficient. Natural soil deposits are anisotropic and nonhomogeneous with respect to the cohesion coefficient [40,41,42,43]. Anisotropy as a basic property of materials considerably affects the bearing capacity of foundations [44]. Due to soil anisotropy, the undrained shear strength changes with failure plane orientation. In the problem of bearing capacity, along with any assumed failure surface, the direction of the principal stresses varies from one point to another. Hence, using the strength values of each orientation of the failure surface would result in more realistic results. Calculation of bearing capacity in this manner is of great importance, particularly for analytical solutions in which the undrained bearing capacity highly depends on one soil parameter (i.e., undrained shear strength) [45].

A few studies have evaluated the effect of nonhomogeneity and anisotropy on the bearing capacity of foundation on the horizontal ground rested on clay [46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] and (c-φ) soil [62, 63].

Skempton [60] calculated the bearing capacity of a foundation on nonhomogeneous clays using empirical formulas. By considering the circular mechanism failure, Raymond [52] provided a solution for estimating the bearing capacity of surface footing on a frictionless soil, assuming a linear cohesion coefficient variation with depth. Bearing capacity of shallow strip footings on nonhomogeneous and anisotropic clays was analyzed by Sreenivasulu and Ranganatham [61] on the assumption of the cylindrical failure surface. By using the limit equilibrium approach and considering a circular failure surface, Menzies [51] presented a correction factor for the effect of cohesion coefficient anisotropy on the bearing capacity of a foundation. Reddy and Srinivasan [55, 56] analyzed the bearing capacity of footings over a single layer and also a two-layered nonhomogeneous and anisotropic clay by assuming a circular failure mechanism. By using circular failure mechanism, Reddy and Srinivasan [54] evaluated the effect of nonhomogeneity and anisotropy on the bearing capacity of c-φ soils, including φ = 0 conditions of soils. By considering a circular failure mechanism and using the upper bound analysis, Chen [59] analyzed the bearing capacity of footing on a single layer and a two-layered nonhomogeneous and anisotropic clay. Although the mathematical analysis is simplified by using the circular mechanism, the best solution is not provided by this mode of failure. Using the slip-line method, a correction coefficient for the bearing capacity foundation on anisotropic clays as a function of the soil strength parameters was proposed by Davis and Christian [48]. Appling the method of characteristic line, Davis and Booker [47] studied the effect of nonhomogeneous clays on the bearing capacity of foundation. Salencon [57] analyzed the bearing capacity of clay taking the variation of cohesion with depth as linear by using upper bound limit analysis. Using limit analysis and assuming a mechanism similar to Prandtl-type mechanism, Reddy and Rao [53] analyzed the bearing capacity of strip footing resting on nonhomogeneous and anisotropic clays. Gourvenec and Randolph [49] analyzed the bearing capacity of strip foundations and circular foundations on nonhomogeneous clays by applying the finite element method. By applying the upper bound approach of limit analysis and considering a translational failure mechanism, Al-Shamrani [46] presented closed-form solutions for the undrained bearing capacity of shallow strip footings on anisotropic clays. Al-Shamrani and Moghal [45] presented a closed-form solution based on the kinematical approach of limit analysis for the undrained bearing capacity of strip footings on anisotropic cohesive soils. Using the discrete element method (DEM) in the framework of the upper bound theory of limit analysis, Yang and Du [58] investigated the effect of nonhomogeneous and anisotropic soils on the bearing capacity coefficient of strip foundation. By applying the limit equilibrium method associated with the Coulomb failure mechanism, Izadi et al. [50] evaluated the effect of variation of cohesion coefficient of marine deposit with a depth on seismic bearing capacity. Meyerhof [62] obtained the bearing capacity of soils with anisotropy in friction by the conventional Terzaghi’s type approach. For this purpose, two extreme values of φ for the outer zones and equivalent φ for the radial shear zone was considered. Applying the upper bound approach of limit analysis and a mechanism similar to Prandtl-type mechanism, Reddy and Rao [63] evaluated the bearing capacity of nonhomogeneous and anisotropic (c-φ) soils. All mentioned investigations indicate that nonhomogeneity and anisotropy have a notable effect on the bearing capacity of the soils.

However, not much research has been done on the effect of nonhomogeneous and anisotropic soil on the bearing capacity of a foundations near or on slopes. Halder and Chakraborty [64], using the lower bound limit analysis technique, evaluated the bearing capacity of a strip footing placed over an embankment of anisotropic clay. It was shown that the anisotropy ratio has a significant effect on the bearing capacity of the shallow foundation. The main objective of the present research is to evaluate the effect of anisotropic and nonhomogeneous soil on the bearing capacity of a strip foundation on a slope. For this purpose, the simplified Coulomb failure mechanism and the limit equilibrium method of analysis, which have not been used in any of the previous studies for this purpose, were utilized. The cohesion coefficient was assumed to be nonhomogeneous and anisotropic. A two-wedge failure mechanism, proposed by Richards et al. [6], was adopted. It should be noted that this failure mechanism was applied by Ghazavi and Eghbali [65] and Ghosh and Debnath [3] to evaluate the bearing capacity of a shallow foundation rested on the horizontal ground. Comparing the results obtained by these researchers with the Finite Element analyses revealed that using this failure mechanism provided acceptable results. The PSO algorithm and MATLAB MathWorks were applied for the optimization in the present solution. Comprehensive comparisons were made with the results of previous studies. Furthermore, the effect of the nonhomogeneity and the anisotropy on bearing capacity factors and the depth and path of the failure zone was evaluated.

Anisotropy and Nonhomogeneity of Soil

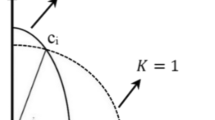
Figure 1 presents the changing pattern of cohesion coefficient anisotropy, based on Casagrande [41], Livneh and Komornik [42], Reddy and Rao [53, 63], and Livneh and Greenstein [66]. The variation of cohesion coefficient with the angle of inclination (i) is given by:

$$ c_{i} = c_{{\text{h}}} + \left( {c_{{\text{h}}} - c_{{\text{v}}} } \right)\sin^{2} i = c_{{\text{h}}} \left( {1 + \left( {K - 1} \right)\sin^{2} i} \right) $$

(1)

Fig. 1

Anisotropy of the cohesion coefficient

where c_i is the cohesion corresponding to an inclination i, c_h and c_v are the cohesion coefficients in the horizontal and vertical directions, respectively, i is the angle between the horizontal direction and the maximum principal stress and K is the anisotropy coefficient, which is c_v/c_h.

The changing pattern of the nonhomogeneity of the cohesion coefficient is shown in Fig. 2.

Fig. 2

Variation of cohesion coefficient with depth

From Fig. 2, it is clear that the variation of the cohesion coefficient with depth is assumed as linear. The cohesion coefficient at depth h from the surface is given by:

$$ c_{{\text{h}}} = c_{{{\text{h}}0}} + \lambda h $$

(2)

where $c_{{{\text{h}}0}}$ is the cohesion coefficient in the horizontal direction at h = 0 and λ is a variation of the cohesion coefficient with depth, which is suggested to be in the range of 0.6–3 kPa/m by Tant and Craig [67] and 5 kPa/m by Wood [68].

Model Definition and Analysis of Procedure

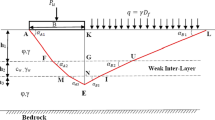
In this study, a footing with the width of B₀ was placed horizontally on an inclined ground surface (Fig. 3). The bearing capacity of the strip footing (q_ult) is normally computed using the following basic formulation:

$$ q_{{{\text{ult}}}} = c_{{\text{v}}} N_{c} + \frac{1}{2}B_{0} \gamma N_{\gamma } $$

(3)

Fig. 3

Failure mechanism and wedges assumed in the present analysis

where N_c and N_γ are bearing capacity factors and γ is the unit weight of the soil.

The failure mechanism presented in Fig. 3 is almost similar to the original two-wedge slip surfaces proposed by Richards et al. [6]. Here, P_U is the vertical load on the foundation and β is the slope inclination. As shown in Fig. 3, the vertical surface CE is assumed to behave like a vertical retaining wall. At the failure stage, the weight of the wedge ACE and active pressure resulting from q_ult are applied from the left side on the wall. On the right-hand side, the weight of the wedge CBE applies lateral passive pressure on the virtual wall. To satisfy equilibrium, the active and passive thrusts acting on the virtual wall must be equal.

In the analytical solution, it is assumed that the failure mechanism consists of an active and passive wedge with their inclination angles considered as the variable of the present analysis. To determine the coefficients of bearing capacity, the failure-wedge geometry of the problem is depicted in Fig. 4. In this figure, φ is the friction angles of the soil; α_A is the slip surface angle in the active zone; α_B is slip surface angle in the passive zone; δ is the friction angle along the surface between the active and passive zones; k_v is the vertical seismic acceleration coefficient; k_h is the horizontal seismic acceleration coefficient; and h is the depth of failure zone.

Fig. 4

Free body diagrams of the active and passive wedges

P_a is the active thrust that acts on the active zone and P_p is the passive resistance exerted on the passive zone.

Using the limit equilibrium method and equating forces on the active and passive zones, the bearing capacity factor is obtained. In the active zone (Fig. 4a), by writing the forces in horizontal and vertical directions, P_a is obtained from Eqs. (4)-(9).

$$ \sum H = 0 \Rightarrow R_{{\text{A}}} \sin \left( {\alpha_{{\text{A}}} - \varphi } \right) - C_{{{\text{AE}}}} \cos \alpha_{{\text{A}}} - P_{{\text{a}}} \cos \delta + \left( {P_{{\text{u}}} + W_{{\text{A}}} } \right)k_{{\text{h}}} = 0 $$

(4)

$$ \sum V = 0 \Rightarrow R_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right) + C_{{{\text{AE}}}} \sin \alpha_{{\text{A}}} + C_{{{\text{CE}}}} - \left( {P_{{\text{u}}} + W_{{\text{A}}} } \right)\left( {1 \pm k_{{\text{v}}} } \right) + P_{{\text{a}}} \sin \delta = 0 $$

(5)

$$ C_{{{\text{AE}}}} = \frac{{c_{{\text{h}}} \left( {1 + \left( {K - 1} \right)\sin^{2} \alpha_{{\text{A}}} } \right)h + 0.5 \lambda h^{2} }}{{\sin \alpha_{{\text{A}}} }} $$

(6)

$$ C_{{{\text{CE}}}} = c_{{\text{h}}} hK + 0.5h^{2} = c_{{\text{v}}} h + 0.5 \lambda h^{2} $$

(7)

$$ W_{{\text{A}}} = \frac{1}{2}B_{0}^{2} \gamma \tan \alpha_{{\text{A}}} $$

(8)

$$ \begin{aligned} & P_{{\text{a}}} = \left( {P_{{\text{u}}} + W_{{\text{A}}} } \right)\left( {\frac{{\left( {1 \pm k_{{\text{v}}} } \right)\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + k_{{\text{h}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) \\ & \quad - c_{{\text{h}}} \left( {1 + \left( {K - 1} \right)\sin^{2} \alpha_{{\text{A}}} } \right)h\left( {\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + \cot \alpha_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) \\ & \quad - \lambda h^{2} \left( {\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + 0.5\cot \alpha_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) - Kc_{{\text{h}}} h\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}} \\ \end{aligned} $$

(9)

where $h = B_{0} \tan \alpha_{{\text{A}}}$ is the depth of the failure mechanism.

The same procedure is followed for the passive zone (Fig. 4b) and P_p is obtained from Eqs. (10)-(15).

$$ \sum H = 0 \Rightarrow P_{{\text{p}}} \cos \delta - R_{{\text{B}}} \sin \left( {\alpha_{{\text{B}}} + \varphi } \right) - C_{{{\text{EB}}}} \cos \alpha_{{\text{B}}} + W_{{\text{B}}} k_{{\text{h}}} = 0 $$

(10)

$$ \sum V = 0 \Rightarrow R_{{\text{B}}} \cos \left( {\alpha_{{\text{B}}} + \varphi } \right) - W_{{\text{B}}} \left( {1 \pm k_{{\text{v}}} } \right) - P_{{\text{p}}} \sin \delta - C_{{{\text{EB}}}} \sin \alpha_{{\text{B}}} - C_{{{\text{CE}}}} = 0 $$

(11)

$$ C_{{{\text{EB}}}} = \frac{{c_{{\text{h}}} \left( {1 + \left( {K - 1} \right)\sin^{2} \alpha_{{\text{B}}} } \right)h_{1} + 0.5 \lambda h_{1}^{2} }}{{\sin \alpha_{{\text{B}}} }} $$

(12)

$$ h_{1} = \frac{{B_{0} \tan \alpha_{{\text{A}}} \tan \alpha_{{\text{B}}} }}{{\tan \alpha_{{\text{B}}} + \tan \beta }} $$

(13)

$$ W_{{\text{B}}} = \frac{1}{2}\frac{{\gamma B_{0}^{2} \tan^{2} \alpha_{{\text{A}}} }}{{\tan \alpha_{{\text{B}}} + \tan \beta }} $$

(14)

$$ \begin{aligned} & P_{{\text{p}}} = \left( {W_{{\text{B}}} } \right)\left( {\frac{{\left( {1 - k_{{\text{v}}} } \right)\sin \left( {\alpha_{{\text{B}}} + \varphi } \right) - k_{{\text{h}}} \cos \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}}} \right) + \frac{1}{2}\lambda h^{2} \frac{{\sin \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}} \\ & \quad + c_{{\text{h}}} \left( {1 + \left( {K - 1} \right)\sin^{2} \alpha_{{\text{B}}} } \right)\left( {\frac{{B_{0} \tan \alpha_{{\text{A}}} \tan \alpha_{{\text{B}}} }}{{\tan \alpha_{{\text{B}}} + \tan \beta }}} \right)\left( {\frac{{\sin \left( {\alpha_{{\text{B}}} + \varphi } \right) + \cot \alpha_{{\text{B}}} \cos \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}}} \right) \\ & \quad + \frac{1}{2}\lambda \left( {\frac{{B_{0} \tan \alpha_{{\text{A}}} \tan \alpha_{{\text{B}}} }}{{\tan \alpha_{{\text{B}}} + \tan \beta }}} \right)^{2} \left( {\frac{{\sin \left( {\alpha_{{\text{B}}} + \varphi } \right) + \cot \alpha_{{\text{B}}} \cos \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}}} \right) \\ & \quad + Kc_{{\text{h}}} h\frac{{\sin \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}} \\ \end{aligned} $$

(15)

Given the equilibrium of two wedges, the active pressure and the passive resistance are equated. Therefore, by equating the active pressure and passive resistance, the ultimate bearing capacity ($q_{{{\text{ult}}}}$) can be obtained as follows:

$$ P_{{\text{a}}} = P_{{\text{p}}} $$

(16)

$$ q_{\text{ult}} = c_{{\text{v}}} N_{c} + \frac{1}{2}B0\gamma N_{\gamma } $$

(17)

$$ N_{c} = v \left( \frac{f}{a} \right) + \frac{e}{a} $$

(18)

$$ N_{\gamma } = \frac{b}{a} $$

(19)

where $\upsilon = \left( {\frac{{\lambda B_{0} }}{{c_{{\text{h}}} }}} \right)$ is the nonhomogeneous coefficient.

Detailed equations for a, b, d, e, and f are given in the “Appendix” section.

From Eqs. (18) and (19), it can be stated that the bearing capacity factors depend on c, φ, c_v, c_h, k_v, k_h, B₀, υ, K, α_A, α_B, λ, and β. Here, all the parameters are constant except α_A and α_B. Therefore, to find the optimum values of N_c and N_γ, the optimization process is performed in terms of α_A and α_B.

The particle swarm optimization (PSO) algorithm and MATLAB MathWorks were applied for the optimization. The PSO, initially developed by Kennedy and Eberhart [69], is a stochastic optimization technique that has been inspired by the behavior of bird flocking, fish schooling and swarming theory. In PSO, a group of specks flies in the job lookup distance to detect their optimum berth. Typically, this optimum berth is characterized by the optimum fitness function. In the PSO, some candidate particles or the potential solutions fly in the problem search space to ensure that their positions are optimum. This optimum position is usually characterized by the optimum of a fitness function. Let V and X denote a particle’s velocity and position in a search space, respectively. Then, the velocity of the ith particle is delimited by V_i = (v_i1; v_i2; v_i3;...; v_id) and the ith particle may be interpreted as X_i = (x_i1; x_i2; x_i3;...; x_id). Also, d denotes the dimension of the problem. The best previous particle of the ith particle is recorded and expressed as P_i = (p_i1; p_i2; p_i3;...; p_id). Here, the index of the best particle among the studied population is represented by P_g = (p_g1, p_g2, p_g3...p_gd). The position and velocity of each particle can be estimated using Eqs. (20) and (21):

$$ X_{id} = X_{id} + V_{id} $$

(20)

$$ V_{id} = \omega \times V_{id} + c_{1} \times {\text{rand}} \times \left( {P_{id} - X_{id} } \right) + c_{1} \times {\text{rand}} \times \left( {P_{gd} - X_{id} } \right) $$

(21)

In these equations, c₁ and c₂ are position constants known as acceleration coefficient, rand is a random number within the range [0,1], and $\omega$ is the inertia weight coefficient, which is calculated using the following equation:

$$ \omega \left( {{\text{gn}}} \right) = \omega_{\max } - \left[ {\frac{{\left( {\omega_{\max } - \omega_{\min } } \right)}}{{{\text{NI}}}}} \right]*{\text{gn}} $$

(22)

where gn is the generation.

The PSO is an appropriate algorithm to solve the low-dimensional problems like the topic of the present study. The efficiency of this algorithm to calculate the bearing capacity of the foundation was proved by Ghosh and Debnath [3] and Debnath and Ghosh [70, 71].

Comparisons

The results of estimated bearing capacity in the presence of k_h and β were compared with those of Hansen [12], Vesic [72], Zhu [10], Kumar and Rao [23], Kumar and Kumar [19] and Yamamoto [39] for the shallow foundation rested on anisotropic and nonhomogeneous soil. The comparison of the results is presented in Figs. 5 and 6. As can be inferred from Figs. 5 and 6, using different approaches for estimating the bearing capacity of shallow foundation rested near or on slopes gave a wide range of values for the bearing capacity factors. In some cases, the difference between the reported values is even more than 100%. This difference, in addition to the different approaches of determining the bearing capacity, is also related to using different failure mechanisms.

Fig. 5

Comparison of N_c with k_h and β for a φ = 30°, β = 10; b φ = 30°, β = 20; c φ = 40°, β = 15; d φ = 40°, β = 30

Fig. 6

Comparison of N_γ with k_h and β for a φ = 30°, β = 10; b φ = 30°, β = 20; c φ = 40°, β = 15; d φ = 40°, β = 30

Delta (δ) is a very effective parameter in the present analysis. Therefore, the results were assessed for three cases, namely δ = 0.5φ, δ = 0.75φ, and δ = φ.

Figure 5 shows that the values of N_c provided by Kumar and Rao [23], who applied the method of stress characteristics, vary within the range of the present results from the cases δ = 0.5φ and δ = 0.75φ. As reported by Kumar and Kumar [19] and Kumar and Ghosh [35], who, respectively, used the limit equilibrium method and the upper bound theory, the values of N_c obtained by them were close to those of Kumar and Rao [23]. Furthermore, Hansen [12] solution overestimated that of Kumar and Rao [23]. Overall, it can be concluded that when δ = 0.5φ, the present solution is conservative. Moreover, when φ = 40° and δ = φ, the present solution overestimates those of Hansen [12] and Kumar and Rao [23]. One explanation for the difference between the results of the present study and those of the previous works may be using different failure mechanisms and methods. Figure 6 shows that when φ = 30°, the values of N_γ obtained by the present solution are close to those of Kumar and Rao [23] for the case δ = 0.5φ; however, when δ = 0.75φ, the values of N_γ of the present study are in good agreement with those of Zhu [10]. It should be noted that Zhu [10] employed the equivalence of limit equilibrium method and limit analysis to determine the bearing capacity factor, N_γ. Furthermore, Hansen [12] and Kumar and Rao [23] have minimum values under static and seismic conditions, respectively. When φ = 40° and β = 10°, the values of N_γ obtained by Kumar and Rao [23] are within the range of the present results from the cases δ = 0.5φ and δ = 0.75φ while the results Zhu [10]and Yamamoto [39] are slightly higher than the present result for δ = 0.75φ. It is of note that the solutions reported by Yamamoto [39] are based on the upper bound method. By increasing the slope inclination to 20°, the results obtained by Hansen [12], Zhu [10], Kumar and Rao [23], Kumar and Kumar [19], and Yamamoto [39] are close to the present results for δ = 0.5φ. According to Figs. 5 and 6 and considering that the obtained results depend on the amount of δ, it seems that acceptable values of the N_γ and N_c can be obtained between the results reported for δ = 0.5φ and δ = 0.75φ.

As the merit of this study, the geometry of the failure mechanism is defined by only few angular parameters and the reason is employing the simple failure mechanism. Moreover, since other techniques need several other assumptions, the features of those solutions might be changeable.

Results for Homogeneous and Isotropic Soil

The variation of the bearing capacity coefficient with k_h for different β and φ is provided in Figs. 7 and 8, respectively. As can be noticed, regardless of the values of β and φ, N_c and N_γ decrease constantly with an increase in k_h. The decrease in N_c and N_γ with k_h tends with increasing the k_h values.

Fig. 7

Comparison of N_c with k_h and β for a φ = 10°, δ = 0.5φ; b φ = 20°, δ = 0.5φ; c φ = 30°, δ = 0.5φ; d φ = 40°, δ = 0.5φ; e φ = 10°, δ = 0.75φ; and f φ = 20°, δ = 0.75φ; g φ = 30°, δ = 0.75φ; h φ = 40°, δ = 0.75φ

Fig. 8

Comparison of N_γ with k_h and β for a φ = 10°, δ = 0.5φ; b φ = 20°, δ = 0.5φ; c φ = 30°, δ = 0.5φ; d φ = 40°, δ = 0.5φ; e φ = 10°, δ = 0.75φ f φ = 20°, δ = 0.75φ; g φ = 30°, δ = 0.75φ; h φ = 40°, δ = 0.75φ

Results for Nonhomogeneous and Anisotropic Soil

The nonhomogeneous coefficient and anisotropy ratio only affect the N_c. To observe the effect of nonhomogeneous coefficient and anisotropy ratio on static bearing capacity coefficient, the anisotropy and nonhomogeneity bearing capacity factor, and the ratio of anisotropic and nonhomogeneity bearing capacity factor to isotropic and homogeneity bearing capacity factor is presented in Tables 1 and 2, respectively. This seismic bearing capacity factor for anisotropic and nonhomogeneous soils is presented in Figs. 9 and 16. Ranges of various parameters are as follows:

$$ \begin{aligned} & \varphi = 30\;{\text{and}}\; 40\quad \delta = 0.5\;{\text{and}}\;0.75\quad \beta = 10,20,30, 40\;{\text{and}}\;50 \\ & k_{{\text{h}}} = 0.1, 0.2\;{\text{and}}\;0.3\quad \upsilon = 0,0.5\;{\text{and}}\;2\quad K = 0.8\;{\text{and}}\;2\quad k_{{\text{v}}} = 0 \\ \end{aligned} $$

Table 1 Anisotropy and nonhomogeneity bearing capacity factor for static conditions

Table 2 Ratio of the anisotropy and nonhomogeneity bearing capacity factor to isotropic and homogeneity bearing capacity factor for static conditions

Fig. 9

Variation of N_c with k_h and β for φ = 10°, δ = 0.5φ and a υ = 0; b υ = 0.5; c υ = 2

According to Table 1, N_c increases with increasing υ and decreasing K. Also, as expected, the bearing capacity increases with increasing φ and decreasing β. From Table 2, it can be concluded that when soil is homogeneous and anisotropic with the anisotropy ratio of 0.8, the N_c is 8.5% to 19% greater than that of the homogeneous and isotropic soil. Meanwhile, N_c for the homogeneous soil with an anisotropy ratio of 2 is 17.5% to 39% less than N_c of the homogeneous and isotropic soil. Hence, this difference shows that the anisotropy of soil has a considerable effect on the value of bearing capacity factor. Similar to the static condition, increasing the nonhomogeneous coefficient and decreasing the anisotropy ratio led to an increase in the seismic bearing capacity. Also, the seismic bearing capacity factor decreased with an increase in the horizontal seismic acceleration coefficient. On the other hand, when υ = 0.5, N_c is 6% to 36% more than that of the homogeneous soil, and this difference increases to about 15% to 125% when υ = 2. This demonstrates that the nonhomogeneity has a significant effect on N_c.

As can be seen from Figs. 9, 10, 11, 12, 13, 14, 15, and 16, when the anisotropy ratio is greater than 1 and it couples with the seismic acceleration coefficient, the value of N_c reduces drastically. Comparing all graphs in each of Figs. 9, 10, 11, 12, 13, 14, 15, and 16 demonstrates the effect of the nonhomogeneous coefficient and the anisotropy ratio on N_c. For example, it can be concluded from Fig. 9 that, when k_h = 0 and β = 10°, N_c increases about 43% with an increase in the nonhomogeneous coefficient from 0.5 to 2, and the increase rate of N_c decreases to 17% with increasing k_h to 0.3. It means that the seismic acceleration coefficient decreases the effect of the nonhomogeneous coefficient on N_c. Furthermore, it can be found from Fig. 9 that for a constant value of the nonhomogeneous coefficient, for example υ = 0.5 and when k_h = 0 and β = 10°, N_c increases about 43% with decreasing the anisotropy ratio from 2 to 0.8. Under these conditions, the reduction tends to increase with an increase in the value of k_h such that it reaches 51% for k_h = 0.3. Thus, overall, the positive effect of the nonhomogeneous coefficient and anisotropy ratio on N_c tends to decrease with an increase in k_h.

Fig. 10

Variation of N_c with k_h and β for φ = 20°, δ = 0.5φ and a υ = 0; b υ = 0.5; c υ = 2

Fig. 11

Variation of N_c with k_h and β for φ = 30°, δ = 0.5φ and a υ = 0; b υ = 0.5; c υ = 2

Fig. 12

Variation of N_c with k_h and β for φ = 40°, δ = 0.5φ and a υ = 0; b υ = 0.5; c υ = 2

Fig. 13

Variation of N_c with k_h and β for φ = 10°, δ = 0.75φ and a υ = 0; b υ = 0.5; c υ = 2

Fig. 14

Variation of N_c with k_h and β for φ = 20°, δ = 0.75φ and a υ = 0; b υ = 0.5; c υ = 2

Fig. 15

Variation of N_c with k_h and β for φ = 30°, δ = 0.75φ and a υ = 0; b υ = 0.5; c υ = 2

Fig. 16

Variation of N_c with k_h and β for φ = 40°, δ = 0.75φ and a υ = 0; b υ = 0.5; c υ = 2

The effect of both k_h and k_v in the value of N_c is presented in Fig. 17. As we expected, the effect of both the seismic acceleration coefficients leads to a more drastic reduction in the value of N_c. The effect of k_v is exactly the same as the effect of k_h, suggesting that k_v reduces the positive effect of the nonhomogeneous coefficient and anisotropy ratio on the value of N_c.

Fig. 17

Variation of N_c with k_h, k_v and β for φ = 20°, δ = 0.5φ and a υ = 0; b υ = 0.5; c υ = 2

Tables 3 and 4 indicate the effect of the nonhomogeneous coefficient and anisotropy ratio on α_A, α_B and h. Here, it is assumed that φ = 10° and 20°, B = 2 m, and k_h = 0. As can be seen from Tables 3 and 4, the active and passive angles and the depth of the failure zone decrease with increasing nonhomogeneous coefficient and anisotropy ratio. The decrease in failure depth with increasing the nonhomogeneous coefficient is in agreement with physical principles since failure takes place in the weaker upper part of the slope. To better understand the effect of anisotropy ratio and the nonhomogeneous coefficient on the location of failure surface, failure surfaces for two conditions of nonhomogeneous and anisotropy are shown in Fig. 18 using the results of Tables 3 and 4. When β = 10° and 30° and φ = 10° and 20°, it is clear that the active zone shrinks and the passive zone moves to the bottom of the slope with increasing the anisotropy ratio. Furthermore, when β = 10° and φ = 10° and 20°, both of the active and passive zones shrink with an increase in the nonhomogeneous coefficient. A similar trend is observed when β = 30° and φ = 10°. In comparison, when β = 30° and φ = 30°, the effect of nonhomogeneous coefficient on the pattern of active and passive zones is similar to that of the anisotropy ratio. Further computation for determining the location of the failure surface for other friction angles of soil (i.e., φ = 30° and 40°) shows that the location of failure surface is similar to what presented in Fig. 18a–c, e.

Table 3 Variation of the active and passive angles and the depth of the failure zone with a constant υ for various values of K

Table 4 Variation of the active and passive angles and the depth of the failure zone with a constant K for various values of υ

Fig. 18

Schematic demonstration of the location of failure surface for different values of anisotropy ratio for a φ = 10° and 20° and β = 10° and b φ = 10° and 20° and β = 30°; and for different values of the nonhomogeneous coefficient for c φ = 10° and 20° and β = 10°; d φ = 10° and β = 30°; e φ = 20° and β = 30°

Table 5 presents the effect of the seismic acceleration coefficient on α_A, α_B and h. Here, it is assumed that φ = 20°, B = 2, K = 0.8, υ = 0.5, and k_v = 0. From Table 5, it is clear that the depth of the failure zone decreases with an increase in the seismic acceleration coefficient and increases with an increase in the slope inclination. Moreover, the active angle increases with increasing k_h, while the passive angle decreases with increasing k_h. Another result inferred from Table 5 is that the active angle increases with an increase in the slope inclination while the passive angle decreases with an increase in the slope inclination.

Table 5 Variation of the active and passive angles and the depth of the failure zone for various values of k_h

Figure 19 represents the location of the failure surface for different values of β and k_h. As can be seen from this figure, when the slope inclination increases, the path of failure in the passive zone deviates more than the vertical surface.

Fig. 19

Schematic demonstration of the location of failure surface for different values of the seismic acceleration coefficient for a β = 10°, b β = 20°, c β = 30°, and d β = 40°

Conclusions

The effect of anisotropy and nonhomogeneity on the bearing capacity of a shallow foundation rested on an inclined ground was evaluated using a simplified Coulomb failure mechanism and the limit equilibrium method. The bearing capacity equation was presented as a function of slope inclination (β), friction angle (φ), anisotropy ratio (K), nonhomogeneous coefficient (υ), slip surface angle in the passive and active zone (α_A and α_B) and seismic acceleration coefficients (k_h and k_v). According to the equation provided to determine the bearing capacity of the shallow foundation, the anisotropy and nonhomogeneity only affect N_c. The main results of this study can be outlined as follows:

• A new approach for calculating the bearing capacity of nonhomogeneous and anisotropic soils on slopes can be provided using the limit equilibrium method combined with the pseudo-static seismic loading approach, and applying the simplified Coulomb failure mechanism.

• Delta (δ) is a very effective parameter in the present analysis. Given that previous researchers have presented a wide range of values for the bearing capacity factors, the present solution for δ = 0.5φ and δ = 0.75φ suggests an acceptable range for calculating bearing capacity factors.

• The bearing capacity factors N_c and N_γ decrease with increasing seismic acceleration coefficient (k_h) and slope inclination (β).

• N_c increases with decreasing anisotropy ratio (K) and increasing the nonhomogeneous coefficient (υ).

• The positive effect of the nonhomogeneous coefficient and anisotropy ratio on the N_c decreases with an increase in the values of k_h and k_v.

• The depth of the failure zone decreases with increasing the nonhomogeneous coefficient, the anisotropy ratio, and the seismic acceleration coefficient, while the depth of the failure zone increases with an increase in the slope inclination.

Appendix: Analytical Functions of Eqs. (18 and 19)

$$ a = \left( {\frac{{\left( {1 - k_{{\text{v}}} } \right)\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + k_{{\text{h}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) $$

(23)

$$ \begin{aligned} b & = \tan \alpha_{{\text{A}}} \left[ {\left( {\frac{{\tan \alpha_{{\text{A}}} }}{{\tan \alpha_{{\text{B}}} + \tan \beta }}} \right)\left( {\frac{{\left( {1 - k_{{\text{v}}} } \right)\sin \left( {\alpha_{{\text{B}}} + \varphi } \right) - k_{{\text{h}}} \cos \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}}} \right)} \right. \\ & \quad \left. { - \left( {\frac{{\left( {1 - k_{{\text{v}}} } \right)\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + k_{{\text{h}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right)} \right] \\ \end{aligned} $$

(24)

$$ \begin{aligned} & e = \frac{1}{K}\left( {1 + \left( {K - 1} \right)\sin^{2} \alpha_{{\text{B}}} } \right)\left( {\frac{{\tan \alpha_{{\text{A}}} \tan \alpha_{{\text{B}}} }}{{\tan \alpha_{{\text{B}}} + \tan \beta }}} \right)\left( {\frac{{\sin \left( {\alpha_{{\text{B}}} + \varphi } \right) + \cot \alpha_{{\text{B}}} \cos \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}}} \right) \\ & \quad + \left( {\tan \alpha_{{\text{A}}} } \right)\frac{{\sin \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}} + \left( {\tan \alpha_{{\text{A}}} } \right)\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}} \\ & \quad + \frac{1}{K}\left( {1 + \left( {K - 1} \right)\sin^{2} \alpha_{{\text{A}}} } \right)\left( {\tan \alpha_{{\text{A}}} } \right)\left( {\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + \cot \alpha_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right) \\ \end{aligned} $$

(25)

$$ \begin{aligned} f & = \left( \frac{1}{K} \right)\left[ {\left( {\tan \alpha_{{\text{A}}} } \right)^{2} \left( {\frac{{\sin \left( {\alpha_{{\text{A}}} - \varphi } \right) + 0.5\cot \alpha_{{\text{A}}} \cos \left( {\alpha_{{\text{A}}} - \varphi } \right)}}{{\cos \left( {\alpha_{{\text{A}}} - \varphi - \delta } \right)}}} \right)} \right. \\ & \quad + \left( {\frac{{\tan \alpha_{{\text{A}}} \tan \alpha_{{\text{B}}} }}{{\tan \alpha_{{\text{B}}} + \tan \beta }}} \right)^{2} \left( {\frac{{0.5\sin \left( {\alpha_{{\text{B}}} + \varphi } \right) + 0.5\cot \alpha_{{\text{B}}} \cos \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}}} \right) \\ & \quad \left. { + \left( {\tan \alpha_{{\text{A}}} } \right)^{2} \left( {\frac{{0.5\sin \left( {\alpha_{{\text{B}}} + \varphi } \right)}}{{\cos \left( {\alpha_{{\text{B}}} + \varphi + \delta } \right)}}} \right)} \right] \\ \end{aligned} $$

(26)