Modelling soil compaction parameters using a hybrid soft computing technique of LSSVM and symbiotic organisms search

Abstract

The soil compaction parameters, i.e., optimum water content (OWC) and maximum dry density (MDD) are essential parameters used in civil engineering projects for monitoring the compaction of soils. The current practice of using laboratory testing to determine the OWC and MDD is time-consuming and costly. Thus, this research suggests a hybrid machine-learning solution to replace traditional soil testing for determining OWC and MDD. The novel method combines the least square support vector machine (LSSVM) and symbiotic organisms search (SOS) algorithm. These two computational intelligence algorithms work together to create an OWC and soil MDD prediction model, LSSVM–SOS. For this purpose, a large database of 13 different soils featuring 6 influencing factors was used. Overall, experimental results show that the proposed LSSVM–SOS has attained the most accurate prediction of the OWC of soils (RMSE = 0.0288, MAE = 0.0199, and R² = 0.9656) and MDD (RMSE = 0.0305, MAE = 0.0206, and R² = 0.9641). These results of the proposed model are significantly better than those obtained from other hybrid LSSVMs constructed with particle swarm optimization, grey wolf optimizer, and slime mould optimization algorithms. According to the findings, the newly created LSSVM–SOS can aid geotechnical engineers in the design phase of civil engineering projects.

Introduction

Soil compaction is the process of pressing soil particles closer together by minimizing air voids while keeping the water content between the soil particles constant. The mechanical properties of soils can be improved in a variety of ways through compaction. Proctor [1] suggested compacting the soil at the desired compaction energy with varying water contents. The compaction curve can thus be used to determine the optimum water content (OWC) and maximum dry density (MDD). These two compaction parameters are frequently utilized in geotechnical practices to maintain the long-term performance of different geotechnical structures, such as highway embankments [2, 3], railway embankments [4, 5], airport runways [6,7,8], and so on [9]. For the construction and maintenance of geotechnical structures, it is consequently essential to comprehend and predict the compaction characteristics of various soils [9, 10].

The OWC and MDD can be determined using laboratory experiments and analytical methods [10]. In the laboratory, at least 4–5 tests must be performed to accurately define the compaction curve. Thus, the laboratory test is tedious and time-consuming [11]. In addition, veteran geotechnical experts and highly qualified personnel are required to conduct the test and attain reliable results. Hence, it is essential to develop intelligent data-driven algorithms for determining the OWC and MDD based on available experimental records [9, 10]. In the past, several prediction models were proposed to determine OWC and MDD of soils. The majority of these models were developed using regression analyses and limited data from specific soils. Wang and Yin [10] stated that these models produced a wide range of prediction accuracies, with coefficients of determination (R²) scattered between 0.64 and 0.98. Furthermore, the prediction precision of these models tended to decline with a bigger database [12].

In recent days, machine learning (ML) techniques have been used to estimate the OWC and MDD of soils in order to handle the issue with a larger database and greater accuracy. The compaction characteristics of 55 soil samples were predicted using artificial neural network (ANN) and evolutionary polynomial regression (EPR) approaches [13, 14]. To estimate the compaction parameters for 212 samples, Ardakani and Kordnaeij [15] employed group method of data handling (GMDH) model. Kurnaz and Kaya [11] used GMDH, support vector machine (SVM), extreme learning machine (ELM), and Bayesian regularization neural network (BRNN) to estimate OWC and MDD of soils based on 451 experimental results of index and standard proctor test. The authors used index properties of soil samples as the influencing parameters for this purpose.

According to the literature, these prediction models exhibited better coefficient of determination (R²) values (ranging from 0.90 to 0.98) than regression analysis models [10]. However, the soil type in these researches was limited. For instance, soft clay with high flexibility was not examined in some research, while fine and coarse-grained soils could not be linked in others. Additionally, the influencing variables were not entirely accounted for in these models. Previous researches have demonstrated that the accuracy of prediction can be assured for a specified soil range; nevertheless, the issue of the limited soil type and the insufficient consideration of soil parameters may lead to inaccuracies in prediction. Therefore, a high-performance soft computing model is required to predict the OWC and MDD of soils taking into account a broad variety of soil types and affecting variables.

Based on the most recent research, it has been determined that hybrid soft computing approaches are ideally suited for predicting the intended output including soil compaction parameters, compression index, California bearing ratio, and so on [15,16,17,18,19,20]. In addition, as the topic of interest is complex, it is necessary to examine various sophisticated ML models in order to discover more accurate estimating models [21,22,23,24,25,26,27,28,29,30]. The least squares support vector machine (LSSVM) is an effective ML algorithm for nonlinear and multivariable modelling [31]. Note that, LSSVM is a regression-based ML model and has been effectively implemented in geotechnical engineering [31,32,33]. However, none of the prior research has used LSSVM to forecast OWC and MDD of soils. Therefore, the purpose of the present work is to address this gap in the literature.

It is pertinent to mention here that the development of an LSSVM model needs the configuration of its hyperparameters, such as the regularization and kernel function parameters. These two factors have a substantial impact on the result of the learning phase and, consequently, influence the predictive capacity of the LSSVM-based model. It is not easy to provide the regularization and kernel function parameters since they must be sought in continuous domains [31]. Consequently, an infinite number of parameter sets exist. Thus, researchers have utilized meta-heuristic algorithms (MHAs) to define parameter adjustment of LSSVM as an optimization problem [31]. Previous researches have proved the effectiveness of MHAs in simulating complicated phenomena in geotechnical and geological engineering.

In this work, a high-performance prediction model of soil compaction parameters was developed using a hybrid approach of LSSVM and symbiotic organisms search (SOS) algorithm. The results of the proposed model were compared with three more hybrid LSSVMs constructed with particle swarm optimization (PSO), grey wolf optimizer (GWO), and slime mould optimization (SMA) algorithms. A vast database of soils with diverse classifications (gravel, sand, silt, clay) was gathered for this purpose from the study of Wang and Yin [10]. For this purpose, a large database of various soil types was collected from a recent work by Wang and Yin [10]. In the said study, the authors [10] compiled a set of 226 soil compaction results from the literature and consolidated them. In the present work, the whole dataset of 226 soil compaction results was used for modelling the OWC and MDD of soils.

Methodology

Least square support vector machine

Suykens et al. [34] introduced LSSVM, a regression-based ML method based on the structural risk reduction principle. LSSVM’s learning phase is quick since it simply involves solving a set of linear equations. To construct a prediction model, the dataset can be prepared in the following form: $D = \left\{ {x_{k} ,y_{k} } \right\}$, $k = 1, 2, \ldots , N$; where $k$ represents the $k$th data sample and $N$ is the total sample count. The goal of the LSSVM learning phase is to develop a mapping function $y\left( x \right)$ that estimates the response variable given a collection of influencing factors $x$. Following is an illustration of an LSSVM model for function approximation.

$$y\left( x \right) = \mathop \sum \limits_{k = 1}^{N} \alpha_{k} K\left( {x_{k} ,x_{l} } \right) + b$$

(1)

where $K$ and $b$ represent the linear system's solution. $k$ and $N$ denote the index and total number of training samples, respectively; $x_{k}$ and $x_{l}$ are training and testing sets input patterns, respectively; $K\left( {x_{k} ,x_{l} } \right)$ is the kernel function. The Radial basis function (RBF) is an extensively used kernel function, given by:

$$k\left( {x_{k} ,x_{l} } \right) = \exp \left( { - \frac{{\left| {\left| {x_{k} - x_{l} } \right|} \right|^{2} }}{{2\sigma^{2} }}} \right)$$

(2)

where $\sigma$ is a kernel parameter. To establish a LSSVM model, it is necessary to solve the following optimization problem:

$$J_{P} \left( {w,e} \right) = \left\{ {\frac{1}{2}w^{T} w + \frac{\gamma }{2}\mathop \sum \limits_{k = 1}^{N} e_{k}^{2} } \right\},$$

(3)

$$y_{k} = w^{T} \emptyset \left( {x_{k} } \right) + b + e_{k}$$

(4)

where $e_{k} \in R$ represents the $k$th error variable; $w$ and $b$ are the two parameters that are used function approximation; $\gamma$ is the regularization constant, and $\emptyset \left( {x_{k} } \right)$ is the mapping function. For further mathematical information regarding LSSVM, studies in the literature can be referred [31, 34, 35].

Brief overview of employed MHAs

In this sub-section, a brief discussion of the employed MHAs, i.e., PSO, GWO, SMA, and SOS is presented. As stated above, all these MHAs are swarm-based and have been extensively used by researchers in recent times.

In the year 1995, Kennedy and Eberhart [36] introduced PSO, inspired by the social foraging behaviour of swarm, like the schooling and shoaling behaviour of fish, flocking behaviour of birds, etc. A review of the literature [18, 26, 37] reveals that this algorithm has been successfully applied in every part of engineering and sciences in order to enhance the performance of conventional soft computing techniques. Generally, PSO performs the search for the optimal solutions through agents called swarms/particles, by deterministic and stochastic approaches. In PSO, N-dimensional search space with $n$ particles, the $i{\text{th}}$ particle is represented as: $x_{i} = \left[ {x_{i1} ,x_{i2} ,x_{i3} , \ldots , x_{iN} } \right]$, where ${\text{i}} = 1,2,3, \ldots ,{\text{n}}$; and the velocity of this particle is represented as $v_{i} = \left[ {v_{i1} ,v_{i2} ,v_{i3} , \ldots , v_{iN} } \right]$, where the fitness of each particle is determined by the specified objective function known as cost function. Each particle is influenced by its ‘best’ position (called personal best, p_best) and the group ‘best’ position (called global best, g_best). Also, every particle has known the position of the best individual of the g_best. Exploration and exploitation processes in PSO are determined by a number of parameters, including the inertia weight, cognitive and social coefficients, and two random parameters. One of the advantages of particle swarm optimization over other derivative-free methods is the reduced number of parameters to tune and constraints acceptance. Refer to the following research for further information [26, 36, 37].

GWO is one of the widely used MHAs, proposed by Mirjalili et al. [38]. It was inspired by the social structure of grey wolf packs. In GWO, the hierarchical structure of the leadership and hunting mechanism of grey wolves is regarded as an important characteristic. Each wolf pack comprises four sorts of grey wolves to imitate the leadership hierarchy: alpha ($\alpha$), beta ($\beta$), delta ($\delta$), and omega ($\omega$) wolves, in which $\alpha$ and $\omega$ wolves are, respectively, the most and least responsible wolves, whereas, $\beta$ and $\delta$ are, respectively, second and third in the pack's hierarchy. Note that, $\alpha$, $\beta$, and $\delta$ wolves occasionally participate in the hunting phase, while $\omega$ wolves encircle the prey based on the positions of the experienced wolves. In GWO, each feasible solution to an optimization problem is specified by the position of a grey wolf. Mathematically, a grey wolf pack is a set of possible solutions for where the positions of $\alpha$, $\beta$ and $\delta$ wolves are the best possible solutions in each iteration, ranked from best to worst. Having the best estimation of a grey wolf position, $\alpha$, $\beta$ and $\delta$ wolves update the position of an $\omega$ wolf in the pack.

As a novel MHA that is based on nature, SMA [39] carries out the simulation of a slime mould’s nutritional phase (a single-celled eukaryote). This program carries out the simulation of the foraging behaviour of slime moulds. Slime moulds search for the food sources (by sensing their odour), then wrap and digest them through the secretion of enzymes. In SMA, the theoretical description of approaching the best solution is a phase of iterations to yield the highest smell concentration. The adaptable weight of the slime mould guarantees swift convergence and avoids being trapped in local extrema. This method allows the advancing of the slime mould in all feasible paths towards the best solution, which emulates the architecture of the slime mould when they eat. Then, the wrapping of the food is carried out using contractions of the intravenous structure within the upper and lower bounds in the subsequent step. More bio-oscillator waves are created in the vein with the highest contraction of food, and as a result, the thickness of this vein increases due to the cytoplasm’s quicker flow. As a response to the negative and positive signals received from veins regarding the concentration of food, the search patterns are modified in SMA.

Cheng and Prayogob [40] presented the SOS algorithm. SOS is a simple and effective, and it leverages a population-based search approach by directing a population of candidate solutions to search for potential optimum regions iteratively until a global optimum solution to a given objective function is discovered. However, it was originally intended for numerical optimization problems in a continuous solution space, despite undergoing numerous changes that have made it more resilient and adaptable to various problem spaces. SOS is inspired by the interplay between species that coexist in a single habitat and continuously struggle and compete for existence or growth.

The original studies of Kennedy and Eberhart [36] for PSO, Mirjalili et al. [38] for GWO, Li et al. [39] for SMA, and Cheng and Prayogob [40] for SOS can be referred to for more details.

Hybrid modelling of LSSVM and OAs

In this work, four optimization algorithms (OAs) were utilized to determine the LSSVM hyper-parameter. As stated above, γ and σ are the two hyperparameters of LSSVM. It is worth mentioning that adequate configuration of γ and σ is required for developing an effective LSSVM model, as these two parameters have a substantial impact on the model’s performance. Also note that, selecting LSSVM hyper-parameters all at once is a difficult operation because they must be searched in continuous domains, resulting in an endless number of paraeter sets. As a result the problem of LSSVM parameter tuning may be stated as an optimization problem.

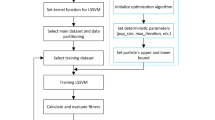
Considering the above points as a reference, PSO, GWO, SMA, and SOS were used to optimize the values of γ and σ and four hybrid LSSVM models, namely LSSVM-PSO, LSSVM-GWO, LSSVM-SMA, and LSSVM-SOS, were constructed. The following are the steps for optimizing LSSVM parameters: (a) initialization of LSSVM; (b) set kernel function; (c) set mimulus and maximum bounds of γ and σ; (d) data partitioning; (e) training dataset selection; (f) initialize MHAs; (g) set deterministic parameters of MHAs, such as swarm size (N_S), number of iterations (i_max), upper and lower bounds (UB and LB), and other parameters; (h) training of LSSVM; (i) calculate and evaluate the fitness value, root mean square error (RMSE); (j) check terminating criteria; (k) obtained optimum values of γ and σ; and (l) testing of hybrid LSSVMs. The development of hybrid LSSVM models is depicted in Fig. 1. Notably, in addition to the hyper-parameters of LSSVM, the deterministic parameters of MHAs also play a significant role in hybrid modelling; thus, they must be carefully calibrated during the optimization process.

Fig. 1

Flow chart for hybrid LSSVM modelling

Descriptive statistics and computational modelling

In order to create a high-performance prediction model of the OWC and MDD, a vast array of experimental results of soil compaction parameters from a recently published work by Wang and Lin [10] were compiled. The collected dataset contains several details including gravel content (C_G), sand content (C_S), fines content (C_F), liquid limit (LL), plastic limit (PL), compaction energy (CE), OWC and MDD. The collected data consists of the following soil types: CH, CL, CL–ML, GC, GM, GP–GC, GW–GC, MH, ML, SC, SM, SP–SC, and SW–SC.

The descriptive details of the soil properties in the current database are presented in Table 1. In addition, the minimum, mean, maximum, and range for OWC and MDD are tabulated in Table 2, separately for CH, CL, CL-ML, GC, GM, GP–GC, GW–GC, MH, ML, SC, SM, SP–SC, and SW-SC soils. The comparative histograms for each variable are displayed in Fig. 2. Note that the normalized values of input soil parameter, OWC, and MDD were considered for this purpose. To better demonstrate, the correlation analysis with colour plot (based on degree of correlation, i.e., R-value) between input soil parameters and OWC, MDD are presented in Tables 3 and 4, respectively. According to the information presented in Tables 3 and 4, the amount of correlation between the parameters can be observed quickly. As can be seen, the contents of gravel and sand (i.e., C_G and C_S) and the CE have a negative correlation with the OWC, whereas C_F and PL exhibit a positive correlation. In contrast, C_F, and plasticity parameters (i.e., LL, and PL) have a negative correlation, but C_G, C_S, and CE have a positive correlation. Moreover, a large number of soil metrics have very little correlation with the OWC and MDD of soils. These occurrences imply that the collected dataset has a vast array of experimental data and can be deemed relevant for data-driven modelling.

Table 1 Descriptive statistics of the collected dataset

Table 2 Descriptive details of OWC and MDD for different soils

Fig. 2

Comparative histogram between input and output parameters

Table 3 Correlation analysis between input soil parameters and OWC

Table 4 Correlation analysis between input soil parameters and MDD.

Subsequent to the data collection, the whole dataset was apportioned into two subsets: (a) a training subset including 80% of the main dataset and (b) a testing subset containing the remaining dataset. Despite the fact that there is no pre-defined criterion or set of criteria for choosing the number of datasets to use in a predictive model, the researchers' decision will be determined primarily by the type of problem at hand. Generally, a model built from a large dataset is often thought to be superior to one built from a small number of observed data points. Taking this into account, 20% of the primary dataset was chosen as the testing dataset. The steps of computational modelling in estimating the soil compaction parameters can be described as follows: (a) selection of the main dataset; (b) data normalization; (c) data partitioning and selection of training and testing subsets; (d) processing though MHAs; (e) computational modelling using LSSVM-PSO, LSSVM-GWO, LSSVM-SMA, and LSSVM-SOS; and (f) prediction of training and testing datasets. Figure 3 depicts the entire process of computational modelling in the form of a flow chart.

Fig. 3

Steps of computational modelling

Results and discussion

This section details the results of the hybrid LSSVM models used to estimate the soil compaction parameters. As stated above, before the models were created, the main dataset was separated into training (181 samples) and testing (45 samples) subsets. Note that, the same training and testing subsets were used to build and validate all models. The results of the built models were then evaluated using a variety of indices. On the contrary, aside from γ and σ, the OA deterministic parameters such as N_S, i_max, UB, LB, and other parameters play a significant role in hybrid modelling, therefore they were appropriately calibrated during the course of optimization. The details of deterministic and hyper-parameters in forecasting soil compaction parameters are described in the following sub-section, followed by a comparative analysis of results.

Model performance

Following the development of hybrid LSSVMs, different indices were determined to evaluate them, including R², performance index (PI), variance account factor (VAF), Willmott's index of agreement (WI), RMSE, mean absolute error (MAE), RMSE to observation's standard deviation ratio (RSR), and weighted mean absolute percentage error (WMAPE) [18, 41,42,43,44,45,46,47,48,49,50,51]. Note that these indices are often used to assess any prediction model's generalization ability from a variety of angles, including correlation accuracy, related error, amount of variance, and so on. The expressions for these indices can be given by:

$$R^{2} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (y_{i} - y_{{{\text{mean}}}} )^{2} - \mathop \sum \nolimits_{i = 1}^{n} (y_{i} - \hat{y}_{i} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} (y_{i} - y_{{{\text{mean}}}} )^{2} }}$$

(5)

$${\text{PI}} = {\text{adj}}.R^{2} + 0.01\;{\text{VAF}} - {\text{RMSE}}$$

(6)

$${\text{VAF}} \left( \% \right) = \left( {1 - \frac{{{\text{var}} (y_{i} - \hat{y}_{i} )}}{{{\text{var}} (y_{i} )}}} \right) \times 100$$

(7)

$${\text{WI}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} (y_{i} - \hat{y}_{i} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left\{ {\left| {\hat{y}_{i} - y_{{{\text{mean}}}} } \right| + \left| {y_{i} - y_{{{\text{mean}}}} } \right| } \right\}^{2} }}} \right]$$

(8)

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} (y_{i} - \hat{y}_{i} )^{2} }$$

(9)

$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\left( {\hat{y}_{i} - y_{i} } \right)} \right|$$

(10)

$${\text{RSR}} = \frac{{{\text{RMSE}}}}{{\sqrt {\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} (y_{i} - y_{{{\text{mean}}}} )^{2} } }}$$

(11)

$${\text{WMAPE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right| \times y_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} y_{i} }}$$

(12)

where $y_{i}$ and $\hat{y}_{i}$ are the actual and predicted ith values; $n$ is the number of observations; and $y_{{{\text{mean}}}}$ is the average of actual value. It is important to note that the value of these indices must match their ideal value for an ideal model, which is provided in Table 5.

Table 5 Ideal values of different indices

As previously stated, selecting LSSVM hyper-parameters and deterministic parameters of OAs is critical for developing the best model; therefore, the values of γ and σ were set within a pre-defined range of upper and lower bounds. In this work, the upper and lower bounds of γ and σ were set to (100 and 0.10) and (50 and 0.10), respectively. The values of γ and σ were generated randomly within the range of upper and lower limits in each iteration using the equation below.

$$\gamma \;{\text{and}}\;\sigma = {\text{rand}} \times \left( {{\text{UB}} - {\text{LB}}} \right) + {\text{LB}}$$

(13)

where UB and LB are the upper and lower bounds and ${\text{rand}}$ represents a uniformly distributed random number generated within the range of 0–1. On the other hand, to construct the optimum hybrid LSSVMs, the value of N_S and i_max were set to 30 and 200, respectively. The values of $c_{1}$ and $c_{2}$, (PSO parameters) and $z$ (SMA parameter) were set to 1 and 2, and 0.2, respectively. For other OAs, the values of exploration and exploitation constants were kept at their original values. The details of LSSVM hyper-parameters and deterministic parameters of OAs are presented in Table 6. The primary dataset was partitioned into training and testing subsets before the model construction; the training subset was used to generate the hybrid models, while the testing subset was utilized to evaluate the predictive potential of the constructed LSSVM models.

Table 6 Details of different parametric for hybrid LSSVMs

Tables 7 and 8 show the predictive outcomes of the constructed hybrid LSSVMs for predicting soil OWC and MDD, respectively. Herein, the performance of the models in predicting the training, testing, and total outputs is presented. It should be emphasized that the performance of each model with the training subset was utilized to describe the goodness of fit of the constructed models, whilst the testing dataset was used to assess their generalization capabilities. Based on the experimental results, the proposed LSSVM-SOS attained the highest R² and lowest RMSE values in OWC and MDD prediction. The proposed LSSVM-SOS achieved the highest accuracy in the training phase, with R² = 0.9783 and RMSE = 0.0231 in OWC prediction and R² = 0.9793 and RMSE = 0.0233 in MDD prediction. These matrices were found to have R² = 0.9160 and RMSE = 0.0450 in OWC prediction and R² = 0.9092 and RMSE = 0.0498 in MDD prediction during the testing phase. Overall, the developed LSSVM-SOS predicts the OWC and MDD of soils with 96.56% and 96.41% accuracy (in terms of R² value), respectively. These results show that the proposed LSSVM-SOS has high predictive performance in both instances. However, in the testing phase, the predictive precision of the developed LSSVM–SMA and LSSVM–PSO were determined to be the second-best models with R² = 0.8935 and R² = 0.8823 for OWC and MDD prediction, respectively.

Table 7 Performance indices for OWC prediction

Table 8 Performance indices for MDD prediction

To better demonstrate, illustrations of actual and estimated values of OWC and MDD are presented in Figs. 4, 5, 6 and 7, respectively. Herein, the scatterplots of the best two prediction models are presented. In the training phase of OWC prediction, the LSSVM-SOS (R² = 0.9783) and LSSVM–GWO (R² = 0.9767) models were found to be the top two models, while the LSSVM–SOS (R² = 0.9160) and LSSVM–SMA (R² = 0.8935) were determined to be the best in the testing phase. On the contrary, the LSSVM–GWO (R² = 0.9785) and LSSVM–PSO (R² = 0.8823) were determined to be the second-best MDD prediction models throughout the training and testing stages, respectively.

Fig. 4

Scatter plot for OWC prediction in the training phase (for best two models)

Fig. 5

Scatter plot for OWC prediction in the testing phase (for best two models)

Fig. 6

Scatter plot for MDD prediction in the training phase (for best two models)

Fig. 7

Scatter plot for MDD prediction in the testing phase (for best two models)

It is crucial to note that a data-driven model is insufficient without a visual depiction of results. Visualizations facilitate the detection of trends, correlation, and outliers in a dataset that are more easily comprehended. Visual depictions are useful for seeing trends in data without having to sift through the granular details. Thus, a graphical depiction of the generated models’ outcomes in the form of a Taylor diagram and accuracy matrix is also presented. These diagrams are incredibly helpful for evaluating a model’s overall correctness comprehensively.

Note that, an accuracy matrix [50] is a heat map matrix which is used to quantify the amount of accuracy attained by a model in terms of different performance criteria. Using this matrix, one can quickly assess the amount of accuracy achieved by a model without examining the values of each index. As specified earlier, several indices must be established to examine the preciseness of a model from various perspectives; however, interpreting findings by studying the values of each index is time-consuming and requires extensive observations. Thus, the accuracy matrix is highly beneficial for the rapid evaluation of results. The accuracy matrix for the generated models for OWC and MDD prediction is depicted in Figs. 8 and 9. Here, the performance of the models on the training (TR), testing (TS), and total (TL) datasets is provided. It can be seen from the accuracy matrix that the suggested LSSVM-SOS is the best prediction model in both scenarios.

Fig. 8

Accuracy matrix for OWC prediction

Fig. 9

Accuracy matrix for MDD prediction

Alternately, the Taylor diagram [52] is a 2-D mathematical diagram used to offer a brief evaluation of a model’s precision. In terms of the coefficient of correlation, ratio of standard deviations, and RMSE, it describes the relationships between the estimated and real observations. In a Taylor diagram, a point represents a model. For an ideal model, the position of the point should agree with the reference point (Ref). Figures 10 and 11 depict the Taylor diagrams for the hybrid LSSVMs created for OWC and MDD prediction. Herein, the models` outcomes are reported for the training and testing subsets. As can be observed, the LSSVM-SOS is the most precise model (as the green marker appears closest to the ‘Ref’ point)) in both phases of OWC and MDD prediction.

Fig. 10

Taylor diagram for OWC prediction: a training and b testing

Fig. 11

Taylor diagram for MDD prediction: a training and b testing

Discussion of results

In the previous sub-section, the predictive performance of the hybrid LSSVMs in forecasting the OWC and MDD of soils is given and reviewed. As mentioned above, many performance indices were calculated to analyse the performance and generalization ability of the constructed hybrid LSSVMs, including LSSVM–PSO, LSSVM–GWO, LSSVM–SMA, and LSSVM–SOS. All proposed LSSVM models suitably forecast the indented output, i.e., OWC and MDD of soils, according to experimental findings. Specifically, the proposed LSSVM-SOS attained the maximum precision in both the training and testing phases; however, the LSSVM–SMA and LSSVM–PSO were determined to be the second-best models for OWC and MDD prediction, respectively.

Nonetheless, the overall accuracy of the developed hybrid LSSVMs was assessed through OBJ criterion. Notably, the OBJ criterion is quite beneficial for determining the overall performance of a data-driven model [53, 54]. The OBJ takes into account R² and MAE values of the training and testing data, and the mathematical expression is given by [53]:

$${\text{OBJ}} = \left( {\frac{{N_{{{\text{TR}}}} - N_{{{\text{TS}}}} }}{{N_{{{\text{TL}}}} }}} \right) \times \left( {\frac{{{\text{MAE}}_{{{\text{TR}}}} }}{{R_{{{\text{TR}}}}^{2} }}} \right) + \left( {\frac{{2 \times N_{{{\text{TR}}}} }}{{N_{{{\text{TL}}}} }}} \right) \times \left( {\frac{{{\text{MAE}}_{{{\text{TS}}}} }}{{R_{{{\text{Ts}}}}^{2} }}} \right)$$

(14)

where $N_{{{\text{TR}}}}$ and $N_{{{\text{TS}}}}$ are the number of samples for the training and testing subsets, respectively; $N_{{{\text{TL}}}}$ is the total number of samples; ${\text{MAE}}_{{{\text{TR}}}}$ and ${\text{MAE}}_{{{\text{TS}}}}$ are the MAE index for the training and testing subsets, respectively; and $R_{{{\text{TR}}}}^{2}$ and $R_{{{\text{TS}}}}^{2}$ are the R² index for the training and testing subsets, respectively.

The values of these indices along with the OBJ value are presented in Table 9. All created hybrid LSSVMs were ranked and listed in the table based on the OBJ value. For OWC prediction, the respective OBJ values for LSSVM–PSO, LSSVM–GWO, LSSVM–SMA, and LSSVM–SOS are 0.0293, 0.0278, 0.0503, and 0.0247. For MDD prediction, the OBJ values for these models are 0.0523, 0.0301, 0.0544, and 0.0269, respectively. These values show that LSSVM-SOS has the lowest OBJ, and therefore, it is the best model from this viewpoint. To better illustrate, Fig. 12 depicts a bar plot of OBJ values for each hybrid LSSVM constructed for OWC and MDD prediction.

Table 9 Evaluation of OBj criterion

Fig. 12

Bar plot of OBj values

Summary and conclusion

The present work proposes a high-performance hybrid model to replace the conventional laboratory tests of soil compaction. In this work, four hybrid LSSVM models, including LSSVM-PSO, LSSVM-GWO, LSSVM-SMA, and LSSVM-SOS, were used to build a prediction model for soil compaction parameters, namely OWC and MDD. Based on the experimental results, the following conclusions can be drawn:

• (a) The proposed LSSVM–SOS was found to be the best model among the created hybrid LSSVM models in terms of R² and RMSE criteria, with R² = 0.9656 and RMSE = 0.0288 for OWC prediction and R² = 0.9641 and RMSE = 0.0305 for MDD prediction.

• (b) The overall performance of the developed LSSVM–SOS shows that it can be utilized as an alternate tool to estimate soil compaction parameters to aid geotechnical engineers in the design phase of civil engineering projects.

• (c) The main advantages of the proposed LSSVM–SOS model include: (1) use of real-life datasets; (2) 13 different soil types were considered; (3) higher prediction accuracy in the testing phase; (4) high degree of reliability; and (5) optimized values of $\gamma$ and $\sigma$ were used.

• (d) However, the restricted search space of the OAs and the need for many runs can be seen as drawbacks of this work. Therefore, in order to broaden the application of hybrid LSSVMs for forecasting the required output in other engineering fields, additional research should be undertaken.

• (e) The future direction of this work may include: (1) a detailed assessment of the accuracy of other hybrid models, via actual data from various areas of geotechnical engineering; (2) evaluation of the LSSVM–SOS model’s superiority over other hybrid LSSVM models; and (3) implementation of advanced and enhanced of meta-heuristic algorithms for a comparative assessment of different hybrid LSSVM models.

Nevertheless, as far as the authors are aware, this work shows for the first time the application of hybrid LSSVM models built using swarm intelligence approaches for forecasting the soil compaction parameters.