A novel liquefaction study for fine-grained soil using PCA-based hybrid soft computing models

Abstract

Earthquake-induced liquefaction is an unpredicted phenomenon that causes catastrophic damages and devastation to the environment, structures, and human life. The assessment of soil liquefaction behavior is a decisive work for geotechnical engineers especially during the designing phase of any civil engineering projects. These decisions implicate tedious and costly experimental procedures and extensive evaluation. Considering these facts, the present study aims to simplify the process of evaluating soil’s liquefaction behavior in a broader domain involving the least experimental datasets. Three PCA (principal component analysis)-based advanced hybrid computational models, namely PCA-ANN, PCA-ANFIS, and PCA-ELM were developed to predict the liquefaction behavior of soils. The dimension reduction technique, i.e. PCA, was used to avoid the multicollinearity effect during the course of the development of the said models. Geotechnical parameters, namely plasticity index, SPT blow count, water content to liquid limit ratio, bulk density, total stress, effective stress, and fine content along with other seismic input variables, such as the ratio of peak ground acceleration and acceleration due to gravity, and magnitude of an earthquake were used to develop the predictive models. The predictive accuracy of the proposed models was evaluated via several fitness parameters. In the end, the best predictive model was determined using a novel tool called Rank Analysis. Based on the results, it has been established that the PCA-ELM hybrid computational model can be considered as a new alternative tool to assist geotechnical engineers in the task of assessing the liquefaction potential of soil during the preliminary design stage in any engineering project.

1 Introduction

Soil liquefaction often termed an earthquake-induced phenomenon leads to loss of strength in soil and changes in in-situ soil to behave as a viscous liquid causing huge ground failures. Poorly drained fine-grained soils such as sand, silt, and gravels are the most susceptible to liquefaction. Civil engineering structures constructed on loose soil terrain tilts or damages easily when liquefaction occurs because soil deposits lose their ability to support the weight of the superstructure along with the structure’s foundations. The occurrence of Alaska and Niigata earthquakes in 1964 led to the extensive study of liquefaction by many researchers. Seed and his co-researchers Seed and Idriss [1]; Seed et al [2] developed a methodology known as the simplified approach for assessing the liquefaction potential of cohesionless soil using laboratory tests data which become the most widely used empirical approach in the world. Seed [3] developed correlations between liquefaction potential and standard penetration test (SPT) value, i.e., N value. Idriss sand Boulanger [4] proposed a semi-empirical approach for determining the liquefaction potential of saturated sands based on blow counts from the SPT. Presently, a simplified approach based on several in-situ tests, such as the cone penetration test (CPT) and small-strain shear wave velocity (Vs) measurement, have been established for assessing soil liquefaction potential. Due to the high cost and excessive effort for setting the experimental set-ups for simulating the liquefaction phenomenon, simplified approaches based on in-situ tests are frequently applied by geotechnical engineers to assess the liquefaction potential of soils. These empirical equations have been proposed for saturated and partially saturated cohesion less soils. Many researchers have performed studies on liquefaction response of fine grained silts and clays and have considered soil to be in saturated conditions. Bray and Sancio [5], Gratchev [6], Boulanger and Idriss [7]. As saturated condition of soil is considered to be the most vulnerable state for liquefaction (least factor of safety) and hence, in reference to the earlier studies, the present study focuses in determining the liquefaction response of fine-grained soil under saturated conditions.

Most of the applicable methods in evaluating the liquefaction potential that is in practice are theoretical and empirical methods which are prominently based on the liquefaction analysis of case histories and finding the occurrence of liquefaction. Any empirical or theoretical methods need large dataset based on extensive laboratory and in-situ testing for proper evaluation of liquefaction involving high-end calculation. The dependency of these methods on extensive experimental results and calculation may arise the risk of uncertainty and error. Many possible factors may cause uncertainty in determining liquefaction. Therefore, accurate and precise prediction of liquefaction is highly significant for designing sub and super-structures, especially when constructed in high-seismic zones. Proper forecasting of soil liquefaction guarantees the safety and serviceability of such engineering projects. Thus, in the process of liquefaction evaluation, it must be assured that the factor of safety of the soil deposits is measured with an appropriate level of accuracy. Nowadays, computational-based techniques are being used frequently for finding the solutions to various engineering problems including the assessment of liquefaction potential of soils. Computational methods are based on the artificial intelligence of the machine and can be defined as the ability of a system to independently find solutions to problems by recognizing patterns in databases with minimal human involvement. In other words, it enables a system to recognize patterns based on provided or existing algorithms and datasets to develop an acceptable and reliable solution. This leads to minimal uncertainty caused due to the use of empirical deterministic methods.

Farookhzad et al [8] used artificial neural networks (ANN) for predicting soil liquefaction and presented a comparison between the empirical approach and the ANN model. It was suggested that the developed neural networks are an influential computational tool that can scrutinize the multifaceted connections between soil’s liquefaction potential and their significant parameters. Samui and Sitharam [9]; used two robust and widely used machine learning tools, ANN and support vector machine (SVM) to predict liquefaction susceptibility of soil based on test data obtained from the 1999 Chi-Chi, Taiwan earthquake. The developed models were applied to various liquefaction case histories that are globally available. Samui [10] used relevance vector machine (RVM) to evaluate the liquefaction potential of soil by using actual CPT data and provided a comparative study of the results obtained from RVM with a widely used ANN model. Xue and Yang [11] determined the liquefaction potential of soil using an integrated fuzzy neural network model acknowledged as Adaptive Neuro-Fuzzy Inference System (ANFIS). Muduli et al [12] used multi-gene genetic programming (MGGP) an evolutionary computational technique for evaluating liquefaction based on cone penetration tests. Samui et al [13] studied the liquefaction behavior of soil using extreme learning machine (ELM). Multivariate Adaptive Regression Spline (MARS) models have also been prominently used by various researchers for assessment of liquefaction of soil deposits. (Zhang et al [14]; Zhang and Goh [15]).

During the early days of liquefaction research, it was assumed that occurrences of liquefaction are merely associated with cohesionless soils, but few instances in the past suggested that liquefaction is not only limited to sandy soils. In-fact, it can be occurred in cohesive soils also, i.e., soils with plasticity and fine content. These instances led to the regress study of liquefaction assessment of fine-grained soil with medium to low plasticity by various researchers (Wang [16]; Andrew and Martin [17]; Bray et al [18]; Paydar and Ahmadi [19]; Marto et al [20]; Ghani and Kumari [21]). A detailed review of these studies reveals that, researchers recommended various geotechnical parameters such as plasticity index (PI), liquid limit (LL), water content (wc), and liquid limit to water content ratio (wc/LL) to study the liquefaction behavior of fine-grained soil [Polito [22]; Seed et al [23]; Bray and Sancio [5]; Boulanger and Idriss [7]; Gratchev [6]; Ghani and Kumari [24]; Ghani and Kumari [25]. In addition, the total stress (TS) and effective stress (ES) have a greater influence on the cyclic stress ratio (CSR) which is a crucial parameter for liquefaction study Idriss and Boulanger [4]. Earthquakes during Northridge 1994, Kocaeli 1999, and Chi-Chi 1999 revealed that fine-grained soil deposits liquefied under the seismic condition irrespective of earlier believes these sites underwent liquefaction Ghani and Kumari [21]. Cyclic testing of soils that liquefied in Adapazari during the Kocaeli 1999, earthquake confirmed that fine-grained soils were susceptible to liquefaction Bray and Sancio [5]. Ghani and Kumari [24, 25] have presented a detailed review of the literature which provides an extended discussion on the liquefaction ability of fine-grained soils. Boulanger and Idriss [26] suggested that silts and clays can be separated into “sand-like” fine-grained soils that can liquefy and “clay-like” fine-grained soils that can undergo cyclic failure for assessing their liquefaction vulnerability, which clearly indicates that fine-grained soil can be susceptible to liquefaction. It was also stated that plasticity index can be considered as a significant discriminating criteria to categorize these two type of fine-grained soils. There are many parameters defined by Ghani and Kumari [24] which influences the liquefaction behavior of fine grained soil. These parameters include intensity of earthquake, percentage of fine content, plasticity index of soil, liquid limit of soil, peak ground acceleration, and SPT blow count. In view of the above the present paper take accounts of all the parameters used by various researchers observed in the literature to develop a computational model to predict the liquefaction behavior based on its interdependencies. Therefore, the development of computational models for the assessment of liquefaction susceptibility of cohesionless and cohesive soils involves a large number of input parameters. One of the prominent problems that arise while developing a model which deals with a large number of variables is the overfitting of the model, due to the presence of multicollinearity between the variables. Overfitting develops large gaps between the training and testing results of the developed model. A dataset with large input variables increases the dimensionality of the problem which leads to an increase in computational cost and time for processing the desired output. To propose an efficient and effective computational model for liquefaction assessment, the above-mentioned problems need to be addressed. Principal component analysis (PCA) is a renowned approach that is used for reducing the dimensionality of datasets and increasing interpretability as well as curtailing any information loss. It does so by generating novel uncorrelated variables known as principal component (PC) that successively maximize variance.

Advancements in liquefaction study techniques have been proposed by many researchers in the past few decades. One of the major concerns in the determination of factor of safety of soil which defines soils liquefaction potential is to accurately predict it as it depends upon several geotechnical parameters. The correlation of these geotechnical parameters with the factor of safety is highly dynamic which needs advanced computational techniques for accurate and precise prediction. To achieve and develop a computational model that can establish the relationship between these parameters and the factor of safety to predict the liquefaction behavior accurately, new hybrid soft computing methods are adopted in the present study. It investigates and compares the performance of ANN, adaptive neuro-fuzzy inference system (ANFIS), and ELM for assessment of liquefaction behavior of soil present in high seismic regions. To boost the predictive performance of the developed computational models, these are integrated with PCA. The PCA-based hybrid computational models are named PCA-ANN, PCA-ANFIS, and PCA-ELM.

2 Theoretical details of empirical techniques, PCA, and soft computing models

The following sections describe the methodologies of the developed soft computing models in detail. The theoretical details of the empirical approach and PCA used in this study are explained which is followed by the methodological approach of the soft computing models including the ANN, ANFIS, and ELM.

2.1 Empirical approach based on Indian Standard Code (IS 1893 Part I: 2016) “Criteria for Earthquake Resistant Design of Structures”

It is considered one of the most common and simplified practices for the evaluation of the liquefaction potential of soil deposits in India. The standard primarily focuses on earthquake risk assessment for earthquake-resistant design of buildings, liquid retaining structures, bridges, embankments, and retaining walls as well as the provisions of this standard are also applicable to critical structures, like nuclear power plants, petroleum refinery plants, and large nuclear dams. This method uses SPT, CPT, or Shear wave velocity (V_S) to evaluate the liquefaction susceptibility of soil deposits. The following subsections focus on SPT-based liquefaction potential. The liquefaction assessment parameter that shows the loading applied by seismic activity on soil, proposed by IS 1893 [27] is presented as Cyclic Stress Ratio (CSR) and can be obtained by the following equation:

$$ CSR = 0.65\left( {\frac{{a_{max} }}{g}} \right)\left( {\frac{{\sigma_{\nu o} }}{{\sigma^{\prime}_{\nu o} }}} \right)r_{d} $$

(1)

where $\sigma_{\nu o}$ represents total vertical overburden stress; $\sigma^{\prime}_{\nu o}$ represents effective vertical overburden stress; z represents the depth (in m) below the ground surface; a_max represents the peak ground acceleration; g represents acceleration due to gravity; and r_d represents the stress reduction factor.

The potential of soil to resist liquefaction is determined by Cyclic Resistance Ratio (CRR), which can be evaluated using the corrected SPT blow count (N₁)₆₀ using the following expression:

$$ CRR_{{}} = \left[ {\frac{1}{{34 - (N_{1} )_{60CS} }} + \frac{{(N_{1} )_{60CS} }}{135} + \frac{50}{{[10(N_{1} )_{60CS} + 45]^{2} }} - \frac{1}{200}} \right] $$

(2)

Further the following equation is used to evaluate factor of safety (FOS), which can be described as:

$$ FOS = \frac{CRR}{{CSR}} $$

(3)

Note that, If FOS < 1, soil will liquefy and for soil layers with FOS ≥1, is said to be safe against liquefaction

2.2 Principal component analysis (PCA)

The PCA was first introduced in an article by Hotelling [28] and since then it has been used in many fields including engineering and sciences. Its prime purpose is reducing the dimensionality of a multivariate dataset and also classifying a smaller number of variables which summarizes the larger dataset and in turn reduces the computational time.

For a given set of m dimensional predictor variable, ${\varvec{u}}_{{\varvec{i}}} = [{\varvec{u}}_{{\varvec{i}}} \left( 1 \right),{\varvec{u}}_{{\varvec{i}}} \left( 2 \right),.......{\varvec{u}}_{{\varvec{i}}} \left( {\varvec{p}} \right)]^{{\varvec{T}}}$where $i = 1,2, \ldots .q$. Principal component analysis transforms the predictor variable (v_i) into a new vector using (4)

$$ \nu_{i} = U^{T} u_{i} $$

(4)

where $U$ represents a $p \times p$ orthogonal matrix, which is used to determine the eigenvectors of the covariance matrix $M$ of the sample, ${\varvec{M}} = \frac{1}{{\varvec{q}}}\mathop \sum \nolimits_{{{\varvec{i}} = 1}}^{{\varvec{q}}} {\varvec{u}}_{{\varvec{i}}} \bullet {\varvec{u}}_{{\varvec{i}}}^{{\varvec{T}}}$ and can be solved using (5).

$$ {\varvec{\lambda}}_{{\varvec{j}}} {\varvec{r}}_{{\varvec{j}}} = {\varvec{Mr}}_{{\varvec{j}}} $$

(5)

where ${\varvec{\lambda}}_{{\varvec{j}}}$ and ${\varvec{r}}_{{\varvec{j}}}$ denote eigenvalue and eigenvector of the covariance matrix ($M$), respectively. The orthogonal component of the predictor variable $\nu_{i}$ is assessed subsequent transformation of $u_{i}$ using equation (4) and the corresponding resultant component is called as the principal component. Principal components selection depends on the obtained eigenvalues and eigenvectors which are further arranged in descending manner and predictor variables are reduced to principle components. Thus, PCA reduces the dimensionality of the complex problem by changing multiple input variables into principal components that are uncorrelated and have sequentially maximum variances.

2.3 Artificial neural network (ANN)

An ANN is one of the widely acknowledged machine learning algorithms which is stimulated by the functionality of the human brain (Goh [29]; Wang and Rahman [30]; Juang and Chen [31]; Wambua et al [32]; Mokhtarzad et al [33]). In general, ANN generates a multifaceted network mapping between input and output variables which can approximate non-linear functions. Amongst the numerous methods available to develop an ANN model, the multilayer perceptron (MLP) neural network is one of the most commonly applied methods, which can solve complex mathematical problems that require nonlinear equations by defining proper weights. The typical MLP consists of at least three layers. The first layer is termed as an input layer, the last layer is termed as an output layer, and the remaining layers present between the input and output layers are called hidden layers. Figure 1 shows a typical representation of ANN architecture. Coulibaly et al [34] suggested that one hidden layer is adequate for an ANN model to approximate multifaceted non-linear functions for given datasets. Observations are drawn from the present study also suggest that one hidden layer was suitable to estimate the relationship between the principal components and factor of safety against liquefaction of the soil deposits. Therefore, the present study uses an ANN model which comprises one input layer, one output layer, and one hidden layer. Once the network is properly trained with adequate datasets it can be validated, and further, the trained network can be used to make predictions for a new set of data that has never been introduced. Due to its efficiency and wide applicability, it is one of the most suitable computational models applied in the field of liquefaction assessment used by various researchers. Successful application of ANN can be found in the literature (Goh [29]; Wang and Rahman [30]; Goh [35]; Farookhzad et al [8]; Samui and Sitharam [9]Kamatchi et al [36];; Kumar et al [37]; Prabakaran et al [38]; Ramezani et al [39]; Kaloop et al [40]; Kaloop et al [41]; Kaloop et al [42]; Kardani et al [43]; Kardani et al [44]; Kardani et al [45]; Kardani et al [46]; Ghani et al [47]; Asteris et al [48]).

Figure 1

A typical architecture of an ANN.

2.4 Adaptive neuro fuzzy inference system (ANFIS)

The Neuro-fuzzy approach is an integrated method that blends the qualities of neural networks and fuzzy systems in a balanced form which overcomes their shortcomings. The blending of a neural network and fuzzy logic into neuro-fuzzy models merges the computational power of neural networks and the advantages of high-level human-like thinking of fuzzy systems. The adaptive and learning capabilities of neural network models and knowledge representation and qualitative approach of fuzzy logic approach are combined by adaptive neuro-fuzzy inference system (ANFIS) models. It has a high generalization capability as neural networks and other machine learning techniques. ANFIS can model the qualitative features of human knowledge in the form of if–then rules and reasoning processes without using precise quantitative analyses. Amongst several fuzzy inference methods, Mamdani, Takagi–Sugeno, and Tsukamoto fuzzy are three prominent approaches that are usually used to develop an ANFIS model. Normally an ANFIS model structures three layers, starting with the input layer with input nodes then followed by hidden layers where nodes functions as membership functions (MFs) and rules, and the output layers with output nodes. Kayadelen [49], Vankatesh et al [50], Xue and Yang [11], Kumar et al [51], Kaya [52]; Kardani et al [53] and Kumar et al [54] have opted for the use of this hybrid of neural network and fuzzy logic computational model in assessing liquefaction response of soil layers.

For ease in understanding we assume that the fuzzy system has two inputs and one output, and it is a first-order Sugeno fuzzy model. Hence, a classic rule set with two fuzzy if then rules can be expressed as following:

$$ Rule\; 1\;:\; if\; a\; is\; A_{1}\; and\; b\; is\; B_{1},\; then\; f_{1}\; = p_{1}\; a\; +\; q_{1}\; b\; +\; r_{1} $$

(6)

$$ Rule\; 2\;:\; if\; a\; is\; A_{2}\; and\; b\; is\; B_{2},\; then\; f_{2}\; =\; p_{2}\; a\; +\; q_{2}\; b\; +\; r_{2} $$

(7)

where $a$ and $b$ are the two inputs, and ${A}_{1}$, ${A}_{2}$, ${B}_{1}$ and ${B}_{2}$ are membership functions associated with inputs $x$ and $y$ associated with the node function. The parameters ${p}_{1}$, $q_{1} ,$ $r_{1}$ and $p_{2}$, $q_{2} ,$ $r_{2}$ are associated with output functions $f_{1}$ and $f_{2}$, respectively. A typical ANFIS Structure is presented in Figure 2, which illustrates that an ANFIS model comprises of five layers. The functionalities of each of these layers are described below:

Figure 2

A Standard representation of ANFIS Structure.

Layer 1: In this layer, the input variables are converted into a fuzzy membership function. Parameters present in layer 1 are denoted as premise parameters. The output of the node can be computed as:

$$ O_{i}^{1} = \mu_{Ai} \left( x \right) = \frac{1}{{1 + (\left( {x - c_{i} } \right)/a_{i} )^{2bi} }} $$

(8)

where $x$ is the input to node $i$, and $i$ is the linguistic label associated with this node and $a_{i}$, $bi$, $c_{i}$ are premise parameters.

Layer 2: Every node available in this layer is z fixed node which is labeled as $X$, whose output is product of all incoming signals.

$$ O_{i}^{2} = w_{i} = \mu_{Ai} \left( x \right)\mu_{Bi} \left( y \right),i = 1,2 $$

(9)

Layer 3: In this layer the firing strengths of FIS rules are normalized. Every node available in this layer calculates the weight, which is normalized. Outputs of this layer are referred as normalized firing strengths and is determined as;

$$ O_{i}^{3} = \overline{{w_{i} }} = \frac{{w_{i} }}{{w_{1} + w_{2} }} $$

(10)

Layer 4: In this layer every node i is termed as an adaptive node with a node function represented below:

$$ O_{i}^{4} = \overline{w}_{i} f_{i} = \overline{{w_{i} }} \left( {p_{i} x + q_{i} y + r_{i} } \right) $$

(11)

where $\overline{w}_{i}$ is the output of the preceding layer and $p_{i}$, $q_{i}$ and $r_{i}$ are the resultant parameters.

Layer 5: The combined output of the ANFIS model is evaluated by the following expression:

$$ O_{i}^{5} = \sum \overline{{w_{i} }} f_{i} = \frac{{\mathop \sum \limits_{i} w{}_{i}^{{}} f_{i} }}{{\mathop {\sum w_{i} }\limits_{i} }}O_{i}^{4} = \overline{w}_{i} f_{i} = \overline{{w_{i} }} \left( {p_{i} x + q_{i} y + r_{i} } \right) $$

(12)

2.5 Extreme learning machine: (ELM)

ELM, proposed by Huang et al [55] is a simple, fast, and powerful machine learning algorithm that is used for regression, classification, clustering as well as function approximation. It is nothing but a feedforward neural network whose learning speed can be thousands of times faster than a conventional feedforward network. ELM consists of a single hidden layer with one or more hidden neurons, where the weights of the input layer and biases of hidden neurons are randomly assigned. These weights and biases remain constant during the training and testing phases. In contrast, the weights of the output layer can be trained very fast. A review of the literature reveals the ELM can yield acceptable predictive performance with low computational cost. A typical structure of ELM is shown in Figure 3.

Figure 3

A Typical structure of ELM network.

A predictive model with $n$ samples and $p$ input features of dataset $X = { }\left\{ {x_{t} \in R^{p} } \right\},{ }t = 1,{ }2,{ } \ldots \ldots .,n$, the output of ELM can be written as:

$$ o_{i} \left( t \right) = { }m_{i}^{T} h\left( t \right) $$

(13)

where $m_{i} \,\epsilon \,R^{q} ,i\,\epsilon \left\{ {1,{ }2, \ldots \ldots ,o} \right\}{ }$ represents the weight vector of output layer, and $h\left( t \right)\,\epsilon \,R^{q} { }$ denotes the vector of hidden neurons outputs for a given input $x\left( t \right)\,\epsilon \,R^{p}$. Therefore, the vector of outputs of hidden neurons can be mathematically expressed as:

$$ h\left( t \right) = { }\left[ {f(w_{1}^{T} x\left( t \right) + b_{1} ){ },{ }f(w_{2}^{T} x\left( t \right) + b_{2} ), \ldots \ldots ,{ }f(w_{q}^{T} x\left( t \right) + b_{q} ){ }} \right] $$

(14)

in which, $b_{1} ,b_{2} , \ldots \ldots ,b_{q}$ are the bias terms of $k$ hidden neurons, $w_{k} \epsilon \,R^{p}$ denotes the weight vector of hidden to output layer and the functions $f\left( {..} \right)$ represents the activation function. Note that the weight vector and biases are generated randomly from a Gaussian distribution. In the nest stage, the $q \times n$ matrix of hidden layer output (${\varvec{H}}$) is formed, whose $i^{th}$ column is the vector of a hidden layer output $h\left( t \right)$. Subsequently, the weight matrix M=$[m_{1} ,m_{2} , \ldots \ldots ,m_{c} ]$ can be calculated through ‘$Moore{-}Penrose{ }pseudo{ }inverse$’ method as follows:

$$ M = \left( {H{ } \times { }H^{T} } \right)^{ - 1} { }H{ } \times { }D^{T} $$

(15)

where $D = \left[ {d\left( 1 \right),d\left( 2 \right), \ldots \ldots ,d\left( n \right)} \right]$ is a $c{ } \times n$ matrix whose $t^{th}$ column is the actual largest vector $d\left( t \right)\,\epsilon \,R^{c}$. As specified all the parameters of the network, the class label for ‘new input’ feature can be calculated as follows.

$$ Y = { }\arg max\left\{ {O_{i} } \right\} $$

(16)

where $i = 1,{ }2, \ldots \ldots ,o$ and $Y$ is the predicted class label. Several applications of this soft computing technique are amiable in the literature and researchers are using this technique to build predictive model as well as classification model in every field of engineering and sciences (Huang et al [56]; Zhu et al [57]; Huang et al [58]; Liu et al [59]; Samui et al [13]; Kumar and Samui [60]; Ceryan and Samui [61]).

3 Study area and data collection

Bihar is documented as a seismically active state of India. The state falls on the boundary of the Himalayan tectonic plate near the border of Bihar–Nepal and it covers seismic zones III, IV, and V. Out of 38 districts in Bihar, 8 districts belong to seismic zone V, 24 districts belong to seismic zone IV, and 6 districts belong to seismic zone III. The majority of the districts fall under multiple seismic zones (i.e., either seismic zone V & IV or seismic zone IV & III). The state has mostly experienced an earthquake in the magnitude of 5–7, but the worst was in the year 1934 with a magnitude of 8.4 which led to extensive destruction and enormous loss of human life. Nepal earthquake in 2015 which caused catastrophic damages in Nepal also caused severe damages in the state due to the closeness of the state from the epicenter. Liquefaction during these earthquakes was also observed in the Madhubani district of Bihar as a consequence on 25th April 2015. The state also exhibits a great example of alluvial soil deposits with a high percentage of fine contents as most of the cities lie near the bank of several rivers. The consecutive flood in the state every year leads to enormous deposition of plastic and non-plastic silts which increases the risk of liquefaction in the considered study area.

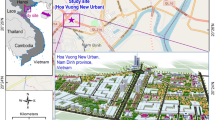
Bihar is a developing state with ongoing infrastructural developments and has a dense population as well as it is acknowledged as a seismic active zone according to the data of the Global Seismic Hazard Assessment Program (GSHAP), therefore it is essential to determine the liquefaction potential of the province with a modern framework so that all aspects are considered. In view of the above, for the present paper, the data obtained from an investigation site, from Darbhanga, Long. 26.1542° N and Lat. 85.8918° E, Madhubani, Long. 26.3483° N Lat. 86.0712° E, Muzaffarpur, Long.26.1197° N Lat. 85.3910° E and Supaul, Long. 26.1234° N Lat. 86.6045° E districts of Bihar, (India) shown in Figure 4 are used to analyze the liquefaction behavior of soil.

Figure 4

Geographical layout of study area showing the site locations in Bihar.

From the data samples collected from these sites, laboratory experiments were performed to obtain their geotechnical parameters to evaluate their liquefaction behavior. Finally, 180 data samples were engaged in developing and validating soft computing models. The details of the statistical characteristics of the variables used in this study are provided in Table 1.

Table 1 Statistical description of dataset.

4 Data processing and analysis

4.1 Statistical analysis

In this sub-section, the values of FOS are correlated with the input variables (IV) i.e., plasticity index (IV 1), SPT blow count (IV 2), Water Content to Liquid Limit Ratio (IV 3), M_w (IV 4), a_max/g (IV 5), Bulk density (IV 6), total stress (IV 7), effective stress (IV 8) and fine content (IV 9), details of which are furnished in the form of pair plot in Figure 5. It is apparent from the correlation plot that the input variables (IV1-IV9) are significantly correlated amid themselves which develops the problem of multicollinearity in the training and testing of computational models.

Figure 5

Correlation plot between input variables (IV1-IV9) and response variable (FOS).

Pearson's correlation coefficient (R), also referred to as Pearson's R is a statistic that measures the linear correlation between two variables and defines the strength of the association amongst the two variables. The collinearity between standard penetration blow count (N₁)₆₀ and target variable was the highest (IV2, R = 0.88). Moreover, input parameters such as plasticity index (IV1, R = 0.25), M_w (IV 4, R=−0.63), a_max/g (IV 5, R=−0.63), effective stress (IV7, R = 0.35), and total stress (IV8, R = 0.35) have significant amount of correlation to the FOS. These values indicate that IV1, IV2, IV4, IV5, IV7, and IV8 are the most influencing factors in estimating the FOS. Also, 2-D scatter density plots between the input variables and factor of safety are presented in Figure 6(a-i), from which the scatteredness of the variables can be visualized. Note that, to maintain the similarity, the normalized values of input and output parameters are considered to draw the 2-D scatter density plots.

Figure 6

(a-i) 2-D scatter density plot between the input variables (IV1 to IV 9) and factor of safety (variables are in normalized form).

4.2 Data processing using PCA

Based on the results of statistical analysis presented in section 4.1, it reveals that the degree of correlation between the variables is on the lower side in many cases. However, in some cases, it is found to be on the higher side. This phenomenon not only increases the computational cost but also yields lower accuracy during computational modeling. In contrast, there might be a possibility that some of the input variables considered in the analysis are less important. Therefore, to avoid the multicollinearity issues and to reduce the number of variables involved in the assessment of liquefaction which enhances the computational cost and time, the Principal Component Analysis is performed in the present study.

The insight behind the application of PCA is to diminish the number of predictor variables using principal components (PCs). These PCs are generated to predict the target variable efficiently thus promoting the development of simple and robust computational models with low computational costs. PCA provides a new set of variables established on the concept of entropy, which possesses the potential to clarify the significant extent of variance in the dataset. Furthermore, the new variables generated using PCA are orthogonal and evades the effect of overfitting and multicollinearity.

For the selection of PCs to perform the analysis, there is no thumb rule available. It depends on the choice of researchers and the type of analysis. For the present study, a cumulative amount of variance of approximately 97% has been opted to select the PCs, which are presented in Table 2. It was observed that six PCs out of the nine input variables to evaluate liquefaction exhibit 97% influence on the factor of safety, which demonstrates the effectiveness of PCA in reducing the dimensionality of the datasets. Therefore, six components (PC1-PC6) are used as input variables to develop the PCA-based predictive models, namely PCA-ANN, PCA-ANFIS, and PCA-ELM to predict the FOS for evaluating soil’s liquefaction potential. The descriptive statistics of PCs are furnished in table 3. Furthermore, the graphical representation of PCs in terms of their standard deviation, proportions of variance, and cumulative proportions along with correlation plot are shown in figure 7, figure 8, and figure 9, respectively.

Table 2 Realizations of principal component analysis.

Table 3 Statistical summary of each principal components.

Figure 7

Plots of PCs with cumulative proportions of variance.

Figure 8

Plots of PCs with standard deviation, proportions of variance, and cumulative proportions.

Figure 9

Correlation plot between principal components (PC1-PC9).

4.3 AI based analysis

For the application of computational analysis normalization of the datasets is considered as one of the most crucial stages. Normalization is performed in the pre-processing stage to cancel out the dimensionality effect of the variables. Therefore, before developing any model, the input and output variables have been normalized between 0 and 1 using the following expression:

$$ x_{NORMALISED} = \left( {\frac{{x - x_{min} }}{{x_{max} - x_{min} }}} \right) $$

(17)

where which $x_{min}$ and $x_{max}$ represent the minimum and maximum value of parameter (x) under consideration, respectively. This approach is called the ‘min-max’ normalization technique. After the normalization has been performed, the dataset is then divided into training and testing subsets. For this, 70% of the whole dataset is extracted at random to build the training subset while the balance 30% data is used as the testing subset.

The prime scope of this study was to scrutinize the feasibility of the three hybrid soft computing models namely PCA-ANN, PCA-ANFIS, and PCA-ELM developed for the assessment of soil liquefaction and their respective comparison to assess its adaptability and applicability. As mentioned, 70% of the main dataset (126 observations) extracted at random is used to train the above models, while the remaining dataset (54 observations) is used to validate (testing) the same. However, the entire process is presented in the form of a flow chart in Figure 10.

Figure 10

Flow chart showing steps of AI Models development.

Furthermore, to assess the performance of the predictive models, eight statistical indicators are determined including the Root mean square error (RMSE), Coefficient of determination (R²), Variance Account Factor (VAF), Performance Index (PI), Nash–Sutcliffe efficiency coefficient (NSE), Willmott`s Index of agreement (WI), Mean Bias Error (MBE) and Expanded Uncertainty (U₉₅). The details of mathematical expressions of the said parameters can be written as:

$$ RMSE = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {F_{A} - F_{P} } \right)} $$

(18)

$$ R^{2} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (F_{A} - F_{MEAN} )^{2} - \mathop \sum \nolimits_{i = 1}^{n} (F_{A} - F_{P} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} (F_{A} - F_{MEAN} )^{2} }} $$

(19)

$$ VAF\left( \% \right) = \left( {1 - \frac{{{\text{var}} (F_{A} - F_{P} )^{2} }}{{{\text{var}} (F_{A} )}}} \right) \times 100 $$

(20)

$$ PI = adj.R^{2} + 0.01VAF - RMSE $$

(21)

$$ NSE = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} (F_{A} - F_{P} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} (F_{A} - F_{MEAN} )^{2} }} $$

(22)

$$ WI = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} (F_{A} - F_{P} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left\{ {\left| {F_{P} - F_{MEAN} } \right| + \left| {F_{A} - F_{MEAN} } \right| } \right\}^{2} }}} \right] $$

(23)

$$ MBE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {F_{A} - F_{P} } \right) $$

(24)

$$ U_{95} = 1.96\surd \left( {SD_{{\hat{y}}}^{2} + RMSE_{{\hat{y}}}^{2} } \right) $$

(25)

where ${F}_{A}$, ${F}_{P}$ and ${F}_{MEAN}$ represent the actual, predicted and mean values of $n$ observations of factor of safety, respectively. Note that, for a prefect model, the value of these indices should be equal to their ideal value as presented in Table 4, which allows us to compare the performance of each model as well as to verify its accuracy and precision.

Table 4 Ideal values of the statistical performance indicators.

5 Results and discussion

PCA-based computational models are developed that can predict the liquefaction behavior of soil with utmost ease and accuracy. A comparative study for the same has been performed to determine the robustness of these hybrid models and their respective results have been presented in this section. The developed computational model uses 180 data cases divided into training and testing data obtained from different sites in Bihar, India. The developed models consider geotechnical parameters which significantly affect the liquefaction resistance of the soil deposits as well as parameters that are related to the intensity of earthquake and ground acceleration as input parameters. The nine input parameters are selected as per the literature observations which includes P, N₆₀, wc/LL, g, ES, TS, ${a}_{max}/g$, and M_W. After the development of these model all the statical performance parameters mentioned in section 4.3 are determined to assess the predictive performance of the models. The best model amongst the three is carefully chosen based on the comparative assessment and their respective predictive power.

5.1 Realizations of computational models

This section has outlined the developments of liquefaction susceptibility in the last 40 decades and has highlighted the previous related research on liquefaction susceptibility considering plasticity and concludes that the plasticity index can confidently classify the behavior of the fine-grained soils as liquefiable or non-liquefiable. The present study focuses on developing a robust computational model for accurate and precise liquefaction classification considering plasticity index as one of the prominent parameters.

The computational model developed and associated with PCA is amongst one of the novel and effective approaches to study liquefaction of cohesive and cohesionless soil deposits. After performing the PCA on the raw datasets, the principal components (PC) were obtained and studied. It was observed that out of nine, six PCs are nearly 97% effective in predicting the factor of safety. Hence, the newly generated PCs were adopted as the input variables for the computational model for predicting soil liquefaction.

For the ANN model, one hidden layer with ten hidden neurons was considered and because of the randomness present in ANN, the numbers of hidden neurons are finalized based on trial-and-error run. The linear function (trainlm) and tangent sigmoid (tansig) function are used as training function and transfer function, respectively. The 'gaussmf’ function with 3 parameters in each function is used as a membership function in ANFIS modelling. In ELM, the sigmoid function is used as an activation function with 10 hidden neurons in the hidden layer. The weight and biases are the only hyperparameters to be set for this model. With the same training data, the ELM model is trained with varying hidden neurons ranges between 5 to 20 and selects the optimum number of hidden neurons using a trial-and-error approach. The final model with 10 hidden neurons is used to construct the predictive model of soil liquefaction.

Note that, to assess the predictive capability of a model, it is reasonable to focus on the outcomes for the testing dataset. The details of statistical indicators for all models are determined which are tabulated in Table 5 and Table 6 or the training and testing dataset, respectively. Based on the results, it was perceived that the PCA-ANN model has achieved the maximum predictive accuracy with RMSE=0.0069, R²=0.9986, VAF=99.8617 and MBE=0 in the training stage, while the same has been drastically decreased in the testing phase (RMSE=0.0886, R²=0.8998, VAF=80.0131, and MBE=0.0339). The performance of the PCA-ANFIS model (RMSE=0.0103, R²=0.9970, VAF=99.6971, and MBE=0) in the training stage is found to be slightly lower than the PCA-ANN model, while higher predicting performance (RMSE=0.0501, R²=0.9769, VAF=93.0074, and MBE=0.0129) is observed in the testing phase compared to PCA-ANN model. In contrast, a balanced result is obtained in PCA-ELM modeling. As can be seen, the accuracy obtained in the training stage (RMSE=0.0.0349, R²=0.9651, VAF=96.5061, and MBE=0) is comparatively lower than PCA-ANN and PCA-ANFIS, however, in the testing phase PCA-ELM outperformed (RMSE=0.0324, R²=0.9724, VAF=96.9180, and MBE=−0.0042) the other two model in respect of each performance parameter.

Table 5 Statical performance detail for the developed hybrid model (Training phase).

Table 6 Statical performance detail for the developed hybrid model (Testing phase).

The other parameters as calculated above also show the dominance of the PCA-ELM model over the other models in the testing phase. Typically, a predictive model with higher accuracy in the testing phase indicates the robustness of the model as well as the predictive ability for a new dataset. From the results furnished in Figure 11 and Figure 12 along with Table 5 and Table 6, it is revealed that the PCA-ANN model achieved the highest predictive accuracy at all levels in the training stage while the accuracy in the testing stage reduced drastically, which indicates the overfitting and local minima trapping issue of PCA-ANN. In contrast, although the PCA-ELM model achieved the lowest accuracy in the training stage, the performance of the same was found to be on the higher side in the testing phase. A detailed review reveals the PCA-ELM model attained slightly higher accuracy in the testing phase compared to the training phase in each case, which not only indicates the robustness of the model but also disposes of the overfitting issue. Therefore, considering the facts and results, it can be established that the PCA-ELM model turns out to be a better predictive model to predict soil liquefaction.

Figure 11

Illustration between actual and predicted FOS for Training data (TR) based on hybrid computational models.

Figure 12

Illustration between actual and predicted FOS for Testing data (TS) based on hybrid computational models.

5.2 Graphical visualization of results and comparative analysis

The visualization of results drawn from the developed models is considered a very effective tool and can be used to quantify the degree of similarity or dissimilarity between them. Such representation of the outcomes permits researchers to explore and explain the results with utmost ease and simplicity. In light of the above, visuals illustration of the results obtained in the study is presented by means of Taylor diagram along with a prominent method of analysis i.e. ‘Rank Analysis’ in the following sub-sections.

5.2a Taylors Diagram: To demonstrate the graphical comparison of the developed hybrid models a mathematical-based plot called “Taylor diagram” was plotted. Taylor`s diagram is designed to indicate the accuracies of various models in a most suitable and compact fashion. It is a summary of a statistical analysis which signifies the fineness of the results and their respective match between the actual data and the data predicted by the developed models. All the statical parameters like correlation coefficient, the root-mean-square-difference, and the ratio of the standard deviations of the two models are indicated by a single point in this illustration. The point that is closer to the ‘reference’ point indicates the perfect predictive model. Figure13(a) and Figure 10(b) present the Taylor diagram for the training and testing dataset respectively. As observed, the position of the PCA-ELM model appears closer to the ‘reference’ point and therefore, can be considered as the best one.

Figure 13

Taylor diagrams exhibiting a statistical comparison of three hybrid model: (a) for training and (b) for testing dataset respectively.

5.2b Rank Analysis: Rank Analysis is one of the most effective and well-organized tools for assessing the overall performance of any computational model with ease and accuracy. During the process of determining the best predictive model, several performance indices are usually evaluated and the conclusions are made based on the comparison amongst the values of each index. This is a complicated process which often leads to an inaccurate conclusion. Therefore, to validate the conclusions based on index parameters, Rank Analysis has been performed. A maximum rank of i, (i is the total number of models under consideration, i.e., 3, in this study) is allotted to the model that has the best value for each index, while, a minimum rank of 1 is allotted to the model that has the worst value for each index, separately for the training and testing dataset. In the subsequent stage, the total performance (i.e. total rank) of all the models is calculated by summing up their ranks of each dataset. And, in the end, the final rank of each model is calculated by summing up the total ranks of the training and testing datasets. Table 7 represents the details of the rank analysis of each proposed model.

Table 7 Rank Analysis of the developed hybrid models.

As can be seen, in the training stage, the PCA-ANN model attained a total rank of 21 and outperformed the other two models by far, while the PCA-ELM model attained a total rank of 24 in the testing phase. However, when the comparisons are made in terms of the final rank obtained by each model, the PCA-ELM model shows the highest predictive accuracy with a final rank of 34 which is followed by PCA-ANFIS and PCA-ANN.

5.3 Discussion of results

The above sub-sections present the results determined for the proposed hybrid computational models in predicting the liquefaction potential of soils. The performance and efficacy of these models are evaluated in meticulously and comprehensively. The performance of developed models was assessed based on several performance indices as indicated above. These parameters calculate the prediction accuracy based on the predicted values of the developed models. Soft computing techniques with their competence in non-linear modelling predict the desired output. This indicates that the developed models consider the minimum and maximum values of input parameters during the course of modelling.

To understand the performance and power of the developed model in a comprehensive manner, eight performance indices, namely, RMSE, R², VAF, PI, NSE, WI, MBE and U95 were determined for training and testing datasets respectively. It is observed that the overall performance of the PCA-ELM model is much better in comparison to the other two models with RMSE=0.0.0349, R²=0.9651, VAF=96.5061, and MBE=0 in the training phase, and RMSE=0.0324, R²=0.9724, VAF=96.9180, and MBE=−0.0042 in the testing phase. From the results, it is evident that there is no uncertainty between the results in the form of any deviation or abnormality in predicted values. Furthermore, to provide a clear perception of the desired output for the proposed model, visual interpretation of results in the form of Taylor diagrams is furnished and discussed. At the end, the performance of the best predictive model is assessed based on a novel approach called ‘Rank Analysis’. It is perceived that the PCA-ELM model attained the maximum final rank of 34 while the PCA-ANN achieved the lowest final rank.

6 Conclusion

Estimating the liquefaction behavior of soil is a vital task in the designing stage of any civil engineering project, which involves tedious and costly experimental processes and calculations. Keeping this in consideration, this research aims to simplify the process of evaluating soil’s liquefaction behavior without conducting the actual field or laboratory test and empirical procedures. The present study proposes and verifies three advanced computational hybrid models (PCA-ANN, PCA-ANFIS, and PCA-ELM) in predicting soil’s liquefaction susceptibility. The main advantages of these proposed models are that they have high generalization capability, less overfitting issue, and very low computational cost. The performance of the proposed models in the testing phase was found to be in good agreement compared to the performance in the training stage. Neither large variations nor unacceptable values have been obtained in the testing phase which satisfies the generalization capability and robustness of the models.

The projected models are the combination of three widely used AI models, namely ANN, ANFIS, and ELM, and dimensionality reduction tool, i.e., PCA. Results of performance indices reveal that the PCA-ELM model has attained the best predictive performance with R²=0.9651, VAF=96.5061, and RMSE=0.0349 in the training phase and R²=0.9724, VAF=96.9180, and RMSE=0.0324 in the testing phase. Also, the rank analysis and Taylor’s diagrams show that the PCA-ELM model outperforms the other models in a comparative study. Therefore, based on the overall performance analysis, the proposed PCA-ELM model can be considered as a new alternative tool to assist geotechnical engineers in the task of assessing the liquefaction potential of soil during the preliminary design stage in any engineering project.