1 Introduction

Materials subjected to high strain loading behave differently compared to the situation of static loading. This sensitivity of materials to the loading rate has created challenges and at the same time opportunities for deeper understanding of strength of materials. Rock blasting for underground excavation, rock drilling, and strain burst of rock are examples of situations in which loading rate plays a role in dictating the material behaviour and the degree of rock fragmentation. Three main methods have been proposed for measuring rock strength under dynamic loading by the International Society for Rock Mechanics (ISRM). These proposed methods include compression test, Brazilian test, and Notched Semi-Circular Bend (NSCB) test. These tests are performed using the Split Hopkinson Pressure Bar (SHPB) to monitor the material behaviour, and measure the loading rate and material strength [1].

A comprehensive review of the SHPB testing of rock has been reported by Xia and Yao [2]. According to their review, John Hopkinson invented the SHPB testing technique in 1872 to investigate the propagation of stress waves along iron wires. Hopkinson’s idea was modified a few times and, finally, Lindholm in 1964 was the person who suggested a testing set up which looks like the system as today’s apparatus [3].

Since the invention of the SHPB apparatus, it has been used extensively to measure material strength under different loading rates. By conducting experimental splitting–tension tests, Hughes et al. [4] concluded that there is a shift of crack initiation time relative to the peak stress. Furthermore, experimental strength versus strain rate data indicates that the dynamic tensile strength of concrete is much higher than the static tensile strength. Dai et al. [5] used SHPB system to measure dynamic compressive and tensile strength of rocks, and to investigate the effect of slenderness of the compressive specimen and friction between the sample and bars on the measured results. Das [6] conducted experimental SHPB tests and presented a rate-dependent constitutive model to predict dynamic behaviour of sandstone under tensile loading. Li et al. [7] performed a set of SHPB experimental tests to study the explosion resistance of high-damping rubber materials. Crack propagation in coal specimens was investigated by Ai et al. [8]. In their work, Brazilian disk coal specimens with vertical and horizontal bedding were studied using the SHPB system. Experimental results suggest that the bedding direction has a major influence on the dynamic mechanical properties such as dynamic tensile strength and strain energy. The path of crack propagation is affected by the bedding plane direction, as well. Feng et al. [9] conducted SHPB tests to study the effect of strain rates on the dynamic flexural properties of rubber concrete. Their results show that adding rubber to the concrete makes the material more flexible and that the crack propagation speed is reduced.

Different constitutive models have been implemented and numerous numerical studies have been performed to investigate the failure and fracture behaviour of brittle materials such as rock and concrete in dynamic loading. Numerical methods including Finite Element Method (FEM), Discrete Element Method (DEM), and hybrid Finite Element and Discrete Element Method (FDEM) have been utilized for the mechanical simulation in the literature. Hughes et al. [4] conducted a comprehensive numerical splitting tensile analysis to investigate the effect of varying the uniaxial tensile strength of concrete on the crack initiation time, stress state, crack growth characteristics, and failure mode. Gálvez et al. [10] used FEM to model the SHPB testing system and to study tensile strength of ceramic materials at high rates of strain. Tedesco et al. [11] used FEM to study direct tension tests of plain concrete in a SHPB system. Their numerical analyses revealed the dynamic states of stress in the specimen prior to failure as well as the mode of failure. Meng and Li [12] investigated the uniformity of axial and radial stress in a specimen under uniaxial compressive loading using the finite-element method. In their work, the role of specimen size and end friction on the stress distribution in the specimen was studied. Zhong et al. [13] investigated the influence of interface friction and specimen configuration on the material dynamic response using SHPB and nonlinear FE analysis.

Discrete element method (DEM) is a powerful technique in numerical modelling of geomaterials [14,15,16]. Cundall [17] developed DEM to simulate the interaction of blocks in a rock mass. Since then, the technique has been employed in the simulation of many geotechnical problems including rock cutting [18, 19], fracture process zone [20], rock spalling [21], rock blasting [22], and rock fracturing [23]. Brara et al. [24] used DEM to study the concrete material tensile behaviour at high strain. Particle Flow Code (PFC) was used by Li et al. [25] to study the effect of impact velocity on the compressive strength of rock. Yin et al. [26] used DEM to study mode I fracture toughness of granite in an SHPB test under different temperature conditions. The results show that DEM is capable of reflecting the mechanical properties of rocks at elevated temperatures. Du et al. [27] used DEM simulation to describe the failure behaviour of hydrostatically confined oblique cylindrical rock specimens under combined compression-shear loading in SHPB test. They investigated the effect of confining pressure and loading rate on the failure mechanism of rock.

Due to rock heterogeneity, the applicability of continuum based models to address rock engineering problems, particularly those that involve dynamic failure of rock, is limited [28]. Munjiza [29] formalized the idea of using a new hybrid finite-discrete element method (FDEM). In the FDEM, each discrete element is discretized into finite elements. In the context of the combined finite-discrete element method, transition from continua to discontinua is done through fracture and fragmentation processes [29]. Rougier et al. [30] used a 3D FDEM to model SHPB experiments on granite material and tried to reproduce the softening behaviour of the specimen. Osthus et al. [31] also used FDEM to simulate the SHPB test. Their work demonstrates good agreement between the FDEM and SHPB experimental tests results.

SHPB test can be simulated using a hybrid-bonded particle–finite element system. In this method, the incident and transmission bars are modelled by finite element, while the brittle material is simulated with a bonded particle system. Bonded Particle Method (BPM) is a simple version of discrete element technique in which the discrete particles are circular in 2D and spherical in 3D [32]. This technique was introduced by Cundall and Strack [33] in their pioneer work in the simulation of soil shear deformation. Fakhimi et al. [34] used the hybrid finite element-bonded particle system to simulate the SHPB test and to evaluate the strength characteristics of sandstone under uniaxial compressive loading. Their work revealed that the experimental strength enhancement cannot be successfully captured if only the inertia of the tested material is considered. For this reason, a micromechanical model was proposed in their work which was capable of reproducing the dynamic results in the SHPB test.

In this study, the CA3 [35] computer program, which is a hybrid-bonded particle-finite-element 3D program, is used to simulate the Brazilian tensile test in an SHPB system. The micromechanical model proposed in [34] is utilized to examine the validity of the model in capturing strength enhancement in tensile failure of rock. The numerical results are presented and compared with the physical tests data reported in the literature.

2 Theoretical Background

A sketch of the SHPB apparatus is shown in Fig. 1. The test begins by shooting the striker bar using a gas gun. The striker bar impacts the incident bar, and as a result, the incident wave is generated. When the incident wave reaches the specimen, it decomposed into the reflected wave and transmitted wave. The combination of incident and reflected waves on one end and transmitted wave on the other end of the specimen causes severe damage to the rock specimen. Through the strain gages installed on the incident and transmission bars, the necessary information about the applied stress on the specimen and the loading rate can be obtained. The length of incident and transmission bars has to be long enough, so that the wave which is propagated along them can be assumed one dimensional.

Fig. 1
figure 1

Schematic view of the split Hopkinson pressure bar apparatus [34]

Full size image

Based on the one-dimensional wave equation for a given point along each of the bars, the strain is given by:

$$\begin{gathered} \varepsilon_{{\text{I}}} = - \frac{1}{c}\dot{u}_{{\text{I}}} \hfill \\ \varepsilon_{{\text{R}}} = \frac{1}{c}\dot{u}_{{\text{R}}} \hfill \\ \varepsilon_{{\text{T}}} = - \frac{1}{c}\dot{u}_{{\text{T}}} \hfill \\ \end{gathered}$$
(1)

where \(\varepsilon\) is the strain, \(\dot{u}\) is the particle velocity, and the subscripts I, R, and T stand for incident, reflected, and transmission bars, respectively. The elastic wave speed along the steel bars can be obtain from the following equation:

$$c = \sqrt {\frac{E}{\rho }}$$
(2)

In Eq. (2), \(E\) is the Young’s modulus and \(\rho\) is the density of the bars.

As shown in Fig. 2, in the case of dynamic equilibrium, the summation of incident and reflected strains (\(\varepsilon_{{\text{I}}}\), \(\varepsilon_{{\text{R}}}\)) must be equal to the transmitted strain (\(\varepsilon_{{\text{T}}}\)) [34]. This ensures that the forces (Fa, Fb) at the two ends of the specimen (points a and b in Fig. 2) are equal. Therefore, we have:

$$\left( {\varepsilon_{{\text{I}}} + \varepsilon_{{\text{R}}} } \right)_{{\text{a}}} = \left( {\varepsilon_{{\text{T}}} } \right)_{{\text{b}}}$$
(3)
Fig. 2
figure 2

Strains of the bars at the two sides of the specimen

Full size image

If the above condition of dynamic equilibrium is satisfied, tensile stress (\(\sigma_{\tau }\)) at the center of the Brazilian specimen can be calculated by the following equation (Fig. 3):

$$\sigma_{\tau } = \frac{2p\left( \tau \right)}{{\pi Dt}}.$$
(4)
Fig. 3
figure 3

Brazilian disk specimen in the SHPB test

Full size image

In Eq. (4), \(\tau\) is the time, D and t are the diameter and thickness of the disk, and \(p\left( \tau \right)\) is the applied load to the specimen which is given by:

$$p\left( \tau \right) = \frac{{F_{{\text{a}}} + F_{{\text{b}}} }}{2} = \frac{EA}{2}\left( {\varepsilon_{{\text{I}}} + \varepsilon_{{\text{R}}} + \varepsilon_{{\text{T}}} } \right)$$
(5a)

Using Eq. (3), Eq. (5a) can be simplified as:

$$p\left( \tau \right) = EA\varepsilon_{{\text{T}}}$$
(5b)

Hughes et al. [4] estimated stress rate (\(\dot{\sigma }\)) and strain rate (\(\dot{\varepsilon }\)) from the following equations:

$$\dot{\sigma } = \frac{{\sigma_{{\tau_{\max } }} }}{{\tau^{\prime}}}$$
(6)

where \(\sigma_{{\tau_{\max } }}\) is the maximum tensile stress at the center of the specimen and \(\tau^{\prime}\) is the time delay between the start and the peak of the transmitted stress wave, and:

$$\dot{\varepsilon } = \frac{{\dot{\sigma }}}{{E_{{\text{S}}} }}$$
(7)

where \(E_{{\text{S}}}\) is the Young’s modulus of the specimen.

An alternative and more accurate method for determination of stress rate is to consider all the stress components (\(\sigma_{x} , \sigma_{y} , \sigma_{z}\)) at the center of the specimen. For the plane stress situation, \(\sigma_{x} = 0\) and \(\sigma_{z}\) stress component can be calculated [4] from the following equation (Fig. 4):

$$\sigma_{z} = - \frac{2P}{{\pi Dt}}\left[ {\frac{{D^{2} }}{{z\left( {D - z} \right)}} - 1} \right]$$
(8a)
Fig. 4
figure 4

Stress components in a Brazilian test

Full size image

Therefore, at the center of the specimen, we have:

$$\sigma_{z} = - \frac{6P}{{\pi Dt}}$$
(8b)
$$\sigma_{y} = \frac{2P}{{\pi Dt}}$$
(9)

The tensile strain at the specimen center is equal to:

$$\varepsilon_{y} = \frac{1}{{E_{{\text{S}}} }}\left( {\sigma_{y} - \nu \sigma_{z} - \nu \sigma_{x} } \right)$$
(10)

Or

$$\varepsilon = \varepsilon_{y} = - \frac{1 + 3\nu }{{E_{{\text{S}}} }}\left[ {\frac{2EA}{{\pi Dt}}\varepsilon_{{\text{T}}} } \right]$$
(11)

where \(\nu\) is the Poisson’s ratio of the rock. By taking derivative from both sides of Eq. (11), the strain rate at the center of the specimen can be obtained using the strain rate in the transmission bar.

3 Micromechanical Model

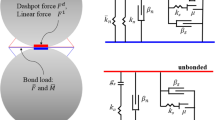
The SHPB test was simulated numerically by the CA3 program [35] which is a hybrid discrete–finite-element code for 3D simulation of geo-materials. The rock was modelled by the bonded particle system [33] which is a discrete element system whose elements are made of spherical particles. The spherical particles interact at the contact points by normal and shear springs. The normal and shear spring constants are shown by kn and ks, respectively. The contact points are assumed to have normal bond (nb) and shear bond (sb) to withstand the deviatoric stresses. A contact point can break in tension or shear if the applied force at the contact point exceeds the normal bond or shear bond. Following the failure of a contact point, it follows the coulomb frictional law with the friction coefficient μ. In summary, five micromechanical parameters are needed for interaction of spherical particles in the CA3 program (Fig. 5).

Fig. 5
figure 5

Micromechanical elements for interaction of two spherical particles

Full size image

While the contact bond model described by the five parameters kn, ks, nb, sb, and μ has been successful in simulating rock strength and its failure in static loading, it has shown difficulty in capturing strength enhancement in dynamic loading; inertia alone could not provide material rate dependency observed in the physical tests. To remedy this problem, Fakhimi et al. [34] proposed a phenomenological micromechanical model in which the contact bond strength increases with the increase in the relative velocity of the particles at the contact point:

$$n_{{\text{b}}} : = n_{{\text{b}}} \times e^{{\left( {\frac{{\beta_{{\text{n}}}^{^{\prime}} }}{{c_{{\text{s}}} }} \times V_{{{\text{nr}}}} } \right)}}$$
(12)
$$s_{{\text{b}}} : = s_{{\text{b}}} \times e^{{\left( {\frac{{\beta_{{\text{s}}}^{^{\prime}} }}{{c_{{\text{s}}} }} \times V_{{{\text{sr}}}} } \right)}}$$
(13)

where \(V_{{{\text{nr}}}} \;{\text{and}} \;V_{{{\text{sr}}}}\) are relative normal and shear velocities of the particles at their contact point, \(\beta_{{\text{n}}}^{^{\prime}} {\text{and}} \beta_{{\text{s}}}^{^{\prime}}\) are two dimensionless micromechanical constants called strength enhancement coefficients, and \(c_{{\text{s}}}\) is the wave speed in the rock specimen defined by:

$$c_{{\text{s}}} = \sqrt {\frac{{E_{{\text{s}}} }}{{\rho_{{\text{s}}} }}}$$
(14)

The sign := in Eqs. (12) and (13) means that the static values of the normal bond and shear bond on the right sides of the equations are replaced with the corresponding dynamic values on the left sides of those expressions in the dynamic analysis. Note that instead of \(\beta_{{\text{n}}}^{^{\prime}} {\text{and}} \beta_{{\text{s}}}^{^{\prime}}\), in the previous publication [34], \(\beta_{{\text{n}}} = \frac{{\beta_{{\text{n}}}^{^{\prime}} }}{{c_{{\text{s}}} }}\) and \(\beta_{{\text{s}}} = \frac{{\beta_{{\text{s}}}^{^{\prime}} }}{{c_{{\text{s}}} }}\) were used which have the dimension of s/m. In the next sections of the paper, the results of numerical and experimental uniaxial compression tests are compared to justify the appropriateness of Eqs. (12) and (13), and then, the model is applied for some tensile Brazilian tests to reveal the usefulness of the model when tensile loading of a rock specimen is involved.

4 Bonded Particle Model

4.1 Calibration

In the bonded particle model, the micromechanical parameters (\(k_{{\text{n}}} ,k_{{\text{s}}} ,n_{{\text{b}}} ,s_{{\text{b}}} \;{\text{and}}\; \mu )\) must be calculated by the calibration procedure. To this end, the macroscopic rock physical properties need to be measured (Table 1), and then, by conducting numerical tests, the micromechanical properties are determined by the procedure such as the one discussed in [36] or by trial and error. Appropriate micro-properties are those that can reproduce the mechanical properties of rock.

Table 1 The macro-mechanical properties of the sandstone
Full size table

Following the procedure discussed in [36], the BPM calibration was successfully performed and the micro properties were obtained (Table 2). The radius of spherical particles in the BPM ranges from 0.15 to 0.225 mm with the average value of 0.1875 mm. Consistent with that for the rock specimen, a density of 2700 kg/m3 was considered for the particles.

Table 2 The micro-mechanical parameters for the numerical specimen
Full size table

The physical dimensions and properties of the Split Hopkinson bars [34] are reported in Table 3. A slenderness ratio \(t/D = 1\) [5] is considered for the specimen in this study. This means that for uniaxial compression and Brazilian tests, the specimen diameter is 12.7 mm (consistent with that in Table 3). Furthermore, the specimen length (in uniaxial compression) and specimen thickness (in Brazilian test) are 12.7 mm.

Table 3 The characteristics of the SHPB apparatus
Full size table

4.2 Calibration Verification

To verify the appropriateness of the calibrated model in mimicking the sandstone behavior, some static uniaxial compressive and Brazilian tests were performed. The prepared specimen for the uniaxial compression test is shown in Fig. 6. The finite-element ring in the middle of the specimen has a very low stiffness and is used to measure the lateral deformation of the bonded particle system. The numerical axial stress–axial strain curve is shown in Fig. 7a. Note that the elastic modulus (27.3 GPa) and the compressive strength (125 MPa) are in good agreement with the physical data reported in Table 1. The numerical lateral deformation data shown in Fig. 7 suggest a Poisson’s ratio of 0.18 which can be compared with that for the sandstone (Table 1).

Fig. 6
figure 6

Numerical uniaxial compression test

Full size image
Fig. 7
figure 7

Numerical uniaxial compression test result: a stress–axial strain curve, b lateral strain–axial strain curve

Full size image

The numerical Brazilian test setup is shown in Fig. 8a, while the load–displacement curve is demonstrated in Fig. 8b. The peak load from this test is 2.7 kN from which the material indirect tensile strength of 10.7 MPa is obtained. This value is closed to the actual tensile strength of the sandstone (Table 1). In summary, the numerical tests results confirm that the macroscopic physical properties of the sandstone can be closely reproduced (Table 4). This suggests that the micromechanical parameters of the bonded particle system (Table 2) are valid.

Fig. 8
figure 8

a Brazilian tensile test setup and b load–displacement curve

Full size image
Table 4 Comparison of the physical properties of sandstone and bonded particle model
Full size table

5 Numerical Simulation Of SHPB System

The incident and transmission bars were assumed to be linear elastic with properties reported in Table 3. The bars were discretized to finite elements. On the other hand, the cylindrical specimen (12.7 mm in length and 12.7 mm in diameter) was assumed to be made of bonded particles. The numerical SHPB test setup for the uniaxial compression test is shown in Fig. 9a. The incident wave as a stress wave is applied to the left end of the incident bar and propagates along the bar until it reaches the specimen. Part of the wave is transmitted through the specimen and the transmission bar, while the other part is reflected back in the incident bar due to the impedance mismatch of the steel bar and the rock specimen. The stress (or strain) at the locations shown in red in Fig. 9 is measured during the numerical test. The test setup in Fig. 9 is similar to that reported in [34] and similar input wave as that in [34] was used in our analysis.

Fig. 9
figure 9

a Uniaxial, b Brazilian, SHPB test setup. Red elements are to show the places where strain gages are mounted in the physical test or stress is measured (recorded) in the numerical tests

Full size image

The numerical test results of the reflected and transmitted waves for three different cases of \(\beta = \beta_{{\text{n}}} = \beta_{{\text{s}}} = 40, 80, 100\; {\text{s}}/{\text{m}}\) (or in dimensionless form: \(\beta^{\prime} = \beta_{{\text{n}}}^{^{\prime}} = \beta_{{\text{s}}}^{^{\prime}} = 12.7 \times 10^{4} , 25.4 \times 10^{4} \;{\text{and}}\; 31.8 \times 10^{4}\)) are shown in Fig. 10. Notice how with a value of \(\beta^{\prime}\) = 25 to 32 \(\times 10^{4}\), not only the peak values but also the shape of the transmitted and reflect experimental waves can be reproduced numerically, suggesting that Eqs. (12) and (13) are capturing the mechanical behavior of the material realistically.

Fig. 10
figure 10

Comparison between the numerical outputs with \(\beta = 40 - 100\frac{{\text{s}}}{{\text{m}}}\left( {\beta^{\prime} = 12.7 \times 10^{4} , 25.4 \times 10^{4} {\text{ and }}\;31.8 \times 10^{4} } \right)\) and the experimental results in uniaxial compressive tests [34]. R and T stand for reflected and transmitted waves, respectively

Full size image

To study the performance of the model in the indirect tensile test, the SHPB test setup of Fig. 9b was used. In a SHPB test, dynamic equilibrium of the specimen needs to be satisfied. To this end, the incident, reflected, and transmitted waves were shifted in time to help to calculate the specimen ends forces (ends a and b in Fig. 11). Time shifting is calculated using the distance of strain gauges from the specimen ends (Fig. 9 and Table 5). To assure dynamic equilibrium, the summation of incident and reflected waves must be equal to the transmitted wave. As it can be realized from Fig. 12, in our numerical simulation, dynamic equilibrium has been achieved reasonably well.

Fig. 11
figure 11

Closed up view of the numerical specimen in the SHPB test

Full size image
Table 5 Time shifting of the waves
Full size table
Fig. 12
figure 12

a Shifted stress data in time to calculate the specimen ends forces; b dynamic equilibrium in the Brazilian test. I, R, and T stand for incident, reflected, and transmitted stress waves, respectively

Full size image

In addition to the incident wave discussed above, two more incident waves were considered in our study to scrutinize the role of strain or stress rate on the strength enhancement. All the three incident waves are depicted in Fig. 13. These incident waves together with different values of micromechanical constants \(\beta_{{\text{n}}}^{^{\prime}} {\text{and}} \beta_{{\text{s}}}^{^{\prime}}\) (Table 6) were used, and several numerical exercised were conducted. Three different methods were applied to measure the strain rate of the specimen. Sample calculation for the incident wave 2 (Fig. 13) with \(\beta_{n}^{^{\prime}} = \beta_{s}^{^{\prime}} = 31.8 \times 10^{4}\) is reported here. In the first method, Eqs. (4) and (5) are used to calculate the stress at the specimen center and, therefore, from Fig. 14a, with the value of the stress rate \(\dot{\sigma } = \frac{{\sigma_{{\tau_{\max } }} }}{{\tau^{\prime}}} = \frac{{33.5 {\text{MPa}}}}{{37 \mu {\text{s}}}} = 905\; {\raise0.7ex\hbox{${{\text{GPa}}}$} \!\mathord{\left/ {\vphantom {{{\text{GPa}}} {\text{s}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{s}}$}},\) the strain rate is calculated as \(\dot{\varepsilon } = \frac{{\dot{\sigma }}}{{E_{{\text{S}}} }} = \frac{905}{{27.3}} = 33.1 \;{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{s}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{s}}$}}.\) In the second method, the slope of linear part of Fig. 14b is utilized to measure the stress rate (1200 GPa/s) and the strain rate is calculated as \(\dot{\varepsilon } = \frac{{\dot{\sigma }}}{{E_{{\text{S}}} }} = \frac{1200}{{27.3}} = 44\; {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{s}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{s}}$}}.\) The strain rate (Fig. 14c) is calculated from Eq. (11) in the third method (\(\dot{\varepsilon } = 65.3 1/{\text{s}})\).

Fig. 13
figure 13

Different incident waves considered in this study

Full size image
Table 6 Six different combinations of \({\varvec{\beta}}_{{\varvec{n}}}^{\user2{^{\prime}}}\) and \({\varvec{\beta}}_{{\varvec{s}}}^{\user2{^{\prime}}}\) coefficients used in this study
Full size table
Fig. 14
figure 14

Estimation of strain rate by a tensile stress in the specimen, b linear method, and c suggested method based on Eq. (11)

Full size image

The micro-cracking processes for the specimen subjected to the wave 2 and with the micro-parameters \(\beta_{{\text{n}}}^{^{\prime}} = 31.8 \times 10^{4} ,\;\beta_{{\text{s}}}^{^{\prime}} = 31.8 \times 10^{4}\) are shown in Fig. 15. Notice that as expected, the cracking are mostly along the specimen diameter and parallel to the direction of applied load. In the same figure, the summation of incident and reflected stress waves is compared with the transmitted stress, confirming that the necessary condition for dynamic equilibrium of the specimen has been fulfilled.

Fig. 15
figure 15

Dynamic equilibrium and micro-cracking processes in the numerical specimen

Full size image

The results of the conducted numerical exercises for different incident waves and different micromechanical constants \(\beta_{{\text{n}}}^{^{\prime}}\) and \(\beta_{{\text{s}}}^{^{\prime}}\) are reported in Table 7. Notice that different approaches used to measure the strain rate do not end up to the same values. Furthermore, as expected, with the increase in the strength enhancement micromechanical constants, greater rock strength is obtained. It is interesting to note that the influence of \(\beta_{{\text{n}}}^{^{\prime}}\) on rock strength seems to be more important compared to that of \(\beta_{{\text{s}}}^{^{\prime}}\) This fact can be realized by comparing the rock strength for the last two tests (under incident wave 1) reported in Table 7. The reason for this observation is that most of the induced micro-cracks at the contact points of the bonded particles are tensile crack (shown in red in Fig. 15) and, therefore, \(\beta_{{\text{n}}}^{^{\prime}}\) which is involved with the tensile strength of contact points should play a more important role compared to the \(\beta_{{\text{s}}}^{^{\prime}}\) parameter. It should be mentioned that the DIF in the last column of Table 7 stands for the dynamic increase factor which is simply the ratio of dynamic strength to the static value.

Table 7 Numerical test results for dynamic increase factor (DIF)
Full size table

The transmitted and reflected wave forms due to the applied incident waves 1, 2, and 3 are shown in Fig. 16. Note that by changing the strength enhancement micromechanical constants, the wave form can be modified. This procedure was followed in the work by Fakhimi et al. [34] for uniaxial compression tests on blue sandstone specimens, and it was shown that the numerical and physical wave forms can be closely matched if the micromechanical constants \(\beta_{{\text{n}}}^{^{\prime}} = \beta_{{\text{s}}}^{^{\prime}} = 12.7 {-} 31.8 ( \times 10^{4} )\) or βn=βs = 40–100 s/m are used (Fig. 10).

Fig. 16
figure 16

The effect of the applied enhancement coefficient β (s/m) (or \(\beta^{\prime}\)) on the response and strength of the specimen using the input corresponding to the incident wave a 1, b 2, and c 3

Full size image

6 Validation

The work in [34] suggests that Eqs. (12) and (13) are capable of reproducing strength enhancement of sandstone under uniaxial compression dynamic loading. To check validity of these equations for tensile loading, the results of our numerical analysis are compared with the physical tests data in Fig. 17. The experimental data are for sandstone specimens and are reported in [6]. The numerical data for \(\beta = \beta_{{\text{n}}} = \beta_{{\text{s}}} = 0\) in Fig. 17 clearly underestimate the physical values, meaning that inertia alone has not been capable enough to capture the material behavior under high strain rate loading. On the other hand, with \(\beta = \beta_{{\text{n}}} = \beta_{{\text{s}}} = 40 - 100\;{\text{s}}/{\text{m}}\), the physical rate dependency of sandstone strength can be reasonably well captured by the proposed phenomenological model. It is interesting to realize that the same values of \(\beta\) were also used in [34] and were able to reproduce the sandstone strength enhancement consistent with the physical observation. In summary, it appears that with the same values of micromechanical strength enhancement parameters, both the compressive and tensile strength of sandstone specimens can be reasonably well simulated.

Fig. 17
figure 17

Comparison of physical and numerical DIF values. The physical data for the sandstone are from [6]

Full size image

DIF values for high strength concrete under tensile and compressive loading were measured and are reported in Fig. 18 [4]. From this figure, it appears that quasi-brittle materials such as concrete demonstrate different rate dependency behaviour under compression and tension; they are more sensitive to the applied strain rate in tension. In Fig. 18, the data points from physical and numerical tests for the blue sandstone are shown as well. The figure clearly indicates that the proposed micromechanical model shows non-identical rate dependency in tension and compression. More physical and numerical data are needed for further elaboration on this finding.

Fig. 18
figure 18

Comparison of DIF values from [4] and our study. The hollow and filled symbols are the results of tensile and compressive loading, respectively

Full size image

Lu et al. [37] performed tensile tests on different rocks and presented a general diagram of the dynamic increase factor versus the loading rate (Fig. 19). The results of the numerical tests of this study for \(\beta = \beta_{{\text{n}}} = \beta_{{\text{s}}} = 40 - 100\;{\text{s}}/{\text{m}}\) are shown in Fig. 19 too. Considering the scatter of the physical tests data, this figure confirms that for the assumed values of the micromechanical enhancement coefficients, the general trend of rock strength rate dependency can be captured with reasonable accuracy within the framework of the proposed micromechanical model.

Fig. 19
figure 19

DIF in tensile tests versus strain rate for different rock specimen [37]. The numerical tests results of this study are shown with dashed lines

Full size image

7 Conclusion

In this investigation, numerical Split Hopkinson pressure bar (SHPB) Brazilian tensile tests under high strain rates were conducted. CA3 which is a hybrid-bonded particle-finite-element program for 3D simulation of geomaterials was used in the study. The rock was modelled by a bonded particle system while the incident and transmitted bars were simulated by finite-element method. The numerical results suggest that a simple contact bond model for the bonded particle system is not able to reproduce reasonable results for the dynamic situation. For this reason, a micromechanical model which allows the bond strength between the particles to increase in proportion to the relative velocity of the particles is suggested. It appears that the proposed model can help to match the numerical reflected and transmitted wave forms with those of the physical data closely. Furthermore, the model can reasonably well reproduce physical dynamic increase factor values reported in the literature.