Improvements to the Prototype Micro-brittle Model of Peridynamics

Abstract

This paper assesses the accuracy and convergence of the bond-based Peridynamic model with brittle failure, known as the prototype micro-brittle (PMB) model. We investigate the discrete equations of this model, suitable for numerical implementation. It is shown that the widely used discretization approach incurs rather large errors. Motivated by this observation, a correction is proposed, which significantly increases the accuracy by cancelling errors associated with the discretization. As an additional result, we derive equations to treat the interactions between differently sized particles, i.e., a non-homogeneous discretization spacing. This presents an important step forward for the applicability of the PMB model to complex geometries, where it is desired to model interesting parts with a fine resolution (small particle spacings) and other parts with a coarse resolution in order to gain numerical efficiency. Validation of the corrected Peridynamic model is performed by comparing longitudinal sound wave propagation velocities with exact theoretical results. We find that the corrected approach correctly reproduces the sound wave velocity, while the original approach severely overestimates this quantity. Additionally, we present simulations for a crack growth problem which can be analytically solved within the framework of Linear Elastic Fracture Mechanics Theory. We find that the corrected Peridynamics model is capable of quantitatively reproducing crack initiation and propagation.

1 Introduction

Peridynamics (PD), originally devised in 1999 by S. A. Silling [1] is is a relatively new approach to solve problems in solid mechanics. In contrast to the most popular numerical methods for solving continuum mechanics problems, namely the Finite Element Method or the Finite Volume Method, PD does not require a topologically connected mesh of elements. Additionally, PD incorporates the description of damage and material failure from the outset. Within the context of mesh-free methods, Peridynamics can be classified as a Total-Lagrangian collocation method with nodal integration. PD features two classes of interaction models, so called bond-based materials and state-based materials. In the bond-based case, interactions exist as spring-like forces between pairs of particles. The interactions only depend on the relative displacement (and potentially its history) of the interacting particle pair and are thus independent of other particles. This is in contrast to the state-based model where pair-wise interactions also depend on the cumulative displacement state of all other particles within the neighborhoods of the two particles which form the pair.

The scope of this paper is to assess the accuracy and convergence of the linear-elastic, bond-based PD model with brittle failure, known as the prototype micro-brittle (PMB) model in the literature. We investigate the discrete equations of this model, suitable for numerical implementation. It is shown that the widely used discretization approach incurs rather large errors. Motivated by this observation, a new discretization scheme is proposed, which significantly increases the numerical accuracy. As an additional result, we derive equations to treat the interactions between differently sized particles, i.e., a non-homogeneous discretization spacing. This presents an important step forward for the applicability of the PMB model to complex geometries, where it is desired to model interesting parts with a fine resolution (small particle spacing) and other parts with a coarse resolution in order to gain numerical efficiency.

We begin by introducing the basic terminology of bond-based PD. In order to be consistent with the major part of the existing PD literature, we use the following symbols: a coordinate in the reference configuration is denoted with ${\boldsymbol X}$, deformed (current) coordinates are denoted by ${\boldsymbol x}$, such that the displacement is given by ${\boldsymbol u} ={\boldsymbol X} -{\boldsymbol x}$. Bold mathematical symbols like the preceding ones denote vectors, while the same mathematical symbol in non-bold font refers to its Euclidean norm, e.g. $x = \vert {\boldsymbol x}\vert$.

The governing equation for a PD continuum is given by

$$\displaystyle{ W({\boldsymbol X},t) = \frac{1} {2}\int \limits _{\mathcal{H}_{\delta }}\omega ({\boldsymbol X}^{{\prime}}-{\boldsymbol X})\,w\left [{\boldsymbol u}({\boldsymbol X}^{{\prime}},t) -{\boldsymbol u}({\boldsymbol X},t),{\boldsymbol X}^{{\prime}}-{\boldsymbol X}\right ]\,\mathrm{d}V _{{\boldsymbol X}^{{\prime}}}, }$$

(1)

where $W({\boldsymbol X},t)$ is the energy density at a point located at ${\boldsymbol X}$ in the reference configuration, and displaced at time t by an amount ${\boldsymbol u}({\boldsymbol X},t)$. $w\left [{\boldsymbol u}({\boldsymbol X}^{{\prime}},t) -{\boldsymbol u}({\boldsymbol X},t)\right ]$ is the micropotential, which describes the strain energy due to the relative displacement of a pair of points located at ${\boldsymbol X}$ and ${\boldsymbol X}^{{\prime}}$. The assumption that the strain energy density depends only on pairs of interacting volume elements leads to the restriction of a fixed Poisson ratio [2] of 1∕3 in 2D (1/4 in 3D). The function $\omega ({\boldsymbol X}^{{\prime}}-{\boldsymbol X})$ is a weight function which modulates the pair interaction strength depending on spatial separation, and $V _{{\boldsymbol X}^{{\prime}}}$ is the volume associated with a point.

Fig. 1

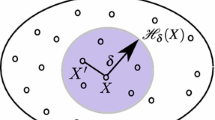
Peridynamics is a method for solving problems in solid mechanics. A body is discretized with a set of integration nodes, which form the reference configuration. Within this reference configuration, each source node interacts with other nodes that are located within a finite horizon $\mathcal{H}_{\delta }$, centered on the source node. The interactions are termed bonds. Peridynamics is a non-local method, because not only nearest, or, adjacent, neighbors are considered. The figure above depicts a single source node i with a horizon given by the radial cutoff δ. Bonds exist between node i and all other nodes j which are inside $\mathcal{H}_{\delta }$. Upon deformation of the bonds, forces are projected along the reference bond vectors $\boldsymbol{\xi }_{\mathit{ij}}$ such that solid material behavior is obtained

Referring to Fig. 1, the integration domain $\mathcal{H}_{\delta }$ is the full disc (full sphere in 3D) around ${\boldsymbol X}$ described by the radial cutoff δ, and is termed the horizon. Within the PD picture, the strain energy is conceptually stored in bonds that are defined between all pairs of points $\left ({\boldsymbol X},{\boldsymbol X}^{{\prime}}\right )$ located within $\mathcal{H}_{\delta }$. Thus, a bond vector in the reference configuration is given by $\boldsymbol{\xi }={\boldsymbol X}^{{\prime}}-{\boldsymbol X}$, and the relative bond displacement due to some deformation at time t is $\boldsymbol{\eta }(t) ={\boldsymbol u}({\boldsymbol X}^{{\prime}},t) -{\boldsymbol u}({\boldsymbol X},t)$. The bond distance vector in the current configuration is therefore written as ${\boldsymbol r}(t) =\boldsymbol{\eta } (t)+\boldsymbol{\xi }$.

With this notation, and dropping the explicit dependence on time, Eq. (1) is written in a more compact form as

$$\displaystyle{ W({\boldsymbol X}) = \frac{1} {2}\int \limits _{\mathcal{H}_{\delta }}\omega (\boldsymbol{\xi })w({\boldsymbol r},\boldsymbol{\xi })\mathrm{d}V _{{\boldsymbol X}^{{\prime}}}, }$$

(2)

The factor of 1∕2 in the above equation arises because each bond is defined twice, once originating at ${\boldsymbol X}$ and pointing to ${\boldsymbol X}^{{\prime}}$, and again via its antisymmetric counterpart pointing from ${\boldsymbol X^{{\prime}}}$ to ${\boldsymbol X}^{{\prime}}$. The forces within the bond-based PD continuum are obtained by taking the derivative of the micropotential with respect to the bond distance vector. The microforce between two bonded points is thus

$$\displaystyle{ {\boldsymbol f}({\boldsymbol r},\boldsymbol{\xi }) = -\frac{\partial w({\boldsymbol r},\boldsymbol{\xi })} {\partial {\boldsymbol r}}, }$$

(3)

yielding the acceleration ${\boldsymbol a}({\boldsymbol X})$ of a point with mass density ρ due to all its neighbors within $\mathcal{H}_{\delta }$:

$$\displaystyle{ \rho {\boldsymbol a}({\boldsymbol X}) =\int \limits _{\mathcal{H}_{\delta }}\omega (\boldsymbol{\xi }){\boldsymbol f}({\boldsymbol r},\boldsymbol{\xi })\mathrm{d}V _{{\boldsymbol X}^{{\prime}}}. }$$

(4)

For implementation in a computer code, Eqs. (2) and (4) need to be discretized. This process requires the division of the continuous body to be simulated into a number of distinct nodes with a given subvolume, subject to the constraint that the sum of all subvolumes equals the total volume of the body. These nodes are termed particles henceforth and the Peridynamic bonds exist between these particles. The most straightforward discretization approach is nodal integration, which is used in almost all publications dealing with PD up to date. Referring to Fig. 1, particle i is connected to all neighbors j within the horizon δ. Dropping the explicit dependence on ${\boldsymbol X}$, the discrete expression for the energy density of a particle i reads:

$$\displaystyle{ W_{i} =\sum \limits _{j\in \mathcal{H}_{\delta }}\omega (\xi _{\mathit{ij}})V _{j}w_{\mathit{ij}}({\boldsymbol r}_{\mathit{ij}},\boldsymbol{\xi }_{\mathit{ij}}), }$$

(5)

and

$$\displaystyle{ {\boldsymbol a}_{i} = \frac{1} {m_{i}}\sum \limits _{j\in \mathcal{H}_{\delta }}\omega (\xi _{\mathit{ij}})V _{i}V _{j}{\boldsymbol f}_{\mathit{ij}}({\boldsymbol r}_{\mathit{ij}},\boldsymbol{\xi }_{\mathit{ij}}). }$$

(6)

These discretizations represent simple Riemann sums, i.e., piecewise constant approximations of the true integrals. The object of this work is to quantify the errors incurred by this approach, but before doing so, we introduce a specific form of the pairwise force function which is compatible with linear elastic continuum behavior and supports a brittle fracture mechanism.

2 Linear Elasticity in Peridynamics

In order to establish the link with linear elasticity, i.e., a Hookean solid, Silling [2] introduced the Prototype Microbrittle Material (PMB) model, with a microforce that depends linearly on the bond stretch $s = \vert \boldsymbol{\xi } +\boldsymbol{\eta } \vert /\vert \boldsymbol{\xi }\vert$. The bond stretch can be thought of as a pairwise one dimensional strain description of the material, and a full strain tensor can indeed be derived from an ensemble of bond stretches [3]. A microforce which is linear in s is therefore in agreement with Hooke’s law.

Here, we employ the following microforce which:

$$\displaystyle{ f(s,\xi ) = -\mathit{cs}/\xi, }$$

(7)

with proportionality constant c. The corresponding micropotential is obtained by integrating the microforce w.r.t. displacement.

$$\displaystyle{ w(s) = -\int f(s,\xi )\mathrm{d}\eta = \frac{1} {2}\mathit{cs}^{2}. }$$

(8)

Note that the expressions for the microforce and the micropotential differ from Silling’s original work by a factor of ξ. This change is purely for consistency reasons, because, in our opinion, the energy density should not contain a reference to a length scale. The modification will be absorbed into the proportionality constant c which is yet to be determined.

The weight function is chosen as a simple step function,

$$\displaystyle{ \omega (\xi _{\mathit{ij}}) = \left \{\begin{array}{@{}l@{\quad }l@{}} 1\quad &\text{if }\xi _{\mathit{ij}} \leq \delta \\ 0\quad &\text{if }\xi _{\mathit{ij}}>\delta \end{array} \right., }$$

(9)

which allows for a compact notation as it can be absorbed into the summation operator of the discretized expressions, i.e., $\sum \limits _{j\in \mathcal{H}_{\delta }}\omega (\xi _{\mathit{ij}}) =\sum \limits _{j\in \mathcal{H}_{\delta }}1$. The effects of using different weight functions have been studied in detail [4]. No significant benefits were observed when using different forms of the weight function for the purpose of simulating structural response problems, however, the weight function affects the dispersion of waves.

Damage and failure are incorporated by keeping track of the history of a bond stretch state. We fail individual bonds by permanently and irreversibly deleting them once they are stretched beyond a critical stretch value s _c .

The remaining constant c is determined by requiring the Peridynamic expression for the energy density, Eq. (2) to be consistent with the result from linear elasticity theory, W _el.:

$$\displaystyle{ \frac{1} {2}\int \limits _{\mathcal{H}_{\delta }}\omega (\xi _{\mathit{ij}})w(s)\mathrm{d}V _{{\boldsymbol X}^{{\prime}}} = W_{\mathit{el}.}, }$$

(10)

In the 3D case of pure dilation or compression, cf. Eq. (32) in the Appendix, we have $W_{\mathit{el}.}^{3D} = 9\mathit{Ks}^{2}/2$, where K is the bulk modulus and s is the strain along any of the Cartesian directions. Note that for isotropic strain field, the strain and the stretch of any bond coincide. Integrating the Peridynamic energy density expression for this strain field in spherical coordinates, we have

$$\displaystyle{ \frac{1} {2}\int \limits _{\mathcal{H}_{\delta }}\omega (\xi _{\mathit{ij}})w(s)\mathrm{d}V = \frac{1} {2}\int \limits _{0}^{\delta }\int \limits _{ 0}^{\pi }\int \limits _{ 0}^{2\pi }\omega (\xi _{\mathit{ ij}})\frac{1} {2}\mathit{cs}^{2}\xi ^{2}\mathrm{d}\xi \sin (\phi )\mathrm{d}\phi \mathrm{d}\theta = \frac{\pi \mathit{cs}^{2}\delta ^{3}} {6}. }$$

(11)

Equating this result with the continuum theory expression for the elastic strain energy, the constant c is obtained as:

$$\displaystyle{ c = \frac{6K} {\pi \delta ^{3}}. }$$

(12)

This approach of determining c is correct for the continuous integral expressions upon which PD theory is based. However, in combination with the discrete expression given by Eq. (5), the results of a numerical computation of the energy density are inaccurate, as exact analytic integration is combined with piecewise constant approximation of the integrals. Furthermore, the analytic integration performed in Eq. (11) assumes that each node is completely contained in the bulk of the body, such that a spherical integration domain exists around the central node. This assumption is certainly not true at the boundaries of the body. The errors incurred by this approach are rather large and, what is worse, does not converge to zero upon increasing δ. This behaviour would be expected, as more as an increase in δ at fixed particle spacing means that more integration nodes are used to sample the field variables. Before we quantify these errors, we introduce an alternative approach to determine c which relies on exact error cancellation such that the energy density is exactly reproduced for a given strain field.

Fig. 2

Piecewise constant approximation of the Peridynamic neighborhood volume. In the original derivation of Peridynamics, the neighborhood boundary $\mathcal{H}_{\delta }$ is defined as a smooth region in space given by the radial cutoff δ. For a piecewise constant approximation of the integrals of the Peridynamic theory suitable for computer implementation, the neighborhood also needs to be defined in a discrete manner: here, we define the piecewise constant neighborhood approximation as the volume of all particles touched by the radial cutoff δ

2.1 An Improved Route for Determining the PMB Proportionality Constant

Instead of deriving the proportionality constant c by exact analytic integration, we propose to use the same integral approximation as is used for discretizing the PD energy density integral or acceleration expression. This means that we use a piecewise constant approximation for Eq. (10), as shown in Fig. 2:

$$\displaystyle{ \frac{1} {2}\int \limits _{\mathcal{H}_{\delta }}w(s)\mathrm{d}V _{{\boldsymbol X}^{{\prime}}} \approx \frac{1} {2}\sum \limits _{j\in \mathcal{H}_{i}}w(s)V _{j} = W_{\mathit{el}.} }$$

(13)

Inserting the micropotential and the 3D pure dilation result for the continuum strain energy density in the above equation, we obtain the proportionality constant as

$$\displaystyle{ c_{i} = \frac{18K} {\sum \limits _{j\in \mathcal{H}_{i}}V _{j}}. }$$

(14)

In this formulation, the dependence of c _i on the horizon δ is now only implicit through the number of particles contributing to the sum in the denominator. A particle at a free surface of a body will have a different number of neighbors compared to a particle in the bulk. This effect is accounted for with our discrete expression for c _i , as opposed to the original expression, Eq. (12), which is only valid for the bulk. This normalization is similar to a Shepard correction of the shape functions encountered in other meshless methods such as Smooth-Particle Hydrodynamics [5, 6], where it restores C ⁰ consistency, i.e., the ability to approximate a constant field. At the same time, it is this local dependence which allows us to easily introduce different spatial resolutions and horizons. It is important at this point to discuss the conservation of momentum. In the original formulation of the PMB model, the proportionality constant c is the same for all interacting particles. Therefore, ${\boldsymbol f}_{\mathit{ij}} = -{\boldsymbol f}_{\mathit{ji}}$, and, as the forces are aligned with the distance vector between particles i and j, both linear and angular momentum are conserved. In the approach proposed here, ${\boldsymbol f}_{\mathit{ij}}$ is not necessarily equal to $-{\boldsymbol f}_{\mathit{ji}}$, as the particle volume sum over $\mathcal{H}_{i}$ is not guaranteed to equal the particle volumes sum over $\mathcal{H}_{j}$. Thus $c_{i}\neq c_{j}$, in general. We therefore enforce symmetry in the following manner:

$$\displaystyle{ c_{\mathit{ij}} = \frac{c_{i} + c_{j}} {2} }$$

(15)

The full expressions for the potential energy of a particle and its acceleration, as required for implementation in a computer code, are then

$$\displaystyle{ E_{i} =\sum \limits _{j\in \mathcal{H}_{i}}V _{i}V _{j}c_{\mathit{ij}}s_{\mathit{ij}}^{2}, }$$

(16)

and

$$\displaystyle{ {\boldsymbol a}_{i} = \frac{1} {m_{i}}\sum \limits _{j\in \mathcal{H}_{i}}V _{i}V _{j}c_{\mathit{ij}}s_{\mathit{ij}} \frac{1} {\xi _{\mathit{ij}}} \frac{{\boldsymbol r}_{\mathit{ij}}} {r_{\mathit{ij}}}. }$$

(17)

We note that the existing body of publications on Peridynamics recognizes that the analytic integration approach for determining the proportionality constant, cf. Eq. (12), is not exact when used together with a discrete set of nodes. Different approaches have been taken to address this problem: Parks et al. [7] describe an algorithm which approximately accounts for the fact that particles near the edge of the horizon have a volume which is only partially within the horizon. Bobaru and Ha [8] describe a similar, yet slightly more accurate algorithm, which rests on the assumption that nodes are placed on quadratic or cubic lattices. Neither of these corrections is able to calculate the sum of volumes enclosed by the horizon exactly. Below, exemplary comparison is made between the algorithm described by Parks et al. and the approach proposed here, which calculates this volume exactly, regardless of whether a regular grid is employed or not.

Fig. 3

This graph shows relative errors of the Peridynamic strain energy density for a pure dilation strain field. Black disks denote results obtained with the original PMB method [2] which uses analytic integration for the determination of the micropotential proportionality constant. Black squares denote the results obtained with the original PMB method and the volume correction approach due to Parks et al. [7]. Red symbols show the results obtained using the here proposed normalization approach for the micropotential constant

3 Results

3.1 Comparison of the Original PMB Model with the Improved Model

This section presents two examples to assess the accuracy of the original PMB model and the normalization procedure proposed in this work. We show that the energy density and speed of sound are exactly reproduced using our method, while the original method yields considerable errors. Finally, we investigate a mode-I crack opening example with our modified PD scheme, where a failure criterion based on the Griffith energy release rate correctly reproduces results from Linear Elasticity Fracture Mechanics Theory.

3.1.1 Energy Density

The ability to reproduce the correct strain energy for a homogeneous deformation is the most basic task any simulation method for solid mechanics should be able to handle with good accuracy. We consider a cube of a material under periodic boundary conditions. The bulk modulus is 1 GPa, and the material is discretized using a cubic lattice with spacing Δ x = 1 m. In order to effect a homogeneous deformation, all directions are scaled using a factor of l = 1.05, leading to volume change of 15.8 %. We measure the Peridynamic strain energy density, W _PD by summing over all bond energies and dividing by the cube volume. The exact strain energy density is calculated using Eq. (32), such that a relative error can be defined:

$$\displaystyle{ \varDelta W = \frac{W_{\mathit{PD}} - W_{\mathit{el}.}^{3D}} {W_{\mathit{el}.}^{3D}} \:. }$$

(18)

Figure 3 shows the relative errors for a range of different horizon cutoffs $\delta \in [2\varDelta x\ldots 6\varDelta x]$, such that the number of particles within the horizon varies from 32 to 924, while the total number of particles in the system is kept constant. This type of convergence is denoted m-convergence in the Peridynamics literature [9]. Two different methods with analytic expressions for the proportionality constant c are compared against the normalization approach proposed here: the original method, cf. Eq. (12), and the volume correction first presented by Parks et al. [7], which approximately accounts for the fact that finite volume region of particles near the edge of the horizon are only partially within within the horizon. We observe that the original approach shows relative errors in excess of 30 %. What is worse, is that the errors do not converge monotonously as one increases the horizon. As more particles are within the horizon, the accuracy of the numerical integration should increase, because the strain field is sampled using more integration points. In this particular case, the horizon is the only discretization resolution variable available due to the scale invariance implied by the absence of free surfaces. The volume correction approach due to Parks et al. fares only slightly better, but generally underestimates the strain energy density. We note that Hu et al. [10] describe similar observations for the strain energy density in bond based Peridynamics with the constant micromodulus function. In contrast, the normalization proposed here reproduces the strain energy density exactly for any micromodulus.

3.1.2 Wave Propagation

The second example investigates the propagation of a pressure pulse. To this end, we consider a bar of size 500 × 4 × 4 m³, discretized using a cubic lattice with Δ x = 1 m. We set K = 1 Pa, $\rho = 1\:\mathrm{kg/m}^{3}$ and δ = 2. 5Δ x. Periodic boundaries are applied along the y- and z-direction in order to suppress free surface effects. The pulse is initiated by a displacement perturbation of Gaussian shape at one end,

$$\displaystyle{ {\boldsymbol x} ={\boldsymbol X} + 0.02\;\mathrm{m}\: \times \:\exp \left (-\frac{{\boldsymbol X} \cdot {\boldsymbol X}} {100\;\mathrm{m}^{2}}\right ){\boldsymbol e}_{x}, }$$

(19)

where ${\boldsymbol e}_{x}$ is the unit vector in the Cartesian x-direction. The simulation is then run until the pressure pulse has reached the right end of the bar. The time-step is set to Δ t = 0. 1 s, which is stable according to CFL analysis. Following [11], the theoretical value for the longitudinal speed of sound is

$$\displaystyle{ c_{l} = \sqrt{\frac{K + \frac{3} {4}G} {\rho }}, }$$

(20)

where $G = 3K(1 - 2\nu )/[2(1+\nu )]$ is the shear modulus, and ν is Poisson’s ratio. As the 3D Peridynamic model under consideration has a fixed Poisson ratio $\nu = 1/4$ [1], we obtain $c_{l} = 4.24\:\mathrm{m/s}$. Figure 4 compares this theoretical prediction with the results of Peridynamics simulation that employ the original analytic integration approach for determining the amplitude constant c of the micropotential, and the normalization approach proposed here. It is evident from this comparison that the original approach severely overestimates the wave propagation speed. This is in agreement with the observation, that the original approach overestimates the energy density, leading to a system which is effectively too stiff. In contrast, the normalization procedure for determining c reproduces the theoretical wave propagation speed very well.

Fig. 4

Sound wave propagation. A horizontally oriented bar of dimensions 500 * 4 * 4 m is loaded using a Gaussian shaped displacement at the left. This initial perturbation causes a Gaussian-shaped pressure pulse to travel to the right at the longitudinal speed of sound. Shown above are theoretical values (vertical dashed lines), where the center of the pressure pulse should be located after elapsed time periods of 50 and 94 s, respectively. The results of the Peridynamics simulations, (i) using the original approach, and (ii) using the normalization for the micropotential amplitude are shown as black and red lines, respectively. We note that the original approach over-predicts the speed of sound by 13 %, while the here proposed normalization approach agrees with the theoretical result within an error margin of less than 1 %

Fig. 5

Generation of non-uniform particle configurations. Top: a volume is meshed using regular tetrahedrons. Form this mesh, a particle configuration is obtained by placing particles at the tetrahedron barycenter, and assigning the tetrahedron’s volume and mass to the particles. Color coding represents volume, increasing from blue to red

To investigate the performance of the normalization approach in the case of non-uniform particle spacing, we now consider a mesh of the same bar as above, which is generated via a stochastic procedure. We use a Delaunay-based meshing algorithm to generate tetrahedral elements. These elements are subsequently replaced by particles. Each particle is assigned the volume of the tetrahedron it replaces. The particle’s mass is obtained from the volume and the mass density, m = Vρ. Figure 5 shows a section of the bar in both the tetrahedron and particle representation. To realize a challenging test, the tetrahedral mesh was intentionally generated such that small angles and large variations in the tetrahedron volumes are achieved. The resulting particle configuration is therefore strongly polydisperse with a ratio of smallest to largest radius of 100. Because no characteristic length-scale (such as the lattice spacing above) is now present, we adjust the Peridynamic horizon for each particle separately, such that the neighborhood contains 30 neighbors. Three different initial tetrahedron meshes of different resolutions are used to conduct a convergence study for our PMB normalization approach. The coarsest mesh contains 17,211 tetrahedrons, and two more finely resolved meshes are obtained by repeated splitting of the elements, such that the finest mesh has 70,381 elements.

Fig. 6

Propagation of a pressure pulse in a long bar which is discretized using irregular particle positions and polydisperse particle size distributions. The geometry and parameters are the same as for Fig. 4, but instead of a regular mesh we employ the discretization approach via a stochastic tetrahedral mesh outlined in Fig. 5. The vertical dashed line indicates the position where the pressure pulse should be, according to the exact wave propagation speed. The Peridynamic simulations show convergence to this exact result upon increasing the number of particles used for discretizing the bar

The results are given in Fig. 6. We observe that pressure pulse is much broader when compared to the results of the uniform particle configuration shown in Fig. 4, and that oscillations travelling behind the main pulse are more pronounced. This is not surprising, as it is well known that wave propagation is affected by discretization effects: partial reflections occur always when a wave is transmitted between regions of space that are discretized using different resolutions. These reflections cause dispersion and reduction in the observed wave speed propagation speed. As the discretization length scale becomes small compared to the wavelength, these effects disappear. We therefore expect convergence of the location of the pressure pulse to its theoretical position at a given time, and return of its shape back to the initial Gaussian shape, as the particles are more finely resolved. The simulation results shown in Fig. 6 support these statements: as the resolution is enhanced, the wave speed tends towards its theoretical value and the pressure pulse shows less oscillations. We therefore conclude that our approach of handling interactions between Peridynamic particles of different size is correct.

3.2 Fracture Energy

Traditionally, continuum mechanics is formulated using a set of partial differential equations which describe temporal and spatial evolution. These equations require smooth solutions with well defined gradients. Therefore, discontinuities in the material, such as cracks, cannot emerge naturally within the solution manifold. In contrast, Peridynamics circumvents this problem by employing an integral description for the evolution equations. Due to its simple form, the PMB model in particular is well suited to model arbitrary crack initiation and propagation phenomena. A number of studies have used the PMB model to study crack propagation speed, crack branching as well as coalescence of individual cracks [12–15]. However, to the best of these authors’ knowledge, no quantitative assessment of the accuracy of PMB simulations relative to analytic solutions for modelling crack initiation and propagation has been published to date. The main reason for this shortcoming is probably the fact that the original formulation of the PMB model using the analytic integration approach for determining the micropotential amplitude inflicts unacceptably large errors already for the energy density. This implies that no quantitatively correct modelling of crack processes could be carried using the original PMB approach. However, the above cited studies demonstrate that the original PMB model is very well suited to qualitatively model complex crack growth phenomena, including the interaction of multiple cracks with each other. In this section, we demonstrate the our normalization approach for determining the micropotential amplitude can be used to quantitatively reproduce analytic solutions obtained from Linear Elastic Fracture Mechanics (LEFM) Theory.

A useful crack propagation theory for numerical simulations must be based on criteria which are independent of the discretization length scale. If length scale-dependent measures such as stress are used instead, no convergence of the loads required to propagate a crack can be achieved because finer resolution always implies a higher stress concentrations. One useful criterion is the Griffith energy release rate, i.e., the energy required to separate a body by generating two free surfaces, one to either side of a crack area. The energy release rate is defined as energy divided by area and is therefore an intensive measure for the resistance of a body against cracking. In the discrete setting of a numerical simulation, the energy release rate incorporates the discretization length scale and thus provides a failure criterion which is independent of discretization. This implies that a crack growth simulation based on such a failure criterion can converge upon discretization refinement. A Peridynamic failure criterion based on the Griffith energy release rate has been first published by Silling and Askari [2]. Here, we roughly follow their approach, but restrict ourselves to plane-strain conditions as LEFM Theory provides useful analytic solutions to compare against in this case.

Because PMB interactions are formulated in terms of bond-wise micropotentials, a failure criterion is required which links the micropotential to the energy release rate. Such an expression can be obtained by considering a pure dilation stretch state of a Peridynamic material and summing the energy stored in all those bonds which cross a hypothetical unit fracture surface. The resulting normalized energy per area, which is a function of the bond stretch and the bulk modulus, can be equated with the energy release rate. From this relation a critical bond stretch can be obtained at which the bond should fail in order to yield a given energy release rate. Figure 7 shows how Peridynamic bonds which are connected to a particular central node interact across a hypothetical fracture surface. An interaction volume is defined as as the spatial volume occupied by these bonds. For a given fracture surface, a manifold of interaction volumes exist. The magnitude of these volumes depends on the distance of the central node away from the fracture surface. Thus, we obtain the Peridynamic energy release rate, G _I, PD , by integrating the product of micropotential and interaction volume over all values of the distance of the central node to the fracture surface. Referring to Fig. 7, this integral is given by:

$$\displaystyle\begin{array}{rcl} G_{I,\mathit{PD}}& =& 2\;\int \limits _{h=0}^{\delta }w(s)\;V _{ c}(h,\delta )\mathrm{d}h \\ & =& 2\;\int \limits _{h=0}^{\delta }\left [\frac{1} {2}\mathit{cs}^{2}\;t\delta ^{2}\arccos \left (\frac{\delta -h} {\delta } \right ) -\left (\delta -h\right )\sqrt{2\,\delta h - h^{2}}\right ]\mathrm{d}h \\ & =& \frac{2} {3}\mathit{cs}^{2}t\delta ^{3}. {}\end{array}$$

(21)

Fig. 7

Peridynamic bond interactions across a hypothetical fracture surface in a 2D plane strain model. Configurations (a) and (b) show two examples for bonds which traverse a hypothetical fracture surface. The total energy which is set free if the hypothetical fracture surface becomes real is the sum of the energies stored in all the bonds between the red and black particle half-spaces. While it is in principle possible to enumerate these bonds and perform an explicit summation, this approach is cumbersome in practice. Instead, we consider the interaction volume to either side of the fracture surface, which is given by the plane thickness multiplied with the circular segment (gray), $V _{c}(h,\delta ) = t\delta ^{2}\arccos \left (\frac{\delta -h} {\delta } \right ) -\left (\delta -h\right )\sqrt{2\,\delta h - h^{2}}$. The energy density of each configuration is given by the product of the the micropotential and the interaction volume. Finally, the energy release rate is obtained by integrating the energy density over all configurations by varying h

Note that the factor of 2 in front of the integral stems from the fact that we have two interaction volumes, one to either side of the hypothetical fracture surface. The factor t above is the thickness of the plane-strain model. Requiring that the Peridynamic energy release rate matches a specified energy release rate, G _I, PD  = G _I we obtain the critical bond stretch at failure as:

$$\displaystyle{ s_{c} = \sqrt{ \frac{3G_{I } } {2\mathit{ct}\delta ^{3}}}. }$$

(22)

A useful test for the above expression is delivered by LEFM Theory, which provides analytic solutions that predict the onset of crack growth for some simple models. One such model is a rectangular patch of an elastic material with an existing sharp crack on one side, which is stretched by applying tractions, see Fig. 8. For prescribed values of the energy release rate and the Young’s modulus, a critical traction is predicted by LEFM Theory when failure should occur by abrupt propagation of the initial crack through the entire patch. For this geometry, the critical traction that leads to failure is known to be [16]

$$\displaystyle{ \sigma _{F} = K_{I} \frac{1} {\sqrt{\pi \,a}}\left (1.12 - 0.23\, \frac{a} {L} + 10.6\, \frac{a^{2}} {L^{2}} - 21.7\, \frac{a^{3}} {L^{3}} + 30.4\, \frac{a^{4}} {L^{4}}\right )^{-1}. }$$

(23)

Fig. 8

Sketch of the geometry used for the crack propagation analysis. A rectangular patch of a linear-elastic material is stretched by applying tractions to the top and bottom side. The patch features an initial crack which serves to effect stress concentration at the crack tip. This geometry and loading scenario can be solved analytically solved for a critical traction which causes the crack to grow using Linear Elastic Fracture Mechanic Theory

Here, σ _F is the traction applied to the top and bottom of the patch which causes the crack to propagate, a is the initial length of the crack, L is the width of the patch, and K _I is the fracture toughness. In plane strain, the fracture toughness can calculated from the Griffith energy release rate G _I , the Young’s modulus of the system, and the Poisson ratio:

$$\displaystyle{ K_{I} = \sqrt{ \frac{G_{I } \,E} {1 -\nu ^{2}}} }$$

(24)

With the values E = 10⁴ Pa, $\nu = 1/3$, $G_{I} = 1\;\mathrm{J}/\mathrm{m}^{2}$, L = 1 m and $a = L/8$, we obtain the failure traction as σ _F  = 146. 9 Pa. This result will serve as the reference solution against which the normalized PMB model presented in this work will be compared. Peridynamic simulations were carried out using a square lattice discretization of this geometry with seven different lattice constants ranging from 0.005 to 0.04 m, resulting in total particle numbers from 1,250 to 80,000. Tractions were realized by gradually applying opposite forces to the top and bottom row of particles, effecting a gradual stretch of the patch. The forces were ramped up in time such that a displacement velocity 10⁴ times slower than the speed of sound in the patch was achieved. Under these conditions, the simulation can be effectively considered quasi-static. Figure 9 shows a snapshot of the simulation with the highest resolution, just before the crack starts to grow. In Fig. 10, the traction values are reported for each resolution, when the crack starts to grow. These data points suggest linear convergence of the critical traction towards the analytic result from above: the extrapolated infinite-resolution simulation value is 144. 4 ± 1. 5 Pa, while the analytic result is 146.9 Pa. The agreement between these results is very good and we attribute the remaining difference to the fact that the initial crack does not, depending on the actual particle spacing, align perfectly with the particles. This observation can also explain the scattering of the data points around the linear fit, because, the simulated initial crack is sometimes shorter or longer by one lattice constant when compared to what it should be. Nevertheless, we note that the simple normalized PMB model is highly successful at predicting the correct stress at the crack tip which causes the crack to grow.

Fig. 9

Peridynamic simulation of crack propagation. Shown is a snapshot of the simulation with the finest resolution. The color-coding represents the yy-component of the stress tensor. The zoomed-in area shows the stress concentration at the crack tip

Fig. 10

Convergence of the critical tractions required to cause abrupt crack propagation. As the particle spacing is reduced, linear convergence towards the exact result σ _F  = 146. 9 PA is observed

4 Discussion

We have shown that the discrete implementations of the original formulation of the Prototype-Microbrittle Model of linear elasticity in Peridynamics suffers from severe inaccuracies. The origin of this deficiency is traced back to the way how the micropotential proportionality constant is derived. The original approach employs exact analytic integration for this quantity. In a numerical implementation, however, field variables depending on the micropotential are evaluated using non-exact integration rule, e.g., piecewise constant integration via the Riemann sum. The inconsistency between these different integration approaches causes inaccuracies. To resolve this problem, we have modified the PMB model such that the same numerical integration rule is used for determining both the micropotential proportionality constant and the field variables. As an additional result, interactions between particles with different sizes and different Peridynamic horizons can be natively treated using our modification. The correctness of the new approach is validated by simulating the propagation of sound waves, where very good agreement with the theoretical prediction is observed. It is instructive to interpret our modification as a normalization procedure, which performs so well because it effects error cancellation. The modified PMB scheme bears strong similarity to other meshless simulation methods such as Smooth-Particle Hydrodynamics, where such a normalization is known as the Shepard correction. Because Peridynamics is most useful for dealing with material discontinuities, we also consider a crack initiation and propagation example. Here, a patch of an elastic material with a pre-existing crack is pulled apart. Once a critical traction is reached, the stress concentration at the existing crack tip cause the crack to grow abruptly and cause complete separation of the patch. Peridynamic simulations of this experiment with the modified PMB model show linear convergence to the exact critical traction as the discretization resolution is enhanced. Much praise has been granted in advance to Peridynamics as a method specifically apt to handle complex crack growth phenomena. The simulations reported herein constitute the the first quantitative demonstration that Peridynamics is indeed able to correctly predict failure in agreement with exact analytic solutions.

Appendix

1.1 Strain Energy Density

In the continuum theory of linear elasticity, the stress tensor $\boldsymbol{\sigma }$ is obtained from a linear relationship between the stiffness tensor ${\boldsymbol C}$ and the strain tensor $\boldsymbol{\epsilon }$,

$$\displaystyle{ \sigma _{\mathit{ij}} = C_{\mathit{ijkl}}\epsilon _{\mathit{kl}}. }$$

(25)

Employing Voigt notation [17] to reduce the dimensionality of the above tensors, the stiffness tensor is expressed as a 6 × 6 matrix in terms of bulk modulus K and Poisson’s ratio ν as,

$$\displaystyle{ {\boldsymbol C} = \frac{3K} {1+\nu } \left [\begin{array}{cccccc} 1-\nu & \nu & \nu & 0 & 0 & 0\\ \nu &1-\nu & \nu & 0 & 0 & 0 \\ \nu & \nu &1-\nu & 0 & 0 & 0 \\ 0 & 0 & 0 &1/2-\nu & 0 & 0 \\ 0 & 0 & 0 & 0 &1/2-\nu & 0 \\ 0 & 0 & 0 & 0 & 0 &1/2-\nu \end{array} \right ], }$$

(26)

and the symmetric stress and strain tensors reduce to vectors with six entries:

$$\displaystyle{ \boldsymbol{\epsilon }= \left [\begin{array}{c} \epsilon _{\mathit{xx}}\\ \epsilon _{\mathit{yy }} \\ \epsilon _{\mathit{zz}}\\ \epsilon _{\mathit{xy }} \\ \epsilon _{\mathit{xz}}\\ \epsilon _{\mathit{zx } } \end{array} \right ];\:\boldsymbol{\sigma }= \left [\begin{array}{c} \sigma _{\mathit{xx}}\\ \sigma _{\mathit{yy }} \\ \sigma _{\mathit{zz}}\\ \sigma _{\mathit{xy }} \\ \sigma _{\mathit{xz}}\\ \sigma _{\mathit{zx } } \end{array} \right ] }$$

(27)

For a general strain state, the energy density is then obtained from a simple dot-product as

$$\displaystyle{ W = \frac{1} {2}\boldsymbol{\sigma } \cdot \boldsymbol{\epsilon }. }$$

(28)

In the following, the volumetric strain energy densities for 3D and 2D plane strain will be derived.

1.2 Pure Dilatation Under Plane Strain Conditions

In the case of pure dilatation by an amount s under plane strain conditions, neither shear nor strain along the z-direction is present. The corresponding strain tensor in Voigt notation is

$$\displaystyle{ \boldsymbol{\epsilon }= \left [\begin{array}{c} s\\ s \\ 0\\ 0 \\ 0\\ 0 \end{array} \right ] }$$

(29)

The plane-strain energy density is therefore

$$\displaystyle{ W_{\mathit{el}.}^{2D} = \frac{1} {2}\boldsymbol{\sigma }\cdot \boldsymbol{\epsilon } = \frac{9\mathit{Ks}^{2}} {4}, }$$

(30)

where the fixed Poisson ratio $\nu = 1/3$, which is applicable to a 2D bond-based Peridynamic model, has been substituted.

1.3 Pure Dilatation in 3D

In the case of 3D pure dilatation no shear is present. Thus,

$$\displaystyle{ \boldsymbol{\epsilon }= \left [\begin{array}{c} s\\ s \\ s\\ 0 \\ 0\\ 0 \end{array} \right ], }$$

(31)

and the volumetric energy density is

$$\displaystyle{ W_{\mathit{el}.}^{3D} = \frac{9\mathit{Ks}^{2}} {2}, }$$

(32)

Note that this result is independent of ν.