A Novel of Low-Frequency Vibration Isolation with High-Static Low-Dynamic Stiffness Characteristic

Abstract

The efficiency of quasi-zero stiffness vibration isolator will decrease when getting overloaded and underloaded. Given the variability of load in general engineering application, this paper aims at presenting a newly designed type of vibration isolation system with positive stiffness in parallel with elements of negative stiffness, which has variable carrying capacity. The vibration isolation performance of system requires overall analysis. Firstly, static analysis is applied to obtain the optimal vibration isolation parameters of the system at the equilibrium position and to verify the high-static low-dynamic stiffness characteristic of the system. Then, the nonlinear dynamic equation of the system is established. Meanwhile, the influence of excitation amplitude on the transmissibility of the system is analyzed under three different conditions by harmonic balance method. Finally, the response curves of the system to sinusoidal excitation and multi-frequency excitation are analyzed by numerical simulation. The result of numerical simulation shows that the vibration isolation system still has good low-frequency vibration isolation characteristics when dealing with different loads. The problem of poor vibration isolation performance of general quasi-zero stiffness isolators under load changes is well solved.

1 Introduction

Low-frequency vibration generally has the characteristics of slow attenuation and long propagation distance, which will bring pose potential hazards to engineering equipment. By introducing negative stiffness element in parallel with positive stiffness element can form an HSLD vibration isolator (Dong et al. 2017, 2018a; Asai et al. 2017), so that the vibration isolation frequency band of the system can extend to low frequency and ultra-low frequency (Sun et al. 2018; Wu et al. 2017; Davis and McDowell 2017). During the past five years, a number of research have been done on the structural design of negative stiffness elements, such as Euler pressure bar (Ding and Chen 2019), torsional spring (Zhou et al. 2015), hydraulic component (Li et al. 2018), cam roller (Sun et al. 2019a) and nonlinear damper (Dong et al. 2018b), and the result reveals that the HSLD vibration isolator has an excellent performance of low-frequency vibration isolation, comparing with the traditional linear isolator. Moreover, the HSLD vibration isolation method has been extended from single degree of freedom (DOF) to multi-DOF vibration isolation (Wang et al. 2017; Li and Xu 2018; Sun et al. 2019b), which show a better effectiveness of low-frequency vibration isolation in multiple directions. However, how to realize the vibration isolation in wider frequency domain on the basis of HSLD is still a problem that domestic and foreign scholars have been committed to solving.

Given the theory that positive and negative stiffness parallel mechanism can cancel each other to form quasi-zero stiffness structure to some extent, Cheng et al. researched the QZS structure of one horizontal tension spring with two vertical positive stiffness springs (Cheng et al. 2017). Xu et al. proposed a QZS vibration isolation system with time-delay control for line spectrum reconstruction of mechanical vibration and noise of underwater vehicles (Li and Xu 2016; Zhou et al. 2018). Wang et al. studied the influence of negative stiffness elements with different structures on low-frequency vibration, such as inclined springs, the buckled beam (Wang et al. 2019a, b; Cai et al. 2020). Valeev studied the solution of QZS problem, from the perspective of manufacturing (Valeev 2018). Jurevicius et al. described the theoretical and experimental investigations of the dynamics of the complex passive low-frequency vibration systems (Jurevicius et al. 2019). Tang et al. studied the impact of shock vibration on QZS isolators (Tang and Brennan 2014). Liu and Yu added an auxiliary system based on the general QZS vibration isolators. The studies show that the addition of the auxiliary system can make the vibration isolator to obtain a wider vibration isolation frequency domain (Liu and Yu 2018).

However, load variation in practical application has a great impact on vibration isolation performance of vibration isolation system (Abolfathi et al. 2015; Ledezma-Ramirez et al. 2015). In general, in parallel vibration isolation system with positive and negative stiffness, elastic elements with positive and negative stiffness need to be adjusted at the same time to achieve variable load, and the structure is complex, which is difficult to realize (Le and Nguyen 2017; Abbasi et al. 2018; Wang et al. 2018). Therefore, since the damage caused by low-frequency vibration to instruments with different loads, and the existing quasi-zero stiffness vibration isolations cannot solve the problem well, a new type of HSLD low-frequency vibration isolation device with variable load has been designed. Low-frequency vibration isolation of different loads can be achieved by adjusting the displacement of inclined guide rod. This paper is organized as follows: In Sect. 2, the static analysis of the model is carried out to show its HSLD characteristics at the static equilibrium position. The HSLD characteristics of the system at the static equilibrium position are studied in Sect. 3. The vibration isolator's transmissibility is given in Sect. 4 to evaluate vibration isolation performance. In Sect. 5, numerical simulation is used to verify the correctness of vibration isolation system theory. Finally, some conclusions are drawn.

2 Description of Low-Frequency Vibration Isolation

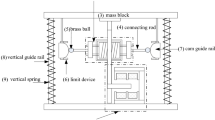
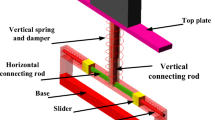
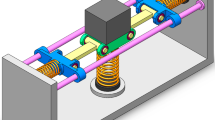
The three-dimensional diagram and structural diagram of the low-frequency vibration isolator are shown in Fig. 1. The isolator is mainly supported by two vertical springs, and two inclined springs are used to reduce the overall stiffness of it in the vertical direction. When bearing a load, the platform will be subjected to the force of vertical spring and inclined spring at the same time. Under this circumstance, this isolator will reach the static equilibrium point when the inclined spring is parallel to the horizontal plane. The correcting element consists of a motor, a screw, a slider, and two pull rods. The inclined spring is installed on the inclined guide bar. The motor rotates to drive the slider to slide up and down in order to pull the bar. The end of the inclined guide rod is connected with the pull rod. Thus, the change in the position of the tie rod makes the end of the guide rod slide inside the slide track, then changing the angle between the inclined spring and the horizontal plane. The change of the included angle causes a corresponding change of the balance position of the structure, as well as the compression amount and bearing capacity of the positive and negative stiffness elastic components at the new-balance position. Given the above premises, by adjusting the inclination angle of the inclined spring, the compression amount of both positive and negative stiffness components can be adjusted. The mechanism of the correcting element is shown in Fig. 2. In Fig. 2a, the vibration isolator is in the overload state at the static equilibrium position, and the negative stiffness components are on horizontal planes. By adjusting the motor, the slider can be moved down, and the pull rod will be pulled to make the angle between the inclined spring and the horizontal plane corresponding to the load. Thus, the load on the object will be in a new-balance position, as shown in Fig. 2b.

Fig. 1

Low-frequency isolator model: (1) loading support; (2) vertical springs; (3) tilt guide bar; (4) tilt springs; (5) telescopic rod; (6) sliding track; (7) slider; (8) leading screw; (9) motor; (10) base

Fig. 2

Low-frequency isolator adjustment schematic: a preadjustment structure diagram, b adjusted structure diagram

3 Static Characteristics of the System

For common quasi-zero stiffness vibration isolation systems, it is necessary to achieve HSLD performance at the equilibrium point, so that the system can meet the low-frequency vibration isolation characteristics. However, for the new vibration isolation system designed in this paper, not only the HSLD characteristic, but also the quasi-zero stiffness characteristic near the equilibrium position should be achieved in order to realize the low-frequency vibration isolation for different loads.

Figure 3 is a schematic diagram of the force exerted on the negative stiffness component of the correcting element. In this diagram, when this part is affected by force F after ignoring the vibration-isolated object, the restoring force in the vertical direction of the system is

Fig. 3

Negative stiffness stress diagram

$$ F = F_{\text{v}} + F_{\text{s}} $$

(1)

$$ F_{\text{v}} = 2k_{\text{v}} (h_{0} + x + y\sin \beta ) $$

(2)

$$ F_{\text{s}} = - \,2k_{\text{s}} x\left( {\frac{{L_{0} }}{{\left( {a - y\cos \beta } \right)^{2} + x^{2} }} - 1} \right) $$

(3)

In the above formulae, F_v and F_S represent the restoring force of vertical spring and the restoring force of inclined spring, respectively; K_v and K_S are the corresponding stiffness of elastic elements with positive and negative stiffness; h₀ represents the distance between the initial position and the initial equilibrium point; θ represents the included angle between the inclined spring and the horizontal plane; a is the horizontal distance between the tilted spring end and the equilibrium point; β is the included angle between the guide track and the horizontal plane; y is the displacement of the end of the inclined guide bar on the guide rail track; L₀ is the original length of the inclined spring; and x is the displacement at the equilibrium point. The above parameters are used to define the following dimensionless parameters:

$$ \hat{F}_{\text{s}} = \frac{{F_{\text{s}} }}{{k_{\text{s}} L_{0} }},\hat{F} = \frac{F}{{k_{\text{v}} L_{0} }} - \frac{{h_{0} }}{{L_{0} }},\hat{x} = \frac{x}{{L_{0} }},\hat{a} = \frac{a}{{L_{0} }},\hat{y} = \frac{y}{{L_{0} }},\alpha = \frac{{k_{\text{s}} }}{{k_{\text{v}} }} $$

Thus, the equation between the dimensionless restoring force and displacement of the system should be:

$$ \hat{F} = 2(\hat{x} + \hat{y}\sin \beta ) - 2\alpha \hat{x}\left[ {\frac{1}{{\sqrt {(\hat{a} - \hat{y}\cos \beta )^{2} + \hat{x}^{2} } }} - 1} \right] $$

(4)

By taking the derivative of Eq. (4), the dimensionless stiffness and displacement of the system can be expressed as

$$ \hat{K} = 2 - 2\alpha \left\{ {\frac{{\left( {\hat{a} - \hat{y}\cos \beta } \right)^{2} }}{{\left[ {\left( {\hat{a} - \hat{y}\cos \beta } \right)^{2} + \hat{x}^{2} } \right]^{{\frac{3}{2}}} }} - 1} \right\} $$

(5)

If the guide bar is not adjusted at this time, the displacement of the guide bar y is 0, and the relationship between stiffness ratio α and initial included angle θ would be expressed as:

$$ \alpha = \frac{{k_{\text{s}} }}{{k_{\text{v}} }} = \frac{a}{{(L_{0} - a)}} = \frac{\cos \theta }{(1 - \cos \theta )} $$

(6)

According to Fig. 4, the range where the dimensionless force is 0 at the equilibrium position is affected by the initial angle, and the included angle is either too small or too large to increase the instability of the system. Meanwhile, it can be found from Fig. 5 that when the initial included angle ranges from 20° to 80°, the average variation of stiffness near the equilibrium position would decrease at first and then increase.

Fig. 4

Dimensionless force–displacement curve of the system at different initial angles

Fig. 5

Dimensionless stiffness-displacement curve of the system at different initial angles

Therefore, in the range between 20° and 80°, there is a minimum value of the average variation of stiffness near the range of the equilibrium position. At this point, vibration isolation efficiency is the best.

The stiffness ratio changes with the initial included angle. On this premise, Eq. (6) should be substituted into Eq. (5). Meanwhile, the researcher set x as quantitative and a as independent variable in order to obtain diagram describing the relationship between geometric parameters and dimensionless stiffness. When the dimensionless stiffness K attains the minimum value, the corresponding point a will attain the minimum value of the average change. At this equilibrium position, the isolation frequency domain reaches the widest state, as shown in Fig. 6.

Fig. 6

Optimal structural parameter ratio

As shown in Fig. 7, by comparing this point with neighboring points, it is verified that this point is the optimal equilibrium point before the position of the guide rod is adjusted. Moreover, this point should be regarded as the midpoint of the up-down displacement of the guide rod in order to reduce the variation range of the overall stiffness of the system.

Fig. 7

Dimensionless force–displacement comparison chart

Given the geometric operation relation shown in Fig. 3, it can be calculated that:

$$ a = y\cos \beta + a_{0} $$

(7)

$$ L = \sqrt {\left( {h_{0} - y\sin \beta } \right)^{2} + \left( {y\cos \beta + a_{0} } \right)^{2} } $$

(8)

$$ \cos \theta = a/L $$

(9)

According to the above formulae, corresponding relation of $\hat{a}$, α, θ can be found out. As shown in Fig. 8, the change of the slide track inclination angle β has less effect on stiffness ratio α, whereas the change of the guide bar displacement y has more effect on stiffness ratio α. When the guide bar displacement y changes within the range of ± 0.1, the initial included angle between the inclined spring and the horizontal plane decreases gradually with the increase of y. Thus, at the same time, the stiffness ratio required a will also increase.

Fig. 8

Changes in the parameters at the initial point

When $\hat{y}\cos \beta \ne 0$, as β has less effect on stiffness ratio a, β is set 45° considering the convenience of subsequent calculation. The value of a and h₀ is defined as unit length, and the corresponding initial angle θ ranges from 43° to 52°; thus, the variation range of the slide rail displacement y will be − 0.11 to 0.08. In the process of sliding track displacement change, it can be found out that the dimensionless force ranges from − 0.11 to 0.08, according to Fig. 9. Moreover, when x > 0.33, the displacement of the guide bar has merely no effect on the dimensionless force. Meanwhile, the dimensionless stiffness–displacement curve of the whole system can be obtained from Fig. 10. At this point, the variation range of the stiffness of the system at the equilibrium position is − 0.48 to 0.48. Therefore, from the perspective of statics, this structure reduces the overall stiffness of the vibration isolation system and correspondingly changes the bearing capacity when the system reaches a new equilibrium position, so as to realize low-frequency vibration isolation for different loads.

Fig. 9

Dimensionless force–displacement when the slider is displaced

Fig. 10

Dimensionless stiffness–displacement when the slider is displaced

4 Dynamic Analysis

4.1 Dynamic Equations of the Isolator

In ideal condition, the parallel isolator with positive and negative stiffness will maintain static equilibrium state when x = 0 and y = 0. At this point, the dynamic stiffness of vibration isolation system is relatively low; thus, it is very sensitive to the change of load. In actual conditions, it is inevitable that the load will be too heavy or too light. When this happens, the isolated object will not be at the equilibrium position in the static equilibrium state, which means the vibration isolation system cannot meet vibration isolation in the ideal state. Assuming that the vibration isolation system is in overload state, then there is supposed to be:

$$ \text{KL}\left[ {(k_{1} ( \pm \hat{u}_{0} ) + k_{3} ( \pm \hat{u}_{0} )^{3} )} \right] = \text{mg} $$

(10)

In the above formula, $\hat{u}_{0}$ represents the deviation from the desired position, and mg represents the difference between the overload mass and the ideal mass. If harmonic force excitation $f = F\cos \left( {\omega t} \right)$ and harmonic displacement excitation $e = Z\cos \left( {\omega t} \right)$ are applied in the system, the nonlinear motion differential equation of the system can be formed as:

$$ mv^{\prime\prime} + cv^{\prime} + F_{1} - \text{mg} = F\cos (\omega t) $$

(11)

$$ mz^{\prime\prime} + cz^{\prime} + F_{2} - \text{mg} = m\omega^{2} Z\cos (\omega t) $$

(12)

In the above two formulae, v is the displacement with the equilibrium position in overload condition as the origin of coordinates, and z = v − e stands for the relative displacement between the isolated object and the base under the harmonic excitation condition. Using Taylor’s expansion, Eqs. (4) and (5) can be approximated to:

$$ k_{1} = 1 - \alpha \left( {\frac{1}{{\hat{a} - \hat{y}\cos \beta }} - 1} \right) $$

(13)

$$ k_{3} = \frac{\alpha }{{2(\hat{a} - \hat{y}\cos \beta )^{3} }} $$

(14)

$$ \hat{y} = \frac{{\hat{u}_{0} }}{\sin \beta } $$

(15)

At this time, the dynamic model of the system can be constructed by applying excitation force to the vibration isolator and the object:

$$ mL_{0} \frac{{\text{d}^{2} \hat{x}}}{{\text{d}t^{2} }} + cL_{0} \frac{{\text{d}\hat{x}}}{{\text{d}t}} + k_{s} L_{0} \left[ {(k_{1} (\hat{x} \pm \hat{u}_{0} ) + k_{3} (\hat{x} \pm \hat{u}_{0} )^{3} )} \right] = \upsilon \rho \cos (\omega t) + \text{mg} $$

(16)

In the above formula, ρ is the amplitude of harmonic excitation. If the input is harmonic force excitation, then $\upsilon = 1$, $\rho = \hat{F}$. If the input is harmonic displacement excitation, then $\upsilon = \varOmega^{2}$, $\rho = \hat{Z}$. The following dimensionless parameters are applied:

$\omega_{n} = \sqrt {k/m}$, $\varOmega { = }\omega /\omega_{\text{n}}$, $\tau { = }\omega_{\text{n}} t$, $\xi {\text{ = c}}/(2m\omega_{n} )$, $\hat{\delta }{ = }\delta /L_{0}$, $\hat{y} = y/L_{0}$, $\hat{F}{ = }F/k_{v} L_{0}$, $\hat{Z} = Z/L_{0}$

By substituting Eqs. (14) and (15) into Eq. (16), the dimensionless differential equation of the system can be formed as:

$$ \hat{v}^{\prime\prime} + 2\xi \hat{v}^{\prime} + 3k_{3} \hat{u}_{0}^{2} \hat{v} \pm 3k_{3} \hat{u}_{0} \hat{v}^{2} + k_{3} \hat{v}^{3} = \hat{F}\cos (\varOmega \tau ) $$

(17)

$$ \hat{z}^{\prime\prime} + 2\xi \hat{z}^{\prime} + 3k_{3} \hat{u}_{0}^{2} \hat{z} \pm 3k_{3} \hat{u}_{0} \hat{z}^{2} + k_{3} \hat{z}^{3} = \varOmega^{2} \hat{Z}\cos (\varOmega \tau ) $$

(18)

The above two formulae can be transformed as:

$$ \hat{n}^{\prime\prime} + 2\xi \hat{n}^{\prime} + 3k_{3} \hat{u}_{0}^{2} \hat{n} \pm 3k_{3} \hat{u}_{0} \hat{n}^{2} + k_{3} \hat{n}^{3} = \upsilon \rho \cos (\varOmega \tau ) $$

(19)

The nonlinear dynamic equation expressed in Eq. (19) is Duffing equation, which is transformed into Duffing equation under asymmetric excitation through parameter transformation. Then the equation $\hat{q} = {\hat{\text{z}}} \pm m_{2} /(3k_{3} )$ is formed and substituted into Eq. (19). Thus, the differential equation of the system can be converted into:

$$ \hat{q}^{\prime\prime} + 2\xi \hat{q}^{\prime} + k_{3} \hat{q}^{3} = \pm \,b_{0} + \upsilon \rho \cos (\varOmega \tau ) $$

(20)

In the above formula, $b_{0} = k_{3} \hat{u}_{0}^{3}$. Thus, the steady-state response solution is solved by applying harmonic balance method. Meanwhile, the higher-grade harmonic term is omit, the constant term and the coefficient of the harmonic terms of each grade are turned to zero, and then the system’s steady-state response solution is obtained. The solution only consists of constant term $A_{0}$, harmonic amplitude term $A_{1}$ and phase difference φ:

$$ {\text{k}}_{3} A_{0}^{3} + \frac{3}{2}k_{3} A_{0} A_{1}^{2} = \pm \,k_{3} $$

(21)

$$ - \,\varOmega^{2} A_{1} + 3k_{3} A_{0} A_{1} + \frac{3}{4}k_{3} A_{1}^{3} = \upsilon \rho \cos (\varphi ) $$

(22)

$$ - 2\xi \varOmega A_{1} = \upsilon \rho \sin (\varphi ) $$

(23)

After obtaining quadratic sum, the researcher gets a polynomial with only the constant term $A_{0}$:

$$ \begin{aligned} & 25{\text{k}}_{3}^{3} A_{0}^{9} - 20{\text{k}}_{3}^{2} \varOmega^{2} A_{0}^{7} - 15{\text{k}}_{3}^{3} b_{0} A_{0}^{6} + 4b_{0} \varOmega^{2} \left( {\varOmega^{2} + 4\xi^{2} } \right)A_{0}^{5} + 16{\text{k}}_{3} b_{0} \varOmega^{2} A_{0}^{4} \\ & \quad + \,3b_{0} (2\upsilon^{2} \rho^{2} - 3{\text{n}}_{0}^{2} )A_{0}^{3} - 4{\text{n}}\varOmega^{2} (\varOmega^{2} + 4\xi^{2} )A_{0}^{2} + 4b_{0}^{2} \varOmega^{2} A_{0} - b_{0}^{3} = 0 \\ \end{aligned} $$

(24)

At this point, Ω has two solutions with positive value. By calculating, the researcher obtains the extremum of the constant term $A_{0}^{f}$ and its corresponding resonant frequency $\varOmega_{0}^{f}$ of the system at the harmonic force excitement condition:

$$ \begin{aligned} & - 20k_{3}^{3} \xi^{2} A_{0}^{f9} + 8k_{3}^{2} \xi^{4} A_{0}^{f7} + 36k_{3}^{2} b_{0} \xi^{2} A_{0}^{f9} - 3k_{3}^{2} \rho^{2} A_{0}^{f5} - 16k_{3} b_{0} \xi^{4} A_{0}^{f4} \\ & \quad - 36k_{3} b_{0}^{2} \xi^{2} A_{0}^{f3} + 3k_{3} b_{0} \rho^{2} A_{0}^{f2} + 8k_{3}^{2} \xi^{4} A_{0}^{f} - 4b_{0}^{3} \xi^{2} = 0 \\ \end{aligned} $$

(25)

$$ \varOmega_{0}^{f} = \sqrt {\frac{{5k_{3}^{2} A_{0}^{f6} - 4k_{3} \xi^{2} A_{0}^{f4} - 4k_{3} b_{0} A_{0}^{f3} + 4b_{0} \xi^{2} A_{0}^{f} - b_{0}^{2} }}{{2k_{3} A_{0}^{f4} - 2b_{0} A_{0}^{f} }}} $$

(26)

In a similar way, the extremum of the constant term $A_{1}^{\text{z}}$ and its corresponding resonant frequency $\varOmega_{1}^{\text{z}}$ in the system at the harmonic displacement excitement condition:

$$ \begin{aligned} & ( - 75k_{3}^{4} \rho^{2} - 80k_{3}^{3} \xi^{2} )A_{0}^{z9} + 32k_{3}^{2} \xi^{4} A_{0}^{z7} + (45k_{3}^{3} b_{0} \rho^{2} + 144k_{3} b_{0} \xi^{2} )A_{0}^{z6} - 64k_{3} b_{0} \xi^{4} A_{0}^{z4} \\ & \quad + (27k_{3}^{2} b_{0}^{2} \rho^{2} - 48k_{3} b_{0}^{2} \xi^{2} )A_{0}^{z3} + 32b_{0}^{2} \xi^{4} A_{0}^{z} + (3k_{3} b_{0}^{3} \rho^{2} - 16b_{0}^{3} \xi^{2} ) = 0 \\ \end{aligned} $$

(27)

$$ \varOmega_{0}^{z} = \sqrt {\frac{{5k_{3}^{2} A_{0}^{z6} - 4k_{3} \xi^{2} A_{0}^{z4} - 4k_{3} b_{0} A_{0}^{z3} + 4b_{0} \xi^{2} A_{0}^{z} - b_{0}^{2} }}{{2k_{3} A_{0}^{z4} + 3k_{3} \rho^{2} A_{0}^{z2} - 2b_{0} A_{0}^{z} }}} $$

(28)

The above process is mainly the calculation under the overload state. When an underload state occurs, ${\hat{\text{u}}}_{0}$ should be transformed into $- \hat{u}_{0}$ in order to obtain steady-state response solution of the system under two harmonic excitation conditions.

4.2 Definition of the Transmissibility

Force transmissibility and displacement transmissibility are the main parameters to measure the performance of vibration isolators. When the harmonic force excitation is applied, dimensionless force ${\hat{\text{f}}}_{\text{m}}$ on low-frequency vibration isolation system consists of dimensionless damping force $\hat{f}_{{\text{md}}}$ and dimensionless elastic force $\hat{f}_{{\text{me}}}$. Thus, it is obvious that:

$$ {\hat{\text{f}}}_{\text{m}} = \hat{f}_{{\text{md}}} + \hat{f}_{{\text{me}}} $$

(29)

Speaking of dimensionless force applied to the system under overload state can be attained:

$$ \hat{q} = \hat{z} \pm m_{2} /(3k_{3}^{\prime } ) = A_{0}^{\prime } + A_{1} \cos (\varOmega \tau + \varphi ) $$

(30)

In the above two equations:

$$ A_{0}^{'} { = }A_{0} \mp {\hat{\text{u}}}_{0} $$

(31)

By substituting Eq. (31) into Eq. (30), the expressions of dimensionless damping force $\hat{f}_{{\text{md}}}$ and dimensionless elastic force $\hat{f}_{{\text{me}}}$ can be attained:

$$ \hat{f}_{{\text{md}}} = 2\xi \hat{q}^{\prime} = - \hat{F}_{{\text{md}}} \sin (\varOmega \tau + \varphi ) $$

(32)

$$ \hat{f}_{{\text{me}}} = b_{1} \hat{v} \pm b_{2} \hat{v}^{2} + k_{3}^{'} \hat{v}^{3} = \hat{F}_{{\text{me}0}} + \hat{F}_{{\text{me}1}} \cos (\varOmega \tau + \varphi ) $$

(33)

In the above two expressions, the amplitude of the dimensionless damping force can be expressed as $\hat{F}_{{\text{md}}} = 2\xi \varOmega A_{1}$. Meanwhile, constant term $\hat{F}_{{\text{me}0}}$ and the amplitude of the harmonic term $\hat{F}_{{\text{me}1}}$ should be expressed as:

$$ \hat{F}_{{\text{me}0}} = b_{1} A_{0}^{'} \pm b_{2} A_{0}^{'2} \pm \frac{{b_{2} A_{1}^{2} }}{2} + k_{3}^{'} A_{0}^{'3} + \frac{3}{2}k_{3}^{'} A_{0}^{'} A_{1}^{2} $$

(34)

$$ \hat{F}_{{\text{me}1}} = b_{1} A_{1} \pm 2b_{2} A_{0}^{'} A_{1} + \frac{3}{4}k_{3}^{'} A_{1}^{3} + 3k_{3}^{'} A_{0}^{'} A_{1} $$

(35)

According to the concept of force transmissibility, the parts in the system dynamics can be ignored in both the overload state and new equilibrium state, so:

$$ T_{\text{f}} = \frac{{\hat{F}_{t} }}{\rho } = \frac{{\sqrt {(2\xi \varOmega A_{1} )^{2} + \hat{F}^{2}_{{\text{me}1}} } }}{\rho } $$

(36)

The force transmissibility of ideal system and equivalent linear system is, respectively:

$$ T_{\text{f}} = \frac{{\sqrt {(k_{3}^{'} A_{1}^{3} )^{2} + \left( {2\xi \varOmega A_{1} } \right)^{2} } }}{\rho } $$

(37)

$$ T_{\text{l}} = \sqrt {\frac{{1 + (2\xi \varOmega )^{2} }}{{(1 - \varOmega^{2} )^{2} + (2\xi \varOmega )^{2} }}} $$

(38)

In a similar way, when the harmonic displacement excitation is applied to a vibration-isolated item in overload state, the dimensionless absolute displacement of the system is:

$$ \hat{q} = \hat{e} \mp \hat{u}_{0} + \hat{z} = A_{0} \mp \hat{u}_{0} + A_{1} \cos (\varOmega \tau + \varphi ) + \rho \cos (\varOmega \tau ) $$

(39)

Thus, the absolute displacement transmissibility of the system should be:

$$ T_{z} = \frac{{\left| {\hat{q}} \right|}}{\rho } = \frac{{\left| {A_{0} \mp \hat{u}_{0} } \right| + \sqrt {A_{1}^{2} + \rho^{2} + 2A_{1} \rho \cos (\varphi )} }}{\rho } $$

(40)

In the above two equations, cos(φ) can be solved through Eq. (22).

The force and displacement transmissibility of the low-frequency vibration isolation system in the ideal state, the overload state, and the new equilibrium state, and the force and displacement transmissibility of the equivalent linear system in such conditions are shown in Figs. 11 and 12. It can be seen from the two sets of figures that the low-frequency vibration isolation system in the three states is better than the equivalent linear system in terms of the amplitude and frequency excitation. And with the excitation amplitude increases, the system stiffness of the overload state and the new equilibrium state will constantly change, showing successively as linear, gradually soft, gradually soft then gradually hard, gradually hard.

Fig. 11

Force transmissibility curve under harmonic excitation conditions

Fig. 12

Displacement transmissibility curve under harmonic displacement excitation conditions

Under the condition of harmonic force excitation, the magnitude relationship of the force transmissibility of the low-frequency vibration isolation system in three states will change in different frequency ranges. When the excitation frequency is in low-frequency band, force transmissibility in ideal state is lower than that in new equilibrium state, whereas the latter is lower than the force transmissibility in overload state. In other words, the vibration efficiency of the system in the ideal and the new equilibrium state is better than that in the overload state. In addition, when the excitation amplitude increases and reaches the high-frequency band, the force transfer rate of the low-frequency vibration isolation system under the three states will tend to be consistent with each other.

In the condition of harmonic displacement excitation, the characteristic changes caused by the excitation amplitude on the system are basically the same as the force transfer rate curve, so only the differences are analyzed. As shown in Fig. 12, the maximum absolute displacement transfer rate of the low-frequency vibration isolation system in the overload state is always greater than that in the new equilibrium state and ideal state. Meanwhile, with the continuous increase of excitation amplitude, the absolute displacement transfer rate of the low-frequency vibration isolation system in the above three states will tend toward infinity.

5 Numerical Simulation

5.1 Simulation of General Equivalent Systems Under Basic Excitation

In this section, there are mainly two kinds of simulation: the first one is the simulation of the general equivalent systems; the second one is the simulation of the low-frequency vibration isolation system in the ideal state, overload state, and new equilibrium state. Given the fact that the newly designed vibration isolator is mainly used in low-frequency vibration isolation, this section focuses on the simulation of the system under sinusoidal excitation vibration condition and random multi-frequency excitation vibration condition.

The parameters used in this simulation are shown in Table 1. A sinusoidal excitation is applied in the general equivalent system. The amplitude of the excitation is 4 mm, while the corresponding frequency is 5 Hz. In Fig. 13, once the system is just sinusoidal excited, its response amplitude increases rapidly and arrives at a stable point when t = 2 s. At this point, the response amplitude is more than twice that of the excitation amplitude. When random multi-frequency excitation is applied, the amplitude of the response curve of the general equivalent linear system is always larger than the excitation amplitude. Thus, it can be seen that the nonnegative stiffness system cannot isolate low-frequency vibration efficiently. Meanwhile, the system can magnify the input excitation amplitude and then aggravate the damage to the item.

Table 1 Parameters and simulation values of vibration isolation system

Fig. 13

Input and output curves of equivalent linear system under sinusoidal excitation and multi-frequency excitation

5.2 Simulation of Low-Frequency Vibration Isolation System Under Basic Excitation

Given the fact that a general equivalent system cannot isolate low-frequency vibrations, a negative stiffness element is added into the system in order to study its response curve in the single-frequency sinusoidal excitation state and random multi-frequency excitation state.

5.3 Simulation of System in Ideal Condition

In Fig. 14, once a sinusoidal excitation is applied in the vibration system, the response amplitude of the system will suddenly increase and be unstable in a short period. However, after 1 s, the response amplitude of the system enters the stable output stage. Meanwhile, the response amplitude is much smaller than the sinusoidal excitation amplitude. When facing with a random multi-frequency excitation, the parallel vibration isolation system with positive and negative stiffness can reduce the input amplitude. At the same time, the range of the response amplitude is approximately ± 5 mm, which shows relatively high vibration isolation ability. Based on the above figures, it is proved that parallel isolator with positive and negative stiffness can effectively isolate vibration when low-frequency excitation is applied in ideal condition.

Fig. 14

Input and output curves of ideal system under sinusoidal excitation and multi-frequency excitation

5.4 Simulation of System in Overload Condition

It is necessary to study the response curve after excitation is applied in the overload condition. Keeping the parameters of the system unchanged, the researcher let $\hat{u}_{0} = 0.05$ and then attain the following response amplitude of the system:

According to Fig. 15, the overload system has higher response amplitude comparing to the ideal system and shows instability. When random multi-frequency excitation is applied, the amplitude of the curve of the system changes sharply, especially near the peaks. At this point, the response amplitude changes rapidly. To sum up, although the overload system cannot realize the same vibration isolation efficiency and performance when these two kinds of excitation are applied, it still has low-frequency vibration isolation ability comparing to the general equivalent linear system.

Fig. 15

Input and output curves of overload system under sinusoidal excitation and multi-frequency excitation

5.5 Simulation of System in New Equilibrium Condition

The inclined guide bar of the newly designed parallel vibration isolator is adjusted with positive and negative stiffness in order to suit the load in overload condition and then attain the response curve of the system, which is shown in Fig. 16.

Fig. 16

Input and output curves of new-balance system under sinusoidal excitation and multi-frequency excitation

At this point, the response curve of the newly designed system is basically the same with that of the overload system. However, the response amplitude of the new system is better than that of the overload system. Therefore, the newly designed parallel vibration isolator is feasible to conduct effective vibration isolation in case of variable loads.

6 Conclusion

This paper concentrates on the design and analysis of a new type of vibration isolation system with positive stiffness in parallel with elements of negative stiffness, which is structurally simple. Unlike previous studies, this paper focuses on the analysis of the effect of different loads and the implementation of an adjustment mechanism to handle a wide range of loads. To ensure zero stiffness under imperfect stiffness matching, a lateral adjustment mechanism is also proposed. Meanwhile, as the bearing capacity of the system can be adjusted according to the load, the system can be widely applied in engineering practices. Here is the conclusion of this paper:

• (1) According to the static analysis, before the guide bar is adjusted, the system’s range of vibration isolation becomes the widest when the structural parameter ratio $\hat{a} = 0.66$ is in the static equilibrium position. However, after the guide bar is adjusted according to the variation of the load, the system still has relatively low natural frequency in the new equilibrium position.

• (2) According to the dynamic analysis, the increase of excitation amplitude can change the stiffness characteristic of the transmissibility of the low-frequency vibration isolation system. When the transmissibility of the system has no unstable solution, which means the excitation amplitude is relatively low, the isolation efficiency of the low-frequency vibration isolator in the ideal state is always higher than that in the new equilibrium state as well as in the overload state.

• (3) Whenever exposed to sinusoidal or multi-frequency excitations, the newly designed system in this paper can always isolate low-frequency vibration effectively in the ideal state. Although the isolation efficiency of the system in the new equilibrium state is lower comparing to that in the ideal state, it is still higher than that in the overload state.