1 Introduction

Delay in MEMS devices is a very common phenomenon, which can be introduced into the system unavoidably or by design. In electrostatic MEMS resonators, many inherent system delays can be introduced through actuators, filters, processor dynamics, and feedback measurements. The desire for improved device features, such as low-cost, low-voltage, high quality factor, and improved reliability have motivated great interest to understand the impact of delays on MEMS. On the other hand, feedback controllers have been deliberately used to stabilize the response, compensate for system parameter changes, and generally to enhance the resonator performance [1–5]. Another challenge is to drive electrostatic MEMS resonators at a sharp response while preventing them from collapse due to pull-in.

Several works have been presented recently on time delay feedback controllers. Pyragas [6] presented a delayed feedback controller to stabilize the unstable periodic orbits of a chaotic system. In another work [7], the improved Pyragas controller was shown to stabilize a torsion-free unstable periodic orbit, which conventional methods cannot do. Masoud et al. [8] demonstrated a delayed controller to reduce pendulation on small ship-mounted telescopic cranes. Nayfeh and Nayfeh [9] utilized time-delay acceleration feedback to enhance stability for controlling machine-tool chatter.

The delayed time in the Pyragas method [6] has been investigated in the case of half of the period of the unstable periodic orbit [10]. Generally, the delayed signal can be displacement, velocity [11], and acceleration [9]. With proper designed time delay, a delayed feedback controller has been proven to stabilize systems including Atomic Force Microscopes (AFM) [12] and magneto-elastic beam systems [13].

Hu et al. [14] studied the dynamics of a controlled Duffing oscillator with delayed feedback with respect to the time delay. Wang and Hu [15] showed that the trivial equilibrium undergoes stability switches as delay time varies. Global stability of displacement feedback [16] and local stability for velocity feedback [17] were studied by using the method of multiple scales and the shooting technique. Also, the analysis on a Single Degree-Of-Freedom (SDOF) system with negative velocity feedback near trivial equilibrium was presented [17], considering quadratic and cubic nonlinearity [18]. It was found that delayed velocity feedback can extend significantly the working frequency ranges of the system compared to with delayed displacement feedback [19]. Delayed feedback of such type was applied to the linear dynamical systems showing that the controller cannot stabilize the unstable motion under some conditions [20].

There are other methods for solving nonlinear dynamic problems with delays, such as energy analysis, which is a combination of the method of Lyapunov’s function and the averaging technique, and pseudo-oscillator analysis, which is based on the idea of an oscillator slightly perturbed. Both of them are limited to undamped oscillators, meaning the damping factor is just perturbed into the system [21].

El-Bassiouny [22, 23] presented the analysis of primary and subharmonic resonances of a cantilever beam under time-delay feedback control using averaging and multiple scales methods. A number of important analytical conclusions were reached on the effect of feedback gains, the time-delay, the coefficient of cubic terms, and external excitations [24].

Qaroush and Daqaq [25] utilized a delayed feedback controller to reduce the vibrations of a macrocantilever beam and a microcantilever sensor. A modified multiple scales perturbation approach demonstrating large time-delay feedback gain was presented. This approach could lead to output peak frequencies not necessarily close to the natural frequency of the system [26]. Erneux [27] investigated strongly nonlinear crane oscillations and lasers subject to optoelectronic feedback by the method of averaging, considering weak damping and weak feedback. Rand et al. [28] utilized a two-variable expansion perturbation scheme to analyze Van der Pol–Hopf bifurcation with delayed feedback. Hamdi and Belhaq [29] investigated nontrivial solutions and bistability in the Duffing oscillator with a delayed displacement feedback via the perturbation method. Nayfeh et al. [30] discussed dynamics of machining using quadratic and cubic stiffness of machine tools, which accounts for the regenerative effects.

In previous works, Younis and Nayfeh [31] used a perturbation method to analytically describe dynamics of a resonant microbeam excited electrically. Alsaleem and Younis [32] investigated theoretically the dynamics of delayed feedback MEMS resonators using a shooting technique and basin-of-attraction analysis and verified their results experimentally [33–35].

In this paper, we use a SDOF model to investigate the dynamics of electrostatic MEMS resonators with the delayed feedback controller of Pyragas [1]. A perturbation method, the method of multiple scales, is used to present analytically the impact on the dynamics of the system by the control gain and delay. The results are then verified using long-time integration, shooting techniques, and basin-of-attraction analysis.

2 Problem formulations

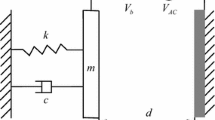
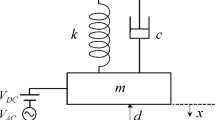
We consider a nonlinear single degree-of-freedom model (Fig. 1) actuated by an electric load composed of a DC component V DC and an AC harmonic component V AC subjected to a viscous damping of coefficient c. The equation of motion governing the behavior of the resonator under a delay feedback controller can be expressed as

(1)

In Eq. (1), ε 0 is the dielectric constant of air, A is the electrode area, \(\hat{\varOmega}\) is the AC excitation frequency, \(\dot{\hat{x}}_{d} = \dot{\hat{x}}(\hat{t} - \hat{\tau} )\), where \(\hat{\tau}\) is the time delay, and G is the amplitude of the velocity feedback controller with unit V s/m (Fig. 2).

Fig. 1
figure 1

A single degree-of-freedom model of an electrically actuated resonator

Full size image
Fig. 2
figure 2

Schematic for the delayed feedback controller

Full size image

Next, we normalize Eq. (1) by introducing the nondimensional variables

$$ t = \frac{\hat{t}}{T^{*}},\qquad \tau= \frac{\hat{\tau}}{T^{*}},\qquad x = \frac {\hat{x}}{d},\qquad x_{d} = \frac{\hat{x}_{d}}{d} $$
(2)

where \(T^{*} = \sqrt{m/k}\).

Substituting Eq. (2) into Eq. (1) yields

$$ \ddot{x} + 2\zeta\dot{x} + x = P\frac{[V_{\mathrm{DC}} + V_{\mathrm{AC}}\cos\varOmega t + G_{V}(\dot{x}_{d} - \dot{x})]^{2}}{(1 - x)^{2}} $$
(3)

where \(\zeta= \frac{c}{2\sqrt{mk}}\); \(\varOmega= \hat{\varOmega} T^{*}\); \(P = \frac{\varepsilon _{0}A}{2kd^{3}}\); \(G_{V} = G\frac{d}{T^{*}}\).

The nondimensional deflection x can be decomposed as

$$ x = \delta+ u $$
(4)

where δ is the equilibrium position of the oscillator normalized to d, due to V DC and u is the dynamic amplitude of the motion. Substituting Eq. (4) into Eq. (3) yields the governing equation of motion

(5)

3 Linearization analysis

Next, we present the linear stability analysis showing vibration characteristics in the neighborhood of the equilibrium position. First, we derive the equilibrium equation of the system in Eq. (5). We set all time-dependent terms equal to zero including the dynamic amplitude u, which leads to

$$ \delta= \frac{PV_{\mathrm{DC}}^{2}}{(1 - \delta)^{2}} $$
(6)

Equation (6) gives the upper mass position under V DC only. Then we set V AC=0 in Eq. (5). Assuming G V is small compared to V DC, \(\frac{1}{(1 - \delta- u)^{2}}\) in the right-hand side of Eq. (5) can be expanded using a Taylor’s series up to the third-order term as

(7)

Also, \([V_{\mathrm{DC}} + G_{V}(\dot{u}_{d} - \dot{u})]^{2}\) can be expanded as

$$ \bigl[V_{\mathrm{DC}} + G_{V}(\dot{u}_{d} - \dot{u}) \bigr]^{2} = V_{\mathrm{DC}}^{2} + 2V_{\mathrm{DC}}G_{V}( \dot{u}_{d} - \dot{u}) + \cdots $$
(8)

Plugging the linear terms of the right-hand side of Eqs. (7) and (8) into Eq. (5), we obtain

(9)

Dropping the equilibrium equation (6) from Eq. (9) and rearranging yield

$$ \ddot{u} + 2\zeta_{0}\dot{u} - 2g\dot{u}_{d} + \omega ^{2}u = 0 $$
(10)

where

$$ \zeta_{0} = \zeta+ g;\quad g = \frac{PV_{\mathrm{DC}}G_{V}}{(1 - \delta)^{2}};\qquad \omega^{2} = 1 - \frac{2PV_{\mathrm{DC}}^{2}}{(1 - \delta)^{3}} $$
(11)

One can see that ω is the nondimensional natural frequency of the parallel-plate resonator after applying V DC. The parameter g can be viewed as the nondimensional controller gain.

We should mention that ζ 0 in Eq. (10) cannot be considered as an effective damping ratio. Instead, the term \(2\zeta_{0}\dot{u} - 2g\dot{u}_{d}\) in Eq. (10) is the complete damping term, because the time delay here is taken into consideration. We need further analysis to uncover the effective damping ratio, which will be presented in Sect. 4.

To study the stability of Eq. (10) we assume the candidate solution to be of the form [36]

$$ u = u_{0}e^{\lambda t} $$
(12)

where u 0 is the amplitude of the solution and λ is the eigenvalue. Note that the delay term is u d =u 0 e λ(t−τ). Plugging Eq. (12) into Eq. (10) yields the following characteristic equation:

$$ \lambda^{2} + \bigl(2\zeta_{0} - 2ge^{ - \lambda\tau} \bigr) \lambda+ \omega^{2} = 0 $$
(13)

Given λ is complex of the form λ=χ+iρ, where χ is the growth or decay rate and ρ is the frequency of oscillations, we split the characteristic equation into real and imaginary parts as

(14)
(15)

If the real part of the eigenvalue χ is negative, the solution is bounded (stable response) as time increases. On the other hand, a positive real part of the eigenvalue leads to unbounded solution (unstable response). Thus, a zero real part of the eigenvalue, or pure imaginary eigenvalue, defines the linear stability boundary. To solve for this boundary condition, we set χ=0 in Eq. (14) and Eq. (15) and obtain

(16)
(17)

Canceling g, we obtain

$$ - \rho^{2} - 2\frac{\zeta\sin(\rho\tau)}{1 - \cos(\rho\tau )}\rho+ \omega^{2} = 0 $$
(18)

We can use Eq. (18) to find the system’s free oscillation frequency ρ for a specific time delay τ. After obtaining the frequency ρ, we use Eq. (17) to find the effective boundary gain g.

A case study of the capacitive device of [32, 33] of properties of Table 1 is considered. Figure 3 shows the stability chart of this system as a function of the nondimensional effective gain g and time delay τ. In Fig. 3, we obviously can see the periodicity. In one period, for example, the interval between 0 and T, the boundary gain g tends toward negative infinity when τ goes to 0 or T, which can also be seen analytically. When τ=0 or T, Eq. (16) yields the unique solution ρ=ω, which leads to g having no bounded solution in Eq. (17) because 1−cos(ρτ) is zero.

Fig. 3
figure 3

Stability chart within four periods (T=2π/ω) for V AC=1 V, V DC=40.2 V

Full size image
Table 1 The parameters of a parallel-plate capacitor [32, 33]
Full size table

Also, in Fig. 3, we can see the least possible negative gain to perturb the system into an unstable state is g=−0.0013 at τ=0.5T. In fact, for τ=0.5T, we have the solutions of Eq. (16) and Eq. (17) as ρ=ω,ζ+2g=0. It indicates that the system needs

$$ \zeta+ 2g > 0 $$
(19)

to reach the stable state.

4 Perturbation analysis

In this section, we use a perturbation method, the method of multiple scales [37], to investigate analytically the response of the resonator for a small motion around the equilibrium position. Therefore, we consider the system is perturbed generating small response u=O(ε). Considering the terms V DC=O(1), V AC=O(ε 3), G V =O(ε 2) and expanding the electrodynamic term on the right-hand side of Eq. (5) up to the third order, we obtain

(20)

Substituting Eqs. (20) and (7) into Eq. (5) yields

(21)

Scaling the damping and dropping the higher order terms beyond the third order in Eq. (21) and the equilibrium terms of Eq. (6) yields the nondimensional equation of motion below

(22)

where

(23)

and the rest of parameters are as defined in Eq. (11).

Since the primary resonance is investigated here, we describe the nearness of the excitation frequency Ω to the natural frequency ω by introducing detuning parameter σ defined by

$$ \varOmega= \omega+ \varepsilon^{2}\sigma $$
(24)

Substituting Eq. (24) into Eq. (22), we obtain

(25)

The equation above is based on considering the system with small damping, weak quadratic and cubic nonlinearities, weak feedback and soft excitation.

Assuming u is a function of ε and time t, we expand u as

(26)

where T 0=t, T 1=εt, T 2=ε 2 t.

As will be proven latter, u is independent of T 1. Therefore the delay term can be written as [36]

(27)

which upon expansion for small ε 2 τ near T 2 becomes

(28)

Next, we use the following differentiation notations:

(29)

Plugging Eqs. (26)–(29) into Eq. (25) yields

(30)

Spiriting terms of equal power in ε up to the third order gives

(31)
(32)
(33)

The solution of Eq. (31) is written as

$$ u_{1}(T_{0},T_{1},T_{2}) = A(T_{1},T_{2})e^{i\omega T_{0}} + \bar{A}(T_{1},T_{2})e^{ - i\omega T_{0}} $$
(34)

Note that |A| is the amplitude of u 1. Substituting Eq. (34) into Eq. (32), we obtain

(35)

where cc represents the complex conjugate terms.

To eliminate the secular term in Eq. (35), we need

$$ - 2i\omega\frac{\partial A}{\partial T_{1}} = 0 $$
(36)

which indicates that A is the function of T 2 only, A=A(T 2).

Thus, Eq. (35) becomes

$$ D_{0}^{2}u_{2} + \omega^{2}u_{2} = - \alpha_{q} \bigl(A^{2}e^{i2\omega T_{0}} + A\bar{A} \bigr) + \mathrm{cc} $$
(37)

Solving the differential equation above with respect to u 2 yields

$$ u_{2}(T_{0},T_{2}) = \frac{\alpha_{q}A^{2}}{3\omega^{2}}e^{i2\omega T_{0}} - \frac{\alpha _{q}A\bar{A}}{\omega^{2}} + \mathrm{cc} $$
(38)

Plugging Eqs. (34) and (38) into Eq. (33) yields

(39)

To eliminate secular terms in Eq. (39), we set

(40)

Writing A in the polar form [37] in terms of amplitude a and phase β, \(A \equiv \frac{1}{2}a(T_{2})e^{i\beta(T_{2})}\), yields

(41)

Separating the imaginary and real terms gives

(42)
(43)

Next, we introduce a new dependent variable φ=σT 2−β in order to transform Eqs. (42) and (43) into an autonomous system of equations as below

(44)
(45)

Note that a′, φ′ are derivatives with respect to T 2.

For steady-state response, a′=0, φ′=0, which yields the following modulation equations governing the amplitude a and phase φ of the dynamic response:

(46)
(47)

After eliminating variable φ, the steady-state frequency response equation can be expressed as

(48)

For each σ representing the deviation from natural frequency of the excitation frequency, we can obtain the resonance amplitude a by solving Eq. (48). There is possibility that a has three nontrivial solutions, corresponding to the softening or hardening nonlinear behavior. From Eq. (48), we can also notice that gsin(ωτ) accompanies σ, and plays the role of changing the effective excitation frequency. Similarly, −g+gcos(ωτ) plays the role of changing the damping ratio, since it accompanies ζ. Accordingly, an effective damping ratio ζ e can be defined as shown below:

$$ \zeta_{e} = \zeta+ g - g\cos(\omega\tau) $$
(49)

Commonly, \(\tau= \frac{T_{r}}{2} = \frac{\pi}{\omega}\) is considered [10] (T r is the period of the response signal), which according to Eq. (49) gives ζ e =|2g+ζ|.

In addition, the solution for u can be expressed as

(50)

Note that a and φ are both constant for steady-state response.

5 Small vibrations and the effective damping ratio

Next, we present stability analysis based on the derived equations from the perturbation analysis of Sect. 4. For convenience, we introduce F 1(a,φ) and F 2(a,φ) to be the right-hand side of Eqs. (44) and (45), respectively. Therefore, Eqs. (44) and (45) are rewritten as

$$ a' = F_{1}(a,\varphi) $$
(51)
$$ a\varphi' = F_{2}(a,\varphi) $$
(52)

For periodic solutions, a and phase φ need to be constants, (a 0,φ 0). To determine the stability of the periodic solution, we evaluate the Jacobian matrix of Eqs. (51) and (52) at (a 0,φ 0) as

$$ J(a_{0}, \varphi_{0}) = \left\vert \begin{array}{c@{\quad}c} \frac{\partial F_{1}}{\partial a} \big|_{(a_{0},\varphi_{0})} & \frac{\partial F_{1}}{\partial\varphi} \big|_{(a_{0},\varphi_{0})} \\ \noalign{\vspace*{6pt}} \frac{1}{a_{0}}\frac{\partial F_{2}}{\partial a} \big|_{(a_{0},\varphi_{0})} & \frac{1}{a_{0}}\frac{\partial F_{2}}{\partial\varphi} \big|_{(a_{0},\varphi_{0})} \end{array} \right\vert $$
(53)

To obtain the eigenvalues, the determinant is set equal to zero

$$ \bigl \vert \lambda I - J(a_{0}, \varphi_{0}) \bigr \vert = 0 $$
(54)

where λ is the eigenvalue and I is the identity matrix. Solving Eq. (54) yields

$$ \lambda^{2} + R\lambda+ S = 0 $$
(55)

where

(56)
(57)

We recall that the coefficient of λ in Eq. (55) is equal to the negative sum of the roots, as R=−(λ 1+λ 2); and the constant term is equal to the multiplication of the roots, as S=λ 1×λ 2. Therefore, the stability condition requires that the real parts of the roots to be negative. Thus, the stability conditions are

$$ R = g - g\cos(\omega\tau) + \zeta> 0 $$
(58)
(59)

These conditions should be satisfied in order to yield periodic solutions.

Note that the stability condition of Eq. (58) is the same as requiring positive effective damping for the system (see Eq. (49)).

When substituting the values of Table 1 into Eq. (59) we find that α c <0, \(\alpha _{q}^{2} > 0\) and terms including \(a_{0}^{2}\) dominate over σ+gsin(ωτ). Thus, S is actually always positive. Hence, one concludes that Eq. (58) determines the system’s stability status alone. For \(\tau= \frac{T_{r}}{2} \approx\frac{\pi}{\omega}\), Eq. (58) becomes

$$ \zeta+ 2g > 0 $$
(60)

or ζ e >0. It is worth to note that Eq. (60) is the same as Eq. (19).

Next, we prove that ζ e represents the effective damping of the system. Toward this, the frequency responses of two different systems with the same ζ e are shown; one is controlled and the other is uncontrolled (Fig. 4). It turns out that they display the same frequency responses. Note that direct long-time integration (LTI) of Eq. (1) is shown as discrete points in Fig. 4, compared to the analytical solution from the method of multiple scales (MMS). One can see they have good agreement. Furthermore, if we generate the time responses at a certain frequency, they appear the same as well (Fig. 5). One can see in Fig. 5 that the two resonators, one controlled and the other uncontrolled, with the same effective damping ratio under the excitation frequency 183 Hz yield the same time responses.

Fig. 4
figure 4

Frequency response curves for τ=T/2 and V AC=3.8 V. (a) ζ=ζ e =0.0103, g=0; (b) ζ=0.0027, ζ e =0.0103, g=0.0038 (triangles: LTI; solid line: MMS)

Full size image
Fig. 5
figure 5

Time response via LTI at f=183 Hz for (a) G=0, ζ=ζ e =0.0103 and (b) G=200 V s/m, ζ=0.0027, ζ e =0.0103

Full size image

Practically, one can utilize the controller gain g and time delay τ to control the system damping ratio as needed. For a specified τ, g relates to ζ e linearly. Figure 6 shows the relation for a system with ζ=0.0103.

Fig. 6
figure 6

The effective damping ratio versus the controller gain for τ=T/2

Full size image

In Fig. 7, we show a 3-D plot for the variation of ζ e as a function of g and τ. One we can see that the variation of ζ e versus g becomes most significant when the time delay is half the period (τ/T=1/2) or odd times the period (such as τ/T=1.5).

Fig. 7
figure 7

A 3-D plot for the effective damping ratio versus the controller gain g and the time delay ratio τ/T

Full size image

6 Moderate and relatively large vibrations

In this section, we investigate the effect of the positive gain on the oscillation response of the capacitive resonator of Table 1. The focus here is on moderate-large response, such that the theories of perturbation and shooting apply. First, we show results for an uncontrolled case with two AC voltage loads. Figure 8 compares the frequency response curve (normalized response versus frequency) obtained by MMS to that of LTI of Eq. (1). For the long-time integration, we use the solution from the previous step as the initial condition to the next frequency step in the frequency sweeping. As shown, the agreement is good among the results of the two approaches.

Fig. 8
figure 8

Frequency-response curves obtained using LTI and MMS for G=0 and V DC=40.2 V for various values of V AC in V

Full size image

Figure 9 demonstrates the effect of applying a control gain via both LTI and MMS. It shows that applying a positive control gain instead of lowering the excitation voltage keeps the bandwidth barely changed, while reducing the response amplitude. Therefore, one can use this feature to enlarge the response bandwidth as shown in Fig. 10. This figure compares the uncontrolled response of the resonator to the controlled response using higher values of V AC such that both actuation methods yield the same maximum response amplitude. Clearly, the controlled response has much larger bandwidth. This remarkable result can be of great advantage in MEMS for sensing and energy-harvesting applications, where both sharp response and wide bandwidth are desirable.

Fig. 9
figure 9

Frequency-response curves obtained using LTI and MMS for V AC=3.8 V, V DC=40.2 V, and τ=T/2. The unit of G is V s/m

Full size image
Fig. 10
figure 10

Frequency-response curves obtained using LTI and MMS for V DC=40.2 V, and τ=T/2. The unit of V AC is V and the unit of G is V s/m

Full size image

Figure 11 shows the positive gain effect on the time response of the resonator in Fig. 11. The output signal has much smaller overshoot and needs less settling time, although rising time increases under the positive gain controller. From perspective of effective damping ratio, positive gain increases the damping ratio, since ζ e =ζ+2g. Thus, ζ e is the analytical explanation for the velocity time-delay feedback controller’s effects on capacitive resonators.

Fig. 11
figure 11

Time responses of (a) uncontrolled system and (b) controlled system, both of which with positive gain G=35 V s/m and τ=T/2 (excitation frequency f=188.9 Hz, V AC=5 V, V DC=40.2 V)

Full size image

Next, we investigate the influence of applying a negative gain on the velocity time-delayed feedback controller. Figure 12 shows both numerical LTI results and MMS analytical solution of the frequency response curves for various negative gains from 0–50 V s/m. This range is equivalent to g from 0 to −0.0001, which lies inside the stability regime according to Fig. 3. One can see good agreement among all the results. Generally, for a specified excitation frequency, increasing the amplitude of the negative gain G causes the displacement x to increase. In addition, the frequency response curve exhibits nonlinear softening behavior, (Fig. 12), if the negative gain is large enough, such as G=−50 V s/m. Therefore, it can be viewed as an alternative way to generate large response signal instead of simply applying larger harmonic load V AC. From the perspective of damping, these dynamic performances can also be explained by recalling that the time-delay feedback controller with negative gain decreases the effective damping ratio ζ e =ζ+2g.

Fig. 12
figure 12

Frequency response curves obtained using LTI and MMS for various values of negative gain for V AC=1 V, V DC=40.2 V and τ=T/2. The unit is of G is V s/m

Full size image

Figure 13 shows the response amplitude at a fixed excitation frequency f=189.5 Hz while changing the value of the negative gain. The figure shows changes of stability occurring approximately within the interval G=−40–70 V s/m. Some of these instabilities are illustrated in Fig. 14, which shows frequency response curves with different values of relatively large negative gains. Note that when G<−71 V s/m, g<−1.34×10−3, which means that the system is operated outside the linearized stability boundaries and inside the instability regime of Fig. 3.

Fig. 13
figure 13

Gain sweeping response of the MMS solution at f=189.5 Hz, V AC=1 V and V DC=40.2 V (solid line: stable; dashed line: unstable)

Full size image
Fig. 14
figure 14

Frequency response curves compared among LTI, MMS and shooting techniques for the resonator with negative controller gains for V AC=1 V, V DC=40.2 V and τ=T/2

Full size image

The curves of Fig. 14 are obtained using MMS, LTI (when possible), in addition to the shooting technique to find periodic motions combined with the Floquet theory [38]. The shooting technique has the capability of predicting periodic solutions regardless of initial conditions, which is especially advantageous for very weak stability scenarios as in this case. According to the shooting technique, the upper stable branches lose stability through a Hopf bifurcation with one or more Floquet multipliers exiting in the unit circle through complex numbers.

In Fig. 13, if we consider the case of G=−20 V s/m, the response curve has a linear shape with no hysteresis. Thus, at f=189.5 Hz, it has one single value of a stable response. When increasing the gain to G=−50 V s/m in Fig. 13, the response exhibits softening behavior with hysteresis. Thus, at f=189.5 Hz, the response can be stable of low value, unstable, or stable at higher value. Increasing the gain further to G=−80 V s/m (Fig. 14a), according to the perturbation results, the frequency-response curve entirely becomes unstable. The results of longtime integration indicate no stable state between 189–191 Hz, which can be due to not finding the proper initial conditions (due to the very weak basin of attraction in this case). However, it is still able to catch periodic solutions where f is slightly away from natural frequency, shown as diamonds in the plots. The shooting technique, on the other hand, does not suffer from such a problem. Results of the shooting technique in Fig. 14 predict instabilities for specific frequency bands around the primary resonance. One should note that these instabilities refer to the loss of stability of the original periodic (period one) solution. The system loses stability through a Hopf bifurcation, which can be supercritical resulting into two new stable periodic solutions of a frequency that is either commensurate with the excitation frequency or incommensurate with it leading to quasiperiodic motion [39]. These post bifurcation scenarios require further bifurcation analysis, which is outside the scope of this work using, for example, the methods of harmonic balance [39], shooting, or finite difference techniques.

It is worth to mention that this loss of stability of the periodic motion is similar in some sense to the bifurcation reported in [40] in the case of large excitation of electrically actuated microbeams in the softening behavior case. It was reported there that the system loses stability through small cascade of period doubling bifurcations, which have very small basins of attractions. The cascade ends with a crisis and vanishes due to the collide with the unstable saddle.

Next, we show examples of the time history response (Fig. 15), which indicates that with a lower effective damping ratio ζ e , the resonator will have higher overshoot and larger settling time.

Fig. 15
figure 15

Time history responses of the uncontrolled system (a) and the controlled system (b) with negative gain G=−50 V s/m (excitation frequency f=191 Hz, V AC=1 V)

Full size image

The final analysis of this paper is concerned with studying the basin of attraction of the solution [35]. The basin-of-attraction results are obtained by integrating the equation of motion, Eq. (1), in time for various initial conditions using a grid of 500×500 initial velocity and displacement. The effect of delayed feedback negative gain on resonator stability is shown in Fig. 16. Figure 16a shows the basin-of-attraction before applying the delayed feedback controller, where it is clear that the resonator is stable and has a big safe area. After applying the negative delayed controller gain, the system starts to lose its stability. The safe area decreases when G=−60 V s/m and decreases more with G=−70 V s/m. Finally, the safe area almost vanishes at G=−80 V s/m and the system becomes practically unstable. This fractal behavior is an outcome of the global bifurcation the system experiences as a result of the collide of the stable periodic orbit with the unstable manifold of the saddle, which results in a multitude of complex dynamical behaviors and the escape from potential well (dynamic pull-in) phenomenon [41, 42].

Fig. 16
figure 16

The basin-of-attraction of the resonator when it is actuated with V DC=40.2 V and V AC=1 V with τ=T/2 at f=189.5 Hz under various values of negative gain

Full size image

7 Summary and conclusions

This paper presented analytical solution for a single degree-freedom resonator model actuated by V DC and V AC with a delay feedback controller. The method of multiple scales is used to obtain analytical explanations for the effect of the control gain and delay. We found that positive control gain can enlarge the response bandwidth of the resonator. Another attractive feature in the case of positive gains is achieving the sharp response of resonators while maintaining large bandwidth. This could be very attractive for a variety of sensing and actuation application in MEMS. Negative control gain can bring the resonator nonlinear behavior or make it stronger so that the system may reach an unstable state when the negative gain is large enough, even though the harmonic load V AC is relatively small (for example, V AC=1 V, V DC=40.2 V). This could lead to attractive applications, such as low-actuation voltage MEMS switches.

We compared the results of the perturbation method to the shooting technique and the basin-of-attraction analysis. The shooting technique performs well in predicting the global stability for the resonator under negative gain control. The basin-of-attraction indicated that, while shooting predicts stable regime in the frequency-response curves for large values of negative gain, the basin-of-attraction of these states are extremely small and fragile. Interestingly, the frequency-response curves agreed with the analytical results from MMS, except that MMS predicts unstable solutions everywhere. The various methods used in this paper shed light on the dynamics of delayed-feedback controlled MEMS resonators.