Nonlinear dynamical responses of forced carbon nanotube-based mass sensors under the influence of thermal loadings

Abstract

This study presents an analytical solution for the nonlinear forced vibration response of bridged carbon nanotube (CNT)-based mass sensors subjected to different types of thermal loading and external harmonic excitations. The structure undergoes a temperature change through its thickness when considering three different distribution patterns of the temperature, namely uniform, linear, and nonlinear. The CNT is modeled as a nonlocal doubly clamped beam that complies with Euler–Bernoulli beam theory and Eringen’s nonlocal elasticity theory. The von Kármán geometric nonlinearity is adopted to account for the mid-plane stretching of end-constrained beams. The extended Hamilton’s principle is used to derive the nonlinear governing equations of motion, boundary conditions, and continuity conditions accounting for the location of the deposited particle. The method of multiple scales (MMS) is employed to perform the nonlinear dynamical analysis of the nanobeam. Analytical expressions of the nonlinear dynamic response of the system exposed to thermal loadings in the case of primary resonance are presented. An important contribution of this work is the provision for closed-form expressions of the resonance frequency and the critical amplitude of the considered system. Simultaneously, validation of the results by MMS is achieved by Galerkin’s procedure and Runge–Kutta method. Then, the effects of the thermal loads and some key parameters on the nonlinear resonance frequency and amplitude shifts are discussed, and some meaningful conclusions are drawn.

1 Introduction

Over the past few decades, the potential applications of carbon nanotubes (CNTs) as high-performance nanostructures in which the vibrational characteristics of CNTs are significant have spread. Due to the advantages of mechanical and thermal properties, the initial discovery of CNTs led to significant transformations in nanotechnology. Further, CNT’s superior properties have led to potential applications in food or medicine, mechanical resonators, environmental monitoring, biosensors, and chemical processing [1,2,3,4,5,6,7,8].

Among the existing sensors, CNT-based mass detectors are used more and more as devices in life and biomedical sciences. In general, an atomic-scale particle deposited on the surface of a resonant mass sensor is detected by capturing the induced shift in resonance frequency or critical amplitudes due to different mass attachments [9,10,11,12,13,14,15]. In recent years, there has been a lot of focus on the nonlinear dynamic characteristics and large amplitude vibrations of nanoscale mass detectors and mechanical resonators. Among those, Ali-Akbari et al. [16] studied the free and forced vibrations of doubly clamped CNT-based mechanical resonator and included the effects of the geometrical properties of the attached particles on the system’s dynamic response. Additionally, Conley et al. [17] investigated the nonlinear dynamics of electrostatically actuated single-walled carbon nanotube (SWCNT) resonators under combined parametric and direct excitations. Moreover, the importance of the dynamic nonlinearity of four beam structures of nanomechanical resonators was discussed by Zhang et al. [18]. Mahdavi et al. [19] examined the dynamic characteristics of a single-layer graphene sheet (SLGS) in the post-buckling regime. In another work [20], the large amplitude of a cantilever CNT was examined by using the harmonic balance method (HBM), coupled with the asymptotic numerical method (ANM). Based on Euler–Bernoulli beam theory, Hajnayeb and Khadem [21] investigated the forced vibrations of a bridged double-walled carbon nanotube (DWCNT) under electrostatic actuation. Using the nonlocal elasticity theory and nonlinear geometrical relations, Li and Wang [22] showed that a graphene–elastic–piezoelectric (GEP) laminated films could be applied in mass detection as a resonant mass sensor. Kim and Lee [23] carried out a study on the nonlinear dynamics of a resonating CNT cantilever with a tip mass subjected to electrostatic excitation for determination of the complex dynamics of the CNT. Jomehzadeh and Saidi [24] presented large amplitude vibration analysis of multilayered graphene sheets with the harmonic balance method based on the Eringen’s theory of nonlocal continuum. Xu and Younis [25] developed an efficient reduced-order model (ROM) for CNTs to analyze static and dynamic behaviors of CNT-based resonators excited by large electrostatic forces. The effects of an axial magnetic field on forced vibrations of double single-walled carbon nanotube (DSWCNT) coupled by a Winkler elastic medium were reported by Stamenković et al. [26]. Mehdipour et al. [27] and Patel and Joshi [28] analyzed the forced oscillation regime of SWCNT and DWCNT mass sensors, respectively. Moreover, the single-layered graphene sheet with deposited nanoparticles under in-plane magnetic field was proposed as a new type of the mass detector by Karličić et al. [29] using the nonlocal Kirchhoff–Love plate theory. Then, on the basis of the nonlocal elasticity theory and MMS, Togun [30] studied nonlinear free and forced vibrations of Euler–Bernoulli nanobeams with attached nanoparticle. Besides the aforementioned studies, several investigations have been also carried out in the open literature dealing with the nonlinear dynamics of nanostructure-based resonators [31,32,33,34,35].

In addition to the effects of forced vibrations and large amplitude responses, other studies showed that the temperature rise also plays an important role in determination of the static and dynamic characteristics of nanoscale structures. Thus, it is of crucial importance to take the thermal effects into consideration in theoretical and experimental studies concerning with nanostructures. During the past two decades, considerable effort has been put into estimating the static and dynamic responses of nanoscale structures in thermal environments [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. In this regard, Ghaffari et al. [51] made an attempt to study the buckling behavior and linear vibration of CNT-based mass detectors subjected to uniform temperature. By utilizing the continuum mechanics model, Kang and his co-workers [52] deeply investigated the influence of the temperature change on the fundamental resonance behavior and resonance frequency shift of CNT-based resonators in a high-temperature environment. They proved a valid improvement of fundamental resonance frequency in nonlinear oscillation regime under thermal loadings. Kang et al. [53] applied finite element method-based nonlinear analysis to model CNT-based mass sensors subjected to thermal loads. Another study was conducted on the nonlinear dynamic behaviors of rotating and propped cantilever nanobeams subjected to thermal stress [54]. Using molecular dynamics simulations and nonlocal elasticity, Shen et al. [55] expressed the influence of the temperature rise on the nonlinear dynamic response of bilayer graphene sheets (BLGSs) and pointed out that the temperature change plays an important role in the nonlinear oscillation regime of BLGSs. Moreover, Koh et al. [56] presented the thermally induced nonlinear vibration of SWCNTs via molecular dynamic simulations. Furthermore, buckling and linear vibration analyses of bridged CNT-based resonators subjected to UTD, LTD, and NLTD were performed by Ghaffari et al. [57] who utilized the Euler–Bernoulli beam theory in conjunction with the Eringen’s nonlocal elasticity. Their results indicated that the assumption of NLTD across the radius of CNTs yields lower values of the natural frequency and the induced shift in the frequency compared to UTD and LTD in the pre-buckling oscillation regime. By contrast, they concluded that in the post-buckling configuration, considering NLTD through the thickness of CNTs estimates higher natural frequencies and frequency shifts compared to UTD and LTD.

In the present work, we focus our attention on the nonlinear forced vibration response of CNT-based mass detectors subjected to different types of thermal loadings. To the best of authors’ knowledge, no previous study regarding the nonlinear dynamic stability of CNT-based mass sensors under various thermal loads has been reported in the literature. The novel contribution of the present work is in the study of the effects of three different temperature rises, i.e., uniform, linear, and nonlinear thermal loadings. Referring to the results and methods of relevant studies, the analysis of nonlinear forced dynamic stability of the CNT under various temperature rises is addressed based on Euler–Bernoulli beam theory and the Eringen’s nonlocal elasticity. The governing equations of the CNT-based resonator are established by the extended Hamilton’s principle. The method of multiple scales is employed to obtain the analytical solutions of the nonlinear forced vibration problem. Afterward, a Galerkin-based numerical technique is adopted to reduce the set of nonlinear governing equations into a time-varying set of ordinary differential equation which is coincident with the nonlinear forced oscillation problem of the nanobeam in thermal environments. Finally, a detailed parametric study is carried out to highlight the impacts of the temperature rise, the excitation force amplitude, the surface temperature difference, the type of temperature profiles, and the deposited mass of the atomic-scale particle on the resonance frequency shift as well as amplitude-based mass detection sensitivity of the bridged CNT-based sensor in different sets of thermal environments for the pre-buckling configuration.

2 Representation of thermal distribution profiles

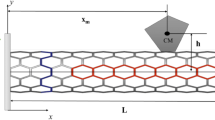
In this effort, the effects of three different temperature profiles are investigated. At the nanoscale, slight changes in the environment can have significant effects on the system’s static and dynamic responses. For this reason, it is important to consider each of the temperature profiles to determine whether the increased complexity into the model results in measurable changes in the response when compared to the simplest case, i.e., a uniform temperature distribution through the thickness of the CNT. The considered profiles are shown in Fig. 1 including uniform, linear, and nonlinear temperature distributions.

Fig. 1

Uniform, linear, and nonlinear temperature distributions through the thickness of the CNT

The first profile that is considered is the uniform temperature distribution (UTD). In that case, for a CNT-based resonator at the ambient temperature of $T_{\mathrm{ref}}$, the temperature rises uniformly to the final value of $T_{\mathrm{UTD}}$ which can be expressed as follows [57]:

$$\begin{aligned} T_{\mathrm{UTD}} =\bar{{T}}=\left( {\frac{T_{i} +T_{o} }{2}} \right) =T_{\mathrm{ref}} +\Delta T_{\mathrm{UTR}} \end{aligned}$$

(1)

where $\Delta T_{\mathrm{UTR}}$ refers to the uniform temperature rise.

Next, the linear temperature distribution (LTD) is considered. When the CNT thickness is thin enough, it is assumed that the temperature varies linearly through the radius of the nanobeam. The linear temperature profile and temperature rise are given as [57]:

$$\begin{aligned} T(r)_{\mathrm{LTD}}= & {} \left( {\frac{T_{o} -T_{i} }{r_{o} -r_{i} }} \right) \left( {r-r_{o} } \right) +T_{o} \end{aligned}$$

(2)

$$\begin{aligned} \Delta T_{\mathrm{LTR}}= & {} \left( {\frac{T_{o} -T_{i} }{r_{o} -r_{i} }} \right) \left( {r-r_{o} } \right) +T_{o} -T_{\mathrm{ref}} \end{aligned}$$

(3)

where $r_{i}$ and $r_{o}$ represent the inner and outer radius, respectively. Also, $T_{i}$ and $T_{o}$ are the inner surface and the outer side temperatures, respectively.

The last temperature distribution to be considered is the nonlinear temperature distribution (NLTD). This distribution is the most complex of the three considered. However, the distribution is more representative of physical systems than the UTD or LTD approximations. Assuming the steady-state, one-dimensional heat conduction equation with a constant heat conduction coefficient for the CNT and the known thermal boundary conditions on the inner and outer surfaces of the nanobeam, the nonlinear temperature distribution and temperature rise across the thickness of the CNT-based mass sensor are obtained as follows [57]:

$$\begin{aligned} T\left( r \right) _{\mathrm{NLTD}}= & {} \frac{\left( {T_{o} -T_{i} } \right) }{Ln\left( {\frac{r_{o} }{r_{i} }} \right) }Ln\left( r \right) +\frac{\left( {T_{o} +T_{i} } \right) }{2}\nonumber \\&-\frac{\left( {T_{o} -T_{i} } \right) }{2Ln\left( {\frac{r_{o} }{r_{i} }} \right) }Ln\left( {r_{i} r_{o} } \right) \end{aligned}$$

(4)

$$\begin{aligned} \Delta T_{\mathrm{NLTR}}= & {} \frac{\left( {T_{o} -T_{i} } \right) }{Ln\left( {\frac{r_{o} }{r_{i} }} \right) }Ln\left( r \right) +\frac{\left( {T_{o} +T_{i} } \right) }{2}\nonumber \\&-\frac{\left( {T_{o} -T_{i} } \right) }{2Ln\left( {\frac{r_{o} }{r_{i} }} \right) }Ln\left( {r_{i} r_{o} } \right) -T_{\mathrm{ref}} \end{aligned}$$

(5)

3 Method of multiple scales for CNT-based mass sensors under thermal loadings

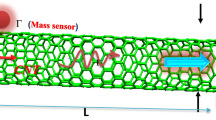
A representative harmonically excited bridged CNT resonator with an atomic-scale particle deposited on its surface is depicted schematically in Fig. 2. The complete system consists of a nanotube of length L, internal radius $r_{i}$, external radius $r_{o}$, and an attached mass of m. The CNT is subjected to external harmonic excitation and three different types of temperature rise, i.e., uniform, linear, and nonlinear thermal loads, as shown in Fig. 1. The vertical and horizontal deflections of the system used to describe the system’s motion are specified by w and u, respectively.

Fig. 2

The system of bridged CNT-based mass detector subjected to thermal loadings with an attached atomic-scale particle under fixed–fixed boundary conditions

Following the same strategy presented in [57] with including the external forces, this system is governed by the following set of nondimensional nonlinear equations of motion:

$$\begin{aligned}&W_{1}^{(4)} +\ddot{{W}}_{1} -\left( \frac{1}{2}\int \limits _0^\eta \left( {{W}'_{1} } \right) ^{2}d\chi \right. \nonumber \\&\left. \quad +\,\frac{1}{2}\int \limits _\eta ^1 {\left( {{W}'_{2} } \right) ^{2}d\chi -T_{n} H} \right) {W}''_{1} +2\bar{{\xi }}\dot{{W}}_{1} \nonumber \\&\quad -\,e^{2}\left[ {\ddot{{W}}}''_{1} -\left( {\frac{1}{2}\int \limits _0^\eta {\left( {{W}'_{1} } \right) ^{2}d\chi +\frac{1}{2}\int \limits _\eta ^1 {\left( {{W}'_{2} } \right) ^{2}d\chi } } } \right) W_{1}^{(4)} \right. \nonumber \\&\left. \quad +\,2\bar{{\xi }}{\dot{{W}}}''_{1} \right] -e^{2}HT_{n} W_{1}^{(4)} =\bar{{F}}_{1} \cos (\Omega \tau ) \end{aligned}$$

(6)

$$\begin{aligned}&W_{2}^{(4)} +\ddot{{W}}_{2} -\left( \frac{1}{2}\int \limits _0^\eta \left( {{W}'_{1} } \right) ^{2}d\chi \right. \nonumber \\&\left. \quad +\,\frac{1}{2}\int \limits _\eta ^1 {\left( {{W}'_{2} } \right) ^{2}d\chi -T_{n} H} \right) {W}''_{2} +2\bar{{\xi }}\dot{{W}}_{2} \nonumber \\&\quad -\,e^{2}\left[ {\ddot{{W}}}''_{2} -\left( {\frac{1}{2}\int \limits _0^\eta {\left( {{W}'_{1} } \right) ^{2}d\chi +\frac{1}{2}\int \limits _\eta ^1 {\left( {{W}'_{2} } \right) ^{2}d\chi } } } \right) W_{2}^{(4)} \right. \nonumber \\&\left. \quad +2\bar{{\xi }}{\dot{{W}}}''_{2} \right] -e^{2}HT_{n} W_{2}^{(4)} =\bar{{F}}_{2} \cos (\Omega \tau ) \end{aligned}$$

(7)

with the boundary conditions and continuity equations expressed as:

$$\begin{aligned} W_{1} (0)=0; \quad {W}'_{1} (0)=0; \quad W_{2} (1)=0; \quad {W}'_{2} (1)=0\nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned}&W_{1} (\eta )=W_{2} (\eta );\,{W}'_{1} (\eta )={W}'_{2} (\eta );\, {W}''_{1} (\eta )={W}''_{2} (\eta ) \nonumber \\&{W}'''_{1} (\eta )-{W}'''_{2} (\eta ) + e^{2}\left[ {\left( {\frac{1}{2}\int _0^\eta {\left( {W_{1}^{\prime }} \right) } ^{2}d\chi +\frac{1}{2}\int _\eta ^1 {\left( {W_{2}^{\prime }} \right) } ^{2}d\chi } \right) } \right. \nonumber \\&\quad \quad -\left. {HT_{n} } \right] \left( {{W}'''_{1} (\eta )-{W}'''_{2} (\eta )} \right) -\mu \ddot{{W}}_{1} (\eta )=0 \nonumber \\ \end{aligned}$$

(9)

The dimensionless parameters used to arrange the normalized form of motion equations, boundary conditions, and continuity equations are written as:

$$\begin{aligned}&\chi =x /{L},\, W_{1,2} =w_{1,2} \sqrt{A / I} ,\, \tau =t\sqrt{{EI} / {m_{0} L^{4}}} ,\, \nonumber \\&\quad 2\bar{{\zeta }}={cL^{2}}/ {\sqrt{m_{0} EI} } \nonumber \\&\Omega ={\Omega ^{*}} / \sqrt{EI} / {m_{0} L^{4}} , \, e={e_{0} a} / {L},\, \eta ={x_{m}} / {L},\nonumber \\&\quad \mu =m / {\left( {m_{0} L} \right) },\bar{{F}}_{1,2} ={F_{1,2}^{*} L^{4}\sqrt{A/ I}} / {EI} \nonumber \\&\left( {T_{n(\mathrm{UTD})} ,T_{n(\mathrm{LTD})} ,T_{n(\mathrm{NLTD})} } \right) \nonumber \\&\quad =\frac{1}{EA}\left( {N_{\mathrm{UTD}}^{T} ,N_{\mathrm{LTD}}^{T} ,N_{\mathrm{NLTD}}^{T} } \right) ,\,H={AL^{2}} / I \nonumber \\ \end{aligned}$$

(10)

where E, I, L, A, and $m_{0}$ are the Young’s modulus, moment of inertia, length, cross-sectional area, and density of the CNT, respectively. The mass and the location of the deposited atomic-scale particle are denoted by m and ${\mu }$, respectively. Also, $w_{1}$ and $w_{2}$ refer to the transverse deflection of the first and the second portions of the nanobeam, respectively. The nonlocal parameter is denoted by $e_{0}a$, which incorporates the small-scale factor. In this case, $e_{0}$ presents a material constant determined experimentally or approximated through matching the dispersion curves of the plane waves with ones of the atomic lattice dynamics. Further, a shows the internal characteristic length. Taking into account the effects of thermal loads, $N^{T}$ is introduced to represent uniform, linear, and nonlinear thermal resultants. The viscous damping coefficient is denoted by c. Moreover, $\Omega ^{*}$ refers to the frequency of the external excitation and $F^{*}_{1,2}$ represents the excitation force amplitudes.

In order to investigate the vibration characteristics of the CNT-based resonator, a schematic configuration of variations in the first natural frequency with respect to the temperature rise is depicted in Fig. 3 for UTD, LTD, and NLTD cases. It can be observed from this figure that for any kind of temperature distribution in the pre-buckling region, the first natural frequency decreases by increasing the temperature change until the thermal load approaches to the critical buckling temperature ($\Delta {\overline{T}}_{cr(\mathrm{UTD})}$, $\Delta \overline{T}_{cr(\mathrm{LTD})}$, $\Delta \overline{T}_{cr(\mathrm{NLTD})}$). This is due to the reduction in the total stiffness of the nanobeam, since the temperature rise has weakening effect on the CNT in the pre-buckling oscillation regime. After the buckling points, augmenting the temperature rise results in higher frequencies for all types of thermal loading. One interesting observation, it can be seen from Fig. 3 that for a fixed value of the temperature rise ($\Delta {\overline{T}}$), the assumption of NLTD yields the lowest values of the natural frequency in the pre-buckling region, while considering NLTD estimates the highest natural frequencies within the range of temperature rise after the critical buckling point. It is worth mentioning that in this paper, we only focus on the pre-buckling regime to investigate the dynamic characteristics of the CNT-based mass detector.

Fig. 3

A schematic of the first natural frequency of the CNT-based mass sensor versus the temperature rise, $\Delta \overline{T}$, illustrating the pre-buckling and post-buckling configurations under various thermal loadings

Here, the method of multiple scales [58] is applied to derive the dynamic nonlinear response of the system. To this end, we assume:

$$\begin{aligned}&W_{1} \left( {\chi ,\,\tau } \right) =\varepsilon W_{11} \left( {\chi ,\,T_{0} ,\,T_{2} } \right) \nonumber \\&\qquad \qquad \qquad \quad +\,\varepsilon ^{3}W_{13} \left( {\chi ,\,T_{0} ,\,T_{2} } \right) +\cdots , \end{aligned}$$

(11)

$$\begin{aligned}&W_{2} \left( {\chi ,\,\tau } \right) =\varepsilon W_{21} \left( {\chi ,\,T_{0} ,\,T_{2} } \right) \nonumber \\&\qquad \qquad \qquad \quad +\,\varepsilon ^{3}W_{23} \left( {\chi ,\,T_{0} ,\,T_{2} } \right) +\cdots , \end{aligned}$$

(12)

where $\varepsilon$ is a small positive parameter. $T_{0}$ and $T_{2}$ denote time scales which can be expressed in the form of $T_{n}= \varepsilon ^{n}\tau$. The time derivatives are written in terms of $T_{0}$ and $T_{2}$ as follows:

$$\begin{aligned} \frac{\partial }{\partial \tau }=D_{0} +\varepsilon ^{2}D_{2} ,\,\,\,\,\,\frac{\partial ^{2}}{\partial \tau ^{2}}=D_{0}^{2} +2\varepsilon ^{2}D_{0} D_{2} \end{aligned}$$

(13)

In conjunction with Eqs. (11)–(13), Eqs. (6)–(9) are now rewritten as the following forms for order $\varepsilon$, considering the truncation of higher-order terms.

$$\begin{aligned}&D_{0}^{2} W_{11} +\left( {1-e^{2}HT_{n} } \right) \frac{\partial ^{4}W_{11} }{\partial \chi ^{4}}\nonumber \\&\quad +\left( {HT_{n} -e^{2}D_{0}^{2} } \right) \frac{\partial ^{2}W_{11} }{\partial \chi ^{2}}=0 \end{aligned}$$

(14)

$$\begin{aligned}&D_{0}^{2} W_{21} +\left( {1-e^{2}HT_{n} } \right) \frac{\partial ^{4}W_{21} }{\partial \chi ^{4}}\nonumber \\&\quad +\left( {HT_{n} -e^{2}D_{0}^{2} } \right) \frac{\partial ^{2}W_{21} }{\partial \chi ^{2}}=0 \end{aligned}$$

(15)

$$\begin{aligned}&W_{11} =0,\,\frac{\partial W_{11} }{\partial \chi }=0\,\,\,\,\,at\,\,\,\chi =0,\nonumber \\&\quad W_{21} =0 ,\, \frac{\partial W_{21} }{\partial \chi }=0\,\,\,\,at\,\,\,\chi =1 \end{aligned}$$

(16)

$$\begin{aligned}&W_{11} =W_{21} ,\,\,\,\,\,\frac{\partial W_{11} }{\partial \chi }=\frac{\partial W_{21} }{\partial \chi }\nonumber \\&\quad \frac{\partial ^{2}W_{11} }{\partial \chi ^{2}}=\frac{\partial W^{2}_{21} }{\partial \chi ^{2}}\,\,at\,\,\, \chi =\eta , \nonumber \\&\left( {1-e^{2}HT_{n} } \right) \left( {\frac{\partial ^{3}W_{11} }{\partial \chi ^{3}}-\frac{\partial ^{3}W_{21} }{\partial \chi ^{3}}} \right) \nonumber \\&\quad -\mu D_{0}^{2} W_{11} =0\,\,\,\,\,\,\,at\,\,\chi =\eta \end{aligned}$$

(17)

The solutions of the problem obtained by Eqs. (14)–(17) are given in the following forms:

$$\begin{aligned} W_{11}= & {} A\left( {T_{2} } \right) e^{i\omega T_{0} }\Phi _{1} \left( \chi \right) +cc \end{aligned}$$

(18)

$$\begin{aligned} W_{21}= & {} A\left( {T_{2} } \right) e^{i\omega T_{0} }\Phi _{2} \left( \chi \right) +cc \end{aligned}$$

(19)

Physically, $A(T_{2})$ is the unknown system response amplitude and cc represents the complex conjugate of the preceding terms. Substituting Eqs. (18) and (19) to Eqs. (14)–(17) and using Eq. (13), the following set of linear equations can be derived as:

$$\begin{aligned}&\left( {1-e^{2}HT_{n} } \right) \Phi _{1}^{(4)}-\omega ^{2}\Phi _{1} \nonumber \\&\quad +\left( {e^{2}\omega ^{2}+T_{n} H} \right) \Phi _{1}^{\prime \prime }=0 \end{aligned}$$

(20)

$$\begin{aligned}&\left( {1-e^{2}HT_{n} } \right) \Phi _{2}^{(4)}-\omega ^{2}\Phi _{2} \nonumber \\&\quad +\left( {e^{2}\omega ^{2}+T_{n} H} \right) \Phi _{2}^{\prime \prime }=0 \end{aligned}$$

(21)

$$\begin{aligned}&\Phi _{1} \left( 0 \right) =0;\,\Phi _{1}^{\prime }\left( 0 \right) =0;\nonumber \\&\quad \Phi _{2} \left( 1 \right) =0;\,\Phi _{2}^{\prime }\left( 1 \right) =0 \end{aligned}$$

(22)

$$\begin{aligned}&\Phi _{1} \left( \eta \right) =\Phi _{2} \left( \eta \right) ,\,\Phi _{1} ^{\prime }\left( \eta \right) =\Phi _{2}^{\prime }\left( \eta \right) , \nonumber \\&\quad \Phi _{1} ^{\prime \prime }\left( \eta \right) =\Phi _{2}^{\prime \prime }\left( \eta \right) \nonumber \\&\left( {1-e^{2}HT_{n} } \right) \left( {\Phi _{1}^{\prime \prime \prime }\left( \eta \right) -\Phi _{2}^{\prime \prime \prime }\left( \eta \right) } \right) \nonumber \\&\quad +\,\mu \omega ^{2}\Phi _{1} \left( \eta \right) =0 \end{aligned}$$

(23)

Considering general solutions of Eqs. (20) and (21), applying the boundary conditions and continuity equations given in Eqs. (22) and (23), and performing an eigenvalue problem analysis, the dimensionless natural frequencies ($\omega )$ of the CNT-based mass detector and the corresponding mode shapes $\varPhi _{1}$ and $\varPhi _{2}$ can be obtained.

Substituting Eqs. (11) and (12) to Eqs. (6)–(9), using Eq. (13), and collecting the coefficients of $\varepsilon ^{3}$, the third-order equations of motion, boundary conditions, and continuity equations of the system can be obtained as follows:

$$\begin{aligned}&D_{0}^{2} W_{13} +\left( {1-e^{2}HT_{n} } \right) \frac{\partial ^{4}W_{13} }{\partial \chi ^{4}}\nonumber \\&\quad +\left( {HT_{n} -e^{2}D_{0}^{2} } \right) \frac{\partial ^{2}W_{13} }{\partial \chi ^{2}}=-2D_{0} D_{2} W_{11} -2\xi D_{0} W_{11} \nonumber \\&\quad +\left[ {\frac{1}{2}\int _0^\eta {\left( {\frac{\partial W_{11} }{\partial \chi }} \right) }^{2}d\chi +\frac{1}{2}\int _\eta ^1 {\left( {\frac{\partial W_{21} }{\partial \chi }} \right) }^{2}d\chi } \right] \frac{\partial ^{2}W_{11} }{\partial \chi ^{2}}\nonumber \\&\quad -\,e^{2}\left[ -2D_{0} D_{2} \frac{\partial ^{2}W_{11} }{\partial \chi ^{2}}-2\xi D_{0} \frac{\partial ^{2}W_{11} }{\partial \chi ^{2}}\right. \nonumber \\&\quad \left. +\left[ {\frac{1}{2}\int _0^\eta {\left( {\frac{\partial W_{11} }{\partial \chi }} \right) }^{2}d\chi +\frac{1}{2}\int _\eta ^1 {\left( {\frac{\partial W_{21} }{\partial \chi }} \right) }^{2}d\chi } \right] \frac{\partial ^{4}W_{11} }{\partial \chi ^{4}} \right] \nonumber \\&\quad +\,F_{1} \cos (\Omega T_{0} ) \nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned}&D_{0}^{2} W_{23} +\left( {1-e^{2}HT_{n} } \right) \frac{\partial ^{4}W_{23} }{\partial \chi ^{4}}\nonumber \\&\quad +\left( {HT_{n} -e^{2}D_{0}^{2} } \right) \frac{\partial ^{2}W_{23} }{\partial \chi ^{2}}=-2D_{0} D_{2} W_{21} -2\xi D_{0} W_{21} \nonumber \\&\quad +\left[ {\frac{1}{2}\int _0^\eta {\left( {\frac{\partial W_{11} }{\partial \chi }} \right) }^{2}d\chi +\frac{1}{2}\int _\eta ^1 {\left( {\frac{\partial W_{21} }{\partial \chi }} \right) }^{2}d\chi } \right] \frac{\partial ^{2}W_{21} }{\partial \chi ^{2}} \nonumber \\&\quad -\,e^{2}\left[ -2D_{0} D_{2} \frac{\partial ^{2}W_{21} }{\partial \chi ^{2}}-2\xi D_{0} \frac{\partial ^{2}W_{21} }{\partial \chi ^{2}}\right. \nonumber \\&\left. \quad +\left[ {\frac{1}{2}\int _0^\eta {\left( {\frac{\partial W_{11} }{\partial \chi }} \right) }^{2}d\chi +\frac{1}{2}\int _\eta ^1 {\left( {\frac{\partial W_{21} }{\partial \chi }} \right) }^{2}d\chi } \right] \frac{\partial ^{4}W_{21} }{\partial \chi ^{4}} \right] \nonumber \\&\quad +\,F_{2} \cos (\Omega T_{0} ) \end{aligned}$$

(25)

$$\begin{aligned}&W_{13} =0,\,\frac{\partial W_{13} }{\partial \chi }=0\,\,\,\,\,at\,\,\,\chi =0,\,\,\,\,\,\,\,\,\,W_{23} =0,\nonumber \\&\quad \frac{\partial W_{23} }{\partial \chi }=0\,\,\,\,at\,\,\,\chi =1 \end{aligned}$$

(26)

$$\begin{aligned}&W_{13} =W_{23} ,\,\,\,\,\,\frac{\partial W_{13} }{\partial \chi }=\frac{\partial W_{23} }{\partial \chi }\,\,,\,\, \frac{\partial ^{2}W_{13} }{\partial \chi ^{2}}=\frac{\partial ^{2}W_{23} }{\partial \chi ^{2}}\,\,\,at\,\,\,\chi =\eta , \nonumber \\&\left( {1-e^{2}HT_{n} } \right) \left( {\frac{\partial ^{3}W_{13} }{\partial \chi ^{3}}-\frac{\partial ^{3}W_{23} }{\partial \chi ^{3}}} \right) \nonumber \\&\quad +\,e^{2}\left[ {\frac{1}{2}\int _0^\eta {\left( {\frac{\partial W_{11} }{\partial \chi }} \right) }^{2}d\chi +\frac{1}{2}\int _\eta ^1 {\left( {\frac{\partial W_{21} }{\partial \chi }} \right) }^{2}d\chi } \right] \nonumber \\&\quad \left( {\frac{\partial ^{3}W_{11} }{\partial \chi ^{3}}-\frac{\partial ^{3}W_{21} }{\partial \chi ^{3}}} \right) \nonumber \\&\quad -\,\mu D_{0}^{2} W_{13} -2\mu D_{0} D_{2} W_{11} =0\,\,\,\,\,\,\,at\,\,\chi =\eta \end{aligned}$$

(27)

The solution of $O(\varepsilon ^{3})$ which consists of the secular and nonsecular terms can be expressed as:

$$\begin{aligned} W_{13}= & {} \Psi _{1} \left( {\chi ,\,T_{2} } \right) e^{i\omega T_{0} }+{\hat{W}}_{1} \left( {\chi ,\,T_{0} ,\,T_{2} } \right) +cc \end{aligned}$$

(28)

$$\begin{aligned} W_{23}= & {} \Psi _{2} \left( {\chi ,\,T_{2} } \right) e^{i\omega T_{0} }+{\hat{W}}_{2} \left( {\chi ,\,T_{0} ,\,T_{2} } \right) +cc \end{aligned}$$

(29)

where ${\hat{W}}_{1}$ and ${\hat{W}}_{2}$ denote the secular terms.

Substituting Eqs. (18), (19), (28), and (29) to Eqs. (24)–(27) and eliminating the secular terms, we have

$$\begin{aligned}&\left( {1-e^{2}HT_{n} } \right) \frac{\partial ^{4}\Psi _{1} }{\partial \chi ^{4}}-\omega ^{2}\Psi _{1} +\left( {HT_{n} +e^{2}\omega ^{2}} \right) \frac{\partial ^{2}\Psi _{1} }{\partial \chi ^{2}}\nonumber \\&\quad =-2i\omega A^{'}\Phi _{1} -2\xi i\omega A\Phi _{1} \nonumber \\&\qquad +\,\frac{3}{2}A^{2}\overline{A} b\frac{\partial ^{2}\Phi _{1} }{\partial \chi ^{2}}+F_{1} \cos \Omega T_{0} \nonumber \\&\qquad -\,e^{2}\left[ {-2i\omega A^{'}\frac{\partial ^{2}\Phi _{1} }{\partial \chi ^{2}}-2\xi i\omega A\frac{\partial ^{2}\Phi _{1} }{\partial \chi ^{2}}+\frac{3}{2}A^{2}\overline{A} b\frac{\partial ^{4}\Phi _{1} }{\partial \chi ^{4}}} \right] \nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned}&\left( {1-e^{2}HT_{n} } \right) \frac{\partial ^{4}\Psi _{2} }{\partial \chi ^{4}}-\omega ^{2}\Psi _{2} +\left( {HT_{n} +e^{2}\omega ^{2}} \right) \frac{\partial ^{2}\Psi _{2} }{\partial \chi ^{2}}\nonumber \\&\quad =-2i\omega A^{'}\Phi _{2} -2\xi i\omega A\Phi _{2} \nonumber \\&\qquad +\,\frac{3}{2}A^{2}\overline{A} b\frac{\partial ^{2}\Phi _{2} }{\partial \chi ^{2}}+F_{2} \cos \Omega T_{0}\nonumber \\&\qquad -\,e^{2}\left[ {-2i\omega A^{'}\frac{\partial ^{2}\Phi _{2} }{\partial \chi ^{2}}-2\xi i\omega A\frac{\partial ^{2}\Phi _{2} }{\partial \chi ^{2}}+\frac{3}{2}A^{2}\overline{A} b\frac{\partial ^{4}\Phi _{2} }{\partial \chi ^{4}}} \right] \nonumber \\ \end{aligned}$$

(31)

$$\begin{aligned}&\Psi _{1} =0,\,\frac{\partial \Psi _{1} }{\partial \chi }=0\,\,\,\,\,at\,\,\,\chi =0,\nonumber \\&\Psi _{2} =0, \, \frac{\partial \Psi _{2} }{\partial \chi }=0\,\,\,\,at\,\,\,\chi =1, \end{aligned}$$

(32)

$$\begin{aligned}&\Psi _{1} =\Psi _{2} ,\,\,\,\,\,\,\,\,\,\,\,\,\frac{\partial \Psi _{1} }{\partial \chi }=\frac{\partial \Psi _{2} }{\partial \chi }\,,\,\,\frac{\partial ^{2}\Psi _{1} }{\partial \chi ^{2}}=\frac{\partial ^{2}\Psi _{2} }{\partial \chi ^{2}}\,\,\,\,\,\,at\,\,\,\chi =\eta , \nonumber \\&\qquad \left( {1-e^{2}HT_{n} } \right) \left( {\frac{\partial ^{3}\Psi _{1} }{\partial \chi ^{3}}-\frac{\partial ^{3}\Psi _{2} }{\partial \chi ^{3}}} \right) \nonumber \\&\qquad +\,\frac{3}{2}e^{2}A^{2}\overline{A} b\left( {\frac{\partial ^{3}\Phi _{1} }{\partial \chi ^{3}}-\frac{\partial ^{3}\Phi _{2} }{\partial \chi ^{3}}} \right) \nonumber \\&\qquad +\,\mu \omega ^{2}\Psi _{1} -2\mu i\omega A^{'}\Phi _{1} =0\,\,\,\,\,\,\,at\,\,\chi =\eta \end{aligned}$$

(33)

In the present work, the normalized excitation frequency $(\varOmega )$ is assumed to be close to the dimensionless first natural frequency ($\omega _{\mathrm{1}})$ of the CNT-based resonator and the detuning parameter, $\sigma$, is introduced. For convenience, the normalized first natural frequency of the CNT is denoted by $\omega$. Detuning parameter $\sigma$ is to quantitatively describe the nearness of $\Omega$ to $\omega$. Accordingly, we have:

$$\begin{aligned} \Omega =\omega +\varepsilon ^{2}\sigma \end{aligned}$$

(34)

Also, the complex amplitude can be given in polar form as follows:

$$\begin{aligned} A={\left( {a\left( {T_{2} } \right) e^{i\theta \left( {T_{2} } \right) }} \right) } / 2 \end{aligned}$$

(35)

where a refers to a real amplitude and $\theta$ is an angle.

Performing algebraic manipulations, using the orthogonality equation, recognizing the solvability condition, and taking the complex amplitude in polar form, the frequency response function of the system can be given by [16]:

$$\begin{aligned} \sigma =\frac{3\Upsilon _{1} }{16\omega \Upsilon _{2} }a^{2}\mp \sqrt{\frac{\left( {f^{*}} \right) ^{2}}{4\omega ^{2}a^{2}}-\left( {\Upsilon ^{*}} \right) ^{2}} \end{aligned}$$

(36)

and the details of $\varUpsilon _{\mathrm {1}}$, $\varUpsilon _{\mathrm {2}}$, $\varUpsilon ^{*}$, and $f^{*}$ are given in [16].

4 Problem solution by Galerkin’s method: numerical analysis

Herein, employing a Galerkin-based numerical technique, the set of nonlinear equations presented in Eqs. (6)–(9) is reduced into a time-varying set of ordinary differential equations. To this end, the transversal motions of the nanobeam, $W_{\mathrm {1}}(\chi ,\tau )$ and $W_{\mathrm {2}}(\chi ,\tau )$, are expressed as a linear combination of a complete set of linearly independent basis functions of the CNT-based resonator, $\Phi _{{1n}}(\chi )$ and $\Phi _{2n}(\chi )$, in the following forms:

$$\begin{aligned} W_{1} \left( {\chi ,\tau } \right)= & {} \sum \limits _{n=1}^N {\Phi _{1n} \left( \chi \right) q_{n} \left( \tau \right) } ,\nonumber \\ W_{2} \left( {\chi ,\tau } \right)= & {} \sum \limits _{n=1}^N {\Phi _{2n} \left( \chi \right) q_{n} \left( \tau \right) } \end{aligned}$$

(37)

where $q_{n}(\tau )$ stands for the reduced generalized coordinates and N is the number of modes. In the present work, N is considered 1, 2, and 3 due to the geometric nonlinearity in the system under investigation.

It is noteworthy to mention that to attain the discretized nonlinear equations of motion, the normalization conditions are used in the following forms:

$$\begin{aligned}&\mu \Phi _{1m} \Phi _{1n} \left| {_{\eta } } \right. +\left( {\int _0^\eta {\Phi _{1m} \Phi _{1n} d\chi } +\int _\eta ^1 {\Phi _{2m} \Phi _{2n} d\chi } } \right) \nonumber \\&\quad -\,e^{2}\left( {\int _0^\eta {\Phi _{1m} {\Phi }''_{1n} d\chi } +\int _\eta ^1 {\Phi _{2m} {\Phi }''_{2n} d\chi } } \right) =1,\,\,\,m=n \nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned}&\mu \Phi _{1m} \Phi _{1n} \left| {_{\eta } } \right. +\left( {\int _0^\eta {\Phi _{1m} \Phi _{1n} d\chi } +\int _\eta ^1 {\Phi _{2m} \Phi _{2n} d\chi } } \right) \nonumber \\&\quad -\,e^{2}\left( {\int _0^\eta {\Phi _{1m} {\Phi }''_{1n} d\chi } +\int _\eta ^1 {\Phi _{2m} {\Phi }''_{2n} d\chi } } \right) =0,\,\,\,m\ne n \nonumber \\ \end{aligned}$$

(39)

Substituting Eq. (37) to Eqs. (6)–(9), multiplying by $\Phi _{{1m}}(\chi )$ and $\Phi _{{2m}}(\chi )$ as weight functions in Galerkin’s method, integrating the outcome from $\chi =0$ to 1, and employing the normalization conditions given in Eqs. (38) and (39), a time-varying set of ordinary differential equations is obtained as:

$$\begin{aligned}&\ddot{{q}}_{m} +\omega _{m}^{2} q_{m} +e^{2}\left[ {\left( {\sum \limits _{s,p}^N {\Xi _{sp} q_{s} q_{p} } } \right) -HT_{n} } \right] \omega _{m}^{2} q_{m}\nonumber \\&\quad -\sum \limits _{i,j,k}^N {\Gamma _{mijk} q_{i} q_{j} q_{k} } \nonumber \\&\quad +\,HT_{n} \left( {\int _0^\eta {\Phi _{1m} {\Phi }''_{1k} \mathrm{d}\chi } +\int _\eta ^1 {\Phi _{2m} {\Phi }''_{2k} \mathrm{d}\chi } } \right) q_{k}\nonumber \\&\quad +\,2\bar{{\zeta }}\sum \limits _{n=1}^N {\left( {\Lambda _{mn} } \right) \dot{{q}}_{n} } =F_{m} \end{aligned}$$

(40)

where

$$\begin{aligned} \Xi _{sp}= & {} \frac{1}{2}\left( {\int _0^\eta {{\Phi }'_{1s} {\Phi }'_{1p} \mathrm{d}\chi } +\int _\eta ^1 {{\Phi }'_{2s} {\Phi }'_{2p} \mathrm{d}\chi } } \right) \end{aligned}$$

(41)

$$\begin{aligned} \Gamma _{mijk}= & {} \frac{1}{2}\left( {\int _0^\eta {{\Phi }'_{1i} {\Phi }'_{1j} \mathrm{d}\chi } +\int _\eta ^1 {{\Phi }'_{2i} {\Phi }'_{2j} \mathrm{d}\chi } } \right) \nonumber \\&\left( {\int _0^\eta {\Phi _{1m} {\Phi }''_{1k} \mathrm{d}\chi } +\int _\eta ^1 {\Phi _{2m} {\Phi }''_{2k} \mathrm{d}\chi } } \right) \end{aligned}$$

(42)

$$\begin{aligned} F_{m}= & {} \int _0^\eta {\Phi _{1m} \bar{{F}}_{1} \mathrm{d}\chi } +\int _\eta ^1 {\Phi _{2m} \bar{{F}}_{2} \mathrm{d}\chi } \end{aligned}$$

(43)

$$\begin{aligned} \Lambda _{mn}= & {} \delta _{mn} -\mu \Phi _{1m} \Phi _{1n} \left| {_{\eta } } \right. \end{aligned}$$

(44)

where $\delta _{mn}$ refers to the Kronecker delta. Moreover, the overdot $({}^{.})$ and the superscript prime $(\,)^{\prime }$ symbolize differentiation with respect to $\tau$ and $\chi$, respectively.

5 Comparative analysis between analytical and numerical responses

In order to verify the accuracy of the MMS used to obtain later results, a comparison is made between the results of the perturbation method and the Galerkin-based numerical method for the proposed system. It should be mentioned that the equations of motion are integrated numerically using the fourth-order Runge–Kutta algorithm at different frequencies. Based on the analytical curve plots, the frequency range is chosen to cover the complete nonlinear frequency characteristic of the mechanical resonator.

Thereafter, using each numerical simulation, the dimensionless maximum steady-state amplitude is extracted and the numerical points are superimposed on the same plot with the analytical curves. This analysis is performed for various physical parameters. Therefore, dynamic characteristics ranging from slightly to extremely nonlinear as the temperature rise ($\Delta \overline{T}$) and the surface temperature difference $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}}$ increase are seen. Figures 4, 5, 6 and  7 illustrate some comparisons between the numerical integration and analytical model. Since the maximum dimensionless displacement occurs at mid-span of the CNT, it is assumed that the nanoscale particle is deposited at the location $\eta = 0.5$. Moreover, in all cases, the particle’s mass is set equal to $m=0.218\hbox { yg}$ and the nonlocal parameter and Q-factor are set to $e_{0}a =2\hbox { nm}$, $Q=5$, respectively.

Since the impacts of various thermal loads on the nonlinear forced vibration response of CNT-based mass detectors are investigated, the focus is paid on the stable branches of frequency response curves to identify the specific ranges of the temperature rise and the surface temperature difference in which the results obtained through the method of multiple scales (MMS) for the stable branches can be verified by using the Galerkin-based numerical technique. Therefore, unstable branches of frequency response curves are not the main target of this work and they have not been captured by Runge–Kutta numerical method in Figs. 4, 5, 6 and 7.

Fig. 4

The amplitude–frequency response of the CNT-based mass sensor subjected to thermal loads in primary resonance condition considering $e_{0}a =2\hbox { nm}$, $Q=5$, $F=2$, $\Delta {\overline{T}}=50\hbox { K}$, $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}} =60\hbox { K}$, $\eta = 0.5$, and $m=0.218\hbox { yg}$, a UTD, b LTD, and c NLTD

In Fig. 4, the frequency response curves are shown for the excitation force amplitude of $F=2$ temperature rise of $\Delta {\overline{T}}=50\hbox { K}$ and the surface temperature difference of $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}} =60\hbox { K}$. This figure compares the results of the perturbation method and long-time integration technique for UTD, LTD, and NLTD cases. As previously mentioned, Galerkin’s method is based on the first three mode approximations to discretize the governing equations of motion. The figure represents excellent agreement between these two methods. This is explained by the fact that low forcing amplitude and small quality factor are chosen, so significant effects of the nonlinearities are not yet seen.

The dynamic responses of the CNT-based mechanical resonator subjected to NLTD obtained by the aforementioned two methods are shown in Fig. 5 for $F=2$, $(T_{o}-T_{i})_{\mathrm{NLTD}} =40\hbox { K}$, and three different values of the temperature rise ($\Delta {\overline{T}}=30\hbox { K}$, $\Delta {\overline{T}}=50\hbox { K}$, and $\Delta {\overline{T}}=70\hbox { K}$). For this set of parameters, the resonator exhibits a strongly hardening behavior as the temperature rises. In particular, this behavior becomes more pronounced as the temperature rise, $\Delta {\overline{T}}$, increases. Thus, for high temperatures, the jumping frequencies predicted by the perturbation technique are higher than those predicted by Galerkin’s method. Additionally, for the given set of parameters, as the average temperature rise ($\Delta {\overline{T}}$) exceeds 50 K, the MMS fails to predict the resonant frequency of the CNT-based resonator at jumping points.

Fig. 5

The amplitude–frequency response of the CNT-based mass sensor subjected to NLTD in primary resonance condition considering $e_{0}a =2\hbox { nm}$, $Q=5$, $F=2$, $(T_{o}-T_{i})_{\mathrm{NLTD}} =40\hbox { K}$, $\eta = 0.5$, and $m= 0.218\hbox { yg}$, a$\Delta {\overline{T}}=30\hbox { K}$, b$\Delta {\overline{T}}=50\hbox { K}$, and c$\Delta {\overline{T}}=70\hbox { K}$

Fig. 6

The amplitude–frequency response of the system subjected to NLTD in primary resonance condition considering $e_{0}a =2\hbox { nm}$, $Q=5$, $F=2$, $\Delta {\overline{T}}=50\hbox { K}$, $\eta = 0.5$, $m= 0.218\hbox { yg}$, and $(T_{o}-T_{i})_{\mathrm{NLTD}} =$a 40 K and b 80 K

A detailed interpretation of the frequency response function curves is elaborated on the system under NLTD in Fig. 6 considering two different values of the surface temperature difference $((T_{o}-T_{i})_{\mathrm{NLTD}} =40\hbox { K}$ and $(T_{o}-T_{i})_{\mathrm{NLTD}} =80\hbox { K})$. As shown in Fig. 6a, the shapes of the peaks and their predicted amplitudes using the analytical model are in excellent correlation with numerical measured points. Indeed, the perturbation technique and Galerkin’s method have a good match for low values of the surface temperature difference. By contrast, MMS cannot accurately predict the dynamical characteristics of the system when the CNT-based resonator is exposed to higher values of the surface temperature difference, as illustrated in Fig. 6b. It is important to mention that the surface temperature difference $(T_{o}-T_{i})$ behaves as an amplification factor to amplify the nonlinear response of the CNT-based mass sensor. Concerning the number of modes, the numerical results are identical with two or three modes and the difference between one and two modes is negligible when compared to the peak amplitude.

Figure 7 indicates the system frequency response when considering two different values of the temperature rise ($\Delta {\overline{T}}=30\hbox { K}$ and $\Delta {\overline{T}}=50\hbox { K}$) and when the excitation force amplitude is raised to $F=3$. As shown, increasing the excitation forcing value enhances the hardening behavior of the system. Consequently, the dynamic behavior of the resonator becomes strongly nonlinear, as shown in Fig. 7, even when the nanostructure is subjected to low values of the temperature rise. Moreover, as the excitation force amplitude rises, the oscillation amplitude increases and the spectral curves obtained analytically begin to bend toward higher frequencies than those predicted by Runge–Kutta method. It is worth noting that in the strongly nonlinear cases of Figs. 5c and 7b, the difference between the numerical results for one mode and the findings for two or three modes is noticeable around resonant frequencies.

Fig. 7

The amplitude–frequency response of the system subjected to NLTD in primary resonance condition considering $e_{0}a =2\hbox { nm}$, $Q=5$, $F=3$, $(T_{o}-T_{i})_{\mathrm{NLTD}} =40\hbox { K}$, $\eta = 0.5$, and $m=0.218\hbox { yg}$, a$\Delta {\overline{T}}=30\hbox { K}$ and b$\Delta {{\overline{T}}}=50\hbox { K}$

Fig. 8

Frequency response function close to the first natural frequency $(\omega _{1})$ considering $e_{0}a = 2\hbox { nm}$, $Q=5$, $F=2$, $(T_{o}-T_{i} )_{\mathrm{LTD,NLTD}} =40\hbox { K}$, $\eta = 0.5$, and $m=0.218\hbox { yg}$, a UTD, b LTD, and c NLTD

6 Investigations on the nonlinear responses of the doubly clamped CNT-based mass detector

In this section, after extensive comparative analyses of the MMS technique versus the numerical simulations, the influences of different parameters such as the temperature change, the surface temperature difference, the external force amplitude, and the type of thermal loading on the frequency response function of the CNT-based resonator are investigated. Since the discrepancy between the results of MMS compared to Galerkin’s method grows as the temperature rise and the surface temperature difference exceed 50 K and 60 K, the maximum values of $\Delta {\overline{T}}$ and $(T_{o}-T_{i} )_{LTD,\,NLTD}$ are set equal to 50 K and 60 K, respectively.

Fig. 9

Frequency response function close to the first natural frequency ($\omega _{1})$ considering $e_{0}a = 2\hbox { nm}$, $Q=5$, $F=2$, $\Delta {\overline{T}}=50\hbox { K}$, $\eta = 0.5$, and $m=0.218\hbox { yg}$, a LTD, and b NLTD

Graphically illustrated in Fig. 8 is the effect of the temperature rise on the distribution of dimensionless vibration amplitude versus the excitation frequency associated with various types of thermal loading. According to this figure, for all three types of thermal loads, a slight reduction in the resonant frequency of the first mode is observed as the temperature increases. Further, by increasing the temperature rise, the forced oscillation amplitude of the CNT increases and this trend is the same for all types of temperature rise. This is due to the reduction in the total stiffness of the CNT, since the geometrical stiffness diminishes when the temperature rises in the pre-buckling region. As a result, by reducing the rigidity of the CNT, the dimensionless nonlinear amplitude peak increases, while the resonant frequency of the nanobeam decreases. A close scrutiny of the obtained results reveals that the amplitude peak of the CNT under LTD is lower than that of NLTD case and higher than that for UTD case. Moreover, the assumption of NLTD across the thickness yields the lowest values of the excitation resonant frequency. Consideration of NLTD through the radius of the nanobeam estimates the smallest values for the rigidity of the CNT-based resonator compared to UTD and LTD. In addition, the nonlinear behavior of the nanostructure subjected to NLTD is more pronounced than that under UTD and LTD.

The plotted curves in Fig. 9 display the variations in the dimensionless nonlinear amplitude with respect to the excitation frequency of the CNT-based resonator under LTD and NLTD for three different values of the surface temperature difference. Enhancing the surface temperature difference leads to increment in the oscillation amplitude. However, this trend is opposite for the variations in the excitation frequency with the surface temperature difference and the frequency decreases as the surface temperature difference rises. This feature is attributed to the fact that the surface temperature difference amplifies the softening behavior of the CNT-based resonator subjected to LTD or NLTD. Also, in increasing the surface temperature difference, the nonlinear hardening effects in the CNT-based resonator increase.

Influences of the magnitude of the external force on the primary resonance of the vibrations of the CNT under UTD, LTD, and NLTD are depicted in Fig. 10. As expected, for all three types of thermal loading, increasing the amplitude of the external force results in an increase in both oscillation amplitudes and resonant frequencies. As evidenced in Fig. 10, the nonlinear behavior of the system is influenced slightly by the excitation force amplitude when considering the three different representations of the thermal loading.

Fig. 10

Frequency response function close to the first natural frequency ($\omega _{{1}})$ considering $Q=5$, $\Delta {\overline{T}}=40\hbox { K}$, $(T_{o}-T_{i} )_{\mathrm{LTD,NLTD}} =60\hbox { K}$, $\eta = 0.5$, and $m=0.218\hbox { yg}$, a UTD, b LTD, and c NLTD

7 Resonant mass sensing for forced vibrations under thermal loading

The principles of mass sensing, based on the resonant frequency shift and large amplitude shift techniques, consist of measuring the induced shifts in the resonant frequency and the nonlinear amplitude resulted by deposited mass on the resonator. To the authors’ knowledge, it is the first time that a CNT subjected to UTD, LTD, and NLTD and excited by an external harmonic force demonstrating nonlinear behavior is investigated for mass sensing applications. The resonant sensing technique is used to derive the frequency and maximum amplitude shifts under various types of thermal loadings. A schematic view of the resonant frequency and nonlinear large amplitude shifts due to an attached atomic-scale particle is illustrated in Fig. 11. As stated earlier, the greatest impacts of the nanoscale particle on the resonant frequency and the nonlinear amplitude are seen when it is attached at the location of $\eta = 0.5$. Accordingly, it is assumed that the nanoscale mass is deposited at the mid-span of the CNT-based resonator. Clearly, adding the mass to the surface of the CNT is accompanied with an increase in the maximum amplitude, while the resonant frequency diminishes when the atomic-scale particle is deposited on the CNT-based resonator. Therefore, the nonlinear amplitude is directly proportional to the value of the attached mass. By contrast, the resonant frequency is inversely proportional to the mass of the particle. As previously mentioned, the maximum values of the temperature rise and the surface temperature difference are assumed to be $\Delta {\overline{T}}=50\hbox {K}$ and $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}}=60\hbox {K}$, respectively.

Fig. 11

Schematic configuration of the shift in the dimensionless resonance frequency close to the first natural frequency $(\omega _{1})$ and nonlinear dimensionless amplitude shift of the sensor due to an attached atomic-scale particle

7.1 Impacts of different thermal loads on the large amplitude-based mass detection sensitivity

In order to investigate the impacts of different parameters on the large amplitude-based mass detection capability, the variations in the deflection amplitude and the nonlinear amplitude shift with respect to the position of the particle are presented in this section for different values of $\Delta {\overline{T}}$, $(T_{o}-T_{i} )_{\mathrm{LTD,NLTD}}$, and ${\mu }$.

The dimensionless oscillation amplitude and the amplitude shift as a function of the mass location are presented in Fig. 12 for the CNT subjected to UTD, LTD, and NLTD considering various temperature rises. As expected, the most sensitive point to add the nanoscale particle is the mid-span of the nanobeam. Inspecting this figure, it is easily deduced that the temperature rise has a significant effect on the maximum amplitude shift of the CNT for all three types of temperature distributions. From Fig. 12, it is revealed that increasing the temperature will raise the nonlinear amplitude shift dramatically. To elaborate more, for higher values of temperature, the CNT-based resonator becomes softer. Thus, by augmenting the temperature the nonlinear amplitude and hence the shift induced in the maximum displacement will increase. In addition, assuming NLTD across the thickness of the CNT leads to higher values of the amplitude shift compared to UTD and LTD, attributed to the fact that the weakening effect of NLTD on the nanoscale structure is more pronounced than that of UTD and LTD.

Fig. 12

Deflection amplitude and nonlinear amplitude-based mass sensing study highlighting the temperature rise for the resonator subjected to various thermal loads considering $e_{0}a = 2\hbox { nm}$, $Q=5$, $F=2$, $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}} =40\hbox { K}$, and $m=0.218\hbox { yg}$, a$\Delta {\overline{T}}=30\hbox { K}$, b$\Delta {\overline{T}}=40\hbox { K}$, and c$\Delta {\overline{T}}=50\hbox { K}$

The plotted curves in Fig. 13 demonstrate the dependency of the maximum amplitude shift to the surface temperature difference for the nanobeam subjected to LTD and NLTD. It is apparent that the surface temperature difference has increasing effect on the change induced in the maximum displacement. As explained earlier, the rigidity of the CNT diminishes by increasing the surface temperature difference, leading to an increment in the maximum displacement. As a result, for both LTD and NLTD cases, increasing the surface temperature difference yields larger values of the maximum displacement shift.

Fig. 13

Deflection amplitude and nonlinear amplitude-based mass sensing study highlighting the surface temperature difference and the type of temperature profile considering $F=2$, $Q=5$, $\Delta {\overline{T}}=50\hbox { K}$, $e_{0}a = 2\hbox { nm}$, and $m=0.218\hbox { yg}$, a LTD, and b NLTD

The obtained results in Figs. 12 and 13 are also presented in Table 1. To evaluate the discrepancy among the effects of three types of thermal loading, namely UTD, LTD, and NLTD, on the maximum amplitude and maximum amplitude shift, the nonlinear temperature distribution (NLTD) is considered as the reference condition. Accordingly, the percentage errors in the dimensionless maximum amplitude $(a_{(\mathrm{UTD})},\,a_{(\mathrm{LTD})})$ and the maximum amplitude shift ($\Delta a_{(\mathrm{UTD})},\,\Delta a_{(\mathrm{LTD})})$ of the CNT with the assumptions of uniform and linear temperature distributions with respect to the nonlinear temperature gradient are defined as:

$$\begin{aligned}&\left( {e_{a(\mathrm{UTD})} ,e_{a(\mathrm{LTD})} } \right) \nonumber \\&\quad =\left( {\frac{\left( {a_{(\mathrm{UTD})} ,a_{(\mathrm{LTD})} } \right) -a_{(\mathrm{NLTD})} }{a_{(\mathrm{NLTD})} }} \right) \times 100\% \end{aligned}$$

(45)

$$\begin{aligned}&\left( {e_{\Delta a(\mathrm{UTD})} ,e_{\Delta a(\mathrm{LTD})} } \right) \nonumber \\&\quad =\left( {\frac{\left( {\Delta a_{(\mathrm{UTD})} ,\Delta a_{(\mathrm{LTD})} } \right) -\Delta a_{(\mathrm{NLTD})} }{\Delta a_{(\mathrm{NLTD})} }} \right) \times 100\% \nonumber \\ \end{aligned}$$

(46)

Table 1 compares the results of UTD, LTD, and NLTD and illustrates the percentage errors in the dimensionless maximum displacement and the maximum displacement shift of the CNT under UTD and LTD with respect to the findings obtained under the NLTD case. As expected, the percent deviations of the results under UTD are higher than those of the LTD case. The obtained results show that the percentage deviations of maximum amplitude and maximum amplitude shift under UTD and LTD are proportional to the temperature rise and the surface temperature difference. By advancing the temperature rise and the surface temperature difference, the maximum displacement and the shift induced in the maximum displacement would rise. Moreover, at a constant value of temperature rise and surface temperature difference, the percent errors in the maximum amplitude and the maximum amplitude shift increase by enhancing the excitation force amplitude for both UTD and LTD cases. Also, it should be stated that the external force magnitude has less important influence on the errors under UTD and LTD, while the effects of the temperature rise and the surface temperature difference are more pronounced.

Table 1 Nonlinear dimensionless amplitude and amplitude-based mass sensitivity difference due to UTD, LTD, and NLTD and percentage error in UTD and LTD with respect to NLTD for different values of $\Delta {\overline{T}},\,(T_{o}-T_{i})_{\mathrm{LTD,NLTD}}$, and the excitation force amplitude F considering $e_{0}a =2\hbox { nm}$, $Q=5$, $\eta = 0.5$, and $m=0.218\hbox { yg}$

In order to perform a crucial study to explain how the value of the deposited mass could affect the resonant amplitude and the resonant amplitude shift, Fig. 14 is plotted. In this case, we plot the variations in the maximum displacement and the maximum displacement shift with respect to the mass location for the CNT-based resonator subjected to UTD, LTD, and NLTD considering three distinct values of the attached mass. A close scrutiny of the obtained results in Fig. 14 reveals that by increasing the mass of the atomic-scale particle, the maximum displacement and hence the maximum displacement shift would rise drastically for all three types of thermal loading.

Fig. 14

Deflection amplitude and nonlinear amplitude-based mass sensing study highlighting the mass ratio considering $e_{0}a = 2\hbox { nm}$, $F=2$, $Q=5$, $\Delta {\overline{T}}=40\hbox { K}$, and $(T_{o}-T_{i} )_{\mathrm{LTD,NLTD}} =40\hbox { K}$, a$\mu =0.002$, b$\mu =0.006$, and c$\mu =0.01$

The illustrated data in Fig. 14 are also tabulated in Table 2. From the obtained results listed in Table 2, it can be seen that by fixing the values of the temperature rise, the excitation force amplitude, and the surface temperature difference, augmenting the mass of the added particle yields higher values of the percentage uncertainties in the dimensionless maximum amplitude and maximum amplitude shift for both UTD and LTD cases. In addition, for both the UTD and LTD cases, the percentage errors in the maximum amplitude shift increase with higher rate compared to the percent errors in the maximum amplitude.

Table 2 The nonlinear dimensionless amplitude and the shift induced in the amplitude due to a deposited atomic-scale particle and the percentage deviations of the results under UTD and LTD from those under NLTD for different mass ratios considering $F=2$, $Q=5$, $\Delta {\overline{T}}=40\hbox { K}$, $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}} =40\hbox { K}$, $e_{0}a = 2\hbox { nm}$, and $\eta = 0.5$

7.2 Influences of various thermal loads on the resonant frequency-based mass detection sensitivity

Through this section, analytical results are presented for resonant frequency-based mass sensing of the CNT-based resonator. The effects of the temperature rise in conjunction with the three types of temperature distribution, the surface temperature difference, the excitation force amplitude, and the mass of the atomic-scale particle on the resonant frequency shift of the nanobeam are examined. Then, a parametric study indicating the significant influences of various parameters on the percentage deviations of the dimensionless resonant frequency and resonant frequency shift for UTD and LTD cases from the reference case (NLTD) is performed.

The maps of the nonlinear dimensionless resonant frequency and frequency shift versus the mass position are shown in Fig. 15 for all types of thermal loadings and three different values of the temperature rise. Irrespective of the thermal loading type and the value of the temperature rise, the highest resonant frequency shifts for the first mode are obtained when the atomic-scale particle is placed at $\eta = 0.5$. Moreover, with the increase in the temperature rise, the nonlinear resonant frequency and frequency shift reduce for all kinds of thermal environment. Physically, this decrease in the system’s resonant frequency is attributed to the mechanical softening caused by thermal loadings in the pre-buckling region. Furthermore, the type of thermal loading has a major role on the resonant frequency-based mass sensing capability, especially at higher values of the temperature rise. As expected, the assumption of NLTD through the radius of the CNT yields lower resonant frequencies and frequency shifts than LTD, while the LTD assumption yields lower shifts than those obtained through the UTD assumption.

Fig. 15

Nonlinear resonance frequency and frequency shifts highlighting the temperature rise for the system subjected to various thermal loads considering $e_{0}a = 2\hbox { nm}$, $Q=5$, $F=2$, $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}} =40\hbox { K}$, and $m=0.218\hbox { yg}$, a$\Delta {\overline{T}}=30\hbox { K}$, b$\Delta {\overline{T}}=40\hbox { K}$, and c$\Delta {\overline{T}}=50\hbox { K}$

A series of benchmark resonant frequency-based responses of the CNT obtained in LTD and NLTD cases are illustrated in Fig. 16 for different values of the surface temperature difference. Using Fig. 16 as a benchmark, one can characterize the impact of the surface temperature difference on the resonant frequency-based dynamics of the CNT resonator. As shown in Fig. 16, for both LTD and NLTD cases, increasing the surface temperature difference leads to a dramatic decrease in the resonant frequency and frequency shift of the nanobeam. Indeed, the resonator exhibits softening behavior in the presence of higher values of the surface temperature difference which is due to the reducing effect of the surface temperature difference on the total stiffness of the CNT in the pre-buckling regime.

Fig. 16

Nonlinear resonance frequency and frequency-based mass sensing study highlighting the surface temperature difference and the type of temperature profile through the thickness of the CNT considering $F=2$, $Q=5$, $\Delta {\overline{T}}=50\hbox { K}$, $e_{0}a = 2\hbox { nm}$, and $m=0.218\hbox { yg}$, a LTD, and b NLTD

The results shown in the plotted curves in Figs. 15 and 16 are also consolidated in Table 3. As highlighted previously, the temperature rise and the surface temperature difference reduce the nondimensional resonant frequency and frequency shift in the pre-buckling oscillation regime. This is predicted because the temperature rise and the surface temperature difference have softening effects on the nanostructure in this region. According to the presented values in Table 3, one can easily find that the nonlinear dimensionless resonant frequency would advance by augmenting the excitation force amplitude. On the contrary, it is interesting to see that higher values of the external force magnitude yield lower nondimensional resonant frequency shifts. In this section, the primary goal is to investigate the impacts of various parameters on the uncertainties in the dimensionless resonant frequency and frequency shift in both UTD and LTD cases with respect to the reference case (NLTD). For UTD and LTD cases, the percent errors in the resonant frequency and the resonant frequency shift are obtained directly by using:

$$\begin{aligned}&\left( {e_{\Omega (\mathrm{UTD})} ,e_{\Omega (\mathrm{LTD})} } \right) \nonumber \\&\quad =\left( {\frac{\left( {\Omega _{(\mathrm{UTD})} ,\Omega _{(\mathrm{LTD})} } \right) -\Omega _{(\mathrm{NLTD})} }{\Omega _{(\mathrm{NLTD})} }} \right) \times 100\% \end{aligned}$$

(47)

$$\begin{aligned}&\left( {e_{\Delta \Omega (\mathrm{UTD})} ,e_{\Delta \Omega (\mathrm{LTD})} } \right) \nonumber \\&\quad =\left( {\frac{\left( {\Delta \Omega _{(\mathrm{UTD})} ,\Delta \Omega _{(\mathrm{LTD})} } \right) -\Delta \Omega _{(\mathrm{NLTD})} }{\Delta \Omega _{(\mathrm{NLTD})} }} \right) \times 100\% \nonumber \\ \end{aligned}$$

(48)

where $\Omega _{(\mathrm{UTD})}$ and $\Omega _{(\mathrm{LTD})}$ represent the dimensionless resonant frequencies in UTD and LTD cases, respectively. Moreover, the dimensionless resonant frequency shifts of the CNT under UTD and LTD are denoted by $\Delta \Omega _{(\mathrm{UTD})}$ and $\Delta \Omega _{(\mathrm{LTD})}$, respectively.

Table 3 Nonlinear dimensionless resonance frequency and frequency-based mass sensitivity difference due to UTD, LTD, and NLTD and percentage error in resonance frequency and shift under UTD and LTD with respect to NLTD for different values of $\Delta {\overline{T}}$, $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}}$, and the excitation force amplitude F for a CNT-based mass sensor under external harmonic excitation considering $e_{0}a =2\hbox { nm}$, $Q=5$, $\eta = 0.5$, and $m=0.218\hbox { yg}$

Fig. 17

Nonlinear resonance frequency and frequency-based mass sensing study highlighting the mass ratio considering $e_{0}a = 2\hbox { nm}$, $F=2$, $Q=5$, $\Delta {\overline{T}}=40\hbox { K}$, and $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}} =40\hbox { K}$, a$\mu =0.002$, b$\mu =0.006$, and c$\mu =0.01$

Table 4 The nonlinear dimensionless resonance frequency and shift of the resonator subjected to UTD, LTD, and NLTD and the percentage deviations of the results under UTD and LTD from those under NLTD for different mass ratios considering $F=2$, $Q=5$, $\Delta {\overline{T}}=40\hbox { K}$, $(T_{o}-T_{i})_{\mathrm{LTD,NLTD}} =40\hbox { K}$, $e_{0}a = 2\hbox { nm}$, and $\eta = 0.5$

As predicted, by increasing the surface temperature difference, the discrepancy among the results under UTD, LTD, and NLTD would rise drastically; thus, the percentage errors in the resonant frequency and frequency shift under both UTD and LTD with respect to NLTD would increase significantly. It is worth mentioning that the increasing effect of the surface temperature difference on the relative errors becomes more pronounced at higher levels of the temperature rise and lower values of the surface temperature difference. As presented in Table 3, for both UTD and LTD, percentage deviations of the resonant frequency degrade by augmenting the excitation force amplitude, while the percent errors in the resonant frequency shift grow with the rise of the applied force magnitude. According to Table 3, it is concluded that when the temperature grows, the percent deviations of the resonant frequency under both UTD and LTD from the results of NLTD would improve considerably.

In Fig. 17, the plotted curves elucidate the impacts of the attached mass on the variations in the dimensionless resonant frequency and frequency shift versus the location of the deposited atomic-scale particle for all three types of temperature profile across the thickness of the CNT. Clearly, an increase in the mass of the atomic-scale particle is accompanied by a reduction in the dimensionless resonant frequency. Unlike the resonant frequency, the induced shift in the nondimensional resonant frequency rises dramatically by advancing the mass of the nanoparticle. This is because the resonant frequency is inversely proportional to the mass of the system. Therefore, an increase in the deposited mass inherently increases the resonant frequency shift of the system subjected to any kind of thermal loading.

To provide extensive analytical results, Table 4 presents the influences of the attached mass on the dimensionless resonant frequency and frequency shift of the nanobeam under the three considered temperature gradients. In addition, regarding the impacts of the deposited mass on the resonant frequency-based dynamics of the CNT, further studies have been carried out to investigate the effects of the added mass on the percentage deviations of the resonant frequency and frequency shift of the nanostructure. As explained earlier, for all types of thermal loading, augmenting the mass of the deposited atomic-scale particle reduces the dimensionless resonant frequency, while the resonant frequency shift is magnified by increasing the attached mass. However, the opposite variation trends of relative errors in the resonant frequency and frequency shift are observed in Table 4. This implies that CNTs with larger attached mass reflect higher values of the percent uncertainties in the resonant frequency, while the percentage errors in the resonant frequency shift diminish when the mass of the atomic-scale particle increases.

8 Conclusions

The nonlinear dynamic behaviors in nanomechanical resonators are more pronounced than their macroscale counterparts systems due to their small size and typically low mechanical damping. This work has detailed the development and limits of applicability of an analytical model to assess the nonlinear dynamics of CNT-based mass sensors subjected to different thermal loadings and external harmonic excitations in the pre-buckling oscillation regime. This model was based on the perturbation technique (MMS), in conjunction with the modal decomposition using Galerkin’s procedure. This approach was used to study the influences of various thermal loadings on the large amplitude/resonant frequency-based mass sensing capabilities of bridged CNT-based resonators excited under primary resonance. Considering Eringen’s nonlocal elasticity and Euler–Bernoulli beam theory (including the von Kármán-type displacement–strain relationship), the nonlinear equations of motion were derived using the Hamilton’s principle. The governing partial differential equations were transformed into a system of coupled nonlinear ordinary differential equations using Galerkin’s decomposition method. The model was compared to numerical simulations using the Runge–Kutta algorithm, demonstrating that the analytical findings corroborated quantitatively and qualitatively with numerical results. Afterward, a parametric study for bridged CNT-based resonators subjected to external harmonic excitation and under different sets of thermal environmental conditions was conducted for the pre-buckling configuration.

In conclusion, for any kind of temperature distribution, the presence of larger $\Delta {\overline{T}}$ and $(T_{o}-T_{i})$ increases the maximum nonlinear amplitude and amplitude shift of the CNT-based mass sensor. On the contrary, the nonlinear resonant frequency and frequency shift decreased as $\Delta {\overline{T}}$ and $(T_{o}-T_{i})$ increased. This feature was attributed to the fact that thermally induced compressive stress reduces the stiffness and hence weakens the CNT. Also, the dimensionless nonlinear amplitude and amplitude shift increase drastically by improving the magnitude of the applied force. Moreover, increasing the excitation force amplitude results in a slight increment in the nondimensional resonant frequency. The trend is reversed for variations in the resonant frequency shift with the excitation force. In addition, the assumption of NLTD yields the highest nonlinear amplitude and amplitude shifts in the pre-buckling regime. Furthermore, the relative discrepancies among the results of UTD, LTD, and NLTD increased as a function of $(T_{o}T_{i})$. For example, changing the value of $(T_{o}T_{i})$ from 40 to 60 K results in increasing the values of $e_{{\varDelta }{a}},{\mathrm{UTD}}$ and $e_{{\varDelta }{a}},{\mathrm{LTD}}$ from 5.1955% and 3.7989% to 8.7634% and 5.4301%, respectively, for the fixed value of $\Delta {\overline{T}}=50\hbox {K}$ and $F=2$. Also, it is concluded that the percentage deviations of the nonlinear amplitude and amplitude shift under UTD and LTD from NLTD would rise dramatically as the temperature grows. We expect that introducing such a design into nanotechnology for mass sensing applications of nanoscale resonating systems can be potentially beneficial in terms of increasing the nonlinear large amplitude-based mass detection sensitivity of these systems in serious thermal environments.