1 Introduction

The exploitation and management of surface and groundwater resources are one of the main components of the development of human societies, agricultural projects, and industrial projects (Torfi et al. 2021). Collection and storage of surface water are one means of conserving water resources, and are usually performed by constructing dams (Abbasi et al. 2019; Sarvarinezhad et al. 2022). Among the various types of dams, earthen dams are the most compatible with the environment (Stephens et al. 2010). The safety of such hydraulic structures should always be monitored due to the use the erodible materials in their bodies. The performance evaluation of a dam is called monitoring. Monitoring means evaluating the performance of a structure and adapting it to pre-determined goals, and appropriate corrective action is taken if necessary (Walder and O'Connor 1997). The monitoring of important hydraulic structures is performed with precision instruments, which are usually installed inside or on the body during construction. Investigation of pore water pressure, horizontal and vertical displacements, and flow seepage are always issues that should be monitored and controlled during the construction and operation of earthen dams (Penman 2018). Predicting the possible behavior of the dam in the future under different loading conditions in the design phases is carried out using numerical simulation. During the construction and exploitation period, hydraulic and geotechnical characteristics may change due to different loading (different values and conditions of water level in the reservoir) conditions (Sousa et al. 2012). Hence, the results of numerical simulation may differ slightly from the observed values of precision instruments (Salmasi and Mansuri 2014). Nowadays, the use of numerical and soft computing models in simulation and estimating the hydraulic and geotechnical behavior of earthen dams has become very popular (Moharrami et al. 2014; Salmasi and Abraham 2020; Sharghi et al. 2019), which can be found in the research of Tayfur et al. (2005) used an artificial neural network (ANN) and finite element method (FEM) to predict piezometric pressure in an earthen dam in Poland. They used the water level in the dam’s reservoir as upstream boundary conditions in FEM and as an input variable in ANN. Their results showed that both ANN and FEM models have good accuracy in estimating piezometric pressure. Ersayın (2006) used ANN to predict piezometric pressure and seepage discharge in the Jeziorsko earth-fill dam (Turkey). He used data on water surface elevation (WSE) upstream and downstream of the dam as model inputs and piezometric pressure inside the dam and seepage discharge collected by collectors as model output. The results of his research showed that the ANN performs well in estimating seepage flow and piezometer pressure. Miao et al. (2012) used the optimized neural network model to predict seepage in the Diyala Earthen Dam (China). They expressed the accuracy of the developed model as satisfactory. Nourani and Babakhani (2013); Sharghi et al. (2018) used the radial neural network method (RBF) to estimate the seepage of the SattarKhan earthen dam (Iran). They compared the results of the RBF model with the results of the numerical solution of Laplace equations based on the finite difference method (FDM). Comparing their results indicate that the RBF method is more accurate than the FDM. Ranković et al. (2014) used a multilayer artificial neural network (MLPNN) model to predict the piezometric pressure in the earthen dam of Iron Gate No. 2. In the development of their ANN, they examined a variety of transfer functions including hyperbolic tangent, sigmoid, linear, and sigmoid logarithm functions. The results of their modeling confirm the appropriate accuracy of the ANN in estimating the piezometric pressure in the dam core. Roushangar et al. (2016) predicted the daily seepage discharge from the Zonoz earthen dam by combining the wavelet model with the Gaussian process regression (GPR) method. For this purpose, they first analyzed the seepage data using the time series wavelet model and then they introduced its results to the GPR model. The results of their research showed that the model developed them has good accuracy in estimating seepage discharge. Sharghi et al. (2018) estimated the seepage discharge in the Sattar Khan earthen dam using MLPNN, support vector machine (SVM), and adaptive inference fuzzy neural system (ANFIS) models. They used the WSE in the reservoir and downstream of the dam as inputs of mentioned soft computing models. Their research showed that all the models used have good accuracy in estimating the seepage discharge. Parsaie et al. (2021) to model and estimate the piezometric pressure and seepage pressure in Shahid Kazemi Bukan earthen Dam developed soft computing models including adaptive multivariate regression (MARS), group method of data handling (GMDH), vector machine support (SVM), Tree M5 algorithm and as well as MLPNN. To design the pattern of input variables, they used time delays of time series water surface level in the dam reservoir. The results of their research showed that soft computing models have very good accuracy in estimating and modeling piezometric pressure, while the accuracy of some of them in modeling and estimating seepage flow is appropriate. The reason is that the phenomenon of seepage in the body and the foundation of the earth dam is very nonlinear.

Bouchehed et al. (2023) successfully utilized three soft computing techniques including support vector regression (SVR), relevance vector machine (RVM), and GPR to predict the seepage discharge through embankment dams. They used piezometer heads (several piezometers in the dam's body) as inputs and seepage discharge as targets.

A review of past research shows that modeling and estimating seepage flow and piezometric pressure in earthen dams at different stages of design and operation is important and many researchers have studied it. The study of the methods used shows that so far few researchers from the point of view of time series analysis have dealt with the problem of hydraulic modeling of earth dams (piezometric pressure) with the help of wavelet theory. Therefore, in this paper, the problem of the piezometric head is studied from the time series point of view. To this end, the wavelet algorithm is used; then soft computing models including MLPNN and SVM are developed based on the results of the wavelet analysis.

2 Material and Methods

2.1 Case Study

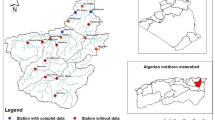
Baft Dam is located 160 km southwest of Kerman and 4 km northeast of Baft city. The dam is a rock-fill Dam with a vertical clay core (Fig. 1). The dam reservoir can store 40 million cubic meters of water. Baft Dam has been constructed to supply drinking water, industrial uses, and agricultural water supply to Baft and Boznjan cities, as well as to control floods and seasonal runoff of the Baft River. Its height from the foundation is 65 m, crest length is 1160 m, reservoir volume is 40 million cubic meters, body volume is 2,700,000 cubic meters, spillway discharge volume is 1055 cubic meters per second, the normal water level in the reservoir is 2352.750 m, and the 850-hectare area is supported by pressure irrigation.

Fig. 1
figure 1

Location, plan, and geographical profile of Baft Dam

Full size image

2.2 Wavelet Transform

Wavelet transform is one of the efficient mathematical transformations used in signal processing. Mathematical transformations are used to obtain additional information from a signal that is not available from the signal itself.

A wavelet is a mathematical function that presents the time scale form of time series and their relationships for time series analysis that includes variables and non-variables. Wavelet analysis offers the use of time intervals for low-frequency information and shorter intervals for high-frequency information. Wavelet analysis can display different aspects of time series data, breakpoints, and discontinuities that other signal analysis methods may not show. A wavelet means a small wave with three characteristics: a limited number of oscillations, a rapid return to travel in both positive and negative directions in its amplitude, and an average of zero. Three properties are necessary conditions for a function wavelet. These properties are called variable acceptance conditions (Nourani et al. 2014). In other words, ψ(x) is a wavelet function if and only if its Fourier transform ψ(ω) satisfies the following condition.

$$\mathop \int \limits_{ - \infty }^{ + \infty } \frac{{\left| {\psi \left( \omega \right)} \right|}}{{\left| \omega \right|^{2} }}{\text{d}}\omega < + \infty$$
(1)

This condition is known as the wavelet acceptance condition ψ(x). The above relation can be considered equivalent to the following formula that must be satisfied.

$$\psi \left( 0 \right) = \mathop \int \limits_{ - \infty }^{ + \infty } \psi \left( x \right){\text{d}}x = 0$$
(2)

This property of a function with a mean of zero is not very restrictive, and thus many functions can be called wavelet functions. ψ(x)is a mother wavelet function in which the functions used in the analysis are scaled and shifted along with the analyzed signal by two mathematical operations: shifting and scaling. Finally, the wavelet coefficients at any point in the signal (b) and for any value on the scale (a) can be calculated by the following equation.

$$\psi_{a.b} \left( x \right) = \frac{1}{\sqrt a }\psi \left( {\frac{x - b}{a}} \right)$$
(3)

Scaling, as a mathematical operator, expands or compresses the signal for the assumed function f(t), if (s < 1) the expanded state is f(st), and if (s > 1), the compressed state is the function f(t). As shown in Eq. 3, in the definition of the wavelet transform, the term of scale (a) is in the denominator, and therefore, if it is (a < 1), the signal is compressed, and if it is (a > 1), the signal is expanded. Also, in the above equation, parameter (b) is modeled as a function of delay or precedence. Finally, the continuous wavelet transform (CWT) can be written as follows:

$${\text{CWT}}_{{\left( {a.b} \right)}} = Wf_{{\left( {a.b} \right)}} = \frac{1}{\sqrt a }\mathop \int \limits_{ - \infty }^{ + \infty } f\left( x \right)\psi \left( {\frac{x - b}{a}} \right){\text{d}}x = \mathop \int \limits_{ - \infty }^{ + \infty } f\left( x \right)\psi_{a.b} \left( x \right){\text{d}}x$$
(4)

2.3 An Overview of the Neural Network Model

The neural network model is one of the most efficient prediction models in the field of modeling hydrological and hydraulic phenomena. The accuracy of this model in various fields of water engineering has been proven by various researchers. for example in water quality and pollution transmission (Nezaratian et al. 2021), scouring (Nou et al. 2022), and sediment transport (Haghiabi 2017). The structure of the neural network applied inputs, number of hidden layers, number of layer neurons, training method, and number of output vectors of each network are effective in evaluating the performance of the model. Also, there is no fixed number of neurons in the hidden layer. The choice of the number of neurons in the latent layer, as well as the number of hidden layers, varies according to the type of problem. In solving hydrological problems, due to severe data changes and data disturbance, backpropagation networks are used due to their high flexibility with an architecture consistent with experience, trial, and error. The number of hidden layers and the number of hidden layer neurons are selected by trial and error and according to the evaluating error of the models. In most water engineering studies, backpropagation multilayer perceptron networks have been used.

In developing the MLPNN, a sigmoidal activating function is usually considered, and the MLPNN is trained by the Levenberg–Marquardt technique due to its greater power and speed than the gradient descent method. Creating a proper network structure is done in three stages: structure consolidation, network training, and network control. The model developed for the MLPNN method has a hidden layer with a sigmoid transfer function.

2.4 An Overview of the Support Vector Machine

The SVM model is an efficient machine learning system based on the theory of constrained optimization that uses the inductive principle of structural error minimization and leads to an overall optimal solution. This model was first proposed by Vapnik (1999), a Russian mathematician. The SVM model is divided into two main groups: (a) the support vector classification model and (b) the support vector regression model (SVR). The SVM classification model is used to solve data classification problems, and the SVM regression model is used to solve prediction problems.

2.5 Support Vector Regression Model (SVR)

As mentioned above, the SVM is based on minimizing the risk structure that is derived from the theory of statistical training. For the application of the SVM in regression problems, Veppnik used an error function to apply SVM to regression problems, which minimizes the errors at a certain distance (ε insensitive) from the actual values.

$$\begin{gathered} L\left( {y,\,f\left( {x,\alpha } \right)} \right) = \left| {y - f\left( {x,\alpha } \right)} \right|_{\varepsilon } = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{for}}\quad \left| {y - f\left( {x - \alpha } \right)} \right| \le \varepsilon } \hfill \\ {\left| {y - f\left( {x - \alpha } \right)} \right| - \varepsilon } \hfill & {i{\text{f}}\quad \left| {y - f\left( {x - \alpha } \right)} \right| > \varepsilon } \hfill \\ \end{array} } \right. \hfill \\ \hfill \\ \end{gathered}$$
(5)

This error function does not take into account values less than \(\varepsilon\). Consider the approximation of the following set of data:

$$D = \left\{ {\left( {x^{1} ,y^{1} } \right), \ldots \left( {x^{i} ,y^{i} } \right)} \right\}\;,\quad \left( {x \in R^{n} ,\,y \in R} \right)$$
(6)

The regression function is estimated by the following function:

$$f\left( x \right) = \left\langle {w,x} \right\rangle + b$$
(7)

which is an internal multiplication. The optimal regression function is expressed by the minimum of the following function.

$$\begin{gathered} \Phi \left( {\omega ,\xi } \right) = \frac{1}{2}\left\| \omega \right\|^{2} + C\sum\nolimits_{i = 1}^{l} {\left( {\xi_{i}^{ - } + \xi_{i}^{ + } } \right)} \hfill \\ {\text{subject}}\;{\text{to}}\;\left\{ \begin{gathered} y_{i} - \left( {\left\langle {\omega ,x_{i} } \right\rangle + b} \right) \le \varepsilon + \xi_{i} \hfill \\ \left( {\left\langle {\omega ,x_{i} } \right\rangle + b} \right) - b \le \varepsilon + \xi_{i}^{*} \hfill \\ \xi_{i} ,\xi_{i}^{*} \ge 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(8)

where C is a predetermined value and is a loose variable that determines the up and down constraints of the system output. If the data is linearly separated, it teaches an optimal level that separates the data without error and with a maximum distance between the page and the nearest training points (backup vectors). If we define training points as input vectors, if the data are linearly separable, the equation is as follows:

$$y = f\left( x \right) = {\text{sign}}\left[ {\sum\nolimits_{i = 1}^{N} {y_{i} a_{i} \left\langle {x_{i} ,x} \right\rangle + b} } \right]\,$$
(9)

where the output of the equation and the class value are the testing samples. The vectors represent input data and the vectors represent the backup vectors. If the data are not linearly separable, samples can be moved to a higher space by applying preprocessing. In this case, relation (12) changes to (13).

$$y = f\left( x \right) = {\text{sign}}\left[ {\sum\nolimits_{i = 1}^{N} {y_{i} a_{i} K\left( {x,x_{i} } \right) + b} } \right]\,$$
(10)

A function is a kernel function that generates internal beats to create machines with different types of nonlinear surfaces in the data space. Different kernels are used for the backup vector machine regression model, which are linear, quadratic, Gaussian, and polynomial. The radial Gaussian kernel (RBF) function is usually better for predicting performance. The equation of this kernel function is as follows:

$$K\left( {x,y} \right) = \exp \left( { - \frac{{\left\| {x_{i} - y_{j} } \right\|}}{{2\sigma^{2} }}} \right)$$
(11)

In constructing an efficient SVM model, the model parameters must be accurately calculated using an optimization method. These parameters are kernel function type, kernel function parameter, regulator parameter C, and accuracy ɛ parameter related to the maximum error in the insensitive region.

2.6 Flowchart of Hybrid Model Development

In this study, two scenarios were considered to estimate the piezometric head in the core of the Baft earth dam. In the first scenario, as the conventional state, the pattern of input variables of the SVM and MLPNN models are designed based on the time delays. In the second scenario, the combined model (combination with wavelet analysis), the signal of input variables is analyzed by wavelet analysis and then introduced as inputs to the mentioned soft computing models. The flowchart of the hybrid model based on a combination with the wavelet algorithm is shown in Fig. 2. In designing the model, the WSE in the dam’s reservoir and its time delays are used as input variables, and the WSE in the piezometer well are used as output.

Fig. 2
figure 2

Flowchart of developing a hybrid neural network model-wavelet

Full size image

3 Results and Discussion

In this section, the results of modeling according to the considered scenarios (first and second scenarios) are presented. To develop MLPNN and SVM, it is necessary to design a pattern of input variables. The design of the input variables is based on the data recorded about the WSE in the dam reservoir in different months and the most important is observable piezometer well (drilled in the core of the earthen dam) data. To estimate the piezometric head in the mentioned well, the time delays of the WSE in the dam’s reservoir are used as inputs. Figure 3 shows the changes in the water level in the dam reservoir as well as the water level in each of the piezometers. As is clear from this figure, during the study period the valve of WSE in the dam’s reservoir varied between 2300 and 2350, while during the same time, the piezometer head in the considered piezometers (well 1) varied between 2342 and 2295. After specifying the pattern of input variables, data preparation is considered. At this stage, the collected data are divided into two categories: training and testing. Eighty percent of the total data were allocated to the training data category for calibration and the remaining 20% to the testing data category used for validation. It should be mentioned that the data confusion approach and random assignment of data to any training and testing data can be used. The next step after data preparation is to design and structure the MLPNN and SVM. In the MLPNN, the number of hidden layers and the number of neurons, and the activation function of each neuron needs to be specified, while in the SVM model, the kernel function needs to be specified. The following is the process of developing a neural network model. As mentioned, the first step after preparing the data is to determine the pattern of input variables. In Table 1, the pattern of input variables based on time delays of WSE in the dam’s reservoir was determined. For this purpose, up to five units of time delay are considered. The design and development of the MLPNN model is a trial-and-error process, although the advice of previous researchers who have worked in this field would be helpful. According to the researchers, firstly, a hidden layer with some neurons equal to the number of input variables is considered. In the next step, another function of the transfer functions is examined. At this stage, one or more suitable transfer functions may be selected, the final choice of which will be determined based on the design experience as well as the performance history of that function in previous studies. At this stage, if the statistical indices of model accuracy are not appropriate, the designer can increase the number of neurons per layer or even the number of hidden layers. In this research, after trial and error, as well as using the experience of research, the appropriate structure for estimating the piezometric head in the earthen dam core is shown in Fig. 4. As shown in this figure, the developed model has two hidden layers, and there are five and three neurons in the first and second hidden layers, respectively. The functions studied in this research are sigmoid, sigmoid tangent, and Gauss, among which the sigmoid tangent function got the best result. The statistical indices of the selected MLPNN model developed for each of the input variable patterns are presented in Table 1. While only the relationship between the WSE in the reservoir and the piezometric head was considered (first row of Table 1), the statistical indices of the MLPNN model developed in the training phase are root-mean-square error (RMSE) = 2.235, R2 = 0.892, and in the testing phase. RMSE = 2.774, R2 = 0.916. By increasing the one-time delay unit (scenario two in the second row of Table 1), the accuracy of the model has not improved significantly in both the training and testing phases. The statistical error index of this model in the testing phase is RMSE = 2.365, and R2 = 0.895. Then, the effect of increasing the time delays of the WSE in the dam reservoir was carefully modeled, and the results are presented in the following rows of Table 1. The structure of the neural network model which has a good function in estimating the piezometric head inside the dam is shown in Fig. 4. The performance of this model in both stages of development is shown in Fig. 5. As can be seen from this figure, the observed values are plotted against the results of the MLPNN model.

Fig. 3
figure 3

Changes in water level in the reservoir and piezometers inside the dam core

Full size image
Table 1 Statistical indices of MLPNN model developed for estimating piezometric head in the core of Baf earthen dam
Full size table
Fig. 4
figure 4

The structure of the MLPNN developed to estimate the piezometric head within the Baft earth dam

Full size image
Fig. 5
figure 5

Performance of SVM and MLPNN in estimating piezometric head within the core of Baft earth dam

Full size image

Here, the development of the SVM model was considered to estimate the piezometric head inside the core of the Baft earthen dam. The same data and scenarios as in Table 1 for the MLPNN model were considered for the development of the SVM model.

In developing the SVM model, the performance of three types of kernel functions, including radial, quadratic, and linear, was evaluated, and in the final stage it was found that the performance of the radial function is better than other kernel functions. Therefore, this function was used in the final structure of the SVM model. Table 2 presents the statistical indices of the accuracy of the SVM model in estimating the piezometric head based on the pattern of input variables. As shown in this table, the SVM model using only the data related to the WSE in the reservoir (without any delay time) can predict the piezometric head in the dam core with statistical error indices including RMSE = 2.243, R2 = 0.891 in the training phase and RMSE = 2.657, R2 = 0.918 in the testing stage. Then, like the MLPNN model, the effect of increasing the input information to the SVM in the form of increasing time delays on the accuracy of modeling was investigated. The results show an increase in time delays in the second to fourth rows of Table 2. Examination of the statistical indices presented in this table shows that increasing the input information (time delays) results in a slight increase in the modeling accuracy. Figure 6 shows the structure of the final SVM model. As can be seen, in addition to the water level figure in the dam reservoir at time T, three other time delays have been used in the structure of the final model. The performance of the SVM model in the training and testing stages is shown in Fig. 5. Comparing the performance of the SVM model with the MLPNN shows that both models have acceptable accuracy in estimating the piezometric head in the core of the Baft earth dam.

Table 2 Statistical indices of developed SVM for predicting piezometric head in Baft earthen dam
Full size table
Fig. 6
figure 6

The structure of the developed SVM to estimate the piezometric head inside the Shahid Baft earthen dam

Full size image

In the following, the effect of data preprocessing using a wavelet algorithm on modeling accuracy is investigated. In preprocessing using the wavelet algorithm, each of the input variables presented in Tables 1 and 2 (time series of data recorded at the water level in the reservoir and its time delays) is a signal that is decomposed by the wavelet algorithm, and its details, including the main signal and the corresponding coefficients, are derived and introduced as input to the soft computing models. In this study, three types of mother wavelets including haar, db, and sym were used to analyze the signal of input variables.

In developing the hybrid model, using wavelet transforms, the different details of input variables (main signal and their degrees of decomposition for different mother wavelets) were derived and different combinations of inputs were examined. In the hybrid model, the degree to which each signal is decomposed depends on the researcher's experience as well as the results of the soft computing models that use these signals and related details as input. However, the experience of previous researchers is also useful and usable. For this purpose, it is suggested that the degree of decomposition of each signal be estimated from the relation \(L=\mathrm{int}\left(\mathrm{long} N\right)\). In this relation, N is the number of observational data in each signal of the time series. Of course, the result of this relationship provides an estimate. Figure 7 shows the result of five degrees of time series decomposition of the WSE in the Baft Dam reservoir using the sym3 wavelet. In this figure, the main signal is shown in the first row, and the multiplier and its decomposed signals are presented in the next rows. Each of the parameters presented in Tables 1 and 2 was analyzed up to five degrees using haar, db, and sym, respectively, and then introduced as input to the MLPNN and SVM models. The accuracy of the Wavelet-MLPNN (WMLPNN) and Wavelet-SVM (WSVM) models developed in this scenario is presented in Tables 3 and 4, respectively. In these tables, the signals were analyzed up to five degrees using haar, db, and the sym introduced to the models. After teaching the models, the average of statistical indices in each scenario was presented (Fig. 8). Examination of these tables shows that the yield of the developed models increased significantly compared to the previous case. Thus, in the training stage, the statistical indices of the WMLPNN model determined by analyzing the input time series with the help of the wavelet wave are RMSE = 1.016 and R2 = 0.973, and in the testing stage are RMSE = 1.340 and R2 = 0.974. Development of the same soft computing model by time series analysis with the help of a db mother wavelet in the training stage results in RMSE = 1.259 and R2 = 0.963, and in the testing stage, RMSE = 1.268 and R2 = 0.959. Based on the sym3 mother wavelet, the error indices of the developed model in training and testing phases are RMSE = 1.073, R2 = 0.972 and RMSE = 1.110, R2 = 0.968, respectively. The statistical indices of the WSVM model by analyzing the input time series with the help of the haar wave are RMSE = 0.657, R2 = 0.989 in the training stage, and the testing stage is RMSE = 1.262, R2 = 0.964. Development of the same soft computing model by analyzing the time series with the help of a db wavelet in the training stage with RMSE = 0.581, R2 = 0.992 and in the testing stage with RMSE = 1.283, R2 = 0.959. Based on the wavelet, the sym3 system has statistical indices of RMSE = 0.827, R2 = 0.983 in the training phase and RMSE = 0.774, R2 = 0.987 in the testing phase. A comparison of the performance of the mother wavelets shows that the performance of the soft computing models is almost the same in all three mother wavelets, although in part the mother wavelet sym3 achieves slightly better accuracy. In addition, a comparison between the WSVM and WMLPNN hybrid models shows that the performance of the hybrid wavelet-support vector machine (WSVM) model is better than the neural-wavelet model.

Fig. 7
figure 7

Sub-signals of time series of water surface elevation in Baft dam reservoir with sym3 mother wavelet

Full size image
Table 3 Statistical indices of WMLPNN model developed for modeling and estimating piezometric level inside the earthen dam
Full size table
Table 4 Statistical indices of developed WSVM for estimating piezometric level in the Baft earthen dam
Full size table
Fig. 8
figure 8

Performance of support vector machine models and artificial neural network in estimating piezometric head within Baft earth dam

Full size image

4 Conclusion

In this research, artificial neural network and support vector machine soft computational models were developed, and their hybrids with wavelet algorithms were used to estimate the piezometric head inside the Baft earth dam. For this purpose, the monthly data recorded from the water surface elevation in the reservoir of Baft earth dam and the piezometric head inside the piezometer well were used. In designing the pattern of input variables, reservoir water level data as well as their time delays up to four units were used. In the development of the aforementioned soft computing models, two approaches were used, namely using raw data and also time series analysis using a wavelet algorithm. In the process of designing and determining the internal structure of the models, different transfer and kernel functions were investigated, which were then used in the development of the radial kernel function of the SVM model and the tangent sigmoid function of the MLPNN model. In the second scenario, where the development of soft computing models was based on the preprocessing of input data using the wavelet algorithm, each of the input signals was decomposed up to five degrees by the mother wavelet, and its details were seen as input to the soft computing models. In this study, three types of mother wavelets including haar, db, and sym were used. The results showed that the development of the MLPNN model in the first scenario (without time series preprocessing by wavelet algorithm) achieved statistical indices around RMSE = 2.235, R2 = 0.892, and the SVM model around RMSE = 2.774, R2 = 0.916. However, if the wavelet algorithm was used for preprocessing the input data, the statistical indices of the above models (combined models WMLPNN and WSVM) improved to RMSE = 0.827, R2 = 0.983, and RMSE = 0.827, R2 = 0.983, respectively, which is significant compared to the previous case. The signal analysis of the input variables using all three mother wavelets and their introduction as input in the development of the aforementioned soft computing models led to almost the same performance, although the performance of the sym3 mother wavelet was slightly better than the others. A comparison of the performance of the WMLPNN with the WSVM also showed that the accuracy of the WMLPNN was significantly better than the WMLPNN.