Introduction

Earth dams are among the world’s oldest hydro-engineering structures. They are constructed to control flood and safeguard land, properties, and living beings. Several investigators have suggested various methods to determine the quantity of seepage and locus of the phreatic line. Kozeny [1] studied the seepage through an earth dam with a horizontal toe drain (under filter) resting on an impervious base assuming the earth dam to have a parabolic upstream face.

Kozeny ignored the resistance of the portion bounded by the parabolic face and upstream straight slope surface conveniently assuming this portion to be comprised of rock-fill materials, though the ignored portion of the earth dam also controls the quantity of seepage and location of the phreatic line [2]. Applying the method of fragments, Pavlovsky [3] determined the quantity of seepage and locus of phreatic line in an earth dam resting on an impervious base without a toe filter. The flow domain has been decomposed into three fragments and the hydraulic resistance of the soil in the upstream side has been considered for finding the flow characteristics. Casagrande [4] made a correction for the entrance condition at the upstream face and recommended the parabolic free surface to start at a point 0.3∆ upstream, where ∆ is equal to base width of the upstream triangular part.

Numerov [5] has analyzed seepage through an earth dam having a straight upstream slope face and a toe drain. The problem has been identified as a Reimann–Hilbert problem. Using Numerov’s solution, one can find the seepage quantity through a levee and location of the phreatic line. However, the solution to the Reimann–Hilbert problem is somewhat intractable for the computation of seepage characteristics [2].

In many cases the seepage may result in excess hydrostatic pressures or uplift pressures beneath elements of the structure or landward strata. Relief wells are often installed to relieve these pressures which might otherwise endanger the safety of the structure [6].

Several investigators [7–9] have applied numerical techniques to determine the quantity of seepage and locus of the phreatic line. Determination of phreatic line by numerical techniques involves iteration and requires special formulation.

In Abdul Hussain et al. [10], optimal design of a homogeneous earth dam were presented in the form of nondimensional design tables/curves. The proposed procedure for the dam design can take care of the optimality as well as feasibility aspects of the problem. This strategy reduces the computing efforts substantially and without this the optimization would have required prohibitively large computer time. The variation in the optimal dam design as the height change is studied. It is concluded that as the dam height increases, flatter side slopes and larger sized drains are necessary.

Based on Chahar’s [11] study, with increase in (flattening of) the upstream slope, top width, or free board the required filter length reduces for a given value of the downstream slope cover, while it increases with increase in the downstream slope. Further, the downstream slope cover or the length of the horizontal drain is less affected by the change in the top width, free board, or upstream slope, while they are more sensitive with the change in the downstream slope.

The purpose of this study is to investigate the effect of hydraulic conductivity ratio (K x /K y ) in seepage rate from earth dam with horizontal drain. 78 different assumed models, were simulated using Seep/w software, with K x /K y  = 1 and 10 and side slopes of 1V:1.5H and 1V:2H (m = 1.5 and 2). So variable parameters consist of horizontal hydraulic conductivity ratio to vertical hydraulic conductivity, upstream and/downstream slopes of dam and horizontal drain length. Also comparison among present study with Mishra and Singh [2], Casagerande [4] and Kozeny [1] will be done to distinguish seepage rate in numerical method and analytical methods.

Materials and Methods

Governing Equations

Seepage discharge obeys Darcy’s law (Eq. 1):

$$ Q = - KA(\partial h/\partial l) $$
(1)

where Q is seepage discharge (m3/s), K is hydraulic conductivity coefficient (m/s), A is the cross sectional area (m2) and \( \partial h/\partial l \) is the flow hydraulic gradient. Poisson’s equation is an equation of water flow in porous media which is the generalized form of Laplace well-known equation (Eq. 2):

$$ K_{x} \frac{{\partial^{2} h}}{{\partial x^{2} }} + K_{y} \frac{{\partial^{2} h}}{{\partial y^{2} }} = q $$
(2)

where K x and K y are the coefficients of hydraulic conductivity in the x and y direction, respectively (m/s), h is the total head (m) and q is the discharge flow rate input/output to the soil (m3/s per unit area, m/s).

Poisson’s equation solution is one of the most complex mathematical problems and numerical methods help for solving differential equations and their conversion into a set of algebraic equations. Seep/w is software to solve Poisson’s equation by the finite element method.

Numerical Simulation

The present seepage problem is solved using the method of finite elements by Seep/w software (v. 2007) applying 3 different ratios for K x /K y , 2 different of upstream and/downstream slopes of dam (m = 1.5 and 2) and 26 different lengths for horizontal drain.

Finite element numerical methods are based on the concept of subdividing a continuum into small pieces, describing the behavior or actions of the individual pieces and then reconnecting all the pieces to represent the behavior of the continuum as a whole. This process of subdividing the continuum into smaller pieces is known as discretization or meshing. The pieces are known as finite elements.

In Geo-Studio Seep/w, the geometry of a model is defined in its entirety prior to consideration of the discretization or meshing. Furthermore, automatic mesh generation algorithms have now advanced sufficiently to enable a well behaved, numerically robust default discretization often with no additional effort required by the user. Of course, it is still wise to view the default generated mesh but any required changes can easily be made by changing a single global element size parameter, by changing the number of mesh divisions along a geometry line object, or by setting a required mesh element edge size [12].

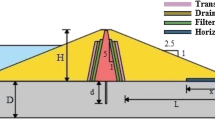
Figures 1 and 2 show two homogeneous earth dam rested on an impervious foundation assumed in this study, for slopes 1V:1.5H and 1V:2H respectively (m = 1.5 and 2). In Figs. 1 and 2, soil material is selected to be isotropic, i.e., K x /K y  = 1, and these two models are assumed as a base models.

Fig. 1
figure 1

Cross section of homogeneous earth dam with slopes 1V:1.5H (m = 1.5)

Full size image
Fig. 2
figure 2

Cross section of homogeneous earth dam with slopes 1V:2H (m = 2)

Full size image

In boundary condition, water level (total head) in upstream is 18 m, water level in downstream was assumed river bed level (zero meters). Also, the foundation’s floor is impermeable (zero flow). Nodes at the horizontal drain have atmospheric pressure (zero pressure). Two dimensional simulation of homogeneous earth dam have about 5,120 elements.

Table 1 presents value of saturated hydraulic conductivity for proposed materials (dam and drain) in this study. Table 2, shows different lengths for horizontal drain selected in this study for two slopes 1V:1.5H and 1V:2H.

Table 1 Saturated hydraulic conductivity for proposed materials
Full size table
Table 2 Different lengths for horizontal drain (values in meter)
Full size table

As mentioned previously, the total number of 78 different models was simulated. For example, Fig. 3 shows a homogeneous earth dam with 19 m of horizontal drain length. As can be seen, around drain, finer elements were selected for more accuracy. Detail of mesh generation around horizontal drain is presented in Fig. 3 too.

Fig. 3
figure 3

Cross section of earth dam with 19 m of horizontal drain length (slope 1V:1.5H or m = 1.5) and detail of mesh generation around horizontal drain

Full size image

Results and Discussion

Figures 4 and 5 show variation of horizontal drain length (d/h w ) versus seepage (q/Kh w ) for slopes 1V:1.5H and 1V:2H respectively (m = 1.5 and 2). In these Figures, h w is water depth in upstream of the dam, d is the distance of the filter from the point of intersection of the upstream reservoir water surface with a sloping face, which is the same as that in Kozeny’s [1] formula, K is hydraulic conductivity of dam material and q is seepage rate in cubic meter per second in unit length of dam (m2/sec). Parameter d was select for future comparison with the other researchers.

Fig. 4
figure 4

Variation of horizontal drain length (dimensionless) versus seepage (dimensionless) for slope 1V:1.5H (m = 1.5)

Full size image
Fig. 5
figure 5

Variation of horizontal drain length (dimensionless) versus seepage (dimensionless) for slope 1V:2H (m = 2)

Full size image

Figure 5 shows that when drain length decreases (d/h w increases), amount of seepage has decreasing in a nonlinear trend. Also, with increasing in K x /K y from 1 to 10, seepage increases from dam body.

Based on Figs. 4 and 5, the present numerical simulation shows good agreement with Casagerande [4], Mishra and Singh [2] in seepage rate. Analytical solutions of Casagerande [4], Mishra and Singh [2] represent lesser of seepage than numerical simulation in this study, but they are all close together. Kozeny’s [1] analytical solution shows higher in seepage rates than three other methods and its agreement with other methods is improper. It is important to note that in analytical methods of Casagerande [4], Mishra and Singh [2], porous media must be isotropic, but in numerical simulation in Seep/w, porous media can be selected as anisotropic. This can be seen from Fig. 4 for K x /K y  = 1 and 10.

Kozeny [1] ignored the hydraulic resistance of the soil in an earth dam bounded by an equipotential parabolic surface and the straight upstream sloping face has been considered in the computation of the seepage and location of the phreatic line. This is the reason that Kozeny [1], results more seepage rate than the others.

Casagrande [4] made a correction for the entrance condition at the upstream face and recommended the parabolic free surface to start at a point 0.3∆ upstream, where ∆ is equal to base width of the upstream triangular part.

In Mishra and Singh [2], unlike in Kozeny’s method, the analysis considers the resistance offered by the soil within the parabolic equipotential surface and the upstream sloping face. Therefore, the seepage computed by the Mishra and Singh [2] method of fragments is less than the seepage computed by Kozeny’s solution.

Comparison between Figs. 4 and 5 demonstrate that for a flatter upstream slope, the Casagrande’s solution is not enough for finding the true seepage losses and required length of the filter.

Trend in increasing of seepage, for drain length ratio = 0.66–1.25 (for 1V:1.5H) and for drain length ratio = 0.73–1.5 (for 1V:2H) are high.

Figure 6 shows variation of horizontal drain length (dimensionless ratio) versus seepage rate (dimensionless ratio) for comparison of two slopes 1V:1.5H (m = 1.5) and 1V:2H (m = 2). Based on Fig. 6, the flatter the upstream slope (for higher value of m), the farther location of the filter from upstream face.

Fig. 6
figure 6

Variation of horizontal drain length (dimensionless) versus seepage (dimensionless) for slope 1V:1.5H (m = 1.5) and 1V:2H (m = 2)

Full size image

Presented graphs have been nondimensionalized and are very simple to be used in determination of the horizontal downstream drainage filter length in a given dam section for a specified downstream slope. The method is simple, straightforward, and does not involve personal skills and judgments, hence it is convenient to use for a new designer.

Figure 7 displays location of phreatic line through an isotropic earth dam without horizontal drain with slope 1V:2H. Intersection of top flow line (phreatic line) with downstream side make saturated zone that is not proper for dam slope stability.

Fig. 7
figure 7

Position of phreatic line through isotropic earth dam without horizontal drain (slope 1V:2H)

Full size image

The function of a filter is to control seepage through an earth dam. A filter is also essential to keep down the top flow line as low as possible in order to increase the dry zone in downstream side in the earth dam for greater stability. Filter function for increasing the dry zone in downstream side, is presented in Figs. 8 and 9 for isotropic and anisotropic (K x /K y  = 10) conditions, respectively.

Fig. 8
figure 8

Position of phreatic line through isotropic earth dam with 27 m of horizontal drain (slope 1V:1.5H)

Full size image
Fig. 9
figure 9

Position of phreatic line through anisotropic earth dam (K x /K y  = 10) with 27 m of horizontal drain (slope 1V:1.5H)

Full size image

Figures 8 and 9 are representative of keep down phreatic line from downstream slope. An earth dam can be prevented from a seepage failure due to softening of the downstream slope by providing a horizontal drainage blanket. Numerical modeling has been obtained in the present work for calculating the downstream horizontal drain in homogeneous isotropic and anisotropic earth dams.

Conclusion

An earth dam can be prevented from a seepage failure due to softening of the downstream slope by providing a rock toe or horizontal drainage blanket. Analytical solutions are not accurate for determining the length of the filtered drainage blanket and downstream slope cover. Based on the study, the following conclusions are drawn:

  1. 1.

    The earth dam portion excluded in Kozeny’s solution reduces the seepage quantity significantly.

  2. 2.

    A filter is essential to keep down the top flow line as low as possible in order to increase the dry zone in downstream side in the earth dam for greater stability.

  3. 3.

    The provision of the filter nearer the upstream side results in higher seepage losses and an increment in the required filter length. If the filter is located away from upstream face, i.e., near the downstream toe, though seepage gets reduced, the saturated zone is increased resulting in a reduction of the dry zone.

  4. 4.

    Comparison between two slopes 1V:1.5H (m = 1.5) and 1V:2H (m = 2), shows the flatter the upstream slope (for higher value of m), the farther location of the filter from upstream face.

  5. 5.

    For a flatter upstream slope, the Casagrande’s correction is not enough for finding the true seepage losses and required length of the filter.