Abstract
Based on Euler–Bernoulli beam theory, this paper investigates large post-buckling deformation of a slender elastic beam with fixed-pinned end. Owing to the asymmetric boundary conditions, it is difficult to establish analytic solution. Based on the Maclaurin series expansion and orthogonal Chebyshev polynomials, the governing differential equation with both sinusoidal nonlinearity and cosinusoidal nonlinearity can be reduced to a polynomial equation, and the geometry condition with sinusoidal nonlinearity can also be simplified to be a cubic polynomial integral equation. The admissible lateral displacement function to satisfy the fixed-pinned boundary conditions is derived in an elegant way. The analytical approximations are obtained with the harmonic balance method. Two approximate formulae for axial load and lateral load are established for small as well as large angle of rotation at the pinned end. These approximate solutions show excellent agreement with those of the shooting method for a large range of the rotation angle at the pinned end. Moreover, due to brevity of expressions, the present analytical approximate solutions are convenient to investigate effects of various parameters on the large post-buckling response of fixed-pinned beams.
Similar content being viewed by others
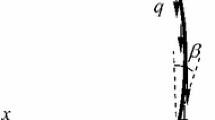
Avoid common mistakes on your manuscript.
1 Introduction
There are many practical cases where post-buckling of structures may occur, such as satellite tethers, marine cables, robotic arms and slender rod in building or bridge. When the slenderness ratio is very large, there is a large displacement within the elastic range. The stability of slender rods has drawn the attention of many scientists since Euler classical contributions in the eighteenth century (Lee 1990; Lee and Oh 2000; Nayfeh and Emam 2008; Vaz and Mascaro 2005; Wang 1981). Studies show that the shear force in the equilibrium state is negligible for the Euler beams with common supporting conditions, such as simply supported, fixed–fixed and cantilever. However, for the asymmetric boundary and the statically indeterminate characteristics of the fixed-pinned beam, the shear force cannot be ignored, which will result in its post-buckling problem in a strong nonlinear problem.
Kocatürk and Akbaş (2010) established a total Lagrangian finite element model of the simply supported beam to study geometrically nonlinear static problem. The solution was obtained numerically by the Newton–Raphson procedure. Then, they studied thermal post-buckling analysis of Timoshenko beams with various boundary conditions (Kocaturk and Akbas 2011). Akbas (2014) investigated the large post-buckling of Timoshenko beams subjected to non-follower axial compression loads. Wang (1996) proposed the perturbation solution of the large post-buckling of an elastic rod with fixed-pinned ends and suffered axial compression. The solutions for buckling, initial post-buckling (perturbation), large loads (asymptotic) and numerical integration of the fixed-pinned rod were developed by Vaz and Silva (2003). Li et al. (2015), Li and Zhou (2005), Song and Li (2007) considered various post-buckling problems for the slender beam with fixed-pinned end by employing shooting method.
Employing the elliptic integration, many scholars obtained the solution of the post-buckling problem of fixed-pinned beams. Yan et al. (2019) derived explicit analytical expressions of buckled beams with fixed-pinned ends. Humer (2013) studied the solution in terms of elliptic integrals for the buckling and post-buckling problem of beams with the influence of axial compressibility and shear deformation. Applying a geometrically exact theory of the elastica, Prechtl et al. (2012) presented a geometrically exact solution to the aforementioned Euler buckling problems. The governing equilibrium equation and Jacobi equation of the elastic rod with various boundary conditions were derived from variational principles by Batista (2015), and their solutions were presented in terms of the Jacobi elliptical functions. Mikata et al. (2007), Singh and Goss (2018) studied the solutions in terms of the Jacobi elliptical functions for a clamped-pinned beam. Sano and Wada (2018) studied snap buckling of an elastic strip with fixed-pinned ends. However, the exact solution was expressed by the elliptic integral of the second kind, which needed to be solved numerically, and was inconvenient for application.
To the authors’ knowledge, the previous researches on the post-buckling problem of a fixed-pinned beam are limited to the solution in terms of numerical form or elliptic integral form. No one has derived a simple and convenient explicit analytical formula for the post-buckling of a fixed-pinned beam. In this paper, the analytical solution for the large post-buckling deformation of a slender elastic beam with fixed-pinned ends is investigated. The governing differential equation is established with Euler–Bernoulli beam theory. Employing the Maclaurin series expansion and orthogonal Chebyshev polynomials, the nonlinear governing equation included sinusoidal function and cosinusoidal function can be reduced to a polynomial equation. A reasonable initial approximation satisfying the boundary conditions is given, and the analytical solutions for the large post-buckling deformation of a fixed-pinned beam are obtained by the harmonic balance method.
2 Mathematical Model and Solution Methodology
The sketch depicted in Fig. 1 shows undeformed and deformed configurations of a slender elastic beam subjected to an axial load, fixed at one end and pinned at the other end. A classic Euler–Bernoulli beam model investigating large post-buckling deflection is written as (Humer 2013; Vaz and Silva 2003; Wang 1996):
and the boundary conditions are
Geometric requirements are
Equation (3) can also be written as
where
and \( S \in \left[ {0,L} \right] \) is the actual curve length, L is the length of the beam, (X, Y) constitutes Cartesian coordinates of the beam, P and Q are the axial load and lateral load and EI is the bending stiffness of the beam, respectively. The analysis of the asymmetrically supported Euler buckling beam with one end clamped and the other end pinned is complicated.
A new independent variable \( \tau = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}s \) is introduced. Then, Eq. (1) can be rewritten in the following dimensionless form:
where
and the boundary conditions are
and the geometry conditions are rewritten as
In the present work, along with the Maclaurin series expansion and the Chebyshev polynomials, and let \( \theta = au \), a new nonlinear equation with no trigonometric function is constructed (Yu et al. 2013):
where
Substituting Eqs. (11) and (12) in Eq. (7), the nonlinear equation could be expressed as
Using Eqs. (10) and (11), the extra condition could be obtained
Following the harmonic balance approximation, a reasonable initial approximation satisfying the boundary conditions could be taken as
where b is the root of Eq. (15). Note that Eq. (15) which is a 3rd algebraic equation could be analytically solved.
In the following step, harmonic balancing process will be performed: substituting Eq. (16) in Eq. (14), and letting the resulting coefficients of the items \( \cos \tau \) and \( \cos 3\tau \) vanish (Sun et al. 2009; Wu et al. 2006; Yu et al. 2012), give
where
From Eq. (17), the analytical approximations for \( \beta \) and \( \gamma \) can be solved and expressed as function of a, as
and the analytical approximate solution for \( \theta \) can be obtained as
3 Results and Discussion
The exact (numeric) solutions \( \beta_{\text{e}} \), \( \gamma_{\text{e}} \), \( \theta_{\text{e}} \) could be obtained by solving Eqs. (3), (4), (7) and (9) with a shooting method. The approximate solutions \( \beta_{0} \),\( \gamma_{0} \) could be calculated, respectively, by Eq. (18). For comparison, exact and approximate values of \( \beta \) and \( \gamma \) with respect to the angle of rotation a are shown in Figs. 2 and 3, respectively. Figures 2 and 3 indicate that Eq. (18) could give excellent approximations to parameters \( \beta \) and \( \gamma \) for small as well as large rotation angle a.
The exact (numeric) solutions \( \theta_{\text{e}} \) and approximate solution \( \theta_{0} \) given in Eq. (19) are displayed in Fig. 4: (a) for a = 0.5, (b) for a = 1.0 and (c) for a = 1.6. From Fig. 4, one could find that Eq. (19) could present excellent approximate accuracy of \( \theta \) for a large range of rotation angle a. Note that a = 1.6 means the angle of rotation in pinned end exceeding \( {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} \) and it is quite a large deformation. Furthermore, if one would like to obtain solutions with higher approximate accuracy, further approximations need to be constructed with Newton harmonic method (Wu et al. 2006; Yu et al. 2012) or the improved Galerkin method (Sun et al. 2015). The length of the formulae, however, must be longer.
Finally, approximate solutions of lateral displacement y and axial displacement x analytically obtained from Eqs. (11), (12) and (16) are plotted in Fig. 5.
4 Conclusions
This paper has focused on large post-buckling deformation of a slender elastic column with fixed-pinned ends, based on the Euler–Bernoulli beam theory. An accurate and brief approach is provided to solve the problem mentioned-above. The approximate solutions have been established. Results for lateral load, axial load, lateral displacement and axial displacement are presented in dimensionless format. Compared with the solution calculated by applying the shooting method, the results obtained by the new method show excellent accuracy for a large range of the rotation angle in the pinned end. The new approach presented here offers analytical approximate solutions which help in analytically investigating the effect of the physical parameters on the post-buckling response of the beam with shear force subjected to terminal forces with fixed-pinned ends. The method and accurate approximations derived here are very useful for robotic arms and slender rod in building or bridge engineering applications. By applying the explicit and analytical formulas, the applied force and deflection can be explicitly analyzed with ease and without numerical integration. However, there is a gap between the model and actual structure for the sake of many hypotheses. Therefore, the more practical and precise models should be constructed by reducing assumptions. An improved analytical approximate method will be investigated to solve other structures with shear deformation, such as beams, bars or plates supported by nonlinear elastic foundation.
References
Akbas SD (2014) Large post-buckling behavior of Timoshenko beams under axial compression loads. Struct Eng Mech 51:955–971
Batista M (2015) On stability of elastic rod planar equilibrium configurations. Int J Solids Struct 72:144–152
Humer A (2013) Exact solutions for the buckling and postbuckling of shear-deformable beams. Acta Mech 224:1493–1525
Kocaturk T, Akbas SD (2010) Geometrically non-linear static analysis of a simply supported beam made of hyperelastic material. Struct Eng Mech 35:677–697
Kocaturk T, Akbas SD (2011) Post-buckling analysis of Timoshenko beams with various boundary conditions under non-uniform thermal loading. Struct Eng Mech 40:347–371
Lee BK (1990) Numerical analysis of large deflections of cantilever beams J Korean Soc. Civ Eng 10:1–7
Lee BK, Oh SJ (2000) Elastica and buckling load of simple tapered columns with constant volume. Int J Solids Struct 37:2507–2518
Li QL, Li SR (2015) Post-buckling behaviors of a hinged-fixed FGM Timoshenko beam under axially distributed follower forces. Chin J Appl Mech 32:90–95
Li SR, Zhou YH (2005) Post-buckling of a hinged-fixed beam underuniformly distributed follower forces. Mech Res Commun 32:359–367
Mikata Y (2007) Complete solution of elastica for a clamped-hinged beam, and its applications to a carbon nanotube. Acta Mech 190:133–150
Nayfeh AH, Emam SA (2008) Exact solution and stability of postbuckling configurations of beams. Nonlinear Dynam 54:395–408
Prechtl G (2012) Geometrically exact solution of a buckling column with asymmetric boundary conditions. PAMM 12:203–204
Sano TG, Wada H (2018) Snap-buckling in asymmetrically constrained elastic strips. Phys Rev E 97(1):013002
Singh P, Goss VGA (2018) Critical points of the clamped-pinned elastica. Acta Mech 229:4753–4770
Song X, Li SR (2007) Thermal buckling and post-buckling of pinned-fixed Euler-Bernoulli beams on an elastic foundation. Mech Res Commun 34:164–171
Sun WP, Lim CW, Wu BS, Wang C (2009) Analytical approximate solutions to oscillation of a current-carrying wire in a magnetic field. Nonlinear Anal Real World Appl 10:1882–1890
Sun Y, Yu Y, Liu B (2015) Closed form solutions for predicting static and dynamic buckling behaviors of a drillstring in a horizontal well. Eur J Mech A Solid 49:362–372
Vaz MA, Mascaro GHW (2005) Post-buckling analysis of slender elastic vertical rods subjected to terminal forces and self-weight. Int J Nonlin Mech 40:1049–1056
Vaz MA, Silva DFC (2003) Post-buckling analysis of slender elastic rods subjected to terminal forces. Int J Nonlin Mech 38:483–492
Wang CY (1981) Large deflections of an inclined cantilever with an end load. Int J Nonlin Mech 16:155–164
Wang CY (1996) Post-buckling of a clamped-simply supported elastica. Int J Nonlin Mech 32:1115–1122
Wu BS, Sun WP, Lim CW (2006) An analytical approximate technique for a class of strongly non-linear oscillators. Int J Non-Linear Mech 41:766–774
Yan WZ, Yu YC, Mehta A (2019) Analytical modeling for rapid design of bistable buckled beams. Theor Appl Mech Lett 9:264–272
Yu Y, Wu B, Lim CW (2012) Numerical and analytical approximations to large post-buckling deformation of MEMS. Int J Mech Sci 55:95–103
Yu Y, Sun Y, Zang L (2013) Analytical solution for initial postbuckling deformation of the sandwich beams including transverse shear. J Eng Mech 139:1084–1090
Funding
The work in this paper is supported by the National Natural Science Foundation of China (Grant No. 41972323), Science and Technology Project of the 13th Five-Year Plan of Jilin Provincial Department of Education (Grant No. JJKH20190126KJ), the Natural Science Foundation of Jilin Province (Grant No. 20170101204JC)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Yu, Y., Chen, L., Yu, P. et al. Analytical Approximate Solution for Large Post-Buckling Behavior of a Fixed-Pinned Beam Subjected to Terminal Force with Shear Force Effect. Iran J Sci Technol Trans Civ Eng 45, 159–164 (2021). https://doi.org/10.1007/s40996-020-00385-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40996-020-00385-x








