Stability and initial post-buckling of a standing sandwich beam under terminal force and self-weight

Abstract

Beams (columns) subjected to axially distributed load (e.g., self-weight) are commonly treated using the classical Euler–Bernoulli beam theory, which ignores the transverse shear effect. Adopting the Engesser and Haringx shear theories, respectively, we study in this article the stability and initial post-buckling of sandwich (or laminated composite) beams under terminal force and axially distributed load. Nonlinear governing equations are derived from geometrical compatibility, equilibrium of forces, and moments. The critical buckling load, modal shapes of deformation, and shear force together with bending moment at buckling can be obtained by using the Galerkin’s method in terms of trigonometric functions, and the initial post-buckled configuration of the beam is determined employing the shooting method. Predictions based on the Engesser theory agree with finite element simulation results, while the Haringx theory overestimates the buckling load. The effects of transverse shear and various different end constraint conditions on static buckling and initial post-buckling of sandwich beams are systematically explored.

1 Introduction

Standing columns (beams) are widely used as structural members such as braces, pipelines, chimneys, and high buildings. In such cases, the standing column is subjected to its own weight (gravity), while accelerating mobile structures could generate body forces equivalent to gravity as a kind of axially distributed load. The axially distributed load developed in the column due to its weight and/or acceleration along column axis affects its potential energy and, consequently, its stability characteristics and natural frequencies. Accordingly, considering the effect of axially distributed load on stability is important in the analysis and design for such column–beam structures.

The stability of a column subjected to gravity was first posed and solved by Euler in 1757 [1], although the solution was erroneous. Later in 1778, Euler himself found the mistake and corrected the solution. One hundred years later, Greenhill analyzed the same problem and obtained an improved solution [2]. When a tip load (terminal force) was added, Timoshenko and Gere [3] and Kato [4] derived approximate formulas, while Wang and Drachman [5] and Wang [6] presented exact analysis in terms of Bessel functions. Noting the difficulty in obtaining exact solutions, Chai and Wang [7] used a differential transformation method to determine the critical buckling load of an axially compressed heavy column having different support (end constraint) conditions. Although the method could convert differential equations into a set of recursive algebraic equations without the need for integration, a fairly large number of terms are required for convergence. Subsequently, making use of generalized hypergeometric functions, Duan and Wang [8] obtained analytical solutions for elastic buckling of a heavy Euler–Bernoulli beam with various combinations of end conditions. These solutions may be used as benchmark solutions to assess the accuracy of approximate formulas and numerical solutions. Recently, Wang [9] used an exact initial value integration method to solve the buckling problem of a braced standing column under tip load and self-weight, whereas Li et al. [10] employed an integral equation method to analyze the buckling of a standing or hanging nonprismatic column subjected to compressive force and distributed axial load. There also exists relevant literature concerning post-buckling of beams under self-weight. Virgin and Plaut [11] studied post-buckling of a linearly elastic cantilevered column under self-weight by means of the perturbation method. Vaz and Mascaro [12] and Liu et al. [13] investigated the post-buckling behavior of a slender rod with double-hinged boundary condition subjected to terminal forces and self-weight. Using the differential quadrature method, Sepahi et al. [14] determined the post-buckling configurations of a beam with one end hinged and the other fixed under terminal forces and self-weight. However, existing researches on the stability or post-buckling of vertical standing columns or beams subjected to axially distributed load and terminal force were carried out using the classical Euler–Bernoulli beam theory. Further, there is yet a study focusing on the stability or post-buckling behavior of a moderately thick standing sandwich (or laminated composite) column under self-weight, for which the effect of transverse shear should not be neglected.

The increasing application of laminated composites and sandwich columns as structural members has stimulated interest in accurate prediction of their stability characteristics. However, as these structures typically have low ratio of transverse shear modulus to in-plane modulus, the classical Euler–Bernoulli beam theory is not applicable for stability analysis. Even for homogenous beams subjected to terminal forces, the critical loads can be overestimated if transverse shear is not included [3]. The effect of transverse shear on post-buckling behavior can likewise be significant [24]. It is expected that this is also applicable for beams under axially distributed load (self-weight).

With transverse shear accounted for, the well-known Timoshenko beam theory has been widely used to solve static and dynamic problems. In this theory, the cross sections posterior to deformation are no longer perpendicular to the central line. Accordingly, two typical approaches—the Engesser theory and the Haringx theory—are often utilized to describe the cross section of shear force [3, 15]. For Euler–Bernoulli beams with deformed cross sections still normal to the central line, the two theories are identical. Up to now, there is still a controversy about which theory is more reasonable. The arguments for and against Engesser and Haringx theories were debated by Zielger [16] and Blaauwendraad [17] who supported the Engesser theory, and Reissner [18] and Aristizabal-Ochoa [19] who supported the Haringx theory. Additionally, Bazant and Beghini [20, 21] found that the Engesser-type buckling formula for short sandwich columns gave much smaller critical loads than the Haringx type. While finite element (FE) computations showed agreement with the Engesser-type formula predictions, the Haringx-type prediction could be obtained with FE simulation somewhat artificially (by updating the core modulus as a function of axial stress in the face sheets). The Engesser theory is the only one that allows using a constant tangential shear modulus for the core when the strains are small enough for the core to remain in the elastic range. Theoretical analysis for sandwich beams by Bazant and Beghini [22] supported the Engesser theory since its predictions agreed well with the experimental data of Fleck and Sridhar [23]. For global buckling of sandwich beams or wide panels having orthotropic phases, the Engesser formula with Huang and Kardomateas shear correction [24] gives conservative predictions, which are very close to the elasticity solution and, in many cases, identical to the elasticity solution for the entire range of face-sheet thickness examined [25]. For structures in building and civil engineering, Blaauwendraad [26] showed that the Haringx theory seriously overestimates the critical loads and the Engesser theory is preferred. Zhang et al. [27] also found that the Engesser theory is more reasonable and preferred for shear beam–columns.

As a summary of existing literature, the Engesser theory is more preferable for sandwich columns and homogenized lattice (or built-up) columns, while the Haringx theory is favored in problems associated with elastomeric bearings and helical springs, for which the theory was initially developed [28, 29].

In this paper, the stability and initial post-buckling of symmetric sandwich (or laminated composite) beams including transverse shear under terminal force and axially distributed load are analyzed for selected boundary conditions. To account for the transverse shear effect, both the Engesser and Haringx theories are employed, leading to two sets of nonlinear differential governing equations for buckling and initial post-buckling. For simplicity, local buckling is not included in the present study. While the buckling problems are directly solved using the Galerkin method in terms of specific trigonometric functions, the initial post-buckling configurations for beams without end lateral forces are determined using the shooting method. For buckling of sandwich beams with clamped–free and clamped–clamped end conditions, predictions from the Engesser and Haringx shear theories compared with FE simulation results are made. The effects of transverse shear and end constraint conditions on both the static buckling and initial post-buckling of sandwich beams are discussed.

2 Mathematical formulation

2.1 Governing equations for a beam with shear

In this section, new governing equations are presented for the stability analysis of sandwich (or laminated composite) beams under self-weight; both the Engesser and Haringx theories are used.

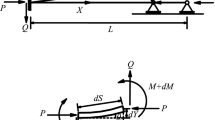
Consider an elastic, initially straight sandwich beam of length l in a buckled configuration between sections i and j, as shown in Fig. 1. The beam is taken as an elastica (inextensible, with bending moment proportional to curvature). Elastic buckling of the beam is conditioned by the end constraints and the magnitude of the terminal force P at its upper end and that of the axially distributed load q contributed by its self-weight. In the buckled configuration, the moments $M_{i}$ and $M_{j}$ (assumed positive counterclockwise) and the axial forces $P_{i}$ and $P_{j}$ together with the equal and opposite lateral forces Q at the ends are set up. A reference Cartesian coordinate system is introduced, with the x-axis coinciding with the neutral axis of the un-deformed beam and the y-axis aligned in the direction of the off-axis deformation. Besides the Euler coordinates x and y, the arc length s, as a Lagrange coordinate, is also used in the following analysis.

The geometric relationship of the sandwich beam is given as:

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}s}=\cos \beta ,\quad \frac{\mathrm{d}y}{\mathrm{d}s}=\sin \beta ,\quad x(s)=\int _0^s {\cos \beta (\eta )} \mathrm{d}\eta ,\quad y(s)=\int _0^s {\sin \beta (\eta )} \mathrm{d}\eta \end{aligned}$$

(1)

where $\beta$ is the slope of the deflected beam axis. From force equilibrium, one has:

$$\begin{aligned} P_i= & {} P \nonumber \\ P_j= & {} P+\int _0^l {q\mathrm{d}\eta } \end{aligned}$$

(2)

Fig. 1

A buckled beam subjected to terminal force and self-weight

The moment m at a distance s (Fig. 1) is:

$$\begin{aligned} \frac{1}{\rho }=\frac{\mathrm{d}\theta }{\mathrm{d}s}=-\frac{m}{\left( {EI} \right) _\mathrm{eq} } \end{aligned}$$

(3)

where $\rho$ is the radius of curvature, $\theta$ is the bending angle defined as the rotation of the cross section due to bending, and $(EI)_\mathrm{eq}$ refers to the equivalent flexural stiffness of the sandwich beam. From moment equilibrium, one obtains:

$$\begin{aligned} m=P_j y(s)-\int _0^s {q\left[ {y(s)-y(\eta )} \right] \mathrm{d}\eta } -Qx(s)-M_j \end{aligned}$$

(4)

When Eq. (4) is differentiated with respect to s, and Eqs. (1), (2), and (3) are used, the general nonlinear governing equation of the sandwich beam can be obtained as:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}s}\left[ {\left( {EI} \right) _\mathrm{eq} \frac{\mathrm{d}\theta }{\mathrm{d}s}} \right] +\left[ {P+\int _s^l {q\mathrm{d}\eta } } \right] \sin \beta -Q\cos \beta =0 \end{aligned}$$

(5)

In the case of an axially uniform beam, Eq. (5) is reduced to:

$$\begin{aligned} \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \sin \beta -\bar{{Q}}\cos \beta =0 \end{aligned}$$

(6)

where the following dimensionless quantities are introduced:

$$\begin{aligned} \xi =\frac{s}{l},\quad (\bar{{P}},\bar{{q}},\bar{{Q}})=\frac{(P,ql,Q)l^{2}}{\left( {EI} \right) _\mathrm{eq} } \end{aligned}$$

(7)

The rest of this paper will focus exclusively on axially uniform sandwich beams.

If transverse shear deformation is neglected, $\theta =\beta$ so that Eq. (5) is reduced to the classic Euler–Bernoulli beam theory [30]. When transverse shear deformation is taken into account, the slope $\beta$ of the deflected beam axis is no longer equal to the bending angle $\theta$. The difference is equivalent to the section shear angle $\gamma _\mathrm{eq}$ based on the Timoshenko beam theory [3]:

$$\begin{aligned} \gamma _\mathrm{eq} =\beta -\theta =\alpha V/(GA)_\mathrm{eq} \end{aligned}$$

(8)

where V is the shear force that rotates as the beam is deflected, $(GA)_\mathrm{eq}$ is the equivalent shear stiffness, and $\alpha$ is the shear correction coefficient. Assuming small shear strains, reasonable for the buckling and initial post-buckling states studied here, one has $\sin \gamma _\mathrm{eq} =\gamma _\mathrm{eq}$ and $\cos \gamma _\mathrm{eq} =1$. It thence follows from Eq. (8) that:

$$\begin{aligned} \sin \beta =\sin (\theta +\gamma _\mathrm{eq} )=\sin \theta +\gamma _\mathrm{eq} \cos \theta \end{aligned}$$

(9)

In the subsequent analysis, two alternative governing equations based separately upon the Engesser shear theory and the Haringx shear theory are derived.

2.1.1 Governing equation based on Engesser shear theory

As shown in Fig. 2a, the Engesser shear theory assumes that the shear force V due to end axial load P and lateral force Q is aligned on the cross section that is normal to the deflected beam axis. Consequently, V is expressed by:

$$\begin{aligned} V=\left[ {P+q(l-s)} \right] \sin \beta -Q\cos \beta \end{aligned}$$

(10)

Inserting Eq. (10) into Eq. (8) leads to:

$$\begin{aligned} \gamma _\mathrm{eq} =\bar{{A}}\left( {\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \sin \beta -\bar{{Q}}\cos \beta } \right) \end{aligned}$$

(11)

where the dimensionless parameter $\bar{{A}}={\alpha (EI)_\mathrm{eq} }/{(GA)_\mathrm{eq} l^{2}}$ is defined as the structural stiffness ratio of bending to shear. Combining (9) with (11) yields:

$$\begin{aligned} \sin \beta =\frac{\sin \theta -\bar{{A}}\bar{{Q}}\cos \theta \cos \beta }{1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \cos \theta } \end{aligned}$$

(12)

Substituting (12) into (6) and multiplying by $\left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \cos \theta } \right)$, a new governing equation based on the Engesser theory is obtained as:

$$\begin{aligned} \left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \cos \theta } \right) \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \sin \theta -\bar{{Q}}\cos \beta =0 \end{aligned}$$

(13)

For buckling, one may adopt the usual assumption that $\beta$ and $\theta$ are small. Therefore, $\sin \theta \cong \theta$, $\cos \theta \cong 1$, and $\cos \beta \cong 1$, so that Eq. (13) becomes:

$$\begin{aligned} \left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \theta -\bar{{Q}}=0 \end{aligned}$$

(14)

Finally, differentiating (14) with respect to $\xi$, a differential equation with $\bar{{Q}}$ eliminated is obtained:

$$\begin{aligned} \left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}^{3}\theta }{\mathrm{d}\xi ^{3}}+\bar{{A}}\bar{{q}}\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\theta }{\mathrm{d}\xi }-\bar{{q}}\theta =0 \end{aligned}$$

(15)

Fig. 2

a Engesser model, with shear force V on cross section normal to deflection curve; b Haringx model, with shear force V on rotated cross section normal to beam axis in initial undeflected state [15]

2.1.2 Governing equation based on Haringx shear theory

Different from the Engesser theory, the Haringx theory assumes that the shear force V is aligned on the cross section that is normal to the beam axis in the initial undeflected state (see Fig. 2b), and thus is expressed by:

$$\begin{aligned} V=\left[ {P+q(l-s)} \right] \sin \theta -Q\cos \theta \end{aligned}$$

(16)

Correspondingly, the equivalent shear angle $\gamma _\mathrm{eq}$ is given by:

$$\begin{aligned} \gamma _\mathrm{eq} =\bar{{A}}\left( {\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \sin \theta -\bar{{Q}}\cos \theta } \right) \end{aligned}$$

(17)

from which one gets:

$$\begin{aligned} \sin \beta =\frac{1}{2}\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \sin 2\theta +\sin \theta -\bar{{A}}\bar{{Q}}\cos ^{2}\theta \end{aligned}$$

(18)

Inserting (18) into (6) leads to the following Haringx-type governing equation:

$$\begin{aligned} \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \left( {\frac{1}{2}\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \sin 2\theta +\sin \theta -\bar{{A}}\bar{{Q}}\cos ^{2}\theta } \right) -\bar{{Q}}\cos \beta =0 \end{aligned}$$

(19)

For buckling, one can assume $\cos \theta \cong 1$, $\sin 2\theta \cong 2\theta$, $\sin \theta \cong \theta$, and $\cos \beta \cong 1$ under the hypothesis of small deformation. Then, Eq. (19) becomes:

$$\begin{aligned} \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \left( {1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \theta -\left( {1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \bar{{Q}}=0 \end{aligned}$$

(20)

To eliminate $\bar{{Q}}$, differentiating (20) twice with respect to $\xi$ yields the following differential equation for buckling:

$$\begin{aligned} \frac{\mathrm{d}^{4}\theta }{\mathrm{d}\xi ^{4}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \left[ {\bar{{A}}\left( {\bar{{P}}+\bar{{q}}(1-\xi )} \right) +1} \right] \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}-2\bar{{q}}\left[ {2\bar{{A}}\left( {\bar{{P}}+\bar{{q}}(1-\xi )} \right) +1} \right] \frac{\mathrm{d}\theta }{\mathrm{d}\xi }+2\bar{{A}}\bar{{q}}^{2}\theta =0\nonumber \\ \end{aligned}$$

(21)

If shear deformation is ignored for buckling analysis, one has $\bar{{A}}=0$. In this case, both the Engesser and Haringx theories are degraded to the classical Euler–Bernoulli theory. And Eq. (15) is reduced to:

$$\begin{aligned} \frac{\mathrm{d}^{3}\theta }{\mathrm{d}\xi ^{3}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\theta }{\mathrm{d}\xi }-\bar{{q}}\theta =0 \end{aligned}$$

(22)

which is identical to the fourth-order differential equation governing the stability of an Euler column [7, 8].

2.2 Modal analysis

Equations governing the initially post-buckling behavior and critical buckling load for static stability are obtained in the previous section based on different shear theories. Correspondingly, the modal shear force, bending moment, and mode shapes at buckling are determined in this section.

2.2.1 Engesser type

With $\sin \beta =\beta$ and $\cos \beta =1$ assumed for buckling, Eq. (10) may be rewritten as:

$$\begin{aligned} \bar{{V}}=\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \beta -\bar{{Q}} \end{aligned}$$

(23)

where $\bar{{V}}={Vl^{2}}/{\left( {EI} \right) _\mathrm{eq} }$ is the dimensionless shear force of the beam cross section. The slope of the beam axis is:

$$\begin{aligned} \beta =\frac{\theta -\bar{{A}}\bar{{Q}}}{1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \end{aligned}$$

(24)

and it follows from Eq. (14) that:

$$\begin{aligned} \bar{{Q}}=\left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \theta \end{aligned}$$

(25)

Inserting the above equation into Eq. (24), one can rewrite the slope of beam axis as:

$$\begin{aligned} \beta =-\bar{{A}}\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\theta \end{aligned}$$

(26)

Similarly, Eq. (23) can be rewritten as:

$$\begin{aligned} \bar{{V}}=\frac{Vl^{2}}{(EI)_\mathrm{eq} }=-\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}} \end{aligned}$$

(27)

2.2.2 Haringx type

For buckling, from Eq. (16), the dimensionless shear force can be written as:

$$\begin{aligned} \bar{{V}}=\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \theta -\bar{{Q}} \end{aligned}$$

(28)

and the beam axis has a slope given by:

$$\begin{aligned} \beta =\left( {1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \theta -\bar{{A}}\bar{{Q}} \end{aligned}$$

(29)

From Eq. (20), one has:

$$\begin{aligned} \bar{{Q}}=\frac{1}{1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] }\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \theta \end{aligned}$$

(30)

Upon inserting (30) separately into (28) and (29), the dimensionless shear force and slope of beam axis are obtained as:

$$\begin{aligned} \bar{{V}}= & {} -\frac{1}{1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] }\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}} \end{aligned}$$

(31)

$$\begin{aligned} \beta= & {} \theta -\frac{\bar{{A}}}{1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] }\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}} \end{aligned}$$

(32)

For both Engesser and Haringx theories, the expression $\bar{{M}}=m/{(EI)_\mathrm{eq} l}=-{\mathrm{d}\theta }/{\mathrm{d}\xi }$ for dimensionless bending moment is employed. To determine the mode shapes at buckling based upon small deformation assumption, from Eq. (1), one can replace x with s and employ $y=\int _0^s {\beta \mathrm{d}\eta }$ to obtain beam lateral deflection. To obtain beam configurations of initial post-buckling, Eq. (1) is used directly with Eq. (12) for the Engesser theory or Eq. (18) for the Haringx theory.

2.3 Beams with classical boundary conditions

Table 1 lists the likely boundary conditions for the beam ends. Accordingly, as shown in Table 2, seven possible combinations of the above boundary conditions are considered in the present study, i.e., clamped–free (CF), clamped–sliding restraint (CS), clamped–hinged (CH), clamped–clamped (CC), hinged–sliding restraint (HS), hinged–hinged (HH), and hinged–clamped (HC).

Table 1 Classical boundary conditions [31]

Table 2 Combination of boundary conditions for sandwich beam

3 Methods of numerical solutions

Governing equations for bucking and initial post-buckling of sandwich beams have been derived based upon Engesser and Haringx shear theories, respectively. Due to nonlinearity of these governing equations, however, analytical solutions are often difficult to obtain. Therefore, numerical methods for solving the problems are given next.

3.1 Solutions of buckling

To find the critical buckling loads $(\bar{{P}}_\mathrm{cr} ,\bar{{q}}_\mathrm{cr})$, one may expand the bending angle $\theta (\xi )$ at buckling in terms of an infinite series. By taking a sufficient number of terms in the series, it is possible to approach the exact solution of the problem. Hence, $\theta (\xi )$ may be truncated as a finite sum as:

$$\begin{aligned} \theta (\xi )=\sum _{m=1}^M {a_m \theta _m (\xi )} ,\quad 0\le \xi \le 1 \end{aligned}$$

(33)

where $a_m$ is unknown coefficient, $\theta _m$ is the corresponding basic function, and M is the number of terms required for convergence.

Table 3 Basic functions of $\theta$ for beams with different boundary conditions

In the present study, specific trigonometric functions are employed as the basic function $\theta _m$ for beams with different combinations of boundary conditions, as shown in Table 3. Subsequently, the Galerkin method is used to translate the differential governing equation into a homogeneous system of algebraic linear equations with the same number of unknown coefficients as Eq. (33). To solve such an eigenvalue problem, the determinant of the coefficient matrix of the system is set to zero. Accordingly, solving the characteristic equation, one can obtain the critical buckling load $\bar{{P}}_\mathrm{cr}$ or $\bar{{q}}_\mathrm{cr}$ by seeking the lowest root of the equation.

Beams with seven combinations of boundary conditions as listed in Table 2 can be classified into two cases: beams with or without lateral force Q. In the following, details for each case are presented to solve the buckling problem.

3.1.1 Beams without lateral force at ends $(\bar{{Q}}=0)$

If one end of the beam is either free or sliding restrained so that the end can move freely laterally, the opposite lateral forces at the beam ends Q must be zero to satisfy the overall equilibrium; namely, the last term on the left-hand side of Eq. (14) or (20) can be eliminated. This situation is applied to beams with boundary conditions of HS, CF, and CS, for which cases the lateral translation of the top end is not constrained. Consequently, the trigonometric functions specified for HS, CF, and CS as shown in Table 3 automatically satisfy the boundary conditions given in Table 1.

Applying Galerkin’s method and using ${\partial \theta }/{\partial a_k }$ as the weighting function, one can solve the Engesser-type differential equation of (14) with $\bar{{Q}}=0$ as:

$$\begin{aligned} \int _0^1 {\left\{ {\left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \theta } \right\} \frac{\partial \theta }{\partial a_k }\mathrm{d}\xi } =0 \end{aligned}$$

(34)

where k varies from 1 to M. In view of Eq. (33), Eq. (34) can be rewritten as a set of homogeneous equations, as:

$$\begin{aligned} \sum _{m=1}^M {\int _0^1 {\left\{ {\left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}^{2}\theta _m }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \theta _m } \right\} \theta _k \mathrm{d}\xi } \cdot a_m } =0,\quad k =1,\ldots ,M \end{aligned}$$

(35)

Setting the determinant of the coefficient matrix of the above system to be zero, one can obtain the critical buckling load parameter $\bar{{P}}_\mathrm{cr}$ or $\bar{{q}}_\mathrm{cr}$ by seeking the lowest root of the equation.

Similarly, the Haringx-type differential equation of (20) with $\bar{{Q}}=0$ can be solved with:

$$\begin{aligned} \sum _{m=1}^M {\int _0^1 {\left\{ {\frac{\mathrm{d}^{2}\theta _m }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \left( {1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \theta _m } \right\} \theta _k \mathrm{d}\xi } \cdot a_m } =0,\quad k=1,\ldots ,M \end{aligned}$$

(36)

3.1.2 Beams with lateral force Q at ends $(\bar{{Q}}\ne 0)$

For beams with boundary conditions of HH, HC, CH, and CC under axially distributed force (e.g., self-weight), the end lateral forces Q are not zero in an asymmetric buckled state. Thus, to eliminate the unknown Q, Eq. (15) of the Engesser type or Eq. (21) of the Haringx type is employed.

By applying Galerkin’s method, Eq. (15) can be solved with:

$$\begin{aligned}&\sum _{m=1}^M \int _0^1 \left\{ \left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}^{3}\theta _m }{\mathrm{d}\xi ^{3}}+\bar{{A}}\bar{{q}}\frac{\mathrm{d}^{2}\theta _m }{\mathrm{d}\xi ^{2}}\right. \nonumber \\&\left. \quad +\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\theta _m }{\mathrm{d}\xi }-\bar{{q}}\theta _m \right\} \theta _k \mathrm{d}\xi \cdot a_m =0,\quad k=1,\ldots ,M \end{aligned}$$

(37)

For beams with double-hinged ends (HH), the corresponding trigonometric function as shown in Table 3 automatically satisfies the boundary conditions given in Table 1. However, for beams with boundary conditions HC, CH, and CC, which share the same basic functions as those of HS, CF, and CS, respectively (see Table 3), all the boundary constraints are satisfied except for the constraint that the lateral translation at the top end is zero. This implies that for HC, CH, and CC, a supplementary constraint equation has to be considered as:

$$\begin{aligned} y(1)=\int _0^1 {\frac{\mathrm{d}y}{\mathrm{d}s}\mathrm{d}\xi } =\int _0^1 {\beta \mathrm{d}\xi } =0 \end{aligned}$$

(38)

Inserting (26) and (33) into (38) leads to:

$$\begin{aligned} \sum _{m=1}^M {\int _0^1 {\left( {\theta _m -\bar{{A}}\frac{\mathrm{d}^{2}\theta _m }{\mathrm{d}\xi ^{2}}} \right) \mathrm{d}\xi } \cdot a_m } =0 \end{aligned}$$

(39)

Table 4 lists detailed expressions of (39) for HC, CH, and CC.

When Eq. (39), which is linear, is taken into account together with Eq. (37) in solving the eigenvalue problem, one finds that a superfluous equation must be removed to determine a unique solution in connection with (39). In the present study, the last equation related to $k=M$ in (37) is replaced with (39), leading to an analogous procedure to determine $a_{m}\, (m=1,\ldots ,M)$. Thus, an eigenvalue problem subjected to a constraint is obtained.

Table 4 Engesser-type supplementary constraint equations for beams with end lateral force Q

Similarly, the Haringx-type differential equation of (21) can be solved with:

$$\begin{aligned}&\sum _{m=1}^M \int _0^1 \left\{ \frac{\mathrm{d}^{4}\theta _m }{\mathrm{d}\xi ^{4}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \left[ {\bar{{A}}\left( {\bar{{P}}+\bar{{q}}(1-\xi )} \right) +1} \right] \frac{\mathrm{d}^{2}\theta _m }{\mathrm{d}\xi ^{2}}\right. \nonumber \\&\left. \quad -\,2\bar{{q}}\left[ {2\bar{{A}}\left( {\bar{{P}}+\bar{{q}}(1-\xi )} \right) +1} \right] \frac{\mathrm{d}\theta _m }{\mathrm{d}\xi }+2\bar{{A}}\bar{{q}}^{2}\theta _m \right\} \theta _k \mathrm{d}\xi \cdot a_m =0,\quad k=1,\ldots ,M \end{aligned}$$

(40)

Similar to those listed in Table 4, the Haringx-type supplementary constraint equations can be obtained by employing Eqs. (32), (33), and (38). As the procedure is analogous to that of the Engesser type, detailed expressions of these equations for HH, HC, CH, and CC are omitted here.

For buckling analysis of all the cases in present study, it has been found to be sufficient to truncate the series expansion at $M =10$. This method is more convenient than those published before and has more broad applicability.

3.2 Solution of initial post-buckling for beams without end lateral force $(\bar{{Q}}=0)$

To determine initial post-buckling, geometrically nonlinear terms should be considered in the governing equation. For beams with boundary conditions HH, HC, CC, and CH (lateral force Q not negligible), the governing equations of both the Engesser and Haringx types for initial post-buckling are highly nonlinear. Explicit expressions of Q are difficult to obtain, especially for statically indeterminate cases such as HC, CC, and CH. As a result, solving the initial post-buckling problem becomes considerably complicated and hence will be discussed in a separate study. The present study considers only beams with $\bar{{Q}}=0$ at the ends, i.e., with boundary conditions HS, CF, and CS.

With $\bar{{Q}}$ eliminated, the governing equation for initial post-buckling, i.e., (13) of the Engesser type or (19) of the Haringx type, is greatly simplified. For instance, Eq. (13) is reduced to:

$$\begin{aligned} \left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \cos \theta } \right) \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \sin \theta =0 \end{aligned}$$

(41)

This second-order nonlinear ordinary differential equation, together with boundary conditions specified at both beam ends (see Table 1), characterizes a two-point boundary value problem (BVP). As it is difficult to obtain an analytical solution, the shooting method is employed to transform the BVP into an initial value problem (IVP) that can be solved using the Runge–Kutta method. A bisection method is cooperatively used to converge to the appropriate initial value, which satisfies the original boundary conditions. Finally, equivalent initial conditions are acquired, and thus a numerical solution of Eq. (41) is obtained.

Similarly, for the Haringx shear formula, Eq. (19) becomes:

$$\begin{aligned} \frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \left( {\frac{1}{2}\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \sin 2\theta +\sin \theta } \right) =0 \end{aligned}$$

(42)

The procedure of solving Eq. (42) is analogous to that described above for Eq. (41).

4 Numerical results and discussions

For stability and initial post-buckling problems of both the Engesser and Haringx types, it is seen from the aforementioned theoretical analysis that the dimensionless buckling loads, modal shapes, and configurations of initial post-buckling depend only on a single dimensionless parameter $\bar{{A}}$ that represents the structural stiffness ratio of bending to shear. A larger value of $\bar{{A}}$ implies that transverse shear occurs more easily. For sandwich beams considered in the present study, the effective bending and shear stiffness of the cross section are presented in “Appendix 1.” For a symmetric sandwich beam, of which the face sheets and the core are taken as isotropic linear elastic, the key parameter $\bar{{A}}$ is mainly dependent on three dimensionless parameters, i.e., the thickness ratio of the face sheet to core $\alpha =f/c$, the slenderness ratio $\eta =t/l$, and the elastic modulus ratio of the core to face sheet ${E_c }/{E_f }$. Here, f and c are separately the thickness of the core and face sheet; l and t are the length and total thickness of the sandwich beam; $E_c$ and $E_f$ are the elastic modulus of the core and face sheet, respectively.

For sandwich beams having either relatively soft or hard cores, the dependence of $\bar{{A}}$ upon $\alpha$ and $\eta$ is presented in Fig. 3. As $\alpha$ is increased, $\bar{{A}}$ increases till $\alpha$ reaches 0.5 at which point the total thickness of the face sheets is equal to that of the core. $\bar{{A}}$ also increases with increasing $\eta$, implying that short beams correspond to larger $\bar{{A}}$. By comparing Fig. 3a with Fig. 3b, it can be seen that different collocation of component materials for sandwich beams results in different order of $\bar{{A}}$ values. For instance, larger ${E_c }/{E_f }$ corresponds to smaller $\bar{{A}}$.

As a case in point, for slender sandwich beams $(\eta =0.02)$ composed of stainless steel face sheets and Rohacell 51 foam core, $\bar{{A}}$ falls in the range of 0.001–0.18. This implies that even for such slender beams, $\bar{{A}}$ cannot be ignored in the aforementioned governing equations. In the following, numerical results are presented, and the influence of $\bar{{A}}$ and boundary conditions on the buckling and initial post-buckling of a sandwich beam subjected to terminal forces and self-weight is discussed in detail.

Fig. 3

Dimensionless parameter $\bar{{A}}$ plotted as a function of $\alpha =f/c$ for selected values of $\eta =t/l$: a sandwich beam with soft core, e.g., stainless steel face sheets and Rohacell 51 foam core; b sandwich beams with hard core, e.g., woven glass–epoxy composite face sheets and closed-cell aluminum foam with porosity of 0.76 as the core [32]. Both the core and face sheet materials are assumed to have a Poisson ratio of 0.3

4.1 Buckling

Consider first dimensionless critical buckling loads, $\bar{{P}}_\mathrm{cr}$ and $\bar{{q}}_\mathrm{cr}$. It is worth noting that beams having the same $\bar{{A}}$ share the same $\bar{{q}}_\mathrm{cr}$ or $\bar{{P}}_\mathrm{cr}$, but they may have different buckling loads, $q_\mathrm{cr}$ or $P_\mathrm{cr}$. The values of $\bar{{q}}_\mathrm{cr}$ with $\bar{{P}}_\mathrm{cr} =0$ and $\bar{{P}}_\mathrm{cr}$ with $\bar{{q}}_\mathrm{cr} =0$ (as listed in Tables 5 and 6, respectively) as well as the concurrent $\bar{{q}}_\mathrm{cr}$ and $\bar{{P}}_\mathrm{cr}$ (as illustrated in Fig. 4) for various beam end supports (i.e., CF, HH, CS, CH, CC, and HC) with $\bar{{A}}=0$ are compared with existing results [8, 9]. Excellent agreement is achieved in all cases, demonstrating the validity and prediction accuracy of the present approach.

Table 5 Comparison of $\bar{{q}}_\mathrm{cr}$ when $\bar{{P}}_\mathrm{cr} =0$ for beams with $\bar{{A}}=0$

Table 6 Comparison of $\bar{{P}}_\mathrm{cr}$ when $\bar{{q}}_\mathrm{cr} =0$ for beams with $\bar{{A}}=0$

Fig. 4

Buckling capacity of beams with $\bar{{A}}=0$ under terminal forces and self-weight

The buckling capacity of beams with hinged–sliding (HS) and hinged–clamped (HC) ends has been rarely reported in the open literature. For $\bar{{A}}=0$, results for both HS and HC cases are presented in Fig. 4. They share the same critical terminal load $\bar{{P}}_\mathrm{cr}$ with those of CF and CH when the self-weight parameter $\bar{{q}}_\mathrm{cr} =0$, but diverge when $\bar{{q}}_\mathrm{cr}$ is increased. When the effect of transverse shear is ignored (i.e., $\bar{{A}}=0)$, the buckling capacity curve of beams with CS ends almost coincides with that of beams with HH. Further, when $\bar{{A}}=0$, it is seen from Fig. 4 that the relationship between $\bar{{P}}_\mathrm{cr}$ and $\bar{{q}}_\mathrm{cr}$ is nearly linear for beams with different end constraints.

Since no results about the buckling of Timoshenko beams (or beams in shear) under self-weight have been hitherto reported, finite element (FE) simulations are employed here to validate the present analytical predictions for beams with $\bar{{A}}\ne 0$. FE calculations are carried out for symmetric sandwich beams satisfying two typical boundary conditions: CF and CC. Eigenvalue analysis is performed using the FE code ABAQUS/Standard to compute the critical buckling loads and eigenmodes. Four-noded plane strain quadrilateral elements with reduced integration (CPE4R) are used for both the face sheets and the core. Perfect bonding between the core and the face sheets is assumed. Boundary conditions are applied using coupling constraints. Mesh convergence has been guaranteed for each calculation. To determine the stability of sandwich beams under combined terminal force and self-weight, a two-step analysis is employed: A general step of static analysis is firstly carried out for calculating the initial stress field under the prescribed “self-weight” with gravity option; subsequently, a linear perturbation step of buckle analysis is applied, and eigenvalue extraction procedure is carried out using the Lanczos solver. For beams under sole self-weight or terminal force, only a buckle analysis is needed to obtain the critical load. Sandwiches consisting of stainless steel face sheets with equal thickness and Rohacell 51 foam core are taken into account, with $\rho _f =8030\,\hbox {kg/m}^{3},\, \upsilon =0.3$ and $E_f =210\,\hbox {GPa}$ for the face sheets, and $\rho _c =51\,\hbox {kg/m}^{3},\, \upsilon =0.3$, and $E_c =70\,\hbox {MPa}$ for the core. Sandwich beams with different values of $\bar{{A}}$ are constructed by changing the ratio of beam length to thickness, according to Eq. (48).

Fig. 5

Comparison of finite element (FE) calculations with analytical predictions for beams under terminal force and self-weight with different $\bar{{A}}$: a clamped–free (CF), and b clamped–clamped (CC) end constraints

Fig. 6

Comparison of FE calculations with analytical predictions: critical buckling load plotted as a function of $\bar{{A}}$ for beams with various boundary conditions under a, c terminal force only ($\bar{{q}}_\mathrm{cr} =0)$ and b, d self-weight only ($\bar{{P}}_\mathrm{cr} =0)$. a, b clamped–free (CF) boundary condition; c, d clamped–clamped (CC) boundary condition

As shown in Figs. 5 and 6, the critical loads predicted by the Engesser theory agree well with FE simulation results, with the difference ranging from 0.14 % at small values of $\bar{{A}}$ to about 5 % at large values of $\bar{{A}}$, while the Haringx theory leads to serious overestimates. This implies that for sandwich beams considered in the present study, the assumption adopted by the Haringx theory that the shear force induced by end axial load and lateral force is aligned on the cross section normal to the beam axis in the initial undeflected state is questionable. Rather, the shear force should be aligned on the cross section normal to the deflected beam axis, as adopted by the Engesser theory. Consequently, the Engesser theory is employed for all subsequent analysis.

From Fig. 5, one can also find that as $\bar{{A}}$ is increased (i.e., the effect of transverse shear becomes more significant), the $\bar{{q}}_\mathrm{cr}$ versus $\bar{{P}}_\mathrm{cr}$ relationship becomes increasingly nonlinear and the buckling capacity decreases. Additionally, the buckling capacity curve is more sensitive to $\bar{{A}}$ for beams with CC ends than those with CF ends. Also, Fig. 6 reveals that the dependence of critical buckling load $\bar{{q}}_\mathrm{cr}$ when $\bar{{P}}_\mathrm{cr} =0$ or $\bar{{P}}_\mathrm{cr}$ when $\bar{{q}}_\mathrm{cr} =0$ upon $\bar{{A}}$ is complicated and highly nonlinear.

For beams with different end constraints under self-weight only, the modal shapes (with lateral deformation normalized by maximum lateral deflection) at buckling are presented in Fig. 7 based on the Engesser theory $(\bar{{A}}\ne 0)$. For comparison, Fig. 7 also includes the corresponding modal shapes predicted using the Euler–Bernoulli beam theory $(\bar{{A}}=0)$. In comparison with modal shapes with $\bar{{A}}=0$, for modal shapes with $\bar{{A}}\ne 0$, the bending deformation is more serious near the bottom end of the beam, and for beams with end lateral force (i.e., HH, CC, CH and HC), the locations of the maximum lateral deflection for the modal shapes with $\bar{{A}}\ne 0$ are closer to the bottom end. Additionally, it should be noted from Fig. 7 that the selected value of $\bar{{A}}$ changes when the end constraints of the beam are varied, because the sensitivity of $\bar{{A}}$ on modal shape also varies.

Fig. 7

Colour online Modal shapes at buckling for beams with different end constraints under only self-weight $(\bar{{P}}_\mathrm{cr} =0)$. Red and black lines refer to modal shapes with $\bar{{A}}=0$ (Euler–Bernoulli beam) and $\bar{{A}}\ne 0$ (Engesser beam), respectively; gray dash lines initial reference state. HS hinged–sliding, CF clamped–free, CS clamped–sliding, HH hinged–hinged, HC hinged–clamped, CH clamped–hinged, CC clamped–clamped

Fig. 8

Sensitivity of $\bar{{A}}$ on critical buckling loads for beams with varying boundary conditions under a self-weight only ($\bar{{P}}_\mathrm{cr} =0)$ and b terminal force only ($\bar{{q}}_\mathrm{cr} =0)$. $\bar{{q}}_{cr0}$ and $\bar{{P}}_{cr0}$ are defined as critical buckling loads for beams with $\bar{{A}}=0$ (i.e., Euler–Bernoulli beams) subjected to self-weight only and terminal force only, respectively

Based on the Engesser theory, the sensitivity of $\bar{{A}}$ on critical buckling loads of beams under self-weight only or terminal force only for different end constraints is presented in Fig. 8. The relationship between the buckling load and $\bar{{A}}$ is nonlinear and highly dependent on end support conditions, as the critical buckling load is more sensitive to $\bar{{A}}$ for beams with stronger end constraints. The order of the sensitivity from weak to strong is HS, CF, and CS beams without end lateral force, followed by HH, HC, CH, and CC beams with end lateral force. The critical buckling load of beams with CC end constraints is most sensitive to $\bar{{A}}$. Additionally, similar to the results in Fig. 4 when $\bar{{A}}=0$, the curves of CS and HH beams in Fig. 8 nearly coincide with each other for both cases (self-weight only and terminal force only), but with different modal shapes. For CF and HS beams subjected to terminal force only, the data for critical buckling loads are quite close to each other, but diverge for beams subjected to self-weight only.

From a designer’s point of view, the critical values of $\bar{{q}}_\mathrm{cr}$ or $\bar{{P}}_\mathrm{cr}$ presented here are of great significance because they furnish the maximum feasible length of a beam.

Fig. 9

Influence of $\bar{{A}}$ on abscissa and ordinate values (i.e., $\bar{{y}}_{\max }$ and $\bar{{x}}_{\max } )$ of the upper end of deflected beam without end lateral force (i.e., CF, CS, and HS beams) under a self-weight only (${\bar{{q}}}/{\bar{{q}}_\mathrm{cr} }=1.10)$ and b terminal force only (${\bar{{P}}}/{\bar{{P}}_\mathrm{cr} }=1.10)$ during initial post-buckling, with $\bar{{y}}_{\max } ={y_{\max } }/l$ and $\bar{{x}}_{\max } ={x_{\max } }/l$

4.2 Initial post-buckling of CF, CS, and HS beams

As previously mentioned, in this section, only results of initial post-buckling for beams without end lateral force (i.e., CF, CS, and HS) are discussed.

Figure 9 presents the influence of $\bar{{A}}$ on the abscissa and ordinate values (i.e., $x_{\max }$ and $y_{\max }$) of the upper end, both normalized with beam length l, for a deflected beam subjected to self-weight only $({\bar{{q}}}/{\bar{{q}}_\mathrm{cr} }=1.10)$ or terminal force only $({\bar{{P}}}/{\bar{{P}}_\mathrm{cr} }=1.10)$ during its initial post-buckling stage. $x_{\max }$ and $y_{\max }$ also represent the maximum coordinate values along the x-axis and the y-axis. As shown in Fig. 9a, for beams subjected to self-weight only, the deflection of a beam with HS ends is nearly independent of $\bar{{A}}$, while in Fig. 9b for beams subjected to terminal force only, the deflection curve of a beam with HS ends is almost coincident with that of a CF beam, both slightly sensitive to $\bar{{A}}$. However, $\bar{{A}}$ affects significantly the deflection of a CS beam during the initial post-buckling stage, especially when it is subjected to self-weight only. This implies that if transverse shear is not included as in the classical Euler–Bernoulli theory, the deflection of beams with CS ends may be substantially underestimated.

Overall, from Fig. 9, it may be concluded that the influence of $\bar{{A}}$ on the horizontal and vertical deflections of the beam upper end, from weak to strong, is ordered as HS, CF, and CS, which is consistent with the previous result in Fig. 8 regarding the influence of $\bar{{A}}$ on critical buckling loads.

Fig. 10

For CF, CS, and HS beams $(\bar{{A}}=0.10)$ without end lateral force, the abscissa and ordinate values of the upper end of deflected beam plotted as a function of a ${\bar{{q}}}/{\bar{{q}}_\mathrm{cr} }$ under self-weight only and b ${\bar{{P}}}/{\bar{{P}}_\mathrm{cr} }$ under terminal force only during initial post-buckling

For a beam with $\bar{{A}}=0.10$ which reflects a moderate degree of transverse shear (see Fig. 8), Fig. 10a, b plots the normalized abscissa and ordinate values of its upper end as functions of self-weight ${\bar{{q}}}/{\bar{{q}}_\mathrm{cr} }$ and terminal force ${\bar{{P}}}/{\bar{{P}}_\mathrm{cr} }$, respectively, which represents the initial post-buckling paths of beams with different boundary conditions. Apparently, the deflection of initial post-buckling is affected by beam boundary conditions. Comparatively speaking, the displacement along the x-axis for a CS beam is the largest and, as illustrated in Fig. 10b for beams subjected to terminal force only, the deflection curves of HS and CF beams are almost identical, similar to the results shown in Figs. 8b and 9b. Generally, beams with stronger end constraints correspond to more serious deflections (in particular, axial shortening along the x-axis during initial post-buckling), and these deflections are more sensitive to $\bar{{A}}$.

Finally, it should be mentioned that because the present initial post-buckling solution is based upon the assumption of small shear strain (i.e., $\sin \gamma _\mathrm{eq} =\gamma _\mathrm{eq}$, $\cos \gamma _\mathrm{eq} =1)$, the results would tend to be less accurate as the loading moves away from the critical point, that is, at the larger values of $\bar{{q}}$ or $\bar{{P}}$.

5 Conclusions

The influence of transverse shear on stability and initial post-buckling of a standing sandwich (or laminated composite) beam under terminal force and axially distributed load (self-weight) is analyzed. By employing the Engesser and Haringx shear theories, nonlinear equations governing the buckling and initial post-buckling behaviors of the sandwich beam are derived, respectively. Critical buckling loads and initial post-buckled configuration of the beam are determined for a total of seven different boundary conditions. Main findings are summarized as follows:

• (1) Dimensionless buckling load, modal shapes, and configuration of initial post-buckling depend mainly on a dimensionless parameter $\bar{{A}}$ of the sandwich beam that represents its structural stiffness ratio of bending to shear.

• (2) The effects of transverse shear should not be neglected for sandwich beams, and compared with finite element calculations, the Engesser theory leads to better predictions than the Haringx theory.

• (3) With transverse shear taken into account, beams exhibit modal shapes quite different from those obtained using the classical Euler–Bernoulli beam theory.

• (4) The dependence of critical buckling load upon $\bar{{A}}$ is highly nonlinear and heavily dependent upon end support conditions, as the critical buckling load of a beam with stronger end constraints is more sensitive to $\bar{{A}}$.

• (5) If transverse shear is not included as in the classical Euler–Bernoulli theory, the post-buckling deflection of the beam may be underestimated. Beams with stronger end constraints correspond to more serious initial post-buckling deflections (in particular, axial shortening along the x-axis), and these deflections are more sensitive to $\bar{{A}}$.

• (6) The present theoretical approach not only provides accurate and simple engineering estimates for the buckling and initial post-buckling of sandwich columns but can also be applied to analyze the stability and initial post-buckling of nonprismatic or even graded beams.

Appendices

Appendix 1: Formulation of dimensionless parameter $\bar{{A}}$ for sandwich beams

A general asymmetric sandwich section (face sheets not having same thickness and/or material) is presented in Fig. 11. The sandwich beam consists of two face sheets having density $\rho _1$ and $\rho _2$, thickness $f_{1}$ and $f_{2}$, elastic modulus $E_{f1}$ and $E_{f2}$, and shear modulus $G_{f1 }$and $G_{f2}$, respectively, and a core of density $\rho _c$, thickness c, elastic modulus $E_{c}$, and shear modulus $G_{c}$. The beam width is uniform, W.

Fig. 11

Section of an asymmetric sandwich beam

It is assumed that the shear stresses are distributed uniformly over the entire beam section of area A. An equivalent shear angle can thence be defined based on the “effective” shear modulus of the section, $\bar{{G}}$, which is defined from the compliances of the constituent phases as:

$$\begin{aligned} {(f_1 +c+f_2 )}/{\bar{{G}}}={f_1 }/{G_{f1} }+c/{G_c }+{f_2 }/{G_{f2}} \end{aligned}$$

(43)

where $G_i ={E_i }/{2(1+\nu _i)}$ $(i =f_{1},\, f_{2}$, and c, denoting upper face sheet, bottom face sheet, and core, respectively).

With respect to the reference axis y through the center of the core (Fig. 11), the neutral axis (N. A.) of the section is defined at a distance e, as:

$$\begin{aligned} e=\frac{E_{f2} f_2 (f_2 +c)-E_{f1} f_1 (f_1 +c)}{2(E_{f1} f_1 +E_c c+E_{f2} f_2 )} \end{aligned}$$

(44)

As a result, the equivalent flexural rigidity of an asymmetric sandwich section $(EI)_\mathrm{eq}$ is given by:

$$\begin{aligned} (EI)_\mathrm{eq} =\left( {E_{f1} \frac{f_1^3 }{12}+E_{f1} f_1 \left( {\frac{f_1 }{2}+\frac{c}{2}+e} \right) ^{2}+E_{f2} \frac{f_2^3 }{12}+E_{f2} f_2 \left( {\frac{f_2 }{2}+\frac{c}{2}-e} \right) ^{2}+E_c \frac{c^{3}}{12}+E_c ce^{2}} \right) W\nonumber \\ \end{aligned}$$

(45)

The shear correction coefficient is calculated from strain energy considerations, accounting for the nonuniform distribution of shear stresses throughout the cross section and the contribution of face sheets [24], as:

$$\begin{aligned} \alpha= & {} \bar{{G}}AW\left( \sum _{i=1,2} \left\{ \frac{E_{fi}^2 }{4(EI)_\mathrm{eq}^2 G_{fi} }\left[ a_i^4 f_i -\frac{2}{3}a_i^2 \left( a_i^3 -b_i^3 \right) +\frac{1}{5}\left( a_i^5 -b_i^5 \right) \right] \right. \right. \nonumber \\&\left. \left. +\,\frac{E_{fi}^2}{(EI)_\mathrm{eq}^2 G_c }\left[ f_i^2 c_i^2 b_i +\frac{2}{15}\frac{E_c^2 }{E_{fi}^2 }b_i^5 +\frac{2}{3}\frac{E_c }{E_{fi} }f_i c_i b_i^3 \right] \right\} \right) \end{aligned}$$

(46)

where

$$\begin{aligned} a_i =f_i +c/2+(-1)^{i+1}e,\,b_i =c/2+(-1)^{i+1}e,\,c_i ={f_i }/2+c/2+(-1)^{i+1}e \end{aligned}$$

(47)

Finally, the nondimensional parameter $\bar{{A}}$, in which the small but nonnegligible shear stiffness of the face sheets and the bending stiffness of the core are taken into account, is obtained as:

$$\begin{aligned} \bar{{A}}= & {} \frac{\alpha \left( {EI} \right) _\mathrm{eq} }{\left( {GA} \right) _\mathrm{eq} l^{2}}=\frac{W}{l^{2}}\left( \sum _{i=1,2} \left\{ \frac{E_{fi}^2 }{4(EI)_\mathrm{eq} G_{fi} }\left[ {a_i^4 f_i -\frac{2}{3}a_i^2 \left( a_i^3 -b_i^3 \right) +\frac{1}{5}\left( a_i^5 -b_i^5\right) } \right] \right. \right. \nonumber \\&\left. \left. +\,\frac{E_{fi}^2 }{(EI)_\mathrm{eq} G_c }\left[ {f_i^2 c_i^2 b_i +\frac{2}{15}\frac{E_c^2 }{E_{fi}^2 }b_i^5 +\frac{2}{3}\frac{E_c }{E_{fi} }f_i c_i b_i^3 } \right] \right\} \right) \end{aligned}$$

(48)

It should be mentioned that with respect to the reference axis y, the axis of mass center is defined at a distance g, as:

$$\begin{aligned} g=\frac{\rho _2 f_2 (c+f_2 )-\rho _1 f_1 (c+f_1 )}{2(\rho _1 f_1 +\rho _c c+\rho _2 f_2 )} \end{aligned}$$

(49)

which is analogous to Eq. (43). Generally, for sandwich beams considered in the present study, the axis of gravity center (G. A.) is coincident with that of mass center, if the gravity field is uniformly distributed.

It is worth noting that for an asymmetric sandwich beam subjected to axially distributed force, only when its neutral axis coincides with its gravity center axis (i.e., $e=g$) and the terminal force is exerted on the line of the neutral axis, can the relevant stability and initial post-buckling problems be solved using the present approach. Otherwise, they belong to problems of eccentric loading, which may be treated as imperfection problems.

For symmetric sandwich beams satisfying $E_{f1} =E_{f2},\, f_1 =f_2$ and $\rho _1 =\rho _2$, one has $e=g=0$.

Appendix 2: Governing equations of buckling in terms of lateral displacement

As a supplementary, buckling governing equations in terms of lateral displacement for a Timoshenko beam are derived. Let the dimensionless lateral displacement be defined as $\bar{{y}}=y/l$. According to Eq. (1), one has:

$$\begin{aligned} \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }=\frac{\mathrm{d}y}{\mathrm{d}s}=\sin \beta \end{aligned}$$

(50)

Rewriting Eq. (6) and substituting Eqs. (8)–(9) into Eq. (50), we obtain the following coupled system of ordinary differential equations as the governing equations of a Timoshenko beam:

$$\begin{aligned}&\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }-\bar{{Q}}\cos \beta =0 \end{aligned}$$

(51a)

$$\begin{aligned}&\frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }=\sin \theta +\gamma _\mathrm{eq} \cos \theta \end{aligned}$$

(51b)

For buckling analysis, based upon the assumption of small deformation, we have $\sin \theta \cong \theta ,\, \cos \theta \cong 1,\, \sin \beta \cong \beta ,\, \cos \beta \cong 1$, and thus ${\mathrm{d}\bar{{y}}}/{\mathrm{d}\xi }=\beta$. Then, the coupled Eqs. (51a) and (51b) may be rewritten as:

$$\begin{aligned}&\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }-\bar{{Q}}=0 \end{aligned}$$

(52a)

$$\begin{aligned}&\frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }=\theta +\gamma _\mathrm{eq} \end{aligned}$$

(52b)

which are the governing equations for the buckling of Timoshenko beams.

For the buckling of Engesser-type shear beams, making use of Eq. (11), we can rewrite the above coupled differential governing equations as:

$$\begin{aligned}&\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }-\bar{{Q}}=0 \end{aligned}$$

(53a)

$$\begin{aligned}&\frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }=\theta +\bar{{A}}\left( {\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }-\bar{{Q}}} \right) \end{aligned}$$

(53b)

Similarly, for the buckling of Haringx-type shear theory, by rewriting Eq. (17), the coupled differential governing equations are obtained as:

$$\begin{aligned}&\frac{\mathrm{d}^{2}\theta }{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }-\bar{{Q}}=0 \end{aligned}$$

(54a)

$$\begin{aligned}&\frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }=\theta +\bar{{A}}\left( {\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \theta -\bar{{Q}}} \right) \end{aligned}$$

(54b)

Finally, through a series of differential operations and rearranging of Eqs. (52b) and Eqs. (B5), we obtain the uncoupled governing equations for buckling of Engesser-type shear beams in terms of lateral displacement $\bar{{y}}$, as:

$$\begin{aligned}&\displaystyle \left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}^{3}\bar{{y}}}{\mathrm{d}\xi ^{3}}+2\bar{{A}}\bar{{q}}\frac{\mathrm{d}^{2}\bar{{y}}}{\mathrm{d}\xi ^{2}}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }-\bar{{Q}}=0 \end{aligned}$$

(55a)

$$\begin{aligned}&\displaystyle \theta =\left( {1-\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }+\bar{{A}}\bar{{Q}} \end{aligned}$$

(55b)

and the uncoupled governing equations for buckling of Haringx-type shear beams in terms of $\bar{{y}}$, as:

$$\begin{aligned}&\left( {1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) ^{2}\frac{\mathrm{d}^{3}\bar{{y}}}{\mathrm{d}\xi ^{3}}+2\bar{{A}}\bar{{q}}\left( {1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) \frac{\mathrm{d}^{2}\bar{{y}}}{\mathrm{d}\xi ^{2}}\nonumber \\&\quad \quad +\left\{ 2\bar{{A}}^{2}\bar{{q}}^{2}+\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] \left( {1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) ^{3}\right\} \frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi } \nonumber \\&\quad \quad +\left\{ {2\bar{{A}}^{3}\bar{{q}}^{2}-\left( {1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \right) ^{3}} \right\} \bar{{Q}}=0 \end{aligned}$$

(56a)

$$\begin{aligned}&\theta =\frac{\frac{\mathrm{d}\bar{{y}}}{\mathrm{d}\xi }+\bar{{A}}\bar{{Q}}}{1+\bar{{A}}\left[ {\bar{{P}}+\bar{{q}}(1-\xi )} \right] } \end{aligned}$$

(56b)

Equations (55a) and (56a) are the “condensed” buckling governing equations in terms of $\bar{{y}}$ for the Engesser and Haringx shear beams, respectively.

Compared with the governing equation in terms of rotation angle $\theta$, i.e., Eq. (14) or Eq. (20), the governing equation in terms of lateral displacement $\bar{{y}}$, i.e., Eq. (55a) or Eq. (56a), appears to be more complicated. With $\theta$ chosen as the principal unknown function and trigonometric functions employed as the base function which automatically satisfy the boundary conditions, it would be more convenient to obtain convergent solutions. Further, since the post-buckling studied in this paper is a highly nonlinear geometric problem, it may be more appropriate to employ $\theta$ as the unknown function.