Generalized Statistical Convergence Based on Fractional Order Difference Operator and Its Applications to Approximation Theorems

Abstract

In this paper, following very recent results of Baliarsingh (Alex Eng J 55(2):1811–1816, 2016), we first introduce the concepts of statistically $\Omega ^{\Delta }$-summability and $\Omega ^{\Delta }$-statistical convergence by means of fractional-order difference operator $\Delta ^{\alpha ,\beta ,\gamma }_{h}$. We also present some important inclusion relations between newly proposed methods. Our present investigation deals essentially with various summability techniques and reveals how these methods lead to a number of approximation by positive linear operators. As an application, we prove a Korovkin type approximation theorem and also present an illustrative example using the generating function type Meyer-König and Zeller operator. Furthermore, we estimate the rate of convergence of approximating linear operators by means of the modulus of continuity and some Voronovskaja type results are derived. Finally, we present some computational and geometrical interpretations to illustrate some of our approximation results.

1 Introduction and Preliminaries

This work is a combination of two mathematical research areas namely statistical summability and approximation process based on positive linear operators. To reveal the novelties presented by this article, we present some new developments and historical comments in summability theory and its applications to approximation theorems.

The theory of summability arises from the process of summation of series and consists fruitful applications in various contexts, for example, approximation theory, probability theory, quantum mechanics, analytic continuation, Fourier analysis, dynamical systems, the theory of orthogonal series, and fixed point theory. Due to the rapid development of sequence spaces some researchers have focused on the notion of statistical convergence which brings a new approach to the concept of ordinary convergence. In 1935, statistical convergence was introduced by Zygmund (1959) under the name of almost convergence. In 1951, Steinhaus (1951) and Fast (1951) independently introduced the notion of statistical convergence. At the last quarter of the twentieth century, statistical convergence and statistical summability have been played the significant role in the development of functional analysis. There are many other generalizations of these concepts which have been investigated by many researchers (Kadak et al. 2017; Edely and Mursaleen 2009; Fridy 1993; Kadak 2016; Mohiuddine 2016; Mursaleen et al. 2012; Connor 1989; Başarır and Konca 2017; Yeşilkayagil and Başar 2016; Nuray et al. 2016; Duman and Orhan 2008).

Let A be a subset of the set $\mathbb {N}$ of natural numbers and $A_{n}=\left\{ j\le n: j\in A \right\}$. The natural density of A is defined by

$$\begin{aligned} \delta (A)=\lim _{n\rightarrow \infty }\frac{1}{n}~|A_{n}| \end{aligned}$$

provided that the limit exists, where $|A_{n}|$ denotes the cardinality of set $A_{n}$. A sequence $x=(x_{j})$ is said to be statistically convergent (st-convergent) to the number L, denoted by $st-\lim x=L$, if, for each $\varepsilon >0,$ the set:

$$\begin{aligned} A_{\varepsilon }=\left\{ j\in \mathbb {N}:|x_{j}-L|\geqq \varepsilon \right\} , \end{aligned}$$

has natural density zero, or equivalently:

$$\begin{aligned} \delta (A_\epsilon )=\lim _{n \rightarrow \infty }\frac{1}{n}\left| \{j\le n: |x_{j}-L|\geqq \varepsilon \}\right| =0. \end{aligned}$$

By $\omega$, we denote the family of all real valued sequences and any subspace of $\omega$ is called a sequence space. We write $\ell _\infty , c$ and $c_0$ for the classical sequence spaces of all bounded, convergent and null sequences, respectively. With respect to the supremum norm $\Vert x\Vert _\infty =\sup _{k}|x_k|$, it is not hard to show that these are Banach spaces. The theory of difference sequence spaces was initially introduced by Kızmaz (1981). As a generalization of difference sequence spaces, the idea of difference operators with natural order m was introduced by Et and Çolak (1995) by defining:

$$\begin{aligned} \lambda (\Delta ^m)=\{x=(x_k): \Delta ^m(x) \in \lambda ,~m \in \mathbb {N}\} \quad (\lambda \in \{\ell _\infty , c, c_0\}), \end{aligned}$$

where

$$\begin{aligned} \Delta ^0x=(x_k), \quad \Delta ^mx=(\Delta ^{m-1} x_{k}-\Delta ^{m-1} x_{k+1}), \end{aligned}$$

and

$$\begin{aligned} \Delta ^mx_k=\sum _{i=0}^{m}(-1)^i\left( {\begin{array}{c}m\\ i\end{array}}\right) x_{k+i}. \end{aligned}$$

Moreover, these well-known difference operators were extended and used year after year in many directions (see Aydin and Başar 2004; Kadak 2017a, b). In 2013, Baliarsingh (2013), Baliarsingh and Dutta (2015) (also see Kadak and Baliarsingh 2015) introduced a new kind of difference sequence spaces with respect to the fractional-order difference operator involving Gamma function, as:

$$\begin{aligned} \Delta ^{(\alpha )} (x_k)= & {} \sum _{i=0}^{\infty }(-1)^{i} \frac{\Gamma (\alpha +1)}{i!\Gamma (\alpha -i+1)} x_{k-i}. \end{aligned}$$

In the year 2016, some new classes of difference sequence spaces of fractional order have been introduced by Baliarsingh (2016) (see Baliarsingh and Nayak 2017).

Given a positive constant h, for each real numbers $\alpha$, $\beta$ and $\gamma ~(\gamma \notin \mathbb N)$, we define generalized difference sequence associating with the fractional order difference operator $\Delta ^{\alpha ,\beta ,\gamma }_h$ as:

$$\begin{aligned} (\Delta^{\alpha ,\beta ,\gamma }_hx)_k=\sum _{i=0}^\infty \frac{(-\alpha )_i~(-\beta )_i}{ i!(-\gamma )_i~h^{\alpha +\beta -\gamma }}x_{k-i}, \end{aligned}$$

(1)

where

$$(u)_k:=\left\{ \begin{array}{lll} 1 , {}{} (u=0\,\,~\text {or}~\,\,k=0), \\ \frac{\Gamma (u+k)}{\Gamma (u)}=u(u+1)(u+2)\dots (u+k-1) , {}{} (k \in \mathbb N).\end{array}\right.$$

We assume without loss of generality, the summation given in (1) is convergent for all $\gamma \notin \mathbb N$ and $\alpha +\beta > \gamma$.

Our main focus of the present study is to generalize the concept of statistical summability using a fractional order linear difference operator $\Delta ^{\alpha ,\beta ,\gamma }_{h}$. In fact, our present investigation shows how newly proposed summability methods lead to a number of approximation processes. We also establish some important approximation results associating with statistically $\Omega ^{\Delta }$-summability and investigate Korovkin and Voronovskaja type approximation results by the help of generalized Meyer-König and Zeller operator. We also present computational and geometrical approaches to illustrate some of our results in this paper.

2 Some New Definitions and Inclusion Relations

In this section, we first give the definitions concerning statistically $\Omega ^{\Delta }$-summability and $\Omega ^{\Delta }$-statistical convergence by means of the fractional order difference operator $\Delta ^{\alpha ,\beta ,\gamma }_{h}$. Secondly, we state and prove two theorems and an illustrative example to determine some inclusion relations between proposed methods.

Let $(\lambda _n)_{n=0}^{\infty }$ be a strictly increasing sequence of positive numbers i.e.

$$\begin{aligned} 0<\lambda _0<\lambda _1< \cdots<\lambda _n< \cdots\,\, ~\text {and}~\,\,\lim _{n \rightarrow \infty }\lambda _n=\infty . \end{aligned}$$

Also, let $x=(x_n)$ be a sequence of real or complex number. We then define the following sum involving difference operator $\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x)$ as follows:

$$\begin{aligned} \Omega ^{\Delta }_n(\lambda x)= & {} \frac{1}{\Delta \lambda _n}\sum _{k=\lambda _{n-1}}^{\lambda _{n}}(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k\\= & {} \frac{1}{\lambda _n-\lambda _{n-1}} \sum _{k=\lambda _{n-1}}^{\lambda _{n}} \sum _{i=0}^{k}\frac{(-\alpha )_i~(-\beta )_i}{ i!(-\gamma )_i~h^{\alpha +\beta -\gamma }}\lambda _{k-i}x_{k-i}, \end{aligned}$$

where $\alpha ,\beta$ and $\gamma \notin \mathbb N$ are real numbers, h is a positive constant such that $|\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda _n)|\ge 0$ and $\lambda _{-n}=0$ for all $n \in \mathbb N$. That is,

$$\begin{aligned} \Omega ^{\Delta }_n(\lambda x)= & {} \frac{1}{\Delta \lambda _n~ h^{\alpha +\beta -\gamma }} \sum _{k=\lambda _{n-1}}^{\lambda _{n}}\Bigg \{\lambda _kx_k- \frac{\alpha \beta }{\gamma } \lambda _{k-1}x_{k-1}+ \frac{\alpha (\alpha -1)~\beta (\beta -1)}{2\gamma (\gamma -1)~} \lambda _{k-2}x_{k-2} \\&-\,\frac{\alpha (\alpha -1)(\alpha -2)~\beta (\beta -1)(\beta -2)}{3!\gamma (\gamma -1)(\gamma -2)} \lambda _{k-3}x_{k-3} +\cdots +\frac{(-\alpha )_k~(-\beta )_k}{k!(-\gamma )_k}\lambda _{0} x_{0} \Bigg \}. \end{aligned}$$

Definition 1

Let $\alpha ,\beta$ and $\gamma \notin \mathbb N$ be real numbers and h be any positive constant. A sequence $x=(x_n)$ is said to be $\Omega ^{\Delta }$-summable to the number L, if

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{1}{\lambda _n-\lambda _{n-1}}\sum _{k=\lambda _{n-1}}^{\lambda _{n}}(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k=L. \end{aligned}$$

We also say that the sequence $x=(x_n)$ is strongly $\Omega _q^{\Delta }$-summable to L, if

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{1}{\lambda _n-\lambda _{n-1}}\sum _{k=\lambda _{n-1}}^{\lambda _{n}}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |^q=0 \quad (0<q<\infty ). \end{aligned}$$

Definition 2

A sequence $x=(x_n)$ is said to be $\Omega ^{\Delta }$-statistical convergent to a number L, if, for every $\epsilon >0,$

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{1}{\lambda _n-\lambda _{n-1}}\left| \left\{ k\le \lambda _n-\lambda _{n-1}:\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |\ge \epsilon \right\} \right| =0. \end{aligned}$$

We denote it by $S_{\Omega ^{\Delta }}-\lim x_n = L.$ We also say that the sequence $x=(x_n)$ is statistically $\Omega ^{\Delta }$-summable to L, if

$$\begin{aligned} st-\lim \Omega ^{\Delta }_n(\lambda x)=L. \end{aligned}$$

Equivalently, we may write

$$\begin{aligned} \lim _{j \rightarrow \infty }\frac{1}{j}\left| \Bigg \{n\le j: \bigg |\frac{1}{\lambda _n-\lambda _{n-1}}\sum _{k=\lambda _{n-1}}^{\lambda _{n}}(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\bigg |\geqq \epsilon \Bigg \}\right| =0. \end{aligned}$$

We write it as $\overline{N}_{\Omega ^{\Delta }}-\lim x_n =L$.

Now, we shall give the following special cases to show the effectiveness of above definitions.

• (1) Let us take $\alpha =2$, $\beta =\gamma$, $h=1$, i.e.

  $$\begin{aligned} (\Delta _{1}^{2,\beta ,\beta }(\lambda x))_k=\lambda _kx_k-2\lambda _{k-1}x_{k-1}+\lambda _{k-2}x_{k-2}. \end{aligned}$$

  Then statistically $\Omega ^{\Delta }$-summability given in Definition 2 is reduced to the $\Lambda ^2$-statistically summability introduced in Braha et al. (2015) (see also Kadak 2016; Alotaibi and Mursaleen 2013).

• (2) Let $\alpha =2$, $\beta =\gamma$, $h=1$, then $\Omega ^{\Delta }$-statistical convergence given in Definition 2 reduces to weighted $\Lambda ^2$-statistically convergence. In addition, the notion of strongly $\Omega _q^{\Delta }$-summability can be interpreted as strongly $\Lambda ^2$-summability (see Kadak 2016; Braha et al. 2015; Mursaleen 2000).

We now present the following theorem which gives the relation between $\Omega ^{\Delta }$-statistical convergence and statistically $\Omega ^{\Delta }$-summability.

Theorem 1

Let$|(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|\le M$for all$k \in \mathbb N.$If a sequence$x=(x_n)$is$\Omega ^{\Delta }$-statistical convergent to the numberL,  then it is statistically$\Omega ^{\Delta }$-summable to the same limit, but not conversely.

Proof

Let $h> 0$ be any constant, $\alpha ,\beta$ and $\gamma \notin \mathbb N$ be real numbers. Let $|(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|\le M$ for all $k \in \mathbb N$. Since $S_{\Omega ^{\Delta }}-\lim x_n = L$, we have

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{1}{\lambda _n-\lambda _{n-1}}\left| \left\{ k\le \lambda _n-\lambda _{n-1}:\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |\ge \epsilon \right\} \right| =0. \end{aligned}$$

We thus find that

$$\begin{aligned} |\Omega ^{\Delta }_n(\lambda x)-L|= & {} \bigg |\bigg (\frac{1}{\lambda _n-\lambda _{n-1}}\sum _{k=\lambda _{n-1}}^{\lambda _{n}}(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k\bigg )-L\bigg |\\= & {} \bigg |\frac{1}{\lambda _n-\lambda _{n-1}} \sum _{k=\lambda _{n-1}}^{\lambda _{n}}[(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L]+\bigg (\frac{1}{\lambda _n-\lambda _{n-1}} \sum _{k=\lambda _{n-1}}^{\lambda _{n}}L-L\bigg )\bigg |\\\le & {} \frac{1}{\lambda _n-\lambda _{n-1}}\Bigg \{\bigg |\sum _{\begin{array}{c} k=\lambda _{n-1} \\ (k\in K_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _{n}}[(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L]\bigg | +\bigg |\sum _{\begin{array}{c} k=\lambda _{n-1} \\ (k\in K^C_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _{n}}[(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L]\bigg |\Bigg \}\\&+\bigg |\frac{1}{\lambda _n-\lambda _{n-1}} \sum _{k=\lambda _{n-1}}^{\lambda _{n}}L-L\bigg |\\\le & {} \frac{1}{\lambda _n-\lambda _{n-1}} \Bigg \{\sum _{\begin{array}{c} k=\lambda _{n-1} \\ (k\in K_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _{n}}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big | +\sum _{\begin{array}{c} k=\lambda _{n-1} \\ (k\in K^C_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _{n}}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |\Bigg \}\\\le & {} \frac{M|K_{\lambda _{n}}(\epsilon ))|+\epsilon |K^C_{\lambda _{n}}(\epsilon )|}{\lambda _n-\lambda _{n-1}}\rightarrow \epsilon ~~(n \rightarrow \infty ), \end{aligned}$$

where

$$\begin{aligned} K_{\lambda _{n}}(\epsilon ):=\{k\le \lambda _n-\lambda _{n-1}: |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|\ge \epsilon \} \end{aligned}$$

and

$$\begin{aligned} K^C_{\lambda _n}(\epsilon ):=\{k\le \lambda _n-\lambda _{n-1}: |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|<\epsilon \}. \end{aligned}$$

That is to say that $x=(x_n)$ is $\Omega ^{\Delta }$-summable to L and hence statistically $\Omega ^{\Delta }$-summable to the same limit. On the other hand the converse is not true, as can be seen by considering the following example.

Example 1

Define the sequence $x=(x_n)$ by

$$\begin{aligned} x_n:=\left\{\begin{array}{ll} 1/m^2, &{}n=m^2-m, m^2-m+1, \dots , m^2-1,~m>1;\\ -1/m^3, &{}n=m^2,~m>1;\\ 0, &{} \text {otherwise}\end{array} \right. \end{aligned}$$

for all $m \in \mathbb N$. Let $\alpha \in (0,1), \beta =\gamma$, $h=1$ and $\lambda _n=n^2$ for all $n\in \mathbb N$. We thus find that

$$\begin{aligned} \nonumber \Omega ^{\Delta }_n(\lambda x)= & {} \frac{1}{2n-1}\Bigg \{n^4x_{n^2}+(1-\alpha )(n^2-1)^2x_{n^2-1}+\bigg [1-\alpha +\frac{\alpha (\alpha -1)}{2}\bigg ](n^2-2)^2x_{n^2-2} \nonumber \\&+ \cdots +\bigg [1-\alpha +\frac{\alpha (\alpha -1)}{2}-\frac{\alpha (\alpha -1)(\alpha -2)}{3!}+\cdots \bigg ](n-1)^4x_{(n-1)^2}\Bigg \}. \end{aligned}$$

(2)

Letting $n \rightarrow \infty$ in (2), we find that $\Omega ^{\Delta }_n(\lambda x) \rightarrow 0$ which yields $st-\lim \Omega ^{\Delta }_n(\lambda x) =0$. On the other hand, for a fixed $\alpha \in (0, 1)$, since

$$\begin{aligned} {S_{\Omega^{\Delta}}}-\text{lim inf }x_{n}=\liminf _{n} \frac{1}{2n-1}\left| \left\{ k\le 2n-1:|\Delta _{h}^{\alpha ,\beta ,\gamma }(x_k)|\ge \epsilon \right\} \right| =0 \end{aligned}$$

and

$$\begin{aligned} {S_{\Omega^{\Delta}}}-\text{lim sup} x_{n}=\limsup _{n} \frac{1}{2n-1}\left| \left\{ k\le 2n-1:|\Delta _{h}^{\alpha ,\beta ,\gamma }(x_k)|\ge \epsilon \right\} \right| =1, \end{aligned}$$

then the sequence $x=(x_n)$ is not $\Omega ^{\Delta }$-statistical convergent.

Theorem 2

• (a) Let us suppose that$x=(x_n)$is strongly$\Omega _q^{\Delta }$-summable$(0<q<\infty )$to the numberL. If the following conditions hold, then the sequencexis$\Omega ^{\Delta }$-statistical convergent toL:

  • (i) $q\in (0, 1)$ and $0\leqq |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|<1$ or

  • (ii) $q\in [1, \infty )$and$1\leqq |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|<\infty$.

• (b) Assume that$x=(x_n)$ is $\Omega ^{\Delta }$-statistical convergent toLand$|(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|\le M$for all$k\in \mathbb N.$If the following conditions hold, then the sequencexis strongly$\Omega _q^{\Delta }$-summable toL:

  • (i) $q\in (0, 1]$ and $M\in [1, \infty )$ or

  • (ii) $q\in [1, \infty )$ and $M\in [0, 1)$.

Proof

• (a) Let $x=(x_n)$ be strongly $\Omega _q^{\Delta }$-summable ($0<q<\infty$) to L. Under the above conditions, we get

  $$\begin{aligned} \frac{1}{\epsilon ~\Delta \lambda _n} \sum _{k=\lambda _{n-1}}^{\lambda _n}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |^q\ge & {} \frac{1}{\epsilon \Delta \lambda _n} \sum _{k=\lambda _{n-1}}^{\lambda _n}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |\\\ge & {} \frac{1}{\epsilon \Delta \lambda _n} \sum _{\begin{array}{c} k=\lambda _{n-1} \\ (k\in K_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _{n}}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |\\\ge & {} \frac{1}{\epsilon \Delta \lambda _n} \sum _{\begin{array}{c} k=\lambda _{n-1}\\ (k\in K_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _{n}}\epsilon \\= & {} \, \frac{1}{\lambda _n-\lambda _{n-1}}|K_{\lambda _{n}}(\epsilon ))| \quad (\epsilon >0) \end{aligned}$$

  which leads us by passing to limit as $n \rightarrow \infty$ that

  $$\begin{aligned} \frac{1}{\lambda _n-\lambda _{n-1}}\left| \left\{ k\le \lambda _n-\lambda _{n-1}:\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |\ge \epsilon \right\} \right| \rightarrow 0. \end{aligned}$$

  Hence, $x=(x_n)$ is $\Omega ^{\Delta }$-statistical convergent to L.

• (b) Let $x=(x_n)$ be $\Omega ^{\Delta }$-statistical convergent to L and

  $$\begin{aligned} |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|\le M \quad\text {for all}~~k\in \mathbb N. \end{aligned}$$

  Thus, clearly, we have

  $$\begin{aligned}&\frac{1}{\Delta \lambda _n} \sum _{k=\lambda _{n-1}}^{\lambda _n}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |^q\\&\quad =\frac{1}{\Delta \lambda _n} \sum _{\begin{array}{c} k=\lambda _{n-1} \\ (k\in K^C_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _n}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |^q+\frac{1}{\Delta \lambda _n} \sum _{\begin{array}{c} k=\lambda _{n-1}\\ (k\in K_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _n}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |^q\\&\quad \le \frac{1}{\Delta \lambda _n} \sum _{\begin{array}{c} k=\lambda _{n-1} \\ (k\in K^C_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _n}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |+\frac{1}{\Delta \lambda _n} \sum _{\begin{array}{c} k=\lambda _{n-1}\\ (k\in K_{\lambda _{n}}(\epsilon )) \end{array}}^{\lambda _n}\big |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L\big |\\&\quad \le \frac{\epsilon ~|K^C_{\lambda _{n}}(\epsilon )|}{\lambda _n-\lambda _{n-1}}+\frac{M|K_{\lambda _{n}}(\epsilon )|}{\lambda _n-\lambda _{n-1}}\rightarrow \epsilon \quad (n \rightarrow \infty ). \end{aligned}$$

  Hence, for $0<q<\infty$, our sequence $x=(x_n)$ is strongly $\Omega _q^{\Delta }$-summable to L .$\square$

3 Applications to Korovkin Type Approximation Theorem

Let C[a, b] be the space of all continuous real valued functions on [a, b]. It is well known that C[a, b] is a Banach space with the norm defined by

$$\begin{aligned} \Vert f\Vert _\infty =\sup \big \{|f(x)|: x\in [a, b]\big \}. \end{aligned}$$

Let $L:C[a, b] \rightarrow C[a, b]$ be a linear operator. Then, L is said to be positive provided by $f \ge 0$ implies $Lf \ge 0$. We also use the notation L(f; x) for the value of Lf at a point x.

The classical Korovkin type approximation theorem (see Korovkin 1953; Bohman 1952) states as follows:

Let $T_n: C[a, b] \rightarrow C[a, b]$ be a sequence of positive linear operators. Then

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert T_{n}(f; x)-f(x)\Vert _\infty =0,\quad \text {for \,all} \quad f\in C[a, b] \end{aligned}$$

if and only if

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert T_{n}(f_{i}; x)-f_i(x)\Vert _\infty =0,\quad \text {for \,each}\,\quad i=0,1,2, \end{aligned}$$

where the test function $f_i(x)=x^i$.

The statistical version of Korovkin theorem was given by Gadjiev and Orhan (2002). With the development of summability methods, this type approximation has been widely used and extended by many authors the reader may refer to (Kadak 2016, 2017a, b; Orhan and Demirci 2014; Srivastava et al. 2012; Edely et al. 2010).

In this section using the test function $f_i(x)=(\frac{x}{1-x})^i$, $i=0, 1, 2$ for $x\in [0, A]$ where $A \leqq \frac{1}{2}$, we try to obtain a Korovkin type approximation theorem which is stronger than that both classical and statistical cases of Korovkin theorem.

Theorem 3

Let$\alpha$, $\beta$and$\gamma \notin \mathbb N$be real numbers andhbe a positive constant. Also let$(T_k)_{k\ge 1}$be a sequence of positive linear operators fromC[0, A] into itself. Then, for all$f\in C[0, A],$

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _{n \rightarrow \infty } \big \Vert ~T_{k}(f(s); x)-f(x)~\big \Vert _{\infty }=0 \end{aligned}$$

(3)

if and only if

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}- & {} \lim _{n \rightarrow \infty } \big \Vert ~T_{k}(1; x)-{1}~ \big \Vert _{\infty }=0\end{aligned}$$

(4)

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}- & {} \lim _{n \rightarrow \infty } \bigg \Vert ~T_{k}~\bigg (\frac{s}{1-s}; x\bigg )-\frac{x}{1-x} ~\bigg \Vert _{\infty }=0\end{aligned}$$

(5)

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}- & {} \lim _{n \rightarrow \infty } \bigg \Vert ~T_{k}~\Bigg (\bigg (\frac{s}{1-s}\bigg )^2; x\Bigg )-\bigg (\frac{x}{1-x}\bigg )^2 ~\bigg \Vert _{\infty }=0. \end{aligned}$$

(6)

Proof

Since each $1, \frac{x}{1-x}, (\frac{x}{1-x})^2$ functions belongs to C[0, A] then the assertions (4), (5) and (6) follow immediately from the first assertion (3). Let us take $f \in C[0, A]$ and $x \in [0, A]$ be fixed. Then there exists a constant $M>0$ such that $|f(x)|\le M$ for all $x \in [0, A]$. Thus, we have

$$\begin{aligned} |f(s)-f(x)|\le 2M \quad (s, x\in [0, A]). \end{aligned}$$

(7)

By continuity of f at x, for given $\varepsilon >0$, there exists a number $\delta =\delta (\varepsilon )>0$ such that for all $s, x\in [0, A]$ satisfying

$$\begin{aligned} \bigg |\frac{s}{1-s}-\frac{x}{1-x}\bigg |<\delta \end{aligned}$$

we have

$$\begin{aligned} |f(s)-f(x)|<\varepsilon \end{aligned}.$$

(8)

Setting $\varphi (s,x)=(\frac{s}{1-s}-\frac{x}{1-x})$. For $|\frac{s}{1-s}-\frac{x}{1-x}|\ge \delta$, then $\varphi ^2(s,x)\ge \delta ^2$. Hence, we derive the consequence from (7) and (8) that

$$\begin{aligned} |f(s)-f(x)|< \varepsilon +\frac{2M}{\delta ^2}\varphi ^2(s,x). \end{aligned}$$

It follows from the linearity and positivity of $T_{k}$ that

$$\begin{aligned} |T_{k}(f(s); x)-f(x)|=\; & {} |T_{k}(f(s)-f(x); x)+f(x) (T_k(f_0; x)-f_0(x))|\\\le & {} T_{k}(|f(s)-f(x)|; x)+M~|T_k(1; x)-1|\\\le & {} \left| T_k\left( \varepsilon +\frac{2M}{\delta ^2}\varphi ^2; x\right) \right| +M~|T_k(1; x)-1|\\\le & {} \varepsilon +\left( \varepsilon +M+ \frac{4M}{\delta ^2}\right) |T_k(1; x)-1|+\frac{4M}{\delta ^2}~\bigg |T_k\bigg (\frac{s}{1-s}; x\bigg )-\frac{x}{1-x}\bigg |\\+ & {} \quad \frac{2M}{\delta ^2}~\bigg |T_k\bigg (\bigg (\frac{s}{1-s}\bigg )^2; x\bigg )-\bigg (\frac{x}{1-x}\bigg )^2\bigg |. \end{aligned}$$

Taking the supremum over $x \in [0, A]$, we obtain

$$\begin{aligned} \nonumber \Vert T_{k}(f(s); x)-f(x)\Vert _\infty\le & {} \varepsilon +N\Bigg \{\bigg \Vert T_k(1; x)-1\bigg \Vert _\infty +\bigg \Vert T_k\bigg (\frac{s}{1-s}; x\bigg )-\frac{x}{1-x}\bigg \Vert _\infty \\+ & {} \quad \bigg \Vert T_k\bigg (\bigg (\frac{s}{1-s}\bigg )^2; x\bigg )-\bigg (\frac{x}{1-x}\bigg )^2\bigg \Vert _\infty \Bigg \} \end{aligned}$$

(9)

where

$$\begin{aligned} N:=\left\{ \varepsilon +M+\frac{4M}{\delta ^2}\right\} . \end{aligned}$$

We now replace $T_k(\cdot ; x)$ by

$$\begin{aligned} \Omega ^{\Delta }_k (T(\cdot ;x))=\frac{1}{\lambda _k-\lambda _{k-1}} \sum _{j=\lambda _{k-1}}^{\lambda _k}\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda T(\cdot ;x))_j \end{aligned}$$

in (9). For a given $\varepsilon ' >0$, we choose a number $\varepsilon >0$ such that $\varepsilon <\varepsilon '$. Then, upon setting

$$\begin{aligned} \mathcal {B}:= & {} \left\{ k\le n:\parallel \Omega ^{\Delta }_k (T(f(s);x))-f(x)\parallel _\infty \ge \varepsilon '\right\} ,\\ \mathcal {B}_{0}:= & {} \left\{ k\le n:\Vert \Omega ^{\Delta }_k (T(1;x))-1\Vert _\infty \ge \frac{\varepsilon ' -\varepsilon }{3N}\right\} ,\\ \mathcal {B}_{1}:= & {} \bigg \{k\le n:\big \Vert \Omega ^{\Delta }_k \big (T\big (\frac{s}{1-s}; x\big )\big )-\frac{x}{1-x}\big \Vert _\infty \ge \frac{\varepsilon ' -\varepsilon }{3N}\big \},\\ \mathcal {B}_{2}:= & {} \left\{ k\le n:\big \Vert \Omega ^{\Delta }_k \big (T\big (\big (\frac{s}{1-s}\big )^2; x\big )\big )-\big (\frac{x}{1-x}\big )^2\big \Vert _\infty \ge \frac{\varepsilon ' -\varepsilon }{3N}\right\} . \end{aligned}$$

Then, it is clear that $\mathcal {B}\subset \mathcal {B}_{0}\cup \mathcal {B}_{1}\cup \mathcal {B}_{2}$ and hence using the conditions (4–6) we obtain

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _{n \rightarrow \infty }\Vert T_{k}(f(s); x) -{f(x)}\Vert _{\infty }=0,\quad\text {for all}~f\in C[0, A], \end{aligned}$$

which completes the proof.

Now we may give an example for Theorem 3. Before giving this example, we present a short introduction related with the generating function type Meyer-Konig and Zeller operators (see Altın et al. 2005).

For a function f on [0, 1), the operators

$$\begin{aligned} M_{n}(f; x)=\sum _{k=0}^{\infty } f\left( \frac{k}{k+n+1}\right) m_{nk}(x) \end{aligned}$$

are known as Meyer-Konig and Zeller operators Meyer-König and Zeller (1960) where

$$\begin{aligned} m_{nk}(x)=\left( {\begin{array}{c}n+k\\ k\end{array}}\right) x^{k}(1-x)^{n+1}. \end{aligned}$$

This operator were also generalized in Altın et al. (2005) using linear generating functions

$$\begin{aligned} L_{n}(f(s); x)=\frac{1}{h_n(x,s)}\sum _{k=0}^{\infty } f\left( \frac{a_{k,n}}{a_{k,n}+b_{n}}\right) \Gamma _{k, n}(s) x^k \end{aligned}$$

(10)

where $0<\frac{a_{k,n}}{a_{k,n}+b_{n}}\le \tilde{A}$, $\tilde{A} \in (0, 1)$, and $h_n(x,s)$ is the generating function for the sequence of $\{\Gamma _{k, n}(s)\}~(s \in I)$ with the form

$$\begin{aligned} h_n(x,s)=\sum _{k=0}^{\infty }~\Gamma _{k, n}(s) ~x^k \quad (s \in I \subset \mathbb R). \end{aligned}$$

We also suppose that the following conditions hold true:

• (i) $h_n(x,s)=(1-x)h_{n+1}(x,s)$;

• (ii) $b_n \Gamma _{k, n+1}(s)=a_{k+1,n}\Gamma _{k+1, n}(s)$ and $\Gamma _{k, n}(s)\ge 0$ for all $s \in I \subset \mathbb R$;

• (iii) $b_n \rightarrow \infty , \frac{b_{n+1}}{b_n}\rightarrow 1$ and $b_n\ne 0$ for all $n\in \mathbb N$;

• (iv) $a_{k+1, n}-a_{k, n+1}=\varphi _n$ where $|\varphi _n|\le m <\infty$, and ${a_{0n}}=0.$

It is easy to see that $L_n$ defined by (10) is positive and linear. We also observe that

$$\begin{aligned} L_{n}(1; x)= & {} 1, \quad L_{n}\left( \frac{s}{1-s}; x\right) =\frac{x}{1-x} \quad \text {and} \\ L_{n}\left( \left( \frac{s}{1-s}\right) ^2; x\right)= & {} \frac{x^2}{(1-x)^2}\frac{b_{n+1}}{b_{n}}+\frac{{\varphi }_n}{b_{n}}\frac{x}{1-x}. \end{aligned}$$

Example 2

Let $\{T_k\}$ be a sequence of positive linear operators from $C[0, \tilde{A}]$ into itself defined by

$$\begin{aligned} T_k(f(s); x)=(1+x_k)~L_k(f(s); x) \end{aligned}$$

(11)

where $x=(x_k)$ is defined as in Example 1. Since $\overline{N}_{\Omega ^{\Delta }}-\lim x_n=0$, it is easy to see that

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}- &{} \lim _n\Vert T_k(1; x)-1\Vert _\infty =0~~ \;\text{and}\\ \overline{N}_{\Omega ^{\Delta }}- &{} \lim _n\left\| T_k\left( \frac{s}{1-s}; x\right) -\frac{x}{1-x}\right\| _\infty =0. \end{aligned}$$

In view of (iii), we have

$$\begin{aligned} T_k\bigg (\bigg (\frac{s}{1-s}\bigg )^2; x\bigg )-\bigg (\frac{x}{1-x}\bigg )^2= & {} (1+x_k)\bigg [\bigg (\frac{x}{1-x}\bigg )^2\frac{b_{k+1}}{b_{k}}+ \left( \frac{{\varphi }_k}{b_{k}}\frac{x}{1-x}\right) \bigg ]-\bigg (\frac{x}{1-x}\bigg )^2\\\le & {} (1+x_k)\Bigg \{\bigg [\frac{b_{k+1}}{b_{k}}-1\bigg ]+\frac{m}{b_{k}}\Bigg \} \end{aligned}$$

which yields that

$$\begin{aligned}&\overline{N}_{\Omega ^{\Delta }}&-\lim _n\bigg \Vert T_k\bigg (\bigg (\frac{s}{1-s}\bigg )^2; x\bigg )-\bigg (\frac{x}{1-x}\bigg )^2\bigg \Vert _\infty =0. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _n\Vert T_k(f_i(s); x)-f_i(x)\Vert _\infty = 0, \quad i=0,1,2. \end{aligned}$$

By taking Theorem 3 into account, and hence by letting $n \rightarrow \infty$, we are led to the fact that

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _n \Vert T_{k}(f(s); x) -{f(x)}\Vert _{\infty }=0. \end{aligned}$$

In view of above example, we say that our proposed method works successfully but classical and statistical forms of Korovkin theorem do not work for this sequence $\{T_k\}$ of positive linear operators.

4 Rates of $\Omega ^{\Delta }$-Statistical Convergence

In this section, we estimate the rate of $\Omega ^{\Delta }$-statistical convergence of positive linear operators defined from C[0, A] into itself.

We first present the following definition.

Definition 3

Let $\alpha$, $\beta$ and $\gamma \notin \mathbb N$ be real numbers and h be a positive constant. Also let $(\theta _n)$ be any non-increasing sequence of positive real numbers. We say that a sequence $x=(x_n)$ is $\Omega ^{\Delta }$-statistical convergent to the number L with the rate $o(\theta _n)$ if, for every $\epsilon >0$,

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{1}{\theta _n~\Delta \lambda _n}\left| \left\{ k\le \lambda _n-\lambda _{n-1}:|(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L|\ge \epsilon \right\} \right| =0. \end{aligned}$$

(12)

In this case, we can write $x_k-L=\Omega ^{\Delta }-o(\theta _n)$.

Lemma 1

Let$(a_n)$and$(b_n)$be positive non-increasing sequences. Assume that$x=(x_k)$and$y=(y_k)$are two sequences such that

$$\begin{aligned}x_k-L_1=\Omega ^{\Delta }-o(a_n)~~\text {and}~~y_k-L_2=\Omega ^{\Delta }-o(b_n).\end{aligned}$$

Then

• (1) $(x_k-L_1)\pm (y_k-L_2)=\Omega ^{\Delta }-o(c_n)$

• (2) $(x_k-L_1)(y_k-L_2)=\Omega ^{\Delta }-o(a_n b_n)$

• (3) $\mu (x_k-L_1)=\Omega ^{\Delta }-o(a_n)$, for any scalar $\mu \in \mathbb R$,

where$c_n=\max _n\{a_n, b_n\}$.

Proof

Assume that $x_k-L_1=\Omega ^{\Delta }-o(a_n)~~\text {and}~~y_k-L_2=\Omega ^{\Delta }-o(b_n)$. In addition, for $\epsilon >0$, let us set

$$\begin{aligned} \mathcal {D}:=\left\{ k\le \lambda _n-\lambda _{n-1}: |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k+(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda y))_k- (L_1+L_2)|\ge \epsilon \right\} , \end{aligned}$$

$$\begin{aligned} \mathcal {D}_{0}:=\left\{ k\le \lambda _n-\lambda _{n-1}:|(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k-L_1|\ge \frac{\epsilon }{2}\right\} \end{aligned}$$

and

$$\begin{aligned} \mathcal {D}_{1}:=\left\{ k\le \lambda _n-\lambda _{n-1}:|(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda y))_k-L_2|\ge \frac{\epsilon }{2}\right\} . \end{aligned}$$

We then observe that $\mathcal {D} \subset \mathcal {D}_{0} \cup \mathcal {D}_{1}$. Thus, we obtain

$$\begin{aligned} \frac{|\mathcal {D}|}{c_n(\lambda _n-\lambda _{n-1})}\le \frac{|\mathcal {D}_0|}{a_n(\lambda _n-\lambda _{n-1})}+\frac{|\mathcal {D}_1|}{b_n(\lambda _n-\lambda _{n-1})}~ \end{aligned}$$

(13)

where $c_n=\max \{a_n, b_n\}$. Now letting $n \rightarrow \infty$ in (13) and using by hypothesis, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{c_n~\Delta \lambda _n }\big |\{k\le \lambda _n-\lambda _{n-1}: |(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda x))_k+(\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda y))_k- (L_1+L_2)|\ge \epsilon \}\big |=0, \end{aligned}$$

as asserted by Lemma 1 (1). Since the other assertions can be proved similarly, we choose to omit the details involved.

We now recall the following basic definition and notation on the modulus of continuity to get the rates of $\Omega ^{\Delta }$-statistical convergence using Definition 3.

The modulus of continuity for a function $f \in C[0, A]$ is defined as follows:

$$\begin{aligned} \omega (f, \delta )=\sup _{|h|<\delta }|f(x+h)-f(x)|. \end{aligned}$$

It is well-known that for any $\delta >0$ and each $s\in [0, A]$,

$$\begin{aligned} |f(s)-f(x)|\le \omega (f, \delta ) \left( \frac{|s-x|}{\delta }+1\right) , \quad (f\in C[0, A]). \end{aligned}$$

(14)

Theorem 4

Let$\alpha$, $\beta$and$\gamma ~( \notin \mathbb N)$be real numbers andhbe a positive constant. Let$\{T_{k}\}$be a sequence of positive linear operators fromC[0, A] into itself. Assume further that$(a_n)$and$(b_n)$be positive non-increasing sequences. Suppose that the following conditions hold true:

• (i) $\Vert T_{k}(1; x)-1\Vert _\infty =\Omega ^{\Delta }-o(a_n)$ on [0, A],

• (ii) $\omega (f, \xi _k)=\Omega ^{\Delta }-o(b_n)$ on [0, A], where $\xi _k:=\sqrt{\Vert T_{k}(\varphi _x(s); x)\Vert }_\infty$ with

  $$\begin{aligned} \varphi _x(s)=\bigg (\frac{s}{1-s}-\frac{x}{1-x}\bigg )^2. \end{aligned}$$

Then we have, for all$f\in C[0, A],$

$$\begin{aligned} \Vert T_{k}(f(s); x)-f(x)\Vert _\infty =\Omega ^{\Delta }-o(c_n) \end{aligned}$$

where$c_n=\max \{a_n, b_n\}$.

Proof

Let $f \in C[0, A]$ and $x \in [0, A]$ be fixed. Since $\{T_k\}$ is linear and monotone, we see (for any $\delta >0$) that

$$\begin{aligned} |T_{k}(f(s); x)-f(x)|\le & {} T_{k}(|f(s)-f(x)|;x)+|f(x)|~|T_{k}(1; x)-1|\\\le & {} \omega (f, \delta )T_{k}\left( \frac{\big |\frac{s}{1-s}-\frac{x}{1-x}\big |}{\delta }+1; x\right) +N~|T_{k}(1; x)-1|\\\le & {} \omega (f, \delta )T_{k}\left( \frac{\big (\frac{s}{1-s}-\frac{x}{1-x}\big )^2}{\delta ^2}+1; x\right) +N~|T_{k}(1; x)-1|\\\le & {} \omega (f, \delta ) \left\{ \frac{1}{\delta ^2}T_{k}(\varphi _x; x)+T_{k}(1; x)\right\} +N~|T_{k}(1; x)-1| \end{aligned}$$

where $N=\Vert f\Vert _\infty$. Taking the supremum over $x \in [0, A]$ on both sides, we get

$$\begin{aligned}&\Vert T_{k}(f(s); x)-f(x)\Vert _\infty \\&\quad \le \omega (f, \delta ) \left\{ \frac{1}{\delta ^2}\Vert T_{k}(\varphi _x; x)\Vert _\infty +\Vert T_{k}(1; x)-1\Vert _\infty +1\right\} +N~\Vert T_{k}(1; x)-1\Vert _\infty . \end{aligned}$$

Now, if we take

$$\begin{aligned} \delta =\xi _k=\sqrt{\Vert T_{k}(\varphi _x; x)\Vert }_\infty \end{aligned}$$

in the last relation, we deduce that

$$\begin{aligned} \Vert T_{k}(f(s); x)-f(x)\Vert _\infty\le & {} \omega (f, \xi _k) \big \{\Vert T_{k}(1; x)-1\Vert _\infty +2 \big \}+N~\Vert T_{k}(1; x)-1\Vert _\infty \\=\; & {} \omega (f, \xi _k)\Vert T_{k}(1; x)-1\Vert _\infty +2 \omega (f, \xi _k)+N~\Vert T_{k}(1; x)-1\Vert _\infty . \end{aligned}$$

Now, we replace $T_{k}(\cdot ; x)$ by

$$\begin{aligned} H_{k}(\cdot ; x):=\Delta _{h}^{\alpha ,\beta ,\gamma }(\lambda T(\cdot ;x))_k. \end{aligned}$$

Using Lemma 1, for a given $\epsilon >0$, we obtain that

$$\begin{aligned}&\frac{1}{c_n (\lambda _n-\lambda _{n-1})}\big |\{k\le \lambda _n-\lambda _{n-1}:\Vert H_k(f(s); x)-f(x)\Vert _\infty \ge \varepsilon \}\big |\\&\quad \le \frac{1}{a_n (\lambda _n-\lambda _{n-1})}\big |\{k\le \lambda _n-\lambda _{n-1}:\Vert H_k(1; x)-1\Vert _\infty \ge \varepsilon /3N\}\big |\\&\qquad +\frac{1}{a_nb_n (\lambda _n-\lambda _{n-1})}\big |\{k\le \lambda _n-\lambda _{n-1}:\omega (f, \xi _k)\Vert H_k(1; x)-1\Vert _\infty \ge \varepsilon /3\}\big |\\&\qquad + \frac{1}{b_n (\lambda _n-\lambda _{n-1})}\big |\{k\le \lambda _n-\lambda _{n-1}:\omega (f, \xi _k)\ge \varepsilon /6\}\big |. \end{aligned}$$

Letting $n \rightarrow \infty$ which leads us to the fact that

$$\begin{aligned} \Vert T_{k}(f(s); x)-f(x)\Vert _\infty =\Omega ^{\Delta }-o(c_n) \quad (f\in C[0, A]), \end{aligned}$$

as desired.

5 A Voronovskaja-Type Theorem

In this section, using the notion of statistically $\Omega ^{\Delta }$-summability we obtain a Voronovskaja-type approximation theorem by the help of $T_k$ family of linear operators defined by (11) for $h_n(x,s)=(1-x)^{-n-1}$, $a_{k,n}=k$, $\Gamma _{k,n}(s)=\left( {\begin{array}{c}n+k\\ k\end{array}}\right)$ and $b_n=n+1$ for all $n \in \mathbb N$.

Lemma 2

Let$\alpha$, $\beta$and$\gamma ~(\notin \mathbb N)$be real numbers andhbe a positive constant. Suppose also that$\eta _x(s)=\left (\frac{s}{1-s}-\frac{x}{1-x}\right )$where$x, s \in [0, A]$. Then, we get

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _n~\big \{(k+1) ~T_k(\eta _x^2; x)\big \}=\frac{x}{(1-x)^2}. \end{aligned}$$

(15)

Proof

Let h be a positive constant, $x \in [0, A]$ and, $\alpha$, $\beta$ and $\gamma ~(\notin \mathbb N)$ be real numbers. Since

$$\begin{aligned} L_k\big (\frac{s}{1-s}; x\big )=\frac{x}{1-x}, \end{aligned}$$

we deduce that

$$\begin{aligned} T_k(\eta _x; x)=(1+x_k)\left[ L_k\bigg (\frac{s}{1-s}; x\bigg )-\frac{x}{1-x}L_k(1; x)\right] =0. \end{aligned}$$

In addition, since

$$\begin{aligned} L_k\left (\frac{s^2}{(1-s)^2}; x\right )=\frac{k+2}{k+1}\bigg (\frac{x}{1-x}\bigg )^2+\frac{1}{k+1}\bigg (\frac{x}{1-x}\bigg ), \end{aligned}$$

we find that

$$\begin{aligned} T_k(\eta _x^2; x)= \;& {} (1+x_k)\left[ L_k\bigg (\frac{s^2}{(1-s)^2}; x\bigg )-2\frac{x}{1-x}L_k\bigg (\frac{s}{1-s}; x\bigg )+\bigg (\frac{x}{1-x}\bigg )^2L_k(1; x)\right] \\=\; & {} (1+x_k)\left[ \frac{1}{k+1}\bigg (\frac{x}{1-x}\bigg )^2+\frac{1}{k+1}\bigg (\frac{x}{1-x}\bigg )\right] \end{aligned}$$

which yields, for all $x \in [0, A]~(A\le 1/2)$, that

$$\begin{aligned} (k+1) T_k(\eta _x^2; x)-\left[ \bigg (\frac{x}{1-x}\bigg )^2+\frac{x}{1-x}\right] = x_k \left[ \bigg (\frac{x}{1-x}\bigg )^2+\frac{x}{1-x}\right] \le 2x_k. \end{aligned}$$

Since

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _{n \rightarrow \infty } 2x_k=0, \end{aligned}$$

the desired result follows, that is,

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _{n \rightarrow \infty } ~(k+1) ~T_k(\eta _x^2; x)=\frac{x}{(1-x)^2}. \end{aligned}$$

Corollary 1

Assume thathis a positive constant,$x \in [0, A]$. Let$\eta _x(s)$be given as in Lemma 2. Then there is a positive constant$M_0(x)$depending only onx, such that

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _{n\rightarrow \infty }~\big \{(k+1)^2 ~T_k(\eta _x^4; x)\big \}= M_0(x). \end{aligned}$$

Theorem 5

Let$\alpha$, $\beta$and$\gamma ~(\notin \mathbb N)$be real numbers andhbe a positive constant. Then, for every$f\in C[0, A]$such that$f', f'' \in C[0, A],$

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _n~\bigg \{(k+1) ~\bigg [T_k\bigg (f\bigg (\frac{s}{1-s}\bigg );x\bigg ) -f\bigg (\frac{x}{1-x}\bigg )\bigg ]\bigg \}=\frac{x}{2(1-x)^2} f''\bigg (\frac{x}{1-x}\bigg ). \end{aligned}$$

Proof

Let $x \in [0, A]$ and $f, f', f'' \in C[0, A]$. Now we consider the following function defined by

$$\theta _x\bigg (\frac{s}{1-s}\bigg )=\left\{ \begin{array}{lll} \frac{f\left( \frac{s}{1-s}\right) -f\left( \frac{x}{1-x}\right) -\left( \frac{s}{1-s}-\frac{x}{1-x}\right) f'\left( \frac{x}{1-x}\right) -\frac{1}{2}\left( \frac{s}{1-s}-\frac{x}{1-x}\right) ^2f''\left( \frac{x}{1-x}\right) }{\left( \frac{s}{1-s}-\frac{x}{1-x}\right) ^2} &{} , &{} s\ne x,\\ 0 &{} , &{} s=x,\end{array} \right. $$

where $\theta _x(\frac{x}{1-x})=0$ and $\theta _x \in C[0, A]$. Using the Taylor formula for $f \in C[0, A]$, we can write

$$\begin{aligned} f\left( \frac{s}{1-s}\right)= \;& {} f\left( \frac{x}{1-x}\right) +\left( \frac{s}{1-s}-\frac{x}{1-x}\right) f'\left( \frac{x}{1-x}\right) +\\&+ \frac{1}{2}\left( \frac{s}{1-s}-\frac{x}{1-x}\right) ^2f''\left( \frac{x}{1-x}\right) +\theta _x\bigg (\frac{s}{1-s}\bigg )\left( \frac{s}{1-s}-\frac{x}{1-x}\right) ^2. \end{aligned}$$

We then observe that the operator $T_k$ is linear and that

$$\begin{aligned} T_k\bigg (f\bigg (\frac{s}{1-s}\bigg ); x\bigg )=\; & {} T_k\bigg (f\bigg (\frac{x}{1-x}\bigg ); x\bigg )+f'\bigg (\frac{x}{1-x}\bigg )T_k\bigg (\bigg (\frac{s}{1-s}-\frac{x}{1-x}\bigg ); x\bigg )\\&+ \frac{1}{2}f''\bigg (\frac{x}{1-x}\bigg )T_k\bigg (\bigg (\frac{s}{1-s}-\frac{x}{1-x}\bigg )^2; x\bigg )\\&+ T_k\bigg (\theta _x\bigg (\frac{s}{1-s}\bigg )\bigg (\frac{s}{1-s}-\frac{x}{1-x}\bigg )^2; x\bigg ). \end{aligned}$$

In view of Lemma 2, one obtains

$$\begin{aligned} T_k\bigg (f\bigg (\frac{s}{1-s}\bigg ); x\bigg )=\; & {} f\bigg (\frac{x}{1-x}\bigg )T_k(1;x)+f'\bigg (\frac{x}{1-x}\bigg ) T_k\bigg (\eta _x; x\bigg )\\&+ \frac{1}{2}f''\bigg (\frac{x}{1-x}\bigg )T_k\bigg (\eta ^2_x, x\bigg )+T_k\bigg (\theta _x\bigg (\frac{s}{1-s}\bigg )\cdot \eta _x^2; x\bigg )\\=\; & {} f\bigg (\frac{x}{1-x}\bigg ) (1+x_k)+\frac{1+x_k}{2}f''\bigg (\frac{x}{1-x}\bigg )\left[ \frac{1}{k+1}\bigg (\frac{x}{1-x}\bigg )^2+\frac{1}{k+1}\bigg (\frac{x}{1-x}\bigg )\right] \\&+ T_k\bigg (\theta _x\bigg (\frac{s}{1-s}\bigg )\cdot \eta _x^2; x\bigg ). \end{aligned}$$

Upon multiplying both sides by $k+1$, we have

$$\begin{aligned} (k+1) ~\bigg [T_k\bigg (f\bigg (\frac{s}{1-s}\bigg );x\bigg ) -f\bigg (\frac{x}{1-x}\bigg )\bigg ]=\; & {} (k+1) f\bigg (\frac{x}{1-x}\bigg ) x_k+\frac{1+x_k}{2}f''\bigg (\frac{x}{1-x}\bigg )\frac{x}{(1-x)^2}\\&+ (k+1)T_k\bigg (\theta _x\bigg (\frac{s}{1-s}\bigg )\cdot \eta _x^2; x\bigg ) \end{aligned}$$

and hence

$$\begin{aligned} \nonumber&\bigg |(k+1) ~\left( T_k\bigg (f\bigg (\frac{s}{1-s}\bigg );x\bigg ) -f\bigg (\frac{x}{1-x}\bigg )\right) -\frac{1}{2}\frac{x}{(1-x)^2} f''\bigg (\frac{x}{1-x}\bigg )\bigg |\\\le & {} (k+1) M_1 x_k+M_2\frac{x_k}{2}+(k+1)\bigg |T_k\bigg (\theta _x\bigg (\frac{s}{1-s}\bigg )\cdot \eta _x^2; x\bigg )\bigg | \end{aligned}$$

(16)

where $M_1=\big \Vert f(\frac{x}{1-x})\big \Vert _\infty$ and $M_2=\big \Vert f''(\frac{x}{1-x})\big \Vert _\infty$. Applying the Cauchy-Schwarz inequality in (16), we obtain

$$\begin{aligned} (k+1) \bigg |T_k\bigg (\theta _x\bigg (\frac{s}{1-s}\bigg )\cdot \eta _x^2; x\bigg )\bigg |\le \sqrt{T_k\bigg (\theta ^2_x\bigg (\frac{s}{1-s}\bigg ); x\bigg )}\sqrt{(k+1)^2T_k(\eta _x^4; x)}. \end{aligned}$$

From Theorem 3, we observe that

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim ~ T_k\bigg (\theta ^2_x\bigg (\frac{s}{1-s}\bigg ); x\bigg )=0. \end{aligned}$$

Using Lemma 2 and Corollary 1, it is not hard to see that

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _n~(k+1) \bigg |T_k\bigg (\theta _x\bigg (\frac{s}{1-s}\bigg )\cdot \eta _x^2; x\bigg )\bigg |=0. \end{aligned}$$

Thus, by taking $n \rightarrow \infty$ in (16), we get

$$\begin{aligned} \overline{N}_{\Omega ^{\Delta }}-\lim _n~\left\{ (k+1) M_1 x_k+\frac{M_2x_k}{2}+(k+1)\bigg |T_k\bigg (\theta _x\bigg (\frac{s}{1-s}\bigg )\cdot \eta _x^2; x\bigg )\bigg |\right\} =0, \end{aligned}$$

which leads us to the desired assertion of Theorem 5.$\square$

6 Computational and Geometrical Approaches

In this section, we provide the computational and geometrical approaches of Theorem 3 with respect to the linear operator $L_n(f;x)$ given in (10) under different choices for the parameters. Here, we have found it to be convenient to investigate our series only for finite sums. More powerful equipments with higher speed can easily compute the more complicated infinite series in a similar manner.

Here, in our computations, we take

• $h_n(x,s)=(1-x)^{-n-1}$ and $\Gamma _{{k,n}} (s) = \left( {\begin{array}{ll} {n + k} \\ k \\ \end{array} } \right);$ 

• $a_{k,n}=k$ and $b_n=n+1$;

• $\alpha =2, \beta =\gamma$ and $h=1$;

• $\lambda (n)=n^2$ for all $n \in \mathbb N$.

Based upon the above choices, we may define the following operator $\Omega _m^{\Delta }(\lambda Lf)$ by

$$\begin{aligned} \Omega _m^{\Delta }(\lambda Lf) =\dfrac{1}{2m-1}\;\sum _{n =(m-1)^2}^{m^2}\Delta _{1}^{2,\beta ,\beta }(\lambda _n L_n(f;x)) \end{aligned}$$

(17)

where

$$\begin{aligned}&L_{n}(f; x)=(1-x)^{n+1}\sum _{k=0}^{\infty } f\left( \frac{k}{k+n+1}\right) ~\left( {\begin{array}{c}n+k\\ k\end{array}}\right) ~x^k. \end{aligned}$$

(18)

Under above conditions, we obtain

$$\begin{aligned} \Omega _m^{\Delta }(\lambda Lf) =\dfrac{1}{2m-1}\left[ m^2L_{m}(f; x)-(m-1)^2L_{m-1}(f; x)\right] . \end{aligned}$$

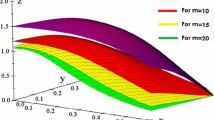
In fact, in Fig. 1, the value of k runs from $k = 0$ to 25 for $m = 5$, $m = 10$ and $m=15$, respectively. As the value of m increases, the sequence

$$\begin{aligned} \Omega _m^{\Delta }(\lambda L(1;x)) \end{aligned}$$

converges towards to the function $f_0(x)=1$.

Fig. 1

The convergence of $\Omega_m^{\Delta}(\lambda L(1;x))$ for different values of $m$

In addition, from Fig. 2, it can be observed that, as the value of m increases, the sequence

$$\begin{aligned} \Omega _m^{\Delta }\bigg (\lambda L\big (\frac{s}{1-s}; x\big )\bigg ) \quad (s,x \in [0,A], ~A\le 1/2) \end{aligned}$$

converges to the function $f_1(x)=\frac{x}{1-x}.$

Fig. 2

The convergence of $\Omega_m^{\Delta}\left(\lambda L\left(\frac{s}{1-s}; x\right)\right)$ for different values of $m$

Similarly, from Fig. 3, it can be easily seen that, as the value of m increases, the sequence

$$\begin{aligned} \Omega _m^{\Delta }\bigg (\lambda L\bigg (\bigg (\frac{s}{1-s}\bigg )^2; x\bigg )\bigg ) \end{aligned}$$

converges to the function $f_2(x)$ given by $f_2(x)=\big (\frac{x}{1-x}\big )^2.$

Fig. 3

The convergence of $\Omega_m^{\Delta}\left(\lambda L\left(\left(\frac{s}{1-s}\right)^2; x\right)\right)$ for different values of $m$

Figures 1, 2 and 3 clearly show that the conditions (4), (5) and (6) of Theorem 3 are satisfied.

Fig. 4

The convergence of $\Omega_m^{\Delta}\left(\lambda L\left(\frac{\cos(3\pi s)}{1+s^2}; x\right)\right)$ for different values of $m$

We also observe from Fig. 4 that, as the value of m increases, the operators given by (17) converge towards the function. Indeed, Fig. 4 shows that the condition (3) holds true for the function

$$\begin{aligned} f(s)=\frac{\cos (3\pi s)}{1+s^2} \end{aligned}$$

in C[0, A] where $A\leqq 1/2$.