Relatively Uniform Weighted Summability Based on Fractional-Order Difference Operator

Abstract

In the present paper, we introduce the notion of relatively uniform weighted summability and its statistical version based upon fractional-order difference operators of functions. The concept of relatively uniform weighted $\alpha \beta$-statistical convergence is also introduced and some inclusion relations concerning the newly proposed methods are derived. As an application, we prove a general Korovkin-type approximation theorem for functions of two variables and also construct an illustrative example by the help of generating function type non-tensor Meyer-König and Zeller operators. Moreover, it is shown that the proposed methods are non-trivial generalizations of relatively uniform convergence which includes a scale function. We estimate the rate of convergence of approximating positive linear operators by means of the modulus of continuity and give a Voronovskaja-type approximation theorem. Finally, we present some computational results and geometrical interpretations to illustrate some of our approximation results.

1 Introduction and Preliminaries

The theory of summability arises from the process of summation of series and is an extremely wide and fruitful field for the application in several branches of functional analysis, in particular, operator theory, analytic continuation, the rate of convergence, quantum mechanics, approximation theory, probability theory, the theory of orthogonal series, and fixed point theory. With the rapid development of sequence spaces, many researchers have focused on the notion of statistical convergence which was independently introduced by Fast [1] and Steinhaus [2] in the same year 1951. Recently, the concepts of statistical convergence and statistical summability have become an active area of research. Also these techniques have been discussed satisfactorily in approximation theory of functions by positive linear operators. For more various approaches to statistical convergence and statistical summability, we refer to [3,4,5,6,7,8].

Let $S \subseteq {\mathbb {N}}$ and

$$\begin{aligned} S_m:=\{n:n\leqq m~~\text {and}~~ n\in S\}. \end{aligned}$$

The natural density (see [9, 10]) of S is defined by

$$\begin{aligned} \delta (S)=\lim _{m\rightarrow \infty }\frac{1}{m}|S_m|, \end{aligned}$$

provided that the limit exists, where $|S_m|$ denotes the cardinality of set $S_m$. A number sequence $u=(u_{n})$ is called statistically convergent ($\delta$-convergent) to the number L, denoted by st-$\lim _m u=L$, if, for every $\epsilon >0,$ the set

$$\begin{aligned} H_{\epsilon }=\big \{n: n\in {\mathbb {N}}~ \text {and}~|u_{n}-L|\geqq \epsilon \big \} \end{aligned}$$

has natural density zero, or equivalently $\delta (H_{\epsilon })=0$. The idea of weighted statistical convergence of single sequences was first given by Karakaya and Chishti [11]. More recently, this notion was modified by Mursaleen et al. [12] (see also the related work by Srivastava et al. [13]) and was further extended by Kadak et al. [14].

Let $s=(s_{k})$ be a sequence of non-negative numbers such that $s_{0}>0$ and $S_m=\sum _{k=0}^m s_k \rightarrow \infty$ as $m \rightarrow \infty$. We say that a sequence $u=(u_{n})$ is weighted statistically convergent (or $S_N$-convergent) to the number L if, for every $\epsilon >0$,

$$\begin{aligned} \lim _{m\rightarrow \infty } \frac{1}{S_m}\bigg |\big \{n\leqq S_m:s_n|u_n-L|\geqq \epsilon \big \}\bigg |=0. \end{aligned}$$

Quite recently, Aktuğlu [15] introduced the notion of $(\alpha ,\beta )$-statistical convergence for single sequences with the help of two sequences $\{\alpha (n)\}_{n\in {\mathbb {N}}}$ and $\{\beta (n)\}_{n\in {\mathbb {N}}}$ of positive numbers which satisfy the conditions: $\alpha$ and $\beta$ are both non-decreasing, $\beta (n)\geqq \alpha (n)$ for all $n\in {\mathbb {N}}$, ($\beta (n)-\alpha (n))\rightarrow \infty$ as $n\rightarrow \infty .$ The set of all pairs $(\alpha ,\beta )$ satisfying above conditions will be denoted by $\Lambda$. A sequence $u=(u_{k})$ is said to be $(\alpha ,\beta )$-statistically convergent to L if, for each $\varepsilon >0$,

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{\left| \left\{ k\in S^{(\alpha ,\beta )}_{n}:|u_{k}-L|\geqq \epsilon \right\} \right| }{\beta (n)-\alpha (n)+1}=0, \end{aligned}$$

where $(\alpha ,\beta ) \in \Lambda$ and $S^{(\alpha ,\beta )}_{n}=[\alpha (n), \beta (n)]$.

The concept of relatively uniform convergence of a sequence of functions was introduced by Moore [16]. In the slight modification by Chittenden [17], the relatively uniform convergence was defined on a closed interval $I \subset {\mathbb {R}}$ as follows:

A sequence $\{f_n(x)\}$ of functions, defined on an interval $I\equiv (a \leqq x \leqq b)$, converges relatively uniformly to a limit function f(x) if there exists a function $\sigma (x)$, called a scale function $\sigma (x)$ defined on I, such that for every $\varepsilon > 0$ there is an integer $n_\varepsilon$ such that for every n greater than $n_\varepsilon$ the inequality

$$\begin{aligned} |f_n(x)-f(x)|\leqq \varepsilon ~|\sigma (x)| \end{aligned}$$

holds uniformly in x on the interval $I \subset {\mathbb {R}}$. For example (see [18]), consider the sequence $(f_n)$ of functions defined on [0, 1] given by

$$\begin{aligned} f_n(x)=\left\{ \begin{array}{ll} \frac{1}{nx} &{} \qquad (x\ne 0),\\ \\ 0 &{} \qquad (x=0). \end{array} \right. \end{aligned}$$

It is clear that $(f_n)$ is not convergent uniformly, but is convergent to $f(x)=0$ uniformly relative to a scale function defined as

$$\begin{aligned} \sigma (x)=\left\{ \begin{array}{ll} \frac{1}{x} &{} \qquad (0<x\leqq 1),\\ \\ 1 &{} \qquad (x=0). \end{array}\right. \end{aligned}$$

Note that uniform convergence is the special case of relatively uniform convergence in which the scale function is a non-zero constant. Very recently, based on the natural density of a set, the notion of relative statistical uniform convergence has been introduced by Demirci and Orhan [18] (see also [19]). In the same year, they gave the definitions of relative modular convergence and statistical relative modular convergence for double sequences of measurable real-valued functions [20].

Let $(f_n)$ be a sequence of functions defined on a compact subset E of real numbers. The sequence $(f_n)$ is said to be statistically relatively uniform convergent to the limit function f defined on E, if there exists a scale function $\sigma (x)$, $|\sigma (x)|>0$, on E such that for every $\epsilon >0$,

$$\begin{aligned} \delta ~\Bigg (n:\sup _{x \in E}\bigg |\frac{f_n(x)-f(x)}{\sigma (x)}\bigg |\ge \epsilon \Bigg )=0. \end{aligned}$$

(1.1)

In this case we write $(st)-f_n \rightrightarrows f (E;\sigma )$.

The idea of fractional-order difference operator was firstly used by Chapman [21] and has since been studied by many researchers [22,23,24,25]. In the year 2016, some new classes of fractional-order difference sequence spaces was introduced by Baliarsingh in [26]. Later on, Kadak [27] has generalized the concept of weighted statistical convergence via (p, q)-integers. In the year 2017, Kadak [28] extended the weighted statistical convergence based on a generalized difference operator involving (p, q)-gamma function.

For our purpose, we will need the following definition involving a fractional-order backward difference operator of functions (see [26]).

Let a, b and c be real numbers and h be any positive constant. Let f(x) be a real-valued function which is differentiable with fractional-order. Based on this function f(x), for the sequence $f_h(\cdot )=(f(x-ih))$, the fractional-order backward difference operator of f corresponding to the decrement ih is defined as

$$\begin{aligned} \Delta ^{a,b,c}_{h} f(x)=\sum _{i=0}^\infty \frac{(-a)_i~(-b)_i}{ i!(-c)_i}\frac{f(x-ih)}{h^{a+b-c}} \end{aligned}$$

(1.2)

where $(-c)_i\ne 0$ for all $i \in {\mathbb {N}}$ and $(r)_k$ denotes the Pochhammer symbol (or shifted factorial) of a real number r which is defined as

$$\begin{aligned} (r)_k:=\left\{ \begin{array}{lll} 1 , &{}&{} (r=0~\text {or}~k=0), \\ \frac{\Gamma (r+k)}{\Gamma (r)}=r(r+1)(r+2)\dots (r+k-1) , &{}&{} (k \in {\mathbb {N}}).\end{array}\right. \end{aligned}$$

(1.3)

From now on, without loss of generality, we can assume that the summation given in (1.2) converges for all $c <a+b$ where $(-c)_i\ne 0$ for all $i \in {\mathbb {N}}$. It is clear that the fractional-order difference operator defined in Eq. (1.2) is linear and hence the integral and fractional-order operators can be obtained through the difference operator $\Delta ^{a,b,c}_{h}$. For example, by choosing $a=2$, $b=c$ in (1.2), we can write

$$\begin{aligned} \lim _{h \rightarrow 0}\Delta ^{2,b,b}_{h} f(x)=\lim _{h \rightarrow 0}\Bigg \{\frac{f(x)-2f(x-h)+f(x-2h)}{h^{2}}\Bigg \}=f''(x), \end{aligned}$$

if it exists. Clearly, for $a=r \in {\mathbb {R}}, b=c$, the fractional derivative operator $(\frac{d}{dx})^r$ and fractional integro operator $(\frac{d}{dx})^{-r}\,(r \notin {\mathbb {N}})$, are immediately obtained via $\Delta ^{a,b,c}_{h}$. For more details see [26].

Our main purpose of the present study is to generalize the uniform convergence of sequences of positive linear operators based on fractional-order linear difference operator $\Delta ^{a,b,c}_{h}$. Also, our present investigation deals essentially with various summability methods for sequences of functions and shows how these methods lead to a number of approximation results. Furthermore, we apply our new type of summability method to prove Korovkin and Voronovskaya type results for functions of two variables with the help of non-tensor Meyer-König and Zeller operators involving generating functions. Several illustrative examples and geometrical interpretations are also given to illustrate some of approximation results in this paper.

2 Some New Definitions and Concerning Inclusion Relations

In this section, we first give the definition of relative uniform weighted $\alpha \beta$-statistical convergence through the weighted $\alpha \beta$-density. Also, we introduce the notion of relatively uniform statistical $\Phi$-summability for function sequences. Secondly, we give some inclusion relations between proposed methods and present an illustrative example to prove that our method is non-trivial generalization of classical and statistical cases of relatively uniform convergence introduced in [18, 19].

Let $p=(p_{k})_{k=0}^\infty$ be a sequence of non-negative real numbers such that

$$\begin{aligned}P_n^{(\alpha ,\beta )}=\sum _{k=\alpha (n)}^{\beta (n)}p_k \rightarrow \infty ~~\text {as}~~n\rightarrow \infty ,~~~~(\alpha ,\beta ) \in \Lambda .\end{aligned}$$

The lower and upper weighted $\alpha \beta$-densities of the set $K \subset {\mathbb {N}}$ are defined by

$$\begin{aligned} {\underline{\delta }}^{(\alpha ,\beta )}_{P_n}(K)=\liminf _{n\rightarrow \infty }\frac{1}{P_n^{(\alpha ,\beta )}}\bigg |\left\{ k\le P_n^{(\alpha ,\beta )}:k\in K\right\} \bigg | \end{aligned}$$

and

$$\begin{aligned} {\overline{\delta }}^{(\alpha ,\beta )}_{P_n}(K)=\limsup _{n\rightarrow \infty }\frac{1}{P_n^{(\alpha ,\beta )}}\bigg |\left\{ k\le P_n^{(\alpha ,\beta )}:k\in K\right\} \bigg |, \end{aligned}$$

respectively. We say that K has weighted $\alpha \beta$-density $\delta ^{(\alpha ,\beta )}_{P_n}(K)$ if

$$\begin{aligned}{\underline{\delta }}^{(\alpha ,\beta )}_{P_n}(K)={\overline{\delta }}^{(\alpha ,\beta )}_{P_n}(K),\end{aligned}$$

in which case $\delta ^{(\alpha ,\beta )}_{{\bar{N}}}(K)$ is equal to this common value. The weighted $\alpha \beta$-density can be restated in the following way:

$$\begin{aligned} \delta ^{(\alpha ,\beta )}_{P_n}(K)=\lim _{n\rightarrow \infty }\frac{1}{P_n^{(\alpha ,\beta )}}\bigg |\left\{ k\le P_n^{(\alpha ,\beta )}:k\in K\right\} \bigg |, \end{aligned}$$

if the limit exists.

Definition 1

Let h be any positive constant, $(\alpha ,\beta ) \in \Lambda$ and $a, b, c \in {\mathbb {R}}$. A sequence $(f_n)$ of functions, defined on a compact subset E of real numbers, is said to be relatively uniform weighted $\alpha \beta$-statistical convergent to the function f on E, if there exists a scale function $\sigma (x)~(|\sigma (x)|>0)$ on E such that, for each $\epsilon >0$,

$$\begin{aligned}\delta ^{(\alpha ,\beta )}_{P_n}\Bigg (\Bigg \{n:\sup _{x \in E}~p_n~\bigg |\frac{\Delta ^{a,b,c}_{h} f_n(x)-f(x)}{\sigma (x)}\bigg |\ge \epsilon \Bigg \}\Bigg )=0,~~~~(\alpha ,\beta ) \in \Lambda .\end{aligned}$$

In this case we denote it by $S_{\Delta }^{(\alpha ,\beta )}(p_n, \sigma )-f_n \rightrightarrows f$.

Definition 2

Let h be any positive constant, $(\alpha ,\beta ) \in \Lambda$ and $a, b, c \in {\mathbb {R}}$. A sequence $(f_n)$ of functions defined on the compact subset $E \subset R$, is said to be uniformly $\Phi$-summable to f on E, if

$$\begin{aligned}\Phi (f_n)=\frac{1}{P_n^{(\alpha , \beta )}}\sum _{k=\alpha (n)}^{\beta (n)}p_k~ \Delta ^{a,b,c}_{h}f_k(x) \rightrightarrows f\end{aligned}$$

as $n \rightarrow \infty$ uniformly in $x\in E$, where $|\Delta ^{a,b,c}_{h}f_k(x)|>0$ for all $k \in {\mathbb {N}}$. Also, we say that $(f_n)$ is uniformly statistical $\Phi$-summable to f, if $(\Phi (f_n))$ is statistically uniform convergent to the same limit function f. That is, for every $\epsilon >0$,

$$\begin{aligned}\delta ~\bigg (\big \{n:\sup _{x \in E}\big |~\Phi (f_n(x))-f(x)~\big |\ge \epsilon \big \}\bigg )=0.\end{aligned}$$

This limit is denoted by ${\overline{N}}_\Phi ~(stat)-f_n \rightrightarrows f$ on E.

Definition 3

A sequence $(f_n)$ of functions, defined on the compact subset $E\subset {\mathbb {R}}$, is said to be relatively uniform statistical $\Phi$-summable to f, if $(\Phi (f_n))$ is relatively uniform statistical convergent to f on E. Equivalently, we may write

$$\begin{aligned} \delta ~\Bigg (\bigg \{n:\sup _{x \in E}~\bigg |\frac{\Phi (f_n(x))-f(x)}{\sigma (x)}\bigg |\ge \epsilon \bigg \}\Bigg )=0,~~~~|\sigma (x)|>0. \end{aligned}$$

We denote it by ${\overline{N}}_\Phi ~-f_n \rightrightarrows f (\sigma , E)$.

Based upon above definitions, we shall give the following special cases and some inclusion relations to show the effectiveness of newly proposed methods.

• Let us take $a=0$, $b=c$, $\alpha (n)=1$, $\beta (n)=n$ and $p_n=1$ for all $n \in {\mathbb {N}}$, the relatively uniform weighted $\alpha \beta$-statistical convergence in Definition 1, is reduced to relatively uniform statistical convergence introduced in [18]. For the case $\sigma (x)$ is non-zero constant, we have its uniformly statistical convergence version (cf. [19]).

• Let $(\lambda _n)$ be a strictly increasing sequence of positive numbers tending to $\infty$ as $n \rightarrow \infty$ such that $\lambda _{n+1}\le \lambda _n +1$ and $\lambda _1=1$. If we take $a=0$, $b=c$, $\sigma (x)=1$, $\alpha (n)=n-\lambda _n+1$ and $\beta (n)=n$, then the relatively uniform statistical $\Phi$-summability given in Definition 3 reduces to the weighted $\lambda$-statistical summability (cf. [29, 30]). Again, if we take $p_n=1$ for all $n \in {\mathbb {N}}$ as an extra condition, we have an analog of $\lambda$-statistical summability for function sequences (cf. [31]).

• Let $\theta =(k_n)$ be an increasing positive number sequence such that $k_0=0$, $0<k_n<k_{n+1}$ and $h_n=k_n-k_{n-1}\rightarrow \infty$, as $n\rightarrow \infty$. It is known that $\theta$ is a lacunary sequence. For $a=0$, $b=c$, $\sigma (x)=1$, $\alpha (n)=k_{n-1}+1$, $\beta (n)=k_n$ and $p_n=1$ for all $n \in {\mathbb {N}}$, relatively uniform statistical $\Phi$-summability is reduced to lacunary statistical summability for function sequences (cf. [28, 32, 33]).

• Take $a=2$, $b=c$, $\sigma (x)=1$, $\alpha (n)=\lambda _{n-1}+1$, $\beta (n)=\lambda _n$, the relatively uniform weighted $\alpha \beta$-statistical convergence reduces to weighted $\Lambda ^{2}$-statistical convergence for function sequences (cf. [27, 34]). In a similar manner, relatively uniform statistical $\Phi$-summability is reduced to $\Lambda ^{2}$-statistical summability (cf. [27, 34]).

As a direct consequence of above mentioned special cases, we can give the following inclusion relations without proof.

Lemma 1

• (a) $f_n \rightrightarrows f$ on E (in the ordinary sense) implies $(st)-f_n \rightrightarrows f (E;\sigma )$, which also implies $S_{\Delta }^{(\alpha ,\beta )}(p_n, \sigma )-f_n \rightrightarrows f$ on E.

• (b) $f_n \rightrightarrows f$ on E (ordinary uniform summable) implies ${\overline{N}}_\Phi ~(stat)-f_n \rightrightarrows f$ on E, which also implies ${\overline{N}}_\Phi ~-f_n \rightrightarrows f(\sigma , E)$.

Theorem 1

Let h be any positive constant, $(\alpha ,\beta ) \in \Lambda$ and $a, b, c \in {\mathbb {R}}$ and, let $\sigma (x)$ be a bounded scale function defined on $E \subset {\mathbb {R}}$. Assume that

$$\begin{aligned}\sup _{x \in E} p_k~\bigg |\frac{\Delta ^{a,b,c}_{h} f_k(x)-f(x)}{\sigma (x)}\bigg |\le M~~~\text {for all }~~k\in {\mathbb {N}}~~~\text {and }~~|\sigma (x)|>0.\end{aligned}$$

If a sequence $(f_n)$ of functions on $E \subset {\mathbb {R}}$ is relatively uniform weighted $\alpha \beta$-statistical convergent to the bounded function f on E, then it is relatively uniform statistical $\Phi$-summable to the same limit function f on E, but not conversely.

Proof

Suppose that $\sup _{x \in E} p_k~\big |\frac{\Delta ^{a,b,c}_{h} f_k(x)-f(x)}{\sigma (x)}\big |\le M~~\text {for all }~k\in {\mathbb {N}}$. From the hypotheses, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{P_n^{(\alpha ,\beta )}}\bigg |\bigg \{k\le P_n^{(\alpha ,\beta )}:\sup _{x \in E}~p_k~\bigg |\frac{\Delta ^{a,b,c}_{h} f_k(x)-f(x)}{\sigma (x)}\bigg |\ge \epsilon \bigg \}\bigg |=0. \end{aligned}$$

Let us set

$$\begin{aligned}K(\epsilon ):=\bigg \{k\le P_n^{(\alpha ,\beta )}:\sup _{x \in E}~p_k~\bigg |\frac{\Delta ^{a,b,c}_{h} f_k(x)-f(x)}{\sigma (x)}\bigg |\ge \epsilon \bigg \}\end{aligned}$$

and

$$\begin{aligned}K^C(\epsilon ):=\bigg \{k\le P_n^{(\alpha ,\beta )}:\sup _{x \in E}~p_k~\bigg |\frac{\Delta ^{a,b,c}_{h} f_k(x)-f(x)}{\sigma (x)}\bigg |< \epsilon \bigg \}.\end{aligned}$$

We then obtain that

$$\begin{aligned} \bigg |\frac{\Phi f_n(x)-f(x)}{\sigma (x)}\bigg |&=\frac{1}{|\sigma (x)|}~\Bigg |\Bigg \{\frac{1}{P_n^{(\alpha , \beta )}}\sum \limits _{k\in I_n^{(\alpha ,\beta )}}p_k~ \Delta ^{a,b,c}_{h}f_k(x)\Bigg \}-f(x)\Bigg |\\&\le \frac{1}{|\sigma (x)|}~\Bigg \{\bigg |\frac{1}{P_n^{(\alpha , \beta )}}\sum _{k\in I_n^{(\alpha ,\beta )}}p_k\big [\Delta _{h}^{a,b,c} f_k(x)-f(x)\big ]\bigg |\\&\quad +\big |f(x)\big |~\bigg |\frac{1}{P_n^{(\alpha , \beta )}}\sum _{k\in I_n^{(\alpha ,\beta )}} p_k-1\bigg |\Bigg \}. \end{aligned}$$

By using the fact that $\frac{1}{P_n^{(\alpha , \beta )}}\sum _{k\in I_n^{(\alpha ,\beta )}} p_k=1$, $\sup _{x\in E}|f(x)/\sigma (x)|<\infty$, and taking supremum over $x \in E$ in the last equation, we get

$$\begin{aligned} \sup _{x \in E}\bigg |\frac{\Phi f_n(x)-f(x)}{\sigma (x)}\bigg |&\le \frac{1}{P_n^{(\alpha , \beta )}}\sum _{\begin{array}{c} k\in I_n^{(\alpha ,\beta )}\\ (k\in K(\epsilon )) \end{array}}\sup _{x \in E}~p_k~\bigg |\frac{\Delta ^{a,b,c}_{h} f_k(x)-f(x)}{\sigma (x)}\bigg |\\&\quad +\frac{1}{P_n^{(\alpha , \beta )}}\sum _{\begin{array}{c} k\in I_n^{(\alpha ,\beta )}\\ (k\in K^C(\epsilon )) \end{array}}\sup _{x \in E}~p_k~\bigg |\frac{\Delta ^{a,b,c}_{h} f_k(x)-f(x)}{\sigma (x)}\bigg |\\&\le \frac{M}{P_n^{(\alpha , \beta )}}~|K(\epsilon )|+\frac{\epsilon }{P_n^{(\alpha , \beta )}}| ~K^C(\epsilon )|\rightarrow 0+\epsilon \cdot 1=\epsilon ~~(n \rightarrow \infty ) \end{aligned}$$

where $I_n^{(\alpha ,\beta )}=[\alpha (n), \beta (n)]$. Therefore, the sequence $(f_n)$ of functions defined on E is relatively uniform statistical $\Phi$-summable to the same limit f on E. $\square$

For converse, we present the following example:

Example 1

Define $f_n:[0, 4] \rightarrow {\mathbb {R}}$ and $\sigma (x)$ by

$$\begin{aligned} f_n(x)=\left\{ \begin{array}{ll} \frac{1}{x}, &{} n=m^2-m, m^2-m+1, \dots , m^2-1;~ m=2,3,4\dots ;~x\in (0, 2)\\ \frac{-m}{x}, &{}n=m^2;~~ m=2,3,4, \dots ;~x\in (0, 2)\\ 0,&{} \text {otherwise or}~x \in [2,4] \cup \{0\} \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \sigma (x)=\left\{ \begin{array}{ll} \frac{1}{x(x-2)(x-4)}, &{} x \in (0, 2)\\ 1, &{}x\in [2,4] \cup \{0\}. \end{array} \right. \end{aligned}$$

In the special case, when $a=2$, $b=c$, $h=2$, $\alpha (n)=1$, $\beta (n)=n$ and $p_n=1$ for all $n \in {\mathbb {N}}$, we have

$$\begin{aligned} \Delta ^{2,b,b}_{2} f_n(x)= & {} \frac{1}{4}\big \{f_n(x)-2f_n(x-2)+f_n(x-4)\big \}\\= & {} \left\{ \begin{array}{ll} \frac{2}{x(x-2)(x-4)}, &{} n=m^2-m, m^2-m+1, \dots , m^2-1; ~x\in (0, 2),\\ \frac{-2m}{x(x-2)(x-4)}, &{}n=m^2, m=2,3,4, \dots ; ~x\in (0, 2),\\ 0,&{} \text {otherwise~or}~x\in [2,4] \cup \{0\}. \end{array}\right. \end{aligned}$$

It is obvious that neither $(\Delta ^{2,b,b}_{h} f_n)$ nor $(f_n)$ converges uniformly on [0, 4]. On the other hand, since

$$\begin{aligned} \Phi (f_n(x))= & {} \frac{1}{n}\sum \limits _{k=1}^n ~\Delta ^{2,b,b}_{2} f_k(x)\\= & {} \left\{ \begin{array}{ll} \frac{s+1}{nx(x-2)(x-4)},&{} n=m^2-m+s; ~s=0,1,2\dots ,m-1 ; ~x\in (0, 2)\\ 0,&{} \text {otherwise~or}~x\in [2,4] \cup \{0\} \end{array}\right. , \end{aligned}$$

we obtain,

$$\begin{aligned}&\lim _{n\rightarrow \infty }\sup _{x \in [0, 4]}~\bigg |\frac{\Phi (f_n(x))-f(x)}{\sigma (x)}\bigg |\\&\quad =\lim _{n\rightarrow \infty }\sup _{x \in [0, 4]}\Bigg |\frac{\frac{s+1}{nx(x-2)(x-4)}}{\frac{1}{x(x-2)(x-4)}}\Bigg | =0,~~s=0,1,2, \dots , m-1, \end{aligned}$$

and hence $(f_n)$ is relatively uniform statistical $\Phi$-summable to $f(x)=0$. However, since

$$\begin{aligned}\liminf _{n \rightarrow \infty } \frac{1}{n}~\Bigg |\Bigg \{n:\sup _{x \in [0, 4]}~\bigg |\frac{\Delta ^{2,b,b}_{2} f_n(x)-f(x)}{\sigma (x)}\Bigg |\ge \epsilon \Bigg \}\Bigg |=0\end{aligned}$$

and

$$\begin{aligned}\limsup _{n \rightarrow \infty } \frac{1}{n}~\Bigg |\Bigg \{n:\sup _{x \in [0, 4]}~\bigg |\frac{\Delta ^{2,b,b}_{2} f_n(x)-f(x)}{\sigma (x)}\ge \epsilon \Bigg \}\Bigg |=1,\end{aligned}$$

then $(f_n)$ is not relatively uniform weighted $\alpha \beta$-statistical convergent to $f(x)=0$.

Based upon above example, it is concluded that proposed method is stronger than the classical and statistical version of relatively uniform convergence introduced in [17, 18].

3 A Korovkin-Type Approximation Theorem

At the beginning of the 1950s, the study of some particular approximation by means of the positive linear operators was extended to general approximation sequences of such operators. The basis of approximation theory through positive linear operators or functionals was developed by Korovkin [35]. This approximation theorem nowadays called Korovkin’s type approximation theorem has been extended in several directions. First of all, Gadjiev and Orhan [36] established the classical Korovkin theorem via statistical convergence. In recent years, with the help of extended summability methods, various approximation results have been proved [14, 23, 30, 34]. For more details on the usage of summability methods in Korovkin-type approximation theorems, refer to [37, 38].

In this section, we shall prove a Korovkin-type approximation theorem related to the notion of relatively uniform statistical $\Phi$-summability for sequence of functions of two variables. First, we give the definitions of fractional-order difference partial operators of f(x, y) defined on $E^2\subset {\mathbb {R}}^2$. Secondly, using the generating function type non-tensor Meyer-König and Zeller operators [39, 40], we show that our proposed method successfully works and is more powerful than the existing Korovkin-type approximation theorem based on (relatively) uniform convergence.

Let a, b and c be real numbers and h be any positive constant. Let $f:E^2 \rightarrow {\mathbb {R}}$ be any real-valued function which has fractional-order partial derivatives. Then, the fractional-order difference partial operators of f(x, y) with respect to x and y are defined by

$$\begin{aligned} \Delta ^{a,b,c}_{h,x} f(x,y)=\sum _{i=0}^\infty \frac{(-a)_i~(-b)_i}{ i!(-c)_i}\frac{f(x-ih,y)}{h^{a+b-c}} \end{aligned}$$

(3.1)

and

$$\begin{aligned} \Delta ^{a,b,c}_{h,y} f(x,y)=\sum _{i=0}^\infty \frac{(-a)_i~(-b)_i}{ i!(-c)_i}\frac{f(x,y-ih)}{h^{a+b-c}} \end{aligned}$$

(3.2)

respectively, where $(-c)_i\ne 0$ for all $i \in {\mathbb {N}}$ and $(r)_k$ denotes the Pochhammer symbol in (1.3). Without loss of generality, we assume that the summations given in (3.1) and (3.2) converge for all $a+b>c$ with $(-c)_i\ne 0$ for all $i \in {\mathbb {N}}$. For instance, taking $a=1$, $b=c$ in (3.1), we would have the first-order partial derivative of f(x, y) with respect to x, that is,

$$\begin{aligned} \lim _{h \rightarrow 0}\Delta ^{1,b,b}_{h,x} f(x,y)=\lim _{h \rightarrow 0}\Bigg \{\frac{f(x,y)-f(x-h,y)}{h}\Bigg \}, \end{aligned}$$

provided that the limit exists (as a finite number).

By $C(D_A)$, we denote the space of all continuous real-valued functions on a fixed compact subset $D_A$ of ${\mathbb {R}}^2$ defined by

$$\begin{aligned}D_A=\big \{(x, y) \in {\mathbb {R}}^2: x\in [0, A], y\in [0, A-x],0<A\le 1/2 \big \}\end{aligned}$$

and equipped with the following norm:

$$\begin{aligned}\Vert f\Vert _{C(D_A)}=\sup _{ (x, y)\in D_A}|f(x, y)|,~\quad ~f \in C(D_A).\end{aligned}$$

Suppose that J is a of positive linear operators from $C(D_A)$ into itself. Then as usual, we say that J is a positive linear operator provided that $f \ge 0$ implies $Jf \ge 0$. Also, we use the notation J(f(u, v); x, y) for the value of Jf at a point $(x, y)\in D_A$.

Throughout the paper, we consider the following families of two dimensional test functions on $D_A$:

$$\begin{aligned}&e_{0}(u,v)=1, \quad e_{1}(u,v)=\frac{u}{1-u-v},\quad e_{2}(u,v)=\frac{v}{1-u-v}\nonumber \\& \quad \text {and}\qquad e_{3}(u,v) =\left( \frac{u}{1-u-v}\right) ^2+\left( \frac{v}{1-u-v}\right) ^2. \end{aligned}$$

(3.3)

Theorem 2

Let h be any positive constant, $(\alpha ,\beta ) \in \Lambda$ and $a, b, c \in {\mathbb {R}}$. Assume that $\{T_{n}\}$ is a sequence of positive linear operators acting from $C(D_A)$ into itself satisfying $|\Delta _{h,x}^{a,b,c} T_n(\cdot ;x,y)|>0$. Assume further that $\sigma _i(x, y)$ is an unbounded scale function on $D_A$ such that $|\sigma _i(x, y)|>0$ for $i=0,1,2,3$. Then, for all $f\in C(D_A)$,

$$\begin{aligned} {\overline{N}}_\Phi ~-T_n(f; x,y) \rightrightarrows f~(\sigma ,D_A) \end{aligned}$$

(3.4)

if and only if

$$\begin{aligned} {\overline{N}}_\Phi ~-T_n(e_i; x,y) \rightrightarrows e_i ~(\sigma _i,D_A) \end{aligned}$$

(3.5)

where $\sigma (x, y)=\max \big \{|\sigma _i(x, y)|; i=0,1,2,3\big \}$ and $e_{i}(\cdot ,\cdot )$ is defined as in (3.3).

Proof

Since each $e_i$ belongs to $C(D_A)$ where $i=0,1,2,3$, then the implication (3.4) $\Rightarrow$ (3.5) is clear. Let $f \in C(D_A)$ and $(x, y) \in D_A$ be fixed. Since f is continuous on $D_A$, given $\epsilon >0$, there exists a number $\delta =\delta (\epsilon )>0$ such that

$$\begin{aligned} |f(u, v)-f(x, y)|<\epsilon \end{aligned}$$

(3.6)

for all $(x, y), (u, v) \in D_A$ satisfying

$$\begin{aligned} \sqrt{\left( \frac{u}{1-u-v}-\frac{x}{1-x-y}\right) ^2+\left( \frac{v}{1-u-v}-\frac{y}{1-x-y}\right) ^2}<\delta . \end{aligned}$$

Also we obtain for all $(x, y), (u, v) \in D_A$ satisfying

$$\begin{aligned} \sqrt{\left( \frac{u}{1-u-v}-\frac{x}{1-x-y}\right) ^2+\left( \frac{v}{1-u-v}-\frac{y}{1-x-y}\right) ^2}\ge \delta \end{aligned}$$

that

$$\begin{aligned} |f(u, v)-f(x, y)|\le \frac{2M}{\delta ^2}\big (\varphi _u^2(x)+\varphi _v^2(y)\big ) \end{aligned}$$

(3.7)

where

$$\begin{aligned} \varphi _u(x)=\frac{u}{1-u-v}-\frac{x}{1-x-y},~~~\varphi _v(y)=\frac{v}{1-u-v}-\frac{y}{1-x-y} \end{aligned}$$

(3.8)

and $M:=\sup _{(x, y) \in D~_A}|f(x, y)|$. Combining (3.6) and (3.7), we get for all $(x, y), (u, v) \in D_A$ and $f \in C(D_A)$ that

$$\begin{aligned} |f(u, v)-f(x, y)|< \epsilon +\frac{2M}{\delta ^2}\big (\varphi _u^2(x)+\varphi _v^2(y)\big ). \end{aligned}$$

It follows from the linearity and positivity of $T_{k}$ that

$$\begin{aligned}&\big |T_{k}(f(u, v); x, y)-f(x,y)\big |\\&\quad =\big |T_{k}(f(u, v)-f(x,y); x,y)+f(x,y) [T_{k}(e_{0}; x, y)-e_{0}(x,y)]\big |\\&\quad \leqq T_{k}\big (|f(u, v)-f(x, y)|; x, y\big )+M~|T_{k}(e_{0}; x, y)-e_{0}(x,y)|\\&\quad \leqq \left| T_{k}\left( \varepsilon +\frac{2M}{\delta ^2}(\varphi _u^2(x)+\varphi _v^2(y)); x, y\right) \right| +M~|T_{k}(e_{0}; x, y)-e_{0}(x,y)|\\&\quad \le \epsilon +(\epsilon +M)~\big |T_{k}(e_{0};x,y)-e_{0}(x,y)\big |\\&\qquad -\frac{4M}{\delta ^2}\left( \frac{x}{1-x-y} \right) \big |T_{k}(e_{1};x,y)-e_{1}(x,y)\big |\\&\qquad + \frac{2M}{\delta ^2}\big |T_{k}(e_{3};x,y)-e_{3}(x,y)\big |\\&\qquad -\frac{4M}{\delta ^2}\left( \frac{y}{1-x-y} \right) \big |T_{k}(e_{2};x,y)-e_{2}(x,y)\big |\\&\qquad +\frac{2M}{\delta ^2}\left( \left( \frac{x}{1-x-y} \right) ^2+\left( \frac{y}{1-x-y} \right) ^2\right) \big |T_{k}(e_{0};x,y) -e_{0}(x,y)\big |\\&\quad \leqq \varepsilon +\left( \varepsilon +M+\frac{4M}{\delta ^2}\right) |T_{k}(e_{0}; x, y)-e_{0}|+\frac{4M}{\delta ^2}|T_{k}(e_{1}; x, y)-e_{1}|\\&\qquad \quad +\frac{4M}{\delta ^2}|T_{k}(e_{2}; x, y)-e_{2}|+\frac{2M}{\delta ^2}|T_{k}(e_{3};x,y)-e_{3}|. \end{aligned}$$

Now multiplying the both sides of the above inequality by $\frac{1}{|\sigma (x, y)|}$ and taking the supremum over $(x,y) \in D_A$, we deduce that

$$\begin{aligned}&\sup _{(x,y) \in D_A} \bigg |\frac{T_{k}(f(u, v); x, y)-f(x,y)}{\sigma (x, y)}\bigg |\nonumber \\&\quad \leqq \sup _{(x,y) \in D_A}\frac{\epsilon }{|\sigma (x, y)|}+ N \sup _{(x,y) \in D_A}\sum _{i=0}^{3}\bigg |\frac{T_{k}(e_{i}(u, v); x, y)-e_{i}(x, y)}{\sigma _i(x, y)}\bigg |, \end{aligned}$$

(3.9)

where $\sigma (x, y)=\max \{|\sigma _i(x, y)|; i=0,1,2,3\}$ and $N:=\varepsilon +M+\frac{4M}{\delta ^2}.$ We now replace $T_k(\cdot ; x, y)$ by $\Phi (T_mf):C(D_A) \rightarrow C(D_A)$ defined by

$$\begin{aligned} \Phi (T_m(\cdot ;x,y))=\frac{1}{P_m^{(\alpha , \beta )}}\sum _{k=\alpha (m)}^{\beta (m)}p_k~ |\Delta ^{a,b,c}_{h,x}T_k(\cdot ;x,y)|,~~(\alpha , \beta )\in \Lambda \end{aligned}$$

in (3.9). For a given $r >0$, we choose a number $\epsilon >0$ such that $\sup \limits _{(x,y) \in D_A}\frac{\epsilon }{|\sigma (x, y)|}<r$. Then, upon setting

$$\begin{aligned} {\mathcal {A}}:= & {} \left\{ m\le n:\sup _{(x,y) \in D_A} \bigg |\frac{\Phi (T_m(f;x,y))-f(x,y)}{\sigma (x, y)}\bigg |\ge r\right\} ,\\ {\mathcal {A}}_{i}:= & {} \left\{ m\le n:\sup _{(x,y) \in D_A} \bigg |\frac{\Phi (T_m(e_{i};x,y))-e_{i}(x,y)}{\sigma _i(x, y)}\bigg |\ge \frac{r- \sup \limits _{(x,y) \in D_A}\frac{\epsilon }{|\sigma (x, y)|}}{4N}\right\} , \end{aligned}$$

where $i=0,1,2,3$. Then, it is clear that ${\mathcal {A}}\subset \bigcup \limits _{i=0}^3{\mathcal {A}}_{i}$ and hence using the hypothesis (3.5), we have

$$\begin{aligned} {\overline{N}}_\Phi ~-T_n(f; x,y) \rightrightarrows f~(\sigma ,D_A), \end{aligned}$$

which completes the proof of Theorem 2. $\square$

Remark 1

In Theorem 2, the condition $|\Delta _{h,x}^{a,b,c} T_n(\cdot ; x,y)|>0$ can not be removed. For example, taking $a \in {\mathbb {N}}$, $b=c$ and $h=1$, since $\Delta _{h,x}^{a,b,c} T_n(e_0;x,y)=0$, then

$$\begin{aligned}{\overline{N}}_\Phi ~-T_n(e_0; x,y) \rightrightarrows 0~(\ne 1)~(\sigma ,D_A).\end{aligned}$$

Therefore, the condition (3.5) does not always hold true for $i=0$.

We now present an illustrative example for Theorem 2. Before giving this example, we give a short introduction associated with the non-tensor type Meyer-König and Zeller operators of two variables (see [40, 41]).

Let us consider the following bivariate non-tensor operators:

$$\begin{aligned} L_{n}(f; x,y)&=\frac{1}{\Omega _n(u,v;x,y)}\nonumber \\&\quad \sum _{k,l=0}^{\infty ,\infty } f\left( \frac{a_{k,l,n}}{a_{k,l,n}+c_{k,l,n}+b_{n}}, \frac{c_{k,l,n}}{a_{k,l,n}+c_{k,l,n}+b_{n}}\right) P^n_{k,l}(u,v)x^ky^l \end{aligned}$$

(3.10)

where $P^n_{k,l}(u,v)>0$ for all $(u,v) \in D_{{\mathcal {A}}}$, ${\mathcal {A}}\in (0, 1)$ and

$$\begin{aligned}\left( \frac{a_{k,l,n}}{a_{k,l,n}+c_{k,l,n}+b_{n}}, \frac{c_{k,l,n}}{a_{k,l,n}+c_{k,l,n}+b_{n}}\right) \in D_{\mathcal A}.\end{aligned}$$

For the double indexed function sequence $\{P^n_{k,l}(u,v)\}_{k,l\in {\mathbb {N}}}$, the generating function $\Omega _n(u,v;x,y)$ is defined by

$$\begin{aligned} \Omega _n(u,v;x,y)=\sum _{k,l=0}^{\infty ,\infty }P^n_{k,l}(u,v)x^ky^l. \end{aligned}$$

Since the nodes are given by

$$\begin{aligned}u=\frac{a_{k, l,n}}{a_{k, l,n}+c_{k, l,n}+b_n}\qquad \text {and} \qquad v= \frac{c_{k, l,n}}{a_{k, l,n}+c_{k, l,n}+b_n} ,\end{aligned}$$

the denominators of

$$\begin{aligned}\frac{u}{1-u-v}=\frac{a_{k, l,n}}{b_n} \qquad \text {and} \qquad \frac{v}{1-u-v}=\frac{c_{k, l,n}}{b_n}\end{aligned}$$

are both independent of k and l, respectively. Throughout the paper, we also suppose that the following conditions hold true (see, for details, [40]):

• (i) $\Omega _n(u,v;x,y)=(1-x-y)~\Omega _{n+1}(u,v;x,y)$;

• (ii) $a_{k+1,l,n} P^n_{k+1,l}(u,v)=b_{n+1}P^{n+1}_{k,l}(u,v)$ and $c_{k,l+1,n} P^n_{k,l+1}(u,v)=b_{n+1}P^{n+1}_{k,l}(u,v)$;

• (iii) $b_n \rightarrow \infty , \frac{b_{n+1}}{b_n}\rightarrow 1$ and $b_n\ne 0$ for all $n\in {\mathbb {N}}$;

• (iv) $a_{k+1,l, n}-a_{k,l, n+1}=\varphi _n$ and $c_{k,l+1, n}-c_{k,l, n+1}=\xi _n$ where $|\varphi _n|\le M_0 <\infty ,$$|\xi _n|\le M_1 <\infty$ and ${a_{0,l,n}}=0, {c_{k,0,n}}=0$ for all $n\in {\mathbb {N}}$.

Note that, choosing $\Omega _n(u,v;x,y)=\frac{1}{(1-x-y)^{n+1}}$, $a_{k,l, n}=k, c_{k,l, n}=l$ and $b_n=n$ in (3.10), we get the non-tensor bivariate MKZ operators (see [42]). Using the positivity and linearity of $L_n$, it can be observed that (see [40])

$$\begin{aligned} L_{n}(e_{0}; x, y)=1,~~~L_{n}\left( e_{1}; x, y\right) =\frac{b_{n+1}}{b_n}e_{1}(x,y),~~~L_{n}\left( e_{2}; x, y\right) =\frac{b_{n+1}}{b_n}e_{2}(x,y) \end{aligned}$$

and

$$\begin{aligned} L_{n}\left( e_{3}; x, y\right) =\frac{b_{n+1}b_{n+2}}{b^2_n}e_{3}(x,y) +\frac{b_{n+1}\varphi _n}{b^2_n}e_{1}(x,y)+\frac{b_{n+1}\xi _n}{b^2_n}e_{2}(x,y). \end{aligned}$$

Example 2

Let $\alpha (n)=1$, $\beta (n)=n$ and $p_n=n$ for all $n \in {\mathbb {N}}$. Define $f_n:[0, 1] \rightarrow {\mathbb {R}}$ and $\sigma (x,y)$ by

$$\begin{aligned} f_n(x,y)=\left\{ \begin{array}{ll} \frac{1}{xy}, &{} n=m^2-m, m^2-m+1, \dots , m^2-1;~(x,y)\in (0,1)\times (0,1)\\ \frac{-m}{xy}, &{}n=m^2;~~ m=2,3,4, \dots ;~(x,y)\in (0,1)\times (0,1)\\ 0,&{} \text {otherwise or}~(x,y)=(0,0)~\text {or}~(x,y)=(1,1) \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \sigma (x,y)=\left\{ \begin{array}{ll} \frac{1}{xy}, &{} (x,y)\in (0,1)\times (0,1)\\ 1, &{}(x,y)=(0,0)~\text {or}~(x,y)=(1,1). \end{array} \right. \end{aligned}$$

For the special case $a= 0$ and $b = c$, one obtains

$$\begin{aligned} \Phi (f_n(x))=\left\{ \begin{array}{ll} \frac{s+1}{nxy},&{} n=m^2-m+s; ~s=0,1,2\dots ,m-1 ; ~(x,y)\in (0,1)\times (0,1)\\ 0,&{} \text {otherwise~or}~(x,y)=(0,0)~\text {or}~(x,y)=(1,1) \end{array}\right. , \end{aligned}$$

which implies that

$$\begin{aligned} {\overline{N}}_\Phi -f_n \rightrightarrows 0~(\sigma , D_{\mathcal A}). \end{aligned}$$

(3.11)

Now, let us suppose that $\{T_n\}$ is the same as taken in Theorem 2 such that

$$\begin{aligned} T_n(f; x,y)=(1+f_n(x,y))~L_n(f; x,y). \end{aligned}$$

(3.12)

Then, observe that

$$\begin{aligned} T_n(e_{0}; x,y)= & {} (1+f_n(x,y)),\nonumber \\ T_n(e_{1}; x,y)= & {} (1+f_n(x,y))~\frac{b_{n+1}}{b_n}\frac{x}{1-x-y},\nonumber \\ T_n(e_{2}; x,y)= & {} (1+f_n(x,y))~\frac{b_{n+1}}{b_n}\frac{y}{1-x-y} \end{aligned}$$

(3.13)

and

$$\begin{aligned}&T_n(e_{3}; x,y)\nonumber \\&\quad =(1+f_n) \bigg [\frac{b_{n+1}b_{n+2}}{b^2_n}\frac{x^2+y^2}{(1-x-y)^2} +\frac{b_{n+1}\varphi _n}{b^2_n}\frac{x}{1-x-y}+\frac{b_{n+1}\xi _n}{b^2_n}\frac{y}{1-x-y}\bigg ]. \end{aligned}$$

(3.14)

Taking into account our assumptions (i)–(iv), we have

$$\begin{aligned} {\overline{N}}_\Phi -T_n(e_{0}; x,y) \rightrightarrows e_{0}~(\sigma _0, D_{{\mathcal {A}}}),\\{\overline{N}}_\Phi -T_n(e_{1}; x,y) \rightrightarrows e_{1}~(\sigma _1, D_{{\mathcal {A}}}),\\{\overline{N}}_\Phi -T_n(e_{2}; x,y) \rightrightarrows e_{2}~(\sigma _2, D_{{\mathcal {A}}}). \end{aligned}$$

We will now show that

$$\begin{aligned} {\overline{N}}_\Phi -T_n(e_{3}; x,y) \rightrightarrows e_{3}~(\sigma _3, D_{{\mathcal {A}}}). \end{aligned}$$

(3.15)

Now let

$$\begin{aligned}B=\sup \limits _{(x, y) \in D_{\mathcal A}}\bigg \{\frac{x^2+y^2}{(1-x-y)^2}, \frac{x}{1-x-y}, \frac{y}{1-x-y}\bigg \}.\end{aligned}$$

By (3.11), (3.14) and the assumption (iv), one obtains

$$\begin{aligned} \sup \limits _{(x, y) \in D_A}\bigg |\frac{T_n(e_{3};x,y)-e_{3}}{\sigma _3(x, y)}\bigg | \le \frac{B}{|\sigma _3|}\Bigg \{\bigg |\frac{b_{n+1}b_{n+2}}{b^2_n}-1\bigg |+(M_0+M_1)\frac{b_{n+1}}{b^2_n}\Bigg \}(1+f_n). \end{aligned}$$

Passing to limit as $n \rightarrow \infty$ in the last inequality and using (iii), the inclusion (3.15) holds true. From (3.13) and (3.15), we can say that our sequence $T_n(f; x,y)$ defined by (3.12) satisfy all assumptions of Theorem 2. Therefore

$$\begin{aligned} {\overline{N}}_\Phi -T_n(f; x,y) \rightrightarrows f~(\sigma ,D_{{\mathcal {A}}}). \end{aligned}$$

In view of above example, we say that our proposed method works successfully but classical and statistical version of relatively uniform convergence do not work for this sequence $\{T_n\}$ of positive linear operators on $D_A$.

4 Rate of Relatively Uniform Weighted $\alpha \beta$-Statistical Convergence

In this section, we estimate the rates of relatively uniform weighted $\alpha \beta$-statistical convergence of positive linear operators defined from $C(D_A)$ into itself by the help of the modulus of continuity.

We now present the following definition.

Definition 4

Let a, b,c be real numbers, h be any positive constant and $(\alpha ,\beta )\in \Lambda$. Let $(\theta _n)$ be a positive non-increasing sequence of real numbers and $\sigma (x,y)$ be a scale function defined on a compact subset $E^2\subset {\mathbb {R}}^2$ satisfying $|\sigma (x,y)|>0$. A sequence $(f_k(x,y))$ of real-valued functions defined on $E^2$ is said to be relatively uniform weighted statistically convergent to f on $E^2$ with the rate of $o(\theta _n)$, if for every $\epsilon >0$,

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{1}{\theta _nP^{(\alpha , \beta )}_n}\left| \left\{ k\le P^{(\alpha , \beta )}_n:\sup _{(x,y) \in E^2}~p_k~\bigg |\frac{\Delta ^{a,b,c}_{h,x} f_k(x,y)-f(x,y)}{\sigma (x,y)}\bigg |\ge \epsilon \right\} \right| =0. \end{aligned}$$

In this case, we denote it by $f_k-f=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma )-o(\theta _n)$ on $E^2$. Taking into account that being little “o” of a sequence (function) is a stronger condition than being big “${\mathcal {O}}$” of a sequence (function), all the results presented in this section can be given when little “o” is replaced by big “${\mathcal {O}}$”.

Lemma 2

Let a, b,c be real numbers, h be any positive constant and $(\alpha ,\beta )\in \Lambda$. Let $(f_k)$ and $(g_k)$ be two function sequences belonging to $C(E^2)$. Suppose that $(\eta _{n})$ and $(\zeta _{n})$ are positive non-increasing sequences of real numbers such that

$$\begin{aligned}f_k-f=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma _0)-o(\eta _n)~~\text {and}~~g_k-g=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma _1)-o(\zeta _n)~~\text {on}~~E^2\end{aligned}$$

where $|\sigma _i(x,y)|>0$, $i=0,1$. Let $\gamma _{n}=\max \{\eta _{n}, \zeta _{n}\}$. Then, the following statements hold:

• (1) $(f_{k}-f)\pm (g_{k}-g)=S_{\Delta }^{(\alpha ,\beta )}(p_k, \max \{|\sigma _i(x,y)|:i=0,1\})-o(\gamma _n)~~\text {on}~~E^2$,

• (2) $(f_{k}-f)(g_{k}-g)=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma _0\sigma _1)-o(\eta _{n} \zeta _{n})~~\text {on}~~E^2$,

• (3) $(\lambda (f_{k}-f))=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma _0)-o(\eta _n)~~\text {on}~~E^2$, for any scalar  $\lambda$.

Proof

Assume that

$$\begin{aligned}f_k-f=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma _0)-o(\eta _n)~~\text {and}~~g_k-g=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma _1)-o(\zeta _n)~~\text {on}~~E^2.\end{aligned}$$

Also, for $\epsilon >0$, define

$$\begin{aligned} {\mathcal {D}}:= & {} \left\{ k\le P^{(\alpha , \beta )}_n :\sup _{(x,y) \in E^2}p_k\Bigg |\frac{\left( \Delta ^{a,b,c}_{h,x} f_k+\Delta ^{a,b,c}_{h,x} g_k \right) (x,y)-(f+g)(x,y)}{\sigma (x,y)}\Bigg |\geqq \epsilon \right\} ,\\ {\mathcal {D}}_{0}:= & {} \left\{ k\le P^{(\alpha , \beta )}_n:\sup _{(x,y) \in E^2}~p_k~\bigg |\frac{\Delta ^{a,b,c}_{h,x} f_k(x,y)-f(x,y)}{\sigma _0(x,y)}\bigg |\ge \frac{\epsilon }{2}\right\} ,\\ {\mathcal {D}}_{1}:= & {} \left\{ k\le P^{(\alpha , \beta )}_n:\sup _{(x,y) \in E^2}~p_k~\bigg |\frac{\Delta ^{a,b,c}_{h,x}g_k(x,y)-g(x,y)}{\sigma _1(x,y)}\bigg |\ge \frac{\epsilon }{2}\right\} . \end{aligned}$$

It is seen that ${\mathcal {D}} \subset {\mathcal {D}}_{0} \cup {\mathcal {D}}_{1}$, which yields, for $n \in {\mathbb {N}}$, that

$$\begin{aligned} \frac{|{\mathcal {D}}|}{\gamma _nP^{(\alpha , \beta )}_n}\le \frac{|{\mathcal {D}}_0|}{\eta _nP^{(\alpha , \beta )}_n}+\frac{|{\mathcal {D}}_1|}{\zeta _nP^{(\alpha , \beta )}_n}, \end{aligned}$$

where $|{\mathcal {D}}|$ denotes the cardinality of the set ${\mathcal {D}}$. Now letting $n \rightarrow \infty$ in the last inequality and using hypothesis, we get

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{1}{\gamma _nP^{(\alpha , \beta )}_n}\left| \left\{ k\le P^{(\alpha , \beta )}_n :\sup _{(x,y) \in D_A}p_k\Bigg |\frac{\left( \Delta ^{a,b,c}_{h,x} f_k+\Delta ^{a,b,c}_{h,x} g_k\right) -(f+g)}{\sigma (x,y)}\Bigg |\geqq \epsilon \right\} \right| =0, \end{aligned}$$

where $\gamma _{n}=\max \{\eta _{n}, \zeta _{n}\}$. Since the other assertions can be proved similarly, we omit the details. $\square$

We now recall the modulus of continuity and auxiliary facts to get the rates of weighted statistically relatively uniform convergence given in Definition 4 by means of the modulus of continuity.

Let $H_{\omega }(D_A)$ denote the space of all real-valued functions f on $D_A$ such that

$$\begin{aligned} |f(u,v)-f(x, y)|\leqq \omega (f; \delta )\bigg [\frac{1}{\delta }\sqrt{\varphi _u^2(x)+\varphi _v^2(y)}+1\bigg ], \end{aligned}$$

(4.1)

where $\varphi _u(x)$, $\varphi _v(y)$ are as defined in (3.8), and $\omega (f; \delta )$ is the modulus of continuity defined by

$$\begin{aligned}\omega (f; \delta )=\sup _{(u, v), (x, y) \in D_A} \left\{ |f(u, v)-f(x, y)|:\sqrt{(u-x)^2+(v-y)^2}\leqq \delta \right\} ,~(\delta >0).\end{aligned}$$

We then observe that any function in $H_{\omega }(D_A)$ is continuous and bounded on $D_A$, and a necessary and sufficient condition for $f \in H_{\omega }(D_A)$ is that $\lim _{\delta \rightarrow 0}\omega (f; \delta )=0$.

Theorem 3

Let a, b,c be real numbers, h be any positive constant and $(\alpha ,\beta )\in \Lambda$. Also, let $\{B_{k}\}$ be a sequence of positive linear operators acting from $H_{\omega }(D_A)$ into $C(D_A)$. Assume that the following conditions hold true : 

• (i) $B_{k}(e_{0})-e_{0} =S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma _0)-o(\eta _n)~~\text {on}~~D_A$, where $e_{0}(u,v)=1$,

• (ii) $\omega (f; \lambda _{k}) =S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma _1)-o(\zeta _n)~~\text {on}~~D_A$, where $\lambda _{k}:=\sqrt{|B_{k}(\psi ; x, y)|}$ with

  $$\begin{aligned}\psi (u, v) =\left( \frac{u}{1-u-v}-\frac{x}{1-x-y}\right) ^2+\left( \frac{v}{1-u-v}-\frac{y}{1-x-y}\right) ^2.\end{aligned}$$

Then, we have, for all $f \in H_{\omega }(D_A)$,

$$\begin{aligned} B_{k}(f)-f=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma )-o(\gamma _n)~~\text {on}~~D_A, \end{aligned}$$

where $\gamma _{n}=\max \{\eta _{n}, \zeta _{n}\}$ and $\sigma (x,y)=\max \{|\sigma _0(x,y)|, |\sigma _1(x,y)|, |\sigma _0(x,y)\sigma _1(x,y)|\}$ for $i=0,1$.

Proof

Let $f \in H_{\omega }(D_A)$ and $(x, y) \in D_A$ be fixed. Then, since $e_{0}(u,v)=1$, by (4.1) and using monotonicity of $\{B_{k}\}$, we see (for any $\delta >0$ and $k\in {\mathbb {N}})$ that

$$\begin{aligned}&\big |B_{k}(f(u, v); x, y)-f(x,y)\big |\\&\quad \leqq B_{k}\big (|f(u, v)-f(x, y)|; x, y\big )+|f(x,y)|~|B_{k}(e_{0}; x, y)-e_{0}(x,y)|\\&\quad \leqq \omega (f; \delta )B_{k}\left( \frac{1}{\delta }\sqrt{\varphi _u^2(x)+\varphi _v^2(y)}+e_{0}(u,v);x,y\right) \\&\qquad + |f(x,y)|~|B_{k}(e_{0}; x, y)-e_{0}(x,y)|\\&\quad \leqq \omega (f; \delta ) \Bigg \{\frac{1}{\delta ^2}B_{k}(\psi ; x, y)+B_{k}(e_{0}; x, y)\Bigg \}+|f(x,y)|~|B_{k}(e_{0}; x, y)-e_{0}(x,y)|. \end{aligned}$$

Now multiplying the both sides of the above inequality by $\frac{1}{|\sigma (x,y)|}$ and taking the supremum over $(x,y) \in D_A$, we obtain

$$\begin{aligned}&\sup _{(x,y) \in D_A}\Bigg |\frac{B_{k}(f; x, y)-f(x,y)}{\sigma (x,y)}\Bigg |\\&\quad \leqq \frac{\omega (f; \delta )}{|\sigma (x,y)|} \Bigg \{\sup _{(x,y) \in D_A}\frac{1}{\delta ^2} \big |B_{k}(\psi ; x, y)\big |+\sup _{(x,y) \in D_A}\big |B_{k}(e_{0}; x, y)-e_{0}(x,y)\big |+1\Bigg \}\\&\qquad +N~\sup _{(x,y) \in D_A}\Bigg |\frac{B_{k}(e_{0}; x, y)-e_{0}(x,y)}{\sigma (x,y)}\Bigg | \end{aligned}$$

where $N:=\sup \limits _{(x,y) \in D_A}|f(x,y)|$. Put $\delta =\lambda _{k}=\sqrt{|B_{k}(\psi ; x, y)|}$ and replace $B_{k}(\cdot ;x,y)$ by $\widetilde{B}_{k}(\cdot ;x,y)=|\Delta ^{a,b,c}_{h,x} B_k(\cdot ;x,y)|$, so we get

$$\begin{aligned}&\sup _{(x,y) \in D_A}p_k\Bigg |\frac{{\widetilde{B}}_{k}(f; x, y)-f(x,y)}{\sigma (x,y)}\Bigg |\nonumber \\&\quad \leqq {\widetilde{N}}\left\{ \sup _{(x,y) \in D_A}p_k\bigg |\frac{\omega (f; \lambda _{k})}{\sigma _1(x,y)}\bigg |+\sup _{(x,y) \in D_A}p_k\bigg |\frac{{\widetilde{B}}_{k}(e_{0}; x, y)-e_{0}}{\sigma _0(x,y)}\bigg |\right. \nonumber \\&\qquad \left. +\sup _{(x,y) \in D_A}p_k\bigg |\frac{\omega (f; \lambda _{k})[{\widetilde{B}}_{k}(e_{0}; x, y)-e_{0}]}{\sigma _0(x,y)\sigma _1(x,y)}\bigg |\right\} ,~~{\widetilde{N}}:=\max \{N, 2\}. \end{aligned}$$

(4.2)

For a given $\epsilon >0$, we consider the following sets:

$$\begin{aligned} {\mathcal {J}}:= & {} \left\{ k \le P^{(\alpha , \beta )}_n:\sup _{(x,y) \in D_A}p_k~\Bigg |\frac{{\widetilde{B}}_{k}(f; x, y)-f(x,y)}{\sigma (x,y)}\Bigg |\ge \epsilon \right\} ,\\ {\mathcal {J}}_{0}:= & {} \left\{ k \le P^{(\alpha , \beta )}_n:\sup _{(x,y) \in D_A}p_k~\bigg |\frac{\omega (f; \lambda _{k})[{\widetilde{B}}_{k}(e_{0}; x, y)-e_{0}]}{\sigma _0(x,y)\sigma _1(x,y)}\bigg |\geqq \frac{\epsilon }{3{\widetilde{N}}}\right\} ,\\ {\mathcal {J}}_{1}:= & {} \left\{ k \le P^{(\alpha , \beta )}_n:\sup _{(x,y) \in D_A}p_k~\bigg |\frac{\omega (f; \lambda _{k})}{\sigma _1(x,y)}\bigg |\geqq \frac{\epsilon }{3{\widetilde{N}}}\right\} ,\\ {\mathcal {J}}_{2}:= & {} \left\{ k \le P^{(\alpha , \beta )}_n:\sup _{(x,y) \in D_A}p_k~\bigg |\frac{{\widetilde{B}}_{k}(e_{0}; x, y)-e_{0}}{\sigma _0(x,y)}\bigg |\geqq \frac{\epsilon }{3\widetilde{N}}\right\} . \end{aligned}$$

Then it is follows from (4.2) that ${\mathcal {J}}\subset {\mathcal {J}}_{0} \cup {\mathcal {J}}_{1}\cup {\mathcal {J}}_{2}$. Now, since $\gamma _{n}=\max \{\eta _{n}, \zeta _{n}\}$, we get, for every $n \in {\mathbb {N}}$, that

$$\begin{aligned} \frac{|{\mathcal {J}}|}{\gamma _nP^{(\alpha , \beta )}_n}\le \frac{|{\mathcal {J}}_0|}{\zeta _n\eta _n P^{(\alpha , \beta )}_n}+\frac{|{\mathcal {J}}_1|}{\zeta _nP^{(\alpha , \beta )}_n}+\frac{|{\mathcal {J}}_2|}{\eta _nP^{(\alpha , \beta )}_n}. \end{aligned}$$

By taking Lemma 2 into account, and hence passing to the limit as $n \rightarrow \infty$ in the last inequality, we see that

$$\begin{aligned} B_{k}(f)-f=S_{\Delta }^{(\alpha ,\beta )}(p_k, \sigma )-o(\gamma _n)~~\text {on}~~D_A, \end{aligned}$$

whence the result. $\square$

5 A Voronovskaja-Type Approximation Theorem

For the pointwise convergence of a sequence of linear positive operators, Voronovskaja theorem (see [43]) concerning the asymptotic behavior of Bernstein polynomials has a crucial role. In this section, based on relatively uniform statistical $\Phi$-summability, we prove a Voronovskaja-type approximation theorem with the help of $T_{n}$ family of linear operators as defined in Example 2.

Lemma 3

Let h be a positive constant, $(\alpha ,\beta ) \in \Lambda$ and $a, b, c\in {\mathbb {R}}$. Then

$$\begin{aligned} {\overline{N}}_\Phi -b_nT_n(\eta _u^2(x); x,y) \rightrightarrows \frac{M_0 x}{1-x-y}~(\sigma , D_A) \end{aligned}$$

(5.1)

and

$$\begin{aligned} {\overline{N}}_\Phi -b_nT_n(\eta _v^2(y); x,y) \rightrightarrows \frac{M_1 y}{1-x-y}~(\sigma , D_A) \end{aligned}$$

(5.2)

where

$$\begin{aligned}\eta _u(x)=\frac{u}{1-u-v}-\frac{x}{1-x-y}\quad \textit{and} \quad \eta _v(y)=\frac{v}{1-u-v}-\frac{y}{1-x-y}.\end{aligned}$$

Proof

Since the proof is similar for (5.2), we consider only (5.1). Suppose that a, b, c are real numbers, $h>0$ and $(x, y) \in D_A$. Since $L_{n}(e_{1})=\frac{b_{n+1}}{b_n}e_{1}$, we can write

$$\begin{aligned} T_{n}\big (\eta _u(x); x, y\big )= & {} (1+f_n(x,y))\left[ L_{n}\left( e_{1}(u,v); x, y\right) -e_{1}(x,y)L_{n}(1; x, y)\right] \nonumber \\= & {} \left[ \frac{b_{n+1}}{b_n}-1\right] e_{1}(x,y)(1+f_n(x,y)). \end{aligned}$$

(5.3)

Also, since

$$\begin{aligned}L_{n}(e_3; x, y) =\frac{b_{n+1}b_{n+2}}{b^2_n}e_{3} +\frac{b_{n+1}\varphi _n}{b^2_n}e_{1}, \end{aligned}$$

we find that

$$\begin{aligned} b_nT_n\left( \eta _u^2(x); x,y\right) =(1+f_n) \left[ \left( \frac{b_{n+1}b_{n+2}}{b_n}-2b_{n+1}+b_n\right) e^2_1 +\frac{b_{n+1}\varphi _n}{b_n}e_{1}\right] . \end{aligned}$$

Using the assumption (iv) and multiplying both sides of above equality by $\frac{1}{|\sigma (x,y)|}$, and also taking supremum over $(x, y) \in D_A$, we get

$$\begin{aligned}&\sup \limits _{(x, y) \in D_A}\left| \frac{b_n\bigg \{T_n\left( \eta _u^2; x,y\right) \bigg \}-\left[ \left( \frac{b_{n+1}b_{n+2}}{b_n}-2b_{n+1}+b_n\right) e^2_1 +\frac{b_{n+1}M_0}{b_n}e_{1}\right] }{\sigma (x, y)}\right| \\&\quad \le \sup \limits _{(x, y) \in D_A} \left| \frac{f_n}{\sigma }\right| \left\{ \bigg |\frac{b_{n+1}b_{n+2}}{b_n}-2b_{n+1}+b_n\bigg |e^2_1+\bigg |\frac{b_{n+1}}{b_n}M_0\bigg |e_{1}\right\} . \end{aligned}$$

Replacing $\{b_nT_n(\eta _u^2)\}$ by

$$\begin{aligned}\Phi \big (b_nT_n(\eta _u^2;x,y)\big )=\frac{1}{P_n^{(\alpha , \beta )}}\sum _{k=\alpha (n)}^{\beta (n)}p_k~ |\Delta ^{a,b,c}_{h,x}(b_kT_k(\eta _u^2;x,y))|\end{aligned}$$

and passing to the limit as $n \rightarrow \infty$ in the last inequality we have

$$\begin{aligned} {\overline{N}}_\Phi -b_n\left\{ T_n(\eta _u^2(x); x,y)\right\} \rightrightarrows \frac{M_0~x}{1-x-y}~(\sigma , D_A). \end{aligned}$$

$\square$

Corollary

Let $(x, y) \in D_A$, and let $\eta _u(x)$ and $\eta _v(y)$ be given as in Lemma 3. Then there are two positive constants $R_0(x)$ and $R_0(y)$ depending only on x and y,  respectively,  such that

$$\begin{aligned} {\overline{N}}_\Phi -b^2_nT_n(\eta ^4_u(x); x,y) \rightrightarrows R_0(x)~(\sigma , D_A) \end{aligned}$$

and

$$\begin{aligned} {\overline{N}}_\Phi -b^2_nT_n(\eta ^4_v(y); x,y) \rightrightarrows R_0(y) ~(\sigma , D_A). \end{aligned}$$

In order to estimate the asymptotic behavior of $T_n$, we present a Voronovskaja-type approximation theorem [43]. For simplicity in notation, we use the followings in next theorem:

$$\begin{aligned}u^*=\frac{u}{1-u-v},~~v^*=\frac{v}{1-u-v},~~ x^*=\frac{x}{1-x-y}~\quad \text {and}~\quad y^*=\frac{y}{1-x-y}.\end{aligned}$$

Theorem 4

Let h be a positive constant, $(\alpha ,\beta ) \in \Lambda$, $(x^*,y^*) \in D_A$ and $a, b, c\in {\mathbb {R}}$. Then,  for every $f\in C_B(D_A)$ such that $f_x, f_y, f_{xx}, f_{xy}, f_{yy} \in C_B(D_A),$

$$\begin{aligned}&{\overline{N}}_\Phi -~b_n ~\big \{T_{n}\left( f;x^*,y^*\right) -f\left( x^*,y^*\right) \big \}\rightrightarrows \frac{1}{2}\left( M_0 x^*f_{xx}(x^*,y^*)\right. \\&\quad \left. +\, M_1 y^*f_{yy}(x^*,y^*)\right) (\sigma , D_A) \end{aligned}$$

where $C_B(D_A)$ denotes the space of all continuous and bounded real-valued functions on the compact subset $D_A$ of ${\mathbb {R}}^2$.

Proof

Let $(x^*,y^*) \in D_A$ and $f_x, f_y, f_{xx}, f_{xy}, f_{yy} \in C_B(D_A)$. By the Taylor formula for $f\in C_B(D_A)$, we have

$$\begin{aligned}&f(u^*, v^*)=f(x^*,y^*)+\left( u^*-x^*\right) f_x(x^*,y^*) +\left( v^*-y^*\right) f_y(x^*,y^*)\\&\qquad \qquad \qquad +\frac{1}{2}\left\{ \left( u^*-x^*\right) ^2f_{xx}(x^*,y^*)+2\left( u^*-x^*\right) \left( v^*-y^*\right) f_{xy}(x^*,y^*) \right. \\&\qquad \qquad \qquad \left. +\,\left( v^*-y^*\right) ^2 f_{yy}(x^*,y^*)\right\} +\theta _{(x^*,y^*)}(u^*,v^*)\sqrt{\left( u^*-x^*\right) ^4+\left( v^*-y^*\right) ^4} \end{aligned}$$

where the function $\theta _{(x^*,y^*)}$ is the remainder,

$$\begin{aligned}\theta _{(x^*,y^*)}(\cdot ,\cdot ) \in C_B(D_A)~~\text {and}~\lim \limits _{(u^*,v^*)\rightarrow (x^*,y^*)}\theta _{(x^*,y^*)}(u^*,v^*)=0.\end{aligned}$$

We thus observe that the operator $T_{n}$ is linear and that

$$\begin{aligned}&T_{n}\big (f(u^*, v^*); x^*,y^*\big )\nonumber \\&\quad =T_{n}\big (f(x^*,y^*);x, y\big )+f_x(x^*,y^*)T_{n}\big (u^*-x^*; x^*,y^*\big )\nonumber \\&\qquad +f_y(x^*,y^*)T_{n}\big (v^*-y^*; x^*,y^*\big )+\frac{1}{2}\bigg \{f_{xx}(x^*,y^*)T_{n}\big ((u^*-x^*)^2; x^*,y^*\big )\nonumber \\&\qquad +f_{yy}(x^*,y^*)T_{n}\big ((v^*-y^*)^2; x^*,y^*\big )\nonumber \\&\qquad +2f_{xy}(x^*,y^*)T_{n}\big (\left( u^*-x^*\right) \left( v^*-y^*\right) ; x^*,y^*\big )\bigg \} \nonumber \\&\qquad +T_{n}\bigg (\theta _{(x^*,y^*)}(u^*,v^*)\sqrt{\left( u^*-x^*\right) ^4+\left( v^*-y^*\right) ^4}; x^*,y^*\bigg ). \end{aligned}$$

(5.4)

Now, we recall that, if $g\in C_B(D_A)$ and if $g(s, t)=g_1(s)g_2(t)$ for all $(s, t) \in D_A$, then

$$\begin{aligned} T_{n}(g(s, t); x, y)=(1+f_{n}(x,y))~L_{n}(g_1(s); x, y)~L_{n}(g_2(t); x, y). \end{aligned}$$

(5.5)

Upon multiplying both sides by $b_n$, $n \in {\mathbb {N}}$, in (5.4), and using (5.3) and (5.5), we get

$$\begin{aligned}&b_n~\big \{T_{n}\left( f\left( u^*,v^*\right) ;x^*,y^*\right) -f\left( x^*,y^*\right) \big \}\\&\quad =b_n f_{n}(x^*,y^*) f(x^*,y^*)+(1+f_n(x^*,y^*))(b_{n+1}-b_n)\big [x^*f_x(x^*,y^*) +y^*f_y(x^*,y^*)\big ]\\&\qquad +\frac{1+f_n(x^*,y^*)}{2}\Bigg \{\bigg [\frac{b_{n+1}b_{n+2}}{b_n}-2b_{n+1}+b_n\bigg ][(x^*)^2f_{xx}(x^*,y^*)+(y^*)^2f_{yy}(x^*,y^*)]\\&\qquad +\frac{b_{n+1}}{b_n}\bigg (x^*f_{xx}(x^*,y^*)\varphi _n+y^*f_{yy}(x^*,y^*)\xi _n\bigg )+2~x^*y^*f_{xy}(x^*,y^*)\frac{(b_{n+1}-b_n)^2}{b_n}\Bigg \}\\&\qquad +b_nT_{n}\bigg (\theta _{(x^*,y^*)}(u^*,v^*)\sqrt{\left( u^*-x^*\right) ^4+\left( v^*-y^*\right) ^4}; x^*,y^*\bigg ). \end{aligned}$$

Taking supremum over $(x^*,y^*) \in D_A$ in (5.4), one obtains

$$\begin{aligned}&\sup \limits _{(x^*, y^*) \in D_A} \bigg |\frac{b_n~\{T_{n} (f\left( u^*,v^*\right) ;x^*,y^*)-f(x^*,y^*)\}}{\sigma (x^*,y^*)}\bigg |\nonumber \\&\quad \le \sup \limits _{(x^*, y^*) \in D_A}\Bigg \{|b_n|~\bigg |\frac{f_{n}(x^*,y^*)f(x^*,y^*)}{\sigma (x^*,y^*)}\bigg |\nonumber \\&\qquad +|1+f_n|~|b_{n+1}-b_n|~\bigg |\frac{x^*f_x(x^*,y^*) +y^*f_y(x^*,y^*)}{\sigma (x^*,y^*)}\bigg |\nonumber \\&\qquad +\bigg |\frac{1+f_n(x^*,y^*)}{2}\bigg |~\Bigg [\bigg |\frac{b_{n+1}b_{n+2}}{b_n}-2b_{n+1}+b_n\bigg |~\bigg |\frac{(x^*)^2f_{xx}(x^*,y^*)+(y^*)^2f_{yy}(x^*,y^*)}{\sigma (x^*,y^*)}\bigg |\nonumber \\&\qquad +\bigg |\frac{b_{n+1}}{b_n}\bigg |~\bigg |\frac{x^*f_{xx}(x^*,y^*)M_0+y^*f_{yy}(x^*,y^*)M_1}{\sigma (x^*,y^*)}\bigg |\nonumber \\&\qquad +2\bigg |\frac{(b_{n+1}-b_n)^2}{b_n}\bigg |~\bigg |\frac{x^*y^*f_{xy}(x^*,y^*)}{\sigma (x^*,y^*)}\bigg |\Bigg ]\Bigg \}\nonumber \\&\qquad +\sup \limits _{(x^*, y^*) \in D_A}\Bigg |\frac{b_nT_{n}\bigg (\theta _{(x^*,y^*)}(u^*,v^*)\sqrt{\left( u^*-x^*\right) ^4+\left( v^*-y^*\right) ^4}; x^*,y^*\bigg )}{\sigma (x^*,y^*)}\Bigg |. \end{aligned}$$

(5.6)

We will now show that

$$\begin{aligned} {\overline{N}}_\Phi -~b_nT_{n}\bigg (\theta _{(x^*,y^*)}(u^*,v^*)\sqrt{\left( u^*-x^*\right) ^4+\left( v^*-y^*\right) ^4}; x^*,y^*\bigg )\rightrightarrows 0~(\sigma , D_A).\nonumber \\ \end{aligned}$$

(5.7)

Applying the Cauchy–Schwarz inequality and using (5.5), we obtain

$$\begin{aligned}&b_nT_{n}\big (\theta _{(x^*,y^*)}(u^*,v^*)\sqrt{\left( u^*-x^*\right) ^4+\left( v^*-y^*\right) ^4}; x^*,y^*\big ) \\&\quad \leqq \left( T_{n}(\theta ^2_{(x^*,y^*)}(u^*,v^*); x^*,y^*)\right) ^{1/2} b_n\left( T_{n}((u^*-x^*)^4; x, y)+T_{n}((v^*-y^*)^4; x^*,y^*)\right) ^{1/2}. \end{aligned}$$

Let us consider $\theta ^2_{(x^*,y^*)}(u^*,v^*)=\gamma _{(x^*,y^*)}(u^*,v^*).$ In this case, we see that

$$\begin{aligned}\gamma _{(x^*,y^*)}(u^*,v^*)\in C_B(D_A)\quad \text {and} \quad \gamma _{(x^*,y^*)}(x^*,y^*)=0.\end{aligned}$$

From Theorem 2, we observe that

$$\begin{aligned} {\overline{N}}_\Phi -~b_nT_{n}\big (\theta ^2_{(x^*,y^*)}(u^*,v^*); x^*,y^*\big ) \rightrightarrows 0~(\sigma , D_A). \end{aligned}$$

(5.8)

Using the above Corollary, the inclusion (5.7) holds true. Now we replace $\big \{b_n(T_{n}f-f)\big \}$ by

$$\begin{aligned} \Phi (b_n(T_nf-f))=\frac{1}{P_n^{(\alpha , \beta )}}\sum _{k=\alpha (n)}^{\beta (n)}p_k~ \big |\Delta ^{a,b,c}_{h,x}(b_k(T_k(f)-f))\big |.\end{aligned}$$

Letting $n \rightarrow \infty$ in (5.6) and considering the assumption (iv), we have

$$\begin{aligned}&\lim _{n\rightarrow \infty }\sup \limits _{(x^*, y^*) \in D_A} \bigg |\frac{\Phi \big (b_n[T_n(f;x^*,y^*)-f(x^*,y^*)]\big )}{\sigma (x^*,y^*)}\\&\qquad -\frac{1}{2}\frac{x^*f_{xx}(x^*,y^*)M_0+y^*f_{yy}(x^*,y^*)M_1}{\sigma (x^*,y^*)}\bigg |\\&\quad \le \lim _{n\rightarrow \infty } \bigg \{|b_n|~|f_n(x^*,y^*)|~N_0+ \frac{|f_n(x^*,y^*)|}{2}\big (M_0~N_1+M_1~N_2\big )\bigg \} \end{aligned}$$

where

$$\begin{aligned}&N_0=\sup \limits _{(x^*, y^*) \in D_A}\bigg |\frac{f(x^*,y^*)}{\sigma (x^*, y^*)}\bigg |,\\&N_1=\sup \limits _{(x^*, y^*) \in D_A}\bigg |\frac{f_{xx}(x^*,y^*)}{\sigma (x^*, y^*)}\bigg |~~\text {and}~~ N_2=\sup \limits _{(x^*, y^*) \in D_A}\bigg |\frac{f_{yy}(x^*,y^*)}{\sigma (x^*, y^*)}\bigg |.\end{aligned}$$

Since ${\overline{N}}_\Phi -f_n\rightrightarrows 0~(\sigma , D_A)$, then

$$\begin{aligned} {\overline{N}}_\Phi -~\bigg \{|b_n|~|f_n(x^*,y^*)|~N_0+ \frac{|f_n(x^*,y^*)|}{2}\big (M_0~N_1+M_1~N_2\big )\bigg \} \rightrightarrows 0~(\sigma , D_A).\nonumber \\ \end{aligned}$$

(5.9)

Using (5.8), (5.9) and Lemma 3, we obtain

$$\begin{aligned} {\overline{N}}_\Phi -~\big \{b_n ~(T_{n}f -f)\big \}\rightrightarrows \frac{1}{2}\left( f_{xx}(x^*,y^*)\frac{M_0 x}{1-x-y}+ f_{yy}(x^*,y^*)\frac{M_1 y}{1-x-y}\right) ~(\sigma , D_A), \end{aligned}$$

the proof is completed. $\square$

6 Computational and Geometrical Interpretations

In this section, using the positive linear operator $L_n(f;x,y)$ given in (3.10), we provide the computational and geometrical interpretations of Theorem 2 by under different choices for the parameters. More powerful equipments with higher speed can easily compute the more complicated infinite series in a similar manner.

Here, in our computations, we take

• $\Omega _n(u,v;x,y)=(1-x-y)^{-n-1}$ and $P^n_{k,l}(u,v)=\frac{(n+k+l)!}{n!~k!~l!}$;

• $a_{k,l,n}=k$, $c_{k,l,n}=l$ and $b_n=n$;

• $a=5/2, b=c$ and $h=\frac{\sqrt{3}}{4}$;

• $\alpha (n)=1$, $\beta (n)=n$ and $p_n=1$ for all $n \in {\mathbb {N}}$;

• $f_n(x,y)$ is given as in Example 2, and $\sigma (x,y)=1$ for all $(x,y) \in D_A$.

Using the above choices, we may define the operator $\Phi (L_m(f;x,y))$ by

$$\begin{aligned} \Phi (L_m(f;x,y)) =\frac{1}{m}\sum _{n=1}^{m}~ |\Delta ^{5/2,b,b}_{\sqrt{3}/4,x}(L_n(f(u,v);x,y))|, \end{aligned}$$

(6.1)

where

$$\begin{aligned} L_{n}(f; x,y)=\frac{1}{(1-x-y)^{n+1}}\sum _{k,l=0}^{\infty ,\infty } f\left( \frac{k}{k+l+n}, \frac{l}{k+l+n}\right) \frac{(n+k+l)!}{n!~k!~l!}x^ky^l.\nonumber \\ \end{aligned}$$

(6.2)

By means of (3.1), for $a=5/2,b=c$ and $h=\frac{\sqrt{3}}{4}$, one gets

$$\begin{aligned} \Delta ^{5/2,b,b}_{\sqrt{3}/4, x}(L_n(f(u,v);x,y))&=\sum _{i=0}^{2}\frac{(-5/2)_i}{i!(\sqrt{3}/4)^{5/2}}L_n\Bigg (f\bigg (u-\frac{\sqrt{3}}{4}i,v\bigg );x,y\Bigg )\\&=\frac{1}{(\sqrt{3}/4)^{5/2}}\left\{ L_n(f;x,y)-\frac{5}{2}L_n\Bigg (f\bigg (u-\frac{\sqrt{3}}{4},v\bigg );x,y\Bigg )\right. \\&\quad \left. +\,\frac{15}{8}L_n\Bigg (f\bigg (u-\frac{\sqrt{3}}{2},v\bigg );x,y\Bigg )\right\} . \end{aligned}$$

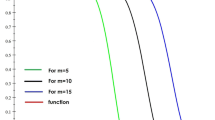
The convergence of $\Phi (L_m(e_0;x,y))$ to the function $e_0(x, y)=1$, is illustrated in Fig. 1 for each values of k and l runs from $k,l = 0$ to 20 for $m = 5$, $m = 10$, $m = 15$ and $m=20$.

Fig. 1

The convergence of $\Phi (L_m(e_0;x,y))$ to $e_0(x,y)=1$

Also, from Fig. 2, it can be observed that, as the value of m increases, the sequence $\Phi (L_m(e_{1};x,y))$ converges to the function $e_{1}(x,y)=\frac{x}{1-x-y}.$

Fig. 2

The convergence of $\Phi (L_m(e_{1};x,y))$ to $e_{1}(x,y)=\frac{x}{1-x-y}$

Similarly, for the test function given by

$$\begin{aligned} e_{3}(u,v)=\left( \frac{u}{1-u-v}\right) ^2+\left( \frac{v}{1-u-v}\right) ^2 \end{aligned}$$

(6.3)

and different values of m, it is also observe that, $\Phi (L_m(e_{3};x,y))$ converges to the function $e_{3}(x,y)$.

Fig. 3

The convergence of $\Phi (L_m(e_{3};x,y))$ to $e_{3}(x,y)=\frac{x^2+y^2}{(1-x-y)^2}$

Figures 1, 2 and 3 clearly show that the conditions (3.5) of Theorem 2 are satisfied for $i=0,1,2,3$.

We observe from Fig. 4 that, as the value of m increases, the operators given by (6.1) converge toward the function. Furthermore, Fig. 4 shows that the condition (3.4) holds true for the function

$$\begin{aligned} f(x,y)=\cos (3\pi xy). \end{aligned}$$

Fig. 4

The convergence of $\Phi (L_m(f;x,y))$ to $f(x,y)=\cos (3\pi xy)$