Reliability Estimation of Modified Weibull Distribution with Type-II Hybrid Censored Data

Abstract

The study deals with the analysis of Type-II hybrid censored data from the modified Weibull distribution. We provide maximum-likelihood estimates of the parameters, reliability, and hazard rate functions along with their standard errors. The confidence intervals along with their widths have also been obtained. Assuming gamma and Jeffrey’s invariant priors for the unknown parameters, Bayes estimates along with its posterior errors and highest posterior density credible intervals are obtained. The Markov Chain Monte Carlo technique has been used to simulate draws from the complicated posterior densities of the parameters. A simulation study is conducted to compare the performances of classical and Bayesian methods of estimation. Finally, a real data analysis is performed for illustrative purpose.

1 Introduction

In reliability and life testing experiments, the equipments are put on test and their failure times are recorded. These failure time observations are then used to draw inferences on various system reliability characteristics. However, due to long life times of today’s products, obtaining times-to-failure data is very time consuming which increases the cost of experimentation as well. To overcome this difficulty, censoring is used in life testing experiments to save the time and cost. Failure censoring schemes are broadly classified as Type-I (time censoring) and Type-II (failure censoring). Suppose, n items are put on test. In Type-I censoring, we fix the time T to terminate the experiment in advanced and observe the life times of those items which fail up to time T, whereas in Type-II censoring scheme, time to terminate the experiment is a random variable and required number of failed items to stop the test is fixed, say m ($m \le n$), so that at the time of the mth failure, the test terminates leaving n − m partially observed failure times. Type-I and Type-II censoring schemes have been extensively studied by numerous authors, including Mann et al. (1974), Lawless (1982), Balakrishnan and Cohen (1991), and Harter et al. (1996).

Since major constraints in life testing experiments are time and cost, therefore, we need a censoring scheme which can make a trade-off between the number of units used and the time required to stop the experimentation without sacrificing the desired efficiency of the statistical inference. Hybrid censoring is one such censoring scheme introduced by Epstein (1954, 1960). The hybrid censoring is also categorized as Type-I and Type-II. If the test is terminated at the random time T ^* = min{X _R:n , T}, where R and T are prefixed numbers, and $X_{R:n}$ indicates the time of Rth failure in a sample of size n. Then, it is called Type-I hybrid censoring scheme. Many studies, including Kundu (2007), Kundu and Pradhan (2009), Dube et al. (2011), Ganguly et al. (2012), Rastogi and Tripathi (2013), and Gupta and Singh (2013), dealt with statistical inference for different life time distributions using Type-I hybrid censoring scheme. On the other hand, if the test is stopped at time T ^** = max{X _R:n , T}, it is known as Type-II hybrid censoring scheme (Childs et al. 2003). With Type-II hybrid censoring scheme, one has the advantage to record the complete life times of at least R units before the experiment is terminated. For more details regarding statistical inferences under Type-II hybrid censoring scheme, one may refer Banerjee and Kundu (2008), Al-Zahrani and Gindwan (2014), and Singh et al. (2014). The detail review of various hybrid censoring schemes is given in Balakrishnan and Kundu (2013). Though many distributions have been considered for drawing inferences with Type-I and Type-II hybrid censored data, to the best of our knowledge, none of the study has reported the inferential statistics on the modified Weibull (MW) distribution under Type-II hybrid censoring scheme. Initially, this distribution was proposed by Lai et al. (2003), and has the following probability density function (PDF):

$$f(x) = \beta x^{\nu - 1} (\nu + \lambda x)\exp (\lambda x - \beta x^{\nu } e^{\lambda x} );\quad x > 0.$$

(1)

The distribution function (DF) of MW distribution is written as:

$$F(x) = 1 - \exp ( - \beta x^{\nu } e^{\lambda x} ).$$

The corresponding reliability and hazard rate functions are as follows:

$$R(x) = \exp ( - \beta x^{\nu } e^{\lambda x} ),$$

(2)

$$h(x) = \beta x^{\nu - 1} (\nu + \lambda x)e^{\lambda x} .$$

(3)

The shape of hazard rate function h(x) of MW distribution depends on the parameter $\nu$. For $\nu \ge 1$, h(x) is increasing in x, whereas for $0 < \nu < 1$, it has bathtub shape. Due to the flexible shape of its hazard rate function, MW distribution has become important life time model for reliability engineers.

In lieu of above considerations, we explore the inferential properties of the modified Weibull distribution with Type-II hybrid censoring data. We provide maximum-likelihood estimators of the parameters, reliability, and hazard functions of MW distribution with Type-II hybrid censored data. Fisher information matrix has been given to construct confidence intervals of the parameters as well as reliability and hazard functions. Bayes estimates and highest posterior density (HPD) intervals of the parameters have been obtained using gamma and Jeffrey’s priors. Markov Chain Monte Carlo (MCMC) technique has been used to generate draws from complex posterior densities of the parameters. The coverage probabilities of confidence and HPD intervals have also been provided. To illustrate the application of MW distribution, a real data analysis is presented. A simulation study is also carried out to access the performances of ML and Bayes methods of estimation. At the end, some concluding remarks are given.

2 Estimation and Confidence Intervals under Type-II Hybrid Censoring Scheme

2.1 Maximum-Likelihood Estimators

Let n units are put on test. Then, under the Type-II hybrid censoring scheme, we have one of the following three types of observations:

Case I: $\left\{ {x_{1:n} < x_{2:n} < \cdots < x_{R:n}} \right\}\quad if\;x_{R:n}>T.$

Case II: $\left\{ {x_{1:\,n} < x_{2:\,n} < \cdots < x_{R:\,n} < x_{R + 1:\,n} < \cdots < x_{k:\,n} < T < x_{k + 1:\,n} } \right\}\;$ if $R \le k < n$, and $x_{k:n} < T < x_{k + 1:n}$

Case III: $\left\{ {x_{1:\,n} < x_{2:\,n} < \cdots < x_{{n:\text{ }n}} < T} \right\}.$

Graphically, it can be presented as shown in Fig. 1:

Fig. 1

Graphical presentation of Type-II hybrid censoring scheme

The likelihood functions for the above three different cases are as follows:

Case I:

$$L_{1} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ) = \frac{n!}{(n - R)!}\prod\limits_{i = 1}^{R} {\beta x_{i}^{\nu - 1} } \left( {\nu + \lambda x_{i} } \right)e^{{\lambda \sum\limits_{i = 1}^{R} {x_{i} } - \beta \sum\limits_{i = 1}^{R} {x_{i}^{\nu } \,e^{{\lambda x_{i} }} } }} \left[ {e^{{ - \beta \,X_{R}^{\nu } e^{{\lambda X_{R} }} }} } \right]^{n - R} .$$

(4)

Case II:

$$L_{2} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ) = \frac{n!}{{\left( {n - K} \right)!}}\prod\limits_{i = 1}^{K} {\beta x_{i}^{\nu - 1} } \left( {\nu + \lambda x_{i} } \right)e^{{\lambda \sum\limits_{i = 1}^{K} {x_{i} } - \beta \sum\limits_{i = 1}^{K} {x_{i}^{\nu } \,e^{{\lambda x_{i} }} } }} \left[ {e^{{ - \beta \,T^{\nu } e^{\lambda T} }} } \right]^{n - K} .$$

(5)

Case III:

$$L_{3} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ) = \prod\limits_{i = 1}^{n} {\beta x_{i}^{\nu - 1} } \left( {\nu + \lambda x_{i} } \right)e^{{\lambda \sum\limits_{i = 1}^{n} {x_{i} } - \beta \sum\limits_{i = 1}^{n} {x_{i}^{\nu } \,e^{{\lambda x_{i} }} } }} .$$

(6)

On combining three likelihood functions, one gets

$$L = L(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ) = \frac{n!}{{\left( {n - D} \right)!}}\prod\limits_{i = 1}^{D} {\beta x_{i}^{\nu - 1} } \left( {\nu + \lambda x_{i} } \right)e^{{\lambda \sum\limits_{i = 1}^{D} {x_{i} } - \beta \sum\limits_{i = 1}^{D} {x_{i}^{\nu } \,e^{{\lambda x_{i} }} } }} \left[ {e^{{ - \beta \,U^{\nu } e^{\lambda U} }} } \right]^{n - D} .$$

(7)

Here, D denotes the number of failure, that is

$$D = \left\{ \begin{aligned} R\quad & {\text{for}}\,{\text{case}}\,{\text{I}} \hfill \\ k\quad &{\text{for}}\,{\text{case}}\,{\text{II}} \hfill \\ n\quad &{\text{for}}\,{\text{case}}\,{\text{III}} \hfill \\ \end{aligned} \right.,$$

and

$$U = \left\{ \begin{aligned} X_{R} & ;\;D = R \\ T & ;\;D > R \\ \end{aligned} \right..$$

The log-likelihood function is

$$\begin{aligned} \log L &= \log C + D\log \beta + (\nu - 1)\sum\limits_{i = 1}^{D} {\log x_{i} } \hfill \\ \quad \,\,&\quad+ \sum\limits_{i = 1}^{D} {\log (\nu + \lambda x_{i} )} + \lambda \sum\limits_{i = 1}^{D} {x_{i} } - \beta \sum\limits_{i = 1}^{D} {x_{i}^{\nu } e^{{\lambda x_{i} }} } \hfill \\ &\quad- \beta \left( {n - D} \right)U^{\nu } e^{\lambda U} . \hfill \\ \end{aligned}$$

(8)

The first derivatives of (8) with respect to β, ν, and λ are as follows:

$$\frac{\partial }{\partial \beta }\log L = \frac{D}{\beta } - \sum\limits_{i = 1}^{D} {x_{i}^{\nu } e^{{\lambda x_{i} }} - (n - D)U^{\nu } e^{\lambda U} } = 0,$$

(9)

$$\frac{\partial }{\partial \nu }\log L = \sum\limits_{i = 1}^{D} {\log x_{i} } + \sum\limits_{i = 1}^{D} {\frac{1}{{(\nu + \lambda x_{i} )}} - \beta \sum\limits_{i = 1}^{D} {x_{i}^{\nu } \log x_{i} } } e^{{\lambda x_{i} }} - \beta (n - D)U^{\nu } \log U\,e^{\lambda U} = 0,$$

(10)

$$\frac{\partial }{\partial \lambda }\log L = \sum\limits_{i = 1}^{D} {\frac{{x_{i} }}{{(\nu + \lambda x_{i} )}}} + \sum\limits_{i = 1}^{D} {x_{i} } - \beta \left. {\left[ {\sum\limits_{i = 1}^{D} {x_{i}^{\nu + 1} } e^{{\lambda x_{i} }} } \right. + \left( {n - D} \right)U^{\nu + 1} e^{\lambda U} } \right] = 0.$$

(11)

Therefore, for fixed ν and λ, the MLE of β say $\hat{\beta }$ can be obtained as:

$$\hat{\beta } = \frac{D}{{\sum\limits_{i = 1}^{D} {x_{i}^{\nu } \,e^{{\lambda x_{i} }} } + (n - D)U^{\nu } e^{\lambda U} }}.$$

(12)

The MLE of ν and λ can be obtained by solving the following non-linear equations:

$$\sum\limits_{i = 1}^{D} {\log x_{i} } + \sum\limits_{i = 1}^{D} {\frac{1}{{\left( {\nu + \lambda x_{i} } \right)}} - \hat{\beta }\sum\limits_{i = 1}^{D} {x_{i}^{\nu } \log x_{i} } } e^{{\lambda x_{i} }} - \hat{\beta }\left( {n - D} \right)U^{\nu } \log U\,e^{\lambda U} = 0,$$

(13)

and

$$\sum\limits_{i = 1}^{D} {\frac{{x_{i} }}{{(\hat{\nu } + \lambda x_{i} )}}} + \sum\limits_{i = 1}^{D} {x_{i} } - \hat{\beta }\left[ {\sum\limits_{i = 1}^{D} {x_{i}^{{\hat{\nu } + 1}} e^{{\lambda x_{i} }} + (n - D)U^{{\hat{\nu } + 1}} e^{\lambda U} } } \right] = 0.$$

(14)

The MLE of β say $\hat{\beta }$ can be obtained by Eq. (12), but Eqs. (13) and (14) are very complicated, so they cannot be expressed explicitly. Thus, some suitable iterative method is required to get $(\hat{\nu },\,\hat{\lambda })$. Now, using the general theory of MLEs, the asymptotic distribution of $\left( {\hat{\beta } - \beta \,\,\,\hat{\nu } - \nu \,\,\,\hat{\lambda } - \lambda } \right)^{\prime }$ is $N_{3} (0,\,\varSigma^{ - 1} )$. Where $\Delta$ is the Fisher’s information matrix whose elements are as follows:

$$\begin{aligned} \Delta_{11} = E\left[ { - \frac{{\partial^{2} \log L}}{{\partial \beta^{2} }}} \right],\;\Delta_{12} = E\left[ { - \frac{{\partial^{2} \log L}}{\partial \beta \partial \nu }} \right] = \Delta_{21} ,\;\Delta_{13} = E\left[ { - \frac{{\partial^{2} \log L}}{\partial \beta \partial \lambda }} \right] = \Delta_{31} ,\;\Delta_{22} = E\left[ { - \frac{{\partial^{2} \log L}}{{\partial \nu^{2} }}} \right],\; \hfill \\ \Delta_{23} = E\left[ { - \frac{{\partial^{2} \log L}}{\partial \nu \partial \lambda }} \right] = \Delta_{32} ,\;{\text{and}}\;\Delta_{33} = E\left[ { - \frac{{\partial^{2} \log L}}{{\partial \lambda^{2} }}} \right]. \hfill \\ \end{aligned}$$

The second derivative with respect to β, ν, and λ are as:

$$\frac{{\partial^{2} }}{{\partial \beta^{2} }}\log L = \frac{ - D}{{\beta^{2} }},$$

(15)

$$\frac{{\partial^{2} }}{{\partial \nu^{2} }}\log L = \sum\limits_{i = 1}^{D} {\frac{ - 1}{{(\nu + \lambda x_{i} )^{2} }}} - \beta \left[ {\sum\limits_{i = 1}^{D} {x_{i}^{\nu } (\log x_{i} )^{2} e^{{\lambda x_{i} }} + (n - D)U^{\nu } (\log U)^{2} e^{\lambda U} } } \right],$$

(16)

$$\frac{{\partial^{2} }}{{\partial \lambda^{2} }}\log L = \sum\limits_{i = 1}^{D} {\frac{{ - x_{i}^{2} }}{{(\nu + \lambda x_{i} )^{2} }}} - \beta \left( {\sum\limits_{i = 1}^{D} {x_{i}^{\nu + 2} e^{{\lambda x_{i} }} + (n - D)U^{\nu + 2} } e^{\lambda U} } \right),$$

(17)

$$\frac{\partial^{2} }{\partial \nu \partial \beta }\log L = \, - \left[ {\sum\limits_{i = 1}^{D} {x_{i}^{\nu } \,\log x_{i} \,e^{{\lambda x_{i} }} \, + \,(n - D)\,U^{\nu } \log U\,e^{\lambda U} } } \right],$$

(18)

$$\frac{\partial^{2} }{\partial \lambda \partial \beta }\log L = \, - \left[ {\sum\limits_{i = 1}^{D} {x_{i}^{\nu + 1} e^{{\lambda x_{i} }} + (n - D)\,U^{\nu + 1} e^{\lambda U} } } \right],$$

(19)

$$\frac{\partial^{2} }{\partial \lambda \partial \nu }\log L = \, - \left[ {\sum\limits_{i = 1}^{D} {\frac{{x_{i} }}{{(\nu + \lambda x_{i} )^{2} }} + \beta \left\{ {\sum\limits_{i = 1}^{D} {x_{i}^{\nu + 1} \,\,\log x_{i} \,e^{{\lambda x_{i} }} + (n - D)U^{\nu + 1} \log Ue^{\lambda U} } } \right\}} } \right].$$

(20)

Using the invariance property of maximum-likelihood estimates, we get the MLEs of the reliability and hazard rate functions as follows:

$$\hat{R}(x) = \exp ( - \hat{\beta }x^{{\hat{\nu }}} e^{{\hat{\lambda }x}} ),$$

$$\hat{h}(x) = \hat{\beta }x^{{\hat{\nu } - 1}} (\hat{\nu } + \hat{\lambda }x)e^{{\hat{\lambda }x}} .$$

The asymptotic sampling distributions of $\left[ {\hat{R}(x) - R(x)} \right]$ and $\left[ {\hat{h}(x) - h(x)} \right]$ are $N(0,R^{\prime}\sum^{ - 1} R)$ and $N(0,h^{\prime}\sum^{ - 1} h)$, where $R^{\prime} = \left( {\frac{\partial R(x)}{\partial \beta },\,\,\frac{\partial R(x)}{\partial \nu },\,\,\frac{\partial R(x)}{\partial \lambda }} \right)$ and $h^{\prime} = \left( {\frac{\partial h(x)}{\partial \beta },\,\,\frac{\partial h(x)}{\partial \nu },\,\,\frac{\partial h(x)}{\partial \lambda }} \right)$.

2.2 Bayesian Estimation

In Bayesian inference, one of the tedious tasks is how to construct prior models for the unknown parameters as there is no unique approach of choosing a priori, and that the choice of a wrong priori may lead to the inappropriate inference. The prior distribution is the key to Bayesian inference and its determination is, therefore, the most important step in drawing the inference (Robert 2007). In practice, informative and non-informative priors are used to represent uncertainties about the model parameters. Berger (1985) pointed out that when there is no information or very difficult to gather regarding the prior variations in the parameters, it is better to use non-informative prior distribution. However, non-informative priors generally lack invariance property under one-to-one transformation, thereby leading to incoherent analysis. On the other hand, informative priors are based on the investigator’s experience about the random behavior of the process under consideration. In lieu of this, we consider the Bayesian method of estimation with both informative and non-informative priors. First, we assume that the parameters β, ν, and λ have ${\text{Gamma}}(a_{1} ,b_{1} )$, ${\text{Gamma}}(a_{2} ,b_{2} )$, and ${\text{Gamma}}(a_{3} ,b_{3} )$ priors, respectively, with PDFs:

$$g_{1} (\beta ) \propto \beta^{{a_{1} - 1}} e^{{ - b_{1} \beta }} ,$$

$$g_{2} (\nu ) \propto \nu^{{a_{2} - 1}} e^{{ - b_{2} \nu }} ,$$

$$g_{3} (\lambda ) \propto \lambda^{{a_{3} - 1}} e^{{ - b_{3} \lambda }} .$$

Based on the above priors, the joint distribution of data and parameters β, ν, and λ is given by,

$$h(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ,\beta ,\nu ,\lambda ) = L(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} \left| {\beta ,\nu ,\lambda } \right.) \cdot g_{1} (\beta ) \cdot g_{2} (\nu ) \cdot g_{3} (\lambda ),$$

$$\begin{aligned} \propto \beta^{{D + a_{1} - 1}} \prod\limits_{i = 1}^{D} {x_{i}^{\nu - 1} \prod\limits_{i = 1}^{D} {(\nu + \lambda x_{i} )e^{{\lambda \sum\limits_{i = 1}^{D} {x_{i} } - \beta \sum\limits_{i = 1}^{D} {x_{i}^{\nu } e^{{\lambda x_{i} }} } }} \cdot e^{{ - \beta (n - D)U^{\nu } e^{\lambda U} }} \nu^{{a_{2} - 1}} \lambda^{{a_{3} - 1}} } } \hfill \quad e^{{ - b_{1} \beta - b_{2} \nu - b_{3} \lambda }} . \hfill \\ \end{aligned}$$

(21)

For drawing Bayesian inference, we need joint posterior distribution of the parameters β, ν, and λ which are very difficult to compute analytically due to multidimensional parameter space. Therefore, Gibbs sampler proposed by Geman and Geman (1984) is used for this purpose. One important advantage with Gibbs sampler is that we only require full conditional posterior distributions of each of the parameters. The full conditional posterior of parameters β, ν, and λ are given by the following:

$$\begin{aligned} W(\beta \left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ,\nu ,\lambda } \right.) & \propto \beta^{{D + a_{1} - 1}} \,e^{{ - \beta \sum\limits_{i = 1}^{D} {x_{i}^{\nu } e^{{\lambda x_{i} }} - \beta (n - D)U^{\nu } e^{\lambda U} - b_{1} \beta } }} \\ & & \propto {\text{Gamma}}\left( {D + a_{1} ,\sum\limits_{i = 1}^{D} {x_{i}^{\nu } e^{{\lambda x_{i} }} + (n - D)U^{\nu } e^{\lambda U} + b_{1} } } \right), \\ \end{aligned}$$

(22)

$$\begin{aligned} W(\nu \left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ,\beta ,\lambda } \right.) \, \propto \, & \nu^{{a_{2} - 1}} \prod\limits_{i = 1}^{D} {x_{i}^{\nu - 1} \prod\limits_{i = 1}^{D} {(\nu + \lambda x_{i} )e^{{ - \beta \sum\limits_{i = 1}^{D} {x_{i}^{\nu } e^{{\lambda x_{i} }} } }} } } \\ & \cdot e^{{ - \beta \left( {n - D} \right)U^{\nu } e^{\lambda U} - b_{2} \nu }} , \\ \end{aligned}$$

(23)

$$\begin{aligned} W\left( {\lambda \left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ,\nu ,\beta } \right.} \right) \propto \lambda^{{a_{3} - 1}} \prod\limits_{i = 1}^{D} {\left( {\nu + \lambda x_{i} } \right)e^{{ - \lambda \left( {b_{3} - \sum\limits_{i = 1}^{D} {x_{i} } } \right)}} } \hfill \\ \cdot e^{{ - \beta \left[ {\sum\limits_{i = 1}^{D} {x_{i}^{\nu } e^{{\lambda x_{i} }} } + \left( {n - D} \right)U^{\nu } e^{\lambda U} } \right]}} . \hfill \\ \end{aligned}$$

(24)

2.2.1 Gibbs Algorithm

• 1. Set starting values for $\nu$ and $\lambda$, and generate $\beta$ from the conditional density $W(\beta \left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ,\nu ,\lambda } \right.)$ given in (22).

• 2. Generate $\nu$ from the conditional density $W(\nu \left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ,\beta ,\lambda } \right.)$ in (23) for the above given simulated value of $\beta$ and starting value of $\lambda$.

• 3. Generate $\lambda$ from the conditional density $W(\lambda \left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{x} ,\nu ,\beta } \right.)$ in (24) for the above simulated values of $\beta$ and $\nu$.

• 4. Repeat steps 1–3 N times and stored the generated draws of $\,\beta ,\,\nu ,\,{\text{and}}\;\lambda$ after the first M-iterations to nullify the effect of the starting values.

• 5. Bayes estimates of the parameters $\,\beta ,\,\nu ,\,{\text{and}}\;\lambda$ are then given by the following:

  $$\,\,\beta^{*} = \frac{1}{N - M}\sum\limits_{i = M + 1}^{N} {\beta_{i} ,\,\,\nu^{*} = \frac{1}{N - M}\sum\limits_{i = M + 1}^{N} {\nu_{i} } \,\,} {\text{and}}\,\,\lambda^{*} = \frac{1}{N - M}\sum\limits_{i = M + 1}^{N} {\lambda_{i} } .$$

• 6. HPD intervals for $\,\beta ,\,\nu \;{\text{and}}\;\lambda$ are obtained using the method proposed by Chen and Shao (1999).

• 7. For computing Bayes estimates and HPD intervals of reliability and hazard functions, we first substituted the generated values of $\,\beta ,\,\nu ,\,{\text{and}}\;\lambda$ in (2) and (3) and then used the procedures as in steps 5 and 6, respectively.

The posterior results under Jeffrey’s priors can be obtained in the same way by setting all gamma priors’ parameters equal to zero i.e., $a_{1} = b_{1} = 0,$ $a_{2} = b_{2} = 0$ and $a_{3} = b_{3} = 0$. Here, it is to be noted that the simulation in steps 2 and 3 is not easy as the inverse distribution function method of generating draws from the posterior densities of $\nu$ and $\lambda$ is not applicable here. Therefore, for simulating parametric draws from these densities, one needs an advanced simulating algorithm. Therefore, we utilize Metropolis–Hastings (MH) algorithm (Metropolis and Ulam 1949; Hastings 1970), one of the MCMC techniques to generate $\nu$ and $\lambda$.

2.2.2 MH Algorithm

Suppose we want to simulate draws $(\theta_{1} ,\,\theta_{2} , \ldots \theta_{N} )$ from the distribution $g\left( \theta \right)$. Given the target density $g\left( \theta \right)$ and an arbitrary proposal density or jumping distribution $q(\theta |\theta^{\prime}) = P(\theta^{\prime} \to \theta )$, i.e., the probability of returning a new sample value $\theta$ given a previous sample value $\theta^{'}$, the algorithm is as follows:

• 1. Set initial value θ° satisfying target density $g(\theta^{ \circ } ) > 0$.

• 2. For t = 1,2,…N, repeat the following steps.

• 3. Set $\theta = \theta^{(t - 1)} .$

• 4. Using current $\theta$ value, sample a point $\theta^{*} \sim \,\,q(\theta^{*} |\theta^{(t - 1)} )$. Here, we assume normal distribution as the proposal density that is $q(\theta^{*} |\theta^{(t - 1)} ) \equiv N(\theta^{(t - 1)} ,\sigma_{\theta } )$. The standard deviation $\sigma_{\theta }$ is chosen, so that the chain explores the whole area of the target density with sufficient acceptance probability.

• 5. Compute the acceptance probability $\rho (\theta^{*} ,\theta^{(t - 1)} ) = \hbox{min} \left\{ {1,\,\log \left( {\frac{{g(\theta^{*} )q(\theta^{(t - 1)} |\theta^{*} )}}{{g(\theta^{t - 1} )q(\theta^{*} |\theta^{(t - 1)} )}}} \right)} \right\}.$

• 6. Generate u from $U(0, 1)$ and take $z = { \log }u$.

• 7. If $z < \rho (\theta^{*} ,\theta^{t - 1} )$, accept $\theta^{*}$ and set $\theta^{(t)} = \theta^{*}$ with probability $\rho (\theta^{*} ,\theta^{t - 1} )$. Otherwise, reject $\theta^{*}$ and set $\theta^{(t)} = \theta^{(t - 1)}$.

3 Real Data Analysis

In this section, an analysis of a real data set is performed. The data set is taken from Lawless (2003), which contains 60 observations on electrical appliance failure times (1000s of cycles) as follows:

0.014, 0.034, 0.059, 0.061, 0.069, 0.08, 0.123, 0.142, 0.165, 0.21, 0.381, 0.464, 0.479, 0.556, 0.574, 0.839, 0.917, 0.969, 0.991, 1.064, 1.088, 1.091, 1.174, 1.270, 1.275, 1.355, 1.397, 1.477, 1.578, 1.649, 1.707, 1.893, 1.932, 2.001, 2.161, 2.292, 2.326, 2.337, 2.628, 2.785, 2.811, 2.886, 2.993, 3.122, 3.248, 3.715, 3.79, 3.857, 3.912, 4.1, 4.106, 4.116, 4.315, 4.510, 4.584, 5.267, 5.299, 5.583, 6.065, 9.701.

First, we compare the fitting of three-parameter MW distribution with some two-parameter distributions, such as Weibull, gamma, and log-normal to this data set. The Kolmogorov–Smirnov (K–S) test, log-likelihood criterion, and Akaike information criterion (AIC) are applied for this purpose. For complete data set, the MLEs of the parameters and fitting summaries of considered models are given in Table 1. While obtaining the MLEs of the three-parameter MW distribution, we found the MLE of $\beta$ in closed form, whereas MLEs of the other two parameters $\nu$ and $\lambda$ are obtained using the optimization function maxLik() of R-software. To check the convergence of this algorithm, the contour plot of the two-dimensional log-likelihood surface for $\nu$ and $\lambda$ corresponding to the considered data set has been drawn in Fig. 2a. The surface is well behaved with a unique maximum. The MLEs of $\nu$ and $\lambda$ are shown in the contour plot. The difference in curvature in the log-likelihood surface along with $\nu$ and $\lambda$ directions can be easily observed. We also draw the individual profile plots of log-likelihood function for $\nu$ and $\lambda$ in Fig. 2b, c, respectively. The values of K–S statistics and associated P values clearly indicate that the MW distribution is a better model for the given data. The values of the log-likelihood and AIC also suggested the same. The fitted density plots and the P–P plots of Kaplan–Meier estimator (KME) (Kaplan and Meier 1958) versus fitted survival functions of the considered models are displayed in Fig. 3a and b. From these plots, it can be seen that the MW distribution is superior to the other distributions in terms of model fitting. More so, the plots of the cumulative hazard function superimposed on nonparametric counterpart given in Fig. 3c confirm that MW distribution is an adequate model for considered data set.

Table 1 MLE along with SE, K–S statistics with corresponding P value, logL, and AIC of the models fitted to the real data

Fig. 2

.

Fig. 3

For real data: a estimated densities plot, b P–P plots of KME verses fitted survival functions, and c empirical and fitted cumulative hazard plots

Now for analyzing this data with MW distribution under Type-II hybrid censoring scheme, three artificially hybrid censored data sets are formed from the complete data with the following censoring schemes:

Scheme 1: R = 48, T = 4 (20 % censored data).

Scheme 2: R = 36, T = 4 (40 % censored data).

Scheme 3: R = 24, T = 1.5 (60 % censored data).

In all the cases, the unknown parameters are estimated using the ML and Bayes methods of estimation. Bayes estimates of $\beta ,\,\nu ,\;{\text{and}}\;\lambda$, and HPD intervals are obtained using gamma and Jeffrey priors. The different estimates of the parameters along with their standard errors and 95 % confidence/HPD intervals are summarized in Table 2.

Table 2 MLEs, Bayes estimates along with their estimated errors (SE/PE), and 95 % confidence/HPD intervals under various Types II hybrid censoring schemes for real data

4 Comparison Study

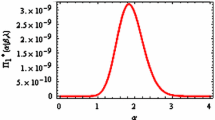
Here, some simulation results for accessing the performances of the classical and Bayesian methods of estimation under various Type-II hybrid censoring schemes for different choices of (R, T) are presented. The comparisons are made on the basis of the average standard errors/posterior errors (ASEs/APEs) of the estimates, average interval lengths (AILs) of the confidence/HPD intervals, and coverage probabilities (CPs). Assuming $\beta = 0.5,\,\nu = 2,\,\,\lambda = 0.2$, two sets of data containing, respectively, n = 30 and 100 observations were generated from (1). We replicate the process 1000 times and obtain average estimates, ASEs/APEs, average confidence/HPD intervals, average interval lengths, and coverage probabilities with different combinations of R and T. For Bayesian estimation, 5000 realizations of the parameters $\beta ,\,\,\nu ,\,\,{\text{and}}\;\lambda$ from the posterior densities in (22), (23), and (24) are generated using Gibbs sampler. While simulating posterior densities of $\nu$ and $\lambda$, we use MH algorithm as discussed in Sect. 2.2. In this algorithm, the initial guess values of the parameters $\nu$ and $\lambda$ are taken as their MLEs. The first 1000 burn-in iterations have been discarded to eliminate the effect of the stating values of the parameters. The graphical diagnostic tools, such as trace and autocorrelation plots, have been employed to check the convergence of the chains. The trace plots of $\beta ,\,\,\nu ,\,\,\text{and}\;\lambda$ in Figs. 4a, 5a, and 6a, respectively show well mixing of the chains. More so, the chains are scattered around their mean values. The autocorrelation plots of $\beta ,\,\,\nu ,\,\,\text{and}\;\lambda$ in Figs. 4b, 5b, and 6b clearly revel that the chains have low autocorrelations. Finally, we have drawn the simulated posterior densities of $\beta ,\,\,\nu ,\,\,\text{and}\;\lambda$ in Figs. 4c, 5c, and 6c, and we found that all posterior distributions are unimodal. The results of the comparison study have been summarized in Tables 3, 4, 5, 6, 7, and 8. The results for reliability and hazard functions for varying values of the mission time x are listed in Tables 9 and 10, respectively. Note that, in Tables 2, 3, 4, 5, 6, 7, and 8, the entries in the bracket [] represent ASEs/APEs and those in the brackets () and {}, respectively, represent average confidence/HPD intervals and their lengths. For all the numerical computations, the programs are developed in the R-software. From the results given in Tables 3, 4, 5, 6, 7, 8, 9, and 10, the following is observed:

Fig. 4

.

Fig. 5

.

Fig. 6

.

Table 3 Average ML estimates, the ASEs, average confidence intervals along with AILs, and CPs with Type-II hybrid censoring for n = 30

Table 4 Average Bayes estimates (ABEs) with gamma priors, the APEs, and average HPD intervals along with AILs and CPs with Type-II hybrid censoring for n = 30

Table 5 Average Bayes estimates with Jeffrey’s prior, the APEs, and average HPD intervals along with AILs and CPs with Type-II hybrid censoring for n = 30

Table 6 Average ML estimates, the ASEs, and average confidence intervals along with AILs and CPs with Type-II hybrid censoring for n = 100

Table 7 Average Bayes estimates with gamma priors, the APEs, and average HPD intervals along with AILs and CPs with Type-II hybrid censoring for n = 100

Table 8 Average Bayes estimates with Jeffrey’s prior, the APEs, and average HPD intervals along with AILs and CPs with Type-II hybrid censoring for n = 100

Table 9 Average ML estimates, ASEs, average confidence intervals along with their AILs, average Bayes estimates with their APEs, average HPD intervals, and CPs of reliability function for fixed n = 50 and varying x

Table 10 Average ML estimates, ASEs, average confidence intervals along with their AILs, average Bayes estimates with their APEs, average HPD intervals, and CPs of hazard rate function for fixed n = 50 and varying x

• The ML estimates in comparison to Bayes are not performing well for small values of n, R, and T. However, for large sample, both the methods of estimation are precisely estimating the parameters, reliability, and hazard functions in terms of ASEs/APEs and AILs and associated CPs of the confidence/HPD intervals.

• The performance of Bayes estimation under gamma priors is better in comparison with those under Jeffrey’s priors as well as ML estimates in terms of AILs and associated CPs of HPD intervals. In all the cases, the HPD intervals under gamma priors cover the true parameters’ values with probability one. Over all, the coverage probabilities of the confidence intervals are observed to be smaller than those of HPD intervals.

• In most of the cases, the CPs of confidence and HPD intervals tend to increase with n, R and T.

• As expected, the average estimated errors and AILs of the various intervals tend to decrease with increase sample size n.

• Bayes estimation with gamma prior provides more efficient estimates as compared with the Jeffrey’s prior as well as the ML method of estimation for all considered combinations of n, R, and T.

• The APEs and the AILs of the HPD intervals based on gamma priors are smaller than those with Jeffrey’s priors.

• As x increases, the reliability function (hazard rate function) decreases (increases). The same trend is observed in the case of their ML and Bayes estimates.

5 Concluding Remarks

In this article, the estimation of the parameters of the modified Weibull distribution under Type-II hybrid censoring scheme is presented. The ML and Bayesian estimation (with gamma and Jeffrey’s priors) methods have been used for this purpose. The performances of different estimators are examined based on small and large samples with different combinations of Type-II hybrid censoring parameters R and T. A real data set analysis is carried out under Type-II hybrid censored scheme to show the applicability of the modified Weibull distribution. Based on the censoring results, it is proposed that the modified Weibull distribution may be a better lifetime model for analyzing the reliability characteristics of real-life systems with Type-II hybrid censoring scheme.