1 Introduction

Lindley distribution was proposed by Lindley (1958) in the context of Bayesian statistics, as a counter example of fiducial statistics. However, due to the popularity of the exponential distribution in statistics especially in reliability theory, Lindley distribution has been overlooked in the literature. Recently, many authors have paid great attention to the Lindley distribution as a lifetime model. From different point of view, Ghitany et al. (2008) showed that Lindley distribution is a better lifetime model than exponential distribution. More so, in practice, it has been observed that many real life system models have increasing failure rate with time. Lindley distribution possesses this property of having increasing hazard-rate function. Al-Mutairi et. al. (2011) developed the inferential procedure of the stress-strength parameter R = P(Y < X), when both stress and strength variables follow Lindley distribution. Gomoz-Deniz and Calderin-Ojeda (2011) developed a discrete Lindley model with its applications in collective risk modeling. Mazucheli and Achcar (2011) studied a competing risk model when the causes of failures follow Lindley distribution. Krishna and Kumar (2011) estimated the parameter of Lindley distribution with progressive Type-II censoring scheme. They also showed that it may fit better than exponential, lognormal and gamma distribution in some real life situations. Recently, Singh and Gupta (2012) studied a k-component load-sharing parallel system model in which each component’s lifetime follows Lindley distribution.

In the recent years, advanced customer expectation and typical global competition are deriving the great attention in improving the reliability of the products. In order to stay competitive, manufactures are being challenged to design, develop, test, and produce high quality and long life products. Hence the manufactures must have the sound knowledge about product failure time distribution. To gain this knowledge, life testing experiments are performed before products are put on the market (Wu and Chang 2003; Balakrishnan and Aggarwala 2000). Major decisions are generally based on life test data, often from a few units due to the cost and time constraints. Moreover, many products last so long that life testing at design conditions is impractical (Wu and Chang 2003). Such situations sometimes arise eventually or sometimes produced with intent.

In reliability/survival analysis, several types of censoring schemes are used. The most rottenly used censoring schemes are Type-I and Type-II censoring. In Type-I censoring, the number of failure observed is random and the termination point of the experiment is fixed, whereas in Type-II censoring the termination point is random, while the number of failures is fixed. The mixture of Type-I and Type-II censoring scheme is known as hybrid censoring scheme and it is quite applicable in reliability acceptance test in MIL-STD-781C (1977). Hybrid sampling scheme was originally introduced by Epstein (1954). Afterwards, this censoring scheme is used by many authors like Chen and Bhattacharya (1988), Childs et al. (2003), Draper and Guttman (1987) and Gupta and Kundu (1998).

Although, this censoring scheme is very useful in reliability/survival analysis, the limited attention has been paid in analyzing hybrid censored lifetime data. Some recent studies on hybrid censoring are Kundu (2007); Banerjee and Kundu (2008); Kundu and Pradhan (2009); Dube et al. (2011) and Ganguly et al. (2012).

In lieu of above considerations, the paper is organized as follows. In Sect. 2, we describe the model under the assumption of hybrid censored data from Lindley lifetime distribution. In Sect. 3, we obtain the maximum likelihood estimator (MLE) of the unknown parameter. It is observed that the MLE is not obtained in closed form, so it is not possible to derive the exact distribution of the MLE. Therefore, we propose to use the asymptotic distribution of the MLE to construct the approximate confidence interval. Further, by assuming Jeffrey’s invariant and gamma priors of the unknown parameter, Bayes estimate along with its posterior standard error (PSE) and highest posterior density credible (HPD) interval of the parameter are obtained in Sect. 4. Markov Chain Monte Carlo (MCMC) technique such as Metropolis–Hastings algorithm has been utilized to generate draws from the posterior density of the parameter. In Sect. 5, a real data set representing the waiting time of the bank customers has been analyzed for illustration purpose. A comparison study is also carried out to judge the performance of classical and Bayesian estimation procedure.

2 Model description

Suppose n identical units are put to test under the same environmental conditions and test is terminated when a pre-chosen number R, out of n items have failed or a pre determined time T, on test has been reached. It is assumed that the failed item not replaced and at least one failure is observed during the experiment. Therefore, under this censoring scheme we have one of the following types of observations:

  • Case I: \( \left\{ {x_{1:n} < \ldots \ldots \ldots < x_{R:n} } \right\} \) if \( x_{R:n} < T \)

  • Case II: \( \left\{ {x_{1:n} < \ldots \ldots \ldots < x_{d:n} } \right\} \) if \( 1 \le d < R \) and \( x_{d:n} < T < x_{d + 1:n} \)

Here, \( x_{1:n} < x_{2:n} < \ldots \) denote the observed failure times of the experimental units. For schematic representation of the hybrid censoring scheme refer to Kundu and Pradhan (2009). It may be mentioned that although we do not observe \( x_{d + 1:n} \), but \( x_{d:n} < T < x_{d + 1:n} \) means that the dth failure took place before T and no failure took place between \( x_{d\,:\,n} \) and T. Let the life time random variable X has a Lindley distribution with parameter θ i.e. the probability density function (PDF) of x is given by;

$$ f_{X} (x\left| \theta \right.)\; = \;\frac{{\theta^{2} }}{{\left( {1\; + \;\theta } \right)}}\left( {1\; + \;x} \right)e^{ - \theta x}; \quad x,\,\theta > 0 $$

Based on the observed data, the likelihood function is given by

Case I:

$$ L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} \left| \theta \right.} \right)\; = \;\frac{{\theta^{2R} }}{{\left( {1\; + \;\theta } \right)^{R} }}\prod\limits_{i = 1}^{R} {\left( {1\; + \;x_{i\,:\,n} } \right)e^{{ - \theta \left\{ {\sum\limits_{i = 1}^{R} {x_{i\,:\,n} } \; + \;\left( {n - R} \right)x_{R\,:\,n} } \right\}}} } \left( {1\; + \;\frac{\theta }{1\; + \;\theta }x_{R:\,n} } \right)^{{^{n - R} }} $$
(1)

Case II:

$$ L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} \left| \theta \right.} \right)\; = \;\frac{{\theta^{2d} }}{{\left( {1\; + \;\theta } \right)^{d} }}\prod\limits_{i = 1}^{d} {\left( {1\; + \;x_{i\,:\,n} } \right)e^{{ - \theta \left\{ {\sum\limits_{i = 1}^{d} {x_{i\,:\,n} } \; + \;(n - d)T} \right\}}} } \left( {1\; + \;\frac{\theta }{1\; + \;\theta }T} \right)^{n - d} \ldots $$
(2)

where \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} \; = \;\left( {x_{1:n} ,\,x_{2:n} ,\, \ldots \ldots \ldots } \right) \)

The combined likelihood for case I and case II can be written as

$$ L\; = \;L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} \left| \theta \right.} \right)\; = \;\frac{{\theta^{2r} }}{{\left( {1\; + \theta } \right)^{r} }}\prod\limits_{i = 1}^{r} {\left( {1\; + \;x_{i\,:\,n} } \right)e^{{ - \theta \left\{ {\sum\limits_{i = 1}^{r} {x_{i\,:\,n} } \; + \;(n - r)c} \right\}}} \left( {1\; + \;\frac{\theta }{1\; + \;\theta }c} \right)^{n - r} } \ldots $$
(3)

where,

$$ r\; = \;\left\{ \begin{array}{ll} R & {\text{for\, case\, I}} \\ d & {\text{for\, case\, II}} \\ \end{array} \right.\quad c = \left\{ \begin{array}{ll} x_{R:n}& {\text{for\, case\, I}} \\ T & {\text{for\, case\, II}} \\ \end{array} \right. $$

3 Maximum likelihood estimate

The log-likelihood function for Eq. (3) can be written as

$$ \log L\; = \;2r\log \left( \theta \right)\; - \;n\log \left( {1\; + \;\theta } \right)\; + \;\left( {n\; - \;r} \right)\log \left[ {1\; + \;\theta \left( {1\; + \;c} \right)} \right]\; + \;\sum\limits_{i = 1}^{r} {\log \left( {1\; + \;x_{i:n} } \right)} \; - \;\theta \left[ {\sum\limits_{i = 1}^{r} {x_{i:n} } \; + \;\left( {n\; - \;r} \right)c} \right] \ldots $$
(4)

The first derivative of Eq. in (4) with respect to θ is given by

$$ \frac{\partial \log L}{\partial \theta }\; = \;\frac{2r}{\theta }\; - \;\frac{n}{1 + \theta }\; + \;\frac{{\left( {n\; - \;r} \right)\left( {1\; + \;c} \right)}}{{1\; + \;\theta \left( {1\; + \;c} \right)}}\; - \;\sum\limits_{i = 1}^{r} {x_{i:n} \; + \;\left( {n\; - \;r} \right)c} \ldots $$
(5)

The second derivative of Eq. (4) with respect to θ is given by

$$ \frac{{\partial^{2} logL}}{{\partial \theta^{2} }}\; = \; - \frac{2r}{{\theta^{2} }}\; + \;\frac{n}{{\left( {1\; + \;\theta } \right)^{2} }}\; + \;\left( {n\; - \;r} \right)\left[ {\frac{{\left( {1\; + \;c} \right)}}{{1\; + \;\theta \left( {1\; + \;c} \right)}}} \right]^{2} \ldots $$
(6)

The MLE of θ will be the solution of the following non-linear equation

$$ \frac{2r}{\theta }\; - \;\frac{n}{1\; + \;\theta }\; + \;\frac{{\left( {n\; - \;r} \right)\left( {1\; + \;c} \right)}}{{1\; + \;\theta \left( {1\; + \;c} \right)}}\; - \;\sum\limits_{i = 1}^{r} {x_{i:n} \; + \left( {n\; - \;r} \right)c} \; = \;0 \ldots $$
(7)

The Eq. (7) can be solved for \( \hat{\theta } \). by using some suitable numerical iterative procedure such as Newton–Raphson method. The observed Fisher’s information is given by

$$ I\left( {\hat{\theta }} \right)\; = \; - \left. {\frac{{\partial^{2} logL}}{{\partial \theta^{2} }}} \right|_{{\theta = \hat{\theta }}} \ldots $$
(8)

Also, the asymptotic variance of \( \hat{\theta } \) is given by

$$ Var\left( {\hat{\theta }} \right)\; = \;\frac{1}{{I\left( {\hat{\theta }} \right)}} \ldots $$
(9)

The sampling distribution of \( \frac{{\left( {\hat{\theta } - \theta } \right)}}{{\sqrt {Var\left( {\hat{\theta }} \right)} }} \) can be approximated by a standard normal distribution. The large-sample \( \left( {1\; - \;\gamma } \right)\; \times \;100\;\% \) confidence interval for θ is given by \( \left[ {\hat{\theta }_{L} ,\hat{\theta }_{U} } \right]\; = \;\hat{\theta }\; \pm \;z_{{\frac{\gamma }{2}}} \sqrt {Var\left( {\hat{\theta }} \right)} \).

4 Bayesian estimation

In many practical situations, it is observed that the behavior of the parameters representing the various model characteristics cannot be treated as fixed constant throughout the life testing period. Therefore, it would be reasonable to assume the parameters involved in the life time model as random variables. Keeping in mind this fact, we have also conducted a Bayesian study by assuming the following independent gamma prior for θ;

$$ g(\theta )\,\alpha \,\theta^{a - 1} e^{ - b\theta } ;\,\theta \; > \;0 $$

Here the hyper parameters a and b are assumed to be known real numbers. Based on the above prior assumption, the joint density function of the sample observations and θ becomes

$$ L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} ,\,\theta } \right)\,\alpha \,\frac{{\theta^{2r + a - 1} }}{{\left( {1\; + \;\theta } \right)^{r} }}e^{{ - \theta \left\{ {\sum\limits_{i = 1}^{r} {x_{i\,:\,n} } \; + \;(n - r)c\; + \;b} \right\}}} \left[ {1\; + \;\frac{\theta }{1\; + \;\theta }c} \right]^{n - r} \ldots $$
(10)

Thus, the posterior density function of θ, given the data is given by

$$ \pi \left( {\theta \left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} } \right.} \right)\; = \;\frac{{L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} \left| \theta \right.} \right)g_{1} \left( {\theta \left| {a,\,b} \right.} \right)}}{{\int\limits_{0}^{\infty } {L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} \left| \theta \right.} \right)g_{1} \left( {\theta \left| {a,\,b} \right.} \right)d\theta } }} \ldots $$
(11)

Therefore, if \( h\left( \theta \right) \) is any function of θ, its Bayes estimate under the squared error loss function is given by

$$ \hat{h}\left( \theta \right)\; = \;E_{{\theta \left| {data} \right.}} \left[ {h\left( \theta \right)} \right]\; = \;\frac{{\int\limits_{0}^{\infty } {h\left( \theta \right)L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} ,\theta } \right)d\theta } }}{{\int\limits_{0}^{\infty } {L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{x} ,\theta } \right)d\theta } }} \ldots $$
(12)

Since it is not possible to compute (11) and therefore (12) analytically. Therefore, we propose the one of the MCMC method such as Metropolis–Hastings algorithm to draw samples from the posterior density function and then to compute the Bayes estimate and HPD credible interval.

4.1 Metropolis–Hastings algorithm

  • Step-1: Start with any value satisfying target density \( f\left( {\theta^{(0)} } \right)\; > \;0 \)

  • Step-2: Using current \( \theta^{(0)} \) value, generate a proposal point (\( \theta{\_}prop \)) from the proposal density \( q\left( {\theta^{(1)} ,\theta^{(2)} } \right)\; = \;P\left( {\theta^{(1)} \to \theta^{(2)} } \right) \) i.e., the probability of returning a value of \( \theta^{(2)} \) given a previous value of \( \theta^{(1)} \).

  • Step-3: Calculate the ratio at the proposal point (\( \theta{\_}prop \)) and current \( \theta^{(i - 1)} \) as:

  • $$ \rho \; = \;\log \left[ {\frac{{f\left( {\theta{\_}prop} \right)q\left( {\theta{\_}prop,\theta^{(i - 1)} } \right)}}{{f\left( {\theta^{(i - 1)} } \right)q\left( {\theta^{(i - 1)} ,\theta{\_}prop} \right)}}} \right] $$

  • Step-4: Generate U from uniform on (0, 1) and take Z = log U.

  • Step-5: If \( Z\; < \;\rho \), accept the move i.e., \( \theta{\_}prop \) and set \( \theta^{(0)} \; = \;\theta{\_}prop \) and return to Step-1. Otherwise reject it and return to Step-2.

  • Step-6: Repeat the above procedure N times and record the sequence of the parameter θ as \( \theta_{1} ,\,\theta_{2} ,\, \ldots \ldots ,\,\theta_{N} \). Further, to remove the autocorrelation between the chains of θ, we only store every fifth generated value. Let the size of the sample we thus store is M = N/5.

  • Step-7: The Bayes estimate of θ and corresponding posterior variance is respectively taken as the mean and variance of the generated values of θ.

  • Step-8: Let \( \theta_{(1)} \; \le \;\theta_{(2)} \; \le \; \ldots \ldots \; \le \;\theta_{(M)} \) denote the ordered value of \( \theta_{(1)} ,\,\theta_{(2)} ,\, \ldots \ldots ,\theta_{(M)} \). Then, following Chen and Shao (1999), the \( (1 - \gamma )\, \times \,100\,\,\% \) HPD interval for θ is \( \left( {\theta_{{\left( {M + i^{*} } \right)}} ,\,\theta_{{\left( {M + i^{*} + \left[ {(1 - \gamma )(M - N)} \right]} \right)}} } \right) \) where, \( i^{*} \) is so chosen that

$$\theta_{{\left( {M + i^{*} + \left[ {(1 - \gamma )(M - N)} \right]} \right)}} \; - \;\theta_{{\left( {M + i^{*} } \right)}} \; = \;\mathop {\min }\limits_{N\,\, \le \,\,i\,\, \le \,\,(M - N) - [(1 - \gamma )(M - N)} \left( {\theta_{{\left( {N + i + \left[ {(1 - \gamma )(M - N)} \right]} \right)}} \; - \;\theta_{{\left( {N + i} \right)}} } \right) $$

5 Data analysis

In this section, we perform a real data analysis for illustrative purpose. We use the data set of waiting times (in minutes) before service of 100 bank customers as discussed by Ghitany et al. (2008). The waiting times in minutes are as follows:

 

0.8, 0.8, 1.3, 1.5, 1.8, 1.9, 1.9, 2.1, 2.6, 2.7, 2.9, 3.1, 3.2, 3.3, 3.5, 3.6, 4.0, 4.1, 4.2, 4.2, 4.3, 4.3, 4.4, 4.4, 4.6, 4.7, 4.7, 4.8, 4.9, 4.9, 5.0, 5.3, 5.5, 5.7, 5.7, 6.1, 6.2, 6.2, 6.2, 6.3, 6.7, 6.9, 7.1, 7.1, 7.1, 7.1, 7.4, 7.6, 7.7, 8.0, 8.2, 8.6, 8.6, 8.6, 8.8, 8.8, 8.9, 8.9, 9.5, 9.6, 9.7, 9.8, 10.7, 10.9, 11.0, 11.0, 11.1, 11.2, 11.2, 11.5, 11.9, 12.4, 12.5, 12.9, 13.0, 13.1, 13.3, 13.6, 13.7, 13.9, 14.1, 15.4, 15.4, 17.3, 17.3, 18.1, 18.2, 18.4, 18.9, 19.0, 19.9, 20.6, 21.3, 21.4, 21.9, 23.0, 27.0, 31.6, 33.1, 38.5

It has been observed by Ghitany et al. (2008) that the Lindley distribution can be effectively used to analyze this data set.

For analyzing this data set with hybrid censoring, we have created three artificially hybrid censored data sets from the above complete (uncensored) data under the following censoring schemes:

  • Scheme 1: R = 75, T = 12 (25 % Censored data)

  • Scheme 2: R = 50, T = 8 (50 % Censored data)

  • Scheme 3: R = 35, T = 6 (65 % Censored data)

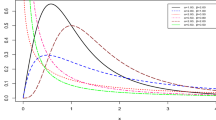
In all the cases, we have estimated the unknown parameter using the ML and Bayes methods of estimation. For obtaining MLE and 95 % confidence interval, we have used nlm() function of R package. The initial/starting value that is used in the nlm() function for the parameter θ is taken as the positive root of the quadratic equation \( m\theta^{2} \; + \;(m\; - \;1)\theta \; - \;2\; = \;0 \), where m is the sample mean. Bayes estimates of θ and HPD intervals are obtained using gamma and Jeffrey priors. The summary for the above three schemes is given in Table 1. For demonstrating the goodness of fit of the hybrid censored data under schemes 1, 2 and 3, the empirical and fitted distribution functions have been plotted in Figs. 1, 2, and 3 (with ML, Jeffrey Bayes and Gamma Bayes methods). It is observed that the goodness of fit to the real data set is quite acceptable even with the 25, 50, and 65 % hybrid censored data.

Table 1 Summary for the three schemes from hybrid censored Lindley distribution for real data
Full size table
Fig. 1
figure 1

Empirical and fitted distribution function (with ML) of waiting time of bank customer with Lindley distribution

Full size image
Fig. 2
figure 2

Empirical and fitted distribution function (with Jeffrey Bayes) of waiting time of bank customer with Lindley distribution

Full size image
Fig. 3
figure 3

Empirical and fitted distribution function (with Gamma Bayes) of waiting time of bank customer with Lindley distribution

Full size image

6 Comparison study

In this section, we present some simulation results for accessing the performances of the classical and Bayesian methods of estimation. The standard error of the estimate and width of the confidence/HPD interval are used for comparison purpose. Assuming \( \theta \; = \;0.5 \), we generated the two sets of data containing respectively n = 30 and 40 observations, and based on these data sets, the MLEs, and Bayes estimate for the parameter have been obtained. We have also considered different values of R and T. For Bayesian estimation, we generated 5,000 realizations of the parameter θ from the posterior density in (11) using Metropolis–Hastings algorithms. The MCMC run of the parameter θ is plotted in Fig. 4, which show fine mixing of the chains. We have also plot the posterior density of θ and found that it is symmetric (Fig. 5). For reducing the autocorrelation among the generated values of θ, we only record every 5th generated values of each parameter. Initially, a strong autocorrelation is observed among the generated chain of θ as shown in Fig. 6. However, the serial correlation is minimized when we record only every 5th generated outcomes (Fig. 7). The results of the comparison study have been summarized in Tables 2, 3, 4, and 5. Note that, in the Tables 1, 2, 3, 4, and 5, the entries in the bracket [] represents SEs/PSEs and that in the brackets () and {} respectively represent confidence/HPD interval and the widths of the interval. For all the numerical computations, the programs are developed in R-environment and are available with the authors. From the results given in Tables 2, 3, 4, and 5, we observe the following:

Fig. 4
figure 4

Plot of generated θ versus iteration of MCMC algorithm

Full size image
Fig. 5
figure 5

Posterior density of θ

Full size image
Fig. 6
figure 6

Plot of autocorrelation of all generated θ

Full size image
Fig. 7
figure 7

Plot of autocorrelation of every 5th stored θ

Full size image
Table 2 Classical and Bayes estimates with their standard errors (SE) and 95 % confidence/HPD intervals (CI) with their widths for the parameter for fixed n = 30, T = 10 and varying R
Full size table
Table 3 Classical and Bayes estimates with their standard errors (SE) and 95 % confidence/HPD intervals (CI) with their widths for the parameter for fixed n = 40, T = 10 and varying R
Full size table
Table 4 Classical and Bayes estimates with their standard errors (SE) and 95 % confidence/HPD intervals (CI) with their widths for the parameter for fixed n = 30, T = 12 and varying R
Full size table
Table 5 Classical and Bayes estimates with their standard errors (SE) and 95 % confidence/HPD intervals (CI) with their widths for the parameter for fixed n = 40, T = 12 and varying R
Full size table

  • Both the methods of estimation considered in the present study are precisely estimating the parameter (in terms of standard error and length of the confidence/HPD interval). The magnitude of the error tend to decrease as we increase any one of n, R and T while keeping the other two as fixed.

  • Bayes estimation with gamma prior provides more precise estimates as compared to the Jeffrey prior and MLEs. Also the performance of MLEs and Jeffrey prior are quite similar.

  • The length of the HPD credible intervals based on Gamma prior are smaller than the corresponding length of the HPD credible intervals based on Jeffrey’s prior.