Impact of human mobility on the transmission dynamics of infectious diseases

Abstract

Spatial heterogeneity is an important aspect to be studied in infectious disease models. It takes two forms: one is local, namely diffusion in space, and other is related to travel. With the advancement of transportation system, it is possible for diseases to move from one place to an entirely separate place very quickly. In a developing country like India, the mass movement of large numbers of individuals creates the possibility of spread of common infectious diseases. This has led to the study of infectious disease model to describe the infection during transport. An SIRS-type epidemic model is formulated to illustrate the dynamics of such infectious disease propagation between two cities due to population dispersal. The most important threshold parameter, namely the basic reproduction number, is derived, and the possibility of existence of backward bifurcation is examined, as the existence of backward bifurcation is very unsettling for disease control and it is vital to know from modeling analysis when it can occur. It is shown that dispersal of populations would make the disease control difficult in comparison with nondispersal case. Optimal vaccination and treatment controls are determined. Further to find the best cost-effective strategy, cost-effectiveness analysis is also performed. Though it is not a case study, simulation work suggests that the proposed model can also be used in studying the SARS epidemic in Hong Kong, 2003.

1 Introduction

Mathematical modeling is considered as one of the most major and effective tools to predict the transmission mechanism of various infectious diseases. The use of mathematical models to describe the dynamics of such diseases was started a long time ago. Kermack and McKendrick (1933) were the first to introduce the mathematical model to analyze the characteristics of epidemic problems. However, this dynamical system approach for epidemiological problems was not so popular until the early 1990s. Some major and recent developments can be found in Diekmann and Heesterbeek (1999), Keeling and Rohani (2008), Makinde (2007), Smith (2008), Thomasey and Martcheva (2008), Okosun et al. (2011), Kar and Mondal (2011), Kar and Jana (2013a, b), Jana et al. (2016a, b).

In the last couple of decades, there is a rapid advancement of transportation system throughout the globe. People now move from one place to another very quickly, and this quick movement of human is an important driver to spread the emerging and re-emerging infectious diseases. For instance, in 2003, SARS epidemic occurred in a wide region of Asia including China due to population dispersal. The H1N1 (swine flu) pandemic in 2009 is now considered to have been the fastest moving pandemic in world history (Lipsitch et al. 2009). Recently, Ebola virus also threatened to become epidemic in vast region of Africa mainly due to the incautious movement of human population. Also, in recent past time, we have witnessed the severe outbreak of many emerging infectious diseases including MERS-CoV, SARS-CoV, Zika, and the very latest addition is novel coronavirus (COVID-19). For these types of diseases, human mobility can influence the disease dynamics mainly in two ways: Movements may cast new pathogens into the susceptible group, or it may enhance the contact rate between the susceptible and infected people. The severe acute respiratory syndrome (SARS) originated in China in 2002 and spread to 29 countries; MERS-CoV originated in Saudi Arabia in 2012 and later, has been identified in 27 countries; and Ebola virus disease began in Sierra Leone in 2014 and spread to several countries via international travel. Presently, novel COVID-19 originated in China and has spread very quickly throughout the globe. Therefore, spatial heterogeneity related to travel is a very important aspect to be considered in infectious disease modeling approach. Some mathematical models on transmission dynamics of infectious diseases due to population dispersal are available in Wang and Mulone (2003), Arino and Van den Driessche (2003), Wang and Zhao (2004), while Wang and Zhao (2005) proposed an age-structured epidemic model and established the conditions of uniform persistence and global extinction of the disease. In the context of developing countries, Cui et al. (2006) proposed a transport-related SIS-type disease model. Later, Wan and Cui (2007) extended this model as an SEIS-type disease model to describe the infection during transportation. However, Meloni et al. (2011) proposed and analyzed a metapopulation model incorporating the mobility of humans. Findlater and Bogoch (2018) studied the effects of human movement, specially via air on the spread of infectious disease. Some other perspective of human movement on the disease dynamics can be found in Wesolowski et al. (2016), Sallah et al. (2017), Kraemer et al. (2019) and the references cited therein. Thus, in recent times, some advancement has been made in developing models with global transportation flows. However, still only a few theoretical and computational approaches have studied the effect of human mobility in the large-scale spreading of the epidemics. But the social and spatial widespread of several infectious diseases demands the re-evaluation and improvement of mathematical models that we use to understand the public health problems throughout the world.

The most important aspect of mathematical epidemiology is to find out the best possible way to control such diseases. From the past epidemic outbreaks for the diseases including pox, cholera, malaria, etc., it can be observed that quarantine and isolation of infected individuals is a very useful control to reduce the level of infection from community (Kar et al. 2013; Jana et al. 2017). In contemporary times, media coverage is also identified as an alternate control measure. People become alert due to media campaign and take necessary precautions to avoid the infectious diseases. The impacts of media on the dynamics of infectious diseases can be found in Sun et al. (2011), Misra et al. (2015). Vaccination is considered as the most important measure in controlling many epidemic diseases including polio, influenza, etc. The use of vaccination on the disease prevalence through different types of compartmental models can be found in Makinde (2007), Buonomo et al. (2008), Kar and Jana (2013a, b), Zhou et al. (2014). Recently, Jana et al. (2016b) proposed an epidemic model of population scattering with vaccination control. However, for any such diseases, treatment of infected individuals is the ultimate control measures to reduce the infection level. Different types of treatment control function and the impact of treatment on the dynamics of diseases are studied well in Wang (2006), Eckalbar and Eckalbar (2011), Jana et al. (2016a) and references therein. But it is observed that the combination of vaccination and treatment is the most efficient way to control such infectious diseases (Kar and Jana 2013a). However, the combined use of vaccination and treatment control still largely remains unexplored.

Following the above literature survey and considering the needs of using mathematical models effectively to investigate the dynamics of the spread of infectious diseases and its possible control measures, in this work we develop an epidemic system with the possibility of infection during transportation and the combined use of treatment and vaccination. We rigorously study the dynamical behavior of the system and try to find out the best strategy to control the spread of the disease. The remaining portion of this article is organized in the following way.

In Sect. 2, the mathematical model is formulated, and in Sect. 3, its dynamical behavior for different scenarios is described. In Sect. 4, formulation of optimal control problem with vaccination and treatment as the control parameters and its simulation works are presented. Next, in Sect. 5, the cost-effectiveness investigation is performed to find out the most beneficial control strategy. At the end, a brief conclusion of this work is drawn.

2 Model formulation

In the context of a very large and developing country like India, with the increase in transportation system among cities, the mass movement of a large number of people creates new opportunities for the spread and establishment of common or novel infectious diseases. Transportation among cities is found to be one of the main factors which affect the outbreak of diseases. In India, there has been accelerated spread of dengue and Chikungunya, both transmitted by the Aedes mosquito, which are particularly well adapted to urbanized areas. India is the country in which the highest prevalence of these two diseases occurs. A range of factors play a role including human mobility among the cities using public transport including bus, trains, air, etc. Thus, the transportation among cities changes the disease dynamics and it motivates us to construct this mathematical model.

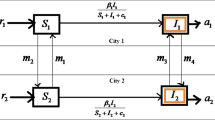
A mathematical model should be a true balance between complexities in the assumptions and simplicity within the formulation. Therefore, to propose and formulate an SIRS-type epidemic model for transmission of a communicable disease with movement of populations, it is assumed that the two cities are similar in terms of population density, economic condition, medical facilities, living environment and disease transmission probability, i.e., the demographic parameters are the same for both the cities. The total population of each city $N_i(i=1, 2)$ is divided into three compartments: susceptible ($S_i$), infected ($I_i$) and recovered ($R_i$). Therefore, total population of each city will be $N_i=S_i+I_i+R_i.$ Some more assumptions are as follows:

• 1. At any time t, the recruitment rate of both the cities is A and its $u_1 (0 \le u_1 \le 1)$ portion is vaccinated.

• 2. The disease transmission rate from the susceptible class to infected class is $\beta$, and populations of city i leave city j at a rate $\alpha$.

• 3. Disease transmission rate is denoted by $\gamma \alpha$, as the populations of the city i travel to the city j.

• 4. Natural and disease-induced mortality rate for the cities and for each class is adopted as d and $\delta$, respectively.

• 5. Natural recovery rate is m for both the cities. Following Zhang and Liu (2008), Jana et al. (2016a), the recoveries due to treatment control $u_2 (0 \le u_2 \le 1)$ for City 1 and City 2 are taken as $ru_2I_1/(1+bu_2I_1)$ and $ru_2I_2/(1+bu_2I_2)$, respectively, where r is the effectiveness of the treatment control and b is the saturation factor. This type of treatment function is used to demonstrate the limited resources.

• 6. The recovery from the disease is not permanent, and the parameter p stands for the rate by which recovered population again moves to susceptible class.

• 7. There is no birth and death during the travels of individuals.

Based on the assumptions made and according to the schematic diagram (Fig. 1), the SIR-type disease model with population dispersal takes the following form:

$$\begin{aligned} \frac{\mathrm{d}S_1}{\mathrm{d}t}& {}= A(1-u_1)-\beta S_1I_1-\mathrm{d}S_1+pR_1-\alpha S_1 +\alpha S_2 -\gamma \alpha S_2 I_2 \nonumber \\ \frac{\mathrm{d}I_1}{\mathrm{d}t}& {}= \beta S_1 I_1-(d+\delta )I_1-\alpha I_1+\alpha I_2 -mI_1\nonumber \\&\quad -\,\frac{ru_2I_1}{1+bu_2I_1}+\gamma \alpha S_2 I_2 \nonumber \\ \frac{\mathrm{d}R_1}{\mathrm{d}t}& {}= Au_1+mI_1+\frac{ru_2I_1}{1+bu_2I_1}-pR_1-\mathrm{d}R_1-\alpha R_1+\alpha R_2 \nonumber \\ \frac{\mathrm{d}S_2}{\mathrm{d}t}& {}= A(1-u_1)-\beta S_2I_2-\mathrm{d}S_2+pR_2-\alpha S_2 +\alpha S_1 -\gamma \alpha S_1 I_1 \nonumber \\ \frac{\mathrm{d}I_2}{\mathrm{d}t}& {}= \beta S_2 I_2-(d+\delta )I_2-\alpha I_2+\alpha I_1 -mI_2\nonumber \\&\quad -\,\frac{ru_2I_2}{1+bu_2I_2}+\gamma \alpha S_1 I_1 \nonumber \\ \frac{\mathrm{d}R_2}{\mathrm{d}t}& {}= Au_1+mI_2+\frac{ru_2I_2}{1+bu_2I_2}-pR_2-\mathrm{d}R_2-\alpha R_2+\alpha R_1 \end{aligned}$$

(1)

and the initial conditions are $S_i(0)\ge 0$, $I_i(0)\ge 0$, $R_i(0)\ge 0$, $i=1,2.$

Fig. 1

Model diagram of the disease transmission

3 Model analysis

Here, we discuss the dynamics of the formulated epidemic system. Uniform boundedness, existence of different equilibria and their stability criteria are discussed. Three distinct cases such as (1) no population dispersal occurs, (2) only susceptible population dispersal occurs and (3) all the classes of population dispersal occur are considered.

3.1 Uniform boundedness of the system

Here, the uniform boundedness nature of the total population is examined.

Theorem 1

All the state variables of the model system (1) are uniformly bounded.

Proof

Assume $X=S_1+I_1+R_1+S_2+I_2+R_2$. Then, it follows from (1)

$$\begin{aligned} \frac{\mathrm{d}X}{\mathrm{d}t}& {}= 2A-\delta (I_1+I_2)-\mathrm{d}X,\\&\mathrm{i.e.,}\frac{\mathrm{d}X}{\mathrm{d}t}+\mathrm{d}X\le 2A. \end{aligned}$$

Now on integration and applying the inequality from Birkhoff and Rota (1982), we have

$$\begin{aligned} 0& {} < X(S_1,I_1,R_1,S_2,I_2,R_2)\le \frac{2A}{d}(1-e^{-\mathrm{d}t})\\&\quad +\,X(S_1(0),I_1(0),R_1(0),S_2(0),I_2(0),R_2(0))e^{-\mathrm{d}t}. \end{aligned}$$

Therefore, as $t\rightarrow \infty$, we get $0<X\le \frac{2A}{d}.$

Hence, the entire solutions of model system (1) which initiate in $R^6_+$ are confined to the region

$$\begin{aligned} R=\left\{ (S_1,I_1,R_1,S_2,I_2,R_2)\in R^6_+{:}\,X=\frac{2A}{d}+\epsilon \right\} \end{aligned}$$

(2)

for any $\epsilon >0$ and $t\rightarrow \infty$. Hence, it is proved. $\square$

3.2 No population dispersal occurs

If there is no occurrence of population dispersal between the cities, then system (1) reduces to a single-city model with three compartments S,  I and R as follows:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}& {}= A(1-u_1)-\beta SI-\mathrm{d}S+pR \nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}& {}= \beta S I-(d+\delta )I-mI-\frac{ru_2I}{1+bu_2I} \nonumber \\ \frac{\mathrm{d}R}{\mathrm{d}t}& {}= Au_1+mI+\frac{ru_2I}{1+bu_2I}-pR-\mathrm{d}R \end{aligned}$$

(3)

with $S(0)\ge 0,I(0)\ge 0, R(0)\ge 0$. The positive invariant region for the system is defined as $D=\{(S,I,R) \in R_{+}^3,S\ge 0, I\ge 0,R\ge 0\}$. The system has a infection-free equilibrium $E_0^0(S^0,0,R^0)$, where $S^0=A \frac{d(1-u_1)+p}{d(d+p)}$, $R^0=\frac{Au_1}{p+d}$. Further, the system has two possible endemic equilibria, $E_1^0(S^1,I^1,R^1)$ and $E_2^0(S^2,I^2,R^2)$ where $S^{1,2}=\frac{(d+\delta +m+ru_2)+bu_2I^{1,2}(d+\delta +m)}{\beta (1+bu_2I^{1,2})}$, $R^{1,2}=\frac{(Au_1+mI^{1,2})(1+bu_2I^{1,2})+ru_2I^{1,2}}{(p+d)(1+bu_2I^{1,2})}$ and $I^1$, $I^2$ (assuming $I^1 \le I^2$) are the roots of the quadratic equation

$$\begin{aligned} c_1I^2+c_2I+c_3=0. \end{aligned}$$

(4)

Here, $c_1=\beta bu_2\{p(\delta +d)+(d+\delta +m)d\}$, $c_2=(p+d)\{\beta(d+\delta +m+ru_2)+d(d+\delta+m) bu_2\}+A\beta bu_1u_2d-\beta \{Abu_2(p+d)+p(m+ru_2)\}$, $c_3=d(p+d)(d+\delta +m+ru_2)-A \beta (p+d(1-u_1))$.

3.2.1 Reproduction number

The infection-free steady state always remains feasible but the existence and feasibility criteria of the above two endemic equilibria are different in different conditions. Before this discussion, we find the explicit form of the basic reproduction number, which is a very important parameter related to the characterization of the different steady states. The next-generation matrix method is applied in order to obtain the basic reproductive ratio (Van den Driessche and Watmough 2002).

Let us write system 3 as follows

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=\varPhi (x)-\varPsi (x), \end{aligned}$$

where $x=(I,R,S)^t$ and $\varPhi (x)=\left( \begin{array}{l} \beta SI \\ 0 \\ 0 \\ \end{array} \right)$, $\varPsi (x)=\left( \begin{array}{l} \left( d+\delta +m\right) I+\frac{ru_2I}{1+bu_2I} \\ (p+d)R-Au_1-mI-\frac{ru_2I}{1+bu_2I} \\ \beta SI+\mathrm{d}S-pR-A(1-u_1) \\ \end{array} \right) .$

Now the Jacobian matrices of $\varPhi$ and $\varPsi$ at the disease-free equilibrium are calculated as

$$\begin{aligned} J(\varPhi ,E^0)=F=\left( \begin{array}{lll} \frac{A \beta \{d(1-u_1)+p\}}{d(d+p)} \quad &{} \quad 0 &{} \quad 0\\ 0 \quad &{} \quad 0 &{} \quad 0\\ 0 \quad &{} \quad 0 &{} \quad 0\\ \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} J(\varPsi ,E^0)=V=\left( \begin{array}{lll} ru_2+d+\delta +m &{} 0 &{} \quad 0 \\ -(m+ru_2) &{} p+d &{} \quad 0 \\ \frac{\beta A\{d(1-u_1)+p\}}{d(d+p)} &{} -p &{} \quad d\\ \end{array} \right) . \end{aligned}$$

Hence, the basic reproduction number which is calculated by the spectral radius of the matrix $(FV^{-1})$ is given by

$$\begin{aligned} R_0^0= \frac{A \beta \{d(1-u_1)+p\}}{d(d+p)(d+\delta +m+ru_2)}. \end{aligned}$$

3.2.2 Existence and stability criteria of equilibrium points

From the quadratic equation (4), it is evident that $c_3<0$ or $> 0$ according to $R_0^0 >1$ or $< 1$. So we may come to the following conclusions:

• 1. If $c_1$ is zero, then Eq. (4) gives a unique value of I and the corresponding equilibrium is feasible if and only if $R_0^0>1.$

• 2. If $c_1\ne 0$, then if

  • (a) $c_2<0$ and $R_0^0<1$, the quadratic equation (4) may have two positive roots for I and in this situation the system has two positive endemic equilibria $E_1^0(S^1,I^1,R^1)$ and $E_2^0(S^2,I^2,R^2).$

  • (b) $R_0^0>1$, then there is exactly one change of sign of Eq. (4) and from Descartes’ rule of sign the system has only one unique feasible equilibrium $E_2^0(S^2,I^2,R^2)$.

In the next two theorems, we state the nature of the infection-free and infected equilibria for system (3).

Theorem 2

The infection-free steady state $E_0^0$of the model system (3) is locally asymptotically stable if $R_0^0<1$and unstable if $R_0^0>1.$

Proof

The characteristic equation of the model system (3) around the infection-free steady state is obtained as

$$\begin{aligned} (\lambda +d)(\lambda +p+d)\left( \lambda -(\beta S^0-(d+\delta +m+ru_2))\right) =0. \end{aligned}$$

Clearly, the above equation has all negative roots if $\beta S^0-(d+\delta +m+ru_2)\le 0$, i.e., if $R_0^0<1$. Hence, the system is asymptotically stable if $R_0^0<1$ and unstable if $R_0^0>1.$$\square$

Theorem 3

The endemic equilibrium point $E_2^0$is locally asymptotically stable if $R_0^0>1$and $\frac{ru_2}{(1+bu_2I^2)^2}>\beta S^2$.

Proof

See “Appendix 1.” $\square$

Note Here, the infection-free steady state moves from stable state to unstable state as $R_0^0$ crosses to 1. Hence, it is concluded that the system passes through a bifurcation at $R_0^0=1$ around the disease-free equilibrium, known as backward bifurcation (detailed calculation is given in Sect. 3.6).

In Fig. 2, we present the phenomenon that system (3) is asymptotically stable at both infection-free and endemic steady states for different parametric conditions.

Fig. 2

Solution curves at both infection-free and infected steady states. Parameter set is $A=0.5,u_1=0.6,r=0.2,u_2=0.5,m=0.03,d=0.01,\delta =0.0014,p=0.78,b=0.005.$ When $\beta =0.001$, $R_0^0<1$ and when $\beta =0.005$, $R_0^0>1$

3.3 When only susceptible individuals dispersal occurs

In this situation, the model system (1) becomes

$$\begin{aligned} \frac{\mathrm{d}S_1}{\mathrm{d}t}& {}= A(1-u_1)-\beta S_1I_1-\mathrm{d}S_1+pR_1-\alpha S_1 +\alpha S_2, \nonumber \\ \frac{\mathrm{d}I_1}{\mathrm{d}t}& {}= \beta S_1 I_1-(d+\delta )I_1 -mI_1-\frac{ru_2I_1}{1+bu_2I_1}, \nonumber \\ \frac{\mathrm{d}R_1}{\mathrm{d}t}& {}= Au_1+mI_1+\frac{ru_2I_1}{1+bu_2I_1}-pR_1-\mathrm{d}R_1, \nonumber \\ \frac{\mathrm{d}S_2}{\mathrm{d}t}& {}= A(1-u_1)-\beta S_2I_2-\mathrm{d}S_2+pR_2-\alpha S_2 +\alpha S_1, \nonumber \\ \frac{\mathrm{d}I_2}{\mathrm{d}t}& {}= \beta S_2 I_2-(d+\delta )I_2 -mI_2-\frac{ru_2I_2}{1+bu_2I_2}, \nonumber \\ \frac{\mathrm{d}R_2}{\mathrm{d}t}& {}= Au_1+mI_2+\frac{ru_2I_2}{1+bu_2I_2}-pR_2-\mathrm{d}R_2. \end{aligned}$$

(5)

After analyzing the above system, it can be concluded that the coordinates of disease-free equilibrium are $E_0^1(S_1^1,0,R_1^1,S_2^1,0,R_2^1)$ and two endemic equilibrium points are $E_1^1(S_1^{*1},I_1^{*1},R_1^{*1},S_2^{*1},I_2^{*1},R_2^{*1})$ and $E_2^1(S_1^{1*},I_1^{1*},R_1^{1*},S_2^{*1},I_2^{*},R_2^{*1})$ where $S_1^1=S_2^2=S^0$, $R_1^1=R_1^2=R^0$, $S_1^{1*,*1}=S_2^{1*,*1}=S^{1,2}$, $I_1^{1*,*1}=I_2^{1*,*1}=I^{1,2}$, $R_1^{1*,*1}=R_2^{1*,*1}=R^{1,2}$. Again applying the next-generation matrix method as earlier, basic reproduction number $R_0^1$ is evaluated as

$$\begin{aligned} R_0^1=\rho (FV^{-1})=\frac{A\beta \{d(1-u_1)+p\}}{d(d+p)(d+\delta +m+ru_2)}. \end{aligned}$$

Next, we investigate the stability of all the feasible equilibria.

Theorem 4

The infection-free steady state $E_0^1$is locally asymptotically stable (unstable) if $R_0^1<1(>1)$.

Proof

The Jacobian matrix of the model system (5) at $E_0^1$ is calculated as

$$\begin{aligned} J(E_0^1)=\left( \begin{array}{ll} A_3 &{}\quad B \\ B &{}\quad A_3 \\ \end{array} \right) \end{aligned}$$

(6)

where

$$\begin{aligned} A_3=\left( \begin{array}{lll} -(d+\alpha ) &{} \quad -\beta S^0 &{} \quad p \\ 0 &{} \quad \beta S^0-(d+\delta +m+ru_2) &{} \quad 0 \\ 0 &{} \quad m+ru_2 &{} \quad -(d+p) \\ \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} B=\left( \begin{array}{lll} \alpha &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 \\ \end{array} \right) . \end{aligned}$$

Following Cui et al. (2006), we may state that the eigenvalues of system (5) are the same as those of the matrices $A_3+B$ and $A_3-B$ where

$$\begin{aligned} A_3+B=\left( \begin{array}{lll} -d &{} \quad -\beta S^0 &{} \quad p \\ 0 &{} \quad \beta S^0-(d+\delta +m+ru_2) &{} \quad 0 \\ 0 &{} \quad m+ru_2 &{} \quad -(d+p) \\ \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} A_3-B=\left( \begin{array}{lll} -(d+2\alpha ) &{} \quad -\beta S^0 &{} \quad p \\ 0 &{} \quad \beta S^0-(d+\delta +m+ru_2) &{} \quad 0 \\ 0 &{} \quad m+ru_2 &{} \quad -(d+p) \\ \end{array}\right) . \end{aligned}$$

The characteristic polynomial of the matrix $A_3+B$ is obtained as $(\lambda +d+p)(\lambda +d+\delta +m+ru_2-\beta S^0)(\lambda +d)=0$, and that of the matrix $A_3-B$ is $(\lambda +d+2 \alpha ) (\lambda +p+d) (\lambda +\delta +d+m+ru_2-\beta S^0)=0$, and all the roots of both the matrices are negative if $R_0^1<1$.

Therefore, all the eigenvalues of system 5 are negative around the disease-free equilibrium. Hence the theorem is proved. $\square$

The stability analysis of the endemic state of system (5) will be investigated in the following theorem.

Theorem 5

The endemic steady state $E_2^1$is locally asymptotically stable if $R_0^1>1$and $\frac{ru_2}{(1+bu_2I_1^{1*})^2}>\beta S_1^{1*}$.

Proof

See “Appendix 2.” $\square$

Note System (5) also passes through a backward bifurcation around its infection-free state $E_0^1.$ Details regarding the backward bifurcation phenomenon are presented in Sect. 3.6.

In Fig. 3, we represent the stability criteria of both the feasible equilibria of system (5).

Fig. 3

Solution curves of system (5) at both the infection-free and infected steady states. The parameters are $A=0.5,r=0.2,u_1=0.6,m=0.03,u_2=0.5,d=0.01,\delta =0.0014,p=0.78,b=0.005,\alpha =0.3.$ When $\beta =0.001$, $R_0^1<1$ and when $\beta =0.005$, $R_0^1>1$

3.4 When population dispersal occurs for all classes

Now we discuss the original model (1) to study the transport-related infection when the populations travel among the cities.

3.4.1 Steady states and their stability analysis

The system possesses a disease-free steady state $E_0^2(S_1^2,0,R_1^2,S_2^2,0,R_2^2)$, where $S_1^2=S_2^2=S^0$, and $R_1^2=R_2^2=R^0$ and two endemic equilibria, namely $E_1^2(S_1^{*2},I_1^{*2},R_1^{*2},S_2^{*2},I_2^{*2},R_2^{*2})$ and $E_2^2(S_1^{2*},I_1^{2*},R_1^{2*},S_2^{2*},I_2^{2*},R_2^{2*})$, where

$$\begin{aligned} S_1^{*2,2*}& {}= S_2^{*2,2*}\\& {}= \frac{ru_2+d+\delta +m+bu_2I_1^{*2,2*}(d+\delta +m)}{(1+bu_2I_1^{*2,2*})(\beta +\gamma \alpha )},\\ R_1^{*2,2*}& {}= R_2^{*2,2*}\\& {}= \frac{Au_1+I_1^{*2,2*}(Abu_1u_2+m+ru_2+mbu_2I_1^{*2,2*})}{(d+p)(1+bu_2I_1^{*2,2*})},\\ I_1^{*2,2*}& {}= I_2^{*2,2*}. \end{aligned}$$

Here, $I_1^{*2}$ and $I_1^{2*}$$\left( I_1^{*2}\le I_1^{2*}\right)$ are the roots of the quadratic equation

$$\begin{aligned} a_1 I^2+a_2 I+a_3=0, \end{aligned}$$

(7)

where $a_1=bu_2(\beta +\gamma \alpha )\{d(d+\delta +m)+(d+\delta )p\}$, $a_2=\{(\beta+\gamma \alpha)(d+\delta+m+ru_2)+d(d+\delta+m)bu_2\}(d+p)+(\beta+\gamma \alpha)Abu_1u_2d-(\beta+\gamma \alpha)\{Abu_2(p+d)+p(m+ru_2)\}$, $a_3=d(d+p)(d+\delta +m+ru_2)-A(\beta +\gamma \alpha )\{d(1-u_1)+p\}.$

The threshold quantity $R_0^2$ of the model system (1) is obtained as $R_0^2=\rho (FV^{-1})=\frac{(\beta +\gamma \alpha )S^0}{(d+\delta +m+ru_2)},$ where $S^0=A \frac{d(1-u_1)+p}{d(d+p)}$. Here, the existence criteria of the endemic equilibrium are the same as for system (5).

Next, we discuss the stability of different equilibria of 1.

Theorem 6

The disease-free steady state $E_0^2$ is locally asymptotically stable if $R_0^2<1.$

Proof

The Jacobian matrix of the model system (1) around the infection-free state $E_0^2$ is obtained as $J(E_0^2)=\left( \begin{array}{ll} P &{} \quad Q \\ Q &{} \quad P \\ \end{array} \right)$ where

$$\begin{aligned}P=\left( \begin{array}{lll} -(d+\alpha ) &{} \quad -(\beta S^0) &{} \quad p \\ 0 &{} \quad \beta S^0-(d+\delta +m+\alpha +ru_2) &{} \quad 0 \\ 0 &{} \quad m+ru_2 &{} \quad -(p+d+\alpha ) \\ \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} Q=\left( \begin{array}{lll} \alpha &{} \quad -\gamma \alpha S^0 &{} \quad 0 \\ 0 &{} \quad \alpha +\gamma \alpha S^0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad \alpha \\ \end{array} \right) .\end{aligned}$$

Now

$$\begin{aligned} P+Q=\left( \begin{array}{lll} -d &{} \quad -(\beta +\gamma \alpha )S^0 &{} \quad p \\ 0 &{} \quad (\beta +\gamma \alpha )S^0-(d+\delta +m+ru_2) &{} \quad 0 \\ 0 &{} \quad m+ru_2 &{} \quad -(p+d) \\ \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} P-Q=\left( \begin{array}{lll} -(d+2 \alpha ) &{} \quad -(\beta -\gamma \alpha )S^0 &{} \quad p \\ 0 &{} \quad (\beta -\gamma \alpha )S^0-(d+\delta +m+ru_2+2 \alpha ) &{} \quad 0 \\ 0 &{} \quad m+ru_2 &{} \quad -(p+d+2\alpha ) \\ \end{array} \right) .\end{aligned}$$

The characteristic equations of the matrices $P+Q$ and $P-Q$ are given in the following:

$$\begin{aligned}&(\lambda +d)(\lambda +p+d)\nonumber \\&\quad \left( \lambda -(\beta +\gamma \alpha )S^0+(d+\delta +m+ru_2)\right) =0, \end{aligned}$$

(8)

$$\begin{aligned}&(\lambda +d+2\alpha )(\lambda +p+d+2 \alpha )\left( \lambda -(\beta -\gamma \alpha )S^0\nonumber \right. \\&\quad \left. +(d+\delta +m+ru_2+2\alpha )\right) =0. \end{aligned}$$

(9)

The roots of Eq. (8) are negative if $(d+\delta +m+ru_2)-(\beta + \gamma \alpha )S^{0}>0$, i.e., if $R_0^2<1$. Again all the roots of (9) are negative if $(\beta -\gamma \alpha )S^{0}-(d+\delta +m+ru_2+2\alpha )<0$, i.e., if $\frac{(\beta -\gamma \alpha )S^0}{d+\delta +m+ru_2+2 \alpha }<R_0^2<1.$ Therefore, all the eigenvalues of $J(E_0^2)$ are negative for $R_0^2<1$. Hence, the theorem is proved. $\square$

Next, we state the stability conditions of the endemic steady state in the next theorem.

Theorem 7

The endemic steady state $E_2^2$is locally asymptotically stable if $R_0^2>1$, $\beta >\gamma \alpha$and $\frac{ru_2}{(1+bu_2I_1^{2*})^2}>(\beta +\gamma \alpha )S_1^{2*}$

Proof

See “Appendix 3.” $\square$

Note In the above three cases, we see that there are one disease-free steady state and two endemic states. Disease-free steady state ($E_0^2$) is stable(unstable) if the reproduction number is less than (greater than) unity but out of two endemic equilibria, one which is smaller in magnitude($I_1^{*2}$) is always unstable and another($I_1^{2*}$) is stable under some parametric conditions.

In Fig. 4, we represent the solution curves of system 1.

Fig. 4

Solution curves of (1) at both infection-free and infected states. The parameters are $A=0.5,r=0.2,u_1=0.6,\delta =0.0014, u_2=0.5,m=0.03,d=0.01,p=0.78,b=0.005,\alpha =0.3$ (when $\beta =0.001$, $R_0^2<1$ and when $\beta =0.005,$$R_0^2>1)$

3.5 Relationship among different reproduction numbers

As our intention is to study the impact of human mobility on the transmission dynamics of infectious diseases, here we compare the basic reproduction number $R_0^2$ due to populations dispersal of all classes of population with $R_0^0$ when no population dispersal occurs. It has been already observed that the basic reproduction numbers are equal in the case of only when susceptible population dispersal occurs and when no population dispersal occurs. Further, from the expressions of $R_0^2$ and $R_0^0,$, it is found that $R_0^2>R_0^0$ for $\gamma >0$ and $R_0^2=R_0^0$ for $\gamma =0$. Further, as $\frac{\partial R_0^2}{\partial \gamma }=\frac{\alpha S_1^2}{d+\delta +m+ru_2}>0$, so $R_0^2$ increases as $\gamma$ increases. As for the higher values of basic reproductive ratio, it is hard to control the disease. Thus, we may conclude that dispersal of populations would make hard to control the disease compare to nondispersal case.

3.6 Backward bifurcation

Here, we discuss the details of backward bifurcation of the model system (1). It has been already noticed that for $R_0^2<1$, system (1) gives two feasible steady states. Next, we state the occurrence of backward bifurcation depending upon some parametric conditions.

Theorem 8

System (1) undergoes a backward bifurcation at $R_0^2=1$if and only if $a_2<0$ [Eq. (7)].

Proof

For sufficiency, let $y=f(x)=a_1x^2+a_2x+a_3$. Now at $R_0^2=1$, $a_3=0$, and the function f(x) passes through the origin. For $a_2<0$, the function $f(x)=0$ has a positive root. If we increase the value of $a_3$ from 0 to $0^+$, the function $f(x)=0$ has two positive roots in some open interval of $a_3$. Therefore, it can be proved that there exist two endemic equilibria when $R_0^2<1$ (for further details, see Jana et al. 2016a).

On the other hand, if $a_2\ge 0$ and $R_0^2<1$, the system has no positive real roots. This completes the proof. $\square$

In Fig. 5, we present the backward bifurcation scenario.

Fig. 5

Bifurcation diagram for the parameter $A=5,r=0.2,\beta =0.01, \alpha =0.004,d=0.1,m=0.01,p=0.01,b=0.01,u_1=0.1,\delta =0.03,u_2=0.28, \gamma =0.001$

4 Optimal control problem

It follows from the form of basic reproductive ratio that to control the disease, it is necessary to increase the treatment as well as the vaccination among the individuals. But the best strategy must be the one where infected individuals are to be reduced with minimum cost. In this regard, optimal control theory is an impressive and powerful tool in finding the best strategy. Here, our objective is to minimize the total infected population of two cities while keeping minimum cost associated with the effective vaccination and suitable treatment. Here, the costs include medicine and drugs, hiring of medical specialist, etc. Therefore, the optimal control theory can be applied to obtain a favorable treatment and vaccination strategy to provide the best protection with moderate cost (Collins and Govinder 2016). In this regard, the objective functional is given as:

$$\begin{aligned}&J(S_1,I_1,R_1,S_2,I_2,R_2,u_1,u_2)\nonumber \\&\quad =\min _{u_1,u_2}\int _{0}^{T}(A_1I_1+A_2I_2+A_3u_1^2+A_4u_2^2) \end{aligned}$$

(10)

subject to system (1).

Here, $A_i,\;i=1,2,3,4$ are the balancing coefficients in the objective functional. The first two terms represent the cost connected with the infected individuals of first and second cities, respectively, and the last two terms represent the cost associated with vaccination and treatment, respectively. We consider the controls $u_1$ and $u_2$ in quadratic forms. This particular form is considered to measure the acuteness of the side effects of the treatment and (see Joshi 2002; Bartl et al. 2010; Tchuenche et al. 2011; Kar and Jana 2013a, b; Laarabi et al. 2015; Collins and Govinder 2016).

Our main aim is to find the pair of optimal controls $(u_1^*,u_2^*)$ such that

$$\begin{aligned} J(u_1^*,u_2^*)=\underset{u_1,u_2\in \varTheta }{\mathrm{min}}J(u_1,u_2) \end{aligned}$$

(11)

where $\varTheta =\{(u_1,u_2){:}\,(u_1,u_2) \text{ is } \text{ Lebesgue } \text{ measurable } \text{ with } 0\le u_1(t),\;u_2(t) \le 1 \text{ for } t\in [0,T]\}$.

The Hamiltonian H is given by

$$\begin{aligned}&H(S_1,I_1,R_1,S_2,I_2,R_2) \nonumber \\&\quad = A_1I_1+A_2I_2+A_3u_1^2+A_4u_2^2\nonumber \\&\quad \quad +\,\lambda _1(t)\frac{\mathrm{d}S_1}{\mathrm{d}t}+\lambda _2(t)\frac{\mathrm{d}I_1}{\mathrm{d}t}\nonumber \\&\quad \quad +\,\lambda _3(t)\frac{\mathrm{d}R_1}{\mathrm{d}t} +\lambda _4(t)\frac{\mathrm{d}S_2}{\mathrm{d}t}\nonumber \\&\quad \quad +\,\lambda _5(t)\frac{\mathrm{d}I_2}{\mathrm{d}t}+\lambda _6(t)\frac{\mathrm{d}R_2}{\mathrm{d}t} \end{aligned}$$

(12)

where the co-state variables $\lambda _i(t)$ (for $i=1,2\ldots 6$) are to be found out using the following set of equations (see Pontryagin et al. 1962):

$$\begin{aligned} \frac{d\lambda _1(t)}{\mathrm{d}t}&=-\frac{\partial H}{\partial S_1} = -[\{-\beta I_1-\alpha -d \}\lambda _1(t)+\beta I_1 \lambda _2(t)\nonumber \\& \quad+\,\left( \alpha -\gamma \alpha I_1\right) \lambda _4(t)+\gamma \alpha I_1 \lambda _5(t) ] \nonumber \\ \frac{d\lambda _2(t)}{\mathrm{d}t}&=-\frac{\partial H}{\partial I_1} = -[A_1-\lambda _1 \beta S_1 -\lambda _2(d+\delta +\alpha +m-\beta S_{1}\nonumber \\&\quad+\,\frac{ru_2}{(1+bu_2I_{1})^2})\nonumber \\&\quad+\,\lambda _3(m+\frac{ru_2}{(1+bu_2I_{1})^2})-\lambda _4\gamma \alpha S_1+\lambda _5 \left( \alpha +\gamma \alpha S_1\right) ] \nonumber \\ \frac{d\lambda _3(t)}{\mathrm{d}t}&=-\frac{\partial H}{\partial R_1} \nonumber \\&= -[\lambda _1 p-\lambda _3 (p+d+\alpha )+\lambda _6 \alpha ] \nonumber \\ \frac{d\lambda _4(t)}{\mathrm{d}t}&=-\frac{\partial H}{\partial S_2} = -[\lambda _1(\alpha -\gamma \alpha I_2)\nonumber \\&\quad+\,\lambda _2\gamma \alpha I_2-\lambda _4(\beta I_2+\alpha +d)+\lambda _5 \beta I_2] \nonumber \\ \frac{d\lambda _5(t)}{\mathrm{d}t}&=-\frac{\partial H}{\partial I_2} = -[A_2-\lambda _1 \gamma \alpha S_2\nonumber \\&\quad+\,\lambda _2(\alpha +\gamma \alpha S_2)-\lambda _4 \beta S_2\nonumber \\&\quad +\,\lambda _5(\beta I_2-(d+\delta +\alpha +m+\frac{ru_2}{(1+bu_2I_2)^2}))\nonumber \\&\quad+\,\lambda _6(m+\frac{ru_2}{(1+bu_2I_2)^2} )] \nonumber \\ \frac{d\lambda _6(t)}{\mathrm{d}t}&=-\frac{\partial H}{\partial R_2} = -[\lambda _3 \alpha +\lambda _4 p-\lambda _6(p+d+\alpha )] \end{aligned}$$

(13)

with the transversality conditions

$$\begin{aligned} {\lambda _i(T)}=0, \quad i=1,2,3,4,5,6. \end{aligned}$$

(14)

Next, the existence of the optimal control pair is studied.

Theorem 9

System (10) has optimal control $\left( u_1^*(t),u_2^*(t)\right)$such that

$$\begin{aligned} J(I_1(t),I_2(t),u_1(t),u_2(t))=\underset{u_1,u_2}{{\rm min}}\,J\left( I_1(t),I_2(t),u_1(t),u_2(t)\right) \end{aligned}$$

subject to the system of Eq. (1).

Proof

Since all the state and co-state variables are nonnegative, the pair $(u_1(t),u_2(t))$ is also nonnegative. Here, also the control domain $\varTheta$ is bounded and closed. So, the optimal control is bounded and hence the existence of a pair of optimal control ($( u_1^*(t), u_2^*(t))$ that minimizes objective functional (10) subject to system (1) is confirmed. $\square$

Now the explicit values of the control parameters are determined in the next theorem.

Theorem 10

The favorable value of the two controls $(u_1^*,u_2^*)$ which reduces the functional J in the domain $\varTheta$ is obtained as $u_1^*=\text{ max }\{0,\text{ min }(\bar{u_1},1)\}$ and $u_2^*=\text{ max }\{0,\text{ min }(\bar{u_2},1)\}$ with $\bar{u_1}=\frac{A(\lambda _1+\lambda _4-\lambda _3-\lambda _6)}{2A_3}$ and $\bar{u_2}$ to be determined as the positive roots of the equation

$$\begin{aligned}&2A_4b^2(I_{1}^{*2})^{2}u_2^3+4A_4bI_{1}^{*2}u_2^2+2A_4u_2\\&\quad -\,rI_{1}^{*2}(\lambda _2+\lambda _5-\lambda _3-\lambda _6)=0. \end{aligned}$$

Proof

Using conditions $\partial H/\partial u_1=0$ and $\partial H/\partial u_2=0$, we obtain the optimal controls $u_1(=\bar{u_1})$ and $u_2(=\bar{u_2})$. On the other hand, these two controls are bounded with lower and upper bound as 0 and 1, respectively, i.e., $u_1=0$ if $\bar{u_1}<0$ and $u_1=1$ if $\bar{u_1}>1$, otherwise $u_1=\bar{u_1}$. Similar result is for the control parameter $u_2$ also. Hence, we obtain the optimum result of the objective functional J [defined in (10)] for the controls pair $(u_1^*,u_2^*)$. $\square$

As we have established that there exists a solution of the system of differential equations (1) and (13), let us assume that $\bar{S_1},\;\bar{I_1},\;\bar{R_1}\;\bar{S_2},\bar{I_2},\;\bar{R_2}$ are the solutions of the initial value problem (1) and $\bar{\lambda _i};\;i=1,2,\ldots ,6$ are the solutions of final value system (13). Next, with the help of computer simulation, some numerical solutions of the optimal control problem are provided.

4.1 Numerical experiments based on the optimal control problem

In this section, we present some numerical simulations using a simulated parameter set $A_1=A_2=A_3= A_4=10, b=0.12, A=50, d=0.05, \alpha =0.012, \beta =0.03, \gamma =0.31, m=0.0953, \delta =0.025, r=2, p=0.018.$ Further, we consider the time duration as 200 units, for which the optimal control is applied. We make a comparison among the four different cases such as (1) only vaccination is applied, (2) only treatment is applied, (3) both the controls are applied simultaneously and (4) no control is applied.

Using Runge–Kutta fourth-order iterative procedure, we solve the original system (1) and the adjoint Eq. (13) simultaneously. We solve the initial value problem (1) using Runge–Kutta forward procedure, whereas Runge–Kutta backward iterative scheme is applied to find the solution of system (13) (see Lenhart and Workman 2007; Jung et al. 2002).

We present the various figures representing the model prediction under different combinations of controls. In Fig. 6, variation in the susceptible population is presented and it is observed that the total size of the susceptible people reduces when the optimal control is applied in comparison to the no control situation. Our ultimate goal is to reduce the infected population, and in Fig. 7, we compare the outcomes of both the cities among the infected population cases, and it is observed that a significant amount of infected populations is reduced when the two controls are adopted optimally in comparison with any of the other three combinations. Similarly, when applying the optimal control among the recovered individuals (Fig. 8), it is observed that application of both the controls provides a sound improvement in the quantity of recovered populations compared to no control case. The graph representing recovered populations for both the cases is strictly monotonically increasing compared to that for no control scenario, which is always a strictly decreasing curve. However, the recovered populations also increase for one control situation but their rate of increment is less compared to both the control cases. In Fig. 9, time evolution of both the control parameters $u_1$ and $u_2$ is presented, and in Fig. 10, time evolution of adjoint variables is presented. Similar to both the control variables, it is easy to substantiate that all the six adjoint variables evaporate at their corresponding final time.

Fig. 6

Comparison of the susceptible populations of each city with different controls

Fig. 7

Comparison of the infected populations of each city with different controls

Fig. 8

Comparison of the recovered populations of each city with different controls

Fig. 9

Time evolution of two controls $u_1$ and $u_2$

Fig. 10

Variation in adjoint variables with time

In Fig. 11, we compare the impact of the parameter $\gamma$ on the infected populations. It is shown that the effect of $\gamma$ is directly proportional to the increase in the infected individuals in each city as lower value of that parameter would enable to reduce the infected populations from each city.

Fig. 11

Variations in infected populations for both the cities as $\gamma$ varies

4.2 Illustrations connected to SARS

In this section, the results are compared with the 2003 SARS epidemic scenario, which occurred in several regions of the eastern and southern Asia. Denphedtnong et al. (2013) presented the cumulative population frequency of SARS in Hong Kong in 2003 for 54 days (within March and April). Here, we use the same values of the parameters as in Denphedtnong et al. (2013) and try to fit the parameter set in the proposed model. It is observed that it is a good model to explain the SARS at that time. In Fig. 12, the model is compared with the SARS outbreak at Hong Kong during 2003. The simulation result shows that our developed model almost approximates that disease dynamics. The parameters used for the simulation of SARS are $A=50,A_1=A_2=A_3=A_4=1,\beta =0.16,b=0.005 ,d=0.5,p= 0.078,\alpha = 0.32 ,\gamma =0.31,\delta =0.24,r=0.2,m=0.0953.$ Due to the absence of suitable vaccination of SARS in 2003 in Hong Kong, we take $u_1=0$.

Fig. 12

Correlation between model prediction and original data of SARS outbreak (where the dotted and solid lines represent original data and model prediction, respectively)

5 Cost-effectiveness study

As here both the vaccination and treatment control parameters are used optimally, in the process of optimal controlling, one must eager to obtain what is the best strategy among four available strategies, viz. application of no control, only treatment control, only vaccination control and both the controls together. In this regard, the cost-effectiveness analysis method is very popularly used to find out the most cost-effective strategy. Some well-known techniques to select the best cost-effective scheme can be found in Okosun et al. (2011, 2013), Agusto (2013), Kar et al. (2019). However, the three techniques, namely (1) infected averted ratio (IAR), (2) average cost-effectiveness ratio (ACER) and (3) incremental cost-effectiveness ratio (ICER), are widely used. Here, only the incremental cost-effectiveness ratio is considered to obtain the most cost-effective plan among the following strategies: (1) Strategy A : only vaccination control is used, (2) Strategy B: only treatment control is used and (3) Strategy C: both the treatment and vaccination controls are used.

5.1 Incremental cost-effectiveness ratio

Now we apply the ICER technique to identify the best cost-effective strategy. The main objective of this method is to make a comparison of the cost-effectiveness of two competing intervention strategies in increasing rank. The ICER values of the different strategies are obtained following the work of Agusto (2013).

From Table 1, it is observed that the ICER value of strategy A is lower than that of strategy B. It implies that scheme B is more costly and less effective compare to Strategy A. Hence, strategy B is excluded from the set of considerations. So now we can compare strategy A and strategy C using Table 2.

Table 1 ICER of all strategies

Table 2 ICER of strategy A and strategy C

From Table 2, it is noticed that the ICER value for the scheme C is lower than that of the strategy A, so strategy A is strongly dominated. This indicates that strategy A is more costly and less effective than strategy C. Therefore, we may conclude that scheme C (i.e., combination of both vaccination and treatment controls optimally) is more cost-effective than strategy A.

6 Concluding remarks

The development of socioeconomic status, globalization, tourism and population dispersal between two places cause the spread of various emerging infectious diseases. In the recent past, several diseases threaten to become epidemic due to population dispersal. In this perspective, a transport-related epidemic model is very much relevant to study. Jana et al. (2016b) proposed and analyzed an infectious disease model with population dispersal between two cities but the effect of treatment control is neglected in that article. But, treatment is an effective control measure and it is used frequently to control almost every infectious disease. From this perspective, in our present article, we formulate and study the behavior of an SIRS-type epidemic system incorporating the infection during transport with treatment control. All possibilities including (1) no population dispersal, (2) only susceptible population dispersal and finally (3) all classes of population dispersal are considered. It has been established that in each of the different cases, the system possesses a infection-free steady state and two possible endemic equilibria depending on some parametric conditions. The existence and the stability criteria of all the feasible equilibria are discussed. It is further shown that in each of the above three cases, the system undergoes a backward bifurcation. The qualitative behavior of a system with a backward bifurcation differs from that of a system with forward bifurcation. Since these behavior differences are important in planning how to control a disease, it is important to determine whether a system can have backward bifurcation so that proper control measure can be applied. The reason for the occurrence of backward bifurcations is consideration of nonlinear treatment function as observed in Jana et al. (2016a). Two most popular control measures to control the spread of infectious diseases are vaccination and treatment (e.g., medicine, surgery, hospitalization, etc). In the present model system, we use these two control measures, to eradicate the disease. The optimal control problem is designed and solved by Pontryagin’s minimum principle. As expected, we observe from our numerical experiment that the application of control is always a better choice than without controls.

An SIR model related to an epidemic system is not new; many researchers including Buonomo and Lacitignola (2011), Zhou et al. (2014), Laarabi et al. (2015), Jana et al. (2016a), etc., describe the epidemic system through SIR model. However, to the best of our knowledge, no attempt has been made to study the behavior of an SIR-type epidemic system considering population dispersal and joint effect of vaccination and treatment control measures. We have examined the joint impact of vaccination and treatment controls through optimal control strategies. In this regard, cost-effectiveness analysis plays an important role in determining the most effective strategy among the different available strategies. Some researchers including Okosun et al. (2011, 2013), Agusto (2013), etc., have used cost-effectiveness strategy with some great success. As here both the vaccination and treatment control parameters are used optimally, in the process of optimal controlling, one must eager to obtain what is the best strategy among four available strategies, viz. application of no control, only treatment control, only vaccination control and both the controls together. From the cost-effectiveness analysis, it is easy to claim that application of both the control measures optimally gives the best result from the point of view of minimizing the effect of the disease with least cost.

Without empirical data used in the model, it is difficult to make any perfect decision. However, our proposed model can be used to determine the optimal level of treatment and vaccination, possibility of backward bifurcation when the actual model parameters are available. The model with population dispersal proposed in this work is a better model to analyze an epidemic system compared to the mathematical models proposed by Cui et al. (2006), Liu and Takeuchi (2006), etc., in the sense of nonlinear saturated treatment function, optimal vaccination and treatment control, etc. Simulation works of this model deliver a very good approximation toward the SARS outbreak of Hong Kong in 2003. Other researchers such as Denphedtnong et al. (2013) and Jana et al. (2016b) also proposed their models which can be applied to describe SARS in 2003, but in our present work, we have established a good estimation of the epidemic SARS in 2003. Although for modeling purpose, in the present article, the population dispersal is considered between two cities only, but in our future research, we would consider multicity dispersal. Similarly, in our future research, we would also consider the demographic parameters of the cities are of different values and that would increase both the realistic phenomenon and the degree of complexity. But still we expect that our proposed model can be used to describe some infectious diseases which threaten to become epidemic mainly due to population scattering.

Appendices

Appendix 1

For local stability analysis, we use the Routh–Hurwitz criteria and we consider the Jacobian matrix of (3) at $E_{2}^{0}(S^{2},I^{2},R^{2})$

$$\begin{aligned} J=\left( \begin{array}{lll} a_{11} &{} \quad a_{12} &{} \quad a_{13} \\ a_{21} &{} \quad a_{22} &{} \quad 0 \\ 0 &{} \quad a_{32} &{} \quad a_{33} \\ \end{array} \right) . \end{aligned}$$

where $a_{11}=-\beta I^{2}-d, a_{12}=-\beta S^{2}, a_{13}=p, a_{21}=\beta I^{2}, a_{22}=\beta S^{2}-(d+\delta +m)-\frac{r u_{2}}{(1+b u_{2} I^{2})^{2}}, a_{23}=0, a_{31}=0, a_{32}=m+\frac{r u_{2}}{(1+b u_{2} I^{2})^{2}}, a_{33}=-(p+d)$.

Now let the characteristic equation of the Jacobian matrix J be $\lambda ^3+c_1\lambda ^2+c_2\lambda +c_3=0$, where

$$\begin{aligned}c_1&=-(a_{11}+a_{22}+a_{33}),\\ c_2&=a_{11}a_{22}+a_{22}a_{33}+a_{33}a_{11}-a_{12}a_{21}\,{{\rm and}}\\ c_3&=a_{12}a_{21}a_{33}-a_{13}a_{21}a_{32}-a_{11}a_{22}a_{33}.\end{aligned}$$

Then, as stated in the Routh–Hurwitz criteria, the eigenvalues of J have negative real parts if $c_{1}$, $c_{3}$ and $c_1c_2-c_3$ all are positive.

Now we calculate the coefficients as

$$\begin{aligned} c_{1}& {}= p+\delta +m+3d+\beta I^2+\frac{ru_2}{(1+bu_2I^2)^2}-\beta S^2,\\ c_2& {}= (\beta I^2+d)(p+d)+\frac{ru_2 \beta I^{2}}{(1+bu_2I^2)^2}\\&\quad +\, (d+\delta +m)(\beta I^2+2d+p)\\&\quad +\,(2d+p) \left( \frac{ru_2}{(1+bu_2I^2)^2} -\beta S^2 \right) \hbox { and}\\ c_3& {}= (p+d)\left( \beta ^{2} S^2 I^2 +p\beta I^2+(\beta I^2+d)(d+\delta +m)\right) \\&\quad +\,(\beta I^2+d) (p+d) \left( \frac{ru_2}{(1+bu_2I^2)^2}-\beta S^2 \right) . \end{aligned}$$

Also,

$$\begin{aligned} c_1c_2-c_3& {}= \left( \frac{ru_2}{(1+bu_2I^2)^2}-\beta S^2 \right) ^{2} (\beta I^{2}+p+2d)\\&\quad +\,\left( \frac{ru_2}{(1+bu_2I^2)^2}-\beta S^2 \right) \left( \beta ^{2} S^{2} I^{2}+(\beta I^{2}+\right. p\\&\quad \left. +\,2d)(p+2\delta +4d+2m+\beta I^{2})\right) \\&\quad +\,(p+\delta +m+3d+\beta I^{2})(d+\delta +m)\\&\quad (\beta I^{2}+p+2d)+\beta ^{2} I^{2} S^{2}\\&\quad (\delta +m+2d+\beta I^{2})+(p+d)((\beta I^{2}+d)\\&\quad (2d+\beta I^{2})+pd) \end{aligned}$$

Now it is easy to note that for $\frac{ru_2}{(1+bu_2I^2)^2}>\beta S^2$, $c_{1},c_{2},c_{3}$ all are positive and also $c_1c_2>c_3$. Thus, for $\frac{ru_2}{(1+bu_2I^2)^2}>\beta S^2$, Routh–Hurwitz criteria are satisfied. Hence, the endemic steady state $E_{2}^{0}$ is locally asymptotically stable for $R^{0}_{0}>1$ and $\frac{ru_2}{(1+bu_2I^2)^2}>\beta S^2$.

Appendix 2

The Jacobian matrix of system (5) at $E_2^1$ is given by

$$\begin{aligned} J(E_2^1)=\left( \begin{array}{ll} A_4 &{} \quad B \\ B &{} \quad A_4 \\ \end{array} \right) \end{aligned}$$

where

$$\begin{aligned} A_4=\left( \begin{array}{lll} -(\beta I_1^{1*}+d+\alpha ) &{} \quad -\,\beta S_1^{1*} &{} \quad p \\ \beta I_1^{1*} &{} \quad \beta S_1^{1*} -(d+\delta +m)-\frac{ru_2}{(1+bu_2I_1^{1*})^2} &{} \quad 0 \\ 0 &{} \quad m+\frac{ru_2}{(1+bu_2I_1^{1*})^2} &{} \quad -(d+p) \\ \end{array} \right) \end{aligned}$$

and B is the same as earlier. We observe that $A_4+B$ is similar as $J(E_2^0)$ and the detailed proof is similar as given in Appendix 1. Hence, $A_4+B$ is stable if $R^{1}_{0}>1$ and $\frac{ru_2}{(1+bu_2I_1^{1*})^2}>\beta S_1^{1*}$.

Now

$$\begin{aligned}A_4-B=\left( \begin{array}{lll} -(\beta I_1^{1*}+d+2\alpha ) &{} \quad -\beta S_1^{1*} &{} \quad p \\ \beta I_1^{1*} &{} \quad \beta S_1^{1*} -(d+\delta +m)-\frac{ru_2}{(1+bu_2I_1^{1*})^2} &{} \quad 0 \\ 0 &{} \quad m+\frac{ru_2}{(1+bu_2I_1^{1*})^2} &{} \quad -(d+p) \\ \end{array} \right) .\end{aligned}$$

Thus, it is enough to verify that the matrix $A_4-B$ fulfills the Routh–Hurwitz criteria. We already checked that $R_0^0=R_0^1$. Now let the characteristic equation of the matrix $A_4-B$ be $\lambda ^3+d_1\lambda ^2+d_2\lambda +d_3=0$, then

$$\begin{aligned} d_1& {}= 3d+2 \alpha +p+\delta +m+\beta I_1^{1*}+\left( \frac{ru_2}{(1+bu_2I_1^{1*})^2}-\beta S_1^{1*}\right) ,\\ d_2& {}= (\beta I_1^{1*}+d+2\alpha )(p+d)+(\beta I_1^{1*}+2d+2\alpha +p ) (d+\delta +m)\\&\quad +\,\frac{ru_2 \beta I_1^{1*}}{(1+bu_2I_1^{1*})^2}+(p+2d+2\alpha )\\&\quad \,\left( \frac{ru_2}{(1+bu_2I_1^{1*})^2}-\beta S_1^{1*}\right) \hbox { and}\\ d_3& {}= (p+d)\left( \beta ^{2} S_1^{1*} I_1^{1*} +p\beta I_1^{1*} +(\beta I_1^{1*}+d+2\alpha )(d+\delta +m)\right) \\&\quad +\,(\beta I_1^{1*}+d+2\alpha ) (p+d) \left( \frac{ru_2}{(1+bu_2I_1^{1*})^2}-\beta S_1^{1*} \right) . \end{aligned}$$

Also after some simplifications, we obtain

$$\begin{aligned} d_1d_2-d_3& {}= \left( \frac{ru_2}{(1+bu_2I_1^{1*})^2}-\beta S_1^{1*} \right) ^{2} (\beta I_1^{1*}+p+2d+2\alpha )\\&\quad +\,\left( \frac{ru_2}{(1+bu_2I_1^{1*})^2}-\beta S_1^{1*} \right) \left( \beta ^{2} S_1^{1*}I_1^{1*}\right. \\&\quad +\,(\beta I_1^{1*}+p+2d+2\alpha )\\&\quad \left. (p+2\delta +4d+2m+2\alpha +\beta I_1^{1*})\right) \\&\quad +\,(p+\delta +m+3d+\beta I_1^{1*}+2\alpha )(d+\delta +m)\\&\quad \,(\beta I_1^{1*}+p+2d+2\alpha )\\&\quad +\,\beta ^{2} S_1^{1*}I_1^{1*}(\delta +m+2d+\beta I_1^{1*}+2\alpha )\\&\quad +\,(p+d)\left( (\beta I_1^{1*}+d+2\alpha )(2d+\beta I_1^{1*}+2\alpha )\right. \\&\left. \quad +\,p(d+2\alpha )\right) \end{aligned}$$

Now it is easy to observe that for $\frac{ru_2}{(1+bu_2I_1^{1*})^2}>\beta S_1^{1*}$, $d_{i}>0, i=1,2,3$ and $d_1d_2>d_3$. Then, all the conditions of Routh–Hurwitz criteria are satisfied for $\frac{ru_2}{(1+bu_2I_1^{1*})^2}>\beta S_1^{1*}$. Hence, $A_4-B$ is stable for $R_0^1>1$, $\frac{ru_2}{(1+bu_2I_1^{1*})^2}>\beta S_1^{1*}$.

Therefore, combining the above two cases, we conclude that the endemic steady state $E_2^1$ is locally asymptotically stable if $R_{0}^{1}>1$ and $\frac{ru_2}{(1+bu_2I_1^{1*})^2}>\beta S_1^{1*}$. Hence, the theorem is proved.

Appendix 3

The Jacobian matrix of system (1) at $E_2^2$ is given by

$$\begin{aligned} J(E_2^2)=\left( \begin{array}{ll} P_3 &{} \quad Q_3 \\ Q_3 &{} \quad P_3 \\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} P_3=\left( \begin{array}{lll} -(d+\beta I_1^{2*}+\alpha ) &{} \quad -(\beta S_1^{2*}) &{} \quad p \\ \beta I_1^{2*} &{} \quad \beta S_1^{2*}-(d+\delta +m+\alpha +\frac{ru_2}{(1+bu_2I_1^{2*})^2}) &{} \quad 0 \\ 0 &{} \quad m+\frac{ru_2}{(1+bu_2I_1^{2*})^2} &{} \quad -(p+d+\alpha ) \\ \end{array} \right) \end{aligned}$$

and

$$\begin{aligned} Q_3=\left( \begin{array}{lll} \alpha -\gamma \alpha I_1^{2*} &{} \quad -\gamma \alpha S_1^{2*} &{} \quad 0 \\ \gamma \alpha I_1^{2*} &{} \quad \alpha +\gamma \alpha S_1^{2*} &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad \alpha \\ \end{array} \right) . \end{aligned}$$

Now to check that the matrix $P_3+Q_3$ satisfies the Routh–Hurwitz criteria, we consider the characteristic equation of the matrix as $\lambda ^3+m_1\lambda ^2+m_2\lambda +m_3=0$, where

$$\begin{aligned} m_{1}& {}= p+\delta +m+3d+\left( \beta +\gamma \alpha \right) I_1^{2*}\\&\quad +\,\frac{ru_2}{(1+bu_2I_1^{2*})^2}-\left( \beta +\gamma \alpha \right) S_1^{2*},\\ m_2& {}= ((\beta +\gamma \alpha )I_1^{2*}+d)(p+d)+\frac{ru_2 (\beta +\gamma \alpha )I_1^{2*}}{(1+bu_2I_1^{2*})^2}\\&\quad +\,(d+\delta +m)((\beta +\gamma \alpha ) I_1^{2*}+2d+p)\\&\quad +\,(2d+p) \left( \frac{ru_2}{(1+bu_2I_1^{2*})^2}- (\beta +\gamma \alpha )S_1^{2*} \right) \hbox { and }\\ m_3& {}= (p+d)\left( (\beta +\gamma \alpha )^{2} S_1^{2*}I_1^{2*} +p(\beta +\gamma \alpha ) I_1^{2*} \right. \\&\quad \left. +\,(d+\delta +m) (d+(\beta +\gamma \alpha ) I_1^{2*})\right) \\&\quad +\,(p+d) (d+(\beta +\gamma \alpha ) I_1^{2*}) \left( \frac{ru_2}{(1+bu_2I_1^{2*})^2}- (\beta +\gamma \alpha )S_1^{2*} \right) . \end{aligned}$$

Also after some simplifications, we obtain

$$\begin{aligned}&m_1m_2-m_3\\&\quad =\left( \frac{ru_2}{(1+bu_2I_1^{2*})^2}-\beta S_1^{2*} \right) ^{2} ((\beta +\gamma \alpha ) I_1^{2*}+p+2d)\\&\qquad +\,\left( \frac{ru_2}{(1+bu_2I_1^{2*})^2}-\beta S_1^{2*} \right) \left( (\beta +\gamma \alpha )^{2} S_1^{2*}I_1^{2*}\right. \\&\qquad \left. +\,((\beta +\gamma \alpha ) I_1^{2*}+p+2d)(p+2\delta +4d+2m+(\beta +\gamma \alpha ) I_1^{2*})\right) \\&\qquad +\,(p+\delta +m+3d+(\beta +\gamma \alpha ) I_1^{2*})(d+\delta +m)\\&\qquad ((\beta +\gamma \alpha ) I_1^{2*}+p+2d)\\&\qquad +\,(\beta +\gamma \alpha )^{2} S_1^{2*} I_1^{2*}(\delta +m+2d+(\beta +\gamma \alpha ) I_1^{2*})\\&\qquad +\,(p+d)(((\beta +\gamma \alpha ) I_1^{2*}+d)(2d+(\beta +\gamma \alpha ) I_1^{2*})+pd). \end{aligned}$$

Now it is easy to note that if $\frac{ru_2}{(1+bu_2I_1^{2*})^2}>\left( \beta +\gamma \alpha \right) S_1^{2*}$, then $m_{i}>0,i=1,2,3$ and $m_{1}m_{2}>m_{3}$, i.e., the Routh–Hurwitz criteria are satisfied.

Now to check the eigenvalue of the matrix $P_3-Q_3$, we consider that the characteristic equation of the matrix $P_3-Q_3$ is $\lambda ^3+n_1\lambda ^2+n_2\lambda +n_3=0$ where

$$\begin{aligned} n_1& {}= p+\delta +m+3d+6\alpha +(\beta -\gamma \alpha )I_1^{2*}\\&\quad +\,\frac{ru_2}{\left( 1+bu_2I_2^{2*}\right) ^{2}}-(\beta -\gamma \alpha )S_1^{2*},\\ n_2& {}= (p+d+2\alpha ) \left( d+2\alpha +(\beta -\gamma \alpha ) I_1^{2*}\right) \\&\quad +\, (d+\delta +m+2\alpha ) \\& \quad \left( p+2d+4\alpha +(\beta -\gamma \alpha ) I_1^{2*}\right) \\&\quad +\,\frac{ru_2(\beta -\gamma \alpha ) I_1^{2*}}{\left( 1+bu_2I_1^{2*}\right) ^{2} }\\&\quad +\,\left( p+2d+4\alpha \right) \\& \quad \left( \frac{ru_2}{\left( 1+bu_2I_1^{2*}\right) ^{2} }\right. \\&\quad \left. -(\beta -\gamma \alpha ) S_1^{2*} \right) \hbox { and}\\ n_3& {}= (p+d+2\alpha ) \left( (\beta -\gamma \alpha )^{2}I_1^{2*}S_1^{2*}\right. \\&\quad +\,pI_1^{2*} (\beta -\gamma \alpha )+ (d+\delta +m+2\alpha )(d+2\alpha \\&\quad \left. +(\beta -\gamma \alpha )I_1^{2*})\right) \\&\quad +\, (p+d+2\alpha )(d+2\alpha +(\beta -\gamma \alpha )I_1^{2*}) \\& \quad \left( \frac{ru_2}{(1+bu_2I_1^{2*})^2}\right. \\&\quad \left. -(\beta -\gamma \alpha )S_1^{2*} \right) . \end{aligned}$$

Moreover, after some simplifications, we obtain

$$\begin{aligned}&n_1n_2-n_3\\&\quad =\left( \frac{ru_2}{(1+bu_2I_1^{2*})^2}-(\beta -\gamma \alpha ) S_1^{2*} \right) ^{2} \\&\qquad ((\beta -\gamma \alpha ) I_1^{2*}+p+2d+4\alpha )\\&\qquad +\,\left( \frac{ru_2}{(1+bu_2I_1^{2*})^2}-(\beta -\gamma \alpha ) S_1^{2*} \right) \left( (\beta -\gamma \alpha )^{2} S_1^{2*}I_1^{2*}\right. \\&\qquad +\,((\beta -\gamma \alpha ) I_1^{2*}+p+2d+4\alpha )\\&\left. \qquad (p+2\delta +4d+2m+8\alpha +(\beta -\gamma \alpha ) I_1^{2*})\right) \\&\qquad +\,(p+\delta +m+3d+6\alpha +(\beta -\gamma \alpha ) I_1^{2*})(d+\delta +m+2\alpha )\\&\qquad ((\beta -\gamma \alpha ) I_1^{2*}+p+2d+4\alpha )+(\beta -\gamma \alpha )^{2} S_1^{2*} I_1^{2*}\\&\qquad (\delta +m+2d+4\alpha +(\beta -\gamma \alpha ) I_1^{2*})\\&\qquad +\,(p+d+2\alpha )(((\beta -\gamma \alpha ) I_1^{2*}+2d+4\alpha )(d+2\alpha \\&\qquad +\,(\beta -\gamma \alpha ) I_1^{2*})+p(d+2\alpha )). \end{aligned}$$

Now if $\beta -\gamma \alpha >0$, and $\frac{ru_2}{(1+bu_2I_1^{2*})^2}>(\beta -\gamma \alpha )S_1^{2*}$, then $n_i>0, i=1,2,3$ and $n_1n_2>n_3$. Then, all the conditions of Routh–Hurwitz criteria are satisfied.

So, combining both the above two results, it may be concluded that the eigenvalues of $J(E_2^2)$ are all negative or have negative real part if $R_0^2>1$, $\beta >\gamma \alpha$ and $\frac{ru_2}{(1+bu_2I_1^{2*})^2}>(\beta +\gamma \alpha )S_1^{2*}$. Hence, the theorem is proved.