1 Introduction

A record of past events in human mankind shows that infectious disease has a profound effect on human populations, including their development and evolution. Individual’s health status is affected by many factors, such as the quantity of time spent in a specific place, availability and access to affordable health care, complex economic and social factors, educational attainments, and lifestyles. Despite significant advances in medical sciences, infectious disease affects both the human and animal population in many parts of the world. As we know, performing experiments on the population is forbidden one can use mathematical model to investigate the transmission, predict the outbreak and even control of epidemics [2]. At present, mathematical models are considered as one of the active topic in public health and biology to determine whether the epidemics can be broken out or not [37]. Many real-world systems often interact and influence each other. There is an enduring relationship between migration and the introduction of diseases. In past decades, many mathematical models were constructed to study the effect of the spatial heterogeneity and migration on disease transmission [13, 15, 18]. Hethcote (1976) [14] proposed two-patch epidemic model with population dispersal. Wang and Zhao [56] and references therein also described the dynamics of disease propagation between different patches resulting from population dispersal. These studies consider meta-population models, in which the population are subdivided into distinct patches, each of which are considered as homogeneous. This type of model formulation process is frequently used for understanding the transmission of disease between and within different population centers. One can use these models to examine the spatial dynamics of city-by-city transmission and to investigate the reason for high levels of synchronicity observed between town, cities, and so forth during disease outbreaks.

Complex network models is another emerging field that is widely studied to investigate epidemic spreading, including rumours, human disease and computer viruses. Complex network is a new branch in statistical physics which provides a reliable model for the intensive study of the epidemic spreading. In complex network modelling nodes represent individuals or organizations and link the interactions among them. Mathematical analysis of such models have revealed the importance of topology for investigating propagation dynamics. Liu et al. [33], Wen-Jie and Xing-Yuan [62] studied the epidemic spreading and discussed the credibility of homogeneous mixing hypothesis. Ren and Wang [46] proposed a network model with time-varying community structure. They found that the time of the epidemic outbreak depends mainly on the mobility rate of the individual. Wen-Jie and Yuan [60] proposed a novel model with two strategies for controlling epidemic disease: quarantine and message delivery. Nian et al. [40] constructed a dynamic network model based on Barabasi-Albert (BA), keeping the same total number of edges. They showed immunization based on node activity is effective and is more feasible in dynamic networks. Wang and Zhao [59] generalized the susceptible-Infected-Susceptible (SIS) model that explores the propagation of multi-messages by considering their correlation degree. These models provided very powerful results but did not display the complete local and global spatial spread dynamics.

These researches motivated our work, yet majority of them are focused on static network models. However, in reality our life is not static. We move from one city to another to perform our job etc. and then we come back to our own city and perform local random movement. The major drawback of these models is that they do not include spatial heterogeneity and local random movement which can also affect the spread of epidemics. The heterogeneity of the spatial environment is considered as an important contributing factor in propagating many contagious diseases. This is barely surprising as populations in actuality are not homogeneous: interactions between individuals are likely to have limited scope. As spatial spread of disease relies on complex interaction between distinct elements (like, diverse nature of a given population and the dynamics innate to a given pathogen/host interaction), mathematical models provide a quality conceptual structure with which emergence of spatial patterns and processes involved can be studied and explained. In modeling geographic effects or spatial dispersal of a disease, a discrimination is usually created between dispersal and diffusion models. Using partial differential equations, one can typically introduce spatial variation in epidemic models. A reaction–diffusion (RD) model describes the proliferation (reaction) and movement (diffusion) of individuals. By diffusion model, dissemination of infection to immediate adjoining neighbours can be studied. This mechanical–biological interaction within and surrounding cells has been previously incorporated into modelling cancer of brain, breast, kidney and pancreas. Here, we apply it to model spread of disease among two connected cities using a mechanically coupled RD model. The spatial spread of diseases like influenza [64], Ebola involves many unusual and distinct components. Therefore, modeling their spread is a complicated task.

The propagation of global pandemic diseases are affected by transportation, and is considered as one of the relevant and crucial problems on the epidemiological multi-group models. Over the last forty years, both the scope and process of migration have experienced significant shifts, and the majority of these changes have transformed the innate characteristics of migration-accompanied infectious disease. In this paper, an effort has been made to decipher the effect of migration on epidemic spread among heterogeneous cities coupled through reaction-diffusion modeling. The aim is to recommend some preventive health-policy measures during an outbreak. Asymptotic infection rate which displays a saturation effect have been rarely considered for network reaction-diffusion modeling [10]. The asymptotic infection rate, \(\frac{\beta I}{S+I+c}\), is a function of the number of infections present at a given point of time. This signifies the fact that the number of contacts an individual carrying the virus can have with other individuals reaches some finite maximum value due to the spatial or social distribution of the population and/or limitation of time. We believe that this is the first work that considers a two-patch reaction-diffusion epidemiological model to mimic the scenario of intra and intercity human dispersal. We also computed basic reproduction numbers for coupled reaction-diffusion systems. We emphasize that this rate and heterogeneous transmission rate has significant contributions to the dynamics of disease spread. Our mathematical analysis are inspired by [8, 9, 16, 21, 25,26,27, 30, 31, 43, 50, 61, 63].

The manuscript is organized as follows: In Sect. 2 two-city susceptible-infected-deceased (SID) model with global and local movement is formulated. In Sect. 3, the existence of equilibrium is analysed and reproduction number is calculated. Global stability using graph theory is discussed in Sect. 4. Numerical results are presented to confirm the analytical findings in Sect. 5. In Sect. 6, we summarize the main contributions of the work.

2 Formulation of epidemic model

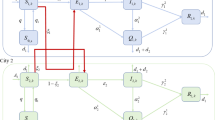
In the model introduced by Upadhyay et al. (2014) [54], there is no intercity travel. Communicable diseases such as sexual diseases and influenza can be passed on easily from one city to other cities. Therefore, considering the effect of both local (within city) and global (across city) population dispersal on the spread of epidemics are relevant and important. In this work, we considered two city models which are connected by road. We do not care about the dynamics taking place in connecting roads. A typical disease is captured by the following Susceptible-Infected-Deceased structure modelling:

$$\begin{aligned} \frac{dS}{dt}= & {} r S\left( 1-\frac{S+I}{K}\right) -\frac{\beta S I}{S+I+c}, \\ \frac{dI}{dt}= & {} \frac{\beta S I}{S+I+c}-a I, \\ \frac{dD}{dt}= & {} a I. \end{aligned}$$

We omit the equation D for further calculation since the above system does not depend on D. The following assumptions are taken into account while formulating the two city epidemiological model:

  1. (i)

    We considered the population that is organized and is interacting among two cities.

  2. (ii)

    Let \((S_1,I_1)\) and \((S_2,I_2)\) denotes the density of susceptible and infective individuals resident in city 1 and city 2 respectively.

  3. (iii)

    The disease is transmitted to a susceptible individual by an effective contact with an infected individual.

  4. (iv)

    We use asymptotic transmission incidence to model disease transmission phenomenon, which, for human is considered more accurate than mass action [10, 38, 54].

  5. (v)

    The virus is spread among the population only and the disease is not inherited genetically.

  6. (vi)

    During travelling there is no birth or death.

Considering above assumptions the epidemic situation in two cities with bidirectional movement can be modeled by the following system of differential equation,

$$\begin{aligned} \frac{dS_1}{dt}= & {} r_1 S_1\left( 1-\frac{S_1+I_1}{K_1}\right) -\frac{\beta _1 S_1 I_1}{S_1+I_1+c_1}+m_1S_2-m_2S_1 \nonumber \\= & {} f_1(S_1,I_1)+m_1S_2-m_2S_1, \end{aligned}$$
(1)
$$\begin{aligned} \frac{dI_1}{dt}= & {} \frac{\beta _1 S_1 I_1}{S_1+I_1+c_1}-a_1 I_1+m_3I_2-m_4I_1\nonumber \\= & {} f_2(S_1,I_1)+m_3I_2-m_4I_1, \end{aligned}$$
(2)
$$\begin{aligned} \frac{dS_2}{dt}= & {} r_2 S_2\left( 1-\frac{S_2+I_2}{K_2}\right) -\frac{\beta _2 S_2 I_2}{S_2+I_2+c_2}+m_2S_1-m_1S_2\nonumber \\= & {} f_3(S_2,I_2)+m_2S_1-m_1S_2, \end{aligned}$$
(3)
$$\begin{aligned} \frac{dI_2}{dt}= & {} \frac{\beta _2 S_2 I_2}{S_2+I_2+c_2}-a_2 I_2+m_4I_1-m_3I_2= f_4(S_2,I_2)+m_4I_1-m_3I_2. \end{aligned}$$
(4)

All the parameters appearing in (1–4) are assumed to be positive constants. A concise description about (1–4) system parameters and variables is presented in Table 1.

Further, we suppose that functions \(S_1,I_1,S_2,I_2\) depend on time as well as on space. The heterogeneity in space and the local movement of individuals plays a crucial role in reflecting epidemiological spread. As an effect of growing international trade, intensive human mobility and inevitable menace of contagious epidemics, in-depth understanding of statistical and dynamical properties of human travel are essentially important [6]. We now assume both susceptible and infectious population perform random movement within their city. We consider habitat \({\varOmega }_1\) and \({\varOmega }_2\) \(\in {\mathbb {R}}^2\) as a bounded identical domain with smooth boundary \(\partial {\varOmega }_1\) and \(\partial {\varOmega }_2\) representing city 1 and city 2 respectively. Two cities are considered to be identical. Here we also assume that \(\beta _1\) and \(\beta _2\) depends on the spatial location \(p_1=(x_1,y_1)\) and \(p_2=(x_2,y_2)\), is positive Hölder continuous function on \({\varOmega }_1\) and \({\varOmega }_2\) respectively. The Laplacian operator \(\nabla ^2=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}\), is used to describe the local Brownian motion in two-dimensional space. It can be interpreted as the non-regular and continuous movement of individuals. Incorporating these facts, Eq. (1–4) can be written in \({\mathbb {R}}^2\) domain as

$$\begin{aligned}&\frac{\partial S_1}{\partial t} = D_{S_1}\nabla ^2 S_1+f_1(S_1(p_1, t),I_1(p_1, t))+m_1 S_2(p_2, t)-m_2 S_1(p_1, t), \nonumber \\&\quad p_1 \in {\varOmega }_1,~~~p_2 \in {\varOmega }_2, \end{aligned}$$
(5)
$$\begin{aligned}&\frac{\partial I_1}{\partial t} = D_{I_1} \nabla ^2 I_1+f_2(S_1(p_1, t),I_1(p_1, t))+m_3 I_2(p_2, t)-m_4 I_1(p_1, t),\nonumber \\&\quad p_1 \in {\varOmega }_1,~~~p_2 \in {\varOmega }_2, \end{aligned}$$
(6)
$$\begin{aligned}&\frac{\partial S_2}{\partial t} = D_{S_2} \nabla ^2 S_2+f_3(S_2(p_2, t),I_2(p_2, t))+m_2 S_1(p_1, t)-m_1 S_2(p_2, t),\nonumber \\&\quad p_1 \in {\varOmega }_1,~~~p_2 \in {\varOmega }_2, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{\partial I_2}{\partial t} = D_{I_2} \nabla ^2 I_2+f_4(S_2(p_2, t),I_2(p_2, t))+m_4 I_1(p_1, t)-m_3 I_2(p_2, t),\nonumber \\&\quad p_1 \in {\varOmega }_1,~~~p_2 \in {\varOmega }_2. \end{aligned}$$
(8)

Now, consider a translation map \(f: {\varOmega }_1 \rightarrow {\varOmega }_2\) with \(p_2=f(p_1)=p_1+L\), L represents a fixed distance from one city to another. As per our knowledge, this situation has not been modelled yet and is an initial step for modelling movement of individuals between both inter and intra city. As all models, this model too is limited by some assumptions like that the cities are identical and people from one city move to another city at exactly the same position obeying some fixed distance law. However, we hope this research work will open many paths towards modelling movement of population in any desired location within a different city. Under this map any position \(p_2\) in city 2 can be reflected by position \(p_1\) in city 1. Mathematically, we can write

$$\begin{aligned} S_2(p_2, t)= & {} \hat{S_2}(p_1, t), ~~ p_1 \in {\varOmega }_1, p_2 \in {\varOmega }_2, \\ I_2(p_2, t)= & {} \hat{I_2}(p_1, t), ~~ p_1 \in {\varOmega }_1, p_2 \in {\varOmega }_2. \end{aligned}$$

Therefore, (5–8) is equivalent to

$$\begin{aligned}&\partial _t S_1- D_{S_1} \nabla ^2 S_1 \nonumber \\&\quad = f_1(S_1(p_1, t),I_1(p_1, t))+m_1 \hat{S_2}(p_1, t)-m_2 S_1(p_1, t)\nonumber \\&\quad =g_1(S_1,I_1,\hat{S_2}),~~ p_1 \in {\varOmega }_1, \end{aligned}$$
(9)
$$\begin{aligned}&\partial _t I_1- D_{I_1} \nabla ^2 I_1 \nonumber \\&\quad = f_2(S_1(p_1, t),I_1(p_1, t))+m_3 \hat{I_2}(p_1, t)-m_4 I_1(p_1, t)\nonumber \\&\quad =g_2(S_1,I_1,\hat{I_2}), ~~ p_1 \in {\varOmega }_1, \end{aligned}$$
(10)
$$\begin{aligned}&\partial _t S_2-D_{S_2} \nabla ^2 S_2 \nonumber \\&\quad = f_3(\hat{S_2}(p_1, t),\hat{I_2}(p_1, t))+m_2 S_1(p_1, t)-m_1 \hat{S_2}(p_1, t)\nonumber \\&\quad =g_3(\hat{S_2},\hat{I_2},S_1),~~ p_1 \in {\varOmega }_1, \end{aligned}$$
(11)
$$\begin{aligned}&\partial _t I_2-D_{I_2} \nabla ^2 I_2 \nonumber \\&\quad = f_4(\hat{S_2}(p_1, t),\hat{I_2}(p_1, t))+m_4 I_1(p_1, t)-m_3 \hat{I_2}(p_1, t)\nonumber \\&\quad =g_4(\hat{S_2},\hat{I_2},I_1), ~~ p_1 \in {\varOmega }_1. \end{aligned}$$
(12)

For the sake of neat and general representation of variables we drop \(\hat{} \) notation i.e. we write \(\hat{S_2}=S_2\) and \(\hat{I_2}=I_2\) we rewrite the Eq. (9–12) as follows

$$\begin{aligned}&\partial _t S_1- D_{S_1} \nabla ^2 S_1 \nonumber \\&\quad = f_1(S_1(x,t),I_1(x,t))+m_1 S_2(x,t)-m_2 S_1(x,t)\nonumber \\&\quad =g_1(S_1,I_1,S_2),~~ x \in {\varOmega }, \end{aligned}$$
(13)
$$\begin{aligned}&\partial _t I_1- D_{I_1} \nabla ^2 I_1 \nonumber \\&\quad = f_2(S_1(x,t),I_1(x,t))+m_3 I_2(x,t)-m_4 I_1(x,t)\nonumber \\&\quad =g_2(S_1,I_1,I_2), ~~ x \in {\varOmega }, \end{aligned}$$
(14)
$$\begin{aligned}&\partial _t S_2-D_{S_2} \nabla ^2 S_2 \nonumber \\&\quad = f_3(S_2(x,t),I_2(x,t))+m_2 S_1(x,t)-m_1 S_2(x,t)\nonumber \\&\quad =g_3(S_2,I_2,S_1),~~ x \in {\varOmega }, \end{aligned}$$
(15)
$$\begin{aligned}&\partial _t I_2-D_{I_2} \nabla ^2 I_2 \nonumber \\&\quad = f_4(S_2(x,t),I_2(x,t))+m_4 I_1(x,t)-m_3 I_2(x,t)\nonumber \\&\quad =g_4(S_2,I_2,I_1), ~~ x \in {\varOmega }. \end{aligned}$$
(16)

The system can be written compactly as,

$$\begin{aligned} \frac{\partial u}{\partial t}= D \nabla ^2 u+ \xi (u), x \in {\varOmega }, \end{aligned}$$
(17)

where \(u=(S_1,I_1,S_2,I_2)^T\), \(D=(D_{S_1}, D_{I_1}, D_{S_2},D_{I_2})^T\) and \(\xi (u)= \begin{pmatrix} g_1(S_1,I_1,S_2)\\ g_2(S_1,I_1,I_2)\\ g_3(S_2,I_2,S_1)\\ g_4(S_2,I_2,I_1) \end{pmatrix}\). The system (17) is analyzed under the initial conditions given by

$$\begin{aligned} S_{10}(x,0)\ge 0,I_{10}(x,0)\ge 0,S_{20}(x,0)\ge 0,I_{20}(x,0)\ge 0, \end{aligned}$$
(18)

where \(x \in {\varOmega }\in {\mathbb {R}}^2\) and zero flux boundary conditions

$$\begin{aligned} \frac{\partial S_1}{\partial \nu }=\frac{\partial I_1}{\partial \nu }=\frac{\partial S_2}{\partial \nu }=\frac{\partial I_2}{\partial \nu }=0. \end{aligned}$$
(19)

\(\nu \) represents the outward unit normal vector on the boundary \(\partial {\varOmega }\) which is assumed to be smooth. Neumann or zero-flux boundary conditions biologically implies that the domain boundary is isolated or insulated from the external environment i.e. there are no fluxes of populations through the boundary [39]. By the standard parabolic theory, (17) admits a unique nonnegative classical solution \((S_1(x,t), I_1(x,t), S_2(x,t), I_2(x,t)) \in C^{2,1}({\bar{{\varOmega }}} \times (0,\infty ))\), and satisfies (17) point wisely. Moreover, from the strong maximum principle and the Hopf boundary lemma for parabolic equations [45] guarantee that \(S_1(x,t), I_1(x,t),S_2(x,t), I_2(x,t)>0\) for all \((x,t) \in {\bar{{\varOmega }}} \times (0,\infty )\).

We now define two travel matrices

$$\begin{aligned} A=(a_{ij})_{2 \times 2}= \begin{pmatrix} 0 &{} m_2\\ m_1 &{} 0 \\ \end{pmatrix},~~ {and}~~ B=(b_{ij})_{2 \times 2}= \begin{pmatrix} 0 &{} m_4\\ m_3 &{} 0 \\ \end{pmatrix}. \end{aligned}$$
(20)

Here, \(a_{ij}\) and \(b_{ij}\) describe the mobility rate of susceptible and infected from a city i to city j respectively. We assume these matrices are irreducible. Biologically, it means individuals in city 1 can travel to city 2 directly or indirectly.

Fig. 1
figure 1

Transfer diagram of the two-city model for disease transmission

Full size image
Table 1 Parameter values of system (17) and their biological meanings. We mostly took hypothetical parameter value which are in ecological permissible range
Full size table

3 Dynamical behaviour of the two-city model

Before studying the stability behavior of our spatial model we give the following result to show the boundedness of system (17) which is important from ecological point of view.

3.1 Some preliminary properties of the spatial model

Proposition 1

All non-negative solutions of model system (1–4) which initiate in \({\mathbb {R}}^{4}_+\) are uniformly bounded, with ultimate bound \((\frac{r_1}{4 \eta }+1)K_1+(\frac{r_2}{4 \eta }+1)K_2\), where \(\eta =min(a_1,a_2)\).

Proof

We define,

$$\begin{aligned} W(t)=S_1(t)+I_1(t)+S_2(t)+I_2(t). \end{aligned}$$
(21)

The time derivative of (21) along the solutions of (1–4) is

$$\begin{aligned} \frac{dW}{dt}=\frac{dS_1}{dt}+\frac{dI_1}{dt}+\frac{dS_2}{dt}+\frac{dI_2}{dt}, \end{aligned}$$
(22)

for each \(\eta >0,\) the following inequality hold:

$$\begin{aligned} \frac{dW}{dt}+\eta W= & {} r_1S_1 \left( 1-\frac{S_1+I_1}{K_1}\right) + r_2S_2\left( 1-\frac{S_2+I_2}{K_2}\right) \nonumber \\&-(a_1-\eta )I_1-(a_2-\eta )I_2+\eta (S_1+S_2), \end{aligned}$$

Taking \(\eta = min(a_1, a_2)\), the above inequality satisfies

$$\begin{aligned} \frac{dW}{dt}+\eta W\le & {} r_1S_1 \left( 1-\frac{S_1}{K_1}\right) + r_2S_2\left( 1-\frac{S_2}{K_2}\right) +\eta S_1+\eta S_2. \nonumber \\ \frac{dW}{dt}+\eta W\le & {} \left( \frac{r_1}{4}+\eta \right) K_1+ \left( \frac{r_2}{4}+\eta \right) K_2=L. \end{aligned}$$
(23)

Using comparison lemma for \(t>{\tilde{T}}>0\) we have

$$\begin{aligned} W(t)\le \frac{L}{\eta }-\left( \frac{L}{\eta }-W({\tilde{T}})\right) e^{-\eta (t-{\tilde{T}})}. \end{aligned}$$
(24)

Then for \({\tilde{T}}=0\), we have

$$\begin{aligned} W(t)\le \frac{L}{\eta }-\left( \frac{L}{\eta }-W(0)\right) e^{-\eta (t)}. \end{aligned}$$
(25)

For large value of t, we have \(W(t)\le \frac{L}{\eta }\) with \(\eta =min(a_1,a_2)\). \(\square \)

For a biologically practical system all population are required to be constrained by a bound in time by their environments. Thus, the feasible region of (1–4) can be chosen as \({\mathcal {E}}=\{(S_1,I_1,S_2,I_2) \in {\mathbb {R}}_+^4 |W(t)=S_1(t)+I_1(t)+S_2(t)+I_2(t) \le \frac{L}{\eta } \}\). It can be easily seen that \({\mathcal {E}}\) is positively invariant with respect to (1–4). Let us denote \({\mathcal {E}}^0\): the interior of \({\mathcal {E}}\), and \(\partial {\mathcal {E}}\): the boundary of \({\mathcal {E}}\).

Proposition 2

All non-negative solution \((S_1,I_1,S_2,I_2)\) of model (17) with initial condition (18), satisfies the following inequality

$$\begin{aligned} \limsup \limits _{t \rightarrow \infty } ~~\max \limits _{{x \in {\bar{{\varOmega }}}}} (S_1(., t)+S_2(., t))\le & {} max \{K, \max _{{\bar{{\varOmega }}}}(S_{10}(x)+S_{20}(x))\}, \\ \limsup \limits _{t \rightarrow \infty } ~~\max \limits _{{x \in {\bar{{\varOmega }}}}} (I_1(., t)+I_2(., t))\le & {} max \left( \frac{\beta K-a(c+K)}{a}, \max _{{\bar{{\varOmega }}}} (I_{10}(x)+I_{20}(x))\right) . \end{aligned}$$

where the meaning of \(a,\beta , K\) can be found in proof.

Proof

By virtue of (13) and (15) we have the following inequality,

$$\begin{aligned} \frac{\partial S_1}{\partial t}\le & {} D_{S_1} {\varDelta }S_1+ r_1 S_1 \left( 1-\frac{S_1}{K_1}\right) +m_1 S_2-m_2 S_1, \end{aligned}$$
(26)
$$\begin{aligned} \frac{\partial S_2}{\partial t}\le & {} D_{S_2} {\varDelta }S_2+ r_2 S_2 \left( 1-\frac{S_2}{K_2}\right) +m_2 S_1-m_1 S_2. \end{aligned}$$
(27)

Since the system (26)- (27) is cooperative, therefore by using comparison principle of parabolic equations [11], one can show \((S_1(x,t),S_2(x,t))\) is a subsolution of the following problem

$$\begin{aligned} \frac{d \bar{S_1}}{d t}= & {} r_1 \bar{S_1} \left( 1-\frac{\bar{S_1}}{K_1}\right) +m_1 \bar{S_2}-m_2 \bar{S_1}, \end{aligned}$$
(28)
$$\begin{aligned} \frac{d \bar{S_2}}{d t}= & {} r_2 \bar{S_2} \left( 1-\frac{\bar{S_2}}{K_2}\right) +m_2 \bar{S_1}-m_1 \bar{S_2}. \end{aligned}$$
(29)

Let \(S=\bar{S_1}+\bar{S_2}\). Adding (28) and (29) and performing straightforward computations, we get

$$\begin{aligned} \frac{d(\bar{S_1}+\bar{S_2})}{d t}= & {} r_1 \bar{S_1} \left( 1-\frac{\bar{S_1}}{K_1}\right) +r_2 \bar{S_2} \left( 1-\frac{\bar{S_2}}{K_2}\right) , \\ \frac{d S}{d t}\le & {} 2 r S \left( 1-\frac{S}{K} \right) , \end{aligned}$$

where \(r=max(r_1,r_2)\), and \(K=max(K_1,K_2)\). Again, using comparison principle one can show S(t) is a subsolution of the following problem

$$\begin{aligned} \frac{d {\bar{S}}}{d t}= & {} 2 r {\bar{S}} \left( 1-\frac{{\bar{S}}}{K} \right) . \end{aligned}$$

We observe that the positive constant

$$\begin{aligned} {\bar{S}}=max \{K, \max _{{\bar{{\varOmega }}}}(S_{10}(x)+S_{20}(x))\}, \end{aligned}$$
(30)

is the supersolution to (28–29). Therefore,

$$\bar{S_1}(t) +\bar{S_2}(t)\le S(t) \le {\bar{S}}(t).$$

Also, \(\lim _{t \rightarrow \infty } {\bar{S}}(t) \le K \). Thus, from well known comparison principle for parabolic equations, we finally have

$$\begin{aligned}&S_1(x,t)+ S_2(x,t)\le \bar{S_1}(t) +\bar{S_2}(t)\le max \{K, \max _{{\bar{{\varOmega }}}}(S_{10}(x)+S_{20}(x))\}:= {\bar{S}}(t), \nonumber \\&\quad \forall x \in {\varOmega }, t \ge 0. \end{aligned}$$
(31)

Hence, we have

$$\begin{aligned} S_1(x,t)+S_2(x,t) \le K =\bar{U_1}:=Sup_{t\ge 0} ||S_1(.,x)+S_2(.,x)||_\infty , \forall x \in {\bar{{\varOmega }}}, \end{aligned}$$

This implies

$$\begin{aligned} \limsup \limits _{t \rightarrow \infty } ~~\max \limits _{x \in {\bar{{\varOmega }}}}( S_1(x, t)+S_2(x, t)) \le max \{K, \max _{{\bar{{\varOmega }}}}(S_{10}(x)+S_{20}(x))\}. \end{aligned}$$

Next, making use of (14) and (16) and putting upper bound of \(S_1\) and \(S_2\) we have the following inequality,

$$\begin{aligned} \frac{\partial I_1}{\partial t}\le & {} D_{I_1} {\varDelta }I_1+ \frac{\beta _1 \bar{U_1} (I_1+I_2) }{\bar{U_1}+(I_1+I_2)+c_1}-a_1 I_1 +m_3 I_2-m_4 I_1, \end{aligned}$$
(32)
$$\begin{aligned} \frac{\partial I_2}{\partial t}\le & {} D_{I_2} {\varDelta }I_2+ \frac{\beta _2 \bar{U_1} (I_1+I_2) }{\bar{U_1}+(I_1+I_2)+c_2}-a_2 I_2+m_4 I_1-m_3 I_2. \end{aligned}$$
(33)

Again, since the system (32)- (33) is cooperative by using comparison principle of parabolic equations [11], one can show \((I_1(x,t), I_2(x,t)) \le (\bar{I_1}(t),\bar{I_2}(t))\), where \((\bar{I_1}(t),\bar{I_2}(t))\) is a solution of the following differential equation

$$\begin{aligned} \frac{d \bar{I_1}}{d t}= & {} \frac{\beta _1 \bar{U_1} (\bar{I_1}+\bar{I_2}) }{\bar{U_1}+(\bar{I_1}+\bar{I_2})+c_1}-a_1 \bar{I_1} +m_3 \bar{I_2}-m_4 \bar{I_1}, \end{aligned}$$
(34)
$$\begin{aligned} \frac{d \bar{I_2}}{d t}= & {} \frac{\beta _2 \bar{U_1} (\bar{I_1}+\bar{I_2}) }{\bar{U_1}+(\bar{I_1}+\bar{I_2})+c_2}-a_2 \bar{I_2}+m_4 \bar{I_1}-m_3 \bar{I_2}. \end{aligned}$$
(35)

Adding (34–35) along with few computations and letting \(I=\bar{I_1}+\bar{I_2}\), we have the following

$$\begin{aligned} \frac{d I}{d t}\le & {} \left( \frac{\beta K}{K+I+c}-a\right) I, \end{aligned}$$

where \(\beta =max(\beta _1,\beta _2)\), \(a=min(a_1,a_2)\) and \(c=min(c_1,c_2)\). Following the same analysis as above, one can show that for \(t \ge 0\) we have the following inequality

$$\begin{aligned}&I_1(x,t)+I_2(x,t) \nonumber \\&\quad \le \bar{I_1}(t)+\bar{I_2}(t) \le max \left( \frac{\beta K-a(c+K)}{a}, \max _{{\bar{{\varOmega }}}} (I_{10}(x)+I_{20}(x)) \right) =:{\bar{I}}(t), \nonumber \\&\qquad \forall x \in {\varOmega }, t \ge 0. \end{aligned}$$
(36)

Hence, we have

$$\begin{aligned}&I_1(x,t)+I_2(x,t) \nonumber \\&\quad \le max \left( \frac{\beta K-a(c+K)}{a}, \max _{{\bar{{\varOmega }}}} (I_{10}(x)+I_{20}(x)) \right) :=\bar{U_2}, \forall x \in {\bar{{\varOmega }}}, \end{aligned}$$
(37)

This implies

$$\begin{aligned} \limsup \limits _{t \rightarrow \infty } ~~ \max \limits _{x \in {\bar{{\varOmega }}}} (I_1(., t)+ I_2(., t)) \le max \left( \frac{\beta K-a(c+K)}{a}, \max _{{\bar{{\varOmega }}}} (I_{10}(x)+I_{20}(x))\right) . \end{aligned}$$

\(\square \)

Definition 1

[7]: The spatial model (17) is said to have the persistence property if for any nonnegative initial data \((S_{10}(x),I_{10}(x), S_{20}(x), I_{20}(x))\), there exists positive constants \(\epsilon _i=\epsilon _i(S_{10},I_{10}, S_{20}, I_{20})\) for \(i=1,2,3,4\), such that corresponding solution, \((S_1,I_1,S_2,I_2)\) of model (17) satisfies,

$$\begin{aligned} \liminf \limits _{t \rightarrow +\infty } \min _{{\bar{{\varOmega }}}} S_1(x,t)\ge & {} \epsilon _1, \liminf \limits _{t \rightarrow +\infty } \min _{{\bar{{\varOmega }}}} I_1(x,t)\ge \epsilon _2,\\ \liminf \limits _{t \rightarrow +\infty } \min _{{\bar{{\varOmega }}}} S_2(x,t)\ge & {} \epsilon _3,\liminf \limits _{t \rightarrow +\infty } \min _{{\bar{{\varOmega }}}} I_2(x,t)\ge \epsilon _4. \end{aligned}$$

Proposition 3

Assume that if

$$\begin{aligned} \beta _1> & {} \frac{((a_1 + m_4) (c_1 + \underline{W_1}))}{\underline{W_1}}, r_1> \frac{\beta _1 \bar{U_2}}{(c_1 + \bar{U_2})}, \nonumber \\ m_2 +\frac{ \beta _1 \bar{U_2}}{(c_1 + \bar{U_2})}< & {} r_1 , K_1 > \frac{r_1 \bar{U_2} (c_1 + \bar{U_2})}{(r_1-m_2) (c_1 + \bar{U_2})-\beta _1 \bar{U_2})}, \end{aligned}$$
(38)
$$\begin{aligned} \beta _2> & {} \frac{((a_2 + m_3) (c_2 + \underline{W_3}))}{\underline{W_3}}, r_2> \frac{\beta _2 \bar{U_2}}{(c_2 + \bar{U_2})},\nonumber \\ m_1 +\frac{ \beta _2 \bar{U_2}}{(c_2 + \bar{U_2})}< & {} r_2 , K_2 > \frac{r_2 \bar{U_2} (c_2 + \bar{U_2})}{(r_2-m_1) (c_2 + \bar{U_2})-\beta _2 \bar{U_2})}, \end{aligned}$$
(39)

(where definition of \(\underline{W_1}\) and \(\underline{W_3}\) are given in the proof) holds, than system (17) has the persistence property.

Proof

From (13), we have

$$\begin{aligned} \frac{\partial S_1}{\partial t}\ge & {} D_{S_1} {\varDelta }S_1+r_1 S_1 \left( 1-\frac{S_1+I_1}{K_1}\right) -\frac{\beta _1 S_1 I_1}{S_1+I_1+c_1}-m_2 S_1, \\ \frac{\partial S_1}{\partial t}\ge & {} D_{S_1} {\varDelta }S_1+r_1 S_1\left( 1-\frac{S_1}{K_1}\right) -\frac{r_1 S_1 \bar{U_2}}{K_1}-\frac{\beta _1 S_1 \bar{U_2}}{\bar{U_2}+c_1}-m_2 S_1, \\ \frac{\partial S_1}{\partial t}\ge & {} D_{S_1} {\varDelta }S_1+S_1\left( r_1 \left( 1-\frac{S_1}{K_1}\right) -\frac{r_1 \bar{U_2}}{K_1}-\frac{\beta _1 \bar{U_2}}{\bar{U_2}+c_{1}}-m_2\right) , \end{aligned}$$

for \(t>t_1\). Since (38) holds, then for small enough \(\epsilon >0\) chosen

$$\begin{aligned} \frac{K_1}{r_1}\left( r_1 \left( 1-\frac{\bar{U_2}}{K_1}\right) -m_2-\frac{\beta _1 \bar{U_2}}{c_1+\bar{U_2}}\right) -\epsilon >0. \end{aligned}$$
(40)

Hence, there exists \(t_2>t_1\) such that for any \(t>t_2\),

$$\begin{aligned} S_1(x,t) \ge \underline{W_1}, \end{aligned}$$
(41)

where \(\underline{W_1}=\frac{K_1}{r_1}\left( r_1 \left( 1-\frac{\bar{U_2}}{K_1}\right) -m_2-\frac{\beta _1 \bar{U_2}}{c_1+\bar{U_2}}\right) -\epsilon \).

Now, we apply lower bound of \(S_1\) to equation (14), and we have

$$\begin{aligned} \frac{\partial I_1}{\partial t}\ge & {} D_I {\varDelta }I_1+\left( \frac{\beta _1 \underline{W_1}}{\underline{W_1}+I_1+c_1}-a_1-m_4 \right) I_1. \end{aligned}$$
(42)

Then there exists \(t_3 > t_2\) such that for any \(t > t_3\),

$$\begin{aligned} I_1(x,t) \ge \underline{W_2}, \end{aligned}$$
(43)

where

$$\begin{aligned} \underline{W_2}= -c_1 + \underline{W_1} \left( \frac{\beta _1}{a_1+m_4}-1\right) -\epsilon . \end{aligned}$$
(44)

Similarly, we can find bounds for \(S_2\) and \(I_2\).

$$\begin{aligned} S_2(x,t)\ge & {} \underline{W_3}=\frac{K_2}{r_2} \left( r_2 \left( 1-\frac{\bar{U_2}}{K_2}\right) -m_1- \frac{\beta _2 \bar{U_2}}{c_2+\bar{U_2}}\right) -\epsilon , \nonumber \\ I_2(x,t)\ge & {} \underline{W_4}=-c_2 + \underline{W_3}\left( \frac{\beta _2}{a_2+m_3}-1\right) -\epsilon . \end{aligned}$$
(45)

Summarizing, we have the following

$$\begin{aligned} \liminf \limits _{t \rightarrow \infty } \min \limits _{{\bar{{\varOmega }}}} S_1(x,t)\ge & {} \underline{W_1}.\nonumber \\ \liminf \limits _{t \rightarrow \infty } \min \limits _{{\bar{{\varOmega }}}} I_1(x,t)\ge & {} \underline{W_2}.\nonumber \\ \liminf \limits _{t \rightarrow \infty } \min \limits _{{\bar{{\varOmega }}}} S_2(x,t)\ge & {} \underline{W_3}.\nonumber \\ \liminf \limits _{t \rightarrow \infty } \min \limits _{{\bar{{\varOmega }}}} I_2(x,t)\ge & {} \underline{W_4}. \end{aligned}$$
(46)

Thus, the model system (17) is persistent. \(\square \)

3.2 Possible equilibria and their existence criteria

Our main interest in this section is the existence and uniqueness of the equilibrium. For this purpose let us first introduce some notations. For a closed linear operator \(Z:D(Z) \subset L^2({\varOmega })\rightarrow L^2({\varOmega })\), where D(Z) is the domain of Z, the spectral spread s(Z) of Z is defined by

$$\begin{aligned} s(Z)=sup\{{\mathbb {R}}e (\lambda ): \lambda \in \sigma _p(Z)\}, \end{aligned}$$

where \(\sigma _p\) denotes the point spectrum of Z.

We will first discuss equilibrium points in City 1 without any migration. There are only two equilibria for the following elliptic problem,

$$\begin{aligned} 0= & {} r_1 S_1\left( 1-\frac{S_1+I_1}{K_1}\right) -\frac{\beta _1 S_1 I_1}{S_1+I_1+c_1}+D_{S_1} \nabla ^2 S_1 , \nonumber \\ 0= & {} \frac{\beta _1 S_1 I_1}{S_1+I_1+c_1}-a_1 I_1+D_{I_1} \nabla ^2 I_1, \end{aligned}$$
(47)

with boundary conditions

$$\begin{aligned} \frac{\partial S_1}{\partial \nu }=\frac{\partial I_1}{\partial \nu }=0, x\in \partial {\varOmega }. \end{aligned}$$

The system has,

  1. 1.

    A disease free equilibrium (DFE) is a time independent solution of the form \(E_{10}=(S_{10}^0,0)\), where \(S_{10}^0>0\) for \(x\in {\varOmega }\). It is obvious that \((S_{10}^0,0)\) is a disease free equilibrium if and only if \(S_{10}^0\) is a positive solution of the equation,

    $$\begin{aligned} D_{S_1}\nabla ^2 S_1+S_1 r_1\left( 1-\frac{ S_1}{K_1}\right) =0, x\in {\varOmega }. \end{aligned}$$
    (48)

    Now, we state the following proposition [48]

Proposition 4

Equation (48) has a positive solution \(S_{10}^0\) if and only if \(s(D_{S_1}\nabla ^2 +r_1)>0\). Moreover, the positive solution \(S_{10}^0\) is unique and it is strictly positive on \({\varOmega }\).

  1. 2.

    An endemic equilibrium \(E_{10}^*(S_{10}^*,I_{10}^*)\) exists iff there is a positive solution to the (47).

For more generality we investigate the existence of endemic equilibrium when \(\beta _1(x), a_1(x), r_1(x)\) are positive Hölder continuous functions on \({\varOmega }\). Before the main result, we state a useful lemma [32],

Lemma 1

Let \({\varOmega }\) be a bounded Lipschitz domain in \({\mathbb {R}}^n\). Let \({\varLambda }\) be a non-negative constant and suppose that \(z\in W^{1,2}({\varOmega })\) is a non-negative weak solution of the inequalities

$$\begin{aligned} 0 \le -\nabla ^2 z+{\varLambda }z~~~~ \text {in}~~~~{\varOmega }, \frac{\partial z}{\partial \nu }\le 0~~~~ \text {on}~~~~ \partial {\varOmega }. \end{aligned}$$

Then, for any \(q \in [1,n/(n-2)]\), there exists a positive constant \(C_0\), depending on \(q, {\varLambda }\) and \({\varOmega },\) such that \(||z||_q \le C_0 inf z\).

Proposition 5

Problem (47) admits at least one positive solution.

Proof

The proof uses the approach given by [53]; [29]; [30]; [42]. But for the reader convenience we summarize the steps of the proof given in Appendix A. \(\square \)

Now, we give two simple observations which give the existence of equilibrium points for the other cities and hence give us an idea about the existence of equilibrium for the entire network.

Remark 1

Suppose that system (17) is at an equilibrium \(E_0=(S_1^0,0,S_2^0,0)\), and given city 1 is at disease free equilibrium, \(E_{10}\). The city 2 that can be accessed from city 1 is also at the DFE. In particular, if outgoing matrices A and B are irreducible, then both cities are at the DFE.

Indeed for showing this, suppose the city 1 is at the DFE, i.e., \(I_1=0\). Then from Eq. (14) we have

$$\begin{aligned} \frac{\partial I_1}{\partial t}=m_3 I_2. \end{aligned}$$

As the city 1 is in disease free equilibrium, \(\frac{\partial I_1}{\partial t}=0\), now since \(m_3>0\) it follows that \(I_2=0\). This implies that the entire system is at disease free equilibrium, \(E_0\).

Remark 2

Suppose that system (17) is at an equilibrium \(E^*=(S_1^*,I_1^*,S_2^*,I_2^*)\), and that the disease is endemic in city 1. Then the disease is also endemic in city 2 that can be accessed from city 1. In particular, if the outgoing matrices A and B are irreducible, then the disease is endemic in both cities.

Indeed for showing this, suppose that the disease is endemic in city 1, i.e., \(I_1>0\). We will prove this result by contradiction. Suppose that \(I_2=0\). Since the system is at equilibrium, from (16) we have

$$\begin{aligned} 0=\frac{\partial I_2}{\partial t}=m_4I_1. \end{aligned}$$

Again since \(m_4>0\), it follows \(I_1=0\), which is a contradiction. Therefore \(I_2>0\) if the disease is endemic in city 1.

Similar results were obtained for the ODE multi-city epidemic model [3]. These results can be extended for n cities in the similar way. Moreover these results give an idea that if the cities are connected and have access to each other then either both cities will be disease-free or both will be in disease endemic situations. We have illustrated this result numerically in Sect. 5.

3.3 Calculation of basic reproduction number

The basic reproduction number, \(R_0\) is interpreted as the expected number of new cases generated by a single infected host in a completely susceptible population [55]. This number is very useful because it assists to figure out whether infectious disease will spread through the population or will die out.

Following the steps in [51] we first calculate the basic reproduction number for system (1–4). For the epidemic (1–4), we define:

$$\begin{aligned} F = \begin{pmatrix} \frac{\beta _1 S_1^0}{S_1^0+c_1} &{} 0\\ 0 &{} \frac{\beta _2 S_2^0}{S_2^0+c_2} \\ \end{pmatrix}, V = \begin{pmatrix} m_4+a_1 &{} -m_3\\ -m_4 &{} m_3+a_2 \\ \end{pmatrix}. \end{aligned}$$
(49)

The basic reproduction number can be calculated by finding the spectral radius of the next generation matrix \(FV^{-1}\).

$$\begin{aligned} R_0^{ODE}=max \{R_{01}^{ODE},R_{02}^{ODE}\}, \end{aligned}$$
(50)

where \(R_{0j}^{ODE}(j=1,2)\) is the basic reproduction number of each city given by

$$\begin{aligned}&R_{01}^{ODE}=\frac{\beta _1(a_2+m_3)S_1^0}{(a_1(a_2+m_3)+a_2 m_4)(c_1+S_1^0)}, \\&R_{02}^{ODE}=\frac{\beta _2(a_1+m_4)S_2^0}{(a_1(a_2+m_3)+a_2 m_4)(c_2+S_2^0)}. \end{aligned}$$

Now, in order to define the basic reproduction number for model (17), we use the approach given by [58]; [44]. We assume that the state variables are near the disease-free steady state, \(E_0\). Let the distribution of initial infection is represented by \(\phi (x)\). Under the affect of mortality, mobility and transfer of individuals in infected compartments, the distribution of those infective members as time evolves becomes \(T(t)\phi (x)\). Thus, the distribution of new infection at time t is \(F(x)T(t)\phi (x)\). Subsequently, the distribution of total new infection is

$$\begin{aligned} \int _0^{\infty } F(x)T(t)\phi (x) dt. \end{aligned}$$
(51)

Define

$$\begin{aligned} {\mathcal {L}}(\phi )(x):=\int _0^{\infty } F(x)T(t)\phi dt=F(x)\int _0^{\infty } T(t)\phi dt. \end{aligned}$$

\({\mathcal {L}}\) is a positive continuous operator which maps the initial infection distribution of the total infective members produced during the infection period. Following [58]; [35] we define spectral radius of \({\mathcal {L}}\) as the basic reproduction number

$$\begin{aligned}&R_0^{HPDE}:=r({\mathcal {L}}) \nonumber \\&\quad (R_0^{HPDE}~\text { represents basic reproduction number in heterogeneous environment})\nonumber \\ \end{aligned}$$
(52)

for model (17).

Now, we define the basic reproduction number \(R_{01}^{HPDE}\) for the system of isolated city 1. We linearize the system around the DFE \(E_{10}=(S_{10}^0,0)\) and obtain the following equation

$$\begin{aligned} \frac{\partial I_1}{\partial t}= & {} D_{I_1}\nabla ^2 I_1+\left( \frac{\beta _1 S_{10}^0}{S_{10}^0+c_1}-a_1\right) I_1,\nonumber \\ \frac{\partial I_1}{\partial \nu }= & {} 0. \end{aligned}$$
(53)

By substituting \(I_1(x,t)=e^{-\lambda t}\xi (x), \lambda \in {\mathbb {R}}\) into the equation and dividing both sides by \(e^{-\lambda t}\), we obtain the following linear eigenvalue problem

$$\begin{aligned}&D_{I_1} \nabla ^2 \xi +\left( \frac{\beta _1 S_{10}^0}{S_{10}^0+c_1}-a_1\right) \xi +\lambda \xi =0, \nonumber \\&\frac{\partial \xi }{\partial \nu }=0. \end{aligned}$$
(54)

By the Krein-Rutman Theorem [20], if \((\lambda , \xi )\) is a solution of (54) with \(\xi \ne 0\) on \({\varOmega }\) then \(\lambda \) is real. Moreover, there exists a least eigenvalue \(\lambda ^*\), with its corresponding eigenfunction \(\xi ^*\) positive on \({\varOmega }\). Also, there is no other eigenvalue \(\lambda \) that has an eigenfunction \(\xi \) which is positive everywhere. Notice that \((\lambda ^*,\xi ^*)\) satisfies

$$\begin{aligned} D_{I_1} \nabla ^2 \xi ^*+\left( \frac{\beta _1(x) S_{10}^0}{S_{10}^0+c_1}-a_1\right) \xi ^*+\lambda ^* \xi ^*=0. \end{aligned}$$

Following [1], \(\lambda ^*\) is given by the variational characterization as:

$$\begin{aligned} \lambda ^*= & {} inf\left\{ \left[ \int _{\varOmega }D_{I_1} \Bigg |\nabla \phi (x)|^2 +\left( a_1-\frac{\beta _1(x) S_{10}^0}{S_{10}^0+c_1}\right) \phi ^2(x)\right] : \right. \nonumber \\&\quad \left. \phi \in W^{1,2}({\varOmega }) ~~~\text {and} \int _{\varOmega }\phi dx=1\right\} , \nonumber \\ R_{01}^{HPDE}= & {} sup \left\{ \frac{\int \frac{\beta _1(x) S_{10}^0}{S_{10}^0+c_1} \phi ^2(x) dx}{\int [D_{I_1}|{\nabla \phi (x)}|^2+a_1 \phi ^2(x)]dx}:{\phi \in W^{1,2}({\varOmega })}\right\} . \end{aligned}$$
(55)

Similarly for city 2,

$$\begin{aligned} R_{02}^{HPDE}=sup \left\{ \frac{\int \frac{\beta _2(x) S_{20}^0}{S_{20}^0+c_2} \phi ^2(x) dx}{\int [D_{I_2}|{\nabla \phi (x)}|^2+a_2 \phi ^2(x)]dx}:{\phi \in W^{1,2}({\varOmega })}\right\} . \end{aligned}$$
(56)

The definition of \(R_0^{HPDE}\) for (17) is closely related to the stability of DFE, \(E_0=(S_1^0,0,S_2^0,0)\). Linearizing the model around \(E_0\), the stability of \(E_0\) can be decided by the sign of the principal eigenvalue of the problem:

$$\begin{aligned} \mu \phi _1= & {} D_{I_1}\nabla ^2 \phi _1+\left( \frac{\beta _1(x) S_1}{S_1+c_1}-(m_4+a_1)\right) \phi _1+m_3 \phi _2, x \in {\varOmega }, \nonumber \\ \mu \phi _2= & {} D_{I_2}\nabla ^2 \phi _2+m_4 \phi _1+\left( \frac{\beta _2(x) S_2}{S_2+c_2}-(m_3+a_2)\right) \phi _2, x \in {\varOmega }, \nonumber \\ \frac{\partial \phi _1}{\partial \nu }= & {} \frac{\partial \phi _2}{\partial \nu }=0,~~ x \in \partial {\varOmega }. \end{aligned}$$
(57)

Since the system is cooperative, (57) has a principal eigenvalue \(\mu _0\) associated with a positive eigenvector [23].

Following [36, 53, 58], the basic reproduction number \(R_0^{HPDE}\) for (17) is defined as the spectral radius \(r(-F{\mathcal {O}}^{-1})\), where \({\mathcal {O}}:D({\mathcal {O}}) \subset C({\bar{{\varOmega }}}; {\mathbb {R}}^2) \rightarrow C({\bar{{\varOmega }}}; {\mathbb {R}}^2)\) is a linear operator \({\mathcal {O}}=\begin{pmatrix} D_{I_1} \nabla ^2 &{} 0\\ 0 &{} D_{I_2} \nabla ^2\\ \end{pmatrix}-V\). F and V are as defined in (49).

$$\begin{aligned}&D({\mathcal {O}})= (\phi _1,\phi _2)\in \cap _{p \ge 1} W^{2,p}({\varOmega };{\mathbb {R}}):\frac{\partial \phi _1}{\partial \nu }=\frac{\partial \phi _2}{\partial \nu }=0, \\&\qquad \text {on} ~~ \partial {\varOmega }~~ \text {and} ~~{\mathcal {O}}(\phi _1,\phi _2)\in C({\bar{{\varOmega }}}; {\mathbb {R}}^2). \end{aligned}$$

However, when the infection coefficients \(\beta _1\) and \(\beta _2\) are spatially independent, the basic reproduction number admits the same value as its ODE counterpart [55]. We state the following result from [58]:

Theorem 1

If each \(D_{S_1}\), \(D_{I_1}\), \(D_{S_2}\) and \(D_{I_2}\) is a positive constant and \(F(x)=F\) and \(V(x)=V\) are independent of \(x \in {\varOmega }\), then basic reproduction number for homogeneous environment \(R_0^{PDE}=r(FV^{-1})=R_0^{ODE}\).

Proof

See [58] for the proof. \(\square \)

Sect. 5 gives numerical evidence for these analytical results.

4 Global stability analysis

In this section, we deduce sufficient conditions under which the disease free and endemic equilibrium globally asymptotically stable in a homogeneous environment. Graph theoretical approaches developed by [28] are utilized in our proof. Before starting, we recall some preliminaries from graph theory.

Consider a weighted directed graph or digraph \(G=(W,E)\) containing a set \(W=\{1,2,3...n\}\) of vertices and a set E of arcs (i, j) leading from source vertex i to destination vertex j and each arc (j, i) is assigned a positive weight \(m_{ij}\). The weight matrix of weighted digraph is given by \(M=(m_{ij})_{n\times n}\) whose entry \(m_{ij}\) equals the weight of arc (j, i) if it exists, and 0 otherwise. A weighted digraph (G, M) is strongly connected if and only if the weight matrix M is irreducible. The Laplacian matrix of (G, M) is defined as \(L = \begin{pmatrix} \sum _{k \ne 1} m_{1k} &{} -m_{12}&{}...&{} -m_{1n}\\ -m_{21} &{}\sum _{k \ne 2} m_{2k} &{}...&{} -m_{2n}\\ : &{} :&{}:&{} :\\ -m_{n1} &{} -m_{n2}&{}...&{} \sum _{k \ne n} m_{nk}\\ \end{pmatrix}\),

Let \(C_i\) denote the cofactor of the \(i^{th}\) diagonal element of L. The result which will be used in our proofs are given as follows [19]:

Proposition 6

Assume \(n\ge 2\). Then

$$\begin{aligned} C_i=\sum _{T \in T_i} W(T), i=1,2,3....,n. \end{aligned}$$
(58)

where \(T_i\) is the set of all spanning trees T of (G, M) that are rooted at vertex i, and W(T) is the weight of T. In particular, if (G, M) is strongly connected, then \(C_i>0\) for \(1 \le i \le n\).

Theorem 2

Assume \(n\ge 2\). Let \(C_i\) be given in the above proposition. Then the following identity holds:

$$\begin{aligned} \sum _{i,j=1}^n C_i m_{ij} G_i(x_i)=\sum _{i,j=1}^n C_i m_{ij} G_j(x_j), \end{aligned}$$
(59)

where \(G_i(x_i)\), \(1 \le i \le n\), are arbitrary functions.

Proposition 7

Assume \(R_0^{ODE} \le 1\). Suppose that infective travel matrix \(B=(b_{ij})\) is irreducible. Then the disease-free equilibrium \(E_0\) is globally asymptotically stable.

Proof

Suppose \(B=(b_{ij})\) is irreducible (see (20)). Let F and V be given as in (49). We observe that V is a non-singular M-matrix since all the off-diagonal entries of V are non-positive and the sum of the entries of each of its columns are positive. Since B is irreducible, then \(V^{-1}>0\) is also irreducible. By Perron-Frobenious Theorem [4], non-negative irreducible matrix \(V^{-1}F\) has a positive left eigenvector \((w_1,w_2)\) corresponding to eigenvalue \(\rho (V^{-1}F)\).

$$\begin{aligned} (w_1,w_2)F^{-1}V=R_0^{ODE}(w_1,w_2) \end{aligned}$$
(60)

and thus

$$\begin{aligned} \frac{1}{R_0^{ODE}}(w_1,w_2)=(w_1,w_2)F^{-1}V \end{aligned}$$
(61)

Let \(d_i=\frac{w_i}{\frac{\beta _iS_i^0}{S_i^0+c_i}}>0\), \(i=1,2\) and \(I=(I_1,I_2)^T\). Set

$$\begin{aligned} {\mathfrak {L}}_1=d_1I_1+d_2 I_2. \end{aligned}$$
(62)

Differentiating \({\mathfrak {L}}_1\) along solutions of system (1–4), we obtain

$$\begin{aligned} {\mathfrak {L}}_1'= & {} d_1 \left( \frac{\beta _1 S_1 I_1}{S_1+I_1+c_1}-a_1 I_1-m_4I_1+m_3I_2\right) \\&+ d_2\left( \frac{\beta _2 S_2 I_2}{S_2+I_2+c_2}-a_2 I_2+m_4I_1-m_3I_2\right) , \\\le & {} d_1\left( \frac{\beta _1 S_1^0 I_1}{S_1^0+c_1}-(a_1+m_4)I_1+m_3I_2 \right) \\&+ d_2\left( \frac{\beta _2 S_2^0 I_2}{S_2^0+c_2}-(a_2 +m_3)I_2+m_4I_1\right) , \\= & {} \left( \frac{w_1}{\beta _1 S_1^0/(S_1^0+c_1)},\frac{w_2}{\beta _2 S_2^0/(S_2^0+c_2)}\right) (F-V)I, \\= & {} (w_1,w_2) (1-F^{-1}V) I, \\= & {} (w_1,w_2) (1-\frac{1}{R_0^{ODE}}) I\le 0, \end{aligned}$$

Therefore, \({\mathfrak {L}}_1\) is a Lyapunov function for system (1–4). Since \(d_i>0\) for \(i=1,2\), \({\mathfrak {L}}_1'=0\) implies that either \(S_i=S_i^0\) or \(I_i=0\) for any \(1\le i\le 2\). When \(S_i=S_i^0\), we have

$$\begin{aligned} 0=(S_i^0)^{'}= & {} r_i S_i^0 \left( 1-\frac{S_i^0+I_i}{K_i}\right) -\frac{\beta _i S_i^0 I_i}{S_i^0+I_i+c_i} \mp m_1S_1^0 \pm m_2S_2^0. \end{aligned}$$

Comparing these equations with

$$\begin{aligned} 0= r_i S_i\left( 1-\frac{S_i}{K_i}\right) \mp m_1 S_1 \pm m_2 S_2. \end{aligned}$$

we have \(I_i=0\). Thus, we showed that \({\mathfrak {L}}_1'=0\) implies \(I_1=I_2=0\). It can be easily verified that the only invariant subset of the set \(\{(S_1,I_1,S_2,I_2) \in {\mathcal {E}} | I_1,I_2=0 \}\) is the singleton \({E_0}\). Therefore, by LaSalle Invariance Principle [24], \(E_0\) is globally asymptotically stable in \({\mathcal {E}}^0\). \(\square \)

Now, we establish the global stability of DFE, \(E_0\) for a homogeneous spatial model system (13–16). For this, we select a Lyapunov function as:

$$\begin{aligned} {\mathcal {V}}_1(t)=\int \int _{\varOmega }{\mathfrak {L}}_1(I_1,I_2)dA, \end{aligned}$$
(63)

where \({\mathfrak {L}}_1(I_1,I_2)\) is given as in (62).

$$\begin{aligned} \frac{d{\mathcal {V}}_1}{dt}= & {} \int \int _{\varOmega }\left[ \frac{\partial {\mathfrak {L}}_1}{\partial I_1}\frac{\partial I_1}{\partial t}+ \frac{\partial {\mathfrak {L}}_1}{\partial I_2}\frac{\partial I_2}{\partial t}\right] dA,\\= & {} \int \int _{\varOmega }\frac{d {\mathfrak {L}}_1}{dt}dA+\int \int _{\varOmega }\left( D_{I_1} \frac{\partial {\mathfrak {L}}_1}{\partial I_1} \nabla ^2 I_1+D_{I_2} \frac{\partial {\mathfrak {L}}_1}{\partial I_2} \nabla ^2 I_2\right) dA, \\= & {} T_1+T_2, \end{aligned}$$

where \(T_1=\int \int _{\varOmega }\frac{d {\mathfrak {L}}_1}{dt}dA\) and \(T_2=\int \int _{\varOmega }\left( D_{I_1} \frac{\partial {\mathfrak {L}}_1}{\partial I_1} \nabla ^2 I_1+D_{I_2} \frac{\partial {\mathfrak {L}}_1}{\partial I_2} \nabla ^2 I_2\right) dA\). We now consider \(T_2\) and determine the sign of each term. We utilize the formula known as Green’s first identity in the plane

$$\begin{aligned} \int \int _{\varOmega }F\nabla ^2G dA= & {} \int _{\varOmega }F \frac{\partial G}{\partial \nu }dS-\int \int _{\varOmega }(\nabla F.\nabla G)dA,\nonumber \\ \int \int \frac{\partial {\mathfrak {L}}_1}{\partial I_1} \nabla ^2 I_1 dA= & {} \int _{\varOmega }\frac{\partial {\mathfrak {L}}_1}{\partial I_1} \frac{\partial I_1}{\partial \nu }dS-\int \int _{\varOmega }\left[ \nabla (\frac{\partial {\mathfrak {L}}_1}{\partial I_1}).\nabla I_1\right] dA,\nonumber \\= & {} -\int \int _{\varOmega }\left[ \nabla \left( \frac{\partial {\mathfrak {L}}_1}{\partial I_1}\right) \nabla I_1\right] dA. \end{aligned}$$
(64)

Now,

$$\begin{aligned} \nabla \left( \frac{\partial {\mathfrak {L}}_1}{\partial I_1}\right) =\frac{\partial ^2 {\mathfrak {L}}_1}{\partial I_1^2}\frac{\partial I_1}{\partial x}{\hat{i}}+\frac{\partial ^2 {\mathfrak {L}}_1}{\partial I_1^2}\frac{\partial I_1}{\partial y}{\hat{j}}. \end{aligned}$$

Hence,

$$\begin{aligned} \int \int _{\varOmega }\frac{\partial {\mathfrak {L}}_1}{\partial I_1} \nabla ^2I_1 dA=-\int \int \frac{\partial ^2 {\mathfrak {L}}_1}{\partial I_1^2} \left[ \left( \frac{\partial I_1}{\partial x}\right) ^2+\left( \frac{\partial I_1}{\partial y}\right) ^2\right] dA\le 0. \end{aligned}$$

Similarly,

$$\begin{aligned} \int \int _{\varOmega }\frac{\partial {\mathfrak {L}}_1}{\partial I_2} \nabla ^2I_2 dA=-\int \int \frac{\partial ^2 {\mathfrak {L}}_1}{\partial I_2^2} \left[ \left( \frac{\partial I_2}{\partial x}\right) ^2+\left( \frac{\partial I_2}{\partial y}\right) ^2\right] dA\le 0. \end{aligned}$$

The above analysis shows that if \(T_1 \le 0\), then \(\frac{{\mathcal {V}}_1(t)}{dt}\le 0\). This implies that \(E_0\) is globally asymptotically stable in presence of diffusion if \(E_0\) is globally asymptotically stable in the absence of diffusion.

Proposition 8

Assume that \(R_0^{ODE}>1\) and suppose that the following assumptions are satisfied for all \(1 \le i , j \le 2\)

  1. 1.

    A, B are irreducible.

  2. 2.

    There exists \(\lambda >0\) such that \(a_{ij} S_j^*=\lambda b_{ij} I_j^*\).

  3. 3.

    \(S_i-\frac{(S_i+I_i)}{K_i}(S_i-S_i^*)<0, S_i \ne S_i^*.\)

  4. 4.

    \(S_i^*(I_i-I_i^*)-I_i^*(S_i-S_i^*)<0, S_i \ne S_i^*, I_i \ne I_i^*\).

Then there exists a unique equilibrium \(E^*\) which is globally asymptotically stable.

Proof

We prove the result when all assumptions are satisfied. For city 1 set

$$\begin{aligned} {\mathcal {L}}_1(S_1,I_1)=S_1-S_1^*-S_1^*ln\frac{S_1}{S_1^*}+I_1-I_1^*-I_1^*ln\frac{I_1}{I_1^*}. \end{aligned}$$
(65)

From equilibrium equation, we obtain

$$\begin{aligned} r_1S_1^*-m_2S_1^*= & {} r_1S_1^*\left( \frac{S_1^*+I_1^*}{K_1}\right) +\frac{\beta _1S_1^*I_1^*}{S_1^*+I_1^*+c_1}-m_1S_2^*, \\ a_1I_1^*+m_4I_1^*= & {} \frac{\beta _1S_1^*I_1^*}{S_1^*+I_1^*+c_1}+m_3I_2^*. \end{aligned}$$

Note that \(1-x+lnx\le 0\) for \(x>0\) and equality holds if and only if \(x=1\). Differentiating \({\mathcal {L}}_1\) along the solution of system (1–4), we obtain

$$\begin{aligned} {\mathcal {L}}_1'= & {} r_1S_1-r_1S_1\left( \frac{S_1+I_1}{K_1}\right) -\frac{\beta _1S_1I_1}{S_1+I_1+c_1}+m_1S_2-m_2S_1 \\&+S_1^*\left( r_1\left( \frac{S_1+I_1}{K_1}\right) +\frac{\beta _1I_1}{S_1+I_1+c_1}-\frac{m_1S_2}{S_1}\right) -(r_1S_1^*-m_2S_1^*) \\&+ \left( \frac{\beta _1S_1I_1}{S_1+I_1+c_1}-a_1I_1+m_3I_2-m_4I_1\right) \\&- I_1^*\left( \frac{\beta _1S_1}{S_1+I_1+c_1}-a_1+\frac{m_3I_2}{I_1}-m_4\right) , \\\le & {} r_1S_1-r_1S_1\left( \frac{S_1+I_1}{K_1}\right) +m_1 S_2 \\&+S_1^*\left( r_1 \left( \frac{S_1+I_1}{K_1}\right) +\frac{\beta _1 I_1}{S_1+I_1+c_1}-\frac{m_1 S_2}{S_1}\right) \\&-(r_1S_1^* \left( \frac{S_1^*+I_1^*}{K_1}\right) +\frac{\beta _1S_1^*I_1^*}{S_1^*+I_1^*+c_1}-m_1S_2^*) \\&+\left( m_3 I_2\right) -I_1^*\left( \frac{\beta _1S_1}{S_1+I_1+c_1}+\frac{m_3I_2}{I_1}\right) +\left( \frac{\beta _1S_1^*I_1^*}{S_1^*+I_1^*+c_1}+m_3I_2^*\right) , \\\le & {} r_1(S_1-\frac{(S_1+I_1)}{K_1}(S_1-S_1^*))+\frac{\beta _1}{S_1+I_1+c_1}[S_1^*(I_1-I_1^*)-I_1^*(S_1-S_1^*)] \\&+m_1S_2^*\left( 1-\frac{S_1^*S_2}{S_2^*S_1}+ln\frac{S_1^*S_2}{S_2^*S_1}\right) +m_1S_2^*\left( \frac{S_2}{S_2^*}+ln\frac{S_2^*}{S_2}-\frac{S_1}{S_1^*}-ln\frac{S_1^*}{S_1}\right) \\&+ m_3I_2^*\left( 1-\frac{I_2I_1^*}{I_2^*I_1}+ln\frac{I_2I_1^*}{I_2^*I_1}\right) +m_3I_2^*\left( \frac{I_2}{I_2^*}+ln\frac{I_2^*}{I_2}-\frac{I_1}{I_1^*}-ln\frac{I_1^*}{I_1}\right) , \\\le & {} m_1S_2^*\left( \frac{S_2}{S_2^*}+ln\frac{S_2^*}{S_2}-\frac{S_1}{S_1^*}-ln\frac{S_1^*}{S_1}\right) +m_3I_2^*\left( \frac{I_2}{I_2^*}+ln\frac{I_2^*}{I_2}-\frac{I_1}{I_1^*}-ln\frac{I_1^*}{I_1}\right) , \\\le & {} m_3I_2^* \left[ \left( \lambda \frac{S_2}{S_2^*}+\lambda ln \frac{S_2^*}{S_2}+\frac{I_2}{I_2^*}+ln\frac{I_2^*}{I_2}\right) -\left( \lambda \frac{S_1}{S_1^*}+\lambda ln\frac{S_1^*}{S_1}+\frac{I_1}{I_1^*}+ln\frac{I_1^*}{I_1}\right) \right] , \\= & {} m_3I_2^*[G_2(S_2,I_2)-G_1(S_1,I_1)], \\= & {} b_{21} I_2^*[G_2(S_2,I_2)-G_1(S_1,I_1)], \end{aligned}$$

where \(G_i(S_i,I_i)=\lambda \frac{S_i}{S_i^*}+\lambda ln \frac{S_i^*}{S_i}+\lambda \frac{I_i}{I_i^*}+\lambda ln \frac{I_i^*}{I_i},~~i=1,2\).

Similarly, if we consider \({\mathcal {L}}_2(S_2,I_2)=S_2-S_2^*-S_2^*ln\frac{S_2}{S_2^*}+I_2-I_2^*-I_2^*ln\frac{I_2}{I_2^*}\) we have \({\mathcal {L}}_2' \le m_4 I_1^*[G_1(S_1,I_1)-G_2(S_2,I_2)]= b_{12} I_1^*[G_1(S_1,I_1)-G_2(S_2,I_2)]\). Consider a weight matrix \(M=(m_{ij})\) with entry \(m_{ij}=b_{ij} I_i\) and denote the corresponding weighted digraph as (G, M). Let \(C_i=\sum _{T \in T_i} W(T) \ge 0\) be as given in proposition 6 with (G, M). Then, by Theorem 2, the following identity holds

$$\begin{aligned} \sum _{i=1}^{2}C_i\sum _{j=1}^2 b_{ij} I_i^*[G_i(S_i,I_i)-G_j(S_j,I_j)]=0. \end{aligned}$$
(66)

Set

$$\begin{aligned} {\mathcal {L}}_3(S_1,I_1,S_2,I_2)= \sum _{i=1}^{2} C_i{\mathcal {L}}_i(S_i,I_i). \end{aligned}$$
(67)

Differentiating (67) and using (66),

$$\begin{aligned} {\mathcal {L}}_3'=\sum _{i=1}^{2}C_i {\mathcal {L}}_i^{'}\le \sum _{i=1}^{2} C_i \sum _{j=1}^{2}b_{ij}I_i^*[G_i(S_i,I_i)-G_j(S_j,I_j)]=0, \end{aligned}$$
(68)

for all \((S_1,I_1,S_2,I_2)\in {\mathcal {E}}^0\). Therefore, \({\mathcal {L}}_3\) is a Lyapunov function for the system (1–4). To prove \(E^*\) is globally asymptotically stable, we need to examine the largest compact invariant set. Since B is irreducible, we know that \(C_i>0\) for \(i=1,2\) and thus \({\mathcal {L}}_3'=0\) implies that \(S_i=S_i^*\), and \(I_1=I_1^*\) for \(i=1,2\). Therefore, the only compact invariant subset of the set where \({\mathcal {L}}_3'=0\) is the singleton \(E^*\). Therefore, by LaSalle Invariance Principle, \(E^*\) is globally asymptotically stable in the interior of \({\mathcal {E}}^0\). \(\square \)

Now, we are in position to prove the global stability of \(E^*\) for spatial model system (13–16). Next, we choose a Lyapunov function as

$$\begin{aligned} {\mathcal {V}}_2(t)=\int \int _{\varOmega }{\mathcal {L}}_3(S_1,I_1,S_2,I_2)dA, \end{aligned}$$
(69)

where \({\mathcal {L}}_3(S_1,I_1,S_2,I_2)\) is given as in (67). Then,

$$\begin{aligned} \frac{d{\mathcal {V}}_2}{dt}= & {} \int \int _{\varOmega }\left[ \frac{\partial {\mathcal {L}}_3}{\partial S_1}\frac{\partial S_1}{\partial t}+ \frac{\partial {\mathcal {L}}_3}{\partial I_1}\frac{\partial I_1}{\partial t}+\frac{\partial {\mathcal {L}}_3}{\partial S_2}\frac{\partial S_2}{\partial t}+ \frac{\partial {\mathcal {L}}_3}{\partial I_2}\frac{\partial I_2}{\partial t}\right] dA,\\= & {} \int \int _{\varOmega }\frac{d{\mathcal {L}}_3}{dt}dA \\&+\int \int _{\varOmega }\left( D_{S_1} \frac{\partial {\mathcal {L}}_3}{\partial S_1} \nabla ^2S_1+D_{I_1} \frac{\partial {\mathcal {L}}_3}{\partial I_1} \nabla ^2 I_1\right. \\&\left. +D_{S_2} \frac{\partial {\mathcal {L}}_3}{\partial S_2} \nabla ^2S_2+D_{I_2} \frac{\partial {\mathcal {L}}_3}{\partial I_2} \nabla ^2 I_2\right) dA, \\= & {} U_1+U_2, \end{aligned}$$

where \(U_1=\int \int _{\varOmega }\frac{d {\mathcal {L}}_3}{dt}dA\) and \(U_2=\int \int _{\varOmega }\left( D_{S_1} \frac{\partial {\mathcal {L}}_3}{\partial S_1} \nabla ^2 S_1+D_{I_1} \frac{\partial {\mathcal {L}}_3}{\partial I_1} \nabla ^2I_1+D_{S_2} \frac{\partial {\mathcal {L}}_3}{\partial S_2} \nabla ^2S_2+D_{I_2} \frac{\partial {\mathcal {L}}_3}{\partial I_2} \nabla ^2I_2 \right) dA\).

$$\begin{aligned} \int \int _{\varOmega }F\nabla ^2G dA= & {} \int _{\varOmega }F \frac{\partial G}{\partial n}dS-\int \int _{\varOmega }(\nabla F.\nabla G)dA,\nonumber \\ \int \int \frac{\partial {\mathcal {L}}_3}{\partial S_1} \nabla ^2 S_1 dA= & {} \int _{\varOmega }\frac{\partial {\mathcal {L}}_3}{\partial S_1} \frac{\partial S_1}{\partial n}dS-\int \int _{\varOmega }\left[ \nabla (\frac{\partial {\mathcal {L}}_3}{\partial S_1}).\nabla S_1\right] dA,\nonumber \\= & {} -\int \int _{\varOmega }\left[ \nabla \left( \frac{\partial {\mathcal {L}}_3}{\partial S_1}\right) .\nabla S_1\right] dA. \end{aligned}$$
(70)

Now,

$$\begin{aligned} \nabla \left( \frac{\partial {\mathcal {L}}_3}{\partial S_1}\right) =\frac{\partial ^2 {\mathcal {L}}_3}{\partial S_1^2}\frac{\partial S_1}{\partial x}{\hat{i}}+\frac{\partial ^2 {\mathcal {L}}_3}{\partial S_1^2}\frac{\partial S_1}{\partial y}{\hat{j}}, \end{aligned}$$
(71)

Hence,

$$\begin{aligned} \int \int _{\varOmega }\frac{\partial {\mathcal {L}}_3}{\partial S_1} \nabla ^2S_1 dA=-\int \int \frac{\partial ^2 {\mathcal {L}}_3}{\partial S_1^2} \left[ \left( \frac{\partial S_1}{\partial x}\right) ^2+\left( \frac{\partial S_1}{\partial y}\right) ^2\right] dA\le 0. \end{aligned}$$
(72)

Similarly,

$$\begin{aligned} \int \int _{\varOmega }\frac{\partial {\mathcal {L}}_3}{\partial I_1} \nabla ^2I_1 dA=-\int \int \frac{\partial ^2 {\mathcal {L}}_3}{\partial I_1^2} \left[ \left( \frac{\partial I_1}{\partial x}\right) ^2+\left( \frac{\partial I_1}{\partial y}\right) ^2\right] dA\le 0,\nonumber \\ \int \int _{\varOmega }\frac{\partial {\mathcal {L}}_3}{\partial S_2} \nabla ^2 S_2 dA=-\int \int \frac{\partial ^2 {\mathcal {L}}_3}{\partial S_2^2} \left[ \left( \frac{\partial S_2}{\partial x}\right) ^2+\left( \frac{\partial S_2}{\partial y}\right) ^2\right] dA\le 0,\nonumber \\ \int \int _{\varOmega }\frac{\partial {\mathcal {L}}_3}{\partial I_2} \nabla ^2I_2 dA=-\int \int \frac{\partial ^2 {\mathcal {L}}_3}{\partial I_2^2} \left[ \left( \frac{\partial I_2}{\partial x}\right) ^2+\left( \frac{\partial I_2}{\partial y}\right) ^2\right] dA\le 0 \end{aligned}$$
(73)

The above analysis indicates that if \(U_1 \le 0\), then \(\frac{d{\mathcal {V}}_2(t)}{dt}\le 0\). Thus, we have the following consequence: if \(E^*\) is globally asymptotically stable in the absence of diffusion, then \(E^*\) will remain globally asymptotically stable in the presence of diffusion.

The same procedure will work for homogeneous coupled reaction-diffusion system with n nodes or cities and any topology or connections.

5 Numerical simulation for two cities

The global dynamical behaviour of two-city model in the interior of \({\mathbb {R}}_4^+\) is investigated numerically. The values of the parameters are hypothetical but are chosen carefully on the basis of the ranges reported in Jorgensen [17] and are ecologically permissible parameter values. The ODEs (1–4) were integrated using Runge-Kutta method and for spatial model we employ explicit standard five-point approximation programmed in the MATLAB R2017a software environment.

5.1 Numerical simulation for non-spatial model and effect of mobility

For the parameter values \(m_1=1.2, m_2=0.2, a_1=0.15, m_3=0.2, m_4=0.1, a_2=0.13\) and other parameters as given in Table 1 we obtain positive equilibrium point as \(E^*=(48.9651, 642.9726, 52.3128, 321.6942)\), which is globally asymptotically stable (c.f. Fig. 2a). If we change the parameter \(m_4=3.1\) we observe that the dynamics changes from stable focus to limit cycle (c.f. Fig. 2b). These figures suggest that change in migration rate can induce bifurcation.

We have used the MATLAB matcont toolbox for plotting equilibrium manifolds of \(E^*\) and are presented in Fig. 3a, b. These diagrams are generated by taking \(m_4\) and \(m_1\) as a bifurcation parameter. In Fig. 3a, variations of the infective \(I_1\) and \(I_2\) populations are given as functions of \(0<m_4<5\), with the values of the other parameters are as given above. When \(0<m_4<0.28826133\) the equilibrium \(E^*\) is stable (all eigenvalues have negative real parts). When \(m_4\approx m_{4{\textit{cr}}1}=0.28826133\) a complex conjugate pair becomes purely imaginary and the equilibrium loses stability through Hopf-bifurcation and becomes unstable giving rise to limit cycle which is orbitally stable (first Lyapunov coefficient is negative). For \(0.28826133<m_4<3.3198113\) the equilibrium, \(E^*\) unstable (two eigenvalues have positive real parts). However, when \(m_4 \approx m_{4{\textit{cr}}2}=3.3198113\) the system again experiences Hopf-bifurcation (supercritical). For \(3.3198113<m_4<5\), \(E^*\) is again stable (all eigenvalues have negative real parts).

Now, we investigate the effect of \(m_1\). As \(m_1\) increases from 0 to 8 two Hopf bifurcations are observed. When \(0<m_1<0.16385636\) we have unstable branches (two eigenvalues are positive and two have negative real parts). At \(m_1 \approx m_{1{\textit{cr}}1} = 0.16385636\) a complex conjugate pair becomes purely imaginary giving rise to the first Hopf point (supercritical). For \(0.16385636<m_1<6.583927\) we observe a stable branch (all eigenvalues have negative real parts). Again at \(m_1 \approx m_{1 {\textit{cr}}2} = 6.583927\) two eigenvalues becomes purely imaginary giving rise to second Hopf point (supercritical). As \(6.583927<m_1<8\) we again observe an unstable branch (two eigenvalues are positive and two have negative real parts). Thus in the present system and for the given parameter values we observe two Hopf-bifurcations, one is stabilizing and other is destabilizing the equilibrium \(E^*\).

Next we draw a Hopf bifurcation curve in \((m_1,m_4)\) plane (c.f. Fig. 4) from first Hopf point (\(m_4\approx m_{4{\textit{cr}}1}=0.28826133\)) in order to detect bifurcations with codimension-2 [22]. No codimension-2 bifurcation is observed. We also performed the continuation of the limit cycle from the first Hopf point when \(m_1,m_4\) are treated as the free parameters. At \(m_1=1.2\) and \(m_4=0.28826131\) Limit point cycle is observed. Limit Point Cycle (LPC) is a fold bifurcation of the cycle from the family of limit cycles bifurcating from the Hopf point, where two limit cycles with different periods are present near LPC point. No other bifurcation point was found in this curve. Identical results were obtained when we carried out the continuation of limit cycles from other Hopf point and hence are not reported. Our simulation results can be compared to the results given by [46]. They derived a critical value with respect to the mobility rate and found that when mobility rate is larger than critical value outbreak occurs before it dies out.

Fig. 2
figure 2

Numerical simulation of the system (1–4), a time series for infectives in both cities showing global stability of \(E^*\) with \( m_4=0.1\), b time series for infectives showing periodic dynamics in two cities with \(m_4=3.1\). Other parameter values are the same as given in text

Full size image
Fig. 3
figure 3

A branch of equilibria displaying existence of Hopf-bifurcations, a in the \((m_4, I_1)\) and \((m_4, I_2)\)-plane, b in the \((m_1, I_1)\) and \((m_1, I_2)\)-plane. Other parameter values are the same as given in text. H: denote a Hopf point

Full size image
Fig. 4
figure 4

The Hopf bifurcation curve in \((m_1,m_4)\) plane. LPC: denote limit point cycle

Full size image

Now, suppose that initially city 1 and 2 are disjoint (zero mobility), and that the disease is present in city 1, while city 2 is such that the disease is absent. For the parameter values given in Table 1 we find that \((R_{01}^{ODE})_{isolated}=\frac{\beta _1 K_1}{a_1(K_1+c_1)}>1\) while \((R_{02}^{ODE})_{isolated}=\frac{\beta _2 K_2}{a_2(K_2+c_2)}<1\). Now we connect both the cities. We observe that mobility can stabilize or destabilize the DFE. We observe that when we set migration \(m_1=1.2,m_2=0.2, m_3=0.2, m_4=0.1\), the infection spreads in both the cities (c.f. Fig. 5a). The effective reproduction number for the whole network is 8.8880 greater than unity. The simulation confirms the instability of the disease-free steady state when \(R_0^{ODE}>1\). Moreover, when we set migration \(m_1=1.2,m_2=3.2, m_3=0.2, m_4=3.1\), the infection is dies out in both the cities (c.f. Fig. 5b). In this case, the effective reproductive number is 0.719094 which is less than unity for the whole network. A change in mobility can induce a bifurcation from \(R_0^{ODE}<1\) to \(R_0^{ODE}>1\) or vice-versa. Therefore, parameters \(m_i\) can play an important role in disease controlling.

Fig. 5
figure 5

a Time series for infectives showing the disease is sustained in two cities when \(m_1=1.2,m_2=0.2, m_3=0.2, m_4=0.1\), b time series for infectives showing disease is disappearing in both cities when \(m_1=1.2,m_2=3.2, m_3=0.2, m_4=3.1\). Other parameter values are the same as those listed in Table 1

Full size image

5.2 Numerical simulation for spatial model

We check the above result for our spatial model system (13–16) without and with spatial heterogeneity. To examine the spatio-temporal dynamics of the system, we carry out intensive numerical simulations for model (13–16) in two-dimensional spaces using finite difference scheme for the 2D Laplacian. We consider two cities to be identical square domains. All our numerical simulations use zero-flux or Neumann boundary conditions and nonzero initial conditions. We discretize the system of size \(200 \times 200\) through \(x \rightarrow (x_0, x_1, x_2, . . . , x_N)\) and \(y \rightarrow (y_0, y_1, y_2, . . . , y_N)\), with \(N = 800\) i.e. the spacing between the lattice points is \({\varDelta }h=0.25\). In the present study, we set \({\varDelta }t =0.001\).

5.2.1 The effect of mobility

We confirm numerically that if the parameters and the diffusion coefficient are constant, the reproduction number is the same as in the ODE case. Again, we suppose that cities 1 and 2 are isolated, and initially the disease spreads in city 1 while disease is absent in city 2, i.e., \(R_{01}^{PDE} \approx 14.304723>1\) while \(R_{02}^{PDE} \approx 0.455555<1\). Now, let us connect the cities. We observe that when we set migration \(m_1=1.2,m_2=0.2, m_3=0.2, m_4=0.1\), the infection spreads in both the cities (c.f. Fig. 6a). The effective reproductive number for the coupled PDE system is \(R_0^{PDE} \approx 8.9035>1\). However, when we set more strong migration rate \(m_1=1.2,m_2=3.2, m_3=0.2, m_4=3.1\), the infection dies out in both the cities (c.f. Fig. 6b). The effective reproductive number for the coupled PDE system is \(R_0^{PDE} \approx 0.7968<1\). We observe that the value of \(R_0^{PDE}\) is almost the same as in the ODE case which is in agreement with the result of Theorem 1.

Now, we are interested in studying the effect of heterogeneity. To capture the seasonality of school contacts, the transmission rate \(\beta _1\) and \(\beta _2\) can be set to be the periodic function. For this, we consider \(\beta _1=2.15(1+cos((\pi x y)/10))\) and \(\beta _2=0.98(1+cos((\pi x y)/10))\), and keep other parameters the same as above. There is no explicit formula for computing the basic reproduction number \(R_0^{HPDE}\) in a spatially heterogeneous infection. Thus, we numerically compute it by using solvepdeeig MATLAB function. If the cities are disconnected, we find \(R_{01}^{HPDE} \approx 23.037539\) while \(R_{02}^{HPDE} \approx 0.748634<1\). When the cities are connected, we observe that the disease spreads in both the cities with small population dispersal and it requires a stronger dispersal rate to reach disease-free state. Even for the migration rate \(m_1=1.2,m_2=3.2, m_3=0.2, m_4=3.1\), we found \(R_0^{HPDE} \approx 1.290126>1\) which implies that the infection does not dies out in both the cities (c.f. Fig. 7a) which was not the case in ODE and spatial model without heterogeneity. From these simulations, we have two implications, (i) the risk of infection could be underestimated if we compute basic reproduction number using constant parameters, (ii) more stronger migration rate from disease endemic city to disease free city is required to achieve overall disease free state in spatially heterogeneous domain (c.f. Fig. 7b). In contrast, [46] showed that the epidemic will die in the first community when the mobility rate is too low. Also, if mobility rate is high enough the epidemic can spread into second community before it die.

Fig. 6
figure 6

Spatial dynamics for the homogeneous system (13–16) varying migration coefficient \(m_2,m_4\) at \(t=100\) days, a \(m_2=0.2, m_4=0.1\) with \(R_{0}^{PDE} \approx 8.9035>1\), b \(m_2=3.2, m_4=3.1\) with \(R_{0}^{PDE} \approx 0.79688<1\). Initial conditions and other parameter values are the same as those listed in Table 1. Blue color represents minimum density and yellow color represents maximum density

Full size image
Fig. 7
figure 7

Spatial dynamics for the heterogeneous system (13–16) with \(\beta _1(x,y)=2.15(1+cos(\pi x y/10)), \beta _2(x,y)=0.98(1+cos(\pi x y/10))\) and varying migration coefficient \(m_2,m_4\) at \(t=100\) days, a \(m_2=3.2, m_4=3.1\) with \(R_0^{HPDE} \approx 1.290126\), b \(m_2=7.2, m_4=7.1\) with \(R_{0}^{HPDE} \approx 0.88655<1\). Initial conditions and other parameter values are the same as those listed in Table 1. Blue color represents minimum density and yellow color represents maximum density

Full size image

Conclusion: Figure 5, 6 and 7 gives an overview of the dynamics of the basic reproduction number with respect to the mobility of the susceptible and infected individuals from City 1 (disease endemic) to City 2 (disease free). These figures show that if the dispersal rate from endemic to disease free city (\(m_2\) and \(m_4\)) increases it can bring effective reproduction numbers down below unity.

5.2.2 Disease dissemination with varying diffusion

In this subsection, we investigate the influence of diffusion coefficients on \(R_0^{HPDE}\) and hence on disease prevalence or absence. Here, we fix the parameter values \(D_{S_1}=1, D_{S_2}=5, D_{I_2}=0.05,\beta _1=2.15(1+cos(\pi x y/10)), \beta _2=0.98(1+cos(\pi x y/10))\) and other parameter values given in Table 1 and vary parameter \(D_{I_1}\). Our numerical computations signify that \(R_0^{HPDE}\) decreases as \(D_{I_1}\) increases and the system undergoes a transition from \(R_0^{HPDE}>1\) to \(R_0^{HPDE}<1\) as \(D_{I_1}\) varies from 0.01 to 10 (c.f. Fig. 8). Similarly, \(R_0^{HPDE}\) decreases as any other diffusion coefficient increases. Hence, the larger the local random diffusion, the smaller is the infection risk.

The finding is in accordance with the previous work [62]. They showed that when the agents move with a high velocity the inhomogeneity of epidemic spreading decreases. Similar results were found in [57] for a time-delayed reaction-diffusion model of dengue fever. However, recently [47] showed that monotonicity of \(R_0^{HPDE}\) with respect to diffusion rates does not hold in general. Moreover, we also observe a change in pattern formation as diffusion coefficient changes from \(D_{I_1}=0.01\) to \(D_{I_2}=10\). Infected population of city 1 gathers into large cluster at \(D_{I_2}=10\).

Fig. 8
figure 8

Spatial dynamics of the system (13–16) varying diffusion coeffcient \(D_{I_1}\) at \(t=300\) days, a \(D_{I_1}=0.01\) , b \(D_{I_1}=1\) and c \(D_{I_1}=10\). Other parameter values are the same as those listed in Table 1. These figures indicate \(R_0^{HPDE}\) is decreasing function of \(D_{I_1}\)

Full size image

5.2.3 The effect of spatial heterogeneity

Next, we take \(\beta _1=2.15(1+pcos(\pi x y/10))\) and \(\beta _2=0.98(1+pcos(\pi x y/10))\), where \(0<p\le 1\) can be interpreted as an order of magnitude of infection heterogeneity. We now fix \(D_{I_1}=0.01\) and other parameters as above. Our numerical computation indicates that if p is increased from 0 to 1 i.e. more heterogeneity of spatial infection, \(R_0^{HPDE}\) increases as a function of p. We calculate the value of \(R_0^{HPDE}\) numerically and found that for (i) \(p=0.1\), \(R_0^{HPDE} \approx 0.876137<1\), (ii) \(p=0.4\), \(R_0^{HPDE}\approx 1.113995>1\), (iii) \(p=0.8\), \(R_0^{HPDE} \approx 1.431082>1\). These simulation shows that infection risk become more intense by heterogeneous spatial disease transmission (c.f. Fig. 9).

Fig. 9
figure 9

Spatial dynamics of the system (13–16) varying magnitude of infection heterogeneity p where \(\beta _1=2.15(1+pcos(\pi x y/10))\) and \(\beta _2=0.98(1+pcos(\pi x y/10))\) at \(t=300\) days, a \(p=0.1\) with \(R_0^{HPDE} \approx 0.876137<1\), b \(p=0.4\) with \(R_0^{HPDE} \approx 1.1139949>1\) and c \(p=0.8\) with \(R_0^{HPDE}\approx 1.431082\). Other parameter values are the same as those listed in Table 1. These figures indicate \(R_0^{HPDE}\) is an increasing function of p

Full size image

Our simulation result are in agreement with [41]. They modified the standard SIRS model on WS small-world network and BA scale-free network and analysed the model theoretically and performed computer simulation on different networks. They found that on increasing the number of links the critical value to contact rate (\(\lambda _c\)) decreases, i.e. for contact rate>critical value to contact rate, infection spreads and becomes persistent. Our simulation result also shows that an increase in heterogeneity (that can be compared to increase in nodes) increases the infectives. However, we did not consider effect of vaccination in controlling the epidemic propagation and can be an important factor.

6 Conclusions and discussions

A complete analysis of a two-city reaction-diffusion model is presented to study the transmission of epidemics. We considered distinct parameters for both the cities. We showed that when the coupled reaction-diffusion system is at an equilibrium and city 1 has disease endemic situations, the city 2 (connected to city 1 directly or indirectly) will be also at an disease endemic level. These conclusions assume that the entire coupled system is at a steady state equilibrium. The formula for calculating basic reproduction number \(R_0^{HPDE}\) for two city reaction-diffusion models is derived using previous findings. This formula permits us to suggest some control measures against disease spread from one city to another and to investigate the effectiveness of present public health policies. The disease free equilibrium (DFE) is globally asymptotically stable if the basic reproduction number for ODE (\(R_0^{ODE}\)) is less than unity i.e. \(R_0^{ODE} \le 1\), and unstable if \(R_0^{ODE}>1\). The health impact and consequences produced by population migration is directly related to two basic factors, (i) the distance between source and the destination [49], and (ii) the size of the mobile population migrating between different disease prevalent cities. We found the existence of codimension-1 bifurcations (two Hopf-points and Limit Point of Cycles) and discussed how endemic equilibrium, \(E^*\) changes its stability through Hopf-bifurcations. We have also shown that a population migration results in the spread of the disease in both cities, even though the disease is not prevalent in one isolated city. We also observed that a more strong population dispersal rate from disease endemic city to disease free city can bring the entire system to disease free situation.

Moreover, for spatially homogeneous infections i.e. if all parameters are constant, we demonstrated numerically that the diffusion coefficients \(D_{I_1}\) and \(D_{I_2}\) has no effect on the value of the basic reproduction number. Although, in a spatially heterogeneous environment, the random diffusion coefficients \(D_{I_1}\) and \(D_{I_2}\) affects the basic reproduction number. We notice that more local random movements among the population reduces the basic reproduction number. Alternatively, more spatial heterogeneity induces higher \(R_0^{HPDE}\) and as a result more infection risk. Numerical simulation shows that infection risk can be understated if spatially constant parameters are used to calculate basic reproduction number.

To see the effect of traveling between and within the cities, comparative degrees of analysis are required. There are a large number of possibilities to extend the present two-city model, in order to quantify the practicality. Complex network provides a powerful platform to study the role of heterogeneous topology such as a small world, scale free and is ignored traditionally. Analytic solution for the complete model is complicated, however the numerical solutions can be used to plan control strategies, for instance by adjusting migration parameters. The development and analysis of such reaction-diffusion network models are still in their beginning. It is worthy to note that in this work we assume that the displacements are made from a point of the first city to exactly the symmetrical point of the other. To generalize it, we have to consider an integral term to allow individuals to go to desired point in the other city. This issue will be addressed in our forthcoming work and can assist us to understand spatial spread of an epidemic more accurately when populations migrate from one location of a city to another city randomly.