1 Introduction

Nowadays, the increasing need for fast product building in the competitive world of marketing was answered by the invention of the rapid prototyping (RP) technique also known as additive manufacturing (AM) or layered manufacturing (LM) [1] which is based on quickly fabricating products and prototypes, layer by layer directly (without an intermediate tool) from a 3D computer-aided design (CAD) model [2,3,4]. Its benefits over conventional subtractive manufacturing techniques (like NC machines) made them widely used in industries such as aerospace, automotive, electronics, and many other fields; Some of their benefits include the capability of fabricating complex models, fast manufacturing, a wide range of material choices, flexibility to reduce build cost, reduced waste of material and tooling utilization, and energy consumption [5,6,7,8,9,10]. AM technique divides into Binder jetting (consists of 3D printing (3DP), Link-jetting, S-print, and M-print), Directed energy deposition (consists of Direct metal deposition (DMD), Laser deposition (LD), and Electron beam direct melting (EBDM), Material extrusion (consists of Fused deposition melting (FDM) or fused filament fabrication (FFF)), Material jetting (consists of Polject, Ink-jetting, and Thermojet), Powder bed fusion (consists of Selective laser sintering (SLS), Selective laser melting (SLM), and Electron beam melting (SBM)), Sheet lamination (consists of Ultrasonic consolidation (UC) and Laminated object manufacture (LOM)), and Vat photo-polymerization (consists of Stereo-lithography (SLA) and Digital light processing (DLP)) [11].

Among the mentioned processes, SLA and FDM due to their ability to create intricate parts, and SLS due to their ability to manufacture fast and low-cost products, are commonly used and popular [12, 13]. The problem with the SLS method, that it produces parts with lower density and strength, is solved by the SLM method which produces denser and stronger parts by melting and re-solidifying the metal powder [14]. SLM process works based on the melting of the powder by high power laser, which starts with distributing powder on a powder bed uniformly. Then a laser beam is used to melt the metallic powder by aiming points in space according to the 3D model definition. Afterward, the previous layer is covered by another layer of powder. This process goes on repeatedly until the structure is completed [15]. As explained, the benefits of the SLM method can make it a useful case study.

The main problem with RP methods is the poor quality of the produced part, which is governed by the surface quality, accuracy, and strength of the part. They often need post-processing such as removing support structures and polishing the surface which leads to a longer time to completely produce a suitable part. The longer the time of production, the higher the cost of production [2, 5]. Properties of the final product (like surface quality, part strength, and so on) are affected by part deposition [5, 6, 16]. Other process parameters (layer thickness and laser power) affect the final properties of the product. For example, the layer-wise nature of AM process causes the staircase effect and therefore volumetric error which can be reduced by choosing the best part build orientation (PBO) and layer thickness [1, 6, 17]. The best condition is when the accuracy and surface quality are at their highest amount and build time and cost are at their lowest amount, but, as mentioned before, more accuracy and better surface quality need more time and hence higher cost [18]. So it is not easy to find the best PBO because there is always a conflict between these properties [19].

The research on the optimization of the PBO in the literature can be divided into two main categories, first, solving the problem of a single objective optimization, and second, solving the problem of multi-objective optimization. For the case of improving the best build orientation for a special objective function (OF), some researchers used an OF in terms of part build orientation, and others just examined different directions to investigate the best one. For example, Alsalla et al. [20] investigated the effect of build orientation on the mechanical properties of the SLM parts. They conducted the fracture toughness test of Edge Notched Bend (SENB) samples. They concluded experimentally that the best direction for the fracture toughness is in the OZ direction (in which the longitude and the thickness of the specimen were, respectively, in the OZ and OY directions). Although, due to the pores at the edges of the SLM parts, its fracture toughness is lower than the conventional product. Hartunian and Eshraghi [21] studied the behavior of SLM parts in different orientations by examining the tensile strength of rectangular parts. They showed that the weakest tensile strength happened in the Z orientation (in which the longitude and the thickness of the specimen were, respectively, in the Z and Y directions). Like the previous two studies, Vishwakarma et al. [22] focused on studying experimentally the effect of the build orientation on the tensile strength and ductility of the SLM parts. They prepared plates in 0°, 45°, and 90° orientations. The result was that the orientation of 90° showed better strength and ductility even in comparison with the conventional melting method. Camposeco-Negrete et al. [23] proposed an experimental work for optimizing printing parameters on the quality, strength, mass, and processing time of polylactic acid (PLA) samples produced by additive manufacturing. The experimental results were analyzed by analysis of variance (ANOVA) and optimized through the Taguchi method.

On the other hand, some other studies optimized a single OF in terms of orientation parameters. For example, Ingole et al. [24] Formulate the cost of FDM manufactured product as an OF in a mathematical term. To achieve the best build orientation, they analyzed this formula for different orientations of different types of actual parts. Morgan et al. [25] studied the effect of build orientation on the volume support of SLM parts. They used volume support in terms of build orientation and optimized it with an unconstraint gradient-based MatLab algorithm. To prove the efficiency of the algorithm, they studied three cases. Ulu et al. [26] prepared an OF for the strength of the additively manufactured part in terms of build orientations. Then they optimized the strength for some study cases to achieve maximum structural robustness employing a surrogate-based model.

Generally, to optimize an OF with the help of an algorithm there should be a relation between OF and build orientation. Some researchers used response surface from the results of the experiment to construct OFs, like the works of [5, 27]. While others tried an analytical relation independent of the experimental results for optimization, like the works of [26, 28]. In the case of multi OF optimization, most of the studies are based on Weighted sum and Pareto front methods [29]. Since the main challenge with the weighted sum method is to choose the proper weight for each OF, using the non-dominant genetic algorithm II (NSGAII) can be a proper solution [30]. Here is the literature research on the multi OF Pareto front-based optimization with the help of the genetic algorithm. Nezhad et al. [31] found the best build orientations based on the Pareto front for SLA parts’ build time, surface quality, and support volume. In addition, they defined the thickness of each layer as a variable in terms of build orientation. Later, Huang et al. [30] worked on the optimization of FDM parts’ build time and surface roughness. They also used compute unified device architecture (CUDA) to enhance solving speed. Khodaygan et al. [28] worked on the optimization of build time and surface quality. Then, they used the kriging meta-model to optimize OFs with the means of NSGAII and the TOPSIS method to rank Pareto front answers. Asadollahi et al. [32] researched the optimization of the build time and material mass with the constraint of surface roughness and mechanical behavior of FDM products. Di Angelo et al. [11] used original methods to estimate the build cost and surface quality in terms of build orientation for FDM parts.

As it is shown in the review of the literature, there is a gap in analyzing multi-objective PBO optimization of three OFs of surface roughness, build time, and mechanical property (specifically, the strength of a part). So, the purpose of the present study is to choose the best PBO by multi-objective optimizing three OFs (surface quality, build time, and mechanical properties (specifically, the strength of a part)) and rank them based on the importance of each OF. To achieve this purpose, analytical OFs are formulated based on the derived relations in the literature, then an SLM part, which was manufactured particularly for this study, is used for the formulation of the part OFs. Since these OFs were computationally expensive, the kriging meta-model is used to approximate OFs. Both the original OFs and the approximated OFs are optimized by NSGAII. In solving the multi-objective PBO optimization problem in AM by a generating method, selecting the best PBO from the obtained optimal Pareto alternatives is a significant challenge for designers. In this work, to find the best PBO from the optimal Pareto fronts, the TOPSIS algorithm is used. For justification purposes, first, the capability of the original OFs was evaluated by a comparison between the results of experimental tests and analytical original OFs optimum orientations. Finally, to illustrate the efficiency of estimated OFs to reduce consumed time was illustrated by conducting an ANOVA for the comparison of the values derived from original and estimated OFs.

2 Methodology

In this section, the method to achieve the best PBO of three OFs is discussed. First, the optimization problem and the variables are described then, the OFs are introduced which are as follows: surface roughness, build time, and mechanical properties (factor of safety). Finally, the description of the NSGAII method used to solve the multi-objective problem optimization is presented.

2.1 Formulation of multi-objective optimization problem

To solve the PBO for a multi-objective problem, first, the “Standard Triangle Language” STL file of the model should be derived from the 3D model. The STL format is used to transfer data from the CAD model to the 3D printer device [33]. As it is shown in Fig. 1, changing the direction of the part causes changes in the coordinates of the normal vectors and the vertexes of the triangular facets. Which can be controlled by the rotation matrix. The variables of the rotation matrix are the angles of the rotation around each ax. Therefore, the variables of this optimization problem are the rotation angles around the x, y, and z axes. So the vertexes’ and the normal vectors’ coordinates of the triangular facets should be derived from the STL file of the 3D models.

Fig. 1
figure 1

STL format of the 3D model a before rotation. b after rotation

Full size image

The general optimization problem is:

$${\text{min}} f\left( x \right) = \left( {f_{1} \left( x \right),f_{2} \left( x \right),f_{3} \left( x \right)} \right)$$
(1)

where x is the vector of decision variables.

$$x=\left({\theta }_{x}.{\theta }_{y}.{\theta }_{z}\right)$$

and the constraints are:

$$0\le {\theta }_{x}\le 180$$
$$0\le {\theta }_{y}\le 180$$
$$0\le {\theta }_{z}\le 180$$

\(f({\theta }_{x}.{\theta }_{y}.{\theta }_{z})\) consists of desired OFs to be optimized and this research consists of three OFs of surface roughness, build time, and mechanical property. \({\theta }_{x}\), \({\theta }_{y}\), and \({\theta }_{z}\) are the design variables and the rotation angle around the x, y, and z-axes, respectively.

2.2 Surface roughness

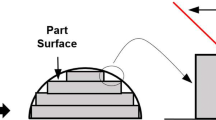
As it was described in the introduction the main problem with AM method is the poor part quality due to the layer-wise nature of this method, which causes the stair-stepping effect. The effect of the stair-step and part orientation is shown in Fig. 2. It is clear that the second position (Fig. 2b) causes poor surface quality, more surface roughness, and stair-stepping effect. Many researchers worked on surface quality, like the works of [2, 3, 5, 30, 34] some of them used interpolation of experimental data [2] or a response surface method, which was constructed by conducting several experiments [5]. The latter used laser power, build orientation, and layer thickness as design variables for an SLS method. Byun and Lee [3] proposed a new mathematical relation between surface roughness and rotation angle based on the previous experimental data, they ignored the effect of removing support structure for different kinds of AM processes except for the SLA process. Among the factors that affect the surface roughness (like layer thickness, removing support structure, and staircase effect) the staircase effect is the main source of errors according to Ahn et al. [35]. Their research proposed a mathematical relation between the average surface roughness and the surface angle, which is as follows:

Fig. 2
figure 2

stair-stepping effect. a before rotation. b after rotation

Full size image
$${R}_{a}=\frac{A}{W}=\frac{L}{2}\left|\frac{\mathrm{cos}\theta -\beta }{\beta }\right| ({0}^{^\circ }\le \theta \le {180}^{^\circ })$$
(2)

where \(A\) is step area, \(W\) is step width, \(L\) is layer thickness, \(\theta\) is the surface angle, and \(\beta\) is profile angle.

This formulation was improved by the works of Khodaygan and Golmohammadi [28] regardless of layers deviations, which can be used for any kind of AM parts, and it is as follows (Eq. 3):

$${Ra}_{i}=\left|\mathrm{cos}\theta \right|=\left|{n}_{3i}\right|$$
(3)

Finally, the mean roughness of the surface is as bellow:

$$R=\frac{{\sum }_{i=1}^{n}{Ra}_{i}{A}_{i}}{{\sum }_{i=1}^{n}{A}_{i}}$$
(4)

where \({Ra}_{i}\) is the surface roughness of each triangle’s facets, \({A}_{i}\) is the area of each triangle’s facet, and n is the number of triangular facets.

(see [28] for details)

To set Eq. (3) in terms of part-build decision variables, the rotation matrix is pre-multiplied by the facet’s third component of normal vectors.

The transformation matrix according to Euler angles, roll \(\left(\alpha \right)\), pitch \(\left(\beta \right)\), and yaw \(\left(\gamma \right)\), is as follows [36]:

$${R}_{\alpha }=\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{cos}\alpha & -\mathrm{sin}\alpha \\ 0& \mathrm{sin}\alpha & \mathrm{cos}\alpha \end{array}\right]$$
(5)
$${R}_{\beta }=\left[\begin{array}{ccc}\mathrm{cos}\beta & 0& \mathrm{sin}\beta \\ 0& 1& 0\\ -\mathrm{sin}\beta & 0& \mathrm{cos}\beta \end{array}\right]$$
(6)
$${R}_{\gamma }=\left[\begin{array}{ccc}\mathrm{cos}\gamma & -\mathrm{sin}\gamma & 0\\ \mathrm{sin}\gamma & \mathrm{cos}\gamma & 0\\ 0& 0& 1\end{array}\right]$$
(7)
$$R\left(x\right)={R}_{\gamma }{R}_{\beta }{R}_{\alpha }$$
(8)

Transformation law for Cartesian components of a vector [37]:

$${\left[n\right]}^{^{\prime}}={\left[R\right]}^{T}\left[n\right]$$

where the transposed of the transformation matrix (the rotation matrix) is as below:

$${R}^{T}\left(x\right)=\left[\begin{array}{ccc}\mathrm{cos}\beta \mathrm{cos}\gamma & -\mathrm{cos}\beta \mathrm{sin}\gamma & \mathrm{sin}\beta \\ \mathrm{cos}\alpha \mathrm{sin}\gamma +\mathrm{sin}\alpha \mathrm{sin}\beta \mathrm{cos}\gamma & \mathrm{cos}\alpha \mathrm{cos}\gamma -\mathrm{sin}\alpha \mathrm{sin}\beta \mathrm{sin}\gamma & -\mathrm{sin}\alpha \mathrm{cos}\beta \\ \mathrm{sin}\alpha \mathrm{sin}\gamma -\mathrm{cos}\alpha \mathrm{sin}\beta \mathrm{cos}\gamma & \mathrm{sin}\alpha \mathrm{cos}\gamma +\mathrm{cos}\alpha \mathrm{sin}\beta \mathrm{sin}\gamma & \mathrm{cos}\alpha \mathrm{cos}\beta \end{array}\right]$$
(9)

In this study, Eq. (3) is used.

2.3 Build time

Many authors worked on the part-build time like the works of [3, 5, 27, 38, 39]. Their studies focused on finding factors that affect the build time the most. For example, the goal of the work of references [3, 34] was to minimize the build time by minimizing the support structure and non-productive time (time to lower the platform after every deposition, the time between ending and starting of a new cycle, time to wipe the nozzle, and so on for an FDM method). Brika et al. [27] considered machine parameters (like laser scan speed, layer thickness, and so on), volume and height of the printed part, and the support structure. While Jibin [38] only calculated scanning time and preparing time (consisting of the height of the part and other preparing time) for build time estimation. Reference [39] worked on the build time of the SLA method and formulated their function based on the waiting time and scanning time (which is dependent on a part cross-section area and the machine’s scanning speed).

While most of the non-productive time is independent of the part orientation, the number of layers, which is proportional to the part height, depends on the part orientation [5]. Therefore, the relation of the build time in this study is based on the work of the reference [28]. They considered the number of layers and support material to be minimized. According to this study, each triangular facets that their normal vectors are negative needs support material. The final relation for the build time, which can be used for any kind of AM parts that demand support material (however, even it can be used for the SLS method, which does not have support material, by applying zero value for the support material in Eq. 10), is as below (Eq. 10):

$$T=K({z}_{\mathrm{max}}-{z}_{\mathrm{min}})(1+S)$$
(10)

where

$$S=\frac{{\sum }_{i=1}^{m}{Z}_{{\mathrm{down}}_{i}}{A}_{{\mathrm{down}}_{i}}}{{\sum }_{i=1}^{m}{A}_{{\mathrm{down}}_{i}}}\left(1+\sum_{i=1}^{m}\left|{{n}_{3}}_{i}\right|\right)$$
(11)
$${A}_{\mathrm{down}}=0.5\left|\left({v}_{1}-{v}_{3}\right)\times \left({v}_{2}-{v}_{3}\right)\right|$$
(12)

And,

$${Z}_{\mathrm{down}}=\frac{{z}_{1}+{z}_{2}+{z}_{3}}{3}$$
$$\vec{n} = \left( {n_{1} ,n_{2} ,n_{3} } \right)$$
$$\overrightarrow {{v_{1} }} = \left( {x_{1} ,y_{1} ,z_{1} } \right)$$
$$\overrightarrow {{v_{2} }} = \left( {x_{2} ,y_{2} ,z_{2} } \right)$$
$$\overrightarrow {{v_{3} }} = \left( {x_{3} ,y_{3} ,z_{3} } \right)$$
(13)

where \(m\) is the number of downward facets, \({n}_{3}\) is the z-component of the facets’ normal vectors, \(v\) is the coordinate of a triangular facet’ vertex, \(S\) is support material, \(K\) is a calibration constant. (see [28] for details).

As mentioned in the previous section, to have Eq. (10) in terms of part-build decision variables, the rotation matrix is pre-multiplied to the facets normal vectors and vertex vectors. In this study, Eq. (10) is used.

2.4 Mechanical properties

References [27, 40,41,42] worked on the mechanical properties of AM products. Reference [27] considered average tensile strength, average elongation, average Vickers hardness, and yield strength to optimize. They used polynomial regression from the experimental data. Lovo et al. [40] proposed a mathematical relation between the tensile strength of trusses that were produced by the FDM technique in terms of part orientation. The optimal tensile strength was achieved by minimizing the angle between the tensile force and build orientation. So, the mentioned relation is as bellow:

$$f=\sum_{i=1}^{n}{\omega }_{i}{f}_{i}=\sum_{i=1}^{n}{\omega }_{i}{\left({t}_{i}\cdot x\right)}^{2}$$
(14)

where

$$x=a\widehat{i}+b\widehat{j}+c\widehat{k}$$
$$\mathrm{cos}\left({\theta }_{i}\right)={t}_{i}\cdot x$$
(15)

\({\omega }_{i}\) are weights of objective functions. \({t}_{i}\) is tensile force direction (truss direction). x is the normal vector of the facets to the build surface plane. \(a\), \(b\), and \(c\) are variables.\({\theta }_{i}\) is the angle between the tensile force and fabrication orientation.

On the other hand, a study [42] declared that the minimum limit of the stress happens in the direction parallel to the printing orientation, based on that, they evaluated mechanical properties as follows:

$$M = \left\{ {\begin{array}{*{20}c} {\left| {\sigma \cdot \cos \left\langle {Z,\sigma } \right\rangle } \right|,} & {\sigma \ge \sigma_{\min } } \\ {0,} & {\sigma < \sigma_{\min } } \\ \end{array} } \right.$$
(16)

where \(\sigma\) is the maximum stress in the critical plane. \({\sigma }_{min}\) is stress limit. Z is z-axes direction.

Ulu et al. [26] considered the strength of a part as mechanical property to be optimized (maximized) and used finite element analysis to achieve this goal. They defined an OF to magnify the weakest element of a part with the help of the factor of safety (FS). To achieve this purpose, they used the inverted value of FS (i.e., FS−1, the ratio of the actual stress to the yield stress), so when the value of FS−1 of the weakest element is added to the sum of the FS−1 values of other elements, it plays a more important role. Their goal was to find a PBO in which the weakest element of a part has the highest strength among different PBOs, which was achieved by minimizing Eq. 17. They named this OF strength of a part. The mathematical relation between strength and build orientation, which can be used for any kind of AM method, is as follows (Eq. 17):

$$f\left(x\right)=\sum_{i=1}^{n}\left[\sum_{k=1}^{6}{\left(\frac{1}{{\mathrm{FS}}_{i}^{k}\left(x\right)}\right)}^{\kappa }\right]$$
(17)

where FS is described below:

$${\text{FS}}_{i} \left( x \right) = \sigma^{Y} /\sigma^{\prime}_{i} \left( x \right)$$
(18)

The transformation law for a Cartesian component of a tensor is as below [37]:

$${\left[\sigma \right]}^{^{\prime}}={\left[R\right]}^{T}\left[\sigma \right]\left[R\right]$$
(19)

The rotation matrix \((R)\) as explained in Sect. 2.2, Eq. (9).

\({\sigma }_{i}\) is the component of each element’s stress matrix that is derived from the FE analysis. \(R\left(x\right)\) is the rotation matrix. \(\sigma^{\prime}_{i}\) is the stress component after transformation. \({\sigma }^{Y}\) is the yield stress component. n is the number of FE analysis elements. \(\kappa\) is a positive large number. (see [26] for details).

Note that Eq. 17 showed that the OF of mechanical property (i.e., strength) consists of FS, which is a factor with no unit, so the strength OF is a factor with no unit. In the present study, Eq. (17) is used to evaluate the mechanical properties (i.e., strength) of the AM product.

2.5 Surrogate-modeling the OFs

All those mentioned OFs are computationally expensive, especially when a part is complicated and needs a lot of numbers of triangular elements to produce a high-quality part from a 3D model. The case of calculating the mechanical properties of the part adds the FE analysis (for the calculation of stress in each element, see Sect. 3), therefore, additional computation is added because seeding the part’s body creates new elements. Again, the number of these elements depends on the complexity of the part. These elements are separated from the elements of the STL file. To make computation simple and at the same time precise, the OFs were modeled through meta-modeling. Kriging meta-model was used in this paper as a suitable surrogate model for an OF with a lot of curvatures like the presented OFs in Sects. 2.2, 2.3, and 2.4. The first step is to generate a sample of orientations. Based on the actual value of the functions, kriging modeling starts. The Latin Hypercube Sampling (LHS) method is applied to generate a sample of orientations. LHS method creates a random sample of orientations, the difference of this method with simple random sampling is its full coverage of each variable range by dividing each range to N equiprobable intervals and selecting a value randomly with a specific probability function [43]. In this paper, 100 sample orientations, between the range of decision variables (0 to π radian), were obtained by the LHS MATLAB command. Which is represented in Fig. 3.

Fig. 3
figure 3

Schematic of 100 sample orientations that are obtained through the LHS method. The angles are in radian

Full size image

The kriging predictor function will be as follows [28, 44]:

$$y\left(x\right)=f(x)+z(x)$$
(20)

where x is the vector of decision variables. \(f(x)\) is a regression model. \(z(x)\) is the deviation from the regression model.

$$f\left(x\right)={b(x)}^{T}\beta$$
(21)
$$b\left(x\right)={\left[{b}_{1}\left(x\right){b}_{2}\left(x\right)\cdots {b}_{k}\left(x\right)\right]}^{T}$$
(22)
$$\beta ={\left[{\beta }_{1}{\beta }_{2}\cdots {\beta }_{k}\right]}^{T}$$
(23)

The correlation between \(z\left({x}^{j}\right)\) and \(z\left({x}^{i}\right)\) depends on the distance between \({x}^{j}\) and \({x}^{i}\),

$$d\left( {x^{j} ,x^{i} } \right) = \mathop \sum \limits_{k = 1}^{m} \theta_{k} \left| {x_{k}^{j} - x_{k}^{i} } \right|^{2}$$
(24)

that leads to the correlation function as follows:

$$C\left( {z\left( {x^{j} } \right),z\left( {x^{i} } \right)} \right) = {\text{exp}}\left[ { - d\left( {x^{j} ,x^{i} } \right)} \right]$$
(25)

So, the other terms can be written as below:

$$z\left(x\right)={c}^{T}\left(x\right){C}^{-1}\left(f-G\beta \right)$$
(26)

where:

$$c\left( x \right) = \left[ {C\left( {x,x^{1} } \right) \cdots C\left( {x,x^{p} } \right)} \right]$$
(27)
$$f=\left[f\left({x}^{1}\right)\cdots f\left({x}^{p}\right)\right]$$
(28)
$$\beta ={\left({G}^{T}{C}^{-1}G\right)}^{-1}{G}^{T}{C}^{-1}f$$
(29)
$${G}_{ij}={g}_{j}\left({x}^{i}\right)$$
(30)
$${\text{Cov}}\left( {z\left( {x^{j} } \right),z\left( {x^{i} } \right)} \right) = \sigma^{2} C\left( {\left[ {C\left( {x^{j} ,x^{i} } \right)} \right]} \right)$$
(31)
$${\sigma }^{2}=\frac{1}{P}{\left(f-G\beta \right)}^{T}{C}^{-1}\left(f-G\beta \right)$$
(32)

where \(\beta\) consists of unknown parameters. \(b\left(x\right)\) contains basis functions. Matrix G has the dimension of \(p\times k\). \({\sigma }^{2}\) is the variance of the \(z\left(x\right)\). \(\theta\) is the correlation vector parameter. \(m\) is the dimension of the decision variables.

Finally, to construct the kriging model \(\theta\) should be found.

2.6 Pareto front-based optimization by NSGAII

As discussed before, since there is always a conflict between OFs, there are solutions that are no worse than the other ones (the non-dominant ones). On the other hand, the solutions must be diverse enough to cover all of the optimal answers. Therefore, the application of the Pareto front becomes necessary. The Evolutionary multi-objective optimization (EMO) algorithms were designed the way to achieve this purpose. The elitist NSGAII as an EMO algorithm was employed in this study to find optimum answers. This algorithm works based on the usual GA algorithm, the difference is that the population is ranked based on the level of being non-dominant. Then the answers with the same level of being non-dominant will be ranked based on the crowding distance. Finally, the upper-ranked population will be selected for the next round [45].

The OFs, decision variables, and constraints are described in Sect. 2.1. In this study, the case study optimization problem was solved for both original and surrogate-modeled OFs of roughness, build time, and mechanical properties. This procedure was completed by MATLAB optimization toolbox, “multi-objective optimization using genetic algorithm” option for both original functions and estimated function by kriging method. Settings options like population size, selection, reproduction, mutation, crossover, migration procedures, and stopping criteria are adjustable. The settings for this research optimization have been set on the population size of 100, Pareto fraction of 1, migration interval of 50, maximum generation of 1000, and stall generations of 100 and 200 for the optimization of original functions and the meta-modeled functions by kriging method, respectively (see Sect. 3).

2.7 Multi-criteria decision-making process by TOPSIS

As mentioned before, the results of the Pareto front are non-dominant, which means that there is no better answer than the other one. But with the help of a multi-criteria decision-making (MCDM) process, it is possible to rank the results of the Pareto front. One of the most useful and powerful methods of the MCDM process is Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). It can especially become helpful for the designers to decide on an option based on the importance (weight) they assign to each OF. As it is obvious from its name, the method orders the results based on the Euclidian distance from the positive ideal solution (Ideal Solution, \({A}^{+}\)) and the negative ideal solution (Nadir Solution, \({A}^{-}\)) and each function’s weights. To employ this method, first, the results must be normalized Eq. (33) as follows:

$${r}_{ij}=\frac{{a}_{ij}}{\sqrt{{\sum }_{k=1}^{m}{{a}_{kj}}^{2}}}$$
(33)

where \({a}_{ij}\) is the matrix of results with m rows (number of results) and n columns (number of objective functions).

The normalized results must be weighted. For this purpose, the weight (\(w\)) matrix is multiplied the normalized (\(r\)) matrix Eq. (34):

$$U={\left[w\right]}_{1\times n}{\left[r\right]}_{m\times n}={\left[{w}_{i}{r}_{ij}\right]}_{n\times m}$$
(34)

From Eq. (34) the ideal solution and the nadir solution will be derived and the alternatives can be ranked based on the amount of \({C}_{i}^{*}\) (Eq. (35)), which is between 0 and 1. The amount of 1 is the highest score and the amount of 0 is the lowest score.

$${C}_{i}^{*}=\frac{{d}_{i}^{-}}{{d}_{i}^{-}+{d}_{i}^{*}}$$
(35)

where \({d}_{i}^{-}\) is the Euclidian distance of each alternative from its nadir solution. \({d}_{i}^{*}\) is the Euclidian distance of each alternative from its positive solution. Finally, the results will be ranked based on their scores [46].

2.8 Comparing results based on ANOVA

To compare the results of the two types of OFs (original and meta-modeled) for the case study, there should be a statistical reference to whether the differences are insignificant (and the meta-modeled OFs are acceptable). To achieve this purpose, the Analysis of variance (ANOVA) is employed. Which is using hypothesis testing and confidence interval procedures. These statistical procedures are used to compare the two groups’ mean based on the fact that the probability of most of the phenomenon and accidents are normally distributed. Figure 4 illustrates the schematic of the normal distribution of the two comparing groups.

Fig. 4
figure 4

Normal distribution of the two comparing groups

Full size image

The statistical hypothesis is as follows:

$${H}_{0}:{\mu }_{1}={\mu }_{2}$$
$${H}_{1}:{\mu }_{1}\ne {\mu }_{2}$$
(36)

where \({\mu }_{1}\) is the mean of group 1 results and \({\mu }_{2}\) is the mean of group 2 results. \({H}_{0}\) is the null hypothesis and \({H}_{1}\) is the alternative hypothesis.

Here, it is assumed that the null hypothesis is the differences in the results of these two groups are insignificant. If the null hypothesis is rejected, it means that the assumption is false and the differences are significant.

The statistical t test for this comparison is formulated for two types of conditions, which are when the real variances are equal and the second condition is when the real variances are not equal. In most cases, the real variances are unknown. To find whether the real variances are equal, the \(F\) test is used.

In this study, the Power of the test value (P-Value) is used to achieve the purpose. P-value is the smallest amount of significance that causes \({H}_{0}\) to be rejected. Also, the interval confidence is assumed to be \(95\%\). The interval confidence is the probability of acceptance of the hypothesis when it is true [47].

2.9 Proposed algorithm

In this section, the process to determine the best PBO is briefly described. As it is shown in Fig. 5, first, the STL format of the product is derived from the CAD model or the actual part that is about to be printed. Then, the coordinates and normal vectors of each element of the STL file of the part are derived. With the derived coordinates and normal vectors, from the mentioned OFs in the previous sections, the OFs are formulated in terms of PBO parameters, which are the angles of rotation along x, y, and z axes. In this step, the constraints of the multi-objective problem are determined, which are the restrictions of the rotation angles along each ax. Then, the LHS method derives the sample of PBO from the specified domain. The determined sample is used to create surrogate OFs by the Kriging method. Then, both the original and meta-modeled OFs are optimized through NSGAII and the results of both optimizations are ranked by the TOPSIS method. Finally, these result is compared with each other by ANOVA and if the P-value indicates that the differences are insignificant, then the meta-modeled OFs are suitable to use instead of computationally expensive original OFs.

Fig. 5
figure 5

The flowchart of the used method in this research

Full size image

3 Case study

In this section, a human tooth as a case study is considered to illustrate the application of the proposed method demonstrated in the previous section. The physical fabricated part and CAD model of the human tooth used for the case study are shown in Fig. 6. The properties of the used powder are reported in Table 1. The tooth was fabricated using the SLM method from the stainless steel 316 powder. Some experimental processes for manufacturing the tooth samples in the different orientations are shown in Fig. 7.

Fig. 6
figure 6

The tooth model used for the case study a actual part. b CAD model of the part

Full size image
Table 1 Properties of SS316 (Stainless steel 316)
Full size table
Fig.7
figure 7

SLM manufacturing process of samples in different build orientations which are used, particularly, in this study and for justification purposes

Full size image

As mentioned before, to derive the OFs of the model, the STL format of the part should be derived. The STL format of the model is shown in Fig. 8.

Fig. 8
figure 8

a schematic of the STL format of the fabricated tooth. b a closer view of the STL format of the part. c triangular facets of the STL format

Full size image

First, the roughness original OF is derived from Eq. (3), and the estimated OF is generated through the Kriging method and the generated samples from the LHS method. The estimated OF of the roughness is presented in Eq. (37). Then, like the previous procedure for the roughness OF, the build time original OF is derived from Eq. (10), and the estimated build time is generated from the Kriging method and the generated samples from the LHS method. The estimated OF of the build time is presented in Eq. (38). Finally, the mechanical properties OF are derived. To derive the mechanical properties OF (i.e., strength), first, the FE analysis of the part should be conducted to derive the stress tensor in each element, which is essential to calculate the strength according to Eq. 17. The FE analysis was conducted through ABAQUS. Before the analysis, the steps below have been taken.

  1. (1)

    The number of triangular facets was reduced in the STL file by Autodesk Fusion 360 software.

  2. (2)

    The reduced file was converted into quad meshes by instant meshes code.

  3. (3)

    The quad mesh file was converted into a Boundary Representation (BRep) solid body by Autodesk Fusion 360 (see Fig. 9).

  4. (4)

    The BRep file was imported in ABAQUS according to the following boundary and loading conditions, which is shown in Fig. 10. Based on the reference [48] chewing pressure for molar teeth was assumed to be 2 MPa. So the pressure applied in the loading section of the FE analysis was 2 MPa. For the boundary condition, the roots of the molar tooth were fixed.

  5. (5)

    The model meshed with a number of 171,161 elements for the analysis.

Fig. 9
figure 9

The BRep solid body of the case study

Full size image
Fig.10
figure 10

The loading and boundary conditions

Full size image

After the mentioned steps, the FE analysis was carried out and the results of each stress component for each element were derived (Fig. 11). According to the reference [49], the Stainless Steel was assumed to be an isotropic material, therefore the usage of Eq. (17) for deriving mechanical properties OF (i.e., strength) will be allowable. Finally, the original OF of the mechanical properties was derived using Eq. (17). The estimated OF was modeled using the Kriging method based on the samples derived from the LHS method, which is presented in Eq. (39).

Fig. 11
figure 11

Sample obtained results from FE analysis. Note that the unit of the pressure is MPa

Full size image

Therefore, the optimization problem formulation for estimated OFs will be as follow:

$$\begin{aligned} {\text{Min}}_{{R_{a} }} \left( {\alpha ,\beta ,\gamma } \right) & = \left( {1.1207 \times 10^{ - 5} } \right) \\ & \times \left[ {0.0619e^{{\left( { - \left( {\alpha + 0.25} \right)^{2} - \left( {\beta + 0.5592} \right)^{2} - \left( {\gamma - 1.3636} \right)^{2} } \right)}} } \right. \\ & - 0.0110e^{{\left( { - \left( {\gamma - 0.5327} \right)^{2} - \left( {\alpha - 0.5869} \right)^{2} - \left( {\beta + 1.2033} \right)^{2} } \right)}} \\ & - 0.0711e^{{\left( { - \left( {\alpha + 1.0742} \right)^{2} - \left( {\beta + 1.1230} \right)^{2} - \left( {\gamma + 0.6086} \right)^{2} } \right)}} \\ & + \left. { \cdots - 0.3158e^{{\left( { - \left( {\alpha + 0.2180} \right)^{2} - \left( {\beta - 0.4669} \right)^{2} - \left( {\gamma - 0.4984} \right)^{2} } \right)}} + 0.494374} \right] \\ \end{aligned}$$
(37)
$$\begin{aligned} {\text{Min}}_{{t_{B} }} \left( {\alpha ,\beta ,\gamma } \right) & = \left( {5.2285 \times 10^{ - 5} } \right) \\ & \times \left[ {1660977766e^{{\left( { - \left( {\alpha + 1.0742} \right)^{2} - \left( {\beta + 1.1230} \right)^{2} - \left( {\gamma + 0.6086} \right)^{2} } \right)}} } \right. \\ & + 649454922e^{{\left( { - \left( {\gamma - 0.5327} \right)^{2} - \left( {\alpha - 0.5869} \right)^{2} - \left( {\beta + 1.2033} \right)^{2} } \right)}} \\ & - 1013100210e^{{\left( { - \left( {\alpha + 0.25} \right)^{2} - \left( {\beta + 0.5592} \right)^{2} - \left( {\gamma - 1.3636} \right)^{2} } \right)}} \\ & + \left. { \cdots - 742140268e^{{\left( { - \left( {\alpha + 0.2180} \right)^{2} - \left( {\beta - 0.4669} \right)^{2} - \left( {\gamma - 0.4984} \right)^{2} } \right)}} + 250570488.49} \right] \\ \end{aligned}$$
(38)
$$\begin{aligned} {\text{Min}}_{{{\text{FS}}^{ - 1} }} \left( {\alpha ,\beta ,\gamma } \right) & = \left( {3.8058195 \times 10^{7} } \right) \\ & \times \left[ {0.00014e^{{\left( { - \left( {\alpha + 1.0742} \right)^{2} - \left( {\beta + 1.1230} \right)^{2} - \left( {\gamma + 0.6086} \right)^{2} } \right)}} } \right. \\ & - 0.00022e^{{\left( { - \left( {\alpha + 0.25} \right)^{2} - \left( {\beta + 0.5592} \right)^{2} - \left( {\gamma - 1.3636} \right)^{2} } \right)}} \\ & + 0.00022e^{{\left( { - \left( {\gamma - 0.5327} \right)^{2} - \left( {\alpha - 0.5869} \right)^{2} - \left( {\beta + 1.2033} \right)^{2} } \right)}} \\ & - 0.00022e^{{\left( { - \left( {\alpha + 0.25} \right)^{2} - \left( {\beta + 0.5592} \right)^{2} - \left( {\gamma - 1.3636} \right)^{2} } \right)}} \\ & + \left. { \cdots + 0.00038e^{{\left( { - \left( {\alpha + 0.2180} \right)^{2} - \left( {\beta - 0.4669} \right)^{2} - \left( {\gamma - 0.4984} \right)^{2} } \right)}} + 0.000083} \right] \\ \end{aligned}$$
(39)

Subjected to

$$0^{ \circ } \le \alpha \le 180^{ \circ }$$
$$0^{ \circ } \le \beta \le 180^{ \circ }$$
$$0^{ \circ } \le \gamma \le 180^{ \circ }$$
(40)

Then the optimization problem for both original and estimated OFs was solved by the NSGAII method. The results of the solved PBO problem for original OFs and estimated OFs are shown in Fig. 12, and Fig. 13, respectively. As it is obvious in both Figs. 12 and 13, the first one shows the optimized results a bit more scattered and the latter one shows the optimized results a bit more uniformly. But, in a conclusion, they are well consistent with each other.

Fig. 12
figure 12

The derived Pareto front for the PBO optimization problem of the original OFs

Full size image
Fig. 13
figure 13

Derived Pareto front for the PBO optimization problem of the estimated OFs

Full size image

The results obtained from the optimization were ranked based on the TOPSIS method with equal weight for each OF (1/3 for the surface roughness (\({R}_{a})\), 1/3 for build time (\({t}_{B})\), and 1/3 for the strength as mechanical properties). Top 10 optimum PBOs with their scores are presented in Tables 2 and 3 for the original OFs and the estimated OFs, respectively. As it is shown in Tables 2 and 3, the best PBO for original OFs and estimated OFs are in the Eulerian angles of \(\left( {78.03^\circ ,23.09^\circ ,93.82^\circ } \right)\) and \(\left( {23.53^\circ ,66.36^\circ ,1.51^\circ } \right)\), respectively. The results show that both methods estimated that around the first quadrant coordinate is the best PBO.

Table 2 Top 10 optimum PBOs with their scores for the original OFs. Note that \(\sum {\mathrm{FS}}^{-1}\) has no unit
Full size table
Table 3 Top 10 optimum PBOs with their scores for the estimated OFs. Note that \(\sum {\mathrm{FS}}^{-1}\) has no unit
Full size table

To evaluate the results obtained from the estimated OFs, the analysis of variance has been conducted. The P-values reported in Table 4 are from the comparison between the values of the original OFs and the estimated OFs in the elite angles derived from the optimization of the original OFs. Based on Table 4, all estimated OFs with P-values of more than 0.05 (which means the difference between the original and estimated OF is statistically insignificant) show that they simulated the original OFs successfully. Therefore, the kriging method is reliable for simulating complicated OFs (especially mechanical properties), and could use instead of time-consuming original OFs. It is consistent with the results of reference [28], in which they used estimated OFs of roughness and time. In the cases that the OFs are computationally expensive, estimated OF is a good approach to achieve close results to the actual ones.

Table 4 P-values of the ANOVA of the comparison between original and estimated OFs optimum PBO results
Full size table

To illustrate the capability of the proposed method (i.e., employing NSGAII and TOPSIS methods for the analytical original OFs used in this study), experimental tests for optimum orientation were conducted to obtain the actual values of the surface roughness, build time, and mechanical property in the optimum orientations. Then, the results were compared with the results derived from the original OFs. Table 5 shows the top 10 optimum results of the experimental tests and analytical OFs with their differences for each property. As it is obvious in Table 5, the results of optimum orientations of experimental tests and analytical OFs are in reasonable agreement. It should be noted that experimental tests may have errors due to the environmental conditions, operator’s error and the impossibility to reach the proper location on the part (especially in the case of mechanical properties experimental tests).

Table 5 Comparison of the results derived from the proposed method and experimental results for justification purposes
Full size table

4 Conclusions

Among the governing parameters for a qualified additively manufactured part and the most important properties of the AM part (part quality, surface quality, cost, build time, support structure, and mechanical properties), the effect of PBO on the surface quality, build time, and mechanical properties of the AM part was considered to be investigated in this paper. The proposed method in this work helps to obtain optimum PBO in which the surface roughness and build time will be minimized, the mechanical properties and specifically, the strength will be maximized. It also helps to decide between the non-dominant answers of the optimized results. To achieve this, each OF was derived from the literature and they were customized for the SLM process. The estimated OF by the Kriging method solves the original OFs problem of being computationally expensive. Then, the OFs were optimized by the multi-objective optimization NSGAII algorithm. Afterwards, the results of the Pareto front obtained from NSGAII can be selected by TOPSIS method according to a designer’s decision, it can be reached by assigning a specific weight for each OF based on their importance. Finally, the results of the estimated OFs were evaluated by comparing them with the original OFs results through ANOVA. By analyzing the results of the case study, it was clear that the estimation of the original OFs could solve the original OFs’ problem of being computationally expensive. Comparison of the results of experimental tests, conducted specifically for this study, and analytical original OFs showed that the original OFs could predict reasonably the optimum orientations. In conclusion, this study provides a convenient and precise method, which can be applied to any kind of AM parts, to increase the surface quality by reducing roughness, improve time consumption by reducing build time, and improve the strength of the manufactured product by increasing the strength all at the same time. It also, helps designers to decide which orientation to choose based on the importance of each property (OF) and to solve the time-consuming problem.