Keywords

7.1 Introduction

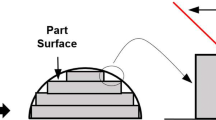
Additive manufacturing (sometimes called 3D printing) refers to a process by which 3D computer-aided design (CAD) models are used to build 3D objects, by adding layer-by-layer material. The manufacturing processes in layers are currently used in several areas to fabricate end-use products in aircraft industry, medical implants, jewelery, footwear industry, automotive industry and fashion products [1, 2]. Additive manufacturing technologies have grown over the years due to their effectiveness in the development of the prototype model in a reduced production time and cost. Depending on the specific 3D printing technology and the complexity of the 3D model, it is important to consider support structures and how they may affect the final result. In this work, a 3D printer using Fused Deposition Modeling (FDM) is considered. FDM extrudes a melted filament onto a build surface along a predetermined path. As the material is extruded, it cools, forming a solid surface providing the foundation for the next layer of material to be built upon. This is repeated layer-by-layer until the object is completed. With FDM printing, each layer is printed as a set of heated filament threads which adhere to the threads below and around it. Each thread is printed slightly offset from its previous layer. This allows a model to be built up to angles of 45\(^{\circ }\), allowing prints to expand beyond its previous layers width. When a feature is printed with an overhang beyond 45\(^{\circ }\), it can sag and requires support material beneath it to hold it up [3, 4]. Thus, the accuracy of the printed object depends on the orientation of the part on the printer platform, that is, the part must have the correct orientation in order to improve the quality of the surface. Different measures can be considered to determine the optimal build orientation taking into account factors such as staircase effect, model precision, build time, structure support and model stability [1, 5]. The optimal build orientation of a model helps in the accuracy of the part, reduces the number of supports generated and the build time of the parts, and consequently decreases the final costs.

Several approaches have been carried out to determine the orientation of a model based on single-objective optimization using objective functions such as the build height, staircase effect, volumetric error, volume of support structures and total contact area of the part with the support structures, surface quality, surface roughness and build deposition time [6, 7]. Recently, multi-objective approaches have been developed to determine the optimal object building orientation in the construction of CAD models, essentially by reducing the multi-objective problem to a single-objective one using classical scalarization methods  [8,9,10,11,12,13]. A genetic algorithm was used in Brika et al. [8] for solving a multi-objective build orientation problem. They optimized several variables, yield and tensile strength, elongation and vickers hardness, for material properties used, surface roughness, support structure and build time and cost. The particle swarm optimization algorithm was used in Li et al. [10] to solve a multi-objective optimization problem in order to get the desired orientations for the support area, construction time and surface roughness. In the paper of Phatak and Pande [11] a genetic algorithm was used to optimize a weighted average of five normalized evaluation criteria (build height, staircase error factor, material utilization factor, part surface area in contact with support structures and volume of support structures) based on their relevance to the rapid prototyping process. In Das et al. [14], the errors related to the staircase effect and the support volume were studied, using weights to find the best orientation of a spherical model. Cheng et al. [15] formulated a multi-objective optimization problem focused on the surface quality and production cost of the parts, obtaining solutions for all types of surfaces, whether with complex geometries or not, or even for curved surfaces. The multi-objetive approach presented by Byun et al. [16] intend to reduce surface roughness, construction time and part cost. The goal was to find the ideal orientation of a 3D model by applying the Technique for Order Preference by Similarity to Ideal Solution and weight methods. Nezhad et al. [17] proposed an Optimized Pareto Based Part Orientation algorithm in order to optimize the minimum construction time, the support volume and surface finish. The applied method does not use weights and optimizes objectives simultaneously and independently. A multi-objective optimization approach, using the Non-dominated Sorting Genetic Algorithm II (NSGA-II) and Multi-Objective Particle Swarm Optimization algorithm, considering as objective functions the surface roughness and the build time, for different models, was developed by Padhye and Deb [18]. Gurrala and Regalla [19] also applied the NSGA-II algorithm to optimize the strength of the model and its volumetric shrinkage as objective functions. Through the Pareto front, they concluded that with the shrinkage of the part their strength increases in the horizontal and vertical directions. A different study addressing how an easily removed support structure might be designed using less material and build time and leaving fewer artifacts on the specimen surface can be seen in Kuo et al. [20]. There, a cost-based formulation is employed to find a compromise between cost and surface profile error induced by specimen weight.

In this work, the optimization of the final printed object surface is addressed, based on the minimization of the staircase effect, the area of the object in contact with the supporting structures and the build time. Here, a multi-objective optimization approach is proposed to obtain the orientation of the Rear Panel Fixed model taking into account the compromise between combinations of two measures mentioned above. We present some preliminary experiments showing the Pareto fronts and discuss different trade-offs between the objectives.

This article is organized as follows. Section 7.2 introduces the orientation problem, the quality measures and the multi-objective optimization approach. The numerical experiments are presented and discussed in Sect. 7.3. Finally, Sect. 7.4 contains the conclusions of this study and some recommendations for future work.

7.2 Multi-objective Approach

7.2.1 Optimization Problem

In this study, a multi-objective optimization to determine the orientation of the construction of a 3D CAD model is used. It intends to simultaneously minimize more than one measure of the quality of the printed object.

The measures involved in this study are the staircase effect, the area of the object in contact with the support structures and the build time.

Although we intend to study three measures of quality, in this study we will perform the multi-objective optimization of the combinations of two objective functions and three objective functions simultaneously. Thus the multi-objective optimization problem is given by

$$\begin{aligned} \begin{array}{ll} \min &{} f\left( \theta _x,\theta _y\right) =\big \{f_1\left( \theta _x,\theta _y\right) , \ldots , f_k\left( \theta _x,\theta _y\right) \big \} \\ \text{ s.t. } &{} 0 \le \theta _x \le 180\\ &{} 0 \le \theta _y \le 180 \end{array} \end{aligned}$$
(7.1)

where k is the number of objective functions and \(\theta _x\) and \(\theta _y\) are the rotation angles along the x-axis and the y-axis, respectively.

In the following, the quality measures based on staircase effect, support area and the required build time are described.

7.2.2 Quality Measures

7.2.2.1 Support Area

A measure of the quality of the printed object is the quantity of support area, since it affects post-processing and surface finish [9]. The support area is defined as the total area of the downward-facing facets that is equivalent to the total contact area of the external supports with the object [7, 9].

The support area, SA, is defined by

$$\begin{aligned} SA=\sum _i A_i\ \left| d^T n_i\right| \ \delta \end{aligned}$$
(7.2)

where \(A_i\) is the area of the triangular face i, d is the unit vector of the direction of construction, \(n_i\) is the normal unit vector of the triangular face i and the initial function is given by \(\delta =1\) if \(d^T n_i < 0\) and \(\delta =0\) if \(d^T n_i > 0\) [9]. In this study, we used the direction vector \(d=(0,0,1)\), because our 3D printer only moves on the x-axis and y-axis, since the base platform (z-axis) is fixed.

7.2.2.2 Staircase Effect

The orientation and layer thickness are the most important factors that affect the superficial roughness [21]. Kattethota et al. [21] studied the staircase effect (SE) of a 3D model based on the deviation between the actual and desired surfaces. It means that the greater the deviation between the two surfaces (real and desired), the greater the length of the layer and the lower the orientation of the construction of the part. The staircase effect, SE, is defined by

$$\begin{aligned} SE=\sum _i\left\{ \begin{array}{lll} \frac{t}{\tan \left( \theta _i\right) },&{}&{} \text {if}\,\, \tan \left( \theta _i\right) \ne 0\\ 0,&{}\,\,\,\,&{} \text {if}\,\, \tan \left( \theta _i\right) = 0\\ \end{array} \right. \end{aligned}$$
(7.3)

where t is the layer thickness and \(\theta _i\) is the angle between triangle facet i of model surface and build orientation (d).

7.2.2.3 Build Time

As considered in Jibin [9] the build time encompasses the scanning time and the preparation time. The scanning time includes solid scanning time, contour scanning time and support scanning time, where the solid and contour scanning times are independent of the part building direction and the support scanning time depends on the volume of supports. The preparation time of the model covers the time required for the platform to move down during the construction of each layer, the scraping time of this and other preparation times. Thus, the preparation time depends on the total number of slices of the solid, which is dependent on the height of the building direction. Therefore, minimizing this height and consequently the number of layers, can decrease the construction time of the part [7, 9].

The build time, BT, is given by

$$\begin{aligned} BT=\max _i\left( d^T v^1_i, d^T v^2_i, d^T v^3_i\right) -\min _i\left( d^T v^1_i, d^T v^2_i, d^T v^3_i\right) \end{aligned}$$
(7.4)

where d is the direction vector and \(v_i^1, v_i^2, v_i^3\) are the vertex triangle facets i.

7.2.3 Multi-objective Genetic Algorithm

In this work, the elitist Non-dominated Sorting Genetic Algorithm II (NSGA-II) proposed by Deb  [22] is used. This is a multi-objective genetic algorithm that mimics the natural evolution of the species. Evolution starts from a population of individuals randomly generated. Each individual represents a potential solution of the multi-objective optimization problem. In NSGA-II, each individual in the current population is evaluated using a Pareto ranking and a crowding measure. First the best rank is assigned to all the non-dominated individuals in the current population. Solutions with the best rank are removed from the current population. Next, the second best rank is assigned to all the non-dominated solutions in the remaining population. In this manner, ranks are assigned to all solutions in the current population. The fittest individuals have a higher probability of being selected to generate new ones by genetic operators. NSGA-II uses a binary tournament selection based on non-domination rank and crowding distance to select a set of parent solutions. When two solutions are selected, the one with the lowest non-domination rank is preferred. Otherwise, if both solutions belong to the same rank, then the solution with the higher crowding distance is selected. Next, genetic operators such as recombination and mutation are applied to create an offspring population. Then, the two populations are merged together to form a combined population that is sorted according to different non-dominated fronts. If the size of the first non-dominated front is smaller then the population size, all members of this front are chosen for the new population. The remaining members of the population are chosen from subsequent non-dominated fronts in the order of their ranking.

The MATLAB® function gamultiobj [23] provided in the Global Optimization Toolbox will be used in order to approximate the Pareto fronts of the multi-objective problems with each combinations of two objective functions. The gamultiobj function implements a multi-objective genetic algorithm that is a variant of the elitist NSGA-II [22]. This function provides a set of algorithm options related with customizing randomization key properties, algorithm properties and termination criteria.

7.3 Experiments

7.3.1 Model

The 3D CAD model used in this study is a Rear Panel Fixed (see Fig. 7.1a) that has vents on either side. The size of the model is different from the side panels, but the side panels for left and right are equal.

Initially, the CAD model is converted into STL (STereoLithography), which is the default file type used by the most common 3D print file formats (see Fig. 7.1b).

Fig. 7.1
figure 1

Rear Panel Fixed model

Full size image

The STL file is an approximation (tessellation) of the CAD model, where the geometric characteristics of the 3D model are depicted. Thus, the model is represented by a mesh of triangles, describing only the surface geometry of a three-dimensional object without any representation of color, texture or other common attributes of the CAD model. It was defined using 3008 triangles, a volume of 46.2 cm\(^3\) and 676 slices for a layer thickness of 0.2 mm (layer thickness used in this work). Figure 7.2a–c depict the SA, SE and BT objective functions landscapes for the Rear Panel Fixed model. These objective functions are nonconvex with multiple local optima. Moreover, it can be observed that the minimizers of each objective function are different. Therefore, these objectives are conflicting each other and there exist different trade-off solutions that represent different compromises between the objectives.

Fig. 7.2
figure 2

Rear Panel Fixed objective functions

Full size image

7.3.2 Implementation Details

Firstly, the combination of two of the quality measures, the support area, the staircase effect and the build time of the part was considered, and the following three multi-objective optimization problems were formulated:

  • SA versus SE—problem (7.1) with \(f_1=SA\) and \(f_2=SE\);

  • SA versus BT—problem (7.1) with \(f_1=SA\) and \(f_2=BT\);

  • SE versus BT—problem (7.1) with \(f_1=SE\) and \(f_2=BT\).

Secondly, a multi-objective optimization of the three objective functions simultaneously is considered, where SA versus SE versus BT denotes solving the problem (7.1) with \(f_1=SA\), \(f_2=SE\) and \(f_3=BT\).

In order to solve the multi-objective optimization problems, the MATLAB® gamultiobj function was used with default values, thus a population size and a maximum number of generations of 50 and 400, respectively. By default, the Pareto fraction is 0.35 and therefore, in each run, 18 non-dominated solutions are found (\(0.35 \times \) population size). In addition, 30 independent runs were performed and the Simplify 3D software [24] (a 3D model printing simulator) was used to represent the solutions found for the Rear Panel Fixed model.

In the following sections the results for the different combinations of two objectives (SA versus SE, SA versus BT, and SE versus BT problems) as well as the results for the three objectives (SA versus SE versus BT problem) are presented.

In all figures, the set of non-dominated solutions obtained among the 30 independent runs are plotted with a blue dot. From this overall set of solutions, the non-dominated ones were selected and marked with a red circle. Representative solutions will be selected to discuss trade-offs between objectives and identify the characteristics associated with these solutions.

7.3.3 Results for the SA versus SE Problem

Figure 7.3 depicts the Pareto front for SA versus SE problem, where the set of non-dominated solutions for all runs are plotted with a blue dot.

Fig. 7.3
figure 3

Pareto front of the Rear Panel Fixed model for the SA versus SE problem

Full size image

Table 7.1 presents the representative non-dominated solutions selected from the Pareto front, that were marked with a red circle in Fig. 7.3.

Table 7.1 Representative non-dominated solutions for the SA versus SE problem
Full size table

Solutions A and G are the extremes of the Pareto front, where solution A has the best SA value and the worst SE value. Conversely, solution G is the worst in terms of SA and the best in terms of SE. These solutions correspond to the lowest values of SA and SE that can be observed in Fig. 7.2a, b, respectively.

From Table 7.1, it is possible to observe that solutions A, B, C and D have very similar orientation angles, although different SA and SE values, verifying a reduction in the staircase effect and an increase in the support area, in particular in the solution D. Solutions D and E are visually very similar, as can be seen in Fig. 7.4b, c, respectively, but the solution E requires more supports. From solutions A to G, there is a significant change in the orientation of the part.

Fig. 7.4
figure 4

Representative solutions for the SA versus SE problem

Full size image

7.3.4 Results for the SA versus BT Problem

Figure 7.5 shows the Pareto front for the model Rear Panel Fixed when SA and BT are the objectives to minimize simultaneously (SA versus BT). Table 7.2 presents the orientation angles and objective values for representative non-dominated solutions selected from the Pareto front. These solutions are shown in Fig. 7.6. It is possible to see that from point A to point B there is no significant change in terms of BT, but there is a great increase in the support area. From solutions B to C, the value of SA increases, while the value of BT decreases. Solution D is one of the extremes of the Pareto front, being minimum of BT function (as it can also be seen in Fig. 7.2c), but it is a bad solution in terms of SA.

Fig. 7.5
figure 5

Pareto front of the Rear Panel Fixed model for the SA versus BT problem

Full size image
Table 7.2 Representative non-dominated solutions for the SA versus BT problem
Full size table
Fig. 7.6
figure 6

Representative solutions for the SA versus BT problem

Full size image

7.3.5 Results for the SE versus BT Problem

In Fig. 7.7, the solutions obtained in the objective space when optimizing SE versus BT problem are presented. Solutions A and F are the extremes of the Pareto front. There is a significant improvement in the BT value, when comparing solutions B and C, although a negligible decrease in SE. From solutions A to F the part is placed lying down, as can be seen in Fig. 7.8, decreasing the height of the part (decreasing BT). Solutions D, E and F are visually similar as can be seen in Fig. 7.8d, e, f (Table 7.3).

Fig. 7.7
figure 7

Pareto front of the Rear Panel Fixed model for the SE versus BT problem

Full size image
Fig. 7.8
figure 8

Representative solutions for the SE versus BT problem

Full size image

7.3.6 Results for the SA versus SE versus BT Problem

In this section, the results of the multi-objective optimization of the three objective functions simultaneously (SA versus SE versus BT problem) are presented. The problem was optimized using the MATLAB® function gamultiobj with default values, as described in the Sect. 7.3.2.

Figure 7.9 shows the non-dominated solutions obtained for the Rear Panel Fixed model. Three solutions regarding the extreme solutions for each objective are represented by A, B and C, corresponding to the angles (90.00, 0.00), (180.00, 44.95), (180.00, 135.00), respectively (corresponding to Figs. 7.6a, 7.8a, f, respectively).

Table 7.3 Representative non-dominated solutions for the SE versus BT problem
Full size table
Fig. 7.9
figure 9

Pareto front of the Rear Panel Fixed model for the SA versus SE versus BT problem

Full size image

In Fig. 7.10 the two-dimensional projections of the Pareto front of the Rear Panel Fixed model for the SA versus SE versus BT problem are presented. It can be seen that the number of non-dominated solutions is larger than the one obtained with two objective combinations.

Fig. 7.10
figure 10

2D Projections of the Pareto front for the SA versus SE versus BT problem

Full size image

7.3.7 Discussion of the Results

The first three combinations of multi-objective optimization problems solved allow to perceive the extremes and the compromise between objectives. Moreover, there are solutions that belong to the Pareto optimal set of the problems solved, i.e., their images belong to the Pareto fronts of the different multi-objective optimization problems. This is the case of solution (90.00, 0.00) that minimizes SA and appears on the Pareto fronts of SA versus SE and SA versus BT problems. In addition, the solution that corresponds to the (180.00, 44.95) orientation was found for the SA versus SE and SE versus BT problems, optimizing the SE function. It is also verified that the solution (180.00, 135.00) optimizes BT, as can be seen in the solutions of SA versus BT and SE versus BT. When BT is one of the objective functions involved in the multi-objective problem (combinations SA versus BT and SE versus BT), some representative solutions put the part lying down, as can be seen in solution D of Fig. 7.6 and in solutions D, E, and F of Fig. 7.8, as expected because BT function intends to minimize its height. However, with the combination SA versus SE, as expected, no solution that position the part lying down exists.

In the multi-objective simultaneous optimization of the three objective functions, all the solutions obtained with the combinations of two objectives and others that represent other trade-offs between objective functions were found.

7.4 Conclusions and Future Work

In this paper, the build orientation optimization of a given object - Rear Panel Fixed model—was addressed based on three quality measures: the total support contact area, the staircase effect and the build time.

First, a multi-objective optimization approach was proposed for three different combinations of two objectives: SA versus SE, SA versus BT, and SE versus BT. Some preliminary experiments were presented for the three different combinations. The Pareto fronts obtained and the different trade-offs between the objectives were discussed. It was also verified that some solutions were found repeatedly in different combinations of objective functions. The results showed the effectiveness of the proposed approach since it was possible to find different solutions to optimize the various combinations.

Then, the three objective functions were optimized simultaneously. From the Pareto front we may conclude that a larger number of solutions was obtained when comparing to the ones obtained through two objective combinations, as well as, new trade-off solutions were found. It was observed that, for all problems, the Pareto fronts have nonconvexities and discontinuities.

In the future, we intend to perform a multi-objective optimization using other objective functions and test more difficult models.