Abstract
We present an approach leading to Finsler geometry without differential calculus of tensors. Several natural examples of such singular Finsler spaces are studied. One class of such examples contains Busemann G-spaces with non-positive curvature. Starting with a singular version of the axiomatics, some simplest properties known in the smooth Finsler geometry are interpreted.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The preface of Busemann’s Geometry of Geodesics [6] contains the following sentence: “... the term Finsler Space means to many not only a type of space, but also a definite approach: The space is considered as a set of linear elements to which euclidean metrics are attached. ... In spite of the great success of Finsler’s thesis, the later development of this aspect lacks simple geometric facts to the extent that their existence in non-Riemannian geometry has been doubted.”
Busemann considers Finsler geometry as a geometry of G-spaces which satisfy appropriate axioms. The first Busemann version of axiomatics leading to G-spaces was made in [7]. Unfortunately, the topology of general G-spaces is still mysterious: it is unknown whether every G-space is a topological manifold and even whether it is finite-dimensional. Positive answers to these questions exist only in special cases. Consequently, speaking about axioms of generalized non-smooth Finsler geometry, one should adjust Busemann’s axioms and take into account the current realities.
The object of the present paper is Finsler spaces in standard and non-standard singular approaches. First let us recall the standard definition. Here standard means the modern definition in terms of differential geometry of manifolds (see, for example, [10] or [9]).
Let \(M^n\) be a \(C^\infty \)-manifold and \(TM^n\) its tangent bundle. A function  is called Finsler metric if it has the following properties:
is called Finsler metric if it has the following properties:
-
(a)
\({\mathcal {F}}\) is \(C^\infty \) on
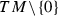 where \(\{0\}\) is the null-section of TM;
where \(\{0\}\) is the null-section of TM; -
(b)
\({\mathcal {F}}\) is positively homogeneous on vectors:
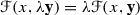 for all \(\lambda > 0\) and all \(\mathbf y \in T_xM\);
for all \(\lambda > 0\) and all \(\mathbf y \in T_xM\); -
(c)
in every point \(x \in M^n\) and for every vector
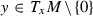 the quadratic form
the quadratic form 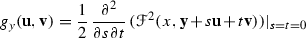 (1)
(1)is positive definite.
Condition (c) means that  is a strongly convex function of the variable \(\mathbf y \) for any fixed \(x \in M^n\).
is a strongly convex function of the variable \(\mathbf y \) for any fixed \(x \in M^n\).
We want to get rid of the \(C^\infty \)-smoothness condition here. In particular, we speak about manifolds with non-necessarily smooth norms in the tangent spaces. Such a weakening of the definition leads to obstructions for the application of the differential calculus of tensors. Our purpose is to show that Finsler geometry in general has a right to existence without differentiation of tensors.
In particular, we present a version of the axiomatics for such non-smooth Finsler geometry. It is preceded by the introduction of necessary notions and by several examples to illustrate the possibility of such a geometry and its methods.
The work was inspired by the author’s recent results on the geometry of Busemann G-spaces with non-positive curvature, showing that such a space is a topological manifold having a tangent space at every point. It occurs that the tangent space has a structure of a normed space with strictly convex norm. The metric of the space is the length metric and one can pick a class of curves with velocity. The velocity of the curve  in the space X at the point
in the space X at the point  ,
,  , is a tangent vector
, is a tangent vector  which can be obtained as a limit of secants to \(\gamma \). If \(\gamma \) has velocity
which can be obtained as a limit of secants to \(\gamma \). If \(\gamma \) has velocity  at all points with continuous norm
at all points with continuous norm  , then its length is
, then its length is

In particular, if \(\gamma \) is a naturally parameterized geodesic segment, then it has unit velocity at all points and
2 Directed segments in metric spaces
Let (X, d) be a metric space. The closed ball with center  and radius \(r > 0\) is denoted by
and radius \(r > 0\) is denoted by  , the corresponding open ball U(p, r) and the sphere S(p, r).
, the corresponding open ball U(p, r) and the sphere S(p, r).
We also consider non-reversible metrics for which the symmetry property  may fail. The triangle inequality for the the non-reversible metric d must be written strongly in the form
may fail. The triangle inequality for the the non-reversible metric d must be written strongly in the form

for all points \(x, y, z \in X\). Hence the closed ball with center  and radius r has two different interpretations:
and radius r has two different interpretations:

and

Corresponding open balls are

and

If the metric is reversible, both balls  and
and  coincide with
coincide with  at all points and for all \(r > 0\).
at all points and for all \(r > 0\).
Both systems of open balls \(U_+\) and \(U_-\) generate topologies on the set X as follows. We say that a subset \(U \subset X\) is positively (correspondingly, negatively) open if for any point \(x \in U\) there exists \(r > 0\) such that  (correspondingly
(correspondingly  . The verification of the topology axioms for the family of positively (negatively) open subsets is standard (it is based on the evident argument: if
. The verification of the topology axioms for the family of positively (negatively) open subsets is standard (it is based on the evident argument: if  then
then  ). We will denote the two topologies by \(\tau _+\) and \(\tau _-\). In general such topologies may be different.
). We will denote the two topologies by \(\tau _+\) and \(\tau _-\). In general such topologies may be different.
Example 2.1
Consider \(X = {\mathbb {R}}\) with the metric
It is easy to check that d is a metric. The open balls of this metric are the following:

and

Evidently, the topologies \(\tau _+\) and \(\tau _-\) are different: semiintervals of type (s, t] are open in the first one and they are not open in the second one.
The map  from the numerical segment
from the numerical segment  to the metric space X is called positively isometric if for any
to the metric space X is called positively isometric if for any  such that \(s < t\) the following equality holds:
such that \(s < t\) the following equality holds:

The map \(\gamma \) is called isometric if for any 

The directed segment
 in the space (X, d) is the image of the numerical segment
in the space (X, d) is the image of the numerical segment  under the positively isometric map
under the positively isometric map  such that \(\gamma (a)= x\) and \(\gamma (b) = y\). The point x is the beginning of the directed segment
such that \(\gamma (a)= x\) and \(\gamma (b) = y\). The point x is the beginning of the directed segment  , the point y is its endpoint. The directed segment
, the point y is its endpoint. The directed segment  is called segment and is denoted
is called segment and is denoted  if \(\gamma \) is isometric. The points x and y are called ends of the segment
if \(\gamma \) is isometric. The points x and y are called ends of the segment  . Every segment
. Every segment  leads to a pair of directed segments
leads to a pair of directed segments  and
and  . On the other hand, the directed segments
. On the other hand, the directed segments  and
and  may be essentially different as point sets when the metric d is asymmetric and
may be essentially different as point sets when the metric d is asymmetric and  .
.
An equivalent definition of the directed segment  and the segment
and the segment  uses the notion of length. Let
uses the notion of length. Let  be a map. Given a subdivision
be a map. Given a subdivision
of the numerical segment  , the corresponding positive variation of the length is
, the corresponding positive variation of the length is

and its negative variation is

We say that \(\gamma \) represents a positively rectifiable curve in X if the set

is bounded. The positive length of a positively rectifiable curve \(\gamma \) is by definition

The map \(\gamma \) represents a rectifiable curve with length \(L(\gamma )\) if it is both positively rectifiable and metrically invertible:

for all pairs  . The image
. The image  is a directed segment
is a directed segment
 where \(x = \gamma (a)\) and \(y = \gamma (b)\) if and only if \(\gamma \) represents a positively rectifiable curve and
where \(x = \gamma (a)\) and \(y = \gamma (b)\) if and only if \(\gamma \) represents a positively rectifiable curve and  . Correspondingly, the segment
. Correspondingly, the segment  is an image of the rectifiable curve \(\gamma \) with length
is an image of the rectifiable curve \(\gamma \) with length  .
.
Definition 2.2
The space (X, d) is called geodesic if for any ordered pair of different points  there exists a directed segment
there exists a directed segment  .
.
For a better understanding of the above definitions, let us consider some examples.
Example 2.3
Let \(V^n\) be a linear space. We consider its elements as vectors and as points at the same time. The linear segment
 is a part of the straight line bounded by x and y, the endpoints of
is a part of the straight line bounded by x and y, the endpoints of  . The Minkowski space is a finite-dimensional linear space \(V^n\) equipped with a norm. In general, the norm
. The Minkowski space is a finite-dimensional linear space \(V^n\) equipped with a norm. In general, the norm  is not necessarily symmetric, strictly convex or smooth. Identifying every vector \(\mathbf x \) with its endpoint in the corresponding affine space \(A^n\) when the origin \(o \in A^n\) is fixed and identified with the null-vector \({{\varvec{\theta }}}\), one gets a metric d on \(A^n\) with
is not necessarily symmetric, strictly convex or smooth. Identifying every vector \(\mathbf x \) with its endpoint in the corresponding affine space \(A^n\) when the origin \(o \in A^n\) is fixed and identified with the null-vector \({{\varvec{\theta }}}\), one gets a metric d on \(A^n\) with

The possible asymmetry of the norm leads to metric asymmetry: the equality  fails in general. Modern Finsler geometry allows non-symmetric metrics, so asymmetry is admissible.
fails in general. Modern Finsler geometry allows non-symmetric metrics, so asymmetry is admissible.
The possible non-smoothness of the norm contradicts in general the standard smoothness assumption in modern Finsler geometry. The possible non-strongness of the convexity also contradicts it: the positive definiteness of the form (1) fails. This condition may be false even if the norm is smooth and strictly convex: when the Gauss–Kroneker curvature (calculated in the sense of the Euclidean metric in the space \(A^n\)) of the boundary sphere  of the ball
of the ball  vanishes in some point x with
vanishes in some point x with  .
.
If the norm in Minkowski space is non-strictly convex, we have non-uniqueness of directed segments. Precisely, if  contains a pair of different points
contains a pair of different points  with
with  , then any two points \(u, v \in A^n\) such that
, then any two points \(u, v \in A^n\) such that
are connected by infinitely many non-linear directed segments  .
.
Example 2.4
(Funk metrics) Let \({\Omega }\) be a bounded convex domain in the affine space \(A^n\). Given two distinct points \(x, y \in {\Omega }\), the point \(z \in \partial {\Omega }\) for which y lies between x and z is uniquely defined. The Funk distance  is
is

The linear segment  is the directed segment in the sense of the Funk metric \(d_\mathrm{F}\). Such a directed segment is unique for any two \(x, y \in {\Omega }\) if \({\Omega }\) is strictly convex. If not, the boundary \(\partial {\Omega }\) contains linear segments, and the directed segment
is the directed segment in the sense of the Funk metric \(d_\mathrm{F}\). Such a directed segment is unique for any two \(x, y \in {\Omega }\) if \({\Omega }\) is strictly convex. If not, the boundary \(\partial {\Omega }\) contains linear segments, and the directed segment  is not unique if z is an interior point of the linear segment lying in \(\partial {\Omega }\).
is not unique if z is an interior point of the linear segment lying in \(\partial {\Omega }\).
Example 2.5
Let  be a non-constant concave monotone non-decreasing function with \(f(0)=0\). Concavity means that
be a non-constant concave monotone non-decreasing function with \(f(0)=0\). Concavity means that

for all pairs  and monotone non-decreasing means that the inequality \(0 \leqslant s < t\) implies
and monotone non-decreasing means that the inequality \(0 \leqslant s < t\) implies  . It is well known that the function
. It is well known that the function  is a reversible metric on \({\mathbb {R}}\). It follows that the function
is a reversible metric on \({\mathbb {R}}\). It follows that the function

is also a metric on \({\mathbb {R}}\) but it is not reversible if f is not the identity function  . All translations \(T_h:{\mathbb {R}} \rightarrow {\mathbb {R}}\) of the type \(T_h(x) = x+h\) are isometries of the metric space \(({\mathbb {R}}, d_{f_{-}})\) independently on the choice of the function f. If \(s < t\) then the point s may be connected with t by a directed segment with length \(L_+=t-s\). The reverse directed segment is possible only if f is linear (
. All translations \(T_h:{\mathbb {R}} \rightarrow {\mathbb {R}}\) of the type \(T_h(x) = x+h\) are isometries of the metric space \(({\mathbb {R}}, d_{f_{-}})\) independently on the choice of the function f. If \(s < t\) then the point s may be connected with t by a directed segment with length \(L_+=t-s\). The reverse directed segment is possible only if f is linear ( for some \(k > 0\)) on the numerical segment
for some \(k > 0\)) on the numerical segment  . In the last case, the length \(L_-\) of the reverse segment is
. In the last case, the length \(L_-\) of the reverse segment is  .
.
If  in the interval
in the interval  for some \(\varepsilon , C > 0\) and \(0< p < 1\) then for any \(s, t \in {\mathbb {R}}\), \(s < t\), there is no rectifiable path from t to s.
for some \(\varepsilon , C > 0\) and \(0< p < 1\) then for any \(s, t \in {\mathbb {R}}\), \(s < t\), there is no rectifiable path from t to s.
Consider the unit circle  as a factor group of \(({\mathbb {R}}, +)\) by the action of \({\mathbb {Z}}\) on \({\mathbb {R}}\) by \((2\pi k)\)-translations: \(x \mapsto T_{2 \pi k}(x)=x+2\pi k\). The metric \(d_{f-}\) generates a new metric \(d_{f,{\mathbb {S}}}\) on \({\mathbb {S}}^1\). Denote
as a factor group of \(({\mathbb {R}}, +)\) by the action of \({\mathbb {Z}}\) on \({\mathbb {R}}\) by \((2\pi k)\)-translations: \(x \mapsto T_{2 \pi k}(x)=x+2\pi k\). The metric \(d_{f-}\) generates a new metric \(d_{f,{\mathbb {S}}}\) on \({\mathbb {S}}^1\). Denote

and consider the class  as a point
as a point  . Then we have for
. Then we have for  and
and  two quantities:
two quantities:

and

The metric  is defined as the minimum
is defined as the minimum

For example, consider the case \(f (x) = \lambda x\) where \(\lambda > 1\). Assume for convenience that \(s< t < s+2\pi \). Then

The point  is connected to
is connected to  by a directed segment
by a directed segment  . Namely, if
. Namely, if

and consequently

then  is the arc of the circle starting from
is the arc of the circle starting from  to
to  counterclockwise. If
counterclockwise. If

then  is the clockwise arc
is the clockwise arc  to
to  . If the equality
. If the equality
holds then both these arcs are directed segments. Speaking about the inverse directed segment  we also have several essentially different situations.
we also have several essentially different situations.
-
If \(t - s < {2 \pi }/({1+\lambda })\), then the counterclockwise arc from
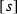 to
to 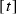 is a directed segment
is a directed segment 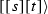 and its inverse arc is an inverse segment
and its inverse arc is an inverse segment 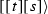 .
. -
If \(t - s = {2 \pi }/({1+\lambda })\), then there is one more directed segment from
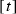 to
to 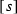 : now both arcs of \({\mathbb {S}}^1\) from
: now both arcs of \({\mathbb {S}}^1\) from 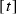 to
to 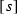 are directed segments.
are directed segments. -
If
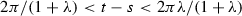 , then the directed segments
, then the directed segments 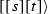 and
and 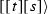 are unique and different. Both are directed counterclockwise.
are unique and different. Both are directed counterclockwise.
The two cases
reduce to the previous ones after redenoting  .
.
Remark 2.6
It is not difficult to extend the metric  considered here to the metric on \({\mathbb {C}}\) with prescribed properties of directed segments connecting points on \({\mathbb {S}}^1\).
considered here to the metric on \({\mathbb {C}}\) with prescribed properties of directed segments connecting points on \({\mathbb {S}}^1\).
The following example constructed by the same scheme as the previous one presents a geodesic space with different topologies \(\tau _+\) and \(\tau _-\)
Example 2.7
Let d be a metric on \({\mathbb {R}}\) from Example 2.1. Then the factorisation of \({\mathbb {R}}\) by the action of \({\mathbb {Z}}\) by k-translations \(t \mapsto t+k\), \(k \in {\mathbb {Z}}\) leads to a geodesic space with different topologies \(\tau _+\) and \(\tau _-\). Neither \(({\mathbb {R}}/{\mathbb {Z}}, \tau _+)\) nor \(({\mathbb {R}}/{\mathbb {Z}}, \tau _+)\) is homeomorphic to \({\mathbb {S}}^1\). The map  is a homeomorphism \(({\mathbb {R}}/{\mathbb {Z}}, \tau _+) \rightarrow ({\mathbb {R}}/{\mathbb {Z}}, \tau _-)\).
is a homeomorphism \(({\mathbb {R}}/{\mathbb {Z}}, \tau _+) \rightarrow ({\mathbb {R}}/{\mathbb {Z}}, \tau _-)\).
3 The spaces of directions and the tangent cones in a geodesic space
Let (X, d) be a (not necessarily reversible) geodesic metric space. We do not suppose uniqueness of  nor coincidence of
nor coincidence of  with \([yx\rangle \) as point sets here. Let \(o \in X\) be an arbitrary point and
with \([yx\rangle \) as point sets here. Let \(o \in X\) be an arbitrary point and  and
and  two directed segments starting from o.
two directed segments starting from o.
Definition 3.1
We say that the directed segments  and
and  have the same joint direction at o if the following holds. Let
have the same joint direction at o if the following holds. Let  be a positively isometric map with image
be a positively isometric map with image  (natural parameterization of
(natural parameterization of  ) and
) and  the corresponding positively isometric map for
the corresponding positively isometric map for  . Then
. Then

The binary relation “to have the same joint direction” is an equivalence relation on the set of all directed segments starting at o. From now on, we omit the word “joint” and use the term “the same direction” meaning namely this definition. Each equivalence class is called a direction at o.
Assume that the set of segments starting at the point \(o \in X\) satisfies the following condition: if

then

for any two segments  and
and  with corresponding natural parameterizations \(\gamma _x\) and \(\gamma _y\). Then we say that the directions at the point o are defined independently of the asymmetry. The geodesic space X is called a space with directions independent of the asymmetry if this property holds at all points of X.
with corresponding natural parameterizations \(\gamma _x\) and \(\gamma _y\). Then we say that the directions at the point o are defined independently of the asymmetry. The geodesic space X is called a space with directions independent of the asymmetry if this property holds at all points of X.
The following example explains the necessity of the independence condition.
Example 3.2
Denote by X the closed subset \(\eta \geqslant \sqrt{\xi }\) of the upper half-plane \(\eta > 0\) of the plane with coordinates \((\xi , \eta )\) bounded by the \(\eta \)-axis \(\gamma _1\) from the left and by the semiparabola \(\gamma _2\) with equation \(\eta = \sqrt{\xi }\) from the right. Consider the function  defined as
defined as

Here  is the length distance between the considered points generated in the set X from the standard Euclidean metric and
is the length distance between the considered points generated in the set X from the standard Euclidean metric and

Note that \(\delta _-\) becomes also the length metric symmetrized as  when it is defined or
when it is defined or  otherwise. In such symmetrization it represents the metric of a non-separable \({\mathbb {R}}\)-tree. Hence \(\delta \) is the length metric on the set X and \((X, \delta )\) is a geodesic space. Both boundary lines: the positive ray \(\gamma _1\) of the \(\eta \)-axis and the semiparabola \(\gamma _2\) from the right side of X are geodesic rays starting from the origin o. The metric \(\delta \) restricted to the boundary rays is reversible on each of them. We have
otherwise. In such symmetrization it represents the metric of a non-separable \({\mathbb {R}}\)-tree. Hence \(\delta \) is the length metric on the set X and \((X, \delta )\) is a geodesic space. Both boundary lines: the positive ray \(\gamma _1\) of the \(\eta \)-axis and the semiparabola \(\gamma _2\) from the right side of X are geodesic rays starting from the origin o. The metric \(\delta \) restricted to the boundary rays is reversible on each of them. We have

and

The equivalence class of the segment  defined as an image of the isometry \(\gamma _x\) will be denoted by
defined as an image of the isometry \(\gamma _x\) will be denoted by  . The following statement is well known for reversible metrics. In fact, the non-reversibility has no influence on its proof.
. The following statement is well known for reversible metrics. In fact, the non-reversibility has no influence on its proof.
Lemma 3.3
Let \(o \in X\) be a point with directions defined independently of the asymmetry. Then the function  defined as
defined as

is well defined and it is a metric on the set of directions at the point o.
The distance \(\overline{\angle }\) is called the upper isosceles angle between the directions  and
and  . The metric \(\overline{\angle }\) is not reversible in general. The upper angle between directions can be defined in a more general way but we will not generalize the definition of upper isosceles angle here because in most situations both quantities do not work as effective tools for calculations.
. The metric \(\overline{\angle }\) is not reversible in general. The upper angle between directions can be defined in a more general way but we will not generalize the definition of upper isosceles angle here because in most situations both quantities do not work as effective tools for calculations.
The lower isosceles angle \(\underline{\angle }\) is also well defined in a similar way, but it does not lead to a metric in general.
Example 3.4
Consider 2-dimensional Minkowski space \(V^2\) with the Randers norm \({\mathcal {F}} = \alpha + \beta \) where

is the Euclidean norm and

is a linear form such that
After rotation of coordinates one can assume that for \(0< b < 1\) the norm \({\mathcal {F}}\) gets the form

The unit sphere  given by
given by

after a transformation of its equation to the form

can be parameterized by the angular parameter \(\phi \):

The upper isosceles angle \(\overline{\angle }\) is equal to the lower isosceles angle \(\underline{\angle }\) and

in the parametrization (5). The difference of the signs in the final items in the numerator leads to the irreversibility of the metric  .
.
Speaking about the tangent cone  to the geodesic space (X, d) one should take into the account that its definition has the following alternative form. If X is an Alexandrov space with bounded (from above or from below) curvature, then its space of directions is a well-defined metric space whose metric is a length metric generated from the angle metric (see [4] for precise definitions and details). In this case the natural meaning of the tangent cone is the Euclidean cone over the space of directions. Such an approach does not work for geodesic spaces in general. Fortunately, there exists another meaning of the tangent cone which we use here.
to the geodesic space (X, d) one should take into the account that its definition has the following alternative form. If X is an Alexandrov space with bounded (from above or from below) curvature, then its space of directions is a well-defined metric space whose metric is a length metric generated from the angle metric (see [4] for precise definitions and details). In this case the natural meaning of the tangent cone is the Euclidean cone over the space of directions. Such an approach does not work for geodesic spaces in general. Fortunately, there exists another meaning of the tangent cone which we use here.
From now on, all the metric spaces are topologically symmetric: the topologies \(\tau _+\) and \(\tau _-\) coincide. Moreover, speaking about directions we mean that all directions are defined independently of the asymmetry.
Definition 3.5
Let (X, d) be a metric space and \(A, B \subset X\) be two closed sets. The Hausdorff distance
 in X is
in X is

where

denotes the symmetric \(\varepsilon \)-neighborhood of the set C.
Remark 3.6
Since the neighborhood \({\mathcal {N}}_\varepsilon (C)\) is the intersection
where

is open in the topology \(\tau _+\) and

is open in \(\tau _-\), it is an open set in \(\tau = \tau _{\pm }\).
Remark 3.7
We allow here the value  .
.
Remark 3.8
Note that the metric \(\mathrm{Hd}\) on the family of closed subsets in X is reversible.
Definition 3.9
Let \((X, d_X),(Y, d_Y)\) be two metric spaces. The Gromov–Hausdorff distance  between them is by definition
between them is by definition

where the infimum is taken among all metric spaces \((Z, d_Z)\) and all isometric embeddings \(f:X \rightarrow Z\) and \(g:Y \rightarrow Z\).
Definition 3.10
Let \((X_t, d_t)\) be a one-parameter family of compact metric spaces. We say that it converges when \(t \rightarrow t_0\)
in the sense of Gromov–Hausdorff to a compact space (X, d), if  . The value \(t_0\) is a real number or \(\pm \infty \) here.
. The value \(t_0\) is a real number or \(\pm \infty \) here.
The version of Definition 3.10 in the non-compact proper case deals with pointed spaces.
Definition 3.11
Let \((X_t, d_t, o_t)\) be a one-parameter family of proper metric spaces with marked points \(o_t\) correspondingly. We say that the space (X, d, o) is a Gromov–Hausdorff limit of this family when \(t \rightarrow t_0\) if for every \(r > 0\) the ball  is a Gromov–Hausdorff limit of \(d_t\)-balls
is a Gromov–Hausdorff limit of \(d_t\)-balls  .
.
In order to estimate the distances \(d_\mathrm{GH}\) it is convenient to use [4, Theorem 7.3.25].
Definition 3.12
([4, Definition 7.3.17]) A correspondence
\(\varphi \) between sets A and B is by definition a subset of the Cartesian product  such that for every \(a \in A\) there exists \(b \in B\) for which \((a, b) \in \varphi \), and conversely, for every \(b \in B\) there exists \(a \in A\) for which \((a, b) \in \varphi \).
such that for every \(a \in A\) there exists \(b \in B\) for which \((a, b) \in \varphi \), and conversely, for every \(b \in B\) there exists \(a \in A\) for which \((a, b) \in \varphi \).
Theorem 3.13
For any two metric spaces X and Y

where

is the distortion of the correspondence \(\varphi \) between X and Y and the infimum is taken among all such correspondences.
The proof of this theorem for the spaces with non-reversible metrics does not differ from the symmetric case presented in [4].
Definition 3.14
Let (X, d) be a proper geodesic space, \(p \in X\) an arbitrary point. Consider a family of spaces \((X, d_t)\), \(t > 0\), where  . The space
. The space  is called the tangent cone to (X, d) at the point p if the pointed space \((X_*, d_*, p_*)\) with some marked point
is called the tangent cone to (X, d) at the point p if the pointed space \((X_*, d_*, p_*)\) with some marked point  is a Gromov–Hausdorff limit of the family \((X, d_t, p)\) when \(t \rightarrow +\infty \). The point \(p_*\) is a vertex of the cone
is a Gromov–Hausdorff limit of the family \((X, d_t, p)\) when \(t \rightarrow +\infty \). The point \(p_*\) is a vertex of the cone  . It is convenient to identify \(p_*\) with p and to consider p as a vertex of
. It is convenient to identify \(p_*\) with p and to consider p as a vertex of  .
.
The following natural example and the consideration after it partially explain the motivation of the paper.
Example 3.15
Let X be a smooth surface in the affine space \(A^n\) equipped with a strictly convex norm. We do not suppose the norm to be reversible, smooth or strongly convex. By its own smoothness, the surface X has a well-defined family of smooth curves and a tangent space  at every point p. This space inherits the norm from the ambient space \(A^n\). The length \(L(\gamma )\) of a smooth curve \(\gamma \) in X calculated by the formula (2) generates a length metric d on X. The topologies \(\tau _+\) and \(\tau _-\) with respect to the metric d coincide, the space (X, d) is proper in these topologies and it is a geodesic space. It is obvious that the metric space
at every point p. This space inherits the norm from the ambient space \(A^n\). The length \(L(\gamma )\) of a smooth curve \(\gamma \) in X calculated by the formula (2) generates a length metric d on X. The topologies \(\tau _+\) and \(\tau _-\) with respect to the metric d coincide, the space (X, d) is proper in these topologies and it is a geodesic space. It is obvious that the metric space  is a tangent cone
is a tangent cone  to the space (X, d) with vertex p, where the metric
to the space (X, d) with vertex p, where the metric  in
in  is induced from \(A^n\).
is induced from \(A^n\).
Definition 3.16
We say that the family \(d_t\),  , of metrics on the set A
uniformly converges to the function
, of metrics on the set A
uniformly converges to the function  if for any \(\varepsilon > 0\) there exists \(T > 0\) such that
if for any \(\varepsilon > 0\) there exists \(T > 0\) such that

for all \(x, y \in A\) and all \(t > T\). The function \(d_*\) is automatically non-negative and satisfies the triangle inequality

It is called a pseudometric if the equality  implies \(d_*(y, x) = 0\). Analogously to the symmetric case, the pseudometric \(d_*\) generates a metric space on the set \(A/\theta \) where \(\theta \) is an equivalence relation on A such that \(a \theta b\) if and only if \(d_*(a, b) = 0\).
implies \(d_*(y, x) = 0\). Analogously to the symmetric case, the pseudometric \(d_*\) generates a metric space on the set \(A/\theta \) where \(\theta \) is an equivalence relation on A such that \(a \theta b\) if and only if \(d_*(a, b) = 0\).
Definition 3.17
We say that the metric space (X, d) satisfies the property of segments prolongability at the point \(p\in X\) if there exists \(r > 0\) such that every point \(x\in U_+(p, r)\), \(x \ne p\), is an interior point of a directed segment \([py\rangle \) with \(d(p, y) = r\). If such r is detected, we say that (X, d) satisfies the r-prolongability of segments at p.
Let (X, d) be a proper geodesic space with \(\tau _+=\tau _-\) and with the property of local uniqueness of directed segments: for every point \(p \in X\) there exists a ball \(B_+(p, r)\) where any ordered pair of points \(x, y \in B_+(p, r)\) defines a unique directed segment  . In particular, for every \(x \in B_+(p, r)\) the directed segment \([px \rangle \) is defined uniquely. For \(x \in B_+(p, r)\) and \(t \geqslant 1\), denote by \(x_t\) the point of the segment \([px\rangle \) such that
. In particular, for every \(x \in B_+(p, r)\) the directed segment \([px \rangle \) is defined uniquely. For \(x \in B_+(p, r)\) and \(t \geqslant 1\), denote by \(x_t\) the point of the segment \([px\rangle \) such that

Define the family of metrics  on the ball \(B_+(p, r)\).
on the ball \(B_+(p, r)\).
Lemma 3.18
Let the space (X, d) satisfy the property of segments r-prolongability at \(p \in X\). Assume that the metrics \(d_t\) are well defined on \(B_+(p, r)\) and the family \(d_t\) converges uniformly to a pseudometric

Then the one-parameter family of pointed spaces  has a limit in the sense of Gromov–Hausdorff when \(t \rightarrow +\infty \).
has a limit in the sense of Gromov–Hausdorff when \(t \rightarrow +\infty \).
Proof
First, let us define a metric space \((Y, d_Y)\) as follows. It follows from the condition, that the function \(d_*\) is a pseudometric on the set \(B_+(p, r)\). We will denote by \(B_*\) the metric space generated from the pseudometric space \((B_+(p, r),d_*)\) as a factor-space by the equivalence relation \(\theta \) as in Definition 3.16. Consider the family of spaces

\(t > 0\). It easily follows from the definition of the metrics \(d_t\) that every space  is isometric to the ball \(B_+(p, sr)\) in
is isometric to the ball \(B_+(p, sr)\) in  when \(s \leqslant t\). Consequently, there is a well-defined inductive limit
when \(s \leqslant t\). Consequently, there is a well-defined inductive limit

We will denote its metric by \(d_Y\). Note that the segments r-prolongability at p implies that the ball \(B_*\) is foliated by directed segments \([py\rangle \) with \(d_*(p, y) = r\). It follows that Y consists of the rays which are infinite continuations of these segments and the r-ball \(B_+(p, r)\) in Y coincides with \(B_*\). We claim that the pointed space \((Y, d_Y, p)\) is exactly the Gromov–Hausdorff limit of the family  .
.
Note that there is a similarity of balls: the ball  of the space
of the space  is similar with the coefficient t to the ball \(B_+(p, r)\) in (X, d). Consequently, to prove
is similar with the coefficient t to the ball \(B_+(p, r)\) in (X, d). Consequently, to prove  , it is sufficient to prove the convergence of r-balls
, it is sufficient to prove the convergence of r-balls  .
.
Given any \(\varepsilon > 0\) denote \(T(\varepsilon )\) a number such such that inequality (6) holds for any \(t \geqslant T(\varepsilon )\) and all pairs \(x, y \in B(p, r)\).
The composition of pseudometric projection \(\mathrm{pr} :(B_+(p, r), d_*) \rightarrow (B_*, d_*)\) with the identity map \(\mathrm{Id}:(B_+(p, r), d_t) \rightarrow (B_+(p, r), d_*)\) has the distortion estimated by

for every \(t \geqslant T(\varepsilon )\). Consequently, it follows from Theorem 3.13 that \((B_+(p, r), d_t)\) \(\xrightarrow [\scriptscriptstyle \mathrm{GH}]{} B_*\).
Finally, it is clear that

and consequently,

This proves the lemma. \(\square \)
The following example demonstrates the essentiality of the condition of segments prolongability at p.
Example 3.19
Consider a subset A of the plane with coordinates \((\rho , \phi )\) which we assume to be Cartesian, bounded by the lines \(\phi \geqslant 0\), \(\rho \geqslant 0\) and \(\rho \leqslant {1}/({\phi +1})\). Define a pseudometric \(d_A\) on A by

and the metric space \((A/\theta , d_A)\). Here \(\theta \) is a pseudometric equivalence with the unique non-trivial class defined by the equality \(\rho =0\).
Geometrically, the space A is isometric to a subspace of the Riemannian surface of branching covering over the Euclidean plane with one singular point in the origin. Its boundary projects to the union of the spiral \(\rho = {1}/({\phi +1})\) in the polar coordinates with the segment \(0 \leqslant \rho \leqslant 1\) of the axis \(\phi = 0\).
All the spaces \((A, d_t)\) are isometric to each other, but the spaces \((A, t {\cdot } d)\) do not converge in the sense of Gromov–Hausdorff because the family of balls B(p, r) in these spaces has no Gromov–Hausdorff limit.
4 Definition and examples
Let (X, d) be a metric space such that
-
X is a geodesic space;
-
the topologies \(\tau _+\) and \(\tau _-\) coincide;
-
the space \((X, \tau )\) is a topological manifold;
-
for any point \(p \in X\) the space of directions is defined independently of the asymmetry, the tangent cone
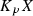 is well defied and it has the structure of a normed linear space with strictly convex norm.
is well defied and it has the structure of a normed linear space with strictly convex norm.
Then the space X is called a singular Finsler space.
Example 4.1
Let (X, d) be a Busemann G-space with non-positive curvature. It is a symmetric geodesic space by definition. Then it is proved in [1] that X is a topological manifold and the tangent cone  is well defined at every point \(p \in X\). Moreover, it is shown in [2] that
is well defined at every point \(p \in X\). Moreover, it is shown in [2] that  has the structure of a normed space with strictly convex norm. It follows that every Busemann G-space with non-positive curvature is a singular Finsler space.
has the structure of a normed space with strictly convex norm. It follows that every Busemann G-space with non-positive curvature is a singular Finsler space.
Example 4.2
The Funk metric (4) leads to a regular Finsler space only if the boundary \(\partial {\Omega }\) is smooth and strongly convex. The Funk space defined with strictly convex boundary surface \(\partial {\Omega }\) is a singular Finsler space which can be non-smooth.
The following example should be viewed as a counterexample because not every quasihyperbolic plane satisfies the definition of singular Finsler space.
Example 4.3
Quasihyperbolic planes which were studied in [5] and [8] are deeply connected with singular Finsler spaces: they lead to a new understanding of the definition of singular Finsler spaces and to some problems. First, we recall the definition and properties of a quasihyperbolic plane.
Remark 4.4
One should not confuse this notion of quasihyperbolic plane with another object introduced by B.A. Rozenfeld also known as a quasi-hyperbolic space.
Let

be the upper Euclidean half-plane and \({\Gamma }\) a group which acts on X by the transformations  , where \(\alpha > 0\), \(\beta \in {\mathbb {R}}\). The group \({\Gamma }\) is generated by positive homotheties
, where \(\alpha > 0\), \(\beta \in {\mathbb {R}}\). The group \({\Gamma }\) is generated by positive homotheties  and x-parallel translations
and x-parallel translations  .
.
The metric space (X, d) with a \({\Gamma }\)-invariant metric d is called a quasihyperbolic plane if it is a Busemann G-space.
The following theorem of Gribanova gives a characterization of quasihyperbolic planes in terms of the linear element. The overall formulation is taken from [3].
Theorem 4.5
Let (X, d) be a quasihyperbolic plane. Then the linear element in X has the form

where the function  satisfies the conditions
satisfies the conditions
-
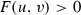 when
when 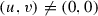 ;
; -
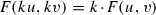 for all \(k \geqslant 0\);
for all \(k \geqslant 0\); -
F is convex;
-
F is smooth in all points
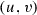 except (0, 0);
except (0, 0); -
tangents for the curve
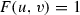 parallel to the line \(v = 0\) touch this curve in a unique point.
parallel to the line \(v = 0\) touch this curve in a unique point.
Conversely, each line element of the form (7) with F satisfying these properties defines a quasihyperbolic plane. The geodesics of the space (X, d) are the intersections of X with
-
the curves
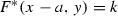 , \(k > 0\), \(a \in {\mathbb {R}}\), where
, \(k > 0\), \(a \in {\mathbb {R}}\), where 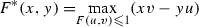
is a function dual to F in coordinates turned over \({\pi }/{2}\), and
-
the tangents to these curves in points of the x-axis.
For two distinct points there exists exactly one geodesic passing through them.
In some sense, the above example presents the class of metrics which is dual to the singular Finsler metrics admitting the action of \({\Gamma }\) on X. In general, a quasihyperbolic plane is not necessarily a singular Finsler space and vice-versa. The stadium space described in [3] is a counterexample: the norm in its tangent space is not strictly convex. Conversely, it follows from the smoothness condition that if the linear element of the space X is strictly convex but not smooth, it is a singular Finsler space but not a quasihyperbolic plane. In that case it admits branching of geodesics.
More examples of singular Finsler spaces arise as smooth submanifolds of a strictly convex normed space as in Example 3.15.
5 Curves with velocity
Let (X, d) be a singular Finsler space,  a parameterization of a rectifiable curve \(\gamma \subset X\), \(a< s_0 < b\) and
a parameterization of a rectifiable curve \(\gamma \subset X\), \(a< s_0 < b\) and  . Let \(t > 0\) and
. Let \(t > 0\) and  be a parameterization of the directed segment from p to
be a parameterization of the directed segment from p to  proportional to the natural parameterization. It defines a vector \(\mathbf w _t\) in the tangent space
proportional to the natural parameterization. It defines a vector \(\mathbf w _t\) in the tangent space  with length
with length  . The vector
. The vector
is called the secant-directing vector of \(\gamma \) at the point p corresponding to the parameter t. If the limit

exists, then we say that the curve \(\gamma \) has an upcoming velocity in the positive direction at the point p. The vector \(\mathbf v _+\) represents this upcoming velocity. Similarly, for \(t < 0\) the vector \(\mathbf v _t\) is defined by

where  is the unit vector in the direction of the continuation of the directed segment
is the unit vector in the direction of the continuation of the directed segment  after the point p, and
after the point p, and

represents the coming velocity from the negative direction at the point p if it exists.
If the vectors \(\mathbf v _+\) and \(\mathbf v _-\) coincide, we say that \(\gamma \) has velocity presented by the velocity vector \(\mathbf v = \mathbf v _+ = \mathbf v _-\) at p. The proof of the following theorem is standard but we review it here to avoid questions.
Theorem 5.1
Let \(\gamma \) be a curve in a singular Finsler space (X, d) represented by a parameterization  such that the velocity vector \(\mathbf v (s)\) exists for all parameters s in
such that the velocity vector \(\mathbf v (s)\) exists for all parameters s in  and such that the function
and such that the function  is continuous. Then \(\gamma \) is positively rectifiable with length
is continuous. Then \(\gamma \) is positively rectifiable with length

Proof
First, we show that the curve \(\gamma \) is positively rectifiable, that is, the length variations (3) are bounded from above. Denote by

the maximal value of the norm of the vector \(\mathbf v \), which is reached at some  since
since  is continuous. It follows from the definition of the vector \(\mathbf v (s)\) as a common limit in (8) and (9) that for any
is continuous. It follows from the definition of the vector \(\mathbf v (s)\) as a common limit in (8) and (9) that for any  there exists
there exists  such that if
such that if  then
then

and

Consequently, applying the triangle inequality, we have

for any  where \(\sigma < \tau \).
where \(\sigma < \tau \).
Picking a finite subcovering
we find the estimate

of the length variation of \(\gamma \) for the subdivision T of the segment  such that
such that  for any two neighbour elements \(t_i, t_{i+1}\) of T and some j depending on i. An arbitrary subdivision T can be accomplished by additional points to get the same estimate of the variation
for any two neighbour elements \(t_i, t_{i+1}\) of T and some j depending on i. An arbitrary subdivision T can be accomplished by additional points to get the same estimate of the variation  (adding points can only enlarge the value of
(adding points can only enlarge the value of  ). Hence, the set of positive length variations is bounded and \(\gamma \) is positively rectifiable.
). Hence, the set of positive length variations is bounded and \(\gamma \) is positively rectifiable.
Denote by \(L_+(\gamma )\) the positive length of \(\gamma \). Next we show that it is exactly of the form (10). First, for any \(\varepsilon > 0\) there exists \(\delta _1 > 0\) such that for any subdivision T of  with diameter \({\Delta } < \delta _1\) the estimate holds
with diameter \({\Delta } < \delta _1\) the estimate holds

Next, consider the function  defined for
defined for  by
by

It is continuous by the condition of Theorem 5.1 and by the definition of \(\mathbf v \). Hence it is uniformly continuous and there exists \(\delta _2\) such that if \(|\tau | < \delta _2\) then

or

for all  . For a subdivision T of
. For a subdivision T of  presented by numbers \(a = s_0< s_1< \cdots< s_{n-1} < s_n\), if the diameter \({\Delta } < \delta _2\), the summing inequalities (11) by \(i = \overline{0, n-1}\) taking \(\tau _i = {\Delta } s_i = s_{i+1}-s_i\) gives
presented by numbers \(a = s_0< s_1< \cdots< s_{n-1} < s_n\), if the diameter \({\Delta } < \delta _2\), the summing inequalities (11) by \(i = \overline{0, n-1}\) taking \(\tau _i = {\Delta } s_i = s_{i+1}-s_i\) gives

Note that the second item under the modulus here is in fact the integral sum for the integral  . The integral exists since the norm
. The integral exists since the norm  is continuous. Finally, there exists \(\delta _3 > 0\) such that
is continuous. Finally, there exists \(\delta _3 > 0\) such that

for any subdivision T with diameter \({\Delta }(T) < \delta _3\). Taking  and an arbitrary subdivision T with \({\Delta }(T)< \delta \) we obtain that
and an arbitrary subdivision T with \({\Delta }(T)< \delta \) we obtain that

proving the theorem because of arbitrariness of \(\varepsilon > 0\). \(\square \)
6 Some questions and problems
We conclude by a short list of questions which are close to the theory developed or may have independent interest.
First, since the singular Finsler geometry is an extension of smooth Finsler geometry, it is natural to ask about the circle of its objects: what is kept in such an extension.
Question 6.1
What objects of the smooth Finsler geometry admit a description without differentiation and hence belong to the singular extension of Finsler geometry?
The first pretenders for singular Finsler geometry are standard measures: different versions of angular measure, areas and volumes. One can speak about different versions of perpendicularity, of course, without symmetry. Note that Busemann studied these values in the symmetric case of G-spaces. The class of singular Finsler spaces has some differences from the class of Busemann G-spaces.
More problematic are Finsler linear connections and corresponding parallelisms. It is hard to imagine what can be an analogue of the Levi-Civita connection. One can try to approximate singular Finsler norms by smooth ones and use some limiting procedure. As a consequence, the following question arises.
Question 6.2
How do the limiting versions of differential quantities depend on the choice of approximation and limiting procedures?
Of course, the version of the extension of Finsler geometry to the singular case described here is not unique. But the question is
Question 6.3
What other manners can be used to extend smooth Finsler geometry to the non-smooth or to the non-strongly convex situation?
Recall that this paper was inspired by the theorem proved in [2]: the tangent cone for a non-positively curved G-space has a structure of normed space with strictly convex norm. The theorem is proved for the reversible case. The following series of problems arises.
Problem 6.4
Let X be a non-positively curved Busemann G-space with non-reversible metric. This means that all the axioms of G-space hold except that the metric symmetry and the axiom of curvature non-positivity holds for the set of directed segments.
-
(a)
Is it true that the topologies \(\tau _+\) and \(\tau _-\) coincide?
-
(b)
Are the spaces of directions defined independently on the asymmetry?
-
(c)
Is the pseudometric \(d_*\) from Lemma 3.18 well defined and is it a metric?
-
(d)
Is the tangent cone
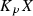 homeomorphic to X and is it a normed space?
homeomorphic to X and is it a normed space?
The following problem results: is the space X a singular Finsler space?
Some questions arise from the consideration of quasihyperbolic spaces. The known researches deal with quasihyperbolic planes, that is, with reversible two-dimensional quasihyperbolic spaces. Going to high dimensions and breaking the symmetry can generate extra obstructions for the description of quasihyperbolic geometry. The obvious is the fact that a quasihyperbolic space is a singular Finsler space only if its norm is strictly convex. The general problem is the following.
Problem 6.5
Let  be the
be the  -dimensional open half-space. Consider the metrics d on X generated by the linear elements of type
-dimensional open half-space. Consider the metrics d on X generated by the linear elements of type
where the function \(F(\mathbf{u }, v)\) is convex and positively homogeneous: \(F(\lambda \mathbf{u }, \lambda v) = \lambda F(\mathbf{u }, v)\) for all pairs  and all \(\lambda > 0\).
and all \(\lambda > 0\).
-
(a)
Find geodesics of the metric d in the general case.
-
(b)
Is there any kind of duality between singular Finsler metrics and quasihyperbolic metrics?
Note that these questions are unanswered for the non-reversible metrics even in the two-dimensional case.
References
Andreev, P.D.: Proof of the Busemann conjecture for \(G\)-spaces of nonpositive curvature. St.-Petersburg Math. J. 26(2), 193–206 (2015)
Andreev, P.D.: Normed space structure on a Busemann \(G\)-space of cone type. Math. Notes 101(2), 193–202 (2017)
Berestovskiǐ, V.N., Halverson, D.M., Repovš, D.: Locally \(G\)-homogeneous Busemann \(G\)-spaces. Differential Geom. Appl. 29(3), 299–318 (2011)
Burago, D., Burago, Yu., Ivanov, S.: A Course in Metric Geometry. Graduate Studies in Mathematics, vol. 33. American Mathematical Society, Providence (2001)
Busemann, H.: Quasihyperbolic geometry. Rend. Circ. Mat. Palermo 2(4), 256–269 (1955)
Busemann, H.: The Geometry of Geodesics. Academic Press, New York (1955)
Busemann, H.: Metric Methods in Finsler Spaces and in the Foundations of Geometry. Annals of Mathematics Studies, vol. 8. Princeton University Press, Princeton (1942)
Gribanova, I.A.: The quasihyperbolic plane. Siberian Math. J. 40(2), 245–257 (1999)
Mo, X.: An Introduction to Finsler Geometry. Peking University Series in Mathematics, vol. 1. World Scientific, Hackensack (2006)
Shen, Z.: Lectures on Finsler Geometry. World Scientific, Singapore (2001)
Acknowledgements
I am very grateful to Athanase Papadopoulos for his invaluable help in preparing this paper. My thanks to the referee for a number of important remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by RFBR, Grant 14-01-00219.
Rights and permissions
About this article
Cite this article
Andreev, P. Foundations of singular Finsler geometry. European Journal of Mathematics 3, 767–787 (2017). https://doi.org/10.1007/s40879-017-0169-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0169-x



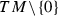 where
where 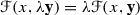 for all
for all 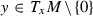 the quadratic form
the quadratic form 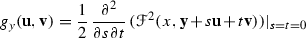
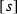 to
to 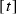 is a directed segment
is a directed segment 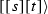 and its inverse arc is an inverse segment
and its inverse arc is an inverse segment 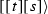 .
.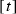 to
to 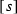 : now both arcs of
: now both arcs of 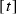 to
to 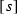 are directed segments.
are directed segments.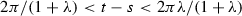 , then the directed segments
, then the directed segments 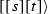 and
and 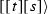 are unique and different. Both are directed counterclockwise.
are unique and different. Both are directed counterclockwise.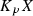 is well defied and it has the structure of a normed linear space with strictly convex norm.
is well defied and it has the structure of a normed linear space with strictly convex norm.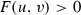 when
when 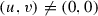 ;
;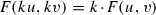 for all
for all 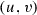 except (0, 0);
except (0, 0);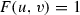 parallel to the line
parallel to the line 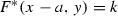 ,
, 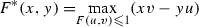
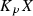 homeomorphic to X and is it a normed space?
homeomorphic to X and is it a normed space?