Abstract
We introduce the notions of spray vector and connection operator to give efficient curvature formulas for a homogeneous Finsler space. Thus the flag curvatures can be computed in the Lie algebra level. Applying these formulas, one can show that in several occasions the structure of the Lie algebra may have influence over the signs of the flag curvatures, regardless of the underlying Finsler metric. Some concrete examples are constructed to illustrate the concepts and the curvature behavior in Finsler geometry.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flag curvature is the most important quantity in Finsler geometry, as it generalises sectional curvature in Riemannian geometry. The sign of the flag curvature governs the behavior of the geodesic flow; it also reflects the topology of the underlying manifold, as indicated by the classical Bonnet–Myers theorem, Cartan–Hadamard theorem, etc.
The computation of curvature in Finsler geometry is usually time consuming. Almost all known computable examples can be divided into the following three classes: Berwald space, which shares the curvature tensor with a Riemannian metric [10, 29]; projectively flat space, whose flag curvature is a scalar function on the tangent bundle and has a short formulahou [10, 26]; \((\alpha ,\beta )\)-metric, which is locally computable using knowledge of Riemannian geometry [5, 27, 28].
In this survey article, we will concentrate on another class of computable Finsler manifolds, namely, homogeneous Finsler spaces. There is a simple evidence showing the importance of homogeneous spaces in Riemannian geometry: almost all known examples of Einstein manifolds are homogeneous [9]. Thus, it is fair to say that the study of homogeneous spaces in Finsler geometry is of equal importance.
These spaces can be thought of as coset spaces of Lie groups, thus the computation of curvature can be done in the Lie algebra level. The study of homogeneous Finsler spaces has a long history [11,12,13,14, 16], but the curvature formula comes very recently [18]. This is interesting, because the curvature formula for a homogeneous Riemannian manifold is relatively easy to deduce, but for the Finsler case is not. We shall not reproduce the proof of the formula here. Interested readers may consult [18] for details. Instead, we will present several applications of the formula, thus leading to new proofs of the results of Hu–Deng [16], Huang [18, 19], and Xu–Deng–Huang–Hu [37]. These results will show that the sign of flag curvature is closely related to the structure of Lie algebras.
In this direction, it is an important achievement in Riemannian geometry to classify homogeneous spaces admitting positively curved Riemannian metrics [2, 7, 8, 30, 33, 34]. The list of such spaces is rather short. Thus it is natural to consider the same problem in Finsler geometry with the expectation that the list could be longer. However, in [37] we proved a disappointing result that the list of even dimensional homogeneous spaces admitting positively curved Finsler metrics is the same as in the Riemannian case. As a consequence, even dimensional homogeneous Finsler spaces of positive constant curvature must be Riemannian spaces. These results will be presented in Sect. 3.
The study of Ricci curvature is also of interest when restricting to homogeneous manifolds. It is well known that a homogeneous space M admits an invariant Riemannian metric with positive Ricci curvature if and only if M is compact and the fundamental group \(\pi _1(M)\) is finite, thus providing a converse to the Bonnet–Myers theorem in the homogeneous case. Lohkamp [23] showed that every smooth manifold admits a \(C^2\) metric with negative Ricci curvature. Accordingly negative Ricci curvature has no topological obstruction. However, this result is not true in the homogeneous case, because Milnor [24] showed that nilpotent Lie groups do not admit invariant metric with \(\mathrm {Ric}\,{<}\,0\). We further extend Milnor’s result to Finsler geometry [19]. This result also provides a negative answer to Shiing-Shen Chern’s question on the existence of Einstein metrics (restricting to the homogeneous case, of course). We shall survey several Ricci curvature related results in Sect. 4.
The paper is organized as follows. Section 2 is an introduction to the concept of homogeneous Finsler space and the curvature formula. Section 3 is devoted to the study of flag curvatures, with an emphasis towards the classification of positively curved homogeneous spaces in even dimensions. Section 4 studies Ricci curvatures of a special class of homogeneous Finsler spaces, namely, Lie groups equipped with left invariant Finsler metrics. Finally, a few concrete examples are provided in Sect. 5 to illustrate the usefulness of the curvature formula. The first example is an infinite family of Finsler metrics on the Lie group E(2). They all have constant flag curvature \(K=0\). According to the Akbar–Zadeh theorem, these examples are locally Minkowskian, but they are non-trivial. The second example is an infinite family of Finsler metrics on the sphere \(S^{7}\). They all have constant Ricci curvature \(+1\) and vanishing S-curvature. Among these metrics only two are Riemannian, as obtained by Jensen [20] and Ziller [38].
2 Homogeneous Finsler spaces
This section is mainly to introduce some basic facts on homogeneous Finsler spaces and to fix notation. Since the concept of homogeneous Finsler space combines the study of homogeneous space with Finsler geometry, the reader is referred to textbooks such as [4, 10] for basics on Finsler geometry, and [15, 21] on homogeneous spaces.
2.1 Finsler metrics and flag curvature
Definition 2.1
Let V be a real linear space of dimension m. A smooth function  is called a Minkowski norm on V, if it satisfies the following two conditions:
is called a Minkowski norm on V, if it satisfies the following two conditions:
-
(Positive 1-homogeneity) \(F(\lambda y)=\lambda F(y)\) for all \(\lambda >0\),
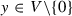 .
. -
(Strong convexity) For each fixed
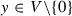 , the Hessian of
, the Hessian of 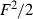 at y is positive definite. In other words, the bilinear function
at y is positive definite. In other words, the bilinear function 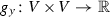 defined by
defined by 
is an inner product on V.
The linear space V endowed with a Minkowski norm F is called a Minkowski space, denoted by (V, F). The set of unit vectors  is called the indicatrix. Notice that the Euclidean norm is a special Minkowski norm, with inner product \(g_y\) independent of y.
is called the indicatrix. Notice that the Euclidean norm is a special Minkowski norm, with inner product \(g_y\) independent of y.
In some cases, the function F is only defined on a cone in  . Such F will be called y-local. Unless otherwise stated, we require F to be y-global, namely, it is defined on the whole
. Such F will be called y-local. Unless otherwise stated, we require F to be y-global, namely, it is defined on the whole  . We may also define \(F(0)=0\), then F is \(C^1\) at 0 in general.
. We may also define \(F(0)=0\), then F is \(C^1\) at 0 in general.
Definition 2.2
Let M be a smooth manifold of dimension m. Let TM be the tangent bundle of M. A smooth function  is called a Finsler metric on M if its restriction to each tangent space is a Minkowski norm. In particular, if the Minkowski norms are all Euclidean, then the Finsler metric is Riemannian.
is called a Finsler metric on M if its restriction to each tangent space is a Minkowski norm. In particular, if the Minkowski norms are all Euclidean, then the Finsler metric is Riemannian.
Now let (M, F) be a Finsler manifold. Let \((x^i)\) be a local chart on M, then we have a natural local coordinate \((x^i,y^i)\) on  . Let
. Let  , then we can express
, then we can express  . Moreover, if we define
. Moreover, if we define  , then we obtain the so-called Cartan tensor
, then we obtain the so-called Cartan tensor
 . The \(g_y\)-trace of \(C_y\) is the mean Cartan tensor
\(I_y\). It can also be expressed as
. The \(g_y\)-trace of \(C_y\) is the mean Cartan tensor
\(I_y\). It can also be expressed as  .
.
The Hilbert form is defined by  . The spray is the unique vector field \(\xi \) on
. The spray is the unique vector field \(\xi \) on  such that
such that

If we introduce the spray coefficients

where \((g^{ij})=(g_{ij})^{-1}\), then one can show that  . The projections of the integral curves of \(\xi \) are called geodesics.
. The projections of the integral curves of \(\xi \) are called geodesics.
The connection coefficients are given by  . Using these coefficients, one can define the Riemann curvature tensor
. Using these coefficients, one can define the Riemann curvature tensor
 , where
, where

Moreover, for each flag (P, y) in \(T_xM\), where  is a tangent plane containing y, the flag curvature
K is defined by
is a tangent plane containing y, the flag curvature
K is defined by

Notice that \(R_y\) is self-adjoint with respect to \(g_y\).
The trace of Riemann curvature tensor is called the Ricci curvature

A Finsler manifold (M, F) is said to be of constant flag curvature, if there is a constant \(\kappa \) such that

Similarly, it is said to have constant Ricci curvature, if for some constant \(\kappa \),

2.2 Isometries and totally geodesic submanifolds
Let (M, F) be a Finsler manifold. A diffeomorphism \(\varphi :M\rightarrow M\) is called an isometry, if it preserves the metric, i.e.

All the isometries naturally form a group, called the full isometry group of (M, F), denoted by  . It is proved in [12] that
. It is proved in [12] that  is a Lie group.
is a Lie group.
An isometry preserves the Hilbert form and the spray vector field, hence it will send geodesics to geodesics.
Recall that a regular submanifold \(M'\) of M is called totally geodesic, if for every \(v\in TM'\), the unique maximal geodesic with tangent vector v lies in \(M'\). By using (1), one can show that for each flag  , the flag curvature of (P, y) as a flag in \(M'\) (with respect to the induced metric) is the same as the flag curvature of (P, y) as a flag in M [3].
, the flag curvature of (P, y) as a flag in \(M'\) (with respect to the induced metric) is the same as the flag curvature of (P, y) as a flag in M [3].
Proposition 2.3
Let (M, F) be a Finsler manifold and \(\mathfrak {G}\) any set of isometries of M. Let U be the set of points of M which are left fixed by all elements of \(\mathfrak {G}\). Then each connected component of U is a totally geodesic submanifold.
Proof
Let x be a point of U. Let V be the subspace of \(T_xM\) consisting of vectors which are left fixed by all elements of \(\mathfrak {G}\). Let W be a neighborhood of the origin in \(T_xM\) such that: (a) the exponential map \(\mathrm{exp}_x\) is a smooth diffeomorphism from  to
to  ; (b) for each point p in \(\exp _x(W)\backslash \{x\}\), there is a unique minimizing (forward) geodesic connecting x and p. For the existence of such neighborhood, one may consult [4].
; (b) for each point p in \(\exp _x(W)\backslash \{x\}\), there is a unique minimizing (forward) geodesic connecting x and p. For the existence of such neighborhood, one may consult [4].
Since for each  , v is fixed by all elements of \(\mathfrak {G}\), we find that the geodesic
, v is fixed by all elements of \(\mathfrak {G}\), we find that the geodesic  ,
,  , is also fixed by all elements of \(\mathfrak {G}\). It follows that
, is also fixed by all elements of \(\mathfrak {G}\). It follows that  is a subset of
is a subset of  .
.
Conversely, for each point p in  , there is a unique minimizing (forward) geodesic connecting x and p. This geodesic must be fixed by all elements of \(\mathfrak {G}\), because x and p do. Consequently, its tangent vector at x lies in W. It follows that
, there is a unique minimizing (forward) geodesic connecting x and p. This geodesic must be fixed by all elements of \(\mathfrak {G}\), because x and p do. Consequently, its tangent vector at x lies in W. It follows that  is a subset of
is a subset of  .
.
As a result, we have  is a regular submanifold of M. So U consists of regular submanifolds of M. It follows that each connected component of U is a regular submanifold of M. Moreover, it is totally geodesic as proved above.\(\square \)
is a regular submanifold of M. So U consists of regular submanifolds of M. It follows that each connected component of U is a regular submanifold of M. Moreover, it is totally geodesic as proved above.\(\square \)
Remark 2.4
The Finsler exponential map is only \(C^1\) at the origin. This is a crucial difference between Finsler geometry and Riemannian geometry. For further results in this direction, one may consult [11].
2.3 Homogeneous Finsler spaces
Definition 2.5
A Finsler manifold (M, F) is called homogeneous, if  acts transitively on M; namely, for every pair of points \(p,q\in M\), there is an isometry f such that \(f(p)=q\).
acts transitively on M; namely, for every pair of points \(p,q\in M\), there is an isometry f such that \(f(p)=q\).
Let G be a subgroup of  that acts transitively on M. It is easy to show that the identity component of G also acts transitively, so we will assume that G itself is connected.
that acts transitively on M. It is easy to show that the identity component of G also acts transitively, so we will assume that G itself is connected.
Now fix a point \(o\in M\), let H be the isotropy subgroup of o, i.e.

Then M can be identified with the coset space G / H (see [15, Chapter II, Proposition 4.3]). Moreover, since \(F(o,f_*y)=F(o,y)\), \(f\in H\), we see that the Minkowski norm \(F|_o\) on \(T_oM\) is invariant by H, thus the indicatrix at o is invariant by H. It follows that H is compact. By passing to the identity component if necessary (thus M is passed to its covering space), we may assume that H is connected.
In summary, the above discussion leads to the consideration of the coset space G / H, where G is a connected Lie group and H is a compact connected subgroup of G. This is really a rich class of manifolds. However, given a pair of such Lie groups G and H, the action of G on \(M=G/H\) may not be effective.
Example 2.6
The coset space  can be described as follows. Consider the action of
can be described as follows. Consider the action of  on the upper half plane M by fractional linear transformations
on the upper half plane M by fractional linear transformations

It is easily shown that the isotropy subgroup of \(\mathrm {i}\) is  , hence M can be viewed as the coset space
, hence M can be viewed as the coset space  . Notice that the matrices \(-A\) and A give rise to the same transformation on M, thus the action of
. Notice that the matrices \(-A\) and A give rise to the same transformation on M, thus the action of  on M is not effective.
on M is not effective.
The Riemannian metric  is invariant by G, so (M, g) is a homogeneous Riemannian space. This reveals the upper half plane model of hyperbolic geometry. One can show that the full isometry group is
is invariant by G, so (M, g) is a homogeneous Riemannian space. This reveals the upper half plane model of hyperbolic geometry. One can show that the full isometry group is  . Clearly, it is more convenient to work with
. Clearly, it is more convenient to work with  .
.
The above example motivates the following alternative definition of homogeneous Finsler space.
Definition 2.7
Suppose G is a connected Lie group which acts almost effectively on the coset space \(M=G/H\), where H is a compact connected Lie subgroup of G. If the Finsler metric F is invariant by G, then the pair (G / H, F) is called a homogeneous Finsler space.
In the following, when we talk about a homogeneous Finsler space, we will always admit the above assumptions.
To assign a G-invariant Finsler metric on G / H, it suffices to assign an H-invariant Minkowski norm on \(T_oM\), and then translate to other tangent spaces by the action of G [13]. Actually, for any \(x\in M\),  , if two elements \(\varphi \) and \(\psi \) in G both send o to x, then we have
, if two elements \(\varphi \) and \(\psi \) in G both send o to x, then we have
To ensure the above two equations do not conflict, we need
Let  and
and  , then the above equation is simply \(F(o, v) = F(o, h_*v)\). This shows that the H-invariance of \(F|_o\) guarantees the definition of \(F|_x\) does not depend on the choice of the isometry sending o to x. Using this fact the G-invariance of F then follows easily.
, then the above equation is simply \(F(o, v) = F(o, h_*v)\). This shows that the H-invariance of \(F|_o\) guarantees the definition of \(F|_x\) does not depend on the choice of the isometry sending o to x. Using this fact the G-invariance of F then follows easily.
A similar argument shows that every G-invariant object on M can be viewed as an H-invariant object on \(T_oM\). For example, the Riemann curvature tensor \(R_y\) is G-invariant, namely,
hence, \(R_y\) can also be viewed as an H-invariant (1, 1) tensor on \(T_oM\), with \(y\in T_oM\).
Now let \(\mathfrak {g}\) and \(\mathfrak {h}\) be the Lie algebras of G and H, respectively. Since H is compact, there exists an  -invariant subspace \(\mathfrak {m}\) of \(\mathfrak {g}\) that is complimentary to \(\mathfrak {h}\), namely, we have the direct sum decomposition
-invariant subspace \(\mathfrak {m}\) of \(\mathfrak {g}\) that is complimentary to \(\mathfrak {h}\), namely, we have the direct sum decomposition
The  -invariance of \(\mathfrak {m}\) is equivalent to
-invariance of \(\mathfrak {m}\) is equivalent to

because H is connected. Notice that the choice of \(\mathfrak {m}\) is by no means unique.
For each \(X\in \mathfrak {g}\), the action of the 1-parameter subgroup
 on M induces a vector field
\(X^*\) on M, called the fundamental vector field corresponding to X. It is a classical result that the space of all fundamental vector fields has a Lie algebra structure isomorphic to
\(\mathfrak {g}\) [21, p. 42, Proposition 4.1]. In particular, the map sending X to
\(X^*(o)\) is linear. If X belongs to
\(\mathfrak {h}\), then
\(\varphi _t(o)=o\),
\(X^*(o)=0\), and vice versa. It follows that
\(\mathfrak {h}\) is the kernel of this map, and this map is a linear isomorphism between \(\mathfrak {m}\) and \(T_oM\). From now on, we will always identify \(T_oM\) with \(\mathfrak {m}\) in this manner.
on M induces a vector field
\(X^*\) on M, called the fundamental vector field corresponding to X. It is a classical result that the space of all fundamental vector fields has a Lie algebra structure isomorphic to
\(\mathfrak {g}\) [21, p. 42, Proposition 4.1]. In particular, the map sending X to
\(X^*(o)\) is linear. If X belongs to
\(\mathfrak {h}\), then
\(\varphi _t(o)=o\),
\(X^*(o)=0\), and vice versa. It follows that
\(\mathfrak {h}\) is the kernel of this map, and this map is a linear isomorphism between \(\mathfrak {m}\) and \(T_oM\). From now on, we will always identify \(T_oM\) with \(\mathfrak {m}\) in this manner.
With this identification, the Minkowski norm \(F|_o\) on \(T_oM\) can also be viewed as a Minkowski norm on \(\mathfrak {m}\), still denoted by F. Recall that for each \(h\in H\) and \(X\in \mathfrak {g}\), \(h_*(X^*)\) is the fundamental vector field corresponding to  (cf. [21, p. 51, Proposition 5.1]). Hence, the H-invariance of \(F|_o\) on \(T_oM\) is equivalent to the
(cf. [21, p. 51, Proposition 5.1]). Hence, the H-invariance of \(F|_o\) on \(T_oM\) is equivalent to the  -invariance of F on \(\mathfrak {m}\). The same argument guarantees that every H-invariant object on \(T_oM\) can be viewed as an
-invariance of F on \(\mathfrak {m}\). The same argument guarantees that every H-invariant object on \(T_oM\) can be viewed as an  -invariant object on \(\mathfrak {m}\). Henceforth, we will use the same symbols \(g_y,C_y,R_y,\ldots \) to denote the corresponding objects on \(T_oM\) and on \(\mathfrak {m}\).
-invariant object on \(\mathfrak {m}\). Henceforth, we will use the same symbols \(g_y,C_y,R_y,\ldots \) to denote the corresponding objects on \(T_oM\) and on \(\mathfrak {m}\).
Lemma 2.8
([13, 18]) The Minkowski norm \(F|_o\) on \(T_oM\) is H-invariant if and only if the Minkowski norm F on \(\mathfrak {m}\) is  -invariant, namely,
-invariant, namely,  for any \(h\in H\),
for any \(h\in H\),  . Moreover, the following conditions are mutually equivalent:
. Moreover, the following conditions are mutually equivalent:
-
(A)
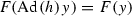 for all
for all 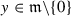 , \(h\in H\);
, \(h\in H\); -
(B)
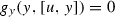 , \(u\in \mathfrak {h}\) for all
, \(u\in \mathfrak {h}\) for all  ;
; -
(C)
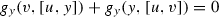 for all \(u\in \mathfrak {h}\),
for all \(u\in \mathfrak {h}\), 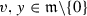 ;
; -
(D)
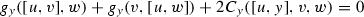 for all \(u\in \mathfrak {h}\),
for all \(u\in \mathfrak {h}\), 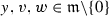 .
.
Proof
The first part is clear. We now prove the mutual equivalence of the four conditions.
-
(A) \(\Rightarrow \) (B): Taking
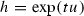 in (A), and differentiating with respect to t at \(t=0\) yields (B).
in (A), and differentiating with respect to t at \(t=0\) yields (B). -
(B) \(\Rightarrow \) (C): Here we may view y as the position vector field on
 and \(g_y\) as a Riemannian metric on \(\mathfrak {m}\). Notice also that u is a constant vector field on \(\mathfrak {m}\) and
and \(g_y\) as a Riemannian metric on \(\mathfrak {m}\). Notice also that u is a constant vector field on \(\mathfrak {m}\) and 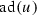 is a linear transformation on \(\mathfrak {m}\). Let D be the flat trivial connection on \(\mathfrak {m}\), then we have
is a linear transformation on \(\mathfrak {m}\). Let D be the flat trivial connection on \(\mathfrak {m}\), then we have 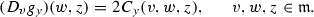
Applying \(D_v\) to (B) and using the fact that \(D_v y = v\),
 , then (C) is proved.
, then (C) is proved. -
(C) \(\Rightarrow \) (D): Applying \(D_w\) to (C) yields (D).
-
(D) \(\Rightarrow \) (B): Taking \(v=w=y\) does the work.
-
(B) \(\Rightarrow \) (A): Consider the curve
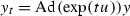 in \(\mathfrak {m}\). It has the property that
in \(\mathfrak {m}\). It has the property that  , hence we have
, hence we have 
Now let
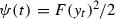 , then we have for each fixed s,
, then we have for each fixed s, 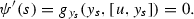
Thus \(\psi \) is a constant function,
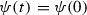 . Consequently,
. Consequently, 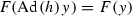 holds for
holds for 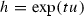 . Since H is connected, it can be generated by elements of the form
. Since H is connected, it can be generated by elements of the form  , hence (A) holds for any \(h\in H\).\(\square \)
, hence (A) holds for any \(h\in H\).\(\square \)
2.4 The flag curvature formula
Fix a nonzero vector \(y\in \mathfrak {m}\), we will attach to it a vector \(\eta \) and a linear operator N on \(\mathfrak {m}\).
Definition 2.9
For each  , there is a unique vector \(\eta \) in \(\mathfrak {m}\) satisfying
, there is a unique vector \(\eta \) in \(\mathfrak {m}\) satisfying

called the spray vector at y. The subscript \(\mathfrak {m}\) in (2) means projection to the subspace \(\mathfrak {m}\). We shall use \(\mathrm {ad}_{\mathfrak {m}}(y)\) to denote the operator on \(\mathfrak {m}\) sending v to  .
.
Definition 2.10
For each nonzero vector y in \(\mathfrak {m}\), there is a unique (1, 1) tensor N on \(\mathfrak {m}\) satisfying

called the connection operator at y.
From the definition of N, it is easy to see that the adjoint operator of N with respect to \(g_y\), denoted by \(N^*\), satisfies the following equation:

There is a simple relation between \(\eta ,N\) and the S-curvature,

where \(I_y\) is the mean Cartan tensor. The reader is refered to [18] for the proof. If the Lie group G is unimodular, then Milnor [24, Lemma 6.3] shows that  . Since \(\mathrm{ad}(y)\) maps \(\mathfrak {h}\) into \(\mathfrak {m}\), we have \(.\) In this case,
. Since \(\mathrm{ad}(y)\) maps \(\mathfrak {h}\) into \(\mathfrak {m}\), we have \(.\) In this case,  coincides with S-curvature.
coincides with S-curvature.
Notice that \(\eta \) and N are defined for each nonzero vector y in \(\mathfrak {m}\). Sometimes it is more convenient to view them as tensor fields on  . Precisely, \(\eta \) can be viewed as a vector field on
. Precisely, \(\eta \) can be viewed as a vector field on  and N is a (1, 1) tensor field on
and N is a (1, 1) tensor field on  . Using the trivial flat connection D on
. Using the trivial flat connection D on  , one can verify that \(N=D\eta /2 - \mathrm {ad}_{\mathfrak {m}}(y)/2\), i.e.,
, one can verify that \(N=D\eta /2 - \mathrm {ad}_{\mathfrak {m}}(y)/2\), i.e.,

This relation gives us an efficient way to compute N in concrete examples.
The spray vector \(\eta \) and connection operator N play an importance role in the curvature formulas of a homogeneous Finsler space. The proofs of the following two theorems could be found in [18].
Theorem 2.11
([18]) Identifying \(T_oM\) with \(\mathfrak {m}\) as above, the Riemann curvature tensor \(R_y\) of a homogeneous Finsler space \((M=G/H,F)\) satisfies the following equation:

where the operator \(\widetilde{R}\) is defined by

namely, for each \(v\in \mathfrak {m}\),

Using the adjoint operator \(N^*\), one can rewrite equation (5) as follows:

Theorem 2.12
([18]) The Ricci curvature of a homogeneous Finsler space \((M=G/H,F)\) is given by

where  is considered as a linear operator on \(\mathfrak {m}\).
is considered as a linear operator on \(\mathfrak {m}\).
3 Flag curvatures
3.1 Naturally reductive metrics
Now we describe a simple and trivial case in which the above flag curvature formula is applicable.
Definition 3.1
Let F be an invariant Finsler metric on the homogeneous space \(M=G/H\). If the spray vector \(\eta \) vanishes identically, i.e.

then the metric F is said to be naturally reductive.
Remark 3.2
If the metric F is Riemannian, then  is independent of y. By polarising (7), one recovers the usual definition of naturally reductiveness in [21], namely
is independent of y. By polarising (7), one recovers the usual definition of naturally reductiveness in [21], namely

It can be shown that, for each nonzero y in \(\mathfrak {m}\), the spray vector \(\eta \) at y is zero if and only if  is a geodesic [18, 22]. Hence, naturally reductive metrics share the same set of geodesics. Consequently these metrics are Berwaldian, and share the same Riemann curvature tensor.
is a geodesic [18, 22]. Hence, naturally reductive metrics share the same set of geodesics. Consequently these metrics are Berwaldian, and share the same Riemann curvature tensor.
Theorem 3.3
If the Finsler metric F on the homogeneous space \(M=G/H\) is naturally reductive, then for each nonzero vector \(y\in \mathfrak {m}\), we have

Proof
This is obvious if the reader is familiar with homogeneous Riemannian spaces (cf. [21]). Here we shall provide a direct proof.
Since \(\eta =0\), we have  , \(D_{\eta }N=0\) and
, \(D_{\eta }N=0\) and  , hence
, hence  .
.
Substituting  to (3) yields
to (3) yields

Permuting u and v in the above equation shows that \(\mathrm {ad}_{\mathfrak {m}}(y)\) is skew-adjoint with respect to \(g_y\). Hence we have
The conclusion then follows from Theorem 2.11.\(\square \)
By using a similar argument, we have
Corollary 3.4
If the Finsler metric F on the homogeneous space \(M=G/H\) is naturally reductive, then we have

which is independent of the metric F.
The following result furnishes a very simple case where the above theorem may be applied.
Theorem 3.5
Let G / H be a homogeneous space. Assume that \(\breve{F}\) is an  -invariant Minkowski norm on \(\mathfrak {g}\) and \(\mathfrak {m}\) is an
-invariant Minkowski norm on \(\mathfrak {g}\) and \(\mathfrak {m}\) is an  -invariant subspace of \(\mathfrak {g}\) complimentary to \(\mathfrak {h}\). Define a Minkowski norm F on \(\mathfrak {m}\) as follows:
-invariant subspace of \(\mathfrak {g}\) complimentary to \(\mathfrak {h}\). Define a Minkowski norm F on \(\mathfrak {m}\) as follows:

Then F is naturally reductive and the flag curvature is nonnegative.
Proof
Álvarez Paiva and Durán [3] introduced the notion of isometric submersion. Here the projection \(\pi :\mathfrak {g}\rightarrow \mathfrak {m}\) is just an isometric submersion between Minkowski spaces \((\mathfrak {g},\breve{F})\) and \((\mathfrak {m},F)\). It can be shown that the infimum in (8) is attained at a unique \(u\in \mathfrak {h}\). We shall denote by \(\breve{y}\) the unique vector \(y+u\) such that \(F(y)=\breve{F}(y+u)\),  . Then it is proved in [3] that \(\pi \) is also an isometric submersion between Euclidean spaces \((\mathfrak {g}, \breve{g}_{\breve{y}})\) and \((\mathfrak {m}, g_y)\), namely,
. Then it is proved in [3] that \(\pi \) is also an isometric submersion between Euclidean spaces \((\mathfrak {g}, \breve{g}_{\breve{y}})\) and \((\mathfrak {m}, g_y)\), namely,

where \(\breve{g}_{\breve{y}}\) and \(g_y\) are the inner products associated to \(\breve{F},F\), respectively.
The  -invariance of F is obvious by definition. Now we prove that F is naturally reductive. Since \(\breve{F}\) is
-invariance of F is obvious by definition. Now we prove that F is naturally reductive. Since \(\breve{F}\) is  -invariant, by an argument similar to Lemma 2.8, we have
-invariant, by an argument similar to Lemma 2.8, we have

Let z belong to \(\mathfrak {m}\) and let \(w=\breve{y}\) for some  , then we have
, then we have

where we have used the fact that  . Notice that \(\breve{g}_{\breve{y}}(\breve{y}, x) = g_y(y,x)\) for any \(x\in \mathfrak {m}\), we have
. Notice that \(\breve{g}_{\breve{y}}(\breve{y}, x) = g_y(y,x)\) for any \(x\in \mathfrak {m}\), we have  for any \(z\in \mathfrak {m}\). Hence F is naturally reductive.
for any \(z\in \mathfrak {m}\). Hence F is naturally reductive.
Now, the Riemann curvature tensor \(R_y\) is independent of the metric F. We know from Riemannian geometry that \(R_y\) has nonnegative eigenvalues, hence the flag curvature is nonnegative.\(\square \)
Remark 3.6
The spaces in this theorem are called normal homogeneous. One may compare the treatment here with [35]. Clearly, the study of normal homogeneous Finsler spaces is almost the same as normal homogenous Riemannian spaces.
3.2 Positively curved spaces
In this subsection, we will try to answer the following question: which homogeneous spaces admit an invariant Finsler metric, whose flag curvature is everywhere positive? We shall first give two lemmas that describe some flags with nonnegative curvature. The first lemma generalizes a result of Milnor [24] and also a result of Hu–Deng [16].
Lemma 3.7
([18]) If a nonzero vector y belongs to the center of \(\mathfrak {g}\), then we may adjust \(\mathfrak {m}\) such that \(y\in \mathfrak {m}\). For this center element \(y\in \mathfrak {m}\), the connection operator N is skew-adjoint with respect to \(g_y\) and we have
with equality holding if and only if y is \(g_y\)-orthogonal to  .
.
Proof
When y belongs to the center of \(\mathfrak {g}\), let \(y=y_1+y_2\) be the decomposition with respect to the direct sum \(\mathfrak {g}=\mathfrak {h}+\mathfrak {m}\). If  , then
, then  . It follows that
. It follows that  is a center both in G and H, contradicting the hypothesis that the action is almost effective. Hence \(y_2\ne 0\).
is a center both in G and H, contradicting the hypothesis that the action is almost effective. Hence \(y_2\ne 0\).
Since  , we find that y is
, we find that y is  -invariant and
-invariant and  . Since
. Since  ,
,  , we have
, we have  and
and  . As a result, \(y_2\) is
. As a result, \(y_2\) is  -invariant. Let \(\mathfrak {m}_1\) be an
-invariant. Let \(\mathfrak {m}_1\) be an  -invariant subspace of \(\mathfrak {m}\) complimentary to \(\mathbb {R}y_2\), and define
-invariant subspace of \(\mathfrak {m}\) complimentary to \(\mathbb {R}y_2\), and define  , then \(\mathfrak {m}'\) is also an
, then \(\mathfrak {m}'\) is also an  -invariant subspace of \(\mathfrak {g}\) complimentary to \(\mathfrak {h}\). The first part is proved.
-invariant subspace of \(\mathfrak {g}\) complimentary to \(\mathfrak {h}\). The first part is proved.
The hypothesis now implies \(\mathrm {ad}_{\mathfrak {m}}(y)=0\) and \(\eta =0\). The connection operator N is determined by the relation

Permuting u and v in (9) shows that N is skew-adjoint with respect to \(g_y\).
Since \(D_{\eta }N=0\) and \([N,\mathrm {ad}_{\mathfrak {m}}(y)]=0\), we have  . Thus
. Thus

Moreover  since y belongs to the center. Thus by Theorem 2.11, we have
since y belongs to the center. Thus by Theorem 2.11, we have
The equality holds if and only if \(Nv=0\). By (9), the condition \(Nv=0\) is equivalent to the property that y is \(g_y\)-orthogonal to  .\(\square \)
.\(\square \)
A slight generalization of Lemma 3.7 is given in [36]. We restate it as follows.
Lemma 3.8
If a nonzero vector \(y\in \mathfrak {m}\) satisfies \(\eta =0\) at y, and there is a vector \(v\in \mathfrak {m}\) such that  , then we have
, then we have
Proof
Since  , \(\eta =0\), \(D_{\eta }N=0\), utilizing (5) we have
, \(\eta =0\), \(D_{\eta }N=0\), utilizing (5) we have

Using the definition of N (see equation (3)), we have

Combining the above two equations yields

Using the definition of N once again, we find that the right-hand side is equal to \(g_y(Nv,Nv)\). Thus the lemma is proved.\(\square \)
Based on the above two lemmas, we now proceed to study homogeneous Finsler spaces with positive flag curvature. Since such spaces are compact by the Bonnet–Myers theorem, from now on we will always assume that G is compact in this subsection.
With the compact assumption, we can fix an  -invariant inner product Q on \(\mathfrak {g}\). Then we have
-invariant inner product Q on \(\mathfrak {g}\). Then we have

Let \(\mathfrak {m}\) be the orthogonal compliment of \(\mathfrak {h}\) with respect to Q, then \(\mathfrak {m}\) is  -invariant.
-invariant.
Suppose that there is a nonzero vector \(y\in \mathfrak {m}\) such that \(\eta =0\) at y. The existence of such y will be clear in context. Fixing such a vector y, there is a unique operator \(P:\mathfrak {m}\rightarrow \mathfrak {m}\) that is self-adjoint with respect to \(Q|_{\mathfrak {m}}\) and satisfies
In general, P is not  -invariant, but we still have
-invariant, but we still have  for any \(u\in \mathfrak {h}\). Actually, since F is
for any \(u\in \mathfrak {h}\). Actually, since F is  -invariant, we get from Lemma 2.8 (C) that
-invariant, we get from Lemma 2.8 (C) that

Thus we have

which in turn forces  .
.
Now equation (3) can be rewritten as

Using (10) and the self-adjoint property of P, we have

Thus we obtain an expression of N as follows:

where  . We shall show that \(B^+v\) always belongs to \(\mathfrak {m}\), thus the projection can be omitted. Actually, for any \(u\in \mathfrak {h}\),
. We shall show that \(B^+v\) always belongs to \(\mathfrak {m}\), thus the projection can be omitted. Actually, for any \(u\in \mathfrak {h}\),

Hence  is perpendicular to \(\mathfrak {h}\), thus belongs to \(\mathfrak {m}\).
is perpendicular to \(\mathfrak {h}\), thus belongs to \(\mathfrak {m}\).
Using a similar argument we can show that the adjoint operator \(N^*\) is given by

where  . However, \(B^-v\) usually does not belong to \(\mathfrak {m}\), so the projection could not be omitted.
. However, \(B^-v\) usually does not belong to \(\mathfrak {m}\), so the projection could not be omitted.
To further simplify (6), we compute

and

Altogether, we can rewrite (6) in the following form (be ware of the assumption that \(\eta =0\) at y)

If  and
and  , then we have
, then we have

Lemma 3.9
Let Q be an  -invariant inner product on \(\mathfrak {g}\). Then the function \(f(z)=F^2(z)/Q(z,z)\) defined on
-invariant inner product on \(\mathfrak {g}\). Then the function \(f(z)=F^2(z)/Q(z,z)\) defined on  must attain its minimum at some nonzero vector \(y\in \mathfrak {m}\) and the spray vector \(\eta \) vanishes at the minimizer y. Suppose further that there is a vector \(v\in \mathfrak {m}\) such that
must attain its minimum at some nonzero vector \(y\in \mathfrak {m}\) and the spray vector \(\eta \) vanishes at the minimizer y. Suppose further that there is a vector \(v\in \mathfrak {m}\) such that  , then we have
, then we have

where \(\lambda \) is the minimal value of f(z).
Proof
By homogeneity, the function \(f(z)=F^2(z)/Q(z,z)\) can be viewed as defined on the indicatrix \(F(z)=1\), hence it must attain its minimum at some  . Denote the minimal value by \(\lambda \), then we have
. Denote the minimal value by \(\lambda \), then we have

Let \(\widetilde{f}(z) = F^2(z) - \lambda Q(z,z)\), then \(\widetilde{f}\) attains minimal value at y, so \(D_w\widetilde{f} = 0\) at y, namely,
Also, the Hessian of \(\widetilde{f}\) must be semi-positive definite at y, so we have
Notice that the left-hand side of (12) can be written as Q(Py, w), comparing with right-hand side yields \(Py=\lambda y\), namely, y is an eigenvector of P with eigenvalue \(\lambda \). Moreover, we get from (13) that \(Q(Pz,z)\geqslant \lambda Q(z,z)\), hence \(\lambda \) is the smallest eigenvalue of P. As a result
Since Q is  -invariant, we know from (10) that
-invariant, we know from (10) that  , hence
, hence

Together with (12) we have

Hence \(\eta =0\) at y.
Now, if the vector v satisfies  , then we have
, then we have  . Since \(B^+v\) always belongs to \(\mathfrak {m}\), we have
. Since \(B^+v\) always belongs to \(\mathfrak {m}\), we have  . Put
. Put  , then we have
, then we have

Similarly we have

Substitute the above two results into (11), then we have

with equality holding if and only if \(w=0\), i.e.,  .\(\square \)
.\(\square \)
Theorem 3.10
([16]) Let G be a connected and simply connected Lie group. If G admits a left invariant Finsler metric of positive flag curvature, then \(\mathrm{rank}(G)=1\) and G is Lie isomorphic to  .
.
Proof
In this case  and \(\mathfrak {g}=\mathfrak {m}\). Let y be the minimizer as in Lemma 3.9, then y is the eigenvector of P with eigenvalue \(\lambda \). If there is a linearly independent vector z such that
and \(\mathfrak {g}=\mathfrak {m}\). Let y be the minimizer as in Lemma 3.9, then y is the eigenvector of P with eigenvalue \(\lambda \). If there is a linearly independent vector z such that  , then we may write \(z=Pv\). The vectors y and v are linearly independent because \(P^{-1}y\) and \(P^{-1}v\) are. By Lemma 3.9, the flag curvature of
, then we may write \(z=Pv\). The vectors y and v are linearly independent because \(P^{-1}y\) and \(P^{-1}v\) are. By Lemma 3.9, the flag curvature of  is nonpositive, contradicting our hypothesis. Thus the rank of G is at most 1 and the universal cover of G is
is nonpositive, contradicting our hypothesis. Thus the rank of G is at most 1 and the universal cover of G is  .\(\square \)
.\(\square \)
Proposition 3.11
([16, 18]) Suppose that G is a compact connected Lie group and H is a closed subgroup of G. Let \(M=G/H\) be a homogeneous space on which G acts almost effectively. If M admits a G-invariant Finsler metric F with strictly positive flag curvature, then
-
if \(\dim M\) is even, then G is semi-simple,
-
if \(\dim M\) is odd, then G is either semi-simple or the center of G is one dimensional.
Proof
Let \(\mathfrak {z}\) be the center of \(\mathfrak {g}\), then by Lemma 3.7 we may assume that \(\mathfrak {z}\subset \mathfrak {m}\).
If \(\dim \mathfrak {z}=0\), then  is semi-simple.
is semi-simple.
If \(\dim \mathfrak {z}=1\), choose a nonzero vector \(y\in \mathfrak {z}\) and let \(\mathfrak {p}\) be the \(g_y\)-orthogonal compliment of \(\mathfrak {z}\) in \(\mathfrak {m}\). Consider the restriction of the operator N on \(\mathfrak {p}\). By Lemma 3.7 we have
This shows that the restriction of N on \(\mathfrak {p}\) is non-singular. Since N is skew-adjoint on \(\mathfrak {p}\), the dimension of \(\mathfrak {p}\) must be even. As a result, M is odd dimensional.
If \(\dim \mathfrak {z}\geqslant 2\), then we can choose linearly independent vectors \(y,v\in \mathfrak {z}\). Since  , Lemma 3.7 shows that \(g_y(R_y(v),v)=0\), contradicting our hypothesis. Hence this case cannot happen.
, Lemma 3.7 shows that \(g_y(R_y(v),v)=0\), contradicting our hypothesis. Hence this case cannot happen.
Since \(\dim G-\mathrm{rank}(G)\) is always even, the proposition is proved.\(\square \)
Before proceeding, we present a simple lemma on group actions.
Lemma 3.12
Suppose that Lie groups G, H, L satisfy \(L\subset H\subset G\) and G acts almost effectively on the coset space \(M=G/H\). Let \(C(L)_0\) be the identity component of the centralizer of L in G. Let \(M_L\) be the set of points in M that are fixed by elements of L. Let \(M_0\) be the connected component of \(M_L\) through o. Then \(C(L)_0\) acts transitively on \(M_0\), and \(M_0= C(L)_0/C(L)_0\cap H\).
Proof
We only need to prove that \(M_0\) is precisely the orbit of \(C(L)_0\), namely,  .
.
For each point x in the orbit of \(C(L)_0\), let \(x=f(o)\) for some \(f\in C(L)_0\). Then for any \(l\in L\), \(lf=fl\). Hence we have  . This shows that x is fixed by all elements in L. Moreover, since the orbit of \(C(L)_0\) is connected, we find that \(x\in M_0\). Thus the orbit
. This shows that x is fixed by all elements in L. Moreover, since the orbit of \(C(L)_0\) is connected, we find that \(x\in M_0\). Thus the orbit  is contained in \(M_0\).
is contained in \(M_0\).
Conversely, for each vector v in \(T_oM_0\), if we identify \(T_oM_0\) with a subspace \(\mathfrak {m}_0\) of \(\mathfrak {m}\) as before, then v is  -invariant. Thus v belongs to the centralizer of \(\mathfrak {l}\), the Lie algebra of L. This shows that \(M_0\) is contained in
-invariant. Thus v belongs to the centralizer of \(\mathfrak {l}\), the Lie algebra of L. This shows that \(M_0\) is contained in  .\(\square \)
.\(\square \)
Now we may prove a refinement of Proposition 3.11.
Theorem 3.13
([37]) Suppose that G is a compact connected Lie group and H is a closed subgroup of G such that G acts almost effectively on G / H. Suppose \(M=G/H\) admits an invariant Finsler metric F with strictly positive flag curvature. Let T be a maximal torus of H and let \(C(T)_0\) be the identity component of the centralizer of T in G. Then
-
If \(\dim M\) is even, then T is a maximal torus of G. In this case, \(\mathrm{rank}(G)=\mathrm{rank}(H)\).
-
If \(\dim M\) is odd, then \(C(T)_0/T\) is isomorphic to \(S^1\),
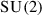 or
or  . In this case \(\mathrm{rank}(G)=\mathrm{rank}(H)+1\).
. In this case \(\mathrm{rank}(G)=\mathrm{rank}(H)+1\).
Proof
Notice that \(C(T)_0\cap H=T\). By Lemma 3.12 and Proposition 2.3, \(M_0=C(T)_0/T\) is a totally geodesic submanifold of M, hence it also has positive flag curvature. But \(M_0=C(T)_0/T\) is a Lie group, the induced metric on \(M_0\) is a left invariant metric, hence by Theorem 3.10, \(\mathrm{rank}(M_0)=1\) and \(M_0\) is isomorphic to \(S^1\),  or
or  .
.
Since \(\dim G-\mathrm{rank}(G)\) is an even number for the compact group G, the theorem follows.\(\square \)
Theorem 3.14
([37]) Let G be a compact connected simply connect Lie group and H a connected closed subgroup of G such that the dimension of \(M=G/H\) is even and G acts almost effectively on M. If M admits a G-invariant Finsler metric of positive flag curvature, then it also admits a G-invariant Riemannian metric of positive sectional curvature.
Proof
Fix an  -invariant inner product Q on \(\mathfrak {g}\). Let \(\mathfrak {m}\) be the orthogonal compliment of \(\mathfrak {h}\) in \(\mathfrak {g}\). Let \(\mathfrak {t}\) be a Cartan subalgebra of \(\mathfrak {h}\), then by the above Theorem 3.13, \(\mathfrak {t}\) is also a Cartan subalgebra of \(\mathfrak {g}\).
-invariant inner product Q on \(\mathfrak {g}\). Let \(\mathfrak {m}\) be the orthogonal compliment of \(\mathfrak {h}\) in \(\mathfrak {g}\). Let \(\mathfrak {t}\) be a Cartan subalgebra of \(\mathfrak {h}\), then by the above Theorem 3.13, \(\mathfrak {t}\) is also a Cartan subalgebra of \(\mathfrak {g}\).
For any \(t_1,t_2\in \mathfrak {t}\), the operators  as linear transforms on \(\mathfrak {m}\), are skew-adjoint with respect to \(Q|_{\mathfrak {m}}\), and commute to each other. So they share the same invariant subspaces. We have the direct sum decomposition
as linear transforms on \(\mathfrak {m}\), are skew-adjoint with respect to \(Q|_{\mathfrak {m}}\), and commute to each other. So they share the same invariant subspaces. We have the direct sum decomposition

where each \(\mathfrak {m}_{\alpha }\) is a 2-dimensional \(\mathrm{ad}(\mathfrak {t})\)-invariant subspace of \(\mathfrak {m}\). Precisely, each \(\alpha \in \mathrm{\Delta }^+\) is a linear function on \(\mathfrak {t}\), called a (positive) root, and \(\mathfrak {m}_{\alpha }\) has a basis \(z_\alpha ,w_{\alpha }\) such that

In other words, \(\mathfrak {m}_{\alpha }\) is the root space of  with eigenvalues
with eigenvalues  . For each linear function \(\theta \) on \(\mathfrak {t}\), we define \(\mathfrak {m}_{\theta }\) to be the root space of
. For each linear function \(\theta \) on \(\mathfrak {t}\), we define \(\mathfrak {m}_{\theta }\) to be the root space of  with eigenvalues
with eigenvalues  , \(t\in \mathfrak {t}\). Thus one can show that
, \(t\in \mathfrak {t}\). Thus one can show that

Choose \(\alpha \in \mathrm{\Delta }^+\) and fix a nonzero vector \(y\in \mathfrak {g}_{\alpha }\). Let \(\mathfrak {t}'\) be the subspace of \(\mathfrak {t}\) annihilated by \(\alpha \). Then for any  , using (14), we have
, using (14), we have  . Recall that the invariance of F implies (see Lemma 2.8 (D))
. Recall that the invariance of F implies (see Lemma 2.8 (D))

It is evident that  is skew-adjoint with respect to \(g_y\). The operators
is skew-adjoint with respect to \(g_y\). The operators  , \(t\in \mathfrak {t}'\), commute to each other, so they also share the same invariant subspaces. We obtain another direct sum decomposition
, \(t\in \mathfrak {t}'\), commute to each other, so they also share the same invariant subspaces. We obtain another direct sum decomposition
where each \(\mathfrak {m}'_{\delta }\) is an \(\mathrm{ad}(\mathfrak {t}')\)-invariant subspace of \(\mathfrak {m}\) and has the form

Consequently, if two vectors \(v, w\in \mathfrak {m}\) belong to two different summands, then they are orthogonal with respect to \(g_y\).
Notice that the first summand \(\mathfrak {m}_{\alpha }\) is the 0-eigenspace of all  , \(t\in \mathfrak {t}'\). If \(\gamma \in \mathrm{\Delta }^+\) and
, \(t\in \mathfrak {t}'\). If \(\gamma \in \mathrm{\Delta }^+\) and  , then \(\mathfrak {m}_{\gamma }\) does not belong to the first summand. So we have \(g_y(y, \mathfrak {g}_{\gamma })=0\). Consequently, for any \(u\in \mathfrak {m}\),
, then \(\mathfrak {m}_{\gamma }\) does not belong to the first summand. So we have \(g_y(y, \mathfrak {g}_{\gamma })=0\). Consequently, for any \(u\in \mathfrak {m}\),  . This shows that \(\eta =0\) at y.
. This shows that \(\eta =0\) at y.
Suppose there is \(\beta \in \mathrm{\Delta }^+\) such that  , and
, and  , then there is a summand in (15) which only contains \(\mathfrak {m}_{\beta }\). So \(\mathfrak {m}_{\beta }\) will be orthogonal to other \(\mathfrak {m}_{\gamma }\), with respect to \(g_y\). Choose a nonzero \(v\in \mathfrak {m}_{\beta }\). Since \(\alpha \pm \beta \) are not roots, we have
, then there is a summand in (15) which only contains \(\mathfrak {m}_{\beta }\). So \(\mathfrak {m}_{\beta }\) will be orthogonal to other \(\mathfrak {m}_{\gamma }\), with respect to \(g_y\). Choose a nonzero \(v\in \mathfrak {m}_{\beta }\). Since \(\alpha \pm \beta \) are not roots, we have  . Moreover, using the above orthogonality one can check that for any \(u\in \mathfrak {m}\),
. Moreover, using the above orthogonality one can check that for any \(u\in \mathfrak {m}\),

As a result, \(N(v)=0\). Now Lemma 3.8 shows that the flag curvature of  is zero. A contradiction.
is zero. A contradiction.
So we have proved that, for any roots \(\alpha \) and \(\beta \) in \(\mathrm{\Delta }^+\), at least one of \(\alpha +\beta ,\alpha -\beta \) is a root. This is what Wallach called the condition (A). Although we consider Finsler metrics instead of Riemannian metrics, the result shows that the underlying homogeneous space should satisfy the same set of requirements. So there is no difference between Finsler and Riemannian geometry in this situation.\(\square \)
Remark 3.15
For more detailed discussion on this topic, one may consult [37]. Xu and Deng also have some progress on the odd dimensional case, see [36].
Corollary 3.16
Let (M, F) be an even dimensional connected and simply connected homogeneous Finsler space. If it has positive constant flag curvature, then it is an even dimensional Riemannian space form.
Proof
By the Sphere Theorem [25], a connected and simply connected Finsler space with positive constant flag curvature must be homeomorphic to a sphere. Comparing with Wallach’s list, one can see that M must be diffeomorphic to a sphere. Moreover, by carefully checking the  action for each case, one can show that the only possible invariant Finsler metric is a multiple of the standard Riemannian one. A detailed analysis of possible invariant Finsler metrics can be found in [37].\(\square \)
action for each case, one can show that the only possible invariant Finsler metric is a multiple of the standard Riemannian one. A detailed analysis of possible invariant Finsler metrics can be found in [37].\(\square \)
4 Left invariant Finsler metrics on Lie groups
In this section, we shall study Ricci curvatures of left invariant Finsler metrics on Lie groups. Now  and \(\mathfrak {m}=\mathfrak {g}\), hence we do not need projection (to \(\mathfrak {m}\), or to \(\mathfrak {h}\)) in this case. A direct consequence of Lemma 3.7 is the following
and \(\mathfrak {m}=\mathfrak {g}\), hence we do not need projection (to \(\mathfrak {m}\), or to \(\mathfrak {h}\)) in this case. A direct consequence of Lemma 3.7 is the following
Corollary 4.1
If a nonzero vector \(y\in \mathfrak {g}\) belongs to the center of \(\mathfrak {g}\), then for any left invariant Finsler metric F on the Lie group G, the Ricci curvature along the y-direction is nonnegative. It is zero if and only if y is \(g_y\)-orthogonal to the subspace  .
.
To describe directions with negative Ricci curvature, we shall prove
Lemma 4.2
Let F be a left invariant Finsler metric on the Lie group G. If a nonzero vector \(y\in \mathfrak {g}\) is \(g_y\)-orthogonal to the subspace  , then the Ricci curvature along the y-direction is nonpositive. It is zero if and only if \(\mathrm {ad}_{\mathfrak {m}}(y)\) is skew-adjoint with respect to \(g_y\).
, then the Ricci curvature along the y-direction is nonpositive. It is zero if and only if \(\mathrm {ad}_{\mathfrak {m}}(y)\) is skew-adjoint with respect to \(g_y\).
Proof
The hypothesis implies that \(\eta =0\) at y. The connection operator N now satisfies

Permuting u and v in (16) shows that N is self-adjoint with respect to \(g_y\), i.e., \(N=N^*\).
By Theorem 2.12, the Ricci curvature along the y-direction is given by

The equality holds if and only if \(N=0\). In view of (16), the condition \(N=0\) is also equivalent to the property that \(\mathrm{ad}(y)\) is skew-adjoint with respect to \(g_y\).\(\square \)
Proposition 4.3
Let F be a left invariant Finsler metric on the Lie group G. If  , then there exists a flag with nonpositive flag curvature; Moreover, if
, then there exists a flag with nonpositive flag curvature; Moreover, if  , then there exists a flag with nonnegative flag curvature as well.
, then there exists a flag with nonnegative flag curvature as well.
Proof
If  , then we may choose a nonzero \(y\in \mathfrak {g}\) that is \(g_y\)-orthogonal to
, then we may choose a nonzero \(y\in \mathfrak {g}\) that is \(g_y\)-orthogonal to  . Then by Lemma 4.2, there is a flag
. Then by Lemma 4.2, there is a flag  with nonpositive flag curvature.
with nonpositive flag curvature.
If  , then since the image of \(\mathrm{ad}(y)\) is included in \([\mathfrak {g},\mathfrak {g}]\), it has dimension \(\leqslant \dim \mathfrak {g}-2\). Thus the kernel of \(\mathrm{ad}(y)\) has dimension \(\geqslant 2\). It follows that there is a vector \(v\in \ker \mathrm{ad}(y)\) that is linearly independent of y.
, then since the image of \(\mathrm{ad}(y)\) is included in \([\mathfrak {g},\mathfrak {g}]\), it has dimension \(\leqslant \dim \mathfrak {g}-2\). Thus the kernel of \(\mathrm{ad}(y)\) has dimension \(\geqslant 2\). It follows that there is a vector \(v\in \ker \mathrm{ad}(y)\) that is linearly independent of y.
By Lemma 4.2, the spray vector \(\eta =0\) at y and the connection operator N is self-adjoint with respect to \(g_y\). Moreover, from (16) we see that N is just the self-ajoint part of the operator  .
.
Now write  with P skew-adjoint, then
with P skew-adjoint, then  and thus
and thus

It follows that  and
and
thereby proving the proposition.\(\square \)
Corollary 4.4
Let F be a left invariant Finsler metric on M on a solvable Lie group G. If all the flag curvatures are strictly negative, then  .
.
Proof
Since \(\mathfrak {g}\) is solvable,  is a proper subspace of \(\mathfrak {g}\). The conclusion then follows from Lemma 4.2 or Proposition 4.3.\(\square \)
is a proper subspace of \(\mathfrak {g}\). The conclusion then follows from Lemma 4.2 or Proposition 4.3.\(\square \)
Remark 4.5
The Riemannian version of this result was given by Wolter [32].
The following theorem refines results of Wolf [31], Milnor [24] and Hu–Deng [16].
Theorem 4.6
([18]) Suppose the Lie group G is nilpotent but not commutative, then for any left invariant Finsler metric on G, there is a direction with positive Ricci curvature and there is also a direction with negative Ricci curvature. In particular, G does not admit any left invariant Einstein–Finsler metric.
Proof
By definition, \(\mathfrak {g}\) is nilpotent indicates that the derived series

must terminate. Let u be a nonzero vector in the last nonzero term of this series, then u belongs to the center \(\mathfrak {z}\) of \(\mathfrak {g}\) and is contained in  . Thus
. Thus  by Corollary 4.1.
by Corollary 4.1.
Now we claim that  is a proper subspace of \(\mathfrak {g}\). Otherwise, we have
is a proper subspace of \(\mathfrak {g}\). Otherwise, we have

This shows that \(\mathfrak {g}\) cannot be nilpotent unless it is commutative, contradicting to our hypothesis. Hence,  is a proper subspace of \(\mathfrak {g}\). There exists a nonzero vector y such that y is \(g_y\)-orthogonal to
is a proper subspace of \(\mathfrak {g}\). There exists a nonzero vector y such that y is \(g_y\)-orthogonal to  . It follows that y is \(g_y\)-orthogonal to
. It follows that y is \(g_y\)-orthogonal to  and \(\mathrm{ad}(y)\ne 0\).
and \(\mathrm{ad}(y)\ne 0\).
Since the eigenvalues of a skew-adjoint operator are pure imaginary or zero, while the eigenvalues of a nilpotent operator are all zero, we conclude that the nonzero linear operator \(\mathrm{ad}(y)\), being nilpotent, could not be skew-adjoint. Hence, by Lemma 4.2,  .\(\square \)
.\(\square \)
Shiing-Shen Chern had asked, does every smooth manifold admit a Ricci-constant Finsler metric? In the homogeneous realm, a similar question could be raised: does every homogeneous space admit an invariant Finsler metric with constant Ricci curvature? The above theorem shows that the answer is negative.
Recall that a Lie group G is called unimodular, if its left invariant Haar measure is also right invariant. For example, all compact Lie groups are unimodular. It was proved in [24, Lemma 6.3] that G is unimodular if and only if  for every \(y\in \mathfrak {g}\).
for every \(y\in \mathfrak {g}\).
Theorem 4.7
If the Lie group G possesses a left invariant Finsler metric with all Ricci curvatures \(\geqslant 0\), then G is unimodular.
Proof
Let \(\mathfrak {u}\) be the unimodular kernel of \(\mathfrak {g}\), namely,

By the Jacobi identity  , we have
, we have  for any v, \(w\in \mathfrak {g}\). Hence
for any v, \(w\in \mathfrak {g}\). Hence  is contained in \(\mathfrak {u}\).
is contained in \(\mathfrak {u}\).
If G is not unimular, then \(\mathfrak {u}\) is a proper subspace of \(\mathfrak {g}\). We can choose a nonzero y in \(\mathfrak {g}\) that is \(g_y\)-orghogonal to \(\mathfrak {u}\) and thus orthogonal to \([\mathfrak {g},\mathfrak {g}]\). By Lemma 4.2,  .
.
If the equality holds, then \(\mathrm{ad}(y)\) is skew-adjoint and  . But y does not belong to \(\mathfrak {u}\), we have
. But y does not belong to \(\mathfrak {u}\), we have  . This contradiction completes the proof.\(\square \)
. This contradiction completes the proof.\(\square \)
Professor Ming Xu told the author that the above theorem can be slightly generalized as follows.
Theorem 4.8
If the homogeneous Finsler space \(M=G/H\) admits an invariant Finsler metric with all Ricci curvatures \(\geqslant 0\), then G is unimodular.
Proof
Let \(\mathfrak {u}\) be the unimodular kernel of \(\mathfrak {g}\). If G is not unimodular, then \(\mathfrak {u}\) is a proper subspace of \(\mathfrak {g}\).
As in the proof of Theorem 4.7,  is contained in \(\mathfrak {u}\). Moreover, since H is compact, there is an
is contained in \(\mathfrak {u}\). Moreover, since H is compact, there is an  -invariant inner product on \(\mathfrak {g}\). With respect to this inner product, \(\mathrm{ad}(h)\) is skew-adjoint, for any \(h\in \mathfrak {h}\). It follows that
-invariant inner product on \(\mathfrak {g}\). With respect to this inner product, \(\mathrm{ad}(h)\) is skew-adjoint, for any \(h\in \mathfrak {h}\). It follows that  . So \(\mathfrak {h}\) is also contained in \(\mathfrak {u}\).
. So \(\mathfrak {h}\) is also contained in \(\mathfrak {u}\).
Denote by \(\mathfrak {u}'\) the \(\mathfrak {m}\)-component of \(\mathfrak {u}\) with respect to the decomposition \(\mathfrak {g}=\mathfrak {h}+\mathfrak {m}\), then \(\mathfrak {u}'\) is a proper subspace of \(\mathfrak {m}\). We may choose a nonzero vector y in \(\mathfrak {m}\) that is \(g_y\)-orthogonal to \(\mathfrak {u}'\). So y is \(g_y\)-orthogonal to  . In particular, y is orthogonal to
. In particular, y is orthogonal to  . So we have
. So we have

Notice that y is orthogonal to  , we have
, we have

Hence \(\eta =0\) at y. These two facts simplify the Ricci curvature to  . Moreover, the connection operator N is determined by
. Moreover, the connection operator N is determined by

Clearly N is self-adjoint with respect to \(g_y\). So  . The equality holds if and only if \(N=0\), if and only if \(\mathrm {ad}_{\mathfrak {m}}(y)\) is skew-adjoint with respect to \(g_y\). Consequently, as a linear operator on \(\mathfrak {m}\), the trace of \(\mathrm {ad}_{\mathfrak {m}}(y)\) is zero. Notice that \(\mathrm{ad}(y)\) maps \(\mathfrak {h}\) into \(\mathfrak {m}\), we have
. The equality holds if and only if \(N=0\), if and only if \(\mathrm {ad}_{\mathfrak {m}}(y)\) is skew-adjoint with respect to \(g_y\). Consequently, as a linear operator on \(\mathfrak {m}\), the trace of \(\mathrm {ad}_{\mathfrak {m}}(y)\) is zero. Notice that \(\mathrm{ad}(y)\) maps \(\mathfrak {h}\) into \(\mathfrak {m}\), we have  . A contradiction.\(\square \)
. A contradiction.\(\square \)
In view of the above results, one may conclude that the behavior of flag curvature and Ricci curvature in Finsler geometry share a common theme with the corresponding concepts in Riemannian geometry. But there are still many differences. For example, Bochner’s theorem plays an important role in discussing nonpositive Ricci curvature in Riemannian geometry. It says that, if a compact Riemannian manifold without boundary has nonpositive Ricci curvature, then every Killing field is parallel. Moreover, if it has one direction of strictly negative Ricci curvature, then every Killing field is zero. Based on this theorem, Alekeseevskii and Kimel’fel’d [1] proved that homogeneous Riemannian manifolds with zero Ricci curvature must be flat. However, so far the Finsler version of Bochner’s theorem is not proved, thus leaving open the window that there may be a Ricci flat homogeneous Finsler space which is not flat. Similarly, due to the auto-vanishing of the Weyl tensor, a three dimensional Riemannian manifold with constant Ricci curvature must have constant sectional curvature. However the same conclusion has not been proved in Finsler geometry, thus there may be a Ricci constant Finsler 3-manifold whose flag curvature is not constant. In the next section we shall provide y-local examples of this type.
5 Examples
5.1 Three dimensional Lie groups
We shall consider the Ricci curvatures of three Lie groups in this subsection. They are E(2),  and
and  .
.
The Lie group E(2) consists of rigid motions of the Euclidean plane, namely,

Its Lie algebra has a basis

Thus the Lie brackets are given by

Let \(\alpha \) be a Euclidean norm on the Lie algebra such that  is orthonormal, namely,
is orthonormal, namely,
Then \(\alpha \) corresponds to a left invariant Riemannian metric on E(2), whose sectional curvature is identically zero (cf. [24]). Now we define a Minkowski norm F on the Lie algebra as follows:

where \(\phi \) is a smooth function defined on  and satisfying
and satisfying

Then F gives rise to a left invariant \((\alpha ,\beta )\)-metric on E(2).
Direct computation shows that the spray vector is given by

It is not identically zero, hence F is not naturally reductive. Moreover, the connection operator is given by

Substituting the above data to the curvature formula, we find that the flag curvature of F is identically zero, regardless of the function \(\phi \) chosen. By the Akbar–Zadeh theorem, the metric F is locally Minkowskian, but since E(2) is not commutative, (M, F) is not covered by a global Minkowski space.
Actually, there is a simple explanation of the vanishing of flag curvature. Notice that the right invariant vector field corresponding to \(E_3\) is parallel with respect to \(\alpha \), the Finsler metric F is affinely equivalent to \(\alpha \), thus it is Berwaldian and the Riemann curvature tensor is the same as \(\alpha \).
In a similar manner, we consider the Lie group  consisting of all
consisting of all  real matrices of determinant 1. Its Lie algebra has a basis
real matrices of determinant 1. Its Lie algebra has a basis  with Lie brackets given by
with Lie brackets given by

Again define the Riemannian metric \(\alpha \) by
and consider the Finsler metric \(F=\alpha \phi (s)\), where  . In this case, the spray vector is given by
. In this case, the spray vector is given by

where  and
and  . Notice that the determinant of the matrix \((g_{ij})\) is a function of s, we find that the mean Cartan torsion is given by
. Notice that the determinant of the matrix \((g_{ij})\) is a function of s, we find that the mean Cartan torsion is given by

where  is the dual of
is the dual of  . Together the above two facts we see that the S-curvature is identically zero, regardless of the function \(\phi \) chosen. Moreover, since
. Together the above two facts we see that the S-curvature is identically zero, regardless of the function \(\phi \) chosen. Moreover, since  is unimodular, the Ricci curvature is computed by
is unimodular, the Ricci curvature is computed by  . We have
. We have

In view of the above equation, it seems reasonable to obtain a family of solutions of the equation

because it is a second order ODE on \(\phi \) (where \(\kappa \) is a constant number). But we claim that, the solutions could not be y-global. Actually, letting \(y=E_3\) (thus \(s=1\)) in (17) yields

Hence, if F has constant Ricci curvature, then necessarily the constant \(\kappa \) is positive. By the Bonnet–Myers theorem,  would be compact, that is a contradiction.
would be compact, that is a contradiction.
Hence, the above Finsler metrics cannot be Einstein. We conjecture that any y-global Finsler metrics on  cannot be Einstein.
cannot be Einstein.
The last example in this subsection is the Lie group  , consisting of matrices of the form
, consisting of matrices of the form  , where the complex numbers a, b satisfy \(|a|^2+|b|^2=1\). The Lie algebra
, where the complex numbers a, b satisfy \(|a|^2+|b|^2=1\). The Lie algebra  has a basis \(E_1,E_2,E_3\) with
has a basis \(E_1,E_2,E_3\) with

Consider the Minkowski norm  again. It is evident that the indicatrix of F can be parametrized by
again. It is evident that the indicatrix of F can be parametrized by

Thus every vector y in \(\mathfrak {su}(2)\) can be written as

In other words, (r, s, t) is a coordinate system on  . Using this coordinate system one can compute that
. Using this coordinate system one can compute that

where  . Using (4), one can show that the matrix of N with respect to the basis
. Using (4), one can show that the matrix of N with respect to the basis  is given by
is given by

where

Clearly,  , so the S-curvature vanishes. As a result, the Ricci curvature is computed by
, so the S-curvature vanishes. As a result, the Ricci curvature is computed by

Thus, the Einstein equation  reduces to the following ODE:
reduces to the following ODE:

The solution is given by

where \(\mu \geqslant 0\) is a constant number. If \(\mu >0\), we can show that the corresponding Finsler metric does not have constant flag curvature (see [17]), but it is still y-local. If \(\mu =0\), then the resulting Finsler metric is Randers type and has constant flag curvature. This special case has been obtained by Bao and Shen [6].
5.2 Einstein metrics on \(S^7\)
The standard action of  on the sphere
on the sphere  is transitive with isotropy subgroup
is transitive with isotropy subgroup  . The 10-dimensional Lie algebra
. The 10-dimensional Lie algebra  has the following basis:
has the following basis:
where \(\mathbf {i},\mathbf {j},\mathbf {k}\) are the standard basis of pure imagenary numbers in \(\mathbb {H}\). It is seen that \(E_8,E_9,E_{10}\) span a subalgebra isomorphic to  . Let \(\mathfrak {m}\) be the subspace spanned by \(E_1\) through \(E_7\).
. Let \(\mathfrak {m}\) be the subspace spanned by \(E_1\) through \(E_7\).
Clearly,  for \(1\leqslant i,j\leqslant 3\). Hence every element in the subspace \(\mathfrak {m}_0\) spanned by \(E_1,E_2,E_3\) is left fixed by the action of
for \(1\leqslant i,j\leqslant 3\). Hence every element in the subspace \(\mathfrak {m}_0\) spanned by \(E_1,E_2,E_3\) is left fixed by the action of  . Moreover,
. Moreover,

where i, j, k is a cyclic permutation of 1, 2, 3. Clearly the subspace \(\mathfrak {m}_1\) spanned by \(E_4,E_5,E_6,E_7\) is also an invariant subspace of  .
.
Now define an inner product \(\overline{g}\) on \(\mathfrak {m}\) by setting \(E_1,E_2,\ldots ,E_7\) as an orthonormal basis. It is easy to see that \(\overline{g}\) is  -invariant. Define a Minkowski norm F on \(\mathfrak {m}=\mathfrak {m}_0 + \mathfrak {m}_1\) as follows:
-invariant. Define a Minkowski norm F on \(\mathfrak {m}=\mathfrak {m}_0 + \mathfrak {m}_1\) as follows:

where \(y_0\) is the \(\mathfrak {m}_0\)-component of \(y\in \mathfrak {m}\). By the invariance of \(\overline{g}\), the  -invariance of F follows easily. Let \(s=\overline{g}(y_0,y_0)/\overline{g}(y,y)\).
-invariance of F follows easily. Let \(s=\overline{g}(y_0,y_0)/\overline{g}(y,y)\).
We list the other Lie brackets (between elements of \(\mathfrak {m}\)) as follows:

where the index i, j, k runs over a cyclic permutation of 1, 2, 3.
Using the above data, it is easily computed that the spray vector \(\overline{\eta }\) for the Riemannian metric \(\overline{g}\) is given by

for  . Notice that \(\overline{\eta }\) always belongs to \(\mathfrak {m}_1\).
. Notice that \(\overline{\eta }\) always belongs to \(\mathfrak {m}_1\).
Now, since \(D_vy=v\), \(D_vy_0 = v_0\), where \(v_0\) is the \(\mathfrak {m}_0\)-component of v, we have

Thus one can easily compute

Further differentiating yields

for any \(w,v\in \mathfrak {m}\).
It is straightforward to verify that, the spray vector \(\eta \) for the Finsler metric F is given by

As a result, the connection operator N is computed as

We shall not present the matrix of N here, but only mention that we still have
 . Hence the S-curvature vanishes, regardless of the function
\(\phi \). Moreover, the Ricci curvature is given by
. Hence the S-curvature vanishes, regardless of the function
\(\phi \). Moreover, the Ricci curvature is given by

Hence, the Einstein equation \(\mathrm {Ric}=6F^2\) reduces to a second order ODE on \(\phi \). Inspection shows that there are two solutions of the form \(\phi (s)=a+bs\), they are given by
The first solution corresponds to the canonical metric on \(S^7\), while the second solution corresponds to the Einstein–Riemannian metric found by Jensen [20]. Ziller [38] proved that they are the only homogeneous Einstein metrics on \(S^7\), in the Riemannian realm.
We do not know if there are other y-global solutions of the Einstein equation, though we believe there are many. Those solutions correspond to non-Riemannian Finsler metrics. Perhaps they are the first examples of Einstein metrics that are not of \((\alpha ,\beta )\) type and not of constant flag curvature.
References
Alekseevskii, D.V., Kimel’fel’d, B.N.: Structure of homogeneous Riemann spaces with zero Ricci curvature. Funct. Anal. Appl. 9(2), 97–102 (1975)
Aloff, S., Wallach, N.R.: An infinite family of 7-manifolds admitting positively curved Riemannian structures. Bull. Amer. Math. Soc. 81(1), 93–97 (1975)
Álvarez Paiva, J.C., Durán, C.E.: Isometric submersions of Finsler manifolds. Proc. Amer. Math. Soc. 129(8), 2409–2417 (2001)
Bao, D., Chern, S.-S., Shen, Z.: An Introduction to Riemann–Finsler Geometry. Graduate Texts in Mathematics, vol. 200. Springer, New York (2000)
Bao, D., Robles, C., Shen, Z.: Zermelo navigation on Riemannian manifolds. J. Differential Geom. 66(3), 377–435 (2004)
Bao, D., Shen, Z.: Finsler metrics of constant curvature on the Lie group \(S^3\). J. London Math. Soc. 66(2), 453–467 (2002)
Bérard-Bergery, L.: Les variétés riemanniennes homogènes simplement connexes de dimension impaire à courbure strictement positive. J. Math. Pures Appl. 55(1), 47–67 (1976)
Berger, M.: Les variétés riemanniennes homogènes normales simplement connexes à courbure strictement positive. Ann. Sc. Norm. Super. Pisa 15, 179–246 (1961)
Besse, A.L.: Einstein Manifolds. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 10. Springer, Berlin (1987)
Chern, S.-S., Shen, Z.: Riemann–Finsler Geometry. Nankai Tracts in Mathematics, vol. 6. World Scientific, Singapore (2005)
Deng, S.: Fixed points of isometries of a Finsler space. Publ. Math. Debrecen 72(3–4), 469–474 (2008)
Deng, S., Hou, Z.: The group of isometries of a Finsler space. Pacific J. Math. 207(1), 149–155 (2002)
Deng, S., Hou, Z.: Invariant Finsler metrics on homogeneous manifolds. J. Phys. A 37(34), 8245–8253 (2004)
Deng, S., Hou, Z.: Naturally reductive homogeneous Finsler spaces. Manuscripta Math. 131(1–2), 215–229 (2010)
Helgason, S.: Differential Geometry, Lie Groups and Symmetric Spaces. Pure and Applied Mathematics. vol. 80, 2nd edn. Academic Press, New York (1978)
Hu, Z., Deng, S.: Curvatures of homogeneous Randers spaces. Adv. Math. 240, 194–226 (2013)
Huang, L.: Einstein Finsler metrics on \(S^3\) with nonconstant flag curvature. Houston J. Math. 37(4), 1071–1086 (2011)
Huang, L.: On the fundamental equations of homogeneous Finsler spaces. Differential Geom. Appl. 40, 187–208 (2015)
Huang, L.: Ricci curvatures of left invariant Finsler metrics on Lie groups. Israel J. Math. 207(2), 783–792 (2015)
Jensen, G.R.: Einstein metrics on principal fibre bundles. J. Differential Geom. 8(4), 599–614 (1973)
Kobayashi, S., Nomizu, K.: Foundations of Differential Geometry. Vols. 1, 2. Interscience, New York (1963, 1969)
Latifi, D.: Homogeneous geodesics in homogeneous Finsler spaces. J. Geom. Phys. 57(5), 1421–1433 (2007)
Lohkamp, J.: Metrics of negative Ricci curvature. Ann. Math. 140(3), 655–683 (1994)
Milnor, J.: Curvatures of left invariant metrics on Lie groups. Adv. Math. 21(3), 293–329 (1976)
Rademacher, H.-B.: A sphere theorem for non-reversible Finsler metrics. Math. Ann. 328(3), 373–387 (2004)
Shen, Z.: Projectively flat Finsler metrics of constant flag curvature. Trans. Amer. Math. Soc. 355(4), 1713–1728 (2003)
Shen, Z.: On projectively flat \((\alpha,\beta )\)-metrics. Canadian Math. Bull. 52(1), 132–144 (2009)
Shen, Z., Yu, C.: On a class of Einstein Finsler metrics. Internat. J. Math. 25(4), # 1450030 (2014)
Szabó, Z.I.: Positive definite Berwald spaces. Structure theorems on Berwald spaces. Tensor (NS) 35(1), 25–39 (1981)
Wallach, N.R.: Compact homogeneous Riemannian manifolds with strictly positive curvature. Ann. Math. 96(2), 277–295 (1972)
Wolf, J.A.: Curvature in nilpotent Lie groups. Proc. Amer. Math. Soc. 15(2), 271–274 (1964)
Wolter, T.H.: Einstein metrics on solvable groups. Math. Z. 206(3), 457–471 (1991)
Wilking, B.: The normal homogeneous space \({\rm SU}(3){\times }{\rm SO}(3)/{\rm U}^\bullet (2)\) has positive sectional curvature. Proc. Amer. Math. Soc. 127(4), 1191–1994 (1999)
Wilking, B., Ziller, W.: Revisiting homogeneous spaces with positive curvature. J. Reine Angew. Math. doi:10.1515/crelle-2015-0053
Xu, M., Deng, S.: Normal homogeneous Finsler spaces. Transform. Groups. doi:10.1007/s00031-017-9428-7
Xu, M., Deng, S.: Towards the classification of odd-dimensional homogeneous reversible Finsler spaces with positive flag curvature. Ann. Mat. Pura Appl. doi:10.1007/s10231-016-0624-1
Xu, M., Deng, S., Huang, L., Hu, Z.: Even dimensional homogeneous Finsler spaces with positive flag curvature (2014). arXiv:1407.3582
Ziller, W.: Homogeneous Einstein metrics on spheres and projective spaces. Math. Ann. 259(3), 351–358 (1982)
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is supported by the National Natural Science Foundation of China Grant No. 11301283.
Rights and permissions
About this article
Cite this article
Huang, L. Flag curvatures of homogeneous Finsler spaces. European Journal of Mathematics 3, 1000–1029 (2017). https://doi.org/10.1007/s40879-017-0157-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0157-1



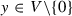 .
.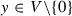 , the Hessian of
, the Hessian of 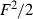 at y is positive definite. In other words, the bilinear function
at y is positive definite. In other words, the bilinear function 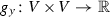 defined by
defined by 
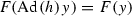 for all
for all 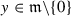 ,
, 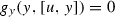 ,
,  ;
;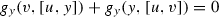 for all
for all 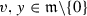 ;
;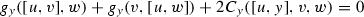 for all
for all 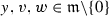 .
.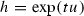 in (A), and differentiating with respect to t at
in (A), and differentiating with respect to t at  and
and 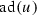 is a linear transformation on
is a linear transformation on 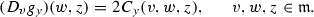
 , then (C) is proved.
, then (C) is proved.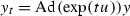 in
in  , hence we have
, hence we have 
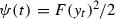 , then we have for each fixed s,
, then we have for each fixed s, 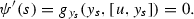
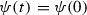 . Consequently,
. Consequently, 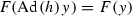 holds for
holds for 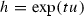 . Since H is connected, it can be generated by elements of the form
. Since H is connected, it can be generated by elements of the form  , hence (A) holds for any
, hence (A) holds for any 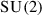 or
or  . In this case
. In this case