1 Introduction

In information technology, computer viruses are known as malicious codes or programs that have the ability to self-replicate and to spread via wired and wireless networks. Nowadays, computer viruses have become a big threat to Internet security, privacy as well as to work and daily life because of the continuous development of the Internet. This leads to urgent requests for effective measures to prevent and control computer viruses. For this purpose, mathematicians and engineers have built many mathematical models to study characteristics and transmission mechanisms of computer viruses (see, for instance, [9, 19,20,21, 25, 26, 38, 40, 41, 44, 46, 49,50,51]). These models are based on basic principles of mathematical epidemiology and the high similarity of the spread of computer viruses and biological viruses in combination with reasonable technical hypotheses, which are not only biologically motivated but also practical. The main approach used here is the use of integer-order and fractional-order differential equations to model the spreading of computer viruses [19,20,21, 25, 40, 41, 44, 46, 49,50,51]. As an important consequence, effective measures for preventing and controlling computer viruses can be suggested. Recently, we have studied dynamics and approximate solutions for some computer virus propagation models [10, 11, 23].

In a previous work [41], Piqueira and Araujo proposed a modified epidemiological model for computer viruses and analyzed its dynamics. This model is represented by

$$\begin{aligned} \begin{aligned}&\dot{S} = -\alpha _{SA}SA - \beta SI + \sigma R,\\&\dot{I} = \beta SI - \alpha _{IA}AI - \delta I,\\&\dot{R} = \delta I - \sigma R,\\&\dot{A} = \alpha _{SA}SA + \alpha _{IA}AI, \end{aligned} \end{aligned}$$
(1)

where the total population denoted by T, is divided into 4 groups, that are

  1. (i)

    S: the group of non-infected computers subjected to possible infection;

  2. (ii)

    A: the group of non-infected computers equipped with anti-virus;

  3. (iii)

    I: the group of infected computers;

  4. (iv)

    R: the group of removed computers due to infection or not.

Note that the parameters are assumed to be positive. We refer the readers to [41] for more details of the model (1) as well as its dynamical properties.

The model (1) has attracted the attention of many researchers in various aspects. In [42], Piqueira and Batistela modified the model (1) by applying the quarantine concept while approximate methods for the model (1) are studied in [12, 18]. Recently, variants of the model (1) in the context of fractional derivatives have also been studied. In a recent work [16], Dokuyucu et al. extended the model (1) with the help of the Atangana-Baleanu fractional derivative in the Caputo sense. Before this work, Singh et al. in [46] had considered the model (1) in the context of the Caputo-Fabrizio derivative having non-singular kernel. In 2017, Bonyah et al. [7] modeled the transmission of computer viruses by combining the model (1) with the Caputo fractional derivative and the beta-derivative; however, dynamics of the proposed fractional-order models has not been discussed in [7]. Although the model (1) has been extended and developed at some levels, to the best of our knowledge, complete dynamical analysis of the model (1) under the Caputo fractional derivative has not been studied yet. This motivates us to conduct this research.

Motivated and inspired by importance of mathematical models of computer viruses in general and the model (1) in particular, in this work we analyze (1) in the context of the Caputo fractional derivative to study memory effects on population dynamics. The derivation of the proposed fractional-order model is explained in terms of memory effect. It should be emphasized that fractional-order models are able to describe complex systems arising in real-world applications more accurately than integer-order ones due to the effective memory function of fractional derivatives [4,5,6, 13, 29, 43, 47]. In recent years, many mathematicians, engineers, biologists and ecologists have proposed a large number of fractional-order differential equation models and studied their applications in both theory and practice (see, for example, [1,2,3, 17, 22, 28, 46] and references therein). Recently, we have proposed and examined some fractional-order differential equations arising in biology and epidemiology [23, 24].

Our main objective is to establish positivity, linear invariant and stability properties including the local and global asymptotic stability (GAS), uniform and Mittag-Leffler stability of the fractional-order model. Here, the positivity and linear invariant are investigated by using some standard techniques. Meanwhile, it is well-known that the stability problem of fractional-order systems is very important but not a simple task. However, by a simple approach, which is based on the Lyapunov stability theory [17, 33, 34, 37, 48] in combination with an appropriate linear Lyapunov function, the stability properties of the proposed fractional-order model are analyzed rigorously. As an important consequence, the dynamics of the fractional-order model is determined fully.

From the mathematical analysis point of view, the proposed fractional-order model (3) is a generalization of the integer-order model (1). Therefore, the dynamics of the integer-order model is also obtained thanks to the dynamical analysis for the fractional-order model. As an important consequence, qualitative studies of the both fractional-order and integer-order models performed in [7] and [41] are improved. On the other hand, the present approach can be extended to investigate fractional-order versions of the model (1) in the context of other fractional derivatives. In practice, the fractional-order model is more flexible than the integer-order one because of the appearance of fractional-order \(\alpha\), which not only expands the space of parameters but also can provide more computer virus transmission scenarios. This is very useful in studying the parameter estimation problem. In Example 2 in Sect. 4, we perform a numerical experiment using synthetic data in order to show advantages of the fractional-order model in the parameter estimation problem. This example shows that the fractional-order model can fit the given data set better than the integer-order model as long as the parameter \(\alpha\) is chosen reasonably. This agrees with an analysis of a fractional-order model using real data of dengue fever, which was performed in [15].

The plan of this work is as follows:

Sect. 2 provides some preliminaries and auxiliary results. Dynamics of the fractional-order model is analyzed in Sect. 3. Numerical experiments are performed in Sect. 4. Some conclusions and remarks are presented in the last section.

2 Preliminaries and auxiliary results

We first recall from [8, 13, 29, 43] the definitions of fractional derivatives in the Caputo sense and their properties.

Let [a, b] be a finite interval of the real line \(\mathbb {R}\) and AC[a, b] be the space of absolutely continuous functions on [a, b]. The left-sided and right-sided Caputo fractional derivatives of order \(0< \alpha < 1\) defined via the Riemann-Liouville fractional integrals of a function \(f(t) \in AC[a, b]\) are given by (see [29, Section 2.4])

$$\begin{aligned} {^C_aD}^{\alpha }_tf(t) = \dfrac{1}{\Gamma (1 - \alpha )}\int _a^t\frac{f'(\tau )d\tau }{(t - \tau )^{\alpha }}, \quad t > a \end{aligned}$$

and

$$\begin{aligned} {^C_bD}^{\alpha }_tf(t) = -\dfrac{1}{\Gamma (1 - \alpha )}\int _t^b\frac{f'(\tau )d\tau }{(\tau - t)^{\alpha }}, \quad t < b \end{aligned}$$

respectively.

Definition 1

( [8]) Suppose that \(\alpha > 0\),  \(t > a\),  \(\alpha , a, t \in \mathbb {R}\). The Caputo fractional derivative is given by

$$\begin{aligned} ^C_aD^{\alpha }_tf(t) = \dfrac{1}{\Gamma (n - \alpha )}\int _a^t\dfrac{f^{(n)}(\xi )}{(t - \xi )^{\alpha + 1 - n}}d\xi , \qquad n - 1< \alpha < n \in \mathbb {N}. \end{aligned}$$

Property 1

(Linearity property [13]). Let \(f(t), g(t): [a, b] \rightarrow \mathbb {R}\) be such that \(^C_aD^{\alpha }_tf(t)\) and \(^C_aD^{\alpha }_tg(t)\) exist everywhere and let \(c_1, c_2 \in \mathbb {R}\). Then, \(^C_aD^{\alpha }_t(c_1f(t) + c_2g(t))\) exists everywhere, hence

$$\begin{aligned} ^C_aD^{\alpha }_t\big (c_1f(t) + c_2g(t)\big ) = c_1 {^C_aD^{\alpha }_tf(t)} + c_2 {^C_aD^{\alpha }_tg(t)}. \end{aligned}$$

Lemma 1

(Generalized mean value theorem [39]). Suppose that \(f(t) \in C[a, b]\) and \(^C_aD_t^{\alpha }f(t) \in C(a, b]\) for \(0< \alpha < 1\), then we have

$$\begin{aligned} f(t) = f(a) + \dfrac{1}{\Gamma (\alpha )}\big ({^C_aD_t^{\alpha }f}(\xi )\big ).(t - a)^{\alpha }, \end{aligned}$$

with \(a \le \xi \le t\) and for all \(t \in (a, b]\).

Theorem 1

([14, Theorem 2.2]) Assume that \(f \in C^1[a, b]\) is such that \(^C_aD^{\alpha }_tf(t) \ge 0\) for all \(t \in [a, b]\) and all \(\alpha \in (\alpha _0, 1)\) with some \(\alpha _0 \in (0, 1)\). Then, f is monotone increasing. Similarly, if \(^C_aD^{\alpha }_tf(t) \le 0\) for all t and \(\alpha\) mentioned above, then f is monotone decreasing.

Consider the following general dynamical system governed by the Caputo fractional differential equations

$$\begin{aligned} ^C_{t_0}D^{\alpha }_ty(t) = f(t, y), \quad y(t_0) = y_0, \quad \alpha \in (0, 1). \end{aligned}$$
(2)

Definition 2

( [34]). A point \(y^*\) is called an equilibrium point of the Caputo fractional dynamical system (2) if and only if \(f(t, y^*) = 0\).

We now consider some concepts of stability for the system (2) based on concepts presented in [1, 13, 17, 30, 34, 36].

Definition 3

(Concepts of stability) The equilibrium point \(y^* = 0\) of the system (2) is said to be

  1. (i)

    stable if for every \(\epsilon > 0\) and \(t_0 \in \mathbb {R}_+\) there exists \(\delta = \delta (\epsilon , t_0) > 0\) such that for any \(y_0 \in \mathbb {R}^n\) the inequality \(\Vert y_0\Vert < \delta\) implies that \(\Vert y(t; t_0, y_0)\Vert < \epsilon\) for \(t \ge t_0\);

  2. (ii)

    local asymptotically stable if it is stable and there exists some \(\gamma > 0\) such that \(\lim _{t \rightarrow \infty }\Vert y(t)\Vert = 0\) whenever \(\Vert y_0\Vert < \gamma\);

  3. (iii)

    uniformly stable if for every \(\epsilon > 0\) there exists \(\delta = \delta (\epsilon ) > 0\) such that for \(t_0 \in \mathbb {R}_+, y_0 \in \mathbb {R}^n\) with \(\Vert y_0\Vert < \epsilon\) the inequality \(\Vert y(t; t_0, y_0)\Vert < \epsilon\) holds for \(t \ge t_0\);

  4. (iv)

    globally asymptotically stable if it is stable and \(\lim _{t \rightarrow \infty }\Vert y(t)\Vert = 0\) for all \(y_0\) satisfying \(\Vert y_0\Vert < \infty\).

Definition 4

(Class-\(\mathcal {K}\) functions [27]) A continuous function \(\alpha : [0, t) \rightarrow [0, \infty )\) is said to belong to class-\(\mathcal {K}\) if it is strictly increasing and \(\alpha (0) = 0\).

Theorem 2

(Lyapunov stability and uniform stability of fractional order systems [17]) Let \(x = 0\) be an equilibrium point for the non-autonomous fractional-order system (2). Let us assume that there exists a continuous Lyapunov function V(y(t), t) and a scalar class-\(\mathcal {K}\) function \(\gamma _1(.)\) such that, \(\forall y \ne 0\)

$$\begin{aligned} \gamma _1(\Vert y(t)\Vert ) \le V(y(t), t) \end{aligned}$$

and

$$\begin{aligned} ^C_{t_0}D^{\beta }_ty(t) \le 0, \quad \text {with} \quad \beta \in (0, 1] \end{aligned}$$

then the origin of the system (2) is Lyapunov stable (stable).

If, furthermore, there is a scalar class-\(\mathcal {K}\) function \(\gamma _2(.)\) satisfying

$$\begin{aligned} V(y(t), t) \le \gamma _2(\Vert y\Vert ) \end{aligned}$$

then the origin of the system (2) is Lyapunov uniformly stable (uniformly stable).

Theorem 3

(Fractional order Barbalat’s lemma [48, Theorem 3]) If a scalar function V(t, y(t)) is positive semi-definite and the Caputo fractional derivative of V(t, y(t)) along the solution y(t) of the system (2) satisfies \(^C_{t_0}D^{\alpha }_tV(t, y(t)) \le -\varphi (\Vert y(t)\Vert )\), where \(\varphi (.)\) belongs to class-\(\mathcal {K}\), then \(y(t) \rightarrow 0\) as \(t \rightarrow +\infty\) if \(y_i(t)\) \(i = 1, 2, \ldots ,n\) are uniformly continuous.

Corollary 1

([48, Corollary 3]) If a scalar function V(t, y(t)) is positive semi-definite and the Caputo fractional derivative of V(t, y(t)) along the solution y(t) of the system (2) satisfies \(^C_{t_0}D^{\alpha }_tV(t, y(t))\) is negative semi-define, then \(y(t) \rightarrow 0\) as \(t \rightarrow +\infty\) if \(f_i(t, y(t))\) \(i = 1, 2, \ldots , n\) for the system (2) are bounded.

Definition 5

(Mittag-Leffler Stability [34]) The solution of (2) is said to be Mittag-Leffler stable if

$$\begin{aligned} \Vert y(t)\Vert \le \{m[y(t_0)]E_{\alpha }(-\lambda (t - t_0)^{\alpha })\}^b \end{aligned}$$

where \(t_0\) is the initial time, \(\alpha \in (0, 1)\), \(\lambda \ge 0\), \(b > 0\), \(m(0) = 0\), \(m(x) \ge 0\), and m(x) is locally Lipschitz on \(x \in \mathbb {B} \in \mathbb {R}^n\) with Lipschitz constant \(m_0\).

Theorem 4

(Theorem 5.1 in [34]) Let \(y = 0\) be an equilibrium point for the system (2) and \(\mathbb {D} \subset \mathbb {R}^n\) be a domain containing the origin. Let \(V(t, y(t)): [0, \infty ) \times \mathbb {D} \rightarrow \mathbb {R}\) be a continuously differentiable function and locally Lipschitz with respect to y such that

$$\begin{aligned} \begin{aligned}&\alpha _1 \Vert y\Vert ^a \le V(t, y(t)) \le \alpha _2\Vert y\Vert ^{ab},\\&{^C_0D_t^{\beta }}V(t, y(t)) \le -\alpha _3\Vert y\Vert ^{ab}, \end{aligned} \end{aligned}$$

where \(t \ge 0\), \(x \in \mathbb {D}\), \(\beta \in (0, 1)\), \(\alpha _1, \alpha _2, \alpha _3, a\) and b are arbitrary positive constants. Then \(x = 0\) is Mittag-Leffler stable. If the assumptions hold globally on \(\mathbb {R}^n\), then \(y = 0\) is globally Mittag-Leffler stable.

3 Fractional-order model and its dynamics

In this section, we consider the model (1) in the context of the fractional Caputo derivative and analyze its dynamics.

3.1 Mathematical formulation

We now introduce a fractional-order version of (1) using the Caputo fractional derivative. Following the approach in [3, 15], we generalize the model (1) by considering the following system

$$\begin{aligned} \begin{aligned}&^C_{0}D^{\alpha }_t S(t) = -\alpha _{SA}^{\alpha }SA - \beta ^{\alpha } SI + \sigma ^{\alpha } R,\\&^C_{0}D^{\alpha }_t I(t) = \beta ^{\alpha } SI - \alpha _{IA}^{\alpha }AI - \delta ^{\alpha } I,\\&^C_{0}D^{\alpha }_t R(t) = \delta ^{\alpha } I - \sigma ^{\alpha } R,\\&^C_{0}D^{\alpha }_t A(t) = \alpha _{SA}^{\alpha }SA + \alpha _{IA}^{\alpha }AI. \end{aligned} \end{aligned}$$
(3)

Note that all the integer-order derivatives in (1) are replaced by the Caputo fractional derivatives and each parameter \(*\) is replaced by \(*^{\alpha }\), respectively. This makes the fractional-order model more flexible. Here, the dimensions of the parameters have been adjusted to ensure that both sides of the system (3) have the same dimension (see [3, 15]).

A simple approach for explaining memory effects on the model (3) is the use of the Grunwald-Letnikov definition for the Caputo fractional derivative \(^C_{0}D^{\alpha }_t y(t)\). Suppose the function \(^C_{0}D^{\alpha }_t y(\tau )\) satisfies suitable smoothness conditions in every finite interval (0, t). We use a grid

$$\begin{aligned} 0 = \tau _0< \tau _1< \ldots < \tau _{n+1} = t = (n + 1)h, \qquad \tau _{n + 1} - \tau _n = h, \end{aligned}$$

and the classical notation of finite differences

$$\begin{aligned} \dfrac{1}{h^\alpha }\Delta ^{\alpha }_hy(t) = \dfrac{1}{h^{\alpha }}\Bigg (y(\tau _{n + 1}) - \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } y(\tau _{n + 1 - \nu })\Bigg ), \end{aligned}$$

where

$$\begin{aligned} c_\nu ^{\alpha } = (-1)^{\alpha - 1}\left( {\begin{array}{c}\alpha \\ \nu \end{array}}\right) , \end{aligned}$$

and

$$\begin{aligned} \left( {\begin{array}{c}\alpha \\ \nu \end{array}}\right) := \dfrac{\alpha (\alpha - 1)(\alpha - 2)\ldots (\alpha - \nu + 1)}{\nu !} \end{aligned}$$

is the usual notation for the binomial coefficients [43, p. 43]. Then, the Grunwald-Letnikov definition reads [43]

$$\begin{aligned} ^C_{0}D^{\alpha }_t y(t) = \lim _{h \rightarrow 0}\dfrac{1}{h^{\alpha }}\Delta ^{\alpha }_h y(t). \end{aligned}$$

Applying Grunwald-Letnikov definition to the model (3), we obtain

$$\begin{aligned} \begin{aligned}&^C_{0}D^{\alpha }_t S(t) = \lim _{h \rightarrow 0}\dfrac{1}{h^{\alpha }}\Bigg (S(\tau _{n + 1}) - \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } S(\tau _{n + 1 - \nu })\Bigg ) = -\alpha _{SA}^{\alpha }S(t)A(t) - \beta ^{\alpha } S(t)I(t) + \sigma ^{\alpha } R(t),\\&^C_{0}D^{\alpha }_t I(t) = \lim _{h \rightarrow 0}\dfrac{1}{h^{\alpha }}\Bigg (I(\tau _{n + 1}) - \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } I(\tau _{n + 1 - \nu })\Bigg ) = \beta ^{\alpha } S(t)I(t) - \alpha _{IA}^{\alpha }A(t)I(t) - \delta ^{\alpha } I(t),\\&^C_{0}D^{\alpha }_t R(t) = \lim _{h \rightarrow 0}\dfrac{1}{h^{\alpha }}\Bigg (R(\tau _{n + 1}) - \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } R(\tau _{n + 1 - \nu })\Bigg ) = \delta ^{\alpha } I(t) - \sigma ^{\alpha } R(t),\\&^C_{0}D^{\alpha }_t A(t) = \lim _{h \rightarrow 0}\dfrac{1}{h^{\alpha }}\Bigg (A(\tau _{n + 1}) - \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } A(\tau _{n + 1 - \nu })\Bigg ) = \alpha _{SA}^{\alpha }S(t)A(t) + \alpha _{IA}^{\alpha }A(t)I(t), \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned}&S(\tau _{n + 1}) \approx \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } S(\tau _{n + 1 - \nu }) + h^{\alpha }\Big [-\alpha _{SA}^{\alpha }S(\tau _{n+1})A(\tau _{n+1}) - \beta ^{\alpha } S(\tau _{n+1})I(\tau _{n+1}) + \sigma ^{\alpha } R(\tau _{n+1})\Big ],\\&I(\tau _{n + 1}) \approx \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } I(\tau _{n + 1 - \nu }) + h^{\alpha }\Big [\beta ^{\alpha } S(\tau _{n+1})I(\tau _{n+1}) - \alpha _{IA}^{\alpha }A(\tau _{n+1})I(\tau _{n+1}) - \delta ^{\alpha } I(\tau _{n+1})\Big ],\\&R(\tau _{n + 1}) \approx \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } R(\tau _{n + 1 - \nu }) + h^{\alpha }\Big [\delta ^{\alpha } I(\tau _{n+1}) - \sigma ^{\alpha } R(\tau _{n+1})\Big ],\\&A(\tau _{n + 1}) \approx \sum _{\nu = 1}^{n + 1}c_\nu ^{\alpha } A(\tau _{n + 1 - \nu }) + h^{\alpha }\Big [\alpha _{SA}^{\alpha }S(\tau _{n+1})A(\tau _{n+1}) + \alpha _{IA}^{\alpha }A(\tau _{n+1})I(\tau _{n+1})\Big ], \end{aligned} \end{aligned}$$

for h small enough. Hence, to determine the value of \(\big (S(\tau _{n+1}),\,\,I(\tau _{n+1}),\,\,R(\tau _{n+1}),\,\,A(\tau _{n+1})\big )\) we must use all the past values of \(\big (S(\tau _{j}),\,\,I(\tau _{j}),\,\,R(\tau _{j}),\,\,A(\tau _{j})\big )\) for \(j = 0, 1, \ldots , n\).

Note that it follows from the original ODE model (1) (corresponding to \(\alpha = 1\)) that

$$\begin{aligned} \begin{aligned}&S(\tau _{n + 1}) \approx S(\tau _n) + h\Big [-\alpha _{SA}S(\tau _{n})A(\tau _{n}) - \beta S(\tau _{n})I(\tau _{n}) + \sigma R(\tau _{n})\Big ],\\&I(\tau _{n + 1}) \approx I(\tau _n) + h\Big [\beta S(\tau _{n})I(\tau _{n}) - \alpha _{IA}A(\tau _{n})I(\tau _{n}) - \delta I(\tau _{n})\Big ],\\&R(\tau _{n + 1}) \approx R(\tau _n) + h\Big [\delta I(\tau _{n}) - \sigma R(\tau _{n})\Big ],\\&A(\tau _{n + 1}) \approx A(\tau _n) + h\Big [\alpha _{SA}S(\tau _{n})A(\tau _{n}) + \alpha _{IA}A(\tau _{n})I(\tau _{n})\Big ] \end{aligned} \end{aligned}$$

for h small enough. So, \(\big (S(\tau _{n}),\,\,I(\tau _{n}),\,\,R(\tau _{n}),\,\,A(\tau _{n})\big )\) is sufficient to compute \(\big (S(\tau _{n+1}),\,\,I(\tau _{n+1}),\,\,R(\tau _{n+1}),\,\,A(\tau _{n+1})\big )\).

We now focus on the positivity, linear invariant and equilibria of (3). Note that thanks to Theorem 3.1 and Remark 3.2 in [35], we obtain the existence and uniqueness of solutions of the system (3).

Theorem 5

(Positivity and linear invariant) The set

$$\begin{aligned} \Omega ^T:= \Big \{(S, I, R, A)\big |S, I, R, A \ge 0;\,\,S + I + R + A = T\Big \} \end{aligned}$$
(4)

is a positively invariant set of the model (3), that is, \(\big (S(t),\, I(t),\, R(t),\, A(t)\big ) \in \Omega ^T\) for all \(t > 0\) if \(\big (S(0),\, I(0),\, R(0),\, A(0)\big ) \in \Omega ^T\).

Proof

First, the system (3) implies that

$$\begin{aligned} _0^C D_t^{\alpha } S\Big |_{S = 0} = \sigma ^{\alpha } R,\quad _0^C D_t^{\alpha } I\Big |_{I = 0} = 0,\quad _0^C D_t^{\alpha } R\Big |_{R = 0} = \delta ^{\alpha } I,\quad _0^C D_t^{\alpha } I\Big |_{A = 0} = 0. \end{aligned}$$

Let \(\big (S(0),\, I(0),\, R(0),\, A(0)\big )\) be any initial data with \(S(0), I(0), R(0), A(0) \ge 0\). Then, the corresponding solution \(\big (S(t),\, I(t),\, R(t),\, A(t)\big )\) cannot escape from the hyperplanes of \(S = 0\), \(I = 0\), \(R = 0\) and \(A = 0\), and on each hyperplane the vector field is tangent to that hyperplane or points toward the interior of \(\mathbb {R}^4_+\). This means that \(S(t), I(t), R(t), A(t) \ge 0\) for \(t > 0\).

Let \(\big (S(0), I(0), R(0), A(0)\big )\) be any initial data belonging to the set \(\Omega ^T\). Set \(T(t) = S(t) + I(t) + R(t) + A(t)\) for \(t \ge 0\). Adding side-by-side the 1st, 2nd, 3rd and 4th equations of (3), we obtain

$$\begin{aligned} _0^C D_t^{\alpha }T(t) = 0, \quad T(0) = T. \end{aligned}$$

This equation has a unique solution, that is, \(T(t) = T\). Hence, \(S(t) + I(t) + R(t) + A(t) = T\) for \(t \ge 0\). The proof is complete. \(\square\)

To determine the set of equilibria of the model (3), we consider the following system

$$\begin{aligned} \begin{aligned}&-\alpha _{SA}^{\alpha }SA - \beta ^{\alpha } SI + \sigma ^{\alpha } R = 0,\\&\beta ^{\alpha } SI - \alpha _{IA}^{\alpha }AI - \delta ^{\alpha } I = 0,\\&\delta ^{\alpha } I - \sigma ^{\alpha } R = 0,\\&\alpha _{SA}^{\alpha }SA + \alpha _{IA}^{\alpha }AI = 0. \end{aligned} \end{aligned}$$

Thanks to the results established in [41], we obtain three solutions of this system

$$\begin{aligned} \begin{aligned}&(S, I, R, A) = (0,\, 0,\, 0,\, T),\\&(S, I, R, A) = (T,\, 0,\, 0, 0),\\&(S, I, R, A) = \bigg (\dfrac{\delta ^{\alpha }}{\beta ^{\alpha }},\,\dfrac{T - (\delta /\beta )^{\alpha }}{1 + (\delta /\sigma )^{\alpha }},\, \dfrac{T - (\delta /\beta )^{\alpha }}{1 + (\sigma /\delta )^{\alpha }},\,0\bigg ), \end{aligned} \end{aligned}$$

which form the set of equilibria of (3).

Proposition 1

(Equilibria) The model (3) always has two disease-free equilibrium points, which are given by

$$\begin{aligned} \begin{aligned}&\mathcal {E}_1^0 = (S, I, R, A) = (0, 0, 0, T),\\&\mathcal {E}_2^0 = (S, I, R, A) = (T, 0, 0, 0). \end{aligned} \end{aligned}$$

Meanwhile, a unique disease-endemic equilibrium point exists if and only if \(T\beta ^{\alpha } > \delta ^{\alpha }\). If existing, it is defined by

$$\begin{aligned} \mathcal {E}^* = (S, I, R, A) = \bigg (\dfrac{\delta ^{\alpha }}{\beta ^{\alpha }},\,\dfrac{T - (\delta /\beta )^{\alpha }}{1 + (\delta /\sigma )^{\alpha }},\, \dfrac{T - (\delta /\beta )^{\alpha }}{1 + (\sigma /\delta )^{\alpha }},\,0\bigg ). \end{aligned}$$

3.2 Stability analysis

In this subsection, we investigate the GAS and uniform stability of the fractional-order model (3).

As an important consequence of Theorem 5, we only need to study dynamics of the following sub-model

$$\begin{aligned} \begin{aligned} \begin{aligned}&^C_{0}D^{\alpha }_t S = -\alpha _{SA}^{\alpha }S(T - S - I - R) - \beta ^{\alpha } SI + \sigma ^{\alpha } R,\\&^C_{0}D^{\alpha }_t I= \beta ^{\alpha } SI - \alpha _{IA}^{\alpha }(T - S - I - R)I - \delta ^{\alpha } I,\\&^C_{0}D^{\alpha }_t R= \delta ^{\alpha } I - \sigma ^{\alpha } R \end{aligned} \end{aligned} \end{aligned}$$
(5)

on its feasible set

$$\begin{aligned} \Omega ^* = \Big \{(S, I, R)\big |S, I, R\ge 0;\,\,S + I + R \le T\Big \}. \end{aligned}$$

Note that the representation \(A = T - S - I - R\) was used to obtain (5). On the set \(\Omega ^*\), the model (5) always possesses two disease-free equilibrium points, which are given by

$$\begin{aligned} \begin{aligned}&E_1^0 = (S, I, R) = (0, 0, 0),\\&E_2^0 = (S, I, R) = (T, 0, 0). \end{aligned} \end{aligned}$$

Also, a unique disease-endemic equilibrium point exists if and only if \(T\beta ^{\alpha } > \delta ^{\alpha }\). If existing, it is given by

$$\begin{aligned} E^* = (S, I, R) = \bigg (\dfrac{\delta ^{\alpha }}{\beta ^{\alpha }},\,\,\dfrac{T - (\delta /\beta )^{\alpha }}{1 + (\delta /\sigma )^{\alpha }},\,\, \dfrac{T - (\delta /\beta )^{\alpha }}{1 + (\sigma /\delta )^{\alpha }}\bigg ). \end{aligned}$$

Lemma 2

(Local asymptotic stability) The equilibrium point \(E_1^0\) of the model (5) is always locally asymptotically stable. Meanwhile, the equilibrium points \(E_2^0\) and \(E^*\) are always unstable.

Proof

It is important to remark that from the linearization theorem for fractional dynamical systems [33], it is sufficient to consider linearized equations around equilibria of the system (5).

The linearized equation around the equilibrium point \(E_1^0\) is given by

$$\begin{aligned} ^C_{0}D^{\alpha }_t Y(t) = J(E_1^0)Y(t), \end{aligned}$$

where \(Y(t) = \big (S(t),\, I(t),\, R(t)\big )^T\) and \(J(E_1^0)\) is the Jacobian matrix of (5) at \(E_1^0\), i.e.,

$$\begin{aligned} J(E_1^0) = \begin{pmatrix} -\alpha _{SA}^{\alpha }T&{}0&{}\sigma ^{\alpha }\\ &{}&{}\\ 0&{}-\alpha _{IA}^{\alpha }T - \delta ^{\alpha }&{}0,\\ &{}&{}\\ 0&{}\delta ^{\alpha }&{}-\sigma ^{\alpha }. \end{pmatrix} \end{aligned}$$

Consequently, all the eigenvalues of \(J(E_1^0)\) are

$$\begin{aligned} \lambda _1 = -\alpha _{SA}^{\alpha }T< 0, \quad \lambda _2 = -\alpha _{IA}^{\alpha }T - \delta ^{\alpha }< 0, \quad \lambda _3 = -\sigma ^{\alpha } < 0. \end{aligned}$$

By the stability results of linear systems [37], we conclude that \(E_1^0\) is always locally asymptotically stable.

Similarly, the Jacobian matrix of (5) at \(E_2^0\) is given by

$$\begin{aligned} J(E_2^0) = \begin{pmatrix} \alpha _{SA}^{\alpha }T&{}(\alpha _{SA}^{\alpha } - \beta ^{\alpha })T&{}\alpha _{SA}^{\alpha }T + \sigma ^{\alpha }\\ &{}&{}\\ 0&{}\beta ^{\alpha } T - \delta ^{\alpha }&{}0\\ &{}&{}\\ 0&{}\delta ^{\alpha }&{}-\sigma ^{\alpha } \end{pmatrix}. \end{aligned}$$

Hence, all the eigenvalues of \(J(E_2^0)\) are

$$\begin{aligned} \lambda _1 = \alpha _{SA}^{\alpha }T > 0, \quad \lambda _2 = \beta ^{\alpha } T - \delta ^{\alpha }, \quad \lambda _3 = -\sigma ^{\alpha }. \end{aligned}$$

This implies that \(E_2^0\) is always stable.

Finally, the Jacobian matrix of (5) at \(E^*\) is

$$\begin{aligned} J(E^*) = \begin{pmatrix} \alpha _{SA}^{\alpha }S^* - \beta ^{\alpha } I^*&{}\alpha _{SA}^{\alpha }S^* - \beta ^{\alpha } S^*&{}\alpha _{SA}^{\alpha }S^* + \sigma ^{\alpha }\\ &{}&{}\\ \beta ^{\alpha } I^* + \alpha _{IA}^{\alpha }I^*&{}\beta ^{\alpha } S^* + \alpha _{IA}^{\alpha }I^* - \delta ^{\alpha }&{}\alpha _{IA}^{\alpha }I^*\\ &{}&{}\\ 0&{}\delta ^{\alpha }&{}-\sigma ^{\alpha } \end{pmatrix}. \end{aligned}$$

Note that \(\beta ^{\alpha } S^* = \delta ^{\alpha }\). This implies that

$$\begin{aligned} J(E^*) = \begin{pmatrix} \alpha _{SA}^{\alpha }S^* - \beta ^{\alpha } I^*&{}\alpha _{SA}^{\alpha }S^* - \delta ^{\alpha }&{}\alpha _{SA}^{\alpha }S^* + \sigma ^{\alpha }\\ &{}&{}\\ \beta ^{\alpha } I^* + \alpha _{IA}^{\alpha }I^*&{}\alpha _{IA}^{\alpha }I^*&{}\alpha _{IA}^{\alpha }I^*\\ &{}&{}\\ 0&{}\delta ^{\alpha }&{}-\sigma ^{\alpha } \end{pmatrix}. \end{aligned}$$

The characteristic polynomial of \(J(E^*)\) is given by

$$\begin{aligned} \begin{aligned} P_{E^*}(\lambda )&= \det \big (J(E^*) - \lambda \mathbb {I}\big ) = \det \begin{pmatrix} \alpha _{SA}^{\alpha }S^* - \beta ^{\alpha } I^* - \lambda &{}\alpha _{SA}^{\alpha }S^* - \delta ^{\alpha }&{}\alpha _{SA}^{\alpha }S^* + \sigma ^{\alpha }\\ &{}&{}\\ \beta ^{\alpha } I^* + \alpha _{IA}^{\alpha }I^*&{}\alpha _{IA}^{\alpha }I^* - \lambda &{}\alpha _{IA}^{\alpha }I^*\\ &{}&{}\\ 0&{}\delta ^{\alpha }&{}-\sigma ^{\alpha } - \lambda \end{pmatrix}\\&= \det \begin{pmatrix} \alpha _{SA}^{\alpha }S^* + \alpha _{IA}^{\alpha }I^* - \lambda &{}\alpha _{SA}^{\alpha }S^* + \alpha _{IA}^{\alpha }I^* - \lambda &{}\alpha _{SA}^{\alpha }S^* + \alpha _{IA}^{\alpha }I^* - \lambda \\ &{}&{}\\ \beta ^{\alpha } I^* + \alpha _{IA}^{\alpha }S^*&{}\alpha _{IA}^{\alpha }I^* - \lambda &{}\alpha _{IA}^{\alpha }I^*\\ &{}&{}\\ 0&{}\delta ^{\alpha }&{}-\sigma ^{\alpha } - \lambda \end{pmatrix}. \end{aligned} \end{aligned}$$

Therefore, \(J(E^*)\) always has an eigenvalue given by

$$\begin{aligned} \lambda ^* = \alpha _{SA}^{\alpha }S^* + \alpha _{IA}^{\alpha }I^*. \end{aligned}$$

If \(E^*\) exists (\(T\beta ^{\alpha } > \delta ^{\alpha }\)), then \(S^*, I^* > 0\). So, \(\lambda ^* > 0\). Consequently, \(E^*\) is always unstable. The proof is complete. \(\square\)

Theorem 6

The equilibrium point \(E_1^0\) of the model (5) is not locally asymptotically stable but also globally asymptotically stable with respect to the set \(\Omega ^* - \{E_2^0,\,E^*\}\).

Proof

Consider a Lyapunov functions \(V: \Omega ^* \rightarrow \mathbb {R}\) defined by

$$\begin{aligned} V(S, I, R) = S + I + R. \end{aligned}$$
(6)

The Caputo fractional derivative of V along solutions of (5) satisfies

$$\begin{aligned} \begin{aligned} ^C_{0}D^{\alpha }_t V(S, I, R)&= {^C_{0}D^{\alpha }_t S} + {^C_{0}D^{\alpha }_t I} + ^C_{0}D^{\alpha }_t R\\&= \Big [-\alpha _{SA}^{\alpha }S(T - S - I - R) - \beta ^{\alpha } SI + \sigma ^{\alpha } R\Big ]\\&\quad + \Big [ \beta ^{\alpha } SI - \alpha _{IA}^{\alpha }(T - S - I - R)I - \delta ^{\alpha } I\Big ] + \big (\delta ^{\alpha } I - \sigma ^{\alpha } R\big )\\&= -\alpha _{SA}^{\alpha }(T - S - I - R)S - \alpha _{IA}^{\alpha }(T - S - I - R)I. \end{aligned} \end{aligned}$$
(7)

Note that all solutions of the system (5) are bounded. Therefore, applying the fractional Barbalat’s lemma (Corollary 1), we obtain

$$\begin{aligned} \lim _{t \rightarrow \infty }\big (S(t),\, I(t),\, R(t)\big ) = E_1^0. \end{aligned}$$

Combining this with the local stability of \(E_1^0\) established in Lemma 2, the GAS of \(E_1^0\) is proved. The proof is completed. \(\square\)

As a consequence of Theorem 6, we also obtain the uniform stability of \(E_1^0\) as follows.

Corollary 2

The equilibrium point \(E_1^0\) of the model (5) is uniform stable.

Proof

Consider the Lyapunov function given by (6). Note that

$$\begin{aligned} \dfrac{1}{T}(S^2 + I^2 + R^2) \le V(S, I, R) = S + I + R \le \sqrt{3}\sqrt{S^2 + I^2 + R^2} \end{aligned}$$

for all \((S, I, R) \in \Omega ^*\). Therefore, we have

$$\begin{aligned} \gamma _1(\Vert y\Vert ) \le V(y) \le \gamma _2(\Vert y\Vert ), \end{aligned}$$

where

$$\begin{aligned} y = \big (S,\,I,\,R\big )^T, \quad \Vert y\Vert = \sqrt{S^2 + I^2 + R^2}, \quad \gamma _1(z) = \dfrac{z^2}{T}, \quad \gamma _2(z) = \sqrt{3}z. \end{aligned}$$

Furthermore, the estimate (7) implies that

$$\begin{aligned} ^C_{0}D^{\alpha }_t V \le 0. \end{aligned}$$

Hence, the function V satisfies Theorem 2. Consequently, the uniform stability of \(E_1^0\) is proved. The proof is complete. \(\square\)

3.3 Dynamics of the fractional-order model

Summarizing the results constructed in Subsections 3.1 and 3.2, we obtain the dynamics of the original fractional-order model (3) as follows.

Theorem 7

(Dynamical analysis of the fractional-order model (3))

  1. (i)

    The set \(\Omega ^T\) given by (4) is a positively invariant set of the model (3).

  2. (ii)

    The model (3) always possesses the disease-free equilibrium points \(\mathcal {E}_1^0\) and \(\mathcal {E}_2^0\) for all the values of the parameters. Additionally, the unique disease-endemic equilibrium point \(\mathcal {E}^*\) exists if and only if \(T\beta ^{\alpha } > \delta ^{\alpha }\).

  3. (iii)

    The equilibrium point \(\mathcal {E}_1^0\) is always locally asymptotically stable, meanwhile, the equilibrium points \(\mathcal {E}_2^0\) and \(\mathcal {E}^*\) are always unstable.

  4. (iv)

    The equilibrium point \(\mathcal {E}_1^0\) is always globally asymptotically stable and uniformly stable.

By using the Lyapunov functions proposed in Subsection 3.2 and Theorem 4, we obtain the Mittag-Leffler stability of the model (3).

Corollary 3

The equilibrium point \(\mathcal {E}_1^0\) is also Mittag-Leffler stable.

Remark 1

From the GAS of the fractional-order model (3) we also obtain the GAS of the original ODE model (1). This provides an improvement for the results constructed in the benchmark work [41].

4 Numerical experiments

In this section, we conduct a set of numerical simulations to support the theoretical findings.

Example 1

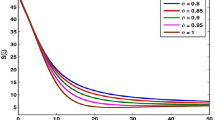
(Dynamics of the fractional-order model) In this example, we observe the behaviour of the fractional-order model to confirm its stability properties. For this purpose, consider the model (3) with parameters given in Table 1.

Table 1 The parameters in numerical experiments
Full size table

The solutions of the fractional-order model (5) generated by the explicit fractional Euler method (see [31, 32]) are depicted in Figs. 1, 2, 3, 4, 5. In these figures, each blue curve represents a phase space corresponding to a specific initial data, the green arrows show the evolution of the model and the color circles indicate the position of the existing equilibrium points. It is clear that all the solutions are stable and converge to the equilibrium point \(E_1^0\). Moreover, the dynamics of the model is confirmed.

Fig. 1
figure 1

The phase spaces of the fractional-order model (5) in Case 1

Full size image
Fig. 2
figure 2

The phase spaces of the fractional-order model (5) in Case 2

Full size image
Fig. 3
figure 3

The phase spaces of the fractional-order model (5) in Case 3

Full size image
Fig. 4
figure 4

The phase spaces of the fractional-order model (5) in Case 4

Full size image
Fig. 5
figure 5

The phase spaces of the fractional-order model (5) in Case 5

Full size image

It is observed from the numerical results in Example 1 that the behaviour of the model (3) depends on \(\alpha\). This means that the fractional-order model (\(\alpha \in (0, 1]\)) is more flexible than the ODE one (\(\alpha = 1\)). On the other hand, the appearance of \(\alpha\) may be useful in studying the parameter estimation problem since it expands the space of parameters and can provide more computer virus spread scenarios. In order to support this assertion, let us consider the following simple example with synthetic data set.

Example 2

(Numerical simulation with synthetic data) Assume that we observe the numbers of computers of the groups S, I, R and A in a system at some points in a time period and the observations are recorded in Table 2.

Table 2 Synthetic data used in numerical simulation
Full size table

Assume that we have obtained the following set of parameters for the fractional-order model (3):

$$\begin{aligned} \beta = 0.1,\quad \delta = 25, \quad \alpha _{SA} = 0.025, \quad \alpha _{IA} = 0.25, \quad \sigma = 75, \quad T = 100. \end{aligned}$$
(8)

Our task now is to choose suitable values of \(\alpha\) such that the solutions of the fractional-order model fit with the synthetic data as much as possible. Figures 6, 7, 8, 9 depict the behavior of the model (3) corresponding to three different values of \(\alpha\), namely, \(\alpha \in \{0.85,\,0.9,\,1.0\}\). From these figures, we see that \(\alpha = 0.85\) and \(\alpha = 0.9\) (fractional order) are better than \(\alpha = 1\) (integer order) and \(\alpha = 0.85\) is the best. This shows the role of \(\alpha\) in the parameter estimation.

This example only works with synthetic data since real data is not available. However, it has shown one of the main advantage of the fractional-order model over the integer-order one. This agrees with an analysis of a fractional-order model using real data of dengue fever, which was performed in [15].

Fig. 6
figure 6

The S-component of the fractional-order model versus the synthetic data

Full size image
Fig. 7
figure 7

The I-component of the fractional-order model versus the synthetic data

Full size image
Fig. 8
figure 8

The R-component of the fractional-order model versus the synthetic data

Full size image
Fig. 9
figure 9

The A-component of the fractional-order model versus the synthetic data

Full size image

5 Conclusions and remarks

In this work, a fractional-order epidemiological model for computer viruses, which is derived from the well-known integer-order epidemiological model (1) and the Caputo fractional derivative, has been considered to analyze memory effects on population dynamics. The positivity, linear invariant, stability properties of the fractional-order model have been analyzed rigorously. It should be emphasized that the stability properties are investigated by using an appropriate linear Lyapunov function in combination with stability theory for fractional dynamical systems. The main result is that the dynamical properties of the fractional-order model have been determined fully. Also, the present approach can be extended to study fractional versions of the model (1) in the context of other fractional derivative operators. Finally, a set of numerical experiments is conducted to support the theoretical findings. The experiments show that there is a good agreement between the numerical results and theoretical ones.

In the near future, we will study applications of the proposed fractional-order model in real-world situations. The present approach will be extended to investigate dynamics of the original ODE model (1) in the context of other fractional derivatives. In addition, numerical methods preserving the mathematical features of the model will also be considered.