New Aspects of Fractional Epidemiological Model for Computer Viruses with Mittag–Leffler Law

Abstract

In this work, we examine a fractional epidemiological model with strong memory effects. We use a fractional derivative with Mittag–Leffler-type kernel to moderate the epidemiological model to narrate the spreading and controlling of the computer viruses. We obtain the solution of the mathematical model by using q-HATM. The existence and uniqueness of the solution of the epidemiological model for computer viruses are examined by employing the fixed-point theory. Finally, to demonstrate the outcomes of the investigation, some graphical results are presented.

1 Introduction

In recent years, computer virus is a major problem in hardware and software technology. The computer virus is a particular kind of computer program which propagates itself and spreads from one computer to another. The file system generally damaged by the viruses and worms employs system vulnerability to look and attack computers. Consequently, for improving the safety and reliability in the computer setups and networks, the test on excellent examination of the computer virus spreading dynamical process is an important instrument. There are mainly two methods to examine the considered problem similar to the biological viruses as microscopic and macroscopic mathematical models. To describe and control the spreading of computer virus, many engineers and scientists suggested several ways to formulate mathematical models [1–18]. In recent work, Singh et al. [19] have reported a new mathematical model for describing spreading of computer virus by making use of a new fractional derivative with the exponential kernel. Fractional order calculus (FOC) has been employed to formulate the mathematical models of real-life problems. Nowadays, the FOC is acting a pivotal role in the areas of physics, computer science, chemistry, earth science, economics, etc. In recent years, many mathematicians and scientists paid their attention in this very special branch of mathematical analysis [20–32]. In 2016, Atangana–Baleanu (AB) fractional derivative was studied by Atangana and Baleanu [33] connected with the Mittag–Leffler function in its kernel. The AB fractional derivative has been used in describing various physical problems such as mathematical model of exothermic reactions having fixed heat source in porous media [34], Biswas–Milovic model in optical communications [35], regularized long-wave equation in plasma waves [36], Fornberg–Whitham equation in wave breaking [37], rumor spreading dynamical model [38], dynamical system for competition between commercial and rural banks in Indonesia [39], etc.

The principal aim of the present study is to suggest a novel epidemiological model for describing the spreading for computer viruses with Mittag–Leffler-type memory. A new numerical algorithm, namely q-HATM [40, 41] is used for solving the epidemiological model of arbitrary order for computer viruses associated with Mittag–Leffler-type kernel. The q-HATM is the combination of q-homotopy analysis method (q-HAM) [42, 43] and Laplace transform method [44,45,46,47].

Motivated and very useful consequences of fractional operators in mathematical modeling of real word problems, we present a fractional modified epidemiological model (FMEM) for computer viruses. The key aim of this investigation is to apply a novel fractional operator in describing the spreading of viruses in computers. The existence and uniqueness of the solution of the FMEM for computer viruses are investigated by using the concept of the well-known fixed-point theory. The article is organized as follows: Sect. 2 presents the key results related to AB fractional derivative. Section 3 is dedicated to the fractional modeling of computer viruses. In Sect. 4, we report the existence and uniqueness of the solution of the FMEM for computer viruses. In Sect. 5, the efficiency of q-HATM is used to obtain the analytical solution of the FMEM for computer viruses. Section 6 reports the numerical results and discussions. Section 7, which is the last portion of the article, points out the conclusions.

2 The AB Fractional Derivative and Its Properties

Definition 2.1

Assume that $S \in H^{1} (\alpha ,\beta ),\,\beta > \alpha ,\,\kappa \in (0,1]$ and differentiable, then the AB fractional derivative in terms of Caputo is presented as [33]

$$ {}_{\quad\alpha }^{\,ABC} D_{\tau }^{\kappa } \left( {S(\tau )} \right) = \frac{B(\kappa )}{1 - \kappa }\int\limits_{\alpha }^{\tau } {S^{\prime } } (\eta )E_{\kappa } \left[ { - \frac{\kappa }{1 - \kappa }(\tau - \eta )^{\kappa } } \right]{\text{d}}\eta . $$

(1)

In Eq. (1), $B(\kappa )$ is satisfying the property $B(0) = B(1) = 1$.

Definition 2.2

Let $S \in H^{1} (\alpha ,\beta ),\,\beta > \alpha ,\,\kappa \in (0,1]$ and non-differentiable, then the AB fractional derivative in Riemann–Liouville sense is presented as [33]

$$ {}_{\quad\alpha }^{\,ABR} D_{\tau }^{\kappa } \left( {S(\tau )} \right) = \frac{B(\kappa )}{1 - \kappa }\frac{\text{d}}{{{\text{d}}\tau }}\int\limits_{\alpha }^{\tau } {S(\eta )E_{\kappa } \left[ { - \frac{\kappa }{1 - \kappa }(\tau - \eta )^{\kappa } } \right]} {\text{d}}\eta . $$

(2)

Definition 2.3

Consider $0 < \kappa < 1$, and S be a function of $\tau$, then the fractional integral operator associated with AB fractional derivative of order $\kappa$ is drafted as [33]

$$ {}_{\;\;\,0}^{AB} I_{\tau }^{\kappa } \left( {S(\tau )} \right) = \frac{(1 - \kappa )}{B(\kappa )}S(\tau ) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {S(\vartheta )} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta ,\quad \tau \ge 0. $$

(3)

3 FMEM of Computer Viruses with Mittag–Leffler Memory

In this section, we extend the epidemiological model for computer viruses formulated by Piqueira and Araujo [5] by using the theory of AB fractional derivative to induce the strong memory in the model description. Here, we denote the total population by T. We divide the total population T into the following four categories:

• Category I: The number of computers which are not infected is inclined to probable infection and is indicated by the symbol $S(\tau ).$

• Category II: The number of computers which are not infected is associated with the anti-virus and represented by the symbol $A(\tau ).$

• Category III: The number of computers which are infected by virus is denoted by the symbol $I(\tau ).$

• Category IV: The number of removed computers because of infection or not is represented by the symbol $R(\tau ).$

In the mathematical formulation of the problem, the influx parameter mortality parameters are taken in the following manner:

$\varpi$ indicates the influx rate, which is representing the involvement of novel computers to the interconnected system, and $\theta$ stands for the proportion coefficient connected to the mortality rate, not due to the virus.

In order to decorate the magnificent report with infected ones, the susceptible category $S(\tau )$ is converted into the infected category with a rate that is pertaining to the chance of susceptible computers. Consequently, $\xi$ represents the equivalent factor and this rate is straightforwardly equivalent to the multiplication of $S(\tau )$ and $I(\tau ).$ The conversion of susceptible into antidotal is straightforwardly equivalent to the product of $S(\tau )$ and $A(\tau )$ with the equivalent factor represented via $\mu_{SA}$. On making use of the anti-virus programs, the computers affected by virus can be got back to normal ones and being converted in the antidotal one with a rate straightforwardly equivalent to the product of $A(\tau )$ and $I(\tau )$ with the equivalent factor indicated via $\mu_{IA}$. Here, we indicate the rate of reducing the computer into the useless and computer is removed from the system by the symbol $\varepsilon$, while we represent the proportion factor of the computers that can be restored and converted into the susceptible category by the symbol $\rho$.

The dynamical process of the spreading of the infection of a recognized virus is investigated with the aid of the present approach and, so, the conversion of antidotal into infected is not studied. Consequently, a scheme of vaccination can be described, and a cost-effective application of anti-virus programs can be clarified with the help of the understudy model.

Considering all these suppositions, the mathematical representations can be presented in the following manner

$$ \begin{aligned} \frac{{{\text{d}}S(\tau )}}{{{\text{d}}\tau }} & = \varpi - \mu_{SA} S(\tau )A(\tau ) - \xi S(\tau )I(\tau ) - \theta S(\tau ) + \rho R(\tau ), \\ \frac{{{\text{d}}I(\tau )}}{d\tau } & = \xi S(\tau )I(\tau ) - \mu_{IA} A(\tau )I(\tau ) - \varepsilon I(\tau ) - \theta I(\tau ), \\ \frac{{{\text{d}}R(\tau )}}{{{\text{d}}\tau }} & = \varepsilon I(\tau ) - \rho R(\tau ) - \theta R(\tau ), \\ \frac{{{\text{d}}A(\tau )}}{{{\text{d}}\tau }} & = \mu_{SA} S(\tau )A(\tau ) + \mu_{IA} A(\tau )I(\tau ) - \theta A(\tau ). \\ \end{aligned} $$

(4)

In considered model, the influx rate is investigated to be $\varpi = 0$, as action of viruses is very fast than the extension of system, so it is assumed that no new computer is involved in the system all the while the spreading of the assessed virus. On the similar manner, the fraction coefficient is taken to be $\theta = 0$, supposing that the machine obsolescence time is very bigger than the time of the virus movement.

Consequently, mathematical model (4) becomes as follows:

$$ \begin{aligned} \frac{{{\text{d}}S(\tau )}}{{{\text{d}}\tau }} & = - \mu_{SA} S(\tau )A(\tau ) - \xi S(\tau )I(\tau ) + \rho R(\tau ), \\ \frac{{{\text{d}}I(\tau )}}{{{\text{d}}\tau }} & = \xi S(\tau )I(\tau ) - \mu_{IA} A(\tau )I(\tau ) - \varepsilon I(\tau ), \\ \frac{{{\text{d}}R(\tau )}}{{{\text{d}}\tau }} & = \varepsilon I(\tau ) - \rho R(\tau ), \\ \frac{{{\text{d}}A(\tau )}}{{{\text{d}}\tau }} & = \mu_{SA} S(\tau )A(\tau ) + \mu_{IA} A(\tau )I(\tau ). \\ \end{aligned} $$

(5)

It is well known that the mathematical models with classical derivatives do not carry the memory of the system, so we extend the mathematical model (5) with the aid of AB fractional derivative, then it reduces as follows:

$$ \begin{array}{*{20}l} {_{0}^{ABC} D_{\tau }^{\kappa } S(\tau ) = - \mu_{SA} S(\tau )A(\tau ) - \xi S(\tau )I(\tau ) + \rho R(\tau ),} \hfill \\ {_{0}^{ABC} D_{\tau }^{\kappa } I(\tau ) = \xi S(\tau )I(\tau ) - \mu_{IA} A(\tau )I(\tau ) - \varepsilon I(\tau ),} \hfill \\ {_{0}^{ABC} D_{\tau }^{\kappa } R(\tau ) = \varepsilon I(\tau ) - \rho R(\tau ),} \hfill \\ {_{0}^{ABC} D_{\tau }^{\kappa } A(\tau ) = \mu_{SA} S(\tau )A(\tau ) + \mu_{IA} A(\tau )I(\tau ).} \hfill \\ \end{array} $$

(6)

The initial conditions associated with fractional model (6) are presented as

$$ S = \alpha_{1} ,\quad I = \alpha_{2} ,\quad R = \alpha_{3} \quad {\text{and}}\quad A = \alpha_{4} \quad {\text{at}}\,\tau = 0. $$

(7)

In this investigation, we have taken $T(\tau ) = S(\tau ) + I(\tau ) + R(\tau ) + A(\tau )$ to be fixed at a time $\tau$. We suppose that $\Psi$ stands for the Banach space of continuous real-valued functions over the interval $\Delta$ having the norm

$$ \left\| {(S(\tau ),I(\tau ),R(\tau ),A(\tau ))} \right\| = \left\| {S(\tau )} \right\| + \left\| {I(\tau )} \right\| + \left\| {R(\tau )} \right\| + \left\| {A(\tau )} \right\|. $$

(8)

In Eq. (8), $\left\| {S(\tau )} \right\| = \sup \left\{ {\left| {S(\tau ):\tau \in \Delta } \right|} \right\}$, $\left\| {I(\tau )} \right\| = \sup \left\{ {\left| {I((\tau ):\tau \in \Delta } \right|} \right\}$, $\left\| {R(\tau )} \right\| = \sup \left\{ {\left| {R(\tau ):\tau \in \Delta } \right|} \right\}$ and $\left\| {A(\tau )} \right\| = \sup \left\{ {\left| {A(\tau ):\tau \in \Delta } \right|} \right\}$. Specially $\Psi = C(\Delta ) \times C(\Delta ) \times C(\Delta ) \times C(\Delta )$, here $C(\Delta )$ is the Banach space of continuous $\Re$ valued functions on the interval $\Delta$ possessing the sup norm.

4 Existence and Uniqueness of a Solution of FMEM for Computer Viruses with Mittag–Leffler Memory

In the present part, we investigate the existence of the solution with the help of the concept of the well-known fixed-point approach.

Firstly, we employ the fractional integral operator on the fractional order model (6), and it gives

$$ \begin{array}{*{20}l} {S(\tau ) - S(0) = {}_{\;\;\,0}^{AB} I_{\tau }^{\kappa } \left\{ { - \mu_{SA} S(\tau )A(\tau ) - \xi S(\tau )I(\tau ) + \rho R(\tau )} \right\},} \hfill \\ {I(\tau ) - I(0) = {}_{\;\;\,0}^{AB} I_{\tau }^{\kappa } \left\{ {\xi S(\tau )I(\tau ) - \mu_{IA} A(\tau )I(\tau ) - \varepsilon I(\tau )} \right\},} \hfill \\ {R(\tau ) - R(0) = {}_{\;\;\,0}^{AB} I_{\tau }^{\kappa } \left\{ {\varepsilon I(\tau ) - \rho R(\tau )} \right\},} \hfill \\ {A(\tau ) - A(0) = {}_{\;\;\,0}^{AB} I_{\tau }^{\kappa } \left\{ {\mu_{SA} S(\tau )A(\tau ) + \mu_{IA} A(\tau )I(\tau )} \right\}.} \hfill \\ \end{array} $$

(9)

On using the representation given in Eq. (3), it reduces to the following system

$$ \begin{aligned} S(\tau ) - S(0) & = \frac{(1 - \kappa )}{B(\kappa )}\left\{ { - \mu_{SA} S(\tau )A(\tau ) - \xi S(\tau )I(\tau ) + \rho R(\tau )} \right\} \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int_{0}^{\tau } {\left\{ { - \mu_{SA} S(\vartheta )A(\vartheta ) - \xi S(\vartheta )I(\vartheta ) + \rho R(\vartheta )} \right\}} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta , \\ I(\tau ) - I(0) & = \frac{(1 - \kappa )}{B(\kappa )}\left\{ {\xi S(\tau )I(\tau ) - \mu_{IA} A(\tau )I(\tau ) - \varepsilon I(\tau )} \right\} \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int_{0}^{\tau } {\left\{ {\xi S(\vartheta )I(\vartheta ) - \mu_{IA} A(\vartheta )I(\vartheta ) - \varepsilon I(\vartheta )} \right\}(\tau - \vartheta )^{\kappa - 1} } {\text{d}}\vartheta , \\ R(\tau ) - R(0) & = \frac{(1 - \kappa )}{B(\kappa )}\left\{ {\varepsilon I(\tau ) - \rho R(\tau )} \right\} \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int_{0}^{\tau } {\left\{ {\varepsilon I(\vartheta ) - \rho R(\vartheta )} \right\}(\tau - \vartheta )^{\kappa - 1} } {\text{d}}\vartheta , \\ A(\tau ) - A(0) & = \frac{(1 - \kappa )}{B(\kappa )}\left\{ {\mu_{SA} S(\tau )A(\tau ) + \mu_{IA} A(\tau )I(\tau )} \right\} \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int_{0}^{\tau } {\left\{ {\mu_{SA} S(\vartheta )A(\vartheta ) + \mu_{IA} A(\tau )I(\vartheta )} \right\}} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta . \\ \end{aligned} $$

(10)

In order to clarify the system, we use the subsequent notations

$$ \begin{array}{*{20}l} {\Omega _{1} (\tau ,S) = - \mu_{SA} S(\tau )A(\tau ) - \xi S(\tau )I(\tau ) + \rho R(\tau ),} \hfill \\ {\Omega _{2} (\tau ,I) = \xi S(\tau )I(\tau ) - \mu_{IA} A(\tau )I(\tau ) - \varepsilon I(\tau ),} \hfill \\ {\Omega _{3} (\tau ,R) = \varepsilon I(\tau ) - \rho R(\tau ),} \hfill \\ {\Omega _{4} (\tau ,A) = \mu_{SA} S(\tau )A(\tau ) + \mu_{IA} A(\tau )I(\tau ).} \hfill \\ \end{array} $$

(11)

Theorem 4.1

The kernels $\Omega _{1} (\tau ,S),\Omega _{2} (\tau ,I),\Omega _{3} (\tau ,R)$ and $\Omega _{4} (\tau ,A)$ fulfill the Lipschitz condition and contraction if the subsequent result is satisfied

$$ 0 \le \left( {\mu_{SA} \beta_{4} + \xi \beta_{2} } \right) < 1. $$

(12)

Proof We initiate with $\Omega _{1} (\tau ,S)$. Let $S(\tau )$ and $S^{*} (\tau )$ are two functions, then we get

$$ \left\| {\varOmega_{1} (\tau ,S) - \varOmega_{1} (\tau ,S^{*} )} \right\| = \left\| { - \mu_{SA} \left\{ {S(\tau ) - S^{*} (\tau )} \right\}A(\tau ) - \xi \left\{ {S(\tau ) - S^{*} (\tau )} \right\}I(\tau )} \right\|. $$

(13)

On utilizing of the inequality of triangular on Eq. (13), it gives

$$ \begin{aligned} \left\| {\Omega _{1} (\tau ,S) -\Omega _{1} (\tau ,S^{*} )} \right\| & \le \left\| {\mu_{SA} \left\{ {S(\tau ) - S^{*} (\tau )} \right\}A(\tau )} \right\| + \left\| {\beta \left\{ {S(\tau ) - S^{*} (\tau )} \right\}I(\tau )} \right\| \\ & \le \left\{ {\mu_{SA} \beta_{4} + \xi \beta_{2} } \right\}\left\| {S(\tau ) - S^{*} (\tau )} \right\| \\ & \le \lambda_{1} \left\| {\left( {S(\tau ) - S^{*} (\tau )} \right)} \right\|. \end{aligned} $$

(14)

Letting $\lambda_{1} = \mu_{SA} \beta_{4} + \xi \beta_{2}$, where $\left\| {S(\tau )} \right\| \le \beta_{1} ,\,\left\| {I(\tau )} \right\| \le \beta_{2} ,\left\| {R(\tau )} \right\| \le \beta_{3}$ and $\left\| {A(\tau )} \right\| \le \beta_{4}$ are bounded functions, then Eq. (14) gives

$$ \left\| {\Omega _{1} (\tau ,S) -\Omega _{1} (t,S^{*} )} \right\| \le \lambda_{1} \left\| {S(\tau ) - S^{*} (\tau )} \right\|. $$

(15)

Thus, the $\Omega _{1} (\tau ,S)$ satisfy the Lipschitz condition and if $0 \le \mu_{SA} \beta_{4} + \xi \beta_{2} < 1$, then it is also a contraction.

In the similar way, we can easily prove the following results

$$ \begin{array}{*{20}l} {\left\| {\Omega _{2} (\tau ,I) -\Omega _{2} (\tau ,I^{*} )} \right\| \le \lambda_{2} \left\| {I(\tau ) - I^{*} (\tau )} \right\|,} \hfill \\ {\left\| {\Omega _{3} (\tau ,R) -\Omega _{3} (\tau ,R^{*} )} \right\| \le \lambda_{3} \left\| {R(\tau ) - R^{*} (\tau )} \right\|,} \hfill \\ {\left\| {\Omega _{4} (\tau ,A) -\Omega _{4} (\tau ,A^{*} )} \right\| \le \lambda_{4} \left\| {A(\tau ) - A^{*} (\tau )} \right\|.} \hfill \\ \end{array} $$

(16)

On making use of the abovementioned kernels, Eq. (10) reduces as follows:

$$ \begin{array}{*{20}l} {S(\tau ) = S(0) + \frac{(1 - \kappa )}{B(\kappa )}\Omega _{1} (\tau ,S) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\Omega _{1} (\vartheta ,S)} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta ,} \hfill \\ {I(\tau ) = I(0) + \frac{(1 - \kappa )}{B(\kappa )}\Omega _{2} (\tau ,I) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\Omega _{2} (\vartheta ,I)} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta ,} \hfill \\ \begin{aligned} R(\tau ) = R(0) + \frac{(1 - \kappa )}{B(\kappa )}\Omega _{3} (\tau ,R) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\Omega _{3} (\vartheta ,R)(\tau - \vartheta )^{\kappa - 1} } {\text{d}}\vartheta , \hfill \\ A(\tau ) = A(0) + \frac{(1 - \kappa )}{B(\kappa )}\Omega _{4} (\tau ,A) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\Omega _{4} (\vartheta ,A)} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta . \hfill \\ \end{aligned} \hfill \\ \end{array} $$

(17)

Now, we present the following recursive formula

$$ \begin{array}{*{20}l} {S_{n} (\tau ) = \frac{(1 - \kappa )}{B(\kappa )}\Omega _{1} (\tau ,S_{n - 1} ) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\Omega _{1} (y,S{}_{n - 1})(\tau - \vartheta )^{\kappa - 1} } {\text{d}}y,} \hfill \\ {I_{n} (\tau ) = \frac{(1 - \kappa )}{B(\kappa )}\Omega _{2} (\tau ,I_{n - 1} ) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\Omega _{2} (\vartheta ,I{}_{n - 1})} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta ,} \hfill \\ R_{n} (\tau ) = \frac{(1 - \kappa )}{B(\kappa )}\Omega _{3} (\tau ,R_{n - 1} ) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\Omega _{3} (\vartheta ,R{}_{n - 1})} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta , \hfill \\ A_{n} (\tau ) = \frac{(1 - \kappa )}{B(\kappa )}\Omega _{4} (\tau ,A_{n - 1} ) + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\Omega _{4} (\vartheta ,A{}_{n - 1})(\tau - \vartheta )^{\kappa - 1} } {\text{d}}\vartheta .\\ \end{array} $$

(18)

The associated initial conditions are presented as

$$ S_{0} (\tau ) = S(0),\quad I_{0} (\tau ) = I(0),\quad R_{0} (\tau ) = R(0),\quad A_{0} (\tau ) = A(0). $$

(19)

The difference formulas are written in the following manner

$$ \begin{aligned} \wp_{1,n} (\tau ) & = S_{n} (\tau ) - S_{n - 1} (\tau ) = \frac{(1 - \kappa )}{B(\kappa )}\left( {\Omega _{1} \left( {\tau ,S_{n - 1} } \right) -\Omega _{1} \left( {\tau ,S_{n - 2} } \right)} \right) \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int_{0}^{\tau } {\left( {\Omega _{1} \left( {\vartheta ,S_{n - 1} } \right) -\Omega _{1} \left( {\vartheta ,S_{n - 2} } \right)} \right)} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta \\ \wp_{2,n} (\tau ) & = I_{n} (\tau ) - I_{n - 1} (\tau ) = \frac{(1 - \kappa )}{B(\kappa )}\left( {\Omega _{2} (\tau ,I_{n - 1} ) -\Omega _{2} (\tau ,I_{n - 2} )} \right) \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\left( {\Omega _{2} (\vartheta ,I_{n - 1} ) -\Omega _{2} (\vartheta ,I_{n - 2} )} \right)\,(\tau - \vartheta )^{\kappa - 1} } {\text{d}}\vartheta , \\ \wp_{3,n} (\tau ) & = R_{n} (\tau ) - R_{n - 1} (\tau ) = \frac{(1 - \kappa )}{B(\kappa )}\left( {\Omega _{3} (\tau ,R_{n - 1} ) -\Omega _{3} (\tau ,R_{n - 2} )} \right) \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\left( {\Omega _{3} (\vartheta ,R_{n - 1} ) -\Omega _{3} (\vartheta ,R_{n - 2} )} \right)(\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta } , \\ \wp_{4,n} (\tau ) & = A_{n} (\tau ) - A_{n - 1} (\tau ) = \frac{(1 - \kappa )}{B(\kappa )}\left( {\Omega _{4} (\tau ,A_{n - 1} ) -\Omega _{4} (\tau ,A_{n - 2} )} \right) \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{t} {\left( {\Omega _{4} (\vartheta ,A_{n - 1} ) -\Omega _{4} (\vartheta ,A_{n - 2} )} \right)} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta . \\ \end{aligned} $$

(20)

It is worth to observe that

$$ \begin{array}{*{20}l} {S_{n} (\tau ) = \sum\limits_{i = 0}^{n} {\wp_{1,i} (\tau )} ,} \hfill \\ {I_{n} (\tau ) = \sum\limits_{i = 0}^{n} {\wp_{2,i} (\tau )} ,} \hfill \\ {R_{n} (\tau ) = \sum\limits_{i = 0}^{n} {\wp_{3,i} (\tau )} ,} \hfill \\ {A_{n} (\tau ) = \sum\limits_{i = 0}^{n} {\wp_{4,i} (\tau )} .} \hfill \\ \end{array} $$

(21)

We can easily obtain the subsequent result

$$\begin{aligned} \left\| {\wp_{1,n} (\tau )} \right\| & = \left\| {S_{n} (\tau ) - S_{n - 1} (\tau )} \right\| \\ & = \left\| {\begin{array}{*{20}l} {\frac{(1 - \kappa )}{B(\kappa )}\left( {\Omega _{1} (\tau ,S_{n - 1} ) -\Omega _{1} (\tau ,S_{n - 2} )} \right)} \hfill \\ { + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\left( {\Omega _{1} (\vartheta ,S_{n - 1} ) -\Omega _{1} (\vartheta ,S_{n - 2} )} \right)(\tau - \vartheta )^{\kappa - 1} \,} {\text{d}}\vartheta } \hfill \\ \end{array} } \right\|. \end{aligned}$$

(22)

On utilization of the triangular inequality on Eq. (22) enables us to get the result

$$ \begin{aligned}\left\| {S_{n} (\tau ) - S_{n - 1} (\tau )} \right\| & \le \frac{(1 - \kappa )}{B(\kappa )}\left\| {\left( {\Omega _{1} (\tau ,S_{n - 1} ) -\Omega _{1} (\tau ,S_{n - 2} )} \right)} \right\| \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\left\| {\int\limits_{0}^{\tau } {\left( {\Omega _{1} (\vartheta ,S_{n - 1} ) -\Omega _{1} (\vartheta ,S_{n - 2} )} \right)\,(\tau - \vartheta )^{\kappa - 1} } {\text{d}}\vartheta } \right\|. \end{aligned} $$

(23)

We have already proved that $\Omega _{1} (\tau ,S)$ holds the Lipchitz condition, so we get

$$ \begin{aligned} \left\| {S_{n} (\tau ) - S_{n - 1} (\tau )} \right\| & \le \frac{(1 - \kappa )}{B(\kappa )}\lambda_{1} \left\| {S_{n - 1} (\tau ) - S_{n - 2} (\tau )} \right\| \\ & \quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\lambda_{1} \int\limits_{0}^{\tau } {\left\| {S_{n - 1} (\vartheta ) - S_{n - 2} (\vartheta )} \right\|(\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta } , \end{aligned} $$

(24)

Then, we have

$$ \left\| {\wp_{1,n} (\tau )} \right\| \le \frac{(1 - \kappa )}{B(\kappa )}\lambda_{1} \left\| {\wp_{1,n - 1} (\tau )} \right\| + \frac{\kappa }{B(\kappa )\varGamma (\kappa )}\lambda_{1} \int\limits_{0}^{\tau } {\left\| {\wp_{1,n - 1} (\vartheta )} \right\|} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta . $$

(25)

On employing the same way, we get

$$ \begin{array}{*{20}l} {\left\| {\wp_{2,n} (\tau )} \right\| \le \frac{(1 - \kappa )}{B(\kappa )}\lambda_{2} \left\| {\wp_{2,n - 1} (\tau )} \right\| + \frac{\kappa }{B(\kappa )\varGamma (\kappa )}\lambda_{2} \int\limits_{0}^{\tau } {\left\| {\wp_{2,n - 1} (\vartheta )} \right\|} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta ,} \hfill \\ {\left\| {\wp_{3,n} (\tau )} \right\| \le \frac{(1 - \kappa )}{B(\kappa )}\lambda_{3} \left\| {\wp_{3,n - 1} (\tau )} \right\| + \frac{\kappa }{B(\kappa )\varGamma (\kappa )}\lambda_{3} \int\limits_{0}^{\tau } {\left\| {\wp_{3,n - 1} (\vartheta )} \right\|} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta ,} \hfill \\ {\left\| {\wp_{4,n} (\tau )} \right\| \le \frac{(1 - \kappa )}{B(\kappa )}\lambda_{4} \left\| {\wp_{4,n - 1} (\tau )} \right\| + \frac{\kappa }{B(\kappa )\varGamma (\kappa )}\lambda_{4} \int\limits_{0}^{\tau } {\left\| {\wp_{4,n - 1} (\vartheta )} \right\|} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta .} \hfill \\ \end{array} $$

(26)

On making use of the abovementioned results, we establish the following theorems.

Theorem 4.2

The exact solution of the FMEM for computer viruses (6) exists if we can find τ₀ such that

$$ \frac{(1 - \kappa )}{B(\kappa )}\lambda_{1} + \frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1)}}\lambda_{1} \tau_{0}^{\kappa} < 1. $$

(27)

Proof From the results (25) and (26), we have

$$ \begin{array}{*{20}l} {\left\| {\wp_{1,n} (\tau )} \right\| \le \left\| {S_{n} (0)} \right\|\left[ {\left( {\frac{(1 - \kappa )}{B(\kappa )}\lambda_{1} } \right) + \left( {\frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1)}}\lambda_{1} \tau^{\kappa} } \right)} \right]^{n} } \hfill \\ {\left\| {\wp_{2,n} (\tau )} \right\| \le \left\| {I_{n} (0)} \right\|\left[ {\left( {\frac{(1 - \kappa )}{B(\kappa )}\lambda_{2} } \right) + \left( {\frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1)}}\lambda_{2} \tau^{\kappa} } \right)} \right]^{n} ,} \hfill \\ {\left\| {\wp_{3,n} (\tau )} \right\| \le \left\| {R_{n} (0)} \right\|\left[ {\left( {\frac{(1 - \kappa )}{B(\kappa )}\lambda_{3} } \right) + \left( {\frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1)}}\lambda_{3} \tau^{\kappa} } \right)} \right]^{n} ,} \hfill \\ {\left\| {\wp_{4,n} (\tau )} \right\| \le \left\| {A_{n} (0)} \right\|\left[ {\left( {\frac{(1 - \kappa )}{B(\kappa )}\lambda_{4} } \right) + \left( {\frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1)}}\lambda_{4} \tau^{\kappa} } \right)} \right]^{n} .} \hfill \\ \end{array} $$

(28)

Thus, the abovementioned solutions exist and are continuous. In order to demonstrate that Eq. (18) is a solution of FMEM for computer viruses (6), we suppose that

$$ \begin{aligned} S(\tau ) - S(0) & = S_{n} (\tau ) - W_{1,n} (\tau ), \\ I(\tau ) - I(0) & = I_{n} (\tau ) - W_{2,n} (\tau ), \\ R(\tau ) - R(0) & = R_{n} (\tau ) - W_{3,n} (\tau ), \\ A(\tau ) - A(0) & = A_{n} (\tau ) - W_{4,n} (\tau ). \\ \end{aligned} $$

(29)

Therefore, we have

$$ \begin{aligned} \left\| {W_{1,n} (\tau )} \right\| & = \left\| {\begin{array}{*{20}l} {\frac{(1 - \kappa )}{B(\kappa )}\left( {\Omega _{1} (\tau ,S) -\Omega _{1} (\tau ,S_{n - 1} )} \right)} \hfill \\ { + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\left( {\Omega _{1} (\tau ,S) -\Omega _{1} (\tau ,S_{n - 1} )} \right)(\tau - \tau )^{\kappa - 1} } d\tau } \hfill \\ \end{array} } \right\|. \\ & \le \frac{(1 - \kappa )}{B(\kappa )}\left\| {\left( {\Omega _{1} (\tau ,S)\, -\Omega _{1} (\tau ,S_{n - 1} )} \right)} \right\| \\ &\quad + \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\left\| {\left( {\Omega _{1} (\vartheta ,S) -\Omega _{1} (\vartheta ,S_{n - 1} )} \right)} \right\|\,} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta \\ & \le \frac{(1 - \kappa )}{B(\kappa )}\lambda_{1} \left\| {S(\tau ) - S_{n - 1} (\tau )} \right\| + \frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1)}}\lambda_{1} \left\| {S(\tau ) - S_{n - 1} (\tau )} \right\|\tau^{\kappa} . \\ \end{aligned} $$

(30)

On making use of the abovementioned process recursively, it gives

$$ \left\| {W_{1,n} (\tau )} \right\| \le \left( {\frac{(1 - \kappa )}{B(\kappa )} + \frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1)}}\tau^{\kappa} } \right)^{n + 1} \lambda_{1}^{n + 1} \beta_{1} . $$

(31)

Then at $\tau_{0}$, we have

$$ \left\| {W_{4,n} (\tau )} \right\| \le \left( {\frac{(1 - \kappa )}{B(\kappa )} + \frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1)}}\tau_{0}^{\kappa} } \right)^{n + 1} \lambda_{1}^{n + 1} \beta_{1} . $$

(32)

Next, on using the limit n tends to infinity, we have

$$ \left\| {W_{1,n} (\tau )} \right\| \to 0. $$

In the same way, we get

$$ \left\| {W_{2,n} (\tau )} \right\| \to 0,\left\| {W_{3,n} (\tau )} \right\| \to 0\quad {\text{and}}\quad \left\| {W_{4,n} (\tau )} \right\| \to 0. $$

Hence, the exact solution of the FMEM for computer viruses (6) exists if condition (27) is satisfied.

Now, we show that the FMEM for computer viruses (6) has a unique solution.

In order to prove the uniqueness of the solutions, we assume that there exists another system of solutions of mathematical model (6) be $S^{ * } (\tau ),I^{ * } (\tau ),R^{ * } (\tau )$ and $A^{ * } (\tau )$ then

$$ \begin{aligned}S(\tau ) - S^{ * } (\tau ) &= \frac{(1 - \kappa )}{B(\kappa )}\left( {\Omega _{1} (\tau ,S) -\Omega _{1} (\tau ,S^{ * } )} \right) \\ &\quad+ \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\left( {\Omega _{1} (\vartheta ,S) -\Omega _{1} (\vartheta ,S^{ * } )} \right)} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta .\end{aligned} $$

(33)

On operating the norm on Eq. (33), we get

$$ \begin{aligned}\left\| {S(\tau ) - S^{ * } (\tau )} \right\| &\le \frac{(1 - \kappa )}{B(\kappa )}\left\| {\Omega _{1} (\tau ,S) -\Omega _{1} (\tau ,S^{ * } )} \right\| \\ &\quad+ \frac{\kappa }{{B(\kappa )\Gamma (\kappa )}}\int\limits_{0}^{\tau } {\left\| {\left( {\Omega _{1} (\vartheta ,S) -\Omega _{1} (\vartheta ,S^{ * } )} \right)} \right\|} (\tau - \vartheta )^{\kappa - 1} {\text{d}}\vartheta . \end{aligned} $$

(34)

The use of the Lipschitz condition of $\Omega _{1} (\tau ,S)$ enables us to get

$$ \left\| {S(\tau ) - S^{ * } (\tau )} \right\|\,\left( {1 - \frac{(1 - \kappa )}{B(\kappa )}} \lambda_{1} - \frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1 )}}\lambda_{1} \tau^{\kappa} \right) \le 0. $$

(35)

Theorem 4.3

The FMEM for computer viruses (6) has a unique solution if

$$ \left( {1 - \frac{(1 - \kappa )}{B(\kappa )}\lambda_{1} - \frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1 )}}\lambda_{1} \tau^{\kappa}} \right) > 0. $$

(36)

Proof From Eq. (35), we have

$$ \left\| {S(\tau ) - S^{ * } (\tau )} \right\|\,\left( {1 - \frac{(1 - \kappa )}{B(\kappa )}\lambda_{1} - \frac{\kappa }{{B(\kappa )\Gamma (\kappa + 1 )}}\lambda_{1} \tau^{\kappa} } \right) \le 0. $$

(37)

If condition (36) holds, then Eq. (37) yields

$$ \left\| {S(\tau ) - S^{ * } (\tau )} \right\| = 0. $$

Thus, we have

$$ S(\tau ) = S^{ * } (\tau ). $$

(38)

On utilizing the similar methodology, we arrive at the following results

$$ I(\tau ) = I^{ * } (\tau ),\quad R(\tau ) = R^{ * } (\tau ),\quad A(\tau ) = A^{ * } (\tau ). $$

(39)

Thus, the proof of the uniqueness theorem is completed.

5 Application of q-HATM to Solve FMEM for Computer Viruses

First of all, we use the Laplace transform on FMEM for computer viruses (6), and it gives

$$ \begin{array}{*{20}l} {L\left[ S \right] - \frac{{\alpha_{1} }}{p} - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ { - \mu_{SA} S(\tau )A(\tau ) - \xi S(\tau )I(\tau ) + \rho R(\tau )} \right] = 0,} \hfill \\ {L\left[ I \right] - \frac{{\alpha_{2} }}{p} - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ {\xi S(\tau )I(\tau ) - \mu_{IA} A(\tau )I(\tau ) - \varepsilon I(\tau )} \right] = 0,} \hfill \\ {L\left[ R \right] - \frac{{\alpha_{3} }}{p} - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ {\varepsilon I(\tau ) - \rho R(\tau )} \right] = 0,} \hfill \\ {L\left[ A \right] - \frac{{\alpha_{4} }}{p} - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ {\mu_{SA} S(\tau )A(\tau ) + \mu_{IA} A(\tau )I(\tau )} \right] = 0.} \hfill \\ \end{array} $$

(40)

The nonlinear operators are given as

$$ \begin{aligned} N_{1} \left[ {\Theta _{1} (\tau ;z)} \right] & = L\left[ {\Theta _{1} (\tau ;z)} \right] - \frac{{\alpha_{1} }}{p} - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ { - \mu_{SA}\Theta _{1} (\tau ;z)} \right.\Theta _{4} (\tau ;z) \\ & \quad \left. { - \xi\Theta _{1} (\tau ;z)\Theta _{2} (\tau ;z) + \rho\Theta _{3} (\tau ;z)} \right] = 0, \\ N_{2} \left[ {\Theta _{2} (\tau ;z)} \right] & = L\left[ {\Theta _{2} (\tau ;z)} \right] - \frac{{\alpha_{2} }}{p} - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ {\xi\Theta _{1} (\tau ;z)} \right.\Theta _{2} (\tau ;z) \\ & \quad \left. { - \mu_{IA}\Theta _{4} (\tau ;z)\Theta _{2} (\tau ;z) - \varepsilon\Theta _{2} (\tau ;z)\,} \right] = 0, \\ N_{3} \left[ {\Theta _{3} (\tau ;z)} \right] & = L\left[ {\Theta _{3} (\tau ;z)} \right] - \frac{{\alpha_{3} }}{p} - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ {\varepsilon\Theta _{2} (\tau ;z)} \right. \\ & \quad \left. { - \rho\Theta _{3} (\tau ;z)} \right] = 0, \\ N_{4} \left[ {\Theta _{4} (\tau ;z)} \right] & = L\left[ {\Theta _{4} (\tau ;z)} \right] - \frac{{\alpha_{4} }}{p} - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ {\mu_{SA}\Theta _{1} (\tau ;z)} \right.\Theta _{4} (\tau ;z) \\ & \quad \left. { + \mu_{IA}\Theta _{4} (\tau ;z)\Theta _{2} (\tau ;z)} \right] = 0, \\ \end{aligned} $$

(41)

and thus, we have

$$ \begin{aligned} \Re_{1,\ell } (\vec{S}_{(\ell - 1)} ) & = L\left[ {S_{(\ell - 1)} } \right] - \frac{{\alpha_{1} }}{p}\left( {1 - \frac{{k_{\ell } }}{n}} \right) \\ & \quad - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ - \mu_{SA} \left( {\sum\limits_{r = 0}^{\ell - 1} {S_{r} A_{(\ell - 1 - r)} } } \right) \right.\\ &\quad \left. - \xi \left( {\sum\limits_{r = 0}^{\ell - 1} {S_{r} I_{(\ell - 1 - r)} } } \right) - \rho R_{(\ell - 1)} \right], \\ \Re_{2,\ell } (\vec{I}_{(\ell - 1)} ) & = L\left[ {I_{(\ell - 1)} } \right] - \frac{{\alpha_{2} }}{p}\left( {1 - \frac{{k_{\ell } }}{n}} \right) \\ & \quad - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ \xi \left( {\sum\limits_{r = 0}^{\ell - 1} {S_{r} I_{(\ell - 1 - r)} } } \right)\right.\\ &\quad \left. - \mu_{IA} \left( {\sum\limits_{r = 0}^{\ell - 1} {A_{r} I_{(\ell - 1 - r)} } } \right) - \varepsilon I_{(\ell - 1)} \right], \\ \Re_{3,\ell } (\vec{R}_{(\ell - 1)} ) & = L\left[ {R_{(\ell - 1)} } \right] - \frac{{\alpha_{3} }}{p}\left( {1 - \frac{{k_{\ell } }}{n}} \right) \\ & \quad - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ {\varepsilon I_{(\ell - 1)} - \rho R_{(\ell - 1)} } \right], \\ \Re_{4,\ell } (\vec{A}_{(\ell - 1)} ) & = L\left[ {A_{(\ell - 1)} } \right] - \frac{{\alpha_{4} }}{p}\left( {1 - \frac{{k_{\ell } }}{n}} \right) \\ & \quad - \frac{{p^{\kappa } + \kappa (1 - p^{\kappa } )}}{{p^{\kappa } }}L\left[ \mu_{SA} \left( {\sum\limits_{r = 0}^{\ell - 1} {S_{r} A_{(\ell - 1 - r)} } } \right) \right.\\ &\quad \left. + \mu_{IA} \left( {\sum\limits_{r = 0}^{\ell - 1} {A_{r} I_{(\ell - 1 - r)} } } \right) \right] \\ \end{aligned} $$

(42)

and $k_{\ell }$ is defined as

$$ k_{\ell } = \left\{ \begin{array}{*{20}l} 0,\quad \ell \le 1, \hfill \\ n,\quad \ell > 1. \hfill \\ \end{array} \right. $$

(43)

Next, the deformation equations of $\ell^{th}$-order are presented as

$$ \begin{array}{*{20}l} {L\left[ {S_{\ell } (\tau ) - k_{\ell } S_{(\ell - 1)} (\tau )} \right] = \hbar \Re_{1,\ell } (\vec{S}_{(\ell - 1)} ),} \hfill \\ {L\left[ {I_{\ell } (\tau ) - k_{\ell } I_{(\ell - 1)} (\tau )} \right] = \hbar \Re_{2,\ell } (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {I}_{(\ell - 1)} ),} \hfill \\ {L\left[ {R_{\ell } (\tau ) - k_{\ell } R_{(\ell - 1)} (\tau )} \right] = \hbar \Re_{3,\ell } (\vec{R}_{(\ell - 1)} ),} \hfill \\ {L\left[ {A_{\ell } (\tau ) - k_{\ell } A_{(\ell - 1)} (\tau )} \right] = \hbar \Re_{4,\ell } (\vec{A}_{(\ell - 1)} ).} \hfill \\ \end{array} $$

(44)

The utilization the inversion of Laplace transform on Eq. (44) enables us to get

$$ \begin{array}{*{20}l} {S_{\ell } (\tau) = k_{\ell } S_{(\ell - 1)} (\tau) + \hbar L^{ - 1} \left[ {\Re_{1,\ell } (\vec{S}_{(\ell - 1)} )} \right],} \hfill \\ {I_{\ell } (\tau) = k_{\ell } I_{(\ell - 1)} (\tau) + \hbar L^{ - 1} \left[ {\Re_{1,\ell } (\bar{I}_{(\ell - 1)} )} \right],} \hfill \\ {R_{\ell } (\tau) = k_{\ell } R_{(\ell - 1)} (\tau) + \hbar L^{ - 1} \left[ {\Re_{1,\ell } (\vec{R}_{(\ell - 1)} )} \right],} \hfill \\ {A_{\ell } (\tau) = k_{\ell } A_{(\ell - 1)} (\tau) + \hbar L^{ - 1} \left[ {\Re_{1,\ell } (\vec{A}_{(\ell - 1)} )} \right].} \hfill \\ \end{array} $$

(45)

We take the initial guess $S_{0} (\tau ) = \alpha_{1}$, $I_{0} (\tau ) = \alpha_{2}$, $R_{0} (\tau ) = \alpha_{3}$, $A_{0} (\tau ) = \alpha_{4}$ and solving Eq. (45) for $\ell = 0,1,2, \ldots ,$ we determine the values of $S_{\ell } (\tau ),I_{\ell } (\tau ),R_{\ell } (\tau )$ and $A_{\ell } (\tau ),\,\forall \ell \ge 1.$

Finally, the solution of FMEM for computer viruses (6) is given as

$$ \begin{array}{*{20}l} {S(\tau ) = S_{0} (\tau ) + S_{1} (\tau )\left( {\frac{1}{n}} \right) + S_{2} (\tau )\left( {\frac{1}{n}} \right)^{2} + \cdots ,} \hfill \\ {I(\tau ) = I_{0} (\tau ) + I_{1} (\tau )\left( {\frac{1}{n}} \right) + I_{2} (\tau )\left( {\frac{1}{n}} \right)^{2} + \cdots ,} \hfill \\ {R(\tau ) = R_{0} (\tau ) + R_{1} (\tau )\left( {\frac{1}{n}} \right) + R_{2} (\tau )\left( {\frac{1}{n}} \right)^{2} + \cdots ,} \hfill \\ {A(\tau ) = A_{0} (\tau ) + A_{1} (\tau )\left( {\frac{1}{n}} \right) + A_{2} (\tau )\left( {\frac{1}{n}} \right)^{2} + \cdots .} \hfill \\ \end{array} $$

(46)

6 Numerical Simulations

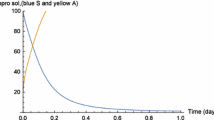
In this part, we present the numerical computation for FMEM for computer viruses (6) as function of time at $\mu_{SA} = 0.025$, $\mu_{IA} = 0.25$, $\xi = 0.1,\,\varepsilon = 9,\,\rho = 0.8,\,\hbar = - 1$ and $n = 3$ for defined values of order of AB fractional operator. The initial conditions are taken as $S(0) = 3,\,I(0) = 95,\,R(0) = 1$ and $A(0) = 1$. The numerical outcomes for different kind of computer populations are present through Figs. 1, 2, 3 and 4. Figure 1 presents the impact of order of AB fractional operator on the group of non-infected computers with the possibility of infection. Figure 2 demonstrates the impact of order of AB fractional operator on the group of infected computers. Figure 3 presents the influence of order of AB fractional operator on the class of removed ones due to the infection or not. Figure 4 presents the effect of order of AB fractional derivative on non-infected computers associated with anti-virus. It can be noticed from Figs. 1, 2, 3 and 4 that there is a significant impact of order of AB fractional operator on different kind of populations of computers due to Mittag–Leffler memory.

Fig. 1

Nature of $S(\tau )$ with respect to $\tau$ for distinct orders of AB fractional derivative

Fig. 2

Nature of $I(\tau )$ with respect to $\tau$ for distinct orders of AB fractional derivative

Fig. 3

Nature of $R(\tau )$ with respect to $\tau$ for distinct orders of AB fractional derivative

Fig. 4

Nature of $A(\tau )$ with respect to $\tau$ for distinct orders of AB fractional derivative

7 Concluding Remarks, Observations and Suggestions

In this work, the FMEM for computer viruses is studied involving Mittag–Leffler memory effects. The existence and uniqueness of the solution of FMEM for computer viruses are examined. The solution of the FMEM for computer viruses is obtained with the aid of q-HATM. To demonstrate the effects of Mittag–Leffler memory on different groups of computer, some numerical simulations are conducted. The numerical outcomes give very clear indications that the use of AB fractional derivative in mathematical modeling of computer viruses is very fruitful, and the q-HATM is a very accurate and easy approach for solving such type of fractional models.