Persistence of periodic solutions from discontinuous planar piecewise linear Hamiltonian differential systems with three zones

Abstract

In this paper, we study the number of limit cycles that can bifurcate from a period annulus in discontinuous planar piecewise linear Hamiltonian differential system with three zones separated by two parallel straight lines. More precisely, we consider the case where the period annulus, bounded by a heteroclinic orbit or homoclinic loop, is obtained from a real center of the central subsystem, i.e. the system defined between the two parallel lines, and two real saddles of the others subsystems. Denoting by H(n) the number of limit cycles that can bifurcate from this period annulus by polynomial perturbations of degree n, we prove that if the period annulus is bounded by a heteroclinic orbit then $H(1)\ge 2$, $H(2)\ge 3$ and $H(3)\ge 5$. Now, if the period annulus is bounded by a homoclinic loop then $H(1)\ge 3$, $H(2)\ge 4$ and $H(3)\ge 7$. For this, we study the number of zeros of a Melnikov function for piecewise Hamiltonian system.

1 Introduction and main result

The most important problem in the qualitative theory of ordinary differential equations is to determine the number and position of limit cycles of differential systems. The classic formulation of such a problem was proposed by Hilber in 1900 for polynomial differential systems and became known as the Hilbert’s 16th problem, see [9]. Currently this problem has been considered for piecewise differential systems. This class of differential systems have piqued the attention of researchers in qualitative theory of differential equations, mainly by their numerous applications, for instance in mechanics, electrical circuits, control theory, neurobiology, etc (see the book [4] and the papers [3, 5, 19, 20]).

For continuous planar piecewise differential systems with two zones, Freire, Ponce, Rodrigo and Torres in [7] proved that such systems have at most one limit cycle. In the discontinuous case, the maximum number of limit cycles is not known, but important partial results about this problem have been obtained, see for instance [1, 2, 8, 14]. Of course, the problem becomes more complicated when we have more than two zones, and there are few works that deal with the discontinuous case (see [10, 11, 17, 21,22,23,24]). However, when restrictive hypotheses such as symmetry and linearity are imposed on the system, the problem becomes more accessible and good results on the number of limit cycles have been obtained. More precisely, for symmetric continuous piecewise linear differential systems with three zones, conditions for nonexistence and existence of one, two or three limit cycles have been obtained (see for instance the book [15]). For the nonsymmetric case, examples with two limit cycles surrounding the only singular point at the origin was found in [12, 16].

Recently, some researchers have been study the number of limit cycles that emerging from a period annulus in a discontinuous piecewise linear near-Hamiltonian differential systems with three zones, given by

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}= H_y(x,y)+\epsilon f(x,y), \\ \dot{y}= -H_x(x,y)+\epsilon g(x,y), \end{array} \right. \end{aligned}$$

(1)

with

$$\begin{aligned}&H(x,y)=\left\{ \begin{array}{ll}\vspace{0.2cm} H^{\scriptscriptstyle L}(x,y)=\dfrac{b_{\scriptscriptstyle L}}{2}y^2-\dfrac{c_{\scriptscriptstyle L}}{2}x^2+a_{\scriptscriptstyle L}xy+\alpha _{\scriptscriptstyle L}y-\beta _{\scriptscriptstyle L}x, \,\, x\le -1, \\ \vspace{0.2cm} H^{\scriptscriptstyle C}(x,y)=\dfrac{b_{\scriptscriptstyle C}}{2}y^2-\dfrac{c_{\scriptscriptstyle C}}{2}x^2+a_{\scriptscriptstyle C}xy+\alpha _{\scriptscriptstyle C}y-\beta _{\scriptscriptstyle C}x, \, -1\le x\le 1, \\ H^{\scriptscriptstyle R}(x,y)=\dfrac{b_{\scriptscriptstyle R}}{2}y^2-\dfrac{c_{\scriptscriptstyle R}}{2}x^2+a_{\scriptscriptstyle R}xy+\alpha _{\scriptscriptstyle R}y-\beta _{\scriptscriptstyle R}x, \,\, x \ge 1, \\ \end{array} \right. \\&f(x,y)=\left\{ \begin{array}{ll} f_{\scriptscriptstyle L}(x,y), \quad x\le -1, \\ f_{\scriptscriptstyle C}(x,y), \quad -1\le x\le 1, \\ f_{\scriptscriptstyle R}(x,y), \quad x \ge 1, \\ \end{array} \right. \\&g(x,y)=\left\{ \begin{array}{ll} g_{\scriptscriptstyle L}(x,y), \quad x\le -1, \\ g_{\scriptscriptstyle C}(x,y), \quad -1\le x\le 1, \\ g_{\scriptscriptstyle R}(x,y), \quad x \ge 1, \\ \end{array} \right. \end{aligned}$$

where the functions $H^i$, $f_i$ and $g_i$ are $\mathbb {C}^{\infty }$, for $i=L,C,R$, and $0\le \epsilon<<1$. When $\epsilon =0$ we say that system (1) is a piecewise Hamiltonian differential system. We call system (1) of left subsystem for $x\le -1$, right subsystem for $x\ge 1$ and central subsystem for $-1\le x\le 1$.

In this direction, i.e. when we have a discontinuous piecewise linear near-Hamiltonian differential system with three zones separated by two parallel straight lines, the best lower bound for its the number of limit cycles is seven. This lower bound was obtained by linear perturbations of a piecewise linear differential system with subsystems without singular points and a boundary pseudo–focus, see [23]. As far as we know, all other papers that estimate the number of limit cycles for these class of piecewise linear differential systems have found at most 1 or 3 limit cycles, see [6, 11, 18, 22]. Now, in [25], 7 and 12 limit cycles were obtained in discontinuous piecewise linear near-Hamiltonian differential systems with three zones perturbed by piecewise quadratic and cubic polynomials, respectively. But, in this paper, the period annulus of the unperturbed piecewise linear Hamiltonian differential system was obtained from a real saddle of the central subsystem and two virtual centers of the others subsystems. For the same type of period annulus, in [22], 10 limit cycles were obtained through cubic perturbations.

The search for examples that present the best quota for the number of limit cycles that a piecewise linear system with three zones can have is what motivates most of the works found in the literature about this topic. However, all cases are interesting in themselves, that is, the search for better quotas for number of limit cycles cannot be used to neglect the study of particular families. We believe that the question of the number of limit cycles must be answered for all subclass of piecewise linear systems with three zones. So the type of singular points of the subsystems and their positions, that is, whether they are real or virtual, is important. Furthermore, there is not much work in the literature dealing with the discontinuous case for these piecewise systems.

In this work, we contribute along these lines. Our goal is to estimated the lower bounds for the number of crossing limit cycles of system (1) that bifurcated from a period annulus of system (1)$|_{\epsilon =0}$, bounded by a heteroclinic orbit or homoclinic loop, obtained by a real center of the central subsystem and two real saddles of the others subsystem, in the cases that f(x, y) and g(x, y) are polynomial functions of degree n, for $n=1,2,3$. More precisely, the main result in this paper is the follow.

Theorem 1

The number of crossing limit cycles of system (1) which can bifurcate from the period annulus of the unperturbed system (1)$|_{\epsilon =0}$ bounded by a homoclinic loop (resp. heteroclinic orbit) is at least three (resp. two) if $n=1$, four (resp. three) if $n=2$ and seven (resp. five) if $n=3$.

For prove the Theorem 1 we will study the number of zeros of the first order Melnikov function associated to system (1), see the Sect. 2 in this paper or [22, 23] for more details about the Melnikov function. Our study is concentrated in the neighborhoods of the homoclinic loop and heteroclinic orbit, since to estimate the zeros of the Melnikov function we consider its expansion at the point corresponding to this orbit. The rest of the paper is organized as follows. In Sect. 3 we obtain a normal form to system (1)$|_{\epsilon =0}$ that simplifies the computations and in Sect. 4 we will prove Theorem 1.

2 Melnikov function

In this section, we will introduce the first order Melnikov function associated to system (1), which will be needed to prove the main result of this paper.

For this purpose, suppose that unperturbed system (1)$|_{\epsilon =0}$ has a period annulus consisting of a family of crossing periodic orbits surrounding the origin such that each orbit of this family passes thought the three zones with clockwise orientation, satisfies the following two hypotheses:

• (H1) There exists an open interval $J=(\alpha ,\beta )$ such that for each $h\in J$ we have four points, $A(h)=(1,a(h))$, $A_1(h)=(1,a_1(h))$, with $a_1(h)<a(h)$, and $A_2(h)=(-1,a_2(h))$, $A_3(h)=(-1,a_3(h))$, with $a_2(h)<a_3(h)$, which are determined by the following equations

  $$\begin{aligned} \begin{aligned}&H^{\scriptscriptstyle R}(A(h))=H^{\scriptscriptstyle R}(A_1(h)), \\&H^{\scriptscriptstyle C}(A_1(h))=H^{\scriptscriptstyle C}(A_2(h)), \\&H^{\scriptscriptstyle L}(A_2(h))=H^{\scriptscriptstyle L}(A_3(h)), \\&H^{\scriptscriptstyle C}(A_3(h))=H^{\scriptscriptstyle C}(A(h)), \end{aligned} \end{aligned}$$

  (2)

  satisfying, for $h\in J$,

  $$\begin{aligned} H^{\scriptscriptstyle R}_y(A(h))\,H^{\scriptscriptstyle R}_y(A_1(h))\,H^{\scriptscriptstyle L}_y(A_2(h))\,H^{\scriptscriptstyle L}_y(A_3(h))\ne 0, \end{aligned}$$

  and

  $$\begin{aligned} H^{\scriptscriptstyle C}_y(A(h))\,H^{\scriptscriptstyle C}_y(A_1(h))\,H^{\scriptscriptstyle C}_y(A_2(h))\,H^{\scriptscriptstyle C}_y(A_3(h))\ne 0. \end{aligned}$$

• (H2) The unperturbed system (1)$|_{\epsilon =0}$ has only crossing periodic orbit $L_h=L_h^{\scriptscriptstyle R}\cup \bar{L}_h^{\scriptscriptstyle C}\cup L_h^{\scriptscriptstyle L}\cup L_h^{\scriptscriptstyle C}$ passing through these points with clockwise orientation (see Figure 1), where

  $$\begin{aligned} \begin{aligned}&L_h^{\scriptscriptstyle R}=\Big \{(x,y)\in \mathbb {R}^2:H^{\scriptscriptstyle R}(x,y)=H^{\scriptscriptstyle R}(A(h)),\,x>1\Big \}, \\&\bar{L}_h^{\scriptscriptstyle C}=\{(x,y)\in \mathbb {R}^2:H^{\scriptscriptstyle C}(x,y)=H^{\scriptscriptstyle C}(A_1(h)),-1\le x\le 1 \quad \text {and}\quad y<0\}, \\&L_h^{\scriptscriptstyle L}=\{(x,y)\in \mathbb {R}^2:H^{\scriptscriptstyle L}(x,y)=H^{\scriptscriptstyle L}(A_2(h)),x<-1\}, \\&L_h^{\scriptscriptstyle C}=\{(x,y)\in \mathbb {R}^2:H^{\scriptscriptstyle C}(x,y)=H^{\scriptscriptstyle C}(A_3(h)),-1\le x\le 1 \quad \text {and}\quad y>0\}. \end{aligned} \end{aligned}$$

Fig. 1

The crossing periodic orbit of system (1)$|_{\epsilon =0}$

Assuming the hypotheses (H1) and (H2), consider the solution of right subsystem from (1) starting at the point A(h). Let $A_{\epsilon }(h)=(1,a_{\epsilon }(h))$ be the first intersection point of this orbit with straight line $x=1$. Denote by $B_{\epsilon }(h)=(-1,b_{\epsilon }(h))$ the first intersection point of the orbit from central subsystem from (1) starting at $A_{\epsilon }(h)$ with straight line $x=-1$, $C_{\epsilon }(h)=(-1,c_{\epsilon }(h))$ the first intersection point of the orbit from left subsystem from (1) starting at $B_{\epsilon }(h)$ with straight line $x=-1$ and $D_{\epsilon }(h)=(1,d_{\epsilon }(h))$ the first intersection point of the orbit from central subsystem from (1) starting at $C_{\epsilon }(h)$ with straight line $x=1$ (see Figure 2).

Fig. 2

Poincaré map of system (1)

We define the Poincaré map of piecewise system (1) as follows,

$$\begin{aligned} H^{\scriptscriptstyle R}(D_{\epsilon }(h))-H^{\scriptscriptstyle R}(A(h))=\epsilon M(h)+\mathcal {O}(\epsilon ^2), \end{aligned}$$

where M(h) is called the first order Melnikov function associated to piecewise system (1). Then, using the same idea of the proof of Theorem 1.1 in [13], it is easy to prove the following theorem.

Theorem 2

Consider system (1) with $0\le \epsilon<<1$ and suppose that the unperturbed system (1)$|_{\epsilon =0}$ has a family of crossing periodic orbits surrounding the origin. Then the first order Melnikov function can be expressed as

$$\begin{aligned} \begin{aligned} M(h)&= \frac{H_y^{\scriptscriptstyle R}(A)}{H_y^{\scriptscriptstyle C}(A)} I_{\scriptscriptstyle C} + \frac{H_y^{\scriptscriptstyle R}(A)H_y^{\scriptscriptstyle C}(A_3)}{H_y^{\scriptscriptstyle C}(A)H_y^{\scriptscriptstyle L}(A_3)} I_{\scriptscriptstyle L} \\&\quad +\frac{H_y^{\scriptscriptstyle R}(A)H_y^{\scriptscriptstyle C}(A_3)H_y^{\scriptscriptstyle L}(A_2)}{H_y^{\scriptscriptstyle C}(A)H_y^{\scriptscriptstyle L}(A_3)H_y^{\scriptscriptstyle C}(A_2)} \bar{I}_{\scriptscriptstyle C} \\&\quad + \frac{H_y^{\scriptscriptstyle R}(A)H_y^{\scriptscriptstyle C}(A_3)H_y^{\scriptscriptstyle L}(A_2)H_y^{\scriptscriptstyle C}(A_1)}{H_y^{\scriptscriptstyle C}(A)H_y^{\scriptscriptstyle L}(A_3)H_y^{\scriptscriptstyle C}(A_2)H_y^{\scriptscriptstyle R}(A_1)} I_{\scriptscriptstyle R}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}&I_{\scriptscriptstyle C}=\int _{\widehat{A_3A}}g_{\scriptscriptstyle C}dx-f_{\scriptscriptstyle C}dy, \quad I_{\scriptscriptstyle L}=\int _{\widehat{A_2A_3}}g_{\scriptscriptstyle L}dx-f_{\scriptscriptstyle L}dy, \\&\bar{I}_{\scriptscriptstyle C}=\int _{\widehat{A_1A_2}}g_{\scriptscriptstyle C}dx-f_{\scriptscriptstyle C}dy\quad \text {and} \quad I_{\scriptscriptstyle R}=\int _{\widehat{AA_1}}g_{\scriptscriptstyle R}dx-f_{\scriptscriptstyle R}dy. \end{aligned}$$

Furthermore, if M(h) has a simple zero at $h^{*}$, then for $0< \epsilon<<1$, the system (1) has a unique limit cycle near $L_{h^{*}}$.

3 Normal form

In order to prove Theorem 1, we will do a continuous linear change of variables which transform system (1)$|_{\epsilon =0}$ in a new system with few parameters. The proposed change of variables is a homeomorphism which keeps invariant the straight lines $x=\pm 1$. Furthermore, this homeomorphism will be a topological equivalence between the systems. More precisely, we have the follow result.

Proposition 3

Suppose that the central subsystem from (1)$|_{\epsilon =0}$ has a center and the other two subsystems have two saddles. Then, after a linear change of variables and a rescaling of the independent variable, we can assume that $\alpha _{\scriptscriptstyle L}=a_{\scriptscriptstyle L}$, $\alpha _{\scriptscriptstyle R}=-a_{\scriptscriptstyle R}$, $b_{\scriptscriptstyle C}=1$, $c_{\scriptscriptstyle C}=-1$ and $a_{\scriptscriptstyle C}=\alpha _{\scriptscriptstyle C}=0$.

Proof

As the central subsystem from (1)$|_{\epsilon =0}$ has a center with clockwise orientation of the orbits, then $a_{\scriptscriptstyle C}^2+b_{\scriptscriptstyle C}c_{\scriptscriptstyle C}<0$ and $b_{\scriptscriptstyle C}>0$. Note that $b_i\ne 0$, for $i=L,R$. In fact, if $b_i=0$ then the saddle of right or left subsystem have a separatrix parallel to straight line $x=0$. System (1)$|_{\epsilon =0}$ has four tangent points given by $P_1=(1,-(a_{\scriptscriptstyle C}+\alpha _{\scriptscriptstyle C})/b_{\scriptscriptstyle C})$, $P_2=(1,-(a_{\scriptscriptstyle R}+\alpha _{\scriptscriptstyle R})/b_{\scriptscriptstyle R})$, $P_3=(-1,(a_{\scriptscriptstyle C}-\alpha _{\scriptscriptstyle C})/b_{\scriptscriptstyle C})$ and $P_4=(-1,(a_{\scriptscriptstyle L}-\alpha _{\scriptscriptstyle L})/b_{\scriptscriptstyle L})$. By hypothesis (H2), we have that the system (1)$|_{\epsilon =0}$ have only crossing points on the straight lines $x=\pm 1$, except in the tangent points. Hence, for all $y\in \mathbb {R}\setminus \{(\pm a_{\scriptscriptstyle C}-\alpha _{\scriptscriptstyle C})/b_{\scriptscriptstyle C},-(a_{\scriptscriptstyle R}+\alpha _{\scriptscriptstyle R})/b_{\scriptscriptstyle R}),(a_{\scriptscriptstyle L}-\alpha _{\scriptscriptstyle L})/b_{\scriptscriptstyle L})\}$, we must have

$$\begin{aligned} \left\langle X_{\scriptscriptstyle L}(-1,y),(1,0)\right\rangle \left\langle X_{\scriptscriptstyle C}(-1,y),(1,0)\right\rangle >0 \end{aligned}$$

and

$$\begin{aligned} \left\langle X_{\scriptscriptstyle R}(1,y),(1,0)\right\rangle \left\langle X_{\scriptscriptstyle C}(1,y),(1,0)\right\rangle >0. \end{aligned}$$

But this implies that $b_{\scriptscriptstyle L}b_{\scriptscriptstyle C}>0$, $b_{\scriptscriptstyle R}b_{\scriptscriptstyle C}>0$, $P_1=P_2$ and $P_3=P_4$. Therefore, as $b_{\scriptscriptstyle C}>0$, we have that

$$\begin{aligned} \begin{aligned}&\quad \alpha _{\scriptscriptstyle L}=\frac{a_{\scriptscriptstyle L}b_{\scriptscriptstyle C}+b_{\scriptscriptstyle L}(\alpha _{\scriptscriptstyle C}-a_{\scriptscriptstyle C})}{b_{\scriptscriptstyle C}},\quad b_{\scriptscriptstyle L}>0,\\&\alpha _{\scriptscriptstyle R}=\frac{-a_{\scriptscriptstyle R}b_{\scriptscriptstyle C}+b_{\scriptscriptstyle R}(a_{\scriptscriptstyle C}+\alpha _{\scriptscriptstyle C})}{b_{\scriptscriptstyle C}}\quad \text {and}\quad b_{\scriptscriptstyle R}>0. \end{aligned} \end{aligned}$$

(3)

Assuming the conditions (3), consider the change of variables

$$\begin{aligned} \left( \begin{array}{c} u\\ v \end{array}\right) =\left( \begin{array}{cc} 1 &{} 0\vspace{0.2cm}\\ \dfrac{a_{\scriptscriptstyle C}}{\omega _{\scriptscriptstyle C}} &{}\,\,\,\,\, \dfrac{b_{\scriptscriptstyle C}}{\omega _{\scriptscriptstyle C}} \end{array}\right) \left( \begin{array}{c} x\\ y \end{array}\right) +\left( \begin{array}{c} 0\vspace{0.2cm}\\ \dfrac{\alpha _{\scriptscriptstyle C}}{\omega _{\scriptscriptstyle C}} \end{array}\right) , \end{aligned}$$

with $\omega _{\scriptscriptstyle C}=\sqrt{-a^2_{\scriptscriptstyle C} - b_{\scriptscriptstyle C}c_{\scriptscriptstyle C}}$. Applying this change of variables and rescaling the time by $\tilde{t}=\omega _{\scriptscriptstyle C}\,t$, we obtain the results after rewriting the parameters. $\square$

Remark 4

Consider the system (1)$|_{\epsilon =0}$ in its normal form, i.e. with $\alpha _{\scriptscriptstyle L}=a_{\scriptscriptstyle L}$, $\alpha _{\scriptscriptstyle R}=-a_{\scriptscriptstyle R}$, $b_{\scriptscriptstyle C}=c_{\scriptscriptstyle C}=1$ and $a_{\scriptscriptstyle C}=\alpha _{\scriptscriptstyle C}=0$. Note that when $\beta _{\scriptscriptstyle C}=0$, we have that the singular point of the central subsystem from (1)$|_{\epsilon =0}$ is at the origin. In this case, assuming the hypotheses (H1) and (H2), the period annulus of system (1)$|_{\epsilon =0}$ has all its periodic orbits passing through the three zones bounded by the orbit $L_0$ of the central subsystem tangent to straight lines $x=\pm 1$ in the points $P_{\scriptscriptstyle R}=(1,0)$ and $P_{\scriptscriptstyle L}=(-1,0)$ (see Fig. 3 (a)).

If $\beta _{\scriptscriptstyle C}\ne 0$, after a reflection around the straight line $x=0$ (if necessary), we can assuming without loss of generality that $-1<\beta _{\scriptscriptstyle C}<0$. In this case, the period annulus of system (1)$|_{\epsilon =0}$ has all its periodic orbits passing through the three zones bounded by the orbit ${{\tilde{L}}}_0$ of the central subsystem tangent to straight lines $x= 1$ in the point $P_{\scriptscriptstyle R}=(1,0)$. Note that, ${{\tilde{L}}}_0$ intercept crosswise the straight line $x= -1$ in two distinct points. Moreover, the period annulus has periodic orbits passing by two zones, which are bounded by ${{\tilde{L}}}_0$ and ${{\hat{L}}}_{0}$, where ${{\hat{L}}}_{0}$ is the orbit of the central subsystem tangent to straight lines $x= -1$ in the point $P_{\scriptscriptstyle R}=(-1,0)$. Observe that ${{\hat{L}}}_{0}$ is contained in the region bounded by ${{\tilde{L}}}_0$ (see Fig. 3 (b)).

In this paper we will study only the case where $\beta _{\scriptscriptstyle C}=0$. The compute for the case $\beta _{\scriptscriptstyle C}\ne 0$ are more complicated and leave for future work.

Fig. 3

Periodic orbits tangent to straight lines $x=\pm 1$ of the system (1)$|_{\epsilon =0}$ with $\alpha _{\scriptscriptstyle L}=a_{\scriptscriptstyle L}$, $\alpha _{\scriptscriptstyle R}=-a_{\scriptscriptstyle R}$, $b_{\scriptscriptstyle C}=c_{\scriptscriptstyle C}=1$ and $a_{\scriptscriptstyle C}=\alpha _{\scriptscriptstyle C}=0$ when $\beta _{\scriptscriptstyle C}=0$ (a) and $\beta _{\scriptscriptstyle C}\ne 0$ (b)

In what follows, we will consider the piecewise linear near–Hamiltonian system system (1) such that (1)$|_{\epsilon =0}$ is in its normal form and the singular point of the central subsystem from (1)$|_{\epsilon =0}$ is at the origin, i.e. we assume system (1) with $\alpha _{\scriptscriptstyle L}=a_{\scriptscriptstyle L}$, $\alpha _{\scriptscriptstyle R}=-a_{\scriptscriptstyle R}$, $b_{\scriptscriptstyle C}=1$, $c_{\scriptscriptstyle C}=-1$, $a_{\scriptscriptstyle C}=\alpha _{\scriptscriptstyle C}=0$, $\beta _{\scriptscriptstyle C}=0$ and

$$\begin{aligned}&f(x,y)=\left\{ \begin{array}{ll} f_{\scriptscriptstyle L}(x,y)=\sum \limits _{i+j=0}^{n}r_{ij}x^{i}y^{j}, \quad x\le -1, \\ f_{\scriptscriptstyle C}(x,y)=\sum \limits _{i+j=0}^{n}u_{ij}x^{i}y^{j}, \quad -1\le x\le 1, \\ f_{\scriptscriptstyle R}(x,y)=\sum \limits _{i+j=0}^{n}p_{ij}x^{i}y^{j}, \quad x \ge 1, \\ \end{array} \right. \end{aligned}$$

(4)

$$\begin{aligned}&g(x,y)=\left\{ \begin{array}{ll} g_{\scriptscriptstyle L}(x,y)=\sum \limits _{i+j=0}^{n}s_{ij}x^{i}y^{j}, \quad x\le -1, \\ g_{\scriptscriptstyle C}(x,y)=\sum \limits _{i+j=0}^{n}v_{ij}x^{i}y^{j}, \quad -1\le x\le 1, \\ g_{\scriptscriptstyle R}(x,y)=\sum \limits _{i+j=0}^{n}q_{ij}x^{i}y^{j}, \quad x \ge 1, \\ \end{array} \right. \end{aligned}$$

(5)

for $n=1,2,3$.

4 Proof of Theorem 1

In order to compute the zeros of the first order Melnikov function, it is necessary to find the open interval J, where it is define. For this, consider the follow proposition.

Proposition 5

Consider the system (1) satisfying the hypotheses (Hi), $i=1,2$. Then $J=(0,\tau _{\scriptscriptstyle R})$, where $\tau _{\scriptscriptstyle R}=(a_{\scriptscriptstyle R}^2-b_{\scriptscriptstyle R}\beta _{\scriptscriptstyle R}-\omega _{\scriptscriptstyle R}^2)/b_{\scriptscriptstyle R}\omega _{\scriptscriptstyle R}$ with $\omega _{\scriptscriptstyle R}=\sqrt{a^2_{\scriptscriptstyle R} + b_{\scriptscriptstyle R}c_{\scriptscriptstyle R}}$, and the period annulus are equivalents to one of the figures of Figs. 4 and 5.

Proof

Firstly, note that if the saddles of the right or left subsystem from (1)$|_{\epsilon =0}$ are virtual or if they are under the straight lines $x=\pm 1$, then we have not periodic orbits passing through the three zones. Let $W^u_{\scriptscriptstyle R}$ and $W^s_{\scriptscriptstyle R}$ (resp. $W^u_{\scriptscriptstyle L}$ and $W^s_{\scriptscriptstyle L}$) be the unstable and stable separatrices of the saddles of the right (resp. left) subsystems from (1)$|_{\epsilon =0}$, respectively. Denote by $P_{\scriptscriptstyle L}^{i}=W^i_{\scriptscriptstyle L}\cap \{(-1,y):y\in \mathbb {R}\}$ and $P_{\scriptscriptstyle R}^{i}=W^i_{\scriptscriptstyle R}\cap \{(1,y):y\in \mathbb {R}\}$, for $i=u,s$. After some compute, is possible to show that

$$\begin{aligned} P_{\scriptscriptstyle L}^{u}=(-1,\tau _{\scriptscriptstyle L}),\quad P_{\scriptscriptstyle L}^{s}=(-1,-\tau _{\scriptscriptstyle L}),\quad P_{\scriptscriptstyle R}^{u}=(1,-\tau _{\scriptscriptstyle R}),\quad P_{\scriptscriptstyle R}^{s}=(1,\tau _{\scriptscriptstyle R}), \end{aligned}$$

where $\tau _{\scriptscriptstyle R}=(a_{\scriptscriptstyle R}^2-b_{\scriptscriptstyle R}\beta _{\scriptscriptstyle R}-\omega _{\scriptscriptstyle R}^2)/b_{\scriptscriptstyle R}\omega _{\scriptscriptstyle R}$, $\tau _{\scriptscriptstyle L}=(a_{\scriptscriptstyle L}^2+b_{\scriptscriptstyle L}\beta _{\scriptscriptstyle L}-\omega _{\scriptscriptstyle L}^2)/b_{\scriptscriptstyle L}\omega _{\scriptscriptstyle L}$, $\omega _{\scriptscriptstyle R}=\sqrt{a^2_{\scriptscriptstyle R} + b_{\scriptscriptstyle R}c_{\scriptscriptstyle R}}$ and $\omega _{\scriptscriptstyle L}=\sqrt{a^2_{\scriptscriptstyle L} + b_{\scriptscriptstyle L}c_{\scriptscriptstyle L}}$. Note that we have a symmetry between the points $P_{\scriptscriptstyle L}^{u}$ and $P_{\scriptscriptstyle L}^{s}$ (resp. $P_{\scriptscriptstyle R}^{u}$ and $P_{\scriptscriptstyle R}^{s}$) with respect to x-axis. Let $\tau$ be the smallest ordinate value between the points $P_{\scriptscriptstyle R}^{s}$ and $P_{\scriptscriptstyle L}^{u}$, i.e. $\tau = \min \{\tau _{\scriptscriptstyle R},\tau _{\scriptscriptstyle L}\}$. Then, less than one reflection around the y-axis, we can assuming that $\tau =\tau _{\scriptscriptstyle R}$.

As the vector field $X_{\scriptscriptstyle C}$ associated with the central subsystem from (1)$|_{\epsilon =0}$ is $X_{\scriptscriptstyle C}(x,y)=(y,-x)$, if the ordinates of the points $P_{\scriptscriptstyle R}^{s}$ and $P_{\scriptscriptstyle L}^{u}$ are distinct, i.e. $\tau _{\scriptscriptstyle R}\ne \tau _{\scriptscriptstyle L}$ (see Fig. 4), then we have a homoclinic loop passing through the points $P_{\scriptscriptstyle R}^{s}$ and $P_{\scriptscriptstyle R}^{u}$. Otherwise, if the ordinates of points $P_{\scriptscriptstyle R}^{s}$ and $P_{\scriptscriptstyle L}^{u}$ are the same, i.e. $\tau _{\scriptscriptstyle R}=\tau _{\scriptscriptstyle L}$ (see Fig. 5), then we have a hetoclinic orbit passing through the points $P_{\scriptscriptstyle R}^{s}$, $P_{\scriptscriptstyle R}^{u}$, $P_{\scriptscriptstyle L}^{s}$ and $P_{\scriptscriptstyle L}^{u}$. Moreover, the central subsystem from (1)$|_{\epsilon =0}$ has a periodic orbit tangent to straight lines $x=\pm 1$ in the points $P_{\scriptscriptstyle R}=(1,0)$ and $P_{\scriptscriptstyle L}=(-1,0)$. The Figs. 4 and 5 shows the possibles phase portraits of the system (1)$|_{\epsilon =0}$.

Fig. 4

Phase portrait of system (1)$|_{\epsilon =0}$ with $\tau _{\scriptscriptstyle R}\ne \tau _{\scriptscriptstyle L}$

Fig. 5

Phase portrait of system (1)$|_{\epsilon =0}$ with $\tau _{\scriptscriptstyle R}=\tau _{\scriptscriptstyle L}$

Consider a initial point of form $A(h)=(1,h)$, with $h\in (0,\tau _{\scriptscriptstyle R})$. By the hypothesis (H2), the system (1)$|_{\epsilon =0}$ has a family of crossing periodic orbits that intersects the straight lines $x=\pm 1$ at four points, A(h), $A_1(h)=(1,a_1(h))$, with $a_1(h)<h$, and $A_2(h)=(-1,a_2(h))$, $A_3(h)=(-1,a_3(h))$, with $a_2(h)<a_3(h)$ satisfying

$$\begin{aligned} \begin{aligned}&H^{\scriptscriptstyle R}(A(h))=H^{\scriptscriptstyle R}(A_1(h)), \\&H^{\scriptscriptstyle C}(A_1(h))=H^{\scriptscriptstyle C}(A_2(h)), \\&H^{\scriptscriptstyle L}(A_2(h))=H^{\scriptscriptstyle L}(A_3(h)), \\&H^{\scriptscriptstyle C}(A_3(h))=H^{\scriptscriptstyle C}(A(h)), \end{aligned} \end{aligned}$$

where $H^{\scriptscriptstyle R}$, $H^{\scriptscriptstyle C}$ and $H^{\scriptscriptstyle L}$ are given by normal form from Proposition 3. More precisely, we have the equations

$$\begin{aligned} \begin{aligned}&\frac{b_{\scriptscriptstyle R}}{2}(h-a_1(h))(h+a_1(h))=0, \\&\frac{1}{2}(a_1(h)-a_2(h))(a_1(h)+a_2(h))=0, \\&\frac{b_{\scriptscriptstyle L}}{2}(a_2(h)-a_3(h))(a_2(h)+a_3(h))=0, \\&\frac{1}{2}(a_3(h)-h)(a_3(h)+h)=0. \end{aligned} \end{aligned}$$

As $a_1(h)<h$, $a_2(h)<a_3(h)$, $b_{\scriptscriptstyle R}>0$ and $b_{\scriptscriptstyle L}>0$, the only solution of system above is $a_1(h)=-h$, $a_2(h)=-h$ and $a_3(h)=h$, i.e. we have the four points given by $A(h)=(1,h)$, $A_1(h)=(1,-h)$, $A_2(h)=(-1,-h)$ and $A_3(h)=(-1,h)$. Moreover, system (1)$|_{\epsilon =0}$ has a periodic orbit $L_h$ passing through these points, for all $h\in (0,\tau _{\scriptscriptstyle R})$. If $h\in [\tau _{\scriptscriptstyle R},\infty )$ then the orbit of the system (1)$|_{\epsilon =0}$ with initial condition in A(h) do not return to straight line $x=1$ to positive times, i.e. the system (1)$|_{\epsilon =0}$ has no periodic orbit passing thought the point A(h). Therefore, if $h\in (0,\tau _{\scriptscriptstyle R})$ the system (1)$|_{\epsilon =0}$ has a period annulus, formed by the periodic orbits $L_h$, limited by one periodic orbit $L_0$ tangent to the straight lines $x=\pm 1$ and a homoclinic loop if $\tau _{\scriptscriptstyle R}\ne \tau _{\scriptscriptstyle L}$ (see Fig. 4) or heteroclinic orbit if $\tau _{\scriptscriptstyle R}=\tau _{\scriptscriptstyle L}$ (see Fig. 5). This complete the proof. $\square$

As $A(h)=(1,h)$, $A_1(h)=(1,-h)$, $A_2(h)=(-1,-h)$ and $A_3(h)=(-1,h)$, we have the follow immediate corollary.

Corollary 6

Let J be the interval of definition of Melnikov function (2). For $h\in J$,

$$\begin{aligned} \frac{H_y^{\scriptscriptstyle R}(A)}{H_y^{\scriptscriptstyle C}(A)}=b_{\scriptscriptstyle R},\quad \frac{H_y^{\scriptscriptstyle R}(A)H_y^{\scriptscriptstyle C}(A_3)}{H_y^{\scriptscriptstyle C}(A)H_y^{\scriptscriptstyle L}(A_3)}=\frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}},\quad \frac{H_y^{\scriptscriptstyle R}(A)H_y^{\scriptscriptstyle C}(A_3)H_y^{\scriptscriptstyle L}(A_2)}{H_y^{\scriptscriptstyle C}(A)H_y^{\scriptscriptstyle L}(A_3)H_y^{\scriptscriptstyle C}(A_2)}=b_{\scriptscriptstyle R} \end{aligned}$$

and

$$\begin{aligned} \frac{H_y^{\scriptscriptstyle R}(A)H_y^{\scriptscriptstyle C}(A_3)H_y^{\scriptscriptstyle L}(A_2)H_y^{\scriptscriptstyle C}(A_1)}{H_y^{\scriptscriptstyle C}(A)H_y^{\scriptscriptstyle L}(A_3)H_y^{\scriptscriptstyle C}(A_2)H_y^{\scriptscriptstyle R}(A_1)}=1. \end{aligned}$$

Then, the first order Melnikov function associated to system (1) can be written as

$$\begin{aligned} \begin{aligned} M(h)&= b_{\scriptscriptstyle R}\int _{\widehat{A_3A}}g_{\scriptscriptstyle C}dx-f_{\scriptscriptstyle C}dy+\frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}} \int _{\widehat{A_2A_3}}g_{\scriptscriptstyle L}dx-f_{\scriptscriptstyle L}dy\\&\quad + b_{\scriptscriptstyle R}\int _{\widehat{A_1A_2}}g_{\scriptscriptstyle C}dx-f_{\scriptscriptstyle C}dy+\int _{\widehat{AA_1}}g_{\scriptscriptstyle R}dx-f_{\scriptscriptstyle R}dy. \end{aligned} \end{aligned}$$

In what follows, we will simplify the expression to the first order Melnikov function associated to system (1) when $n=1,2,3$. For this, we will distinguish two cases. In the first one, we consider the case when $n=1$. In this case, we will find an expression for the Melnikov function associated with system (1) without assuming specific values for its parameters. For the second one, i.e. when $n=2,3$, we assuming the values $b_{\scriptscriptstyle L}=a_{\scriptscriptstyle L}=b_{\scriptscriptstyle R}=c_{\scriptscriptstyle R}=1$, $c_{\scriptscriptstyle L}=a_{\scriptscriptstyle R}=0$ and $\beta _{\scriptscriptstyle R}=-2$ for the parameters of system (1). This was necessary due to the complexity of the compute involved.

For this, we define the functions:

$$\begin{aligned} \begin{aligned} f_0(h)&= h, \\ f_1(h)&= (h^2+1)\arccos \bigg (\frac{h^2-1}{h^2+1}\bigg ), \\ f_2(h)&= (h^2-1)\log \bigg (\frac{1+h}{1-h}\bigg ), \\ f_3(h)&= (h^2-4)\log \bigg (\frac{2+h}{2-h}\bigg ), \\ f_4(h)&= h^3, \\ f_5(h)&= h^2(h^2+1)\arccos \bigg (\frac{h^2-1}{h^2+1}\bigg ), \\ f_6(h)&= h^2(h^2-1)\log \bigg (\frac{1+h}{1-h}\bigg ), \\ f_7(h)&= h^2(h^2-4)\log \bigg (\frac{2+h}{2-h}\bigg ), \\ f_{\scriptscriptstyle R}^{\scriptscriptstyle S}(h)&= (h^2-\tau _{\scriptscriptstyle R}^2)\log \bigg (\frac{h+\tau _{\scriptscriptstyle R}}{\tau _{\scriptscriptstyle R}-h}\bigg ), \\ f_{\scriptscriptstyle L}^{\scriptscriptstyle S}(h)&= (h^2-\tau _{\scriptscriptstyle L}^2)\log \bigg (\frac{h+\tau _{\scriptscriptstyle L}}{\tau _{\scriptscriptstyle L}-h}\bigg ),\\ \end{aligned} \end{aligned}$$

(6)

with $h\in (0,1)$ for $f_i(h)$, $i=0,\dots ,7$, and $h\in (0,\tau _{\scriptscriptstyle R})$ for $f_j^{\scriptscriptstyle S}(h)$, $j=R,L$.

Theorem 7

The first order Melnikov function M(h) associated with system (1) when $n=1$ can be expressed as

$$\begin{aligned} M_{11}(h)=k_0f_0(h)+k_1f_1(h)+k_{\scriptscriptstyle R}f_{\scriptscriptstyle R}^{\scriptscriptstyle S}(h)+k_{\scriptscriptstyle L}f_{\scriptscriptstyle L}^{\scriptscriptstyle S}(h), \end{aligned}$$

(7)

if $\tau _{\scriptscriptstyle R}\ne \tau _{\scriptscriptstyle L}$, or

$$\begin{aligned} M_{12}(h)=k_0f_0(h)+k_1f_1(h)+k_{\scriptscriptstyle R} f_{\scriptscriptstyle R}^{\scriptscriptstyle S}(h), \end{aligned}$$

(8)

if $\tau _{\scriptscriptstyle R}=\tau _{\scriptscriptstyle L}$, with $h\in (0,\tau _{\scriptscriptstyle R})$. The functions $f_0,f_1,f_{\scriptscriptstyle R}^{\scriptscriptstyle S},f_{\scriptscriptstyle L}^{\scriptscriptstyle S}$ are given in (6). Here the coefficients $k_0$, $k_1$, $k_{\scriptscriptstyle R}$ and $k_{\scriptscriptstyle L}$ depend on the parameters of system (1).

Proof

The orbit $(x_{\scriptscriptstyle R}(t),y_{\scriptscriptstyle R}(t))$ of the system (1)$|_{\epsilon =0}$, such that $(x_{\scriptscriptstyle R}(0),$ $y_{\scriptscriptstyle R}(0))=(1,h)$, is given by

$$\begin{aligned} \begin{aligned} x_{\scriptscriptstyle R}(t)=\,&-\frac{e^{-t \omega _{\scriptscriptstyle R}}}{2\omega _{\scriptscriptstyle R}}(b_{\scriptscriptstyle R} h-b_{\scriptscriptstyle R}e^{2t \omega _{\scriptscriptstyle R}}h-2e^{t \omega _{\scriptscriptstyle R}}\omega _{\scriptscriptstyle R}+b_{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}-2b_{\scriptscriptstyle R}e^{t \omega _{\scriptscriptstyle R}}\tau _{\scriptscriptstyle R}\\&+b_{\scriptscriptstyle R}e^{2t \omega _{\scriptscriptstyle R}}\tau _{\scriptscriptstyle R}), \\ y_{\scriptscriptstyle R}(t)=\,&-\frac{e^{-t \omega _{\scriptscriptstyle R}}}{2\omega _{\scriptscriptstyle R}}(-a_{\scriptscriptstyle R}h+a_{\scriptscriptstyle R}e^{2t \omega _{\scriptscriptstyle R}}h-\omega _{\scriptscriptstyle R}h- e^{2t \omega _{\scriptscriptstyle R}}\omega _{\scriptscriptstyle R}h-a_{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}\\&+2a_{\scriptscriptstyle R}e^{t \omega _{\scriptscriptstyle R}}\tau _{\scriptscriptstyle R}-a_{\scriptscriptstyle R}e^{2t \omega _{\scriptscriptstyle R}}\tau _{\scriptscriptstyle R}-\omega _{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}+e^{2t \omega _{\scriptscriptstyle R}}\omega _{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}). \end{aligned} \end{aligned}$$

The flight time of the orbit $(x_{\scriptscriptstyle R}(t),y_{\scriptscriptstyle R}(t))$, from $A(h)=(1,h)$ to $A_1(h)=(1,-h)$, is

$$\begin{aligned} t_{\scriptscriptstyle R}=\frac{1}{\omega _{\scriptscriptstyle R}}\log \bigg (\frac{h+\tau _{\scriptscriptstyle R}}{\tau _{\scriptscriptstyle R}-h}\bigg ). \end{aligned}$$

Now, for $g_{\scriptscriptstyle R}$ and $f_{\scriptscriptstyle R}$ defined in (4) and (5), respectively, we have

$$\begin{aligned} \begin{aligned} I_{\scriptscriptstyle R}^1&=\int _{\widehat{AA_1}}g_{\scriptscriptstyle R}dx-f_{\scriptscriptstyle R}dy \\&=\int _{0}^{t_{\scriptscriptstyle R}}(g_{\scriptscriptstyle R}(x_{\scriptscriptstyle R}(t), y_{\scriptscriptstyle R}(t)) x'_{\scriptscriptstyle R}(t) - f_{\scriptscriptstyle R}(x_{\scriptscriptstyle R}(t), y_{\scriptscriptstyle R}(t)) y'_{\scriptscriptstyle R}(t))dt \\&= \alpha _1f_0(h)+\alpha _2f_{\scriptscriptstyle R}^{\scriptscriptstyle S}(h), \end{aligned} \end{aligned}$$

(9)

with

$$\begin{aligned} \alpha _1 =\frac{1}{\omega _{\scriptscriptstyle R}}(2 (p_{00} + p_{10}) \omega _{\scriptscriptstyle R} + b_{\scriptscriptstyle R} (p_{10} + q_{01}) \tau _{\scriptscriptstyle R})\quad \text {and}\quad \alpha _2 = \frac{b_{\scriptscriptstyle R}}{2\omega _{\scriptscriptstyle R}}(p_{10} + q_{01}). \end{aligned}$$

The orbit $(x_{\scriptscriptstyle C1}(t),y_{\scriptscriptstyle C1}(t))$ of the system (1)$|_{\epsilon =0}$, such that $(x_{\scriptscriptstyle C1}(0),y_{\scriptscriptstyle C1}(0))=(1,-h)$, is given by

$$\begin{aligned} \begin{aligned} x_{\scriptscriptstyle C1}(t)&=\cos (t) - h \sin (t), \\ y_{\scriptscriptstyle C1}(t)&=-h \cos (t) - \sin (t). \end{aligned} \end{aligned}$$

The flight time of the orbit $(x_{\scriptscriptstyle C1}(t),y_{\scriptscriptstyle C1}(t))$, from $A_1(h)=(1,-h)$ to $A_2(h)=(-1,-h)$, is

$$\begin{aligned} t_{\scriptscriptstyle C1}=\arccos \Bigg (\frac{h^2-1}{h^2+1}\Bigg ). \end{aligned}$$

Now, for $g_{\scriptscriptstyle C}$ and $f_{\scriptscriptstyle C}$ defined in (4) and (5), respectively, we obtain

$$\begin{aligned} \begin{aligned} {\bar{I}}_{\scriptscriptstyle C}^1 =&\int _{\widehat{A_1A_2}}g_{\scriptscriptstyle C}dx-f_{\scriptscriptstyle C}dy\\ =&\int _{0}^{t_{\scriptscriptstyle C1}}(g_{\scriptscriptstyle C}(x_{\scriptscriptstyle C1}(t), y_{\scriptscriptstyle C1}(t)) x'_{\scriptscriptstyle C1}(t) - f_{\scriptscriptstyle C}(x_{\scriptscriptstyle C1}(t), y_{\scriptscriptstyle C1}(t)) y'_{\scriptscriptstyle C1}(t))dt,\\ =&-2v_{00}+\alpha _3f_0(h)+\alpha _4f_1(h), \end{aligned} \end{aligned}$$

(10)

with

$$\begin{aligned} \alpha _3 = v_{01}-u_{10} \quad \text {and}\quad \alpha _4 = \frac{u_{10} + v_{01}}{2}. \end{aligned}$$

The orbit $(x_{\scriptscriptstyle L}(t),y_{\scriptscriptstyle L}(t))$ of the system (1)$|_{\epsilon =0}$, such that $(x_{\scriptscriptstyle L}(0),y_{\scriptscriptstyle L}(0))=(-1,-h)$, is given by

$$\begin{aligned} \begin{aligned} x_{\scriptscriptstyle L}(t)=\,&\frac{e^{-t \omega _{\scriptscriptstyle L}}}{2\omega _{\scriptscriptstyle L}}(b_{\scriptscriptstyle L} h-b_{\scriptscriptstyle L}e^{2t \omega _{\scriptscriptstyle L}}h-2e^{t \omega _{\scriptscriptstyle L}}\omega _{\scriptscriptstyle L}+b_{\scriptscriptstyle L}\tau _{\scriptscriptstyle L}-2b_{\scriptscriptstyle L}e^{t \omega _{\scriptscriptstyle L}}\tau _{\scriptscriptstyle L}\\&+b_{\scriptscriptstyle L}e^{2t \omega _{\scriptscriptstyle L}}\tau _{\scriptscriptstyle L}), \\ y_{\scriptscriptstyle L}(t)=\,&\frac{e^{-t \omega _{\scriptscriptstyle L}}}{2\omega _{\scriptscriptstyle L}}(-a_{\scriptscriptstyle L}h+a_{\scriptscriptstyle L}e^{2t \omega _{\scriptscriptstyle L}}h-\omega _{\scriptscriptstyle L}h- e^{2t \omega _{\scriptscriptstyle L}}\omega _{\scriptscriptstyle L}h-a_{\scriptscriptstyle L}\tau _{\scriptscriptstyle L}\\&+2a_{\scriptscriptstyle L}e^{t \omega _{\scriptscriptstyle L}}\tau _{\scriptscriptstyle L}-a_{\scriptscriptstyle L}e^{2t \omega _{\scriptscriptstyle L}}\tau _{\scriptscriptstyle L}-\omega _{\scriptscriptstyle L}\tau _{\scriptscriptstyle L}+e^{2t \omega _{\scriptscriptstyle L}}\omega _{\scriptscriptstyle L}\tau _{\scriptscriptstyle L}). \end{aligned} \end{aligned}$$

The flight time of the orbit $(x_{\scriptscriptstyle L}(t),y_{\scriptscriptstyle L}(t))$, from $A_2(h)=(-1,-h)$ to $A_3(h)=(-1,h)$, is

$$\begin{aligned} t_{\scriptscriptstyle L}=\frac{1}{\omega _{\scriptscriptstyle L}}\log \bigg (\frac{h+\tau _{\scriptscriptstyle L}}{\tau _{\scriptscriptstyle L}-h}\bigg ). \end{aligned}$$

Now, for $g_{\scriptscriptstyle L}$ and $f_{\scriptscriptstyle L}$ defined in (4) and (5), respectively, we have

$$\begin{aligned} \begin{aligned} I_{\scriptscriptstyle L}^1&=\int _{\widehat{A_2A_3}}g_{\scriptscriptstyle L}dx-f_{\scriptscriptstyle L}dy \\&=\int _{0}^{t_{\scriptscriptstyle L}}(g_{\scriptscriptstyle L}(x_{\scriptscriptstyle L}(t), y_{\scriptscriptstyle L}(t)) x'_{\scriptscriptstyle L}(t) - f_{\scriptscriptstyle L}(x_{\scriptscriptstyle L}(t), y_{\scriptscriptstyle L}(t)) y'_{\scriptscriptstyle L}(t))dt \\&= \alpha _5f_0(h)+\alpha _6f_{\scriptscriptstyle L}^{\scriptscriptstyle S}(h), \end{aligned} \end{aligned}$$

(11)

with

$$\begin{aligned} \alpha _5 =\frac{1}{\omega _{\scriptscriptstyle L}}(2 (r_{10}-r_{00}) \omega _{\scriptscriptstyle L} + b_{\scriptscriptstyle L} (r_{10} + s_{01}) \tau _{\scriptscriptstyle L})\quad \text {and}\quad \alpha _6 = \frac{b_{\scriptscriptstyle L}}{2\omega _{\scriptscriptstyle L}}(r_{10} + s_{01}). \end{aligned}$$

The orbit $(x_{\scriptscriptstyle C2}(t),y_{\scriptscriptstyle C2}(t))$ of the system (1)$|_{\epsilon =0}$, such that $(x_{\scriptscriptstyle C2}(0),$ $y_{\scriptscriptstyle C2}(0))=(-1,h)$, is given by

$$\begin{aligned} \begin{aligned} x_{\scriptscriptstyle C2}(t)&=-\cos (t) + h \sin (t), \\ y_{\scriptscriptstyle C2}(t)&=h \cos (t) + \sin (t). \end{aligned} \end{aligned}$$

The flight time of the orbit $(x_{\scriptscriptstyle C2}(t),y_{\scriptscriptstyle C2}(t))$, from $A_3(h)=(-1,h)$ to $A(h)=(1,h)$, is

$$\begin{aligned} t_{\scriptscriptstyle C2}=\arccos \Bigg (\frac{h^2-1}{h^2+1}\Bigg ). \end{aligned}$$

Now, for $g_{\scriptscriptstyle C}$ and $f_{\scriptscriptstyle C}$ defined in (4) and (5), respectively, we obtain

$$\begin{aligned} \begin{aligned} I_{\scriptscriptstyle C}^1=&\int _{\widehat{A_3A}}g_{\scriptscriptstyle C}dx-f_{\scriptscriptstyle C}dy \\ =&\int _{0}^{t_{\scriptscriptstyle C2}}(g_{\scriptscriptstyle C}(x_{\scriptscriptstyle C2}(t), y_{\scriptscriptstyle C2}(t)) x'_{\scriptscriptstyle C2}(t) - f_{\scriptscriptstyle C}(x_{\scriptscriptstyle C2}(t), y_{\scriptscriptstyle C2}(t)) y'_{\scriptscriptstyle C2}(t))dt \\ =&\,\,2v_{00}+\alpha _3f_0(h)+\alpha _4f_1(h). \end{aligned} \end{aligned}$$

(12)

Hence, by Corollary 6, the first order Melnivov function associated to system (1) is given by

$$\begin{aligned} M_{11}(h) = b_{\scriptscriptstyle R} I^{1}_{\scriptscriptstyle C}+\frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}}I^{1}_{\scriptscriptstyle L}+b_{\scriptscriptstyle R} {\bar{I}}^{1}_{\scriptscriptstyle C}+I^{1}_{\scriptscriptstyle R}. \end{aligned}$$

(13)

Replacing (9), (10), (11) and (12) in (13) we obtain (7), with

$$\begin{aligned} k_0=\alpha _1 + 2 b_{\scriptscriptstyle R}\alpha _3 + \frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}} \alpha _5,\quad k_1=2 b_{\scriptscriptstyle R} \alpha _4,\quad k_{\scriptscriptstyle R}=\alpha _2\quad \text {and}\quad k_{\scriptscriptstyle L}=\frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}}\alpha _6. \end{aligned}$$

Finally, replacing $\tau _{\scriptscriptstyle L}=\tau _{\scriptscriptstyle R}$ on function $M_{11}(h)$ in (7) we obtain the expression (8) with

$$\begin{aligned}&k_0=\alpha _1 + 2 b_{\scriptscriptstyle R}\alpha _3 + \frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}\omega _{\scriptscriptstyle L}} (2 (r_{10}-r_{00}) \omega _{\scriptscriptstyle L} + b_{\scriptscriptstyle L} (r_{10} + s_{01}) \tau _{\scriptscriptstyle R}), \\&k_1=2 b_{\scriptscriptstyle R} \alpha _4,\quad \text {and}\quad k_{\scriptscriptstyle R}=\alpha _2+\frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}}\alpha _6. \end{aligned}$$

$\square$

For the study of the case when $n=2,3$, let us consider system (1), with

$$\begin{aligned} H(x,y)=\left\{ \begin{array}{ll}\vspace{0.2cm} H^{\scriptscriptstyle L}(x,y)=\dfrac{y^2}{2}+xy+y-\alpha x, \quad x\le -1, \\ \vspace{0.2cm} H^{\scriptscriptstyle C}(x,y)=\dfrac{x^2}{2}+\dfrac{y^2}{2}, \quad \quad \quad -1\le x\le 1, \\ H^{\scriptscriptstyle R}(x,y)=\dfrac{y^2}{2}-\dfrac{x^2}{2}+2x, \quad \quad \quad x \ge 1, \\ \end{array} \right. \end{aligned}$$

(14)

for $\alpha \in \{1,2\}$. We can see that the central subsystem from (1)$|_{\epsilon =0}$ has a center at the origin, the right subsystem has a saddle at the point (2, 0) and if $\alpha =1$ (resp. $\alpha =2$) the left subsystem has a saddle at the point $(-2,1)$ (resp. $(-3,2)$). Moreover, we have that if $\alpha =1$ (resp. $\alpha =2$) then $P_{\scriptscriptstyle L}^{u}=(-1,1)$ (resp. $P_{\scriptscriptstyle L}^{u}=(-1,2)$), $P_{\scriptscriptstyle L}^{s}=(-1,-1)$ (resp. $P_{\scriptscriptstyle L}^{s}=(-1,-2)$), $P_{\scriptscriptstyle R}^{u}=(1,-1)$, $P_{\scriptscriptstyle R}^{s}=(1,1)$ and the central subsystem from (1)$|_{\epsilon =0}$ has a periodic orbit tangent to straight lines $x=\pm 1$ in the points $P_{\scriptscriptstyle R}=(1,0)$ and $P_{\scriptscriptstyle L}=(-1,0)$.

For $A(h)=(1,h)$, with $h\in (0,1)$, the system (1)$|_{\epsilon =0}$ has a family of crossing periodic orbits $L_h$ that intersects the straight lines $x=\pm 1$ at four points, i.e. the hypothesis (H1) is satisfied. More precisely, by equations on (2), for each $h\in (0,1)$ we have the four points given by $A(h)=(1,h)$, $A_1(h)=(1,-h)$, $A_2(h)=(-1,-h)$, $A_3(h)=(-1,h)$ and a periodic orbit

$$\begin{aligned} \begin{aligned} L_h=&\,\,\Big \{(x,y)\in \mathbb {R}^2:H^{\scriptscriptstyle R}(x,y)=\frac{(3 + h^2)}{2},\, x>1\Big \} \\&\cup \Big \{(x,y)\in \mathbb {R}^2:H^{\scriptscriptstyle C}(x,y)=\frac{(1 + h^2)}{2},\, -1\le x\le 1 \quad \text {and}\quad y<0\Big \}\\&\cup \Big \{(x,y)\in \mathbb {R}^2:H^{\scriptscriptstyle L}(x,y)=\frac{(2\alpha + h^2)}{2},\, x<-1\Big \}\\&\cup \Big \{(x,y)\in \mathbb {R}^2:H^{\scriptscriptstyle C}(x,y)=\frac{(1 + h^2)}{2},\, -1\le x\le 1 \quad \text {and}\quad y>0\Big \} \end{aligned} \end{aligned}$$

passing through these points. Therefore, if $h\in (0,1)$ the system (1)$|_{\epsilon =0}$ has a period annulus, formed by the periodic orbits $L_h$, limited by one periodic orbit tangent to the straight lines $x=\pm 1$, when $h=0$, and a heteroclinic orbit (resp. homoclinic loop) if $\alpha =1$ (resp. $\alpha =2$) when $h=1$.

The next theorem provide us a simpler formula for the Melnikov function associated to system (1) with f(h), g(h) and H(h) given by (4), (5) and (14), respectively, when $n=2,3$ and $\alpha \in \{1,2\}$. Its proof follows exactly the same steps of the proof of Theorem 7, (with the obvious changes, of course) and will be omitted to simplify the text.

Theorem 8

The first order Melnikov function associated with system (1), with H(h) given in (14), can be expressed when $\alpha =1$ as

$$\begin{aligned} M_{21}(h)= & {} \sum _{i=0}^{2}k_if_i(h)+k_4f_4(h),\quad \quad \,\, \text {if}\quad n=2, \\ M_{31}(h)= & {} \sum _{i=0}^{2}k_if_i(h)+\sum _{i=4}^{6}k_if_i(h),\quad \text {if}\quad n=3, \end{aligned}$$

and when $\alpha =2$ as

$$\begin{aligned} M_{22}(h)= & {} \sum _{i=0}^{4}k_if_i(h),\quad \text {if}\quad n=2, \\ M_{32}(h)= & {} \sum _{i=0}^{7}k_if_i(h),\quad \text {if}\quad n=3, \end{aligned}$$

for $h\in (0,1)$, where the functions $f_i$, for $i=0,\dots ,7$ are given in (6). Here the coefficients $k_i$, for $i=0,\dots ,7$, depend on the parameters of system (1).

Before proving the Theorem 1, we will need the following results.

Consider the function $F:\mathbb {R}\rightarrow \mathbb {R}$ given by

$$\begin{aligned} F(h)=\sum _{j=0}^{n}C_j(\delta ) (h-\tau )^j+\mathcal {O}((h-\tau )^{n+1}), \end{aligned}$$

(15)

with $\tau \ge 0$ and the coefficients $C_j(\delta )$, $j=0,\dots ,n$, depending on the parameters $\delta =(\delta _1,\dots ,\delta _m)\in \mathbb {R}^m$. Then we have the follow proposition.

Proposition 9

Suppose that there exist an integer $k\ge 1$ and $\tilde{\delta }\in \mathbb {R}^{m}$ with $m\ge k+1$ such that

$$\begin{aligned} C_{j}(\tilde{\delta })=0,\quad j=0,\dots ,k-1,\quad C_{k}(\tilde{\delta })\ne 0 \end{aligned}$$

and

$$\begin{aligned} \text {rank}\,\frac{\partial (C_{0},\dots ,C_{k})}{\partial (\delta _1,\dots ,\delta _m)}\tilde{(\delta )}=k+1. \end{aligned}$$

(16)

Then the function (15) has exactly k real positive simple roots in a neighborhood of $h=\tau$ for all $\delta$ near $\tilde{\delta }$.

Proof

By the condition (16) we can assume that

$$\begin{aligned} \text {det}\,\frac{\partial (C_{0},\dots ,C_{k})}{\partial (\delta _1,\dots ,\delta _{k+1})}(\tilde{\delta })\ne 0, \end{aligned}$$

Then the change of parameters $\tilde{C}_i=C_i(\delta _1,\dots ,\delta _{k+1},\tilde{\delta }_{k+2},\dots ,\tilde{\delta }_{m})$, $i=0,\dots ,k$, has inverse $\delta _j(\tilde{C}_{0},\dots ,\tilde{C}_{k})$, $j=1,\dots ,k+1$, and can write (15) as

$$\begin{aligned} F(h)=\tilde{C}_0+\tilde{C}_1(h-\tau )+\dots +\tilde{C}_k(h-\tau )^k+\mathcal {O}((h-\tau )^{k+1}), \end{aligned}$$

(17)

with $\tilde{C}_k(\tilde{\delta })\ne 0$ and $\tilde{C}_j(\tilde{\delta })=0$, $j=0,\dots ,k-1$.

Let $0<|\tilde{C}_k-C_k(\tilde{\delta})|\ll 1$ and $0<\tau -h_k\ll 1$ such that

$$\begin{aligned} \tilde{C}_k(h_k-\tau )^k>0. \end{aligned}$$

Take $\tilde{C}_{k-1}$ such that $|\tilde{C}_{k-1}|\ll |\tilde{C}_{k}|$, $\tilde{C}_{k-1}\tilde{C}_{k}<0$ and

$$\begin{aligned} \tilde{C}_{k-1}(h_{k}-\tau )^{k-1}+\tilde{C}_k(h_{k}-\tau )^k>0. \end{aligned}$$

Now, as $\tilde{C}_{k-1}\tilde{C}_{k}<0$, we can choose $h_{k-1}$, such that $0<\tau -h_{k-1}\ll \tau -h_k\ll 1$ and

$$\begin{aligned} \tilde{C}_{k-1}(h_{k-1}-\tau )^{k-1}+\tilde{C}_k(h_{k-1}-\tau )^k<0. \end{aligned}$$

Therefore, the equation

$$\begin{aligned} \tilde{C}_{k-1}(h-\tau )^{k-1}+\tilde{C}_k(h-\tau )^k=0 \end{aligned}$$

has a root $h_k^{*}$, with $h_{k}<h_k^{*}<h_{k-1}$. Continuing with this reasoning, there are $\tilde{C}_0,\dots ,\tilde{C}_{k}$, such that

$$\begin{aligned} \tilde{C}_0\tilde{C}_{1}<0,\,\,\tilde{C}_1\tilde{C}_{2}<0,\dots ,\,\,\tilde{C}_{k-1}\tilde{C}_{k}<0,\,\,|\tilde{C}_0|\ll |\tilde{C}_{1}|\ll \dots \ll |\tilde{C}_{k}|, \end{aligned}$$

and the equation (17) has k real positive roots. Moreover, as $\tilde{C}_k(\tilde{\delta })\ne 0$ and by Rolle’s theorem, for all $\delta$ near $\tilde{\delta }$ we can choose the $\tilde{C}_j$ and $h_j$, $j=0,\dots ,k$, such that equation (17) has exactly k real positive simple roots near $h=\tau$. $\square$

Lemma 10

Let $f:\mathbb {R}\rightarrow \mathbb {R}$ be a function of class $\mathbb {C}^{k+1}$, $k\ge 1$. Then

$$\begin{aligned} f(x)\log (\tau -x)=\mathcal {P}(x)\log (\tau -x)+\mathcal {R}(x), \end{aligned}$$

where $\mathcal {P}(x)=\sum _{i=0}^{k}\frac{f^{(i)}(\tau )}{i!}(x-\tau )^i$ is the Taylor’s polynomial of f at $x=\tau$ of degree k and $\mathcal {R}(x)=\log (\tau -x)(f(x)-\mathcal {P}(x))$. Moreover, $\lim _{x\rightarrow \tau }\mathcal {R}(x)=0$.

Proof

To prove the lemma, it suffices to show that $\lim _{x\rightarrow \tau }\mathcal {R}(x)=0$. By the Taylor’s formula with Lagrange remainder, there is $c\in \mathbb {R}$ such that

$$\begin{aligned} \mathcal {R}(x)=\frac{f^{(k+1)}(c)}{(k+1)!}\log (\tau -x)(x-\tau )^{k+1}. \end{aligned}$$

By the L’Hospital rule

$$\begin{aligned} \begin{aligned} \lim _{x\rightarrow \tau }\mathcal {R}(x)=&\,\frac{f^{(k+1)}(c)}{(k+1)!}\lim _{x\rightarrow \tau }\log (\tau -x)(x-\tau )^{k+1}\\ =&\,\frac{f^{(k+1)}(c)}{(k+1)!}\lim _{x\rightarrow \tau }\frac{\log (\tau -x)}{(x-\tau )^{-(k+1)}}\\ =&\,\frac{f^{(k+1)}(c)}{(k+1)!}\lim _{x\rightarrow \tau }\frac{(\tau -x)^{-1}}{(k+1)(x-\tau )^{-(k+2)}}\\ =&\,\,-\frac{f^{(k+1)}(c)}{(k+1)!(k+1)}\lim _{x\rightarrow \tau }(x-\tau )^{(k+1)}=0. \end{aligned} \end{aligned}$$

$\square$

Proof of Theorem 1

To prove the Theorem 1, firstly, we begin with the case $n=1$. For this case, we have two sub-cases. The first one is when $\tau _{\scriptscriptstyle R}=\tau _{\scriptscriptstyle L}$ (i.e. we have a heteroclinic orbit) and the second one is when $\tau _{\scriptscriptstyle R}\ne \tau _{\scriptscriptstyle L}$ (i.e. we have an homoclinic loop). For the cases $n=2,3$, again, we have two sub-cases. The first one is when $\alpha =1$ (i.e. we have a heteroclinic orbit) and the second one is when $\alpha =2$ (i.e. we have an homoclinic loop).

Case $n=1$. Consider the Melnikov functions $M_{11}(h)$ and $M_{12}(h)$ given by the Theorem 7. By Lemma 10 we can expand these functions at $h=\tau _{\scriptscriptstyle R}$ as

$$\begin{aligned}&M_{11}(h)=\sum _{j=0}^{3}C_{11}^j(h-\tau _{\scriptscriptstyle R})^j+\sum _{j=1}^ {2}D_{11}^j\log (\tau _{\scriptscriptstyle R}-h)(h-\tau _{\scriptscriptstyle R})^j \end{aligned}$$

(18)

$$\begin{aligned}&+ \mathcal {O}((h-\tau _{\scriptscriptstyle R})^4),\nonumber \\&M_{12}(h)=\sum _{j=0}^{2}C_{12}^j(h-\tau _{\scriptscriptstyle R})^j+\sum _{j=1}^{2}D_{12}^j\log (\tau _{\scriptscriptstyle R}-h)(h-\tau _{\scriptscriptstyle R})^j\nonumber \\&+\mathcal {O}((h-\tau _{\scriptscriptstyle R})^3), \end{aligned}$$

(19)

where

$$\begin{aligned} C_{11}^0&= \tau _{\scriptscriptstyle R} \bigg (\frac{2 b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}} (r_{10}-r_{00}) + 2 (p_{00} + p_{10} + b_{\scriptscriptstyle R} ( v_{01}-u_{10})) + \frac{\tau _{\scriptscriptstyle L}b_{\scriptscriptstyle R}}{\omega _{\scriptscriptstyle L}}\\&\quad (r_{10} + s_{01}) + \frac{\tau _{\scriptscriptstyle R}b_{\scriptscriptstyle R}}{\omega _{\scriptscriptstyle R}}(p_{10} + q_{01})\bigg ) + b_{\scriptscriptstyle R} (u_{10} + v_{01})(1 + \tau _{\scriptscriptstyle R}^2)\\&\quad \arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg ) + \frac{b_{\scriptscriptstyle R}}{2\omega _{\scriptscriptstyle L}}(r_{10} + s_{01}) (\tau _{\scriptscriptstyle R}-\tau _{\scriptscriptstyle L}) (\tau _{\scriptscriptstyle L} + \tau _{\scriptscriptstyle R})\\&\quad \log \bigg (\frac{\tau _{\scriptscriptstyle L} + \tau _{\scriptscriptstyle R}}{\tau _{\scriptscriptstyle L} - \tau _{\scriptscriptstyle R}}\bigg ),\\ C_{11}^1&= \frac{2 b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}}(r_{10}-r_{00}) + 2 (p_{00} + p_{10} -2 b_{\scriptscriptstyle R} u_{10} ) + \frac{\tau _{\scriptscriptstyle L}b_{\scriptscriptstyle R}}{\omega _{\scriptscriptstyle L}}(p_{10} \\&\quad + q_{01}) +b_{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}\bigg (2 (u_{10} + v_{01})\arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg )+\frac{\log (2\tau _{\scriptscriptstyle R})}{\tau _{\scriptscriptstyle R}}(p_{10} \\&\quad + q_{01})+\frac{1}{\tau _{\scriptscriptstyle L}}(r_{10} + s_{01})\log \bigg (\frac{\tau _{\scriptscriptstyle L} + \tau _{\scriptscriptstyle R}}{\tau _{\scriptscriptstyle L} - \tau _{\scriptscriptstyle R}}\bigg )\bigg ),\\ C_{11}^2&= \frac{b_{\scriptscriptstyle R}}{2}\bigg (2 (u_{10} + v_{01}) \bigg (\arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg )-\frac{2\tau _{\scriptscriptstyle R}}{1+\tau _{\scriptscriptstyle R}^2}\bigg ) + \frac{1}{\omega _{\scriptscriptstyle R}}(p_{10} + q_{01}) \\&\quad (1 + \log (2) + \log (\tau _{\scriptscriptstyle R})) + \frac{1}{\omega _{\scriptscriptstyle L}}(r_{10} + s_{01})\bigg (\frac{2\tau _{\scriptscriptstyle R}\tau _{\scriptscriptstyle L}}{\tau _{\scriptscriptstyle L}^2-\tau _{\scriptscriptstyle R}^2}+ \log \bigg (\frac{\tau _{\scriptscriptstyle L} + \tau _{\scriptscriptstyle R}}{\tau _{\scriptscriptstyle L} - \tau _{\scriptscriptstyle R}}\bigg )\bigg )\bigg ),\\ \\ C_{11}^3&=\frac{b_{\scriptscriptstyle R}}{8\omega _{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}}(p_{10} + q_{01})+\frac{2b_{\scriptscriptstyle R}}{3}\bigg (\frac{\tau _{\scriptscriptstyle L}^3}{\omega _{\scriptscriptstyle L}(\tau _{\scriptscriptstyle L}^2-\tau _{\scriptscriptstyle R}^2)^2}(r_{10} + s_{01}) -\frac{2}{(1+\tau _{\scriptscriptstyle R}^2)^2} \\&\quad (u_{10} + v_{01})\bigg ), \\ C_{12}^0&= \tau _{\scriptscriptstyle R} \bigg (\frac{2 b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}} ( r_{10}-r_{00}) + 2 (p_{00} + p_{10} + b_{\scriptscriptstyle R} (v_{01}-u_{10})) + \frac{\tau _{\scriptscriptstyle R}b_{\scriptscriptstyle R}}{\omega _{\scriptscriptstyle L}}\\&\quad (r_{10} + s_{01}) + \frac{\tau _{\scriptscriptstyle R}b_{\scriptscriptstyle R}}{\omega _{\scriptscriptstyle R}}(p_{10} + q_{01})\bigg ) + b_{\scriptscriptstyle R} (u_{10} + v_{01})(1 + \tau _{\scriptscriptstyle R}^2)\\&\quad \arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg ),\\ C_{12}^1&= \frac{2 b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}}(r_{10}-r_{00}) + 2 (p_{00} + p_{10} + b_{\scriptscriptstyle R} ( v_{01}-u_{10})) + \frac{\tau _{\scriptscriptstyle R}b_{\scriptscriptstyle R}}{\omega _{\scriptscriptstyle L}}(r_{10} \\&\quad + s_{01}) + \frac{\tau _{\scriptscriptstyle R}b_{\scriptscriptstyle R}}{\omega _{\scriptscriptstyle R}}(p_{10} + q_{01}) + 2 \tau _{\scriptscriptstyle R}b_{\scriptscriptstyle R} (u_{10} + v_{01})\\&\quad \bigg (\arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg )-\frac{\tau _{\scriptscriptstyle R}^2+1}{\tau _{\scriptscriptstyle R}}\bigg )+\frac{\tau _{\scriptscriptstyle R}b_{\scriptscriptstyle R}\log (2\tau _{\scriptscriptstyle R})}{\omega _{\scriptscriptstyle R}\omega _{\scriptscriptstyle L}}\\&\quad ((p_{10} + q_{01}) \omega _{\scriptscriptstyle L} + (r_{10} + s_{01}) \omega _{\scriptscriptstyle R}),\\ C_{12}^2&= b_{\scriptscriptstyle R} (u_{10} + v_{01})\bigg (\arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg )-\frac{2\tau _{\scriptscriptstyle R}}{\tau _{\scriptscriptstyle R}^2+1}\bigg )\\&\quad + \frac{b_{\scriptscriptstyle R}}{2\omega _{\scriptscriptstyle R}\omega _{\scriptscriptstyle L}}((p_{10} + q_{01}) \omega _{\scriptscriptstyle L} + (r_{10} + s_{01}) \omega _{\scriptscriptstyle R}) (1 + \log (2) + \log (\tau _{\scriptscriptstyle R})). \end{aligned}$$

and $D_{1i}^j$, $i=1,2$ and $j=1,2$, depending on the parameters of system (1), whose expressions have been omitted for simplicity. Moreover, as

$$\begin{aligned} \lim _{h\rightarrow \tau _{\scriptscriptstyle R}}\log (\tau _{\scriptscriptstyle R}-h)(h-\tau _{\scriptscriptstyle R})^j=0,\quad j=1,2, \end{aligned}$$

the factors of the expansions in (18)–(19) that have $\log (\tau _i-h)$, $i=R,L$, can be disregarded in the study of the number of zeros. Therefore, will consider only the coefficients $C_{1i}^j$, $i=1,2$ and $j=0,1,2,3$.

When $\tau _{\scriptscriptstyle R}\ne \tau _{\scriptscriptstyle L}$, for

$$\begin{aligned} p_{00}&= -p_{10}+\frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle L}}(r_{00} - r_{10} + b_{\scriptscriptstyle L} (u_{10} - v_{01}))-\frac{b_{\scriptscriptstyle R}\tau _{\scriptscriptstyle L}}{2\omega _{\scriptscriptstyle L}}(r_{10} + s_{01})\\&\quad -\frac{b_{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}}{2\omega _{\scriptscriptstyle R}}(p_{10} + q_{01})-\frac{b_{\scriptscriptstyle R}}{2\tau _{\scriptscriptstyle R}}(u_{10} + v_{01}) (1 + \tau _{\scriptscriptstyle R}^2) \arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg )\\&\quad +\frac{b_{\scriptscriptstyle R}}{4\omega _{\scriptscriptstyle L}\tau _{\scriptscriptstyle R}}(r_{10} + s_{01}) (\tau _{\scriptscriptstyle L}^2 - \tau _{\scriptscriptstyle R}^2) \log \bigg (\frac{\tau _{\scriptscriptstyle L} + \tau _{\scriptscriptstyle R}}{\tau _{\scriptscriptstyle L} - \tau _{\scriptscriptstyle R}}\bigg ), \\ q_{01}&= -\frac{1}{2\omega _{\scriptscriptstyle L}\tau _{\scriptscriptstyle R}^2\log (2\tau _{\scriptscriptstyle R})}\bigg ((-4 (u_{10} + v_{01}) \omega _{\scriptscriptstyle L} -2 (r_{10} + s_{01})\tau _{\scriptscriptstyle L}) \omega _{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}+2 (u_{10} \\&\quad + v_{01}) \omega _{\scriptscriptstyle L}\omega _{\scriptscriptstyle R}(\tau _{\scriptscriptstyle R}^2-1)\arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg )+2p_{10}\omega _{\scriptscriptstyle L}\tau _{\scriptscriptstyle R}^2\log (2\tau _{\scriptscriptstyle R})\\&\quad +(r_{10} + s_{01}) \omega _{\scriptscriptstyle R}(\tau _{\scriptscriptstyle R}^2+\tau _{\scriptscriptstyle L}^2)\log \bigg (\frac{\tau _{\scriptscriptstyle L} + \tau _{\scriptscriptstyle R}}{\tau _{\scriptscriptstyle L} - \tau _{\scriptscriptstyle R}}\bigg ) \bigg ),\\ s_{01}&=-r_{10}\quad \text {and}\quad u_{10}\ne -v_{01}, \end{aligned}$$

we have that

$$\begin{aligned} C_{11}^0=C_{11}^1=C_{11}^2=0,\quad C_{11}^3\ne 0\quad \text {with}\quad \text {rank}\frac{\partial (C_{11}^0,C_{11}^1,C_{11}^2,C_{11}^3)}{\partial (p_{00},q_{10},s_{01},u_{10})}=4. \end{aligned}$$

This implies, by Proposition 9, that $C_{11}^0$, $C_{11}^1$, $C_{11}^2$ and $C_{11}^3$ can be taken as free coefficients, satisfying

$$\begin{aligned} C_{11}^0C_{11}^1<0,\quad C_{11}^1C_{11}^2<0,\quad C_{11}^2C_{11}^3<0 \end{aligned}$$

and

$$\begin{aligned} 0<|C_{11}^0|\ll |C_{11}^1|\ll |C_{11}^2|\ll |C_{11}^3|, \end{aligned}$$

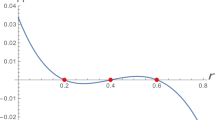
such that the function $M_{11}(h)$ has exactly three positive roots near $h=\tau _{\scriptscriptstyle R}$. Therefore, the number of limit cycles from system (1) that can bifurcate of the period annulus near the homoclinic loop in $h=\tau _{\scriptscriptstyle R}$, for $n=1$ and $\tau _{\scriptscriptstyle R}\ne \tau _{\scriptscriptstyle L}$, is at least three.

When $\tau _{\scriptscriptstyle R}=\tau _{\scriptscriptstyle L}$, for

$$\begin{aligned} p_{00}&= -p_{10} +\frac{b_{\scriptscriptstyle R}}{b_{\scriptscriptstyle R}}(r_{00} - r_{10} + b_{\scriptscriptstyle L}( u_{10} - v_{01}))-\frac{b_{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}}{2\omega _{\scriptscriptstyle L}}(r_{10} + s_{01})\\&\quad -\frac{b_{\scriptscriptstyle R}\tau _{\scriptscriptstyle R}}{2\omega _{\scriptscriptstyle R}}(p_{10} + q_{01})-\frac{b_{\scriptscriptstyle R}}{2\tau _{\scriptscriptstyle R}}(u_{10} + v_{01}) (1 + \tau _{\scriptscriptstyle R}^2) \arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg ), \\ s_{01}&= -r_{10}-\frac{\omega _{\scriptscriptstyle L}}{\omega _{\scriptscriptstyle R}}(p_{10} + q_{01})+\frac{\omega _{\scriptscriptstyle L}}{\tau _{\scriptscriptstyle R}^2\log (2\tau _{\scriptscriptstyle R})}(u_{10} + v_{01}) \bigg (2 (\tau _{\scriptscriptstyle R} + \tau _{\scriptscriptstyle R}^3) \\&\quad - (\tau _{\scriptscriptstyle R}^2-1)\arccos \bigg (\frac{\tau _{\scriptscriptstyle R}^2-1}{\tau _{\scriptscriptstyle R}^2+1}\bigg )\bigg ),\\ u_{10}&\ne -v_{01}, \end{aligned}$$

we have that

$$\begin{aligned} C_{12}^0=C_{12}^1=0,\quad C_{12}^2\ne 0\quad \text {with}\quad \text {rank}\frac{\partial (C_{12}^0,C_{12}^1,C_{12}^2)}{\partial (p_{00},s_{01},u_{10})}=3. \end{aligned}$$

As in the previous case, by Proposition 9, we can choose $C_{12}^0,C_{12}^1,$ and $C_{12}^2$ such that the function $M_{12}(h)$ has exactly two positive roots near $h=\tau _{\scriptscriptstyle R}$. Therefore, the number of limit cycles from system (1) that can bifurcate of the period annulus near the heteroclinic orbit in $h=\tau _{\scriptscriptstyle R}$, for $n=1$ and $\tau _{\scriptscriptstyle R}=\tau _{\scriptscriptstyle L}$, is at least two.

Case $n=2,3$and $\alpha =1$. Consider the Melnikov functions $M_{21}$ and $M_{31}$ given by the Theorem 8. By Lemma 10 we can expand these functions at $h=1$ as

$$\begin{aligned} M_{21}(h)= & {} \sum _{j=0}^{3}C_{21}^j(h-1)^j+\sum _{j=1}^{2}D_{21}^j\log (1-h)(h-1)^j\\&+\,\,\mathcal {O}((h-1)^4),\\ M_{31}(h)= & {} \sum _{j=0}^{5}C_{31}^j(h-1)^j+\sum _{j=1}^{4}D_{31}^j\log (1-h)(h-1)^j \\&+\,\,\mathcal {O}((h-1)^6), \end{aligned}$$

where

$$\begin{aligned} C_{21}^0&= 2 p_{00} + \frac{1}{3} (2 p_{02} + 9 p_{10} + 14 p_{20} + 3 q_{01} + 4 q_{11} - 6 r_{00} - 2 r_{02} + 9 r_{10} \\&\quad + r_{11} - 14 r_{20} + 3 s_{01} + 2 s_{02} - 4 s_{11}) + (\pi - 2) u_{10} + (2 + \pi ) v_{01},\\ C_{21}^1&= 2 p_{00} + 2 p_{02} + 3 p_{10} + q_{01} - 2 r_{00} - 2 r_{02} + 3 r_{10} - r_{11} - 2 r_{20} + s_{01} \\&\quad - 2 s_{02} - 4 u_{10} + \pi u_{10} + \pi v_{01} + (p_{10} + q_{01} + r_{10} + r_{11} - 4 r_{20} + s_{01}) \\&\quad \log (2) + (q_{11} + s_{02} - s_{11}) \log (4) + p_{20} (2 + \log (16)), \\ C_{21}^2&= \frac{1}{2} (4 p_{02} + p_{10} + q_{01} - 2 q_{11} - 4 r_{02} + r_{10} - 3 r_{11} + 4 r_{20} + s_{01} - 6 s_{02} \\&\quad + 2 s_{11} + (\pi - 2) (u_{10} + v_{01}) + (p_{10} + q_{01} + r_{10} + r_{11} - 4 r_{20} + s_{01})\\&\quad \log (2) + (q_{11} + s_{02} - s_{11}) \log (4) + p_{20} (\log (16) - 4)),\\ C_{21}^3&= \frac{1}{24} (16 p_{02} + 3 p_{10} - 20 p_{20} + 3 q_{01} - 10 q_{11} - 16 r_{02} + 3 r_{10} - 13 r_{11} \\&\quad + 20 r_{20} + 3 s_{01} - 26 s_{02} + 10 s_{11} - 8 (u_{10} + v_{01})), \\ C_{31}^0&= \frac{1}{6} (12 p_{00} + 4 p_{02} + 18 p_{10} + 5 p_{12} + 28 p_{20} + 45 p_{30} + 6 q_{01} + 3 q_{03} \\&\quad + 8 q_{11} + 11 q_{21} - 12 r_{00} - 4 r_{02} + 18 r_{10} + 2 r_{11} + 6 r_{12} - 28 r_{20} \\&\quad - 6 r_{21} + 45 r_{30} + 6 s_{01} + 4 s_{02} + 6 s_{03} - 8 s_{11} - 6 s_{12} + 11 s_{21} \\&\quad + 3 ( 4 v_{01} - 8 u_{30} + 8 v_{03} + 2 (\pi - 2) u_{10} + \pi (u_{12} + 3 u_{30} + 2 v_{01} \\&\quad + 3 v_{03} + v_{21}))), \\ C_{31}^1&= 2 p_{00} + 2 p_{02} + 3 p_{10} + 3 p_{12} + 2 p_{20} - 7 p_{30} + q_{01} + 3 q_{03} - 3 q_{21} \\&\quad - 2 r_{00} - 2 r_{02} + 3 r_{10} - r_{11} + r_{12} - 2 r_{20} + 6 r_{21} - 7 r_{30} + s_{01} + 6 s_{12} \\&\quad - 3 s_{21} + (\pi - 4) u_{10} - 2 (u_{12} + 5 u_{30} - 3 v_{03} + v_{21}) + \pi (u_{12} + 3 u_{30} \\&\quad + v_{01} + 3 v_{03} + v_{21}) + (p_{10} + 12 p_{30} + q_{01} + r_{10} + r_{11} + r_{12} - 4 r_{20} \\&\quad - 4 r_{21} + 12 r_{30} + s_{01} - 4 s_{12}) \log (2) + s_{02} ( \log (4) - 2) + q_{11} \log (4) \\&\quad - s_{11} \log (4) + s_{03} (\log (8) - 3) + (p_{20} + q_{21} + s_{21}) \log (16),\\ \\ C_{31}^2&= \frac{1}{4} (8 p_{02} + 2 p_{10} + 13 p_{12} - 8 p_{20} - 63 p_{30} + 2 q_{01} + 15 q_{03} - 4 q_{11} \\&\quad - 21 q_{21} - 8 r_{02} + 2 r_{10} - 6 r_{11} + 2 r_{12} + 8 r_{20} + 34 r_{21} - 63 r_{30} \\&\quad + 2 s_{01} - 12 s_{02} - 18 s_{03} + 4 s_{11} + 34 s_{12} - 21 s_{21} + 2 (\pi - 2) u_{10} \\&\quad + 2 \pi (2 u_{12} + 6 u_{30} + v_{01} + 6 v_{03} + 2 v_{21}) - 4 (3 u_{12} + 9 u_{30} + v_{01} \\&\quad - 3 v_{03} + 3 v_{21}) + (p_{10} + p_{12} + 4 p_{20} + 9 p_{30} + q_{01} + r_{10} + r_{11} + r_{12} \\&\quad - 4 r_{20} - 2 r_{21} + 9 r_{30} + s_{01} - 2 (s_{11} + s_{12})) \log (4) + (q_{11} + s_{02}) \\&\quad \log (16) + (q_{03} + q_{21} + s_{03} + s_{21}) \log (64)),\\ \\ C_{31}^3&= \frac{1}{24} (16 p_{02} + 3 p_{10} - 20 p_{20} - 156 p_{30} + 3 q_{01} + 48 q_{03} - 10 q_{11} - 52 q_{21} \\&\quad - 16 r_{02} + 3 r_{10} - 13 r_{11} + 3 r_{12} + 20 r_{20} + 84 r_{21} - 156 r_{30} + 3 s_{01} \\&\quad - 26 s_{02} - 39 s_{03} + 10 s_{11} + 84 s_{12} - 52 s_{21} - 8 u_{10} + 4 (3 \pi - 10) u_{12} \\&\quad + 12 \pi (v_{21} + 3 (u_{30} + v_{03}) ) - 8 (15 u_{30} + v_{01} + 3 v_{03} + 5 v_{21}) \\&\quad - 12 (3 p_{30} - 3 q_{03} + q_{21} - 2 r_{21} + 3 r_{30} - 2 s_{12} + s_{21}) \log (2) + 4 p_{12} \\&\quad (8 + \log (8))), \\ C_{31}^4&= \frac{1}{48} (4 r_{20} - p_{10} - 4 p_{20} - q_{01} - 2 q_{11} - 13 q_{21} - r_{10} - r_{11} - r_{12} \\&\quad + 22 r_{21} - 39 r_{30} - s_{01} - 2 s_{02} - 3 s_{03} + 2 s_{11} + 22 s_{12} - 13 s_{21} \\&\quad + 8 u_{10} + 2 (3 \pi - 8) u_{12} + 6 (3 \pi - 8) u_{30} + 8 v_{01} + 2 (3 \pi - 8) \\&\quad (3 v_{03} + v_{21}) - 6 (q_{21} - 2 r_{21} + 3 r_{30} - 2 s_{12} + s_{21}) \log (2) + 9 q_{03} \\&\quad (3 + \log (4)) + p_{12} (9 + \log (64)) - 3 p_{30} (13 + \log (64))),\\ \\ C_{31}^5&= \frac{1}{960} (5 p_{10} + 20 p_{12} + 20 p_{20} + 5 q_{01} + 60 q_{03} + 10 q_{11} + 5 r_{10} + 5 r_{11} \\&\quad + 5 r_{12} - 20 r_{20} + 20 r_{21} + 5 s_{01} + 10 s_{02} + 15 s_{03} - 10 s_{11} + 20 s_{12} \\&\quad - 32 (2 u_{10} + u_{12} + 3 u_{30} + 2 v_{01} + 3 v_{03} + v_{21})), \end{aligned}$$

and $D_{n1}^j$, $n=2,3$ and $j=1,\dots ,4$, depending on the parameters of system (1), with H(h) given in (14), whose expressions have been omitted for simplicity. As in the case $n=1$, will consider only the coefficients $C_{n1}^i$, $n=2,3$ and $i=0,\dots ,5$.

When $n=2$, for

$$\begin{aligned} \begin{aligned}&p_{00} = \frac{1}{6} (6 r_{00} -2 p_{02} - 9 p_{10} - 14 p_{20} - 3 q_{01} - 4 q_{11} + 2 r_{02} - 9 r_{10} - r_{11} \\&\quad \quad + 14 r_{20} - 3 s_{01} - 2 s_{02} + 4 s_{11} + 6 u_{10} - 3 \pi u_{10} - 6 v_{01} - 3 \pi v_{01}),\\&p_{10} = \frac{1}{\log (8)}(8 p_{20} - 4 p_{02} + 4 q_{11} + 4 r_{02} + 4 r_{11} - 8 r_{20} + 8 s_{02} - 4 s_{11} \\&\quad \quad + 6 (u_{10} + v_{01}) - (4 p_{20} + q_{01} + r_{10} + r_{11} + s_{01}) \log (8) - (q_{11} - 2 r_{20} \\&\quad \quad + s_{02} - s_{11})\log (64)),\\&p_{20} = \frac{1}{8 (2 \log (2) - 1)} (4 q_{11} -4 p_{02} + 4 r_{02} + 4 r_{11} - 8 r_{20} + 8 s_{02} - 4 s_{11} \\&\quad \quad + 6 u_{10} + 6 v_{01} +\log (2)(- 8 q_{11} - 8 r_{02} - 8 r_{11} + 16 r_{20} - 16 s_{02} \\&\quad \quad + 8 s_{11}) + 4 p_{02} \log (4) + \log (8)(\pi u_{10} + \pi v_{01})),\\&u_{10} \ne - v_{01}, \end{aligned} \end{aligned}$$

we have that

$$\begin{aligned} C_{21}^0=C_{21}^1=C_{21}^2=0, \quad C_{21}^3\ne 0\quad \text {with}\quad \text {rank}\frac{\partial (C_{21}^0,C_{21}^1,C_{21}^2,C_{21}^3)}{\partial (p_{00},p_{10},p_{20},u_{10})}=4. \end{aligned}$$

As in the previous cases, by Proposition 9, we can choose $C_{21}^0,C_{21}^1,C_{21}^2$ and $C_{21}^3$ such that the function $M_{21}(h)$ has exactly three positive roots near $h=1$. Therefore, the number of limit cycles from system (1) (with f(h), g(h) and H(h) given by (4), (5) and (14), respectively) that can bifurcate of the period annulus near the heteroclinic orbit in $h=1$, for $n=2$ and $\alpha =1$, is at least three.

When $n=3$, it is possible choose parameters value $p_{00}$, $p_{10}$, $p_{12}$, $p_{20}$, $u_{12}$ and $u_{10}$, such that

$$\begin{aligned} C_{31}^0=C_{31}^1=C_{31}^2=C_{31}^3=C_{31}^4=0,\quad C_{31}^5\ne 0 \end{aligned}$$

with

$$\begin{aligned} \text {rank}\frac{\partial (C_{31}^0,C_{31}^1,C_{31}^2,C_{31}^3,C_{31}^4,C_{31}^5)}{\partial (p_{00},p_{10},p_{12},p_{20},u_{12},u_{10})}=6. \end{aligned}$$

As in the previous cases, the number of limit cycles from system (1) (with f(h), g(h) and H(h) given by (4), (5) and (14), respectively) that can bifurcate of the period annulus near the heteroclinic orbit in $h=1$, for $n=3$ and $\alpha =1$, is at least five.

Case $n=2,3$and $\alpha =2$. Consider the Melnikov functions $M_{22}$ and $M_{32}$ given by Theorem 8. By Lemma 10 we can expand these functions at $h=1$ as

$$\begin{aligned} M_{22}(h)= & {} \sum _{j=0}^{4}C_{22}^j(h-1)^j+\sum _{j=1}^{2}D_{22}^j\log (1-h)(h-1)^j\\&+\mathcal {O}((h-1)^5),\\ M_{32}(h)= & {} \sum _{j=0}^{7}C_{32}^j(h-1)^j+\sum _{j=1}^{4}D_{32}^j\log (1-h)(h-1)^j \\&+\mathcal {O}((h-1)^8), \end{aligned}$$

where $C_{n2}^i$ and $D_{n2}^j$, $n=2,3$, $i=0,\dots ,7$ and $j=1,\dots ,4$, depending on the parameters of system (1), with H(h) given in (14), whose expressions have been omitted for simplicity. As in the case $\alpha =1$, will consider only the coefficients $C_{n2}^i$, $n=2,3$ and $i=0,\dots ,7$.

When $n=2$, it is possible choose parameters value $p_{00}$, $p_{10}$, $p_{20}$, $s_{01}$ and $u_{10}$, such that

$$\begin{aligned} C_{22}^0=C_{22}^1=C_{22}^2=C_{22}^3=0,\quad C_{12}^4\ne 0 \end{aligned}$$

with

$$\begin{aligned} \text {rank}\frac{\partial (C_{22}^0,C_{22}^1,C_{22}^2,C_{22}^3,C_{22}^4)}{\partial (p_{00},p_{10},p_{20},s_{01},u_{10})}=5. \end{aligned}$$

As in the previous cases, the number of limit cycles from system (1) (with f(h), g(h) and H(h) given by (4), (5) and (14), respectively) that can bifurcate of the period annulus near the homoclinic loop in $h=1$, for $n=2$ and $\alpha =2$, is at least four.

Finally, when $n=3$, it is possible choose parameters value $p_{00}$, $p_{10}$, $p_{12}$, $p_{20}$, $s_{01}$, $u_{12}$, $r_{10}$ and $u_{10}$, such that

$$\begin{aligned} C_{32}^0=C_{32}^1=C_{32}^2=C_{32}^3=C_{32}^4=C_{32}^5=C_{32}^6=0,\quad C_{32}^7\ne 0 \end{aligned}$$

with

$$\begin{aligned} \text {rank}\frac{\partial (C_{32}^0,C_{32}^1,C_{32}^2,C_{32}^3,C_{32}^4,C_{32}^5,C_{32}^6,C_{32}^7)}{\partial (p_{00},p_{10},p_{12},p_{20},s_{01},u_{12},r_{10},u_{10})}=8. \end{aligned}$$

As in the previous cases, the number of limit cycles from system (1) (with f(h), g(h) and H(h) given by (4), (5) and (14), respectively) that can bifurcate of the period annulus near the homoclinic loop in $h=1$, for $n=3$ and $\alpha =2$, is at least seven. $\square$