Stability of Morse-Smale maps

Abstract

$C^r(B,B)$ is the space of $C^r$ maps of a Banach manifold B to itself, bounded together with their derivatives up to the order r. It is chosen a topological subspace $KC^r (B,B)$ satisfying certain compactness and reversibility conditions, the subspace depending on the class of problems in view. A large class of maps in $KC^r(B,B),$ called Morse-Smale maps and the notion of stability relative to the largest invariant set A(f) are defined, and it is proved that the Morse-Smale maps are stable relatively to A(f) and form an open set in $KC^r (B,B), r\ge 1.$ Examples of $KC^r (B,B)$ can be constructed with maps arising from flows of retarded functional differential equations, of certain types of neutral functional differential equations and parabolic PDE and some other special PDE. Also, if B is compact, the set of all $C^r-$diffeomorphisms of B is a particular example of $KC^r (B,B)$ and the main result yields the proof for the stability of Morse–Smale diffeomorphisms of a compact manifold, originally established in Palis (Topology 8:385–405, 1969) and Palis and Smale (in: Global analysis proc symp pure math, vol 14, AMS, Providence, RI, 1970).

1 Introduction

We will deal in this paper with smooth maps $f: B\rightarrow E,\ B$ being a Banach manifold imbedded in a Banach space E. The maps f belong to $C^r (B, E),$ the Banach space of all $E-$valued $C^r-$maps defined on B which are bounded together with their derivatives up to the order $r \ge 1$. Let $C^r(B, B)$ be the subspace of $C^r(B, E)$ of all maps leaving B invariant, that is, $f(B) \subset B.$ Denote by A(f) the set

$$\begin{aligned} A(f) = \{ x \in B: \hbox { there exists a sequence }(x=x_1, x_2, \dots ) \in B, \\ \sup \limits _j||x_j|| < \infty \hbox { and } f(x_j)=x_{j-1}, j=2, 3, \dots \}. \end{aligned}$$

Special subspaces $KC^r(B, B)$ of $C^r(B, B)$ will be introduced satisfying the following compactness and reversibility properties: "any $f \in KC^r(B, B)$ is reversible, has A(f) compact and given a neighborhood U of A(f) in B,  there exists a neighborhood $\mathfrak {w}(f)$ of f in $KC^r(B, B)$ such that $A(g) \subset U$ for all $g \in \mathfrak {w}(f)$" (reversibility for a $C^1$ map f means f/A(f) and df/A(f) are injective maps). The choice of the classes $KC^r(B, B)$ depends on the problems in view. In each case we need to assume appropriate hypotheses on the data in order to obtain the required compactness and reversibility properties for the elected $KC^r(B, B).$

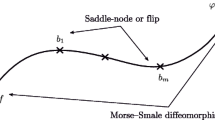
Global unstable manifolds of hyperbolic periodic points of a map $f \in KC^r(B, B)$ are introduced using the reversibility of f. When the nonwandering set $\Omega (f)$ (see sect. 2) is a finite set of hyperbolic periodic points with finite dimensional unstable manifolds transversal to the local stable manifolds, the map f is called a Morse-Smale map (see Definition 4.2). We denote by MS the set of Morse-Smale maps of $KC^r(B, B).$

From the dynamic point of view, a Morse-Smale map f exhibits the simplest orbit structure, specially the "gradient like" ones, that is, the $f \in MS$ for which there exists a continuous Liapunov function $V: B \rightarrow {\mathbb {R}}$ such that if $x \in B$ and $f(x) \ne x,$ then $V(f(x)) < V(x).$ In this case $\Omega (f)$ is equal to Fix(f),  the set of all fixed points of f.

In Palis [12], and in Palis-Smale [15] the authors proved very important stability theorems for (and existence of) Morse-Smale diffeomorphisms defined on a compact manifold M. They showed that any Morse-Smale diffeomorphism f is stable. That is, there exists a neighborhood $\vartheta (f)$ of f in ${Diff}^r(M),$ the set of all $C^r-$diffeomorphisms of $M, \ r \ge 1,$ such that for each $g \in \vartheta (f)$ corresponds a homeomorphism $h=h(g): M \rightarrow M$ and $h \cdot f = g \cdot h$ holds on M.

We say that $f \in KC^r(B, B)$ is stable relatively to A(f) if there exists a neighborhood $\vartheta (f)$ of f in $KC^r(B, B)$ such that to each $g \in \vartheta (f)$ corresponds a homeomorphism $h= h(g): A(f) \rightarrow A(g)$ and $h \cdot f = g \cdot h$ holds on A(f).

1.1 Main result (openess and stability)

"The set MS is open in $KC^r(B, B)$ and any $f \in MS$ is stable relatively to A(f)."

The main motivation is the study of certain maps arising from flows of some infinite dimensional dynamical systems which appear naturally in several physical as well as mathematical contexts. That class includes retarded functional differential equations (RFDE),certain types of neutral functional differential equations (NFDE), parabolic partial differential equations (parabolic PDE) and some other special PDE. The basic theory of RFDE and NFDE can be seen in Hale [2] and parabolic PDE in Henry [5]. A framework for the dynamics of maps in infinite dimensions can also be found in Hale [3].

As a first general example, let $E= C^0([-1,0], {\mathbb {R}}^n)$ be the Banach space of all continuous maps $\varphi :[-1,0] \rightarrow {\mathbb {R}}^n,$ the norm in E being the sup norm, and $\mathfrak {X}^r=C^r(E, {\mathbb {R}}^n), \ r \ge 1,$ be the Banach space of all $C^r-$functions defined in E with values in ${\mathbb {R}}^n$ which are bounded together with their derivatives up to the order $r; \mathfrak {X}^r$ is endowed with the usual topology. Given $F \in \mathfrak {X}^r,$ let us consider the RFDE ${\dot{x}} = F(x_t)$ where, for each fixed $t, \ x_t$ designates the resriction of a function x as $x_t(\theta ) = x(t+\theta ), \ -1 \le \theta \le 0.$ For any $\varphi \in E,$ let $x_t(\varphi ), \ t\ge 0,$ be the solution such that $x_0=\varphi$ and denote $T_F(t)\varphi = x_t(\varphi ).$ If this function is defined for $t\ge 0,$ then $T_F(t): E \rightarrow E$ is a strongly continuous semigroup and for $t \ge 1 \ T_F(t)$ is a compact map $(f=T_F(1): B \rightarrow E, \ B=E,$ in notation of the first paragraph). The RFDE can also be defined on manifolds (see [2, 11] and Example 2.2).

A general situation for a parabolic PDE can also be described; let us suppose $u \in {\mathbb {R}}^k, \ x \in {\mathbb {R}}^n, \ \Omega$ be a bounded open set in ${\mathbb {R}}^n$ with smooth boundary $\partial \Omega , \Delta$ be the Laplacian operator, D be a $k\times k$ positive diagonal matrix, and consider the problem

$$\begin{aligned}&u_t - D\Delta u = F(x, u, \hbox {grad} \ u) \ \hbox {in} \ \Omega , \\&\quad u=0 \ \hbox {on} \ \partial \Omega \ \hbox {(or other usual boundary condition).} \end{aligned}$$

Let $W= H_0^1(\Omega ) \cap H^2(\Omega )$ be the domain of $-\Delta$ and $E=W^\alpha , \ 0\le \alpha \le 1,$ be the domain of the fractional power $(-\Delta )^\alpha$ of $-\Delta$ with the graph norm (see [5] for details). Under suitable conditions on F and $\alpha ,$ this PDE generates a strongly continuous semigroup $T_F (t)$ on E which is compact for $t> 0.$ Call $f=T_F(1).$

The map f and the set A(f) contain much of the interesting informations about the semigroup $T_F (t)$ (see [8, 9, 11]). If A(f) is not a compact set, very little is known at this time. The compactness of A(f) and the reversibility of f will play a fundamental role in the sequel.

More specific examples motivated the author in the present paper:

The Levin-Nohel RFDE on S ¹

Let $G:{\mathbb {R}}\rightarrow {\mathbb {R}}$ and $a:[0,1] \rightarrow {\mathbb {R}}$ be analytic functions, G being periodic, $a(1)=0, \ a(s) \ge 0, {\dot{a}}(s)\le 0, \ \ddot{a}(s)>0.$ If $g(x)={G^\prime }(x)$ is derivative of G, the Levin-Nohel equation on $S^1$ is given by

$$\begin{aligned} {\dot{x}} = -\int ^0_{-1} a(-\theta ) g(x(t+\theta )) d\theta . \end{aligned}$$

The above RFDE admits a Liapunov function

$$\begin{aligned} V(\varphi ) = G(\varphi (0)) -\frac{1}{2} \int ^0_{-1} {{\dot{a}}(-\theta ) \big [ \int ^0_\theta g(\varphi (s)) ds \big ]^2} d\theta \end{aligned}$$

whose derivative ${\dot{V}}$ along the solution is given by

$$\begin{aligned} {\dot{V}}(\varphi )=\frac{1}{2} {\dot{a}}(1) \big [ \int ^0_{-1} g(\varphi (\theta ))d\theta \big ]^2 - \frac{1}{2} \int ^0_{-1} \ddot{a}(-\theta )\big [ \int ^0_\theta g(\varphi (s))ds\big ]^2 d\theta \le 0. \end{aligned}$$

The case in which g has four simple zeros on $S^1$ was studied by Hale and Rybakowski in [4] and they described the possible topological types of the corresponding A(f) ( in the present case the time one map f is reversible and A(f) is compact) for $^{{\cdot }{\cdot }}$generic$^{{\cdot }{\cdot }}G$. They found five classes for A(f), three of them stable under perturbations of G and the remaining two classes having saddle connections. The pictures for A(f) are the following:

1.2 The Chafee-Infante parabolic PDE

Consider the following scalar parabolic PDE

$$\begin{aligned} u_t = u_{xx} + \lambda (u-u^3 ) \ \ \ \ 0<x<\pi , \ t>0 \end{aligned}$$

$$\begin{aligned} u=0 \ \hbox {at } \ x=0, \pi , \end{aligned}$$

where $\lambda$ is a real parameter. This equation defines a strongly continuous semi-group $T_\lambda (t), \ t\ge 0,$ on $H^1_0 (0,\pi )$ (see Henry [5] for details). The Liapunov function $V: H^1_0 (0, \pi ) \rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} V(\varphi ) = \int ^\pi _0 \big [ \frac{1}{2} \varphi ^2_x - \lambda \big ( \frac{\varphi ^2}{2} - \frac{\varphi ^4}{4}\big )\big ]dx \end{aligned}$$

has the following derivative along the solutions:

$$\begin{aligned} {\dot{V}}(u(t,\cdot )) = - \int ^\pi _0 u^2_t dx \le 0. \end{aligned}$$

Henry (see [5]) described the invariant set $A(f) \in H^1_0 (0, \pi )$ for $\lambda$ in the intervals $n^2 < \lambda \le (n+1)^2 , \ n=0, 1, 2$ and 3 . The time one map $f=f(\lambda )$ is reversible and has $(2n+1)$ hyerbolic fixed points when $\lambda$ satisfies $n^2< \lambda < (n+1)^2$ and pictures for A(f) are the following:

When $n^2 < \lambda \le (n+1)^2 , \ A(f)$ is a n-dimensional compact set.

The values $\lambda = (n+1)^2, \ n=0, 1, 2, \dots$ correspond to a kind of "bifurcation" of A(f); two more fixed points bifurcate from 0 and the dimension of A(f) increases when $\lambda$ passes through a bifurcation value. The description of A(f) for $n>3$ has been done by J. Hale and A. Nascimento (private communication).

1.3 The elastic beam equation

Ball [1] studied a model for the transverse motion of an elastic beam with ends fixed in space. The corresponding non linear equation

$$\begin{aligned} u_{tt} + \alpha u_{xxxx} - \big [\lambda + k \int _0^l u^2_s (s, t) ds \big ] u_{xx} + \delta u_t =0 \end{aligned}$$

has $\alpha , k, \delta$ and $\lambda$ as positive constants and the boundary conditions are stated for hinged or clamped ends. In each case, the equation defines a flow in a suitable Banach space, with a Liapunov function (the energy) nonincreasing along solutions.

Taking f as the time-one map (which is reversible in this case), the number of fixed points and the dimension of A(f) depend on $\lambda$ (which is proportional to the axial load). Some conjectures about pictures for A(f) are made in [1] but to settle them new techniques would seem to be necessary. For the case $u=u_{xx}=0$ at $x=0, l$ (hinged ends) A(f) can be defined in some detail.

1.4 The Navier-Stokes equation

In [7] Ladyzhenskaia proved that the set A(f) corresponding to the semigroup $T_F (t)$ generated by the Navier-Stokes equation F in a two dimensional domain is a compact set and $f= T_F (1)$ is a compact map. The dimension of A(f) may increase as the Reynolds number Re increases and it seems that the dynamical system $F= F(Re)$ is in fact the object of investigation in turbulence theory dealing with flows at large values of Re. How does A(f) change as the viscosity $\nu \rightarrow 0,$ i.e. as $Re \rightarrow +\infty$ ?

As applications of the main result we mention:

• 1. If B is compact, the set of all $C^r$-diffeomorphisms of B is a particular example of $KC^r (B,B)$ and the main result yields the proof for the stability of Morse-Smale diffeomorphisms of a compact manifold, originally established in [12, 15].

• 2. If S is the set of time one maps of all analytic RFDE defined on a compact manifold, the Morse-Smale maps f of S are stable relatively to A(f) and form an open set in S.

Section 2 is presented just to show that there exists a large class of problems in which it is possible to find B and to choose subspaces of $C^r(B, B)$ with the properties of a $KC^r(B, B).$ On the other side, in the definition of MS the unstable manifolds are assumed to have finite dimension and we see, in Sect. 3, that in many application this is the case since A(f) has finite Hausdorff dimension. The remaining sections are concerned with the tools to be used in the proof of the main result.

2 The dynamics of some non linear maps

Let B be a connected Banach manifold embedded in a Banach space E, with norm $|| \cdot ||,$ and $U \subset B$ an open set.

We will deal, often, with continuous maps $f: U \rightarrow B$ which are compact maps, that is, which send bounded sets into relatively compact sets.

Given a map $f: U\rightarrow B,$ one can define

$$\begin{aligned} A(f;U)=\{ x \in U: \hbox {there exists a sequence } (x=x_1, x_2, \dots ) \in U, \\ sup_j ||x_j||< \infty \ \hbox {and} \ f(x_j) = x_{j-1}, \ j=2, 3, \dots \}. \end{aligned}$$

When $U=B, \ f:B \rightarrow B,$ then A(f; B) is simply denoted by A(f).

Remark

$A(f;U) \subset f(A(f;U)) \subset f^2 (A(f;U)) \subset \dots .$ A subset $M \subset U$ is said to be negatively invariant with respect to $f:U\rightarrow B$ if any $x \in M$ has a negative bounded orbit on M, that is, if there exists a sequence $(x=x_1, x_2, \dots ) \in M, \ sup_j ||x_j || < \infty$ and $f(x_j) = x_{j-1}, j= 2, 3, \dots .$

It is easy to prove the following:

Proposition 1.1

A(f; U) is negatively invariant; if $M\subset U$ is negatively invariant then $f(M) \supset M$ and $A(f;U) \supset M.$ If $M\subset U$ is bounded then M is negatively invariant if and only if $f(M) \supset M.$

Let us denote by$A_n (f;U)$ the set

$$\begin{aligned} A_n (f;U) = \{ x \in U | \hbox { there exists a sequence } (x=x_1 , x_2 , \dots ) \in U, \\ f(x_j) = x_{j-1} , \ j \ge 2, \ \hbox {and} \ sup_j ||x_j || \le n \}. \end{aligned}$$

It is clear that $A_n (f; U) \subset A(f; U).$

Denote $A_n(f;B) = A_n (f).$

Proposition 1.2

The set $A_n(f;U)$ is negatively invariant and if f is compact, $A_n(f, U)$ is relatively compact.

Proof

It is clear that $f[A_n (f;U)] \supset A_n(f;U)$ then $\overline{f[A_n(f;U)]} \supset \overline{A_n(f;U)};$ if f is compact it follows that $\overline{A_n(f;U)}$ is compact.

Proposition 1.3

If $f: U \rightarrow B$ is compact then $A_n(f;U)$ is compact.

Proof: It is sufficient to prove that $A_n(f;U)$ is closed. Take $y= \lim x^\nu , x^\nu \in A_n(f;U).$ We have the sequences:

$$\begin{aligned} x^1&=x^1_1, x^1_2, \dots , x^1_j, \dots \\ x^2&=x^2_1, x^2_2, \dots , x^2_j, \dots \\ \vdots&\hbox { } \\ x^\nu&=x^1_1, x^\nu _2, \dots , x^\nu _j, \dots \end{aligned}$$

such that $f(x_j^\nu )= x_{j-1}^\nu , j \ge 2, \ \nu \ge 1.$ Since f is compact and $sup || x_j^\nu || \le n,$ each vertical sequence has a limit point ${\overline{x}}_j$ defined by a subsequence of $x^\nu _j$ (j fixed), that is,

$$\begin{aligned} \lim _\nu x^\nu _j = {\overline{x}}_j \hbox { (using the same indices).} \end{aligned}$$

One has the sequence

$$\begin{aligned} y= {\overline{x}}_1, {\overline{x}}_2 , \dots \end{aligned}$$

and by continuity $f({{\overline{x}}}_j)= {\overline{x}}_{j-1} , j \ge 2,$ that is, $y \in A_n(f;U).$

Corollary 1.4

If $f: U \rightarrow B$ is compact, then A(f; U) is a countable union of compact sets. When $U=B,$ the same holds for A(f).

Proof

$A(f;U) = \bigcup \limits _{n\ge 1} A_n (f;U)$ and $A(f) = \bigcup \limits _{n\ge 1} A_n(f).$

A subset $M\subset U$ is said to be positively invariant with respect to $f: U \rightarrow B$ if $f(M) \subset M$ (the positive orbit of a point of M remains in M). M is invariant if it is negatively and positively invariant. A(f) is the largest invariant set of any $f: B \rightarrow B.$

If the positive orbit $\gamma ^+(x) = \{ f^n(x), n \ge 0\}$ is contained in U one can define w(x),  the $w-$limit set of $x: y \in w(x)$ if $y=\lim _{j \rightarrow \infty } f^{n_j}(x)$ for some sequence $n_j \rightarrow \infty$ as $j \rightarrow \infty$. Analogously, one can define $\alpha (x),$ the $\alpha -$limit set of x, since there is defined a negative bounded orbit $\gamma ^-(x) \subset U$. We say that $z \in \alpha (x)$ if $z=\lim _{i\rightarrow \infty } x_{n_i}, \ n_i \rightarrow \infty$ as $i \rightarrow \infty ,$ for some subsequence $x_{n_i}$ of some sequence

$$\begin{aligned} (x=x_1, x_2, \dots ) \in \gamma ^-(x), \ \sup _j ||x_j || < \infty , \ f(x_j) = x_{j-1}, j\ge 2. \end{aligned}$$

In what follows we will consider continuous maps $f: B \rightarrow B.$ A point $z \in A(f)$ is a non wandering point if given a neighborhood $\mathfrak {w}$ of z in A(f) and $n_0 \in N$, there exists $n>n_0$ such that $f_n(\mathfrak {w}) \cap \mathfrak {w} \ne \Phi .$ It is clear that the non wandering set $\Omega (f),$ the set of all non wandering points, is closed in A(f).

Proposition 1.5

If $B \subset E$ is bounded (and connected) and $f: B \rightarrow B$ is compact, then the largest invariant set A(f) is nonempty, compact (and connected) and $A(f) = \bigcap \limits _{n\ge 1} f^n(B).$

Proof

Let us denote by $A_i, i\ge 1,$ the relatively compact sets $A_i = f^i(B).$ One has $A_1 = f(B) \supset f({\overline{A}}_1) \supset \overline{f(A_1)} = {\overline{A}}_2$ since $f(A_1) \subset f({\overline{A}}_1)$ and $f({\overline{A}}_1)$ is closed. By induction $A_{i-1} \supset {\overline{A}}_i , \ i>1,$ imply $A_i = f(A_{i-1}) \supset f({\overline{A}}_i) \supset \overline{f(A_i)} = {\overline{A}}_{i+1}.$ We have, then, $\bigcap \limits _{i\ge 1} A_i \supset \bigcap \limits _{i\ge 1}{\overline{A}}_{i+1}$ and $\bigcap \limits _{i\ge 1} A_i \subset \bigcap \limits _{i\ge 1} {\overline{A}}_{i} \subset \bigcap \limits _{i\ge 1}{\overline{A}}_{i+1}$; finally $I=\bigcap \limits _{i\ge 1} A_i = \bigcap \limits _{i\ge 1}{\overline{A}}_{i+1} = \bigcap \limits _{i\ge 1} {\overline{A}}_{i}$ which is connected and compact because is the intersection of the non increasing sequence of connected and compact sets ${\overline{A}}_1 \supset {\overline{A}}_2 \supset {\overline{A}}_3 \supset \dots .$ It is clear that $A(f) \subset I;$ but, conversely, let $x \in f(B) \cap f^2(B) \cap \dots$ and consider the sequences

$$\begin{aligned} x&=x^1_1, x^1_2 \\ x&=x^2_1, x^2_2, x^2_3 \\ \vdots&\hbox { } \\ x&=x^n_1, x^n_2, x^n_3, \dots \hbox { in which } f(x^n_{i+1})=x^n_i. \end{aligned}$$

In the first vertical sequence $( x^1_2 , x^2_2, x_2^3, \dots , x_2^n, \dots )$ one observes that $x_2^n \in A_1$ for $n\ge 2; \ x_2^n \in A_2$ for $n\ge 3$, and so on. Since ${\overline{A}}_1$ is compact that sequence has a limit point ${\overline{x}}_1 \in {\overline{A}}_1$ and by the above observations, ${\overline{x}}_1 \in {\overline{A}}_i , i\ge 1,$ then ${\overline{x}}_1 \in I.$ But f is continuous, then $f({\overline{x}}_1 )=x.$ Using the same argument, starting from ${\overline{x}}_1 \in I$ we construct ${\overline{x}}_2 \in I$ and $f({\overline{x}}_2) = {\overline{x}}_1$ and so on, we get the sequence

$$\begin{aligned} (x, {\overline{x}}_1 , {\overline{x}}_2 , \dots ), \ f({\overline{x}}_1 )=x \ \hbox { and } f({\overline{x}}_i)=f({\overline{x}}_{i-1}), \ i\ge 2, \end{aligned}$$

that is, $x \in A(f)$ and $A(f) = I.$ It is clear that A(f) is the largest invariant set and if $x \in B,$ the sequence $(x, f(x), f^2(x), \dots )$ is such that $f^i(x) \in A_1$ for $i\ge 1$ and then there exists a limit point ${\overline{x}} \in {\overline{A}}_1 ;$ but since $f^i(x) \in A_2$ for $i\ge 2$, it follows that ${\overline{x}} \in {\overline{A}}_2 ,$ and so on, ${\overline{x}} \in {\overline{A}}_j$ for all $j \ge 1 ,$ which shows that ${\overline{x}} \in A(f) \ne \Phi .$

The following result is easy to prove:

Corollary 1.6

If $B \subset E$ is bounded and if $f: B\rightarrow B$ is compact then for any $x \in B, w(x)$ is non empty, compact and invariant (then $w(x) \subset A(f)$).

Definition 1.7

A continuous map $f: B \rightarrow B$ is said to be $C^0-$reversible if it is one-to-one on A(f). If in addition f is $C^1$ and the derivative $df: TB \rightarrow TB$ is one-to-one on $A(df), \ f$ is said to be reversible.

Proposition 1.8

If $f: B\rightarrow B$ is $C^0-$reversible and A(f) is compact then $\Omega (f)$ is compact and invariant. Also, if $x \in A(f),$ the w and $\alpha -$limit sets w(x) and $\alpha (x)$ are non empty, compact and invariant sets contained in $\Omega (f).$

Proof

If $y \in \Omega (f),$ it is easy to see that $f^i(y) \in \Omega (f)$ for all $i\ge 1.$ Since f is $C^0-$reversible, A(f) is compact and $g = {f}/{A(f)}$ is a homeomorphism, then all points of the (unique) negative orbit of $y, \ (y, g^{-1}(y), g^{-2}(y), \dots )$ belong to $\Omega (f)$ and $\Omega (f)$ is invariant. But $\Omega (f)$ is closed, then it is compact.

Given $x \in A(f),$ the homeomorphism $g: A(f) \rightarrow A(f)$ shows, by standard arguments, that w(x) and $\alpha (x)$ are $\ne \Phi$, compact and invariant sets. Since $\{ g^i (x): -\infty< i < \infty \} \subset \Omega (f)$ and $\Omega (f)$ is closed, $\alpha (x)$ and w(x) are in $\Omega (f).$

The next Lemma 1.9 and Theorem 1.10 were shown to me by D. Henry.

Let (X, d) be a complete metric space , The Kuratowski measure of noncompactness of a nonempty and bounded subset A or X is the non negative number $\alpha (A) = \inf \{ d^\prime \in {\mathbb {R}}: A \hbox { has a finite cover of diameter } < d^\prime \}.$

It is known that (see [3])

• (i) $\alpha (A) = 0$ if and only if ${\overline{A}}$ is compact

• (ii) $\alpha ( A_1 \cup A_2) = max [ \alpha (A_1), \alpha (A_2)]$

A continuous map $f: X \rightarrow X$ is a set contraction if there exists $0 \le \theta < 1$ such that $\alpha (f(A)) \le \theta \cdot \alpha (A)$ for all bounded sets $A\subseteq X.$

If $f: X\rightarrow X$ is continuous, and $M \subset X,$ one says that M is $f-$invariant (or simply invariant) if any $x \in M$ has one negative bounded orbit contained in M and $f(M) \subset M.$

Lemma 1.9

If (X, d) is a complete metric space, $A_k \ (k\ge 1)$ are nonempty closed bounded sets with $A_1 \supset A_2 \supset A_3 \supset \dots$ and $\alpha (A_k) \rightarrow 0$ as $k \rightarrow \infty ,$ then $A_\infty = \bigcap \limits _{k \ge 1} A_k$ is a nonempty compact set and for any $\epsilon > 0$ there exists $n_\epsilon$ so $A_\infty \subset A_n \subset \epsilon -$neighborhood of $A_\infty$ for $n \ge n_\epsilon .$ If all the $A_k$ are connected then $A_\infty$ is also connected.

Proof

The key result is $A_\infty \ne \emptyset .$ Let $p_k \in A_k \ (k= 1, 2, \dots )$; we show there is a convergent subsequence $p_{k^{\prime }} \rightarrow p$ in X. Since $p_{k^\prime } \in A_{k^\prime } \subset A_n$ for all $k^{\prime } \ge n, \ p \in A_n ;$ this holds for each n so $p \in A_{\infty }.$

Now let $\epsilon _n > \alpha (A_n), \ \epsilon _n \rightarrow 0; \ A_n$ may be covered by finitely many sets $\{S_i^n : i=1,2, \dots ,N_n\}$ with diam $S_i^n \le \epsilon _n .$ Since $\{p_k\}_{k \ge 1} \subset A_1$ there exists $i_1 \in \{ 1, 2, \dots , N_1 \}$ so $S^1_{i_1}$ contains infinitely many of the $p_k$ - thus there is a subsequence $\{p^1_k \}$ or $\{p_k \}$ contained in a set of diameter $\le \epsilon _1$. Except possibly for the first term, all $p_k^1 \in A_2$ so there is a set of diameter $\le \epsilon _2$ in $A_2$ containing infinitely many of the $p^1_k$. Thus there is a subsequence $\{p^2_k \}$ ou $\{ p^1_k \},$ in a set of diameter $\le 2$.

Continuing, we find subsequences $\{p_k^n\} \subset \{p_k^{n-1}\} \ \subset \dots \subset \{p_k^1 \} \subset \{p_k\}$ and $d(p_k^n , p_j^n) \le \epsilon _n$ for all j, k. The diagonal sequence $[{\tilde{p}}_n = n^{th} \ \hbox { term of } \{ p_k^n \} ]$ is therefore a Cauchy sequence. Then $A_\infty = \bigcap \limits _{k\ge 1} {A_k}$ is nonempty and closed; since $\alpha (A_\infty ) \le \alpha (A_k)$ for all $k, \ \alpha (A_\infty ) = 0$ so $A_\infty$ is compact. Suppose $\epsilon >0$ and there exist $k_\nu \rightarrow \infty , \ k_\nu < k_{\nu +1},$ with $A_{k_\nu } \subset \!\!\!\!\!/ \ \epsilon -$neighborhood of $A_\infty .$

Let $A^\prime _\nu = A_{k_\nu } -(\epsilon -$neighborhood of $A_\infty )$; $A^\prime _\nu$ is nonempty, closed, $A^\prime _{\nu +1} \subset A^\prime _\nu , \ \alpha (A^\prime _\nu )\le \alpha (A_{k_\nu }) \rightarrow 0$ so $\bigcap \limits _{\nu \ge 1} A^\prime _\nu = A^\prime _\infty$ is nonempty. But $A^\prime _\infty \subset A_\infty$ while $A^\prime _\infty \cap (\epsilon -$neighborhood of $A_\infty )= \Phi ,$ a contradiction.

Finally suppose $A_1 , A_2, \dots$ are connected but $A_\infty$ is not connected. There is a continuous $\varphi : A_\infty \xrightarrow {\text {onto}} \{ 0, 1\}$ and there is a continuous $\Phi : A_1 \rightarrow [0,1]$ with ${\Phi } / {A_\infty } = \varphi .$ Then for each $k < \infty , \ A^{\prime \prime }_k = A_k \cap \Phi ^{-1}(\frac{1}{2})$ is nonempty and closed and, as above, $A^{\prime \prime }_\infty =\cap _{k\ge 1} A^{\prime \prime }_k$ is nonempty. But $A^{\prime \prime }_\infty \subset A_\infty \cap \Phi ^{-1} (1 / 2),$ which is empty $[(1 / 2) \notin \Phi (A_\infty ) = \{0,1\}].$

Theorem 1.10

Let (X, d) be a complete metric space and ${{\mathcal {B}}}$ a bounded open set in X. Suppose $f: X \rightarrow X$ is continuous and satisfies

• (i) given $x \in X, \ f^n(x) \in {{\mathcal {B}}}$ for all sufficiently large n; 

• (ii) for some integer $m \ge 1, \ {\overline{f^m ({{\mathcal {B}}})}} \subset {{\mathcal {B}}}$ and $f^m /{{\mathcal {B}}}$ is a set contraction (there exists $\theta < 1$ so $\alpha (f^m (S))\le \theta \cdot \alpha (S)$ for $S \subset {{\mathcal {B}}}).$

Then $K(f;{{{\mathcal {B}}}})= \bigcap \limits _{i\ge 0} f^m ({{\mathcal {B}}})$ is a nonempty compact $f-$invariant set, it is connected when ${{{\mathcal {B}}}}$ is connected, and contains every compact $f$-invariant set and in fact every $f$-invariant set S such that $S-{{\mathcal {B}}}$ is precompact. If $\{ x_k : k=0, -1, -2, \dots \} \subset {{\mathcal {B}}}$ with $f(x_k) = x_{k+1}$ for each $k<0,$ then $x_0 \in K(f; {{{\mathcal {B}}}})$ (indeed all $x_k \in K(f; {{{\mathcal {B}}}})= A( f / {{{\mathcal {B}}}} ; {{{\mathcal {B}}}})).$ Given $\epsilon > 0$ there exists an integer $n (\epsilon )$ so $K(f; {{{\mathcal {B}}}}) \subset f^n ({{{\mathcal {B}}}}) \subset \epsilon -$neighborhood of $K(f; {{{\mathcal {B}}}})$ for $n \ge n(\epsilon )$ [and of course $K(f;{{{\mathcal {B}}}}) \subset {f^n} ({{{\mathcal {B}}}})$ for every n].

Assume further that f is uniformly continuous on a $\delta _0-$neighborhood of ${{{\mathcal {B}}}}$ for some $\delta _0.$ Given $\epsilon >0$ there exist $\delta >0$ and $n_0 >0$ so any $g:X \rightarrow X$ with $d(f(x), g(x)) < \delta$ on a $\delta _0-$neighborhood of ${{{\mathcal {B}}}}$, satisfies $g^n({{{\mathcal {B}}}}) \subset \epsilon -$neighborhood of $K(f; {{{\mathcal {B}}}})$ for all $n \ge n_0.$ If g also satisfies (i) and (ii) then $K(g; {{{\mathcal {B}}}}) \subset \epsilon -$neighborhood of $K(f; {{{\mathcal {B}}}}).$

Proof

First assume $m=1.$ Let $B_0 =\overline{{{\mathcal {B}}}}, \ B_{n+1} = \overline{f(B_k)}$ for $k\ge 0.$ Since $\overline{f({{{\mathcal {B}}}})} \subset {{{\mathcal {B}}}}, B_1 \subset B_0$ and $B_{k+1} \subset B_k$ for all $k>0.$ The $B_k$ are nonempty closed bounded sets and $\alpha (B_k) \le \theta ^k \alpha ({{{\mathcal {B}}}})$ and $\alpha (B_k) \rightarrow 0$ as $k \rightarrow \infty$ so $B_\infty = \bigcap \limits _{k \ge 0} B_k$ is a nonempty compact set (and connected if ${{{\mathcal {B}}}}-$hence each $B_k-$ is connected). Also $B_{k+1} \supset f(B_k) \supset f(B_\infty )$ for all k so $B_\infty \supset f(B_\infty );$ and $x \in B_\infty$ implies $x \in B_k$ for all k so $f(x) \in f(B_k) \subset B_{k+1}$ for all k,  then $f(x) \in B_\infty .$ Thus $B_\infty = f(B_\infty )$ is $f-$invariant. Also, given $\epsilon >0$ there exists $n(\epsilon )$ so $B_\infty \subset f^n({{{\mathcal {B}}}}) \subset \epsilon -$neighborhood of $B_\infty$ for $n\ge n(\epsilon ).$ Note that there exists $\epsilon _0 >0$ so $dist(x; B_\infty ) < \epsilon _0$ implies $f^n(x) \in {{{\mathcal {B}}}}$ for all $n\ge 0.$

Suppose S is an invariant set such that $S - {{\mathcal {B}}}$ is pre-compact.If $x \in \overline{S-{{\mathcal {B}}}}$ there exists $n_x$ so $f^n(x) \in {{\mathcal {B}}}$ for $n \ge n_x.$ If $n^\prime _x = n_x + n(\epsilon _0)$ then $f^{n^\prime _x}(x) \in \epsilon _0-$neighborhood of $B_\infty$ so there is a neighborhood $U_x$ of x with $f^{n^\prime _x}(U_x) \subset \epsilon _0-$neighborhood of $B_\infty ,$ hence $f^k(U_x) \subset {{\mathcal {B}}}$ for all $k\ge n^\prime _x .$ By compactness of $\overline{S-{{\mathcal {B}}}},$ there is an open $U \supset \overline{S-{{\mathcal {B}}}}$ and an integer $n^\prime$ such that $f^k(U) \subset {{\mathcal {B}}}$ for all $k \ge n^\prime .$ Since S is invariant, we have in fact $S \subset {{\mathcal {B}}}$ so $S \subset B_k$ for all k,  so $S \subset B_\infty .$ Write $K(f; {{{\mathcal {B}}}})$ or K(f) in place of $B_\infty ,$ the largest compact invariant set or the largest invariant subset of ${{\mathcal {B}}}$ or $A(f / {{{\mathcal {B}}}}; {{{\mathcal {B}}}}).$

Now consider the case $m>1.$ The above argument applies with $f^m$ in place of f, so the set $K(f^m)$ is defined, and it is easy to see we only need to prove $f(K(f^m)) = K(f^m)$ [we know that $K(f^m)$ is $f^m-$invariant]. Let ${\tilde{K}}(f) = \bigcup \limits _{i=0}^{m-1} f^i (K(f^m));$ this is a nonempty compact set, $f^m({\tilde{K}}(f)) = {\tilde{K}}(f)$ so ${\tilde{K}}(f) = K(f^m).$ Also $f({\tilde{K}}(f)) = \bigcup \limits _{i=1}^m f^i(K(f^m)) = {\tilde{K}}(f)$ so $K(f^m)$ is $f-$invariant, not only $f^m-$invariant.

For simplicity, suppose again $m=1$. Now suppose f is uniformly continuous on a $\delta _0-$neighborhood of ${{{\mathcal {B}}}}: \ d(f(x), f(y)) \le w(d(x,y))$ when $dist(x, {{{\mathcal {B}}}})< \delta _0, \ dist(y, {{{\mathcal {B}}}}) < \delta _0,$ with $w(\cdot )$ a continuous positive increasing function, $w(0)=0.$ Then there exist $w_k \ (k\ge 1: w_1=w)$ with similar properties and $d(f^k(x), f^k(y)) \le w_k(d(x,y))$ for x, y in a $\delta _0^{(k)}-$neighborhood of ${{{\mathcal {B}}}}$ [say $w_k = w\circ w_{k-1}$ and $w_{k-1}(\delta _0^{(k)}) =\delta _0].$ If $\delta$ is sufficiently small (given n) then $d(f(x), g(x)) < \delta$ on a $\delta _0-$neighborhood of ${{{\mathcal {B}}}}$ implies $g^k({{{\mathcal {B}}}})\subset \delta _0^{(k)}$ for $k=1,2,\dots ,n$ and $d(f^k(x), g^k(x)) < \delta ^{(k)}$ for $k=1, 2, \dots , n, \ x \in {{{\mathcal {B}}}} \ [\delta ^{(1)} = \delta , \ \delta ^{(k)} = w_k(\delta ^{(k-1)}) + \delta ].$ Indeed this is trivial for $k=1,$ and if true for $(k-1)$ then

$$\begin{aligned} d(f^k(x), g^k(x))&\le d(f(f^{k-1}(x)), f(g^{k-1}(x)))+d(f(g^{k-1}(x)), g(g^{k-1}(x))) \\&< [w(\delta ^{(k-1)})+\delta ] = \delta ^{(k)} \hbox { for } x \in {{{\mathcal {B}}}}. . \end{aligned}$$

If $\delta ^{(k)}< \delta _0^{(k)}$ then $g^k({{{\mathcal {B}}}}) \subset \delta _0^{(k)}-$neighborhood of ${{{\mathcal {B}}}}.$ Choosing $\delta$ small, $\delta (K) < \delta _0^{(k)}$ for $k=1, 2, \dots , n.$ Now given $\epsilon >0$ so $f^k(\epsilon ^\prime -$neighborhood of $K(f)) \subset [\epsilon / 2-$neighborhood of K(f)] for all $k \ge 1 \ (0<\epsilon ^\prime<\epsilon < (1/2) \ dist(K(f), \partial {{{\mathcal {B}}}}),$ without loss of generality). Also there exists an integer $n^\prime \ge 1$ so $f^k({{{\mathcal {B}}}}) \subset [(\epsilon ^\prime / 2)-$neighborhood of K(f)] for all $k \ge n^\prime .$ Choose $\delta > 0$ so small that $d(f^k(x), g^k(x)) < \epsilon ^\prime / 2$ for $k=1, 2, \dots , n^\prime$ and $x \in {{\mathcal {B}}}.$ Then $g^k({{{\mathcal {B}}}}) \subset [\epsilon$-neighborhood of K(f)] for $k \ge n^\prime$. Indeed $g^{n^\prime }({{{\mathcal {B}}}}) \subset [(\epsilon ^\prime / 2)$-neighborhood of $f^{n^\prime } ({{{\mathcal {B}}}})] \subset [\epsilon ^\prime$-neighborhood of K(f)],  so $g^{n^\prime }$ maps the $\epsilon ^\prime$-neighborhood of K(f) to itself, and for $1 \le k\le n^\prime , \ g^k(\epsilon ^\prime$-neighborhood of $K(f)) \subset [(\epsilon ^\prime / 2)$-neighborhood of $f^k(\epsilon ^\prime$-neighborhood of $K(f))] \subset [((\epsilon +\epsilon ^\prime )/2)$-neighborhood of K(f)].

As a final remark in this section we see that the Proposition 1.5 and Corollary 1.6 can be generalized for set contractions instead of compact maps.

Corollary 1.11

If B is bounded (and connected) and $f: B\rightarrow B$ is a set contraction, then the largest invariant set A(f) is nonempty, compact (and connected) and $A(f) = \bigcap \limits _{n\ge 1} f^n(B).$

Corollary 1.12

If B is bounded and $f:B\rightarrow B$ is a set contraction then for any $x \in B, \ w(x)$ is nonempty, compact and invariant (then $w(x) \subset A(f)).$

Example 1.13

Let $f:{\mathbb {R}}^k \rightarrow {\mathbb {R}}^k$ a continuous map such that given $x \in {\mathbb {R}}^k, \ f^n(x)$ belongs to the unit open ball ${{{\mathcal {B}}}}$ for some $n=n(x)$ and $\overline{f({{\mathcal {B}}})} \subset {{{\mathcal {B}}}},$ Then f satisfies the hypothesis of Theorem 1.10.

3 Compact retractions and the dimension of the largest invariant set

Let $B\subset E$ be a Banach manifold imbedded in a Banach space E. A retraction $\beta :B \rightarrow B$ is a continuous map such that $\beta ^2=\beta .$ It is clear that $\beta (B)$ is closed in B.

In [11] we find the proof of the following result:

Proposition 2.1

Let $\beta :B \rightarrow B$ be a smooth retraction. Then $\beta (B)$ is an imbedded submanifold of B.

Example 2.2

Let M be a compact submanifold of an Euclidean space ${\mathbb {R}}^n$ and $B = C^0(I,M)$ be the totality of all continuous paths $\varphi :I=[-m,0] \rightarrow M,$ for some fixed $m>0.$ B is a bounded Banach manifold imbedded in the Banach space $E = C^0(I, {\mathbb {R}}^n)$ of all continuous maps $\varphi : I \rightarrow {\mathbb {R}}^n, \ || \ \ ||$ being the sup norm. A retarded functional differential equation on M (see [2, 11]) is a map $F: B \rightarrow TM, \ F(\varphi )$ being a tangent vector to the manifold M at the point $\varphi (0).$ When F is $C^1 ,$ the flow map $f: B \rightarrow B$ defined by $f(\varphi )=x_m(\varphi ), \varphi \in B,$ is compact and $C^1 \ (t \rightarrow x_t(\varphi )$ is the solution of RFDE F such that $x_0(\varphi ) = \varphi ).$ If F is analytic, f is also analytic and reversible.

The map $\alpha : B \rightarrow B$ defined by

$$\begin{aligned} \alpha (\varphi )={\widetilde{{\varphi (0)}}}, \ \widetilde{\varphi (0)}(\theta ) = \varphi (0) \ \ \hbox { for all } \theta \in I , \end{aligned}$$

satisfies $\alpha ^2 = \alpha$ then is a compact $C^1 -$retraction and $\alpha (B)$ is diffeomorphic to M. Moreover, $\alpha$ is homotopic to the identity map of B,  the homotopy $F: [0,1] \times B \rightarrow B$ being defined by $F(\lambda , \varphi ) = \varphi (\lambda \cdot \theta ), \ 0 \le \lambda \le 1, \ \theta \in [-m, 0].$

The next arguments and statements appearing in this section follow closely the works of Mallet-Paret and Ma$\tilde{\hbox {n}}$é about the subject (see [8,9,10]). We recall them here for a sake of completeness.

Let us denote by ${\mathscr {R}}$ (B) the set of all compact and $C^1$ retractions, homotopic to the identity, defined on a bounded Banach manifold $B \subset E.$ If $\alpha : B \rightarrow B$ belongs to ${\mathscr {R}}$ $(B), \ \alpha (B)$ is an imbedded compact submanifold of B (then a finite dimension manifold).

Let ${{\hat{\alpha }}} : B \rightarrow \alpha (B)$ be the map defined by ${{\hat{\alpha }}} (x) = \alpha (x)$ for all $x \in B,$ and $i: \alpha (B) \rightarrow B$ be the inclusion of $\alpha (B)$ into B.

Since $\alpha ^2 = \alpha ,$ the following diagram

is commutative and induces another commutative diagram

where ${\check{H}}^{*} (\cdot )$ denotes $\check{C}$ech cohomology. The equality $i^* \cdot {\hat{\alpha }}^* = id$ shows that ${\hat{\alpha }}^*$ is injective.

Let $f:B\rightarrow B$ be any compact map homotopic to $\alpha \in$ ${\mathscr {R}}$ (B) (then homotopic to the identity of B) and consider the restriction of ${{\hat{\alpha }}}$ to the compact set A(f):

$$\begin{aligned}{}[{{\hat{\alpha }}} / A(f)]: A(f) \rightarrow \alpha (B). \end{aligned}$$

Let $J:A(f) \rightarrow B$ be the inclusion map; the composition ${{\hat{\alpha }}} \cdot J = [{{\hat{\alpha }}} / A(f)]$ shows that $[{{\hat{\alpha }}} / A(f)]^* = J^* \cdot {\hat{\alpha }}^{*} .$ We will prove that $J^*$ is injective and since ${\hat{\alpha }}^{*}$ is also injective the same holds for $[{{\hat{\alpha }}} / A(f)]^* .$ In fact, to the sequence of inclusions $i_m : {\overline{A}}_m = \overline{f^m(B)} \rightarrow B, \ m \ge 1,$ corresponds the sequence of induced maps $i^*_m .$ By the continuity property of Čech cohomology, if the $i^*_m$ are injective maps then, since $A(f) = \cap _{m \ge 1}{\overline{A}}_m ,$ the map $J^*$ is necessarily injective. To show that the $i^*_m$ are injective maps one considers the composition $B\xrightarrow {{g_m}} {\overline{A}}_m \xrightarrow {{i_m}}B, \ g_m(x) = f^m(x),$ that is , $(f^m)^* = g_m^* \cdot i_m^* ,$ and since by hypothesis f is homotopic to the identity, one has $f^* = id$ and $(f^m)^* = (f^*)^m = id.$ The relation $g_m^* \cdot i_m^* = (f^m)^* = id$ shows finally that the $i_m^*$ are injective maps and we have the following result:

Proposition 2.3

$[{{\hat{\alpha }}} / A(f) ]^* : {\check{H}}^{*}(\alpha (B)) \rightarrow \ {\check{H}}^{*}(A(f))$ is an injective map.

Corollary 2.4

The topological dimension of A(f) is greater or equal to $\dim \alpha (B).$

Proof

Since $\alpha (B)$ is a compact manifold, Ȟ$^{\dim \alpha (B)} (\alpha (B))$ is non trivial; using the fact that $[{{\hat{\alpha }}} / A(f)]^*$ is injective we see that Ȟ$^{\dim \alpha (B)} (A(f))$ is also non trivial and as a consequence, the topological dimension of A(f) is greater or equal to $\dim \alpha (B)$.

Corollary 2.5

$[{{\hat{\alpha }}} / A(f)]: A(f) \rightarrow \alpha (B)$ is onto.

Proof

Suppose $[{{\hat{\alpha }}} / A(f)]$ is not surjective; then there exists a point $p\in \alpha (B)$ which is not in the image of $[{{\hat{\alpha }}}/A(f)]$, that is, the following composition of maps is well defined:

$$\begin{aligned} A(f) \overset{\beta }{\longrightarrow } (\alpha (B)-\{p\}) \overset{i}{\longrightarrow } \alpha (B) \end{aligned}$$

where $\beta (x)=[{{\hat{\alpha }}}/A(f)](x)$ for all $x\in A(f)$. The composition $i \cdot \beta = [{{\hat{\alpha }}}/A(f)]$ induces $\beta ^* \cdot i^* = [{{\hat{\alpha }}}/A(f)]^*$. If $*=n= \dim \alpha (B)$ we obtain, for the cohomology with ${\mathbb {Z}}_2$ coefficients, $\check{H}^n(\alpha (B))={\mathbb {Z}}_2$ and ${\check{H}}^n(\alpha (B)-\{p\})=0$ which is a contradiction since $[{{\hat{\alpha }}}/A(f)]^*$ is one-to-one.

Corollary 2.6

For any $\alpha$ and $\gamma$ in ${{{\mathcal {R}}}}(B)$, $dim \ \alpha (B)= dim \ \gamma (B)$. Moreover, if

$[{{\hat{\alpha }}}/A(\gamma )], d[{{\hat{\alpha }}}/A(\gamma )]$ are injective then $\alpha (B)$ is diffeomorphic to $\gamma (B)$. In particular the integer $n=dim \ \alpha (B)$ depends only on B.

Proof

$[{{\hat{\alpha }}}/A(\gamma )]: A(\gamma )=\gamma (B) \rightarrow \alpha (B)$ is onto, then $\dim A(\gamma ) \ge \dim \alpha (B)$; by symmetry $A(\gamma )$ and $A(\alpha )=\alpha (B)$ have the same dimension. The map $[{{\hat{\alpha }}}/A(\gamma )]$ is then injective and onto hence a homeomorphism; since it is also a local diffeomorphism it follows that $[{{\hat{\alpha }}}/A(\gamma )]$ is a diffeomorphism between $\gamma (B)$ and $\alpha (B)$.

Theorem 2.7

(Mallet-Paret, Mañé). Let E be a Banach space, $U \subset E$ an open set and $f:U \rightarrow E$ a $C^1$ map. If $\Lambda \subset E$ is a compact set such that $f(\Lambda ) \supset \Lambda$ and df(x) is the sum of a contraction and a compact operator for all $x\in \Lambda$, then $\Lambda$ has finite limit capacity. In particular, $\Lambda$ has finite Hausdorff dimension.

The above results apply to RFDE on compact manifolds (Example 2.2).

Theorem 2.8

Let F be an RFDE defined on a compact manifold M (see [2] Ch.13, [9, 10]) and A(F) be the largest invariant set of the flow map of F. Then the Hausdorff dimension of A(F) is finite, is always larger than or equal to that of M and for all $p\in M$ there exists a global solution $x: {\mathbb {R}}\rightarrow M$ of F such that $x(0)=p$. Moreover, if A(F) is a manifold without boundary then $dim \ A(F) = dim \ M$.

Proof

Consider Example 2.2 and apply Corollaries 2.4, 2.5, 2.6 and Theorem 2.7; to complete the proof, we only need to show that in Example 2.2 the map $f:B \rightarrow B$ (defined by $f(\varphi )=x_r(\varphi )$ for all $\varphi \in B$) is homotopic to the compact $C^1$-retraction $\alpha _0$ introduced in that example. In fact, one observes that if $\Phi _t^{(\lambda )} (t \ge 0)$ is the semiflow on $B=C^0([-r,0],M)$ defined by the RFDE $\dot{x}(t)=\lambda F(x_t)$, then $\Phi _r^{(1)}=f$ and $\Phi _r^{(0)}=\alpha _0$.

4 Hyperbolic periodic points of smooth maps. Fundamental local results

Let $x=f(x)$ be a fixed point of a $C^r$-map $f:B \rightarrow B, r \ge 1, B \subset E$ being a Banach manifold imbedded in the Banach space E. The fixed point is said to be hyperbolic if the spectrum $\sigma (df(x))$ of the derivative df(x) is disjoint from the unit circle of the complex plane. Under the above hypothesis one can define local unstable and local stable $C^r$-manifolds denoted by $LW^u(x)$ and $LW^s(x)$, respectively (see th. 5.1, [6 p. 53]).

Proposition 3.1

Let $x=f(x)$ be a hyperbolic fixed point of a reversible $C^r$ map $f:B \rightarrow B$. The set $W^u(x)=\bigcup _{i \ge 0} f^i(LW^u(x))$ is an injectively immersed $C^r$-submanifold of B.

The manifold $W^u(x)$ is the (global) unstable manifold of the hyperbolic fixed point x. It is easy to see that $W^u(x)$ is invariant under f so $W^u(x) \subset A(f).$

For instance, if the given $C^r$ map $f: B \rightarrow B$ is compact, the derivative df(x) at the hyperbolic fixed point x is a linear compact operator and $W^u(x)$ is finite dimensional; $LW^s(x)$ is finite codimension and positively invariant. The manifolds $LW^s(x)$ and $LW^u(x)$ are always transversal at the point x.

If $g=f^n , n\ge 1,$ is a power of bounded map $f:B \rightarrow B$, it is easy to see that $A(f) = A(g).$ If f/A(f) is injective then g/A(g) is also injective. If f is compact, g is compact and if f is reversible, g is reversible.

$x \in B$ is a periodic point of f if it is a fixed point of some iterate of f; the smallest integer $m > 0$ with $f^m(x) = x$ is the period of x. It is clear that the orbit ${\tiny {\mathscr {O}}}$ $(x)=\{ x, f(x), f^2(x), \dots , f^{m-1}(x)\}$ of a periodic point x is a finite set with m points. Fix(f) and Per(f) will denote, respectively, the set of all fixed points and of all periodic points of f. We have, obviously, $Fix(f) \subset Per(f) \subset \Omega (f).$

A periodic point x with period m is said to be a hyperbolic periodic point if ${\tiny {\mathscr {O}}}$ (x) is hyperbolic, that is, if all points $y \in {\tiny {\mathscr {O }}}(x)$ are hyperbolic fixed points of $f^m$. We can talk about $LW^u(y), LW^s(y)$ for all $y \in$ ${\tiny {\mathscr {O}}}$ (x). The unstable manifold of y is $W^u(y) = \cup _{i\ge 0} \ f^{mi}(LW^u(y)).$

Definition 3.2

A hyperbolic periodic point x of f is a source if $LW^s(x) \cap A(f) = \{x\};$ is a sink if $LW^u(x) = \{x\};$ otherwise x is a saddle.

Proposition 3.3

Let f be a smooth $C^0$-reversible map and x be a hyperbolic periodic source (sink; saddle). Then $y \in$ is ${\tiny {\mathscr {O}}}$ (x) is also a source (sink; saddle).

Proof

By the theory of local invariant manifolds we have always the relations:

$$\begin{aligned} f(LW^u(x)) \subset LW^u(f(x)) \hbox { and } f(LW^s(x)) \subset LW^s(f(x)) \end{aligned}$$

which show that x is a sink if and only if $y \in$ ${\tiny {\mathscr {O}}}$ (x) is also a sink. But, since f is one-to-one on A(f) it follows that x is a source if and only if $y \in$ ${\tiny {\mathscr {O}}}$ (x) is a source.

Let x be a hyperbolic fixed point of a smooth map $f: B \rightarrow B$ and assume $\dim LW^u(x) < \infty .$ If x is not a sink there exists an open disc $B^u$ in $LW^u(x)$ such that $\overline{B^u} \subset LW^u(x)$ and $f^{-1} / B^u$ is a contraction. It follows that $f^{-l}(B^u) \subset B^u.$ As usually, a fundamental domain for $LW^u(x)$ is the compact set $G^u(x)=\overline{B^u} - f^{-1}(B^u).$ If $y \in LW^u(x) - \{x \},$ there exists an integer k such that $f^k(y) \in G^u(x).$ Any neighborhood $N^u(x)$ of $G^u(x)$ such that $N^u(x) \cap LW^s(x) = \Phi$ is called a fundamental neighborhood for $LW^u(x).$

If the hyperbolic fixed point is not a source we will consider a neighborhood $V = B^s \times B^u$ of x, $B^s$ being an open disc in $LW^s(x)$ such that $f / B^s$ is a contraction and $\overline{B^s} \subset LW^s(x).$ In order to define the concept of fundamental domain for $LW^s (x)- G^s(x) ,$ we assume the following hypothesis: "A(f) is compact and f is $C^0$-reversible."

We then define

$$\begin{aligned} G^s(x) = \overline{B^s \cap A(f)} - f(B^s \cap A(f)) \end{aligned}$$

and since f/A(f) is a homeomorphism, $G^s(x)$ is compact. It is clear that $x \notin G^s(x)$ so $LW^u(x) \cap G^s(x)=\Phi$ and there exists a neighborhood $N^s(x)$ of $G^s(x)$ which does not intersect $LW^u(x); \ N^s(x)$ is called a fundamental neighborhood for $LW^s(x).$

Remark

• (1) Any point of $W^s \cap A(f) = [ \bigcup \limits _{i\ge 0} f^{-i}(LW^s(x)) ] \cap A(f)$ reaches $B^s \cap A(f)$ after finitely many iterations of f/A(f) or its inverse.

• (2) Given $y \in B^s \cap A(f) - \{ x \},$ there exists an integer k such that ${\tilde{f}}^k(y) \in G^s(x), \ {\tilde{f}}$ being the restriction of f to A(f).

In fact, if $y \notin f(B^s \cap A(f))$ there is nothing to prove. If $y \in f(B^s \cap A(f))$ one considers the sequence $y=y^0, y^1, y^2, \dots f(y^i) = y^{i-1} \ i\ge 1,$ and there exists a first integer $i_0$ such that $y^{i_0} \notin B^s \cap A(f)$ ( if $y^i \in B^s \cap A(f)$ for all $i\ge 1$ then $y \in LW^u(x) \cap B^s = \{x\}).$ If $y^{i_0} \in \overline{B^s \cap A(f)}, \ y^{i_0} \in G^s(x);$ if $y^{i_0} \notin \overline{B^s \cap A(f)}$ then $y^{i_0 -1} \in B^s \cap A(f) - f(B^s \cap A(f)) \subset G^s(x).$

Given two submanifolds $i_1: W_1 \rightarrow B$ and $i_2: W_2 \rightarrow B$ one says that $W_1$ and $W_2$ are $\epsilon -C^1$ close manifolds if there exists a diffeomorphism $\gamma :W_1 \rightarrow W_2$ such that $i_1: W_1 \rightarrow B$ and $i_2 \circ \gamma :W_1 \rightarrow B$ are $\epsilon -C^1$ close maps.

The local $\lambda$-lemma (see [12]) holds, mutatis mutandis, for any smooth map f defined in the neighborhood of a hyperbolic fixed point such that $LW^u(x)$ has finite dimension.

Proposition 3.4

(local $\lambda$-lemma). Let x be a hyperbolic fixed point of a smooth map $f: B\rightarrow B, \ \dim LW^u(x) < \infty ,$ and $B^u$ be an imbedded open disc in $LW^u(x),$ containing x. Let q be a point of $LW^s(x), \ q\ne x$, and $D^u$ be a disc centered at q, transversal to $LW^s(x),$ such that $\dim D^u = \dim LW^u(x).$ Then there is an open set V of B containing $B^u$ such that given $\epsilon >0$ there exists $n_0 \in N$ such that if $n>n_0$ the connected component of $f^n(D^u) \cap V$ through $f^n(q)$ and the open disc $B^u$ are $\epsilon -C^1$ close manifolds.

Proof

(see [12,13,14]).

It is interesting to remark that we do not need to assume compactness or reversibility for the smooth map f but the proof uses, strongly, the finite dimensionality of $LW^u(x).$

In the same hypothesis of the local $\lambda$-lemma, let x be a hyperbolic fixed point of a smooth map $f: B\rightarrow B$ and $LW^u(x)$ be the local finite dimensional unstable manifold of x. The unstable set is the union $W^u(x)=\bigcup \limits _{n\ge 0} f^n(LW^u(x)).$ The topological boundary of the invariant set $W^u(x)$ is the set $\partial W^u(x)$ of all $y \in B$ such that $y = lim \ f^{n_i} (y_i), \ n_i \rightarrow \infty$ as $i\rightarrow \infty ,$ the $y_i$ belonging to a fundamental domain $G^u(x)$ for $LW^u(x).$ Remark that if A(f) is compact $\partial W^u(x)$ is an invariant set because it is obviously positively invariant and given $y=lim f^{n_i}(y_i) \in \partial W^u(x),$ the $f^{n_i -1}(y_i)$ belong to A(f). The compactness of A(f) implies there exists a limit point $x_1 \in A(f)$ of $f^{n_i -1}(y_i)$ and $f(x_1)=y;$ by induction, one constructs a sequence $(y = x_0, x_1, x_2, \dots ) \in \partial W^u(x)$ satisfying $f(x_i) = x_{i-1} , \ i\ge 1,$ then $\partial W^u(x)$ is negatively invariant and $\partial W^u(x) \subset A(f).$

Remark 3.5

The $w$-limit sets of points of $G^u(x)$ are contained in $\partial W^u(x)$ but the converse is not true, in general, as it happens in many situations.

Proposition 3.6

Let x be a hyperbolic fixed point of a smooth map f and assume $\dim LW^u(x) < \infty .$ Then $W^u(x)$ is invariant and $\overline{W^u}(x) = \partial W^u(x) \cup W^u(x).$ If in addition A(f) is compact then $\partial W^u(x)$ and $\overline{W^u}(x)$ are invariant sets.

Proof

Let $y \in \overline{W^u}(x)$ be the limit of a sequence $x_\nu \rightarrow y, \ x_\nu \in W^u(x).$ If $y \in W^u(x)$ we have the inclusion $\overline{W^u}(x) \subset \partial W^u(x) \cup W^u(x)$ and the proof is over; assume that $y \notin W^u(x).$ By the definition of $W^u(x),$ for each $x_\nu \in W^u(x)$ corresponds an integer $n_\nu$ and $y_\nu \in G^u(x)$ such that $x_\nu = f^{n_\nu }(y_\nu ), \ \nu \ge 1.$ We want to conclude that $n_\nu \rightarrow \infty$ as $\nu \rightarrow \infty .$ If $n_\nu < M$ for all $\nu \ge 1$ and for some integer M, we construct the sets $f^j(G^u(x)), 0 \le j \le M,$ and have two possibilities: either $y \in f^j(G^u(x))$ for some $j, 0 \le j\le M,$ then $y \in W^u(x)$ which is a contradiction, or $y \notin f^j(G^u(x))$ for all $0\le j\le M,$ then there exists a neighborhood U of y such that $U \cap f^j(G^u(x)) = \Phi$ for all $j= 0,1,2,\dots ,M,$ and $x_\nu = f^{n_\nu }(y_\nu ) \notin U$ for all $\nu \ge 1$ which is also a contradiction since $x_\nu \rightarrow y.$ Then $n_\nu \rightarrow \infty$ as $\nu \rightarrow \infty$ and $y \in \partial W^u(x).$ It was showed that $\overline{W^u(x)} \subset \partial W^u(x) \cup W^u(x).$ The prove is complete since the inclusion $\overline{W^u(x)} \supset \partial W^u(x) \cup W^u(x)$ is trivial.

Let us denote by $C^r(B,E)$ the Banach space of all $C^r$ maps $f: B\rightarrow E$ such that f are bounded with bounded derivatives up to the order $r \ge 1.$ We give to $C^r(B,B) \subset C^r(B,E)$ the induced topology. We say that $x= f^n(x)$ is a non degenerate $n$-periodic point if n is the period of x and $1 \notin$ spectrum of $df^n(x).$

Proposition 3.7

Let $x = x(f)$ be a non degenerate $n$-periodic point of a $C^r$ map $f: B \rightarrow B, \ r \ge 1.$ There exist neighborhoods U of x in B and $\vartheta (f)$ of f in $C^r(B,B)$ such that any $g \in \vartheta (f)$ has in U only one $n-$-periodic point x(g) and no other $m$-periodic point with $m\le n.$ Moreover, if x is hyperbolic, the local stable and unstable manifolds depend continuously on $g \in \vartheta (f);$ in particular if $LW^u(x(f))$ is finite dimensional, on has $\dim LW^u(x(f)) = \dim LW^u(x(g))$ for all $g \in \vartheta (f).$

Proof

Assume, first of all, $x= x(f)$ is a fixed point. The map

$$\begin{aligned} F: C^r(B, E) \times B \rightarrow E \end{aligned}$$

defined by

$$\begin{aligned} F(g,y) = g(y) - y \end{aligned}$$

is differentiable$\cdot$ and $DF(f,x) (h,u) = d f(x) u - u+h(x).$ But $F(f,x) = f(x)-x = 0$ and $1 \notin \sigma (df(x))$ then there exist neighborhoods $\vartheta (f)$ of f in $C^r(B,B)$ and U(x) of x in B,  and a function $y^*: \vartheta (f)\rightarrow U(x)$ such that $g(y^*(g)) = y^*(g)$ for all $g \in \vartheta (f).$

The properties related with the local invariant manifolds follow from the general results of the theory of invariant manifolds. Finally, if $x= x(f)$ is a periodic point, we use the continuity of the map $f \rightarrow f^n$ to finish the proof.

Proposition 3.8

Let P be a hyperbolic periodic point of a smooth map $f, \ \dim LW^u(P) < \infty ,$ and $N^u(P)$ a fundamental neighborhood for $LW^u(P).$ Then, there exists a neighborhood W of P such that

$$\begin{aligned} \bigcup \limits _{n\ge 0} f^{-n}(N^u(P)) \cup LW^s(P) \supset W. \end{aligned}$$

Proof

Let p be the period of P and $h = f^p.$ If the proposition is not true, there exists a sequence $x_\nu \rightarrow P$ as $\nu \rightarrow \infty$ such that $x_\nu \notin LW^S(P)$ and $x_\nu \notin \bigcup _{n\ge 0} f^{-n}(N^u(P)).$ Let $V=B^s \times B^u$ be a neighborhood of P considered in the construction of $N^u(P).$ Let $k_\nu$ be the first integer such that $z_{k_\nu } = h^{k_\nu }(x_\nu ) \notin V;$ such a first integer does exist, otherwise $x_\nu \in LW^s(P)$. The sequence $k_\nu \rightarrow \infty$ as $\nu \rightarrow \infty$; in fact, if $k_\nu \le M$ for all $\nu \ge 1,$ since $h^{k_\nu }(P)= p$ and $h^{k_\nu }$ is continuous there exists a neighborhood ${\tilde{V}}$ of $P, \ {\tilde{V}} \subset V$ such that $h^{k_\nu }({\tilde{V}}) \subset V$ for all $k_\nu \le M$ which is an absurd because the $x_\nu \in {\tilde{V}}$ for all $\nu \ge \nu _0$ imply $h^{k_\nu }(x_\nu ) \in V$ giving a contradiction.

We may assume the neighborhood V is chosen such that $h(x_s , x_u) = (L_s x_s + \Phi _s(x_s, x_u), \ L_u x_u + \Phi _u (x_s, x_u))$ verifies $||L_s||, \ ||L_u^{-1}||< a< 1, \ \big \Vert \frac{\partial \Phi _i}{\partial x_j} \big \Vert \le k, \ a+k <1, \ i, j = u, s.$ Since $x_\nu \rightarrow P,$ there exists $\nu _1$ such that for all $\nu \ge \nu _1$ one has $||x_\nu ||\le \frac{1}{\nu }$ and if $h(x_s, x_u) = ({\overline{x}}_s, {\overline{x}}_u), \ {\overline{x}}_s = B^s, \ {\overline{x}}_u \in B^u,$ one obtains, also, $||{\overline{x}}_s|| = ||L_s x_s + \Phi _s(x_s, x_u)|| \le a(\frac{1}{\nu }) = k(\frac{1}{\nu }) < \frac{1}{\nu }.$

The canonical projections of $h^{k_\nu -1}(x_\nu )$ on $B^u$ and $B^s$ are $\pi _u(h^{k_\nu -1}(x_\nu ))$ and $\pi _s(h^{k_\nu -1}(x_\nu )),$ respectively; since $\overline{B^u}$ is compact, there is a limit point Z for $\pi _u(h^{k_\nu -1}(x_\nu ))$, that is, at least for a subsequence one has $\lim _{\nu \rightarrow \infty } \pi _u(h^{k_\nu -1}(x_\nu )) =Z$ and $||\pi _s(h^{k_\nu -1}(x_\nu ))|| < \frac{1}{\nu }$ for all $\nu \ge \nu _1.$ The above argument shows us that there exists a subsequence of $h^{k_\nu -1}(x_\nu )$ which has $z \in \overline{B^u}$ as limit and $h^{k_\nu }(x_\nu ) = h(h^{k_\nu -1}(x_\nu )) \rightarrow h(Z).$ That limit point Z is not P because $h(Z) \notin V,$ then Z reaches $N^u(P)$ after a finite number of iterations of h and, by continuity, each $h^{k_\nu -1}(x_\nu ),$ for large $\nu$, reaches $N^u(P)$ after a finite number of iterations of h that is $x_\nu \in \cup _{n\ge 0} \ f^{-n}(N^u(P))$ which is a contraction. The proof is then complete.

Proposition 3.9

Let P be a hyperbolic $p$-periodic point of a map$f \in C^r(B,B),\ r \ge 1, \ \dim LW^u(P) < \infty ,$ and $N^u(P)$ a fundamental neighborhood for $LW^u(P).$ Then, there exist neighborhoods U of P in B and $\vartheta (f)$ of f in $C^r(B,B)$ such that $N^u(P)$ is a fundamental neighborhood for $LW^u(P^*), P^* = P^*(g)$ being the unique hyperbolic $p$-periodic point in U corresponding to $g \in \vartheta (f).$ Moreover, there exists a neighborhood $W_0$ of P such that for all g in $\vartheta (f)$ one has

$$\begin{aligned} \bigcup \limits _{n\ge 0} g^{-n}(N^u(P)) \cup LW^s(P^*(g)) \supset W_0. \end{aligned}$$

Proof

The first statement is a consequence of Proposition 3.7. Assume that the remaining statement is not true; then there exist sequences $x_\nu \rightarrow P$ and $g_\nu \rightarrow f$ such that

$$\begin{aligned} x_\nu \notin LW^s(P^*(g_\nu )) \end{aligned}$$

and

$$\begin{aligned} x_\nu \notin \bigcup \limits _{n\ge 0} g_\nu ^{-n}(N^u(P)). \end{aligned}$$

As before, let $k_\nu$ be the first integer such that $g_\nu ^{pk_\nu }(x_\nu ) \notin V = B^s \times B^u;$ such a first integer does exist because $x_\nu \notin LW^s (P^*(g_\nu )).$ Call $h = f^p$ and $h_\nu = g_\nu ^p;$ if $k_\nu \le M$ for $\nu \ge 1, \ h^{k_\nu }(P)=P$ implies the existence of ${\tilde{V}},$ neighborhood of P,  such that $h^{k_\nu }({\tilde{V}}) \subset V;$ then $f^{pk_\nu }(x_\nu ) \in V$ for large $\nu$ and $g_\nu \rightarrow f$ implies $g_\nu ^{pk_\nu }(x_\nu ) \in V$ which contradicts the definition of $k_\nu .$ We know that $g_\nu ^{pk_\nu }(x_\nu ) = h_\nu ^{k_\nu }(x_\nu ) \notin V$ but $g_\nu ^{p(k_\nu -1)}(x_\nu ) = h_\nu ^{k_\nu -1}(x_\nu ) \in V$ for all $\nu \ge 1$. The convergence $h_\nu \rightarrow h$ is in the $C^1$-norm then we can choose V such that $h_\nu (x_s , x_u)=(L_s^\nu x_s + \Phi ^\nu _s(x_s, x_ u), \ L^\nu _u x_s + \Phi ^\nu _u (x_s, x_u)), \ ||L_s||< a< 1, \ \big | \frac{\partial \Phi _s}{\partial x_j} \big | \le k, \ 0<a+k<1$ and given $\epsilon >0, \ \exists \ \nu _0$ such that $\nu > \nu _0$ implies $|| L_s - L^\nu _s|| < \epsilon$ and $\Big | \frac{\partial \Phi _s^\nu }{\partial x_j} - \frac{\partial \Phi _s}{\partial x_j} \Big | < \epsilon , \ j=u, s.$ It follows that for a suitable $\epsilon > 0, \ ||L^\nu _s || \le a + \frac{\epsilon }{2} < 1$ and $\Big | \frac{\partial \Phi _s^\nu }{\partial x_j} \Big |< k + \frac{\epsilon }{2}, \ (a + \frac{\epsilon }{2}) + (k + \frac{\epsilon }{2}) = (a + k+\epsilon )<1.$ The same argument used in the last Proposition 3.8 shows that $h_\nu ^{k_\nu -1}(x_\nu ) \rightarrow {\overline{Z}}.$ If ${\overline{Z}}=P, \ h({\overline{Z}})=h(P)=P=h(h^{k_\nu -1}(x_\nu ))$ and since $h_\nu \rightarrow h, \ |h_\nu (h_\nu ^{k_\nu -1}(x_\nu )) - h(h_\nu ^{k_\nu -1}(x_\nu )) | < \epsilon$ that is $|h_\nu ^{k_\nu }(x_\nu ) -P| < \epsilon$ which is an absurd since $h_\nu ^{k_\nu }(x_\nu ) \notin V.$ Since ${\overline{Z}} \ne P$ and ${\overline{Z}} \in LW^u(P),$ with a finite number of iterations of ${\overline{Z}}$ by $h/LW^u(P)$ or its inverse one reaches $N^u(P)$ and with the same number, for large $\nu , x_\nu$ reaches $N^u(P)$ by using $h_\nu$ and $x_\nu \in \cup _{n\ge 0} \ g_\nu ^{-n}(N^u(P))$ which is a contradiction. The proof is complete.

To state dual results corresponding to Propositions 3.8 and 3.9 we need to assume reversibility for f and some compactness hypothesis in the set of maps to be considered.

Proposition 3.10

Let P be a hyperbolic periodic point of a $C^0$-reversible and smooth map f such that A(f) is compact; let $N^s(P)$ be a fundamental neighborhood for$LW^s(P).$ Then there exists a neighborhood W of P such that

$$\begin{aligned} \bigcup \limits _{n\ge 0} f^n(N^s(P)) \cup LW^u(P) \supset W \cap A(f). \end{aligned}$$

Proof

Let p be the period of $P (f^p(P) = P)$ and V the neighborhood used in the construction of $N^s(P).$ If Proposition 3.10 is not true, there exists a sequence $x_\nu \rightarrow P, \ x_\nu \in A(f), \ x_\nu \notin LW^u(P)$ and $x_\nu \notin \cup _{n>0} \ f^n(N^s(P)).$ Each $x_\nu$ defines a unique sequence $(x_\nu = x_\nu ^0, x_\nu ^1, x_\nu ^2, \dots ) \in A(f), \ f^p(x_\nu ^i)= x_\nu ^{i-1}, \ i\ge 1.$

Let $k_\nu$ be the first integer such that $x_\nu ^{k_\nu } \notin V$ (if $x_\nu ^i \in V$ for all $i, \ x_\nu \in LW^u(P)).$ See that $k_\nu \rightarrow \infty$ as $\nu \rightarrow \infty ;$ if $k_\nu \le M$ let ${\tilde{f}} = f/ A(f)$ be the homeomorphism obtained restricting f to $A(f), \ {\tilde{f}}^{-pk_\nu }(P)=P,$ and given $V \cap A(f),$ there exists ${\tilde{V}} = {\tilde{V}}(P)$ such that ${\tilde{f}}^{-pk_\nu }({\tilde{V}} \cap A(f)) = V \cap A(f)$ and for large $\nu \ge \nu _0, \ x_\nu \in {\tilde{V}} \cap A(f)$ then ${\tilde{f}}^{-pk_\nu }(x_\nu ) \in V \cap A(f)$ which is a contradiction.

We have limit points $x_\nu ^{k_\nu -1} \rightarrow x, \ x_\nu ^{k_\nu } \rightarrow y, \ {\tilde{f}}^p(y) = x$ and $x \ne P$ (if $x=P \Rightarrow y=P$(contradiction since $y \notin V$)). It is easy to see that $x \in A(f) \cap LW^s(P)$ since there exists a sequence $x, f^p(x), f^{2p}(x), \dots ,$ constructed using $x_\nu ^{k_\nu -1} , x_\nu ^{k_\nu - 2},$ and so on.

With finite number of iterations by ${\tilde{f}}^p, \ x$ reaches $N^s(P).$ Since $x_\nu ^{k_\nu -1} \rightarrow x$ the same happens with $x_\nu ^{k_\nu -1}$ and $x_\nu \in \cup _{n\ge 0} \ f^n(N^s(P))$ and obtain a contradiction. The proof is complete.

Consider now a (not unique) topological subspace $KC^r(B,B)$ of $C^r(B,B)$ satisfying the following compactness and reversibility properties: "Any $f \in KC^r(B,B)$ is reversible, has A(f) compact and given a neighborhood U of A(f) in B, there exists a neighborhood $\mathfrak {w}(f)$ of f in $KC^r(B,B)$ such that $A(g) \subset U$ for all $g \in \mathfrak {w}(f)$."

Proposition 3.11

Let P be a hyperbolic $p$-periodic point of a map $f \in KC^r(B,B), \ r \ge 1,$ and $N^s(P)$a fundamental neighborhood for $LW^s (P).$ Then, there exist neighborhoods U of P in B and $\vartheta (f)$ of f in $KC^r(B,B)$ such that $N^s(P)$ is a fundamental neighborhood for $LW^s(P^*), \ P^* = P^*(g)$ being the unique hyperbolic $p$-periodic point in U corresponding to $g \in \vartheta (f).$ Moreover, there exists a neighborhood $W_0$ of P such that for all $g \in \vartheta (f)$ one has

$$\begin{aligned} \bigcup \limits _{n\ge 0}g^n(N^s(P)) \cup LW^u(P^*(g)) \supset W_0 \cap A(g). \end{aligned}$$

Proof

The first statement follows from Proposition 3.7. If the second statement is not true there exist sequences $x_\nu \rightarrow P$ and $g_\nu \rightarrow f$ such that $x_\nu \in A(g_\nu ),$

$$\begin{aligned} x_\nu \notin LW^u(P^*(g_\nu )) \hbox { and } x_\nu \notin \bigcup \limits _{n\ge 0}g_\nu ^n(N^s(P)). \end{aligned}$$

Following the same arguments as in the proof of proposition 3.10, each $x_\nu$ defines a unique sequence

$$\begin{aligned} (x_\nu = x_\nu ^0, x_\nu ^1, x_\nu ^2, \dots ) \in A(g_\nu ), \ g_\nu ^p(x_\nu ^{i})= x_\nu ^{i-1}, \ i \ge 1. \end{aligned}$$

Let $k_\nu$ be the first integer such that $x_\nu ^{k_\nu } \notin V, \ V$ being a neighborhood of P used in the construction of $N^s(P)$ (if $x_\nu ^i \in V$ for all $i\ge 0, \ x_\nu \in LW^u(P^*(g_\nu ))).$ The sequence $g_\nu$ may be chosen in order to obtain $A(g_\nu )$ in a $(1/ \nu )$-neighborhood of A(f), then $x_\nu ^{k_\nu }$ approaches A(f) as $\nu \rightarrow \infty .$ Since A(f) is compact there exists a sequence $y_\nu \in A(f)$, each $y_\nu$ giving the minimum for the distances between the $x_\nu ^{k_\nu }$ and A(f). The sequence $y_\nu$ has a limit point $y \in A(f)$ and it is clear that $x_\nu ^{k_\nu } \rightarrow y$ as $\nu \rightarrow \infty ,$ then $y \notin V.$ See that $k_\nu \rightarrow \infty$ as $\nu \rightarrow \infty$ (if $1 \le k_\nu \le M$ and since $x_\nu ^{k_\nu -1} \rightarrow f^p(y), \ x_\nu ^{k_\nu -2} \rightarrow f^{2p}(y),$ etc, one obtains $f^{Mp}(y) = P$ which implies $y=P \in V$-contradiction) then $P \in w(y)$ with respect to $f^p$ and $y \in A(f) \cap LW^s(p), \ y \ne P.$ With a finite number of iterations of y by $f^p / A(f)$ one reaches $N^s(P)$ and with the same number, for large $\nu , x_\nu ^{k_\nu }$ reaches $N^s(P)$ using $g_\nu ^p ,$ then $x_\nu \in \cup _{n\ge 0} \ g_\nu ^n \ (N^s(P)),$ which is a contradiction. The proof is complete.

Proposition 3.12

Assume it is given a topological subspace S of $C^r(B,B)$ such that any $f \in S$ is reversible, has A(f) compact and admits a neighborhood $\vartheta (f)$ in S such that $\cup _{g \in \vartheta (f)} \ A(g)$ is relatively compact. Then S has the properties of a $KC^r(B,B).$

Proof

If the proposition were not true, there would exist a neighborhood $U_0$ of A(f),  a sequence $f_\nu \rightarrow f, \ f_\nu \in S$ and points $x_\nu \in A(f_\nu )$ such that $x_\nu \notin U_0.$ But the elements of the sequence $(x_\nu )$ eventually belong to $\cup _{g \in \vartheta (f)} \ A(g)$ for a suitable neighborhood $\vartheta (f)$ of f in S; so $(x_\nu )$ has a limit point $x^0.$ Since $x_\nu \in A(f_\nu )$ there exists a sequence

$$\begin{aligned} ( x_\nu = x_\nu ^0 , x_\nu ^1 , x_\nu ^2 , \dots , x_\nu ^i, \dots ) \in A(f_\nu ) \end{aligned}$$

such that $f_\nu (x_\nu ^i) = x_\nu ^{i-1}$ for $i \ge 1.$ Choosing an appropriate subsequence of the $(x_\nu ^0),$ hence the $(x_\nu ^i)$ for each i, one obtains a sequence of limit points

$$\begin{aligned} (x^0, x^1, x^2, \dots ), \ x_\nu ^i \rightarrow x^i, \ i\ge 0. \end{aligned}$$

But $||f(x^1)-x^0|| \le ||f(x^1) - f(x_\nu ^1)|| + || f(x_\nu ^1) - f_\nu (x_\nu ^1)|| + ||x_\nu ^0 - x^0||,$ that is, $f(x^1) = x^0;$ analogously $f(x^i) = x^{i-1}, \ i\ge 2,$ and $x^0 \in A(f) - U_0 = \Phi$ which is a contradiction.

Remark 3.13

Recall the Example 2.2 in which $B= C^0(I,M).$ Let $S \subset C^r(B ,B)$ be the set of all analytic flow maps $f_F$ of analytic (RFDE) $F \in \mathfrak {X}^r$ (see [2] p. 330) defined on an analytic compact manifold M. Then S is a particular $KC^r(B,B), \ r \ge 1$. The reversibility of $f_F$ follows from the analiticity of F,  and each $f_F$ being compact implies $A(f_F)$ is a compact set. The "continuity" of $A(f_F)$ with respect to $f_F$ follows from Proposition 3.12.

In fact, the map $f: F \in \mathfrak {X}^r \rightarrow f_F \in C^r(B,B)$ is well defined,continuous and injective. Moreover, $\mathfrak {X}^r$ is homeomorphic to $f(\mathfrak {X}^r)$ with the relative topology since $f_{F_\nu } \rightarrow f_F$ (in the topology of $C^r(B,B))$ implies $F_\nu \rightarrow F$ in $\mathfrak {X}^r.$ By Arzela’s theorem and the above homeomorphism we see that the topological subspaces ${\tilde{S}} = f(\mathfrak {X}^r)$ and S satisfy the hypothesis of Proposition 3.12.

5 Morse-Smale maps. Openess and $\Omega$-stability

In this section we will state and prove some fundamental results related with the local and global behavior of the invariant manifold of hyperbolic (fixed and periodic) points of some special smooth maps. Let $C^r(B,E)$ be the Banach space of all $C^r$-maps $f: B \rightarrow E,$ bounded with bounded derivatives up to the order $r\ge 1.$ As above considered, we will deal with special spaces $KC^r(B,B)$ which are topological subspaces of $C^r(B,E).$

To obtain global unstable manifolds we saw that it was sufficient to assume reversibility; when the non wandering set $\Omega (f)$ of a map f belonging to one space $KC^r(B,B), \ r \ge 1,$ is a finite set of (hyperbolic periodic) points with finite dimension unstable manifolds satisfying a transversality condition (see Definition 4.2) we say that f is a Morse-Smale map. The purpose of this section is to study some properties of the Morse-Smale maps.

The choice of the class $KC^r(B,B)$ depends on the case we are studying; for instance, maps arising from retarded functional differential equations, neutral functional differential equations, semi-linear parabolic equations, hyperbolic equations, can be considered. In each case we need to assume the appropriate hypothesis on the equations in order to obtain the compactness properties of $KC^r(B,B).$

Proposition 4.1

Let $P, Q \in \hbox {Per}(f)$ be distinct hyperbolic periodic points of a reversible map f such that $\dim LW^u(P), \ \dim LW^u (Q) < \infty .$ If A(f) is compact and $\overline{W^u}(Q) \cap W^u(P) \ne \Phi ,$ then there exists $x \in \overline{W^u}(Q) \cap LW^s(P)$ such that $x \in {\tiny {\mathscr {O}}} (P).$

Proof

From the hypothesis it follows that $P \in \overline{W^u}(Q)$ so there exists a sequence $z_i = f^{n_i}(y_i) \rightarrow P$ with $n_i\rightarrow \infty$ as $i \rightarrow \infty , \ y_i \in G^u(Q).$ The points P and Q are fixed points of the power $g=f^{[p,q]}, \ p$ and q being the periods of P and Q and [p, q] its least common multiple. Since Q is a limit point of a sequence $(Z_i = Z_i^0, Z_i^1, Z_i^2, \dots ) \in W^u(Q), \ g(Z_i^\nu )=Z_i^{\nu -1}, \ \nu \ge 1,$ there exists a first integer $k_i$ such that $Z_i^{k_i} \notin {\overline{U}}_0, \ {\overline{U}}_0$ being a suitable bounded and closed neighborhood of P, chosen together with closed neighborhood ${\overline{U}}_n$ of $f^n(p), \ 1 \le n \le p-1 ,$ satisfying the condition $g({\overline{U}}_i) \cap {\overline{U}}_j = \Phi , \ 0\le i\ne j \le p-1.$

Since $Z_i^{k_i} \in W^u(Q) \subset A(f)$ then the sequence $Z_i^{k_i}$ has a limit point x;  but $Z_i^{k_i} \notin \ int \ {\overline{U}}_0,$ that is, $Z_i^{k_i} \in A(f) - \ int\ {\overline{U}}_0$ which is closed, then $x \in A(f) - \ int \ {\overline{U}}_0$ and $x \ne P.$

We remark now that $k_i \rightarrow \infty$ as $i \rightarrow \infty$ because if $k_i \le M$ for all $i \ge 1,$ there exists a neighborhood ${\tilde{V}}$ of P such that ${\overline{g}}^{k_i}({\tilde{V}}) \subset {\overline{U}}_0$ for all $k_i \le M ,$ but $Z_i \rightarrow P$ implies $Z_i \in {\tilde{V}}$ for large i and since $g^{k_i}(Z_i^{k_i}) = Z_i$ one obtains $Z_i^{k_i} \in {\overline{U}}_0$ which is a contradiction.

Given $l\ge 1, \ g^l(x) \in {\overline{U}}_0 ;$ in fact, for large $i, \ k_i > l$ and $g^l(x) = g^l( \ lim \ Z_i^{k_i}) = \ lim \ g^l( Z_i^{k_i}) = \ lim \ (Z_i^{k_i-l}) \in {\overline{U}}_0,$ then $x \in \overline{W^u(Q)} \cap LW^s(P).$ Finally, since $g(x) \in {\overline{U}}_0 , \ x \notin {\tiny \mathscr {O }}(P) - \{ P\};$ otherwise $x \in {\overline{U}}_j$ for some $0<j\le p-1$ which implies $g(x)=x \in {\overline{U}}_j \cap {\overline{U}}_0 \ne \Phi .$

Definition 4.2

Let f be an element of the topological space $KC^r(B,B), \ r \ge 1.$ We say that f is a Morse-Smale map $(f \in MS)$ if:

• (1) $\Omega (f)$ is finite ( then $\Omega (f) = \ Per(f)).$

• (2) If $P \in \ Per (f), \ P$ is hyperbolic and $\dim W^u(P) < \infty .$

• (3) If P and Q belong to Per(f) then $W^u(Q) \pitchfork LW^s(P)$ ($\pitchfork$ means transversal).

Remark

It is clear that if f is $C^0$-reversible one has $\Omega (f)$ finite implies $\Omega (f) = \ Per(f).$ In fact , $\Omega (f)$ is invariant, then the negative orbit of $x_0 \in \Omega (f) - \ Per(f)$ has a infinite number of points otherwise $x_0 \in \ Per(f).$ This is a contradiction. But, even without assuming $C^0$-reversibility one has: $\Omega (f)$ finite implies $\Omega (f) = \ Per(f).$ For otherwise there exists $x_0 \in \Omega (f) - \ Per(f)$ and $x_i = f^i(x_0) \ (i \ge 0)$ are in $\Omega (f) \ (f(\Omega (f)) \subset \Omega (f),$ always, by continuity of f). Since $\Omega (f)$ is finite, the $x_i \ (0\le i < m)$ are distinct but $x_m \in \{ x_0, x_1, \dots , x_{m-1}\}.$ Since $x_0 \notin \ Per(f), \ x_m \ne x_0$ and $x_m = x_{m-p}$ for some $p \in \{1, \dots , m-1\}$ and then $\{f^i(x_0) : i \ge m-p\} = \{ x_{m-p}, \dots , x_{m-1}\}$ is bounded away from $x_0$ and $x_0 \notin \Omega (f)$ which is a contradiction.

As a corollary of the of the local $\lambda$-lemma (see Proposition 3.4) one can easily prove the following:

Proposition 4.3

(global $\lambda$-lemma—see [12]). Let $f:B \rightarrow B$ be a smooth reversible map and assume A(f) is compact. Let $W^u(P)$ be the global unstable manifold of a hyperbolic fixed point $P, \ \dim W^u(P)=r,$ and $N \subset A(f)$ be an injectively immersed invariant submanifold of B with a point q of transversal intersection with $LW^s(P).$ Then, for any given cell neighborhood $B^r$ imbedded in $W^u(P),$ centered in P, and any $\epsilon > 0,$ there exists one $r$-cell in $N, \ \epsilon - C^1$ close to $B^r$.

Proof

The reversibility of f able us to define the global unstable manifold $W^u(P) \subset A(f)$ and f/A(f) is a homeomorphism. The proof follows from the local $\lambda$-lemma.

Remark

We don’t need N imbedded if $N = \cup _{k\ge 0} N_k, \ N_0 \subset N_1 \subset \dots ,$ with each $N_k$ imbedded.

Corollary 4.4

Let $P_i \in \ Per(f), \ i=1, 2, 3,$ be hyperbolic points. If $W^u(P_1)$ and $LW^s(P_2), W^u(P_2)$ and $LW^s(P_3)$ have $Q_1, Q_2 \notin \ Per(f)$ of transversal intersections then $W^u(P_1)$ and $LW^s(P_3)$ also have a point $Q_3 \notin \ Per(f)$ of transversal intersection.

Corollary 4.5

Let $P \in \ Per(f)$ be hyperbolic. If $W^u(P)$ meets $LW^s(P)$ in a point $Q \notin {\tiny \mathscr {O }} (P)$ of transversal intersection, then $\Omega (f)$ is not finite.

Proofs

(Easy)

Let us introduce now the set MR of all elements of the topological space $KC^r(B,B), \ r \ge 1,$ such that

• 1. $\Omega (f)$ is finite ( then $\Omega (f) = \ Per(f)).$

• 2. $P \in \ Per(f) \Rightarrow P$ is hyperbolic and $\dim W^u(P) < \infty .$

• 3. If $P, Q \in \ Per(f)$ and $W^u(P) \cap LW^s(Q) \ne \Phi$ then there exists a point of transversal intersection.

It is clear that $MS \subset MR$ and if $f\in MR, \ A(f)$ is the union of all unstable manifolds of $P \in Per(f).$

Proposition 4.6

If $f \in MR,$ there exist in $\ Per(f)$ at least one sink and at least one source. Moreover, $A(f) = \cup _{P \in Per(f)} \ W^u(P).$

Note. It is possible the source and the sink are identical, case in which A(f) is a single point.

Proof

If there are no sources in $Per(f) = \Omega (f)$ then there exists a cycle with transversal intersections and unstable manifolds with the same dimension. Using the global $\lambda$-lemma and their corollaries one concludes that $\Omega (f)$ is not finite. The same argument shows the existence of a sink.

Proposition 4.7

Let $f \in MR$ and $P, Q \in Per(f)$ such that $P \ne Q$ and $\overline{W^u(Q)} \cap W^u(P) \ne \Phi .$ then there exists a sequence $P_1, P_2, \dots , P_n \in Per(f), \ P_1 =P, \ P_n = Q,$ such that

$$\begin{aligned} W^u(P_{i+1}) \cap LW^s(P_i) \ne \Phi , \ \ 1 \le i \le n-1. \end{aligned}$$

Proof

We start with some remarks:

• (a) If $x \in \overline{W^u(Q)} \cap W^u(P), \ x$ is assumed to be in $LW^u(P).$

• (b) $\overline{W^u(Q)} \cap W^u(P) \ne \Phi$ if and only if $\partial W^u(Q) \cap W^u(P) \ne \Phi .$

• (c) P cannot be a source $(LW^s(P) \cap A(f) = \{P\}).$ In fact, the Proposition 4.3 implies that $\overline{W^u(Q)} \cap W^u(P)\ne \Phi \Rightarrow LW^s(P)\cap A(f)\ne \{P\}.$

• (d) If P is a sink $(LW^u(x)=\{x\})$ it is enough to define $P=P_1$ and $Q=P_2.$

Finally, P is a saddle, then by Proposition 4.3 there exists $x \in \overline{W^u(Q)} \cap LW^s(P)$ and $x \notin {\tiny \mathscr {O} }(P);$ we may assume

$$\begin{aligned} x \in \partial W^u(Q) \cap LW^s(P) \end{aligned}$$

otherwise we are done. But $\partial W^u(Q) \subset A(f)$ then $x \in A(f),$ that is, $x \in W^u(P_2)$ for some $P_2 \in Per(f)$ which implies

$$\begin{aligned} W^u(P_2) \cap LW^s(P) \ne \Phi \ \hbox {and } W^u(P_2) \cap \partial W^u(Q) \ne \Phi . \end{aligned}$$

If $P_2 = Q$ the proposition is proved. If $P_2 \ne Q$ we repeat the argument and get the sequence $(P_1 = P, P_2, P_3, \dots ).$ Remark that in this sequence $P_i \ne P_j$ otherwise $\Phi = W^u(P_i) \cap LW^s(P_i) \ne {\tiny \mathscr {O }}(P_i)$ and $\Omega (f)$ is not finite by Corollary 4.5. Since $\Omega (f)$ is finite we reach the given point Q.

Proposition 4.8

Let $f \in MR.$ Then for each $P \in Per(f),\ W^u(P)$ is imbedded in B. In particular, f as a map from $W^u(P)$ into itself is differentiable.

Proof

If $W^u(P)$ is not imbedded we have $\partial W^u(P) \cap W^u(P) \ne \Phi$ and then there exists $x \in W^u(P) \cap LW^s(P), \ x \notin {\tiny \mathscr {O }}(P),$ with transversality $(f \in MR)$, then $\Omega (f)$ is not finite.

As in the case of diffeomorphisms [12] we introduce in the set of orbits of periodic points a partial order using the following definition:

Definition 4.9

Let $f \in MR$ and $P, Q \in Per(f).$ Then ${\tiny {\mathscr {O}}}$ $(P) \le$ ${\tiny {\mathscr {O}}}$ (Q) if $\overline{W^u(Q)} \cap W^u(P) \ne \Phi .$

The above definition does not depend on the choice of the particular representatives of ${\tiny {\mathscr {O}}}$ (P) and ${\tiny {\mathscr {O}}}$ (Q). If $P_1 \in$ ${\tiny {\mathscr {O}}}$ (P) and $Q_1 \in$ ${\tiny {\mathscr {O}}}$ (Q) we see that $\overline{W^u(Q)} \cap W^u(P) \ne \Phi$ if and only if $W^u(Q) \cap LW^s(P) \ne \Phi ,$ if and only if $W^u(Q_1) \cap LW^s(P_1) \ne \Phi .$ The relation ${\tiny {\mathscr {O}}}$ $(P) \le$ ${\tiny {\mathscr {O}}}$ (Q) is obviously reflexive and transitive by using the global $\lambda$-lemma and their corollaries. Finally if $W^u(Q) \cap LW^s(P) \ne \Phi$ and $W^u(P) \cap LW^s(Q) \ne \Phi$ for $Q \notin$ ${\tiny {\mathscr {O}}}$ (P) we obtain a kind of cycle and the global $\lambda$-lemma shows that $\Omega (f)$ is infinite which is a contradiction. Then, ${\tiny {\mathscr {O}}}$ $(P) ={\tiny {\mathscr {O}}} (Q)$ and $\le$ is a partial order.

The set of orbits of all periodic points of a map $f \in MR$ toghether with the above define partial order is called the phase diagram D(f) of f. For $P,Q \in Per(f),$ a chain connecting Q to P in the phase diagram of f is a sequence $P_0, \dots , P_n$ with $P_i \in Per(f), \ P_i \notin$ ${\tiny {\mathscr {O}}}$ $(P_{i+1}), \ P_1 = P$ and $P_n = Q,$ such that $W^u(P_{i+1}) \cap LW^s(P_i) \ne \Phi .$ The integer n is the length of the chain.

Q is said to have $k$-behavior relative to P (write $beh(Q|P) = k)$ if the maximum length of chains connecting Q to P is $k \in N;$ complete the definition by setting $beh(Q|P) = 0$ iff $W^u(Q) \cap LW^s(P) = \Phi .$ If $Q \in$ ${\tiny {\mathscr {O}}}$ (P) then $beh(Q|P)=0$ but not conversely because if P, Q are fixed points and sinks we have $beh(Q|P)=0$ and $Q \notin$ ${\tiny {\mathscr {O}}}$ (P). It is also clear that for distinct orbits ${\tiny {\mathscr {O}}}$ $(P) \le$ ${\tiny {\mathscr {O}}}$ (Q) implies $beh(Q|P)>0.$

Using some ideas appearing in [12] we will show that given $f \in MR,$ there is a neighborhood $\vartheta (f)$ of f in $KC^r(B,B)$ such that $g \in \vartheta (f)$ implies $g \in MR$ and there is an isomorphism between phase diagrams, that is, a bijection $\rho (g): D(f) \rightarrow D(g)$ between the phase diagrams of f and g which is ordering and indices preserving, that means: $P, Q \in Per(f),$ ${\tiny {\mathscr {O}}}$ $(P) \le {\tiny {\mathscr {O }}}(Q),$ implies ${\tiny {\mathscr {O}}}$ $(\rho (g)P) \le$ ${\tiny {\mathscr {O}}}$ $(\rho (g)Q)$ and $\dim W^u(P) = \dim W^u(\rho (g)P).$

Since $f \in MR,$ by Proposition 3.7 each $g \in \vartheta _1(f)$ defines a map

$$\begin{aligned} \rho (g): Per(f) \rightarrow Per(g) \subset \Omega (g) \\ P \rightarrow P^* = \rho (g)P. \end{aligned}$$

We will construct neighborhoods V of A(f) and $\vartheta (f)$ of f such that

$$\begin{aligned} \Omega (g) \cap V = \rho (g) [\ Per(f) \cap V] \end{aligned}$$

for all $g \in \vartheta (f).$ We will proceed by induction on the phase diagram of f.

For each sink $S_i$ of f, choose a neighborhood $V_0(S_i) \subset LW^s(S_i)$ and $\epsilon _0(S_i) >0$ such that if $||g-f||_r < \epsilon _0(S_i)$ then $V_0(S_i) \subset LW^s(S^*_i),$ where $S^*_i = \rho (g)S_i.$ Let $V_0=\cup V_0(S_i)$ and $\epsilon _0 = min \ \{\epsilon _0(S_i) | S_i$ is a sink of $f\}$. In $V_0$ we trivially have $\Omega (g) \cap V_0 = \rho (g) [Per(f) \cap V_0]$ for all $|g-f|_r < \epsilon _0.$ If, now, S is a saddle near sinks ($beh(S | S_i) \le 1$ for all sinks $S_i),$ by the compactness of the fundamental domain $G^u(S),$ there exist $n_0$ and a fundamental neighborhood $N^u(S)$ such that given $x \in N^u(S), \ f^n(x) \in V_0$ for some $n \le n_0.$ The same happens with g near f; by Proposition 3.9, $\cup _{n\ge 0} g^{-n}(N^u(S)) \cup LW^s(S^*)$ contains a neighborhood $U_1(S)$ of S in B,  for all g belonging to a suitable $\epsilon _1(S)$-neighborhood of f in $KC^r(B,B).$ Consider $V_1(S) = V_0 \cup [ \cup _{n=1}^{n_0} f^{-n}(V_0)] \cup U_1(S)$ and $\epsilon _1(S)$ for each saddle S near sinks and finally $V_1 = \cup V_1(S)$ and $\epsilon _1 = min \{\epsilon _1(S)\}$ for all saddles near sinks. In $V_1$ we have

$$\begin{aligned} \Omega (g) \cap V_1 = \rho (g) \ [Per(f) \cap V_1 ]. \end{aligned}$$

By induction, assume now that we have constructed $V_k, \epsilon _k$ corresponding to the points in Per(f) whose behavior with respect to sinks of f is $\le k,$ so that $\Omega (g) \cap V_k = \rho (g) [Per(f) \cap V_k]$ for $|g-f|_r < \epsilon _k.$ Let $P_{k+1}$ a point next to these in the phase-diagram of f. Again, by the compacity of $G^u(P_{k+1})$ there exists $n_1(P_{k+1})$ such that $f^n(x) \in V_k$ for all $x \in G^u(P_{k+1})$ and some $1\le n \le n_1(P_{k+1}).$ Using inverse images of $V_k$ by f one define $N^u(P_{k+1})$ and $\epsilon _{k+1}(P_{k+1});$ for $|g-f|_r < \epsilon _{k+1}(P_{k+1})$ the same happens with g. Use again Proposition 3.9 to obtain $U_{k+1}(P_{k+1}) =$ neighborhood of $P_{k+1} \subset LW^s(P^*_{k+1}) \cup \ \cup _{n\ge 0} \ g^{-n}(N^u(P_{k+1})).$

Define $U_{k+1} = \cup U_{k+1}(P_{k+1})$ and $\epsilon _{k+1} = min \{ \epsilon _{k+1}(P_{k+1})\}, \ n_1 = max \{ n_1(P_{k+1})\};$ finally

$$\begin{aligned} V_{k+1} = V_k \cup [\cup _{n=1}^{n_1} \ f^{-n} (V_k)] \cup U_{k+1} \end{aligned}$$

and in $V_{k+1}$ we have

$$\begin{aligned} \Omega (g) \cap V_{k+1} = \rho (g) \ [Per(f) \cap V_{k+1}] \end{aligned}$$

for all $|g-f|_r < \epsilon _{k+1}.$ The induction is complete. Remark that in $V_{k+1}$ there are no other non-wandering points besides $P_i \in Per(f)$ and the corresponding $P^*_i$ of g. The procedure reaches the sources and we define the above mentioned neighborhoods V of A(f) and $\vartheta (f)$ of f such that

$$\begin{aligned} \Omega (g) \cap V = \rho (g) [Per(f) \cap V] \end{aligned}$$

for all $g \in \vartheta (f).$ But $f \in KC^r(B,B)$ and we reduce $\vartheta (f),$ if necessary, and obtain $A(g) \subset V$ for all $g \in \vartheta (f).$ Then, since $\Omega (g) \subset A(g) \subset V,$ it follows that $\Omega (g) = Per(g)$ for all $g \in \vartheta (f)$ and we have finished the proof of the following:

Theorem 4.10

The set MR is open in $KC^r(B,B), \ r \ge 1.$ Moreover, if $f \in MR$ there is a neighborhood $\vartheta (f)$ of f in $KC^r(B,B)$ such that for each $g \in \vartheta (f)$ the map $\rho (g): \ Per(f) \rightarrow \ Per(g)$ above considered is a diagram isomorphism. In particular, f is $\Omega$-stable.

Consider again a smooth map $f \in MR$. If $P_k, P_{k+1} \in \ Per(f)$ satisfy $beh(P_k | P_{k+1})=1$ and of $G^s(P_{k+1})$ is a fundamental domain (then compact) for $LW^s(P_{k+1})$ we have that $W^u(P_k) \cap G^s(P_{k+1})$ is also compact. In fact, if $x_\nu \rightarrow x, \ x_\nu \in W^u(P_k) \cap G^s(P_{k+1}),$ it is clear that $x \in G^s(P_{k+1})$ and if $x \notin W^u(P_k)$ (then $x \in \partial W^u(P_k)),$ there exists ${\tilde{P}} \in \ Per(f)$ such that $x \in W^u({\tilde{P}}), \ {\tilde{P}} \ne P_{k+1}$ and ${\tilde{P}} \ne P_k;$ but by Proposition 4.1 $\overline{W^u(P_k)} \cap W^u({\tilde{P}}) \ne \Phi$ implies $W^u(P_k) \cap LW^s({\tilde{P}}) \ne \Phi ,$ then $beh(P_k | P_{k+1} ) > 1$ giving us a contradiction, that is, $x \in W^u(P_k).$

The Proposition 3.11 combined with Theorem 4.10, Proposition 3.4 and the arguments used in Lemma 1.11 of [12] prove the following:

Proposition 4.11

Let $f \in MS, \ P \in Per(f)$ and $\dim W^u(P)=m.$ Fix a cell neighborhood $B^m$ of P in $LW^u(P).$ Given $\epsilon >0,$ there exist neighborhoods V of P, and $\vartheta (f)$ of f in $KC^r(B,B), r\ge 1,$ such that if for some $Q \in Per(f), \ W^u(Q^*(g)) \cap V \ne \Phi$ then $W^u(Q^*(g)) \cap V$ is fibered by $m$-cells $\epsilon - C^1$ close to $B^m, \ g \in \vartheta (f)$ and $Q^*(g) = \rho (g) Q.$

From Theorem 4.10 and Proposition 4.11 we obtain the main result of this section:

Theorem 4.12

The set MS of all $r$-differentiable Morse-Smale maps is open in MR (then in $KC^r(B,B)), \ r\ge 1.$ Moreover, if $f \in MS,$ then its phase-diagram is stable (up to a diagram isomorphism) under small $C^r$ perturbations of f in $KC^r(B,B).$

Remark

In the language used by Palis and Takens in [16], it follows, improving Proposition 4.11, that we really have an Unstable Foliation of $U= V \cap A(f)$ for $f \in MS$ at $P \in Per(f),$ that is, a continuous foliation ${\mathscr {F}}^{u} (P) : x \in U \rightarrow$ ${\mathscr {F}}^{u}_x(P)$ such that:

• (a) the leaves are $C^1$ discs, varying continuously in the $C^1$ topology and ${\mathscr {F}}^{u}_P (P) = W^u(P) \cap U,$

• (b) each leaf ${\mathscr {F}}^{u}_x (P)$ containing $x \in U,$ is contained in U, 

• (c) ${\mathscr {F}}^{u}(P)$ in $f$-invariant; that is, $f({\mathscr {F}}^{u}_x (P)) \supset {\mathscr {F}}^{u}_{f(x)}(P), \ x$ and f(x) in U.

Moreover, using the reversibility property of the MS maps, this unstable foliation can be easily globalized through saturation by f. The same happens for g in a suitable neighborhood $\vartheta (f)$ of f in MS (then in $KC^r(B,B)).$

By induction on the phase diagram of $f \in MS$ and using the global $\lambda$-lemma we easily obtain (see Proposition 3.l of [16]) a so called compatible system of global unstable foliations ${\mathscr {F}}^{u}(P_1),$ ${\mathscr {F}}^{u}(P_2), \dots , {\mathscr {F}}^{u}(P_n),$ for any maximal chain $(P_1, P_2, \dots , P_n) \in Per(f),$ ${\tiny {\mathscr {O}}}$ $(P_i) \le {\tiny {\mathscr {O}}}$ $(P_{i+1}), i=1, 2, \dots , n-1, \ P_1$ being a source and $P_n$ being a sink. The compatibility means that "if a leaf F of ${\mathscr {F}}^{u}(P_k)$ intersects a leaf ${\tilde{F}}$ of ${\mathscr {F}}^{u}(P_l), k < l \le n,$ then $F \supset {\tilde{F}};$ moreover, the restriction of ${\mathscr {F}}^{u}(P_l)$ to a leaf of ${\mathscr {F}}^{u}(P_k)$ is a $C^1$ foliation."

6 Stability

In this section we will prove a stability theorem for Morse-Smale maps. Palis [12] and Palis and Smale [15] proved stability theorems for Morse-Smale diffeomorphisms defined on a compact manifold. It is possible to adapt some of the J. Palis techniques of [12] to prove that MS maps defined on a Banach manifold B are stable relatively to the largest invariant set. We start with the following definition:

Definition 5.1

A map f in $KC^r(B,B)$ is stable relatively to A(f) if there exists a neighborhood $\vartheta (f)$ of f in $KC^r(B,B)$ such that to each $g \in \vartheta (f)$ one can find a homeomorphism $h=h(g): A(f) \rightarrow A(g)$ satisfying the conjugacy condition $h \cdot f = g \cdot h$ on A(f).

The properties of $f \in MS,$ specially the reversibility of f and the compactness of A(f),  the finite dimensionality of the unstable manifolds $W^u(P), \ P \in Per(f),$ the existence of compatible systems of global unstable foliations and the parametrized version of the Isotopy Extension Theorem are the main tools to be used in the proof of the next Theorem 5.3.

In order to recall the Isotopy Extension Theorem (IET) one needs some more notation (see [16]).

Let N be a $C^r$ compact manifold $r \ge 1,$ and A an open set of $R^s.$ Let M be a $C^\infty$ manifold with $\dim M > \dim N.$ We indicate by $C_A^k(N \times A, M \times A)$ the set of $C^k$ mappings $f: N \times A \rightarrow M \times A$ such that $\pi = \pi ^\prime \cdot f,$ endowed with the $C^k$ topology, $1 \le k\le r.$ Here, $\pi$ and $\pi ^\prime$ denote the natural projections $\pi : N \times A \rightarrow A, \ \pi ^\prime : M \times A \rightarrow A.$ Let $Diff^k_A(M\times A)$ be the set of $C^k$ diffeomorphisms $\varphi$ of $M \times A$ such that $\pi = \pi ^\prime \cdot \varphi ,$ again with the $C^k$ topology.

Lemma 5.2

(Isotopy Extension Theorem). Let $i \in C^k_A(N \times A, M \times A)$ be an imbedding and $A^\prime$ a compact subset of A. Given neighborhoods U of $i(N \times A)$ in $M \times A$ and V of the identity in $Diff^k_A(M\times A),$ there exists a neighborhood W of i in $C^k_A(N\times A, M\times A)$ such that for each $j \in W$ there exists $\varphi \in V$ satisfying $\varphi \cdot i=j$ restricted to $N\times A^\prime$ and $\varphi (x) = x$ for all $x \notin U.$

Theorem 5.3

Any Morse-Smale map f in $KC^r(B,B)$ is stable relatively to A(f).

Proof

By Theorem 4.12 (openess) there exists a neighborhood of f in $KC^r(B,B)$ containing only Morse-Smale maps. We saw, also, that if $P_k, P_{k+1} \in Per(f)$ satisfy $beh(P_k, P_{k+1})=1$ then $W^u(P_k) \cap G^s(P_{k+1})$ is compact. If $P_1$ is a source and $beh(P_1, P_{k+1})=k,$ there exists a maximal chain $(P_1, P_2, \dots , P_{k+1})$ such that $beh(P_i, P_{i+1}) = 1, \ i=1, 2, \dots , k.$ Recall that $G^s(P_{k+1}) = \overline{B^s \cap A(f)} - f(B^s\cap A(f)).$ Since the compact set A(f) is equal to the union of all global unstable manifolds of periodic points of f (Prop. 4.6) and $\Omega (f) = Per(f)$ is finite, we may assume that $B^s = B^s(P_{k+1})$ have been chosen in a such way that A(f) is transversal to $\partial B^s$ (besides being transversal to $B^s$) which means that all global unstable manifolds are transversal to $\partial B^s$ and $B^s.$ From the transversality condition it follows that $W^u(P) \cap \overline{B^s}$ is a manifold with boundary, the interior being $W^u(P) \cap B^s$ and the boundary being $W^u(P) \cap \partial B^s, \ P \in Per(f).$ Call $S_E = S_E(P) = \partial B^s \cap G^s(P);$ we have also $S_E = \partial B^s \cap A(f).$ In fact, $S_E \subset \partial B^s \cap \overline{B^s \cap A(f)} \subset \partial B^s \cap A(f)$ trivially. For the reverse inclusion, let $x \in \partial B^s \cap A(f);$ since $f(B^s) \subset B^s$ and $x \notin B^s, \ x \notin f(B^s \cap A(f))$ while $x \in \overline{B^s} \cap A(f),$ so we only need to prove $x \in \overline{B^s \cap A(f)}.$ For some $Q, \ x \in W^u(Q) \cap \partial B^s,$ and these meet transversally so there exist $x^\prime \in W^u(Q) \cap B^s$ arbitrarily close to x, i.e. $x \in \overline{W^u(Q) \cap B^s} \subset \overline{A(f) \cap B^s}.$ We have incidentally proved $\overline{A(f) \cap B^s} = A(f) \cap \overline{B^s},$ which will be needed later. Remark finally that, using the relative topology of $A(f) \cap LW^s(P),$ we have $\partial G^s(P) = S_E \cup S_I, \ S_I = S_I(P)=f(S_E),$ "$\partial$" relative to $A(f) \cap LW^s(P).$ In fact, $G^s(P) = (B^s \cup \partial B^s) \cap A(f) - f(B^s \cap A(f)) = [B^s \cap A(f) - f(B^s \cap A(f))] \cup S_E = [(Int \ G^s(P)) \cup f(S_E)] \cup S_E = Int \ G^s(P) \cup (S_E \cup S_I).$

The stable set $W^s(P)$ is the set of all points $x\in B$ such that $w(x) = \{P\}.$ Any point $z \in W^s(P) \cap A(f)$ reaches $G^s(P) - S_I(P)$ after a finite number of iterations of ${\overline{f}}$ or $({\overline{f}})^{-1}, \ {\overline{f}} = f / A(f).$

Given any bounded imbedded disc $D \subset W^u(P) = W^u(P;f),$ for $g \ C^1$-close to f there is a disc $D^* \subset W^u(P^*(g))=W^u(P^*; g) \ C^1$-close to $D, P^* \in D^*,$ where $P^* = \rho (g)P;$ we say $W^u(P^*; g)$ is $C^1$-close to $W^u(P;f)$ "on compact sets."

Let $P_2$ be a periodic point of f with behavior $\le 1$ with respect to sources and consider a pair $(P_1, P_2)$ such that $P_1$ is a source and $beh(P_1 / P_2) =1.$ The manifolds $W^u(P_1 ; f)$ and $W^u(P^*_1 ; g)$ are $C^1$-close on compact sets and let $h^\prime _1$ be the corresponding diffeomorphism; also $LW^s(P_2;f)$ and $LW^s(P^*_2; g)$ are $C^1$-close for g in a suitable neighborhood of $f, \ P^*_2=\rho (g)P_1^*.$ By the implicity function theorem and the transversality conditions $W^u(P_1;f) \pitchfork LW^s(P_2; f), \ W^u(P_1^*; g) \pitchfork LW^s(P^*_2;g),$ there is a well defined diffeomorphism ${\overline{h}}_2$ from $G^s(P_2; f) \cap W^u(P_1; f)$ into $LW^s(P^*_2;g) \cap W^u(P^*_1; g).$ Define a differentiable map $h_2$ from $G^s(P_2 ; f) \cap W^u(P_1; f)$ into $W^u(P^*_1; g)$ equal to ${\overline{h}}_2$ on $W^u(P_1; f) \cap S_E(P_2)$ and equal to ${\tilde{h}}_2 = g \cdot {\overline{h}}_2 \cdot f^{-1}$ on $W^u(P_1; f) \cap S_I(P_2).$ To construct $h_2$ we use IET (Lemma 5.2) just observing that $(h^\prime _1)^{-1} \cdot {\overline{h}}_2$ maps $W^u(P_1; f) \cap S_E(P_2)$ into $W^u(P_1; f)$ and $(h^\prime _1)^{-1} \cdot {\tilde{h}}_2 = (h^\prime _1)^{-1} \cdot (g \cdot {\overline{h}}_2 \cdot f^{-1})$ maps $W^u(P_1; f)\cap S_I(P_2)$ into $W^u(P_1; f),$ both are near the corresponding inclusion maps and so can be extended to an imbedding of $G^s(P_2;f) \cap W^u(P_1; f)$ into $W^u(P_1; f).$ The property we obtain for $h_2$ is that $h_2 f(x) = g h_2(x)$ for all $x \in W^u(P_1; f)\cap S_E(P_2);$ in fact, $gh_2(x) = g{\overline{h}}_2(x)$ and $h_2f(x)=h_2(f(x))={\tilde{h}}_2(f(x))= g{\overline{h}}_2 f^{-1}(f(x)) = g{\overline{h}}_2(x).$ This map $h_2$ can be extended to $z \in W^s(P_2;f) \cap W^u(P_1; f)$ since there exists a unique $n \in {\mathbb {Z}}$ such that

$$\begin{aligned} ({\overline{f}})^n(z) \in (G^s(P_2; f) - S_I(P_2)) \cap W^u(P_1 ; f); \end{aligned}$$

define $h_2(z) = g^{-n}(h_2(f^n(z)))$ and $h_2(P_2) = P_2^*.$

We do the same with all sources $F_i \in Per(f)$ such that $beh(F_i | P_2)=1$ and $h_2$ is defined on $W^s(P_2;f) \cap A(f).$ For the remaining points ${\tilde{P}}_2 \in Per(f)$ with behavior $\le 1$ with respect to sources proceed analogously and obtain $h_2$ defined on $W^s({\tilde{P}}_2;f) \cap A(f)$ satisfying $h_2f = gh_2$ and $h_2({\tilde{P}}_2) = {\tilde{P}}^*_2.$

The next step is the consideration of $P_3 \in Per(f)$ with behavior $\le 2$ with respect to sources and we will construct a homeomorphism $h_3$ on $W^s(P_3;f) \cap A(f)$ starting with $G^s(P_3) - S_I(P_3).$ For the sources with behavior 1 relative to $P_3$ the procedure is equal to that above. Let now $P_1$ be a source in Per(f) such that $beh(P_1|P_3) = 2.$ We have at least one sequence $(P_1 P_2 P_3)$ such that $beh(P_1 | P_2) = beh(P_2 | P_3) = 1.$ Since $beh(P_2 | P_3)=1$ we define a diffeomorphism $\bar{\bar{h}}_3$ on $G^s(P_3;f) \cap W^u(P_2 ;f)$ exactly as we did above with $h_2.$ But $W^u(P_1;f)$ approaches $W^u(P_2; f)$ and it is well defined a foliation on $W^u(P_1;f)$ induced by $W^u(P_2;f);$ the same happens with $W^u(P_1^*; g)$ relatively to $W^u(P_2^* ; g)$ for g near f in MS. The existence of a compatible system of global unstable foliations guarantees that $W^u(P_1;f)$ intersects $LW^s(P_3; f)$ with its leaves accumulating in the (compact) set $W^u(P_2;f) \cap G^s(P_3;f).$ To each leaf ${\mathscr {F}}_x$ of $W^u(P_1;f) \cap G^s(P_3;f)$ near $W^u(P_2;f) \cap G^s(P_3;f)$ corresponds a unique point $x \in LW^s(P_2;f) \cap W^u(P_1;f)$ near $P_2$. Using $h_2$ (defined in the $P_2$ level), to ${\mathscr {F}}_x$ corresponds a unique leaf ${\mathscr {F}}^{ \ \ *}_{h_2(x)}$ of $W^u(P_1^*;g) \cap G^s(P^*_3;g).$ Consider the map ${\bar{\bar{h}}}_3$ defined on $G^s(P_3;f) \cap W^u(P_2;f)$ and use the $C^1$-closeness on compact sets of $W^u(P_2;f)$ with the leaves of $W^u(P_1;f)$ [respectively of $W^u(P_2^*;g)$ with the leaves $W^u(P_1^*;g)]$ to obtain a diffeomorphism $i_X :{ {\mathscr {F}}}_x \rightarrow W^u(P_2;f) \cap G^s(P_3;f)$ [respectively $i^*_X: { {\mathscr {F}}}^{\ \ *}_{h_2(x)} \rightarrow W^u(P^*_2;g) \cap G^s(P^*_3;g)]$ and construct ${{\bar{h}}}_3 = (i^*_x)^{-1} \cdot {\bar{{\bar{h}}}}_3 \cdot i_x$ which is an extension of ${\bar{{\bar{h}}}}_3$ to the leaf ${\mathscr {F}}_x$. As before, one considers ${{\bar{h}}}_3$ locally defined on $W^u(P_1;f) \cap G^s(P_3;f) \cap S_E(P_3)$ and defines ${\tilde{h}}_3 = g \cdot {{\bar{h}}}_3 \cdot f^{-1}$ (locally) on $W^u(P_1;f) \cap G^s(P_3;f) \cap S_I(P_3).$ Using again the IET to the local foliation $x \rightarrow { {\mathscr {F}}}_X, \ x$ in a neighborhood of $P_2$ in $LW^s(P_2;f) \cap W^u(P_1;f),$ one obtains a continuous (local) extension $h_3$ of ${\bar{{\bar{h}}}}_3$ coinciding with ${{\bar{h}}}_3$ on $W^u(P_1;f) \cap G^s(P_3;f) \cap S_E(P_3)$ and with ${\tilde{h}}_3$ on $W^u(P_1;f) \cap G^s(P_3;f)\cap S_I(P_3).$ Notice that $W^u(P_1;f) \cap LW^s(P_3;f)$ and $W^u(P_1^*;g) \cap LW^s(P_3^*;g)$ are $C^1$-close on compact sets. In order to extend $h_3$ (defined on the leaves of $W^u(P_1;f) \cap G^s(P_3;f)$ near $W^u(P_2;f) \cap G^3(P_3;f))$ to $W^u(P_1;f) \cap G^s(P_3).$ we extract a small tubular neighborhood of $W^u(P_2;f) \cap G^s(P_3;f)$ in $\overline{W^u(P_1;f) \cap LW^s(P_3;f)}$ and apply again the IET for diffeomorphisms near the identity. In this way we can continuously extend $h_3$ to a full neighborhood of $W^u(P_2;f) \cap G^s(P_3;f)$ so that it satisfies the conjugacy equation $h_3 f = g h_3$ for points of $W^u(P_1;f) \cap G^s(P_3;f) \cap S_E(P_3).$

We proceed, in an analogous way, with all possible sequences $(P_1, P_2^\prime , P_3) \in Per(f)$ such that $beh(P_1 | P_2^\prime ) = beh(P_2^\prime | P_3) = 1.$ Consider, finally, the remaining sources $P^\prime _1 \in Per(f)$ in the same conditions as $P_1$ and obtain a continuous $h_3$ defined on $G^s(P_3)$ with the equality $h_3 f = gh_3$ holding on $S_E(P_3)$ and then, a continuous $h_3$ defined on $A(f) \cap W^s(P_3), \ h_3(P_3) = P_3^*,$ with the desired conjugacy property $h_3 f = gh_3.$

The last step showed us, clearly, the full induction procedure. Assume we have constructed all maps $h_k$, satisfying $h_k(P_k) = P^*_k$ and $h_k f = gh_k$ on $A(f) \cap W^s(P_k)$ for all $P_k \in Per(f)$ such that $beh(F_i |P_k) \le k-1, \ k \ge 3,$ where the $F_i$ are all sources of Per(f);  let $P_{k+1} \in Per(f)$ be such that $beh (F_i | P_{k+1}) \le k$ for all sources $F_i \in Per(f).$ Let $(F_1, P_2, \dots , P_k, P_{k+1})$ be a sequence such that $F_1$ is a source and $beh(F_1 | P_2) = beh(P_2 | P_3) = \dots = beh(P_k , P_{k+1})=1.$ We start the construction of $h_{k+1}$ on $W^u(P_k;f) \cap G^s(P_{k+1}),$ extend locally $h_{k+1}$ to $W^u(P_{k-1}) \cap G^s(P_{k+1})$ and by a second induction procedure extend $h_{k+1}$ to $W^u(P_{k-2}) \cap G^s(P_{k+1}), \dots , W^u(F_1) \cap G^s(P_{k+1}),$ as we did in the case $k=2.$ Do the same with all maximal sequences $(F_1, P_2^\prime , P_3^\prime ,\dots , P_{k+1})$ with $F_1$ and $P_{k+1}$ fixed and, finally, with the remaining sources $F_i$ to obtain $h_{k+1}$ defined on $G^s(P_{k+1})$ verifying the equality $h_{k+1}f = g h_{k+1}$ on $S_E(P_{k+1}).$ By forcing the conjugacy $h_{k+1} f = g h_{k+1}$ extend $h_{k+1}$ to $A(f) \cap W^s(P_{k+1}).$ The induction is complete and we reach the sinks. Since the disjoint union

$$\begin{aligned} \bigcup \limits _{P \in Per(f)} A(f) \cap W^s(P) \end{aligned}$$

is equal to A(f) the map $H= h_2 \cup h_3 \cup \dots$ is well defined on $A(f), \ H(P) = P^*,$ and $Hf(x) = gH(x)$ for all $x \in A(f).$

The final step is to check the continuity of $H: A(f) \rightarrow A(g).$ Remark, first of all, that if H is continuous in f(x) then H is continuous in $x \in A(f);$ in fact let $z_i \rightarrow x, \ z_i \in A(f);$ since f is continuous, $f(z_i) \rightarrow f(x)$ and the fact that H is continuous at f(x) implies $Hf(z_i) \rightarrow Hf(x)$ that is $gH(z_i) \rightarrow g H(x) .$ But $H(z_i) \in A(g), \ H(x) \in A(g)$ and g is reversible, then, $H(z_i) \rightarrow H(x).$ Given, now, $x \in A(f),$ it is clear that $x \in A(f) \cap W^s(P_k)$ for some $P_k \in Per(f);$ it is sufficient to verify the continuity of H at the points x of a neighborhood of $P_k$ in $A(f) \cap W^s(P).$ If $P_k$ is a source or a sink the continuity is trivial. Assume $P_k$ is a saddle and let $x_n \rightarrow x, \ x_n \in {\mathscr {F}}^{u}_{x_n}(P_k)$ and $x \in {\mathscr {F}}^{ u}_x(P_k), \ { \mathscr {F}}^{ \ u}(P_k)$ being the global unstable foliation at $P_k$ above considered. But, by the definition of $H= h_2 \cup h_3 \cup \dots$ and by the constructions of the maps $h_k,$ we see that the set of accumulation points of $\{H(x_n)\}$ is contained in $LW^s(P_k^* ; g)$ and $H(x_n) \in { \mathscr {F}}^{\ u^*}_{h_k(x_n)}(P^*_k), \ {\mathscr {F}}^{ \ u^*}(P^*_k)$ being the global unstable foliation at $P^*_k$. Then $H(x_n) \rightarrow { \mathscr {F}}^{ \ u^*}_{h_k(x_n)}(P^*_k) \cap LW^s(P^*_k ; g) = h_k(x) = H(x)$ proving the continuity of H. Similarly, $H^{-1}$ is also continuous and the proof is complete.

Corollary 5.4

([12, 15]). Let B be a compact manifold and $Diff^r(B)$ the set of all $C^r$-diffeormorphisms of $B, \ r \ge 1.$ Then the Morse-Smale diffeomorphisms of $Diff^r(B)$ are stable and form an open set.

Proof

Rermark that $Diff^r (B)$ satisfies the conditions to be a $KC^r(B,B) \subset C^r(B,B).$ In fact $A(f) = B$ for all $f \in Diff^r(B)$ and the reversibility is trivial. The result follows from Theorem 5.3.

Theorem 5.5

Let $KC^r (B, B)$ be the subspace S, set of flow maps of all analytic $RFDE \ F \in \mathfrak {X}^r, \ r \ge 1,$ defined on an analytic compact manifold M. The Morse-Smale maps f of S are stable relatively to A(f) and form an open set in S.

Proof

Follows from Remark 3.13, Theorems 4.12 and 5.3.