1 Introduction

In real-world lifetime phenomena, researchers often face a finite range of variations. Bounded domain distributions result from such finite variations. For a detailed discussion of such distributions, please refer to [1,2,3,4]. Bounded domain distributions are valuable in investigating lifetime phenomena such as yearly flood flow, yearly precipitation data, and reliability analysis. The best conventional bounded domain probability models in this regard are the beta, triangular, epsilon, PERT, uniform, arcsin, Bates, Topp–Leone, Kumaraswamy, triangular, von Mises distributions, epsilon-Lindley, and raised cosine. Applications of such distributions include wavelet, beamforming, and pattern synthesis, as well as storage volume of a reservoir of capacity \(0< z < z_\textrm{max}\), modeling failure rate phenomena such as bathtub shape (BTS), inverted bathtub shape (IBTS), increasing failure rate (IFR), decreasing failure rate (DFR), working life expectancy modeling, and environmental data assessment.

Our motivational tactic starts with an overview of constrained function. The earliest phase on this path is to pick up the odd link function \( \mathcal {D}(x;\Theta ) =ln\left( \frac{1-\mathcal {G}(x)}{\mathcal {G}(x)}\right) \), which fulfills the provisions such as (i) \( \mathcal {D}(x) \) is differentiable and monotonically non-decreasing (ii) \( \mathcal {D}(x) \rightarrow a\) as \( x \rightarrow 0 \) and \( \mathcal {D}(x) \rightarrow b\) as \( x \rightarrow \infty \) with a baseline cumulative distribution function (CDF) \( \mathcal {G}(x) \). Our second motivation deals with the selection of baseline distribution, i.e., the log-logistic distribution (LLD) studied by Verhulst [5], which has wide applications in modeling stochastic lifetime phenomena, such as in time-to-event analysis, especially in survival analysis, color, e.g., the modeling of mortality rate after cancer diagnosis or treatment [6], demography for modeling population, economics for the distribution of wealth or income inequality, engineering for reliability analysis, and hydrology for modeling stream flow rates and precipitation [6]. In this regard, we took the CDF of LLD, which is constructed on the interval \( (0, \infty ) \) as \( \mathcal {G}(x|\alpha ,\beta )=\frac{x^{\beta }}{x^{\beta }+\alpha ^{\beta }}\). Incorporating the baseline CDF into \( \mathcal {D}(x|\alpha , \beta , \theta ) \), yields \( \mathcal {D}(x|\alpha , \beta , \theta )=\beta ln(\frac{\alpha }{x}) \). The next motivation is the extraction of the CDF of Fréchet distribution (FD), a model of extreme values (EVs). Extreme events are rare, but they may have a very high impact on the observed experiments [7]. This model has been used in modeling the data that appear in various spheres of life such as accelerated life monitoring, sea waves, horse racing, rainfall, environmental disasters, earthquakes, wind speeds, sea currents, track race records, relief periods and survival times data, and so on. Although the above model has multiple applications in various fields of study, it must first be defined as follows to extract it:

$$\begin{aligned} f(t;\theta )=\theta t^{-\theta -1} e^{-t^{-\theta }}, t> 0, \theta > 0, \end{aligned}$$

with the corresponding CDF given by

$$\begin{aligned} e^{-\left( \mathcal {D}(x;\alpha ,\beta )\right) ^{-\theta }}= \int _{0}^{\mathcal {D}(x;\alpha ,\beta )}\theta y^{-\theta -1} e^{-y^{-\theta }} \textrm{d}y, \alpha> 0, \beta> 0, \theta > 0, \end{aligned}$$

However, it is important to note that the above is not a CDF according to the defined odd link function. To propose a bounded CDF under the name FLD, we must first introduce a constraint \( 0< x < \alpha \), then define the CDF as

$$\begin{aligned} \mathcal {F}(x;\alpha , \beta ,\theta )=1-e^{-(\mathcal {D}(x,\alpha ,\beta ))^{-\theta }}; \end{aligned}$$

on incorporating the \( \mathcal {D}(.) \) into the above expression, we get

$$\begin{aligned} \mathcal {F}_{\text {FLD}}(x;\alpha ,\beta , \theta )= 1-e^{-(\beta \, ln ( \frac{\alpha }{x}))^{-\theta }}, \beta> 0,\theta > 0, 0< x < \alpha , \end{aligned}$$
(1)

which after differentiation yields the PDF of FLD as

$$\begin{aligned} f_{\text {FLD}}(x;\alpha , \theta , \beta )= \frac{\beta \theta }{x} \left( \beta \, ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta -1} e^{-(\beta \, ln ( \frac{\alpha }{x}))^{-\theta }}. \end{aligned}$$
(2)

An interesting feature appears when we set \( \alpha = 1 \), which in turn yields a two-parameter unit FLD defined as

$$\begin{aligned} f_{\text {FLD}}(x;1, \theta , \beta )= \frac{\beta \theta }{x} (\beta \, ln ( \frac{1}{x}))^{-\theta -1} e^{-\left( \beta \, ln \left( \frac{1}{x}\right) \right) ^{-\theta }}, \beta> 0,\theta > 0, 0< x < 1. \end{aligned}$$
(3)

Similarly, the survival function (SF) is

$$\begin{aligned} \mathcal{S}\mathcal{F}_{\text {FLD}}(x;\alpha , \theta ,\beta )=e^{-(\beta \, ln ( \frac{\alpha }{x}))^{-\theta }}. \end{aligned}$$
(4)

The hazard rate function (HRF) describes the immediate future failure given that the unit has not failed at time x, and stated as

$$\begin{aligned} \mathcal {H}_{\text {FLD}}(x;\alpha , \beta ,\theta )=\frac{\beta \theta }{x} \left( \beta \, ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta -1}. \end{aligned}$$
(5)

The reversed hazard rate function (RHRF) describes the probability of an immediate past failure, given that the unit has already failed at time x. For the FLD in Eq. (3), the RHRF is

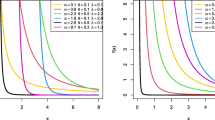
$$\begin{aligned} \mathfrak {R}_{\text {FLD}}(x; \alpha ,\beta , \theta )=\frac{\beta \theta }{x\left( 1-e^{-\left( \beta \, ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}\right) } \left( \beta \, ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta -1} e^{-\left( \beta \, ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}. \end{aligned}$$
(6)

Likewise, the concerned functions, for instance, the PDF and HRF, are highly adaptable in respective performance, will be depicted in the coming sections. More explicitly, the PDF takes on several forms, similar to symmetrical, right skewed, left skewed, L-shape and U-shape curves, see Figs. 1 and 2. Besides, we observe a positive, negative skewness, leptokurtic, mesokurtic, and platykurtic nature of the curvature, which undoubtedly suggests that it is conceived to establish the light and thick tailed prodigy, see Fig. 4. Such incidents are usually widespread in reliability presentations, queuing theory, and environmental phases. Our application segment will assist the readers for realistic predictions about the subsequent generation’s future in a healthier sense. Unlike the Weibull distribution, the suggested model may show the BTS, which is uncommon in competing models such as LLD, gamma distribution (GD), inverse gamma distribution (IGD), three-parameter Weibull distribution (3P WD), three-parameter Kappa (3P Kappa) distribution, exponentiated exponential distribution (EED), FD and log-normal distribution (LND). One can visualize these eminent qualities from HRF plots, probability graphs and four real lifetime data applications, and it also has closed-form CDF and HRF functions. It can efficiently be used in lifetime data analysis, whose detail is given in the application section, which endorses the suitability of the proposed model both in IFR and BTS functions. Also, it portrays negatively, positively, and symmetric shapes of a density function, which is not seen in the corresponding models except MWD. Fourthly, due to its closed CDF or SF one can easily generates random numbers from it. A final motivation is its flexibility in exhibiting a unit domain distribution by fixing \(\alpha = 1\). In addition, the notations and acronyms used in this study are listed in Appendix-\(\hbox {A}_{0}\).

Fig. 1
figure 1

FLD PDF graphs

Full size image

The rest of the manuscript is managed as follows. Section 2 is reserved for studying the curve behavior of PDF and HRF as well as characterizations based of five different lifetime gadgets. The percentile function, rth moment via moment generating function, various entropies, Lorenz, Bonferroni, scaled total time on test transform (TTT), conditional moments, mean deviation (MD), residual life (RL) functions, stress, and strength function are studied in Sect. 3. Section 4 studies the estimation of parameters. Section 5 deals with the competing models and applications. The conclusion is drawn in Sect. 6.

Fig. 2
figure 2

FLD PDF graphs

Full size image

2 Curve Behavior of PDF and HRF Along with Characterizations

2.1 Shapes and Distribution of Curve

In this segment, we shall scrutinize the graphs of PDF and HRF of the FLD distribution as well as the characterization constructed on failure rate functions. For exploring the curve behavior of PDF and HRF, we shall first define the logarithmic form of Eq. (2), which after differentiation about x and equating to zero yields

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}x}(ln(f(x)))=(ln (f(x)))'=-\frac{1}{x}+\frac{1+\theta }{x\, ln\left( \frac{\alpha }{x}\right) }-\frac{\beta \theta \left( \beta ln\left( \frac{\alpha }{x}\right) \right) ^{-1-\theta }}{x}=0. \end{aligned}$$
(7)

Since a closed-form solution is not possible, computational package can be used to find the mode numerically. Furthermore, we observed that \((\ln (f(x)))'\), at extreme points exhibit a non-monotone behavior. For \( \theta =0 \), the mode of the distribution lies at \( x=\alpha e^{-1} \). It is also observed that

$$\begin{aligned} \lim _{x\rightarrow 0} e^{-(\beta ln\frac{\alpha }{x})^{-\theta }}\sim e^{-(\frac{\beta }{x})^{-\theta }}, \lim _{x\rightarrow \alpha } e^{-(\beta ln\frac{\alpha }{x})^{-\theta }}\sim e^{-(\beta (x-a))^{-\theta }}. \end{aligned}$$

So, as \( x\rightarrow 0 \), we have

$$\begin{aligned} \lim _{x\rightarrow 0}f(x)\sim \frac{\beta \theta }{x}\left( \frac{\beta }{x}\right) ^{-\theta -1} e^{-\left( \frac{\beta }{x}\right) ^{-\theta }}, \,\,\, \, 0<x<\infty , \end{aligned}$$

and

$$\begin{aligned} \lim _{x\rightarrow \alpha }f(x)\sim \beta \theta \left( \beta (x-\alpha )\right) ^{-\theta -1} e^{-\left( \beta (x-\alpha )\right) ^{-\theta }} \, \, \, \, 0<x<\alpha . \quad \text {as} \quad x\rightarrow \alpha . \end{aligned}$$

Consequently, the HRF asymptotic form, as \( x\rightarrow 0 \), is

$$\begin{aligned} \mathcal {H}(x)\sim \frac{\beta \theta }{x}\left( \frac{\beta }{x}\right) ^{-\theta -1}, 0<x<\infty , \end{aligned}$$

and as \( x\rightarrow \alpha \)

$$\begin{aligned} \mathcal {H}(x)\sim \beta \theta \left( \beta (x-\alpha )\right) ^{-\theta -1}, 0<x<\alpha . \end{aligned}$$

After the differentiation of Eq. (5) with respect to x and setting the resultant derivative to zero, we get

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}x}(ln(\mathcal {H}(x)))=\frac{\theta \left( 1+\theta -ln\left( \frac{\alpha }{x}\right) \right) \left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}{x^2 ln\left( \frac{\alpha }{x}\right) ^2} =0. \end{aligned}$$
(8)

From the earlier equation, the mode of HRF is \( x = \alpha e^{-\theta -1}\), which depends upon on \(\alpha \) and \(\theta \) only. Moreover, its second derivative is

$$\begin{aligned} \frac{\textrm{d}^2}{\textrm{d}x^2}(ln(\mathcal {H}(x)))=\frac{\theta \left( (1+\theta ) (2+\theta )-3 (1+\theta ) ln\left( \frac{\alpha }{x}\right) +2 ln\left( \frac{\alpha }{x}\right) ^2\right) }{x^3\left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{\theta } (ln \left( \frac{\alpha }{x}\right) )^3}=0, \end{aligned}$$
(9)

which implies that the change points (CP) are: \(\hbox {CP}_{1}=\alpha e^{\frac{1}{4} \left( -3-3 \theta -\sqrt{-7-6 \theta +\theta ^2}\right) }\) and \(\hbox {CP}_{2}=\alpha e^{\frac{1}{4} \left( -3-3 \theta +\sqrt{-7-6 \theta +\theta ^2}\right) }\) (Fig. 3).

Fig. 3
figure 3

FLD HRF graphs

Full size image

2.2 Characterizations

As lifetime phenomena are usually related to reliability and HRF that should be as far as possible to be realistic, such a realistic mechanism can only be obtained if the model is characterizable. Characterization assists scholars in finding the genuine model by using any particular property. For a comprehensive study, readers are referred to [8,9,10]. In this regard, we characterize the proposed model by statistical lifetime gadgets like hazard rate, reverse hazard rate, Mills’ ratio, and elasticity functions which are quite well known in physical sciences and criminological sciences as well as in lifetime data analysis. In this regard, respective characterizing conditions are defined in different propositions one by one as follows.

Definition 1

Let \( X:\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be a continuous stochastic variate with PDF \( \textrm{f}(x) \) iff the HRF fulfills the subsequent equation

$$\begin{aligned} \frac{f'(x)}{\textrm{f}(x)}=\frac{\mathcal {H}'(x)}{\mathcal {H}(x)}-\mathcal {H}(x), \end{aligned}$$

and RHRF \( \mathfrak {R}(x) \) fulfills the stated condition

$$\begin{aligned} \frac{f'(x)}{f(x)}=\frac{\mathfrak {R'(x)}}{\mathfrak {R}(x)}+\mathfrak {R}(x), \end{aligned}$$

respectively.

Proposition 1

Let \( X:\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be a continuous stochastic variate with the PDF (2)iff its HRF defined by 5 is twice differentiable and satisfies the expression

$$\begin{aligned} \frac{\mathcal {H}'(x)}{(\mathcal {H}(x))^{2}}= & {} \frac{\left( 1+\theta -ln\frac{\alpha }{x}-\theta (\beta ln (\frac{\alpha }{x}))^{-\theta }\right) x }{ ln(\frac{\alpha }{x})\beta \theta (\beta ln (\frac{\alpha }{x}))^{-\theta -1}e^{-(\beta ln (\frac{\alpha }{x}))^{-\theta }}\beta \theta (\beta ln (\frac{\alpha }{x}))^{-\theta -1}}+1. \end{aligned}$$
(10)

Proof

The proof is given in Appendix A1. \(\square \)

Proposition 2

Let \( X:\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be a continuous stochastic variate with the PDF 2 iff Eq. 6 is twice differentiable and satisfies the given expression

$$\begin{aligned} \frac{\mathfrak {R}'(x)}{(\mathfrak {R}(x))^{2}}=\frac{e^{-\left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }} \theta \left( \beta ln\left( \frac{\alpha }{x}\right) \right) ^{-2 \theta } \left( -\theta +\left( 1+\theta -ln \left( \frac{\alpha }{x}\right) \right) \left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{\theta }\right) \left( 1-e^{-\left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}\right) }{ \left( ln \left( \frac{\alpha }{x}\right) \right) ^2\left( \beta \theta \left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-1-\theta }e^{-\left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}\right) ^2}-1. \end{aligned}$$
(11)

Proof

The proof is given in Appendix A1. \(\square \)

Definition 2

Let \( X:\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be a continuous stochastic variate having absolutely continuous CDF and PDF iff the Mills ratio defined as: \(\mathfrak {M}(x)=\frac{1}{\mathcal {H}(x)} \) is twice differentiable function and satisfies the following equation:

$$\begin{aligned} \frac{f'(x)}{f(x)}+\frac{\mathfrak {M'}(x)+1}{\mathfrak {M}(x)}=0. \end{aligned}$$

Proposition 3

Let \( X:\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be a continuous stochastic variate with PDF as defined in Eq. 2 iff its Mills ratio \(\mathfrak {M}(x)=\frac{x}{\beta \theta (\beta ln (\frac{\alpha }{x}))^{-theta-1}} \)is twice differentiable and satisfies

$$\begin{aligned} \mathfrak {M}'(x)=\frac{e^{-\left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }} \theta \left( \beta ln\left( \frac{\alpha }{x}\right) \right) ^{-2 \theta } \left( -\theta +\left( 1+\theta -ln \left( \frac{\alpha }{x}\right) \right) \left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{\theta }\right) \left( e^{-\left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}\right) }{ \left( ln \left( \frac{\alpha }{x}\right) \right) ^2\left( \beta \theta \left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-1-\theta }e^{-\left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}\right) ^2}+1. \end{aligned}$$
(12)

Proof

The proof is given in Appendix A1. \(\square \)

Definition 3

Let \( X:\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be an absolutely continuous stochastic variate with CDF and PDF, the elasticity function, \( \mathfrak {E}(x)=x\mathfrak {R}(x) \), of a twice differentiable distribution function satisfies the differential equation,

$$\begin{aligned} \frac{f'(x)}{f(x)}=\frac{\mathfrak {E'}(x)}{\mathfrak {E}(x)}+\frac{\mathfrak {E}(x)}{x}-\frac{1}{x}. \end{aligned}$$

Proposition 4

Let \( X:\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be an absolutely continuous random variate with PDF and CDF as defined in Eqs. 2 and 4 iff its elasticity function is defined \(\mathfrak {E}(x)=x\mathfrak {R}(x) \) which is twice differentiable and satisfies the given expression

$$\begin{aligned}{} & {} \mathfrak {E}'(x)-\left( -\frac{1}{x}+\frac{1+\theta }{x ln \left[ \frac{\alpha }{x}\right] }-\frac{\beta \theta \left( \beta ln \left[ \frac{\alpha }{x}\right] \right) ^{-1-\theta }}{x}-\frac{e^{-\left( \beta ln \left[ \frac{\alpha }{x}\right] \right) ^{-\theta }} \beta \theta \left( \beta ln \left[ \frac{\alpha }{x}\right] \right) ^{-1-\theta }}{\left( 1-e^{-\left( \beta ln\left[ \frac{\alpha }{x}\right] \right) ^{-\theta }}\right) x}\right) \mathfrak {E}(x)\nonumber \\{} & {} \quad =\frac{\beta \theta (\beta ln(\frac{\alpha }{x}))^{-\theta -1}e^{-\left( \beta ln (\frac{\alpha }{x})\right) ^{-\theta }}}{x(1-e^{-\left( \beta ln (\frac{\alpha }{x})\right) ^{-\theta }})}. \end{aligned}$$
(13)

Proof

The proof is given in Appendix A1. \(\square \)

The following theorem was used in [11] to characterize different univariate continuous distributions. Here, we discuss characterizations of FLD distributions through Theorem [11] on the basis of simple relationship between two functions of X.

Theorem 1

Let \( (\mathcal {S}:\mathcal {F};{\textbf {P}}) \) be a given probability space, and let \( \mathbb {W} = \left[ c, d\right] \) be an interval for some \( c < d (c = -\infty ; d = \infty \) might as well be allowed). Let \(X:\mathcal {S} \rightarrow \mathbb {W} \) be a continuous random variable with distribution function \( \mathcal {F} \), and let p and q be two real functions defined on \( \mathbb {W} \) such that

$$\begin{aligned} \mathbb {E}\left( p(X)|X\ge x\right) =\mathbb {E}\left( q(X)|X\ge x\right) \psi (x), x\in \mathbb {W}, \end{aligned}$$

is defined with some real function \( \psi \). Assume that \( p, q \in \mathcal {C}^{1}(\mathbb {W}), \lambda \in \mathcal {C}^{2}(\mathbb {W}) \) and \( \mathcal {F} \) is a twice continuously differentiable and strictly monotone function on the set \( \mathbb {W} \). Finally, assume that the equation \( q \psi = p \) has no real solution in the interior of \( \mathbb {W} \). Then \( \mathcal {F} \) is uniquely determined by the functions p, q and \( \psi \), particularly

$$\begin{aligned} \mathcal {F}=\int _{0}^{x}\mathcal {C}|\frac{\psi '(u)}{\psi (u)q(u)-p(u)}|exp(-r(u))\textrm{d}u, \end{aligned}$$

where the function r is a solution of the differential equation \( r'=\frac{\psi 'q}{\psi q-p} \) and \(\mathcal {C}\) is a constant to make \( \int _{\mathbb {W}}\textrm{d}\mathcal {F}=1. \)

Proposition 5

Let \( X:\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be a continuous random variable, and let \( q(x) = \frac{3}{e^{2(\beta ln \frac{\alpha }{x})^{-\theta }}} \) and \( p(x)= \frac{2}{e^{(\beta ln \frac{\alpha }{x})^{-\theta }}} \) for \( x \in (0;\alpha ) \). The random variable X has PDF (2) iff there exist functions \( \psi \) and p defined in Glanzel Theorem satisfying the differential equation

$$\begin{aligned} \frac{\psi '(x)}{\psi (x)q(x)-p(x)}=\frac{e^{2(\beta ln (\frac{\alpha }{x}))^{-\theta }}\beta \theta (\beta ln (\frac{\alpha }{x}))^{-\theta -1}}{x}. \, \, \, 0< x < \alpha \end{aligned}$$
(14)

Proof

The proof is given in Appendix A1. \(\square \)

Corollary 1

Let \( X;\mathcal {S} \longrightarrow \left( 0,\infty \right) \) be a continuous random variable, and let \( q(x) =\frac{3}{e^{2(\beta ln \frac{\alpha }{x})^{-\theta }}} \) and \( p(x)= \frac{2}{e^{(\beta ln \frac{\alpha }{x})^{-\theta }}} \) for \( x \in (0;\alpha ) \). The random variable X has the PDF (2) iff the \( \psi \) has the form \( \psi (x)= e^{(\beta ln \frac{\alpha }{x})^{-\theta }} \).

Remark 1

Since solution of differential Eq. 14 is

$$\begin{aligned} \psi (x)=\int \frac{e^{(\beta ln (\frac{\alpha }{u}))^{-\theta }}\beta \theta (\beta ln (\frac{\alpha }{u}))^{-\theta -1}}{u} \textrm{d}u +\textsf{D}, \end{aligned}$$

where \( \textsf{D} \) is an integral constant.

3 Lifetime Variate’s Mathematical and Statistical Properties

This section is reserved only for the mathematical and statistical properties of the proposed model, which are quite helpful in the lifetime phenomenon. These properties include the quantile, moment generating function, moments, conditional moments, mean deviation, entropy, residual and reverse residual, Bonferroni, Lorenz curves, scaled TTT, and stress and strength probability.

3.1 Percentile Function

Let X be a continuous variate with CDF \( \mathcal {F}_{X}: R \rightarrow [0, 1]\). Now, from this definition a percentile function \( \mathcal {P} \) generally sends back a threshold measurement x. In this regard, inverse of the FLD percentile function yields \(x=\mathcal {P}(p)\) as follows:

$$\begin{aligned} \mathcal {P}_{p}=\mathcal {F}^{-1}(p)=\alpha e^{-\frac{(-1)^{-1/\theta } ln[1-p]^{-1/\theta }}{\beta }}, \end{aligned}$$
(15)

where \(p\in (0,1)\). The median is \(\alpha e^{-\frac{(-1)^{-1/\theta } ln[0.5]^{-1/\theta }}{\beta }}. \)

Fig. 4
figure 4

Skewness and Kurtosis graphs

Full size image

3.2 Raw Moments from Moment Generating Function

In physical sciences, computing engineering, and environmental modeling, the term raw moment of any model is a computable measure related to the center, dispersion, skewness, and kurtosis of the model’s graph. It not only addresses the curve behavior of a function but also assists in characterizing the probability functions. In order to generate moments from the MGF, we shall first define the MGF of a continuous random variable X\(\sim \text {FLD}(\alpha ,\beta ,\theta )\) as \(\mathcal {M}_{X}(t)=\mathbb {E}(e^{tX})=\int _{0}^{\alpha } e^{tx} f(x) \textrm{d}x \), where \(|t|<1\). Now, on incorporating Eq. (2) we get

$$\begin{aligned} \mathcal {M}_{X}(t)=\int _{0}^{\alpha }e^{tx}\frac{\beta \theta }{x} (\beta \, ln ( \frac{\alpha }{x}))^{-\theta -1} e^{-(\beta \, ln ( \frac{\alpha }{x}))^{-\theta }}\textrm{d}x. \end{aligned}$$

Let \( y = \left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }, \textrm{d}y = \frac{ \theta \beta \left( \beta ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta -1}\textrm{d}x}{x} \), if \(x=0, y=0\), \(x=\alpha , y=\infty \), so when \(x=\alpha e^{-\frac{y^{-1/\theta }}{\beta }} \alpha \), on simplification we get

$$\begin{aligned} \mathcal {M}_{X}(t)=\sum _{r=0}^{\infty } \sum _{m=0}^{\infty } \frac{ \alpha ^r\left( \frac{-r}{\beta }\right) ^m}{m!}\Gamma \left[ 1-\frac{m}{\theta }\right] \frac{t^r}{r!}. \end{aligned}$$

The rth raw moment for FLD distribution can be expressed as the coefficient of \( \frac{t^{r}}{r!} \)

$$\begin{aligned} \mu _{r}^{'}=\sum _{m=0}^{\infty } \frac{ \alpha ^r\left( \frac{-r}{\beta }\right) ^m}{m!}\Gamma \left[ 1-\frac{m}{\theta }\right] , \end{aligned}$$

where \( \Gamma [a]=\int _{0}^{\infty }t^{a-1}e^{-t} \textrm{d}t \) is a gamma function. On the basis of these, we are able to assess the skewness (departure from symmetry, \( \frac{\mu _{3}}{\mu _{2}^{3/2}} \)) and kurtosis (degree of peakedness \(\frac{\mu _{4}}{\mu _{2}^{2}}\)), where \( \mu \) is the moment about mean. Since expressions for these ratios are not in closed form, the plots are portrayed in Fig. 4, indicating that the proposed model is negatively and positively skewed and symmetric. Moreover, the model is also leptokurtic, mesokurtic, and platykurtic in behavior.

3.3 Entropy

The measure of the degree of uncertainty is commonly known as entropy. It has many significant chattels that agree with our innate belief of haphazardness. For studying this, we like to mention some of its properties which are (1) It may be positive or negative. (2) It vanishes if and only if it is a particular event. (3) Entropy is augmented by the accumulation of an independent constituent and lessened by acclimatizing. However, adding this belief to continuous probability models postures some contests. The entropy is specially combatted in physics, computing engineering, and statistics, where it measures the number of ways a thermodynamic system is arranged, the total amount of information in each received message, and measures uncertainty and dispersion, respectively. A number of research papers and monographs have appeared over the past 60 years, discussing and extending the original work of Shannon. In this research work, we will discuss some of them under the following names.

3.3.1 Shannon’s Entropy

The SE is a significant and famous notion in the field of physical sciences and computing engineering, and its applications are generally seen in the field of financial analysis, data compression, mathematics, statistics, and computing sciences. For continuous variable X, it can be expressed as

$$\begin{aligned} \mathcal{S}\mathcal{E}=-\int _{-\infty }^{\infty }\textrm{f}(x)ln(\textrm{f}(x))\textrm{d}x. \end{aligned}$$

Incorporating the PDF in the above equation and simplifying it, we get

$$\begin{aligned} \mathcal{S}\mathcal{E}= & {} -ln (\beta )-ln(\theta )+\frac{(\theta +1)\gamma }{\theta } +1+ln(\alpha )+\frac{1}{\beta }\Gamma \left( 1-\frac{1}{\theta }\right) , \\ \mathcal{S}\mathcal{E}= & {} ln\left( \frac{\alpha }{\beta \theta }\right) +\frac{(\theta +1)\gamma }{\theta } +1+\frac{1}{\beta }\Gamma \left( 1-\frac{1}{\theta }\right) , \end{aligned}$$

where \(\gamma \) is the Euler constant and \( \frac{1}{\theta } < 1\).

3.3.2 Cumulative Residual Entropy

Another measure of randomness of a random variable X called the CRE, where the PDF of the random variable X is swapped by the CDF/SF in Shannon’s definition. The CDF/SF is more consistent than the PDF, because the PDF is obtained as the derivative of the CDF/SF. If X is a random variable, then we can define the CRE as

$$\begin{aligned} \mathcal {CRE}=-\int _{-\infty }^{\infty }\mathcal {S}(x)ln(\mathcal {S}(x))\textrm{d}x; \end{aligned}$$

for FLD, it can be expressed as

$$\begin{aligned} \mathcal {CRE}=-\int _{0}^{\alpha }e^{-\left( \beta \, ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}ln\left( e^{-\left( \beta \, ln \left( \frac{\alpha }{x}\right) \right) ^{-\theta }}\right) \textrm{d}x, \end{aligned}$$

which on simplification yields

$$\begin{aligned} \mathcal {CRE}=\frac{\alpha }{\beta \theta }\sum _{m=0}^{\infty }\frac{(\frac{-1}{\beta })^{m}}{m!}\Gamma \left( 1-\frac{m+1}{\theta }\right) . \end{aligned}$$

provided \( \theta > m+1.\)

3.3.3 Tsallis Entropy

TE was presented by Tsallis [12] in 1988, and it is a generalization of Boltzmann–Gibbs statistics. For a nonnegative continuous random variable X with the PDF 2, Tsallis entropy of order \( \lambda \) is defined by \( \mathcal{T}\mathcal{E}_{\lambda }(X)= \frac{1}{\lambda - 1}\left( 1-\int _{0}^{\alpha } \left( \textrm{f}(x)\right) ^{\lambda }\textrm{d}x \right) ; \lambda \ne 1, \lambda > 1\). For FLD, it can be expressed as

$$\begin{aligned} \mathcal{T}\mathcal{E}_{\lambda }(X)=\frac{1}{\lambda -1}\left( 1-\left( \frac{\theta \beta }{\alpha }\right) ^{\lambda -1}\lambda ^{\frac{1-(1+\theta ) \lambda }{\theta }}\sum _{m=0}^{\infty } \frac{\left( \frac{(\lambda -1)\lambda ^{\frac{1}{\theta }}}{\beta }\right) ^m}{m!}\Gamma \left( \frac{-1-m+\lambda +\theta \lambda }{\theta }\right) \right) , \end{aligned}$$

provided \( (\theta +1)\lambda > m+1.\)

3.3.4 Cumulative Residual Tsallis Entropy

Based on the TE, Sati and Gupta [13] proposed a CRTE of order \( \lambda \), which is given by \( \mathcal {CRTE}_{\lambda }(X)= \frac{1}{\lambda - 1}\left( 1-\int _{0}^{\alpha } \left( \mathcal {F}(x)\right) ^{\lambda }\textrm{d}x \right) ; \lambda \ne 1, \lambda > 1\)

$$\begin{aligned} \mathcal {CRTE}_{\lambda }(X)=\frac{1}{\lambda -1}\left( 1-\alpha \sum _{m=0}^{\infty } \frac{\left( -\frac{\lambda ^{\frac{1}{\theta }}}{\beta }\right) ^m}{m!}\Gamma \left( 1-\frac{m}{\theta }\right) \right) , \end{aligned}$$

provided \( \theta > m.\)

Fig. 5
figure 5

FLD Shannon’s and cumulative residual entropy graphs

Full size image

3.3.5 Rényi Entropy

The RE measures the assortment, uncertainty, or randomness of a system. The entropy is identified after Alfréd Rényi, who looked for the most general definition of information measures that maintain additivity for independent events. It is applied in ecology and statistics as the index of diversity [14], in quantum information as a measure of complex system [15] and in heart rate variability for detecting CAN [16]. The RE of order \( \lambda \), where \( \lambda \ge 0, \lambda \ne 0\) is defined as \( \mathcal{R}\mathcal{E}= \frac{1}{1-\lambda } ln \int _{\Re } \textrm{f}^{\lambda }(x) \textrm{d}x.\) For the FLD, it can be expressed as

$$\begin{aligned} \mathcal{R}\mathcal{E}_{\lambda }(X)=&\frac{1}{1-\lambda } \left( \left( \frac{1-(1+\theta ) \lambda }{\theta }\right) ln[\lambda ]+(1-\lambda )ln\left[ \frac{\alpha }{\theta \beta }\right] \right. \\&\left. ln \left[ \sum _{m=0}^{\infty } \frac{\left( -\frac{(1-\lambda )\lambda ^{\frac{1}{\theta }}}{\beta }\right) ^m}{m!}\Gamma \left[ \frac{-1-m+\lambda +\theta \lambda }{\theta }\right] \right] \right) , \end{aligned}$$

provided \( (\theta +1)\lambda > m+1.\)

3.3.6 Mathai–Haubold Entropy

An inaccuracy measure through disturbance or distortion of systems can be calculated via an entropy known as MHE proposed by [17] is defined as \( \mathcal {MHE}=\frac{\int _{\Re }\textrm{f}^{2-\lambda }(x)\textrm{d}x-1}{\lambda -1} \). For the FLD it can be expressed as

$$\begin{aligned}{} & {} \mathcal {MHE}_{\lambda }(X)\\{} & {} = \frac{(2-\lambda )^{\frac{\lambda -1}{\theta }+\lambda -2}\left( \frac{\theta \beta }{\alpha }\right) ^{2-\lambda -1}\sum _{m=0}^{\infty } \frac{\left( -\frac{(2-\lambda -1)(2-\lambda )^{\frac{1}{\theta }}}{\beta }\right) ^m}{m!}\Gamma \left[ \frac{1-m-\theta (-2+\lambda )-\lambda }{\theta }\right] -1}{\lambda -1}, \end{aligned}$$

provided \( \frac{1}{\theta }>\frac{m+\theta (\lambda -2)+\lambda }{\theta }.\)

Fig. 6
figure 6

Tsallis and cumulative residual Tsallis entropy graphs

Full size image
Fig. 7
figure 7

Rényi and Mathai–Haubold entropy graphs

Full size image

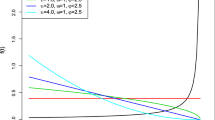
Interpretations of Entropy From Figs. 5, 6, and 7, it is obvious that entropy occupies both negative and positive amount. Both cases are observed in all types of entropies, i.e., FLD is maximum entropy distribution and also has negative entropy, which indicates that the model also exhibits ordered pattern in entropy and it requires energy to achieve this state, i.e., negative entropy. However, the amount of entropy in positives cases is too low, which indicates that disorder exists very negligibly, small.

3.4 Conditional Moments and Mean Deviations

For lifetime probability models, the rth conditional moment is defined as \( \mathbb {E}(X^{r}|X > t), r =1, 2,..., \) which has crucial and substantial concern in forecasting. So for this purpose the rth partial moments of the variate X defined as \(\delta _{r}(t)\) for any real \(r > 0\) is given as

$$\begin{aligned} \delta _{r}(t)&=\int _{-\infty }^{t}x^{r}\textrm{f}(x)\textrm{d}x, \\&=\sum _{m=0}^{\infty } \frac{\alpha ^r \left( -\frac{r}{\beta }\right) ^m \left( \Gamma \left[ 1-\frac{m}{\theta }\right] -\Gamma \left[ 1-\frac{m}{\theta },\left( \beta ln\left[ \frac{\alpha }{t}\right] \right) ^{-\theta }\right] \right) }{m!}, \end{aligned}$$

where \( \Gamma (a,b)=\int _{b}^{\infty }t^{a-1}e^{-t} \) is an incomplete gamma function. Now, the rth conditional moment of the FLD distribution can be obtained as

$$\begin{aligned} \mathbb {E}(X^{r}|X>t)&=\frac{1}{\mathcal {S}(t)} \left\{ \mathbb {E}(X^{r})-\int _{0}^{t}x^{r}\textrm{f}(x)\textrm{d}x\right\} , \\&=\frac{1}{\mathcal {S}(t)}\lbrace \mu '_{r}-\delta _{r}(t)\rbrace . \end{aligned}$$

The partial moments methodology is quite useful in finding the average deviance between the median and mean, where the median/mean aberration yields key evidence about typical of population. These partial moments can be used in many fields like economics and insurance. It delivers vital evidence about a population’s attributes via the first partial moment. Now in this regard, the MD about the mean (\( \mu ' \)) and median (\(\tilde{\mu }\)) are expressed as

$$\begin{aligned} \mathcal{M}\mathcal{D}_{\mu '}= \mathbb {E}\mid X-\mu _{1}'\mid =2\mu _{1}'\mathcal {F}(\mu _{1}')-2\delta _{1}(\mu _{1}'), \end{aligned}$$
(16)

where \( \delta _{r}(t)=\int _{-\infty }^{t}x^{r} \textrm{f}(x)\textrm{d}x \) and

$$\begin{aligned} \mathcal{M}\mathcal{D}_{\tilde{\mu }}=\mathbb {E}\mid X-\tilde{\mu }\mid =\mu _{1}'-2\delta _{1}(\tilde{\mu }), \end{aligned}$$
(17)

respectively, which in turn assists researchers to determine the volume of diffusion in a population, also \(\mu _{1}'=\mathbb {E}(X),\) \(\tilde{\mu }= \mathbb {M}\)(X)=\(\mathcal {P}\)(\(\frac{1}{2})\), and \(\delta _{1}(t)\) is the first complete moment defined as above with \(r=1\).

3.5 Residual Lifetime Function and Its Characteristics

If \( t > 0\) is the survival time, then RL and RRL stochastic variates from time t till the time of failure and the time passed from the failure of a section given that its life \(\le t \), are stated, respectively, as \( \mathcal{R}\mathcal{L}(t):=( X -t|X > t) \) and \( \bar{\mathcal {RRL}}(t):=( t - X|X \le t) \). The SF of the \(\mathcal{R}\mathcal{L} \) is \( \mathcal{S}\mathcal{F}_{\mathcal{R}\mathcal{L}_{(t)}}, t \ge 0 \); for the FLD distribution, it is given as

$$\begin{aligned} \mathcal{S}\mathcal{F}_{\mathcal{R}\mathcal{L}_{(t)}}(x)= & {} \frac{\mathcal {SF }(x+t)}{\mathcal {SF }(t)}=\frac{e^{-(\beta \, ln ( \frac{\alpha }{x+t}))^{-\theta }}}{e^{-(\beta \, ln ( \frac{\alpha }{t}))^{-\theta }}}, \\ \mathcal{S}\mathcal{F}_{\mathcal{R}\mathcal{L}_{(t)}}(x)= & {} e^{-(\beta \, ln ( \frac{\alpha }{x+t}))^{-\theta }-(\beta \, ln ( \frac{\alpha }{t}))^{-\theta }}, \end{aligned}$$

and the corresponding PDF is

$$\begin{aligned} \textrm{f}_{\mathcal{R}\mathcal{L}_{(t)}}(x)=\frac{\beta \theta }{x+t} \left( \beta \, ln \left( \frac{\alpha }{x+t}\right) \right) ^{-\theta -1}e^{-(\beta \, ln ( \frac{\alpha }{x+t}))^{-\theta }-(\beta \, ln ( \frac{\alpha }{t}))^{-\theta }}, \end{aligned}$$

and HRF of \( \mathcal{R}\mathcal{L}_{(t)} \) is given by

$$\begin{aligned} \mathcal {H}_{\mathcal{R}\mathcal{L}_{(t)}}(x)=\frac{\beta \theta }{x+t}\left( \beta \, ln \left( \frac{\alpha }{x+t}\right) \right) ^{-\theta -1}. \end{aligned}$$

As MRL, suggests how much retentive apparatus will last for a specific point of time, is a vital gauge in reliability appraisal and modeling. It deals with condensed data for various decision-making malfunctions, such as fixing burn-in tests, planning enhanced life tests, determining warranty policy, and making maintenance decisions. Keeping in view the significance of the function, one can define it as

$$\begin{aligned} \mathcal {K}(t)= & {} \mathbb {E}(\mathcal{R}\mathcal{L}_{(t)})=\frac{1}{\mathcal{S}\mathcal{F}(t)}\int _{t}^{\alpha }x\textrm{f}(x)\textrm{d}x\\= & {} \frac{1}{\mathcal{S}\mathcal{F}(t)} \lbrace \mathbb {E}(X)-\int _{0}^{t}x\textrm{f}(x)\textrm{d}x\rbrace -t, \end{aligned}$$

where

$$\begin{aligned} \delta _{r}(t)=\int _{-\infty }^{t}x^{r}\textrm{f}(x)\textrm{d}x. \end{aligned}$$
Fig. 8
figure 8

FLD MRL function graphs

Full size image

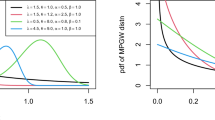
The MRL function is muscularly linked to the failure rate function; the MRL classes are also related to the classes defined via the HRF. From Fig. 3, its is obvious that purported model belongs to BFR, which suggests that the linked MRL has an IBTS shape, see Fig. 8.

$$\begin{aligned} \mathcal {M}ean= & {} \mathcal {M}(t)=\frac{1}{\mathcal {S}(t)} \left\{ \mathbb {E}(X)-\alpha \sum _{m=0}^{\infty }\frac{\left( \frac{-1}{\beta }\right) ^{m}}{m!}\right. \\{} & {} \quad \left. \left( \Gamma \left( 1-\frac{m}{\theta }\right) -\Gamma \left( 1-\frac{m}{\theta }, \left( \beta ln\left( \frac{\alpha }{x}\right) \right) ^{-\theta }\right) \right) \right\} -t, \end{aligned}$$

Gupta and Kirmani [18] stated the substantial importance of the variance of RL function which compelled us to calculate it for FLD as (Fig. 9)

$$\begin{aligned} \mathcal {VAR}(t)= & {} \mathbb {V}ariance(\mathcal{R}\mathcal{L}_{(t)})\\= & {} \frac{2}{\mathcal{S}\mathcal{F}(t)}\int _{t}^{\alpha }x\mathcal{S}\mathcal{F}(x)\textrm{d}x-2t\mathcal {K}(t)-\left( \mathcal {K}(t)\right) ^{2}, \\ \mathcal {VAR}(t)= & {} \frac{1}{\mathcal{S}\mathcal{F}(t)} \left\{ \mathbb {E}(X^{2})-\alpha ^{2} \sum _{m=0}^{\infty }\frac{\left( \frac{-1}{\beta }\right) ^{m}}{m!}\right. \\{} & {} \quad \left. \left( \Gamma \left( 1-\frac{m}{\theta }\right) -\Gamma \Big (1-\frac{m}{\theta }\Big \rbrace -t^{2}-2t\mathcal {K}(t)-\left( \mathcal {K}(t)\right) ^{2} \right) \right\} . \end{aligned}$$
Fig. 9
figure 9

FLD variance of residual life function graphs

Full size image

3.6 Reversed Residual Life Function and Its Features

Similarly, we have also calculated the SF of the RRL function \(\mathcal{R}\mathcal{V}_{(t)}\), \( t \ge 0 \) for the FLD as

$$\begin{aligned} \mathcal{S}\mathcal{F}_{\mathcal{R}\mathcal{V}_{(t)}}(x)=\frac{\mathcal {F}(t-x)}{\mathcal {F}(t)}=\frac{1-e^{-(\beta \, ln ( \frac{\alpha }{t-x}))^{-\theta }}}{1-e^{-(\beta \, ln ( \frac{\alpha }{t}))^{-\theta }}}, 0\le x \le t, \end{aligned}$$

and the corresponding PDF is

$$\begin{aligned} f_{\mathcal{R}\mathcal{V}_{(t)}}(x)=\frac{\beta \theta }{(t-x)(1-e^{-(\beta \, ln ( \frac{\alpha }{t}))^{-\theta }})}\left( \beta \, ln \left( \frac{\alpha }{t-x}\right) \right) ^{-\theta -1}e^{-(\beta \, ln ( \frac{\alpha }{t-x}))^{-\theta }}. \end{aligned}$$

The HRF of \( \mathcal{R}\mathcal{V}_{(t)} \) is given by

$$\begin{aligned} \mathcal {H}_{\mathcal{R}\mathcal{V}_{(t)}}(x)=\frac{\beta \theta }{(t-x)(1-e^{-(\beta \, ln ( \frac{\alpha }{t-x}))^{-\theta }})}\left( \beta \, ln \left( \frac{\alpha }{t-x}\right) \right) ^{-\theta -1}e^{-(\beta \, ln ( \frac{\alpha }{t-x}))^{-\theta }}, \end{aligned}$$

with average and dispersion measures as

$$\begin{aligned} \mathbb {M}ean(\mathcal{R}\mathcal{V}_{(t)})= & {} \mathcal{L}\mathcal{W}(t)=\mathbb {E}(\mathcal{R}\mathcal{V}_{(t)})=t-\frac{1}{\mathcal {F}(t)}\int _{0}^{t}x\textrm{f}(x)\textrm{d}x=t-\frac{\delta _{1}(t)}{\mathcal {F}(t)}, \\ \mathbb {V}ariance(\mathcal{R}\mathcal{V}_{(t)})= & {} \mathcal {W}(t)=2 t \mathcal{L}\mathcal{W}(t)-(\mathcal{L}\mathcal{W}(t))^{2}-\frac{2}{\mathcal {F}(t)}\int _{0}^{t}x\mathcal {F}(x)\textrm{d}x, \\ \mathcal {W}(t)= & {} 2 t \mathcal{L}\mathcal{W}(t)-(\mathcal{L}\mathcal{W}(t))^{2}-t^{2}+\frac{\delta _{2}(t)}{\mathcal {F}(t)}. \end{aligned}$$

3.7 Lorenz Curve

Suppose X is a nonnegative random variable, then the Lorenz curve for the FLD is expressed, for a given probability \(\mathfrak {p}\), as

$$\begin{aligned} \mathcal {Z}(\textrm{p})=\frac{1}{\mu _{1}'}\delta _{1}(\textrm{q}). \end{aligned}$$

3.8 Bonferroni Curve

Suppose X be a nonnegative random variable, then the Bonferroni curve for FLD can be expressed as

$$\begin{aligned} \mathcal {B}(\textrm{p})=\frac{1}{\textrm{p}\mu _{1}'}\delta _{1}(\textrm{q}), \end{aligned}$$

where \(\mu _{1}'=\mathbb {E}(X)\), and \(\textrm{p}=\mathcal {P}(\textrm{p})\) is the percentile function of X at percentile \(\textrm{p}\) and \( \textrm{q}=\mathcal {F}^{-1}(\textrm{p}) \).

3.9 Scaled Total Time on Test

The scaled TTT is important for the aging properties of the underlying distribution and can be applied to solve geometrically some stochastic maintenance problems. TTT for a CDF \( \mathcal {F} \) can be defined as \( \mathcal{S}\mathcal{F}_{\mathcal {F}}(\mathcal {F}(t))=\frac{1}{\mathbb {E}(X)}\int _{0}^{t} \mathcal{S}\mathcal{F}(y)\textrm{d}y\)  see [19]. Therefore, for the FLD it can be expressed as

$$\begin{aligned} \mathcal{S}\mathcal{F}_{\mathcal {F}}(\mathcal {F}(t)) =\frac{1}{\mathbb {E}(X)}\lbrace t e^{-(\beta \, ln ( \frac{\alpha }{t}))^{-\theta }}+\delta _{1}(t)\rbrace . \end{aligned}$$

3.10 Stress–Strength Reliability for the FLD Distribution

In this subsection, the mathematical form of stress–strength R for the FLD is calculated as \( \mathcal {R} = \mathcal {P}\left( Y < X\right) \). It gauges the constituent reliability when it is exposed to random stress, Y, given that its strength is X. In this perspective, R can be believed as a measure of system execution and spontaneously develops electrical and electronic systems. For comprehensive study about stress–strength reliability, readers may see [20]. Let \( X \sim \text {FLD}(\alpha , \beta , \theta _{1}) \) and \( Y \sim \text {FLD}(\alpha , \beta , \theta _{2}) \) denote the strength–stress random variable. Hence, the parameter R for the FLD is obtained as

$$\begin{aligned} \mathcal {R} = \mathcal {P}\left( Y<X\right)&= \int _{x=0}^{\alpha }\int _{y=0}^{x}f(x;\alpha ,\beta ,\theta _{1})f(y;\alpha ,\beta ,\theta _{2})\textrm{d}x \textrm{d}y \\&= \int _{x=0}^{\alpha }f(x;\alpha ,\beta ,\theta _{1})\mathcal {F}(x;\alpha ,\beta ,\theta _{2})\textrm{d}x, \end{aligned}$$

which after simplification yields

$$\begin{aligned} \mathcal {R}&=1-\int _{x=0}^{\alpha } \frac{\beta \theta }{x} (\beta \, ln ( \frac{\alpha }{x}))^{-\theta _{1}-1} e^{-(\beta \, ln ( \frac{\alpha }{x}))^{-\theta _{1}}}e^{-(\beta \, ln ( \frac{\alpha }{x}))^{-\theta _{2}}}\textrm{d}x,\\&=1-\int _{z=0}^{\infty }e^{-z}e^{-z^{\frac{\theta _{2}}{\theta _{1}}}}\textrm{d}z, =1-\sum _{m=0}^{\infty }\frac{(-1)^{m}}{m!}\Gamma \left( 1+m \frac{\theta _{2}}{\theta _{1}}\right) , \end{aligned}$$

provided \( m \frac{\theta _{2}}{\theta _{1}}>-1. \)

4 Estimation of Model Parameters

4.1 Likelihood Method

Statistical implications are usually passed through three dissimilar methods like interval and point estimation as well as hypothesis testing. Even though abundant of approaches for the estimation of parameters were available in the statistical literature, the maximum likelihood method of estimation is the most excellently adaptable one. It owns projected chattels when fabricating the confidence regions and intervals as well as in test statistics. Asymptotic theories of these estimators convey simple calculations that toil well in the limited information contained in the samples. Statisticians frequently pursue to estimate quantities like the density of a test statistic that depends on the sample size so as to obtain better estimate distributions. The subsequent calculations for the MLEs in distribution theory can be handled either logically or mathematically. In this section, we are trying to cope with parameters estimation via the MLE method from the whole sample. Suppose \( x_{1},...,x_{n}\) is a stochastic realization of size n from the FLD distribution given by Eq. (2). The logarithmic form of likelihood function of the FLD is expressed as

$$\begin{aligned} \ell _{n}(\Theta )= & {} n ln(\beta )+n ln (\theta )-\sum _{i=1}^{n}ln(x_{i})-(\theta +1)\sum _{i=1}^{n}\beta ln \left( \frac{\alpha }{x_{i}}\right) \nonumber \\{} & {} - \sum _{i=1}^{n}\left( \beta ln \left( \frac{\alpha }{x_{i}}\right) \right) ^{-\theta }, \end{aligned}$$
(18)

on partially differentiating Eq. (18) with respect to \( ``\theta \)” and “\(\beta \),” respectively, and equating it to zero, we get

$$\begin{aligned} \frac{\partial \ell _{n}(\Theta )}{\partial \theta }= & {} \frac{n}{\theta }-\sum _{i=1}^n ln\left( \beta ln \left( \frac{\alpha }{x_i}\right) \right) -\sum _{i=1}^n -ln \left( \beta ln \left( \frac{\alpha }{x_i}\right) \right) \left( \beta ln \left( \frac{\alpha }{x_i}\right) \right) {}^{-\theta }=0, \nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial \ell _{n}(\Theta )}{\partial \beta }= & {} \frac{n}{\beta }-\frac{n (1+\theta )}{\beta }+\sum _{i=1}^n \theta ln \left( \frac{\alpha }{x_i}\right) \left( \beta ln\left( \frac{\alpha }{x_i}\right) \right) {}^{-1-\theta }=0. \end{aligned}$$
(20)

Because this expression cannot be worked out rationally, we desire to apply a computational package like Mathematica [12.0]. Therefore, we started estimation by utilizing the NMaximized commands. But, we have examined that we are unable to attain the fairly accurate estimate of \( \alpha \) from Eq. (18). Since \( \alpha \) is not based on x and it is the highest value in the domain of x, so we assume that the MLE for \( \alpha \) as \( \hat{\alpha } = max(x_{1}, x_{2},..., x_{n}) + \xi \, \) where \( \xi > 0 \) represents some arbitrary constants. However, when start estimation of parameter, \( \alpha \) of the FLD, using limited sample information, we assume that all the components in the sample are the stochastic variate. Therefore, we should assume that the sample should be encompassed of independent observations on the random variable in demand. As the value of parameter \( \alpha \) defines in the domain of attraction of the FLD random variable, during the process of estimation, it is a stipulation that \( \alpha \) should be greater than the greatest element in the sample. That is why, we are looking for the vigorous value of \( \hat{\alpha } \) which will perhaps be recognized under the condition that \( \hat{\alpha } \) is greater than the greatest element in the sample. Likewise, the convergence of anticipated model’s MLE is based on the massive value of \( \hat{\alpha }\), which seems to be in accordance with the distribution theory of standard epsilon models; for comprehensive study, the reader is referred to [1]. Furthermore, the regularity conditions of MLEs, the FLD (\(\alpha , \beta , \theta \)) model fulfill the regularity conditions as declared by [21](pp. 419). Thus, the confidence interval belt MLE vector of \(\hat{\Theta }\)=(\(\hat{\alpha }\),\(\hat{\beta }\),\(\hat{\theta }\)) is consistent and asymptotically normal family, i.e., \(\sqrt{n}[\hat{\Theta }^{T}-\Theta ^{T}]\sim \text {TVN}[0,I^{-1}]\), where \(\text {I}^{-1}\) is the inverse of the expected Fisher information matrix, which generates variance–covariance matrix based on the expectation of second-order log-likelihood derivatives.

5 Competing Models and Applications

In this section, we have studied four data sets ranging from lifetime perspective to participation aspects. The sources of data sets are mentioned in their respective section.

5.1 Models for Comparisons

For comparison purposes, we have studied ten competing models, including MWD [22], 3P Kappa distribution studied by [23], 3P WD [24], EED [25], WD and GD taken from Wikipedia, IGD [26], FD [7], LND [27], and LLD [6].

5.2 Detection of Hazard Rate Pattern

For failure rate identification pattern, the researchers usually prefer to use the TTT-transform, which helps to examine the shapes of the hazard rate of a given data. In this concern, Barlow and Campo [28] first applied it, for statistical inference problems under order restrictions. When modeling a data set, Aarset [29] used this test as a selection method [30]. As the developed model exhibits IBTS together with IFR, so we prefer to select various data sets exhibiting BTS or IFR.

5.3 Goodness-of-Fit and Discrimination Criterion

In this subsection, diverse standard discriminations are adopted, which are built on the log-likelihood (\( -l\)) function. Let q denote the number of parameters to be fitted and \( \hat{\Theta } \) be the MLEs of \( \Theta \), n is the size of data set, the number of classes is denoted by k, \(z_{j}=\mathcal {F}_{X}(x_{j}) \) and the \(x_{j}, j= 1,2,3,\ldots ,n \) being the arranged observations. Then, the expressions for respective information criteria are given as

$$\begin{aligned} \text {AIC}= & {} 2 q -2\ell (\hat{\Theta }), \quad \text {AICc}=\text {AIC}+\frac{2q(q+1)}{n-q-1}, \quad {\text {BIC} = q ln(n)-2\ell (\hat{\Theta })} \\ \text {HQIC}= & {} -2 \ell (\hat{\Theta })+2q \log (\log (n)),\, \, \text {CAIC}=-2\ell (\hat{\Theta })+\frac{2 q n}{n-q-1}. \end{aligned}$$

The finest model will be accepted if it possesses the least values of these gadgets. Additionally, brilliance of rival models is also confirmed through various goodness-of-fit test statistics which include both the parametric and nonparametric tests like KS, \( \chi ^{2} \), \({W}_{0}^{*}\) and \({A}_{0}^{*}\). Their corresponding expressions are given as follows:

$$\begin{aligned} \text {KS}= & {} \max \left\{ \frac{j}{k}-z_{j},z_{j}-\frac{j-1}{k} \right\} ,\chi ^{2}=\sum _{j=1}^k \frac{(o_{j}-e_{j})^{2}}{e_{j}}, \\ W_{0}^{*}= & {} \sum _{j=1}^{k}\left( z_{j}-\frac{2j-1}{2k}\right) ^{2}+\frac{1}{ 12k}, \\ A_{0}^{*}= & {} \left( \frac{2.25}{k^{2}}+\frac{3}{4 k}+1\right) \left\{ -k- \frac{1}{k}\sum _{j=1}^{k}(2j-1)\ln (z_{j}(1-z_{k-j+1})) \right\} . \end{aligned}$$

Moreover, the VTS, suggested by [31], is also applied. For comprehensive procedural understanding, the readers are referred to [32]. The evaluations of the competing models are described in Table 14.

5.4 Application with Real Lifetime Data Sets

Example 1

The lengths of power failures, in minutes, are recorded in this data set, and the data are extracted from the book [33](pp. 51) with the following measurements: 22, 18, 135, 15, 90, 78, 69, 98, 102, 83, 55, 28, 121, 120, 13, 22, 124, 112, 70, 66, 74, 89, 103, 24, 21, 112, 21, 40, 98, 87, 132, 115, 21, 28, 43, 37, 50, 96, 118, 158, 74, 78, 83, 93, 95.

Table 1 Data set I descriptive summary
Full size table
Table 2 Data set I theoretical measures
Full size table
Table 3 Data set I goodness-of-fit measure based on listed MLEs
Full size table
Fig. 10
figure 10

Empirical TTT plots

Full size image

Analytical Discussion About Data Set I Table 1  displays some descriptive features like SS, \( \bar{\text {X}} \), \( \tilde{\text {X}} \), \( \hat{\sigma } \), \( \hat{\text {SK}} \), \( \hat{\text {KU}} \) and SE of the data, which reveals a close coordination between descriptive and theoretical results given by Table 2. The proposed model has a minimum value of \( \chi ^{2} \) goodness-of-fit statistic as compared to rest of the models values. Also, FLD has minimum value of \({A}_{0}^{*}\), \({W}_{0}^{*} \) and the KS statistic that supports the suitability of suggested model. Take note of that the parameter \( \alpha \) is the highest value in the domain of Eq. 2, i.e., it is nonnegative only if \( x\in (0, \alpha ) \), which implies that the value of parameter \( \alpha \) must fulfill the necessity that \( \alpha > max_{i=1,2,3,...,n}(x_{i}) \), see [2]. In this regard, while finding the MLEs we observed that \( \hat{\alpha } \) is larger than the \( max_{i=1,2,3,...,n}(x_{i}) \) for any data set, which can be visualized in the related tables. Moreover, it is noteworthy that data portray an IFR behavior as portrayed in Fig. 10 along with maximum entropy model as exhibited in Table 13. So, such narrative demands a model that can not only model the positive skewness, leptokurtic behavior, IFR but also the maximum entropy issue in a pleasant way. In addition, for drawing valid conclusion, we have grouped the observation by using R as [13,22], (22,41.7], (41.7,73.4], (73.4,87.3], (87.3,98], (98,117], (117,158] and the frequencies are listed as 8, 5, 6, 7, 7, 5, 7, respectively. Moreover, Tables 3 and 15 (see Appendix A2) portray that the developed model is the most suitable one, with least values for all statistics and highest p value for \( \chi ^{2} \) and with the smallest KS statistics. Furthermore, the VTS and histogram that are portrayed in Table 13 and Fig. 11, respectively, also support the above results. Hence, our proposed model seems to be a natural choice for such data sets.

Example 2

This data set is extracted from the book [34](pp. 12). This data set mentions the death times (in weeks) of patients with cancer (Aneuploid Tumor) of the tongue, with the measurements: 1, 3, 3, 4, 10, 13, 13, 16, 16, 24, 26, 27, 28, 30, 30, 32, 41, 51, 61, 65, 67, 70, 72, 73, 74, 77, 79, 80, 81, 87, 87, 88, 89, 91, 93, 93, 96, 97, 100, 101, 104, 104, 108, 109, 120, 131, 150, 157, 167, 231, 240, 400.

Table 4 Data set II descriptive summary
Full size table
Table 5 Data set II theoretical measures
Full size table
Table 6 Data set II goodness-of-fit measure based on listed MLEs
Full size table
Fig. 11
figure 11

Histogram of data set I and II

Full size image

Discussion on the Fit of Data Set II It is evident from Table 4 that the data portray a maximum entropy, see Table 14, positive skewness and high kurtosis in such a way that skewness to kurtosis ratio is 0.2131. However, the theoretical aspect as given in Table 6 also portrays the same results. But Table 13 endorses both positive and negative entropies. Moreover, Table 5 also affirms the above statement. In addition, we have made frequency distribution of the above data set by R computational package.  For this purpose, we have created different classes, such as [1,16], (16,31.1, (31.1,71.7], (71.7,87], (87,96.4],(96.4,117],(117,400] along with respective frequencies 9, 6, 7, 9, 6, 7, 8. In this regard, Tables 6 and 16 (see Appendix A2) display that the proposed model is highly recommended in moderate tailed behavior and BTS data set as portrayed in 10. Also, these tables provide enough evidence about the appropriateness of the proposed model, with reasonably small values of all the statistics with least loss of information attitude by depicting minimum value of all information criteria. Furthermore, Vuong test statistics and histogram as portrayed in Table 13 and Fig. 11, respectively, indicate that the MWD and 3P WD are reasonably good competitors of the proposed model. Moreover, our claims are further consolidated by the above findings.

Example 3

The third data set is extracted from the book [34](pp. 12). This data set mentions the death times (in weeks) of patients with cancer (Aneuploid Tumor) of the tongue, with measurements: 159, 189, 191, 198, 200, 207, 220, 235, 245, 250, 256, 261, 265, 266, 280, 343, 356, 383, 403, 414, 428, 432, 317, 318, 399, 495, 525, 536, 549, 552, 554, 557, 558, 571, 586, 594, 596, 605, 612, 621, 628, 631, 636, 643, 647, 648, 649, 661, 663, 666, 670, 695, 697, 700, 705, 712, 713, 738, 748, 753, 40, 42, 51, 62, 163, 179, 206, 222, 228, 249, 252, 282, 324, 333, 341, 366, 385, 407, 420, 431, 441, 461, 462, 482, 517, 517, 524, 564, 567, 586, 619, 620, 621, 622, 647, 651, 686, 761, 763.

Table 7 Data set III descriptive summary
Full size table
Table 8 Data set III theoretical measures
Full size table
Table 9 Data set III goodness-of-fit measure based on listed MLEs
Full size table

Discussion About the Third Data Set From Tables 7  and 8, the theoretical and observed descriptive statistics show a remarkable closeness to each other and it seems that third data set is being simulated by the proposed model. Furthermore, BFR can be observed from Fig. 10. For more authoritative advocacy of the proposed model, we have calculated the \( \chi ^{2} \) by making classes of data set via the command bins of R computational package as [40,238], (238,352], (352,495], (495,595], (595,650], (650,763] with the respective frequencies 17, 16, 17, 16, 17,17. Moreover, from Tables 9 and 17 (see Appendix A2), it is evident that our proposed model gives more viable results as compare to the competing models.

Example 4

The fourth data set measures the exact times of failure which is reported by [35] with the measurements:14, 34, 59, 61, 69, 80, 123, 142, 165, 210, 381, 464, 479, 556, 574, 839, 917, 969, 991, 1064, 1088, 1091, 1174, 1270, 1275, 1355, 1397, 1477, 1578, 1649, 1702, 1893, 1932, 2001, 2161, 2292, 2326, 2337, 2628, 2785, 2811, 2886, 2993, 3122, 3248, 3715, 3790, 3857, 3912, 4100, 4106, 4116, 4315, 4510, 4584, 5267, 5299, 5583, 6065, 9701.

Table 10 Data set IV descriptive summary
Full size table
Table 11 Data set IV theoretical measures
Full size table
Table 12 Data set IV goodness-of-fit measure based on listed MLEs
Full size table

Discussion and Analysis of the Fourth Data It is evident from Tables 10 and 11  that the theoretical and empirical measures are closely associated, indicating positive skewness and high kurtosis behaviors. Therefore, these data require a model that can work very well in positively skewed, moderate kurtosis and BFR distributions, as shown in Fig. 10. Furthermore, grouped data with the classes such as [14,184], (184,962], (962,1370], (1370,2120], (2120,3010],(3010,4110], (4110,9701]   and the observed frequencies of each class, which are 9, 8, 9, 8, 9, 8, 9, respectively, also used for comparison purposes. So in this regard, Tables 12 and 18 (see Appendix A2) portray the comparison of the compared distributions. From these tables, it is evident that our proposed model is the suitable one, with least values for all statistics and highest p value for \(\chi ^{2}\) statistics. However, encouraging aspects for the proposed model are its VTS values that ensure that our proposed model is better strategy than other competing models (Fig. 12, Table 13).

Comparison Via Vuong Test The brief summary of theVTS is portrayed in Table 14, where the possible paired values of the FLD with their competitor models are given. From these values, it is clear that the proposed model is suitable choice among these best competitors. Moreover, another encouraging aspect of the proposed model is having a least loss of information model which can be seen from Tables 15, 16, 17, and 18 of criterion, see Appendix A2.

Table 13 Theoretical entropy when \(\lambda =0.75 \)
Full size table
Table 14 Comparison via VTS
Full size table
Fig. 12
figure 12

Histogram of data set III and IV

Full size image

6 Conclusion

The Fréchet log-logistic distribution introduced in this study is a notable bounded distribution. It can be used as a restricted substitute for the beta probability model because the unit support model is a limit case of the FLD, which is an uncommon form for a restricted domain model. Thus, this proposed model offers a flexible explanation to the dilemma of demonstrating constrained qualities. We have also shown that the PDF and HRF of the FLD are very accommodating in their curve shapes. The multiple skewed and kurtosis patterns shown in the PDF of the FLD indicate its versatility. We found that the FLD’s HRF can approve a variety of shapes ranging from BTS to IFR with a left skewed J-shape, which normally comprises two phases: the lengthy usable period phase and the wear-out phase. These forms of the FLD’s HRF make this model an appropriate choice for modeling determinations in a wide range of practical issues. The proposed model adopts a mathematically manipulated able form of its fundamental functions, including CDF, HRF, and SF, based on which we also characterize the FLD, indicating that all of the estimated parameters are reliable. Finally, in the applications section, we explored the FLD model for modeling the failure time of a product, device, or human in respective units. Based on the empirical findings, we can infer that this suggested model outperforms the other competing models for all given data sets.