1 Introduction

Modeling of lifetime data is an important issue for statisticians in a wide range of scientific and technological fields such as medicine, engineering, biology, actuarial science, industrial reliability, etc. The basic idea behind compounding is that the lifetime of a system with N(a discrete random variable) components and the lifetime of ith component (say Xi), independent of N, follow several lifetime distributions. Then the maximum (or minimum) time of failures of components of the system depending on the condition whether they are parallel (or in series), see Adamidis and Loukas (1998). By compounding some continuous distributions (such as the exponential, gamma or Weibull distribution) with some discrete distributions (such as binomial, geometric or zero-truncated Poisson), several new distributions were introduced in the literature, for example see Maurya and Nadarajah (2021).

Pareto’s distribution was first proposed for modeling the income data, and then used to analyze the size of city’s population and the firms size. It has also been an appropriate fit to numerous data in many scientific fields such as physics, technology, biology etc., whenever the Pareto’s law is found, for details see Nadarajah (2005). To generate a distribution that has the ability to model lifetimes data with a heavy tail, based on the composition of the Pareto distribution with the class of discrete distributions power series, De Morais (2009) introduced a class of continuous distributions called Pareto power series (PPS). He also discussed various of its statistical properties along with its reliability features. Three special cases of the PPS, called; Pareto-Poisson, Pareto-geometric and Pareto-logarithmic distributions have also been investigated. Moreover, several lifetime distributions have been introduced as an extension of the Pareto distribution, for example, Asgharzadeh et al. (2013) introduced the Pareto Poisson-Lindley distribution and studied several of its properties. Nassar and Nada (2013) presented the beta Pareto-geometric distribution. Elbatal et al. (2017) proposed the exponential Pareto power series distributions.

To the best of our knowledge, we have not encountered any work related to discussing any statistical properties of the Pareto-Poisson (PP) distribution and/or estimating its parameters under complete (or incomplete) sampling. So, by demonstrating that the PP distribution may be used as a survival model utilizing complete and Type-II censored samples, the purpose of this study is to close this gap. The objectives of the present study are three-fold. First, we shall exclusively focus on discussing some several characteristics of the PP distribution such as: quantile function, median, mode, quartiles, mean deviations, moments, generating functions, entropies, mean residual life, order statistics and stress-strength reliability. Second objective aimed to derive both point and interval estimators of the PP parameters, when the scale Pareto parameter is known, using likelihood and Bayesian estimation methods. Two-sided approximate confidence intervals for the unknown parameters, using asymptotic normal approximation of the frequentist estimators, are constructed. Using independent gamma priors, the Bayes estimators of the PP parameters are developed against symmetric and asymmetric loss functions. Since Bayes estimators cannot be obtained analytically, Markov chain Monte Carlo (MCMC) techniques are considered to compute the Bayes estimates and to construct associated highest posterior density intervals are computed. To check the convergence of MCMC chains, Gelman and Rubin’s convergence diagnostic statistic is used. A comparison between the proposed methodologies is made through a simulation study in terms of their root mean squared-error (RMSE), relative absolute bias (RAB), average confidence lengths (ACLs) and coverage probabilities (CPs). Lastly, two real data sets of different features; the first includes the failure times of some mechanical components and the other represents the active repair times for airborne communication transceiver, are discussed to show how the proposed methods can be applied in real practice. Some specific recommendations are also drawn from the numerical findings.

The rest of the paper is organized as follows: In Section 2, we define the PP distribution and its statistical properties. Frequentist and Bayes estimators for parameter estimation are developed in Sections 3 and 4, respectively. The simulation results are reported in Section 5. Section 6 presents two real applications of the proposed distribution. Some conclusions are addressed in Section 7.

2 The Pareto–Poisson Distribution

In this section, we introduce the PP distribution, which is a member of the Pareto power series family of distributions, and investigate some of its useful mathematical and statistical properties such as: moments, entropies, generation function, reliability function, failure rate function, mean residual-life function stress-strength reliability and order statistics.

First suppose that Y1,Y2,...,YN are independent random variables (rv)s following the Pareto distribution whose probability density function (PDF), \(g\left (y;\alpha ,\lambda \right )=\alpha {{\lambda }^{\alpha }}{{y}^{-\left (\alpha +1 \right )}},\ y\geqslant \lambda \), with shape parameter α > 0 and scale parameter λ > 0. Following De Morais (2009), suppose that the index N is a rv follows a distribution in the power series class whose the following probability mass function

$$ P\left( N=n \right)=\frac{{{a}_{n}}{{\beta }^{n}}}{C(\beta )},\ n=1,2,\dots, $$

where an > 0 (depends only on n) and \( C(\beta )=\sum \nolimits _{n=1}^{\infty }{{{a}_{n}}}{{\beta }^{n}},\ \beta >0 \) is finite.

If one set \(X_{(1)}={\min \limits } \left [ {{Y}_{1}},{{Y}_{2}},...,{{Y}_{N}} \right ]\), then the conditional distribution of X(1) given N = n follows the Pareto density with shape parameter nα and scale parameter λ. Then, the cumulative distribution function (CDF) of X(1)|N = n (say G(⋅)) can be defined as

$$ {{G}_{\left. {{X}_{(1)}} \right|N=n}}\left( x \right)=1-{{\left( \frac{\lambda }{x} \right)}^{\alpha n}},\ x\geqslant \lambda , $$
(2.1)

and the joint PDF of X(1) and N (say g(⋅)) is given by

$$ {g}_{(X_{(1)},N)}(x,n)=\frac{\alpha n{{a}_{n}}{{\beta }^{n}}}{xC(\beta )}{{\left( \frac{\lambda }{x} \right)}^{\alpha n}},\ x\geqslant \lambda. $$
(2.2)

Setting n = 1 in Eqs. 2.2 and 2.1, the PDF and CDF of the PPS distribution are given by

$$ f\left( x;\alpha ,\lambda ,\beta \right)=\frac{\alpha \beta {{\lambda }^{\alpha }}{C}^{\prime}\left( \beta {{\left( {\lambda }/{x} \right)}^{\alpha }} \right)}{{{x}^{\alpha +1}}C(\beta )},\ \alpha,\beta>0,\ x\geqslant \lambda, $$
(2.3)

and

$$ F\left( x;\alpha ,\lambda ,\beta \right)=1-\frac{{C}^{\prime}\left( \beta {{\left( {\lambda }/{x} \right)}^{\alpha }} \right)}{C(\beta )},\ \alpha,\beta>0,\ x\geqslant \lambda, $$
(2.4)

respectively.

As a result, by setting C(β) = eβ − 1 and \( {C}^{\prime }(\beta )={{e}^{\beta }} \) in Eqs. 2.3 and 2.4, the PDF and CDF of three-parameter PP distribution are given respectively by

$$ f\left( x;\alpha ,\lambda ,\beta \right)=\frac{\alpha \beta {{\lambda }^{\alpha }}}{{{x}^{\alpha +1}}}\frac{{{e}^{\beta {{\left( \frac{\lambda }{x} \right)}^{\alpha }}}}}{\left( {{e}^{\beta }}-1 \right)},\ \alpha,\beta,\lambda >0,\ x\geqslant\lambda, $$
(2.5)

and

$$ F\left( x;\alpha ,\lambda ,\beta \right)=\frac{{{e}^{\beta }}-{{e}^{\beta {{\left( \frac{\lambda }{x} \right)}^{\alpha }}}}}{\left( {{e}^{\beta }}-1 \right)},\ \alpha,\beta,\lambda >0,\ x\geqslant\lambda, $$
(2.6)

where α is the shape parameter and (β,λ) are the scale parameters. Moreover, when \( \beta \rightarrow {0^{+}} \), the Pareto distribution can be obtained as a special case from the PP distribution.

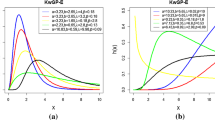
Using some specified values of α, λ and β, some shapes of the PP density function (2.5) are displayed in Fig. 1. It shows that the PP density has a heavy tail. Also, from Eqs. 2.3 and 2.4, one can be easily seen that \( \lim _{x\rightarrow {\infty }} F(t+x)/({{1-{F}(x)}}) = 1 \), which means that the PP distribution has also a long right tail.

Figure 1
figure 1

Several shapes of the PP density using some specific parameter values

Full size image

2.1 Quantile, Median and Mode

To generate random samples from the PP distribution, suppose that U is a rv of standard uniform distribution. From Eq. 2.6, it can be shown that the following transformation of U has a PP distribution. Thus, the quantile function x = Q(p) = F− 1(p), for 0 < p < 1, of the PP distribution is given by

$$ {{x}_{p}}=\lambda {{\left[ \frac{1}{\beta }\log \left[ {{e}^{\beta }}-p\left( {{e}^{\beta }}-1 \right) \right] \right]}^{{-1}/{\alpha } }},\ 0<p<1. $$
(2.7)

In particular, the first, second (median) and third quartiles of the PP distribution (say Q1(⋅), Q2(⋅) and Q3(⋅)) can be obtained by putting p = 0.25, 0.50 and = 0.75 in Eq. 2.7, respectively.

The mode of the PP distribution, x0, is obtained by finding the first derivative of its logarithm PDF, \(\log f\left (x \right )\) with respect to x and equating it to zero. Hence, the mode of the PP distribution is defined by

$$ {{x}_{0}}=\lambda {{\left[-\frac{1}{{\alpha\beta}}{\left( \alpha +1 \right)}\right]}^{{-1}/{\alpha }}}, $$

is always exists and unique.

2.2 Moments

Moments used to describe the characteristics of a distribution, so they are necessary and important in any statistical analysis. So, in this section, the r − th moment about zero of PP distribution is derived. However, the r − th moment \( ({{{\mu }}^{\prime }_{r}}) \) of a rv X has density function (2.5) is given by

$$ \begin{array}{@{}rcl@{}} {{{\mu }}^{\prime}_{r}}=E({{X}^{r}})&=&{\int}_{X}{{{X}^{r}}f(x)dx},\text{ }x\in \mathbb{R}^{+},\\ &=&\frac{\alpha ~\beta ~{{\lambda }^{\alpha }}}{({{e}^{\beta }}-1)}~{\int}_{\lambda }^{\infty }{{{x}^{r-\alpha -1~}}}\exp (\beta {{({\lambda }/{x} )}^{\alpha }})~dx, \end{array} $$
(2.8)

using the following Taylor’s series expansion

$$ \begin{array}{@{}rcl@{}} \exp \left( \beta {{\left( {\lambda }/{x} \right)}^{\alpha }} \right)=\sum\limits_{J=0}^{\infty }{\frac{{{\beta }^{J}}{{\lambda }^{\alpha J}}}{{{x}^{\alpha J}}{\Gamma} (J+1)}}, \end{array} $$
(2.9)

then, from Eqs. 2.8 and 2.9, the r − th moment of PP distribution for r = 1,2,3,... can be expressed as

$$ \begin{array}{@{}rcl@{}} {{{\mu }}^{\prime}_{r}}=\frac{\alpha {{\lambda }^{r}}~}{({{e}^{\beta }}-1)}\sum\limits_{J=0}^{\infty }{\frac{{{\beta }^{J+1}}}{\left( \alpha \left( J+1 \right)-r \right){\Gamma} (J+1)}},\ \alpha >r. \end{array} $$
(2.10)

Setting r = 1, the mean of X, where \(X\sim \text {PP}{(\alpha ,\lambda ,\beta )}\), is

$$ \begin{array}{@{}rcl@{}} {{{\mu }}^{\prime}_{1}}=E\left( X \right)=\frac{\alpha \lambda ~}{({{e}^{\beta }}-1)}\sum\limits_{J=0}^{\infty }{\frac{{{\beta }^{J+1}}}{\left( \alpha \left( J+1 \right)-1 \right){\Gamma} (J+1)}},\ \alpha >1. \end{array} $$
(2.11)

Similarly, setting r = 1 and r = 2, the variance of X is given by \(V(X)={{{\mu }}^{\prime }_{2}}-{{\left ({{{{\mu }}^{\prime }}_{1}} \right )}^{2}}\) where

$$ {{{\mu }}^{\prime}_{2}}=E\left( {{X}^{2}} \right)=\frac{\alpha {{\lambda }^{2}}~}{({{e}^{\beta }}-1)}\sum\limits_{J=0}^{\infty }{\frac{{{\beta }^{J+1}}}{\left( \alpha \left( J+1 \right)-2 \right){\Gamma} (J+1)}},\ \alpha >2. $$

Using the cumulants, denoted by \({\mathcal {C}_{r}}\), the coefficient of skewness and kurtosis can be calculated from the ordinary moments of X. As \(X\sim \text {PP}{(\alpha ,\lambda ,\beta )}\), the first four cumulants of a rv X are given by

$$ {\mathcal{C}_{r}}={{{\mu }}^{\prime}_{r}}-\sum\limits_{i=0}^{r-1}{\left( \begin{array}{lllllll} r-1 \\ i-1 \end{array} \right)}{\mathcal{C}_{i}}{{{\mu }}^{\prime}_{r-i}}. $$
(2.12)

Putting r = 1,2,3,4 into (2.12), then one gets the four cumulants \( \mathcal {C}_{r},\ r=1,2,3,4 \) as

$$ \begin{array}{@{}rcl@{}} {\mathcal{C}_{1}}&=&{{{\mu }}^{\prime}_{1}},\\ {\mathcal{C}_{2}}&=&{{{\mu }}^{\prime}_{2}}-{{\left( {{{{\mu }}^{\prime}}_{1}} \right)}^{2}},\\ {\mathcal{C}_{3}}&=&{{{\mu }}^{\prime}_{3}}-3{{{\mu }}^{\prime}_{2}}{{{\mu }}^{\prime}_{1}}+{{\left( {{{{\mu }}^{\prime}}_{1}} \right)}^{3}},\\ \text{and}\\ {\mathcal{C}_{4}}&=&{{{\mu }}^{\prime}_{4}}-4{{{\mu }}^{\prime}_{3}}{{{\mu }}^{\prime}_{1}}-3{{\left( {{{{\mu }}^{\prime}}_{2}} \right)}^{2}}+12{{{\mu }}^{\prime}_{2}}{{\left( {{{{\mu }}^{\prime}}_{1}} \right)}^{2}}-6{{\left( {{{{\mu }}^{\prime}}_{1}} \right)}^{4}}. \end{array} $$

Once the cumulants \( \mathcal {C}_{2} \), \( \mathcal {C}_{3} \) and \( \mathcal {C}_{3} \) of the PP distribution obtained, the corresponding coefficients of skewness (denoted by κ1), and kurtosis (denoted by κ2), of PP distribution can easily be evaluated, respectively, as \({{\kappa }_{1}}={{\mathcal {C}_{3}}}/{\mathcal {C}_{2}^{{3}/{2}}}\) and \({{\kappa }_{2}}={{\mathcal {C}_{4}}}/{\mathcal {C}_{2}^{2}} \).

2.3 Moment Generating Function

The moment generating (MG) function of X provides the basis of an alternative route to analytic results compared with working directly with the CDF (or PDF) of X. However, the MG function denoted by MX(t), is given by

$$ \begin{array}{@{}rcl@{}} {{M}_{X}}\left( t \right)=E\left( {{e}^{tX}} \right)&={\int}_{-\infty}^{\infty }{{e}^{tx}}f\left( x \right)dx. \end{array} $$
(2.13)

Applying the Maclaurin series expansion for etx, we get \( {{e}^{tx}}=\sum \nolimits _{r=0}^{\infty }{\frac {{{(tx)}^{r}}}{r!}} \). If X is a non-negative rv follows the PP distribution, then (2.13) can be rewritten as

$$ \begin{array}{@{}rcl@{}} {{M}_{X}}\left( t \right)&=&\displaystyle\sum\limits_{r=0}^{\infty }{\text{ }\frac{{{t}^{r}}}{r!}}\text{ }{\int}_{\lambda}^{\infty }{{{x}^{r}}f\left( x \right)dx},\\ &=&\sum\limits_{r=0}^{\infty }{\frac{{{t}^{r}}}{r!}}\text{ }{{{\mu }}^{\prime}_{r}}. \end{array} $$
(2.14)

However, substituting (2.10) in (2.14), the MG function of the PP distribution can be expressed as

$$ {{M}_{X}}\left( t \right)=\sum\limits_{r=0}^{\infty }{\sum\limits_{J=0}^{\infty }{\frac{\alpha {{\lambda }^{r}}{{t}^{r}}~{{\beta }^{J+1}}}{\left( \alpha \left( J+1 \right)-r \right)({{e}^{\beta }}-1)J!r!}}}. $$

Practically, it is easier to work with the logarithm of the MG function which is called the cumulant generating function. Using the MG function for |t| < 1, the cumulant generating function, \({{C}_{X}}\left (t \right )\), of a rv X follows the PP distribution is given by

$$ \begin{array}{@{}rcl@{}} {{C}_{X}}\left( t \right)=\log \left[ {{M}_{X}}\left( t \right) \right]=\log \left[ \sum\limits_{r=0}^{\infty }{\frac{{{t}^{r}}}{r!}}{{{{\mu }}^{\prime}}_{r}} \right]. \end{array} $$
(2.15)

From Eqs. 2.10 and 2.15, the cumulant generating function of PP distribution is given by

$$ {{C}_{r}}\left( t \right)=\log \left[ \sum\limits_{r=0}^{\infty }{\sum\limits_{J=0}^{\infty }{\frac{\alpha {{\lambda }^{r}}{{t}^{r}}~{{\beta }^{J+1}}}{\left( \alpha \left( J+1 \right)-r \right)({{e}^{\beta }}-1)J!r!}}} \right]. $$

2.4 Mean Deviation

The mean deviation about the mean and the median are useful measures of variation for a population. Let μ and M be the mean and median of the PP distribution respectively. The mean deviations about the mean μ (say \({\mathcal {D}_{1}}(X)\)) and about the median M(say \({\mathcal {D}_{2}}(X)\)) can be calculated respectively as

$$ \begin{array}{@{}rcl@{}} {\mathcal{D}_{1}}\left( X \right)=E\left( \left| X-\mu \right| \right)&=&{\int}_{-\infty }^{\infty }{\left| X-\mu \right|f\left( x \right)dx}\\ &=&2\mu F\left( \mu \right)-2\varphi \left( \mu \right), \end{array} $$
(2.16)

and

$$ \begin{array}{@{}rcl@{}} {\mathcal{D}_{2}}\left( X \right)=E\left( \left| X-M \right| \right)&=&{\int}_{-\infty }^{\infty }{\left| X-M \right|f\left( x \right)dx}\\ &=&\mu -2\varphi \left( M \right). \end{array} $$
(2.17)

For short, set \( \eta =\left (\mu \text { or }M \right ) \), using (2.5), one gets

$$ \begin{array}{@{}rcl@{}} \varphi \left( \eta \right)&={\int}_{\lambda }^{\eta }{x f\left( x \right)dx},\\ &=\alpha ~\beta ~{{\lambda }^{\alpha }}~{{({{e}^{\beta }}-1)}^{-1~}}{\int}_{\lambda }^{\eta }{{{x}^{-\alpha ~}}\exp \left( \beta {{\left( {\lambda }/{x} \right)}^{\alpha }} \right)dx}. \end{array} $$
(2.18)

Using the Taylor’s series expansion (2.9), based on some algebraic manipulations, Eq. 2.18 can be rewritten as

$$ \begin{array}{@{}rcl@{}} \varphi \left( \eta \right)=\frac{\alpha }{({{e}^{\beta }}-1)}\sum\limits_{J=0}^{\infty }{\frac{{{\beta }^{J+1}}{{\lambda }^{\alpha (J+1)}}\left[ {{\eta }^{1-\alpha (J+1)}}-{{\lambda }^{1-\alpha (J+1)}} \right]}{(1-\alpha (J+1)){\Gamma} (J+1)}}. \end{array} $$
(2.19)

Substituting (2.19) into (2.16) and (2.17), the mean deviations about the mean μ and about the median M of PP distribution are given, respectively, by

$$ {\mathcal{D}_{1}}\left( X \right)=2\mu \left[ \frac{{{e}^{\beta }}-\exp \left( \beta {{({\lambda }/{\mu } )}^{\alpha }} \right)}{\left( {{e}^{\beta }}-1 \right)} \right]-2\varphi \left( \mu \right), $$

and

$$ {\mathcal{D}_{2}}\left( X \right)=\mu -2\varphi \left( M \right), $$

where φ(μ) and φ(M) can be easily obtained from Eq. 2.19 by replacing η by μ or M, respectively.

2.5 Hazard and Reversed Hazard Functions

The hazard h(⋅) and reverse hazard r(⋅) functions of the PP distribution are given respectively by

$$ \begin{array}{@{}rcl@{}} h\left( x;\alpha,\lambda,\beta\right)& = &\frac{f\left( x;\alpha,\lambda,\beta\right)}{R\left( x;\alpha,\lambda,\beta\right)}\\ & = &\frac{\alpha \beta {{\lambda }^{\alpha }}}{{{x}^{\alpha +1}}}{{\left[ 1\! - \exp \left( \! -\beta {{\left( {\lambda }/{x} \!\right)}^{\alpha }} \right) \right]}^{-1}},\!\ \alpha ,\beta ,\lambda \!>\!0,\ \!\!x\!\geqslant\!\lambda, \end{array} $$
(2.20)

and

$$ \begin{array}{@{}rcl@{}} r\left( x;\alpha,\lambda,\beta\right)&=&\frac{f\left( x;\alpha,\lambda,\beta\right)}{F\left( x;\alpha,\lambda,\beta\right)}\\ &=&\frac{\alpha \beta {{\lambda }^{\alpha }}}{{{x}^{\alpha +1}}}{{\left[ \exp \left( -\beta \left[ {{\left( {\lambda }/{x} \right)}^{\alpha }}-1 \right] \right)-1 \right]}^{-1}},\ \alpha ,\beta ,\lambda >0,\ x\geqslant\lambda, \end{array} $$

where F(⋅), f(⋅) and R(⋅) are obtained in Eqs. 2.1, 2.2 and 2.23, respectively.

To show that h(⋅) is monotonically decreasing function depending on the PP parameters, the Glaser’s theorem is used, see Glaser (1980). First, define the following function

$$ \phi(x)=-\frac{{f}^{\prime}\left( x;\alpha ,\lambda ,\beta \right)}{f\left( x;\alpha ,\lambda ,\beta \right)}, $$
(2.21)

where \( {f}^{\prime }(x) \) is the first derivative of f(x) with respect to x.

From Eq. 2.5, Eq. 2.21 is equivalent straightforward to

$$ \phi(x)={{x}^{-1}}\left[ \alpha \beta {{\lambda }^{\alpha }}{{x}^{-\alpha }}+\alpha +1 \right], $$

then its first derivative will be

$$ \phi^{\prime}(x)=-{{x}^{-2}}\left[\alpha(\alpha+1)\beta {{\lambda }^{\alpha }}{{x}^{-\alpha }}+\alpha +1 \right]. $$
(2.22)

From Eq. 2.22, it can be easily seen that the hazard function of PP distribution, for 0 < α < 1, is decreasing function for all given x > 0 values. Plots of hazard function (2.20) for various values of the model parameters α, β and λ are displayed in Fig. 2. It shows that the hazard rate plots of the PP distribution have decreasing shape in x for all given values of α, β and λ.

Figure 2
figure 2

Hazard rate of the PP distribution using some specific parameter values

Full size image

2.6 Reliability and Mean Residual Life

The reliability (or survival) R(⋅) function of PP distribution is given by

$$ \begin{array}{@{}rcl@{}} R\left( x;\alpha,\lambda,\beta\right)&=&1-F\left( x;\alpha,\lambda,\beta\right)\\ &=&\frac{\exp \left( \beta {{\left( {\lambda }/{x} \right)}^{\alpha }} \right)-1}{\left( {{e}^{\beta }}-1 \right)},\ \alpha ,\beta ,\lambda >0,\ x\geqslant\lambda. \end{array} $$
(2.23)

In the context of reliability studies, the mean-residual-life mR(⋅) function is known as the average remaining life span, which is a component survived up to distinct time t is defined as

$$ \begin{array}{@{}rcl@{}} {{m}_{R}}(t)&=&\frac{1}{R\left( t \right)}\left( {\int}_{t}^{\infty }{xf\left( x \right)dx}-t \right)\\ &=&\frac{1}{R\left( t \right)}\left( {{{{\mu }}^{\prime}}_{1}}-t-{{\int}_{0}^{t}}{xf\left( x \right)dx} \right),\ t>0, \end{array} $$
(2.24)

where R(t) and \( {{{\mu }}^{\prime }_{1}} \) are defined in Eqs. 2.23 and 2.11, respectively.

However, let X be a PP lifetime rv, then the mean-residual-life of X is given by

$$ {{m}_{R}}(t)=\frac{1}{R\left( t \right)}\left( {{{{\mu }}^{\prime}}_{1}}-t-\alpha \sum\limits_{J=0}^{\infty }{\frac{{{\beta }^{J+1}}{{\lambda }^{\alpha \left( J+1 \right)}}{{t}^{1-\alpha \left( J+1 \right)}}}{\left( {{e}^{\beta }}-1 \right)\left( 1-\alpha \left( J+1 \right) \right){\Gamma} (J+1)}} \right),\ t>0. $$

2.7 Entropies

Entropy is an important metric used to measure the amount of uncertainty associated with a rv X. It has been used in many fields such as survival analysis, information theory, computer science and econometrics. So, this section deals with two well-known entropies namely Rényi and δ-entropies. Recently, the considered entropies have also been discussed by Amigó et al. (2018) and Elshahhat et al. (2021).

The Rényi entropy of ζth order, say ρζ, is defined as

$$ {{\rho }_{\zeta }}(x)=\frac{1}{1-\zeta }\log \left( {\int}_{-\infty }^{\infty }{{{\left( f\left( x \right) \right)}^{\zeta }}dx} \right),\text{ }\zeta >0,\text{ }\zeta \ne \text{1}. $$

If \( X\sim \text {PP}(\alpha ,\beta ,\lambda ) \), using the Taylor’s series expansion (2.9), we get

$$ \begin{array}{@{}rcl@{}} {\int}_{\lambda }^{\infty }{{{\left( f\left( x \right) \right)}^{\zeta }}dx}& = &{\int}_{\lambda }^{\infty }{{{\left[ \frac{\alpha \beta {{\lambda }^{\alpha }}}{{{x}^{\alpha +1}}}\frac{\exp \left( \beta {{\left( {\lambda }/{x} \right)}^{\alpha }} \right)}{\left( {{e}^{\beta }}-1 \right)} \right]}^{\zeta }}}dx\\ & = &{{\alpha }^{\zeta }}{{\beta }^{\zeta }}{{\lambda }^{\zeta \alpha }}{{\left( {{e}^{\beta }} - 1 \right)}^{-\zeta }}{\int}_{\lambda }^{\infty }{{{x}^{-\zeta \left( \alpha +1 \right)}}\exp \left( \zeta \beta {{\left( {\lambda }/{x} \right)}^{\alpha }} \right)dx}\\ & = &{{\alpha }^{\zeta }}{{\left( {{e}^{\beta }} - 1 \right)}^{-\zeta }}\sum\limits_{J=0}^{\infty }{\frac{{{\zeta }^{J}}{{\beta }^{\zeta +J}}{{\lambda }^{\alpha \left( J+\zeta \right)}}}{\Gamma (J + 1)}}\left[ \frac{{{\lambda }^{{{J}^{*}}}}}{\zeta \left( \alpha + 1 \right) + \alpha J - 1} \right], \end{array} $$
(2.25)

where \( {{J}^{*}}=1-\zeta \left (\alpha +1 \right )-\alpha J. \)

Hence, from Eq. 2.25, the Rényi entropy of X becomes

$$ {{\rho }_{\zeta }}(x)=\frac{1}{1-\zeta }\log \left( {{\alpha }^{\zeta }}{{\left( {{e}^{\beta }}-1 \right)}^{-\zeta }}\sum\limits_{J=0}^{\infty }{\frac{{{\zeta }^{J}}{{\beta }^{\zeta +J}}{{\lambda }^{\alpha \left( J+\zeta \right)+{{J}^{*}}}}}{\left( \zeta \left( \alpha +1 \right)+\alpha J-1 \right){\Gamma} (J+1)}} \right),\text{ }\zeta >0,\text{ }\zeta \ne \text{1}\text{.} $$
(2.26)

Thus, the δ-entropy, denoted by \( {{I}_{\delta }}\left (X \right ) \), of a lifetime rv X follows PP(α,β, λ) is given by

$$ {{I}_{\delta }}\left( X \right)=\frac{1}{\delta -1}\log \left( 1-{\int}_{0}^{\infty }{{{\left( f\left( x \right) \right)}^{\delta }}dx} \right),\ \delta >0,\ \delta \ne \text{1,} $$

and then it follows the Rényi entropy given by Eq. 2.26.

2.8 Order Statistics

In this subsection, closed-form expressions for the PDF and CDF of the rth order statistic of the PP distribution are obtained. In particular, the distribution of the smallest X(1) and largest X(n) order statistics are also obtained. Suppose \({{X}_{(1)}}\leqslant {{X}_{(2)}}\leqslant \cdots \leqslant {{X}_{(n)}}\) represent the order statistics of a random sample of size n obtained from Eqs. 2.5 and 2.6.

Thus, the PDF and CDF of \({{X}_{(r)}},\ r=1,2,\dots ,n,\) denoted by f(r)(x) and F(r)(x) are given respectively by

$$ \begin{array}{@{}rcl@{}} {{f}_{\left( r \right)}}\left( x \right)&=&C_{r}^{-1}f\left( x \right){{\left( F\left( x \right) \right)}^{r-1}}{{\left[ 1-F\left( x \right) \right]}^{n-r}}\\ &=&C_{r}^{-1}\sum\limits_{q=0}^{n-r}{{{\left( -1 \right)}^{q}}\left( \begin{array}{lllllll} n-r \\ q \end{array} \right)}\text{ }f\left( x \right){{\left[ F\left( x \right) \right]}^{r+q-1}}, \end{array} $$
(2.27)

and

$$ \begin{array}{@{}rcl@{}} {{F}_{\left( r \right)}}\left( x \right)=\Pr \left( {{X}_{\left( r \right)}}\le x \right)&=&\sum\limits_{r=0}^{n}{\left( \begin{array}{lllllll} n \\ r \end{array} \right)}{{\left( F\left( x \right) \right)}^{r}}{{\left[ 1-F\left( x \right) \right]}^{n-r}}\\ &=&\sum\limits_{r=0}^{n}{\sum\limits_{q=0}^{n-r}{{{\left( -1 \right)}^{q}}}\left( \begin{array}{lllllll} n \\ r \end{array} \right)\left( \begin{array}{lllllll} n-r \\ q \end{array} \right)}{{\left( F\left( x \right) \right)}^{r+q}}, \end{array} $$
(2.28)

where \({{C}_{r}}=B\left (r,n-r+1 \right )\).

Substituting (2.) and (2.6) into (2.27) and (2.28), the PDF of the rth order statistic from PP distribution is given by

$$ {{f}_{(r)}}\left( x \right) = C_{r}^{-1}\sum\limits_{q=0}^{n-r}{{{\left( -1 \right)}^{q}}\left( \begin{array}{lllllll} n - r \\ q \end{array} \right)}\frac{\alpha \beta {{\lambda }^{\alpha }}\exp \left( \beta {{\left( {\lambda }/{x} \right)}^{\alpha }} \right)}{{{x}^{\alpha +1}}{{\left( {{e}^{\beta }} - 1 \right)}^{r+q}}}{{\left[ {{e}^{\beta }} - {{e}^{\beta {{\left( {\lambda }/{x} \right)}^{\alpha }}}} \right]}^{r+q-1}}, $$
(2.29)

and

$$ {{F}_{(r)}}\left( x \right)=\sum\limits_{r=0}^{n}{\sum\limits_{q=0}^{n-r}{{{\left( -1 \right)}^{q}}}\left( \begin{array}{lllllll} n \\ r \end{array} \right)\left( \begin{array}{lllllll} n-r \\ q \end{array} \right)}{{\left[ \frac{{{e}^{\beta }}-{{e}^{\beta {{\left( {\lambda }/{x} \right)}^{\alpha }}}}}{\left( {{e}^{\beta }}-1 \right)} \right]}^{r+q}}. $$
(2.30)

In particular, by setting r = 1 and r = n in Eqs. 2.29 and 2.30, the PDFs of smallest X(1) and largest X(n) order statistics are given, respectively, by

$$ {{f}_{\left( 1 \right)}}\left( x \right)=C_{1}^{-1}\sum\limits_{q=0}^{n-1}{{{\left( -1 \right)}^{q}}\left( \begin{array}{lllllll} n-1 \\ q \end{array} \right)}\frac{\alpha \beta {{\lambda }^{\alpha }}}{{{x}^{\alpha +1}}}\frac{{{e}^{\beta {{\left( {\lambda }/{x} \right)}^{\alpha }}}}}{\left( {{e}^{\beta }}-1 \right)}{{\left[ \frac{{{e}^{\beta }}-{{e}^{\beta {{\left( {\lambda }/{x} \right)}^{\alpha }}}}}{\left( {{e}^{\beta }}-1 \right)} \right]}^{q}}, $$

and

$$ {{f}_{\left( n \right)}}\left( x \right)=C_{n}^{-1}\frac{\alpha \beta {{\lambda }^{\alpha }}}{{{x}^{\alpha +1}}}\frac{{{e}^{\beta {{\left( {\lambda }/{x} \right)}^{\alpha }}}}}{\left( {{e}^{\beta }}-1 \right)}{{\left[ \frac{{{e}^{\beta }}-{{e}^{\beta {{\left( {\lambda }/{x} \right)}^{\alpha }}}}}{\left( {{e}^{\beta }}-1 \right)} \right]}^{n-1}}. $$

2.9 Stress-Strength Reliability

Stress-strength model describes the life of a component which has a random strength (say X1) that is subjected to a random stress (say X2). The component fails when the stress applied to it exceeds the strength and it continues to operate satisfactorily whenever X1 > X2.

Suppose X1 and X2 have independent PP rv s such as \( {{X}_{1}}\sim {\text {PP}}\left ({{\alpha }_{1}}, \lambda ,{{\beta }_{1}} \right ) \) and \( {{X}_{2}}\sim {\text {PP}}\left ({{\alpha }_{2}}, \lambda ,{{\beta }_{2}} \right ) \). Then the stress-strength parameter, say \( \mathcal {R} \), where \( \mathcal {R}=\Pr \left ({{X}_{1}}>{{X}_{2}} \right ) \), is defined as

$$ \mathcal{R}={\int}_{0}^{\infty }{{{f}_{1}}\left( x \right){{F}_{2}}\left( x \right)dx}. $$
(2.31)

However, using Eqs. 2.5 and 2.6, the PDF and CDF of X1 and X2 can be expressed, respectively, as

$$ {{f}_{1}}\left( x \right)=\frac{{{\alpha }_{1}}{{\beta }_{1}}{{\lambda }^{{{\alpha }_{1}}}}}{{{x}^{{{\alpha }_{1}}+1}}}\frac{\exp \left( {{\beta }_{1}}{{\left( {\lambda }/{x} \right)}^{{{\alpha }_{1}}}} \right)}{\left( {{e}^{{{\beta }_{1}}}}-1 \right)},\ {{\alpha }_{1}},{{\beta }_{1}}>0,\text{ }x\geqslant\lambda , $$
(2.32)

and

$$ {{F}_{2}}\left( x \right)=\frac{{{e}^{{{\beta }_{2}}}}-\exp \left( {{\beta }_{2}}{{\left( {\lambda }/{x} \right)}^{{{\alpha }_{2}}}} \right)}{\left( {{e}^{{{\beta }_{2}}}}-1 \right)},\text{}{{\alpha }_{2}},{{\beta }_{2}}>0,\ x\geqslant\lambda, $$
(2.33)

where α1 and α2 are the shape parameters and β1,β2 and λ are the scale parameters.

Substituting (2.32) and (2.33) into (2.31), the stress-strength parameter \( \mathcal {R} \) becomes

$$ \begin{array}{@{}rcl@{}} \mathcal{R}&=&\frac{{{\alpha }_{1}}{{\beta }_{1}}{{\lambda }^{{{\alpha }_{1}}}}}{\left( {{e}^{{{\beta }_{1}}}}-1 \right)\left( {{e}^{{{\beta }_{2}}}}-1 \right)}{\int}_{\lambda }^{\infty }{\frac{1}{{{x}^{{{\alpha }_{1}}+1}}}\exp \left( {{\beta }_{1}}{{\left( {\lambda }/{x} \right)}^{{{\alpha }_{1}}}} \right)}\left[ \exp \left( {{\beta }_{2}} \right)\right.\\ &&\left.-\exp \left( {{\beta }_{2}}{{\left( {\lambda }/{x} \right)}^{{{\alpha }_{2}}}} \right) \right]dx. \end{array} $$
(2.34)

For the integral term in Eq. 2.34 (say \( \mathcal {G} \)), using the Taylor’s series expansion (2.9), after some algebraic manipulations, we get

$$ \begin{array}{@{}rcl@{}} \mathcal{G}&=&\sum\limits_{J=0}^{\infty }{\frac{{\beta_{1}^{J}}{{\lambda }^{{{\alpha }_{1}}J}}{{e}^{{{\beta }_{2}}}}}{\Gamma (J+1)}{\int}_{\lambda }^{\infty }{{{x}^{-{{\alpha }_{1}}(J+1)-1}}dx}}\\ &&-\sum\limits_{J=0}^{\infty }{\sum\limits_{s=0}^{\infty }{\frac{{\beta_{1}^{J}}{\beta_{2}^{s}}{{\lambda }^{{{\alpha }_{1}}J}}{{\lambda }^{{{\alpha }_{2}}s}}}{\Gamma (J+1){\Gamma} (s+1)}{\int}_{\lambda }^{\infty }{{{x}^{-{{\alpha }_{1}}(J+1)-{{\alpha }_{2}}s-1}}dx}}}\\ &=&\sum\limits_{J=0}^{\infty }{\frac{{\beta_{1}^{J}}{{\lambda }^{{{\alpha }_{1}}J}}{{e}^{{{\beta }_{2}}}}}{\Gamma (J+1)}\left[ \frac{{{\lambda }^{-{{\alpha }_{1}}(J+1)}}}{{{\alpha }_{1}}(J+1)} \right]}\\ &&-\sum\limits_{J=0}^{\infty }{\sum\limits_{s=0}^{\infty }{\frac{{\beta_{1}^{J}}{\beta_{2}^{s}}{{\lambda }^{{{\alpha }_{1}}J}}{{\lambda }^{{{\alpha }_{2}}s}}}{\Gamma (J+1){\Gamma} (s+1)}\left[ \frac{{{\lambda }^{-{{\alpha }_{1}}(J+1)-{{\alpha }_{2}}s}}}{{{\alpha }_{1}}(J+1)+{{\alpha }_{2}}s} \right]}}. \end{array} $$
(2.35)

Thus, using (2.35), the stress-strength parameter \( \mathcal {R} \) of PP distribution is given by

$$ \begin{array}{@{}rcl@{}} \mathcal{R}&=&\frac{{{\alpha }_{1}}{{\beta }_{1}}{{\lambda }^{{{\alpha }_{1}}}}}{\left( {{e}^{{{\beta }_{1}}}}-1 \right)\left( {{e}^{{{\beta }_{2}}}}-1 \right)}\left[ \sum\limits_{J=0}^{\infty }{{{\psi }_{J}}\left( \lambda ,{{\alpha }_{1}},{{\beta }_{1}},{{\beta }_{2}} \right)}\right.\\ &&\left.-\sum\limits_{J=0}^{\infty }{\sum\limits_{s=0}^{\infty }{{{\psi }_{J,s}}\left( \lambda ,{{\alpha }_{1}},{{\alpha }_{2}},{{\beta }_{1}},{{\beta }_{2}} \right)}} \right], \end{array} $$
(2.6)

where \( {{\psi }_{J}}\left (\lambda ,{{\alpha }_{1}},{{\beta }_{1}},{{\beta }_{2}} \right )=\frac {{\beta _{1}^{J}}{{\lambda }^{-{{\alpha }_{1}}}}{{e}^{{{\beta }_{2}}}}}{{{\alpha }_{1}}(J+1){\Gamma } (J+1)} \) and \( {{\psi }_{J,s}}\left (\lambda ,{{\alpha }_{1}},{{\alpha }_{2}},{{\beta }_{1}},{{\beta }_{2}} \right )=\) \(\frac {{\beta _{1}^{J}}{\beta _{2}^{s}}{{\lambda }^{-{{\alpha }_{1}}}}}{\left ({{\alpha }_{1}}(J+1)+{{\alpha }_{2}}s \right ){\Gamma } (J+1){\Gamma } (s+1)} \).

The likelihood estimation method is the most widely-used in statistical inference and the associated estimators included various desirable properties such as efficiency, consistency, invariance property and convergence properties as well as its intuitive appeal. When the prior information of test items exists, the Bayesian procedure provide some advantages compared with the traditional likelihood technique. One of the most common censoring plans in reliability experiments is termed as Type-II censoring. This censoring has several advantages, for example; (i) reducing the test cost, (ii) reaching a test decision in shorter time and/or with fewer observations, and (iii) the remaining units removed early can be used for other tests. Therefore, in the next two sections, we shall be considering the maximum likelihood and Bayesian estimation methods to derive both point and interval estimators of the unknown PP parameters in presence of data collected under Type-II censoring. Following De Morais (2009), we assume that the PP distribution involves only two unknown parameters α and β, while the scale λ parameter is assumed known.

3 Maximum Likelihood Estimators

Under Type-II (or failure) censoring, the life-test terminated after a specified number of failures (say k) is reached. Suppose that \( \underline {\mathbf {x}}=({{X}_{(1)}},{{X}_{(2)}},...,\) X(k)) is Type-II censored sample of size k obtained from a life-test of n independent units (put on a test at time) taken from a continuous population. Hence, following Lawless (2003), the likelihood function of Type-II censored sample, \( X_{(i)},\ i=1,2,\dots ,k \), is defined as

$$ L(\underline{\mathbf{x}}|\theta)=\frac{n!}{(n-k)!}\underset{i=1}{\overset{k}{\mathop{\Pi}}}\left[f({{x}_{(i)}};\theta)\right]{{\left[1-F({{x}_{(k)}};\theta)\right]}^{n-k}}. $$
(3.1)

If one setting k = n in Eq. 3.1, the Type-II censoring returned to the complete sampling. However, suppose that \( \underline {\mathbf {x}} \) lifetimes being identically distributed having PDF and CDF of PP distribution as defined in Eqs. 2.5 and 2.6, respectively, then the likelihood function (3.1) can be written (up to proportional) as

$$ L\left( \underline{\mathbf{x}}|\alpha,\beta \right)\propto \frac{{{\left( \alpha \beta {{\lambda }^{\alpha }} \right)}^{k}}}{{{\left( {{e}^{\beta }}-1 \right)}^{n}}}\exp \left( \beta \sum\nolimits_{i=1}^{k}{{{(\lambda{x_{(i)}^{-1}})}^{\alpha }}} \right){{\left[ \exp \left( \beta {{(\lambda{x_{(k)}^{-1}})}^{\alpha }} \right)-1 \right]}^{n-k}}\underset{i=1}{\overset{k}{\mathop{\Pi }}} x_{\left( i \right)}^{-\alpha }. $$
(3.2)

The corresponding log-likelihood function, \( \ell (\cdot )\propto \log L(\cdot ) \), of Eq. 3.2 becomes

$$ \begin{array}{@{}rcl@{}} \ell \left( \underline{\mathbf{x}}|\alpha,\beta \right)&\!\propto& k\log \left( \alpha \beta {{\lambda }^{\alpha }} \right)-n\log \left( {{e}^{\beta }}-1 \right)-\alpha \sum\nolimits_{i=1}^{k}{\log }\left( {{x}_{\left( i \right)}} \right) \\ &&\!+\beta \sum\nolimits_{i=1}^{k}{{{\!(\lambda{x_{(i)}^{-1}} )}^{\alpha }}} + \left( n - k \right)\log \left[ \exp\! \left( \beta {{(\lambda{x_{(k)}^{-1}} )}^{\alpha }} \right)\! - \!1 \right]\!. \end{array} $$
(3.3)

Upon differentiating (3.3) partially with respect to α and β, we have two likelihood equations as

$$ \begin{array}{@{}rcl@{}} \frac{\partial \ell }{\partial \alpha }&=\frac{k}{\alpha }+k\log (\lambda)-\sum\nolimits_{i=1}^{k}{\log }({{x}_{(i)}})+\beta \sum\nolimits_{i=1}^{k}{{{(\lambda{x_{(i)}^{-1}})}^{\alpha }}}\log (\lambda{x_{(i)}^{-1}} ) \\ &+\beta (n-k ){{(\lambda{x_{(k)}^{-1}})}^{\alpha }}\log (\lambda{x_{(k)}^{-1}})e^{\beta {{(\lambda{x_{(k)}^{-1}} )}^{\alpha }} }{{\left[e^{\beta {{(\lambda{x_{(k)}^{-1}})}^{\alpha }}}-1 \right]}^{-1}}, \end{array} $$
(3.4)

and

$$ \begin{array}{@{}rcl@{}} \frac{\partial \ell }{\partial \beta }&=&\frac{k}{\beta }-\frac{n{{e}^{\beta }}}{({{e}^{\beta }}-1)}+\sum\nolimits_{i=1}^{k}{{{(\lambda{x_{(i)}^{-1}})}^{\alpha }}}\\ &&+(n-k){{(\lambda{x_{(k)}^{-1}})}^{\alpha }}e^{\beta {{(\lambda{x_{(k)}^{-1}})}^{\alpha }}}{{\left[e^{\beta {{(\lambda{x_{(k)}^{-1}})}^{\alpha }}}-1 \right]}^{-1}}. \end{array} $$
(3.5)

It can be seen that, from Eqs. 3.4 and 3.5, the MLEs \(\hat {\alpha }\) and \( \hat {\beta } \) have been derived in a system of two nonlinear equations, respectively. Thus, a very simple iterative method like Newton-Raphson (N-R) procedure may be used to maximize Eqs. 3.4 and 3.5 to obtain the desired MLEs of α and β. Unfortunately, due to the MLEs of \(\hat {\alpha }\) and \( \hat {\beta } \) cannot be obtained in closed form, then the corresponding exact distribution (or exact confidence intervals) of α and β is also not available. Numerically, we suggest to apply the ’maxLik’ package for any given data set \( x_{(i)},\ i = 1,2,\dots ,k, \) proposed by Henningsen and Toomet (2011). This package utilizes the N-R iterative method via ‘maxNR()’ function to implement the maximum likelihood calculations of \(\hat {\alpha }\) and \( \hat {\beta } \). On the other hand, the EM algorithm can also be easily incorporated to estimate the target parameters.

To construct the 100(1 − γ)% two-sided asymptotic confidence intervals (ACIs) of α and β, the Fisher’s information matrix, Iij(⋅), i,j = 1,2, of their MLEs must be obtained as

$$ {{\mathbf{I}}_{ij}}({\Theta})=E\left[-\frac{{{\partial }^{2}}\ell \left( \left. \mathbf{\underline{x}}\right|{\Theta} \right)}{\partial {{\theta_{i}}\partial{\theta_{j}}}} \right],\ i,j=1,2,\ {\Theta }={{({\alpha },{\beta })}^{\mathbf{T}}}. $$
(3.6)

Clearly, the exact solutions of the expectation in Eq. 3.6 is tedious to obtain. Hence, by dropping E in Eq. 3.6, the approximated variances and covariances of \(\hat {\alpha }\) and \( \hat {\beta } \) are given by

$$ {{\mathbf{I}}^{-1}}(\hat{\Theta })=\left[ \begin{array}{lllllll} -{\mathcal{L}_{\alpha \alpha }} & -{\mathcal{L}_{\alpha \beta }} \\ -{\mathcal{L}_{\beta \alpha }} & -{\mathcal{L}_{\beta \beta }} \end{array} \right]_{\left( \hat{\alpha },\hat{\beta } \right)}^{-1}=\left[ \begin{array}{lllllll} {{{\hat{\sigma }}}^{2}}_{{\hat{\alpha }}} & {{{\hat{\sigma }}}_{\hat{\alpha }\hat{\beta }}} \\ {{{\hat{\sigma }}}_{\hat{\beta }\hat{\alpha }}} & {{{\hat{\sigma }}}^{2}}_{{\hat{\beta }}} \end{array} \right]. $$
(3.7)

Taking the second-partial derivative of Eq. 3.3 with respect to α and β, the Fisher’s elements of Eq. 3.7, locally at their MLEs \(\hat {\alpha }\) and \( \hat {\beta } \), are given by

$$ \begin{array}{@{}rcl@{}} {\mathcal{L}_{\alpha \alpha }}&=-\frac{k}{{{\alpha }^{2}}}+\beta \sum\nolimits_{i=1}^{k}{{{(\lambda x_{(i)}^{-1} )}^{\alpha }}}{{\log }^{2}}(\lambda x_{(i)}^{-1} )+\beta (n-k ){{(\lambda x_{(k)}^{-1} )}^{\alpha }}{{\log }^{2}}(\lambda x_{(k)}^{-1} ) \\ & \times {{e}^{\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}}}\left[ {{e}^{\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}}}-\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}-1 \right]{{\left[ {{e}^{\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}}}-1 \right]}^{-2}}, \end{array} $$
(3.8)
$$ \begin{array}{@{}rcl@{}} {\mathcal{L}_{\beta \beta }}=-\frac{k}{{{\beta }^{2}}}+\frac{n{{e}^{\beta }}}{{{({{e}^{\beta }}-1 )}^{2}}} - (n-k ){{(\lambda x_{(k)}^{-1})}^{2\alpha }}{{e}^{\beta {{(\lambda x_{(k)}^{-1})}^{\alpha }}}}{{\left[ {{e}^{\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}}} - 1 \right]}^{-2}}, \end{array} $$
(3.9)

and

$$ \begin{array}{@{}rcl@{}} {\mathcal{L}_{\alpha \beta }}&=\sum\nolimits_{i=1}^{k}{{{(\lambda x_{(i)}^{-1} )}^{\alpha }}}\log (\lambda x_{(i)}^{-1} )+(n-k){{(\lambda x_{(k)}^{-1} )}^{\alpha }}\log (\lambda x_{(k)}^{-1} ) \\ &\times {{e}^{\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}}}\left[ {{e}^{\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}}}-\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}-1 \right]{{\left[ {{e}^{\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }}}}-1 \right]}^{-2}}. \end{array} $$
(3.10)

To evaluate the MLEs \( \hat \alpha \) and \( \hat \beta \) for any given data set (X(1),X(2),...,X(k)), the ‘maxLik’ package that utilizes the N-R iterative method in computations, proposed by Henningsen and Toomet (2011), is recommended. In N-R iterative, from the parameter space limits, the initial value of each unknown parameter is taken.

Under some regularity conditions, the asymptotic normality of MLEs \( \hat {\Theta } \) is approximately bivariate normal as \( \hat {\Theta }\sim N({\Theta } ,\mathbf {I}^{-1}(\hat {\Theta })) \). Hence, using the large sample theory, the 100(1 − γ)% two-sided ACIs for α and β can be obtained, respectively, by

$$ \left( \hat{\alpha }\mp {{z}_{\gamma /2}}\sqrt{{{{\hat{\sigma }}}^{2}}_{{\hat{\alpha }}}} \right)\quad\text{and}\quad\left( \hat{\beta }\mp {{z}_{\gamma /2}}\sqrt{{{{\hat{\sigma }}}^{2}}_{{\hat{\beta }}}} \right), $$

where zγ/2 is an upper (γ/2)% of the standard normal distribution.

4 Bayes Estimators

Bayes’ procedure has been grown to become the most popular approach in many fields; including but not limited to engineering, clinical, biology, etc. In this section, we consider the Bayesian estimation method to obtian the point and interval estimates of α and β when the data sampled from Type-II censoring.

4.1 Prior Information and Loss Functions

The selection of prior distribution of an unknown parameter is an significant issue in Bayesian inference. A conjugate prior distribution is established when a member of a family of distributions is selected such that the posterior distribution also belongs to the same family. Gamma distribution, depending on its parameter values, can provide variety of shapes. Thus, it also can be considered as suitable prior of model parameter than other complex prior distributions, see Kundu (2008). Therefore, the gamma density priors are considered to adapt support of the PP parameters. Under the assumption of α and β are assumed to be stochastically independent gamma distributed as \( \alpha \sim Gamma({{a}_{1}},{{b}_{1}}) \) and \( \beta \sim Gamma({{a}_{2}},{{b}_{2}}) \), the joint prior PDF of α and β is given by

$$ \pi \left( \alpha ,\beta \right)\propto {{\alpha }^{{{a}_{1}}-1}}{{\beta }^{{{a}_{2}}-1}}\exp \left( -\left( \alpha {{b}_{1}}+\beta {{b}_{2}} \right) \right),\text{ }\alpha ,\beta >0,\text{ }{{a}_{1}},{{a}_{2}},{{b}_{1}},{{b}_{2}}>0, $$
(47)

where ai and bi for i = 1,2 are the shape and scale hyperparameters, respectively. They have been chosen to represent prior knowledge about α and β. Improper gamma prior of α and β can be obtained from Eq. 4.1 by setting ai = bi = 0, i = 1,2.

The choice of the loss function is an important aspect of the Bayes paradigm. Here, we consider three different type of loss functions, called squared-error loss (SEL), linear-exponential loss (LL) and general-entropy loss (GEL) functions. The most commonly symmetric loss function is the SEL function (which is denoted by lS(⋅)) is defined as

$$ l_{S}({\Theta},\tilde{\Theta})=(\tilde{\Theta}-{\Theta})^{2}. $$
(4.2)

Under SEL function (4.2), the Bayes estimate \( \tilde {\Theta }_{S} \) (say) of Θ, is the posterior mean and is given by

$$ \begin{array}{@{}rcl@{}} \tilde{\Theta}_{S}=E[{\Theta}(\alpha,\beta)|\textbf{x}]. \end{array} $$

The LL function (which is denoted by lL(⋅)) and GEL function (which is denoted by lG(⋅)) are the most commonly asymmetric loss functions and are given, respectively, by

$$ l_{L}({\Theta},\tilde{\Theta})=\exp (\nu(\tilde{\Theta}-{\Theta}))-\nu(\tilde{\Theta}-{\Theta}) -1,\ \nu\neq0, $$
(4.3)

and

$$ l_{G}({\Theta},\tilde{\Theta})\propto\left( \frac{\tilde{\Theta}}{\Theta}\right)^{\upsilon}-\upsilon\log\left( \frac{\tilde{\Theta}}{\Theta}\right)-1,\ \upsilon\neq0. $$
(4.4)

The direction and degree of symmetry using LL function are determined based on the sign and size of the shape parameter ν such as if ν > 0 means that overestimation is more serious than underestimation and ν < 0 means the opposite. When \( \nu \rightarrow 0\), the Bayes LL estimate will close to the Bayes SEL estimate. Under (4.3), the Bayes estimate \( \tilde {\Theta }_{L} \) of Θ is given by

$$ \tilde{\Theta}_{L}=-\frac{1}{\nu}{\log\left[E_{\Theta}\left( \exp({-\nu{\Theta}})|\textbf{x} \right) \right]}, $$

provided the above exception exists, and is finite. Under (4.4), the minimum error occurs when \( \tilde {\Theta }={\Theta } \). For υ > 0, a positive error has a more serious effect than a negative error and opposite for υ < 0. Putting υ = − 1 in Eq. 4.4, the Bayes GEL estimate coincides with the Bayes SEL estimate.

Under (4.4), the Bayes estimate \( \tilde {\Theta }_{G} \) of Θ is given by

$$ \tilde{\Theta}_{G}=\left[E_{\Theta}\left( {\Theta}^{-\upsilon}|\textbf{x} \right) \right]^{-1/\upsilon}, $$

provided the above exception exists, and it is finite. For more discussion on Bayesian loss functions, the readers may refer to the recent excellent book presented by Berger (2013). Although we are interested to drive the Bayes estimates using the SEL and GEL functions, yet other loss functions can be easily considered.

4.2 Posterior Analysis

According to the continuous Bayes’ theorem, the joint posterior density (say Φ(⋅)) of α and β is given by

$$ {{\Phi }}\left( \left. \alpha,\beta\right|\underline{\mathbf{x}} \right)=C^{-1}\pi \left( \alpha ,\beta \right)L\left( \left. \underline{\mathbf{x}}\right|\alpha,\beta \right), $$
(4.5)

where \( C={\int \limits }_{0}^{\infty }{\int \limits }_{0}^{\infty }\pi \left (\alpha ,\beta \right )L\left (\left .\underline {\mathbf {x}} \right |\alpha ,\beta \right ) \text{d}\alpha \ \text {d}\beta \) is the normalizing constant.

Combining (3.2) and (4.1), the joint posterior density (4.5) of α and β is given by

$$ \begin{array}{@{}rcl@{}} {\Phi} (\left. \alpha ,\beta \right|\underline{\mathbf{x}} )&=&C^{-1} {{\alpha }^{k+{{a}_{1}}-1}}{{\beta }^{k+{{a}_{2}}-1}}{{\lambda }^{k\alpha }}{{e}^{-\alpha {{b}_{1}}}}{{({{e}^{\beta }}-1 )}^{-n}}{{\left[ \exp (\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }} )-1 \right]}^{n-k}} \\ & &\times \exp \left[ -\beta ({{b}_{2}}-\sum\nolimits_{i=1}^{k}{{{(\lambda x_{(i)}^{-1} )}^{\alpha }}} ) \right]\underset{i=1}{\overset{k}{\mathop{\Pi }}} x_{(i)}^{-\alpha }. \end{array} $$
(4.6)

Conspicuously, because of the nonlinear form of the likelihood function (3.2), the marginal posterior distributions corresponding to α and β cannot be obtained explicitly. Thus, we propose to use MCMC techniques to generate samples from Eq. 4.6 and use them to compute the Bayes estimators of α and β and to construct their highest posterior density (HPD) intervals. To implement MCMC methodology, from Eq. 4.6, the full conditionals \( {\Phi }_{\alpha }^{*}(\cdot ) \) and \( {\Phi }_{\beta }^{*}(\cdot ) \) of α and β are given, respectively, by

$$ {\Phi}_{\alpha}^{*}(\alpha|\beta,\underline{\mathbf{x}})\propto{{\alpha }^{k+{{a}_{1}}-1}}{{\lambda }^{k\alpha }}\exp (-(\alpha b_{1}^{*}+\beta b_{2}^{*}(\alpha) ) ){{\left[ \exp (\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }} )-1 \right]}^{n-k}}, $$
(4.7)

and

$$ {\Phi}_{\beta}^{*}(\beta|\alpha,\underline{\mathbf{x}})\propto{{\beta }^{k+{{a}_{2}}-1}}{{({{e}^{\beta }}-1 )}^{-n}}{{e}^{-\beta b_{2}^{*}(\alpha )}}{{\left[ \exp (\beta {{(\lambda x_{(k)}^{-1} )}^{\alpha }} )-1 \right]}^{n-k}}, $$
(4.8)

where \( b_{1}^{*}=({{b}_{1}}+\sum \nolimits _{i=1}^{k}{\log ({{x}_{(i)}} )} ) \) and \( b_{2}^{*}(\alpha )=({{b}_{2}}-\sum \nolimits _{i=1}^{k}{{{(\lambda x_{(i)}^{-1} )}^{\alpha }}}) \).

From Eqs. 4.7 and 4.8, the conditional posterior distributions of α and β, respectively, cannot be reduced to any familiar distributions. Via R version 4.0.4, the diagram plot of the posterior distributions \( {\Phi }_{\alpha }^{*}(\cdot ) \) and \( {\Phi }_{\beta }^{*}(\cdot ) \) of α and β (when (α,λ,β) = (2,1,2)), respectively, Fig. 3 shows that the distributions (4.7) and (4.8) behave similarly to the normal distribution. Therefore, the Metropolis-Hasting (M-H) algorithm with normal proposal distribution is proposed to simulate MCMC samples, see for example Gelman et al. (2004).

Figure 3
figure 3

Diagram plot of the conditional PDFs of α and β

Full size image

To compute the Bayes MCMC estimates (or constructing associated HPD intervals) of α and β, do the below steps of M-H algorithm for sample generation process:

Step 1: :

Start with an initial guess \( {{\alpha }^{(0)}=\hat {\alpha }} \) and \( {{\beta }^{(0)}=\hat {\beta }} \).

Step 2: :

Set j = 1.

Step 3: :

Generate α∗ and β∗ from normal proposal distributions \( N(\hat \alpha ,\hat \sigma _{\hat \alpha }^{2}) \) and \( N(\hat \beta ,\hat \sigma _{\hat \beta }^{2}) \), respectively.

Step 4: :

Calculate τ1 and τ2 as \( \tau _{1} = \frac {{{\Phi }_{\alpha }^{*}\left ({\left . {\alpha ^{*} } \right |\beta ^{(j-1)} ,\underline {\mathbf {x}}} \right )}}{{{\Phi }_{\alpha }^{*}\left ({\left . {\alpha ^{(j - 1)} } \right |\beta ^{(j-1)} ,\underline {\mathbf {x}}} \right )}}\) and \( \tau _{2} = \frac {{{\Phi }_{\beta }^{*}\left ({\left . {\beta ^{*} } \right |\alpha ^{(j)} ,\underline {\mathbf {x}}} \right )}}{{{\Phi }_{\beta }^{*}\left ({\left . {\beta ^{(j - 1)} } \right |\alpha ^{(j)} ,\underline {\mathbf {x}}} \right )}}. \)

Step 5: :

Generate u1 and u2 from uniform U(0,1) distribution.

Step 6: :

If \( u_{1} \leqslant \min \limits \{1,\tau _{1}\} \), set α(j) = α∗ else set α(j) = α(j− 1). Similarly if \( u_{2} \leqslant \min \limits \{1,\tau _{2}\} \), set β(j) = β∗ else set β(j) = β(j− 1).

Step 7: :

Put j = j + 1.

Step 8: :

Redo Steps 2-7 \( {\mathscr{B}} \) times to get \( {\mathscr{B}} \) draws of α and β.

To ignore the effect of choosing the initial guess value, the first simulated varieties with size \( {{\mathscr{B}}_{0}} \) are removed. Then, the remaining samples, α(j) and β(j) for \( j={\mathscr{B}}_{0}+1,\dots ,{\mathscr{B}} \), of the unknown parameters α and β, respectively, can be further utilized to develop the Bayesian inference. Thus, the approximate Bayes estimates of α or β (say 𝜗) based on SEL, LL and GEL functions are given, respectively, by

$$ \begin{array}{@{}rcl@{}} \tilde{\vartheta}_{S}=\frac{{\sum}_{j=\mathcal{B}_{0}+1}^{\mathcal{B}}{\vartheta^{(j)}}}{\mathcal{B}-\mathcal{B}_{0}},\ \tilde{\vartheta}_{L}=-\frac{1}{\nu}\log\left[\frac{{\sum}_{j=\mathcal{B}_{0}+1}^{\mathcal{B}}{e^{-{\nu}\vartheta^{(j)}}}}{\mathcal{B}-\mathcal{B}_{0}}\right],\ \text{and}\ \tilde{\vartheta}_{G}=\left[\frac{{\sum}_{j=\mathcal{B}_{0}+1}^{\mathcal{B}}{\left( \vartheta^{(j)}\right)^{-\upsilon}}}{\mathcal{B}-\mathcal{B}_{0}}\right]^{-1/\upsilon}, \end{array} $$

where \( {\mathscr{B}}_{0} \) is burn-in. Bayes point estimates of α and β based on various loss functions can be easily obtained via useful ’coda’ package which proposed by Plummer et al. (2006).

According to the procedure proposed by Chen and Shao (1999), the HPD intervals of α and β under Type-II censored data are constructed. First, one must be ordered the simulated MCMC samples of 𝜗(j) for \( j=1,\dots ,{\mathscr{B}}, \) after burn-in as \( \vartheta _{({\mathscr{B}}_{0}+1)},\dots ,\vartheta _{({\mathscr{B}})} \). Thus, the 100(1 − γ)% two-sided HPD interval of 𝜗 is given by

$$ \left( {{\vartheta }_{({{j}^{*}})}},{{\vartheta }_{({{j}^{*}}+(1-\gamma )(\mathcal{B}-{{\mathcal{B}}_{0}}))}} \right), $$

where \( {{j}^{*}}={{{\mathscr{B}}}_{0}}+1,\dots ,{\mathscr{B}} \) is chosen such that

$$ {{\vartheta }_{\left( {{j}^{*}}+[(1-\gamma )(\mathcal{B}-{{\mathcal{B}}_{0}})] \right)}}-{{\vartheta }_{({{j}^{*}})}}=\underset{1\leqslant j\leqslant \gamma \left( \mathcal{B}-{{\mathcal{B}}_{0}} \right)}{\mathop{\min }} \left( {{\vartheta }_{\left( i+[(1-\gamma )(\mathcal{B}-{\mathcal{B}_{0}})] \right)}}-{{\vartheta }_{\left( i \right)}} \right). $$

5 Simulation Study

To evaluate the performance of the proposed estimation methods, an intensive Monte Carlo simulation study is conducted. For fixed λ = 0.1, by considering two different sets of parametric values, namely (α,β) = (0.25,0.75) and (0.5,0.9), a large 1,000 Type-II censored samples for different combinations of n(complete sample size) and k(Type-II censored sample size ) are generated from the PP model such as n = 60, 100 and 200 where the failure percentage k is taken as (k/n)% = 50, 75 and 100% for each n. When (k/n)% = 100%, it means that the simulated Type-II censored sampling has been extended to the complete sampling. However, based on 1,000 replications, the MLEs and their ACIs of α and β are calculated.

To see the impacts of the priors on the PP parameters, two informative sets of hyperparameters of α and β are used, namely Prior 1: (a1,a2) = (1,3), bi = 4 and Prior 2: (a1,a2) = (2.5,7.5), bi = 10 when (α,β) = (0.25,0.75) as well as Prior 1: (a1,a2) = (2.5,4.5), bi = 5 and Prior 2: (a1,a2) = (5,9), bi = 10 when (α,β) = (0.5,0.9). In this numerical study, the hyperparameters (ai,bi), i = 1,2 are chosen in such a way that the prior average fits the expected value of the associated target parameter, see Kundu (2008). Practically, it is preferable to use MLEs rather than the Bayesian estimates, whenever the improper gamma prior information is available, due to the latter is more computationally costly.

Using the M-H algorithm proposed in Section 4, 12,000 MCMC samples (with discarded the first 2,000 samples as burn-in) are generated. Then, based on 10,000 MCMC samples, the average of Bayes MCMC estimates and 95% HPD interval estimates are calculated. In this study, the shape parameter values of LL and GEL functions are taken as ν = υ = (− 5,5). To monitor whether MCMC simulated sample is sufficiently close to the target posterior, we purpose to consider the Gelman and Rubin’s convergence diagnostic statistic. Similar to a classical analysis of variance, this diagnostic measures whether there is a significant difference between the variance-within chains and the variance-between chains. When MCMC outputs are far from 1, this indicates a lack of convergence, for more details see Gelman and Rubin (1992). Figure 4, by running two chains corresponding to both given sets of (α,β) when (n,k) = (100,50), shows that the MCMC iterations reach 1 after about the first 2,000 iterations and thus the proposed simulations converged well. It also presents that the burn-in sample size is a good size to ignore the effect of initial guesses.

Figure 4
figure 4

Gelman and Rubin’s statistic for MCMC iterations of α and β

Full size image

For each test setup, the average estimates of the unknown PP parameters α and β (say 𝜗) with their RMSEs and RABs are calculated using the following formulae, respectively, as:

$$ \begin{array}{@{}rcl@{}} \overline{\hat\vartheta}&=&\frac{1}{M}\sum\nolimits_{j=1}^{M}{\hat\vartheta^{(j)}},\ \text{RMSE}(\hat\vartheta)=\sqrt{\frac{1}{M}\sum\nolimits_{j=1}^{M}(\hat\vartheta^{(j)}-\vartheta)^{2}},\quad \text{and} \\\text{RAB}(\hat\vartheta)&=&\frac{1}{M}\sum\nolimits_{j=1}^{M}\frac{1}{\vartheta}{\left|\hat\vartheta^{(j)}-\vartheta\right|}, \end{array} $$

where M is the amount of generated sequence data and \( \hat \vartheta ^{(j)} \) is the calculated maximum likelihood (or Bayes) estimate at the jth sample of α or β.

Further, the corresponding ACLs and CPs related to the ACIs (or HPD intervals) of α and β are obtained, respectively, as

$$ \text{ACL}_{\vartheta}\left( 1-\gamma \right)\%=\frac{1}{M}\sum\nolimits_{j=1}^{M}{\left( {{U}({\hat\vartheta^{(j)}})}-{{L}({\hat\vartheta^{(j)}})} \right)}, $$

and

$$ \text{CP}_{\vartheta}\left( 1-\gamma \right)\%=\frac{1}{M}\sum\nolimits_{j=1}^{M}{{{\mathbf{1}}_{\left( {{L}({\hat\vartheta^{(j)}})};{{U}({\hat{\vartheta }^{(j)}})} \right)}}}\left( {\vartheta} \right), $$

where 1(⋅) is the indicator function, L(⋅) and U(⋅) denote the lower and upper bounds, respectively, of (1 − γ)% asymptotic (or HPD) interval of 𝜗. Performance of the point estimates is judged based on their RMSE and RAB values. Also, the performance of the intervals estimates is judged using their ACLs and CPs. The average point estimates of α and β, RMSEs, and RABs are reported in Tables 1 and 2, respectively. In addition, the ACLs of 95% asymptotic and HPD interval estimates of α and β are listed in Table 3. All numerical computations were performed using R software version 4.0.4 with two recommended packages namely ‘maxLik’ and ‘coda’ packages. All R-environment scripts that support the findings of this study are available from the corresponding author upon reasonable request.

Table 1 Average estimates (first-line), RMSEs (second-line) and RABs (third-line) of α
Full size table
Table 2 Average estimates (first-line), RMSEs (second-line) and RABs (third-line) of β
Full size table

From Tables 1 and 2, we observe that the proposed estimates of the parameters α and β have very good performance in terms of minimum RMSEs and RABs. Also, as n is large, various estimates of α and β are quite close to the corresponding true parameter values. As n (or k) increases, the performance of both classical and Bayes estimates becomes better. Due to the simulated random normal variates using M-H algorithm, it is observed that the Bayes estimates of α and β become even better compared to the other method. Moreover, using gamma conjugate priors, the Bayesian estimates performed better than the frequentist estimates. Since the variance of prior 2 is lower than prior 1, the Bayesian estimates based on prior 2 have performed superior than those obtained from the other in terms of the smallest RMSEs, RABs and ACLs and highest CPs.

Furthermore, from Table 3, the ACLs of both of 95% ACI/HPD intervals for α and β narrowed down while the corresponding CPs increase when (k/n)% increases. Also, in respect of shortest ACLs and highest CPs, the HPD intervals of α and β performed better than the asymptotic intervals due to the gamma prior information.

Table 3 The ACLs(CPs) of 95% ACI/HPD intervals for α and β
Full size table

One of the main issues in Bayesian analysis is assessing the convergence of a MCMC chain. Therefore, the trace and autocorrelation plots of the simulated MCMC draws of the unknown PP parameters α and β are displayed (when (n,k) = (100,75)) in Fig. 5. The trace plots of MCMC outputs look like random noise and also when the autocorrelation values close to zero, the lag value increases. It also indicates that the MCMC draws are mixed adequately and thus the estimation results are reasonable.

Figure 5
figure 5

Trace (left-pandel) and Autocorrelation (right-panel) for MCMC outputs of α and β

Full size image

To sum up, simulation results pointed out that the proposed estimation methodologies work well in terms of their RMSEs and RABs (for point estimates) and in terms of their ACLs and CPs (for interval estimates). Finally, Bayesian estimation method utilizing the M-H algorithm sampler to estimate the PP distribution parameters is recommended.

6 Engineering Applications

In real practice, based on complete sampling, we aim to demonstrate the usefulness of the proposed model compared to other common lifetime models in the literature. For this purpose, we shall analyze two real data sets obtained from an engineering field. First data (Data-I) consists of the failure times of twenty mechanical components, see Murthy et al. (2004). Other data (say Data-II) consists of 40 records of the active repair times (in hours) for airborne communication transceiver, see Jorgensen (2012). For computational convenience we multiply each original data unit in Data-I and -II by one hundred. The new transformed datasets are presented in Table 4.

Table 4 New transformed Data-I and -II
Full size table

Practically, to identify the failure rate shapes based on both observed data sets I and II, the scaled Total Time on Test (TTT) plot is used. According to Aarset (1987), the scaled TTT transform is defined as

$$ K(u)=\frac{G^{-1}(u)}{G^{-1}(1)},\ 0<u<1, $$
(6.1)

where \( G^{-1}(u)={\int \limits }_{0}^{F^{-1}(u)}R(t)dt \). The corresponding empirical version of Eq. 6.1 is given by

$$ K_{n}(k/n)=\frac{{\sum}_{i=1}^{k}x_{(i)}+(n-k)x_{(k)}}{{\sum}_{i=1}^{n}x_{(i)}},\ r=1,2,\dots,n, $$

where x(i) represents the ith order statistic of the observed data. Graphically, the scaled TTT transform is displayed by plotting (k/n,Kn(k/n)).

Using both data sets I and II in Table 4, plots of the empirical and estimated scaled TTT transforms of the PP distribution are provided in Fig. 6. It shows that the scaled TTT transform is concave and convex. It also indicates that an increasing failure rate function for the fitting PP lifetime model is suitable for Data-I, whereas a decreasing failure rate function is suitable for Data-II. Also, plots in Fig. 6 support our same findings as shown in Fig. 2.

Figure 6
figure 6

Empirical and estimated scaled TTT-Transform plot of the PP distribution

Full size image

Using data sets I and II, we examine goodness-of-fit of the PP distribution and compare the fit results with common flexible distributions that exhibit various failure rates, namely: Weibull (W), gamma (G), exponentiated-exponential (EE), exponentiated Pareto (EPr), alpha power exponential (APE), exponential Poisson (EP), Weibull–Poisson (WP), exponentiated-exponential Poisson (EEP), generalized exponential Poisson (GEP), geometric exponential Poisson (GoEP) and quasi xgamma-Poisson (QXgP) distributions. The corresponding PDFs of these distributions (for x > 0 and α,β,λ > 0) are reported in Table 5.

Table 5 Some competing lifetime models of the PP distribution
Full size table

Several criteria of model selection such as: negative log-likelihood (NL), Akaike information (AI), Bayesian information (BI), consistent Akaike information (CAI), Hannan-Quinn information (HQI), Kolmogorov-Smirnov (KS) with its P-value, Anderson-Darling (AD) and Cramér von Mises (CvM) statistics are used. Using ‘AdequacyModel’ package, the maximum likelihood estimates with their standard errors (SEs) of unknown model parameters along with their goodness measures are calculated and provided in Table 6, for details see Marinho et al. (2019). It is evident that the PP distribution has the smallest values of all fitted selection criteria with the highest P-value than the comparative distributions. It also implies that the PP distribution fits both given data sets well satisfactorily and gives the best fit with respect to all given criteria. If one needs to compare two (or more) statistical models based on the Bayes approach, it is preferable to consider the Watanabe-Akaike information criterion.

Table 6 The MLEs(SEs) and selection criteria of the PP distribution and other competing models
Full size table

For more exploration, to assess the goodness-of-fit of the proposed model compared to other models, the probability–probability plots of all competitive distributions are displayed in Fig. 7. It shows that all fitted points of the PP distribution from data sets I and II are almost close to the straight line, thus the PP distribution gives a better fit than other distributions.

Figure 7
figure 7

The probability–probability plots of the competitive distributions

Full size image

Moreover, the relative histograms of both data sets and the fitted densities as well as the plot of fitted and empirical reliability functions are displayed in Fig. 8. It is clear that the PP life distribution appears to capture the general pattern of the histograms best. Likewise, the fitted survival function of the PP model fits the empirical function for both given data sets quite well.

Figure 8
figure 8

Fitted densities (left-panel), fitted survival functions (right-panel) of the competitive distributions

Full size image

7 Conclusions

By compounding the Pareto and Poisson distributions, we have presented the three-parameter Pareto-Poisson distribution. Various properties of the proposed distribution such as: moments, percentile function, stress-strength measure, entropies and order statistics have been obtained. Under Type-II censored data, when λ known, the model parameters have been estimated using the maximum likelihood and Bayesian estimation methods. To assess the convergence of MCMC chains, the Gelman and Rubin’s diagnostic has been used. Simulation results showed that the performance of the proposed estimators is satisfactory. Two engineering applications from mechanical and communication fields have been analyzed to provide the usefulness of the proposed distribution, showing that it provides a better fits than eleven competitive lifetime distributions namely: Weibull, gamma, exponentiated-exponential, exponentiated Pareto, alpha power exponential, exponential Poisson, Weibull–Poisson, exponentiated-exponential Poisson, generalized exponential Poisson, geometric exponential Poisson and quasi xgamma-Poisson distributions. We can also say that the Pareto-Poisson distribution is high flexible and is the most suitable model for the both real data sets among others. Finally, we recommend to utilize the proposed distribution as a survival model to utility of its ability to model lifetimes data with a heavy tail shaped. As a future research, it is useful to compare the proposed model with some other literature lifetime models in presence of data collected under Type-II censored sampling.