On the Neighbor-Distinguishing Indices of Planar Graphs

Abstract

Let $\textit{G}$ be a simple graph with no isolated edges. The neighbor-distinguishing edge coloring of $\textit{G}$ is a proper edge coloring of $\textit{G}$ such that any pair of adjacent vertices have different sets consisting of colors assigned on their incident edges. The neighbor-distinguishing index of $\textit{G}$, denoted by $\chi '_{a}(G)$, is the minimum number of colors in such an edge coloring of $\textit{G}$. In this paper, we show that if $\textit{G}$ is a connected planar graph with maximum degree $\Delta \ge 14$, then $\Delta \le \chi '_a(G)\le \Delta +1$, and $\chi '_a(G)=\Delta +1$ if and only if $\textit{G}$ contains a pair of adjacent vertices of maximum degree. This improves a result in [W. Wang, D. Huang, A characterization on the adjacent vertex distinguishing index of planar graphs with large maximum degree, SIAM J. Discrete Math. 29(2015), 2412–2431], which says that every connected planar graph $\textit{G}$ with $\Delta \ge 16$ has $\Delta \le \chi '_a(G)\le \Delta +1$, and $\chi '_a(G)=\Delta +1$ if and only if $\textit{G}$ contains a pair of adjacent vertices of maximum degree.

1 Introduction

Graphs considered in this paper are finite and simple. A graph G is called planar if G can be drawn in the plane without any two of its edges crossing. A graph G that is already drawn in the plane in this manner is a plane graph. Let G be a plane graph with vertex set V(G), edge set E(G), face set F(G), minimum degree $\delta (G)$, and maximum degree $\Delta (G)$ (for short, $\Delta$). Let $|G |=|V(G)|$ and $\Vert G\Vert =|E(G)|$ denote the order and size of the graph G, respectively. For positive integers p, q with $p\le q$, let [p, q] denote the set of integers $\{p,p+1,\ldots , q\}$.

A proper edge k-coloring of a graph G is a mapping $\phi$ from E(G) to [1, k] such that any two adjacent edges are assigned distinct colors. The chromatic index $\chi '(G)$ of G is the smallest k such that G has a proper edge k-coloring. For a proper edge k-coloring $\phi$ of G and $v\in V(G)$, denote by $C_{\phi }(v)=\{\phi (uv) |uv \in E(G)\}$ the set of colors of edges incident with v. The proper edge k-coloring $\phi$ is called neighbor-distinguishing (or $\phi$ is an NDE-k-coloring) if $C_{\phi }(u)\ne C_{\phi }(v)$ for each edge $uv\in E(G)$. Two adjacent vertices u and v are said to be conflict if $C_{\phi }(u)=C_{\phi }(v)$. The neighbor-distinguishing index $\chi '_{a}(G)$ of G is the smallest k such that G has an NDE-k-coloring.

A graph G is called normal if it contains no isolated edges. If G has an NDE-coloring, then G is normal. It holds trivially that $\chi '_{a}(G)\ge \chi '(G)\ge \Delta$ for any graph G. Moreover, if G contains two adjacent vertices of maximum degree, then $\chi '_{a}(G)\ge \Delta +1$. Zhang, Liu and Wang [11] introduced the NDE-coloring of graphs and proposed the following conjecture:

Conjecture 1

If G is a connected graph with $|G |\ge 3$ and $G\ne C_{5}$, then $\chi '_{a}(G) \le \Delta +2$.

Balister et al. [2] affirmed Conjecture 1 for bipartite graphs and subcubic graphs. Akbari et al.  [1] proved that $\chi '_{a}(G)\le 3\Delta$ for any graph G. This result is gradually improved to that $\chi '_{a}(G)\le 2.5\Delta +5$ in [10], to that $\chi '_{a}(G)\le 2.5\Delta$ in [9], and to that $\chi '_{a}(G)\le 2\Delta +2$ in [7]. Using probabilistic method, Hatami [4] showed that every graph G with sufficiently large $\Delta$ has $\chi '_{a}(G)\le \Delta +300$. Recently, Joret and Lochet [6] improved this result by replacing 300 with 19. Suppose that G be a planar graph. Bonamy et al. [3] showed that if $\Delta \ge 12$, then $\chi '_{a}(G)\le \Delta +1$. Furthermore, in 2015, Wang and Huang [8] showed that (1) if $\Delta \ge 15$, then $\chi '_{a}(G)\le \Delta +1$; and (2) if $\Delta \ge 16$, then $\chi '_{a}(G)=\Delta +1$ if and only if G contains a pair of adjacent vertices of maximum degree.

This paper focuses on improving the result of Wang and Huang [8]. Namely, we will show the following:

Theorem 1

Let G be a planar graph with $\Delta \ge 14$. Then $\Delta \le \chi '_a(G)\le \Delta +1$; and $\chi '_a(G)=\Delta +1$ if and only if G contains a pair of adjacent vertices of maximum degree.

2 Notation

Let G be a plane graph and $H\subseteq G$. If the boundary vertices of a face f of H are $u_1,u_2,\ldots ,u_k$ in a cyclic ordering, then we write $f=[u_1u_2\cdots u_k]$. For $x\in V(H)\cup F(H)$, let $d_{H}(x)$ denote the degree of x in H. A vertex of degree k (at least k, at most k, respectively) in H is called a k-vertex ($k^{+}$-vertex, $k^{-}$-vertex, respectively). Similarly, we can define k-face, $k^{+}$-face and $k^{-}$-face. For a vertex $v\in V(H)$, let $N_{H}(v)$ denote the set of neighbors of v in H. Let $N_{k}^{H}(v)$ denote the set of k-vertices adjacent to v in H, and set $d_{k}^{H}(v)=|N_{k}^{H}(v)|$. Set $N^{H}_{i_{1},i_{2},\ldots , i_{k}}(v)=N^{H}_{i_{1}}(v)\cup N^{H}_{i_{2}}(v)\cup \ldots \cup N^{H}_{i_{k}}(v)$. Similarly, we can define $N_{k^{+}}^{H}(v)$, $N_{k ^{-}}^{H}(v)$, $d_{k^{+}}^{H}(v)$ and $d_{k^{-}}^{H}(v)$. For a face $f\in F(H)$, let $d_{k}^{H}(f)$ ($d_{k^{+}}^{H}(f)$, $d_{k^{-}}^{H}(f)$, respectively) denote the number of k-vertices ($k^{+}$-vertices, $k^{-}$-vertices, respectively) incident with f in H. If no confusion is caused in the context, we omit the letter G in $d_{G}(v),d_{k}^{G}(v), d_{k^{+}}^{G}(v)$, $d_{k^{-}}^{G}(v)$, $d_{k}^{G}(f)$, $d_{k^{+}}^{G}(f)$ and $d_{k^{-}}^{G}(f)$.

A 3-cycle in the plane graph H is special if it has one 2-vertex, and bad if it has two 3-vertices. A 4-cycle in H is special if it has two 2-vertices. A 3-face in H is special or bad if its boundary forms a special or bad 3-cycle. A 4-face in H is special if its boundary forms a special 4-cycle. A vertex v of H is called small if $d_{H}(v)\in [1,5]$.

Given a graph G, denote by $n_{i}(G)$ the number of i-vertices in V(G) for $i\in [1,\Delta (G)]$. We say that G is smaller than a graph H if $(\Vert G\Vert$, $n_{t}(G)$, $n_{t-1}(G)$, $\ldots$, $n_{1}(G))$ precedes $(\Vert H\Vert , n_{t}(H)$, $n_{t-1}(H)$, $\ldots$, $n_{1}(H))$ regarding the standard lexicographic order, where $t=\max \{\Delta (G)$, $\Delta (H)\}$. A graph is called minimal regarding a given property P if no smaller graph meets the property P.

Suppose that $\phi$ is an NDE-k-coloring of the graph G and $uv\in E(G)$. If $d_{G}(u)\ne d_{G}(v)$, then $C_{\phi }(u)\ne C_{\phi }(v)$. An edge uv is said to be legally colored if its color is different from that of its adjacent edges in E(G) and no pair of new conflict vertices are produced.

3 Proof of Theorem 1

It suffices to show that $\chi '_a(G)=\Delta +1$ if and only if G contains adjacent $\Delta$-vertices. The necessity is clear by the foregoing discussion. To prove sufficiency, it is enough to show that if G is a planar graph with $\Delta \ge 14$ and without adjacent $\Delta$-vertices, then $\chi '_a(G)\le \Delta$. Assume that this is not true. Let G be a minimal counterexample of Theorem 1, that is, G has no NDE-$\Delta$-coloring, while any other planar graph H smaller than G admits an NDE-$\Delta$-coloring. Obviously, G is connected. Since G contains no adjacent $\Delta$-vertices, it is easy to derive that no 1-vertex is adjacent to a $\Delta$-vertex. Let $C=[1,\Delta ]$ denote a set of $\Delta$ colors. Then $|C |\ge 14$.

3.1 Structural Properties of G

In all of the figures of this section, black bullets represent vertices which have no incident edges in E(G) other than those shown, but white bullets represent vertices which might be adjacent to other vertices in V(G) not in the configuration. A cut vertex v is called nontrivial if there exist at least two components of $G-v$ with order at least 2. We denote simply $\{1,2,3,4,5,6,14\}$ by $\{1-6,14\}$; $\{1,3,4,5,6,13,14\}$ by $\{1,3-6,13,14\}$; etc.

Claim 1

G does not contain any nontrivial cut vertex.

Claim 2

There is no edge $uv\in E(G)$ with $d(u)= 1$ and $d(v)\le 7$.

Claim 3

If v is a k-vertex with $k\in [2,5]$, then $d_{5^{-}}(v)=d_{k}(v)\le 1$.

Claim 4

There is no edge $uv\in E(G)$ with $d(u)=d(v)=2$.

Claim 1 is given in [8]. Claims 2–4 are established in [5].

Claim 5

Let $v\in V(G)$.

• (1) If $d_{1}(v)\ge k \in [1,4]$, then $d_{s}(v)=0$ for $s\in [2,k+1]$.

• (2) If $d(v)\le \Delta -1$, then $d_{2}(v)\le 1$.

• (3) v is not incident with any special 4-cycle.

• (4) If v is incident with a special 3-cycle, then $d_{2}(v)=1$.

Proof

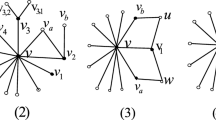
• (1) Assume that $d_{s}(v)\ge 1$ for $s\in [2,k+1]\subseteq [2,5]$. Let $v_1,v_2,\ldots ,v_{k+1}$ be the neighbors of v such that $d(v_{i})=1$ for $i\in [1,k]$ and $d(v_{k+1})=s$. Let $N(v_{k+1})=\{u_{1},u_{2},\ldots ,u_{s-1},v\}$, as depicted in Fig. 1 a. By Claim 3, we consider two cases below:

  Case 1$d_{s}(v_{k+1})=0$. We split $v_{k+1}$ into one 1-vertex $x_{1}$ and one $(s-1)$-vertex $x_{2}$ such that $x_{1}$ is adjacent to v and $x_{2}$ is adjacent to $u_{1},u_{2},\ldots ,u_{s-1}$, yielding a smaller graph H. Then $\Vert H\Vert =\Vert G\Vert$, $n_s(H)<n_s(G)$, $n_{s-1}(H)>n_{s-1}(G)$ and $n_{1}(H)>n_{1}(G)$. By the minimality of G, H has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i$ for $i\in [1,k]$. Note that $\varphi (vx_{1})\notin [1,k]$. Sticking $x_{1}$ and $x_{2}$, we restore the graph G. If $\varphi (vx_{1})\notin C_{\varphi }(x_{2})$, then $\varphi$ is an NDE-$\Delta$-coloring of G. Otherwise, we exchange the colors of $vx_{1}$ and $vv_{j}$ for $j\in [1,k]\backslash (C_{\varphi }(x_{2})\backslash \{\varphi (vx_{1})\})$ to obtain an NDE-$\Delta$-coloring of G, which is a contradiction.

  Case 2$d_{s}(v_{k+1})=1$, i.e., $d(u_{s-1})=d(v_{k+1})=s$. Then $s\in [3,5]$ by Claim 4. Let $H=G-v_{k+1}u_{s-1}$. Then $\Vert H\Vert <\Vert G\Vert$, $n_s(H)<n_s(G)$ and $n_{s-1}(H)>n_{s-1}(G)$. By the minimality of G, H has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i$ for $i\in [1,k]$. Note that $\varphi (vv_{k+1})\notin [1,k]$. If $C_{\varphi }(u_{s-1})\ne C_{\varphi }(v_{k+1})$, then we color $v_{k+1}u_{s-1}$ properly. Otherwise, we exchange the colors of $vv_{t}$ and $vv_{k+1}$ for $t\in [1,k]\backslash (C_{\varphi }(v_{k+1})\backslash \{\varphi (vv_{k+1})\})$ and color $v_{k+1}u_{s-1}$ properly. So we always get an NDE-$\Delta$-coloring of G, which is a contradiction.

• (2) Assume that $d_{2}(v)\ge 2$. Let $v_1,v_2$ be the neighbors of v with $d(v_{1})=d(v_{2})=2$. We consider the following three cases.

  Case 1 Each $v_{i}$ $(i=1,2)$ is not incident with a 3-face and $v, v_{1},v_{2}$ are not incident with a 4-face (see Fig. 1b). Let $N(v_{1})=\{v,w\}$ and $N(v_{2})=\{v,u\}$. We get a smaller graph H by contracting $vv_{1}$ and $vv_{2}$. By the minimality of G, H has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vw)=1$ and $\varphi (vu)=2$. Reversely we subdivide vw, vu with $v_{1},v_{2}$ respectively. By coloring $vv_{1}$ and $v_{2}u$ with 2, $vv_{2}$ and $v_{1}w$ with 1, we get an NDE-$\Delta$-coloring of G, which is a contradiction.

  Case 2v, $v_{1}$, $v_{2}$ are incident with a 4-face $[vv_{1}uv_{2}]$ (see Fig. 1c). We get a smaller graph H by splitting each $v_{i}$ $(i=1,2)$ into two 1-vertices $x_{i}$ and $y_{i}$ such that $x_{i}$ is adjacent to v and $y_{i}$ is adjacent to u. By the minimality of G, H has an NDE-$\Delta$-coloring $\varphi$. Next, we can stick $x_{i}$ and $y_{i}$ together for $i=1,2$, and exchange the colors of $vx_{1}$ and $vx_{2}$ if necessary. This gives an NDE-$\Delta$-coloring of G, which is a contradiction.

  Case 3 Some $v_{i}$, say $v_{2}$, is incident with some 3-face $[vv_2v_3]$ (see Fig. 1d). Let $N(v_{1})=\{v,u\}$. We get a smaller graph H by splitting $v_{1}$ into two 1-vertices $x_{1}$ and $y_{1}$ such that $x_{1}$ is adjacent to v and $y_{1}$ is adjacent to u. By the minimality of G, H has an NDE-$\Delta$-coloring $\varphi$. Sticking $x_{1}$ and $y_{1}$, we restore the graph G. If $\varphi (vx_1)\ne \varphi (uy_1)$, then $\varphi$ is an NDE-$\Delta$-coloring of G. Otherwise, $\varphi (vx_1)=\varphi (uy_1)$. If $\varphi (v_2v_3)\ne \varphi (vx_1)$, then we exchange the colors of $vx_{1}$ and $vv_{2}$. If $\varphi (v_2v_3)=\varphi (vx_1)$, then we recolor $v_2v_3$ and $vx_1$ with $\varphi (vv_3)$, $vv_3$ with $\varphi (v_2v_3)$. So we always get an NDE-$\Delta$-coloring of G, which is a contradiction.

  In view of the proof of Cases 2 and 3 in the statement (2), we can prove the statements (3) and (4). $\square$

Fig. 1

Configurations used in the proof of Claim 5

Claim 6

There is no edge $uv\in E(G)$ such that $6\le d(v)\le 7$ and $d(u)\le 5$.

Proof

Assume that G contains an edge uv with $6\le d(v)=k \le 7$ and $d(u)=s\le 5$. Let $N(v)=\{v_{1}, v_{2},\ldots ,v_{k-1},u\}$ and $N(u)=\{u_{1}, u_{2},\ldots ,u_{s-1},v\}$. By Claim 3, u has at most one conflict vertex, say $u_{1}$ (if it exists). Let $H=G-uv$, which has an NDE-$\Delta$-coloring $\varphi$ such that $\varphi (vv_{i})=i$ for $i\in [1,k-1]$ and $\varphi (uu_{j})=a_{j}$ for $j\in [1,s-1]$.

Without loss of generality, assume that $k=7$ and $s=5$ (for other cases, we have an easier proof). Let $a_{j}\in [1,10]$ for $j\in [1,4]$. Suppose that uv cannot be legally colored. That is, $C_{\varphi }(v_{i})=\{1-6,i+10\}$ for $i\in [1,4]$ or $C_{\varphi }(u_{1})=\{a_{1},a_{2},a_{3},a_{4},14\}$ and $C_{\varphi }(v_{i})=\{1-6,i+10\}$ for $i\in [1,3]$.

Case 1$C_{\varphi }(v_{i})=\{1-6,i+10\}$ for $i\in [1,4]$. For each $i\in [1,4]$, we recolor $vv_{i}$ with a color $b_{i}\in [7,14]\backslash \{i+10\}$ such that $v_{i}$ does not conflict with its neighbors, and color uv with a color in $[11,14]\backslash \{b_{i},i+10\}$.

If $C_{\varphi }(u_{1})\notin \{\{a_{1},a_{2},a_{3},a_{4},t\}\ |\ t\in [11,14]\}$, then we have at least $2\times 4=8$ different ways to recolor or color some edges incident with v. So assume that $C_{\varphi }(u_{1})=\{a_{1},a_{2},a_{3},a_{4},11\}$. Notice that uv can be colored with a color in $[12,14]\backslash \{b_{i},i+10\}$. Then there are at least $1\times 4=4$ different ways to recolor or color some edges incident with v. Since v has at most two conflict vertices other than $v_{1},v_{2},v_3,v_4$, $\varphi$ can be extended to G, which is a contradiction.

Case 2$C_{\varphi }(u_{1})=\{a_{1},a_{2},a_{3},a_{4},14\}$ and $C_{\varphi }(v_{i})=\{1-6,i+10\}$ for $i\in [1,3]$. For each $i\in [1,3]$, we recolor $vv_{i}$ with a color $b_{i}\in [7,14]\backslash \{i+10\}$ such that $v_{i}$ does not conflict with its neighbors, and color uv with a color in $[11,13]\backslash \{b_{i},i+10\}$.

If there exists a color $b_{i}\notin [11,13]$ for $i\in [1,3]$, then we have at least four different ways to recolor or color some edges incident with v. So assume that $b_{i}\in [11,13]$ for all $i\in [1,3]$. We claim that there exists $b_{s}\ne b_{t}$ for $s,t\in [1,3]$. Otherwise, $b_{1}=b_{2}=b_{3}\in [11,13]$, contradicting the choice of $b_{i}$. Say $b_{1}\ne b_{2}$. Next, we recolor $vv_{1}$ with $b_{1}$, $vv_{2}$ with $b_{2}$, and color uv with $[11,13]\backslash \{b_{1},b_{2}\}$. Then we have at least $3+1=4$ different ways to recolor or color some edges incident with v. Since v has at most three conflict vertices other than $v_{1},v_{2},v_3$, we can extend $\varphi$ to G, which is a contradiction. $\square$

In the following discussion, if v is a l-vertex of G, then we denote by $v_1,v_2,\ldots , v_l$ the neighbors of v with $d(v_1)\le d(v_2)\le \cdots \le d(v_l)$.

Claim 7

Let v be a k-vertex of G with $k=8$ or 9.

• (1) If $d_{4^{-}}(v)\ge 1$, then $d_{5^{-}}(v)\le k-7$.

• (2) v is not in a bad 3-cycle.

Proof

• (1) Assume that $d_{s^{-}}(v)\ge k-6$. Let $d(v_{1})=s\le 4$, $d(v_{p})\le 5$ for $p\in [2,k-6]$, and $N(v_1)=\{u_{1}, u_{2},\ldots ,u_{s-1},v\}$. Then $G-vv_{1}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i-1$ for $i\in [2,k]$. By Claim 3, we consider the following two cases.

  Case 1$d_{s}(v_{1})=0$. Then $v_{1}$ has no conflict vertices. Without loss of generality, assume that $\varphi (v_{1}u_{j})=a_{j}\in [1,k+j-1]\subseteq [1,k+2]$ for $j\in [1,s-1]$. First, we can color $vv_{1}$ with any color in $[k+3,14]$. Second, for each $i\in [2,k-6]$, $v_{i}$ has at most one conflict vertex by Claim 3. Recolor $vv_{i}$ with a color $b_{i}\in [k,14]\backslash C_{\varphi }(v_{i})$ such that $v_i$ does not conflict with its neighbors, and color $vv_{1}$ with a color in $[k+3,14]\backslash \{b_{i}\}$. So there are at least $(14-k-2)+(14-k-3)\times (k-6-1)=-k^{2}+17k-65=7$ different ways to recolor or color some edges incident with v. As v has at most $k-(k-6)=6$ conflict vertices, $\varphi$ can be extended to G, which is a contradiction.

  Case 2$d_{s}(v_{1})=1$, i.e., $d(u_{s-1})=d(v_{1})=s$. By Claims 3 and 6, each vertex in $(N(v_{1})\cup N(u_{s-1}))\backslash \{v_{1},u_{s-1}\}$ is an $8^{+}$-vertex. Recolor $v_{1}u_{s-1}$ with a color in $[1,k-1]\backslash (C_{\varphi }(v_{1})\cup C_{\varphi }(u_{s-1}))$. Let $a\in C_{\varphi }(u_{s-1})\backslash C_{\varphi }(v_{1})$. Note that if $vv_{1}$ can be colored with some color in $[k,14]\backslash \{a,\varphi (v_{1}u_{1})$, $\ldots ,\varphi (v_{1}u_{s-2})\}$, then $u_{s-1}$ and $v_{1}$ do not conflict with each other. Without loss of generality, assume that $\{a,\varphi (v_{1}u_{1}),\ldots ,\varphi (v_{1}u_{s-2})\}\subseteq [1,k+2]$. Analogous to the analysis of Case 1, $\varphi$ can be extended to G, which is a contradiction.

• (2) Assume that v is in a bad 3-cycle. If $d(v)=8$, then $d_{5^{-}}(v)\le 1$ by (1). Otherwise, $d(v)=9$. Let $d(v_{1})=d(v_{2})=3$ and $v_{1}v_{2}\in E(G)$. Then $G-v_{1}v_{2}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i$ for $i\in [1,9]$. If $C_{\varphi }(v_1)\ne C_{\varphi }(v_2)$, then we color $v_{1}v_{2}$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$. Notice that if $vv_{1}$ or $vv_{2}$ can be recolored, then we can establish an NDE-$\Delta$-coloring of G by coloring $v_1v_2$ properly. Then $vv_{1}$ or $vv_{2}$ can be recolored with any color in [10, 14]. So there are at least $2\times 5=10$ different ways to recolor some edges incident with v. As v has at most seven conflict vertices, we can extend $\varphi$ to G, which is a contradiction. $\square$

Claim 8

Let v be a 10-vertex of G.

• (1) If $d_{4^{-}}(v)=m$ and $d_{k^{-}}(v)\ge 1$, then $d_{6^{+}}(v)\ge (5-k)m+1$ for $k\in [1,4]$.

• (2) v is not in a bad 3-cycle.

Proof

• (1) Assume that $d_{6^{+}}(v)\le (5-k)m$. Let $d(v_{1})=k\le 4$, $d(v_{p})\le 4$ for $p\in [2,m]$, and $N(v_1)=\{u_{1}, u_{2},\ldots ,u_{k-1},v\}$. Then $G-vv_{1}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i-1$ for $i\in [2,10]$. By Claim 3, we consider the following two cases.

  Case 1$d_{k}(v_{1})=0$. Then $v_1$ has no conflict vertices. Without loss of generality, assume that $\varphi (v_{1}u_{j})=a_{j}\in [1,9+j]\subseteq [1,8+k]$ for $j\in [1,k-1]$. First, we can color $vv_{1}$ with any color in $[9+k,14]$. Second, for each $i\in [2,m]$, $v_i$ has at most one conflict vertex by Claim 3. Recolor $vv_{i}$ with a color $b_{i}\in [10,14]\backslash C_{\varphi }(v_{i})$ such that $v_{i}$ does not conflict with its neighbors, and color $vv_{1}$ with a color in $[9+k,14] \backslash \{b_{i}\}$. So we have at least $(6-k)+(m-1)(5-k)=(5-k)m+1$ different ways to recolor or color some edges incident with v. As v has at most $(5-k)m$ conflict vertices, $\varphi$ can be extended to G, which is a contradiction.

  Case 2$d_{k}(v_{1})=1$, i.e., $d(u_{k-1})=d(v_{1})=k$. By Claims 3 and 6, each vertex in $(N(v_{1})\cup N(u_{k-1}))\backslash \{v_{1},u_{k-1}\}$ is an $8^{+}$-vertex. Recolor $v_{1}u_{k-1}$ with a color in $[1,9] \backslash (C_{\varphi }(v_{1})\cup C_{\varphi }(u_{k-1}))$. Let $a\in C_{\varphi }(u_{k-1})\backslash C_{\varphi }(v_{1})$. Note that if $vv_{1}$ can be colored with some color in $[10,14]\backslash \{a,\varphi (v_{1}u_{1}),\ldots$, $\varphi (v_{1}u_{k-2})\}$, then $u_{k-1}$ and $v_{1}$ do not conflict with each other. Without loss of generality, assume that $\{a,\varphi (v_{1}u_{1}),\ldots ,\varphi (v_{1}u_{k-2})\}\subseteq [1,8+k]$. Analogous to the analysis of Case 1, $\varphi$ can be extended to G, which is a contradiction.

• (2) Assume that v is in a bad 3-cycle. Let $d(v_{1})=d(v_{2})=3$ and $v_{1}v_{2}\in E(G)$. Then $G-v_{1}v_{2}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i$ for $i\in [1,10]$. If $C_{\varphi }(v_1)\ne C_{\varphi }(v_2)$, then we color $v_{1}v_{2}$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$. Notice that if $vv_{1}$ or $vv_{2}$ can be recolored, then we can establish an NDE-$\Delta$-coloring of G by coloring $v_{1}v_{2}$ properly. First, we can recolor $vv_{1}$ or $vv_{2}$ with any color in [11, 14]. Second, we recolor $vv_{1}$ with 11, $vv_{2}$ with 12. So we have at least $2\times 4+1=9$ different ways to recolor some edges incident with v. While v has at most eight conflict vertices, we can extend $\varphi$ to G, deriving a contradiction. $\square$

Claim 9

Let v be an 11-vertex of G.

• (1) If $d_{4^{-}}(v)=m$ and $d_{k^{-}}(v)\ge 1$, then $d_{6^{+}}(v)\ge (4-k)m+1$ for $k\in [1,3]$.

• (2) If v is in a bad 3-cycle, then $d_{6^{+}}(v)\ge 9$.

Proof

(1) Assume that $d_{6^{+}}(v)\le (4-k)m$. Let $d(v_{1})=k\le 3$, $d(v_{p})\le 4$ for $p\in [2,m]$, and $N(v_1)=\{u_{1}, u_{2},\ldots ,u_{k-1},v\}$. Then $G-vv_{1}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i-1$ for $i\in [2,11]$. $\square$

Remark 1

If $d(v_{2})\le 3$, or $d(v_{2})=4$ and $d_{4}(v_{2})$ $=0$, then we can recolor $vv_{2}$ with a color $b_{2}\in [11,14]\backslash C_{\varphi }(v_{2})$ such that $v_{2}$ does not conflict with its neighbors. If $d(v_{2})=4$ and $d_{4}(v_{2})=1$, say, $x_{2}\in N(v_{2})$ with $d(x_{2})=d(v_{2})=4$, then we recolor $v_{2}x_{2}$ with a color in $[1,10]\backslash (C_{\varphi }(v_{2})\cup C_{\varphi }(x_{2}))$. Let $\alpha _{2}\in C_{\varphi }(x_{2})\backslash C_{\varphi }(v_{2})$. Then we can recolor $vv_{2}$ with a color $b_{2}\in [11,14]\backslash ((C_{\varphi }(v_{2})\backslash \{\varphi (v_2x_2),\varphi (vv_2)\})\cup \{\alpha _{2}\})$. Hence, there exists a color $b_2\in [11,14]$ such that if $vv_{2}$ is recolored with $b_2$, then $v_{2}$ does not conflict with its neighbors.

Now, by Claim 3, we have to consider the following two cases.

Case 1$d_{k}(v_{1})=0$. Then $v_1$ has no conflict vertices. Without loss of generality, assume that $\varphi (v_{1}u_{j})=a_{j}\in [1,10+j]\subseteq [1,9+k]$ for $j\in [1,k-1]$. First, we can color $vv_{1}$ with any color in $[10+k,14]$. Second, for each $i\in [2,m]$, $v_i$ has at most one conflict vertex by Claim 3. As in Remark 1, we can recolor $vv_{i}$ with a color $b_{i}\in [11,14]$ such that $v_{i}$ does not conflict with its neighbors, and color $vv_{1}$ with a color in $[10+k,14]\backslash \{b_{i}\}$. So there are at least $(5-k)+(m-1)(4-k)=(4-k)m+1$ different ways to recolor or color some edges incident with v. As v has at most $(4-k)m$ conflict vertices, $\varphi$ can be extended to G, which is a contradiction.

Case 2$d_{k}(v_{1})=1$, i.e., $d(u_{k-1})=d(v_{1})=k$. By Claims 3 and 6, each vertex in $(N(v_{1})\cup N(u_{k-1}))\backslash \{v_{1},u_{k-1}\}$ is an $8^{+}$-vertex. Recolor $v_{1}u_{k-1}$ with a color in $[1,10]\backslash (C_{\varphi }(v_{1})\cup C_{\varphi }(u_{k-1}))$. Let $a\in C_{\varphi }(u_{k-1})\backslash C_{\varphi }(v_{1})$. Note that if $vv_{1}$ can be colored with some color in $[11,14]\backslash \{a,\varphi (v_{1}u_{1}),\ldots$, $\varphi (v_{1}u_{k-2})\}$, then $u_{k-1}$ and $v_{1}$ do not conflict with each other. Without loss of generality, assume that $\{a,\varphi (v_{1}u_{1}),\ldots ,\varphi (v_{1}u_{k-2})\}\subseteq [1,9+k]$. Analogous to the analysis of Case 1, $\varphi$ can be extended to G, which is a contradiction.

(2) Assume that $d_{6^{+}}(v)\le 8$. Let $d(v_{1})=d(v_{2})=3$ and $v_{1}v_{2}\in E(G)$. Then $G-v_{1}v_{2}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i$ for $i\in [1,11]$. If $C_{\varphi }(v_1)\ne C_{\varphi }(v_2)$, then we color $v_{1}v_{2}$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$. Notice that if $vv_{1}$ or $vv_{2}$ can be recolored, then we can establish an NDE-$\Delta$-coloring of G by coloring $v_{1}v_{2}$ properly. First, we can recolor $vv_{1}$ or $vv_{2}$ with any color in [12, 14]. Second, we recolor $vv_{1}$ with 12, $vv_{2}$ with 13 or 14. Third, we recolor $vv_{1}$ with 13, $vv_{2}$ with 14. So we have at least $2\times 3+2+1=9$ different ways to recolor some edges incident with v. As v has at most eight conflict vertices, we can extend $\varphi$ to G, which is a contradiction. $\square$

Claim 10

Let v be a 12-vertex of G.

• (1) If $d_{1}(v)\ge 1$ and $d_{3^{-}}(v)\ge 2$, then $d_{6^{+}}(v)\ge 2d_{4^{-}}(v)+1$.

• (2) If $d_{2^{-}}(v)\ge 1$, then $d_{6^{+}}(v)\ge d_{3^{-}}(v)+1$.

• (3) If v is in a bad 3-cycle, then $d_{6^{+}}(v)\ge 5$.

• (4) If v is in a special 3-cycle and $d_{3^{-}}(v)\ge 2$, then $d_{6^{+}}(v)\ge 5$.

Proof

• (1) Assume that $d_{6^{+}}(v)\le 2d_{4^{-}}(v)$. Let $d(v_{1})=1$ and $d(v_{2})\le 3$. Then $G-vv_{1}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i-1$ for $i\in [2,12]$.

  First, we can color $vv_{1}$ with any color in [12, 14]. Second, $v_2$ has at most one conflict vertex by Claim 3. Analogous to the analysis of Remark 1 in Claim 9(1), we can recolor $vv_{2}$ with a color $b_2\in [12,14]$ such that $v_2$ does not conflict with its neighbors, and color $vv_{1}$ with any color in $[12,14]\backslash \{b_2\}$. Third, for each $v_i$ with $d(v_i)\le 4$ and $i\ge 3$, $v_i$ has at most one conflict vertex by Claim 3. By Remark 1 in Claim 9(1), we can recolor $vv_{i}$ with a color $b_{i}\in \{1,12-14\}$ such that $v_{i}$ does not conflict with its neighbors. If $b_{i}\in [12,14]$, then we color $vv_{1}$ with any color in $[12,14]\backslash \{b_{i}\}$. If $b_{i}=1$, then we recolor $vv_{2}$ with $b_2\in [12,14]$ and color $vv_{1}$ with any color in $[12,14]\backslash \{b_2\}$. So at least $3+2(d_{4^{-}}(v)-1)=2d_{4^{-}}(v)+1$ different ways can be used to recolor or color some edges incident with v. As v has at most $2d_{4^{-}}(v)$ conflict vertices, $\varphi$ can be extended to G, which is a contradiction.

• (2) Assume that $d_{6^{+}}(v)\le d_{3^{-}}(v)$. Let $d(v_{1})\le 2$ and x be the neighbor of $v_{1}$ other than v (if it exists). Then $G-vv_{1}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i-1$ for $i\in [2,12]$. Suppose that $\varphi (v_{1}x)\in [1,12]$, if x exists.

  First, $v_1$ has no conflict vertex by Claim 4. Then we can color $vv_{1}$ with any color in $\{13,14\}$. Second, for each $v_{i}$ with $d(v_{i})\le 3$ and $i\ge 2$, $v_i$ has at most one conflict vertex by Claim 3. As for Remark 1 in Claim 9(1), we can recolor $vv_{i}$ with a color $b_{i}\in [12,14]$ such that $v_{i}$ does not conflict with its neighbors, and color $vv_{1}$ with a color in $\{13,14\}\backslash \{b_{i}\}$. So we have at least $2+(d_{3^{-}}(v)-1)=d_{3^{-}}(v)+1$ different ways to recolor or color some edges incident with v. As v has at most $d_{3^{-}}(v)$ conflict vertices, $\varphi$ can be extended to G, which is a contradiction.

• (3) Assume that $d_{6^{+}}(v)\le 4$. Let $d(v_{1})=d(v_{2})=3$ and $v_{1}v_{2}\in E(G)$. Then $G-v_{1}v_{2}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i$ for $i\in [1,12]$. If $C_{\varphi }(v_1)\ne C_{\varphi }(v_2)$, then we color $v_{1}v_{2}$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$. Notice that if $vv_{1}$ or $vv_{2}$ can be recolored, then we can establish an NDE-$\Delta$-coloring of G by coloring $v_{1}v_{2}$ properly. First, $vv_{1}$ or $vv_{2}$ can be recolored with any color in $\{13,14\}$. Second, we recolor $vv_{1}$ with 13, $vv_{2}$ with 14. So we have at least $2\times 2+1=5$ different ways to recolor some edges incident with v. While v has at most four conflict vertices, we can extend $\varphi$ to G, deriving a contradiction.

• (4) Assume that $d_{6^{+}}(v)\le 4$. Let $d(v_{1})=2$, $d(v_{2})\le 3$ and $vv_1v_xv$ is a special 3-cycle with $d(v_x)\ge 8$. Then $G-vv_{1}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i-1$ for $i\in [2,12]$. We consider the following two cases.

Case 1$\varphi (v_{1}v_x)\notin [12,14]$. First, we can color $vv_{1}$ with any color in [12, 14]. Second, $v_2$ has at most one conflict vertex by Claim 3. As for Remark 1 in Claim 9(1), we can recolor $vv_{2}$ with a color $b_{2}\in [12,14]$ such that $v_{2}$ does not conflict with its neighbors, and color $vv_{1}$ with a color in $[12,14]\backslash \{b_{2}\}$. So we have at least $3+2=5$ different ways to recolor or color some edges incident with v. As v has at most four conflict vertices, we can extend $\varphi$ to G, which is a contradiction.

Case 2$\varphi (v_{1}v_x)\in [12,14]$, say $\varphi (v_{1}v_x)=12$. First, $vv_{1}$ can be colored with any color in $\{13,14\}$. Second, $v_2$ has at most one conflict vertex by Claim 3. As for Remark 1 in Claim 9(1), we can recolor $vv_{2}$ with a color $b_{2}\in [12,14]$ such that $v_{2}$ does not conflict with its neighbors, and color $vv_{1}$ with a color in $\{13,14\} \backslash \{b_{2}\}$. Third, we exchange the colors of $v_1v_x$ and $vv_x$, and color $vv_1$ with any color in $\{13,14\}$. Hence, we have at least $2+1+2=5$ different ways to recolor or color some edges incident with v. Since v has at most four conflict vertices, we can extend $\varphi$ to G, which is a contradiction. $\square$

Claim 11

Let v be a k-vertex of G with $k\in [13,\Delta -1]$ and $d_{1}(v)\ge 1$. If $d_{2^{-}}(v)\ge s$ for $s\in [2,4]$, then $d_{6^{+}}(v)\ge d_{(s+1)^{-}}(v)+1$.

Proof

Assume that $d_{6^{+}}(v)\le d_{(s+1)^{-}}(v)$. Let $d(v_{1})=1$ and $d(v_{i})\le 2$ for $i\in [2,s]$. Then $G-vv_{1}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i-1$ for $i\in [2,k]$. If $d(v_{i})=2$ for $i\in [2,s]$, then $d_{2}(v_{i})=0$ by Claim 4.

First, we can color $vv_{1}$ with any color in $\{k,k+1\}$. Second, for each i with $i\in [2,s]$, we recolor $vv_{i}$ with a color $b_{i}\in \{k,k+1\}\backslash C_{\varphi }(v_{i})$ and color $vv_{1}$ with $\{k,k+1\}\backslash \{b_{i}\}$. Third, for each $v_{i}$ with $d(v_{i})\le s+1\le 5$ and $i\ge s+1$, Analogous to the analysis of Remark 1 in Claim 9(1), we can recolor $vv_{i}$ with a color $c_{i}\in ([1,s-1]\cup \{k,k+1\})\backslash C_{\varphi }(v_{i})$ such that $v_{i}$ does not conflict with its neighbors. If $c_{i}\in [1,s-1]$, say $c_{i}=j$, then we recolor $vv_{j+1}$ with a color $b_{j}\in \{k,k+1\}\backslash C_{\varphi }(v_{j+1})$, and color $vv_{1}$ with $\{k,k+1\}\backslash \{b_{j}\}$. If $c_{i}\in \{k,k+1\}$, then we color $vv_{1}$ with $\{k,k+1\}\backslash \{c_{i}\}$. So there are at least $2+(s-1)+(d_{(s+1)^{-}}(v)-s)=d_{(s+1)^{-}}(v)+1$ different ways to recolor or color some edges incident with v. As v has at most $d_{(s+1)^{-}}(v)$ conflict vertices, $\varphi$ can be extended to G, which is a contradiction. $\square$

Claim 12

Let v be a k-vertex of G with $k\ge 8$.

• (1) v is in at most one bad 3-cycle. Further, if v is in a bad 3-cycle, then $d_{2^{-}}(v)=0$.

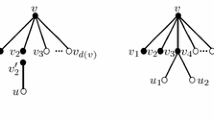
• (2) If v is in $G_1$ of Fig. 2a, then $d_{3^{-}}(v)=2$.

• (3) G does not contain a configuration Fig. 2b.

• (4) G does not contain a configuration Fig. 2c.

Fig. 2

Configurations used in Claim 12(2)–(4)

Proof

• (1) First, we show that v is in at most one bad 3-cycle. Assume that v is in two bad 3-cycles. Let $d(v_i)=3$ for $i\in [1,4]$ and $v_1v_2,v_3v_4\in E(G)$. We denote by $u_i$ the third neighbor of $v_i$ for $i\in [1,4]$. Then $G-v_1v_2$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_i)=i$ for $i\in [1,k]$. If $C_{\varphi }(v_1) \ne C_{\varphi }(v_2)$, then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$, i.e., $\varphi (v_1u_1)=2$ and $\varphi (v_2u_2)=1$. Note that $\varphi (v_3u_3)\ne 4$ or $\varphi (v_4u_4)\ne 3$, say $\varphi (v_3u_3)\ne 4$. Remove the color of $v_3v_4$. Recolor $vv_3$ with a color in $\{1,2\}\backslash \{\varphi (v_3u_3)\}$, say 1, $vv_1$ with 3. Then we color $v_1v_2$, $v_3v_4$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

  Next, we show that if v is in a bad 3-cycle, then $d_{2^{-}}(v)=0$. Assume that $d_{2^{-}}(v)\ge 1$. Let $d(v_1)=d(v_2)=3$, $d(v_3)\le 2$ and $v_1v_2\in E(G)$. We denote by $u_i$ the third neighbor of $v_i$ for $i=1,2$. Then $G-v_1v_2$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_i)=i$ for $i\in [1,k]$. If $C_{\varphi }(v_1) \ne C_{\varphi }(v_2)$, then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$, i.e., $\varphi (v_1u_1)=2$ and $\varphi (v_2u_2)=1$. Recolor $vv_3$ with a color in $\{1,2\}\backslash C_{\varphi }(v_3)$, say 1, and $vv_1$ with 3. Then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

• (2) Assume that $d_{3^{-}}(v)\ge 3$, say $d(v_4)=3$, as shown in Fig. 2a. We use the same symbols as in Fig. 2a. Then $G-v_1v_2$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_i)=i$ for $i\in [1,k]$. If $C_{\varphi }(v_1) \ne C_{\varphi }(v_2)$, then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$, i.e., $\varphi (v_1v_3)=2$ and $\varphi (v_2v_3)=1$. As for Remark 1 in Claim 9(1), we recolor $vv_4$ with a color $\alpha \in [1,3]$ such that $v_4$ does not conflict with its neighbors. If $\alpha \in [1,2]$, say $\alpha =1$, then we recolor $vv_1$ with 4. If $\alpha =3$, then we recolor $vv_1$ with 4, $vv_3$ with 1, $v_2v_3$ with 3. Then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

• (3) Assume that the configuration Fig. 2b exists in G. It follows from Claims 3, 6 and 12(1) that $d(v_{4})\ge 8$. Then $G-v_{1}v_{2}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i$ for $i\in [1,k]$. If $C_{\varphi }(v_1)\ne C_{\varphi }(v_2)$, then we color $v_{1}v_{2}$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$, i.e., $\varphi (v_1u_1)=2$ and $\varphi (v_2u_2)=1$. By Claim 3, we consider the following two cases.

  Case 1$d_{3}(v_{3})=0$. If $|\{1,2\}\cap C_{\varphi }(v_3)|\le 1$, say $1\notin C_{\varphi }(v_3)$, then we recolor $vv_{3}$ with 1, $vv_{1}$ with 3. Otherwise, $\{1,2\}\subseteq C_{\varphi }(v_3)$, say $\varphi (v_{3}v_{4})=1$ and $\varphi (v_{3}u_{3})=2$. We recolor $vv_{1}$ and $v_3v_{4}$ with 4, $vv_{4}$ with 1. Then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

  Case 2$d_{3}(v_{3})=1$, i.e., $d(u_{3})=d(v_{3})=3$. By Claims 2, 3 and 6, each vertex in $N(u_{3})\backslash \{v_{3}\}$ is an $8^{+}$-vertex. Remove the color of $v_{3}u_{3}$. Let $\alpha \in C_{\varphi }(u_{3})\backslash C_{\varphi }(v_{3})$. If $|\{1,2\}\cap \{\varphi (v_{3}v_{4}),\alpha \}|\le 1$, say $1\notin \{\varphi (v_{3}v_{4}),\alpha \}$, then we recolor $vv_{3}$ with 1, $vv_{1}$ with 3. Otherwise, $\{\varphi (v_{3}v_{4}),\alpha \}=\{1,2\}$, say $\varphi (v_{3}v_{4})=1$ and $\alpha =2$. We recolor $vv_{1}$ and $v_{3}v_{4}$ with 4, $vv_{4}$ with 1. Then we color $v_1v_2$, $v_3u_3$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

• (4) Assume that the configuration Fig. 2c exists in G. Then $G-v_{1}v_{2}$ has an NDE-$\Delta$-coloring $\varphi$ with $\varphi (vv_{i})=i$ for $i\in [1,k]$. If $C_{\varphi }(v_1)\ne C_{\varphi }(v_2)$, then we color $v_{1}v_{2}$ properly to get an NDE-$\Delta$-coloring of G. Suppose that $C_{\varphi }(v_1)=C_{\varphi }(v_2)=\{1,2\}$, i.e., $\varphi (v_1u_1)=2$ and $\varphi (v_2u_2)=1$. We deal with the following three cases by symmetry.

Case 1$d_{4}(v_{3})=0$. By Claims 2, 3 and 6, $d(v_4),d(v_5), d(u_3)\ge 8$. If $|\{1,2\}\cap C_{\varphi }(v_{3})|\le 1$, say $1\notin C_{\varphi }(v_{3})$, then we recolor $vv_{3}$ with 1, $vv_{1}$ with 3. Then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G. Otherwise, $\{1,2\} \subseteq C_{\varphi }(v_{3})$. By symmetry, we consider the following two possibilities.

• $\varphi (v_{3}v_{4})=1$ and $\varphi (v_{3}v_{5})=2$. Let $\gamma \in \{4,5\}\backslash (\varphi (v_{3}u_{3}))$, say $\gamma =4$. We exchange the colors of $vv_{4}$ and $v_{3}v_{4}$, and recolor $vv_{1}$ with 4. Then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

• $\varphi (v_{3}v_{4})=1$ and $\varphi (v_{3}u_{3})=2$. If $\varphi (v_{3}v_{5})\ne 4$, then we exchange the colors of $vv_{4}$ and $v_{3}v_{4}$, and recolor $vv_{1}$ with 4. If $\varphi (v_{3}v_{5})=4$, then we exchange the colors of $vv_{4}$ and $v_3v_{4}$, the colors of $vv_{5}$ and $v_3v_{5}$, and recolor $vv_{1}$ with 5. Then we color $v_1v_2$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

Case 2$d_{4}(v_{3})=1$ and $d(u_{3})=4$. By Claims 2, 3 and 6, each vertex in $(N(v_{3})\cup N(u_{3}))\backslash \{v_{3},u_{3}\}$ is an $8^{+}$-vertex. Remove the color of $v_{3}u_{3}$. Let $\alpha \in C_{\varphi }(u_{3})\backslash C_{\varphi }(v_{3})$. If $|\{1,2\}\cap \{\varphi (v_3v_4),\varphi (v_3v_5),\alpha \}|\le 1$, say $1\notin \{\varphi (v_3v_4),\varphi (v_3v_5),\alpha \}$, then we recolor $vv_{3}$ with 1, $vv_{1}$ with 3. Then we color $v_1v_2$, $v_3u_3$ properly to get an NDE-$\Delta$-coloring of G. Otherwise, $\{1,2\} \subseteq \{\varphi (v_3v_4),\varphi (v_3v_5),\alpha \}$. By symmetry, we consider the following two possibilities.

• $\varphi (v_{3}v_{4})=1$ and $\varphi (v_{3}v_{5})=2$. Let $\gamma \in \{4,5\}\backslash \{\alpha \}$, say $\gamma =4$. We exchange the colors of $vv_{4}$ and $v_{3}v_{4}$, and recolor $vv_{1}$ with 4. Then we color $v_{1}v_{2}$, $v_3u_3$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

• $\varphi (v_{3}v_{4})=1$ and $\alpha =2$. If $\varphi (v_{3}v_{5})\ne 4$, then we exchange the colors of $vv_{4}$ and $v_{3}v_{4}$, and recolor $vv_{1}$ with 4. If $\varphi (v_{3}v_{5})=4$, then we exchange the colors of $vv_{4}$ and $v_3v_{4}$, the colors of $vv_{5}$ and $v_3v_{5}$, and recolor $vv_{1}$ with 5. Then we color $v_{1}v_{2}$, $v_3u_3$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

Case 3$d_{4}(v_{3})=1$ and $d(v_{5})=4$. By Claims 2, 3 and 6, each vertex in $(N(v_{3})\cup$ $N(v_{5}))\backslash \{v_{3},v_{5}\}$ is an $8^{+}$-vertex. Remove the color of $v_{3}v_{5}$. Let $\beta \in C_{\varphi }(v_{5})\backslash C_{\varphi }(v_{3})$. If $|\{1,2\}\cap \{\varphi (v_{3}v_{4}),\varphi (v_{3}u_{3}),\beta \}|\le 1$, say $1 \notin \{\varphi (v_{3}v_{4}),\varphi (v_{3}u_{3}),\beta \}$, then we recolor $vv_{3}$ with 1, $vv_{1}$ with 3. Then we color $v_1v_2$, $v_3v_5$ properly to get an NDE-$\Delta$-coloring of G. Otherwise, $\{1,2\} \subseteq \{\varphi (v_3v_4),\varphi (v_3u_3),\beta \}$. By symmetry, we consider the following two possibilities.

• $\varphi (v_3v_4)=1$ and $\varphi (v_3u_3)=2$. We exchange the colors of $vv_{4}$ and $v_{3}v_{4}$, and recolor $vv_{1}$ with 4. Then we color $v_1v_2$, $v_3v_5$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

• $1\in \{\varphi (v_3v_4), \varphi (v_3u_3)\}$ and $\beta =2$. If $5\notin C_{\varphi }(v_{3})$ or $C_{\varphi }(v_{5})\backslash (\varphi (v_3v_5))\ne \{1,2$, $5\}$, then we recolor $vv_{3}$ with 2, $vv_{2}$ with 3. If $5\in C_{\varphi }(v_{3})$ and $C_{\varphi }(v_{5})\backslash (\varphi (v_3v_5))=\{1,2,5\}$, then we recolor $vv_5$ with 3, $vv_3$ with 2, $vv_2$ with 5. Then we color $v_1v_2$, $v_3v_5$ properly to get an NDE-$\Delta$-coloring of G, which is a contradiction.

$\square$

3.2 Discharging Analysis on H

Let H be the graph obtained from G by removing all 1-vertices. Note that $d_{H}(v)=d_{G}(v)-d_{1}^{G}(v)$. By Claims 2, 7–11, we give the relationship between $d_{G}(v)$ and $d_{H}(v)$ in Table 1. It follows that $\delta (H)\ge 2$. By Claim 1, H is 2-connected. Some structural properties of H are collected as follows.

Table 1 The relation between $d_{G}(v)$ and $d_{H}(v)$

Claim 13

Let v be a vertex of H. Then the following statements hold.

• (0) If $2\le d_H(v)\le 6$, then $d_{G}(v)=d_{H}(v)$.

• (1) If $d_H(v)=2$, then $d_{5^-}^H(v)=0$.

• (2) If $d_H(v)=k$ for $k\in [3,5]$, then $d_{5^{-}}^{H}(v)=d_{k}^{H}(v)\le 1$.

• (3) If $d_H(v)=6,7$, then $d_{5^{-}}^{H}(v)=0$.

• (4) Let $d_H(v)=8$. If $d_{4^{-}}^{H}(v)\ge 1$, then $d_{5^{-}}^{H}(v)\le 1$.

• (5) Let $d_H(v)=9$. Then v is not in a bad 3-cycle. If $d_{4^{-}}^{H}(v)\ge 1$, then $d_{5^{-}}^{H}(v)\le 2$.

• (6) Let $d_{H}(v)=10$. Then v is not in a bad 3-cycle. If $d_{3^{-}}^{H}(v)\ge 1$, then $d_{6^{+}}^{H}(v)\ge 2d_{4^{-}}^{H}(v)+1$. If $d_{4^{-}}^{H}(v)\ge 1$, then $d_{6^{+}}^{H}(v)\ge d_{4^{-}}^{H}(v)+1$.

• (7) Let $d_{H}(v)=11$. If $d_{3^{-}}^{H}(v)\ge 1$, then $d_{6^{+}}^{H}(v)\ge d_{4^{-}}^{H}(v)+1$. If v is in a bad 3-cycle, then $d_{6^{+}}^{H}(v)\ge 9$.

• (8) Let $d_{H}(v)=12$. If $d_{2}^{H}(v)\ge 1$, then $d_{6^{+}}^{H}(v)\ge d_{3^{-}}^{H}(v)+1$. If v is in a bad 3-cycle, then $d_{6^{+}}^{H}(v)\ge 5$. If v is in a special 3-cycle and $d_{3^{-}}^{H}(v)\ge 2$, then $d_{6^{+}}^{H}(v)\ge 5$.

Proof

• (0) holds clearly by Table 1. Both (1) and (2) hold by Claims 3, 4, 13(0).

• (3) It holds trivially if $d_G(v)=d_H(v)$. If $d_G(v)> d_H(v)$, by Table 1, then $d_G(v)=8$, 9 or $d_G(v)\ge 13$. If $d_G(v)=8$, then $d^G_{1}(v)=1$. By Claim 7(1), $d^G_{5^{-}}(v)=1$, further to say that $d_{5^{-}}^{H}(v)=d^G_{5^{-}}(v)-d^G_{1}(v)=0$. If $d_G(v)=9$, then $d^G_{1}(v)=2$. By Claim 7(1), $d^G_{5^{-}}(v)\le 2$, further to say that $d_{5^{-}}^{H}(v)=d^G_{5^{-}}(v)-d^G_{1}(v)\le 2-2=0$. If $d_G(v)\ge 13$, then $d^G_{1}(v)\ge 6$. By Claim 5(1), $d^G_{s}(v)=0$ for $s\in [2,5]$, further to say that $d_{5^{-}}^{H}(v)=0$.

• (4) It holds trivially if $d_G(v)=d_H(v)$. If $d_G(v)> d_H(v)$, by Table 1, then $d_G(v)=9$ or $d_G(v)\ge 13$. If $d_G(v)=9$, then $d^G_{1}(v)=1$. By Claim 7(1), $d^G_{5^{-}}(v)\le 2$, further to say that $d_{5^{-}}^{H}(v)=d^G_{5^{-}}(v)-d^G_{1}(v)\le 1$. If $d_G(v)\ge 13$, then $d^G_{1}(v)\ge 5$. By Claim 5(1), $d^G_{s}(v)=0$ for $s\in [2,5]$, further to say that $d_{5^{-}}^{H}(v)=0$.

• (5) It holds trivially if $d_G(v)=d_H(v)$. If $d_G(v)=10$, then $d^G_{1}(v)=1$. By Claim 8(1), $d^H_{6^{+}}(v)=d^G_{6^{+}}(v)\ge 4d^G_{4^{-}}(v)+1=4d^H_{4^{-}}(v)+5$, further to say that $d_{4^{-}}^{H}(v)=0$. If $d_G(v)=11$, then $d^G_{1}(v)=2$. By Claim 9(1), $d^H_{6^{+}}(v)=d^G_{6^{+}}(v)\ge 3d^G_{4^{-}}(v)+1=3d^H_{4^{-}}(v)+7$, further to say that $d_{4^{-}}^{H}(v)=0$. If $d_G(v)\ge 12$, then $d^G_{1}(v)\ge 3$. By Claim 5(1), $d^G_{s}(v)=0$ for $s\in [2,4]$, further to say that $d_{4^{-}}^{H}(v)=0$.

• (6) It holds trivially if $d_G(v)=d_H(v)$. If $d_G(v)=11$, then $d^G_{1}(v)=1$. By Claim 9(1), $d^H_{6^{+}}(v)=d^G_{6^{+}}(v)\ge 3d^G_{4^{-}}(v)+1=3d^H_{4^{-}}(v)+4$, further to say that $d_{4^{-}}^{H}(v)\le 1$. If $d_G(v)=12$, then $d^G_{1}(v)=2$. By Claim 10(1), $d^H_{6^{+}}(v)=d^G_{6^{+}}(v)\ge 2d^G_{4^{-}}(v)+1=2d^H_{4^{-}}(v)+5$, further to say that $d_{4^{-}}^{H}(v)\le 1$. If $d_G(v)\ge 13$, then $d^G_{1}(v)\ge 3$. By Claim 5(1), $d^G_{s}(v)=0$ for $s\in [2,4]$, further to say that $d_{4^{-}}^{H}(v)=0$.

• (7) It holds trivially if $d_G(v)=d_H(v)$. If $d_G(v)=12$, then $d^G_{1}(v)=1$. By Claim 12(1), v is not in a bad 3-cycle. If $d^H_{3^{-}}(v)\ge 1$, implying $d^G_{3^{-}}(v)\ge 2$, by Claim 10(1), then $d_{6^{+}}^{H}(v)=d^G_{6^{+}}(v)\ge 2d^G_{4^{-}}(v)+1\ge 2d_{4^{-}}^{H}(v)+3$. If $d_G(v)\ge 13$, then $d^G_{1}(v)\ge 2$. By Claim 5(1), $d^G_{s}(v)=0$ for $s\in [2,3]$, further to say that $d_{3^{-}}^{H}(v)=0$.

• (8) It holds trivially if $d_G(v)=d_H(v)$. If $d_G(v)\ge 13$, then $d^G_{1}(v)\ge 1$. By Claim 12(1), v is not in a bad 3-cycle. By Claim 5(1), $d^G_{2}(v)=0$, further to say that $d_{2}^{H}(v)=0$. $\square$

Using Euler’s formula $|V(H)|-|E(H)|+ |F(H)|=2$, we can deduce

$$\begin{aligned} \sum \limits _{v\in V(H)}(d_{H}(v)-6)+\sum \limits _{f\in F(H)}(2d_{H}(f)-6)=-12. \end{aligned}$$

We first define the weight function w on H by $w(x)=d_H(x)-6$ if $x\in V(H)$ and $w(x)=2d_H(x)-6$ if $x\in F(H)$. Next, we design some discharging rules and redistribute weights accordingly. Once the discharging is finished, the resultant weight function $w'$ is produced, so that the sum of all weights is kept fixed when the discharging is in process. However, we can show that $w'(x)\ge 0$ for all $x\in V(H)\cup F(H)$. This leads to the following contradiction:

$$\begin{aligned} 0\le \sum \limits _{x\in V(H)\cup F(H)}w'(x)=\sum \limits _{x\in V(H)\cup F(H)}w(x)=-12<0, \end{aligned}$$

and hence demonstrates the nonexistence of such a counterexample.

The discharging rules are defined as follows:

(R1):

Every 4-face f gives 2 to its incident 2-vertex if $d_{2}^{H}(f)=1$; otherwise, it gives 1 to each incident small vertex.

(R2):

Every $5^{+}$-face f gives 2 to each incident 2-vertices, and $\frac{\omega (f)-2d_{2}^{H}(f)}{d_{3}^{H}(f)+d_{4}^{H}(f)+d_{5}^{H}(f)}$ to each incident small vertex of degree at least 3.

For a small vertex u, let $\beta (u)$ denote the total sum of charges transferred into u after (R1)-(R2) were carried out.

(R3):

Let v be an $8^{+}$-vertex adjacent to a small k-vertex u. If $d_{k}^{H}(u)=1$, then v gives max$\{\frac{6-d_H(u)-\beta (u)}{d_H(u)-1},0\}$ to u; if $d_{k}^{H}(u)=0$, then v gives max$\{\frac{6-d_H(u)-\beta (u)}{d_H(u)},0\}$ to u.

For $x,y\in V(H)\cup F(H)$, let $\tau (x\rightarrow y)$ denote the charge transferred from x to y according to the above rules.

Observation 1

(Wang and Huang [8]) Let f be a face of H and v be a small vertex incident with f.

• (1) Every face f is incident with at most $\lfloor \frac{2d_H(f)}{3}\rfloor$ small vertices.

• (2) Let $d_H(f)=5$. If $d_{2}^{H}(f)\ge 1$, then $\tau (f\rightarrow v)\ge 1$. Otherwise, $\tau (f\rightarrow v)\ge \frac{4}{3}$.

• (3) Let $d_H(f)=6$. If $d_{2}^{H}(f)\ge 1$, then $\tau (f\rightarrow v)\ge 2$. Otherwise, $\tau (f\rightarrow v)\ge \frac{3}{2}$.

• (4) Let $d_H(f)\ge 7$. Then $\tau (f\rightarrow v)\ge 2$.

Observation 2

Let v be an $8^{+}$-vertex of H, u be a small vertex adjacent to v, and $G_1$ be the configuration of Fig. 2a.

• (1) Let $d_H(u)=2$. If v is in a special 3-face, then $\tau (v\rightarrow u)\le 1$. Otherwise, $\tau (v\rightarrow u)=0$.

• (2) Let $d_H(u)=3$. If v is in $G_{1}$, then $\tau (v\rightarrow u)\le \frac{3}{2}$. Otherwise, $\tau (v\rightarrow u)\le 1$.

• (3) If $d_H(u)=4$, then $\tau (v\rightarrow u)\le \frac{2}{3}$.

• (4) If $d_H(u)=5$, then $\tau (v\rightarrow u)\le \frac{1}{4}$.

• (5) If v is in a bad 3-face and u is not in this bad 3-face, then $\tau (v\rightarrow u)\le \frac{1}{2}$.

• (6) If v is in $G_{1}$ and u is not in $G_{1}$, then $\tau (v\rightarrow u)\le \frac{1}{3}$.

Proof

Both (3) and (4) hold clearly by Observation 1 and (R3).

• (1) If v is in a special 3-face, then $d_{2}^{H}(v)=1$ by Claim 5(4). Then the faces incident with u are this special 3-face and a $4^{+}$-face. By (R1) and (R2), $\beta (u)\ge 2$. Hence, $\tau (v\rightarrow u)\le \frac{6-2-2}{2}=1$. Otherwise, the faces incident with u are all $4^{+}$-faces. By (R1) and (R2), $\beta (u)\ge 4$. Hence, $\tau (v\rightarrow u)\le \frac{6-2-4}{2}=0$.

• (2) If $d^H_3(u)=0$, then $\tau (v\rightarrow u)=\frac{6-3-\beta (u)}{3}\le 1$. Suppose that $d^H_3(u)=1$. Let v, $w_1$, $w_2$ be the neighbors of u in the clockwise order with $d_H(w_1)=3$. Let $f_{uvw_1}$ be the face with uv and $uw_1$ as boundary edges. Similarly, we can define $f_{w_1uw_2}$ and $f_{vuw_2}$. If $f_{uvw_1}$ or $f_{w_1uw_2}$ is a $4^+$-face, by (R1) and Observation 1, then $\beta (u)\ge 1$. Hence, $\tau (v\rightarrow u)\le \frac{6-3-1}{3-1}=1$. Suppose that $d_{H}(f_{uvw_1})=d_{H}(f_{w_1uw_2})=3$. Then v is in a bad 3-face $vuw_1v$. By Claim 12(1), $d_2^{H}(v)=0$. If $f_{vuw_2}$ is a 4-face with $d^H_2(f_{vuw_{2}})=0$, or a $5^+$-face, by (R1) and Observation 1, then $\beta (u)\ge 1$. Hence, $\tau (v\rightarrow u)\le \frac{6-3-1}{3-1}=1$. Suppose that $d_H(f_{vuw_{2}})= 3$. Then u is incident with three 3-faces, i.e., v is in $G_1$, and $\tau (v\rightarrow u)=\frac{6-3-0}{3-1}=\frac{3}{2}$.

• (5) If v is in a bad 3-face, then $d_2^{H}(v)=0$ by Claim 12(1). Then $d_{H}(u)=3,4,5$. If $d_{H}(u)=3$, then vu is not incident with a 3-face by Claim 12(3). By (R1) and Observation 1, $\beta (u)\ge 2$. Hence, $\tau (v\rightarrow u)\le \frac{6-3-2}{3-1}=\frac{1}{2}$. If $d_{H}(u)=4$, then one of the faces incident with vu is at least a $4^{+}$-face by Claim 12(4). By (R1) and Observation 1, $\beta (u)\ge 1$. Hence, $\tau (v\rightarrow u)\le \frac{6-4-1}{4-1}=\frac{1}{3}<\frac{1}{2}$. If $d_{H}(u)=5$, then $\tau (v\rightarrow u)\le \frac{1}{4}<\frac{1}{2}$ by Observation 2(4).

• (6) If v is in $G_{1}$, then $d_{3^{-}}^{H}(v)=2$ by Claim 12(2). Then $d_{H}(u)=4,5$. If $d_{H}(u)=4$, then one of the faces incident with vu is at least a $4^{+}$-face by Claim 12(4). By (R1) and Observation 1, $\beta (u)\ge 1$. Hence, $\tau (v\rightarrow u)\le \frac{6-4-1}{4-1}=\frac{1}{3}$. If $d_{H}(u)=5$, then $\tau (v\rightarrow u)\le \frac{1}{4}<\frac{1}{3}$ by Observation 2(4). $\square$

Observation 3

Suppose that $v\in V(H)$ is an $8^{+}$-vertex which is not in any bad 3-face. Let $v_{i},v_{i+1},v_{i+2},\ldots ,v_{i+s},v_{i+s+1}$ be $s+2$ consecutive neighbors of v. If $d_{H}(v_{i+j})\in [3,5]$ for $j\in [1,s]$ and $s\ge 2$, then $\sum \limits _{j=1}^{s}\tau (v\rightarrow v_{i+j})\le \frac{s}{3}+1$. In particular,

• (1) If neither $v_{i+1}$ nor $v_{i+s}$ is in a bad 3-face, then $\sum \limits _{j=1}^{s}\tau (v\rightarrow v_{i+j})\le \frac{s}{3}+\frac{2}{3}$.

• (2) If exactly one of $v_{i+1}$ and $v_{i+s}$ is in a bad 3-face, then $\sum \limits _{j=1}^{s}\tau (v\rightarrow v_{i+j})\le \frac{s}{3}+\frac{5}{6}$.

• (3) If $s=2$ and $d_H(v_{i}),d_H(v_{i+3})\notin [3,5]$, then $\tau (v\rightarrow v_{i+1})+\tau (v\rightarrow v_{i+2})\le \frac{3}{2}$.

Proof

Let $f_{t}$ be the face with $vv_{t}$ and $vv_{t+1}$ as boundary edges for $t\in [i,i+s]$.

Let $j\in [i+2,i+s-1]$ and $d_{H}(v_j)=k$. If $d_{k}^{H}(v_{j})=0$, then $f_{j-1}$ and $f_{j}$ incident with $vv_{j}$ are either 4-faces without 2-vertices or $5^{+}$-faces. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-k-2}{k}\le \frac{1}{3}$ by (R1) and Observation 1. If $k\ge 4$ and $d_{k}^{H}(v_{j})=1$, then $d_{5^{-}}^{H}(v_{j})=d_{k}^{H}(v_{j})=1$ by Claim 13(2). Then one of $f_{j-1}$ and $f_{j}$ is at least a $4^{+}$-face. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-k-1}{k-1}\le \frac{1}{3}$ by (R1) and Observation 1. If $k=3$ and $d_{3}^{H}(v_{j})=1$, then one of $f_{j-1}$ and $f_{j}$ is a $4^{+}$-face and the other is a $5^{+}$-face. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-3-1-\frac{4}{3}}{3-1}=\frac{1}{3}$ by (R1) and Observation 1.

Let $j\in \{i+1,i+s\}$, say $j=i+1$. If $d_H(v_{j})\ge 4$, then $\tau (v\rightarrow v_{j})\le \frac{2}{3}$ by Observation 2(3)–(4). If $d_H(v_{j})=3$ and $d_{3}^{H}(v_{j})=0$, then $d_{5^{-}}^{H}(v_{j})=d_{3}^{H}(v_{j})=0$ by Claim 13(2). Hence, $d_H(f_j)\ge 4$ and $\tau (v\rightarrow v_{j})\le \frac{6-3-1}{3}=\frac{2}{3}$ by (R1) and Observation 1. Suppose that $d_H(v_{j})=3$ and $d_{3}^{H}(v_{j})=1$. Let v, $w_1$, $w_2$ be the neighbors of $v_j$ in the clockwise order. If $d_H(w_1)=3$, then $d_H(f_{j-1})\ge 4$. By Claim 13(1)–(3), $d_H(w_2)\ge 8$ and $d_H(f_j)\ge 4$. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-3-2}{3-1}=\frac{1}{2}$ by (R1) and Observation 1. If $d_H(w_2)=3$, then $d_{5^{-}}^{H}(w_{2})=d_{3}^{H}(w_{2})=1$ by Claim 13(2). Then $f_{j}$ is either a 5-face without 2-vertices or a $6^{+}$-face. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-3-\frac{4}{3}}{3-1}=\frac{5}{6}$ by (R1) and Observation 1. Specially, suppose that $v_j$ is not in a bad 3-face. For $l\in \{1,2\}$ with $d_{H}(w_l)=3$, the faces incident with $v_jw_l$ are all $4^{+}$-faces. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-3-2}{3-1}=\frac{1}{2}$ by (R1) and Observation 1.

Consequently, $\sum \limits _{j=1}^{s}\tau (v\rightarrow v_{i+j})\le 2\cdot \frac{5}{6}+\frac{1}{3}(s-2)=\frac{s}{3}+1$. In particular,

• (1) If neither $v_{i+1}$ nor $v_{i+s}$ is in a bad 3-face, then $\sum \limits _{j=1}^{s}\tau (v\rightarrow v_{i+j})\le 2\cdot \frac{2}{3}+\frac{1}{3}(s-2)=\frac{s}{3}+\frac{2}{3}$.

• (2) If exactly one of $v_{i+1}$ and $v_{i+s}$ is in a bad 3-face, then $\sum \limits _{j=1}^{s}\tau (v\rightarrow v_{i+j})\le \frac{2}{3}+\frac{5}{6}+\frac{1}{3}(s-2)=\frac{s}{3}+\frac{5}{6}$.

• (3) If neither $v_{i+1}$ nor $v_{i+2}$ is in a bad 3-face, then $\tau (v\rightarrow v_{i+1})+\tau (v\rightarrow v_{i+2})\le \frac{4}{3}<\frac{3}{2}$ by (1). If exactly one of $v_{i+1}$ and $v_{i+2}$ is in a bad 3-face, then $\tau (v\rightarrow v_{i+1})+\tau (v\rightarrow v_{i+2})\le \frac{3}{2}$ by (2). Suppose that $v_{i+1}$ and $v_{i+2}$ are all incident with bad 3-faces. Then $d_H(v_{i+1})=d_H(v_{i+2})=3$ and $d_{3}^{H}(v_{i+1})=d_{3}^{H}(v_{i+2})=1$. Let $v,x_1,x_2$ be the neighbors of $v_{i+1}$ in the clockwise order. Let v, $y_1$, $y_2$ be the neighbors of $v_{i+2}$ in the clockwise order. If $d_H(x_1)=3$, then $f_{i}$ is either a 4-face without 2-vertices or a $5^{+}$-face. By Claim 13(1)-(3), $d_H(x_2)\ge 8$ and $d_H(f_{i+1})\ge 4$. Hence, $\tau (v\rightarrow v_{i+1})+\tau (v\rightarrow v_{i+2})\le \frac{6-3-2}{3-1}+\frac{6-3-1}{3-1}=\frac{3}{2}$ by (R1) and Observation 1. If $d_H(y_2)=3$, then $\tau (v\rightarrow v_{i+1})+\tau (v\rightarrow v_{i+2})\le \frac{3}{2}$ by symmetry. If $d_H(x_2)=d_H(y_1)=3$, then $f_{i+1}$ is either a 6-face without 2-vertices or a $7^{+}$-face. Hence, $\tau (v\rightarrow v_{i+1})+\tau (v\rightarrow v_{i+2})\le \frac{6-3-\frac{3}{2}}{3-1}+\frac{6-3-\frac{3}{2}}{3-1}=\frac{3}{2}$ by (R1) and Observation 1. $\square$

Let $f\in F(H)$. If $d_H(f)=3$, then $\omega '(f)=\omega (f)=2\times 3-6=0$. If $d_H(f)=4$, then by (R1), f gives at most 2 to all its incident small vertices. Hence, $\omega '(f)\ge \omega (f)-2=2\times 4-6-2=0$. If $d_H(f)\ge 5$, then by (R2),

$$\begin{aligned} \omega '(f)\ge & {} \omega (f)-2d_{2}^{H}(f)-\frac{\omega (f)-2d^{H}_{2}(f)}{d_{3}^{H}(f)+d_{4}^{H}(f)+d_{5}^{H}(f)}(d_{3}^{H}(f)\\&+d_{4}^{H}(f)+d_{5}^{H}(f))=0. \end{aligned}$$

Let $v\in V(H)$ be a k-vertex. Then $k\ge 2$. Let $v_{0},v_{1},\ldots ,v_{k-1}$ denote the neighbors of v in the clockwise order. For $0\le i\le k-1$, we use $f_{i}$ to denote the incident face of v in H with $vv_{i}$ and $vv_{i+1}$ as boundary edges, where all indices are taken as modulo k. If $6\le k\le 7$, then $\omega '(v)=\omega (v)=k-6\ge 0$ by (R3) and Claim 13(3).

Case 1$2\le k\le 5$. If $d_{k}^{H}(v)=1$, then $d_{7^{-}}^{H}(v)=1$ by Claim 13(1)-(3). Hence, by (R1)-(R3), $\omega '(v)\ge k-6+\beta (v)+(k-1)\frac{6-k-\beta (v)}{k-1}=0$. If $d_{k}^{H}(v)=0$, then $d_{7^{-}}^{H}(v)=0$ by Claim 13(1)-(3). Hence, by (R1)-(R3), $\omega '(v)\ge k-6+\beta (v)+k\cdot \frac{6-k-\beta (v)}{k}=0$.

Case 2$k=8$. Then $\omega (v)=2$. If $d_{4^{-}}^{H}(v)\ge 1$, then $d_{5^{-}}^{H}(v)\le 1$ by Claim 13(4). Then v is not in a bad 3-face. Hence, $\omega '(v)\ge 2-d_{5^{-}}^{H}(v)\ge 2-1=1$ by Observation 2(1)-(3). If $d_{4^{-}}^{H}(v)=0$, then $\omega '(v)\ge 2-\frac{1}{4}d_{5}^{H}(v)\ge 2-\frac{1}{4}\times 8=0$ by Observation 2(4).

Case 3$k=9$. Then $\omega (v)=3$ and v is not in a bad 3-face by Claim 13(5). If $d_{4^{-}}^{H}(v)\ge 1$, then $d_{5^{-}}^{H}(v)\le 2$ by Claim 13(5). Hence, $\omega '(v)\ge 3-d_{5^{-}}^{H}(v)\ge 3-1\times 2=1$ by Observation 2(1)-(4). If $d_{4^{-}}^{H}(v)=0$, then $\omega '(v)\ge 3-\frac{1}{4}d_{5}^{H}(v)\ge 3-\frac{1}{4}\times 9=\frac{3}{4}$ by Observation 2(4).

Case 4$k=10$. Then $\omega (v)=4$ and v is not in a bad 3-face by Claim 13(6). If $d_{3^{-}}^{H}(v)\ge 1$, then $d_{6^{+}}^{H}(v)\ge 2d_{4^{-}}^{H}(v)+1$ by Claim 13(6), which implies that $d_{4^{-}}^{H}(v)\le 3$. Hence, $\omega '(v)\ge 4-d_{4^{-}}^{H}(v)-\frac{1}{4}(10-d_{4^{-}}^{H}(v)-d_{6^{+}}^{H}(v))\ge \frac{7}{4}-\frac{1}{4}d_{4^{-}}^{H}(v)\ge 1$ by Observation 2(1)-(4). If $d_{3^{-}}^{H}(v)=0$ and $d_{4}^{H}(v)\ge 1$, then $d_{6^{+}}^{H}(v)\ge d_{4}^{H}(v)+1$ by Claim 13(6), which implies that $d_{4}^{H}(v)\le 4$. Hence, $\omega '(v)\ge 4-\frac{2}{3}d_{4}^{H}(v)-\frac{1}{4}(10-d_{4}^{H}(v)-d_{6^{+}}^{H}(v))\ge \frac{7}{4}-\frac{1}{6}d_{4}^{H}(v)\ge \frac{13}{12}$ by Observation 2(3)-(4). If $d_{4^{-}}^{H}(v)=0$, then $\omega '(v)\ge 4-\frac{1}{4}d_{5}^{H}(v)\ge 4-\frac{1}{4}\times 10=\frac{3}{2}$ by Observation 2(4).

Case 5$k=11$. Then $\omega (v)=5$. If v is in a bad 3-face, then $d_{6^{+}}^{H}(v)\ge 9$ by Claim 13(7). Hence, $\omega '(v)\ge 5-\frac{3}{2}\times 2=2$ by Observation 2. Otherwise, v is not in a bad 3-face.

Case 5.1$d_{3^{-}}^{H}(v)\ge 1$. By Claim 13(7), $d_{6^{+}}^{H}(v)\ge d_{4^{-}}^{H}(v)+1$, which implies that $d_{4^{-}}^{H}(v)\le 5$. Hence, $\omega '(v)\ge 5-d_{4^{-}}^{H}(v)-\frac{1}{4}(11-d_{4^{-}}^{H}(v)-d_{6^{+}}^{H}(v))\ge \frac{5}{2}-\frac{1}{2}d_{4^{-}}^{H}(v)\ge 0$ by Observation 2(1)-(4).

Case 5.2$d_{3^{-}}^{H}(v)=0$. Let $p=d_{6^{+}}^{H}(v)$, $v_{i_1},v_{i_2},\ldots ,v_{i_p}$ be $6^{+}$-vertices with $0=i_1< i_2<\cdots <i_p$, and $n_j=|\{l |i_{j}+1\le l\le i_{j+1}-1,4\le d_{H}(v_l)\le 5\}|$ for $j\in [1,p]$. Then $i_{p+1}-1=10$ and $\sum \limits _{j=1}^{p}n_{j}=11-p$. If $p\ge 4$, then $\omega '(v)\ge 5-\frac{2}{3}(11-p)=\frac{2}{3}p-\frac{7}{3}\ge \frac{1}{3}$ by Observation 2(3)–(4). Assume that $p\le 3$. Note that every vertex in $N_{H}(v)\backslash \{v_{i_1},v_{i_{2}},\ldots ,v_{i_{p}}\}$ is not in a bad 3-face. By Observations 2 and 3, $\sum \limits _{l=i_{j}+1}^{i_{j+1}-1}\tau (v\rightarrow v_{l})\le \frac{n_{j}}{3}+\frac{2}{3}$ for $j\in [1,p]$. Hence, $\omega '(v)\ge 5-\sum \limits _{j=1}^{p}(\frac{n_{j}}{3}+\frac{2}{3})=\frac{4-p}{3}\ge \frac{1}{3}.$

Case 6$k=12$. Then $\omega (v)=6$ and $d_{2}^{H}(v)\le 1$ by Claim 5(2). If v is in a bad 3-face, then $d_{6^{+}}^{H}(v)\ge 5$ by Claim 13(8). Hence, $\omega '(v)\ge 6-\frac{3}{2}\times 2-\frac{1}{2}(12-2-d_{6^{+}}^{H}(v))=\frac{1}{2}d_{6^{+}}^{H}(v)-2\ge \frac{1}{2}$ by Observation 2. So assume that v is not in a bad 3-face.

Case 6.1$d_{2}^{H}(v)=1$. By Claim 13(8), $d_{6^{+}}^{H}(v)\ge d_{3^{-}}^{H}(v)+1$. Then $\omega '(v)\ge 6-d_{3^{-}}^{H}(v)-\frac{2}{3}(12-d_{3^{-}}^{H}(v)-d_{6^{+}}^{H}(v))=\frac{2}{3}d_{6^{+}}^{H}(v)-\frac{1}{3}d_{3^{-}}^{H}(v)-2$ by Observation 2. If $d_{6^{+}}^{H}(v)\ge 5$, then $\omega '(v)\ge \frac{1}{3}d_{6^{+}}^{H}(v)-\frac{5}{3}\ge 0$. If $d_{3^{-}}^{H}(v)\ge 4$, then $\omega '(v)\ge \frac{1}{3}d_{3^{-}}^{H}(v)-\frac{4}{3}\ge 0$. Assume that $d_{3^{-}}^{H}(v)\le 3$ and $d_{6^{+}}^{H}(v)\le 4$. Let $p=d_{6^{+}}^{H}(v)$ and $v_{i_1},v_{i_2},\ldots ,v_{i_p}$ be $6^{+}$-vertices with $0=i_1< i_2<\cdots <i_p$.

Suppose that v is in a special 3-face. If $2\le d_{3^{-}}^{H}(v)\le 3$, then $d_{6^{+}}^{H}(v)\ge 5$ by Claim 13(8). Otherwise, $d_{3^{-}}^{H}(v)=1$. Let $v_{i_{p}+1}$ be a 2-vertex, $n_j=|\{l|i_{j}+1\le l\le i_{j+1}-1,4\le d_{H}(v_l)\le 5\}|$ for $j \in [1,p-1]$, and $n_p=|\{l|i_{p}+2\le l\le i_{p+1}-1,4\le d_{H}(v_l)\le 5\}|$. Then $i_{p+1}-1=11$ and $\sum \limits _{j=1}^{p}n_{j}=11-p$. By Observations 2 and 3, $\sum \limits _{l=i_{j}+1}^{i_{j+1}-1}\tau (v\rightarrow v_{l})\le \frac{n_{j}}{3}+\frac{2}{3}$ for $j\in [1,p-1]$, and $\sum \limits _{l=i_{p}+2}^{i_{p+1}-1}\tau (v\rightarrow v_{l})\le \frac{n_{p}}{3}+\frac{2}{3}$. Hence, $\omega '(v)\ge 6-1-\sum \limits _{j=1}^{p}(\frac{n_{j}}{3}+\frac{2}{3})=\frac{4-p}{3}\ge 0.$

Suppose that v is not in a special 3-face. Let $v_{i_{p+1}}$ be a 2-vertex and $n_j=|\{l|i_{j}+1\le l\le i_{j+1}-1,3\le d_{H}(v_l)\le 5\}|$ for $j \in [1,p+1]$. Then $i_{p+2}-1=11$ and $\sum \limits _{j=1}^{p+1}n_{j}=11-p$. If $d_{3^{-}}^{H}(v)=1$, then each vertex in $N_{H}(v)\backslash \{v_{i_1},v_{i_{2}},\ldots ,v_{i_{p+1}}\}$ is a 4-vertex or a 5-vertex. By Observations 2 and 3, $\omega '(v)\ge 6-\sum \limits _{j=1}^{p+1}(\frac{n_{j}}{3}+\frac{2}{3})=\frac{5-p}{3}\ge \frac{1}{3}$. If $d_{3^{-}}^{H}(v)=2$, then there is $s\in [1,p+1]$ such that a 3-vertex is in $\{v_{i_s+1},\ldots ,v_{i_{s+1}-1}\}$. By Observations 2 and 3, $\omega '(v)\ge 6-(\frac{n_{s}}{3}+\frac{5}{6})-\sum \limits _{j\in [1,p+1]}^{j\ne s}(\frac{n_{j}}{3}+\frac{2}{3})=\frac{9-2p}{6}\ge \frac{1}{6}.$ Suppose that $d_{3^{-}}^{H}(v)=3$. If there is $s\in [1,p+1]$ such that two 3-vertices are in $\{v_{i_s+1},\ldots ,v_{i_{s+1}-1}\}$, by Observations 2 and 3, then $\omega '(v)\ge 6-(\frac{n_{s}}{3}+1)-\sum \limits _{j\in [1,p+1]}^{j\ne s}(\frac{n_{j}}{3}+\frac{2}{3})=\frac{4-p}{3}\ge 0.$ Otherwise, there are $s,t\in [1,p+1]$ such that two 3-vertices are in $\{v_{i_s+1},\ldots ,v_{i_{s+1}-1}\}$ and $\{v_{i_t+1},\ldots ,v_{i_{t+1}-1}\}$, respectively. By Observations 2 and 3, $\omega '(v)\ge 6-(\frac{n_{s}}{3}+\frac{5}{6})-(\frac{n_{t}}{3}+\frac{5}{6})-\sum \limits _{j\in [1,p+1]}^{j\ne s,t}(\frac{n_{j}}{3}+\frac{2}{3})=\frac{4-p}{3}\ge 0.$

Case 6.2$d_{2}^{H}(v)=0$. Let $p=d_{6^{+}}^{H}(v)$, $v_{i_1},v_{i_2},\ldots ,v_{i_p}$ be $6^{+}$-vertices with $0=i_1< i_2<\cdots <i_p$, and $n_j=|\{l|i_{j}+1\le l\le i_{j+1}-1,3\le d_{H}(v_l)\le 5\}|$ for $j\in [1,p]$. Then $i_{p+1}-1=11$ and $\sum \limits _{j=1}^{p}n_{j}=12-p$. If $p\ge 6$, then $\omega '(v)\ge 6-(12-p)=p-6\ge 0$ by Observation 2. If $p\le 3$, then $\omega '(v)\ge 6-\sum \limits _{j=1}^{p}(\frac{n_{j}}{3}+1)=\frac{6-2p}{3}\ge 0$ by Observations 2 and 3.

Suppose that $p=4$. If there are five consecutive vertices $v_{i+1},v_{i+2},\ldots ,v_{i+5}\in N_{3,4,5}^H(v)$, then $\omega '(v)\ge 6-(\frac{5}{3}+1)-(12-4-5)=\frac{1}{3}$ by Observations 2 and 3. If there are $s,t\in [1,4]$ with $n_s=4$ and $n_t=2$, then $\omega '(v)\ge 6-(\frac{4}{3}+1)-\frac{3}{2}-(12-4-6)=\frac{1}{6}$ by Observations 2 and 3. If there are $s,t\in [1,4]$ with $n_s=n_t=3$, then $\omega '(v)\ge 6-2\times (\frac{3}{3}+1)-(12-4-6)=0$ by Observations 2 and 3. If there are $s,t,r\in [1,4]$ with $n_s=3$ and $n_t=n_r=2$, then $\omega '(v)\ge 6-(\frac{3}{3}+1)-2\times \frac{3}{2}-(12-4-7)=0$ by Observations 2 and 3. Otherwise, $n_1=n_2=n_3=n_4=2$. By Observations 2 and 3, $\omega '(v)\ge 6-4\times \frac{3}{2}=0$.

Suppose that $p=5$. If there are three consecutive vertices $v_{i+1},v_{i+2},v_{i+3}\in N_{3,4,5}^H(v)$, Observations 2 and 3 implies that $\omega '(v)\ge 6-(\frac{3}{3}+1)-(12-5-3)=0$. Otherwise, there are $s,t\in [1,5]$ with $n_s=n_t=2$. By Observations 2 and 3, $\omega '(v)\ge 6-2\times \frac{3}{2}-(12-5-4)=0$.

Case 7$k\ge 13$. If v is in $G_{1}$, then $\omega '(v)\ge k-6-2\times \frac{3}{2}-\frac{1}{3}(k-2-d_{6^{+}}^{H}(v))=\frac{1}{3}(2k-25+d_{6^{+}}^{H}(v))\ge 0$ by Observation 2. So assume that v is not in $G_1$.

Suppose that v is in a bad 3-face. By Claim 12(1), $d^H_2(v)=0$ and v is in at most one bad 3-face. If $d_{6^{+}}^{H}(v)\ge 1$, then $\omega '(v)\ge k-6-2\times 1-\frac{1}{2}(k-2-d_{6^{+}}^{H}(v))=\frac{1}{2}(k-14+d_{6^{+}}^{H}(v))\ge 0$ by Observation 2. Otherwise, $d_{6^{+}}^{H}(v)=0$. Assume that $d_H(v_j)=s\in [3,5]$ for $j\in [2,k-1]$. If $d_{s}^{H}(v_{j})=0$, then $f_{j-1}$ and $f_{j}$ are 4-faces without 2-vertices or $5^{+}$-faces. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-s-2}{s}\le \frac{1}{3}$ by (R1) and Observation 1. If $d_{s}^{H}(v_{j})=1$ and $s\ge 4$, then $d_{5^{-}}^{H}(v_{j})=d_{s}^{H}(v_{j})=1$ by Claim 13(2). Then at least one of $f_{j-1}$ and $f_{j}$ is a $4^{+}$-face. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-s-1}{s-1}\le \frac{1}{3}$ by (R1) and Observation 1. If $s=3$ and $d_{3}^{H}(v_{j})=1$, then one of $f_{j-1}$ and $f_{j}$ is a $4^{+}$-face and the other is a $5^{+}$-face. Hence, $\tau (v\rightarrow v_{j})\le \frac{6-3-1-\frac{4}{3}}{3-1}=\frac{1}{3}$ by (R1) and Observation 1. Therefore, $\sum \limits _{j=2}^{k-1}\tau (v\rightarrow v_{j})\le \frac{k-2}{3}$, and $\omega '(v)\ge k-6-2\times 1-\frac{k-2}{3}=\frac{1}{3}(2k-22)\ge \frac{4}{3}$. So assume that v is not in a bad 3-face.

Case 7.1v is in a special 3-face. By Claim 5(4), $d^H_2(v)=1$. Let $p=d_{6^{+}}^{H}(v)$, $v_{i_1},v_{i_2},\ldots ,v_{i_p}$ be $6^{+}$-vertices with $0=i_1< i_2<\cdots <i_p$, and $v_{i_{p}+1}$ be a 2-vertex. Let $n_j=|\{l |i_{j}+1\le l\le i_{j+1}-1,3\le d_{H}(v_l)\le 5\}|$ for $j \in [1,p-1]$, and $n_p=|\{l|i_{p}+2\le l\le i_{p+1}-1,3\le d_{H}(v_l)\le 5\}|$. Then $i_{p+1}-1=k-1$ and $\sum \limits _{j=1}^{p}n_{j}=k-p-1$. By Observations 2 and 3, $\sum \limits _{l=i_{j}+1}^{i_{j+1}-1}\tau (v\rightarrow v_{l})\le \frac{n_{j}}{3}+1$ for $j\in [1,p-1]$, and $\sum \limits _{l=i_{p}+2}^{i_{p+1}-1}\tau (v\rightarrow v_{l})\le \frac{n_{p}}{3}+1$. If $p\le 3$, then $\omega '(v)\ge k-6-1-\sum \limits _{j=1}^{p}(\frac{n_{j}}{3}+1)=\frac{2k-2p-20}{3}\ge 0.$ If $p\ge 6$, then $\omega '(v)\ge k-6-1-(k-p-1)=p-6\ge 0$ by Observation 2.

Suppose that $p=4$. If there are five consecutive vertices $v_{i+1},v_{i+2},\ldots ,v_{i+5}\in N_{3,4,5}^H(v)$, then $\omega '(v)\ge k-6-1-(\frac{5}{3}+1)-(k-1-4-5)=\frac{1}{3}$ by Observations 2 and 3. If there are $s,t\in [1,4]$ with $n_s=4$ and $n_t=2$, then $\omega '(v)\ge k-6-1-(\frac{4}{3}+1)-\frac{3}{2}-(k-1-4-6)=\frac{1}{6}$ by Observations 2 and 3. If there are $s,t\in [1,4]$ with $n_s=n_t=3$, then $\omega '(v)\ge k-6-1-2\times (\frac{3}{3}+1)-(k-1-4-6)=0$ by Observations 2 and 3. If there are $s,t,r\in [1,4]$ with $n_s=3$ and $n_t=n_r=2$, then $\omega '(v)\ge k-6-1-(\frac{3}{3}+1)-2\times \frac{3}{2}-(k-1-4-7)=0$ by Observations 2 and 3. Otherwise, $n_1=n_2=n_3=n_4=2$. Then $k=13$. By Observations 2 and 3, $\omega '(v)\ge 13-6-1-4\times \frac{3}{2}=0$.

Suppose that $p=5$. If there are three consecutive vertices $v_{i+1},v_{i+2},v_{i+3}\in N_{3,4,5}^H(v)$, then $\omega '(v)\ge k-6-1-(\frac{3}{3}+1)-(k-1-5-3)=0$ by Observations 2 and 3. Otherwise, there are $s,t\in [1,5]$ with $n_s=n_t=2$. By Observations 2 and 3, $\omega '(v)\ge k-6-1-2\times \frac{3}{2}-(k-1-5-4)=0$.

Case 7.2v is not in a special 3-face. Let $q=d^H_2(v)+d_{6^{+}}^{H}(v)$, $v_{i_1},v_{i_2},\ldots ,v_{i_q}$ be $6^{+}$-vertices or 2-vertices with $0=i_1< i_2<\cdots <i_q$, and $n_j=|\{l|i_{j}+1\le l\le i_{j+1}-1,3\le d_{H}(v_l)\le 5\}|$ for $j \in [1,q]$. Then $i_{q+1}-1=k-1$ and $\sum \limits _{j=1}^{q}n_{j}=k-q$. By Observations 2 and 3, $\sum \limits _{l=i_{j}+1}^{i_{j+1}-1}\tau (v\rightarrow v_{l})\le \frac{n_{j}}{3}+1$ for $j\in [1,q]$. If $q\le 4$, then $\omega '(v)\ge k-6-\sum \limits _{j=1}^{q}(\frac{n_{j}}{3}+1)=\frac{2k-2q-18}{3}\ge 0.$ If $q\ge 6$, then $\omega '(v)\ge k-6-(k-q)=q-6\ge 0$ by Observation 2.

Suppose that $q=5$. If there are three consecutive vertices $v_{i+1},v_{i+2},v_{i+3}\in N_{3,4,5}^H(v)$, then $\omega '(v)\ge k-6-(\frac{3}{3}+1)-(k-5-3)=0$ by Observations 2 and 3. Otherwise, there are $s,t\in [1,5]$ with $n_s=n_t=2$. By Observations 2 and 3, $\omega '(v)\ge k-6-2\times \frac{3}{2}-(k-5-4)=0$. $\square$