Spectral Collocation Methods for Nonlinear Volterra Integro-Differential Equations with Weakly Singular Kernels

Abstract

A spectral Jacobi-collocation approximation is proposed and analyzed for nonlinear integro-differential equations of Volterra type with weakly singular kernel, and a rigorous error analysis is provided for the spectral methods to show both the errors of approximate solutions and the errors of approximate derivatives of the solutions decaying exponentially in infinity-norm and weighted $L^2$-norm. Numerical results are presented to confirm the theoretical prediction of the exponential rate of convergence.

1 Introduction

In this paper, we consider the following nonlinear Volterra integral-differential equation (VIDEs) of the second kind with weakly singular kernel

$$\begin{aligned} y'(t)={\widehat{f}}(t,y(t))+\int ^t_{0}(t-\tau )^{-\mu }{\widehat{K}}(t,\tau ,y(\tau ))\hbox {d}\tau +{\widehat{g}}(t), \quad t\in [0,T], \end{aligned}$$

(1.1)

subject to the initial condition given by

$$\begin{aligned} \begin{aligned} y(0)=y_0, \end{aligned} \end{aligned}$$

(1.2)

where $0<\mu < 1$, ${\widehat{f}}:[0,T]\times {\mathbb {R}}\rightarrow {\mathbb {R}}$, kernel function ${\widehat{K}}: S\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ (where $S:=\{(t,\tau ):0\le \tau \le t\le T\})$ and ${\widehat{g}}(t): [0,T]\rightarrow {\mathbb {R}}$ are known, y(t) is the unknown function to be determined.

Equation (1.1) arised as model equation for describing turbulent diffusion problems. Due to the fact that the solutions of Eq. (1.1) usually have a weak singularity at $t = 0$, and its nonlinear, the numerical treatment of the Volterra integro-differential equation (1.1) is not simple. As shown in [1], the second derivative of the solution y(t) behaves like $y''(t)\sim t^{-\mu }$.

The given function f in (1.1) is continuous for all t and y, and satisfies the Lipschitz conditions:

$$\begin{aligned} \mid {\hat{f}}(t,y_1)-{\hat{f}}(t,y_2)\mid \le M\mid y_1-y_2\mid , \end{aligned}$$

(1.3)

${\widehat{g}}(x) \in C[0, T]$, and ${\widehat{K}}$ is continuous for all S and Lipschitz continuous with its third argument. Under these conditions, (1.1) possess a unique solution.

Volterra integro-differential equations have been widely used in mathematical models of certain biological and physical phenomena. Due to the wide application of these equations, efficient numerical methods are urgently needed, and there have been many types of methods, such as piecewise polynomial collocation methods [2, 3], spline collocation methods [4], polynomial spline collocation methods [5,6,7], spectral Galerkin method [8,9,10], spectral Jacobi-collocation approximation [11,12,13,14,15,16]. Yet so far, to the authors knowledge, spectral collocation methods for the nonlinear Volterra integral-differential equation with singular kernel had few results.

In this paper, we investigate the Jacobi-collocation methods for the Eq. (1.1) and provide a rigorous error analysis for the spectral methods, which shows that both the errors of approximate solutions and the errors of approximate derivatives of the solutions decay exponentially in $L^\infty$-norm and weighted $L^2$-norm.

The paper is organized as follows. In Sect. 2, we outline the Jacobi-collocation methods for nonlinear Volterra integro-differential equations with weakly singular kernels Eq. (1.1). In Sect. 3, we describe some useful lemmas for establishing the convergence. In Sect. 4, we show the convergence analysis. Numerical results are performed to demonstrate the convergence analysis in Sect. 5. In the final section, we give a conclusion.

2 Jacobi-Collocation Method

Let $\omega ^{\alpha ,\beta }(x) = (1-x)^\alpha (1+x)^\beta$ be a weight function in the usual sense, for $\alpha ,\beta >-1$. As defined in [17,18,19], the set of Jacobi polynomials $\{J_n^{\alpha ,\beta }(x)\}^\infty _{n=0}$ forms a complete $L^2_{\omega ^{\alpha ,\beta }}(-1,1)$-orthogonal system, where $L^2_{\omega ^{\alpha ,\beta }}(-1,1)$ is a weighted space defined by

$$\begin{aligned} L^2_{\omega ^{\alpha ,\beta }}(-1,1)=\{v: v \text { is measurable and } \parallel v\parallel _{\omega ^{\alpha ,\beta }}<\infty \}, \end{aligned}$$

equipped with the norm

$$\begin{aligned} \parallel v\parallel _{\omega ^{\alpha ,\beta }}=\left( \int ^1_{-1}|v(x)|^2\omega ^{\alpha ,\beta }(x)\hbox {d}x\right) ^{\frac{1}{2}}, \end{aligned}$$

and the inner product

$$\begin{aligned} (u,v)_{\omega ^{\alpha ,\beta }}=\int ^1_{-1}u(x)v(x)\omega ^{\alpha ,\beta }(x)\hbox {d}x, \quad \forall u,v\in L^2_{\omega ^{\alpha ,\beta }}(-1,1). \end{aligned}$$

For a given $N\ge 0$, $\{{\theta }_k\}_{k=0}^N$ and $\{\omega ^{\alpha ,\beta }_k\}_{k=0}^N$ are denoted as the Jacobi–Gauss points and corresponding Jacobi weights, respectively. Then, the Jacobi–Gauss integration formula are defined as follows:

$$\begin{aligned} \int _{-1}^1f(x)\omega ^{\alpha ,\beta }(x)\hbox {d}x\approx \sum \limits _{k=0}^Nf({\theta }_k){\omega ^{\alpha ,\beta }_k}. \end{aligned}$$

(2.1)

Similarly, $\{{\tilde{\theta }}_k\}_{k=0}^N$ denotes the Legendre points, and $\{{\omega }_k\}_{k=0}^N$ the corresponding Legendre weights (i.e., Jacobi weights $\{\omega ^{0,0}_k\}_{k=0}^N$). Then, we have the Legendre-Gauss integration formula

$$\begin{aligned} \int _{-1}^1f(x)\hbox {d}x\approx \sum \limits _{k=0}^Nf({\tilde{\theta }}_k){\omega }_k. \end{aligned}$$

(2.2)

For $N>0$, $\{x_i^{\alpha ,\beta }\}^N_{ i=0}$ denotes the collocation points, which is a set of $(N +1)$ Jacobi Gauss points, with weight $\omega ^{\alpha ,\beta }(x)$. Let $\mathcal {P}_N$ be the space of polynomials of degree at most N. For any $v \in C[-1, 1]$, one can define the Lagrange interpolating polynomial $I^{\alpha ,\beta }_N v \in \mathcal {P}_N$, such that

$$\begin{aligned} I^{\alpha ,\beta }_N v(x)=\sum ^N_{i=0}v(x_i)F_i(x),\quad 0\le i\le N, \end{aligned}$$

where

$$\begin{aligned} I^{\alpha ,\beta }_N v(x_i)=v(x_i),\quad 0\le i\le N. \end{aligned}$$

and $F_i(x)$ is the Lagrange interpolation basis function associated with $x_i$.

To apply the theory of orthogonal polynomials, we consider variable substitution

$$\begin{aligned} t= & {} \frac{1}{2}T(1+x),\quad x=\frac{2t}{T}-1,\\ \tau= & {} \frac{1}{2}T(1+s),\quad s=\frac{2\tau }{T}-1, \end{aligned}$$

and let

$$\begin{aligned} u(x)= & {} y\left( \frac{1}{2}T(1+x)\right) ,\quad g(x)={\widehat{g}}\left( \frac{1}{2}T(1+x)\right) ,\\ f(t,u)= & {} {\widehat{f}}\left( \frac{1}{2}T(1+x),y\left( \frac{1}{2}T(1+x)\right) \right) ,\\ K(x,s,u)= & {} \left( \frac{T}{2}\right) ^{-\mu }{\widehat{K}}\left( \frac{1}{2}T(1+x),\frac{1}{2}T(1+s),y(\frac{1}{2}T(1+s))\right) , \end{aligned}$$

then we get

$$\begin{aligned} \begin{aligned}&u'(x)=f(x,u(x))+\int ^x_{-1}(x-s)^{-\mu }K(x,s,u(s))\hbox {d}s+g(x), \quad 0<\mu < 1,\\&u(x)=\int ^x_{-1}u'(s)\hbox {d}s+u(-1),\quad x\in I=[-1,1]. \end{aligned} \end{aligned}$$

(2.3)

Set the collocation points as the set of $(N + 1)$ Jacobi–Gauss points, $\{x_i^{-\mu ,-\mu }\}^N_{ i=0}$ associated with Jacobi weight $\omega ^{-\mu ,-\mu }$. Assume that (2.3) holds at $x_i^{-\mu ,-\mu }$:

$$\begin{aligned} \begin{aligned} u'(x_i^{-\mu ,-\mu })&=f(x_i^{-\mu ,-\mu },u(x_i^{-\mu ,-\mu }))\\&\quad +\int ^{x_i^{-\mu ,-\mu }}_{-1}(x_i^{-\mu ,-\mu }-s)^{-\mu }K(x_i^{-\mu ,-\mu },s,u(s))\hbox {d}s+g(x_i^{-\mu ,-\mu }),\\ u(x_i^{-\mu ,-\mu })&=\int ^{x_i^{-\mu ,-\mu }}_{-1}u'(s)\hbox {d}s+u(-1). \end{aligned} \end{aligned}$$

(2.4)

The main difficulty in obtaining high order of accuracy lies in the computation of the integral term in (2.4). Furthermore, for small values of $x_i$, there is little information available for u(s). To overcome this difficulty, we transfer the integral interval $[-1, x_i^{-\mu ,-\mu }]$ to a fixed interval $[-1, 1]$, then make use of some appropriate quadrature rule. More precisely, we first set

$$\begin{aligned} s(x,\theta )=\frac{1+x}{2}\theta +\frac{x-1}{2}\theta ,\quad -1\le \theta \le 1. \end{aligned}$$

(2.5)

Then, (2.4) becomes

$$\begin{aligned} u'(x_i^{-\mu ,-\mu })= & {} f(x_i^{-\mu ,-\mu },u(x_i^{-\mu ,-\mu }))\nonumber \\&+\int ^{1}_{-1}(1-\theta )^{-\mu } {\widetilde{K}}(x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta ),u(s(x_i^{-\mu ,-\mu },\theta )))\hbox {d}\theta \nonumber \\&+\,g(x_i^{-\mu ,-\mu }),\nonumber \\ u(x_i^{-\mu ,-\mu })= & {} \left( \frac{1+x_i^{-\mu ,-\mu }}{2}\right) \int ^{1}_{-1}u'(s(x_i^{-\mu ,-\mu },\theta ))\hbox {d}\theta +u(-1), \end{aligned}$$

(2.6)

where

$$\begin{aligned} \begin{aligned}&{\widetilde{K}}(x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta ),u(s(x_i^{-\mu ,-\mu },\theta )))\\&\quad =\left( \frac{1+x_i^{-\mu ,-\mu }}{2}\right) ^{1-\mu }{K}(x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta ),u(s(x_i^{-\mu ,-\mu },\theta ))). \end{aligned} \end{aligned}$$

Next, using Jacobi–Gauss integration formula, the integration term in (2.6) can be approximated by

$$\begin{aligned} \begin{aligned}&\int ^{1}_{-1}(1-\theta )^{-\mu } {\widetilde{K}}(x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta ),u(s(x_i^{-\mu ,-\mu },\theta )))\hbox {d}\theta \\&\quad \approx \sum ^N_{k=0}{\widetilde{K}}(x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta _k),u(s(x_i^{-\mu ,-\mu },\theta _k)))\omega ^{-\mu ,0}_k, \end{aligned} \end{aligned}$$

(2.7)

where the set $\{\theta _k\}^N _{i=0}$ is the Jacobi–Gauss points corresponding Jacobi weights $\omega ^{-\mu ,0}_k$. Similarly,

$$\begin{aligned} \int ^{1}_{-1}u'(s(x_i^{-\mu ,-\mu },\theta ))\hbox {d}\theta \approx \sum ^N_{k=0}u'(s(x_i^{-\mu ,-\mu },\tilde{\theta }_k))\omega _k, \end{aligned}$$

(2.8)

where the set $\{\tilde{\theta }_k\}^N_{k=0}$ is the Legendre-Gauss points corresponding Legendre weights $\{\omega _k\}^N_{k=0}$.

We use $u_i, u'_i, 0 \le i \le N$ to approximate the function value $u(x_i),u'(x_i), 0 \le i \le N$, and use

$$\begin{aligned} U(x)=\sum ^N_{j=0}u_jF_j(x),\quad U'(x)=\sum ^N_{j=0}u'_jF_j(x), \end{aligned}$$

(2.9)

where $F_j(x)$ is the Lagrange interpolation basis function associated with $\{x_i^{-\mu ,-\mu }\}^N_{ i=0}$ which is the set of $(N +1)$ Jacobi–Gauss points. Combining the above equations yields

$$\begin{aligned} \begin{aligned} u'_i&=f\left( x_i^{-\mu ,-\mu },\sum ^N_{j=0}u_jF_j(x_i^{-\mu ,-\mu })\right) \\&\quad +\sum ^N_{k=0}{\widetilde{K}}\left( x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta _k), \sum ^N_{j=0}u_jF_j(s(x_i^{-\mu ,-\mu },\theta _k))\right) \omega ^{-\mu ,0}_k\\&\quad +g(x_i^{-\mu ,-\mu }),\\ u_i&=\left( \frac{1+x_i^{-\mu ,-\mu }}{2}\right) \sum ^N_{k=0} \left( \sum ^N_{j=0}u'_jF_j(s(x_i^{-\mu ,-\mu },\tilde{\theta }_k))\right) \omega _k+u_{0}. \end{aligned} \end{aligned}$$

(2.10)

The numerical scheme (2.10) leads to a nonlinear system; we can obtain the values of $\{u_i\}^N_{ i=0}$ and $\{u'_i\}^N_{ i=0}$ by solving the nonlinear equation system.

3 Some Useful Lemmas

In this section, we present some useful lemmas for convergence analysis in Sect. 4. Here and below, C denotes a positive constant which is independent of N, and whose particular meaning will become clear by the context in which it arises.

Lemma 3.1

(see [17]) Let integrate the product $u\varphi$ is computed by $(N + 1)$-point Gauss quadrature formula relative to the Jacobi weight. If $u \in H^m(I)$ for some $m\ge 1$ and $\varphi \in {\mathcal {P}}_N$, then

$$\begin{aligned} \left| \int ^1_{-1}u(x)\varphi (x)\hbox {d}x-(u,\varphi )_{\omega ^{\alpha ,\beta },N}\right| \le CN^{-m}|u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(I)}\Vert \varphi \Vert _{L^2_{\omega ^{\alpha ,\beta }}(I)}, \end{aligned}$$

(3.1)

where

$$\begin{aligned} |u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(I)}= & {} \left( \sum ^m_{j=\min (m,N+1)}\Vert u^{(j)}\Vert ^2_{{\omega ^{\alpha ,\beta }}(I)}\right) ^{1/2},\nonumber \\ (u,\varphi )_{\omega ^{\alpha ,\beta },N}= & {} \sum ^N_{j=0}u(x_j)\varphi (x_j)\omega ^{\alpha ,\beta }_j. \end{aligned}$$

(3.2)

Lemma 3.2

(see [17]) Assume $u \in H^{m,N}_{\omega ^{-\mu ,-\mu }}(I)$, $I^{-\mu ,-\mu }_Nu$ is denoted as the interpolation polynomial associated with the $(N + 1)$ Jacobi–Gauss points $\{x_j\}^N_{j =0}$, namely,

$$\begin{aligned} I^{-\mu ,-\mu }_Nu(x)=\sum ^N_{j=0}u(x_j)F_j(x). \end{aligned}$$

Then, we have

$$\begin{aligned}&\Vert u-I^{-\mu ,-\mu }_Nu\Vert _{L^2_{\omega ^{-\mu ,-\mu }}(I)}\le CN^{-m}|u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(I)}, \end{aligned}$$

(3.3a)

$$\begin{aligned}&\Vert u-I^{-\mu ,-\mu }_Nu\Vert _{L^\infty (I)}\le {\left\{ \begin{array}{ll}CN^{1-\mu -m}|u|_{{H}^{m,N}_{\omega ^{c}}(I)},\quad &{}0\le \mu< \frac{1}{2},\\ CN^{\frac{1}{2}-m}\log N|u|_{{H}^{m,N}_{\omega ^{c}}(I)},\quad &{}\frac{1}{2}\le \mu < 1, \end{array}\right. } \end{aligned}$$

(3.3b)

where $\omega ^c=\omega ^{-\frac{1}{2},-\frac{1}{2}}$ denotes the Chebyshev weight function.

Lemma 3.3

(see [20]) Let $\{F_j(x)\}^N_{j=0}$ denote the Nth degree Lagrange basis polynomials associated with the Jacobi–Gauss points. Then,

$$\begin{aligned} \Vert I^{\alpha ,\beta }_N\Vert _{L^\infty (I)}\le \max _{x\in [-1,1]}\sum ^N_{j=0}\mid F_j(x)\mid = {\left\{ \begin{array}{ll}\mathcal {O}(\log N),&{}\quad -1<\alpha ,\beta \le -\frac{1}{2},\\ \mathcal {O}(N^{\gamma +\frac{1}{2}}),&{}\quad \gamma =\max (\alpha ,\beta ),\text { otherwise}. \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.4)

Lemma 3.4

(Gronwall inequality, see [21] Lemma 7.1.1) For $L \ge 0$, $0< \mu < 1$, u and v defined on $[-1, 1]$ satisfying

$$\begin{aligned} u(x)\le v(x)+L\int ^x_{-1}(x-\tau )^{-\mu }u(\tau )\hbox {d}\tau , \quad u(x),v(x)>0. \end{aligned}$$

Then, there exists a constant $C = C(\mu )$ such that

$$\begin{aligned} u(x)\le v(x)+CL\int ^x_{-1}(x-\tau )^{-\mu }v(\tau )\hbox {d}\tau ,\quad \text {for}\quad -1\le x<1. \end{aligned}$$

If a nonnegative integrable function E(x) satisfies

$$\begin{aligned} E(x)\le L \int ^x_{-1}E(s)\hbox {d}s+J(x),\quad -1<x\le 1, \end{aligned}$$

then

$$\begin{aligned} \begin{aligned}&\Vert E\Vert _{L^\infty (I)}\le C\Vert J\Vert _{L^\infty (I)},\\&\Vert E\Vert _{{\omega ^{\alpha ,\beta }}(I)}\le C\Vert J\Vert _{{\omega ^{\alpha ,\beta }}(I)},\quad q\ge 1. \end{aligned} \end{aligned}$$

(3.5)

Lemma 3.5

(see [22, 23]) For $r>0$, $\kappa \in (0, 1)$ and $v\in C^{r,\kappa }(I)$, then exists a polynomial function $\mathcal {T}_Nv \in \mathcal {P}_N$ and $C_{r,\kappa } > 0$ such that

$$\begin{aligned} \Vert v-\mathcal {T}_Nv\Vert _{L^\infty (I)}\le C_{r,\kappa }N^{-(r+\kappa )}\Vert v\Vert _{r,\kappa }, \end{aligned}$$

(3.6)

where $\Vert \cdot \Vert _{r,\kappa }$ is the standard norm in $C^{r,\kappa }(I)$, as stated in [22, 23], $\mathcal {T}_N$ is denoted as a linear operator from $C^{r,\kappa }(I)$ into $\mathcal {P}_N$.

Lemma 3.6

(see [24]) For $\kappa \in (0, 1)$, $\mathcal {M}$ is defined by

$$\begin{aligned} (\mathcal {M}v)(x)=\int ^x_{-1}(x-t)^{-\mu }K(x,t)v(t)\hbox {d}t. \end{aligned}$$

Then, for any function $v \in C(I)$ and $0< \kappa < 1 -\mu$, the following estimate hold

$$\begin{aligned} \frac{|\mathcal {M}v(x')-\mathcal {M}v(x'')|}{|x'-x''|}\le C\max _{x\in [-1,1]}|v(x)|,\quad x', x'' \in [-1, 1],\quad x'\ne x''. \end{aligned}$$

This implies that

$$\begin{aligned} \parallel \mathcal {M}v\parallel _{0,\kappa }\le C\max _{x\in [-1,1]}|v(x)|,\quad 0<\kappa <1-\mu . \end{aligned}$$

Lemma 3.7

(see [25]) Let $\{F_j(x)\}^N_{j=0}$ denote the $N-th$ degree Lagrange basis polynomials associated with the Jacobi–Gauss points, for every bounded function v, there exists a constant C, independent of v, such that

$$\begin{aligned} \sup _{N}\parallel \sum ^N_{j=0}v(x_j)F_j(x)\parallel _{L^2_{\omega ^{\alpha ,\beta }}(I)}\le C\max _{x\in [-1,1]}|v(x)|. \end{aligned}$$

Lemma 3.8

(see [26]) Assume $f \ge 0$ is a measurable function, for $1< p \le q < \infty$, u, v are nonnegative weight functions the Hardy’s inequality

$$\begin{aligned} \left( \int _a^b |(Tf)(x)|^qu(x)\hbox {d}x\right) ^{1/q}\le \left( \int _a^b |f(x)|^pv(x)\hbox {d}x\right) ^{1/p}, \quad -\infty \le a < b \le \infty \end{aligned}$$

holds if and only if

$$\begin{aligned} \sup _{a<x<b}\left( \int _x^b u(t)\hbox {d}t\right) ^{1/q}\left( \int _a^xv^{1-p'}(t)\hbox {d}t\right) ^{1/p'}<\infty ,\quad p'=\frac{p}{p-1}, \end{aligned}$$

where

$$\begin{aligned} (TF)(x)=\int ^x_ak(x,t)f(t)\hbox {d}t \end{aligned}$$

with k(x, t) a given kernel.

4 Convergence Analysis

In this section, we provide a rigorous error analysis for the Jacobi-collocation methods, which shows that both the errors of approximate solutions and the errors of approximate derivatives of the solutions decay exponentially in $L^\infty$-norm and weighted $L^2$-norm. First, we show the convergence analysis in $L^\infty$-norm.

Theorem 4.1

Assume u(x) the sufficiently smooth exact solution of the nonlinear Volterra integro-differential equation (2.3), f(x, u) and K(x, t, u) satisfies the Lipschitz conditions. U(x) and $U'(x)$ are the numerical solution of the spectral collocation scheme (2.10) with a polynomial interpolation (2.9). If $-\mu$ associated with the weakly singular kernel satisfies $0<\mu < 1$ and $u \in H^{m+1}_{\omega ^{-\mu ,-\mu }} (I)$, then

$$\begin{aligned} \begin{aligned}&\parallel U'(x)-u'(x)\parallel _{L^\infty (I)}\\&\quad \le {\left\{ \begin{array}{ll}C N^{\gamma -\frac{1}{2}-m}\left( K^*+N^\frac{1}{2}\mathcal {{U}}\right) , &{} 0<\mu<\frac{1}{2},\\ CN^{-m}\log N\left( K^*+N^\frac{1}{2}\mathcal {{U}}\right) ,&{} \frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

(4.1)

$$\begin{aligned} \begin{aligned}&\parallel U(x)-u(x)\parallel _{L^\infty (I)}\\&\quad \le {\left\{ \begin{array}{ll}C N^{\gamma -\frac{1}{2}-m}\left( K^*+N^\frac{1}{2}\mathcal {{U}}\right) , &{} 0<\mu<\frac{1}{2},\\ CN^{-m}\log N\left( K^*+N^\frac{1}{2}\mathcal {{U}}\right) ,&{}\frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

(4.2)

where

$$\begin{aligned} K^*= & {} \max _{x\in [-1,1]}|K(x,s(x,\theta ),u(s(x,\theta )))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}. \end{aligned}$$

(4.3)

$$\begin{aligned} \mathcal {{U}}= & {} |u'|_{{H}^{m,N}_{\omega ^{c}}(I)}+|u|_{{H}^{m,N}_{\omega ^{c}}(I)}. \end{aligned}$$

(4.4)

Proof

First, by Eq. (2.10), we have

$$\begin{aligned} \begin{aligned} u'_i&=f(x_i^{-\mu ,-\mu },u_i)+\sum ^N_{k=0}{\widetilde{K}}\left( x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta _k), U(s(x_i^{-\mu ,-\mu },\theta _k))\right) \omega ^{-\mu ,0}_k\\&\quad +g(x_i^{-\mu ,-\mu })\\&=f(x_i^{-\mu ,-\mu },u_i)+\int ^{x_i^{-\mu ,-\mu }}_{-1}(x-s)^{-\mu } {K}(x_i^{-\mu ,-\mu },s,U(s))\hbox {d}s\\&\quad +g(x_i^{-\mu ,-\mu })+I_{i,1},\\ u_i&=\int ^{x_i^{-\mu ,-\mu }}_{-1}U'(s)\hbox {d}s+u(-1), \end{aligned} \end{aligned}$$

(4.5)

where

$$\begin{aligned} \begin{aligned}I_{i,1}&= \sum ^N_{k=0}{\widetilde{K}}\left( x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta _k), U(s(x_i^{-\mu ,-\mu },\theta _k))\right) \omega ^{-\mu ,0}_k\\&\quad - \int ^{1}_{-1}(1-\theta )^{-\mu } {\widetilde{K}}(x_i^{-\mu ,-\mu },s(x_i^{-\mu ,-\mu },\theta ),U(s(x_i^{-\mu ,-\mu },\theta )))\hbox {d}s.\end{aligned} \end{aligned}$$

(4.6)

Using Lemma 3.1 and Lipschitz condition, we obtain

$$\begin{aligned} \begin{aligned}&\mid I_{i,1}(x)\mid \le CN^{-m}|{{\widetilde{K}}}(x,s(x,\theta ),U(s(x,\theta )))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}\\&\quad \le CN^{-m}\left( |{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)} +|{K}(x,s,U(s))-{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}\right) . \end{aligned}\nonumber \\ \end{aligned}$$

(4.7)

Using the definition of $|\cdot |_{{H}^{m,N}(I)}$ in (3.2) and the Lipschitz conditions, we have

$$\begin{aligned} \begin{aligned}&|{K}(x,s,U(s))-{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}\\&\quad =\left( \sum ^m_{j=\min (m,N+1)}\left\| \frac{\partial ^j{K}(x,s,U)}{\partial U^j}-\frac{\partial ^j{K}(x,s,u)}{\partial u^j}\right\| ^2_{L_{\omega ^{-\mu ,0}}^2(I)}\right) ^\frac{1}{2}\\&\quad \le \sum ^m_{j=\min (m,N+1)}L_i\left\| U-u\right\| _{L_{\omega ^{-\mu ,0}}^2(I)}\\&\quad \le C\left\| U-u\right\| _{L_{\omega ^{-\mu ,0}}^2(I)}. \end{aligned} \end{aligned}$$

(4.8)

Then, (4.7) can be rewritten as

$$\begin{aligned}&\mid I_{i,1}(x)\mid \le CN^{-m}|{K}(x,s(x,\theta ),U(s(x,\theta )))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}\nonumber \\&\quad \le CN^{-m}\left( |{K}(x,s,u(s))|_{{H}^{m,N}(I)}+\left\| U-u\right\| _{L_{\omega ^{-\mu ,0}}^2(I)} \right) \nonumber \\&\quad \le CN^{-m}\left( |{K}(x,s,u(s))|_{{H}^{m,N}(I)}+\left\| U-u\right\| _{L^\infty (I)} \right) . \end{aligned}$$

(4.9)

Subtracting (2.4) from (4.5), we have equations:

$$\begin{aligned} \begin{aligned} u'_i-u'(x_i^{-\mu ,-\mu })&=f(x_i^{-\mu ,-\mu },u_i)-f(x_i^{-\mu ,-\mu },u(x_i^{-\mu ,-\mu }))\\&\quad +\int ^{x_i^{-\mu ,-\mu }}_{-1}(x-s)^{-\mu } {K}(x_i^{-\mu ,-\mu },s,U(s))\hbox {d}s\\&\quad - \int ^{x_i^{-\mu ,-\mu }}_{-1}(x-s)^{-\mu } {K}(x_i^{-\mu ,-\mu },s,u(s))\hbox {d}s+I_{i,1},\\ u_i-u(x_i^{-\mu ,-\mu })&=\int ^{x_i^{-\mu ,-\mu }}_{-1}U'(s)-u'(s)\hbox {d}s, \end{aligned} \end{aligned}$$

(4.10)

By the Lipschitz conditions, we have

$$\begin{aligned} \begin{aligned} |u'_i-u'(x_i^{-\mu ,-\mu })|&\le M|u_i-u(x_i^{-\mu ,-\mu })|\\&\quad +L_0\int ^{x_i^{-\mu ,-\mu }}_{-1}(x-s)^{-\mu } |U(s)- u(s)|\hbox {d}s+I_{i,1},\\ u_i-u(x_i^{-\mu ,-\mu })&=\int ^{x_i^{-\mu ,-\mu }}_{-1}U'(s)-u'(s)\hbox {d}s. \end{aligned} \end{aligned}$$

(4.11)

Let

$$\begin{aligned} e(x)=U(x)-u(x),\quad e'(x)=U'(x)-u'(x), \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned} |u'_i-u'(x_i^{-\mu ,-\mu })|&\le M\left| \int ^{x_i^{-\mu ,-\mu }}_{-1}e'(x)\hbox {d}s\right| \\&\quad +L_0\int ^{x_i^{-\mu ,-\mu }}_{-1}(x-s)^{-\mu } |e(s)|\hbox {d}s+I_{i,1},\\ u_i-u(x_i^{-\mu ,-\mu })&=\int ^{x_i^{-\mu ,-\mu }}_{-1}e'(s)\hbox {d}s. \end{aligned} \end{aligned}$$

(4.12)

Multiplying $F_i(x)$ on both sides of (4.12) and summing up from 0 to N yields

$$\begin{aligned} \begin{aligned} |U'(x)-I_N^{-\mu ,-\mu }u'(x)|&\le MI_N^{-\mu ,-\mu }|\int ^{x}_{-1}e'(x)\hbox {d}s|\\&\quad +L_0I_N^{-\mu ,-\mu }\int ^{x}_{-1}(x-s)^{-\mu } |e(s)|\hbox {d}s+J_1(x),\\ U(x)-I_N^{-\mu ,-\mu }u(x)&=I_N^{-\mu ,-\mu }\int ^{x}_{-1}e'(s)\hbox {d}s, \end{aligned} \end{aligned}$$

(4.13)

where

$$\begin{aligned} J_1(x)=\sum _{i=0}^{N} I_{i,1}F_i(x). \end{aligned}$$

Consequently,

$$\begin{aligned} \begin{aligned} |e'(x)|&\le M\int ^{x}_{-1}|e'(x)|\hbox {d}s\\&\quad +L_0\int ^{x}_{-1}(x-s)^{-\mu } |e(s)|\hbox {d}s+J_1(x)+J_2(x)+J_4(x)+J_5(x),\\ e(x)&=\int ^{x}_{-1}e'(s)\hbox {d}s+J_3(x)+J_6(x), \end{aligned} \end{aligned}$$

(4.14)

where

$$\begin{aligned}\begin{aligned}&J_2(x)=I_N^{-\mu ,-\mu }u'(x)-u'(x),\\&J_3(x)=I_N^{-\mu ,-\mu }u(x)-u(x),\\&J_4(x)=MI_N^{-\mu ,-\mu }\int ^{x}_{-1}|e'(s)|\hbox {d}s-M\int ^{x}_{-1}|e'(s)|\hbox {d}s,\\&J_5(x)=L_0\left( I_N^{-\mu ,-\mu }\int ^{x}_{-1}(x-s)^{-\mu } \left| e(s)\right| \hbox {d}s-\int ^{x}_{-1}(x-s)^{-\mu } \left| e(s)\right| \hbox {d}s\right) ,\\&J_6(x)=I_N^{-\mu ,-\mu }\int ^{x}_{-1}e'(s)\hbox {d}s-\int ^{x}_{-1}e'(s)\hbox {d}s.\end{aligned} \end{aligned}$$

Due to the second equation of (4.14), we have

$$\begin{aligned} \begin{aligned} \mid e'(x)\mid&\le M\int ^{x}_{-1}\left| e'(s)\right| \hbox {d}s+ L_0\int ^{x}_{-1}(x-s)^{-\mu } \int ^{s}_{-1}\left| e'(\tau )\right| d \tau \hbox {d}s\\&\quad +L_0\int ^{x}_{-1}(x-s)^{-\mu } \left| J_3(x)+J_5(x)\right| \hbox {d}s\\&\quad +J_1(x)+J_2(x)+J_4(x)+J_5(x).\\ \end{aligned} \end{aligned}$$

(4.15)

Taking advantage of Dirichlet’s formula

$$\begin{aligned} \int ^x_{-1}\int ^\tau _{-1}\Phi (\tau ,s)\hbox {d}s\hbox {d}\tau =\int ^x_{-1}\int ^x_s\Phi (\tau ,s)\hbox {d}\tau \hbox {d}s, \end{aligned}$$

we get

$$\begin{aligned} \begin{aligned} \mid e'(x)\mid&\le M\int ^{x}_{-1}\left| e'(s)\right| \hbox {d}s+ L_0\int ^{x}_{-1}\left( \int ^x_\tau (x-s)^{-\mu }\hbox {d}s\right) \left| e'(\tau )\right| \hbox {d}\tau \\&\quad +L_0\int ^{x}_{-1}(x-s)^{-\mu } \left| J_3(x)+J_6(x)\right| \hbox {d}s\\&\quad +J_1(x)+J_2(x)+J_4(x)+J_5(x), \end{aligned} \end{aligned}$$

(4.16)

for $-1\le s\le x,x\in [-1,1]$, we have

$$\begin{aligned} \int ^x_\tau (x-s)^{-\mu }\hbox {d}s\le \frac{2^{1-\mu }}{1-\mu }. \end{aligned}$$

(4.17)

By Gronwall inequality, we have

$$\begin{aligned} \parallel e'(x) \parallel _{L^\infty (I)}\le C\sum ^6_{i=1}\parallel J_i(x) \parallel _{L^\infty (I)}. \end{aligned}$$

(4.18)

According to the second equation of (4.14), we obtain

$$\begin{aligned} \parallel e(x) \parallel _{L^\infty (I)}\le 2\parallel e'(x)\parallel _{L^\infty (I)}+\parallel J_3(x) \parallel _{L^\infty (I)}+\parallel J_6(x) \parallel _{L^\infty (I)}. \end{aligned}$$

(4.19)

Using Lemma 3.3, the estimates (4.9), we have

$$\begin{aligned} \begin{aligned} \parallel J_1\parallel _{L^\infty (I)}&\le {\left\{ \begin{array}{ll}C N^{\frac{1}{2}-\mu }\max _{0\le i\le N}|I_{i,1}|,\quad 0<\mu<\frac{1}{2},\\ C \log N\max _{0\le i\le N}|I_{i,1}|,\quad \frac{1}{2}\le \mu<1,\end{array}\right. }\\&\le {\left\{ \begin{array}{ll}C N^{\frac{1}{2}-\mu -m}(\max _{x\in [-1,1]}|{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}\\ +2\Vert e'(x)\Vert _{L^\infty (I)}+\Vert J_3(x) \Vert _{L^\infty (I)}+\Vert J_6(x) \Vert _{L^\infty (I)}),\quad 0<\mu<\frac{1}{2},\\ C N^{-m}\log N(\max _{x\in [-1,1]}|{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}\\ +2\Vert e'(x)\Vert _{L^\infty (I)}+\Vert J_3(x) \Vert _{L^\infty (I)}+\Vert J_6(x) \Vert _{L^\infty (I)}),\quad \frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

(4.20)

Due to Lemma 3.2,

$$\begin{aligned} \begin{aligned}&\parallel J_2\parallel _{L^\infty (I)}\le {\left\{ \begin{array}{ll}C N^{1-\mu -m}|u'|_{{H}^{m,N}_{\omega ^{c}}(I)},\quad 0<\mu<\frac{1}{2},\\ C N^{\frac{1}{2}-m}\log N|u'|_{{H}^{m,N}_{\omega ^{c}}(I)},\quad \frac{1}{2}\le \mu<1,\end{array}\right. }\\&\parallel J_3\parallel _{L^\infty (I)}\le {\left\{ \begin{array}{ll}C N^{1-\mu -m}|u|_{{H}^{m,N}_{\omega ^{c}}(I)},\quad 0<\mu<\frac{1}{2},\\ C N^{\frac{1}{2}-m}\log N|u|_{{H}^{m,N}_{\omega ^{c}}(I)},\quad \frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

(4.21)

Using Lemma 3.2 (3.3b) with $m = 1$,

$$\begin{aligned} \begin{aligned}&\parallel J_4\parallel _{L^\infty (I)}\le {\left\{ \begin{array}{ll}C N^{-\mu }|\int ^{x}_{-1}|e'(s)|\hbox {d}s|_{{H}^{1}_{\omega ^{c}}(I)}\le \parallel e'(x)\parallel _{L^\infty (I)},\quad 0<\mu<\frac{1}{2},\\ C N^{-\frac{1}{2}}|\int ^{x}_{-1}|e'(s)|\hbox {d}s|_{{H}^{1}_{\omega ^{c}}(I)}\le \parallel e(x)\parallel _{L^\infty (I)},\quad \frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

(4.22)

Similarly,

$$\begin{aligned} \begin{aligned}&\parallel J_6\parallel _{L^\infty (I)}\le {\left\{ \begin{array}{ll}C N^{-\mu }\parallel e'\parallel _{L^\infty (I)},\quad 0<\mu<\frac{1}{2}, \\ C N^{-\frac{1}{2}}\parallel e'\parallel _{L^\infty (I)},\quad \frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

(4.23)

We now estimate the term $J_6(x)$. In the virtue of Lemmas 3.5, and 3.6, we have

$$\begin{aligned} \begin{aligned}&\parallel J_6\parallel _{L^\infty (I)}= \parallel (I_N^{-\mu ,-\mu }-I)\mathcal {M}e\parallel _{L^\infty (I)}\\&\quad =\parallel (I_N^{-\mu ,-\mu }-I)(\mathcal {M}e-\mathcal {T}_N\mathcal {M}e)\parallel _{L^\infty (I)}\\&\quad \le \left( 1+\parallel I_N^{-\mu ,-\mu }\parallel _{L^\infty (I)}\right) CN^{-\kappa }\parallel \mathcal {M}e\parallel _{0,\kappa }\\&\quad \le {\left\{ \begin{array}{ll}C N^{\frac{1}{2}-\mu -\kappa }\parallel e\parallel _{L^\infty (I)},\quad 0<\mu<\frac{1}{2},\quad \frac{1}{2}-\mu<\kappa<1-\mu ,\\ C N^{-\kappa }\log N\parallel e\parallel _{L^\infty (I)},\quad \frac{1}{2}\le \mu<1,\quad 0<\kappa<1-\mu ,\end{array}\right. } \\&\quad \le {\left\{ \begin{array}{ll}C N^{\frac{1}{2}-\mu -\kappa }(2\Vert e'(x)\Vert _{L^\infty (I)}+\Vert J_3(x) \Vert _{L^\infty (I)}+\Vert J_4(x) \Vert _{L^\infty (I)}),\quad 0<\mu<\frac{1}{2},\\ C N^{-\kappa }\log N(2\Vert e'(x)\Vert _{L^\infty (I)}+\Vert J_3(x) \Vert _{L^\infty (I)}+\Vert J_4(x) \Vert _{L^\infty (I)}),\quad \frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

(4.24)

Provided that N is sufficiently large. Combining (4.20), (4.21), (4.22), (4.23) and (4.24) gives

$$\begin{aligned} \begin{aligned}&\parallel U'(x)-u'(x)\parallel _{L^\infty (I)}\\&\quad \le {\left\{ \begin{array}{ll}C N^{\frac{1}{2}-\mu -m}\left( \max _{x\in [-1,1]}|{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)} +N^\frac{1}{2}(|u'|_{{H}^{m,N}_{\omega ^{c}}(I)}+|u|_{{H}^{m,N}_{\omega ^{c}}(I)})\right) ,\\ 0<\mu<\frac{1}{2},\\ C N^{-m}\log N\left( \max _{x\in [-1,1]}|{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)} +N^\frac{1}{2}(|u'|_{{H}^{m,N}_{\omega ^{c}}(I)}+|u|_{{H}^{m,N}_{\omega ^{c}}(I)})\right) ,\\ \frac{1}{2}\le \mu<1.\end{array}\right. }\end{aligned}\\ \begin{aligned}&\parallel U(x)-u(x)\parallel _{L^\infty (I)}\\&\quad \le {\left\{ \begin{array}{ll}C N^{\frac{1}{2}-\mu -m}\left( \max _{x\in [-1,1]}|{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}\ +N^\frac{1}{2}(|u'|_{{H}^{m,N}_{\omega ^{c}}(I)}+|u|_{{H}^{m,N}_{\omega ^{c}}(I)})\right) ,\\ 0<\mu<\frac{1}{2},\\ C N^{-m}\log N\left( \max _{x\in [-1,1]}|{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)} +N^\frac{1}{2}(|u'|_{{H}^{m,N}_{\omega ^{c}}(I)}+|u|_{{H}^{m,N}_{\omega ^{c}}(I)})\right) ,\\ \frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

We have the desired estimate (4.1) and (4.2). $\square$

Now, we show the convergence analysis in $L^2_{\omega ^{-\mu ,-\mu }}$-norm.

Theorem 4.2

If the hypotheses given in Theorem 4.1 hold, then

$$\begin{aligned} \begin{aligned}&\parallel U'(x)-u'(x)\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\\&\quad \le {\left\{ \begin{array}{ll}C N^{-m}\left( N^{\frac{1}{2}-\mu -\kappa }K^*+N^{1-\mu -\kappa }\mathcal {U}+\mathcal {V}\right) , 0<\mu<\frac{1}{2},\\ C N^{-m}\left( \log NN^{-\kappa }K^*+\log NN^{\frac{1}{2}-\kappa }\mathcal {U}+\mathcal {V}\right) , \frac{1}{2}\le \mu <1.\end{array}\right. }\end{aligned} \end{aligned}$$

(4.25)

$$\begin{aligned} \begin{aligned}&\parallel U(x)-u(x)\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\\&\quad \le {\left\{ \begin{array}{ll}C N^{-m}\left( N^{\frac{1}{2}-\mu -\kappa }K^*+N^{1-\mu -\kappa }\mathcal {U}+\mathcal {V}\right) , 0<\mu<\frac{1}{2},\\ C N^{-m}\left( \log NN^{-\kappa }K^*+\log NN^{\frac{1}{2}-\kappa }\mathcal {U}+\mathcal {V}\right) ,\frac{1}{2}\le \mu <1,\end{array}\right. } \end{aligned} \end{aligned}$$

(4.26)

for any $\kappa \in (0, 1-\mu )$, where

$$\begin{aligned} \mathcal {V}=\mathcal {U}+K^*+\Vert u\Vert _{H^{2}_{\omega ^c}(I)}. \end{aligned}$$

Proof

In the virtue of Gronwall’s Lemma 3.4 and the Hardy inequality Lemma 3.8, from (4.16), we have

$$\begin{aligned} \parallel e'\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\le C\sum ^6_{i=1} \parallel J_i\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}. \end{aligned}$$

(4.27)

By Lemma 3.7, we get

$$\begin{aligned} \begin{aligned} \parallel J_1\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}&\le C\max _{x\in [-1,1]}|I(x)|\\&\le CN^{-m}\left( \max _{x\in [-1,1]}|{K}(x,s,u(s))|_{{H}^{m,N}_{\omega ^{-\mu ,0}}(I)}+\Vert e'(x)\Vert _{L^\infty (I)}\right) . \end{aligned}\end{aligned}$$

(4.28)

Using the convergence result in Theorem 4.1 with $m = 1$, we obtain

$$\begin{aligned}\parallel e'\parallel _{L^\infty (I)}\le C\Vert u\Vert _{H^{2}_{\omega ^c}(I)}. \end{aligned}$$

So that

$$\begin{aligned} \parallel J_1\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\le CN^{-m}\left( K^*+\Vert u\Vert _{H^{2}_{\omega ^c}(I)}\right) . \end{aligned}$$

(4.29)

Due to Lemma 3.2,

$$\begin{aligned} \begin{aligned}&\parallel J_2\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\le CN^{-m}| u'|_{H^{m;N}_{\omega ^c}(I)},\\&\parallel J_3\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\le CN^{-m}| u|_{H^{m;N}_{\omega ^c}(I)}.\end{aligned} \end{aligned}$$

(4.30)

Using Lemma 3.2 with $m = 1$,

$$\begin{aligned} \begin{aligned} \parallel J_4\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}&\le CN^{-1}\left| \int ^{x}_{-1}e'(s)\hbox {d}s\right| _{H^{1}_{\omega ^{-\mu ,-\mu }}(I)}\le CN^{-1}\parallel e'\parallel _{L^2_{\omega ^{-\mu ,-\mu }}(I)}. \end{aligned} \end{aligned}$$

(4.31)

Similarly

$$\begin{aligned} \begin{aligned} \parallel J_6\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}&\le CN^{-1}\left| \int ^{x}_{-1}e'(s)\hbox {d}s\right| _{H^{1}_{\omega ^{-\mu ,-\mu }}(I)} \le CN^{-1}\parallel e'\parallel _{L^2_{\omega ^{-\mu ,-\mu }}(I)}. \end{aligned} \end{aligned}$$

(4.32)

In the virtue of Lemmas 3.5, 3.6 and 3.7, we get

$$\begin{aligned} \begin{aligned}&\parallel J_5\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}=\parallel (I^{-\mu ,-\mu }_N-I)\mathcal {M} e\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\\&\quad =\parallel (I^{-\mu ,-\mu }_N-I)(\mathcal {M} e-\mathcal {T}_Ne\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)} \\&\quad \le \parallel I^{-\mu ,-\mu }_N(\mathcal {M} e-\mathcal {T}_Ne)\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}+\parallel \mathcal {M} e-\mathcal {T}_Ne\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\\&\quad \le C\parallel \mathcal {M} e-\mathcal {T}_Ne\parallel _{ L^\infty (I)}\\&\quad \le CN^{-\kappa }\parallel \mathcal {M} e\parallel _{0,\kappa },\quad \kappa \in (0, 1-\mu )\\&\quad \le CN^{-\kappa }\parallel e\parallel _{ L^\infty (I)},\quad \kappa \in (0, 1-\mu ), \end{aligned} \end{aligned}$$

(4.33)

From Theorem 4.1, we obtain that

$$\begin{aligned} \begin{aligned}&\parallel J_6\parallel _{ L^2_{\omega ^{-\mu ,-\mu }}(I)}\\&\quad \le {\left\{ \begin{array}{ll}C N^{\frac{1}{2}-\mu -m-\kappa }\left( K^*+N^\frac{1}{2}\mathcal {{U}}\right) , &{}0<\mu<\frac{1}{2},\quad \kappa \in (0, 1-\mu ),\\ C N^{-m-\kappa }\log N\left( K^*+N^\frac{1}{2}\mathcal {{U}}\right) ,&{} \frac{1}{2}\le \mu <1,\quad \kappa \in (0, 1-\mu ).\end{array}\right. } \end{aligned} \end{aligned}$$

(4.34)

The desired estimates (4.25) and (4.26) follows from the above estimates and (4.27).$\square$

5 Numerical Experiments

In this section, numerical results are performed to demonstrate the convergence analysis. In all our computations, we use Gauss-Seidel-type iteration technique to solve the nonlinear algebraic equations.

Example 5.1

Consider the following nonlinear Volterra integro-differential equations with weakly singular kernels

$$\begin{aligned}\begin{aligned} y'(t)=g(t)-\int ^t_0(t-\tau )^{-\frac{1}{3}}y^3(\tau )\hbox {d}\tau ,\quad 0\le t\le T. \end{aligned} \end{aligned}$$

where

$$\begin{aligned} g(t)=\frac{2}{3}(t+2)^{-1/3}+\frac{3}{2}(2+t)^2(2t)^\frac{2}{3}-\frac{3}{5}(2+t)(2t)^\frac{5}{3}+\frac{3}{32}(2t)^\frac{8}{3}. \end{aligned}$$

This equation has the exact solution $y(t)=(2+t)^{2/3}$.

Fig. 1

Example 1: Numerical solution and exact solution of Example 1 (left). The errors in $L^\infty$ and weighted $L^2$ norms versus different N (right)

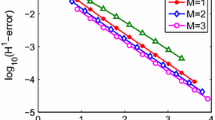
We have illustrated the obtained numerical results of Jacobi spectral collocation method for $N = 10$ and $\gamma = 0.4$ in Fig. 1(left). We can see that the numerical result of our approximation solution is in good agreement with exact solution. Fig. 1(right) illustrates $L^\infty$ and weighted $L^2_{\omega }$ errors of Jacobi spectral collocation method versus the number N of the steps. We can see that the errors decay exponentially in $L^\infty$-norm and weighted $L^2$-norm.

Example 5.2

We also consider the following nonlinear Volterra integro-differential equations with weakly singular kernels as

$$\begin{aligned} \begin{aligned}&y'(t)=f(t)-\int ^{t}_0(t-\tau )^{-\mu } \tan ( y(t))\hbox {d}{\tau },\quad 0\le t\le 2,\quad 0<\mu <1, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} f(t)=\frac{(1-\mu )t^{-\mu }}{1+(t^{2-2\mu })}+ \sqrt{\pi } \left( \frac{t}{2}\right) ^{2-2\mu }\frac{\Gamma (1-\mu )}{\Gamma (\frac{3}{2}-\mu )}. \end{aligned}$$

The exact solution is $y(t)= \arctan (t^{1-\mu })$.

Fig. 2

Example 2: Numerical solution and exact solution of $y(t)= atan(t^{1-\mu })$ with $\mu =0.4$ (left). The errors in $L^\infty$ and weighted $L^2$ norms versus different N (right)

We also illustrated comparison between approximate solution and exact solution which are in good agreement in Fig. 2 (left). The exponential rate of convergence is observed in $L^\infty$ and weighted $L^2$ norms in Fig. 2 (right).

6 Conclusion

In this paper, a spectral Jacobi-collocation approximation is proposed and analyzed for nonlinear integro-differential equations of Volterra type with weakly singular kernel, and a rigorous error analysis is provided for the spectral methods to show both the errors of approximate solutions and the errors of approximate derivatives of the solutions decaying exponentially in infinity-norm and weighted $L^2$-norm. Numerical results are presented to confirm the theoretical prediction of the exponential rate of convergence. Numerical tests are presented to confirm the theoretical results. The main advantage of the present scheme is simple to implement and easy to apply to multidimensional problems.