The Jacobi Collocation Method for a Class of Nonlinear Volterra Integral Equations with Weakly Singular Kernel

Abstract

A Jacobi spectral collocation method is proposed for the solution of a class of nonlinear Volterra integral equations with a kernel of the general form $x^{\beta }\, (z-x)^{-\alpha } \, g(y(x))$, where $\alpha \in (0,1), \beta >0$ and g(y) is a nonlinear function. Typically, the kernel will contain both an Abel-type and an end point singularity. The solution to these equations will in general have a nonsmooth behaviour which causes a drop in the global convergence orders of numerical methods with uniform meshes. In the considered approach a transformation of the independent variable is first introduced in order to obtain a new equation with a smoother solution. The Jacobi collocation method is then applied to the transformed equation and a complete convergence analysis of the method is carried out for the $\displaystyle L^{\infty }$ and the $L^2$ norms. Some numerical examples are presented to illustrate the exponential decay of the errors in the spectral approximation.

1 Introduction

This work is concerned with the numerical solutions to a general class of nonlinear second kind Volterra integral equations

$$\begin{aligned} y(z) = f(z) - \int _0^z {\frac{{{x^\beta }}}{{{{(z - x)}^\alpha }}}g(y(x))dx},\quad 0<\alpha <1,~\beta >0,\quad z \in [0,T], \end{aligned}$$

(1)

which have important applications in nonlinear problems of heat conduction, boundary layer heat transfer, chemical kinetics and theory of superfluidity (see e.g. [4, 6, 17–19]). The above class of equations has been considered by the authors in [1]. The kernel of these equations, $x^{\beta } (z-x)^{-\alpha } g(y(x))$, with $\alpha \in (0,1)$ and  $\beta >0$, possesses two types of singularities (depending on the value of $\beta$) and their solutions are typically not regular.

In previous works a particular case of (1), with to $\alpha =2/3, ~\beta =1/3, ~f(z)=1$ and $g(y)=y^4$ was considered. We will refer to it as Lighthill’s equation. The derivative of its solution behaves like $y'(t)\sim t^{-1/3}$, near the origin (cf. Example 1). As it would be expected, the typical nonsmooth properties of y cause a drop in the global convergence orders of numerical methods based on uniform meshes like collocation and product integration methods [3]. Some classical techniques can be used to recover the optimal convergence orders and this was done for Lighthill’s equation. A collocation method with graded meshes was proposed in [10]; the application of a hybrid collocation method, where the basis for the approximating space also includes some fractional powers, was considered in [22]; the use of extrapolation techniques combined with low order methods was investigated in [12]. We also refer to [2], where a Nyström-type method was applied after a smoothing transformation.

Recently, in [1], a method has been used for the general equation (1) where an initial integral over a small interval is calculated analytically, by using a series solution available near the origin; this combined with a product integration-type method leads to optimal convergence rates. In the present work we consider spectral approximations.

In the last decade the use of spectral methods for the solution of Volterra integral equations (VIEs) has raised more attention from researchers. We refer to [23] for a comprehensive study on the topic of spectral approximations and associated algorithms. It is known that an exponential convergence order can be achieved with spectral approximations in the case of linear and nonlinear Volterra integral equations with smooth kernels (see [24, 28]). This is also true for linear VIEs of the second kind with weakly singular kernel $(z-x)^{-\mu }, 0 < \mu < 1$, under the assumption that the underlying solution is smooth enough ([8],[7]). In 2010, Chen and Tang [9] developed their work by analyzing a Jacobi spectral collocation method for linear VIEs of the second kind with weakly singular kernel $(z-x)^{-\mu }, 0 < \mu < 1$, and with nonsmooth solutions. Some function transformations and variable transformations were employed to change the equation into a new one defined on the standard interval $[-1,1]$, so that the solution of the new equation possessed better regularity properties and the Jacobi orthogonal polynomials theory could be applied. In [15], Li and Tang analyzed a spectral Jacobi-collocation approximation for the particular case of the Abel-Volterra integral equation, that is, with singular kernel $(z-x)^{-1/2}$, where nonsmooth solutions were considered. In their convergence analysis, unlike in [9], only a coordinate transformation (and no solution transformation) is used. We also refer to [27] where some spectral and pseudo-spectral Jacobi-Galerkin approaches were considered for the smooth linear second kind Volterra integral equation. More recently, in [16], this work has been extended to linear Abel-type VIEs with nonsmooth solutions.

In the present work, we investigate the application of the Jacobi collocation method to the general equation (1). First a variable transformation is used on the original equation so that a new equation with a smoother solution is obtained. We note that the use of smoothing techniques for (linear) integral equations with Abel-type kernels was first considered in [11]. In the present case, it happens that the integral term in the transformed equation is suitable for the application of a Gauss-type quadrature with Jacobi weights. Finally, a Jacobi-type collocation condition is imposed on the transformed integral equation [cf. (25)].

The paper is organized as follows. In Sect. 2 first the regularity properties of the solution to equation (1) are discussed. Then the Jacobi collocation method is described. In Sect. 3 some auxiliary results are presented and in Sect. 4 a complete convergence analysis of the method is carried out for the $\displaystyle L^{\infty }$ and the $L^2$ norms. In order to illustrate the theoretical results some numerical examples are considered in Sect. 5.

Throughout the text, the same letter C will be used for all the constants, with different values.

2 The Jacobi-Collocation Method

2.1 Smoothness of the Solution

In [1] it is shown that if $0<\alpha <1, ~~\beta >1 - \alpha , f$ is bounded and g satisfies a local Lipschtiz condition then (1) has a unique continuous (local) solution y(z) on some interval [0, T]. Furthermore, if g(z) is a positive nonlinear function then it can be shown that, under certain conditions, this interval can be extended to $[0, +\infty )$. If $g(z)<0$ then the solution may blow up at some finite z. The theoretical results of Sects. 3–4 are valid independently of the sign of g.

The following lemma concerns Volterra integral equations which can be expressed in terms of the so-called “cordial” operators, which were introduced by Vainikko in [25].

Here we consider a partial result from [26] which will be useful in our analysis.

Lemma 1

Consider the following nonlinear Volterra integral equation

$$\begin{aligned} u(z)=f(z) + \int _0^z z^{-1} ~\varphi (x/z) {g}(x,z, u(x)) dx,\quad 0\le z\le T, \end{aligned}$$

(2)

where $\varphi \in L^1(0,1)$. Let $\Delta _{{T}}=\{(x,z):0\le x\le z\le {T}\}$, and assume that $f\in C^m([0,{T}])$ and $g\in C^m(\Delta _{{T}}\times {\mathscr {D}}),{\mathscr {D}}\subset {\mathbb {R}}$, for an $m\in {\mathbb {N}}$. Let $u^*\in C([0,{T}])$ be a solution of (2) on [0, T] and define

$$\begin{aligned} a(x,z)=[\partial g(x,z,u)/\partial u]_{u=u^*(x)},\quad (x,z)\in \Delta _{{T}}, \end{aligned}$$

(3)

so that $a(0,0)=0$. Then $u^*$ is also in $C^m([0,{T}])$.

It will be of interest to consider the application of the previous lemma to the following nonlinear Volterra integral equation, of which (1) is a particular case with $\gamma =1$,

$$\begin{aligned} y(z) = f(z) - \int _0^z {\frac{{{x^\beta }}}{{{{(z^\gamma - x^\gamma )}^\alpha }}}\, g(y(x))dx},\quad z \in [0,T], \end{aligned}$$

(4)

with $\beta >0$,   $\alpha \,\gamma -\beta < 1$. It can be rewritten as

$$\begin{aligned} y(z) = f(z) + \int _0^z z^{-1}\varphi (x/z)\, \overline{g}(x,z, y(x))),y(x)dx, \end{aligned}$$

(5)

which is of the form (2), with

$$\begin{aligned} \varphi (r)= & {} r^{\beta }(1-r^\gamma )^{-\alpha }\in L^1(0,T),\quad \overline{g}(x,z, y(x))=-z^{1+\beta -\alpha \,\gamma } g(y(x)). \end{aligned}$$

(6)

Using (3), we have

$$\begin{aligned} a(x,z)=[\displaystyle {\partial \overline{g}(x,z,y)/\partial y]_{y=y(x)}=-z^{1+\beta -\alpha \,\gamma }} g'(y(x)), \end{aligned}$$

which yields $a(0,0)=0$. Here y is the unique solution of (4) on [0, T].

Now Lemma 1 can be applied to draw some conclusions on the regularity properties of the solution to (1). We consider $\gamma =1$ an analyze the function $z^{\eta },~ \eta = 1+\beta -\alpha$, for the values of interest, that is, for $0<\alpha <1, \beta >0$.

• Case I   Let $\eta \ge 1$, that is, $\beta -\alpha \ge 0$, and let $\beta -\alpha$ be an integer. Then $z^{\eta }$ will be in the class $C^{\infty }$. By Lemma 1, we may conclude that if $f\in C^m([0,T])$ and $g\in C^m({\mathscr {D}})$ then the solution of equation (1) satisfies $y\in C^m([0,T])$.

• Case II  Let Let $\eta > 1$ with $\eta$ not being an integer. This corresponds to $\beta -\alpha >0$ but with $\beta -\alpha$ not in $\mathbf {Z}$. Let $\bar{m}$ denote the integer part of $\beta -\alpha$. Then the function $z^{\eta }$ will only have $\bar{m}+1$ continuous derivatives on $\Delta _{{T}}$. Therefore, Lemma 1 can be applied with $f\in C^m([0,T])$ and $g\in C^m({\mathscr {D}})$, for $m\le \bar{m}+1$.

• Case III    Let $0<\eta < 1$, that is, $0<\beta <\alpha <1$. In this case, $z^{\eta }$ is just continuous and the function $\displaystyle \overline{g}(x,z,y)=-z^{1+\beta -\alpha } g(y)$ [cf. (6) ] will not be smooth with respect to z.

Remark 1

We consider the following equation

$$\begin{aligned} y(t)=1-C\, \displaystyle {\int _0^{t}\frac{s^{\frac{1-\mu }{1+\mu }}y^m(s)}{(t-s)^{\frac{1}{1+\mu }}}ds},\quad t>0, \end{aligned}$$

(7)

where $C>0$,   $\mu <1$. We see that (7) is of the form (1), with

$$\begin{aligned} \displaystyle {\gamma =1, ~~\beta ={\frac{1-\mu }{1+\mu }}<1, \quad \alpha ={\frac{1}{1+\mu }},\quad g(s)= s^m}, \end{aligned}$$

therefore it falls into Case III. It can be shown ([10]) that the exact solution y to (7) is such that its first derivative satisfies $y'(t) \sim t^{-\frac{\mu }{1+\mu }}$ near the origin. Below we will generalize this result. We note that the first example of Sect. 5 (Lighthill’s equation) is of the type (7), with $\mu =1/2$.

A variable transformation

Defining

$$\begin{aligned} x = {s^{\sigma }}\quad \text {and} \quad z={t^{\sigma }},\quad \sigma >1,\sigma \in {\mathbb {N}}, \end{aligned}$$

(8)

then (1) is transformed into the following integral equation

$$\begin{aligned} \overline{y}(t) = \overline{f}(t) - \sigma \int _0^t {\frac{{{s^{\beta \sigma + \sigma - 1}}}}{{{{({t^\sigma } - {s^\sigma })}^\alpha }}}g(\overline{y}(s))ds},\quad t \in [0,T^{1/\sigma }], ~\,0 <\alpha <1,~~\beta >0, \end{aligned}$$

(9)

where

$$\begin{aligned} \overline{y}(t) = y({t^\sigma }),\quad \overline{f}(t) = f({t^\sigma }). \end{aligned}$$

(10)

It can be shown that (9) has a unique continuous solution on the interval $\displaystyle [0,T^{1/\sigma }]$. We now analyze the regularity of the transformed equation (8).

Since (9) is of the form (4), therefore it admits the representation

$$\begin{aligned} \overline{y}(t) = \overline{f}(t) + \int _0^t t^{-1} \varphi (t^{-1}s)\overline{g}(t,s,\overline{y}(s))ds, \end{aligned}$$

(11)

where

$$\begin{aligned} \varphi (r)= & {} r^{\beta \sigma +\sigma -1}(1-r^{\sigma })^{-\alpha }\in L^1(0,T^{1/\sigma }),\\ \overline{g}(t,s,\overline{y}(s))= & {} -\sigma t^{\sigma (1+\beta -\alpha )}g(\overline{y}(s)). \end{aligned}$$

Let us consider the case when $\alpha \in ]0,1[$ and $\displaystyle 0<1+\beta -\alpha <1$ and let $\overline{f}\in C^m([0,T^{1/\sigma }]), g(\overline{y})\in C^m([0,T^{1/\sigma }])$, for a certain m. Let $\sigma$ be an integer satisfying $\sigma >\frac{m}{1+\beta -\alpha }$. Then $\overline{g}\in C^m(\Delta _{T^{1/\sigma }}\times {\mathscr {D}})$ and, by Lemma 1, it follows that $\overline{y}\in C^m([0,T^{1/\sigma }])$ ($m\ge 1$).

If there exist $p, q \in \mathbf {N},~ q\ge 2$  (p,  q  coprimes), such that $1+\beta -\alpha =p/q$, then we simply take $\sigma =q$.

Remark 2

In particular, by taking into account (10) we can also conclude that, in the case $\displaystyle 0<1+\beta -\alpha < 1$, the first derivative of the solution of (1) satisfies, for $\displaystyle t\in (0,T],$

$$\begin{aligned} \displaystyle {y'(t)=\frac{1}{\sigma }\, t^{\frac{1}{\sigma }-1}\, \overline{y}'(t^{1/\sigma })},\quad (\sigma \ge 2). \end{aligned}$$

(12)

The case when only some derivatives of y are continuous (Case II), can be dealt with in a similar way.

2.2 The Collocation Method

Before we define the Jacobi collocation method, we need to introduce some notations. Let $\displaystyle \varLambda =[-1,1]$ and $\displaystyle {{\omega }^{\alpha _1 ,{\beta }_1 }(x)} = {(1 - x)^{\alpha _1} }{(1 + x)^{\beta _1} }$ be a weight function, for $\alpha _1 ,\beta _1 > - 1$. The Jacobi polynomials, denoted as $\{ J_N^{\alpha _1 ,\beta _1 }(x)\} _{N = 0}^\infty$, form a complete $L_{{\omega ^{\alpha _1,\beta _1 }}}^2(\varLambda )$ orthogonal system, where $L_{{\omega ^{\alpha _1,\beta _1 }}}^2(\varLambda )$ is a weighted space defined by

$$\begin{aligned} L_{{\omega ^{\alpha _1,{\beta }_1 }}}^2(\varLambda ) = \{ v:v\,\,\hbox {is\,\,measurable\,\,and}\,\,{\left\| v \right\| _{{\omega ^{\alpha _1 ,{\beta }_1}}}} < \infty \}, \end{aligned}$$

(13)

equipped with the norm

$$\begin{aligned} {\left\| v \right\| _{{\omega ^{\alpha _1 ,{\beta }_1 }}}} = {\left( \int _{ - 1}^1 {{{\left| {v(x)} \right| }^2}} {\omega ^{\alpha _1 ,{\beta }_1 }}(x)dx\right) ^{\frac{1}{2}}} \end{aligned}$$

(14)

and the inner product

$$\begin{aligned} {(u,v)_{{\omega ^{\alpha _1 ,{\beta }_1 }}}} = \int _{ - 1}^1 {u(x)v(x)} {\omega ^{\alpha _1 ,{\beta }_1 }}(x)dx,\quad \forall u,v \in L_{{\omega ^{\alpha _1 ,{\beta }_1 }}}^2( \varLambda ). \end{aligned}$$

(15)

For a given positive integer N, we denote by $\displaystyle \{ {x_i}\} _{i = 0}^N=\{ {x_i^{\alpha _1,~\beta _1}}\} _{i = 0}^N$ the points of the Gauss-Jacobi quadrature formula, which are the roots of the Jacobi polynomial $\displaystyle J_{N+1}^{\alpha _1,~\beta _1}$, while the weights of the formula will be denoted by $\displaystyle \{ {w_i}\} _{i = 0}^N=\{ {w^{\alpha _1,~\beta _1}(x_i)}\} _{i = 0}^N$. Thus the Gauss-Jacobi quadrature rule with $N+1$ points has the form:

$$\begin{aligned} \int _{ - 1}^1 {u(x){\omega ^{\alpha _1 ,{\beta }_1 }}(x)dx} \sim \sum \limits _{i = 0}^N {{w_i}u({x_i})} ,\,\,\,\,\,u \in L_{{\omega ^{\alpha _1 ,{\beta }_1 }}}^2(\varLambda ). \end{aligned}$$

Let ${{\mathscr {P}}_N}$ denote the space of all polynomials of degree not exceeding N. For any $v \in C(\varLambda )$, we can define the Lagrange interpolating polynomial $I_N^{\alpha _1 ,{\beta }_1 }v \in {{\mathscr {P}}_N}$ as

$$\begin{aligned} I_N^{\alpha _1 ,{\beta }_1 }v(x) = \sum \limits _{i = 0}^N {v({x_i}){L_i}(x)}, \end{aligned}$$

(16)

where the set $\displaystyle \{{L_i}(x)\}_{i=0}^N$ is the Lagrange interpolation basis associated with the zeros of the Jacobi polynomial of degree $\displaystyle N+1$, that is, the points $\{ {x_i}\} _{i = 0}^N.$

In order to apply the theory of orthogonal polynomials, we consider the variable transformations $\displaystyle t =T^{1/\sigma }\frac{{x + 1}}{2},\quad s =T^{1/\sigma }\frac{{\tau + 1}}{2}\quad (x,~\tau \in [-1,1]),$ so that (9) becomes

$$\begin{aligned} Y(x) = F(x) -\sigma \left( \frac{T^{\frac{1}{\sigma }}}{2}\right) ^{\sigma (\beta -\alpha +1)} \int _{-1}^{x}\frac{(\tau +1)^{\beta \sigma +\sigma -1}g(Y(\tau ))}{\left( (x+1)^{\sigma }-(\tau +1)^{\sigma }\right) ^{\alpha }}d\tau ,\quad x\in [-1,1],\nonumber \\ \end{aligned}$$

(17)

where

$$\begin{aligned} \displaystyle Y(x)=\overline{y}\left( T^{1/\sigma }\frac{{x + 1}}{2}\right) ,\quad F(x)=\overline{f}\left( T^{1/\sigma }\frac{{x + 1}}{2}\right) . \end{aligned}$$

Using the formula $a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+\cdots +b^{n-1})$, we can rewrite equation (17) as follows

$$\begin{aligned} Y(x) = F(x) -\int _{- 1}^x (x-\tau )^{-\alpha }\widetilde{k}(x,\tau )g(Y(\tau ))d\tau , \quad x\in [-1,1], \end{aligned}$$

(18)

with the kernel $\displaystyle \widetilde{k}$ being given by

$$\begin{aligned} \widetilde{k}(x,\tau )= \sigma \left( \frac{T^{\frac{1}{\sigma }}}{2}\right) ^{\sigma (\beta -\alpha +1)}\frac{{(\tau +1)^{\beta \sigma +\sigma -1}}}{(P_{\sigma -1} (x,\tau ))^\alpha },\quad 0<\alpha <1, ~\beta >0,~ \sigma \ge 2, \end{aligned}$$

(19)

where

$$\begin{aligned} P_{\sigma -1}(x,\tau )=(x+1)^{\sigma -1}+(x+1)^{\sigma -2}(\tau +1) +\cdots +(x+1)(\tau +1)^{\sigma -2}+(\tau +1)^{\sigma -1}. \end{aligned}$$

Then by using the linear transformation $\frac{{1+ x}}{2}\theta +\frac{{x-1}}{2} = \tau (x,\theta ),\quad x,~\theta \in [ - 1,1],$ we rewrite the integral term in (18) in the form

$$\begin{aligned} \int _{- 1}^{x} (x-\tau )^{-\alpha }\widetilde{k}(x,\tau )g({Y}(\tau ))d\tau = \int _{ - 1}^1 {{{(1 - {\theta }^2)}^{-\alpha }}k({x},\theta )g({Y}(\tau ({x},\theta )))d\theta }, \end{aligned}$$

where

$$\begin{aligned} k(x,\theta )=\sigma \left( \frac{(x+1)T^{\frac{1}{\sigma }}}{2}\right) ^{\sigma (\beta -\alpha +1)} \frac{(1+\theta )^{(\beta +1)\sigma +\alpha -1}}{[2^{\sigma -1} +2^{\sigma -2}(1+\theta )+\cdots +(1+\theta )^{\sigma -1}]^{\alpha }}. \end{aligned}$$

(20)

Hence, the equation (18) becomes

$$\begin{aligned} Y(x) = F(x) - \int _{ - 1}^1 {{{(1 - {\theta }^2)}^{ - \alpha }}k({x},\theta )g({Y}(\tau ({x},\theta )))d\theta }, \quad x\in [-1,1]. \end{aligned}$$

(21)

In the Jacobi-collocation method we seek an approximate solution $\displaystyle \overline{U}_N(x) \in {{\mathscr {P}}_N}$, such that $\displaystyle \overline{U}_N(x)$ satisfies the equation (21) at the collocation points $\displaystyle x_i$:

$$\begin{aligned} \overline{U}_{N}({x_i}) = F({x_i}) - \int _{ - 1}^1 {{{(1 - {\theta }^2)}^{ - \alpha }}k({x_i},\theta )g({ \overline{U}_{N}}(\tau ({x_i},\theta )))d\theta }, \end{aligned}$$

(22)

where $\displaystyle x_i,~i=0,1,\ldots ,N$, are the zeros of the Jacobi polynomial of degree $N+1$.

The integral term in the above equation can be approximated by an $(N+1)$-point Gauss quadrature formula with the Jacobi weights $\displaystyle w_j= w^{-\alpha ,-\alpha }(x_j)=(1-{x_j}^2)^{-\alpha }=(1-x_j)^{-\alpha } (1+x_j)^{-\alpha }~j=0,1,\ldots ,N$:

$$\begin{aligned} \int _{ - 1}^1 {{{(1 - {\theta }^2)}^{-\alpha }}k({x_i},\theta )g({\overline{U}_{N}}(\tau ({x_i},\theta )))d\theta } \sim \sum \limits _{j = 0}^N {{w_j}} k(x_i,{x_j})g({\overline{U}_{N}}(\tau ({x_i},{x_j}))). \end{aligned}$$

(23)

In order to linearize the scheme (22), we shall use Lagrange interpolation to approximate the nonlinear part of the kernel

$$\begin{aligned} g(\overline{U}_{N}(\tau ({x_i},\theta ))) \sim \sum \limits _{k = 0}^N g (\overline{U}_{N}(\tau ({x_i},x_k ))){L_k}(\tau ({x_i},\theta ))= I_N^{-\alpha ,-\alpha }\left( g \left( \overline{U}_{N}(\tau ({x_i},\theta ))\right) \right) ,\nonumber \\ \end{aligned}$$

(24)

where the operator $I_N^{-\alpha ,-\alpha }$ is defined by (16). Then from (23) and (24), the full collocation scheme becomes

$$\begin{aligned} {\hat{U}_{N}}({x_i}) = {F}({x_i}) - \sum \limits _{j = 0}^N {{w_j}} k({x_i},{x _j})I_N^{-\alpha ,-\alpha }g({\hat{U}_{N}}(\tau ({x_i},{x _j}))),\quad i=0,1,\ldots ,N. \end{aligned}$$

(25)

After solving (25), an approximate solution of (21) will be given by

$$\begin{aligned} Y(x)\sim U_{N}(x)=\sum _{i=0}^N \hat{U}_N(x_i)L_i(x), \end{aligned}$$

(26)

where the functions $L_i(x)$ are defined as in (16).

3 Some Preliminaries and Useful Lemmas

In this section we obtain some preliminary results that will be needed in the convergence analysis of the method. First we introduce some weighted Hilbert spaces. Let $\partial _x^{k}v$ denote the kth order derivative of v(x). For a non-negative integer m, define

$$\begin{aligned} \displaystyle H^{m}_{{\omega }^{{\alpha }_1,{\beta _1}}}(\varLambda )=\left\{ v\in L^2_{\omega ^{{\alpha _1},{\beta _1}}}(\varLambda ):\quad \left\| v \right\| _{m,{{\omega }^{\alpha _1,\beta _1}}}<\infty \right\} , \end{aligned}$$

with

$$\begin{aligned} \left| v\right| _{k,{\omega }^{{\alpha }_1 ,{\beta }_1 } }=\left\| \partial _x^{k}v \right\| _{{{\omega }^{{\alpha }_1,{\beta }_1 }}}, \quad {\left\| v \right\| _{m,{\omega ^{{\alpha }_1 ,{\beta }_1}}}} = {\left( \sum \limits _{k = 0}^m {\left| v \right| _{k,{\omega ^{{\alpha }_1 ,{\beta }_1}}}^2} \right) ^{\frac{1}{2}}}, \end{aligned}$$

where the norm $\displaystyle \Vert \quad \Vert _{{{\omega }^{{\alpha }_1,{\beta }_1 }}}$ is defined by (14). We also introduce the seminorms

$$\begin{aligned} \left| v\right| _{H_{\omega ^{{\alpha }_1 ,{\beta }_1}}^{m;N}}= \left( \sum _{k=\min {(m,N+1)}}^{m}\left\| \partial _x^{k}v \right\| _{{_{\omega ^{{\alpha _1},{\beta _1}}}}}^{2}\right) ^{1/2}. \end{aligned}$$

(27)

For any $\displaystyle u,~v\in C(\varLambda )$, a discrete and a continuous inner product are defined, respectively, by

$$\begin{aligned}&{<}v,\phi {>}_N =\sum _{j=0}^N w_jv(x_j)\phi (x_j)\\&\text {and}\\&{<}v,\phi {>}_{w^{{\alpha }_1,{\beta }_1}}= \int _{-1}^{1}w^{{\alpha }_1,{\beta }_1}(x)v(x)\phi (x)dx. \end{aligned}$$

The first lemma gives error estimates for the interpolation polynomial and for the Gauss-Jacobi quadrature formula.

Lemma 2

Let $\displaystyle v\in H^{m}_{w^{{\alpha }_1,{\beta }_1}}(\varLambda ),~m\ge 1$. The following error estimates hold

$$\begin{aligned}&{\left\| {v - I_N^{{\alpha }_1 ,{\beta }_1 }v } \right\| _{{\omega ^{{\alpha }_1 ,{\beta }_1}}}} \le C{N^{ - m}}{\left| v \right| _{H^{m;N}_{{\omega ^{{\alpha }_1 ,{\beta }_1}}}}},\end{aligned}$$

(28)

$$\begin{aligned}&\left| {<}v,\phi {>}_{w^{{\alpha }_1,{\beta }_1}}-{<}v,\phi {>}_N\right| \le C\, N^{-m} \left| v\right| _{H^{m;N}_{{\omega }^{{\alpha }_1,{\beta _1}}}} \left\| \phi \right\| _{{\omega }^{{\alpha }_1,{\beta _1}}}, \nonumber \\&\forall \phi \in {\mathscr {P}}_N. \end{aligned}$$

(29)

From [5] we have the following results concerning the Lebesgue constant.

Lemma 3

Let $\displaystyle \{L_j\}_{j=0}^N$ be the N-th order Lagrange interpolation polynomials associated with the Jacobi collocation points $\displaystyle \{x_i\}_{i=0}^N$. Then

$$\begin{aligned} \Vert I_N^{{\alpha }_1,{\beta }_1}\Vert _{\infty }:=\max _{x\in \varLambda }\sum _{j=0}^N|L_j(x)|= \left\{ \begin{array}{ll} {\mathscr {O}}\left( \log (N)\right) ,&{} -1<{\alpha }_1,~{\beta }_1\le -1/2 ,\\ {\mathscr {O}}\left( N^{\gamma +1/2}\right) , &{} \gamma = \max \{{\alpha }_1,{\beta }_1\},~\text {otherwise}. \end{array}\right. \end{aligned}$$

(30)

Lemma 4

Let $\displaystyle \{L_j\}_{j=0}^N$ be the N-th order Lagrange interpolation polynomials associated with the Jacobi collocation points $\displaystyle \{x_i\}_{i=0}^N$. For every bounded function v, there exists a constant C independent of v such that

$$\begin{aligned} \sup _{N}\left\| \sum _{j=0}^N L_j(x)v(x_j)\right\| _{{\omega }^{{\alpha }_1,{\beta _1}}}\le C\Vert v\Vert _{\infty }. \end{aligned}$$

(31)

Given $r\ge 0$ and $\kappa \in [0,1]$ $\displaystyle , {\mathscr {C}}^{r,\kappa }(\varLambda )$ will denote the space of functions whose $\mathrm r^{th}$ derivatives are H$\ddot{\text {o}}$lder continuous with exponent $\kappa$, endowed with the usual norm

$$\begin{aligned} \Vert v\Vert _{r,\kappa }=\max _{0\le k\le r}\max _{x\in \varLambda }|\partial _x^k v(x)|+\sup _{x,y\in \varLambda , x\ne y}\frac{\left| \partial _x^r v(x)-\partial _x^r v(y)\right| }{\left| x-y\right| ^{\kappa }}. \end{aligned}$$

For any function $\displaystyle v\in {\mathscr {C}}^{r,\kappa }(\varLambda )$, we have the following density result ([20], [21]):

Lemma 5

Let r be a non-negative integer and $\kappa \in (0,1)$. Then, there exists a constant ${{c}}_{r,\kappa }>0$ such that, for any function $\displaystyle v\in {\mathscr {C}}^{r,\kappa }(\varLambda )$, there exists a polynomial function ${\mathscr {T}}_N v\in {\mathscr {P}}_N$ satisfying

$$\begin{aligned} \left\| v-{\mathscr {T}}_N v\right\| _{\infty } \le {{c}}_{r,\kappa }N^{-(r+\kappa )}\Vert v\Vert _{r,\kappa }. \end{aligned}$$

(32)

Now, we need to prove the compactness of the linear weakly singular integral operator $\displaystyle {\mathscr {M}}v$, from $C(\varLambda )$ into $C^{0,\kappa }(\varLambda )$, defined by

$$\begin{aligned} \left( {\mathscr {M}}v\right) (x)=\int _{-1}^{x}(x-s)^{-\alpha } \widetilde{k}(x,s)v(s)ds, \end{aligned}$$

(33)

for any $\displaystyle 0<\kappa <1-\alpha <1$ and where $\widetilde{k}$ is defined in (19).

Lemma 6

Let $\displaystyle {\mathscr {M}}$ be defined by (33). Then, for any function $v\in {\mathscr {C}}(\varLambda )$, there exists a positive constant C such that

$$\begin{aligned} \left\| {\mathscr {M}}v\right\| _{0,\kappa } \le C\Vert v\Vert _{\infty },\quad 0 <\kappa <1-\alpha ,\,\quad \alpha \in (0,1), \end{aligned}$$

(34)

where $\Vert .\Vert _{\infty }$ is the standard norm in $\displaystyle C(\varLambda )$.

Proof

In order to prove (34), we only need to show that $\displaystyle {\mathscr {M}}$ is Hölder continuous with exponent $\displaystyle \kappa$, that is,

$$\begin{aligned} \nonumber \frac{\displaystyle |\left( {\mathscr {M}}v\right) (x_1)-\displaystyle \left( {\mathscr {M}}v\right) (x_2)|}{|x_1-x_2|^{\kappa }}\le C\Vert v\Vert _{\infty }, \quad -1\le x_1< x_2\le 1, \end{aligned}$$

for $0<\kappa <1-\alpha$. Let us analyze $\displaystyle {\mathscr {M}}v(x_1)-\displaystyle {\mathscr {M}}v(x_2)$, with $\displaystyle -1\le x_1< x_2\le 1.$ We have

$$\begin{aligned} \left( {\mathscr {M}}v\right) (x_1)-\displaystyle \left( {\mathscr {M}}v\right) (x_2)= & {} \int _{-1}^{x_1}(x_1-s)^{-\alpha }\widetilde{k}(x_1,s)v(s)ds -\int _{-1}^{x_2}(x_2-s)^{-\alpha }\widetilde{k}(x_2,s)v(s)ds\\= & {} c^{*}\int _{-1}^{x_1}(s+1)^{\beta \sigma +\sigma -1} \left( (x_1+1)^{\sigma }-(s+1)^{\sigma }\right) ^{-\alpha }v(s)ds\\- & {} c^*\int _{-1}^{x_2}(s+1)^{\beta \sigma +\sigma -1} \left( (x_2+1)^{\sigma }-(s+1)^{\sigma }\right) ^{-\alpha }v(s)ds\\= & {} E_1+E_2, \end{aligned}$$

where $\displaystyle c^*=\sigma \left( \frac{T^{\frac{1}{\sigma }}}{2}\right) ^{\sigma (\beta -\alpha +1)}$ and

$$\begin{aligned} E_1= & {} c^*\int _{-1}^{x_1}\left( [(x_1+1)^{\sigma }-(s+1)^{\sigma }]^{-\alpha }\right. \\&\left. -\,[(x_2+1)^{\sigma }-(s+1)^{\sigma }]^{-\alpha }\right) (s+1)^{\beta \sigma +\sigma -1}v(s)ds,\\ E_2= & {} c^*\int _{x_1}^{x_2}[(x_2+1)^{\sigma }-(s+1)^{\sigma }]^{-\alpha }(s+1)^{\beta \sigma +\sigma -1}v(s)ds. \end{aligned}$$

Using the variable transformation $\varsigma =(s+1)^{\sigma }$ we obtain the following bounds for $\displaystyle |E_1|$:

$$\begin{aligned} |E_1|\le & {} c_1^*\int _{0}^{(x_1+1)^{\sigma }}\left( \left( (x_1+1)^{\sigma } -\varsigma \right) ^{-\alpha }-\left( (x_2+1)^{\sigma }-\varsigma \right) ^{ -\alpha }\right) \varsigma ^{\beta }v(\varsigma ^{1/{\sigma }}-1)d\varsigma \\\le & {} c_1^*(x_1+1)^{\beta \sigma } \left( \frac{(x_1+1)^{\sigma (1-\alpha )}}{1-\alpha }-\frac{(x_2 +1)^{\sigma (1-\alpha )}}{1-\alpha }+\frac{\left( (x_2+1)^{\sigma } -(x_1+1)^{\sigma }\right) ^{1-\alpha }}{1-\alpha }\right) \\&\times \Vert v\Vert _{\infty }\\\le & {} c^{**}(x_1+1)^{\beta \sigma } \frac{(x_2-x_1)^{\eta }+(x_2-x_1)^{1-\alpha }}{1-\alpha } \Vert v\Vert _{\infty }, \end{aligned}$$

where $\eta =\min \{1,\sigma (1-\alpha )\}$ and $\sigma (1-\alpha )>1-\alpha$. From the last error inequality, and using the fact that $\sigma >1, -1\le x_1<x_2\le 1$ and $0<\kappa <1-\alpha ,$ we obtain

$$\begin{aligned} \frac{|E_1|}{|x_1-x_2|^{\kappa }}\le & {} 2^{\beta \sigma }c^{**} \frac{|x_1-x_2|^{\eta -\kappa }+ |x_1-x_2|^{1-\alpha -\kappa }}{1-\alpha } \Vert v\Vert _{\infty }\le C \Vert v\Vert _{\infty }. \end{aligned}$$

(35)

A bound for $\displaystyle |E_2|$ can be obtained as follows

$$\begin{aligned} |E_2|\le & {} c_1^*\displaystyle \int _{(x_1+1)^{\sigma }}^{(x_2+1)^{\sigma }}\left( (x_2+1)^{\sigma } -\varsigma \right) ^{-\alpha }\varsigma ^{\beta }v(\varsigma ^{1/{\sigma }} -1)d\varsigma \\\le & {} c_1^*\frac{(1+x_2)^{\sigma \beta }\Vert v\Vert _{\infty }}{1-\alpha } \left( (x_2+1)^{\sigma }-(x_1+1)^{\sigma }\right) ^{1-\alpha }\\\le & {} c^{***}\frac{(1+x_2)^{\sigma \beta }\Vert v\Vert _{\infty }}{1-\alpha } \left| x_2-x_1\right| ^{1-\alpha }. \end{aligned}$$

From the above inequality and by similar arguments to the ones used to bound $\displaystyle |E_1|$, it follows that

$$\begin{aligned} \frac{|E_2|}{|x_1-x_2|^{\kappa }}\le & {} 2^{\beta \sigma } c^{***} \frac{|x_1-x_2|^{1-\alpha -\kappa }}{1-\alpha } \Vert v\Vert _{\infty }\le C \Vert v\Vert _{\infty }. \end{aligned}$$

(36)

From (35) and (36) we obtain (34). $\square$

We now need a result on the regularity of the kernel $k(x,\theta )$, defined by (20).

Lemma 7

Consider (9), with $\displaystyle \overline{f} \in C^m([0,T^{1/\sigma }]), \overline{g}\in C^m(\Delta _{T^{1/\sigma }}\times {\mathscr {D}}), m\ge 1$. Let $\displaystyle \left\{ x_i\right\} _{i=0}^N$ be the set of the $N+1$ zeros of the Jacobi polynomial $\displaystyle J_{N+1}^{-\alpha ,~-\alpha }$ of degree $N+1$. Then, we have that

$$\begin{aligned} \frac{\partial ^{p}}{\partial \theta ^p}k(x_i,\theta ) \in L^2_{w^{-\alpha ,-\alpha }}(\varLambda ),~~p=0,1,\ldots ,m. \end{aligned}$$

Thus, there exist $\displaystyle K_p^*>0,~ p=0,1,\ldots ,m$, and $K^{**}$ so that

$$\begin{aligned} K_p^*=\max _{0\le i\le N}\left\| \frac{\partial ^{p}}{\partial \theta ^p}k(x_i,\theta ) \right\| _{w^{-\alpha ,-\alpha }}^2,~~p=0,1,\ldots ,m \end{aligned}$$

(37)

and

$$\begin{aligned} \max _{0\le i\le N}|k(x_i,.)|_{H^{m;N}_{\omega ^{-\alpha ,-\alpha }}}\le K^{**}. \end{aligned}$$

(38)

Proof

Let $\displaystyle \varsigma =(\beta +1)\sigma +\alpha -1-m$.  From Sect. 2, we know that the integer $\sigma$ can be chosen to satisfy $\displaystyle {\sigma >\frac{m}{1+\beta - \alpha }},$ which implies

$$\begin{aligned} \varsigma =(\beta +1)\sigma +\alpha -1-m \ge (\beta +1)\frac{(m+1)}{1+\beta -\alpha }+\alpha -1-m=\frac{\alpha (\beta +2-\alpha + m)}{1+\beta -\alpha }. \end{aligned}$$

Since $\alpha \in ]0,1[$, then from the last inequality we obtain $\varsigma \ge 0$. Then it is straightforward to prove that the functions $\displaystyle \frac{\partial ^{p}}{\partial \theta ^p}k(x_i,\theta ),~p=0,1,\ldots , m$, are continuous.

We have

$$\begin{aligned} \left\| \frac{\partial ^{p}}{\partial \theta ^p}k(x_i,\theta ) \right\| _{w^{-\alpha ,-\alpha }}^2= & {} \int _{-1}^1(1-\theta ^2)^{-\alpha }\left| \frac{\partial ^{p}}{\partial \theta ^p}k(x_i,\theta )\right| ^2d\theta \\ {}\le & {} \max _{\theta \in [-1,1]}\left| \frac{\partial ^{p}}{\partial \theta ^p}k(x_i,\theta )\right| \int _{-1}^1(1-\theta ^2)^{-\alpha }d\theta \\\le & {} \frac{\sqrt{\pi }\varGamma (1-\alpha )}{\varGamma (3/2-\alpha )} \max _{\theta \in [-1,1]}\left| \frac{\partial ^{p}}{\partial \theta ^p}k(x_i,\theta )\right| \end{aligned}$$

and this gives (37). The inequality (38) is easily obtained by using the definition of seminorm in (27). $\square$

4 Convergence Analysis

In this section we analyze the convergence of the approximate solution obtained by the Jacobi collocation scheme (25) to the exact solution of the integral equation (21).

Error estimate in $L^{\infty }$

Theorem 1

Assume that in (1) the nonlinear function g and all its derivatives up to order m satisfy a local Lipschitz condition. In (9) let $\displaystyle \overline{f} \in C^m([0,T^{1/\sigma }])$,  $\overline{g}\in C^m(\Delta _{T^{1/\sigma }}\times {\mathscr {D}})$, for some $m\in \mathbb {N}$.

Let Y be the exact solution of the Volterra integral equation (18) and let $\displaystyle U_N$ be the approximate solution of (18) obtained by the Jacobi collocation scheme (25).

Then for $Y\in H^m_{{\omega }^{{-\alpha },{-\alpha }}}(\varLambda )\cap H^m_{{\omega }^{C}}(\varLambda )$ we have

$$\begin{aligned} \Vert Y-U_{N}\Vert _{\infty }\le \left\{ \begin{array}{lll} CN^{-\alpha +1-m}{\bar{\chi }}_2, \quad &{}0 < \alpha <1/2, \\ C {\bar{\chi }}_0 N^{\frac{1}{2}-m}, &{}\quad ~~~ \alpha =\frac{1}{2},\\ C \log (N)N^{\frac{1}{2}-m}\bar{\chi }_1, \quad &{}1/2< \alpha < 1, \end{array}\right. \end{aligned}$$

(39)

where ${\bar{\chi }}_0,{\bar{\chi }}_1$ and ${\bar{\chi }}_2$ are given by (67) and (69), respectively, and can be bounded by some constants that does not depend on N.

Proof

At the collocation points $x=x_i$ we have $\displaystyle U_N(x_i)=\hat{U}_N(x_i)$. Then, by subtracting (25) from (21) we obtain

$$\begin{aligned} \nonumber Y({x_i})- & {} {U_{N}}({x_i})=-\left\langle k(x_i,\theta ),g({Y}(\tau ({x_i},{\theta }))) \right\rangle _{{\omega }^{{-\alpha },{-\alpha }}}+\left\langle k(x_i,.),I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},.))) \right\rangle _N \\\nonumber= & {} -\left\langle k(x_i,\theta ),g({Y}(\tau ({x_i},{\theta })))-I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},{\theta }))) \right\rangle _{{\omega }^{{-\alpha },{-\alpha }}} \\\nonumber+ & {} \left\langle k(x_i,.), I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},.))) \right\rangle _N-\left\langle k(x_i,\theta ),I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},{\theta }))) \right\rangle _{{\omega }^{{-\alpha },{-\alpha }}}.\\ \end{aligned}$$

(40)

Let $\displaystyle e(x)=Y(x) - {U_{N}}(x)$, then we will have

$$\begin{aligned} \nonumber e(x_i) = -\left\langle k(x_i,\theta ),g({Y}(\tau ({x_i},{\theta })))-I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},{\theta }))) \right\rangle _{{\omega }^{{-\alpha },{-\alpha }}}+{J_{i}},\\ \end{aligned}$$

(41)

where

$$\begin{aligned} {J_{i}}= \left\langle k(x_i,.),I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},.))) \right\rangle _N-\left\langle k(x_i,\theta ),I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},{\theta }))) \right\rangle _{{\omega }^{{-\alpha },{-\alpha }}}. \end{aligned}$$

Multiplying $L_i(x)$ on both sides of (41) and summing up from $i=0$ to $i=N$ yields

$$\begin{aligned}&I_N^{-\alpha ,-\alpha }\left( Y-U_{N}\right) (x)=I_N^{-\alpha ,-\alpha }\left( Y(x)\right) -U_{N}(x)=\nonumber \\&\sum _{i=0}^NL_i(x){J_{i}}-I_N^{-\alpha ,-\alpha }\left( \int _{-1}^x \widetilde{k}(x,\tau )(x-\tau )^{-\alpha }\left( g(Y(\tau ))-I_N^{-\alpha ,-\alpha }g(U_{N}(\tau ))\right) d\tau \right) .\nonumber \\ \end{aligned}$$

(42)

Let

$$\begin{aligned} \widetilde{\varphi }(x)=\int _{-1}^x \widetilde{k}(x,\tau )(x-\tau )^{-\alpha }\left( g(U_{N}(\tau ))-I_N^{-\alpha ,-\alpha }g(U_{N}(\tau ))\right) d\tau \end{aligned}$$

(43)

and

$$\begin{aligned} \varphi (x)=\int _{-1}^x \widetilde{k}(x,\tau )(x-\tau )^{-\alpha }\left( g(Y(\tau ))-g(U_{N}(\tau ))\right) d\tau . \end{aligned}$$

(44)

Then, after adding and subtracting $\displaystyle \widetilde{\varphi }(x), \displaystyle \varphi (x)$ and $\displaystyle Y(x)$ onto the right-hand side of (42), it follows that

$$\begin{aligned} |e(x)|\le & {} \int _{-1}^x |\widetilde{k}(x,\tau )|(x-\tau )^{-\alpha }|g (Y(\tau ))-g(U_{N}(\tau ))|d\tau \\+ & {} |Y(x)-I_N^{-\alpha -\alpha }(Y)(x)|+|{\widetilde{\varphi }}(x)-I_N^{-\alpha ,-\alpha } ({\widetilde{\varphi }})(x)|+|\widetilde{\varphi }(x)|\\+ & {} |\varphi (x)-I_N^{-\alpha ,-\alpha }(\varphi )(x)| +\left| \sum _{i=0}^NL_i(x){J_{i}}\right| . \end{aligned}$$

Using the fact that the nonlinear function g satisfies a local Lipschitz condition on [0, T] we have

$$\begin{aligned} |e(x)|\le & {} L \int _{-1}^x |\widetilde{k}(x,\tau ) |(x-\tau )^{-\alpha }|e(\tau )|d\tau +I_1(x)+I_2(x)+I_3(x)+I_4(x)+I_5(x),\nonumber \\ \end{aligned}$$

(45)

where

$$\begin{aligned}&I_1(x)=|Y(x)-I_N^{-\alpha ,-\alpha }(Y)(x)|,\end{aligned}$$

(46)

$$\begin{aligned}&I_2(x)=|\sum _{i=0}^NL_i(x){J_{i}}|,\end{aligned}$$

(47)

$$\begin{aligned}&I_3(x)=|{\widetilde{\varphi }}(x)-I_N^{-\alpha ,-\alpha } ({\widetilde{\varphi }})(x)|,\end{aligned}$$

(48)

$$\begin{aligned}&I_4(x)=|{\varphi }(x)-I_N^{-\alpha ,-\alpha }({\varphi })(x)|,\end{aligned}$$

(49)

$$\begin{aligned}&I_5(x)=|\widetilde{\varphi }(x)|. \end{aligned}$$

(50)

For $\sigma >1$ the kernels $\widetilde{k}(x,\tau )$ and $k(x,\theta )$, defined by (19) and (20), respectively, are continuous for $\tau \in [-1,x]\, \mathrm{and}\, \theta , x \in \varLambda$, which implies that they are bounded in their respective domains. Thus, from (45) we have

$$\begin{aligned} \Vert e\Vert _{\infty }\le & {} L\max _{(x,\tau )\in \varLambda \times \varLambda } |\widetilde{k}(x,\tau )|\int _{-1}^x(x-\tau )^{-\alpha } \Vert e\Vert _{\infty } d\tau \\+ & {} \left( \Vert I_1\Vert _{\infty }+\Vert I_2\Vert _{\infty }+\Vert I_3\Vert _{\infty } +\Vert I_4\Vert _{\infty }+\Vert I_5\Vert _{\infty }\right) . \end{aligned}$$

Then, using a standard Gronwall inequality we have

$$\begin{aligned} \Vert e\Vert _{\infty } \le C\left( \Vert I_1\Vert _{\infty }+\Vert I_2\Vert _{\infty }+\Vert I_3\Vert _{\infty } +\Vert I_4\Vert _{\infty }+\Vert I_5\Vert _{\infty }\right) . \end{aligned}$$

(51)

In what follows we bound $\displaystyle \Vert I_j\Vert _{\infty }, j = 1, \ldots , 5$.

In order to simplify the notation, we must consider two cases: $\displaystyle \frac{1}{2}\le \alpha <1$ and $\displaystyle 0<\alpha <\frac{1}{2}.$

• Case 1: $\displaystyle \frac{1}{2}\le \alpha <1$

Bound for $\Vert I_1\Vert _{\infty }$

In order to bound $\Vert I_1\Vert _{\infty }$ we use a result from [5]. Let $I_N^CY\in {\mathscr {P}}_N$ be the interpolant of Y at any of the three families of Chebyshev-Gauss points. Then, from [5] we have

$$\begin{aligned} \Vert Y-I_N^CY\Vert _{\infty }\le C\,N^{\frac{1}{2}-m}|Y|_{H_{w^{C}}^{m;N}}, \end{aligned}$$

(52)

where $\displaystyle w^{C}(x)=w^{-\frac{1}{2},-\frac{1}{2}}(x)$ is the Chebyshev weight function.

Noting that $I_N^{-\alpha ,-\alpha }p(x)=p(x),\quad \forall ~ p\in {\mathscr {P}}_N$ and by adding and subtracting $\displaystyle I_N^CY$, we obtain, for $\frac{1}{2}< \alpha <1$,

$$\begin{aligned} \Vert I_1\Vert _{\infty }= & {} \Vert Y-I_N^{-\alpha ,-\alpha }Y\Vert _{\infty }= \Vert Y-I_N^{-\alpha ,-\alpha }Y+I_N^{-\alpha ,-\alpha }\left( I_N^CY\right) -I_N^CY\Vert _{\infty }\\\le & {} \left( 1+\Vert I_N^{-\alpha ,-\alpha }\Vert _{\infty }\right) \Vert Y-I_N^CY\Vert _{\infty }. \end{aligned}$$

Using Lemma 3 and inequality (52) leads to

$$\begin{aligned} \Vert I_1\Vert _{\infty } \le C\log (N) N^{\frac{1}{2}-m}|Y|_{H^{m;N}_{w^{C}}}. \end{aligned}$$

(53)

Thus

$$\begin{aligned} \Vert I_1\Vert _{\infty }\le & {} \left\{ \begin{array}{ll} C\,N^{\frac{1}{2}-m}|Y|_{H_{w^{C}}^{m;N}}, &{}\alpha =\frac{1}{2},\\ C\log (N) N^{\frac{1}{2}-m}|Y|_{H^{m;N}_{w^{C}}}, &{}\frac{1}{2}< \alpha <1.\end{array}\right. \end{aligned}$$

Bound for $\displaystyle \Vert I_2\Vert _{\infty }$

Recall from (41) that

$$\begin{aligned} \displaystyle J_i=J(x_i)=\left\langle k(x_i,.),I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},.))) \right\rangle _N-\left\langle k(x_i,\theta ),I_N^{-\alpha ,-\alpha }g({U_{N}}(\tau ({x_i},{\theta }))) \right\rangle _{{\omega }^{{-\alpha },{-\alpha }}}. \end{aligned}$$

Hence, by using (29) and (31), we have

$$\begin{aligned} \nonumber \mathop {\max \limits _{0\le i\le N}}| J(x_{i})|\le & {} C N^{-m} \mathop {\max \limits _{0 \le i \le N}}|k(x_i,\theta )|_{H^{m; N}_{{\omega }^{-\alpha ,-\alpha }}}\mathop {\max \limits _{0 \le i \le N}} \Vert I_N^{-\alpha ,-\alpha }g(U_{N}(\tau (x_i,\theta )))\Vert _{{\omega }^{-\alpha ,-\alpha }}\\ \nonumber\le & {} C N^{-m}K^{**} {\max \limits _{0 \le i \le N}} \Vert g(U_{N}(\tau (x_i,\theta )))\Vert _\infty \\\le & {} C K^{**} N^{-m} \left( L\Vert e\Vert _{\infty }+\Vert g(Y)\Vert _{\infty }\right) , \end{aligned}$$

(54)

where $\displaystyle K^{**}$ is defined in Lemma 7.

Thus, combining (54) with Lemma 3, yields

$$\begin{aligned} \nonumber \Vert I_2\Vert _{\infty }= & {} \left\| \sum _{i=0}^NL_i(x){J_{i}}\right\| _{\infty } \le C\mathop {\max \limits _{0\le i\le N}}\left| {J_{i}}\right| \Vert I_N^{ -\alpha ,-\alpha }\Vert _{\infty }\\\le & {} C K^{**}N^{-m}\log (N)\left( L\Vert e\Vert _{\infty }+\Vert g(Y)\Vert _{\infty }\right) . \end{aligned}$$

(55)

Bound for $\displaystyle \left\| I_3\right\| _{\infty }$

Let us consider the operator ${\mathscr {M}}$ defined by (33) with $\mu =-\alpha$ and $\displaystyle v(x)= g(U_{N}(x))-I_N^{-\alpha ,-\alpha }g(U_{N}(x))$.

From Lemma 6 the function $\displaystyle {\mathscr {M}}v$ is Hölder continuous with exponent $\displaystyle 0<\kappa <1-\alpha$. Then $\displaystyle {\mathscr {M}}v \in {\mathscr {C}}^{0,\kappa }(\varLambda )$, and from Lemma 5 there exists a constant $\displaystyle c_{0,\kappa }$ and a polynomial function $\displaystyle {\mathscr {T}}_N({\mathscr {M}}v) \in {\mathscr {P}}_N$ such that (32) is valid, thus we obtain

$$\begin{aligned} \Vert I_3\Vert _{\infty }= & {} \left\| \left( I_N^{-\alpha ,-\alpha }-I\right) {\mathscr {M}} (v)\right\| _{\infty }=\left\| \left( I^{-\alpha ,-\alpha }_N-I\right) \left( {\mathscr {M}}v -{\mathscr {T}}_N({\mathscr {M}}v)\right) \right\| _{\infty }\\\le & {} c_{0,\kappa }\left( 1+ \Vert I^{-\alpha ,-\alpha }_N\Vert _{\infty }\right) N^{-\kappa }\Vert {\mathscr {M}} v\Vert _{0,\kappa }. \end{aligned}$$

From Lemma 6, with $0<\kappa <1-\alpha$, it follows

$$\begin{aligned} \Vert I_3\Vert _{\infty }\le & {} c_{0,\kappa }(1+ \Vert I^{-\alpha ,-\alpha }_N\Vert _{\infty })N^{-\kappa }\Vert g(U_{N})-I_N^{ -\alpha ,-\alpha }g(U_{N})\Vert _{\infty }. \end{aligned}$$

(56)

By using the same procedure as in the bounding of $\Vert I_1\Vert _{\infty }$ we can obtain the following bound

$$\begin{aligned} \Vert g(U_{N})-I_N^{-\alpha ,-\alpha }g(U_{N})\Vert _{\infty }\le & {} \left\{ \begin{array}{ll} C\,N^{\frac{1}{2}-m}|g(U_{N})|_{H_{w^{C}}^{m;N}}, &{}\quad \alpha =\frac{1}{2},\\ C\log (N) N^{\frac{1}{2}-m}|g(U_{N})|_{H^{m;N}_{w^{C}}}, &{}\quad \frac{1}{2}< \alpha <1.\end{array}\right. \end{aligned}$$

By using the definition of seminorm (27) we have

$$\begin{aligned} |g(U_{N})|_{H^{m;N}_{w^{C}}}\le & {} |g(Y)-g(U_{N})|_{H_{w^{C}}^{m;N}(\varLambda )} +|g(Y)|_{H^{m;N}_{w^{C}}}\nonumber \\= & {} \left( \sum _{k=\min {(m,N+1)}}^{m}\left\| \frac{\partial ^k{g}}{\partial {y^k}}\left( U_{N}-Y\right) \right\| _{\omega ^{C}}^{2}\right) ^{\frac{1}{2}}+ |g(Y)|_{H^{m;N}_{w^{C}}}. \end{aligned}$$

(57)

Since the nonlinear function g and its derivatives of orders $\displaystyle 1,2,\ldots ,m$ satisfy a Lipschitz condition, we have

$$\begin{aligned} \left\| \frac{\partial ^k{g}}{\partial {y^k}}(U_{N}-Y) \right\| _{{\omega ^{{C}}}}^{2} \le L_k \left\| U_{N}-Y \right\| _{\omega ^{{C}}}^2,\quad \min {(m,N+1)}\le k \le m. \end{aligned}$$

(58)

Therefore, combining (58) with (57) yields

$$\begin{aligned} |g(U_{N})|_{H^{m;N}_{w^{C}}}\le & {} L'\Vert e\Vert _{{L^2_{\omega ^{{C}}} (\varLambda )}}+|g(Y)|_{H^{m;N}_{w^{C}}}\nonumber \\\le & {} L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m;N}_{w^{C}}}. \end{aligned}$$

(59)

From (57), (59) and Lemma 3, we obtain

$$\begin{aligned} \Vert g(U_{N})-I_N^{-\alpha ,-\alpha }g(U_{N})&\Vert _{\infty } \le \nonumber \\&\left\{ \begin{array}{ll} C\log (N) N^{\frac{1}{2}-m}\left( L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m;N}_{w^{C}}}\right) , ~~\frac{1}{2}< &{}\quad \alpha <1, \\ C\,N^{1/2-m}\left( L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m;N}_{w^{C}}}\right) ,&{}\quad \alpha =\frac{1}{2}. \end{array}\right. \end{aligned}$$

(60)

Finally, using (60) and Lemma 5 in (56), we have

$$\begin{aligned} \Vert I_3\Vert _{\infty }\le & {} \left\{ \begin{array}{ll} C\,N^{\frac{1}{2}-m-\kappa }\log (N)\left( L''\Vert e\Vert _{\infty }+|g(Y) |_{H^{m;N}_{w^{C}}}\right) ,&{}\quad \alpha =\frac{1}{2},\\ C(\log (N))^2 N^{1/2\frac{1}{2}-m-\kappa }\left( L''\Vert e\Vert _{\infty } +|g(Y)|_{H^{m;N}_{w^{C}}}\right) ,&{}\quad \frac{1}{2} < \alpha <1.\end{array}\right. \end{aligned}$$

(61)

Bound for $\displaystyle \Vert I_4\Vert _{\infty }$

Similarly to $\Vert I_3\Vert _{\infty }$, we again consider the operator ${\mathscr {M}}$ defined by (33), with $\mu =-\alpha$ but now with $v(x)=g(Y(x))-g(U_{N}(x))$. Then we can rewrite $I_4$ as follows

$$\begin{aligned} I_4=\left( I^{-\alpha ,-\alpha }_N-I\right) \left( {\mathscr {M}}v\right) (x)= \left( I^{-\alpha ,-\alpha }_N-I\right) \left( {\mathscr {M}} v-{\mathscr {T}}_N({\mathscr {M}}v)\right) (x). \end{aligned}$$

(62)

From (62) and Lemma 5, with $r=0$ and $\kappa \in (0,1-\alpha )$, we have

$$\begin{aligned} \Vert I_4\Vert _{\infty }\le c_{0,\kappa }\left( 1+ \Vert I^{-\alpha ,-\alpha }_N\Vert _{\infty }\right) N^{-\kappa }\Vert {\mathscr {M}} v\Vert _{0,\kappa }. \end{aligned}$$

(63)

On the other hand, from Lemmas 3 and 6, with $0<\kappa <1-\alpha$, and using the fact that g is Lipschitz continuous, yields

$$\begin{aligned} \Vert I_4\Vert _{\infty }\le & {} c_{0,\kappa }(1+ \Vert I^{-\alpha , -\alpha }_N\Vert _{\infty })N^{-\kappa }\Vert g(Y)-g(U_{N})\Vert _{\infty }\nonumber \\\le & {} c_{0,\kappa }N^{-\kappa }(1+\Vert I_N^{-\alpha , -\alpha }\Vert _{\infty })L\Vert e\Vert _{\infty }\nonumber \\\le & {} CN^{-\kappa }\log (N)\Vert e\Vert _{\infty }. \end{aligned}$$

(64)

Bound for $\displaystyle \Vert I_5\Vert _{\infty }$

We have

$$\begin{aligned} \Vert I_5\Vert _{\infty }= & {} \left\| \int _{-1}^x \widetilde{k}(x,\tau )(x-\tau )^{-\alpha } \left( g(U_{N}(\tau ))-I_N^{-\alpha ,-\alpha }g(U_{N}(\tau ))\right) d\tau \right\| _{\infty }\\\le & {} \frac{K 2^{1-\alpha }}{1-\alpha } \Vert g(U_{N})-I_N^{-\alpha ,-\alpha } g(U_{N})\Vert _{\infty }, \end{aligned}$$

where $\displaystyle K=\max _{(\tau ,x)\in [-1,x]\times \varLambda }|\widetilde{k}(x,\tau )|$. From (60) we obtain

$$\begin{aligned} \Vert I_5\Vert _{\infty }\le & {} \left\{ \begin{array}{ll} C\,N^{\frac{1}{2}-m}\left( L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m;N}_{w^{C}}}\right) ,&{}\quad \alpha =\frac{1}{2},\\ C\log (N) N^{\frac{1}{2}-m}\left( L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m;N}_{w^{C}}}\right) ,&{}\quad \frac{1}{2}< \alpha <1.\end{array}\right. \end{aligned}$$

(65)

Finally, using the bounds (53), (55), (61), (64) and (65) in (51), then, for sufficiently large N, we obtain that

$$\begin{aligned} \Vert e\Vert _{\infty }\le & {} \left\{ \begin{array}{ll} C {\bar{\chi }}_0 N^{\frac{1}{2}-m},&{}\quad \alpha =\frac{1}{2},\\ C {\bar{\chi }}_1 N^{\frac{1}{2}-m}\log (N), &{}\quad \frac{1}{2}<\alpha <1, \end{array}\right. \end{aligned}$$

(66)

with $\displaystyle \chi _0$ and $\displaystyle \chi _1$ given by

$$\begin{aligned} {\bar{\chi }}_0= & {} |Y|_{H^{m;N}_{w^{C}}} +\log (N)N^{-\frac{1}{2}}\Vert g(Y)\Vert _{\infty }+ N^{-\kappa }\log (N)|g(Y)|_{H^{m;N}_{w^{C}}}+ |g(Y)|_{H^{m;N}_{w^{C}}},\nonumber \\ {\bar{\chi }}_1= & {} |Y|_{H^{m;N}_{w^{C}}} +N^{-\frac{1}{2}}\Vert g(Y)\Vert _{\infty }+ N^{-\kappa }\log (N)|g(Y)|_{H^{m;N}_{w^{C}}}+ |g(Y)|_{H^{m;N}_{w^{C}}}, \end{aligned}$$

(67)

and the desired result follows.

• Case 2: $\displaystyle 0<\alpha <\frac{1}{2}$

In this case, attending to Lemma 3 and using similar arguments to the ones employed for Case 1, we obtain the following estimates:

$$\begin{aligned}&\Vert I_1\Vert _{\infty } \le CN^{-m-\alpha +1}|Y|_{H^{m;N}_{w^{C}}},\\&\Vert I_2\Vert _{\infty }\le CK^{**}N^{-m-\alpha +\frac{1}{2}}\left( L\Vert e\Vert _{\infty }+\Vert g(Y) \Vert _{\infty }\right) ,\\&\Vert I_3\Vert _{\infty }\le CN^{\frac{1}{2}-m-\kappa }(N^{-\alpha +\frac{1}{2}})^2 \left( L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m;N}_{w^{C}}}\right) , \\&\Vert I_4\Vert _{\infty }\le CN^{-\alpha +\frac{1}{2}-\kappa }\Vert e\Vert _{\infty }, \\&\Vert I_5\Vert _{\infty }\le CN^{1-m-\alpha }\left( L''\Vert e\Vert _{\infty } +|g(Y)|_{H^{m;N}_{w^{C}}}\right) . \end{aligned}$$

Therefore, using the above inequalities in (51) we obtain the desired result:

$$\begin{aligned} \Vert e\Vert _{\infty }\le C {\bar{\chi }}_2 N^{-\alpha +1-m}, ~~ 0<\alpha <\frac{1}{2}, \end{aligned}$$

(68)

with $\displaystyle {\bar{\chi }}_2$ given by

$$\begin{aligned} {\bar{\chi }}_2=|Y|_{H^{m;N}_{w^{C}}} +N^{-\frac{1}{2}}\Vert g(Y)\Vert _{\infty }+ N^{-\kappa -\alpha +\frac{1}{2}}\, |g(Y)|_{H^{m;N}_{w^{C}}} +C N^{\alpha -1}|g(Y)|_{H^{m;N}_{w^{C}}}. \end{aligned}$$

(69)

The proof of Theorem 1 is now complete. $\square$

Error estimate in $L^{2}(\varLambda )$

To obtain an error estimate in the weighted $L^2$ norm, we need a generalized Hardy inequality with weights [8].

Lemma 8

For all measurable functions $f\ge 0$, the generalized Hardy’s inequality

$$\begin{aligned} \left( \int _a^b {{\left| {(Tf)(x)} \right| }^q}u(x)dx\right) ^{1/q} \le C\left( \int _a^b {{{\left| {f(x)} \right| }^p}v(x)dx}\right) ^{1/p} \end{aligned}$$

(70)

holds if and only if

$$\begin{aligned} \mathop {\sup }\limits _{a < x < b} {\left( \int _x^b {u(t)dt} \right) ^{1/q}}{\left( \int _a^x {{v^{1 - p'}}(t)dt} \right) ^{1/p'}} < \infty , \,\,\,\,\,\,p' = \frac{p}{{p - 1}},~~1 < p \le q < \infty . \end{aligned}$$

Here $\displaystyle T$ is an operator of the form

$$\begin{aligned} (Tf)(x) = \int _a^x {k(x,t)f(t)dt}, \end{aligned}$$

where k(x, t) is a given kernel, u and v are weight functions, and $- \infty \le a < b \le \infty$.

We will need the following Gronwall’s inequality [15].

Lemma 9

Suppose that $\displaystyle L\ge 0, \displaystyle 0<\alpha <1$. Let v(x) be a non-negative, locally integrable function defined on $\varLambda$ satisfying

$$\begin{aligned} u(x)\le v(x)+L\int _{-1}^x(x-\tau )^{-\alpha }u(\tau )d\tau . \end{aligned}$$

Then, there exists a constant $\displaystyle C$ such that

$$\begin{aligned} u(x)\le v(x)+ C \int _{-1}^x(x-\tau )^{-\alpha }v(\tau )d\tau ,\quad -1\le x<1. \end{aligned}$$

Theorem 2

Assume that in (1) the nonlinear function g and all its derivatives up to order m satisfy a local Lipschitz condition. In (9) let $\displaystyle \overline{f} \in C^m([0,T^{1/\sigma }])$,  $\overline{g}\in C^m(\Delta _{T^{1/\sigma }}\times {\mathscr {D}})$, for some $m\in \mathbb {N}$.

Let Y be the exact solution of the Volterra integral equation (18) and let $\displaystyle U_N$ be the approximate solution of (18) obtained by the Jacobi collocation scheme (25). Then, for $Y\in H^m_{{\omega }^{{-\alpha },{-\alpha }}}(\varLambda )\cap H^m_{{\omega }^{C}}(\varLambda )$ we have

$$\begin{aligned} \Vert Y-U_{N}\Vert _{w^{-\alpha ,~-\alpha }}\le \left\{ \begin{array}{ll} C \rho _1 N^{\frac{1}{2}-m},&{} \frac{1}{2}< \alpha < 1, \\ C\rho _0 N^{\frac{1}{2}-m}, &{} \alpha =\frac{1}{2},\\ C\rho _2 N^{-\alpha +1-m}, &{} 0<\alpha <\frac{1}{2}, \end{array}\right. \end{aligned}$$

(71)

where $\rho _0,\rho _1$ and $\rho _2$ are given by (81), (82) and (83), respectively, and can be bounded by some constant that does not depend on N.

Proof

Using the generalization of Gronwall’s inequality (see Lemma 9) in (45), we obtain

$$\begin{aligned} \left| {e(x)} \right|\le & {} L\int _{ - 1}^x \left| {{\tilde{k}}(x,\tau )} \right| {{(x - \tau )}^{-\alpha }({I_1} + {I_2} + {I_3}+ {I_4} + {I_5})(\tau )} d\tau \nonumber \\&\quad +\,{I_1}(x) + {I_2}(x) + {I_3}(x)+{I_4}(x) + {I_5}(x), \end{aligned}$$

(72)

with $\displaystyle I_1,~I_2,~I_3,~I_4$ and $\displaystyle I_5$ defined by (46), (47), (48), (49) and (50), respectively. Then

$$\begin{aligned} {\left\| e \right\| _{{w^{-\alpha ,-\alpha }}}}\le & {} L\left\| \int _{ - 1}^x \left| {{\tilde{k}}(x,\tau )} \right| {{(x - \tau )}^{-\alpha }({I_1} + {I_2} + {I_3}+ {I_4} + {I_5})(\tau )} d\tau \right\| _{{w^{-\alpha ,-\alpha }}}\nonumber \\&\quad +\, C\left( {\left\| {{I_1}} \right\| _{{w^{-\alpha ,-\alpha }}}} + {\left\| {{I_2}} \right\| _{{w^{-\alpha ,-\alpha }}}} + {\left\| {{I_3}} \right\| _{{w^{-\alpha ,-\alpha }}}}+ {\left\| {{I_4}} \right\| _{{w^{-\alpha ,-\beta }}}}+{\left\| {{I_5}} \right\| _{{w^{-\alpha ,-\alpha }}}}\right) .\nonumber \\ \end{aligned}$$

(73)

Now, by using Hardy’s inequality (70), we will have the following bound

$$\begin{aligned} {\left\| e\right\| _{{w^{-\alpha ,-\alpha }}}}\le & {} C({\left\| {{I_1}} \right\| _{{w^{-\alpha ,-\alpha }}}} + {\left\| {{I_2}} \right\| _{{w^{-\alpha ,-\alpha }}}} + {\left\| {{I_3}} \right\| _{{w^{-\alpha ,-\alpha }}}}\nonumber \\&+\,{\left\| {{I_4}} \right\| _{{w^{-\alpha ,-\alpha }}}}+{\left\| {{I_5}} \right\| _{{w^{-\alpha ,-\alpha }}}}). \end{aligned}$$

(74)

Bound for $\displaystyle {\left\| I_1 \right\| _{{w^{-\alpha ,-\alpha }}}}$

From (28) it follows

$$\begin{aligned} {\left\| {{I_1}} \right\| _{{w^{-\alpha ,-\alpha }}}} = {\left\| {Y- I_N^{-\alpha ,-\alpha }Y} \right\| _{{w^{-\alpha ,-\alpha }}}} \le C{N^{ - m}}{\left| Y \right| _{H_{{w^{-\alpha ,-\alpha }}}^{m;N}}}. \end{aligned}$$

(75)

Bound for $\displaystyle {\left\| I_2 \right\| _{{w^{-\alpha ,-\alpha }}}}$

From (55), (54) and Lemma 4 we obtain

$$\begin{aligned} \left\| {{I_2}} \right\| _{{w^{-\alpha ,-\alpha }}}= & {} \left\| \sum \limits _{i = 0}^\infty {{L_i}(x)J(x_i) } \right\| _{{w^{-\alpha ,-\alpha }}} \le C\Vert J\Vert _{\infty }\nonumber \\\le & {} C{N^{ - m}}{K^{**}}\left( L{\left\| e \right\| _\infty } + {\left\| {{g(Y)}} \right\| _\infty }\right) , \end{aligned}$$

(76)

with $K^{**}$ defined by (38).

Bound for $\displaystyle {\left\| I_3\right\| _{{w^{-\alpha ,-\alpha }}}}$

Let $\displaystyle v(x)=g(U_N(x))-I_N^{-\alpha ,-\alpha }(g(U_N(x))$. Similarly to the arguments used for the infinity norm, for $\alpha \in [\frac{1}{2},1$), we use (60) and Lemma 3 to obtain

$$\begin{aligned} {\left\| {{I_3}} \right\| _{{w^{-\alpha ,-\alpha }}}}= & {} {\left\| {(I_N^{-\alpha ,-\alpha }- I)({\mathscr {M}}v-{{\mathscr {T}}_N}({\mathscr {M}}v))} \right\| _{{w^{-\alpha ,-\alpha }}}} \le C{\left\| {{\mathscr {M}}v - {{\mathscr {T}}_N}{\mathscr {M}}v} \right\| _\infty }\nonumber \\\le & {} C{N^{-\kappa }}{\left\| {{\mathscr {M}}v} \right\| _{0,\kappa }} \le C{N^{-\kappa }}{\left\| {{g(U_{N})} - I_N^{-\alpha ,-\alpha }g(U_{N})} \right\| _\infty }\nonumber \\\le & {} \left\{ \begin{array}{ll} C\,N^{\frac{1}{2}-m-\kappa }\left( L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m; N}_{w^{C}}}\right) ,&{}\quad \alpha =\frac{1}{2},\\ C\log (N) N^{\frac{1}{2}-m-\kappa }\left( L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m; N}_{w^{C}}}\right) , &{}\quad \frac{1}{2}< \alpha <1.\end{array}\right. \end{aligned}$$

(77)

On the other hand, if $\alpha \in (0,\frac{1}{2})$, from Lemma 3 it follows that

$$\begin{aligned} {\left\| {{I_3}} \right\| _{{w^{-\alpha ,-\alpha }}}}\le CN^{-\alpha +1-\kappa -m}\left( L''\Vert e\Vert _{\infty }+|g(Y_{1})|_{H^{m; N}_{w^{C}}}\right) . \end{aligned}$$

(78)

Bound for $\displaystyle {\left\| I_4\right\| _{{w^{-\alpha ,-\alpha }}}}$

By similar arguments to the ones used to bound $\displaystyle {\left\| I_3\right\| _{{w^{-\alpha ,-\alpha }}}}$, but now with $\displaystyle v(x)=g(Y(x))-g(U_N(x))$, we obtain

$$\begin{aligned} {\left\| {{I_4}} \right\| _{{w^{-\alpha ,-\alpha }}}}= & {} {\left\| {(I_N^{-\alpha ,-\alpha }- I)({\mathscr {M}}v - {{\mathscr {T}}_N}({\mathscr {M}}v))}\right\| _{{w^{-\alpha ,-\alpha }}}}\le C{\left\| {{\mathscr {M}}v - {{\mathscr {T}}_N}{\mathscr {M}}v} \right\| _\infty }\nonumber \\ {}\le & {} C{N^{-\kappa }}{\left\| {{\mathscr {M}}v} \right\| _{0,\kappa }} \le C{N^{-\kappa }}\Vert {g(Y(\tau )) - g(U_{N}(\tau ))}\Vert _\infty \le C{N^{-\kappa }}{\left\| e \right\| _\infty }. \end{aligned}$$

(79)

Bound for $\displaystyle {\left\| I_5\right\| _{{w^{-\alpha ,-\alpha }}}}$

By using the inequalities (28) and (59), it follows that

$$\begin{aligned} \left\| I_5\right\| _{{w^{-\alpha ,-\alpha }}}\le & {} C K_0^*\Vert g(U_{N})-I_N^{-\alpha ,-\alpha }g(U_{N})\Vert _{{\omega }^{{-\alpha }, {-\alpha }}} \le CN^{-m}K_0^*|g(U_{N})|_{H^{m;N}_{w^{-\alpha , -\alpha }}}\nonumber \\\le & {} CN^{-m}K_0^*\left( L''\Vert e\Vert _{\infty }+|g(Y)|_{H^{m; N}_{w^{-\alpha ,-\alpha }}}\right) , \end{aligned}$$

(80)

whith $K_0^*$ defined by (37). Then, using (75), (76), (77), (79) and (80) in (74), we obtain, for sufficiently large N, that

$$\begin{aligned} \Vert e\Vert _{w^{-\alpha ,-\alpha }}\le & {} \left\{ \begin{array}{ll} C \rho _1 N^{\frac{1}{2}-m}, \quad \frac{1}{2}<&{}\alpha <1,\\ C \rho _0 N^{\frac{1}{2}-m}, \quad &{} \alpha =\frac{1}{2}, \end{array}\right. \end{aligned}$$

with $\rho _0, \rho _1$ given by

$$\begin{aligned} {\rho }_0&= C\Big (N^{-\frac{1}{2}}\big (\left| Y \right| _{H^{m;N}_{w^{-\alpha ,-\alpha }}}+\left\| {{g(Y)}} \right\| _\infty +\left| g(Y) \right| _{H^{m;N}_{w^{-\alpha ,-\alpha }}}\big )\nonumber \\&\quad +\, N^{-\kappa }|g(Y)|_{H^{m;N}_{w^{c}}}+\left( N^{-m}+N^{\frac{1}{2} -m-\kappa }+N^{-\kappa }\right) {\bar{\chi }}_0 \Big ),\end{aligned}$$

(81)

$$\begin{aligned} {\rho }_1&= C\Big ( N^{-\frac{1}{2}}\big ( \left| Y \right| _{H^{m;N}_{w^{-\alpha ,-\alpha }}}+\left\| {{g(Y)}} \right\| _\infty +\left| g(Y) \right| _{H^{m;N}_{w^{-\alpha , -\alpha }}}\big ) \nonumber \\&\quad +\, N^{-\kappa }\log (N)|g(Y)|_{H^{m;N}_{w^{c}}}+ \left( N^{-m}+\log (N).N^{\frac{1}{2}-m-\kappa }+N^{-\kappa }\right) \log (N){\bar{\chi }}_1 \Big ).\nonumber \\ \end{aligned}$$

(82)

On the other hand, for $\alpha \in (0,\frac{1}{2})$, using (75), (76), (78), (79) and (80) in (74), for sufficiently large N, we have

$$\begin{aligned} \Vert e\Vert _{w^{-\alpha ,-\alpha }}\le C \rho _2 N^{-\alpha +1-m}, \end{aligned}$$

with $\displaystyle \rho _2$ given by

$$\begin{aligned} \rho _2&= C\Big (N^{\alpha -1}\left( \left| Y \right| _{H^{m;N}_{w^{-\alpha ,-\alpha }}}+\left\| {{g(Y)}} \right\| _\infty +\left| g(Y) \right| _{H^{m;N}_{w^{-\alpha ,-\alpha }}}\right) \nonumber \\&\quad +\, N^{-\kappa }|g(Y)|_{H^{m;N}_{w^{c}}}+\left( N^{-m}+N^{1-\alpha -m-\kappa }+N^{-\kappa }\right) {\bar{\chi }}_2\Big ). \end{aligned}$$

(83)

The proof of Theorem 2 is complete. $\square$

5 Numerical Results

The Jacobi collocation method has been considered for three examples on the interval [0, T], with $T=1$. The numerical results on the tables together with the semi-logarithmic error graphs illustrate the performance of the Jacobi collocation method. In the first two examples the exact solution is not known. Therefore, in order to compute the absolute errors $|Y(x)-U_N(x) |=|\bar{y}(t)-U_N(t)|$, with $t=T^{\frac{1}{\sigma }}\frac{x+1}{2}$, we have taken as the exact solution $\bar{y}(t)$ the approximation $U_N(t)$, obtained by the Jacobi collocation method with $N=32$. To estimate the $L^{\infty }$ error, we have computed the absolute error at the points $x_i= - 1 + 2\frac{i - 1}{1000},\, i=1,..,1001$.

The first example is given by Lighthill’s equation [17].

Example 1

$$\begin{aligned} y(z)=1- \frac{\sqrt{3}}{\pi }\displaystyle {\int _0^{z}\frac{x^{\frac{1}{3}}y^4(x)}{(z-x)^{\frac{2}{3}}}dx},\quad z\in [0,1]. \end{aligned}$$

(84)

In [10] it is shown that y is smooth away from zero. Near the origin it admits the following series solution:

$$\begin{aligned} y(z) = 1 - 1.460998{z^{\frac{2}{3}}} + 7.249416{z^{\frac{4}{3}}} - 46.449738{z^2} + 332.755232{z^{\frac{8}{3}}} + \cdots \end{aligned}$$

(85)

for $z \in [0,R)$, where R is a positive number satisfying $R < 0.070784$. By using the variable transformation $\displaystyle x = {s^{3}}$, and then setting $z= t^{3}$, we obtain

$$\begin{aligned} \overline{y}(t) = 1-\frac{3\sqrt{3}}{\pi }\int _0^t\frac{s^3 \overline{y}^4(s)}{(t^{3}-s^{3})^{\frac{2}{3}}}ds,\,\,\,\,\,\,\,\,\, t \in [0,1], \end{aligned}$$

(86)

where $\displaystyle \overline{y}(t)=y(t^{3})$. Then, the solution of the transformed equation (86) is smooth near the origin, therefore the Jacobi collocation method can be applied to the new equation.

Example 2

$$\begin{aligned} y(z) = 1 - \int _0^z {\frac{{{x^{\frac{1}{3}}}{y^4}(x)}}{{{{(z - x)}^{\frac{1}{2}}}}}} dx,~~z \in [0,1] \end{aligned}$$

(87)

In this case it can be shown that $y(t) \sim t^{5/6}$ for t near the origin (cf. [1]). By using the variable transformation $x = {s^6}$ and setting $z = {t^6}$, then (87) can be rewritten as

$$\begin{aligned} \overline{y}(t) = 1 - 6\int _0^t {\frac{{{s^7}{\overline{y}^4}(s)}}{{{{({t^6} - s^6)}^{\frac{1}{2}}}}}}ds,\,\,\,\,\,\ t\in [0,1], \end{aligned}$$

(88)

where $\displaystyle \overline{y}(t)= y(t^6).$

Table 1 Example 1. The Jacobi collocation method with $N+1$ collocation points

Fig. 1

Example 1. The logarithms of $L^{2}$ errors (stars) and $L^{\infty }$ errors (dots) versus N. Left results for Ligthill’s equation (84). Right results for the transformed equation (86)

Example 3

$$\begin{aligned} y(z) = \sqrt{z} + \frac{{21\sqrt{2} }}{{32}}\pi {z^2} - \int _0^z {\frac{{{x^{\frac{1}{4}}}{y^3}(x)}}{{{{(z - x)}^{\frac{3}{4}}}}}}dx ,\,\,\ z\in [0,1]. \end{aligned}$$

(89)

This example has been taken from [2] and the exact solution of (89) is $\displaystyle y(z) = \sqrt{z}$. Thus, using the variable transformation $\displaystyle x = {s^2}$ and setting $z = {t^2}$, then (89) is transformed into

$$\begin{aligned} \overline{y}(t) = t + \frac{{21\sqrt{2} }}{{32}}\pi {t^4} - 2\int _0^t {\frac{{{s^{\frac{3}{2}}}{\overline{y}^3}(s)}}{{{{({t^2} - {s^2})}^{\frac{3}{4}}}}}} ds,\,\,\,t \in [0,1], \end{aligned}$$

(90)

with $\displaystyle \overline{y}(t) = y({t^2}) =t.$

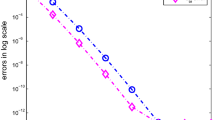
The results in Table 1 illustrate the performance of the Jacobi collocation method applied to equations (84) and (86), respectively. The values displayed show, as it was expected, a big improvement when we apply the Jacobi collocation method to the transformed equation (whose solution is smooth). In Fig. 1, the logarithms of the absolute errors in both $L^{\infty }$ and $L^2$ norms, versus N (the number of collocation points) are displayed. Again the exponential rate of convergence is observed for both nonlinear problems. The results confirm the exponential rate of convergence of the method for equation (86).

Table 2 Examples 2 and 3

Fig. 2

Examples 2 and 3. The logarithms of $L^{2}$ errors (stars) and the $L^{\infty }$ errors (dots) versus the number of collocation points ($N+1$). Left Logarithm of errors for the equation (88). Right Logarithm of errors for the equation (90)

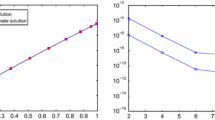
In order to obtain approximate solutions to the equations (87) and (89), the Jacobi collocation method has been applied to their respective transformed equations: (88) (with $\displaystyle \alpha _1=\beta _1=-\frac{1}{2}$) and (90) (with $\displaystyle \alpha _1=\beta _1=-\frac{3}{4}$). Table 2 shows the errors of the approximate solutions of (88) and (90) in $L^{\infty }$ and weighted $L^2$ norms. In Fig. 2, for Examples 2 and 3, we have plotted the logarithm of the absolute errors in both $L^{\infty }$ and $L^2$ norms, versus N. Again the exponential rate of convergence is observed for both nonlinear problems.

6 Conclusions

In this work we have considered a spectral Jacobi-collocation approximation for a class of nonlinear Volterra integral equations defined by (1), which has recently been introduced in [1]. When the underlying solutions of the VIEs have a nonsmooth behaviour at the origin, we first use an appropriate change of the independent variable in order to obtain an equivalent equation with smooth solution. Then the proposed method is applied to the transformed equation. We have provided a convergence analysis of the method in the weighted $L^2$ and $L^{\infty }$ norms and numerical results were presented to confirm the theoretical prediction of the exponential rate of convergence.