1 Introduction

Investigations of laminar boundary layer flow about a flat plate in a uniform stream of fluid continues to receive considerable attention because of its importance in many practical applications in a broad spectrum of engineering systems such as geothermal reservoirs, cooling of nuclear reactors, thermal insulation, combustion chamber, rocket engine, etc. Blasius [1] was the first to investigate and presented a theoretical result for the boundary layer flow over a flat plate in a uniform stream. The behavior of boundary layer flow due to a moving flat surface immersed in an otherwise quiescent fluid was first studied by Sakiadis [2], who investigated it theoretically by both exact and approximate methods. Bataller [3] studied the effects of thermal radiation on the laminar boundary layer about a flat plate via fourth-order Runge-Kutta algorithm together with shooting method. Apart from these works, various aspects of flow and heat transfer of viscous fluid over a flat plate were investigated by many researchers (see [4–8]).

When modeling the boundary layer flow and heat transfer about a flat plate, the boundary conditions that are usually applied are either a specified surface temperature or a specified surface heat flux. However, there are boundary layer flow and heat transfer problems in which the surface heat transfer depends on the surface temperature. This situation arises in conjugate heat transfer problems and when there is Newtonian heating of the convective fluid from the surface. Newtonian heating occurs in many important engineering devices, for example, in heat exchangers, where the conduction in a solid tube wall is greatly influenced by the convection in the fluid flowing over it. On the basis of above discussions and applications, Bataller [9] analyzed the effects of thermal radiation on the laminar boundary layer about a flat plate in a uniform stream of fluid, and about a moving plate in a quiescent ambient fluid both under a convective surface boundary condition. Later, Aziz [10] investigated the heat transfer problems for boundary layer flow concerning with a convective boundary condition. Ishak et al. [11] studied the steady laminar boundary layer flow over a moving plate in a moving fluid with convective surface boundary condition and in the presence of thermal radiation. In this problem they combine two problems i.e., Blasius flow and Sakiadis flow using the composite velocity (\(U=U_w +U_\infty )\) which was introduced by Afzal et al. [12]. Makinde [13, 14] studied the hydromagnetic flow over a vertical flat plate with a convective boundary condition, in this analysis he studied both heat and mass transfer analysis. Further, they extended their work and investigate the MHD mixed convection flow of a vertical plate embedded in a porous medium with a convective boundary condition. Recently, Ramesh et al. [15] obtained a numerical solution for MHD mixed convection flow of a viscoelastic fluid over an inclined surface with a non-uniform heat source/sink. Rajesh and Chamkha [16] studied the effects of ramped wall temperature on unsteady two-dimensional flow past a vertical plate with thermal radiation and chemical reaction. Chamkha et al. [17] investigated the coupled heat and mass transfer by MHD free convection flow along a vertical plate with stream-wise temperature and species concentration variations.

The aim of this paper is to extend the work by Ishak et al. [11] in the absence of radiation effect and by considering the angle of inclination. Appropriate similarity transformations reduce the governing partial differential equations into a set of nonlinear ordinary differential equations. The resulting equations are solved numerically using the shooting method. Variations of several pertinent emerging parameters are analyzed in detail. To the authors’ knowledge, no previous attempts have been made to analyze this problem.

2 Problem formulation

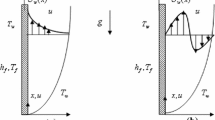
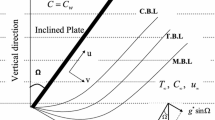
We consider a steady two-dimensional flow of a stream of cold incompressible fluid about a vertical plate which is inclined with an acute angle \(\alpha \), and the temperature \(T_\infty \) over the upper surface of the flat plate with a constant free stream velocity \(U_\infty \) and moving flat plate with constant velocity \(U_w \), while the lower surface of the plate is heated by convection from a hot fluid at temperature \(T_f \) which provides a heat transfer coefficient \(h_f \). Further, it is assumed that the viscous dissipation and radiation effects are neglected. The velocity and temperature profiles in the fluid flow must obey the usual boundary layer equations are given by Ishak et al. [11]

$$\begin{aligned} \frac{\partial \,u}{\partial \,x}+\frac{\partial \,v}{\partial \,y}=0, \end{aligned}$$
(1)
$$\begin{aligned} \rho \left( {u\frac{\partial \,u}{\partial \,x}+v\frac{\partial \,u}{\partial \,y}}\right) =\mu \frac{\partial ^2\,u}{\partial \,y^2}+g\beta \left( T-T_\infty \right) \cos \alpha , \end{aligned}$$
(2)
$$\begin{aligned} \rho \,c_p \left( {u\frac{\partial \,T}{\partial \,x}+v\frac{\partial \,T}{\partial \,y}}\right) =k\frac{\partial ^2\,T}{\partial \,y^2}, \end{aligned}$$
(3)

where \(u\) and \(v\) are the velocity components of the fluid along \(x\) and \(y\) directions respectively. \(\mu , \quad \rho \) and \(c_p \)are the co-efficient of viscosity of the fluid, density of the fluid, and specific heat of fluid, respectively. \(g\) is the acceleration due to gravity, \(\beta \) is the volumetric coefficient of thermal expansion, \(T\) is the temperature of the fluid, \(k\) is the thermal conductivity.

The appropriate boundary conditions for the flow problem are given by [11]

$$\begin{aligned} u=U_w ,\,\,v=0,\,\,-k\frac{\partial T}{\partial y}=h_f (T_f -T)\,\text{ at }\,y=0 \end{aligned}$$
$$\begin{aligned} u\rightarrow U_\infty , \quad T\rightarrow T_\infty ,\,\,\text{ as }\,y\rightarrow \infty . \end{aligned}$$
(4)

where \(T_f \) is the hot fluid temperature and \(h_f \) is the heat transfer coefficient.

In order to reduce the number of independent variables and to get the dimensionless equations, we define the new variables as,

$$\begin{aligned} \psi =\sqrt{Ux\nu } f(\eta ),\,\,\eta =\sqrt{\frac{U}{\nu \,x}} y, \quad \theta (\eta )=\frac{T-T_\infty }{T_f -T_\infty }, \end{aligned}$$
(5)

and the stream function is defined by

$$\begin{aligned} u=\frac{\partial \psi }{\partial y}\,\text{ and }\,v=-\frac{\partial \psi }{\partial x}, \end{aligned}$$
(6)

with the above transformations, the equation of continuity (1) is identically satisfied and Eqs. (2) and (3) reduce to the following forms as:

$$\begin{aligned} 2f^{\prime \prime \prime }+\,ff^{\prime \prime }+2Gr\,\theta \,\cos \alpha =0,\end{aligned}$$
(7)
$$\begin{aligned} \!\!\!\!\!2\theta ^{\prime \prime }+\Pr f\theta ^{\prime } =0 \end{aligned}$$
(8)

where a prime denotes differentiation with respect to \(\eta \) and \(Gr=\frac{g\beta (T_f -T{ }_\infty )x}{U^2}\) is the local Grashof number (Kierkus [18]), \(\Pr =\nu /\alpha \) is the Prandtl number. From Eq. (7) we note that, when \(\alpha =90^\circ \), our problem reduces to the horizontal flat plate case, while when \(\alpha =0^\circ \), it reduces to the vertical flat plate. To exit Eqs. (1–4), here we take \(h_f =\frac{c}{\sqrt{x} }\), where \(c\) is a constant.

The boundary conditions defined as in (4) will become,

$$\begin{aligned} f=0, \quad f^\prime =\lambda , \quad \theta ^{\prime } \,=-Bi(1-\theta ) \quad \quad \mathrm{at} \quad \quad \eta =0, \nonumber \\ f^\prime \rightarrow 1-\lambda , \quad \theta \rightarrow 0 \quad \quad \mathrm{as} \quad \quad \eta \rightarrow \infty . \end{aligned}$$
(9)

where \(Bi=\frac{c}{k}\sqrt{\frac{\nu }{U}} \) is the Biot number and \(\lambda =\frac{U_w }{U}\) is the velocity ratio parameter. Here, one can observe that when \(\lambda =0\), the problem reduces to the Blasius flow (stationary flat plate) and when \(\lambda =1\), the problem reduces to the Sakiadis flow (moving flat plate), respectively.

3 Results and discussion

The nonlinear coupled differential Eqs. (7) and (8) along with the boundary conditions (9) are solved numerically using Runge-Kutta method along with the shooting technique. The accuracy of the employed numerical method is tested by direct comparisons with the values of \(\theta (0)\) (at \(\lambda =0)\) with those reported by [9–11] in Table 1, for the special case of the present problem and an excellent agreement between the results is found. Also, it provides a sample of our results for \(\theta (0)\) when the direction of free stream is fixed (i.e., \(\lambda =1)\) which is presented in Table 2. The numerical computations are executed for several values of the dimensionless parameters involved in the equations viz. the angle of inclination (\(\alpha )\), Prandtl number (\(\Pr )\), local Grashof number (\(Gr)\) and the Biot number (\(Bi)\). Some figures are plotted to illustrate the computed results and also to give the physical explanations.

Table 1 Comparison results of \(\theta (0)\) for different values of Biot number \((Bi)\) when \(\Pr =0.72,\,Gr=0.5\) and \(\lambda =0\) (stationary flat plate)
Full size table
Table 2 Computations values of \(\theta (0)\) for different values of Biot number \((Bi)\) when \(\Pr =0.72,\,Gr=0.5\) and \(\lambda =1\) (moving flat plate)
Full size table

The variations of the dimensionless velocity and temperature profiles for different values of the angles of inclination (\(\alpha =0^\circ ,30^\circ ,90^\circ )\) are presented in Figs. 1 and 2, respectively. For \(\lambda =0\), it is observed that boundary layer flow for the velocity decreases with the increase of the angle of inclination. This is due to the fact that as the angle of inclination increases, the effect of the buoyancy force due to thermal variations decreases by a factor of \(\cos \alpha \). Also, we notice that the effect of the buoyancy force (which is maximum for \(\alpha =0)\) overshoots the main stream velocity significantly. At \(\lambda =1\), the similar effect can be found as shown in Fig. 1. Further, we observe that the temperature increases as the angle of inclination increases as shown in Fig. 2. One can note that if \(\alpha =90^\circ \), the problem reduces to the horizontal flat plate (at \(\lambda =0)\) and the horizontal moving flat plate (at \(\lambda =1)\), while when \(\alpha =0^\circ \) the problem reduces to the vertical flat plate (at \(\lambda =0)\) and the vertical moving flat plate (at \(\lambda =1)\) and when \(\alpha =30^\circ \), the problem reduces to the inclined flat plate (at \(\lambda =0)\) and the inclined moving flat plate (at \(\lambda =1)\).

Fig. 1
figure 1

Effect of \(\alpha \) on velocity profiles

Full size image
Fig. 2
figure 2

Effect of \(\alpha \) on temperature profiles

Full size image

Figure 3 depicts the variation in the velocity profiles for different values of the Grashof number. It is found that for a fixed value of \(\alpha (\alpha =30^\circ )\), both the stationary flat plate (\(\lambda =0)\) and the moving flat plate (\(\lambda =1)\), the velocity increases with the increase in the Grashof number. The physical interpretation gives that if \(Gr>0\), it means heating of the fluid or cooling of the boundary surface, and if \(Gr<0\), it means cooling of the fluid or heating of the boundary surface, and \(Gr=0\), corresponds to the absence of free convection current. The graph of the temperature profiles for different values of the Grashof number is plotted in Fig. 4. It is observed from this figure that the temperature in the thermal boundary layer decreases with the increase in the Grashof number. This result shows the thinning of the thermal boundary layer. This is due to the fact that the buoyancy force enhances the fluid velocity and increases the boundary layer thickness with the increase in the value of \(Gr\).

Fig. 3
figure 3

Effect of \(Gr\) on velocity profiles

Full size image
Fig. 4
figure 4

Effect of \(Gr\) on temperature profiles

Full size image

Figure 5 illustrates the influence of the Prandtl number on the temperature profiles in the boundary layer for both a stationary flat plate (\(\lambda =0)\) and a moving flat plate (\(\lambda =1)\). As in the theory of boundary layer flow, the numerical results show that an increase in the Prandtl number results in a decrease of the thermal boundary layer thickness and in general, lower average temperature within the boundary layer. The reason is that smaller values of \(\Pr \) are equivalent to increasing the thermal conductivity of the fluid, and therefore, heat is able to diffuse away from the heat surface more rapidly than for higher values of \(\Pr \). In heat transfer problems, the Prandtl number controls the relative thickening of the momentum and the thermal boundary layers. In Fig. 6, the variation of the temperature profiles for various values of the Biot number is presented. It is observed that the temperature field increases rapidly near the boundary by increasing the Biot number. Physically speaking, the Biot number is expressed as the convection at the surface of the body to the conduction within the surface of the body. When the thermal gradient are applied to the surface, then the ratio governing the temperature inside a body varies significantly, while the body heats or cools over time.

Fig. 5
figure 5

Effect of \(\Pr \) on temperature profiles

Full size image
Fig. 6
figure 6

Effect of \(Bi\) on temperature profiles

Full size image

From Table 3, we can seen that the values of \(\theta ^\prime (0)\) are negative, which means that the heat flows from the fluid to the solid surface. This is not surprising since the fluid is hotter than the solid surface. Also, one can observe that when the value of \(Bi\) increases from 0.1 to 50, the temperature gradient \(-\theta ^\prime (0)\) increases significantly. However, a further increase in \(Bi\) has only a minor effect on the \(-\theta ^\prime (0)\), when \(Bi\rightarrow \infty \) (i.e., for large value),

Table 3 Computations values of \(-{\theta }'(0)\) for different values of Biot number \((Bi)\)with \(\Pr =0.72,\,Gr=0.5\) and \(\alpha =30^\circ \)
Full size table

4 Conclusions

In the present investigation, the mathematical modeling for boundary layer flow and heat transfer past an inclined stationary/moving flat plate with a convective boundary condition is considered. Using similarity transformations, the governing equations of the problem are reduced to a coupled third-order nonlinear ordinary differential equations and are solved numerically using the shooting method. The obtained numerical solutions are compared with previously published results and are found to be in excellent agreement. The influence of the different parameters on the velocity profiles and temperature profiles are illustrated and discussed. The numerical results give a view towards understanding the response characteristics of the angle of inclination. It is found that when the effect of increasing the angle of inclination in is to decrease the velocity and increase the temperature. The new result of the present investigation is that the temperature of the stationary flat plate is higher than the temperature of the moving flat plate when the plate is inclined at angle \(30^\circ (\alpha )\).