Introduction

The flow of fluid between two porous disks has a huge application in industries. This type of flow has been used in the manufacturing of semiconductors, in the engines of gas turbines, storage devices for computers, etc. Researchers have too much interest in this area because of the theoretical and practical importance. Eringen [1] was the first who proposed the basics of micropolar fluids. Such fluids are a subclass of microfluids. The model micropolar fluids are used to define the flow of liquid crystals, flow of blood, flow in capillaries and microchannels, porous medium, etc. Eringen [2] updated his theory of micropolar fluid in the year 1966. Eringen [3] and Lukaszewicz [4] have also discussed micropolar fluid. Rashidi et al. [5] studied nanofluid flow in the model of rotating porous disks. They discussed the effect of different physical parameters of the flow and magnetic field. Mahanthesh et al. [6] highlighted hydromagnetic nanofluid in their study. They represented the effects of physical constraints by graphs and discussed them in detail. Soid et al. [7] analyzed MHD flow in a stretching and shrinking disk. They adopted the MATLAB software tool for solving equations. They analyzed the impact of the magnetic field parameter and suction parameter on the shear stress. Aziz et al. [8] modelled MHD 3D flow in a rotating disk. They adopted the ND solve mechanism for solving the equations. Agarwal and Mishra [9] presented MHD forced flow and heat transfer in the problem of rotating disks by using HPM. They also compared HPM results with numerical results to prove the accuracy of HPM. Krishna and Chamkha [10] discussed MHD squeezing flow of nanofluid between parallel disks. They adopted Galerkin’s optimal homotopy asymptotic method. They examined the consequence of the key parameters and showed them with graphs. Ibrahim [11] chose time-dependent viscous fluid in the study of the rotating disks. He solved the equations numerically by using the finite difference method. Gupta [12] studied flow due to disk rotation. They used the HPM method in their model. Turkyilmazoglu [13] developed the fluid flow and heat transfer in the problem of the rotating disk. Agarwal [14] analyzed flow between parallel disks with uniform porosity. Venerus [15] studied squeeze flow between porous disks. He considered flow in the liquid films. Waqas et al.[16], Asma et al. [17], Devaki et al. [18], Upadhya [19], and Lin and Ghaffari [20] have also discussed the model of disks in a different manner.

Recently, many researchers devoted their time to researching the micropolar fluid flow property but few of them have discussed the flow of micropolar fluid in rotating disks because of the complexity of obtained differential equations. Agarwal [21] discussed the micropolar fluid in her problem. She analyzed heat mass transfer with flow profile on various parameters. Doh and Muthtamilselvan [22], Takhar et al. [23], Sajid et al. [24], Sadiq et al.[25], Mohyud-Din et al. [26], Bhat and Katagi [27, 28], Pasha et al. [29], Gupta [30], Ahmad et al. [31] and Kushal et al. [32,33,34,35,36,37,38] used micropolar fluid as a source fluid in their studies.

Mostly, in the above-mentioned research, equations are solved numerically by using different numerical methods. Few of them used the analytical method for solving equations. Here the author used the differential transform method (DTM) to obtain the solution for ODEs. Zhou [39] introduced the theory of DTM on linear and nonlinear equations in the experiment of electric circuits. Usman et al. [40], Keimanesh et al. [41], Hatami and Jing [42], Agarwal [43], Gupta et al. [44], Balazadeh et al. [45], and Gupta and Agarwal [46] applied DTM in their research. Awati et al. [47] applied the homotopy analysis method to get the approximate solution in their model. Agarwal [48], Gupta [49], and Ganji et al. [50] used HAM and HPM to obtain the solution.

The main goal of this research is to examine the MHD flow of a micropolar fluid, which is filled between two disks. The nonlinear partial differential equations are reformed into a system of nonlinear ODEs by suitable transformation. Such obtained ODEs are solved analytically by using the differential transform method. The effect of Reynolds number, micropolar parameter, and magnetic field parameter on flow profile is discussed and presented by graphs. The values of skin friction and couple stress is compared with numerical method results and literature, which are displayed in tabular form. The novelty of the current study is to discuss the magnetic field effect on velocity and microrotation profiles.

Mathematical Formulation

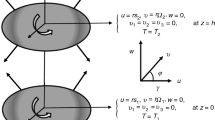
An axisymmetric, laminar, and steady flow of a micropolar fluid, which is filled between two porous disks is considered. Both disks are resting on the plane \(z=-d\) and \(z=d\) respectively. A micropolar fluid is chosen as an electrically conducting fluid in the presence of a transverse magnetic field, which is applied perpendicularly on the disks. Let \(u, v, w\) be the radial, transverse, and axial velocity and \({N}_{1}, {N}_{2},{N}_{3}\) be microrotation components in the cylindrical coordinate system as shown in Fig. 1.

Fig. 1
figure 1

Flow geometry

Full size image

The velocity and microrotation profiles are taken as follows [23]:

$$u=u\left(r,z\right), v=0, w=w(r,z)$$
$${N}_{1}=0, { N}_{2}=N\left(r,z\right),{N}_{3}=0.$$
(1)

The equations of continuity, flow, and microrotation are given by [23]

$$\frac{u}{r}+\frac{\partial u}{\partial r}+\frac{1}{d}\frac{\partial w}{\partial \eta }=0$$
(2)
$$\rho \left(u\frac{\partial u}{\partial r}+\frac{w}{d}\frac{\partial u}{\partial \eta }\right)=-\frac{\partial p}{\partial r}-\frac{\kappa }{d}\frac{\partial N}{\partial \eta }+\left(\mu +\kappa \right)\left(\frac{{\partial }^{2}u}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial u}{\partial r}-\frac{u}{{r}^{2}}+\frac{1}{{d}^{2}}\frac{{\partial }^{2}u}{\partial {\eta }^{2}}\right)-{\sigma }_{e}{B}^{2}u$$
(3)
$$\rho \left(u\frac{\partial w}{\partial r}+\frac{w}{d}\frac{\partial w}{\partial \eta }\right)=-\frac{1}{d}\frac{\partial p}{\partial \eta }+\kappa \left(\frac{\partial N}{\partial r}+\frac{N}{r}\right)+\left(\mu +\kappa \right)\left(\frac{{\partial }^{2}w}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{{d}^{2}}\frac{{\partial }^{2}w}{\partial {\eta }^{2}}\right)$$
(4)
$$\rho j\left(u\frac{\partial N}{\partial r}+\frac{w}{d}\frac{\partial N}{\partial \eta }\right)=\kappa \left(\frac{1}{d}\frac{\partial u}{\partial \eta }-\frac{\partial w}{\partial r}\right)-2\kappa N+{\alpha }_{1}\left(\frac{{\partial }^{2}N}{\partial {r}^{2}}-\frac{N}{{r}^{2}}+\frac{1}{r}\frac{\partial N}{\partial r}+\frac{1}{{d}^{2}}\frac{{\partial }^{2}N}{\partial {\eta }^{2}}\right)$$
(5)

where \(\eta =\frac{z}{d}\) be the variable of similarity, \(B\) be the strength of the magnetic field, \(\rho \) is the density of fluid, \(p\) be the pressure, \(j\) be the micro inertia, \(\mu \) be the viscosity, \(\kappa \) be the gyro-viscosity, \({\alpha }_{1}\) be the coefficient of gyro-viscosity.

The boundary conditions of the problem are as follows:

$$u\left(r,1\right)=0, u\left(r, -1\right)=0, w\left(r,1\right)=-V$$
$$w\left(r,-1\right)=V, N\left(r,1\right)=0, N\left(r,-1\right)=0$$
(6)

A stream function defined by [23] is as follows:

$$\Psi \left(r,\eta \right)=\frac{V}{2}{r}^{2}f\left(\eta \right),$$
(7)

Therefore \(u(r, \eta )\) and \(w(r, \eta )\) is defined by

$$u\left(r, \eta \right)=\frac{Vr}{2d}{f}^{\prime}(\eta )$$
(8)
$$w\left(r, \eta \right)=-Vf(\eta )$$
(9)

Let

$$N\left(r, \eta \right)=\frac{Vr}{2{d}^{2}}g(\eta )$$
(10)

Now substitute the values of \(u, w, N\) from Eqs. (8)-(10) into Eqs. (3)-(5). After simplification and eliminating \(p\), we get

$$\left(1+R\right){f}^{iv}+{R}_{o}f{f}^{{\prime}{\prime}{\prime}}-R{g}^{{\prime}{\prime}}+{R}_{o}{{M}_{n}}^{2}{f}^{{\prime}{\prime}}=0$$
(11)
$$\alpha {g}^{\mathrm{{\prime}}\mathrm{{\prime}}}-\beta {R}_{o}\left(\frac{1}{2}{f}^{\mathrm{{\prime}}}g-f{g}^{\mathrm{{\prime}}}\right)+R\left({f}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}-2g\right)=0$$
(12)

where \({M}_{n}\left[=\sqrt{\frac{{\sigma }_{e}{B}^{2}d}{\rho V}}\right]\) be magnetic field parameter, \(R\left[=\frac{\kappa }{\mu }\right]\) be the micropolar parameter, \({R}_{o}\left[=\frac{\rho Vd}{\mu }\right]\) be the suction/injection-based Reynolds number, \(\alpha \left[=\frac{{\alpha }_{1}}{\mu {d}^{2}}\right], \beta \left[=\frac{j}{{d}^{2}}\right]\) be the micropolar variables.

From Eq. (6), the reduced form of boundary conditions is given by

$$f\left(1\right)=1,f\left(-1\right)=-1, {f}^{\prime}\left(1\right)=0,$$
$${f}^{\prime}\left(-1\right)=0, g\left(1\right)=0,g\left(-1\right)=0.$$
(13)

The shear stress and couple stress on the disks is calculated by

$${\tau }_{ss}={\left[-(\mu +\kappa )\left(\frac{\partial u}{\partial z}\right)\right]}_{z=\pm d}=-\mu (1+R)\frac{rV}{2{d}^{2}}{f}^{{\prime}{\prime}}(\pm 1)$$
(14)
$${\tau }_{cs}={\left[-{\alpha }_{1}\left(\frac{\partial u}{\partial z}\right)\right]}_{z=\pm d}=-{\alpha }_{1}\frac{rV}{2{d}^{3}}{g}^{\mathrm{^{\prime}}}(\pm 1)$$
(15)

From Eqs. (11), (12) and (13), it is clear that \({f}^{\prime}\) is even and \(g\) is odd function so that we can say that axial velocity is symmetric along the central line and the microrotation is asymmetric. Therefore, we can consider this model under the region \(0\le \eta \le 1\).

So reduced boundary conditions can be written as

$$f\left(0\right)=0,f\left(1\right)=1,{f}^{\prime}\left(0\right)=0,$$
$${f}^{\prime}\left(1\right)=0,g\left(0\right)=0, g\left(1\right)=0.$$
(16)

Methodology of DTM

\(k\) Times differentiation of \(f\left(x\right)\) in this method is given by

$$F\left(k\right)=\frac{1}{k!}{\left(\frac{{d}^{k}f(x)}{d{x}^{k}}\right)}_{x={x}_{0}}$$
(17)

The inverse transformation of \(F(k)\) is defined by

$$f\left(x\right)=\sum_{k=0}^{\infty }F\left(k\right){(x-{x}_{0})}^{k}$$
(18)

\(f(x)\) can be shown in the form of finite series and hence Eq. (18) can be expressed as

$$f\left(x\right)=\sum_{k=0}^{n}F\left(k\right){(x-{x}_{0})}^{k}$$
(19)

From Eq. (17) and Eq. (18), we get

$$f\left(x\right)=\sum_{k=0}^{\infty }{(x-{x}_{0})}^{k}\frac{1}{k!}{\left(\frac{{d}^{k}f(x)}{d{x}^{k}}\right)}_{x={x}_{0}}$$

Which represents the Taylor series form of \(f\left(x\right)\) at \(x={x}_{0}\). Following theorems \({T}_{i} (i\le 10)\) can be concluded from Eq. (17) and Eq. (18):

\({T}_{1}\): If \(f\left(x\right)=g(x)\pm h(x)\) then F \(\left(\lambda \right)=G(\lambda )\pm H(\lambda )\).

\({T}_{2}\): If \(f\left(x\right)=cg(x)\) then \(F\left(\lambda \right)=cG(\lambda )\), where \(c\) is a constant.

\({T}_{3}\): If \(f\left(x\right)=\frac{{d}^{m}g(x)}{d{x}^{m}}\) then \(F\left(\lambda \right)=\frac{\left(\lambda +m\right)!}{\lambda !}G(\lambda +m)\).

\({T}_{4}\): If \(f\left(x\right)=g\left(x\right)h(x)\) then \(F\left(\lambda \right)=\sum_{{\lambda }_{1}=0}^{\lambda }G({\lambda }_{1})H(\lambda -{\lambda }_{1})\)

\({T}_{5}\): If \(f\left(x\right)={e}^{ix}\) then \(F\left(\lambda \right)=\frac{{x}^{\lambda }}{\lambda !}\)

\({T}_{6}\): If \(f\left(x\right)={x}^{n}\) then \(F\left(\lambda \right)=\delta (\lambda -n)\) where \(\delta \left(\lambda -n\right)=\left\{\begin{array}{c}1, \lambda =n\\ 0, \lambda \ne n\end{array}\right.\)

\({T}_{7}\): If \(f\left(x\right)={g}_{1}\left(x\right){g}_{2}\left(x\right)\dots \dots \dots .{g}_{n}(x)\) then

$$F\left(\lambda \right)=\sum_{{\lambda }_{n-1}=0}^{\lambda }\sum_{{\lambda }_{n-2}=0}^{{\lambda }_{n-1}}\sum_{{\lambda }_{1}=0}^{{\lambda }_{2}}{G}_{1}\left({\lambda }_{1}\right){G}_{2}\left({\lambda }_{2}-{\lambda }_{1}\right)\dots \dots \dots \dots .{G}_{n}(\lambda -{\lambda }_{n-1})$$

\({T}_{8}\): If \(f\left(t\right)={(1+t)}^{m}\) then \(F\left(\lambda \right)=\frac{m\left(m-1\right)\dots \dots \dots (m-\lambda +1)}{\lambda !}\)

\({T}_{9}\): If \(f\left(t\right)={\text{sin}}(\omega t+\alpha )\) then \(F\left(\lambda \right)=\frac{{\omega }^{\lambda }}{\lambda !}{\text{sin}}\left(\frac{\pi \lambda }{2}+\alpha \right)\)

\({T}_{10}\): If \(f\left(t\right)={\text{cos}}(\omega t+\alpha )\) then \(F\left(\lambda \right)=\frac{{\omega }^{\lambda }}{\lambda !}{\text{cos}}\left(\frac{\pi \lambda }{2}+\alpha \right)\)

Application of DTM

Initially, we will transform Eqs. (11) and (12) under the above-mentioned theorem. Then we get the following iterative equations:

$$\left(1+R\right)\left(k+4\right)\left(k+3\right)\left(k+2\right)\left(k+1\right)F\left(k+4\right)+{R}_{o}\left(\sum_{l=0}^{k}(l+3)(l+2)(l+1)F(l+3)F(k-l)\right)-R\left(\left(k+2\right)\left(k+1\right)G\left(k+2\right)\right)+{R}_{o}{{M}_{n}}^{2}\left(k+2\right)\left(k+1\right)F\left(k+2\right)=0$$
(20)
$$\alpha \left(k+2\right)\left(k+1\right)G\left(k+2\right)-\beta {R}_{o}\left(\frac{1}{2}\sum_{l=0}^{k}\left(l+1\right)F\left(l+1\right)G\left(k-l\right)-\sum_{l=0}^{k}F\left(l\right)\left(k-l+1\right)G\left(k-l+1\right)\right)+R\left\{\left(k+2\right)\left(k+1\right)F\left(k+2\right)-2G\left(k\right)\right\}=0$$
(21)

The transformed boundary conditions are as follows:

$$F\left(0\right)=0, F\left(1\right)=a, F\left(2\right)=0,$$
$$F\left(3\right)=b, G\left(0\right)=0, G\left(1\right)=c.$$
(22)

where \(a, b, c\) can be evaluated by using appropriate boundary conditions mentioned in Eq. (16). We will get the approximate solution of \(f(\eta )\) and \(g(\eta )\) by using iteration from Eqs. (20) and (21).

Results and Discussion

In this division, the author highlights the impact of the different physical factors on the radial velocity \({f}^{\prime}(\eta )\), the axial velocity \(f(\eta )\) and the microrotation profile \(g(\eta )\). For the validation of the differential transform method, the author presented comparative data of the outcomes achieved by DTM with the outcomes evaluated by the numerical method as well as results available in previous studies. This comparison is tabulated in Tables 1, 2 and 3.

Table 1 Comparison between DTM and NM results, when \(\alpha =1, \beta =0.001, R=1, {R}_{o}=1, {M}_{n}=2\)
Full size table
Table 2 Values of coefficient of skin friction \((-{f}^{{\prime}{\prime}}\left(1\right))\), when \(\alpha =1, \beta =0.001, {M}_{n}=1\)
Full size table
Table 3 Values of coefficient of couple stress \(({g}{\prime}(1)\)), when \(\alpha =1, \beta =0.001, {M}_{n}=1\)
Full size table

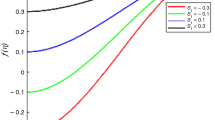
In the Fig. 2, \({f}^{\prime}(\eta )\) is discussed for various numeric values of magnetic field parameter \({M}_{n}\), by assigning other variables as a fixed value like micropolar variables \(\alpha =1, \beta =0.001\) micropolar parameter \(R=1\) and the Reynolds number \({R}_{o}=1\). The figure shows the decreasing behavior of the radial velocity from the lower to the upper disk. In addition, the radial velocity is increasing with a rise in the value of \({M}_{n}\) up to approximately the middle of both the disks and decreases with a rise in the numeric value of \({M}_{n}\) thereafter. The reason behind is that, on increasing the magnetic field parameter, Lorentz force increases automatically which create resistive force within the fluid, hence velocity decreases near the upper disk. In Fig. 3, the effect of \({M}_{n}\) on \(f(\eta )\) is displayed on the same above-mentioned fixed values. This figure illustrates that \(f(\eta )\) is increasing throughout the gap length. One more observation can be seen from this figure which is, that the axial velocity has an increasing behavior with a rise in the values of \({M}_{n}\) in the entire gap length. Figure 4 elucidates the variation of the microrotation \(g(\eta )\) for various values of \({M}_{n}\) for the same fixed parameters. One observation can be made that the behavior of the microrotation is very close to the normal graph. In addition, increasing the value of \({M}_{n}\), it has an increasing behavior. The results of Figs. 3 and 4 are in the good agreement with the physical reason due to the applied magnetic field in the transverse direction which promotes both the velocity and the microrotation profiles.

Fig. 2
figure 2

Radial velocity graph for different \({M}_{n}\)

Full size image
Fig. 3
figure 3

Axial velocity graph for different \({M}_{n}\)

Full size image
Fig. 4
figure 4

Microrotation graph for different \({M}_{n}\)

Full size image

Figures 5, 6 and 7 displays the variation of both profiles for distinct values of the micropolar parameters \(R\) after keeping other variables as constant like micropolar variables \(\alpha =1, \beta =0.001\), micropolar parameter \(R=1\), the magnetic field parameter \({M}_{n}=3\), the Reynolds number \({R}_{o}=-1\). We can observe from Fig. 5 that the radial velocity is falling continuously from \(\eta =0\) to \(\eta =1\). One more thing can be observed that the radial velocity profile is increasing from the lower disk to the approximately middle of both the disks as we increase the value of \(R\) but as the velocity crosses its middle its behavior is reversed. The variation of \(f(\eta )\) is reflected in Fig. 6. A continuous increasing behavior of velocity can be seen from \(\eta =0\) to \(\eta =1\). In addition, the axial velocity also rises with a rise in the values of \(R\) in the entire gap. The nature of \(g(\eta )\) can be seen in Fig. 7. As per the graph, \(g(\eta )\) has incremental nature with an increase in the micropolar parameter. One more observation can be made that the peak of the graph is shifting towards the upper disk on increasing the values of \(R\).

Fig. 5
figure 5

Radial velocity graph for different \(R\) when Ro = −1

Full size image
Fig. 6
figure 6

Axial velocity graph for different \(R\) when \({R}_{o}=-1\)

Full size image
Fig. 7
figure 7

Microrotation graph for different \(R\) when \({R}_{o}=-1\)

Full size image

The variation of \(R\) when the Reynolds number is fixed at \({R}_{o}=1\), on different profiles are reflected in Figs. 8, 9 and 10 when other variables are having a fixed value mentioned above. The falling behavior of the radial velocity is displayed in Fig. 8. It is also clear from figure that the radial velocity profile is decreasing with rise in \(R\) in the neighbourhood of the lower disk but it has reversing nature thereafter. Figure 9 presents the variation of \(f(\eta )\) for various value of the micropolar parameter. As per this figure, the value of the velocity profile is rising rapidly from the lower boundary to the upper boundary. One more observation can be made that velocity is decreasing with rise in \(R\) in the entire gap. The nature of the microrotation profile is shown in Fig. 10. This figure explains that \(g(\eta )\) increases rapidly up to the approximate middle of the path and decreases up to the upper disk thereafter. It can also be analyzed that on rising the values of the micropolar parameter, the microrotation profile is also rising.

Fig. 8
figure 8

Radial velocity graph for different \(R\) when \({R}_{o}=-1\)

Full size image
Fig. 9
figure 9

Axial velocity graph for different \(R\) when \({R}_{o}=1\)

Full size image
Fig. 10
figure 10

Microrotation graph for different \(R\) when \({R}_{o}=1\)

Full size image

The impact of \({R}_{o}\) on the radial, axial velocity and microrotation profile are displayed in Figs. 11, 12 and 13. The variation of the radial velocity \({f}^{\prime}(\eta )\) is reflecting in Fig. 11 for various values of \({R}_{o}\) by choosing other variables as a constant. This figure describes that the radial velocity is falling rapidly from \(\eta =0\) to \(\eta =1\). It can also be depicted that velocity is increasing with rising the values of \({R}_{o}\) near the lower disk while decreasing with rising the values of \({R}_{o}\) near the upper disk. The variation of the axial velocity \(f(\eta )\) can be seen in Fig. 12. This figure explaining the rising behavior of the axial velocity in the entire gap length as well as with respect to the distinct values of \({R}_{o}\). The variation of \(g(\eta )\) for different values of \({R}_{o}\) is presenting in Fig. 13. This graph describes the approximately normal behavior of the microrotation profile. It can also be depicted that the microrotation profile is increasing with rising the values of \({R}_{o}\).

Fig. 11
figure 11

Radial velocity graph for different \({R}_{o}\)

Full size image
Fig. 12
figure 12

Axial velocity graph for different \({R}_{o}\)

Full size image
Fig. 13
figure 13

Microrotation graph for different \({R}_{o}\)

Full size image

Conclusion

The MHD flow of a micropolar fluid between two porous disks is discussed. The obtained higher-order nonlinear ODEs are evaluated by using DTM. The obtained outcomes are compared with the formerly available work which verifies the exactness and validity of the DTM. The author makes the following conclusions:

  • The nature of the radial and the axial velocities are similar for the entire gap length. Its behavior is similar concerning the different parameters except for the distinct values of microrotation parameter while \({R}_{o}=1\).

  • The nature of the microrotation profile is very close to the normal graph from the lower to the upper disk. Also, it has an increasing behavior with respect to all physical parameters.

  • The comparison of numeric values with literature shows that DTM is a better way for evaluating nonlinear ODEs.

In future study, we may generalize this model for the micropolar nanofluid with the effects of the magnetic fields.