1 Introduction

Nonlinear evaluation equations provide a powerful framework for understanding and analyzing complex systems found in fields such as neuroscience, climate science, social networks, and biological systems (Ermentrout and Terman 2010; Wang et al. 2020; Ghergu and Radulescu 2011). These equations enable researchers to capture the intricate interactions and emergent behaviors observed in these systems. These equations play a crucial role in developing advanced machine learning and artificial intelligence algorithms (Weinan et al. 2021). A multitude of efficacious techniques have emerged, offering a diverse array of avenues to construct precise solutions for nonlinear partial differential equations (PDEs). This rich assortment includes the \((G^{\prime }/G)\)-expansion method (Zayed and Gepreel 2009), the modified exp-function method (Naher et al. 2012), the exponential rational function method (Raza et al. 2021), the unified method (Raza et al. 2021), the Hirota bilinear method (Lü and Chen 2021), the simplified Hirota bilinear method (Rafiq et al. 2023), the Bäcklund transformation method (Kaplan and Ozer 2018), the extended simple equation technique (Khater et al. 2019), generalized projective Riccati equations method (Rafiq et al. 2023), extended direct algebraic method (Raza and Zubair 2019), the generalized Kudryashov method (Rafiq et al. 2023), the extended simple equation method (Alotaibi et al. 2023), inverse engineering method (Zubair et al. 2018) and so many.

Within the vast expanse of literature, a remarkable assortment of solution types have been unearthed, each bearing its own distinct characteristics and allure. Among these discoveries lie periodic solutions, rational solutions, hyperbolic type solutions, rogue wave solutions, breather wave solutions, solitary wave solutions, with a particular emphasis on soliton solutions (Raza et al. 2022). Within the realm of solitons, a captivating array of manifestations unfolds, including bright soliton solutions, dark soliton solutions, kink soliton solutions, multi-soliton solutions, and the intriguing entity known as the lump soliton, to name but a few (Rafiq et al. 2021; Wang et al. 2023; Ahmad et al. 2020; Tala-Tebue et al. 2018). The breadth and depth of these findings continue to captivate the minds of researchers and pave the way for further exploration into the profound intricacies of nonlinear phenomena.

Real-world phenomena such as water waves, solitons, and heat conduction can be accurately described by the ill-posed Boussinesq equation (Younas et al. 2022). Understanding and solving ill-posed equation helps overcome challenges in accurately modeling and predicting complex physical systems (Tchier et al. 2017). The ill-posed Boussinesq equation presents mathematical and computational difficulties, requiring innovative techniques for stable and reliable solutions. Solving the ill-posed Boussinesq equation provides insights into wave propagation, nonlinear dynamics, and the behavior of solitons, aiding in the development of technologies and applications in areas such as oceanography, fluid dynamics, and materials science (Holm 2015; Seadawy and Cheemaa 2020; Younas et al. 2020; Rizvi et al. 2021). The mathematical form of ill-posed Boussinesq equation is

$$\begin{aligned} w_{tt}-w_{xx}-(w^2)_{xx}-w_{xxxx}=0, \end{aligned}$$
(1)

where w(x, t) is a wave profile of real valued functions in x and t. The present equation under consideration aims to analyze the propagation of lengthy waves in the shallow water gravity (Daripa 1998). It is important to note that the well-posed Boussinesq equation is distinct from Eq. (1) due to the presence of an additional dispersion term \(w_{xxxx}\). A comprehensive physical description of Eq. (1) has been presented in Bona et al. (2002). In addition, a detailed study of the well-posed Boussinesq equation has been systematically presented in Ma et al. (2009), along with the presentation of its Wronskian solutions. The ill-posed Boussinesq equation has been solved using numerical techniques, specifically filtering techniques, as reported in Daripa and Hua (1999). The filtering techniques have been effectively applied to find the solution of the equation, thereby limiting the growth of mistakes and providing a more efficient approximate solution (Daripa 1998). Moreover, the Lie point symmetry analysis and reductions of Eq. (1) have been meticulously studied in Gao and Tian (2015). It is important to note that although the Kadomtsev–Petviashvili and Belashov–Karpman equations have the applications in physics of waves on shallow water and are obtained from the 3D Boussinesq equation, interesting results have been obtained for other physical systems described by classes of these equations, as well-studied in Karpman and Belashov (1991). In Tchier et al. (2017), undertake an investigation into the dynamics of solitons pertaining to the ill-posed Boussinesq equation. In reference Yaşar et al. (2016), considerable attention has been devoted to the exploration of nonlinear self-adjointness, conservation laws, and exact solutions of the aforesaid ill-posed Boussinesq equation.

The present study offers an in-depth analysis of the ill-posed Boussinesq equation, which manifests in non-linear lattices and shallow water waves. The simplified Hirota technique (Khater and Lu 2021; Khater 2021a, b) is employed to scrutinize the aforementioned equation, which procures multi-wave solutions in one, two, and three soliton profiles. The benefit of this approach is that the need for the bilinear form, which is typically arduous to obtain, is obviated (Kumar and Mohan 2022; Jannat et al. 2022; Boutiara et al. 2022; Khater et al. 2021a, b, c). Additionally, a thorough discourse pertaining to the stability analysis of the equation being examined is put forth.

The paper is structured as follows: Sect. 2 focuses on the utilization of the simplified Hirota’s method to determine multi-wave soliton solutions. Section 3 presents the stability analysis of the considered equation, accompanied by visual representations. In Sect. 4 we explain the graphical representation of the obtained solutions. In the final section, we summarize all the discoveries and conclusions derived from the study.

2 Algorithm of the suggested technique

It’s important to note that the simplified Hirota method is a specialized technique used in the study of soliton solutions and requires a strong background in nonlinear dynamics and mathematics (Manzetti 2018). The general steps of the simplified Hirota’s method for establishing the multi-wave structures of soliton solutions are:

$$\begin{aligned} Q(x,t,w,w_{x},w_{t},w_{2x},\ldots )=0, \end{aligned}$$
(2)

the general structure of nonlinear evolution equations that include two independent variables x and t. Solve Eq. (2) for the dispersion relation between \(a_{i}\) and \(b_{i}\) after substituting

$$\begin{aligned} w(x,t)=e^{\psi _{i}},\quad where\quad {\psi }_{i}=a_{i}x-b_{i}t \quad and\quad i=1, 2, 3,\ldots , N, \end{aligned}$$
(3)

into the linear terms. The N-soliton solutions can be obtained using the subsequent transformation.

$$\begin{aligned} w(x,t)=k(ln \phi )_{x}\quad or\quad w(x,t)=k(ln \phi )_{2x}, \end{aligned}$$
(4)

where \(\phi =\phi (x,t)\) is defined as an auxiliary function. The function \(\phi (x,t)\) takes the following form for a single wave soliton solutions:

$$\begin{aligned} w(x,t)=1+\alpha _{1}e^{\psi _{1}},\quad where\quad {\psi }_{1}=a_{1}x-b_{1}t. \end{aligned}$$
(5)

The function \(\phi (x,t)\) takes the following form for a two wave soliton solutions:

$$\begin{aligned} w(x,t)=1+\alpha _{1}e^{\psi _{1}}+\alpha _{2}e^{\psi _{2}}+\alpha _{1}\alpha _{2}r_{12}e^{\psi _{1}+\psi _{2}}, \end{aligned}$$
(6)

where \(r_{12}\) is phase shift and \({\psi }_{2}=a_{2}x-b_{2}t\). The function \(\phi (x,t)\) takes the following form for a three wave soliton solutions:

$$\begin{aligned} w(x,t)= & {} 1+\alpha _{1}e^{\psi _{1}}+\alpha _{2}e^{\psi _{2}}+\alpha _{3}e^{\psi _{3}}+\alpha _{1}\alpha _{2}r_{12}e^{\psi _{1}+\psi _{2}}+\alpha _{1}\alpha _{3}r_{13}e^{\psi _{1}+\psi _{3}}\nonumber \\{} & {} + \alpha _{2}\alpha _{3}r_{23}e^{\psi _{2}+\psi _{3}}+\alpha _{1}\alpha {2}\alpha _{3}r_{123}e^{\alpha _{1}\psi _{2}+\psi _{3}}, \end{aligned}$$
(7)

where \({\psi }_{3}=a_{3}x-b_{3}t\). The discovery of three Sliton solutions proves the existence of N-soliton for any order \(N\ge 1\). For \(\alpha _{1}=\alpha _{2}=\alpha _{3}= 1\), we construct multi-soliton solutions of Eq. (2). The singular multi-soliton solutions of Eq. (2) can be construct, for \(\alpha _{1}=\alpha _{2}=\alpha _{3}= -1\).

2.1 Application of the protechnique: multi-wave structures

In this section, we will explore the application of the simplified Hirota’s method to the ill-posed Boussinesq equation Eq. (1). To generate multi-soliton solutions in the form of kink solutions (Wazwaz 2007), we set \(\alpha _{1}=\alpha _{2}=\alpha _{3}= 1\) and then substitute the values accordingly.

$$\begin{aligned} w(x,t)=e^{\psi _{i}},\quad where\quad {\psi }_{i}=a_{i}x-b_{i}t. \end{aligned}$$
(8)

By substituting Eq. (8) into the linear terms of Eq. (1), we derive the dispersion relation, which yields the following relationship:

$$\begin{aligned} b_{i}=\pm a_{i}\sqrt{a^{2}_{i}+1}, \end{aligned}$$
(9)

as a result

$$\begin{aligned} \psi _{i}=a_{i}x- a_{i}\sqrt{a^{2}_{i}+1}t. \end{aligned}$$
(10)

In order to obtain the multi-soliton solutions of Eq. (1), we make the assumption that

$$\begin{aligned} \quad w(x,t)=k(ln (h(x,t)))_{2x}, \end{aligned}$$
(11)

where k is a constant that will be determined. We examine the following type of auxiliary function for one soliton solution:

$$\begin{aligned} h(x,t)=1+e^{\psi _{1}},\quad \alpha _{1}=1\quad and\quad \psi _{1}=a_{1}x- a_{1}\sqrt{a^{2}_{1}+1}t. \end{aligned}$$
(12)

By inserting Eq. (11) into Eq. (1) and solving for k then we obtained the possible value for \(k=6\). We collect the following single soliton solution by inserting Eqs. (11) and (12) in Eq. (1).

$$\begin{aligned} w(x,t)=6\Bigg (\frac{a^{2}_{1}e^{a_{1}x- a_{1}\sqrt{a^{2}_{1}+1}t}}{1+e^{a_{1}x- a_{1}\sqrt{a^{2}_{1}+1}t}}-\frac{a^{2}_{1}\big (e^{a_{1}x- a_{1}\sqrt{a^{2}_{1}+1}t}\big )^2}{\big (1+e^{a_{1}x- a_{1}\sqrt{a^{2}_{1}+1}t}\big )^2}\Bigg ) \end{aligned}$$
(13)

Two soliton solutions are developed using the given auxiliary function

$$\begin{aligned} h(x,t)=1+e^{\psi _{1}}+e^{\psi _{2}}+a_{12}e^{\psi _{1}+\psi _{2}}, \quad \alpha _{1}=\alpha _{2}=1, \end{aligned}$$
(14)

and replace the values of \(\psi _{1}\) and \(\psi _{2}\) from Eq. (10). By inserting Eq. (13) into Eq. (1) and solving for the phase shift \(a_{12}\), given below

$$\begin{aligned} a_{12}=\frac{\sqrt{a^2_{2}+1}\sqrt{a^2_{1}+1}-2a^2_{1}+3a_{1}a_{2}-2a^2_{2}-1}{\sqrt{a^2_{2}+1}\sqrt{a^2_{1}+1}-2a^2_{1}-3a_{1}a_{2}-2a^2_{2}-1}, \end{aligned}$$
(15)

which generally refers to

$$\begin{aligned} a_{ij}=\frac{\sqrt{a^2_{j}+1}\sqrt{a^2_{i}+1}-2a^2_{i}+3a_{i}a_{j}-2a^2_{j}-1}{\sqrt{a^2_{j}+1}\sqrt{a^2_{i}+1}-2a^2_{i}-3a_{i}a_{j}-2a^2_{2}-1},\quad 1\le i<j\le 3 \end{aligned}$$
(16)

given that

$$\begin{aligned} \sqrt{a^2_{j}+1}\sqrt{a^2_{i}+1}-2a^2_{i}-3a_{i}a_{j}-2a^2_{2}-1\ne 0. \end{aligned}$$
(17)

Similarly, two-soliton solutions are derived by inserting Eqs. (13) and (14) in Eq. (1).

$$\begin{aligned}{} & {} w(x,t)\nonumber \\{} & {} \quad =6\Bigg (\frac{a^2_{1}e^{\psi _{1}}+a^2_{2}e^{\psi _{2}}+a_{12}(a_{1}+a_{2})^2e^{\psi _{1}+\psi _{2}}}{1+e^{\psi _{1}}+e^{\psi _{2}}+a_{12}e^{\psi _{1}+\psi _{2}}}-\Big (\frac{a_{1}e^{\psi _{1}}+a_{2}e^{\psi _{2}}+a_{12}(a_{1}+a_{2})e^{\psi _{1}+\psi _{2}}}{1+e^{\psi _{1}}+e^{\psi _{2}}+a_{12}e^{\psi _{1}+\psi _{2}}}\Big )^2\Bigg ). \end{aligned}$$
(18)

Three-soliton solutions are developed using the given auxiliary function

$$\begin{aligned} h(x,t)=1+e^{\psi _{1}}+e^{\psi _{2}}+e^{\psi _{3}}+a_{12}e^{\psi _{1}+\psi _{2}}+a_{13}e^{\psi _{1}+\psi _{3}}+a_{23}e^{\psi _{2}+\psi _{3}}+b_{123}e^{\psi _{1}+\psi _{2}+\psi _{3}}, \end{aligned}$$
(19)

where \(\alpha _{1}=\alpha _{2}=\alpha _{3}=1\), and replace the values of \(\psi _{1}\), \(\psi _{2}\), \(\psi _{3}\), \(a_{13}\), and \(a_{23}\) respectively from Eqs. (10) and (16).

Continued as previously, we determine

$$\begin{aligned} b_{123}=a_{12}a_{13}a_{23}. \end{aligned}$$
(20)

We can construct three-soliton solution by inserting Eqs. (18) and (19) in Eq. (1). This clarifies that Eq. (1) yields N-soliton solutions for defined \(N\ge 1\).

Fig. 1
figure 1

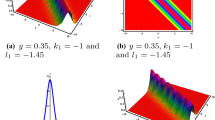
Graphical representation of one-soliton solution given in Eq. (13) using a 3D plot, b 2D plot at \(t=0.2\), c density plot and \(a_1=0.8\)

Full size image
Fig. 2
figure 2

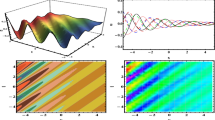
Graphical representation of two-soliton solution given in Eq. (18) using a 3D plot, b 2D plot at \(t=0.2\) and c density plot at \(a_1=0.3, a_2=1.5\)

Full size image

3 Stability analysis

Suppose the perturbed solution of the form

$$\begin{aligned} w(x,t)=M_1+\phi u(x,t), \end{aligned}$$
(21)

it is evident that any constant value \(M_1\) can serve as a stable solution for Eq. (1). We get the following result by substituting Eq. (21) into Eq. (1).

$$\begin{aligned} u_{4x}+2\phi ^{2}(u_{x})^{2}+(\phi +2\phi ^{2}+2M_{1}\phi )u_{xx}-\phi u_{tt}=0, \end{aligned}$$
(22)

linearization Eq. (22) yields

$$\begin{aligned} u_{4x}+(\phi +2\phi ^{2}+2M_{1}\phi )u_{xx}-\phi u_{tt}=0, \end{aligned}$$
(23)

consider Eq. (23) which has a solution in the form

$$\begin{aligned} u(x,t)=e^{(ikx+\theta t)}, \end{aligned}$$
(24)

inserting Eq. (24) into Eq. (23) and solving for \(\phi \), we obtain k, where k is the normalised wave number.

$$\begin{aligned} \theta (k)=\pm \sqrt{1-(1+2\phi +M_{1})k^{2}}. \end{aligned}$$
(25)

In the context of dispersion relations, the sign of the real part of \(\theta (k)\) serves as an indicator of the stability or instability of the solution (Hoffacker and Tisdell 2005). A positive real part suggests instability, as the solution will grow without bound, while a negative real part implies stability, as the solution will approach zero as time goes on. When a complex function is considered stable, it means that the values of both its real and imaginary parts do not exhibit unbounded growth or divergence as the independent variable varies. Instead, these parts remain within certain bounds or limits. From Eq. (25) we consider

$$\begin{aligned} \theta (k)=-\sqrt{1-(1+2\phi +M_{1})k^{2}},\quad where\quad M_{1}<-2\phi , \end{aligned}$$
(26)

this shows stable behavior (Fig. 3) for all values of k. And this will be unstable for all values of k, if we consider square root with plus sign. When the real part of \(\theta (k)\) is zero, it implies that the system or function under consideration exhibits a critical balance between growth and decay (Berk et al. 1996). Perturbations or disturbances may cause the function to oscillate or exhibit periodic behavior around this balance point, without significant divergence or convergence.

Fig. 3
figure 3

Graphically illustration of the stability analysis for Eq. (26) by using suitable physical parameter values \(M_{1}=-3\) and \(\phi =1\) for green line, \(M_{1}=-5\) and \(\phi =2\) for blue line and \(M_{1}=-7\), and \(\phi =3\) for red line

Full size image

4 Discussion on the graphical illustration of derived solutions

In the present study, we have undertaken an investigation of the ill-posed Boussinesq equation, which is known to manifest in the context of nonlinear lattices and shallow water waves. The graphical representation of the obtained solutions is exhibited, highlighting their significance in the burgeoning domains of nonlinear science. By utilizing the simplified Hirota methodology, we are able to successfully achieve solutions for models with one-soliton, two-soliton, and three-soliton, while taking into account their respective constraint conditions. The derived one-soliton solution of the investigation is illustrated in Fig. 1 through a graphical representation, which has been achieved by employing a suitable physical parameter value of \(a_1=0.8\). Figure 2 displays a graphical representation of the investigated two-soliton solution, utilizing appropriate physical parameters where the values of \(a_1\) and \(a_2\) are 0.3 and 1.5, respectively.

Multi-solitons are of great significance in comprehending shallow water waves, as they represent a collection of solitary waves that offer valuable insights into their behavior. The development of multi-soliton solutions enhances our understanding of the dynamics of shallow water waves, encompassing their interaction and propagation characteristics. Additionally, a comprehensive investigation of the stability analysis of the model under consideration has been conducted, and the outcomes have been presented in the form of a graph, as depicted in Fig. 3 which has been achieved by employing a suitable physical parameter values \(M_{1}=-3\) and \(\phi =1\) for green line, \(M_{1}=-5\) and \(\phi =2\) for blue line and \(M_{1}=-7\), and \(\phi =3\) for red line.

5 Concluding remarks

In this manuscript, the dynamic analysis of the ill-posed Boussinesq equation has been investigated. This equation arises in nonlinear lattices and shallow water waves. To obtain multi-wave structures, such as one-soliton, two-soliton and three-soliton solutions, the simplified Hirota method has been employed. To visually represent the obtained solutions and their physical features, these results have been visually demonstrated through 3D, 2D and density plots. In addition, a comprehensive discussion on the stability analysis of the equation under study has been presented. These results are innovative and have not been previously investigated in the context of this equation. The methodology used is concise, straightforward, and efficient, and as a result, it makes a significant contribution to comprehending the complexity of multi-wave profiles in nonlinear physical science models.