The Combined Effects of Wall Properties and Space Porosity on MHD Two-Phase Peristaltic Slip Transport Through Planar Channels

Abstract

In this article, a theoretical investigation is analyzing the effects of the complaint wall properties, the slip conditions, the space porosity, and the transverse magnetic field on the magnetohydrodynamic peristaltic transport of viscous compressible flow carrying out some rigid spherical suspension particles flowing through space porous medium in a horizontal elastic rectangular channel. The flexible channel walls are taken as a sinusoidal wave. The expressions describing the peristaltic transport are mathematically analyzed using the perturbation technique with a small amplitude wave ratio. The analytical study describes the influence of various wall parameters such as damping force, wall tension, and wall elasticity and flow parameters as compressibility parameter, slip parameter, suspension parameter, Reynolds number, space porosity, and magnetic field parameter on the net axial velocity. The reversal flow occurs at the channel core and boundaries due to the slip and the magnetic field effects. Biological, geophysical, and industrial fluid dynamics applications are important models for the peristaltic transport described in this work.

Introduction

Recent theoretical articles studying the action of the peristaltic transport of biofluids through a channel or tube draw the interest of many researchers. In the beginning, it is important to know the nature of the peristaltic transport which is considered as a fluid dynamic process, in which the fluid transport from one place to another occurs as a result of area contraction or expansion along the flexible walls of a distensible channel. The resulting wave takes the shape of a sinusoidal wave. Many applications in the physiological and industrial fields are widely depending on the type of two-phase flow, in which the interaction between the fluid flow and suspended particles through the porous medium will occur. Particularly, physiological applications take serious attention in the study, such as urine motion in the ureter from kidney to the bladder, chyme movement through gastrointestinal system, food movement in the esophagus, the ovum motion in the female’s fallopian tube, and the blood transport through the small blood vessels like the motion in arterioles, venules, and also the capillaries. The peristaltic system can also exist in the case of lymph motion via the lymphatic vessels. Furthermore, some worms use the peristaltic movement as a method of movement. Also, this phenomenon is applied in the propulsion of some industrial fluids, for instance, roller, finger pumps, heart–lung machine, and blood pump machine. For this reason, in the current years, scientific studies are handling the peristaltic movement of incompressible liquids whereas few articles deal with the compressible peristaltic transport. As a result, this study concentrates on this type under the effect of several physical parameters. To extend the interests of the study, the flow of rarefied gases in micro-domains is also included.

There are numerous physiological applications related to the compliant collapsible tubes and their effects on the behavior of the fluid flow carrying some particulate suspensions through a porous medium such as the dynamics of internal blood flowing through veins above the heart and arteries under a cuff, and the pressure pulse propagation in the cerebrospinal fluid system and the blood flow in the cardiovascular system. The elastic properties of the collapsing tubes in the real physiological systems are related to the muscle effect. In the laboratory, this model can be described according to the “tube law”. It means rubber tubes of finite length are used and reveal a rich variety of self-excited oscillations indicating the related dynamical system.

To illustrate the importance of peristaltic transport in the physiological field, a literature survey of the relevant works has been provided. Several experimental and theoretical attempts in this area have been provided such as Latham [1], Fung and Yih [2] and Shapiro et al. [3]. They were amongst earlier researchers who introduced studies for the peristaltic movement system. A comprehensive literature review on the theoretical investigations was classified accordingly with the model geometry, the fluid type, Reynolds number, wave amplitude, wavelength, and the shape of wave taken into consideration. The experimental studies for peristaltic motion have been analyzed by Rath [4], Srivastava and Srivastava [5,6,7,8] and Srivastava and Saxena [9]. It was remarkable that the prior studies were concentrated on the peristaltic movement of incompressible viscous and non-Newtonian fluids. There are a few related studies explaining the flow of compressible fluids peristaltically. Aarts and Ooms [10] was the first who introduced the principles of peristaltic pumping of compressible liquids to improve the oil extraction process from porous rocks using the ultrasound technique. It is noticed that a similar action between the ultrasonic radiation and the peristaltic mechanism on the liquid motion. The compressibility has a powerful effect on the liquid flow. Tsiklauri and Beresnev [11] have explained the relaxation time impact on the peristaltic locomotion for the compressible liquid of the Maxwell model. Antanovskii and Ramkissoon [12] have studied the discharge of a compressible fluid through a long flexible wall tube motivated by pulsatile force in addition to the wall relaxation and contraction by applying the lubrication technique. Elshehawey et al. [13] investigated the action of the peristaltic movement of a compressible liquid through a porous medium via tapered pore. The perturbation methodology is used. The results disclosed that the net flow rate was depending on the ultrasonic radiation, furthermore, liquid compressibility has a large impact on the net flow generated. Eldesoky and Mousa [14] have analyzed the peristaltic process for Maxwell fluid flowing via a porous medium tube. The calculations too disclosed that liquid compressibility, porosity parameter, and relaxation time have impacted the net flow rate. Hayat et al. [15] have indicated the influence of the rheological characteristics and compressibility of Jeffrey fluid traveling peristaltically through a circular pipe. The increase in the relaxation time has reduced the streamwise velocity and caused the reversal flow near the walls. Eldesoky and Mousa [16] have studied the applications of the peristaltic system for compressible fluids in the field of aerospace. In addition, Eldesoky [17] investigates the influence of different properties like wall slip conditions and permeability parameters on the peristaltic locomotion of compressible fluid of the Maxwell model, it was noticed that energy is dissipated through the traveling wave of compressible fluid at the surface of the tube wall. Felderhof [18] has indicated the dissipation rate occurred. Ricard and Nuñez [19] has illustrated the stability effect of the long wave peristaltic action for compressible fluid using extended lubrication theory with a small parameter.

The two-phase flow has an essential action in many engineering applications and especially in the biological field. Solid particles were constructed within the kidneys or appeared because of shattering larger kidney stones producing dusty peristaltic transport via the ureter. This effect has been indicated as Jiménez-Lozano et al. [20]. Hung and Brown [21] were the first who tried to study two-phase peristaltic transport. Researches of Srivastava and Srivastava [7], Srivastava and Saxena [9] and Mekheimer et al. [22] have worked on this topic. The previous articles deal with incompressible viscous peristaltic motion in a rectangle duct or circular tube. Eldesoky et al. [23] were the first who concentrated their study on the interaction of the liquid compressibility and the suspended solid particles for the peristaltic wave mechanism. It was remarkable that the net axial velocity increases with increasing particle concentration. Eldesoky et al. [24] have analyzed the mutual effects of the particle concentration and the thermal characteristics on the peristaltic locomotion in the presence of a catheter through a pipe using the low Reynolds long wave technique. The results showed that the increase in the catheter size has reduced the mean flow velocity but the thermal properties were enhanced. Whereas, Eldesoky et al. [25] added the porosity effect to the magnetohydrodynamics (MHD), heating, and dusty suspensions properties on the peristaltic flow of the blood via a two-dimensional channel under the assumptions of the perturbation scheme. The more dust led to more decrease in the fluid temperature and also the magnetic force has changed the fluid temperature depending on the time and position. Zeeshan et al. [26] have examined the simultaneous effects of the ionization slip properties with hall current, suspension concentration, and thermal heating on the peristaltic motion of the two-phase MHD flow in the presence of the space porosity. The results showed that the Darcy factor was reducing the temperature distribution, whereas, the increase in the particle volume fractions have decreased the velocity profiles.

Selection the compliant walls indicates the effectiveness of the wall properties on the flow behavior in the collapsible tubes and particularly in the critical positions in the living creatures such as the wavy transport in the cardiovascular system, the urine transport in the bladder membrane and particularly if dusty solid stones are flowing within the urine from kidney to the bladder. Wall compliance properties have received good concentration amongst the latest investigations studying the peristaltic process of biofluids. Pandey and Chaube [27] have explained the various influences of the properties of the walls on peristaltic movement for couple stress fluid, but the case of non-Newtonian fluid was studied by Javed et al. [28]. The elasticity of the flexible walls and the heat transfer effects were discussed for the incompressible peristaltic waves by Radhakrishnamacharya and Srinivasulu [29]. Elnaby and Haroun [30] have presented a discussion about a new model to illustrate the action of wall properties on peristaltic movement fluids.

According to the compressible flow area of study, wall properties have been handled in few articles as Mekheimer and Abdel‐Wahab [31] who investigated the influence of different parameters of the wall on the compressible flow generated by surface acoustic wave (SAW) in micro-channel.

Also, there is a special concentration on the peristaltic motion of magnetohydrodynamic (MHD) flow of physiological fluids, such as pump machine of blood and also MHD peristaltic compressor. Sud et al. [32] illustrates the magnetic field effect on the flow of blood. The rise in the magnetic field has enhanced blood velocity. Whereas Akbar [33] has discussed the magnetic field impact on the peristaltic flow of nano-Eyring-Powell fluid. Abbasi et al. [34] have introduced a further model of changing the viscosity of the MHD fluid moving peristaltically. Moreover, Sinha et al. [35] did a similar study including the mutual effects of wall slip and heat exchange. The results showed that the slipping at walls boosted the mean streamwise velocity. Srinivas et al. [36] studied the combined influences of transverse magnetic flux, the wall slip conditions, and the heat transfer on the peristaltic movement of an incompressible MHD Newtonian fluid in a porous channel with elastic features. The long-wavelength technique with a low-Reynolds number was applied. The thermal temperature gradient in the divergent portion was large. According to the compressible flow study Mekheimer et al. [37] were concerned with magnetic field action in their research. The Hartmann number and the permeability parameter have enhanced the net discharge and the mean streamwise velocity at walls. Recent articles handling the simultaneous effects of dusty fluid with MHD in presence of different factors of nanofluid, hall current, porous medium and wall slip properties are presented for instance (Elmaboud et al. [38, 39]; Abdelsalam and Vafai [40, 41]; Abdelsalam and Bhatti [42, 43]; Abd Elmaboud et al [44]). Recently, Eldesoky et al. [46] have analyzed the different influences of the relaxation time, the slip conditions, and the elastic features for the flexible channel on the peristaltic motion of compressible fluid of the Maxwellian model. It was found that the higher concentration of particles caused resistance to the flow and assistance of the reflux occurrence. Then, Eldesoky et al. [46] analyzed the various effects of heat transfer, elastic wall properties, slip conditions on the peristaltic flow of compressible liquid in a tube and the results showed that the liquid compressibility, flexible wall features, and heat transfer have strong effectiveness in changing the dynamic behavior of the flow. Abumandour et al. [47] have also studied the interaction between the magnetic flux and the elastic wall properties on the peristaltic movement of the MHD flow by using the perturbation approach. The results showed that the damping coefficient will resist the flow but the rise in the magnetic flux has reduced the flow rate.

In Sadaf and Abdelsalam [48], the performance of the injected nanoparticles is investigated in a mixed flexible peristaltic blood model using average lubrication methodology. It was found that the hybrid nanoparticles were affecting the heat transfer rate rather than the set nanoparticles. Bhatti et al. [49] have investigated the Sutterby fluid model to understand the mechanism of the blood hemodynamics under the effect of the nanomaterials characteristics on the runoff of the gyrotactic microorganisms through the blood flow in a narrow artery. The accurate perturbation technique up to the third order was performed on the model's governing equations. The results showed that the non-Newtonian property has a resisting impact on the fluid flow and the temperature distribution was high in the transition from a convergent to a divergent position through the artery. Abdelsalam and Bhatti [50] have analyzed the convective flow of a non-Newtonian nanofluid carrying some oxytocic microorganisms using the homotopy perturbation methodology (HPM). Elmaboud et al. [51] have entered the electromagnetic force field and the heat flux on the two layers' immiscible flow. The analytical methodology is the homotopy analysis method (HAM). The results showed that the electric field boosted the net flow whereas, the magnetic force did not. Abdelsalam and Mekheimer [52] have investigated the case of rotating channel with constant angular velocity and carrying couple stress fluid moving peristaltically under the exact solution of (HPM). Eldesoky et al. [53] have combined the mutual effects of thermal heating and magnetic flux in the presence of small circular suspensions through the blood flow in a catheter tube under the approximation of the long wave technique. The results showed that the heat was enhancing the net axial velocity while the suspension concentration caused a reduction in the flow rate.

Towards what is best for the author’s survey, it is worth saying that there has not been any attempt to study the combined influences of wall properties, slip condition, magnetic field on peristaltic locomotion of MHD compressible liquid mixed with suspended particulate through the porous area of a planar rectangular channel. Therefore, the authors pay attention to this study for compressible fluid flow as it receives less interest.

The main goal of this investigation is to determine the wall slip, wall properties, fluid compressibility, magnetic field, and space porosity effects on the wavy peristaltic pumping of a compressible fluid mixed with suspended particles inside a micro-channel with compliant walls and, also, study the effect of suspended particles concentration. This study is divided into three cases which will be shown later. The problem model is introduced as a spring-backed flexible wall. A perturbation approach with a small amplitude wave ratio is taken and neglecting the pressure gradient of the order zero at the beginning. This theoretical investigation is very useful in understanding a number of diverse physical problems concerned with biofluid peristaltic transport through the human organs; also, this study may be valid for molecular gases (compressible liquid) flowing in Nano-channels. The undertaken problem in the present form approaches to the real system containing the wall slip, the space porosity, the transverse magnetic field, and the wall properties in the presence of suspended particles that appear in the peristaltic flow for the blood through the artery. The chosen model represents a model similar to the blood motion in the flexible arteries. The elastic features are presented as spring-backed walls. The particulate suspensions refer to the red blood cells concentration in the blood and the plasma is the main flow. The fats in the blood are constructing the porous medium and the magnetic field effect appears in the magnetic resonance imaging MRI units. The current model can be reduced to reach the model investigated by Mekheimer and Abdel‐Wahab [31].

Mathematical Formulation of the Problem

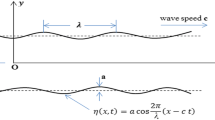
Suppose a peristaltic wave of compressible viscous flow carrying out some rigid spherical particles whose number density is sufficiently sizable to define average characteristics of dusty particles. The rectangular channel has elastic walls with uniform width $(2d)$. The channel is containing a porous area and is exposed to a transverse magnetic field. The model of a spring-backed compliant wall under the previous physical parameters is presented in Fig. 1. Selection of $(x-y)$ as Cartesian coordinates. The flow is energized by means of a small amplitude ratio sinusoidal wave with a constant wave speed $c$ on the compliant walls of the channel.

Fig. 1

Schematic graph for the geometry of a two-dimensional peristaltic transport through spring-backed flexible channel walls

The system of the governing equations describing the two-phase flow in the existence of the magnetic force and the space porosity is expressed as Srivastava and Srivastava [7, 8], Eldesoky et al. [23] and Drew [54].

Fluid Phase

Continuity Equation

$$ \frac{{\partial (1 - C)\rho_{f} }}{\partial t} + u_{f} \frac{{\partial (1 - C)\rho_{f} }}{\partial x} + v_{f} \frac{{\partial (1 - C)\rho_{f} }}{\partial y} + \rho_{f} \left( {\frac{{\partial (1 - C)\,u_{f} }}{\partial x} + \frac{{\partial (1 - C)\,v_{f} }}{\partial y}} \right) $$

(1)

where $[C]$ refers to the constant volume fraction of the solid particles as Srivastava and Srivastava [6] so that Eq. (1) become as follows:

$$ \frac{{\partial \rho_{f} }}{\partial t} + u_{f} \frac{{\partial \rho_{f} }}{\partial x} + v_{f} \frac{{\partial \rho_{f} }}{\partial y} + \rho_{f} \left( {\frac{{\partial u_{f} }}{\partial x} + \frac{{\partial v_{f} }}{\partial y}} \right) = 0 $$

(2)

X-momentum

$$ \begin{aligned} \left( {1 - C} \right)\rho_{f} \left[ {\frac{{\partial u_{f} }}{\partial t} + u_{f} \frac{{\partial u_{f} }}{\partial x} + v_{f} \frac{{\partial u_{f} }}{\partial y}} \right] & = - (1 - C)\frac{\partial p}{{\partial x}} + (1 - C)\mu_{s} \left( {\frac{{\partial^{2} u_{f} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{f} }}{{\partial y^{2} }}} \right) \\ & \quad + \frac{{(1 - C)\,\mu_{s} }}{3}\frac{\partial }{\partial x}\left( {\frac{{\partial u_{f} }}{\partial x} + \frac{{\partial v_{f} }}{\partial y}} \right) \\ & \quad + C\,S\,(u_{P} - u_{f} ) - \frac{{\mu_{s} \,u_{f} }}{K} - \sigma \,B_{o}^{\,\,2} \,u_{f} \, \\ \end{aligned} $$

(3)

Y-momentum

$$ \begin{aligned} \left( {1 - C} \right)\rho_{f} \left[ {\frac{{\partial v_{f} }}{\partial t} + u_{f} \frac{{\partial v_{f} }}{\partial x} + v_{f} \frac{{\partial v_{f} }}{\partial y}} \right] & = - (1 - C)\frac{\partial p}{{\partial y}} + (1 - C)\,\mu_{s} \left( {\frac{{\partial^{2} v_{f} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{f} }}{{\partial y^{2} }}} \right) \\ & \quad + \frac{{(1 - C)\,\mu_{s} }}{3}\frac{\partial }{\partial y}\left( {\frac{{\partial u_{f} }}{\partial x} + \frac{{\partial v_{f} }}{\partial y}} \right) \\ & \quad + C\,S\,(v_{p} - v_{f} ) - \frac{{\mu_{s} \,v_{f} }}{K} \\ \end{aligned} $$

(4)

Particulate Phase

Continuity Equation

$$ \frac{\partial }{\partial x}\left\{ {C\,u_{p} } \right\} + \frac{\partial }{\partial y}\left\{ {C\,v_{p} } \right\} = 0 $$

(5)

X-momentum

$$ C\,\rho_{p} \left[ {\frac{{\partial u_{p} }}{\partial t} + u_{p} \frac{{\partial u_{p} }}{\partial x} + v_{p} \frac{{\partial u_{p} }}{\partial y}} \right] = - C\frac{\partial p}{{\partial x}} + C\,S\,(u_{f} - u_{p} ) $$

(6)

Y-momentum

$$ C\rho_{p} \,\left[ {\frac{{\partial v_{p} }}{\partial t} + u_{p} \frac{{\partial v_{p} }}{\partial x} + v_{p} \frac{{\partial v_{p} }}{\partial y}} \right] = - C\,\frac{\partial p}{{\partial y}} + C\,S\,(v_{f} - v_{p} ) $$

(7)

where $[x$] is the streamwise direction and [$y]$ is the normal direction of the channel walls. $[{B}_{o}]$ refers to the transverse magnetic field. $[\sigma ]$ denotes the coefficient of electrical conductivity. $[K]$ is the permeability of the porous area. $\left[{u}_{f}, {v}_{f}, {u}_{{\varvec{p}}},\mathrm{and} {v}_{{\varvec{p}}}\right]$ refer to the liquid phase and particle phase velocities in the [$x$ and $y]$ directions, respectively. $[{\rho }_{f}\mathrm{and} {\rho }_{p}]$ refer to the actual liquid and particles densities, respectively. [$p]$ is the liquid pressure. [µ_s] refers to suspended particles effective viscosity, and $[S]$ means the drag coefficient as a result of the interface forces associated with the two phases of flow.

The constitutive equation expressing the action of fluid compressibility takes the form of Srivastava and Saxena [9]

$$ \frac{1}{\rho }\frac{\partial \rho }{{\partial \left( {1 - C} \right)p}} = k^{*} $$

(8)

where [${k}^{*}]$ is the fluid compressibility and Eq. (8) was solved to obtain a relation for the fluid density as follows:

$$ \rho_{f} = \rho_{o} e^{{\left[ {\left( {1 - C} \right)k^{*} \left( {p - p_{c} } \right)} \right]}} $$

(9)

where $[{\rho }_{o}]$ refers to the constant density at reference pressure [${p}_{c}$].

The geometry of the wall surface can be described as Elnaby and Haroun [30]

$$ \eta (x,t) = a\cos \frac{2\pi }{\lambda }(x - ct) $$

(10)

where $[\eta (x,t)]$ refers to the transverse displacement of the channel wall. $[a]$ refers to the amplitude of the wave. $[\lambda ]$ denotes the wavelength, and $[c]$ is the wave speed.

$[ \eta (x, t) \mathrm{and} -\eta (x, t) ]$ are defined at the upper and lower boundaries as follows:

$$ y = \pm \left( {d + \eta } \right) = \pm \left( {d + a cos\frac{2 \pi }{\lambda }\left( {x - ct } \right)} \right) $$

(11)

where $[2d]$ is the channel width.

Compliant walls are represented as a spring-backed flexible wall prototype restricted to just propagate in the normal direction. The flexible wall equation can be expressed as

$$ L\left( \eta \right){ } = p - p_{o} $$

(12)

where $[L$] refers to differential operator representing the action of the complaint wall forces, according to Mekheimer and Abdel‐Wahab [31].

$$ L = - T\frac{{\partial^{2} }}{{\partial x^{2} }} + m\frac{{\partial^{2} }}{{\partial t^{2} }} + D\frac{\partial }{\partial t} + B\frac{{\partial^{4} }}{{\partial x^{4} }} + K_{1} $$

(13)

where $[T]$ denotes longitudinal wall tension per unit width. $[m]$ refers to wall mass per unit area, [$D]$ denotes damping forces factor,$[B$] denotes the wall flexural rigidity coefficient, [${K}_{1}]$ is the stiffness of spring, $[p]$ is the interface pressure at the boundaries, and [${p}_{o}]$ is the outside wall surface pressure in consequence of muscles tension. Addition of some terms to Eq. (13) for calculation of spring basics may exist but they do not modify the mathematical model, therefore, so that the study remains uncomplicated these terms are neglected as Mittra and Prasad [55]. Supposing that$[{p}_{o}=0 ]$, and channel walls are non-extensible. Thus, just lateral motions exist perpendicular to unreformed locations and no horizontal displacement occurs. The suspension concentration is supposed to be small [$C\le 0.59]$, then the collision of the particles with each other can be ignored. Diffusivity terms expressing the particles interfere as Brownian motion was ignored as Batchelor [56]. Drag coefficient relation is taken in the following form:

$$ S = \frac{9}{2}\frac{{\mu_{0} }}{{a_{0}^{2} }}\lambda^{\prime}(C)\;{\text{and}}\;\lambda^{\prime}(C) = \frac{{4 + 3\left[ {8C - 3C^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} + 3C}}{{\left[ {2 - 3C} \right]^{2} }} $$

(14)

where [µ₀] refers to the dynamic fluid viscosity. ${[a}_{o}]$ denotes the particulate radius. Tam [57] has introduced an expression for [$\lambda {^{\prime}}(C)]$ which serves in the calculations of the fractional volume of the suspended particles. Noting that, it is valid for small particulate Reynolds number.

Charm and Kurland [58] have presented an experimental expression for estimation the effective viscosity of the suspensions as follows:

$$ \mu_{S} (C) = \mu_{0} \frac{1}{1 - qC} $$

(15a)

$$ q = 0.07{\text{e}} \,^{{\left[ {2.49\,\,C + \frac{1107}{{T_{1} }}{\text{e}}^{{\,\,\left( { - 1.69\,C} \right)}} } \right]}} $$

(15b)

where $[{T}_{1}]$ refers to the absolute temperature in $(^\circ K).$ Charm and Kurland [58] have experimentally examined Eq. (15) and deduced that this equation was suitable for the blood suspensions up to 10\%.

The slip of fluid takes place on the wall boundaries and non-permeability conditions are fitted for the fluid on channel walls.

Boundary conditions: according to the physical explanation of the current model problem, walls of the channel were supposed to be elastic but extensible and just vertical displacements of the walls occur.

Thus, the boundary conditions at $y=\pm \left(d+\eta \right)$ are expressed as follows:

• 1. Wall slip condition is

  $$ u_{f} = \mp A\frac{{\partial u_{f} }}{\partial y}\,\,\,\, $$

  (16)

• 2. Impermeability of wall is

  $$ \left. \begin{gathered} v_{f} = \pm \frac{\partial \eta }{{\partial t}} \hfill \\ v_{p} = \pm \frac{\partial \eta }{{\partial t}}\,\,\, \hfill \\ \end{gathered} \right\}\,\, $$

  (17)

• 3. Pressure gradient interaction at the channel boundaries is

  $$ \begin{aligned} \left( {1 - C} \right)\frac{\partial L}{{\partial x}} = \left( {1 - C} \right)\frac{\partial P}{{\partial x}} & = - \left( {1 - C} \right)\rho_{f} \left( {\frac{{\partial u_{f} }}{\partial t} + u_{f} \frac{{\partial u_{f} }}{\partial x} + v_{f} \frac{{\partial u_{f} }}{\partial x}} \right) + \left( {1 - C} \right)\mu_{\,s} \left( {\frac{{\partial^{2} u_{f} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{f} }}{{\partial y^{2} }}} \right) \\ & \quad + \frac{{\left( {1 - C} \right)\mu_{s} }}{3}\frac{\partial }{\partial x}\left( {\frac{{\partial u_{f} }}{\partial x} + \frac{{\partial v_{f} }}{\partial y}} \right) + C\,S\left( {u_{p} - u_{f} } \right) - \frac{{\mu_{s} }}{K}u_{f} - \sigma \,u_{f} B_{o}^{2} \\ \end{aligned} $$

  (18)

Dimensionless parameters are presented as follows:

$$ \left. \begin{gathered} \overline{x} = \frac{x}{d},\,\,\overline{y} = \frac{y}{d},\,\,\,\overline{{u_{f} }} = \frac{{u_{f} }}{c},\,\,\overline{{v_{f} }} = \frac{{v_{f} }}{c},\,\,\overline{{u_{p} }} = \frac{{u_{p} }}{c},\,\, \hfill \\ \overline{{v_{p} }} = \frac{{v_{p} }}{c},\overline{\eta } = \frac{\eta }{d},\overline{t} = \frac{ct}{d},\overline{p} = \frac{P}{{\rho_{o} c^{2} }},\overline{{p_{c} }} = \frac{{P_{c} }}{{\rho_{o} c^{2} }} \hfill \\ \end{gathered} \right\}, $$

(19)

Dimensionless elastic wall parameters are

$$ \overline{D} = \frac{D d}{{\rho_{o} \upsilon_{s} }},\overline{B} = \frac{B}{{\rho_{o } d \upsilon_{s}^{2} }},\overline{{K_{1} }} = \frac{{K_{1} d\,^{3} }}{{\rho_{o } \,\upsilon_{s}^{\,2} }},\overline{m} = \frac{m}{{\rho_{o } d}},\overline{T} = \frac{T \,d}{{\rho_{o} \,\upsilon_{s}^{2} }}. $$

(20)

Permeability parameter of the porous area is $\overline{K} = \frac{K}{{d^{\,2} }}$ whereas dimensionless fluid parameters are supposed to be as follows: the Reynolds number in presence of the suspended particulates $R = \frac{{c\,\,d\,\rho_{0} }}{{(1 - C)\,\mu_{S} }},\,$ the compressibility coefficient $\chi = k^{*} \rho_{0} \,c^{2} ,$ the wave number $\alpha = \frac{2\,\pi \,d}{\lambda },$ the amplitude ratio $\varepsilon = \frac{a}{d},$ the suspension factors $M = \frac{{S\,d^{\,2} }}{{(1 - C)\,\mu_{S} }},$ $N = \frac{{S\,d^{\,2} \rho_{o} }}{{(1 - C)\,\rho_{p} \,\mu_{S} }}$, Hartmann number $H_{a} = \sqrt {\frac{\sigma }{{\mu_{S} }}} \,B_{o} \,d$, the kinematic viscosity $\upsilon_{s} = \frac{{\mu_{\,s} }}{{\rho \,_{o} }}$, and the Knudsen number $Kn = \frac{A}{d}$ where [A] denotes molecules mean free path.

Thus, Eqs. (l–7), (9–11), and (16–18) after dropping the overbars eventually take the following form:

$$ \frac{{\partial \rho_{f} }}{\partial t} + u_{f} \frac{{\partial \rho_{f} }}{\partial x} + v_{f} \frac{{\partial \rho_{f} }}{\partial y} + \rho_{f} \left( {\frac{{\partial u_{f} }}{\partial x} + \frac{{\partial v_{f} }}{\partial y}} \right) = 0 $$

(21)

$$ \begin{aligned} &\left( {1 - C} \right)R\rho_{f} \left[ {\frac{{\partial u_{f} }}{\partial t} + u_{f} \frac{{\partial u_{f} }}{\partial x} + v_{f} \frac{{\partial u_{f} }}{\partial y}} \right] = - \left( {1 - C} \right)R\frac{\partial p}{{\partial x}} + \left[ {\frac{{\partial^{2} u_{f} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{f} }}{{\partial y^{2} }}} \right] \\ & \quad + \frac{1}{3}\frac{\partial }{\partial x}\left[ {\frac{{\partial u_{f} }}{\partial x} + \frac{{\partial v_{f} }}{\partial y}} \right] + C M\left( {u_{p} - u_{f} } \right) - \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)\,u_{f} }}{(1 - C)}\,\, \\ \end{aligned} $$

(22)

$$ \begin{aligned} \left( {1 - C} \right)\,R\,\rho_{f} \left[ {\frac{{\partial \,v_{f} }}{\partial t} + u_{f} \frac{{\partial \,v_{f} }}{\partial x} + v_{f} \frac{{\partial \,v_{f} }}{\partial y}} \right] & = - \left( {1 - C} \right)\,R\frac{\partial \,p}{{\partial \,y}} + \left[ {\frac{{\partial^{\,2} \,v_{f} }}{{\partial \,x^{2} }} + \frac{{\partial \,^{2} \,v_{f} }}{{\partial \,y^{2} }}} \right] \\ & \quad + \frac{1}{3}\frac{\partial }{\partial y}\left[ {\frac{{\partial \,u_{f} }}{\partial x} + \frac{{\partial \,v_{f} }}{\partial y}} \right] + C M\left( {v_{p} - v_{f} } \right) - \frac{{v_{f} }}{(1 - C)\,K} \\ \end{aligned} $$

(23)

$$ C R \left[ {\frac{{\partial u_{p} }}{\partial t} + u_{p} \frac{{\partial u_{p} }}{\partial x} + v_{p} \frac{{\partial u_{p} }}{\partial y}} \right] = - C R\frac{\partial p}{{\partial x}} + C N\left( {u_{f - } u_{p} } \right) $$

(24)

$$ C R\left[ {\frac{{\partial v_{p} }}{\partial t} + u_{p} \frac{{\partial v_{p} }}{\partial x} + v_{p} \frac{{\partial v_{p} }}{\partial y}} \right] = - \,\,C R\frac{\partial p}{{\partial y}} + C N\left( {v_{f} - v_{p} } \right) $$

(25)

with

$$ \rho_{f} = e^{{\left( {1 - C} \right) \chi (p - p_{0} )}} $$

(26)

$$ \eta = \varepsilon \,\,{\text{c}} \,o\,s\,\,\alpha \,\,\left( {x - t} \right) $$

(27)

Also, boundary conditions at $y = \pm \left( {1 + \eta } \right)$ take the form

$u_{f} = \mp Kn\frac{{\partial u_{f} }}{\partial y}$, $v_{f} = \pm \varepsilon \, \alpha \,\,\sin \alpha \left( {x - t} \right)$ and $v_{p} = \pm \varepsilon \, \alpha \,\,\sin \alpha \left( {x - t} \right)$

$$ \left( {1 - C} \right)\frac{\partial }{\partial x}\left( {m\frac{{\partial^{2} }}{{\partial t^{2} }} + \frac{D}{{\left( {1 - C} \right) R}}\frac{\partial }{\partial t} + \frac{B}{{\left( {1 - C} \right)^{2} R^{2} }}\frac{{\partial^{4} }}{{\partial x^{4} }} - \frac{T}{{\left( {1 - C} \right)^{2} R^{2} }}\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{K_{1} }}{{\left( {1 - C} \right)^{2} R^{2} }}} \right)\eta = \frac{1}{R}\left( {\frac{{\partial^{2} u_{f} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{f} }}{{\partial y^{2} }}} \right) $$

(28)

$$ - \left( {1 - C} \right)\rho_{f} \left( {\frac{{\partial u_{f} }}{\partial t} + u_{f} \frac{{\partial u_{f} }}{\partial x} + v_{f} \frac{{\partial u_{f} }}{\partial x}} \right) + \frac{1}{3R}\frac{\partial }{\partial x}\left( {\frac{{\partial u_{f} }}{\partial x} + \frac{{\partial v_{f} }}{\partial y}} \right) + \frac{CM}{R}\left( {u_{\,p} - u_{f} } \right) - \frac{{(\frac{1}{K} + H_{a}^{2} )\,u_{f} }}{(1 - C)\,R} $$

(29)

Solution Technique

Following the principles of the perturbation analysis method, the system of governing Eqs. (21)–(27) is solved in the form of a power series for $\varepsilon$ under the boundary conditions (28) and (29) to obtain first and second-order systems of equations. Supposing that, the existence of the flow is mainly depending on the peristaltic wave with small amplitude ratio $\left(\varepsilon \right)$. Then developing the series for the following properties $p, {u}_{f}, {v}_{f}, {u}_{p}, {v}_{p},\mathrm{ and} {\rho }_{f}$ to be as follows

$$ p = p_{0} + \varepsilon p_{1} (x,y,t) + \varepsilon^{2} p_{2} (x,y,t) + \cdots $$

(30)

$$ u_{f} = \varepsilon u_{f1} (x,y,t) + \varepsilon^{2} \,\,u_{f2} (x,y,t) + \cdots $$

(31)

$$ v_{f} = \varepsilon v_{f1} (x,y,t) + \varepsilon^{2} \,\,v_{f2} (x,y,t) + \cdots . $$

(32)

$$ u_{p} = \varepsilon u_{p1} (x,y,t) + \varepsilon^{2} \,\,u_{p2} (x,y,t) + \cdots . $$

(33)

$$ v_{p} = \varepsilon v_{p1} (x,y,t) + \varepsilon^{2} \,\,v_{p2} (x,y,t) + \cdots $$

(34)

$$ \rho_{f} = 1 + \varepsilon \rho_{f1} (x,y,t) + \varepsilon^{2} \rho_{f2} (x,y,t) + \cdots $$

(35)

A substitutive manner of Eqs. (30)–(35) into Eqs. (21)–(27) and (28)–(29) are performed. Then similar $\varepsilon , {\varepsilon }^{2}$ terms are collected to consist of two sets of differential equations associated with their relevant boundary conditions for ${p}_{1}, {\rho }_{f1}, {u}_{\left(f, p\right)1}, {v}_{\left(f, p\right)1}, {u}_{\left(f, p\right)2}, {v}_{\left(f, p\right)2}, {\rho }_{f2},\mathrm{ and} {p}_{2}$.

Terms of ${\varvec{\varepsilon}}$

$$ \frac{{\partial u_{f1} }}{\partial t} + \frac{{\partial u_{f1} }}{\partial x} + \frac{{\partial v_{f1} }}{\partial y} = 0 $$

(36)

$$ \begin{aligned} \left( {1 - C} \right)R \frac{{\partial u_{f1} }}{\partial t} & = - \left( {1 - C} \right)R\frac{{\partial p_{1} }}{\partial x} + \left( {\frac{{\partial^{2} u_{f1} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{f1} }}{{\partial y^{2} }}} \right) \\ & \quad + \frac{1}{3}\frac{\partial }{\partial x}\left( {\frac{{\partial u_{f1} }}{\partial x} + \frac{{\partial v_{f1} }}{\partial y}} \right) + C M \left( {u_{p1} - u_{f1} } \right) - \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)u_{f1} }}{(\,1 - C\,)}\,\, \\ \end{aligned} $$

(37)

$$ \left( {1 - C} \right)R \frac{{\partial v_{f1} }}{\partial t} = - \left( {1 - C} \right)R\frac{{\partial p_{1} }}{\partial y} + \left( {\frac{{\partial^{2} v_{f1} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{f1} }}{{\partial y^{2} }}} \right) + \frac{1}{3}\frac{\partial }{\partial y}\left( {\frac{{\partial u_{f1} }}{\partial x} + \frac{{\partial v_{f1} }}{\partial y}} \right) + C M \left( {v_{p1} - v_{f1} } \right) - \frac{{v_{f1} }}{(\,1 - C\,)\,K}\, $$

(38)

$$ C R \frac{{\partial u_{p1} }}{\partial t} = - C R\frac{{\partial p_{1} }}{\partial x} + C N \left( {u_{f1} - u_{p1} } \right) $$

(39)

$$ C R \frac{{\partial v_{p1} }}{\partial t} = - C R\frac{{\partial p_{1} }}{\partial y} + C N \left( {v_{f1} - v_{p1} } \right) $$

(40)

$$ \rho_{f1} = \left( {1 - C} \right) \chi p_{1} $$

(41)

Terms of ${{\varvec{\varepsilon}}}^{2}$

$$ \frac{{\partial u_{f2} }}{\partial t} + u_{f1} \frac{{\partial \rho_{f1} }}{\partial x} + v_{f1} \frac{{\partial \rho_{f1} }}{\partial y} + \frac{{\partial u_{f2} }}{\partial x} + \frac{{\partial v_{f2} }}{\partial y} + \rho_{f1} \left( {\frac{{\partial u_{f1} }}{\partial x} + \frac{{\partial v_{f1} }}{\partial y}} \right) = 0 $$

(42)

$$ \left( {1 - C} \right)R \left[ {\frac{{\partial \,u_{f2} }}{\partial t} + u_{f1} \frac{{\partial \,u_{f1} }}{\partial x} + v_{f1} \frac{{\partial \,u_{f1} }}{\partial y} + \rho_{f1} \frac{{\partial \,u_{f1} }}{\partial t}} \right] = - \left( {1 - C} \right)\,\,R\frac{{\partial \,p_{\,2} }}{\partial x} + \left( {\frac{{\partial^{\,2} \,u_{f2} }}{{\partial x^{\,2} }} + \frac{{\partial \,^{2} \,u_{f2} }}{{\partial y^{\,2} }}} \right) + \frac{1}{3}\frac{\partial }{\partial x}\left( {\frac{{\partial u_{f2} }}{\partial x} + \frac{{\partial v_{f2} }}{\partial y}} \right) + C M \left( {u_{p2} - u_{f2} } \right) - \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)\,u_{f2} }}{(\,1 - C\,)}\,\, $$

(43)

$$ \left( {1 - C} \right)\,R\,\,\left[ { \frac{{\partial \,v_{f2} }}{\partial \,t} + u_{f1} \frac{{\partial \,v_{f1} }}{\partial \,x} + v_{f1} \frac{{\partial \,v_{f1} }}{\partial \,y} + \rho_{f1} \frac{{\partial \,v_{f1} }}{\partial \,t}} \right] = - \left( {1 - C} \right)\,R\,\frac{{\partial \,p_{2} }}{\partial y} + \left( {\frac{{\partial^{\,\,2} \,v_{f2} }}{{\partial \,x^{\,2} }} + \frac{{\partial^{\,\,2} \,v_{f2} }}{{\partial \,y^{\,2} }}} \right) + \frac{1}{3}\frac{\partial }{\partial y}\left( {\frac{{\partial u_{f2} }}{\partial x} + \frac{{\partial v_{f2} }}{\partial y}} \right) + C M \left( {v_{p2} - v_{f2} } \right) - \frac{{\,v_{f2} }}{(\,1 - C\,)\,K} $$

(44)

$$ C R \left[ {\frac{{\partial u_{p2} }}{\partial t} + u_{p1} \frac{{\partial u_{p1} }}{\partial x} + v_{p1} \frac{{\partial u_{p1} }}{\partial y}} \right] = - C R\frac{{\partial p_{2} }}{\partial x} + C N \left( {u_{f2} - u_{p2} } \right) $$

(45)

$$ C R \left[ {\frac{{\partial v_{p2} }}{\partial t} + u_{p1} \frac{{\partial v_{p1} }}{\partial x} + v_{p1} \frac{{\partial v_{p1} }}{\partial y}} \right] = - C R\frac{{\partial p_{2} }}{\partial y} + C N \left( {v_{f2} - v_{p2} } \right) $$

(46)

$$ \rho_{f2} = \left( {1 - C} \right) \chi p_{2} + \frac{{\left( {1 - C} \right)^{2} \chi^{2} p_{1}^{2} }}{2} $$

(47)

Applying Taylor series expansion about $y= \pm 1$ to prepare the systems of boundary conditions:

$$ u_{f} \left( {x, \pm \eta ,t} \right) = u_{f} \left( {x, \pm 1,t} \right) \pm \eta \left( {x,t} \right)\frac{{\partial u_{f} \left( {x, \pm 1,t} \right)}}{\partial y} + \frac{{\eta^{2} \left( {x,t} \right)}}{2}\frac{{\partial^{2} u_{f} \left( {x, \pm 1,t} \right)}}{{\partial y^{2} }} + \ldots $$

(48)

$$ v_{f} \left( {x, \pm \eta ,t} \right) = v_{f} \left( {x, \pm 1,t} \right) \pm \eta \left( {x,t} \right)\frac{{\partial v_{f} \left( {x, \pm 1,t} \right)}}{\partial y} + \frac{{\eta^{2} \left( {x,t} \right)}}{2}\frac{{\partial^{2} v_{f} \left( {x, \pm 1,t} \right)}}{{\partial y^{2} }} + \ldots $$

(49)

$$ v_{p} \left( {x, \pm \eta ,t} \right) = v_{p} \left( {x, \pm 1,t} \right) \pm \eta \left( {x,t} \right)\frac{{\partial v_{p} \left( {x, \pm 1,t} \right)}}{\partial y} + \frac{{\eta^{2} \left( {x,t} \right)}}{2}\frac{{\partial^{2} v_{p} \left( {x, \pm 1,t} \right)}}{{\partial y^{2} }} + \ldots $$

(50)

Applying the previous expansions of (48)–(49), and (50) into the boundary Eqs. (28)–(29) then presenting cosine and sine in the form of exponentials. Finally, these boundary conditions are as follows.

For ${\varvec{\varepsilon}}$ Terms

$$ u_{f1} \left( { \pm 1} \right) = \mp Kn\frac{{\partial u_{f1} \left( { \pm 1} \right)}}{\partial y} $$

(51)

$$ v_{f1} \left( { \pm 1} \right) = \mp \frac{i\alpha }{2}\left( {e^{{i\alpha \left( {x - t} \right)}} - e^{{ - i\alpha \left( {x - t} \right)}} } \right) $$

(52)

$$ v_{p1} \left( { \pm 1} \right) = \mp \frac{i\alpha }{2}\left( {e^{{i\alpha \left( {x - t} \right)}} - e^{{ - i\alpha \left( {x - t} \right)}} } \right) $$

(53)

$$ - \left( {1 - C} \right)R \frac{{\partial u_{f1} \left( { \pm 1} \right)}}{\partial t} + \frac{1}{R}\left( {\frac{{\partial^{2} u_{f1} \left( { \pm 1} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} u_{f1} \left( { \pm 1} \right)}}{{\partial y^{2} }}} \right) + \frac{1}{3R}\frac{\partial }{\partial x}\left( {\frac{{\partial u_{f1} \left( { \pm 1} \right)}}{\partial x} + \frac{{\partial v_{f1} \left( { \pm 1} \right)}}{\partial y}} \right) + \frac{CM}{R} \left( {u_{p1} \left( { \pm 1} \right) - u_{f1} \left( { \pm 1} \right)} \right) - \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)}}{(\,1 - C\,)}\,u_{f1} \left( { \pm 1} \right) = \left( {1 - C} \right)\left[ { - \frac{{i\delta_{a} }}{2} \left( {e^{{i\,\alpha \,\,\left( {x - t} \right)}} - e^{{ - \,i\,\alpha \,\left( {x - t} \right)}} } \right) + \frac{{\delta_{b} }}{2} \left( {e^{{i\alpha \left( {x - t} \right)}} + e^{{ - i\alpha \left( {x - t} \right)}} } \right)} \right] $$

(54)

where $\delta_{a} = m\, \alpha^{3} - \frac{{B\,\alpha^{5} }}{{\left( {1 - C} \right)^{2} R^{2} }} - \frac{{T\,\alpha^{3} }}{{\left( {1 - C} \right)^{2} R^{2} }} - \frac{{K_{1} \,\alpha }}{{\left( {1 - C} \right)^{2} R^{2} }}$ and $\delta_{b} = \frac{{D\alpha^{2} }}{{\left( {1 - C} \right) R}}$.

For ${{\varvec{\varepsilon}}}^{2}$ Terms

$$ u_{f2} \left( { \pm 1} \right) \pm \frac{1}{2}\left( {e^{{i\alpha \left( {x - t} \right)}} + e^{{ - i\alpha \left( {x - t} \right)}} } \right)\frac{{\partial u_{f1} \left( { \pm 1} \right)}}{\partial y} = \mp Kn\frac{{\partial u_{f2} \left( { \pm 1} \right)}}{\partial y} - \frac{Kn}{2}\left( {e^{{i\alpha \left( {x - t} \right)}} + e^{{ - i\alpha \left( {x - t} \right)}} } \right)\frac{{\partial^{2} u_{f1} \left( { \pm 1} \right)}}{{\partial y^{2} }} $$

(55)

$$ v_{f2} \left( { \pm 1} \right) \pm \frac{1}{2}\left( {e^{{i\alpha \left( {x - t} \right)}} + e^{{ - i\alpha \left( {x - t} \right)}} } \right)\frac{{\partial v_{f1} \left( { \pm 1} \right)}}{\partial y} = 0 $$

(56)

$$ v_{p2} \left( { \pm 1} \right) \pm \frac{1}{2}\left( {e^{{i\alpha \left( {x - t} \right)}} + e^{{ - i\alpha \left( {x - t} \right)}} } \right)\frac{{\partial v_{p1} \left( { \pm 1} \right)}}{\partial y} = 0 $$

(57)

It is worth remarking that the first and the second-orders of the boundary conditions are sufficient for solving the current problem and the 3rd order is not important so that it is neglected.

Using the expressions of Aarts and Ooms [10] for the solution of the two sets of equations according to the following nonlinear approaches:

$$ u_{f1} (x,y,t) = U_{f1} (y) e^{i\alpha (x - t)} + \overline{U}_{f1} (y) e^{ - i\alpha (x - t)} $$

(58)

$$ v_{f1} (x,y,t) = V_{f1} (y) e^{i\alpha (x - t)} + \overline{V}_{f1} (y) e^{ - i\alpha (x - t)} $$

(59)

$$ u_{p1} (x,y,t) = U_{p1} (y) e^{i\alpha (x - t)} + \overline{U}_{p1} (y) e^{ - i\alpha (x - t)} $$

(60)

$$ v_{p1} (x,y,t) = V_{p1} (y) e^{i\alpha (x - t)} + \overline{V}_{p1} (y) e^{ - i\alpha (x - t)} $$

(61)

$$ p_{1} (x,y,t) = P_{1} (y) e^{i\alpha (x - t)} + \overline{P}_{1} (y) e^{ - i\alpha (x - t)} $$

(62)

$$ \rho_{f1} (x,y,t) = \left( {1 - C} \right)\chi \,\,P_{1} (y)\, e^{i\alpha (x - t)} + \left( {1 - C} \right)\chi \,\overline{P}_{1} \,(y) \,e^{ - i\alpha (x - t)} $$

(63)

and

$$ u_{f2} (x,y,t) = U_{f20} (y) \, + \,\,U_{f2} (y)\, e^{2i\alpha (x - t)} + \overline{U}_{f2} (y) \,e^{ - 2i\alpha (x - t)} $$

(64)

$$ v_{f2} (x,y,t) = V_{f20} (y) + \,V_{f2} (y)\, e^{2i\alpha (x - t)} + \overline{V}_{f2} (y)\, e^{ - 2i\alpha (x - t)} $$

(65)

$$ u_{p2} (x,y,t) = U_{p20} (y) + \,U_{p2} (y)\, e^{2i\alpha (x - t)} + \overline{U}_{p2} (y)\, e^{ - 2i\alpha (x - t)} $$

(66)

$$ v_{p2} (x,y,t) = V_{p20} (y)\, + \,\,V_{p2} (y) \,e^{2i\alpha (x - t)} + \overline{V}_{p2} (y) \,e^{ - 2i\alpha (x - t)} $$

(67)

$$ p_{2} (x,y,t) = P_{20} (y) + P_{2} (y)\, e^{2i\alpha (x - t)} + \overline{P}_{2} (y)\, e^{ - 2i\alpha (x - t)} $$

(68)

$$ \rho_{f2} (x,y,t) = D_{20} (y) + D_{2} (y) \,e^{2i\alpha (x - t)} + \overline{D}_{2} (y) \,e^{ - 2i\alpha (x - t)} $$

(69)

The overbars refer to variable’s complex conjugate, knowing that the peristaltic flow has particularly a nonlinear (second-order) action as Aarts and Ooms [10] and just trivial solution obtained because of adding a non-oscillatory term into 1st order whereas non-oscillatory terms such as ${U}_{f20}\left(y\right), {V}_{f20}\left(y\right), {U}_{p20}\left(y\right), {V}_{p20}\left(y\right), {P}_{20}\left(y\right), \mathrm{ and } {D}_{20}(y)$ were just added into the second and higher orders and cannot be neglected in the current solution after time averaging through the period.

Equations (58) through (63) are substituted into the first-order system of (36–41) and their corresponding boundary conditions (51–54) resulting in the following first set of equations.

The First-order Set Is

$$ V^{\prime}_{f1} + i \alpha U_{f1} = \left( {1 - C} \right)i \alpha \chi P_{1} . $$

(70)

$$ - i\alpha \left( {1 - C} \right)RU_{f1} = - i\alpha \left( {1 - C} \right)RP_{1} + U^{\prime\prime}_{f1} - \alpha^{2} U_{f1} + \frac{1}{3}i\alpha \left[ {V^{\prime}_{f1} + i\alpha U_{f1} } \right] + CM\left[ {U_{p1} - U_{f1} } \right] - \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)\,U_{f1} }}{(\,1 - C\,)}\,\,. $$

(71)

$$ - i\alpha \left( {1 - C} \right)RU_{f1} - i\alpha \left( {1 - C} \right)RV_{f1} = - \left( {1 - C} \right)RP^{\prime}_{1} + V^{\prime\prime}_{f1} - \alpha^{2} V_{f1} + \frac{1}{3}\frac{d}{dy}\left[ {V^{\prime}_{f1} + i\alpha U_{f1} } \right] + CM\left[ {V_{p1} - V_{f1} } \right] - \frac{{V_{f1} }}{(\,1 - C\,)\,K}\, $$

(72)

$$ - i\alpha RU_{p1} = - i\alpha RP_{1} + N\left[ {U_{f1} - U_{p1} } \right] $$

(73)

$$ - i\alpha RV_{p1} = - R P^{\prime}_{1} + N\left[ {V_{f1} - V_{p1} } \right] $$

(74)

And boundary conditions for 1st order (ɛ¹) are

$$ U_{f1} \left( { \pm 1} \right) = \mp Kn\frac{{\partial U_{f1} \left( { \pm 1} \right)}}{\partial y} $$

(75)

$$ V_{f1} \left( { \pm 1} \right) = \mp \frac{i\alpha }{2} $$

(76)

$$ V_{p1} \left( { \pm 1} \right) = \mp \frac{i\alpha }{2} $$

(77)

$$ \frac{{\partial^{2} U_{f1} \left( { \pm 1} \right)}}{{\partial y^{2} }} - \left[ {\frac{4}{3}\alpha^{2} - \left( {1 - C} \right)i\alpha R + \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)}}{(\,1 - C\,)}\,\,} \right]U_{f1} \left( { \pm 1} \right) + \,\frac{i\alpha }{3}\frac{{\partial V_{f1} \left( { \pm 1} \right)}}{\partial y} + CM\left( {U_{p1} \left( { \pm 1} \right) - U_{f1} \left( { \pm 1} \right)} \right) = \left( {1 - C} \right)R \delta $$

(78)

where

$$ \delta = \frac{ - i\alpha }{{2\left( {1 - C} \right)^{2} R^{2} }}\left[ {\left( {1 - C} \right)^{2} R^{2} m \alpha^{2} - B\alpha^{4} - T\,\alpha^{2} + i D\alpha R \left( {1 - C} \right) - K_{1} } \right] $$

(78a)

Now, the main concern is to find out the solution for the equations of ${U}_{\left(f, p\right)1}, {V}_{\left(f, p\right)1}, \mathrm{ and } {P}_{1}$.

Following the method introduced by Mekheimer and Abdel‐Wahab [31], the equations of the velocity and the pressure are obtained. Thus, the first-order solution for Eqs. (70)–(74) subject to the boundary conditions (75)–(78) is obtained as follows:

$$ U_{f1} (y) = R_{6} C_{1} \cosh (L_{1} y) + R_{7} C_{2} \cosh (L_{2} y\,) $$

(79)

$$ V_{f1} (y) = C_{1} \sinh (L_{1} \,y) + C_{2} \sinh (\,L_{2} \,y) $$

(80)

$$ P_{1} (y) = R_{4} C_{1} \cosh (L_{1} y) + R_{5} C_{2} \cosh (L_{2} y\,) $$

(81)

$$ U_{p1} (y) = R_{8} C_{1} \cosh (L_{1} y) + R_{9} C_{2} \cosh (L_{2} y\,) $$

(82)

$$ V_{p1} (y) = R_{10} C_{1} \sinh (L_{1} y) + R_{11} C_{2} \sinh (L_{2} y) $$

(83)

where

$$ \left. {\begin{array}{*{20}l} {\Gamma^{2} = \beta^{2} - \frac{{H_{a}^{2} }}{(1 - C)}} \hfill \\ {S = \frac{{H_{a}^{2} }}{(1 - C)}} \hfill \\ \end{array} } \right\} $$

(83a)

$$ \beta^{2} = \left[ {\alpha^{2} + \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)}}{(\,1 - C\,)}\, - i \alpha R \left( {1 - C} \right) - \frac{i \alpha R C M}{{N - i R \alpha }} } \right] $$

(83b)

$$ \left. {\begin{array}{*{20}l} {\gamma = \left( {1 - C} \right)R - \frac{{\left( {1 - C} \right)i \alpha \chi }}{3} + \frac{C M R}{{N - i \alpha R}}} \hfill \\ {B_{1} = 1 - \frac{{i \alpha \left( {1 - C} \right)\chi }}{\gamma }\,} \hfill \\ { \upsilon^{2} = \beta^{2} - \frac{{\beta^{2} - \alpha^{2} }}{{B_{1} }}} \hfill \\ {Z = \upsilon^{2} + \Gamma^{2} + \frac{S}{{B_{1} }}\,} \hfill \\ \end{array} } \right\} $$

(83c)

$$ \left. {\begin{array}{*{20}l} {Z = \upsilon^{2} + \Gamma^{2} + \frac{S}{{B_{1} }}} \hfill \\ {L_{1}^{2} = \frac{{Z + \sqrt {Z^{2} - 4\Gamma^{2} \upsilon^{2} } }}{2}} \hfill \\ {L_{2}^{2} = \frac{{Z - \sqrt {Z^{2} - 4\Gamma^{2} \upsilon^{2} } }}{2}} \hfill \\ \end{array} } \right\} $$

(83d)

$$ \left. {\begin{array}{*{20}l} {A_{1} = (1 - C)\,\,\chi \,\left( {\frac{{L_{1}^{2} - \Gamma }}{{L_{1} \,\gamma }}^{2} } \right) + \frac{{i\,L_{1} }}{\alpha }\,} \hfill \\ {A_{2} = (1 - C)\,\,\chi \,\left( {\frac{{L_{2}^{2} - \Gamma }}{{L_{2} \,\gamma }}^{2} } \right) + \frac{{i\,L_{2} }}{\alpha }} \hfill \\ \end{array} } \right\} $$

(83e)

$$ \left. {\begin{array}{*{20}l} {R_{1} = \left[ { - \,\left( {\frac{{L_{1}^{2} - \Gamma }}{{L_{1} \,}}^{2} } \right) - \frac{{i\,A_{1} \,L_{1}^{2} }}{\alpha } + \frac{{i\,A_{1} \,\beta^{2} }}{\alpha }} \right]\,,\,\,R_{2} = \left[ { - \,\left( {\frac{{L_{2}^{2} - \Gamma }}{{L_{2} \,}}^{2} } \right) - \frac{{i\,A_{2} \,L_{2}^{2} }}{\alpha } + \frac{{i\,A_{2} \,\beta^{2} }}{\alpha }} \right],} \hfill \\ {R_{3} = \left[ {\gamma - \frac{{\,i \, \beta^{2} (1 - C)\,\,\chi }}{\alpha }} \right]\,,\,\,\,\,R_{4} = \,\left( {\frac{{L_{1}^{2} - \Gamma }}{{L_{1} \,\gamma }}^{2} } \right) + \frac{{R_{1} }}{{R_{3} }}\,,\,\,\,\,R_{5} = \,\left( {\frac{{L_{2}^{2} - \Gamma }}{{L_{2} \,\gamma }}^{2} } \right) + \frac{{R_{2} }}{{R_{3} }}\,\,,\,\,} \hfill \\ {R_{6} = \left[ {\frac{{(1 - C)\,\,\chi \,R_{1} }}{{R_{3} }} + A_{1} } \right]\,,\,\,\,\,\,R_{7} = \left[ {\frac{{(1 - C)\,\,\chi \,R_{2} }}{{R_{3} }} + A_{2} } \right]\,,\,\,\,\,R_{8} = \left[ {\frac{{ - i\,\alpha \,R\,R_{4} \, + \,N\,R_{6} }}{N - i\,\alpha \,R\,}} \right]\,,} \hfill \\ {\,R_{9} = \left[ {\frac{{ - i\,\alpha \,R\,R_{5} \, + \,N\,R_{7} }}{N - i\,\alpha \,R\,}} \right]\,\,,\,\,\,R_{10} = \left[ {\frac{{N - \,R\,R_{4} \,L_{1} }}{N - i\,\alpha \,R\,}} \right]\,\,,\,\,\,\,R_{11} = \left[ {\frac{{N - \,R\,R_{5} \,L_{2} }}{N - i\,\alpha \,R\,}} \right]\,} \hfill \\ \end{array} } \right\} $$

(83f)

$$ w = \left[ {\frac{4}{3}\,\alpha^{2} - \,i\,\alpha \,(\,1 - C\,)R + \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)}}{(\,1 - C\,)}} \right]\, $$

(83g)

$$ \left. \begin{gathered} g_{1} = \cosh L_{1} + K_{n} L_{1} \sinh L_{1} \, \hfill \\ g_{2} = \cosh L_{2} + K_{n} \,L_{2} \,\sinh L_{2} \, \hfill \\ g_{3} = \left( {R{}_{6}\,L_{1}^{2} \, - \,w\,R{}_{6}\, + C\,M\,R{}_{8} - C\,M\,R{}_{6}\, + i\,\alpha \,L_{1} } \right)\cosh L_{1} \hfill \\ g_{4} = \left( {R{}_{7}\,L_{2}^{2} \, - \,w\,R{}_{7}\, + C\,M\,R{}_{9} - C\,M\,R{}_{7}\, + i\,\alpha \,L_{2} } \right)\cosh L_{2} \hfill \\ \end{gathered} \right\} $$

(83h)

$$ \left. \begin{gathered} G = R_{6} \,g_{1} \,g_{4} - R_{7} \,g_{2} \,g_{3} \, \hfill \\ C_{1} = - \left( {1 - C} \right)R\delta \frac{{R_{7} \,g_{2} }}{G} \hfill \\ C_{2} = \left( {1 - C} \right)R\delta \frac{{R_{7} \,g_{1} }}{G}\, \hfill \\ \end{gathered} \right\} $$

(83i)

The Second-order Set Is

$$ V_{f20}^{\prime } = - \left( {1 - C} \right)\chi \left[ {P_{1} \,\overline{{V_{f1}^{\prime } }} + \overline{{P_{1} }} \,V_{f1}^{\prime } + V_{f1} \overline{{P^{\prime}_{1} }} + \overline{{V_{f1} }} P^{\prime}_{1} } \right]\,\, $$

(84)

$$ U_{f20}^{\prime \prime } = \left( {1 - C} \right)R\left[ {\left( {1 - C} \right)i\alpha \chi P_{1} \overline{{U_{f1} }} - \left( {1 - C} \right)i\alpha \chi \overline{{P_{1} }} U_{f1} } \right.\left. { + V_{f1} \overline{{U_{f1}^{\prime } }} + \overline{{V_{f1} }} U_{f1}^{\prime } } \right] + CM\left[ {U_{f20} - U_{p20} } \right] + \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)}}{(\,1 - C\,)}U_{f20} \,\, $$

(85)

$$ \begin{aligned} - \left( {1 - C} \right)RP_{20}^{\prime } + \frac{4}{3}V_{f20}^{\prime \prime } & = \left( {1 - C} \right)R\left[ {\left( {1 - C} \right)i\alpha \chi P_{1} \,\overline{{V_{f1} }} - \left( {1 - C} \right)i\alpha \chi \overline{{P_{1} }} \,V_{f1} - i\alpha U_{f1} \overline{{V_{f1} }} } \right. \\ & \quad \left. { + i\alpha \overline{{U_{f1} }} V_{f1} + V_{f1} \overline{{V_{f1}^{\prime } }} + \overline{{V_{f1} }} V_{f1}^{\prime } } \right]\\ &\quad + CM\left[ {V_{f20} - V_{p20} } \right] + \frac{1}{(\,1 - C\,)\,K}\,\,\,V_{f20} \\ \end{aligned} $$

(86)

$$ U_{f20} - U_{p20} = \frac{R}{N}\left[ {V_{p1} \overline{{U^{\prime}_{p1} }} + \overline{{V_{p1} }} U^{\prime}_{p1} } \right] $$

(87)

$$ V_{f20} - V_{p20} = \frac{R}{N}\left[ { - i \alpha \overline{{V_{p1} }} U_{p1} + i \alpha V_{p1} \overline{{U_{p1} }} + V_{p1} \overline{{V^{\prime}_{p1} }} + \overline{{V_{p1} }} V^{\prime}_{p1} } \right] + \frac{R}{N} P^{\prime}_{20} $$

(88)

The boundary conditions for the second order $\left({\varepsilon }^{2}\right)$ are

$$ U_{f2o} \left( { \pm 1} \right) \pm \frac{1}{2}\left( {\overline{{U_{f1} }}^{\prime } \left( { \pm 1} \right) + U_{f1}^{\prime } \left( { \pm 1} \right)} \right) = \mp Kn\left[ {U_{f2o}^{\prime } \left( { \pm 1} \right) \pm \frac{1}{2}\left( {\overline{{U_{f1} }}^{\prime \prime } \left( { \pm 1} \right) + U_{f1}^{\prime \prime } \left( { \pm 1} \right)} \right)} \right] $$

(89)

$$ V_{p20} \left( { \pm 1} \right) \pm \frac{1}{2}\left[ {V^{\prime}_{p1} \left( { \pm 1} \right) + \overline{{V^{\prime}_{p1} }} \left( { \pm 1} \right)} \right] = 0 $$

(90)

$$ V_{f20} \left( { \pm 1} \right) \pm \frac{1}{2}\left[ {V^{\prime}_{f1} \left( { \pm 1} \right) + \overline{{V^{\prime}_{f1} }} \left( { \pm 1} \right)} \right] = 0 $$

(91)

Then, the solution of Eqs. (84)–(88) subject to their boundary conditions (89)–(91) is given by

$$ U_{f2o} \left( y \right) = R E\left( y \right) + D_{2} Cosh\,\sqrt {\delta_{c} } \,y + D_{3} \,Sinh\,\sqrt {\delta_{c} } \,y $$

(92)

$$ V_{f20} (y) = - \left( {1 - C} \right)\chi \,\,\left[ {P_{1} (y) \overline{{V_{f1} }} (y) + \overline{{P_{1} }} (y) V_{f1} (y)} \right] $$

(93)

$$ P_{20} (y) = D + \frac{4}{{3 R\,Z_{1} }}V_{f20}^{\prime } (y) - \frac{{\left( {1 - C} \right)}}{{Z_{1} }}\int {F_{1} (y)dy} - \frac{C M}{{N\,Z_{1} }}\int {F_{2} (y)dy} + \frac{\chi }{{K\,R\,Z_{1} }}\int {F_{3} (y)dy} \,\, $$

(94)

$$ U_{p2o} \left( y \right) = U_{f2o} \left( y \right) + \frac{R}{N}\left[ {V_{p1} \overline{{u_{p1} ^{\prime}}} + \overline{{V_{p1} }} U_{p1} ^{\prime}} \right] $$

(95)

$$ V_{p20} (y) = - \left( {1 - C} \right)\chi \left[ {P_{1} (y)\,\, \overline{{V_{f1} }} (y) + \overline{{P_{1} }} (y) \,\,V_{f1} (y)} \right] - \frac{R}{N}\left[ {F_{2} (y) + P_{20}^{\prime } (y)} \right] $$

(96)

$$ \begin{aligned} E(y) & = (1 - C)\left[ {\frac{{\delta_{1} }}{2}\left( {\frac{{\cosh \left( {L_{1} + \overline{{L_{1} }} } \right)y}}{{\left( {L_{1} + \overline{{L_{1} }} } \right)^{2} - \delta_{c} }} + \frac{{\cosh \left( {L_{1} - \overline{{L_{1} }} } \right)y}}{{\left( {L_{1} - \overline{{L_{1} }} } \right)^{2} - \delta_{c} }}} \right)} \right. + \frac{{\delta_{2} }}{2}\left( {\frac{{\cosh \left( {L_{1} + \overline{{L_{2} }} } \right)y}}{{\left( {L_{1} + \overline{{L_{2} }} } \right)^{2} - \delta_{c} }} + \frac{{\cosh \left( {L_{1} - \overline{{L_{2} }} } \right)y}}{{\left( {L_{1} - \overline{{L_{2} }} } \right)^{2} - \delta_{c} }}} \right) \\ & \quad + \frac{{\delta_{3} }}{2}\left( {\frac{{\cosh \left( {L_{2} + \overline{{L_{1} }} } \right)y}}{{\left( {L_{2} + \overline{{L_{1} }} } \right)^{2} - \delta_{c} }} + \frac{{\cosh \left( {L_{2} - \overline{{L_{1} }} } \right)y}}{{\left( {L_{2} - \overline{{L_{1} }} } \right)^{2} - \delta_{c} }}} \right) + \frac{{\delta_{4} }}{2}\left( {\frac{{\cosh \left( {L_{2} + \overline{{L_{2} }} } \right)y}}{{\left( {L_{2} + \overline{{L_{2} }} } \right)^{2} - \delta_{c} }} + \frac{{\cosh \left( {L_{2} - \overline{{L_{2} }} } \right)y}}{{\left( {L_{2} - \overline{{L_{2} }} } \right)^{2} - \delta_{c} }}} \right) \\ & \quad + \frac{{\delta_{5} }}{2}\left( {\frac{{\cosh \left( {L_{1} + \overline{{L_{1} }} } \right)y}}{{\left( {L_{1} + \overline{{L_{1} }} } \right)^{2} - \delta_{c} }} - \frac{{\cosh \left( {L_{1} - \overline{{L_{1} }} } \right)y}}{{\left( {L_{1} - \overline{{L_{1} }} } \right)^{2} - \delta_{c} }}} \right) + \frac{{\delta_{6} }}{2}\left( {\frac{{\cosh \left( {L_{2} + \overline{{L_{1} }} } \right)y}}{{\left( {L_{2} + \overline{{L_{1} }} } \right)^{2} - \delta_{c} }} - \frac{{\cosh \left( {L_{2} - \overline{{L_{1} }} } \right)y}}{{\left( {L_{2} - \overline{{L_{1} }} } \right)^{2} - \delta_{c} }}} \right) \\ & \quad + \frac{{\delta_{7} }}{2}\left( {\frac{{\cosh \left( {L_{1} + \overline{{L_{2} }} } \right)y}}{{\left( {L_{1} + \overline{{L_{2} }} } \right)^{2} - \delta_{c} }} - \frac{{\cosh \left( {L_{1} - \overline{{L_{2} }} } \right)y}}{{\left( {L_{1} - \overline{{L_{2} }} } \right)^{2} - \delta_{c} }}} \right) + \frac{{\delta_{8} }}{2}\left( {\frac{{\cosh \left( {L_{2} + \overline{{L_{2} }} } \right)y}}{{\left( {L_{2} + \overline{{L_{2} }} } \right)^{2} - \delta_{c} }} - \frac{{\cosh \left( {L_{2} - \overline{{L_{2} }} } \right)y}}{{\left( {L_{2} - \overline{{L_{2} }} } \right)^{2} - \delta_{c} }}} \right) \\ & \quad + \frac{C\,M}{N}\left[ {\frac{{\delta_{9} }}{2}\left( {\frac{{\cosh \left( {L_{1} + \overline{{L_{1} }} } \right)y}}{{\left( {L_{1} + \overline{{L_{1} }} } \right)^{2} - \delta_{c} }} - \frac{{\cosh \left( {L_{1} - \overline{{L_{1} }} } \right)y}}{{\left( {L_{1} - \overline{{L_{1} }} } \right)^{2} - \delta_{c} }}} \right) + \frac{{\delta_{10} }}{2}\left( {\frac{{\cosh \left( {L_{1} + \overline{{L_{2} }} } \right)y}}{{\left( {L_{1} + \overline{{L_{2} }} } \right)^{2} - \delta_{c} }} - \frac{{\cosh \left( {L_{1} - \overline{{L_{2} }} } \right)y}}{{\left( {L_{1} - \overline{{L_{2} }} } \right)^{2} - \delta_{c} }}} \right)} \right. \\ & \quad \left. {\left. { + \frac{{\delta_{11} }}{2}\left( {\frac{{\cosh \left( {L_{2} + \overline{{L_{1} }} } \right)y}}{{\left( {L_{2} + \overline{{L_{1} }} } \right)^{2} - \delta_{c} }} - \frac{{\cosh \left( {L_{2} - \overline{{L_{1} }} } \right)y}}{{\left( {L_{2} - \overline{{L_{1} }} } \right)^{2} - \delta_{c} }}} \right) + \frac{{\delta_{12} }}{2}\left( {\frac{{\cosh \left( {L_{2} + \overline{{L_{2} }} } \right)y}}{{\left( {L_{2} + \overline{{L_{2} }} } \right)^{2} - \delta_{c} }} - \frac{{\cosh \left( {L_{2} - \overline{{L_{2} }} } \right)y}}{{\left( {L_{2} - \overline{{L_{2} }} } \right)^{2} - \delta_{c} }}} \right)} \right]} \right] \\ \end{aligned} $$

(96a)

$$ Z_{1} = \frac{{\left( {1 - C} \right)N + C M}}{N} $$

(96b)

$$ F_{1} \,(y)\, = \left[ \begin{gathered} (1 - C)\,i \alpha \chi P_{1} (y) \overline{{V_{f1} }} (y) - (1 - C)\,\,i \alpha \chi \overline{{P_{1} }} (y) V_{f1} (y) \hfill \\ - i \alpha U_{f1} (y) \overline{{V_{f1} }} (y) + i \alpha \overline{{U_{f1} }} (y) V_{f1} (y) + V_{f1} \overline{{V^{\prime}_{f1} }} (y) + \overline{{V_{f1} }} V^{\prime}_{f1} (y) \hfill \\ \end{gathered} \right] $$

(96c)

$$ F_{2} (y) = \left[ { - i \alpha \overline{{V_{p1} }} (y) U_{p1} (y) + i \alpha V_{p1} (y) \overline{{U_{p1} }} (y) + V_{p1} \overline{{V_{p1}^{\prime } }} (y) + \overline{{V_{p1} }} V_{p1}^{\prime } (y)} \right] $$

(96d)

$$ F_{3} (y) = \left[ {P_{1} (y)\,\, \overline{{V_{f1} }} (y) + \overline{{P_{1} }} (y) \,\,V_{f1} (y)} \right] $$

(96e)

$$ D = P_{20} (y) - \frac{4}{{3 RZ_{1} }}V_{f20}^{\prime } (y) + \frac{{\left( {1 - C} \right)}}{{Z_{1} }}\int {F_{1} (y)dy} + \frac{C M}{{NZ_{1} }}\int {F_{2} (y)dy\, - \frac{\chi }{{K\,R\,Z_{1} }}\int {F_{3} (y)dy} \,} {\text{at }}y = - 1 $$

(96f)

$$ \delta_{c} = \frac{{\left( {\frac{1}{K} + H_{a}^{2} } \right)}}{(\,1 - C\,)} $$

(96g)

$$ \begin{aligned} D_{2} & = - \frac{1}{{2\left( {Cosh\,\sqrt {\delta_{c} } + Kn\,\sqrt {\delta_{c} } \,Sinh\,\sqrt {\delta_{c} } \,} \right)}}\left\{ {R\,\,[E(1) - E( - 1)]} \right. \\ & \quad \left. { + Kn\left[ {R\,E^{\prime}(1) - R\,E^{\prime}( - 1) + \beta_{3} - \beta_{4} } \right] + \beta_{1} + \beta_{2} } \right\} \\ \end{aligned} $$

(96h)

$$ \begin{aligned} D_{3} & = - \frac{1}{{2\left( {Sinh\sqrt {\delta_{c} } + Kn\,\sqrt {\delta_{c} } \,Cosh\,\sqrt {\delta_{c} } \,} \right)}}\left\{ {R\,\,[E(1) - E( - 1)]} \right. \\ & \quad \left. { + Kn\left[ {R\,E^{\prime}(1) + R\,E^{\prime}( - 1) + \beta_{3} + \beta_{4} } \right] + \beta_{1} - \beta_{2} } \right\} \\ \end{aligned} $$

(96i)

$$ \left. \begin{gathered} \beta_{1} = \frac{1}{2}\left( {U_{f1}^{\prime } \left( 1 \right) + \overline{{U_{f1} \left( 1 \right)}}^{\prime } } \right) \hfill \\ \beta_{2} = \frac{ - 1}{2}\left( {U_{f1}^{\prime } \left( { - 1} \right) + \overline{{U_{f1} \left( { - 1} \right)}}^{\prime } } \right) \hfill \\ \beta_{3} = \frac{1}{2}\left( {U_{f1}^{\prime \prime } \left( 1 \right) + \overline{{U_{f1} \left( 1 \right)}}^{\prime \prime } } \right) \hfill \\ \beta_{4} = \frac{ - 1}{2}\left( {U_{f1}^{\prime \prime } \left( { - 1} \right) + \overline{{U_{f1} \left( { - 1} \right)}}^{\prime \prime } } \right) \hfill \\ \end{gathered} \right\} $$

(96j)

$$ \left. \begin{gathered} \delta_{1} = \overline{{R_{6} }} \overline{{C_{1} }} C_{1} L_{1} + \overline{{L_{1} }} \overline{{C_{1} }} C_{1} R_{6} \,\,,\,\delta_{2} = \overline{{R_{7} }} \overline{{C_{2} }} C_{1} L_{1} + \overline{{L_{2} }} \overline{{C_{2} }} C_{1} R_{6} \hfill \\ \delta_{3} = \overline{{R_{6} }} \overline{{C_{1} }} C_{2} L_{2} + \overline{{L_{1} }} \overline{{C_{1} }} C_{2} R_{7} \,\,,\delta_{4} = \overline{{R_{7} }} \overline{{C_{2} }} C_{2} L_{2} + \overline{{L_{2} }} \overline{{C_{2} }} C_{2} R_{7} \hfill \\ \delta_{5} = \overline{{C_{1} }} R_{6} C_{1} L_{1} + \overline{{L_{1} }} \overline{{C_{1} }} \overline{{R_{6} }} C_{1} \,,\,\,\delta_{6} = \overline{{C_{1} }} R_{7} C_{2} L_{2} + \overline{{L_{1} }} \overline{{C_{1} }} \overline{{R_{6} }} C_{2} \hfill \\ \delta_{7} = \overline{{C_{2} }} R_{1} C_{1} L_{1} + \overline{{L_{1} }} \overline{{C_{1} }} \overline{{R_{6} }} C_{1} \,,\,\delta_{8} = \overline{{C_{2} }} R_{7} C_{2} L_{2} + \overline{{L_{2} }} \overline{{C_{2} }} \overline{{R_{7} }} C_{2} \hfill \\ \delta_{9} = R_{10} C_{1} \overline{{R_{8} }} \overline{{C_{1} }} \overline{{L_{1} }} + \overline{{R_{10} }} \overline{{C_{1} }} R_{8} L_{1} C_{1} \hfill \\ \delta_{10} = R_{10} C_{1} \overline{{R_{9} }} \overline{{C_{2} }} \overline{{L_{2} }} + \overline{{R_{11} }} \overline{{C_{2} }} R_{8} L_{1} C_{1} \hfill \\ \delta_{11} = R_{11} C_{2} \overline{{R_{8} }} \overline{{C_{1} }} \overline{{L_{1} }} + \overline{{R_{10} }} \overline{{C_{1} }} R_{9} L_{2} C_{2} \hfill \\ \delta_{12} = R_{11} C_{2} \overline{{R_{9} }} \overline{{C_{2} }} \overline{{L_{2} }} + \overline{{R_{11} }} \overline{{C_{2} }} R_{9} L_{2} C_{2} \hfill \\ \end{gathered} \right\} $$

(96k)

The net axial streamwise velocities may now be written as

$$ < V_{f\,x} (y) > \,\, = \varepsilon^{2} U_{f20} (y) $$

(97)

$$ < U_{p} (y) > = \varepsilon^{2} U_{p20} (y) $$

(98)

The mean velocity perturbation function G(y) according to Fung and Yih [2] and Srivastava and Srivastava [6] takes the form

$$ G(y) = - \frac{200}{{\alpha^{2} R^{2} }}\left( {E(y) - E(1)} \right) $$

(99)

It is noticed for the current problem that the results of Fung and Yih [2] can be obtained in case of $[\chi = 0]$ incompressible liquids under the assumption of the absence of the wall properties $[B, D, T, {K}_{1},\mathrm{ and} m]$, the magnetic field parameter $[{H}_{a}]$, and the space porosity parameter $[K]$ in case of non-slip wall conditions and free from solid suspensions $[C=0]$. It is also remarked that the results of Mekheimer and Abdel‐Wahab [31] can be covered if $[C=0], {[H}_{a}=0], \mathrm{and} [1/K =0]$.

Results and Discussion

Validation Section

Results are compared with the article of Mekheimer and Abdel‐Wahab [31]. The mathematical calculations and the results are obtained for the present analysis under the assumptions of ignoring the effect of particles suspensions $[\mathrm{C}=0]$, transverse magnetic field $[{\mathrm{H}}_{\mathrm{a}}=0]$ and free from porosity [$1/\mathrm{K }=0]$. Figure 2 shows the results from the present study under the previous assumptions which exactly matches with Mekheimer and Abdel‐Wahab [31].

Fig. 2

The variation of the streamwise velocity under different factors of the wall and flow properties

Studying the behavior of the net flow requires analytical calculations for the combined effects of the magnetic field, the space porosity, the wall properties, the slip parameters, the suspension parameter, and the compressibility parameter on the viscous compressible peristaltic transport in a flexible channel. These calculations are mathematically carried out in the previous section. In this section, results are graphically plotted for the velocity profiles to show these effects on the mean axial velocity and the reversal flow. There are three divisions of this study: the first case is showing the influences of all parameters such as the magnetic field, the wall parameters, the slip parameter, the compressibility parameter, the flow parameters, and the suspension parameters except the effect of the space porosity, which does not exist in this case. The second case of the discussion is handling the same previous effects but taking into consideration the effect of space porosity parameter in the absence of the magnetic field. The final case is to study the influence of all parameters in the presence of the space porosity parameter and the magnetic field parameter. Each case is described graphically as follows.

In the first case, Fig. 3 shows the effect of various parameters on the mean axial velocity in the presence of the magnetic field and the absence of the porosity effect (Table 1).

Fig. 3

The net streamwise velocity distributions along the y-axis and the medium is free from porosity

Table 1 Corresponding to Fig. 3

Figure 3 indicates explicitly the effects of the various parameters on the mean streamwise velocity $< {V}_{fx}{ / \varepsilon }^{2} >$ then plotting the velocity profiles along the y-axis. These parameters are the flow and wall parameters. The flow parameters are the compressibility parameters $[\chi ]$, the Reynolds number $[R]$, the wall slip $[Kn]$, the suspensions parameter $[C]$, the magnetic field parameter called Hartmann number $[{H}_{a}]$. The wall compliance parameters are the flexural wall rigidity $[B]$, the longitude wall tension $[T]$. $[{K}_{1}]$ represents the wall stiffness. The parameter $[D]$ represents the dissipative feature of the wall. The choice $D=0$ implies that the wall moves up and down, with no damping force on it.

It is noticed in Fig. 3a that there is a high resistance for the flow. The rise in the wall damping $[D]$ is reducing the mean streamwise velocity. Whereas the wall stiffness $[{k}_{1}]$ and the compressibility factor $[\chi ]$ are enhancing the streamwise velocity profiles as illustrated in Fig. 3b, c. Obviously, it is noted in Fig. 3d that the velocity profile near the boundaries increases by increasing the longitude tension parameter $[T]$ but it is reduced near the center with raising the wall tension $[T]$. In contrast, no-slip conditions mean that the fluid particles stick with the solid walls. The slip conditions mean that the fluid velocity at the wall is allowed to slip along the contour of the surface (move on the surface and tangent to the surface). and this condition is defined by the Knudsen number $[Kn]$. Its effect is shown in Fig. 3e as $\left[Kn\right]$ boosts the net streamwise velocity. Figure 3g shows that the mean axial velocity is enhanced by increasing the magnetic parameter $[{H}_{a}]$. The suspension parameter $[C]$ effect is illustrated in Fig. 3f, as the increase in the concentration $[C]$ reduces the path area then the mean axial velocity is raised as shown.

Now, the second case of the study is illustrated graphically. Figure 4 shows the simultaneous effects of the various physical parameters on the net streamwise velocity in the presence of the porosity parameter $[K]$ and the absence of the magnetic field parameter $\left[{H}_{a}\right]$.

Fig. 4

The streamwise velocity profiles versus y axis in the absence of the magnetic flux

Figure 4a shows the effect of the damping parameter which resists the flow. The parameters $[{k}_{1}, \chi ,\boldsymbol{ }and$ $Kn]$ have similar effects on the mean streamwise velocity. There is a proportional relation between these parameters and velocity profile as shown in Fig. 4b, d, e. The effects of longitude wall tension $[T]$ and suspension parameter $[C]$ are shown in Fig. 4c, f. There is a significant effect near the boundaries as these parameters are boosting the net streamwise velocity. This effect is less at the channel core where the velocity profiles close to each other and the relationship between these parameters and mean velocity remains proportional. The range of the permeability parameter of the porous medium is [$0 \le k \le \infty$]. At $[K=\infty$], this means that $\left[\frac{1}{K}=0\right].$ Then, the open path will be free from porosity. But $\left[K=0\right]$ means that [$\frac{1}{K}=\infty ]$. Then, the path is fully filled with the space porosity which is closing the path. It is noted in Fig. 4g that the mean axial velocity is enhanced by increasing $K$ (Table 2).

Table 2 Corresponding to Fig. 4

Finally, the combined effects of the magnetic flux [${H}_{a}]$ and the space porosity $[K]$ are taken into consideration in the graphical plots beside the wall properties, the wall slip conditions, and the compressibility parameter as shown in Fig. 5 (Table 3).

Fig. 5

The mean streamwise velocity distribution along the y-axis in the presence of the magnetic flux and the space porosity

Table 3 Corresponding to Fig. 5

The time average flow velocity $< {V}_{fx}{ / \varepsilon }^{2}>$ is graphically discussed under the assumption of existing the magnetic field $[{H}_{a}]$ and the space porosity $[K]$ as follows.

Figure 5a shows the effect of the damping parameter $[D]$ which also is resisting the flow. It is noticed that the reversal flow begins to occur for higher values of $[D]$. As the parameters $\left[{K}_{1}, T, C,\boldsymbol{ }\chi ,\boldsymbol{ }\mathrm{and}\boldsymbol{ } K n\right]$ are increasing, the net streamwise velocity is enhanced near the boundaries as illustrated in Fig. 5b–e, g. This effect is small at the channel core. It is also noticed in Fig. 5d that, for small values of the compressibility parameter $[ \chi =0.001]$, the velocity profile seems to be constant along the y-axis and it is plotted as a straight line. The rise in the magnetic flux $[{H}_{a}]$ reduces the mean streamwise velocity as shown in Fig. 5f. Finally, Fig. 5h shows that as permeability parameter $[K]$ is increased then the path will let the flow be easier with low resistance. Therefore, the net streamwise velocity is enhanced.

Conclusion

This paper is analyzing the combined effects of the wall properties $[ D, T, \mathrm{and} {K}_{1}]$, the magnetic field $[{H}_{a}]$, the wall slip [$Kn]$, the liquid compressibility $[\chi ]$, and the space porosity $[K]$ interacted with a solid suspensions $[C]$ in the presence of the peristaltic transport through a rectangular channel. The used methodology is the analytical perturbation technique under the assumption of a small amplitude ratio. The governing equations are solved under a certain procedure to obtain mathematical relations for both fluid and particles velocities. The mean streamwise velocity profiles are plotted for three cases of study.

In the first case of the study, the influences of the parameters [$D, T, {K}_{1}, Kn, \chi , \mathrm{and } C]$ on the mean axial velocity in the presence of magnetic field parameter [${H}_{a}]$ are investigated and neglecting the effect of the space porosity as the path of motion is open “free from porosity”$[K=\infty \mathrm{ so that } 1/K=0]$.

The second case is studying the effects of the same parameters of the first case but the space porosity $K$ is the parameter of effect and neglecting the effect of the magnetic field.

The third case is combining the effects of the space porosity [$K]$ and magnetic field [${H}_{a}]$ in addition to the wall and flow parameters $[D, T, {K}_{1}, K n, \chi , \mathrm{ and } C]$ as cases 1 and 2.

The following are some important observations:

• In the three cases the damping parameter has significant resistance effect as the mean streamwise velocity is reduced by increasing $[D]$.

• The reversal flow occurs at higher values of the damping parameter $[D]$.

• For the first case of the study, the parameters $[{K}_{1}, \chi , Kn, C, \mathrm{and } {H}_{a}$] have a proportional relation with the mean axial velocity.

• In the first case of the study, the rise in the wall tension [$T]$ enhances the mean streamwise velocity near the boundaries. Whereas, at the center this effect is the opposite as the mean velocity is reduced.

• For the second case of the study, as the compressibility parameter $[\chi ]$ and the permeability parameter [$K]$ increase, the streamwise velocity is enhanced in such a manner.

• The increase in the parameters $[{K}_{1}, T, Kn, \mathrm{and } C]$ boosts the mean streamwise velocity near the boundaries and causes a minor increase at the center.

• For the third case of the study, as permeability $[K]$ increases, this mean flow has less restriction to the flow then the mean streamwise velocity increases.

• By increasing [${H}_{a}]$, the mean streamwise velocity is reduced.

• For higher values of the compressibility parameter $[\chi \ge 0.1 \mathrm{ up to } 1]$, the mean axial velocity increases.

• For small values of the compressibility parameter as $[\chi =0.001]$, the velocity profile seems to be constant.

• The mean streamwise velocity is enhanced by increasing the parameters $[T, {K}_{1}, Kn, \mathrm{and } C]$.