A New Algorithm of Residual Power Series (RPS) Technique

Abstract

Approximate analytic solutions of time–space fractional heat and wave equations are described. A new algorithm of Residual power series technique is introduced to obtain approximate solutions of such problems. The solution was obtained without reducing fractional differential equations to time fractional or space fractional differential equations. Some interesting results are presented to verify the efficiency and reliability of the developed algorithm.

Introduction

The Fractional differential equations (FDEs) are now increasingly attractive in many fields [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. The FDEs introduce a new non-integer derivative which depends on the history of the previous time. The differential equation with fractional derivative operator has successfully been fitted to experimental data [15]. Because of the rapid progress in various fields of science and engineering, researchers have directed the modern techniques in classical and fractional differential equations to obtain approximate solutions for many linear and nonlinear differential equations [16,17,18,19,20,21,22,23,24]. One of these techniques is the Residual power series (RPS) technique, which is easy to use and the accuracy of the results obtained. Residual power series (RPS) technique is a useful tool for generating the solution of FDEs [25,26,27,28,29,30,31,32]. The authors in [33] have found the approximate solutions of space–time fractional differential equations by (RPS) method. They reduce fractional differential equations to time fractional or space fractional differential equations.

In this paper, we will use a new algorithm of the RPS method for solving a time–space fractional heat equation:

$$ D_{t}^{\beta } u\left( {x,t} \right) = D_{x}^{\gamma } u\left( {x,t} \right),\quad 0 < \beta \le 1, 1 < \gamma \le 2, $$

(1)

with nonhomogeneous initial conditions

$$ u(x,0) = f_{00} (x),\quad x > 0, $$

(2)

$$ u(0,t) = w_{00} (t),\quad u_{x} (0,t) = w_{01} (t),\quad t > 0 $$

(3)

and a time–space fractional wave equation:

$$ D_{t}^{\beta } u\left( {x,t} \right) = D_{x}^{\gamma } u\left( {x,t} \right),\quad 1 < \beta \le 2, 1 < \gamma \le 2, $$

(4)

with nonhomogeneous initial conditions

$$ u(x,0) = f_{00} (x),\quad u_{t} (x,0) = f_{01} (x),\quad x > 0, $$

(5)

$$ u(0,t) = w_{00} (t),\quad u_{x} (0,t) = w_{01} (t),\quad t > 0 . $$

(6)

Preliminaries

In order to consider the solutions to the time–space fractional problems, the fractional order derivatives and integral of Riemann–Liouville and, Caputo are presented [34,35,36,37].

Definition 2.1

The fractional integral operator of Riemann–Liouville of a function $f(x)$ is denoted as

$$ J_{a}^{\beta } f(x) = \frac{1}{\varGamma (\beta )}\int\limits_{a}^{x} {(x - \zeta )^{\alpha - 1} f(\zeta )\,d\zeta } , \quad \beta > 0,\,\,\,x > 0. $$

Definition 2.2

The fractional derivative operator of Caputo sense of a function $f(x)$ is denoted as

$$\begin{aligned} & D^{\beta } f(x) = I^{n - \beta } D^{n} f(x)\\ & \qquad = \frac{1}{\varGamma (n - \beta )}\int\limits_{0}^{x} {(x - \zeta )^{n - \beta + 1} f^{(n)} (\zeta )d\zeta } ,\quad n - 1 < \beta \le n,\quad x > 0.\end{aligned} $$

For some examples of Caputo derivatives we have:$D^{\beta } A = 0,$ where $A$ is constant

$$ D^{\beta } \tau^{n} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {(n \le \beta - 1),} \hfill \\ {\frac{\varGamma (n + 1)}{\varGamma (n - \beta + 1)}\tau^{n - \beta } ,} \hfill & {(n > \beta - 1).} \hfill \\ \end{array} } \right. $$

$D_{t}^{\beta } e^{\mu \,\tau } = \mu^{n} \,\tau^{n - \beta } E_{1,n - \beta + 1} (\mu \,\tau ),$ where $E_{\alpha ,\beta } (\mu \,\tau )$ is Mittag–Leffler function [34].

$$ D_{x}^{\gamma } (\sin x) = \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} x^{2k - \gamma + 1} }}{\varGamma (2k - \gamma + 2)}} ,\quad 0 < \gamma \le 1, $$

and

$$ D_{x}^{\gamma } (\sin x) = \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} x^{2k - \gamma + 3} }}{\varGamma (2k - \gamma + 4)}} ,\quad 1 < \gamma \le 2. $$

Definition 2.3

The kh-truncated series $u_{kh} (x,t)$ of the RPS method [32, 33] take the following form:

$$ u_{kh} (x,t) = \sum\limits_{n = 0}^{i - 1} {\frac{{a_{n} (x)}}{n\,!}} + \sum\limits_{n = 1}^{k} {\sum\limits_{m = 0}^{h} {f_{nm} (x)\frac{{t^{n\beta + m} }}{\varGamma (n\,\beta + m + 1)}} } ,\quad t > 0,\quad n - 1 < \beta \le n, $$

(7)

and

$$ u_{kh} (x,t) = \sum\limits_{n = 0}^{i - 1} {\frac{{b_{n} (t)}}{n\,!}} + \sum\limits_{n = 1}^{k} {\sum\limits_{m = 0}^{h} {w_{nm} (t)\frac{{x^{n\gamma + m} }}{\varGamma (n\,\gamma + m + 1)}} } ,\quad x > 0,\quad n - 1 < \gamma \le n $$

(8)

Solution of Time–Space Heat Like Equation

In this section, we suggest a new algorithm of RPS technique to get approximate solutions of time–space heat like equation with nonhomogeneous initial conditions.

Example 3.1

Consider the following time–space heat like equation

$$ D_{t}^{\beta } u(x,t) = D_{x}^{\gamma } u(x,t),\quad 0 < \beta \le 1, \quad 1 < \gamma \le 2, $$

(9)

with nonhomogeneous initial conditions

$$ u(x,0) = f_{00} (x) = \sin x,\quad x > 0, $$

(10)

$$ u(0,t) = w_{00} (t) = 0,\quad u_{x} (0,t) = w_{01} (t) = e^{ - t} , \quad t > 0. $$

(11)

By using Eqs. (9) and (10), the k0-truncated series $u_{k0} (x,t)$ take the following form:

$$ u_{k0} (x,t) = f_{00} (x) + \sum\limits_{n = 1}^{k} {f_{n0} (x)\frac{{t^{n\beta } }}{\varGamma (n\beta + 1)}} ,\quad t > 0,\quad 0 < \beta \le 1. $$

(12)

By using Eqs. (9) and (11), the kh-truncated series $u_{kh} (x,t)$ take the following form:

$$ u_{kh} (x,t) = w_{00} (t) + x\,w_{01} (t)\, + \sum\limits_{n = 1}^{k} {\sum\limits_{m = 0}^{h} {w_{nm} (t)\frac{{x^{n\gamma + m} }}{\varGamma (n\gamma + m + 1)}} } ,\quad x > 0,\quad 1 < \gamma \le 2. $$

(13)

We employed the new RPS technique to solve Problem (9)–(11) by using the new term

$$ u\left( {x,t} \right) = \frac{1}{2}\left( {f_{00} (x) + w_{00} (t) + x\,w_{01} (t)\,} \right) + \frac{1}{2}\left( {\sum\limits_{n = 1}^{\infty } {f_{i0} (x)\frac{{t^{n\,\beta } }}{\varGamma (n\,\beta + 1)}} + \sum\limits_{n = 1}^{\infty } {\sum\limits_{m = 0}^{1} {w_{nm} (t)\frac{{x^{n\gamma + m} }}{\varGamma (n\,\gamma + m + 1)}} } } \right). $$

(14)

Let $u_{kh} \left( {x,t} \right)$ is the kh-truncated series of u(x, t), then

$$ u_{kh} (x,t) = \frac{1}{2}\left( {f_{00} (x) + w_{00} (t) + x\,w_{01} (t)\,} \right) + \frac{1}{2}\left( {\sum\limits_{n = 1}^{k} {f_{i0} (x)\frac{{t^{n\,\beta } }}{\varGamma (n\,\beta + 1)}} + \sum\limits_{n = 1}^{k} {\sum\limits_{m = 0}^{h} {w_{nm} (t)\frac{{x^{n\gamma + m} }}{\varGamma (n\,\gamma + m + 1)}} } } \right). $$

(15)

By using Eq. (15) the approximate solution $u_{00} \left( {x,t} \right)$ of RPS method is

$$ u_{00} \left( {x,t} \right) = \frac{1}{2}\left( {f_{00} (x) + w_{00} (t) + x\,w_{01} (t)\,} \right). $$

(16)

The kh residual function $Res_{kh} \left( {x,t} \right)$ is define as

$$ \text{Re} s_{kh} (x,t) = D_{t}^{\beta } u_{kh} - D_{x}^{\gamma } u(x,t)_{kh} . $$

(17)

To get the required coefficients $w_{ij}$(t), i = 1, 2, 3,…, k, and j = 1, 2, 3,…, k, substitute Eq. (15) into Eq. (17), and solve the following equation

$$ D_{x}^{{\left( {k - 1} \right)\gamma }} D_{x}^{h} Res_{kl} \left( {0,t} \right) \, = 0. $$

(18)

To determine $w_{10}$(t), substituting k = 1 and h = 0 into Eq. (17) then:

$$ \text{Re} s_{10} (x,t) = D_{t}^{\beta } u_{10} - D_{x}^{\gamma } u_{10} (x,t), $$

(19)

where

$$ u_{10} \left( {x,t} \right) = \frac{1}{2}\left( {f_{00} (x) + w_{00} (t) + x\,w_{01} (t)\,} \right) + \frac{1}{2}\left( {f_{10} (x)\frac{{t^{\beta } }}{\varGamma (\beta + 1)} + w_{10} (t)\frac{{x^{\gamma } }}{\varGamma (\gamma + 1)}} \right). $$

(20)

Using Eq. (18) when k = 1and h = 0, we get

$$ w_{10} (t) = f_{10} (0) - D_{x}^{\gamma } f_{10} (0)\frac{{t^{\beta } }}{\varGamma (\beta + 1)}. $$

(21)

To determine w₂₀(t), substituting k = 2 and h = 0 into Eq. (17) then

$$ \text{Re} s_{u20} = D_{t}^{\beta } u_{20} - D_{x}^{\gamma } u_{20} , $$

(22)

where

$$ u_{20} \left( {x,t} \right) = \frac{1}{2}\left( {f_{00} (x) + w_{00} (t) + w_{01} (t)\,x} \right) + \frac{1}{2}\left( {f_{10} (x)\frac{{t^{\beta } }}{\varGamma (\beta + 1)} + w_{10} (t)\frac{{x^{\gamma } }}{\varGamma (\gamma + 1)}} \right). $$

(23)

Using Eq. (18) when k = 1 and h = 1, we get

$$ w_{20} (t) = D_{x}^{\gamma } f_{10} (0) + D_{x}^{\gamma } f_{20} (0)\frac{{t^{\beta } }}{\varGamma (\beta + 1)} - D_{x}^{\gamma } (D_{x}^{\gamma } f_{20} (0))\frac{{t^{2\beta } }}{\varGamma (2\beta + 1)}. $$

(24)

To determine w₁₁(t), substituting k = 1 and h = 1 into Eq. (17) then

$$ \text{Re} s_{u11} = D_{t}^{\beta } u_{11} - D_{x}^{\gamma } u_{11} , $$

(25)

where

$$ u_{11} \left( {x,t} \right) = \frac{1}{2}\left( {f_{00} (x) + w_{00} (t) + w_{01} (t)\,x} \right) + \frac{1}{2}\left( {f_{10} (x)\frac{{t^{\beta } }}{\varGamma (\beta + 1)} + w_{11} (t)\frac{{x^{\gamma + 1} }}{\varGamma (\gamma + 2)}} \right). $$

(26)

Using Eq. (18) when k = 1and h = 1, we get

$$ w_{11} (t) = D_{t}^{\beta } (e^{ - t} ) + D_{x}^{{}} f_{10} (0) - D_{x} (D_{x}^{\gamma } f_{10} (0))\frac{{t^{\beta } }}{\varGamma (\beta + 1)}. $$

(27)

To determine w₂₁(t), substituting k = 2 and h = 1 into Eq. (17) then:

$$ \text{Re} s_{u21} = D_{t}^{\beta } u_{21} - D_{x}^{\gamma } u_{21} (x,t), $$

(28)

where

$$ u_{21} (x,t) = \frac{1}{2}\left( {\sin x + x\,e^{ - t} } \right) + \frac{1}{2}\left( {f_{20} (x)\frac{{t^{\,2\beta } }}{\varGamma (2\beta + 1)} + w_{21} (t)\frac{{x^{2\gamma + 1} }}{\varGamma (2\gamma + 2)}} \right). $$

(29)

Using Eq. (18) when k = 2 and h = 1 we get

$$ \begin{aligned} w_{21} (t) & = D_{t}^{\beta } (w_{11} (t)) + D_{x}^{\gamma } (D_{x} f_{10} (0)) + (D_{x}^{\gamma } (D_{x} f_{20} (0) - D_{x}^{\gamma } (D_{x} (D_{x}^{\gamma } f_{10} (0)))\frac{{t^{\beta } }}{\varGamma (\beta + 1)} \\ & \quad - D_{x}^{\gamma } (D_{x} (D_{x}^{\gamma } f_{20} (0)))\frac{{t^{2\beta } }}{\varGamma (2\beta + 1)}, \\ \end{aligned} $$

(30)

and so on. We will get $f_{10} (x),\,f_{20} (x), \ldots ,f_{k0} (x)$ from the next step by using Eq. (12).

To get the required coefficients $f_{ij} \left( x \right)$(t), i = 1, 2, 3,…, k, and j = 1, 2, 3,…, k, substitute Eq. (12) into Eq. (7), and solve the following equation

$$ D_{t}^{{\left( {k - 1} \right)\beta }} Res_{uk0} \left( {x,0} \right) \, = 0. $$

(31)

To determine $f_{10}$(x), substituting k = 1 into Eq. (17) then:

$$ \text{Re} s_{u10} = D_{t}^{\beta } u_{10} - D_{x}^{\gamma } u_{10} (x,t), $$

(32)

where

$$ u_{10} \left( {x,t} \right) = f_{00} (x) + f_{10} (x)\frac{{t^{\beta } }}{{\varGamma \left( {1 + \beta } \right)}} . $$

(33)

Using Eq. (31) when k = 1, we get

$$ f_{10} (x) = \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} x^{2k - \gamma + 3} }}{\varGamma (2k - \gamma + 4)}} . $$

(34)

To determine $f_{20}$(x), substituting k = 2 into Eq. (17) then

$$ \text{Re} s_{u20} = D_{t}^{\beta } u_{20} - D_{x}^{\gamma } u_{20} , $$

(35)

where

$$ u_{20} \left( {x,t} \right) = f_{00} (x) + f_{10} \frac{{t^{\beta } }}{{\varGamma \left( {1 + \beta } \right)}} + f_{20} \frac{{t^{2\beta } }}{{\varGamma \left( {1 + 2\beta } \right)}}. $$

(36)

Using Eq. (31) when k = 2, we get

$$ f_{20} (x) = \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 2} x^{2k - 2\gamma + 5} }}{\varGamma (2k - 2\gamma + 6)}} . $$

(37)

And so on. By substitute the coefficients $f_{10} (x),\,f_{20} (x), \ldots ,f_{k0} (x)$ into Eqs. (21), (24), (27), and (30), then $w_{10} (t) = 0,$$w_{20} (t) = 0,$$w_{30} (t) = 0,$,…, $w_{k0} (t) = 0,$$w_{11} (t) = \sum\nolimits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} t^{k - \beta + 1} }}{\varGamma (k - \beta + 2)}} ,\quad w_{21} (t) = \sum\nolimits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 2} t^{k - 2\beta + 2} }}{\varGamma (k - 2\beta + 3)}} ,\quad w_{31} (t) = \sum\nolimits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 3} t^{k - 3\beta + 3} }}{\varGamma (k - 3\beta + 4)}} , \ldots ,$ and so on.

So, we get the new RPS solution:

$$ \begin{aligned} u(x,t) & = \frac{1}{2}\left( {\sin x + x\,e^{ - t} } \right)\\ & + \frac{1}{2}\left( {\sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} x^{2k - \gamma + 3} }}{\varGamma (2k - \gamma + 4)}} \frac{{t^{\beta } }}{\varGamma (\beta + 1)} + \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 2} x^{2k - 2\gamma + 5} }}{\varGamma (2k - 2\gamma + 6)}} \frac{{t^{2\,\beta } }}{\varGamma (2\beta + 1)} + \cdot \cdot \cdot } \right) \hfill \\ & \quad +\frac{1}{2}\left( {\sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} t^{k - \beta + 1} }}{\varGamma (k - \beta + 2)}} \frac{{x^{\gamma + 1} }}{\varGamma (\gamma + 2)} + \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 2} t^{k - 2\beta + 2} }}{\varGamma (k - 2\beta + 3)}} \frac{{x^{2\gamma + 1} }}{\varGamma (2\gamma + 2)} - \cdot \cdot \cdot } \right). \hfill \\ \end{aligned} $$

  we can write the last solution as:

$$ \begin{aligned} u(x,t) & = \frac{1}{2}\left( {\sin x + x\,e^{ - t} } \right)\\ & \quad + \frac{1}{2}\left( { - x^{3 - \gamma } E_{2,4 - \gamma } ( - x^{2} )\frac{{t^{\beta } }}{\varGamma (\beta + 1)} + x^{5 - 2\gamma } E_{2,6 - 2\gamma } ( - x^{2} )\frac{{t^{2\beta } }}{\varGamma (2\beta + 1)} + \cdots } \right) \\ & \quad + \frac{1}{2}\left( { - t^{1 - \beta } E_{1,2 - \beta } ( - t)\frac{{x^{\gamma + 1} }}{\varGamma (\gamma + 2)} + t^{2 - 2\beta } E_{1,3 - 2\beta } ( - t)\frac{{x^{2\gamma + 1} }}{\varGamma (2\gamma + 2)} - \cdots } \right). \\ \end{aligned} $$

In a closed form, we can get the solution of Problem (9)–(11) as

$$ \begin{aligned} u(x,t) & = \frac{1}{2}\left( {\sin x + x\,e^{ - t} } \right) + \frac{1}{2}\left( {\sum\limits_{k = 1}^{\infty } {( - 1)^{k} } x^{k\,(2 - \gamma ) + 1} E_{2,k\,(2 - \gamma ) + 1} ( - x^{2} )\frac{{t^{\,k\beta } }}{\varGamma (k\beta + 1)}} \right) \\ & \quad + \frac{1}{2}\left( {\sum\limits_{k = 1}^{\infty } {( - 1)^{k} } t^{k\,(1 - \beta )} E_{1,k(1 - \beta ) + 1} ( - t)} \right), \\ \end{aligned} $$

(38)

As $\beta \to 1$ and $\gamma \to 2$, we have a classical exact solution $\,u(x,t)\,\, = \sin x\,\,e^{ - t} .$

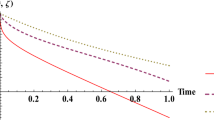
Table 1 provide the numerical results for the convergence of the new developed algorithm of RPS method. Figure 1 provides an excellent approximation with the exact solution. Figures 2, 3, and 4 are the geometric behavior of the solutions. We can get a higher accuracy by getting more components (Table 2).

Table 1 The comparison results of the residual errors for Example 3.1 at $\beta = 1,\gamma = 2$

Fig. 1

a Exact solution (classical case) b RPS solution $u_{31} \left( {x,t} \right)$ for Example 3.1 ($\beta = 1, \gamma = 2$)

Fig. 2

The RPS solution $u_{31} \left( {x,t} \right)$ for Example 3.1a$\beta = 1, \gamma = 1.5$b$\beta = 1, \gamma = 1.75$

Fig. 3

The RPS solution $u_{31} \left( {x,t} \right)$ for Example 3.1a$\beta = 0.5, \gamma = 2$b$\beta = 0.75, \gamma = 2$

Fig. 4

The RPS solution $u_{31} \left( {x,t} \right)$ for Example 3.1a$\beta = 0.5, \gamma = 1.5$b$\beta = 0.75, \gamma = 1.75$

Table 2 The numerical values of the approximate solutions ${\text{u}}_{31}$ for Example 3.1

Solution of Time–Space Wave Like Equation

In this section, we suggest a new algorithm of RPS technique to get approximate solutions of time–space wave like equation with nonhomogeneous initial conditions.

Example 4.1

Consider the following time–space wave like equation

$$ D_{t}^{\beta } u = D_{x}^{\gamma } u,\quad 1 < \beta \le 2,\,\,\,1 < \gamma \le 2\,\,\,x > 0\quad t > 0,\,\, $$

(39)

with nonhomogeneous initial conditions

$$ u(x,0) = f_{00} (x) = 0,\quad u_{t} (x,0) = f_{01} (x) = \cos x, $$

(40)

$$ u(0,t) = \,w_{00} (x) = \sin t,\quad u_{x} (0,t) = w_{01} (x) = 0. $$

(41)

According to RPS method, the solution of Eqs. (39), (40) and (41) can be define as

$$ u(x,t) = \frac{1}{2}\left( {\sin t + t\,\,\cos x} \right) + \frac{1}{2}\left( {\sum\limits_{n = 1}^{k} {\sum\limits_{m = 0}^{1} {f_{nm} (t)\frac{{t^{n\beta + m} }}{\varGamma (n\beta + m + 1)}} } + \sum\limits_{n = 1}^{k} {\sum\limits_{m = 0}^{1} {w_{nm} (t)\frac{{x^{n\gamma + m} }}{\varGamma (n\beta + m + 1)}} } } \right). $$

(42)

The kh-truncated series of the RPS method, denoted by $u_{kh} (x,t)$), is defined as

$$ u_{kh} (x,t) = \frac{1}{2}\left( {\sin t + t\,\cos x} \right) + \frac{1}{2}\left( {\sum\limits_{n = 1}^{k} {\sum\limits_{m = 0}^{h} {f_{nm} (t)\frac{{t^{n\beta + m} }}{\varGamma (n\beta + m + 1)}} } + \sum\limits_{n = 1}^{k} {\sum\limits_{m = 0}^{h} {w_{nm} (t)\frac{{x^{n\gamma + m} }}{\varGamma (n\gamma + m + 1)}} } } \right). $$

(43)

By Applying the method which found in Sect. 3, we can get unknown coefficients $w_{kh} (t),\,\,$ and $f_{kh} (x)$ where $k = 1,2,3, \ldots$ and $h = 0,1$ as follows:

$$ f_{10} (x) = 0,\,\,f_{20} (x) = 0,f_{30} (x) = 0, \ldots ,f_{k0} (x) = 0, $$

$$ f_{11} (x) = \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} x^{2k - \gamma + 2} }}{\varGamma (2k - \gamma + 3)}} , \quad f_{21} (x) = \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 2} x^{2k - 2\gamma + 4} }}{\varGamma (2k - 2\gamma + 5)}} , $$

$$ w_{10} (t) = \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} t^{2k - \beta + 3} }}{\varGamma (2k - \beta + 4)}} \,,\,\,\,w_{20} (t) = \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 2} t^{2k - 2\beta + 5} }}{\varGamma (2k - 2\beta + 6)}} , $$

$$ w_{11} (t) = 0,\,\,w_{21} (t) = 0,w_{31} (t) = 0, \ldots ,w_{k0} (t) = 0. $$

So, we have the new RPS solution of problem (39)–(41) as follows: 

$$ \begin{aligned} u(x,t) = & \frac{1}{2}\left( {\sin t + t\,\,\cos x} \right) \\ & \quad + \frac{1}{2}\left( {\sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} x^{2k - \gamma + 2} }}{\varGamma (2k - \gamma + 3)}} \frac{{t^{\,\beta + 1} }}{\varGamma (\beta + 2)} + \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 2} x^{2k - 2\gamma + 4} }}{\varGamma (2k - 2\gamma + 5)}} \frac{{t^{2\,\beta + 1} }}{\varGamma (2\beta + 2)} + \cdots } \right) \\ & \quad \frac{1}{2}\left( {\sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 1} t^{2k - \beta + 3} }}{\varGamma (2k - \beta + 4)}} \,\frac{{x^{\,\gamma } }}{\varGamma (\gamma + 1)} + \sum\limits_{k = 0}^{\infty } {\frac{{( - 1)^{k + 2} t^{2k - 2\beta + 5} }}{\varGamma (2k - 2\beta + 6)}} \frac{{x^{2\gamma } }}{\varGamma (2\,\gamma + 1)} + \cdots } \right). \\ \end{aligned} $$

we can rewrite the last solution in the form

$$ \begin{aligned} u(x,t) = & \frac{1}{2}\left( {t\,\,\cos x + \sin t} \right) + \frac{1}{2}\left( { - x^{2 - \gamma } E_{2,3 - \gamma } ( - x^{2} )\frac{{t^{\,\beta + 1} }}{\varGamma (\beta + 2)} + x^{4 - 2\gamma } E_{2,5 - 2\gamma } ( - x^{2} )\frac{{t^{2\,\beta + 1} }}{\varGamma (2\beta + 2)} + \cdots } \right) \\ & \quad + \frac{1}{2}\left( { - t^{3 - \beta } E_{2,4 - \beta } ( - t^{2} )\,\frac{{x^{\gamma } }}{\varGamma (\gamma + 1)} + t^{5 - 2\beta } E_{2,6 - 2\beta } ( - t^{2} )\,\frac{{x^{2\gamma } }}{\varGamma (2\,\gamma + 1)} + \cdots } \right). \\ \end{aligned} $$

(44)

In a closed form, we get the solution of problem (39)–(41) as

$$ \begin{aligned} u(x,t) = & \frac{1}{2}\left( {t\,\,\cos x + \sin t} \right) + \frac{1}{2}\left( {\sum\limits_{k = 1}^{\infty } {( - 1)^{k} } x^{k(2 - \gamma )} E_{2,k(2 - \gamma ) + 1} ( - x^{2} )\frac{{t^{k\beta + 1} }}{\varGamma (k\beta + 2)}} \right) \\ & \quad + \frac{1}{2}\sum\limits_{k = 1}^{\infty } {( - 1)^{k} } t^{k(2 - \beta ) + 1} E_{2,k(2 - \beta ) + 2} ( - t^{2} )\frac{{x^{k\gamma } }}{\varGamma (k\beta + 1)}. \\ \end{aligned} $$

As $\beta \to 2$ and $\gamma \to 2$, we have a classical exact solution in the form $u(x,t) = \cos x\,\sin t$.

Figure 5 provides an excellent approximation with the exact solution. Figures 6, 7, and 8 are the geometric behavior of the solutions. We can get a higher accuracy by getting more components (Table 3).

Fig. 5

a Exact solution (classical case) b The RPS solution $u_{31} \left( {x,t} \right)$ for Example 4.1 ($\beta = 2, \gamma = 2$

Fig. 6

The RPS solution $u_{31} \left( {x,t} \right)$ for Example 4.1a$\beta = 2, \gamma = 1.5$b$\beta = 2, \gamma = 1.75$

Fig. 7

The RPS solution $u_{31} \left( {x,t} \right)$ for Example 4.1a$\beta = 1.5, \gamma = 2$b$\beta = 1.75, \gamma = 2$

Fig. 8

The RPS solution $u_{31} \left( {x,t} \right)$ for Example 4.1a$\beta = 1.5, \gamma = 1.5$b$\beta = 1.75, \gamma = 1.75$

Table 3 The numerical values of the approximate solutions ${\text{u}}_{31}$ for Example 4.1

Conclusions

A new algorithm of RPS method successfully been used to give new approximate solutions for time–space fractional heat equation and time–space fractional wave equation. The fractional equations are solved by nonhomogeneous initial conditions without reducing fractional differential equations to time fractional or space fractional differential equations. The behavior of the solution seems to be extremely interesting. The natural frequency of the solutions varies with the change of fractional derivatives. Finally, it is noted that the new algorithm of RPS method is a very effective technique for solving time–space fractional problems.