Periodic Oscillation and Bifurcation Analysis of Pendulum with Spinning Support Using a Modified Continuous Piecewise Linearization Method

Abstract

The large-amplitude oscillation of a pendulum with spinning support was investigated using a modified continuous piecewise linearization method (CPLM). In contrast to previous studies, the present study investigated the response of the spinning support pendulum when the non-dimensional rotation parameter (${\Lambda}$) is greater than one. The analysis showed that the natural frequency increased monotonically with Λ, while the oscillation history produced a distinct qualitative change as ${\Lambda}$ increases from ${\Lambda} < 1$ to ${\Lambda} > 1$, confirming the presence of a bifurcation at ${\Lambda} = 1$. It was also observed that the response exhibits a bi-stable equilibrium and a double-well potential when ${\Lambda} > 1$. Finally, the modified CPLM solution was shown to produce a maximum error of less than 0.30% for ${\text{A}} \le 179^\circ$ and ${\Lambda} \le 1$, which is better than other published results. This shows the potential of the modified CPLM to obtain accurate periodic solutions of complex nonlinear systems.

Introduction

The simple pendulum is a well-known mechanical system with nonlinear response for oscillations beyond the small-angle regime. Therefore, the simple pendulum has been used to study many important nonlinear phenomena. An even more interesting mechanical system is the pendulum with spinning support. Practical applications of the pendulum with spinning support include vibration absorbers [1], fly-ball governors [1] and breaking symmetry in quantum mechanics [2]. The spinning support pendulum differs from the simple pendulum in the sense that its support has a constant rotational speed while the support of the simple pendulum is fixed. Hence, unlike the case of a simple pendulum, the nonlinear oscillations of the spinning support pendulum is parameter dependent; the parameter being the rotational speed of the support or its non-dimensional form.

Several studies have been conducted on the simple pendulum (e.g. Refs. [3,4,5,6,7] and many references cited therein) but only relatively few studies have been conducted on the spinning support pendulum [1, 2, 8,9,10,11]. A plausible explanation is because the restoring force of the spinning support pendulum has a more complex nonlinearity, which can be represented as $f\left( {\sin \varphi ,\sin 2\varphi } \right)$. At present, there are many approximate analytical schemes for estimating the periodic solution of nonlinear oscillators and they include: Lindstedt–Poincare method [12], Modified Lindstedt–Poincare method [11, 13], Homotopy perturbation method [10], Adomain decomposition method [11], Laplace-Adomain decomposition method [14], Homotopy analysis method [8], Harmonic balance method [12], Global residue harmonic balance method [15], Variational iteration method [11], Max–min approach [11], Amplitude–frequency formulation [11, 16], Energy balance method [11], Variational approach [11, 17], Hamiltonian approach [9,10,11], Differential transform method [10], Cubication method [18], Micken iteration method [1] and Continuous piecewise linearization method [19, 20]. In spite of the numerous approximate analytical schemes for the solution of nonlinear oscillators, only few investigations on the large-amplitude oscillations (i.e. $90^\circ < A < 180^\circ$) of the spinning support pendulum have been reported [1, 8]. In Liao and Chwang [8] second-order solutions were derived using the homotopy analysis method. The solution for the frequency–amplitude relation was derived in terms of Bessel functions, which makes the derivation of higher-order approximations complicated. In Lai et al. [1] a combination of Taylor and Chebyshev series was applied to transform the original nonlinear oscillator with trigonometric nonlinearity to an equivalent oscillator with cubic–quintic nonlinearity. The equivalent cubic-quintic oscillator was then solved by means of a modified Micken iteration method. The frequency–amplitude relation obtained for the second-order approximation is complex but produced slightly more accurate results than the second-order approximation of the homotopy analysis method in Liao and Chwang [8]. Other studies [9,10,11] on the spinning support pendulum focus on small- and moderate-amplitude oscillations.

Nayfeh and Mook [12] posed an exercise on the spinning support pendulum in which they suggested a qualitative investigation for cases where the non-dimensional rotation is less than, equal to and greater than unity. However, the exercise did not consider periodic solutions for cases where the non-dimensional rotation is equal to and greater than unity. Also, large-amplitude oscillations were not considered in this exercise. The existing studies [1, 8] on the large-amplitude oscillations of the spinning support pendulum only considered cases in which the non-dimensional rotation parameter is less than unity i.e. low-rotational speed of the support. Cases in which non-dimensional rotation parameter is greater than unity are important for design of high speed fly-ball governors and for analysis of breaking symmetry in quantum mechanics [2]. Hence, in the present study, frequency–amplitude solutions and oscillation histories for cases of large-amplitude oscillations where the non-dimensional rotation is less than, equal to and greater than unity were investigated using a modified CPLM algorithm [20]. The modified CPLM solution is much simpler than the other published approximate analytical solutions [1, 8] for the large-amplitude oscillations of the spinning support pendulum and it is shown to produce results that are accurate for all possible amplitudes.

Mathematical Description of Pendulum with Spinning Support

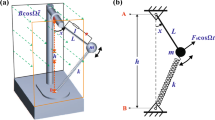
The pendulum with spinning support is depicted in Fig. 1. The system consists of a massless rod of length $l$ attached at one end to a ball of mass $m$ and at the other end to a vertical spinning support, which is spinning at a constant speed of ${\Omega}$ rad/s. The kinetic and potential energy of the system at any point are expressed as [9]:

Fig. 1

Diagrammatic illustration of the oscillation of a pendulum with spinning support

$$ T = \frac{1}{2}m\left( {l^{2} \dot{\varphi }^{2} + l^{2} {\Omega}^{2} \sin^{2} \varphi } \right) $$

(1a)

$$ V = mgl\left( {1 - \cos \varphi } \right) $$

(1b)

The system Lagrangian is obtained from Eqs. (1a, 1b) as:

$$ L = T - V = \frac{1}{2}m\left( {l^{2} \dot{\varphi }^{2} + l^{2} \Omega^{2} \sin^{2} \varphi } \right) - mgl\left( {1 - \cos \varphi } \right) $$

(2)

The equation governing the oscillation of the spinning support pendulum is then obtained from the Lagrange equation given as:

$$ \frac{d}{dt}\left( {\frac{\partial L}{{\partial \dot{\varphi }}}} \right) - \frac{\partial L}{\partial \varphi } = 0 $$

(3)

Substituting Eq. (2) in Eq. (3) and after simplification, we arrive at Eq. (4).

$$ \ddot{\varphi } + \omega_{0}^{2} \left( {1 - \varLambda \cos \varphi } \right)\sin \varphi = 0 $$

(4)

where $\omega_{0} = \sqrt {g/l}$, $g = 9.81\left[ {m/s^{2} } \right]$ and ${\Lambda} = \left( {{\Omega}/\omega_{0} } \right)^{2}$. The initial conditions are given as $\varphi \left( 0 \right) = A \epsilon \left[ {0^\circ ,180^\circ } \right]$ and $\dot{\varphi }\left( 0 \right) = 0$. Equation (4) also represents the oscillation of a simple pendulum subjected to a horizontal force that is proportional to the sine of its angular displacement [12]. Another oscillator governed by Eq. (4) is the frictionless motion of a small mass sliding up and down a circular ring that is rotating about its vertical axis with a constant spin [21]. It should be noted that for the special case when ${\Lambda} = 0$ the present system becomes a simple pendulum. In that case, an exact solution is possible in terms of the Jacobi elliptic cosine function and the exact time period can be expressed in terms of the complete elliptic integral of the first kind. However, no exact solution has been derived for the spinning support pendulum.

From Eq. (4), it is evident that the restoring force of the system is $f\left( \varphi \right) = \omega_{0}^{2} \left( {1 - {\Lambda}\cos \varphi } \right)\sin \varphi$. The compliance curve for the restoring force is shown in Fig. 2a for different values of ${\Lambda}$ and it can be seen that the restoring force is strongly dependent on ${\Lambda}$. Also illustrated in Fig. 2b is the restoring force per unit displacement given as $df/d\varphi = \omega_{0}^{2} \left[ {\cos \varphi + {\Lambda}\left( {1 - 2\cos^{2} \varphi } \right)} \right]$. Both plots suggest a more complex response when ${\Lambda} > 1$, and this may account for the lack of solutions for the case when ${\Lambda} > 1$. The present study is an attempt to bridge this gap using a simple analytical algorithm.

Fig. 2

Plot of a compliance and b restoring force per unit displacement for the spinning support pendulum; $- \,180^\circ \le \varphi \le 180^\circ$; $\omega_{0} = 1.0$

Modified Continuous Piecewise Linearization Method

The CPLM algorithm is an iterative analytical approach that can be used to derive periodic solutions of nonlinear conservative oscillators. It is based on a piecewise discretization and linearization approach that was first applied to solve nonlinear impact models [22,23,24]. It was first proposed by Big-Alabo [19] but the original formulation was limited to nonlinear oscillators in which the slope of the restoring force is always positive i.e. Duffing-type oscillators. The original formulation of the CPLM has been applied to investigate the relativistic oscillator [25] and to analyze the coupled nonlinear vibrations of a two-mass system [26]. The main advantage of the CPLM is its ability to combine simplicity with accuracy notwithstanding the complexity of the nonlinear restoring force of the conservative oscillator. In a recent study [20] on the large-amplitude oscillations of the simple pendulum, the CPLM algorithm was modified to handle nonlinear oscillators characterized by positive and negative slope restoring force. This modified CPLM has been applied in the present investigation of the spinning support pendulum and the basic idea is presented as follows.

Equation (4) can be expressed in standard form as:

$$ \ddot{\varphi } + f\left( \varphi \right) = 0 $$

(5)

where $f\left( \varphi \right) = \omega_{0}^{2} \left( {1 - {\Lambda}\cos \varphi } \right)\sin \varphi$. According to the CPLM algorithm [19], the linearized restoring force for each $n$ discretization of $f\left( \varphi \right)$ can be expressed as Eq. (6).

$$ F_{rs} \left( \varphi \right) = K_{rs} \left( {\varphi - \varphi_{r} } \right) + F_{r} $$

(6)

where $K_{rs} = \left[ {f\left( {\varphi_{s} } \right) - f\left( {\varphi_{r} } \right)} \right]/\left( {\varphi_{s} - \varphi_{r} } \right)$ and $F_{r} = f\left( {\varphi_{r} } \right)$. In reality, $K_{rs}$ represents the restoring force per unit displacement of the nonlinear oscillator. Also, $r = 0,1,2, \ldots , n - 1$ and $s = r + 1$ are the start and end states of each discretization respectively. Hence, using the expression for $f\left( \varphi \right)$ we get: $K_{rs} = \omega_{0}^{2} \left[ {\sin \varphi_{s} - \sin \varphi_{r} + 0.5{\Lambda}\left( {\sin 2\varphi_{r} - \sin 2\varphi_{s} } \right)} \right]/\left( {\varphi_{s} - \varphi_{r} } \right)$ and $F_{r} = \omega_{0}^{2} \left( {1 - {\Lambda}\cos \varphi_{r} } \right)\sin \varphi_{r}$.

Based on the original CPLM formulation [19], $K_{rs}$ must be positive always. However, as shown in Fig. 2, $K_{rs}$ can be positive or negative depending on the values of ${\Lambda}$ and ${\text{A}}$. Hence, Eq. (6) is expressed as [20]:

$$ F_{rs} \left( \varphi \right) = \pm \,\left| {K_{rs} } \right|\left( {\varphi - \varphi_{r} } \right) + F_{r} $$

(7)

Using Eqs. (7), the discretized linear ODE for Eq. (5) can be written as:

$$ \ddot{\varphi } \pm \left| {K_{rs} } \right|\varphi = \pm \,\left| {K_{rs} } \right|\varphi_{r} - F_{r} $$

(8)

The solution to Eq. (8) depends on whether the sign is positive or negative. This modification generalizes the original CPLM algorithm so that it can solve a wider range of nonlinear vibration models. However, it is important to note that the CPLM, as a closed-form analytical algorithm, is limited to the solution of conservative oscillators.

Solution for Positive Linearized Stiffness

The solution for positive linearized stiffness ($K_{rs} > 0$) has been derived previously [19] and only the final solutions are presented here. When $K_{rs} > 0$ the solution for the displacement and velocity can be expressed as:

$$ \varphi \left( t \right) = R_{rs} \sin \left( {\omega_{rs} t + \varphi_{rs} } \right) + C_{rs} $$

(9a)

$$ \dot{\varphi }\left( t \right) = \omega_{rs} R_{rs} \cos \left( {\omega_{rs} t + {\varphi}_{rs} } \right) $$

(9b)

where $\omega_{rs} = \sqrt {K_{rs} }$, $C_{rs} = \varphi_{r} - F_{r} /K_{rs}$ and $R_{rs} = \left[ {\left( {\varphi_{r} - C_{rs} } \right)^{2} + \left( {\dot{\varphi }_{r} /\omega_{rs} } \right)^{2} } \right]^{1/2}$. The initial conditions and other parameters are determined based on the oscillation stage. For the oscillation stage when $\dot{\varphi } < 0$ the initial conditions for each discretization are $\varphi_{r} = \varphi_{r} \left( 0 \right) = A - r\Delta \varphi$ and

$$ \dot{\varphi }_{r} = \dot{\varphi }_{r} \left( 0 \right) = - \,\sqrt {\left| {2\mathop \smallint \limits_{A}^{{\varphi_{r} }} - f\left( \varphi \right)d\varphi } \right|} = - \,\omega_{0} \left( {\sqrt {{\Lambda}\sin^{2} \varphi_{r} + 2\cos \varphi_{r} } - \sqrt {{\Lambda}\sin^{2} A + 2\cos A} } \right); $$

where $\Delta \varphi = A/n$ and the other parameters are calculated as:

$$ \begin{aligned} & {\varphi}_{rs} = \left\{ {\begin{array}{*{20}l} {0.5\pi } \hfill & \quad\quad\qquad\qquad\,\,{\dot{\varphi }_{r} = 0} \hfill \\ {\pi\,+\,\tan^{ - 1} \left[ {\omega_{rs} \left( {\varphi_{r} - C_{rs} } \right)/\dot{\varphi }_{r} } \right]} \hfill & \quad\quad\qquad\qquad\,\,{\dot{\varphi }_{r} < 0} \hfill \\ \end{array} } \right. \\ & \Delta t = \left\{ {\begin{array}{*{20}l} {\left( {0.5\pi - {\varphi}_{rs} } \right)/\omega_{rs} } \hfill & {\left( {\varphi_{s} - C_{rs} } \right) \ge R_{rs} } \hfill \\ {\left( {0.5\pi + \cos^{ - 1} \left[ {\left( {\varphi_{s} - C_{rs} } \right)/R_{rs} } \right] - {\varphi}_{rs} } \right)/\omega_{rs} } \hfill & {\left( {\varphi_{s} - C_{rs} } \right) < R_{rs} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$

For the oscillation stage when $\dot{\varphi } > 0$ the initial conditions are $\varphi_{r} = \varphi_{r} \left( 0 \right) = - A + r\Delta \varphi$ and $\dot{\varphi }_{r} = \dot{\varphi }_{r} \left( 0 \right) = \sqrt {\left| {2\mathop \smallint \limits_{A}^{{\varphi_{r} }} - f\left( \varphi \right)d\varphi } \right|} = \omega_{0} \left( {\sqrt {{\Lambda}\sin^{2} \varphi_{r} + 2\cos \varphi_{r} } - \sqrt {{\Lambda}\sin^{2} A + 2\cos A} } \right)$ and the other parameters are calculated as:

$$ \begin{aligned} & {\varphi}_{rs} = \left\{ {\begin{array}{*{20}l} { - \,0.5\pi } \hfill &\quad\quad\qquad\qquad\,\, {\dot{\varphi }_{r} = 0} \hfill \\ {\tan^{ - 1} \left[ {\omega_{rs} \left( {\varphi_{r} - C_{rs} } \right)/\dot{\varphi }_{r} } \right]} \hfill &\quad\quad\qquad\qquad\,\, {\dot{\varphi }_{r} < 0} \hfill \\ \end{array} } \right. \\ & \Delta t = \left\{ {\begin{array}{*{20}l} {\left( {0.5\pi - {\varphi}_{rs} } \right)/\omega_{rs} } \hfill & {\left( {\varphi_{s} - C_{rs} } \right) \ge R_{rs} } \hfill \\ {\left( {0.5\pi - \cos^{ - 1} \left[ {\left( {\varphi_{s} - C_{rs} } \right)/R_{rs} } \right] - {\varphi}_{rs} } \right)/\omega_{rs} } \hfill & {\left( {\varphi_{s} - C_{rs} } \right) < R_{rs} } \hfill \\ \end{array} } \right. \\ \end{aligned} $$

Hence, the time at the end of each discretization is $t_{s} = t_{r} + \Delta t$ and the end conditions $\varphi_{s}$ and $\dot{\varphi }_{s}$ are calculated by replacing $r$ with $s$ in the formulae for initial conditions.

Solution for Negative Linearized Stiffness

When $K_{rs} < 0$ the solution for the displacement and velocity can be expressed in terms of exponential functions as follows [20]:

$$ \varphi \left( t \right) = A_{rs} e^{{\omega_{rs} t}} + B_{rs} e^{{ - \omega_{rs} t}} + C_{rs} $$

(10a)

$$ \dot{\varphi }\left( t \right) = \omega_{rs} \left( {A_{rs} e^{{\omega_{rs} t}} - B_{rs} e^{{ - \omega_{rs} t}} } \right) $$

(10b)

where $\omega_{rs} = \sqrt {\left| {K_{rs} } \right|}$; $C_{rs} = \varphi_{r} + F_{r} /\left| {K_{rs} } \right|$. Applying the initial conditions, $A_{rs}$ and $B_{rs}$ are derived from Eqs. (10a, 10b) as: $A_{rs} = \frac{1}{2}\left( {\varphi_{r} + \dot{\varphi }_{r} /\omega_{rs} - C_{rs} } \right)$ and $B_{rs} = \frac{1}{2}\left( {\varphi_{r} - \dot{\varphi }_{r} /\omega_{rs} - C_{rs} } \right)$. The initial and end conditions are determined in the same way as for $K_{rs} > 0$ above. After applying the end condition in Eq. (10a) the time interval for each discretization was derived as:

$$ \Delta t = \left\{ {\begin{array}{*{20}l} {\frac{1}{{\omega_{rs} }}\log_{e} \left[ {\frac{{\left( {\varphi_{s} - C_{rs} } \right) \pm \sqrt {\left( {\varphi_{s} - C_{rs} } \right)^{2} - 4A_{rs} B_{rs} } }}{{2A_{rs} }} } \right]} \hfill & { \left( {\varphi_{s} - C_{rs} } \right) > 2\sqrt {A_{rs} B_{rs} } } \hfill \\ {\frac{1}{{\omega_{rs} }}\log_{e} \left( {\frac{{\varphi_{s} - C_{rs} }}{{2A_{rs} }} } \right) } \hfill & {\left( {\varphi_{s} - C_{rs} } \right) \le 2\sqrt {A_{rs} B_{rs} } } \hfill \\ \end{array} } \right. $$

(11)

Hence, the time at the end condition is calculated as $t_{s} = t_{r} + \Delta t$. In Eq. (11) above, the sign before the square root is positive for the oscillation stage when $\dot{\varphi } > 0$ and vice versa. Note that if $\dot{\varphi }_{r} = 0$, then $A_{rs} = B_{rs} = \frac{1}{2}\left( {\varphi_{r} - C_{rs} } \right)$ and the displacement can be expressed as Eq. (12).

$$ \varphi \left( t \right) = \left( {\varphi_{r} - C_{rs} } \right)\cosh \left( {\omega_{rs} t} \right) + C_{rs} $$

(12)

Therefore,

$$ \Delta t = \frac{1}{{\omega_{rs} }}{ \cosh }^{ - 1} \left( {\frac{{\varphi_{s} - C_{rs} }}{{\varphi_{r} - C_{rs} }}} \right) $$

(13)

Solution for Zero Linearized Stiffness

The linearized stiffness for each discretization is normally positive or negative, but in rear situations, one or two discretization around the critical point(s) of the compliance curve may have an approximately zero stiffness. A discretization with zero stiffness is probable when the interval of each discretization is very small i.e. for very large $n$. The zero stiffness discretization can be eliminated by increasing or decreasing $n$. However, if we want to account for $K_{rs} = 0$ in the modified CPLM algorithm, then from Eq. (8) we get:

$$ \ddot{\varphi } = - F_{r} $$

(14)

The solution to Eq. (14) is:

$$ \varphi \left( t \right) = H_{rs} + G_{rs} t - \frac{1}{2}F_{r} t^{2} $$

(15)

where $G_{rs} = \dot{\varphi }_{r} + F_{r} t_{r}$ and $H_{rs} = \varphi_{r} - \dot{\varphi }_{r} t_{r} - \frac{1}{2}F_{r} t_{r}^{2}$ are integration constants determined from the initial conditions. Hence, the time interval is derived from Eq. (15) as:

$$ \Delta t = \frac{{G_{rs} + \sqrt {G_{rs}^{2} + 2F_{r} \left( {H_{rs} - \varphi_{s} } \right)} }}{{F_{r} }} $$

(16)

Results and Discussions

Estimating the Natural Frequency

To verify the accuracy of the modified CPLM solution for the spinning support pendulum a comparison of natural frequency estimates for ${\Lambda} < 1$ and $0^\circ < A < 180^\circ$ was carried out as shown in Tables 1, 2 and 3. For all simulations $\omega_{0} = 1.0$ was assumed. Since the focus of the present study is on large-amplitude oscillations, frequency estimates for small- to moderate-amplitude oscillations are only provided for ${\Lambda} = 0.1$ (see Table 1) to demonstrate that the present method is applicable to the entire range of possible amplitudes i.e. $0^\circ < A < 180^\circ$. For ${\Lambda} = 0.5$ and ${\Lambda} = 0.9$ results are presented for amplitudes in the range of $90^\circ < A < 180^\circ$. Tables 1, 2 and 3 compare results of ‘exact’ numerical solution, the second-order approximation of Lai et al. [1] and the present method ($n = 100$). The numerical results used are those reported in Ref. [1] except for amplitudes greater than $170^\circ$ for which results were not reported. For all other numerical results, the NDSolve function in Mathematica was used to integrate Eq. (4) numerically. The absolute error in the numerical results obtained using the NDSolve function is in the order of $10^{ - 8}$.

Table 1 Comparison of frequency estimates for ${\Lambda} = 0.1$

Table 2 Comparison of frequency estimates for ${\Lambda} = 0.5$

Table 3 Comparison of frequency estimates for ${\Lambda} = 0.9$

Tables 1, 2 and 3 show that the maximum errors of the present method for amplitudes up to 170° are 0.0751%, 0.0903% and 0.0961% for ${\Lambda} = 0.1$, ${\Lambda} = 0.5$ and ${\Lambda} = 0.9$ respectively. The corresponding maximum errors of the second-order approximation of Lai et al. [1] are 1.4270%, 0.788% and 0.9384% respectively. The error in the method of Lai et al. [1] increases gradually at first and then rapidly for $A \ge 150^\circ$. In contrast, the error in the present method increases gradually with amplitude up to $180^\circ$. Hence, the error in the present method is significantly smaller than the error in the method of Lai et al. [1] for $150^\circ \le A < 180^\circ$. Notwithstanding, the above comparison shows that the method of Lai et al. [1] and the present method are both sufficiently accurate for the response of the spinning support pendulum when ${\Lambda} < 1$ and $0^\circ < A < 180^\circ$. Yet the present method is much simpler than the method of Lai et al. [1] and does not require higher order approximations. Furthermore, the present method can give accurate predictions of the response of the spinning support pendulum for ${\Lambda} > 1$; an investigation that seems not to have been given proper attention in the archived literature.

Figure 3 is a plot of the time period against the non-dimensional rotation parameter for three different cases of large-amplitude oscillations: $A = 170^\circ$, $175^\circ$ and $179^\circ$. The time period estimates of the present method agrees with exact numerical solutions, confirming that the present method works extremely well even when ${\Lambda} \ge 1$. Figure 3 shows that the time period decreases with increase in ${\Lambda}$ for each of the amplitudes considered. It was also observed that the trend in the time period remains the same for ${\Lambda} < 1$ and ${\Lambda} \ge 1$. The implication is that the rotation of the support to which the pendulum is attached causes an increase in the frequency of the pendulum as the rotational speed increases, but there is no observed qualitative change in the frequency-rotational speed relationship as the rotational speed increases from low (${\Lambda} < 1$) to high (${\Lambda} > 1$) speed.

Fig. 3

Dependence of time period on non-dimensional rotation parameter. Solid line—present method, markers—numerical solution

Estimating the Oscillation Plots

Further investigation was conducted to determine the displacement and velocity profiles during large-amplitude oscillations. Plots generated based on the present method were compared with exact numerical solutions as shown in Figs. 4, 5, 6 and 7. The blue colour represents the displacement profile while the green colour represents the velocity profile.

Fig. 4

Displacement and velocity profile for ${\Lambda} = 0.50$ and ${\text{A}} = 170^\circ$

Fig. 5

Displacement and velocity profile for ${\Lambda} = 1.0$ and ${\text{A}} = 170^\circ$

Fig. 6

Displacement and velocity profile for ${\Lambda} = 1.5$ and ${\text{A}} = 170^\circ$

Fig. 7

Displacement and velocity profile for ${\Lambda} = 10.0$ and ${\text{A}} = 170^\circ$

Figures 4, 5, 6 and 7 show that the large-amplitude oscillation of the spinning support pendulum exhibits an-harmonic response. The latter is further amplified by an increase in the rotational speed. When ${\Lambda} < 1$ (low rotational speed), the velocity profile has a single turning point in each half-cycle (see Fig. 4). For ${\Lambda} = 1$, a single turning point was also observed although a relatively constant velocity occurred around the turning point (see Fig. 5). The relatively constant velocity is due to the inflexion of the compliance response around the origin as shown in Fig. 2a. Physically, this behaviour implies that the pendulum approaches and returns from the amplitude without a significant change in its velocity. When ${\Lambda} > 1$ (high rotational speed), the velocity profile shows three turning points in each half-cycle consisting of two maximum points and one minimum point (see Figs. 6, 7). A local minimum velocity was observed at $\varphi = 0^\circ$ and this observed response seemed to be counter-intuitive at first glance because it is contrary to the general belief that the velocity of a conservative system reaches its maximum when its displacement is zero. An examination of the compliance response in Fig. 2a showed that the compliance exhibits an oscillation around the origin when ${\Lambda} > 1$. The oscillation in the compliance response is responsible for the observed behaviour in the velocity profile.

Bifurcation Analysis of the Large-Amplitude Response of the Spinning Support Pendulum

To investigate further the qualitative change observed in the oscillation profile as the rotational speed increases from ${\Lambda} < 1$ to ${\Lambda} > 1$, a phase diagram was plotted as shown in Fig. 8. The phase plots show how the velocity flattens across the $\varphi = 0$ line when ${\Lambda} = 1$, and afterwards exhibits an oscillation across the $\varphi = 0$ line when ${\Lambda} > 1$. From Eq. (1b), the potential energy is zero when $\varphi = 0^\circ$. The corresponding kinetic energy obtained from Eq. (1a) is $T = \frac{1}{2}ml^{2} \dot{\varphi }_{lmin}^{2}$, where $\dot{\varphi }_{lmin}$ is the local minimum velocity. At the maximum velocity ($\dot{\varphi }_{max}$), the kinetic energy is also maximum and given as $T_{max} = \frac{1}{2}m\left( {l^{2} \dot{\varphi }_{max}^{2} + l^{2} {\Omega}^{2} \sin^{2} \varphi } \right)$ where $\left| {\dot{\varphi }_{max} } \right| > \left| {\dot{\varphi }_{lmin} } \right|$ and $\sin^{2} \varphi > 0$. This analysis agrees with the observations in Figs. 6 and 7.

Fig. 8

Phase diagram as a function of non-dimensional rotation parameter when ${\text{A}} = 170^\circ$

For ${\Lambda} < 1$, Fig. 2a shows that $f\left( \varphi \right) = 0$ has only one solution in the range $- \,180^\circ < \varphi < 180^\circ$, which is $\varphi = 0$. This critical point has a stable equilibrium (i.e. it is a center) because $df/d\varphi > 0$ as shown in Fig. 2b. Also, the phase plot in Fig. 8 shows the single center when ${\Lambda} \le 1$ and $A = 170^\circ$. For ${\Lambda} > 1$, Fig. 2a shows that there are three critical points in the range $- \,180^\circ < \varphi < 180$. For instance, when ${\Lambda} = 2.0$ the critical points are: $\varphi = 0^\circ$, $- \,60^\circ$ and $+ \,60^\circ$. From Fig. 2b, $df/d\varphi < 0$, $> 0$ and $> 0$ respectively for the critical points. This means that an unstable equilibrium (i.e. saddle point) exists at $\varphi = 0^\circ$ and two centers occur at $\varphi = - \,60^\circ$ and $+ \,60^\circ$. The maximum kinetic energy occurs at the centers and the potential energy is minimum at these points but not necessarily equal to zero as explained above. Hence, a qualitative change is observed in the behaviour of the spinning support pendulum as the rotational speed increases from ${\Lambda} < 1$ to ${\Lambda} > 1$, and this confirms the existence of a bifurcation at ${\Lambda} = 1$.

The phase plot when ${\Lambda} > 1$ is typical of a bi-stable Duffing oscillator [27], which is characterized by a double-well potential. Therefore, we consider the potential function (i.e. $E\left( \varphi \right) = \smallint f\left( \varphi \right)d\varphi = - \omega_{0}^{2} \left[ {\cos \varphi + \left( {{\Lambda}/2} \right)\sin^{2} \varphi } \right]$) plot as shown in Fig. 9. When ${\Lambda} \le 1$, the potential function has a minimum value at $\varphi = 0^\circ$, but when ${\Lambda} > 1$, the potential function exhibits a double-well potential with a local maximum potential at $\varphi = 0^\circ$ and the minimum potential occurring when $\left| \varphi \right| > 0^\circ$. The double-well potential behaviour is well known in nonlinear oscillators with negative linear stiffness [17, 19], but Fig. 9 shows that the spinning support pendulum exhibits a double-well potential when ${\Lambda} > 1$. This qualitative change in the potential response of the system from ${\Lambda} < 1$ to ${\Lambda} > 1$ is due to bifurcation of the system at ${\Lambda} = 1$.

Fig. 9

Dependence of potential function on the non-dimensional rotation parameter

Conclusions

The large-amplitude oscillation of the pendulum with spinning support was investigated using the modified CPLM algorithm. A comparison of time period estimates obtained using the modified CPLM with exact numerical results showed that the error in the modified CPLM is negligible. Typically, the maximum relative error was found to be less that 0.3% for amplitudes up to 179° when the rotational speed is low (${\Lambda} < 1$). Since the spinning support pendulum is a parameter dependent system, investigations were conducted to unravel the effect of the dimensionless rotation parameter (${\Lambda}$) on the oscillation response of the pendulum. It was observed that the time period of oscillation varied inversely with ${\Lambda}$. The implication is that increasing the speed of rotation of the support leads to an increase in the oscillation frequency of the pendulum.

Investigations on the displacement and velocity profiles focussed on large-amplitude oscillations where ${\Lambda} > 1$. Such cases represent a scenario where the rotational speed of the support is greater than $\omega_{0} = \sqrt {g/l}$ and is therefore considered to be high. The results obtained showed a qualitative change in the oscillation response for ${\Lambda} > 1$ compared to the case of ${\Lambda} \le 1$. Therefore, a qualitative analysis was conducted and the presence of a bifurcation at ${\Lambda} = 1.0$ was established. The bifurcation accounts for the observed qualitative change in the oscillation profile as the rotational parameter increases from ${\Lambda} < 1$ to ${\Lambda} > 1$. Additionally, the qualitative analysis showed that the response of the spinning support pendulum for ${\Lambda} > 1$ is characterized by a bi-stable equilibrium which creates a double-well potential in the potential response.

The present study also shows the prospects of the modified CPLM in obtaining accurate periodic solution for nonlinear conservative oscillators and its ability to capture essential an-harmonic response in the oscillation plot. Given the simplicity and accuracy of the modified CPLM, it is recommended to both students and experts in the field of nonlinear dynamics.

Appendix

Pseudocode Algorithm for Modified CPLM Solution for Pendulum with Spinning Support

The pseudocode algorithm above is for the negative velocity oscillation stage (i.e. $\dot{\varphi } < 0$) when the pendulum swings from $+ \,A$ to $- \,A$. This stage constitutes the first half-cycle of the oscillation. For the remaining half-cycle when the pendulum swings from $- \,A$ back to $+ \,A$ a similar algorithm is applicable and the necessary changes can be made by referring to “Modified Continuous Piecewise Linearization Method” section.