Exact Solution of the Weak Shock Wave in Non-ideal Gas

Abstract

In the present paper the exact solution of quasilinear hyperbolic system of equations governing the propagation of weak shock waves in a one dimensional non-ideal adiabatic gas flow with generalized geometries is derived. Here the density ahead of the shock front is assumed to vary according to a power law of the distance. The effect of van der Waals parameter on the radius of weak shock wave is analyzed. An analytical expression for the total energy carried by weak shock wave in non-ideal gas is also derived.

Indroduction

Ideal gas is considered under the assumption that the volume occupied by the gas molecules and the forces between the constituent molecules are negligible but real gases do not follow these assumptions. van der Waals derived the equation of state as: $\left( p+a\varrho ^{2}\right) \left( 1-b\varrho \right) =\varrho RT$, for real gases, where p, $\varrho$ stands for the pressure and density of the gas, T is the absolute temperature, R is the universal gas constant and a and b are the material dependent characteristic parameters. The constants a and b respectively measure the attraction between the gas molecules and volume occupied by each molecule. The van der Waals model is very near to the behavior of real gases for wide range of temperature and pressure. In case of compressible flows, the pressure of gas is taken to be very high consequently the term $a\varrho ^{2}$ may be negligible as compared to the gas pressure p, this results in equation of state for non-ideal gas as $p\left( 1-b\varrho \right) =\varrho RT$. It is noticed that non-ideal gas possesses more general thermodynamic properties than ideal gas, so dealing the system of equations governing the propagation of weak waves supplemented with equation of state $p\left( 1-b\varrho \right) =\varrho RT$, is more complex and applicable than the ordinary gasdynamics case.

The study of nonlinear hyperbolic system of partial differential equations governing the propagation of weak shock waves in real situations has always been an interesting research field due to its important applications. In treatment for kidney stone disease, weak converging shock waves are focused on the stone to break it into enough small pieces that can be eliminated naturally. It is also used in orthopedics and cancer treatment. When high speed train enters into a long train tunnel then weak shock waves are formed in front of it. Due to various important applications of weak shock waves in real situations, a continuous improvement in the subject is desirable. In past decades, many attempts have been made to study the propagation of weak and strong shock waves in different material media. The major break-through in the study of shock wave was made by Courant and Friedrichs [1] and Whitham [2]. They have analyzed the problem of propagation of weak and strong shock waves in ordinary gas dynamics. Sharma and Shyam [3] have studied the growth and decay of weak discontinuities in radiating gas dynamics. Anile [4] proposed the generalized wave front expansion method for the solution of the problem of weak shock waves and the results obtained were in close agreement to many experimental results. Murata [5] has presented a closed form solution of the blast wave problem for ordinary gasdynamics case. Singh et al. [6] gave the exact solution of planar and non planar weak shock wave problem in gas dynamics with generalized geometries. Bira and Sekhar [7] obtained the exact solution of the problem of weak shock wave in isentropic magnetogasdynamics using the method of Lie group transformation. Chadha and Jena [8] discussed the steepening of shock wave in dusty gas. Arora and Siddiqui [9] investigated the behavior of weak shocks in a non-ideal gas. Vishwakarma and Nath [10] have used the similarity method to discuss the propagation of shock wave in non-ideal dusty gas. Wu and Roberts [11] discussed the problem of structure and stability of a spherical shock wave in van der Waals gas. Some authors [12, 13] obtained the solution of weak shock wave in different material media by using the Lie group of transformations. Arora et. al [14] investigated the behaviour of strong shock wave in non - ideal gas using similarity transformation technique. Siddiqui and Arora [15] used similarity transformation to obtain the exact solution of spherical shock wave problem in relaxing gas. Recently Bira et al. [16], Kuila and Sekhar [17] and Ambika and Radha [18] have studied the propagation of shock wave and elementary wave interaction in different material media. To find the closed form solution for the problem associated to the propagation of weak shock wave in non-ideal gas is a challenging problem for researchers and scientist today. In the present paper, an attempt has been made to obtain the exact solution of the problem of propagation of weak shock wave and an analytical expression for the density, velocity and pressure are obtained in terms of position and time. The energy carried by weak shock wave in non-ideal gas is also derived.

Basic Equations and Jump Conditions

The governing equations describing an unsteady inviscid adiabatic one dimensional flow in non-ideal gas with generalized geometries is given by Singh et al. [6] as

$$\begin{aligned} \frac{\partial \varrho }{\partial t}+\vartheta \frac{\partial \varrho }{\partial x}+\varrho \left( \frac{\partial \vartheta }{\partial x}+\frac{j}{x}\vartheta \right)= & {} 0, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \vartheta }{\partial t}+\vartheta \frac{\partial \vartheta }{\partial x}+\frac{1}{\varrho }\frac{\partial p}{\partial x}= & {} 0, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial p}{\partial t}+\vartheta \frac{\partial p}{\partial x}+a^{2}\varrho \left( \frac{\partial \vartheta }{\partial x}+\frac{j}{x}\vartheta \right)= & {} 0, \end{aligned}$$

(3)

where $\varrho$, $\vartheta$ and p are density, flow velocity and pressure of the non-ideal gas respectively and t, x stand for time and spatial coordinates respectively. The entity $a=\left( \gamma p/\left( \varrho \left( 1-b\varrho \right) \right) \right) ^{1/2}$ is the equilibrium speed of sound in non-ideal gas. $j=0$ , 1 and 2 respectively correspond to the planar, cylindrically symmetric and spherically symmetric flows. The entity $\gamma =c_{p}/c_{\upsilon }$ is the ratio of specific heat at constant pressure and specific heat of gas at constant volume.

Let R be the position of the shock front from the centre of disturbance at time t, then the propagation velocity of shock front, s, is given by

$$\begin{aligned} s=\frac{dR}{dt}. \end{aligned}$$

(4)

If $\varrho _{0}$ denotes undisturbed gas density and $\varrho$, $\vartheta$ and p denote the density, velocity and pressure of non-ideal gas just behind the shock respectively. Then the following Rankine-Hugoniot conditions [5, 6] across the shock front are satisfied.

$$\begin{aligned} \varrho= & {} \frac{\gamma +1}{\gamma -1}\left[ 1+\frac{2b\varrho _{0}}{\gamma -1}+\frac{2\left( 1-b\varrho _{0}\right) }{\gamma -1}\frac{1}{M^{2}}\right] ^{-1}\varrho _{0}, \end{aligned}$$

(5)

$$\begin{aligned} \vartheta= & {} \frac{2}{\gamma +1}\left[ 1-b\varrho _{0}-\frac{\left( 1-b\varrho _{0}\right) }{M^{2}}\right] s, \end{aligned}$$

(6)

$$\begin{aligned} p= & {} \frac{2\left( 1-b\varrho _{0}\right) }{\gamma +1}\left[ 1-\frac{\left( \gamma -1\right) }{2\gamma }\frac{1}{M^{2}}\right] \varrho _{0}s^{2}, \end{aligned}$$

(7)

where $M=\frac{s}{a}$, called mach number.

In the present problem, the undisturbed density $\varrho _{0}$ is taken to vary according to the power law of the radius of the shock front R after the disturbance and is given as

$$\begin{aligned} \varrho _{0}=\varrho _{a}R^{\kappa }, \end{aligned}$$

(8)

where $\varrho _{a}$ and $\kappa$ are constants. The constant $\kappa$ is to be determined later.

Exact Solution of the Weak Shock Wave problem

The expression for the pressure behind the shock front satisfying the RH conditions (5)–(7) is given as

$$\begin{aligned} p=\frac{\left( 1-b\varrho _{0}\right) \left[ M^{2}-\left( \gamma -1\right) /\left( 2\gamma \right) \right] \left[ M^{2}\left( \gamma -1\right) /2+b\varrho _{0}\left( M^{2}-1\right) +1\right] }{\left[ M^{2}-b\varrho _{0}M^{2}-\left( 1-b\varrho _{0}\right) \right] ^{2}}\varrho u^{2}. \end{aligned}$$

(9)

By Eq. (9), Eqs. (2) and (3), can we written as

$$\begin{aligned} \frac{\partial \vartheta }{\partial t}+\vartheta \frac{\partial \vartheta }{\partial x}+K_{1}\left( \frac{\vartheta ^{2}}{\varrho }\frac{\partial \varrho }{\partial x}+2\vartheta \frac{\partial \vartheta }{\partial x}\right)= & {} 0, \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial \vartheta }{\partial t}+\vartheta \frac{\partial \vartheta }{\partial x}+K_{2}\left( \frac{\partial \vartheta }{\partial x}+\frac{j}{x}\vartheta \right) \vartheta= & {} 0, \end{aligned}$$

(11)

where $K_{1}$ and $K_{2}$ are given as

$$\begin{aligned} K_{1}= & {} \frac{\left( 1-b\varrho _{0}\right) \left[ M^{2}-\left( \gamma -1\right) /\left( 2\gamma \right) \right] \left[ M^{2}\left( \gamma -1\right) /2+b\varrho _{0}\left( M^{2}-1\right) +1\right] }{\left[ M^{2}-b\varrho _{0}M^{2}-\left( 1-b\varrho _{0}\right) \right] ^{2}}, \end{aligned}$$

(12)

$$\begin{aligned} K_{2}= & {} \frac{\left( \gamma -1\right) \left[ \left( \gamma -1\right) M^{2}+2\right] +b\varrho _{0}\left[ \left( 3\gamma -1\right) M^{2}-2\left( \gamma -1\right) \right] }{2\left[ \left( \gamma -1\right) M^{2}+2-b\varrho _{0}\left( \left( \gamma -1\right) M^{2}+2\right) \right] }. \end{aligned}$$

(13)

Combining (10) and (11) and after integration we have the resulting equation as,

$$\begin{aligned} f\left( t\right) =\varrho \vartheta ^{\psi }x^{-j\chi }, \end{aligned}$$

(14)

where $f\left( t\right)$ is function of time only and $\psi$ and $\chi$ are given as

$$\begin{aligned} \psi= & {} \left( 2K_{1}-K_{2}\right) /K_{1}, \end{aligned}$$

(15)

$$\begin{aligned} \chi= & {} K_{2}/K_{1}. \end{aligned}$$

(16)

By Eqs. (12) and (1), we have

$$\begin{aligned} \frac{\psi }{\vartheta }\frac{\partial \vartheta }{\partial t}-\left( 1-\psi \right) \frac{\partial \vartheta }{\partial x}-\frac{j\left( \chi +1\right) }{x}\vartheta -\frac{1}{f}\frac{df}{dt}=0. \end{aligned}$$

(17)

Solving Eqs. (11) and (13), we have

$$\begin{aligned} \vartheta =-\eta \frac{x}{f}\frac{df}{dt}, \end{aligned}$$

(18)

where $\eta$ is a constant given as

$$\begin{aligned} \eta =\frac{1}{\left( \psi K_{2}+\chi +1\right) j+\left( 1+\psi K_{2}\right) }, \end{aligned}$$

(19)

also

$$\begin{aligned} f\left( t\right) =f_{0}t^{-\tau }, \end{aligned}$$

(20)

where $f_{0}$ is arbitarary constant and $\tau$ is given as

$$\begin{aligned} \tau =\frac{\psi }{\left( \psi -1\right) \eta -j\left( \chi +1\right) \eta +1}. \end{aligned}$$

(21)

Rankine–Hugoniot condition (6) yields the radius of the shock front given as

$$\begin{aligned} R=t^{\frac{\gamma +1}{2\left( 1-2b\varrho _{0}-\frac{\left( 1-b\varrho _{0}\right) }{M^{2}}\right) }\eta \tau }. \end{aligned}$$

(22)

Rankine–Hugoniot condition (5) yields the following value of $\kappa$ which is given as

$$\begin{aligned} \kappa =\frac{2\left( j+1\right) \left( \left( 1-b\varrho _{0}\right) /M^{2}+b\varrho _{0}-1\right) }{\gamma +1}. \end{aligned}$$

(23)

The effect of van der Waals parameter on the radius of weak shock wave is shown in Figs. 1, 2 and 3. The effect of van der Waals parameter of the gas on the radius of the weak shock wave in planar, cylindrically symmetric and spherically symmetric flows is shown in Figs. 1, 2 and 3 respectively. The values of the constants appearing in the computations are taken as: $\varrho _{0}=3.0$ and $\gamma =1.4$, $M=1.02$, 1.04, 1.06 and $b=0.0$, 0.02, 0.04. Here, $b=0.0$ corresponds to the ordinary gas dynamics case. It is observed that an increase in the value of van der Waals excluded volume and Mach number causes to increase the radius of the weak shock wave.

Fig. 1

Behavior of radius of weak shock wave for $j = 0$

Fig. 2

Behavior of radius of weak shock wave for $j= 1$

Fig. 3

Behavior of radius of weak shock wave for $j = 2$

The solution of weak shock wave problem in non-ideal gas is given by

$$\begin{aligned} \varrho= & {} \frac{f_{0}t^{-\tau +\psi }x^{j\chi -\psi }}{\chi ^{\psi }\tau ^{\psi }}, \end{aligned}$$

(24)

$$\begin{aligned} \vartheta= & {} \eta \tau \frac{x}{t}, \end{aligned}$$

(25)

$$\begin{aligned} p= & {} \frac{\left( 1-b\varrho _{0}\right) \left[ M^{2}-\left( \gamma -1\right) /\left( 2\gamma \right) \right] \left[ M^{2}\left( \gamma -1\right) /2+b\varrho _{0}\left( M^{2}-1\right) +1\right] }{\left[ M^{2}-b\varrho _{0}M^{2}-\left( 1-b\varrho _{0}\right) \right] ^{2}}\nonumber \\&\times \frac{1}{\left( \eta \tau \right) ^{\psi -2}}f_{0}x^{\left( j\chi -\psi +2\right) }t^{\left( \chi -\tau -2\right) }. \end{aligned}$$

(26)

Fig. 4

Density profile of weak shock wave for $j= 2$

Fig. 5

Velocity profile of weak shock wave for $j= 2$

Fig. 6

Pressure profile of weak shock wave for $j= 2$

Distribution of flow parameters, density, velocity and pressure in non-ideal gas are presented in the Figs. 4, 5 and 6 respectively. It is observed that the effect of increasing value of van der Walls parameter is to increase the density and to decrease the velocity and pressure in the disturbed region which is in close agreement with the results obtained by Arora et. al [14].

After determining the physical variables, density, velocity and pressure behind the shock front, we can also calculate the total energy carried by the weak shock wave in a non-ideal gas at any time as [6]

$$\begin{aligned} E=4\pi \intop _{0}^{R}\left\{ \frac{1}{2}\varrho \vartheta ^{2}+\frac{\left( 1-b\varrho \right) }{\gamma -1}p\right\} x^{j}dx. \end{aligned}$$

(27)

Putting the value of the density, velocity and pressure from Eqs. (24), (25) and (26) in (27), we have

$$\begin{aligned} E=gt^{\frac{\left( \gamma +1\right) \left( j\left( \chi +1\right) -\psi +3\right) \eta \tau +2\left( \psi -\tau -2\right) \left( 1-b\varrho _{0}-\left( 1-b\varrho _{0}\right) /M^{2}\right) }{2\left( 1-b\varrho _{0}-\left( 1-b\varrho _{0}\right) /M^{2}\right) }}, \end{aligned}$$

where

$$\begin{aligned} g=\frac{\left( \gamma -1\right) +2\left( \left( \left( \gamma -1\right) -\left( \gamma -1\right) b\varrho _{0}+2\left( 1-b\varrho _{0}\right) /M^{2}\right) /\left( \gamma -1\right) \right) }{2\left( j\left( \chi +1\right) -\psi +3\right) \left( \left( \gamma -1\right) +2b\varrho _{0}+2\left( 1-b\varrho _{0}\right) /M^{2}\right) \left( \eta \tau \right) ^{\psi -2}}. \end{aligned}$$

Fig. 7

Behavior of energy of weak shock wave for $j= 0$

Fig. 8

Behavior of energy of weak shock wave for $j= 1$

Fig. 9

Behavior of energy of weak shock wave for $j= 2$

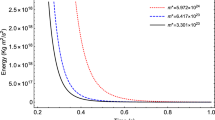
The effect of Mach number on the energy carried by weak shock wave in non-ideal gas for spherically symmetric, cylindrically symmetric and planar flows is shown in Figs. 7, 8 and 9 respectively. The values of the constants appearing in the computations are taken as: $\varrho _{0}=1.0$ and $\gamma =1.4$, $M=1.02,$ 1.04, 1.06, 1.08 and $b=0.02$. Here, it is observed that an increase in the value of Mach number causes to increase the energy of the weak shock wave in spherically symmetric, cylindrically symmetric and planar flows. The variation in energy carried by weak shock wave in planar, cylindrically symmetric and spherically symmetric flows have similar trend but energy carried by weak shock wave is more in planar case as compared to cylindrically symmetric and spherically symmetric flows. The energy carried out by weak shock wave in cylindrically symmetric flow is more than as compared to spherically symmetric flow.

Conclusion

In the present article the exact analytical solution for the problem of weak shock wave in a non-ideal gas has been derived. The solution of Euler equations in a non-ideal gas obtained here is a new one. The behavior of variations of the radius and energy of weak shock wave in a non-ideal gas are similar to that as in an ideal. Here, it is observed that the solution of weak shock wave problem for adiabatic non-ideal gas given by Eqs. (18–20) reduces to the solution presented by Singh et al. [6] for $b=0.0$.