1 Introduction

It was the first time that the impact of bursting bombs’ shock waves was detected during World War II. Despite the lack of obvious traces of violence, it was discovered that castaways’ lungs had been damaged as a result of water bomb blasts. Following that, the first systematic experiments on the implementation of shock waves in medicine were conducted.

A propagation of disturbances which travels faster than sound is known as shock wave. The characteristics of a surface discontinuity in a solution of quasi-linear first-order hyperbolic system of partial differential equations can be explained by shock waves. Due to the existence of discontinuity in solution, it is complicated to formulate the problem of ideal gas and fluid flow mathematically in physics. As a result, in gas dynamics, shock wave theory is incorporated into the hypothesis of generalized solutions of integral conservation laws systems.

Researchers have attempted to examine the propagation of shock waves several times during the last few decades. Classical work of Taylor [1, 2], Taylor [3], Sakurai [4, 5], and Rogers [6] created a comprehensive mathematical technique for understanding blast wave propagation in the context of a hyperbolic system. In the two monographs Courant and Friedrichs [7] and Whitham [8], we find the major development in the theory of shock waves. They looked into the topic of weak and powerful shock waves propagating in standard gas dynamics. Research in the field of weak shock waves has always been a fascinating subject because of its vital applications, such as the treatment of numerous ailments such as kidney stones, orthopedics, cancer etc. To treat the evolution of weak shock waves, Anile [9] developed the generalized wave front expansion, which is based on an asymptotic technique. Many researchers like Poslavskii [10] and Farshi and Trubnikov [11] have derived a precise solution to the one-dimensional gas dynamical system of equations having issue with shock wave propagation. Sharma, Ram and Sachdev [12] presented an exact solution which is uniformly valid for the whole flow field that lies behind the decaying shock wave. They analyzed the interaction of a shock of any strength with a centered simple wave passing over it and captured the entire history of decay with an incredible accuracy even for strong shocks. In the study of finding precise solution to gas dynamical equations involving discontinuities using an analytical approach, the disturbance is assumed to have been of little range, so the theory of small disturbance utilized within this can come up with precise solution in the entire disturbed domain governed by the following fundamental assumptions: the gas is assumed to be ideal and its heat conductivity and viscosity are ignored. The fact that weak discontinuity propagation is a subcategory of nonlinear waves that may be handled analytically is one of the most exciting element of the theory. In the case, where the density of the gas in the disturbed region varies according to relative change in distance and time from the source of the disturbance, Murata [13] gave a closed form of the precise solution for the problem of strong shock waves. Sharma and Radha [14] obtained an exact solution of Euler equations with the help of Lie group analysis for ideal gas dynamics. Singh, Ram and Singh [15] found a precise solution to the weak shock wave problem in gas dynamics using generalized geometries for ideal fluid motion. In 2018, Chaudhary and Singh [16] worked on finding precise solution of the weak shock waves for non-ideal gases.

The stellar atmospheric structure and dynamic processes are dominated by applied gravity. In astrophysics, a field of gravity, the process of unsteady gaseous motion mentioned in this work, is extremely essential. The transient process is one of the most important dynamical issue in the solar atmosphere. Singh, Ram and Singh [17] employed a systematic perturbation approach to investigate the pattern of the flow generated by the motion of a planar piston traveling at constant velocity in a gas which is non-ideal with the field of weak gravity. Also, Chaudhary, Ram and Singh [18] obtained a precise solution to the planar piston problem for a dusty gas under the field of weak gravity. Recently, in 2019, Nath and Singh [19] addressed the problem of a cylindrical shock wave which propagates in rotating axisymmetric for perfect gas in isothermal flow under an azimuthal magnetic field and discovered approximate analytical solution by expanding flow parameters in power series. In 2020, Nath and Singh [20] found approximate analytical answer to the problem of propagation of an ionizing cylindrical shock wave in rotating axisymmetric for non-ideal gas in isothermal flow with an azimuthal magnetic field. In the same year, Husain, Singh and Haider [21] focused on developing an analytical formula for the total energy influenced by Van der Waals excluded volume in the presence of dust-laden particles, as well as establishing an efficient precise solution to the blast wave problem in real gas flow under the effect of dust-laden particles. Then, in 2021, Nath and Singh [22] obtained an approximate analytical solution for the problem of propagation of ionizing cylindrical magnetogasdynamic shock wave in axially symmetric rotating self-gravitating ideal gas under isothermal flow condition. In 2022, Arora and Singh [23] applied the method of power series to explore the shock waves propagation with generalized geometries caused by a violent explosion in a hazy gas.

In the current study, an analytical approach is used to investigate the propagation of an unsteady one-dimensional flow of a non-viscous perfect gas with generalized geometries under a weak gravitational field. The distribution of density of the mass in the medium in this case is supposed to be in the form of a function of power of the radial distance from the weak shock wave’s propagation point. In terms of three variables velocity, density, and pressure in the interrupted zone, a precise solution to the problem is obtained. The closed form precise solution of the given problem using this method represents the novelty of the current analysis. The effects of weak gravitational field on the flow variables and energy are studied. In addition, results of the total energy investigation for the different stellar masses are plotted against time. The obtained results are physically and experimentally true. The method used in the present study is more interesting from a physical and mathematical point of view. The suggested method has a wider application in such types of physical problems, which is justifiable.

2 Governing equations

In the local outer region of the volume of a star, we propose a co-ordinate system. In this system, the origin is on the star’s center and the x-axis is in the direction of the radius of the star for the motion of gas which is transient. The equations that govern for an unsteady one-dimensional motion of a non-viscous fluid in the this region are as follows [15, 17]:

$$\begin{aligned}{} & {} \rho _{t} + u\rho _{x} + \rho \left( u_{x}+\frac{n}{x}u \right) = 0, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} u_{t}+u u_{x} + \frac{1}{\rho }p_{x} +\frac{Gm^*}{x^2}=0, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \left( p\rho ^{-\gamma } \right) _{t} + \left( p\rho ^{-\gamma } \right) _{x} = 0, \end{aligned}$$
(3)

where t and x are only the independent variables and they represent time and space co-ordinate, respectively. The notations u, p and \(\rho\) are dependent variables and they represent particle’s velocity, pressure and density, respectively, and their typical units are considered. \(m^*\) is the mass of the star, G is the gravitational constant, \(\gamma\) is the polytropic index. The values of constant n are 0, 1 and 2 according as the motion is planar, cylindrical and spherical, respectively.

The relation \(p = \rho {\mathcal{R}} T\) is the equation of state which is added to the system of Eqs. (1)–(3). Here, temperature is denoted by T and the symbol \({\mathcal{R}}\) denotes the gas constant. Equations (1)–(3), including the gravitational constant, involve another quantity \(u_{g}\) with velocity dimension which is given by [17, 24]:

$$\begin{aligned} u_{g}=\sqrt{\frac{Gm^*}{x}}. \end{aligned}$$
(4)

If there is weak gravity, the gravitational velocity given in Eq. (4) is smaller than the particle’s velocity u and the sonic velocity \(a= \left( \frac{\gamma p}{\rho }\right) ^{1/2}\), and the basic flow resembles a Riemann flow. It is simple to demonstrate how gravity affects the flow field in this case. Let us introduce a small parameter which is dimensionless:

$$\begin{aligned} \epsilon = \frac{u^2_{g}}{u^2} \ll 1. \end{aligned}$$
(5)

Let us assume the position of shock front as \(x = R(t)\) and speed of the shock as \(\frac{\text{d}R}{\text{d}t}= U\), where R(t) is propagating into the local region characterized by the following conditions:

$$\begin{aligned} \rho = \rho _{0}\left( x\right) ,\ p = p_{0}\left( x\right) ,\ u = u_{0}\left( x\right) = 0, \end{aligned}$$
(6)

where \(\rho _{0}\), \(p_{0}\) and \(u_{0}\) are the evaluation of flow parameters density, pressure and velocity just ahead of the shock front, respectively.

3 Rankine–Hugoniot conditions

The law of conservation of mass, momentum, and energy across the shock front determine the RH conditions at the shock, which are stated as [13, 15]:

$$\begin{aligned}{} & {} \frac{\rho }{\rho _{0}} = \frac{\gamma +1}{\gamma -1}\left( 1+\frac{2}{\gamma -1}\frac{1}{M^2}\right) ^{-1}, \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \frac{u}{a_{0}} = \frac{2M}{\gamma +1}\left( 1-\frac{1}{M^2}\right) , \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \frac{p}{p_{0}} = \frac{2}{\gamma +1}\left( 1-\frac{\gamma -1}{2\gamma }\frac{1}{M^2}\right) \gamma M^2 , \end{aligned}$$
(9)

where M = \(\frac{U}{a_{0}}\) is the Mach number. The effective sound speed \(a_{0}\) just ahead of the shock is given by \(\left( \frac{\gamma p_{0}}{\rho _{0}}\right) ^{1/2}\). In the present problem, the density \(\rho _{0}\) varies according to the power function of radius of the shock front and R is as follows:

$$\begin{aligned} \rho _{0}=\rho _{a}R^{\zeta }, \end{aligned}$$
(10)

where \(\rho _{a}\) and \(\zeta\) are constants.

Above RH conditions (7)–(9) agree with Singh, Ram and Singh [15], also if we take the case of strong shock waves it will reduce to the same as given by Murata [13].

4 Precise solution for the weak shock problem with weak gravitational field

We find a relation among pressure p, velocity u and density \(\rho\) in the flow field which satisfy RH conditions (7)–(9) as:

$$\begin{aligned} p \lambda = \rho u^2, \end{aligned}$$
(11)

where \(\lambda\) is the constant which is given as:

$$\begin{aligned} \lambda =\frac{\left( M^2-1\right) ^2}{\left( 1+\frac{\gamma -1}{2}M^2\right) \left( M^2-\frac{\gamma -1}{2\gamma }\right) }, \end{aligned}$$
(12)

inserting Eq. (11) into Eqs. (2) and (3), we get:

$$\begin{aligned}{} & {} u_{t}+u u_{x} + \frac{1}{\lambda }\left( \frac{u^2}{\rho }\rho _{x} +2u u_{x}\right) =-\frac{Gm^*}{x^2}, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} u_{t}+u u_{x} + \frac{\gamma -1}{2}u\left( u_{x} +\frac{n}{x}u\right) =0, \end{aligned}$$
(14)

on combining Eqs. (13) and (14) and then using the relations (4) and (5) in the resulting equation, we get:

$$\begin{aligned}{} & {} \frac{\alpha }{u}u_{x} + \frac{1}{\rho }\rho _{x}+\left( \epsilon \lambda -\frac{\gamma -1}{2}\lambda n\right) \frac{1}{x}=0, \end{aligned}$$
(15)

where \(\alpha =2-\frac{\gamma -1}{2}\lambda\) is a constant. On integrating Eq. (15), we find:

$$\begin{aligned} Q(t)=\rho u^\alpha x^{\epsilon \lambda -\frac{\gamma -1}{2}\lambda n }, \end{aligned}$$
(16)

where Q(t) is a function of t.

Using Eq. (16) into Eq. (1), we get:

$$\begin{aligned} \frac{\alpha }{u}u_{t} - \left( 1-\alpha \right) u_{x} - \left( 1+\frac{\gamma -1}{2}\lambda \right) \frac{nu}{x}+ \lambda \epsilon \left( \frac{u}{x}\right) -\frac{1}{Q}\frac{\text{d}Q}{\text{d}t}=0. \end{aligned}$$
(17)

Combining Eqs. (14) and (17), we get:

$$\begin{aligned} u = -\omega \frac{x}{Q}\frac{\text{d} Q}{\text{d} t}, \end{aligned}$$
(18)

where \(\omega = \left[ \left( 1+\frac{\gamma -1}{2}\frac{\lambda }{\beta }\right) n + \frac{\lambda \epsilon }{\beta }+1\right] ^{-1}\) and \(\beta = 1 + \frac{(\gamma -1)\alpha }{2}\).

Putting Eq. (18) into (17), and on integrating the resulting equation, we deduce:

$$\begin{aligned} Q(t) = Q_{0}t^{-\frac{\Omega }{\omega }}, \end{aligned}$$
(19)

where \(Q_{0}\) is arbitrary constant and \(\Omega = \left[ 1-\left( \frac{\gamma -1}{2}\right) ^{2}\frac{n\lambda }{\beta }\right] ^{-1}\). Let us take Eqs. (7) and (8). Equation (7) gives the following analytical expression:

$$\begin{aligned} R(t) = t^{\frac{\gamma +1}{2}\frac{M^2}{M^2-1}\Omega } . \end{aligned}$$
(20)

The value of \(\zeta\) obtained with help of RH conditions (7) and (8) is given by:

$$\begin{aligned} \zeta =\frac{2(n+1)\left( \frac{1}{M^2}-1\right) }{(\gamma +1)}. \end{aligned}$$
(21)

Now, the precise solution for the given system of gas dynamic problem with the weak shock waves is given as:

$$\begin{aligned}{} & {} u = \left[ 1-\left( \frac{\gamma -1}{2}\right) ^{2}\frac{n\lambda }{\beta }\right] ^{-1}\frac{x}{t}, \end{aligned}$$
(22)
$$\begin{aligned}{} & {} \rho = Q_{0}\left[ 1-\left( \frac{\gamma -1}{2}\right) ^{2}\frac{n\lambda }{\beta }\right] ^{\alpha } x^{-\left[ \alpha +\lambda \epsilon -n\left( \frac{\gamma -1}{2}\right) \lambda \right] }t^{\alpha -\frac{\Omega }{\omega }} , \end{aligned}$$
(23)
$$\begin{aligned}{} & {} p = \frac{Q_{0}}{\lambda }\left[ 1-\left( \frac{\gamma -1}{2}\right) ^{2} \frac{n\lambda }{\beta }\right] ^{\alpha -2}x^{2-\left[ \alpha +\lambda \epsilon -n\left( \frac{\gamma -1}{2}\right) \lambda \right] }t^ {-2+\alpha -\frac{\Omega }{\omega }}. \end{aligned}$$
(24)

Equations (22)–(24) give a precise solution of our considered problem. The solution that we have obtained in presence of gravitational field will reduce to a solution obtained in ideal gas dynamics by Singh, Ram and Singh [15] in the absence of gravitational field.

5 Behavior of energy

Under a weak gravitational field, the total energy transported by motion of the wave is represented as [25]:

$$\begin{aligned} E =4\pi \int _{0}^{R}\left( \frac{1}{2}\rho u^2 + \frac{1}{\gamma -1}p - \frac{Gm^*}{x}\rho \right) x^n dx , \end{aligned}$$
(25)

where E shows the sum of the gas’s internal, kinetic and gravitational potential energy as a function of time.

Put the values of u, \(\rho\) and p from Eqs. (22)–(24) into Eq. (25), we get:

$$\begin{aligned} E = gt^{\alpha -2-\chi + \Delta \left( 3+\sigma \right) }-ht^{\alpha -\chi +\Delta \sigma }, \end{aligned}$$
(26)

where

\(g = \frac{4\pi Q_{0}\left[ \frac{1}{2}+\frac{1}{(\gamma -1)\lambda }\right] \left[ 1-\left( \frac{\gamma -1}{2}\right) ^{2}\frac{n\lambda }{\beta }\right] ^{\alpha -2}}{3+\sigma }\),

\(h = \frac{4\pi Gm^* Q_{0}\left[ 1-\left( \frac{\gamma -1}{2}\right) ^{2} \frac{n\lambda }{\beta }\right] ^{\alpha }}{\sigma }\),

\(\Delta = \frac{\gamma +1}{2}\frac{M^2}{M^2-1}\Omega\), \(\sigma = n - \left[ \alpha + \lambda \epsilon - n\left( \frac{\gamma -1}{2}\right) \lambda \right]\), \(\chi = \frac{\Omega }{\omega }\).

It may be noted here that the total energy carried by the wave varies with respect to time t and the term containing negative coefficient h shows the effect of gravity on the total energy that is decreasing in the strength of total energy. Due to gravity, energy behaves opposite to behavior of energy presented by Singh, Ram and Singh [15].

6 Results and discussion

Eqs. (22)–(24) represent the precise solution of the one-dimensional gas dynamical system of equations under the influence of the weak gravitational field. Following are the typical values for physical quantities used in our computation: \(\gamma\)=1.4, M=1.2, G=\(6.67408 \times 10^{-11} Nm^{2}/Kg^{2}\) and \(\epsilon\) has been taken small i.e. \(\epsilon \ll 1.\) When there is no gravity, density is increasing behind the shock front on the other hand pressure decreases. In the presence of gravity, the increasing process of density is speeding up and pressure behavior is just reversed. This is, of course, what is expected physical point of view. The given solution will reduce to a solution obtained in ideal gas dynamics by Singh, Ram and Singh [15] in the absence of gravitational field. Eqs. (22)–(24) demonstrate that gravity causes the pressure to increase everywhere in the flow field behind the shock which is same as presented by Nath, Dutta and Pathak [25] for non-ideal medium.

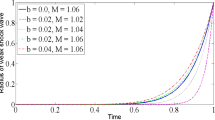
For different stellar masses, Figs. 1, 2 and 3 represent the behavior of the energy for \(n=0, 1, 2,\) respectively, under the influence of weak gravity. In each graph, energy is plotted against the time for three different planets and energy measured in \(\text{kg m}^{2}/\text{s}^{2}\) and the time in seconds. Figures 1, 2 and 3 show that total energy is decreasing as the time passes due to the presence of weak gravity. It is totally opposite to behavior of total energy presented by Singh, Ram and Singh [15] in the absence of gravity. For the planar geometry shown in Fig. 1, it can be observed that value of energy is decreasing as the time increases for all the planets. In case of cylindrical geometry represented by Fig. 2, the behavior of energy is same as in the case of planar geometry but the process of decreasing in the value of energy is slow. In the case of spherical geometry represented by Fig. 3, the process of decreasing in the value of energy is more slower than that in other geometries.

Fig. 1
figure 1

Behavior of the energy for the different value of \(m^{*}\) in planar geometry

Full size image
Fig. 2
figure 2

Behavior of the energy for the different value of \(m^{*}\) in cylindrical geometry

Full size image
Fig. 3
figure 3

Behavior of the energy for the different value of \(m^{*}\) in Spherical geometry

Full size image

7 Conclusion

In the present study, we find the solution of one-dimensional weak shock wave problem in the presence of weak gravitational field using an analytical approach by placing an assumption for the pressure to satisfy one of the Rankine–Hugoniot conditions automatically. The effect of weak gravitational field on the flow parameters presented analytically in Eqs. (22)–(24). Figs. 1, 2 and 3 are showing the effect of weak gravity on total energy, which have calculated in Eq. (26) for the plane, cylindrical and spherical geometry, respectively. On the basis of these findings, we may draw the following conclusions which agree with the physical and experimental points of view:

  1. 1.

    Weak gravity causes an increase in pressure everywhere behind the shock. When the value of gravity increases, the density drops near the shock but increases toward the inner boundary surface.

  2. 2.

    Total energy strength decreases with passes of time and process is delayed for different stellar masses which is shown in Figs. 1, 2 and 3.

  3. 3.

    In the absence of gravity, the results agree with the solution obtained by Singh, Ram and Singh [15].

  4. 4.

    The results presented are supported by physical evidence, and the methodology employed in the finding of it is new.

  5. 5.

    From a physical perspective, the strategy adopted in the present work is more intriguing. It seems reasonable that the recommended approach has a larger range of applications in such types of physical problems. This approach can also be used to investigate how a weak gravitational field affects strong shock waves.