Introduction

Nonlinear singular boundary value problems (SBVPs) have been studied by many mathematicians, physicists and engineers. They used different methods in order to achieve the most accurate numerical solutions and that require the least CPU time. In recent years, a wide spectrum of papers have been devoted to solve such problems. For instance, Motsa and Sibanda [25] presented a novel approach to solve nonlinear SBVP arising in physiology for the study of tumour growth. They used successive linearization method (SLM) and compared their numerical results to those obtained by other methods such as ordinary cubic spline method [16], finite differences (see Pandey and Singh [29] and the references therein), Adomian decomposition method (ADM) [33], third degree B-spline [3], non-polynomial cubic splines [20], and cubic B-spline collocation [16]. Moreover, other papers proposed alternate computational methods based on Bernstein polynomials, via the transformation of the original problem to an eigenvalue problem then applying an open domain MATLAB collocation code “bvpsuite” to solve the nonlinear SBVPs [30]. In [33], Singh and Kumar used a new technique based on Green’s function and the Adomian decomposition method (ADM) for solving nonlinear singular boundary value problems (SBVPs). In [27] Niu et al. used a simplified reproducing kernel method and least squares approach for solving nonlinear singular boundary value problems. Other techniques include piecewise shooting reproducing kernel method [7, 8], mixed decomposition-spline approach [22], variational iteration method [15, 34], topological techniques [6], Padé approximation and collocation methods [1], a fourth order method [4], and other novel numerical methods such as those in [2, 5, 10, 11, 17,18,19,20, 23, 24, 31, 32].

Some applications of nonlinear singular boundary value problems (SBVPs) for ordinary differential equations arise in many branches of applied mathematics, engineering such as chemical reactions, sciences such as nuclear physics and many others. For instance, it arises in the theory of electro-hydrodynamics and in the radial stress on a rotationally symmetric shallow membrane cap. In addition, it describes the equilibrium of the isothermal gas sphere and finds the distribution of heat sources in the human head. Last but not least, it has application for finding the steady-state oxygen diffusion in a spherical cell (see [9] and [33] and the references therein).

In this paper, a recently introduced iterative method based on Green’s functions and fixed-point iteration schemes, such as Picard’s and Mann’s procedures, is presented for the approximate solution of a generalized class of nonlinear SBVPs (see [13, 14, 18, 21, 22] and the references therein). Five examples are considered and the results are compared with other numerical methods. The objective is to show that the iterative procedure yields relatively highly accurate approximate solutions and converges rapidly. Proof of convergence as well as rate of convergence are also included in our study.

An outline of the paper is as follows. To begin with, we will present the definition and construction of the Green’s function and then designate the fixed-point iteration method. A proof of convergence of the scheme as well as its rate of convergence will be included. Moving on, we will investigate five different nonlinear SVBPs to show the efficiency and high accuracy of the method. Finally, we will summarize our findings.

Description of the Iteration Method

Green’s Function

To construct the Green’s function for certain SBVPs, consider first the following linear second order equation:

$$\begin{aligned} \displaystyle {L[u]=u^{\prime \prime }(x)+p(x)u^{\prime }(x)+q(x)u(x)=f(x), } \end{aligned}$$
(1)

for \(a<x<b\) with boundary conditions

$$\begin{aligned} \begin{array}{l} \displaystyle { B_a[u]=a_0u(a)+a_1u^{\prime }(a)=\alpha ,} \\ \displaystyle {B_b[u]=b_0u(b)+b_1u^{\prime }(b)=\beta }. \end{array} \end{aligned}$$
(2)

The general solution is given by \(u=u_h+u_p\) where \(u_h\) is the solution to \(L[u]=0\) subject to the boundary conditions (2), and \(u_p\) is the solution to \(L[u]=f(x)\) satisfying the corresponding homogeneous boundary conditions

$$\begin{aligned} \displaystyle {B_a[u]=B_b[u]=0. } \end{aligned}$$
(3)

To find \(u_p\), we first seek a solution for

$$\begin{aligned} \displaystyle {L[u]=\delta (x-s), } \end{aligned}$$
(4)

subject to the conditions (3); this solution is referred to as the Green’s function G(x|s). Then

$$\begin{aligned} \displaystyle {u_p=\int _{a}^{b} G(x|s) \; f(s)\; ds}. \end{aligned}$$
(5)

Let \(u_1 , u_2\) be two linearly independent solutions of \(L[u]=0.\) The Green’s function satisfies the homogeneous equation for \(x\not =s\) and hence will be a linear combination of the solutions \(u_1, u_2:\)

$$\begin{aligned} \begin{array}{cc} G(x|s)= &{} \left\{ \begin{array}{cc} c_1u_1(x)+c_2u_2(x), &{} a<x< s \\ d_1u_1(x)+d_2u_2(x), &{} s<x< b \end{array} \right. . \end{array} \end{aligned}$$

The constants \(c_1,c_2,d_1,d_2\) are determined using the following conditions:

  1. (i)

    Homogeneous BCs:

    $$\begin{aligned} B_a[G(x|s)]=B_b[G(x|s)]=0. \end{aligned}$$
  2. (ii)

    Continuity of G at \(x=s:\)

    $$\begin{aligned} c_1u_1(s)+c_2u_2(s) = d_1u_1(s)+d_2u_2(s). \end{aligned}$$
  3. (iii)

    Jump discontinuity of \(G^\prime \) at \(x=s\):

    $$\begin{aligned} d_1u_1^{\prime }(s) + d_2 u_2^{\prime }(s)- c_1u_1^{\prime }(s)-c_2u_2^{\prime }(s)=1. \end{aligned}$$

For nonlinear SBVPs

$$\begin{aligned} \displaystyle {u^{\prime \prime }(x) + p(x) u^{\prime }(x) + q(x)u(x) = f(x, u(x), u^{\prime }(x)), } \end{aligned}$$
(6)

the particular solution satisfies

$$\begin{aligned} \displaystyle {u_p=\int _{a}^{b}G(x|s) \; f(s, u_p(s), u_p^{\prime }(s)) \; ds, } \end{aligned}$$
(7)

where G is the Green’s function corresponding to (6).

Picard’s Green’s Scheme (PGS)

In this section, we will describe and detail our proposed method. Let’s consider a class of SVBPs of the form:

$$\begin{aligned} \displaystyle {L[u]=u^{\prime \prime }+\frac{p}{x} \, u^{\prime }=f(x,u,u^{\prime }), } \end{aligned}$$
(8)

with the boundary conditions (2). Let G be the Green’s function for the linear term and define the integral operator

$$\begin{aligned} \displaystyle { K[u_p]= \int _{a}^{b}G(x|s) \; L[u_p] \; ds. } \end{aligned}$$
(9)

Using (7), we can rewrite the latter equation as:

$$\begin{aligned} \displaystyle {K[u_p]=\int _{a}^{b}G(x|s) \left[ L[u_p]-f(s,u(s),u^{\prime }(s))\right] ds + u_p. } \end{aligned}$$
(10)

For convenience, let’s drop \(u_p\) and denote it by u. It follows that

$$\begin{aligned} \displaystyle {K[u]=\int _{a}^{b}G(x|s) \left[ L[u]-f(s,u(s),u^{\prime }(s))\right] ds + u. } \end{aligned}$$
(11)

Applying Picard’s iteration on K[u], namely

$$\begin{aligned} u_{n+1} = K [u_n], \;\;\;\;\; n \ge 0, \end{aligned}$$

yields the following iterative procedure:

$$\begin{aligned} \displaystyle {u_{n+1}=u_n+\int _{a}^{b}G(x|s)\left[ L[u_n]-f(s,u_n(s),u_n^{\prime }(s))\right] ds, } \end{aligned}$$
(12)

where \(L[u_n]\) is the linear term for the second order differential equation. The initial iterate \(u_0\) is chosen to satisfy the corresponding homogenous equation in (8), \(L[u]=0\), and the specified boundary conditions.

Mann’s Green’s Embedded Method (MGS)

Next, we apply the following Mann’s iterative algorithm for the approximation of fixed points, using the operator defined in (9):

$$\begin{aligned} \displaystyle {u_{n+1}=(1-\alpha _n) u_n + \alpha _n K[u_n]}, \;\;\;\;\; n \ge 0. \end{aligned}$$

Following the very similar steps as in the previous subsection, this results in the iterative scheme (MGS):

$$\begin{aligned} \displaystyle {u_{n+1}=u_n+ \alpha _n \; \int _{a}^{b}G(x|s)\left[ L[u_n]-f(s,u_n(s),u_n^{\prime }(s))\right] ds,} \end{aligned}$$
(13)

where \(\left\{ \alpha _{n}\right\} \) is a sequence of numbers that control the stability and speed up the convergence of the scheme. The starting function \(u_0\) is chosen to be the solution for the corresponding homogenous equation \(L[u]=0\) subject to the specified boundary conditions (2).

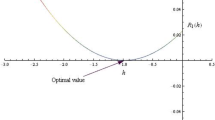
The optimal values of the sequence \(\left\{ \alpha _{n}\right\} \) is found by minimizing the \(L^2\)-norm of the residual error, \(R_n(x;\alpha _n)\), of the \(n^{th}\) iteration \(u_n\), namely

$$\begin{aligned} \Vert R_n(x;\alpha _n)\Vert ^2_{L^2} = \frac{1}{b-a}\int _a^b R_n^2(x;\alpha _n) \;dx, \end{aligned}$$
(14)

where for each n, \(R_n(x;\alpha _n)\) is given by

$$\begin{aligned} R_n(x;\alpha _n) = L[u_n] - f(x,u_n(x),u_n^{\prime }(x)). \end{aligned}$$
(15)

It is worth mentioning that with the proper choice of the parameters \(\alpha _n\)’s, the stability of the scheme can be controlled. For more details on the stability see [11].

Convergence Analysis of the PGS

This section includes the convergence analysis of the Picard’s scheme. The analysis is based on the contraction principle [28]. Without loss of generality, we prove convergence of the PGS that applies to the following boundary value problem:

$$\begin{aligned} \displaystyle {u^{\prime \prime }(x) + \frac{p}{x} \, u^\prime (x) = f(x, u(x), u^{\prime }(x)}, \end{aligned}$$
(16)

where \(p \ge 2\), and complimented with the boundary conditions:

$$\begin{aligned} \displaystyle {u^\prime (0) = \alpha , \;\;\; \; u(1) = \beta }. \end{aligned}$$
(17)

First, we construct the Green’s function for (16) using the properties detailed in Sect. 2.1. Solving the corresponding homogeneous equation of (16), which is a Cauchy–Euler equation, we have

$$\begin{aligned} \begin{array}{cc} G(x|s)= &{} \left\{ \begin{array}{cc} A + B \, x^{1-p}, &{} 0<x< s \\ C + D \, x^{1-p}, &{} s<x< 1 \end{array} \right. . \end{array} \end{aligned}$$
(18)

Applying the corresponding homogenous BCs of (17), that is \(u^\prime (0) = u(1) = 0\), we get the two equations

$$\begin{aligned} \displaystyle {B=0, \;\;\;\; C+D=0}. \end{aligned}$$
(19)

The continuity of the Green’s function gives the equation

$$\begin{aligned} \displaystyle {A + B \, s^{1-p} = C + D \, s^{1-p}}. \end{aligned}$$
(20)

The unit jump discontinuity of the first derivative of the Green’s function results in the equation

$$\begin{aligned} \displaystyle {D (1 - p) s^{-p} - B (1 - p) s^{-p} = 1}. \end{aligned}$$
(21)

Solving the system of equations in (19)–(21), we get the Green’s function

$$\begin{aligned} \begin{array}{cc} G(x|s)= \left\{ \begin{array}{ll} \frac{1}{p-1} \left( s^p - s\right) , &{} 0<x< s \\ \frac{s^p}{p-1} \left( 1 - x^{1-p}\right) , &{} s<x< 1 \end{array} \right. . \end{array} \end{aligned}$$
(22)

Substituting this latter Green’s function in the PGS iterative procedure given in (12), we get the following PGS procedure that corresponds to the BVP in (16), (17):

$$\begin{aligned} \displaystyle {u_{n+1}}= & {} \displaystyle {u_n + \int _{0}^{x} \frac{s^p}{p-1} \left( x^{1-p} - 1 \right) \left[ u_n^{\prime \prime }(s) + \frac{p}{s} \, u_n^\prime (s) - f\left( s, u_n(s), u_n^{\prime }(s)\right) \right] ds} \nonumber \\&+ \displaystyle { \int _{x}^{1} \frac{1}{p-1} \left( s - s^p \right) \left[ u_n^{\prime \prime }(s) + \frac{p}{s} \, u_n^\prime (s) - f\left( s, u_n(s), u_n^{\prime }(s)\right) \right] ds.} \end{aligned}$$
(23)

The next theorem gives convergence of the scheme.

Theorem 1

Assume that \(\displaystyle {f\left( x, u, u^{\prime }\right) }\) is a continuous function whose derivative is bounded with respect to u. Assume that

$$\begin{aligned} \displaystyle {K := \frac{1}{2 (p - 1)} L_c < 1,} \end{aligned}$$

where

$$\begin{aligned} \displaystyle {L_c = \max _{[0, 1] \times R^2} \left| \frac{\partial f}{\partial u}\right| }. \end{aligned}$$

Then, the iterative sequence \(\left\{ u_n(x)\right\} _{n=1}^{\infty }\), given by (23), where \(x \in [0, 1]\) and using any bounded starting function on [0, 1], converges uniformly to the exact solution, u(x), of problem (16)–(17).

Proof

In order to prove the convergence, we will use the function space C[0, 1] equipped with the maximum norm defined by \(\displaystyle {\Vert u\Vert = \max _{0 \le x \le 1} \left| u(x)\right| }\).

Direct integration leads to

$$\begin{aligned} \begin{array}{lll} \displaystyle {\int _0^x \!\!\frac{s^p}{1-p} \left( x^{1-p} \!-\! 1 \right) \left[ u_n^{\prime \prime }(s) + \frac{p}{s} \, u_n^\prime (s) \right] ds} &{} = &{} \displaystyle {\frac{x^{1-p} - 1}{1-p} \int _{0}^{x} \left[ s^p u_n^{\prime \prime }(s) + p s^{p-1} \, u_n^\prime (s) \right] ds} \\ &{} = &{} \displaystyle {\frac{x^{1-p} - 1}{1-p} \int _{0}^{x} \left( s^p \; u_n^\prime (x)\right) ^\prime \, ds } \\ &{} = &{} \displaystyle {\frac{x - x^p}{1-p} \; u_n^\prime (x)}. \end{array} \end{aligned}$$
(24)

Integrating twice by parts we get

$$\begin{aligned}&\displaystyle {\int _x^1 \frac{1}{p-1} \left( s^p - s \right) u_n^{\prime \prime }(s) \; ds}\nonumber \\&\quad = \displaystyle {\frac{1}{p-1}\left[ (1-p) u_n(1) + \left( p x^{p-1}-1\right) u_n(x) + \left( x - x^p\right) u_n^\prime (x) \right. } \nonumber \\&\qquad + \displaystyle { \left. p(p-1) \, \int _x^1 s^{p-2} \, u_n(s) \; ds\right] }. \end{aligned}$$
(25)

Integrating once by parts we get

$$\begin{aligned} \begin{array}{lll} &{}\displaystyle {\int _x^1 \frac{1}{p-1} \left( s^p - s \right) \frac{p}{s} \; u_n^{\prime }(s) \; ds}\\ &{}\quad = \displaystyle {\frac{p}{p-1}\left[ \left( 1 - x^{p-1}\right) u_n(x) - (p-1) \, \int _x^1 s^{p-2} \, u_n(s) \; ds\right] }. \end{array} \end{aligned}$$
(26)

Substituting the results of (24)–(26) into the iterative scheme (PGS) given in (23), we have

$$\begin{aligned} \displaystyle {u_{n+1}}= & {} \displaystyle {u_n(1) + \int _{0}^{x} \frac{s^p}{1-p} \left( x^{1-p} - 1 \right) \, f\left( s, u_n(s), u_n^{\prime }(s)\right) ds} \nonumber \\&+ \displaystyle { \int _{x}^{1} \frac{1}{p-1} \left( s^p - s \right) \, f\left( s, u_n(s), u_n^{\prime }(s)\right) ds.} \end{aligned}$$
(27)

Equivalently, we have

$$\begin{aligned} \begin{array}{lll} \displaystyle {u_{n+1}}= & {} \displaystyle {\beta + \int _{0}^{1} G(x|s) \, f\left( s, u_n(s), u_n^{\prime }(s)\right) ds,} \end{array} \end{aligned}$$
(28)

where \(\beta =u_n(1)\), from (17), and

$$\begin{aligned} \begin{array}{cc} G(x|s)= &{} \left\{ \begin{array}{cc} \displaystyle {\frac{s^p}{1-p} \left( x^{1-p} - 1 \right) } , &{} 0<s< x \\ \displaystyle {\frac{1}{p-1} \left( s^p - s \right) }, &{} x<s< 1 \end{array} \right. . \end{array} \end{aligned}$$
(29)

Define \(T_G: C[0,1] \rightarrow C[0,1]\) to be the right side of Eq. (28):

$$\begin{aligned} \displaystyle {T_G(u) \equiv \beta + \int _{0}^{1} G(x|s) \, f\left( s, u(s), u^{\prime }(s)\right) ds. } \end{aligned}$$
(30)

According to Banach-Picard fixed point theorem, to prove convergence it suffices to show that \(T_G\) is a contractive mapping. Therefore, we have

$$\begin{aligned} \displaystyle {\left| T_G(u) - T_G(v)\right| = \left| \int _0^1 G(x|s) \, \left[ f(s,u,u^{\prime }) - f(s,v,v^{\prime })\right] \; ds \right| .} \end{aligned}$$
(31)

Simple integration gives

$$\begin{aligned} \displaystyle {\int _0^1 G(x|s) \; ds = \frac{1}{2 (p + 1)} (x^2 - 1) \equiv g(x). } \end{aligned}$$
(32)

The maximum value of the absolute value of the function g(x) on the interval [0, 1] occurs either at the critical points or endpoints.

$$\begin{aligned} \displaystyle {|g(x)| \le \frac{1}{2 (p + 1)}. } \end{aligned}$$
(33)

Using (32) and (33), we have from (31)

$$\begin{aligned} \begin{array}{lll} \displaystyle {\left| T_G(u) - T_G(v)\right| }\le & {} \displaystyle { \frac{1}{2(p+1)} \; \int _0^1 \left| f(s,u,u^{\prime }) - f(s,v,v^{\prime })\right| \; ds.} \end{array} \end{aligned}$$
(34)

Applying the Mean Value Theorem for f, we obtain

$$\begin{aligned} \begin{array}{lll} \displaystyle { \left| T_G(u) - T_G(v)\right| } &{} \le &{} \displaystyle { \frac{1}{2(p+1)} \; \max _{0 \le x \le 1} \left| f(x,u(x),u^\prime (x)) - f(x,v(x),v^\prime (x)) \right| }\\ &{} \le &{} \displaystyle { \frac{1}{2(p+1)} L_c \; \Vert u - v\Vert } \end{array} \end{aligned}$$
(35)

where \(\displaystyle { \Vert u - v \Vert = \max _{0 \le x \le 1} |u(x) - v(x)|}\) and \(\displaystyle {L_c = \max _{[0, 1] \times R^3} \left| \frac{\partial }{\partial u}f(x, u, u^\prime )\right| }\). From the hypothesis of the theorem, namely that \(\displaystyle {K := \frac{1}{2(p+1)} L_c < 1,}\) it follows that

$$\begin{aligned} \displaystyle { \left\| T_G(u) - T_G(v)\right\| \le K \; \Vert u - v\Vert ,} \end{aligned}$$
(36)

with \(0< K < 1\). This proves that \(T_G\) is a contraction mapping.

In regard to the rate of convergence, we have

$$\begin{aligned} \begin{array}{lll} \displaystyle { \left\| u_{n+1} - u_n \right\| } &{} = &{} \displaystyle {\left\| T_G(u_n) - T_G(u_{n-1})\right\| } \\ &{} \le &{} \displaystyle {K \; \Vert u_n - u_{n-1}\Vert } \\ &{} \le &{} \displaystyle {K^n \; \Vert u_1 - u_{0}\Vert .} \end{array} \end{aligned}$$
(37)

If \(m> n > 0,\) then

$$\begin{aligned} \begin{array}{lll} \displaystyle { \left\| u_{m} - u_n \right\| } &{} = &{} \displaystyle { \left\| u_{m} - u_{m-1} \right\| + ... + \left\| u_{n+1} - u_{n} \right\| }\\ &{} \le &{} \displaystyle {\left( K^{m-1} + ... + K^n \right) \; \Vert u_1 - u_{0}\Vert } \\ &{} \le &{} \displaystyle {K^n \left( 1 + K + K^2 + ...\right) \Vert u_1 - u_0\Vert } \\ &{} = &{} \displaystyle {\frac{K^n}{1 - K} \; \Vert u_1 - u_{0}\Vert .} \end{array} \end{aligned}$$
(38)

If we let \(m \rightarrow \infty \), we get the error estimate:

$$\begin{aligned} \displaystyle { \left\| u^{\star } - u_n \right\| \le \frac{K^n}{1 - K} \; \Vert u_1 - u_{0}\Vert .} \end{aligned}$$
(39)

\(\square \)

Numerical Examples

In this section, we will implement the Picard’s Green’s scheme for the solution of a nonlinear second order SBVPs. We will compare our numerical results with existing numerical solutions to confirm the validity and high accuracy of the strategy.

Example 1

Consider the following nonlinear SBVP describing the equilibrium of isothermal gas sphere [4], which is taken from Singh and Kumar [33]:

$$\begin{aligned} \displaystyle { u^{\prime \prime }(x) = -\frac{2}{x} u^{\prime }(x) + u^5(x),} \end{aligned}$$
(40)

where \(0< x < 1\) and subject to

$$\begin{aligned} u^\prime (0) =0 , \; \;\; u(1) =\sqrt{\frac{3}{4}}. \end{aligned}$$
(41)

The exact solution is given by \(u(x)=\sqrt{\frac{3}{3+x^2}}\).

Constructing the Green’s function for the linear equation \(L[u]=u^{\prime \prime }=0\) and complimented with the homogeneous BCs \(u^{\prime }(0)=0\) and \(u(1)=0\), results in the subsequent form of the PGS (12).

$$\begin{aligned} \displaystyle u_{n+1}= & {} u_n - \int _{0}^{x} s^2 \left( 1-\frac{1}{x}\right) \left[ u^{\prime \prime }_n(s)+\frac{2}{s} u^{\prime }_n(s) - u^5_n(s) \right] ds \nonumber \\&- \int _{x}^{1} s (s - 1) \left[ u^{\prime \prime }_n(s)+\frac{2}{s} u^{\prime }_n(s) - u^5_n(s) \right] ds . \end{aligned}$$
(42)

The initial iterate is the solution of \(L[u]=0\) subject to the BCs (41), which is found to be \(u_0=\sqrt{\frac{3}{4}}\).

For quantitative comparison, we now define \(E_n\) as the results obtained via the Picard Green’s function approach (PGS), while \(V_n[19]\), \({W}_{n}[6]\), and \(Z_n[23]\) are those obtained by the techniques proposed by Singh and Kumar [33], Geng [8], and Niu et al. [27] respectively. Numerical results of this SBVP, as reported in Table 1 below, confirm that our strategy is more accurate than the latter three methods combined.

Table 1 Maximum absolute errors for Example 1 using PGS, compared with the methods in [8, 27, 33]
Full size table

It can be shown that the contraction constant for the corresponding PGS is \(\displaystyle {K=\frac{L_c}{2(p+1)}}\) which is equal to 5 / 6. This yield slow convergence since K is close to 1. Thus, the results by the PGS may be improved if we use the MGS (23). The best choice for the value of \(\alpha \) to minimize the absolute error in \(E_3\) is found to be \(\alpha ^*=1.43\); for simplicity this value is kept constant for the other iterations. The results are displayed in Table 2.

Table 2 Maximum absolute errors for Example 1 using MGS with \(\alpha =1.43\), compared with the methods in [8, 27, 33]
Full size table

Example 2

Consider the following nonlinear SBVP, which is taken from Singh and Kumar [33]:

$$\begin{aligned} \displaystyle { u^{\prime \prime }(x) = -\frac{2}{x} \, u^{\prime }(x) -e^{-u(x)},} \end{aligned}$$
(43)

where \(0 < x \le 1\) and subject to

$$\begin{aligned} u^\prime (0) =0 , \; \;\; 2u(1)+u^\prime (1) =0. \end{aligned}$$
(44)

This problem is known as the Emden-Fowler equation of the second kind and arises in the study of distribution of heat sources in the human head [9]. The exact solution is not known explicitly.

The Green’s function for the linear equation \(L[u]=u^{\prime \prime }=0\) subject to homogeneous BCs, results in the subsequent form of the PGS (12).

$$\begin{aligned} \displaystyle u_{n+1}= & {} u_n -\int _{0}^{x} s^2 \left( \frac{1}{2}-\frac{1}{x}\right) \left[ u^{\prime \prime }(s)+\frac{2}{s} \, u^{\prime }(s) + e^{-{u(s)}} \right] ds\nonumber \\&- \int _{x}^{1} s \left( \frac{s}{2}-1\right) \left[ u^{\prime \prime }(s)+\frac{2}{s} \, u^{\prime }(s) + e^{-{u(s)}} \right] ds, \end{aligned}$$
(45)

where the initial iterate is found to be \(u_0=0\). Table 3 confirms that the PGS strategy is more accurate, when comparing the numerical results \(E_n\) of this SBVP using our introduced procedure and the numerical results \(V_n\) obtained by Singh and Kumar [33] method and \(Z_{10}\) obtained by Niu et al. approach [27].

Table 3 Residual errors for Example 2 using our scheme and methods in [27, 33]
Full size table

Example 3

Consider the following nonlinear SBVP, which is taken from Khuri and Sayfy [18]:

$$\begin{aligned} \displaystyle { u^{\prime \prime }(x) = -\frac{1}{x} u^{\prime }(x) -e^{u(x)},} \end{aligned}$$
(46)

where \(0< x < 1\) and subject to

$$\begin{aligned} u^\prime (0) =0 , \; \;\; u(1) =0. \end{aligned}$$
(47)

The exact solution is given by \(u(x)=2\ln \left( {\frac{A+1}{Ax^2+1}}\right) \), where \(A=3-2\sqrt{2}.\)

Similar to the previous example, the problem is also known as the Emden-Fowler equation of the second kind. The Green’s function for the linear equation \(L[u]=u^{\prime \prime }=0\), results in the subsequent form of the PGS (12).

$$\begin{aligned} \displaystyle u_{n+1}= & {} u_n-\int _{0}^{x} s \ln {x} \left[ u^{\prime \prime }(s)+\frac{1}{s} u^{\prime }(s) + e^{{u(s)}}\right] ds\nonumber \\&- \int _{x}^{1} s \ln {s} \left[ u^{\prime \prime }(s)+\frac{1}{s} u^{\prime }(s) + e^{{u(s)}}\right] ds, \end{aligned}$$
(48)

where the initial iterate is found to be \(u_0=0\).

Again \(E_n\) is defined as the results of our PGS approach, while \(T_n\), \(V_n[3]\), \({{W}_{n}[6]}\) and \(Z_{64}[23]\) are the results obtained by the techniques proposed by Singh and Kumar [33], Caglar and Caglar and Ozer [3], Geng [8], and Niu et al. [27] respectively. A comparison is summarized in Table 4.

Table 4 Maximum errors for Example 3 using our scheme and methods in [3, 8, 27, 33]
Full size table

Example 4

Consider the following nonlinear SBVP arising in the study of steady-state oxygen diffusion in spherical cell [34], which is taken from Singh and Kumar [33]:

$$\begin{aligned} \displaystyle { u^{\prime \prime }(x) = -\frac{\alpha }{x} \; u^{\prime }(x) +\frac{nu(x)}{u(x)+k},} \end{aligned}$$
(49)

subject to

$$\begin{aligned} u^\prime (0) =0 , \; \;\; 5u(1)+u^\prime (1) =5, \end{aligned}$$
(50)

where \(n=0.76129\) is the reaction rate and \(k=0.03119\) is the Michaelis constant (see [16, 18, 34]).

This above nonlinear SBVP arises in the study of steady-state oxygen diffusion in a spherical cell. The exact solution is not known explicitly. The Green’s function for the linear equation \(L[u]=u^{\prime \prime }=0\) subject to homogeneous BCs, results in the subsequent form of the PGS (12):

$$\begin{aligned} \displaystyle u_{n+1}= & {} u_n-\int _{0}^{x} s^2 \left( \frac{4}{5}-\frac{1}{x}\right) \left[ u^{\prime \prime }(s)+\frac{\alpha }{s} \, u^\prime (s) -\frac{nu(s)}{u(s)+k} \right] ds\nonumber \\&-\int _{x}^{1} s \left( \frac{4}{5} s - 1 \right) \left[ u^{\prime \prime }(s)+\frac{\alpha }{s} \, u^\prime (s) -\frac{nu(s)}{u(s)+k} \right] ds, \end{aligned}$$
(51)

where initial iterate \(u_0=1\), and \(\alpha =1\). \(E_n\) is defined as the maximum absolute error of our PGS approach while \(V_n\) is the maximum absolute error obtained by the technique proposed by Singh and Kumar [33]. The results in Table 5 below confirm that the Green’s function approach is more accurate than the other existing method.

Table 5 Residual errors for Example 4 using our scheme and method in [33]
Full size table

Example 5

Finally we consider the following nonlinear SBVP, which is also taken from Singh and Kumar [33]:

$$\begin{aligned} \displaystyle { u^{\prime \prime }(x) = -\frac{3}{x} u^{\prime }(x) +\frac{1}{2}-\frac{1}{8u^2(x)},} \end{aligned}$$
(52)

where \(0 < x \le 1\) and subject to

$$\begin{aligned} u^\prime (0) =0 , \; \;\; u(1)=1 . \end{aligned}$$
(53)

This nonlinear SBVP arises in the radial stress on a rotationally symmetric shallow membrane cap [15]. The exact solution is not known explicitly. The Green’s function for the linear equation \(L[u]=u^{\prime \prime }=0\) subject to homogeneous BCs, results in the subsequent form of the PGS (12).

$$\begin{aligned} \displaystyle u_{n+1}= & {} u_n-\int _{0}^{x} s^3 \left( \frac{1}{2}-\frac{1}{2x^2}\right) \left[ u^{\prime \prime }(s)+\frac{3}{s} \, u^\prime (s) + \frac{1}{8u^2}-\frac{1}{2} \right] ds \nonumber \\&-\int _{x}^{1} s \left( \frac{s^2}{2}-\frac{1}{2}\right) \left[ u^{\prime \prime }(s)+\frac{3}{s} \, u^\prime (s) + \frac{1}{8u^2}-\frac{1}{2} \right] ds, \end{aligned}$$
(54)

where the initial iterate is \(u_0=1\). \(E_n\) is defined as the maximum absolute error of Green’s function approach while \(R_n\) is the maximum absolute error obtained by the proposed technique in Singh and Kumar [33]. After comparing the results in the Table 6, we assure that the PGS strategy is more accurate.

Table 6 Residual errors for Example 5 using our scheme and the method in [33]
Full size table

Conclusion

In this paper, a recent approach based on embedding Green’s function into fixed-point iteration, is used to solve an extended class of second order nonlinear singular boundary value problems. Five test problems have been considered that demonstrate the efficiency of the scheme. The results confirmed the convergence of the scheme numerically. This claim has been justified by proving convergence of the proposed scheme as well as its rate of convergence. Moreover, the scheme seems to be computationally highly accurate for solving the given class of nonlinear SBVPs, when it compared with other existing methods. In future work, we plan to apply the proposed approach to optimal control problems (see [12, 26]).