Introduction

Nanotechnology is an industrial revolution and one of the hottest fields of research. In the last few years, carbon nanotubes (CNTs) have attracted extensive research activities due to their exceptional mechanical, physical, chemical and thermal properties. CNTs were first discovered by Iijima [1] in 1991.

Carbon nanotubes (CNTs) are unique nanostructured materials that comprise a basic element of nanotechnology. Given their extraordinary mechanical and physical properties, together with their large aspect ratio and low density, CNTs are ideal components of nanodevices. Carbon nanotube research is one of the most promising domains in the fields of mechanics, physics, chemistry, and materials science. A wide range of applications of CNTs have been reported in the literature, including applications in nanoelectronics, nanodevices, and nanocomposites [1–8]. It is important to have accurate theoretical models for the vibrational behavior of CNTs. The natural frequencies of CNTs play an important role in nanomechanical resonators.

Since the vibrations of CNTs are of considerable importance in a number of nanomechanical devices such as oscillators, charge detectors, field emission devices and sensors, many researches have been so far devoted to the problem of the vibration of CNTs [9–12]. A good review on the vibration of CNTs is given by Gibson et al. [13] including a concise review of as many of the relevant publications as possible. Based on the theory of thermal elasticity mechanics, Wang et al. [14] studied the vibration and instability analysis of fluid-conveying single-walled carbon nanotubes (SWNTs) considering the thermal effect.

However, most of the investigations conducted on the vibration of CNTs have been restricted to the linear regime and fewer works were done on the nonlinear vibration of these materials. Recently, Fu et al. [15] studied the nonlinear vibrations of embedded nanotubes using the incremental harmonic balanced method (IHBM). In that work, single-walled nanotubes (SWNTs) and double-walled nanotubes (DWNTs) considered for the study.

Multi walled carbon nanotubes (MWCNT) composite nanofibers with various MWCNT contents were fabricated by electrospinning process and their microwave absorption properties were evaluated in the frequency range of 8–12 GHz at room temperature [16].

Mathematical modelling is a vantage point to reach a solution in an engineering problem, so the accurate modelling of nonlinear engineering problems is an important step to obtain accuratre solutions [17–19]. Most differential equations of engineering problems do not have exact analytic solutions so approximation and numerical methods must be used. Recently some different methods have been introduced to solving these equations, such as the Variational Iteration Method (VIM) [20], Local Fractional Variational Iteration Method (LFVIM) [21, 22], Adomian Decomposition Method (ADM) [23], Homotopy Perturbation Method (HPM) [24], Local Fractional Homotopy Perturbation Method (LFHPM) [25, 26], Parameterized Perturbation Method (PPM) [27], Differential Transformation Method (DTM) [28, 29], Two Dimensional Extended Differential Transform (TDEDT) [30], Modified Homotopy Perturbation Method (MHPM) [31], Least Square Method (LSM) [32–34], Collocation Method (CM) [35], Galerkin Method (GM) [36], Optimal Homotopy Asymptotic Method (OHAM) [37], asymptotic perturbation method [38], local fractional Fourier series method [39, 40] and Differential Quadrature Method (DQM) [41–43].

Nonlocal discrete and continuous models were developed for vibration analyses of two and three-dimensional ensembles of SWCNTs subjected to laterally applied loads by Kiani [44]. Using nonlocal Rayleigh beam theory, the discrete and continuous equations of motion for two and three-dimensional ensembles of SWCNTs were developed, and then solved in their corresponding space and time domains.

A linear model was developed to take into account the van der Waals forces between adjacent SWCNTs because of their bidirectional transverse displacements Kiani [45]. Using Hamilton’s principle, the discrete equations of motion of free vibration of the nanostructure were obtained based on the nonlocal Rayleigh, Timoshenko, and higher-order beam theories.

Transverse wave characteristics within 3D ensembles of SWCNTs was aimed to be carefully studied by Kiani [46]. He used nonlocal continuum theory of Eringen and Hamilton’s principle to develop the nonlocal-discrete equations of motion of the problem based on the Rayleigh, Timoshenko, and higher-order beam theories.

In this study, the nonlocal continuum theory is utilized to simulate the nonlinear vibration of a SWCNT conveying fluid, employing Pasternak-type elastic foundation. To solve the governing equations of the problem, one of the strong numerical methods named the Keller Box Method (KBM) is used. The effects of the flow velocity, vibration amplitude, nonlocal parameter and stiffness of the medium on the nonlinear frequency variation are illustrated.

Mathematical Formulation

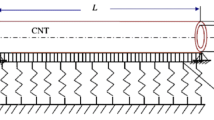
A single-walled carbon nanotube with fluid flow embedded in elastic medium is shown in Fig 1. The nanotube is assumed to be simply supported at both ends and the effect of gravity is negligible.

Fig. 1
figure 1

A single-walled carbon nanotube with fluid flow

Full size image

For Euler–Bernoulli beam theory, the relationship among the transverse shear force Q, the bending moment of the model M, and the longitudinal force N are [47]:

$$\begin{aligned} \frac{\partial Q}{\partial x}=\frac{\partial ^{2}M}{\partial ^{2}x}+N\frac{\partial ^{2}w}{\partial ^{2}x} \end{aligned}$$
(1)

N and M are the stress resultants defined as follows:

$$\begin{aligned} M=\int {z\cdot \sigma _{xx}}dA_c =\int {z\cdot E\varepsilon _{xx}}dA_c,\quad N=\int {\sigma _{xx}}dA_c =\int {E\varepsilon _{xx}}dA_c \end{aligned}$$
(2)

where E is the Young’s modulus of the SWCNT.

The nonlocal continuum theory, presented by Eringen in 1983, shows a more precise constitutive rule for small-scale structures in comparison with the common local elastic theories. This definition of nonlocal elasticity is based on lattice dynamics and observations on phonon dispersion. The nonlocal constitutive equation for the uniaxial bending stress state forms as:

$$\begin{aligned} \sigma _{xx}=E\varepsilon _{xx} +(e_{0}a)^{2}\frac{\partial ^{2}\sigma _{xx}}{\partial x^{2}} \end{aligned}$$
(3)

The parameter \((e_{0}a)\) shows the small-scale effect which is called the nonlocal parameter. In which the parameter \(e_0\) is estimated such that the relations of the nonlocal elasticity model could provide a good approximation of atomic dispersion curves of plane waves with those of atomic lattice dynamics, and a expresses represents an internal length such as lattice parameter and granular size

$$\begin{aligned} M-(e_{0}a)^{2}\frac{\partial ^{2}M}{\partial x^{2}}=\int {zE\varepsilon _{xx} dA_c} \end{aligned}$$
(4)

Based on the Euler–Bernoulli continuum theory, the displacement field of the model is expressed as:

$$\begin{aligned} u(x,z,t)=u(x,t)-z\cdot \frac{\partial w}{\partial x},\quad w(x,z,t)=w(x,t) \end{aligned}$$
(5)

Also the von-Karman strain based on the displacement field is approximately expressed [48]:

$$\begin{aligned} \varepsilon _{xx} \equiv \frac{\partial u(x,z,t)}{\partial x}+\frac{1}{2}\left( \frac{\partial w(x,z,t)}{\partial x}\right) ^{2}=\frac{\partial ^{2}u}{\partial x^{2}}-z\cdot \frac{\partial ^{2}w}{\partial x^{2}}+\frac{1}{2}\left( \frac{\partial w(x,z,t)}{\partial x}\right) ^{2} \end{aligned}$$
(6)

From Eqs. (3) and (6), the nonlocal stress resultant can be defined as:

$$\begin{aligned} M-(e_0 a)^{2}\frac{\partial ^{2}M}{\partial x^{2}}=EI\frac{\partial ^{2}w}{\partial x^{2}} \end{aligned}$$
(7)

where the following relation has been used

$$\begin{aligned} \int {zdA_c} =0,\quad \int {z^{2}} dA_c =I \end{aligned}$$
(8)

The equations of motion can now be expressed in terms of displacements. Substituting for the second derivative of M from Eq. (1) into Eq. (8), we obtain

$$\begin{aligned} M=(e_0 a)^{2}\left[ \frac{\partial Q}{\partial x}-N\frac{\partial ^{2}w}{\partial x^{2}}\right] +EI\frac{\partial ^{2}w}{\partial x^{2}} \end{aligned}$$
(9)

Now, substituting for M from Eq. (9) into Eq. (7), the governing equation of motion is readily identified as

$$\begin{aligned} EI\frac{\partial ^{4}w}{\partial x^{4}}+\frac{\partial Q}{\partial x}-N\frac{\partial ^{2}w}{\partial x^{2}}-(e_0 a)^{2}\left[ {\frac{\partial ^{3}Q}{\partial x^{3}}-N\frac{\partial ^{4}w}{\partial x^{4}}} \right] =0 \end{aligned}$$
(10)

Hence, the governing equations for a fluid-conveying SWCNT can be written as

$$\begin{aligned}&m_c \frac{\partial ^{2}w}{\partial t^{2}}+EI\frac{\partial ^{4}w}{\partial x^{4}}+k_e w-k_p \frac{\partial ^{2}w}{\partial x^{2}}+F\frac{\partial ^{2}w}{\partial x^{2}}+m_f \left( 2v\frac{\partial ^{2}w}{\partial x\partial t}+v^{2}\frac{\partial ^{2}w}{\partial x^{2}}+\frac{\partial ^{2}w}{\partial t^{2}}\right) \nonumber \\&\quad -\,(e_0 a)^{2}\left[ m_c \frac{\partial ^{4}w}{\partial t^{2}\partial x^{2}} +k_e \frac{\partial ^{2}w}{\partial x^{2}}-k_p \frac{\partial ^{4}w}{\partial x^{4}}+F\frac{\partial ^{4}w}{\partial x^{4}}\right. \nonumber \\&\quad \left. +\,m_f \left( 2v\frac{\partial ^{2}w}{\partial x^{3}\partial t}+v^{2} \frac{\partial ^{4}w}{\partial x^{4}}+\frac{\partial ^{4}w}{\partial x^{2}\partial t^{2}}\right) -\frac{EA_c }{2L}\cdot \frac{\partial ^{4}w}{\partial x^{4}}\cdot \int _0^L {\left( \frac{\partial w}{\partial x}\right) ^{2}dx} \right] \nonumber \\&\quad -\frac{EA_c }{2L}\frac{\partial ^{2}w}{\partial x^{2}}\int _0^L {\left( \frac{\partial w}{\partial x}\right) ^{2}dx} =0 \end{aligned}$$
(11)

The deflection of the nanotube is subjected to the following boundary conditions:

$$\begin{aligned} w(0,t)= & {} \frac{\partial ^{2}w(0,t)}{\partial x^{2}}=0\quad \hbox {at}\quad \hbox {x}=0 \nonumber \\ w(L,t)= & {} \frac{\partial ^{2}w(L,t)}{\partial x^{2}}=0\quad \hbox {at}\quad \hbox {x}=\hbox {L} \end{aligned}$$
(12)

\(\hbox {w}(\hbox {x},\hbox {t})\) can be expanded as:

$$\begin{aligned} w(x,t)=q(t).\phi _1(x) \end{aligned}$$
(13)

\(\Phi _{1}\) performs as the normalized mode functions of the nanotube from the linear vibration analysis due to the specified boundary conditions.

Substituting Eq. (13) in Eq. (11) leads to:

$$\begin{aligned} {\ddot{q}}(t)+\frac{\left[ {1+e^{2}\left( K_e +K_p -T-U^{2}\right) +K_e +K_p -T-U^{2}} \right] \cdot \omega _0^2}{1+e^{2}}\cdot q(t)+\frac{\omega _0^2}{4r^{2}}\cdot q^{3}(t)=0\nonumber \\ \end{aligned}$$
(14)

These equations can be made dimensionless by using the following definitions

$$\begin{aligned} \omega _0= & {} \frac{\pi ^{2}}{L^{2}}\sqrt{\frac{EI}{m_c+m_f}},\quad e=\frac{\pi }{L}(e_0 a),\quad K_e =\frac{L^{4}}{\pi ^{4}}\frac{1}{EI}k_e,\quad K_p =\frac{L^{2}}{\pi ^{2}}\frac{1}{EI}k_p, \nonumber \\ T= & {} \frac{L^{2}}{\pi ^{2}}\frac{1}{EI}F,\quad U=\frac{L}{\pi }\sqrt{\frac{m_f }{EI}},\quad r=\sqrt{\frac{I}{A_c}} \end{aligned}$$
(15)

Flexural and shear frequencies are two types of frequencies in nonlocal Timoshenko theory.

To study the flexural vibration characteristics of composite beams, one may resort to the Timoshenko beam model [49]. Such a model assumes that, during transverse vibration, each plane cross section of the beam remains plane but not necessarily normal to the centerline of the beam. These assumptions constitute a first order approximation to rotary inertia and transverse shear deformation.

The Bernoulli-Euler beam model neglects both rotary inertia and transverse shear deformation.

Standard tests like ASTM D790 are available to characterize the flexural moduli of composite beams [50]. The advantages of this method are derived from the ease of running and instrumenting. This test, however, is not recommended for thick beam samples as the presence of both transverse shear and transverse normal deformations would adversely affect the results. Such effects are more pronounced in composite beams which have a small transverse shear modulus as compared to the flexural modulus. Fischer et al. [51] proposed a method for the simultaneous determination of both flexural and shear moduli of thick beams using a three-point bending test.

In the proposed model,the vibration mode is classified into the two distinct groups: flexural and torsional modes. In the flexural mode, the effect of rotatory inertia reduces the natural frequencies,which is more significant for higher modes.The natural frequencies for the torsional mode exist independently. The natural frequencies generally increase with increasing thickness ratio, and there is dynamic optimal thickness ratio for the torsional mode, which is the best thickness ratio for attaining a strongest beam for the vibration.

Numerical Procedure

In this study, Keller Box Method (KBM) is used as an efficient numerical method for solving the problem using Maple 15.0 software. The Keller Box scheme is a face-based method for solving partial differential equations that has numerous attractive mathematical and physical properties. It is shown that these attractive properties collectively follow from the fact that the scheme discretizes partial derivatives exactly and only makes approximations in the algebraic constitutive relations appearing in the PDE. The exact Discrete Calculus associated with the Keller-Box scheme is shown to be fundamentally different from all other mimetic (physics capturing) numerical methods. Actually, Keller Box is a variation of the finite volume approach in which unknowns are stored at control volume faces rather than at the more traditional cell centers. The name alludes to the fact that in space-time, the unknowns sit at the corners of the space-time control volume which is a box in one space dimension on a stationary mesh. The original development of the method [52] dealt with parabolic initial value problems such as the unsteady heat equation. The method was made better known by Bradshaw et al. [53] as a method for the solution of the boundary layer equations.

Keller Box method is one of the important techniques for solving the parabolic flow equation, especially the boundary layer equations [54]. This scheme is implicit with second order accuracy in both space and time and allows the step size of time and space to be arbitrary (nonuniform). This makes it efficient and appropriate for the solution of parabolic partial differential equations. The disadvantage of the method is that the computational effort per time step is expensive due to its step which has to replace the higher derivative by first derivatives, so that the second-order diffusion equation can be written as a system of two first-order equations [55].

There are a large variety of numerical methods which are used to solve mathematical physical problems. Two particular methods, the Box scheme and the Crank-Nicolson scheme, seem to dominate in most practical applications. Keller [56] himself preferred and stressed the Box scheme. This scheme was devised in Keller [52] for solving diffusion problems, but it has subsequently been applied to a broad class of problems. It has been tested extensively on laminar flows, turbulent flows, nonlinear vibration, separating flows and many other such problems [57].

Results and Discussion

Figure 2 shows the behavior of nonlinear frequency for different values of nonlocal parameters. The figure shows that the nonlinear frequency increases with an increase of the nonlocal parameter. The reason is that the nonlocal theory introduces a more flexible model and with increasing the flexibility, the effect of the nonlinearity on the model becomes more significant. The Pasternak model expresses the base of the SWCNT. The Pasternaktype foundation, also named the two-parameter foundation model, models the interaction between the medium and the nanotube using two different parameters. These two paramters are: Winkler constant (\(K_{e}\)) which shows normal pressure and Pasternak constant (\(K_{p}\)), which express transverse shear stress due to the interaction of shear deformation of the surrounding elastic medium.

Fig. 2
figure 2

The variation of nonlinear frequency against the maximum nonlinear amplitude for different nonlocal parameters

Full size image
Fig. 3
figure 3

The variation of nonlinear frequency against the maximum nonlinear amplitude for different axial tensions

Full size image

Figure 3 shows the nonlinear frequency variation against the nonlinear amplitude as a function of axial tension. It is shown that that axial tension of the SWCNT can decrease the difference between the nonlinear and the linear resonant frequency, and this effect is profound for high vibration amplitude. It means that increasing the axial tension F can control the nonlinearity.

Fig. 4
figure 4

The variation of nonlinear frequency against the maximum nonlinear amplitude for different Winkler constants

Full size image
Fig. 5
figure 5

The variation of nonlinear frequency against the maximum nonlinear amplitude for different Pasternak constants

Full size image

Figures 4 and 5 display the influences of Winkler constants (\(K_{e}\)) and Pasternak constants (\(K_{p}\)) on nonlinear frequency variation. Figure 4 indicated that by increasing the Winkler constant, the nonlinear frequency decreases, especially for low vibration amplitudes. This means that as the nanotube vibrates in a stiff medium, the nonlinear frequency turn to the linear frequency. It means that for low amplitudes and stiff elastic foundations, the linear simulation of the SWCNT shows a precise theoretical model for transverse flow-induced vibrations.

Figure 5 depicts the effects of Pasternak constant on the nonlinear frequency. It can be seen an increase in the shear stiffness of the medium results in the decrease of the nonlinear frequency for the small vibration amplitudes, and also the nonlinear flow-induced frequency reduces to the linear.

Fig. 6
figure 6

The variation of nonlinear frequency against the dimensionless fluid velocity for different nonlocal parameters

Full size image

The influence of the effect nonlocal parameter on the nonlinear frequency variation against the flow velocity is shown in Fig. 6. It is resulted that the influence of the nonlocal parameter is greater at higher flow velocities in comparison with lower flow velocities. This effect is more significant when the nonlocal parameter increases.

Fig. 7
figure 7

The variation of nonlinear frequency against the dimensionless fluid velocity for different axial tensions

Full size image

Figure 7 illustrates the nonlinear frequency variation against the flow velocity for various axial tensions. The result shows that for low flow velocities, the effect of axial tension on the nonlinear frequency variation is little. For high flow velocities, the nonlinear frequency variation decreases with increment in axial tensions.

Fig. 8
figure 8

The variation of nonlinear frequency against the dimensionless fluid velocity for different Winkler constants

Full size image

Figure 8 depicts the influence of the Winkler constant on the nonlinear frequency variation against the flow velocities. It shows that the nonlinear frequency variation does not change greatly for low fluid velocities and the mediums with rigid elastic properties origin the difference between the nonlinear and linear frequency to remain unchanged with respect to flow velocity. Furthermore, for flexible mediums, the nonlinear frequency variation increases with the flow velocity.

Fig. 9
figure 9

The variation of nonlinear frequency against the dimensionless fluid velocity for different Pasternak constant

Full size image

The effect of the Pasternak constant on the nonlinear frequency variation with the dimensionless flow velocity is shown in Fig. 9. The result shows that for low fluid velocities (\(\hbox {U}<0.5\)) and as the shear stiffness of the elastic medium increases, the nonlinear frequency variation decreases and for the higher flow velocities it remains constant. This shows that the nonlinear vibration behavior of the SWCNT is independent of the fluid flow.

Conclusion

In this paper, the Keller Box Method (KBM) is used to solve the nonlinear vibration model of a fluid-conveying singel-walled carbon nanotube embedded in a Pasternak foundation. The results show that the axial tension restricts the nonlinear effect and limits the flow induced-vibration of the nanotube at high flow velocity and for high vibration amplitudes.

It is resulted that influence of the nonlocal parameter is greater at higher flow velocities in comparison with lower flow velocities. Also, It can be concluded that by increasing the Winkler constant, the nonlinear frequency decreases, especially for low vibration amplitudes.