Introduction

Carbon nanotubes (CNTs) are an allotrope of carbon. They take the form of cylindrical carbon molecules and have novel properties that make them potentially useful in a wide variety of applications in nanotechnology, electronics, optics, and other fields of materials science. In the recent few years, carbon nanotubes (CNTs) have been one of the most promising studies in the field of mechanics, physics, chemistry, materials science, and so on. They exhibit extraordinary strength and unique electrical properties, and are efficient conductors of heat.

The discovery of CNTs by Iijima [1], especially the discovery of the single-wall nanotube (SWNT) and the successful composition of the CNT in the macrography scale, has received considerable attention in recent years. At the present, CNT has been the chief research subject in the area of the fullerene, and it has been one of the most promising researches in the field of mechanics, physics, chemistry, materials science, and so on. Because of their novel electronic, mechanical, and other physical and chemical properties, CNT holds substantial promise as building blocks for nanoelectronics, nanodevices, and nanocomposites [2–4]. For example, the stiffness of CNT is 100 times as that of the steel, but the weight is one-sixth times as that of the steel. It is foreseen to be the most promising one-dimensional nanophase materials in the 21st century. Therefore, it is necessary and significant to study its mechanical property.

The classic elastic continuum models have been presented to investigate the vibration behavior of CNTs. Yoon et al. [5] examined the effect of moving internal fluid on free vibration and flow induced flutter instability of cantilever CNTs according to the continuum elastic model. It was resulted that the resonance frequencies were related to the fluid-flow velocity. Structural instability of the CNTs could happen at a critical flow velocity.

A theoretical approach based on a continuum elastic model is studied by Natsuki et al. [6] to investigate the sound wave propagation in both single- and double-walled CNTs filled with fluids and found that there exist several critical frequencies, and free wave speed of the fluids influences the wave propagation in fluid-filled CNTs.

Reddy et al. [7] examined the influence of fluid flow on the free vibration and instability of fluid-conveying single-walled CNTs (SWCNTs). Wang et al. [8] studied the Timoshenko beam model and the DQ method for free vibration analysis of multi-walled CNTs (MWCNTs). Zhang et al. [9]. used a double-elastic beam model for transverse vibrations of double-walled carbon nanotubes under compressive axial load according to the Euler–Bernoulli beam theory. The effect of internal moving fluid and compressive axial load on the nonlinear vibration and stability of conveying CNTs is presented by Rasekh and Khadem [10].

The nonlocal Euler–Bernoulli elasticity theory [11] as a modifying theory for nanostructers and nanoscale models have been greatly used to model CNTs due to the nanoscale effects. In this theory, the small scale effects are captured by assuming that the stress at a point is a function of the strains at all other points of the domain. Several references are found related to the nonlocal elasticity theory [12, 13].

Most of the studies are limited to linear vibration at present; however, the deformations of CNTs are nonlinear in nature. Only when considering the nonlinearities in geometry and physics, the more precise dynamic properties of CNTs can be obtained, and then, the nanostructures can receive more wide applications. Fortunately, more and more researchers have begun to realize these ideas, and the nonlinear mechanical behaviors of CNTs have received considerable attentions in recent years. Pantano and Boyce investigated the effect of the characteristic wavelike or wrinkles on the bending mode of CNTs under considering the geometric nonlinearity and explained the phenomenon that the curve modes of CNTs decrease with the increase in the diameter of CNTs. Fu et al. [14] analyzed the nonlinear vibration for embedded CNTs and got the amplitude frequency response curves of the nonlinear free vibration for the SWCNTs and DWCNTs. Yan et al. [15] showed that the radial vibration modes of the inner and outer tubes of simply supported DWCNTs and concluded that the system had twice dynamical mode transitions as the frequency increased.

MWCNTs composite nanofibers with various MWCNT contents were fabricated by electrospinning process, and their microwave absorption properties were evaluated in the frequency range of 8–12 GHz at room temperature [16].

Mathematical modeling is a vantage point to reach a solution in an engineering problem, so the accurate modeling of nonlinear engineering problems is an important step to obtain accurate solutions [17–21]. Most differential equations of engineering problems do not have exact analytic solutions, so approximation and numerical methods must be used. Recently, some different methods have been introduced to solving these equations, such as the variational iteration method (VIM) [22, 23], homotopy perturbation method (HPM) [24, 25], parameterized perturbation method (PPM) [26], differential transformation method (DTM) [27, 28], modified homotopy perturbation method (MHPM) [29], least square method (LSM) [30–32], collocation method (CM) [33, 34], galerkin method (GM) [35], optimal homotopy asymptotic method (OHAM) [36, 37], and differential quadrature method (DQM) [38].

In this study, the nonlocal continuum theory is utilized to simulate the nonlinear vibration of an SWCNT conveying fluid, employing Pasternak-type elastic foundation. To solve the governing equations of the problem, one of the newest analytical methods named the PPM is used. This method is one of the strong and effect method for solving nonlinear problems and is investigated and developed by some authors to solve nonlinear equations arising in engineering problems.

This approach can be used as an efficient and practical technique for solving such nonlinear problems in vibration field. Comparisons revealed that PPM is a powerful approach for solving these problems. In addition, the results showed that the main attributions of this method are very straightforward calculations and low computational burden compared with previous analytical and numerical approaches.

It can be found that PPM is very efficient but straightforward technique, while you just employ a transformation equation and solve the original equation without the separation of linear and nonlinear terms. This method can be easily extended to other strongly nonlinear vibration equations and can be found widely applicable in engineering and science.

The obtained results show good agreement with the numerical simulation and also with a previous study. The effects of the vibration amplitude, flow velocity, nonlocal parameter, and stiffness of the medium on the nonlinear frequency variation are illustrated.

Mathematical modeling

Figure 1 shows an SWCNT conveying fluid, as a hollow cylindrical tube in a Pasternak-type elastic medium. The nanotube is assumed to be simply supported at both ends, and the effect of gravity is negligible.

Fig. 1
figure 1

Single-walled carbon nanotube embedded in a Pasternak-type foundation model

Full size image

For the Euler–Bernoulli beam theory, the relationships among the transverse shear force Q, the bending moment of the model M, and the longitudinal force N are [39]:

$$ \frac{\partial Q}{\partial x} = \frac{{\partial^{2} M}}{{\partial^{2} x}} + N\frac{{\partial^{2} w}}{{\partial^{2} x}} $$
(1)

N and M are the stress resultants, defined as follows:

$$ M = \int {z.\sigma_{xx} } {\text{d}}A_{c} = \int {z.E\varepsilon_{xx} } {\text{d}}A_{c} ,\;\;\;\;N = \int {\sigma_{xx} } {\text{d}}A_{c} = \int {E\varepsilon_{xx} } {\text{d}}A_{c} $$
(2)

where E is Young’s modulus of the SWCNT.

The nonlocal continuum theory, presented by Eringen in 1983, shows a more precise constitutive rule for small-scale structures in comparison with the common local elastic theories. This definition of nonlocal elasticity is based on lattice dynamics and observations on phonon dispersion. The nonlocal constitutive equation for the uniaxial bending stress state forms as:

$$ \sigma_{xx} = E\varepsilon_{xx} + (e_{0} a)^{2} \frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} $$
(3)

The parameter \( (e_{0} a) \) shows the small-scale effect, which is called the nonlocal parameter, in which the parameter \( e_{0} \) is estimated such that the relations of the nonlocal elasticity model could provide a good approximation of atomic dispersion curves of plane waves with those of atomic lattice dynamics, and \( a \) represents an internal length, such as lattice parameter and granular size

$$ M - (e_{0} a)^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} = \int {zE\varepsilon_{xx} {\text{d}}A_{c} } $$
(4)

Based on the Euler–Bernoulli continuum theory, the displacement field of the model is expressed as:

$$ u(x,z,t) = u(x,t) - z.\frac{\partial w}{\partial x},\;\;\;\;w(x,z,t) = w(x,t) $$
(5)

In addition, the von Karman strain based on the displacement field is approximately expressed [40]:

$$ \varepsilon_{xx} \equiv \frac{\partial u(x,z,t)}{\partial x} + \frac{1}{2}\left( {\frac{\partial w(x,z,t)}{\partial x}} \right)^{2} = \frac{{\partial^{2} u}}{{\partial x^{2} }} - z.\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w(x,z,t)}{\partial x}} \right)^{2} $$
(6)

From Eqs. (3) and (6), the nonlocal stress resultant can be defined as

$$ M - (e_{0} a)^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} = EI\frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(7)

where the following relation has been used

$$ \int {z{\text{d}}A_{c} } = 0,\;\;\;\;\int {z^{2} } {\text{d}}A_{c} = I $$
(8)

The equations of motion can now be expressed in terms of displacements. Substituting for the second derivative of M from Eq. (1) into Eq. (8), we obtain

$$ M = (e_{0} a)^{2} \left[ {\frac{\partial Q}{\partial x} - N\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right] + EI\frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(9)

Now, substituting for M from Eq. (9) into Eq. (7), the governing equation of motion is readily identified as

$$ EI\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{\partial Q}{\partial x} - N\frac{{\partial^{2} w}}{{\partial x^{2} }} - (e_{0} a)^{2} \left[ {\frac{{\partial^{3} Q}}{{\partial x^{3} }} - N\frac{{\partial^{4} w}}{{\partial x^{4} }}} \right] = 0 $$
(10)

Hence, the governing equations for a fluid-conveying SWCNT can be written as

$$ \begin{array}{l} m_{c} \frac{{\partial^{2} w}}{{\partial t^{2} }}\, +\, EI\frac{{\partial^{4} w}}{{\partial x^{4} }}\, +\, k_{\text{e}} w - k_{\text{p}} \frac{{\partial^{2} w}}{{\partial x^{2} }}\, +\, F\frac{{\partial^{2} w}}{{\partial x^{2} }}\, +\, m_{f} \left( {2v\frac{{\partial^{2} w}}{\partial x\partial t}\, +\, v^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}\, +\, \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \hfill \\ - (e_{0} a)^{2} \left[ {m_{c} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }}\, +\, k_{\text{e}} \frac{{\partial^{2} w}}{{\partial x^{2} }} - k_{\text{p}} \frac{{\partial^{4} w}}{{\partial x^{4} }}\, +\, F\frac{{\partial^{4} w}}{{\partial x^{4} }}\, +\, m_{f} \left( {2v\frac{{\partial^{2} w}}{{\partial x^{3} \partial t}}\, +\, v^{2} \frac{{\partial^{4} w}}{{\partial x^{4} }}\, +\, \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right) - \frac{{EA_{c} }}{2L}.\frac{{\partial^{4} w}}{{\partial x^{4} }}.\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} {\text{d}}x} } \right] \hfill \\ - \frac{{EA_{c} }}{2L}\frac{{\partial^{2} w}}{{\partial x^{2} }}\int_{0}^{L} {\left( {\frac{\partial w}{\partial x}} \right)^{2} {\text{d}}x} = 0 \hfill \\ \end{array} $$
(11)

The deflection of the nanotube is subjected to the following boundary conditions:

$$ \begin{aligned} w(0,t) = \frac{{\partial^{2} w(0,t)}}{{\partial x^{2} }} = 0\quad {\text{ at }}x{ = 0} \hfill \\ w(L,t) = \frac{{\partial^{2} w(L,t)}}{{\partial x^{2} }} = 0\quad {\text{ at }}x{\text{ = L}} \hfill \\ \end{aligned} $$
(12)

W(x,t) can be expanded as:

$$ w(x,t) = q(t).\phi_{1} (x) $$
(13)

Φ1 performs as the normalized mode functions of the nanotube from the linear vibration analysis due to the specified boundary conditions.

Substituting Eq. (13) in Eq. (11) leads to:

$$ \ddot{q}(t) + \frac{{\left[ {1 + e^{2} (K_{{\text{e}}} + K_{{\text{p}}} - T - U^{2} ) + K_{{\text{e}}} + K_{{\text{p}}} - T - U^{2} } \right].\omega _{0}^{2} }}{{1 + e^{2} }}.q(t) + \frac{{\omega _{0}^{2} }}{{4r^{2} }}.q^{3} (t) = 0 $$
(14)

These equations can be made dimensionless using the following definitions

$$ \omega_{0} = \frac{{\pi^{2} }}{{L^{2} }}\sqrt {\frac{EI}{{m_{c} + m_{f} }}} ,\;\;e = \frac{\pi }{L}(e_{0} a),\;\;K_{\text{e}} = \frac{{L^{4} }}{{\pi^{4} }}\frac{1}{EI}k_{\text{e}} ,\;\;K_{\text{p}} = \frac{{L^{2} }}{{\pi^{2} }}\frac{1}{EI}k_{\text{p}} ,\;\;T = \frac{{L^{2} }}{{\pi^{2} }}\frac{1}{EI}F,\;\;U = \frac{L}{\pi }\sqrt {\frac{{m_{f} }}{EI}} ,\;\;r = \sqrt {\frac{I}{{A_{c} }}} $$
(15)

Analytical solution

The PPM was first proposed in 1999 in [41]. An expanding parameter is introduced by a linear transformation

$$ f = \varepsilon u + a $$
(16)

where ε is the perturbation parameter, by substituting Eq. (16) into an original equation to have no secular term in the equation; we can obtain the unknown constant parameters a and b. Then, the solution is expanded in the form

$$ u = \sum\limits_{i = 0}^{n} {\varepsilon^{i} u_{i} } = u_{0} + \varepsilon u_{1} + \varepsilon^{2} u_{1} + \cdots $$
(17)
$$ q = A_{0} \cos (\omega t) - \frac{1}{8}\frac{{A_{0}^{3} \cos (\omega t)\alpha_{2} }}{{\omega^{2} }} + \frac{1}{8}\frac{{A_{0}^{3} \cos^{3} (\omega t)\alpha_{2} }}{{\omega^{2} }} $$
(18)
$$ q = 0.9771563284\cos (0.04831221268\pi^{2} t) + 0.02284367164\cos^{3} (0.04831221268\pi^{2} t) $$
(19)

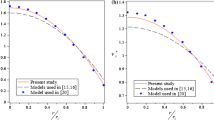
To validate the present solution of the problem and find the accuracy, the comparison between our solution and numerical result is done. Good agreement between the present PPM and the numerical solution is observed in Fig. 2.

Fig. 2
figure 2

Comparison between PPM solution and numerical result

Full size image

Fourth-order Runge–Kutta numerical method

It is obvious that the type of the current problem is the boundary value problem (BVP), and the appropriate numerical method needs to be selected. The numerical solution is performed using the algebra Maple package to solve the present problem. The available methods in this software are a combination of the base scheme (midpoint or trapezoid), and a method enhancement scheme (deferred corrections or Richardson extrapolation). The trapezoid method is generally efficient for typical problems, but the midpoint method can handle harmless end-point singularities that the trapezoid method cannot. The midpoint method, also known as the fourth-order Runge–Kutta method, improves the Euler method by adding a midpoint in the step, which increases the accuracy by one order [42]. Thus, the fourth-order Runge–Kutta method is used as a suitable numerical technique in this study.

Results and discussion

In this section, the effects of the nonlocal parameters (e 0 a), axial tensions (F), Winkler constants (K e), and Pasternak constants (K p) on nonlinear frequency are studied in the following figures.

Figure 3 shows the behavior of nonlinear frequency for different values of nonlocal parameters. The figure shows that the nonlinear frequency increases with an increase in the nonlocal parameter. The reason is that the nonlocal theory introduces a more flexible model, and with increasing the flexibility, the effect of the nonlinearity on the model becomes more significant. The Pasternak model expresses the base of the SWCNT. The Pasternak-type foundation, also named the two-parameter foundation model, models the interaction between the medium and the nanotube using two different parameters. These two parameters are: Winkler constant (K e), which shows normal pressure and Pasternak constant (K p), which express transverse shear stress due to the interaction of shear deformation of the surrounding elastic medium.

Fig. 3
figure 3

Variation of nonlinear frequency against the maximum nonlinear amplitude for different nonlocal parameters

Full size image

Figure 4 shows the nonlinear frequency variation against the nonlinear amplitude as a function of axial tension. It is shown that the axial tension of the SWCNT can decrease the difference between the nonlinear and the linear resonant frequency, and this effect is profound for high vibration amplitude. It means that increasing the axial tension F can control the nonlinearity.

Fig. 4
figure 4

Variation of nonlinear frequency against the maximum nonlinear amplitude for different axial tensions

Full size image

Figures 5 and 6 show the influences of Winkler constants (K e) and Pasternak constants (K p) on nonlinear frequency variation. Figure 5 indicated that by increasing the Winkler constant, the nonlinear frequency decreases, especially for low vibration amplitudes. This means that as the nanotube vibrates in a stiff medium, the nonlinear frequency turns to the linear frequency. It means that for low amplitudes and stiff elastic foundations, the linear simulation of the SWCNT shows a precise theoretical model for transverse flow-induced vibrations.

Fig. 5
figure 5

Variation of nonlinear frequency against the maximum nonlinear amplitude for different Winkler constants

Full size image
Fig. 6
figure 6

Variation of nonlinear frequency against the maximum nonlinear amplitude for different Pasternak constants

Full size image

Figure 6 shows the effects of Pasternak constant on the nonlinear frequency. It can be seen an increase in the shear stiffness of the medium results in the decrease in the nonlinear frequency for the small vibration amplitudes, and also the nonlinear flow-induced frequency reduces to the linear. The influence of the effect nonlocal parameter on the nonlinear frequency variation against the flow velocity is shown in Fig. 7. It is resulted that the influence of the nonlocal parameter is greater at higher flow velocities in comparison with lower flow velocities. This effect is more significant when the nonlocal parameter increases.

Fig. 7
figure 7

Variation of nonlinear frequency against the dimensionless fluid velocity for different nonlocal parameters

Full size image

Figure 8 shows the nonlinear frequency variation against the flow velocity for various axial tensions. The result shows that for low flow velocities, the effect of axial tension on the nonlinear frequency variation is little. For high flow velocities, the nonlinear frequency variation decreases with increment in axial tensions.

Fig. 8
figure 8

Variation of nonlinear frequency against the dimensionless fluid velocity for different axial tensions

Full size image

Figure 9 shows the influence of the Winkler constant on the nonlinear frequency variation against the flow velocities. It shows that the nonlinear frequency variation does not change greatly for low fluid velocities, and the mediums with rigid elastic properties origin the difference between the nonlinear and linear frequencies to remain unchanged with respect to flow velocity. Furthermore, for flexible mediums, the nonlinear frequency variation increases with the flow velocity. The effect of the Pasternak constant on the nonlinear frequency variation with the dimensionless flow velocity is shown in Fig. 10. The result shows that for low fluid velocities (U < 0.5) and as the shear stiffness of the elastic medium increases, the nonlinear frequency variation decreases, and for the higher flow velocities, it remains constant. This shows that the nonlinear vibration behavior of the SWCNT is independent of the fluid flow.

Fig. 9
figure 9

Variation of nonlinear frequency against the dimensionless fluid velocity for different Winkler constants

Full size image
Fig. 10
figure 10

Variation of nonlinear frequency against the dimensionless fluid velocity for different Pasternak constant

Full size image

Conclusion

In this study, the PPM is used to solve the nonlinear vibration model of a fluid-conveying SWCNT embedded in a Pasternak foundation. The approximate solution for the nonlinear frequency variation is obtained by the proposed technique. The present results are in excellent agreement with the numerical ones. In addition, this method is powerful and efficient technique for finding science and engineering nonlinear differential equations.

The results show that the nonlinear flow-induced frequency alters from the linear frequency greatly when the amplitude, flow velocity, and nonlocal parameter are high, while for the CNTs embedded in the mediums of high Pasternak parameters, the nonlinearity of the model does not demonstrate a significant effect on the frequency. Moreover, the axial tension restricts the nonlinear effect and limits the flow induced-vibration of the nanotube at high flow velocity and for high vibration amplitudes.