Cross Entropy for Discrete Z-numbers and Its Application in Multi-Criteria Decision-Making

Abstract

Decisions are based on information, and the reliability of information affects the quality of decision-making. Z-number, produced by Zadeh, considers the fuzzy restriction and the reliability restriction of decision information simultaneously. Many scholars have conducted in-depth research on Z-number, and the concept has great application potential in the field of economic management. However, certain problems with the basic operations of Z-number still exist. Entropy is a measure of information uncertainty, and research on entropy and Z-number continues to be rare. This study initially defines the cross entropy of fuzzy restriction and that of the reliability of Z-numbers. On this basis, a comprehensive weighted cross entropy is constructed, which is used to compare two discrete Z-numbers from the perspective of information entropy. Furthermore, one extended Technique for Order Preference by Similarity to Ideal Solution approach is developed to solve a multi-criteria decision-making problem under discrete Z-context. An example of the ranking of job candidates for human resource management is then presented to illustrate the availability of the proposed method along with the sensitivity and comparative analyses for verifying the validity and applicability of the proposed method.

1 Introduction

Decision-making is one of the most basic attributes of human social behaviour [1, 2]; however, it is often uncertain for issues related to the economy and society [3, 4]. Zadeh proposed the concept of fuzzy sets in 1965 to handle fuzzy information [5]. Atanassov developed the concept of intuitionistic fuzzy sets [6]. Smarandache extended the intuitionistic fuzzy set to propose the concept of neutrosophic sets [7, 8]. Furthermore, hesitant fuzzy sets and picture fuzzy sets have been created [9, 10]. Nearly all of the proposed methods have used one or more numerical functions, such as membership function, to describe the ambiguity of information. These previous studies are based on fully reliable decision information [11]. However, the decision information in the real world is often partially reliable [12, 13], and the effect of information reliability on decision-making must be considered [14, 15]. In 2011, Zadeh constructed Z-number by [16] to describe the fuzzy and reliability restrictions of information simultaneously. Moreover, Z-numbers are usually combined with natural language in practical applications; such a combination is in line with people’s decision-making habits [16].

A Z-number, marked as $Z = \left( {A,B} \right)$, is a complex concept where the fuzzy component $A$ is the fuzzy restriction of the value on a certain random variable $X$, and the reliability component $B$ plays a role in the fuzzy restriction of the probability measure of $A$. For example, a decision maker (DM) decides, ‘It likely takes about 5 h to take a high-speed train from Beijing to Shanghai’. This evaluation can be formalised as $Z = \left( {{\text{about}}\; 5\;{\text{h,}}\;{\text{likely}}} \right)$. Many scholars have conducted in-depth research on Z-number since it was proposed by Zadeh.

Although stating the problem described by Z-number is relatively easy, the calculation principle of Z-number is complicated [16]. Yager [17] discussed some specific underlying probability distributions of some particular decision-making situations to understand and fully utilise the Z-number. Aliev et al. [18] investigated the approximate reasoning of Z-number on the basis of if–then rules. Shen et al. [19] used the smallest enclosing circle method to investigate the multi-criteria decision-making (MCDM) problem under Z-numbers. Furthermore, Aliev et al. [11, 14] discussed the arithmetic operations of discrete and continuous Z-numbers. Aliev et al. [20] proposed t-norm and t-conorm aggregation operators of Z-numbers. Some related theoretical research has been recently conducted [13, 21,22,23,24]. The common feature of these studies is that they follow the original meaning of Z-number and discuss the arithmetic operations of Z-numbers in depth. These methods follow the classical fuzzy theory and probability theory, which often result in high complexity of the operation process.

Some scholars have attempted to simplify the operation of Z-numbers via certain conversion operations. Kang et al. [25] regarded Z-number as a pair of classical fuzzy numbers. Jiang et al. [26] proposed a score function of Z-number, which deeply considered its fuzzy restriction. Kang et al. [27] converted Z-number into a real number to compare two Z-numbers. A common flaw in these studies is that they all split the two components of Z-numbers and ignored the intrinsic link between the two, thereby causing serious information loss and distortion. Kang et al. [28] proposed a method of converting Z-number into one classical fuzzy number. On the basis of this conversion method, many studies have been completed in recent years [29, 30]. Kang et al. [31] recently implemented the stable strategies analysis in evolutionary games based on the utility of Z-number. Although the conversion method of Z-number in [28] has achieved remarkable results in reducing computational complexity, such a conversion method may cause serious information loss during the information fusion to a certain extent, given that the underlying probability distribution is neglected.

The distance measure and the outranking relation of Z-numbers are also important research fields. Aliyev [32] proposed a distance measure by regarding Z-number as a pair of fuzzy numbers; however, he did not consider the underlying probability distributions of Z-numbers. Shen and Wang [13] developed a comprehensive weighted distance measure of Z-numbers; however, they did not consider the difference of the fuzzy restriction components of Z-numbers. Yang and Wang [33] presented a stochastic multi-criteria decision-aiding model where the underlying probability distribution is acquired by constructing a mathematical model with the minimum variance. However, this method is unsuitable because Zadeh did not indicate that the variance of the underlying probability distribution should be minimised when introducing a Z-number. Yang and Wang’s approach added information that cannot be obtained on the basis of existing knowledge, which is contrary to Jaynes’s principle of maximum entropy [34].

Entropy is a measure of information uncertainty. Shannon initially proposed the use of information entropy based on probability theory to measure information uncertainty [35]. Zadeh proposed the concept of fuzzy entropy to measure the uncertainty of the fuzzy event [5, 36]. Shang and Jiang [37] proposed a fuzzy cross-entropy measure between discrete fuzzy numbers. Wei [38] introduced the picture fuzzy cross entropy and applied it to MCDM problems. Although fuzzy entropy can be used effectively to measure the uncertainty of fuzzy information [38,39,40], these previous studies have ignored information reliability. Recently, Kang et al. [41] developed a method for measuring the uncertainty of Z-numbers; however, they did not consider the underlying probability distributions of Z-numbers. Z-numbers describe the ambiguity and reliability of information, which also contains the underlying probability distributions. Therefore, using fuzzy and probability entropy for measuring the information uncertainty contained in Z-numbers is appropriate and meaningful. However, research on the combination of entropy theory and Z-numbers is thus far limited.

To fill the gap of the previous studies, the present work proposes a Z-number comparison method based on cross entropy under the guidance of entropy theory and maximum entropy principle and applies the proposed method to an MCDM problem. Briefly, the motivation for this study includes the following points.

• (1) Shang and Jiang proposed the cross entropy for discrete fuzzy numbers [37]. The present study extends their definition define a novel fuzzy cross entropy for the fuzzy restriction of discrete Z-numbers to compare the fuzzy restriction of Z-numbers effectively.

• (2) On the basis of Jaynes’s theory, the existing research is unreasonable for solving the underlying probability distributions of Z-numbers. We only need to select the underlying probability distributions that meet the restriction of Z-number and have the largest information entropy. Therefore, this study constructs a mathematical model to solve the underlying probability distributions of discrete Z-numbers.

• (3) Zadeh stated that the reliability component was the fuzzy restriction on the probability measure. Hence, the cross entropy of the reliability restriction should consider the underlying probability distributions and the corresponding fuzzy restriction. On this basis, this study defines the cross entropy of the reliability.

• (4) The uncertainty of Z-numbers is the sum of fuzzy and reliability restrictions. Therefore, one comprehensive weighted cross-entropy measure is presented in this study. On the basis of this formula, an extended Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) under discrete Z-valuation is developed in presenting an example of human resource management (HRM) to show the validity of the proposed method.

The remainder of this paper is organised as follows. In Sect. 2, some basic concepts, including discrete fuzzy number, discrete Z-number, entropy and cross entropy, are briefly reviewed. Section 3 defines the cross entropy of fuzziness and reliability restrictions, such that one comprehensive weighted cross entropy of discrete Z-numbers is constructed. Section 4 develops a TOPSIS approach in the context of discrete Z-number for solving MCDM problems. Section 5 presents one illustrative example, and sensitivity and comparative analyses are implemented simultaneously on the proposed approach and other existing methods. Finally, conclusions are summarised and certain future research points are outlined in Sect. 6.

2 Preliminaries

This section reviews some basic concepts and definitions that are related to discrete fuzzy number, discrete Z-number, entropy and cross entropy, which will be the basis in the later analysis.

2.1 Discrete Fuzzy Number

Definition 1

[11, 42,43,44,45] A fuzzy set $A$ whose membership function is a mapping $\mu_{A} :R \to \left[ {0,1} \right]$ is a discrete fuzzy number if it has a finite support $\text{supp}\left( A \right) = \left\{ {x_{i} |1 \le i \le n,\quad n \in N^{*} } \right\}$, where $x_{1} < x_{2} < \cdots < x_{n}$ is satisfied, and two indices $s$ and $t\left( {1 \le s \le t \le n} \right)$ exist, such that

• (1) $\mu_{A} \left( {x_{i} } \right) = 1,\quad \forall x_{i} \in \left\{ {x_{i} |x_{1} \le x_{i} \le x_{n} ,s \le i \le t} \right\}$;

• (2) $\mu_{A} \left( {x_{i} } \right) \le \mu_{A} \left( {x_{j} } \right),\quad \forall x_{i} ,x_{j} \in \left\{ {x_{i} |x_{1} \le x_{i} \le x_{n} ,1 \le i \le j \le s} \right\}$;

• (3) $\mu_{A} \left( {x_{i} } \right) \ge \mu_{A} \left( {x_{j} } \right),\quad \forall x_{i} ,x_{j} \in \left\{ {x_{i} |x_{1} \le x_{i} \le x_{n} ,t \le i \le j \le n} \right\}$.

2.2 Discrete Z-number

Definition 2

[11] A discrete Z-number is an ordered pair $Z = \left( {A,B} \right)$, where certain conditions must be satisfied as follows:

• (1) $A$ is a discrete fuzzy number whose membership function is the mapping $\mu_{A} :\left\{ {x_{i} \in R|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$;

• (2) $B$ is a discrete fuzzy number whose membership function is the mapping $\mu_{B} :\left\{ {b_{i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$.

2.3 Entropy and Cross Entropy

Definition 3

[35] Given the probability distribution $P = \left\{ {p_{i} |p_{i} \ge 0,1 \le i \le n,n \in N^{*} } \right\}$ of discrete random variable $X$ and $\sum\nolimits_{i = 1}^{n} {p_{i} } = 1$, the information entropy of $P$ is

$$H\left( P \right) = - C\sum\limits_{i = 1}^{n} {p_{i} \ln p_{i} } ,$$

(1)

where $C$ is a positive constant that merely amounts to the choice of a unit of measure. Therefore, the quantities of the form $H\left( P \right) = - \sum\limits_{i = 1}^{n} {p_{i} \ln p_{i} }$ play the central role in information uncertainty [35].

On the basis of Shannon’s information entropy, the cross entropy of discrete random variables and that of discrete fuzzy numbers are introduced as follows. Firstly, the cross entropy in Definition 4 describes the difference between the probability distributions of two discrete random variables. Secondly, the cross entropy in Definition 5 describes the difference between two discrete fuzzy numbers. In the following discussion, the method of measuring the uncertainty of Z-numbers will be explored on the basis of the two definitions.

Definition 4

[40, 46, 47] Let $P = \left\{ {p_{i} |p_{i} \ge 0,1 \le i \le n,n \in N^{*} } \right\}$ and $Q = \left\{ {q_{i} |q_{i} \ge 0,1 \le i \le n,n \in N^{*} } \right\}$ be the given probability distributions of two discrete random variables, where $\sum\nolimits_{i = 1}^{n} {p_{i} } = 1$ and $\sum\nolimits_{i = 1}^{n} {q_{i} } = 1$. Then, the cross entropy of $P$ and $Q$ is defined as:

$$H\left( {P,Q} \right) = \sum\limits_{i = 1}^{n} {p_{i} \ln \frac{1}{{q_{i} }}} .$$

(2)

Definition 5

[37,38,39] Let $A_{1}$ and $A_{2}$ be the given discrete fuzzy numbers whose membership functions are $\mu_{{A_{1} }} :\left\{ {x_{1i} \in R|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{A_{2} }} :\left\{ {x_{2i} \in R|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$, respectively. Then, the cross entropy of $A_{1}$ and $A_{2}$ is defined as

$$H\left( {A_{1} ,A_{2} } \right) = \sum\limits_{i = 1}^{n} {\left( {\mu_{{A_{1} }} \left( {x_{1i} } \right)\ln \frac{{\mu_{{A_{1} }} \left( {x_{1i} } \right)}}{{\frac{1}{2}\left( {\mu_{{A_{1} }} \left( {x_{1i} } \right) + \mu_{{A_{2} }} \left( {x_{2i} } \right)} \right)}} + \left( {1 - \mu_{{A_{1} }} \left( {x_{1i} } \right)} \right)\ln \frac{{\left( {1 - \mu_{{A_{1} }} \left( {x_{1i} } \right)} \right)}}{{1 - \frac{1}{2}\left( {\mu_{{A_{1} }} \left( {x_{1i} } \right) + \mu_{{A_{2} }} \left( {x_{2i} } \right)} \right)}}} \right)} ,$$

(3)

which indicates the degree of discrimination of $A_{1}$ from $A_{2}$.

However, the aforementioned cross entropy is not symmetric for $H\left( {A_{1} ,A_{2} } \right)$ in terms of its arguments. Shang and Jiang [37] developed a symmetric discrimination information measure as follows:

$$I\left( {A_{1} ,A_{2} } \right) = H\left( {A_{1} ,A_{2} } \right) + H\left( {A_{2} ,A_{1} } \right).$$

(4)

In addition, $I\left( {A_{1} ,A_{2} } \right) \ge 0$ and $I\left( {A_{1} ,A_{2} } \right) = 0$ exist if and only if $A_{1} = A_{2}$.

3 Cross Entropy of Discrete Z-numbers

Zadeh [16] introduced the concept of Z-number to describe the uncertainty of the evaluation information, which characterises fuzzy and reliability restrictions of information simultaneously. In addition, Shannon [35] indicated that information uncertainty could be summarised by entropy. Consequently, certain concepts of cross entropy about ambiguity and reliability are presented in this section to describe the uncertainty of Z-numbers.

3.1 Cross Entropy of Fuzziness Restriction

The definition of cross entropy for fuzzy sets is independent of the content of the information in [37], in which their formula for computing the cross entropy between two fuzzy sets is convenient regardless of the value interval limit of $X$. However, some novel dilemmas still exist if the same formula is now used to calculate the cross entropy of fuzziness restriction in Z-numbers.

Remark 1

The membership functions of the fuzzy restriction of two discrete Z-numbers $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$ are, respectively, as follows:

$$\mu_{{A_{1} }} = 0/1 + 0.5/2 + 1/3 + 0.5/4 + 0/5,$$

$$\mu_{{A_{2} }} = 0/6 + 0.5/7 + 1/8 + 0.5/9 + 0/10.$$

In view of Definition 5, the cross entropy of $A_{1}$ and $A_{2}$ is

$$H\left( {A_{1} ,A_{2} } \right) = 0.$$

As presented above, this cross entropy is undesirable. The value limit regarding the fuzzy restriction of Z-number should be considered when describing the difference between two Z-numbers. Consequently, the fuzzy restriction measure of Z-numbers must be further discussed.

Definition 6

Given two discrete fuzzy numbers $A_{1}$ and $A_{2}$ with their respective membership functions $\mu_{{A_{1} }} :\left\{ {x_{1i} \in R|1 \le i \le n,n \in {\text{N}}^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{A_{2} }} :\left\{ {x_{2i} \in R|1 \le i \le n,n \in {\text{N}}^{*} } \right\} \to \left[ {0,1} \right]$, the cross-entropy core $E$ of $A_{1}$ and $A_{2}$ is defined as follows:

$$E = \left[ {{\text{e}}_{ij} } \right]_{n \times n} ,$$

(5)

that is a $n \times n$-dimensional matrix, of which each element is pure cross entropy independent of the content of information (i.e. the value of $X$) and ${\text{e}}_{ij}$ is equal to

$${\text{e}}_{ij} = \mu_{{A_{1} }} \left( {x_{1i} } \right)\ln \frac{{\mu_{{A_{1} }} \left( {x_{1i} } \right)}}{{\frac{1}{2}\left( {\mu_{{A_{1} }} \left( {x_{1i} } \right) + \mu_{{A_{2} }} \left( {x_{2j} } \right)} \right)}} + \left( {1 - \mu_{{A_{1} }} \left( {x_{1i} } \right)} \right)\ln \frac{{\left( {1 - \mu_{{A_{1} }} \left( {x_{1i} } \right)} \right)}}{{1 - \frac{1}{2}\left( {\mu_{{A_{1} }} \left( {x_{1i} } \right) + \mu_{{A_{2} }} \left( {x_{2j} } \right)} \right)}}.$$

(6)

Definition 7

Let $X$ be the universe of discourse and $A$ be the given discrete fuzzy number with its membership function $\mu_{A} :\left\{ {x_{i} \in R|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$. The value strategy vector $S_{A}$ of $A$ is defined as follows:

$$S_{A} = \left[ {s_{i} } \right]_{1 \times n} ,$$

(7)

where $s_{i} = \left( {x_{i} - \hbox{min} \left( X \right)} \right)/\left( {\hbox{max} \left( X \right) - \hbox{min} \left( X \right)} \right)$ ($x_{i} \in \text{supp}\left( A \right) = \left\{ {x_{i} |1 \le i \le n,n \in N^{*} } \right\}$) is the value strategy of $A$.

Definition 8

Given two discrete fuzzy numbers $A_{1}$ and $A_{2}$ with their respective membership functions $\mu_{{A_{1} }} :\left\{ {x_{1i} \in R|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{A_{2} }} :\left\{ {x_{2i} \in R|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$, the cross entropy of $A_{1}$ and $A_{2}$ is defined as follows:

$$H^{f} \left( {A_{1} ,A_{2} } \right) = S_{1} ES_{2}^{T} ,$$

(8)

where $S_{1}$ and $S_{2}$ are the value strategy vectors of $A_{1}$ and $A_{2}$, respectively; and $E$ is the cross-entropy core of $A_{1}$ and $A_{2}$.

However, this cross entropy is not symmetric for $H^{f} \left( {A_{1} ,A_{2} } \right)$ in terms of its arguments. Thus, we develop a symmetric discrimination information measure as follows:

$$H^{F} \left( {A_{1} ,A_{2} } \right) = \left| {H^{f} \left( {A_{1} ,A_{2} } \right) - H^{f} \left( {A_{1} ,A_{1} } \right)} \right| + \left| {H^{f} \left( {A_{2} ,A_{1} } \right) - H^{f} \left( {A_{2} ,A_{2} } \right)} \right|.$$

(9)

Then, $H^{F} \left( {A_{1} ,A_{2} } \right) \ge 0$ and $H^{F} \left( {A_{1} ,A_{2} } \right) = 0$ exist if and only if $A_{1} = A_{2}$. The proof process is simple and therefore omitted.

Example 1

Let $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$ be two discrete Z-numbers whose membership functions of fuzzy restriction are, respectively, as follows:

$$\mu_{{A_{1} }} = 0/1 + 0.5/2 + 1/3 + 0.5/4 + 0/5,$$

$$\mu_{{A_{2} }} = 0/6 + 0.5/7 + 1/8 + 0.5/9 + 0/10,$$

with their value strategy vectors, respectively, as follows:

$$S_{1} = \left[ {0.1,0.2,0.3,0.4,0.5} \right],$$

$$S_{2} = \left[ {0.6,0.7,0.8,0.9,1} \right]$$

and cross-entropy core of

$$E = \left[ {\begin{array}{*{20}c} 0 & {0.2876} & {0.6930} & {0.2876} & 0 \\ {0.1438} & 0 & {0.1438} & 0 & {0.1438} \\ {0.6930} & {0.2876} & 0 & {0.2876} & {0.6930} \\ {0.1438} & 0 & {0.1438} & 0 & {0.1438} \\ 0 & {0.2876} & {0.6930} & {0.2876} & 0 \\ \end{array} } \right].$$

In view of Definition 8, the cross entropy of the fuzzy restriction of $Z_{1}$ and $Z_{2}$ can be calculated as

$$H^{f} \left( {A_{1} ,A_{2} } \right) = S_{1} ES_{2}^{T} = 1.2866.$$

Furthermore, we have

$$H^{F} \left( {A_{1} ,A_{2} } \right) = 2.9484.$$

Thus, the value limit interval of $X$ plays a role in the calculation of the cross entropy of the fuzzy restriction between Z-numbers. The outcome is consistent with our aim, which aids us overcome the dilemma stressed in Remark 1.

3.2 Cross Entropy of Reliability Restriction

Zadeh believed that an underlying probability distribution in Z-number exists [16]. On this basis, Yager [17] discussed some special probability distributions in some specific decision scenarios. However, Aliev et al. [11] constructed one goal linear programming for acquiring the underlying probability distributions. The construction of a suitable method for solving the underlying probability distributions in Z-number is essential for Z-number operations. Consequently, this subsection initially proposes a nonlinear programming model based on Jaynes’s maximum entropy theory to solve the underlying probability distributions. Thereafter, the cross entropy of the reliability restriction between Z-numbers is discussed.

For a given discrete Z-number $Z = \left( {A,B} \right)$ associated with a real-valued random variable $X$, the first component $A$ is a fuzzy restriction of $X$. The second component $B$ is a reliability restriction of the probability measure of $X$. Their membership functions are as follows:

$$\mu_{A} :\left\{ {x_{i} \in R|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right],$$

$$\mu_{B} :\left\{ {b_{i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right],$$

According to Zadeh, we assume that the underlying probability distribution is

$$P_{X} = \left\{ {p_{i} |p_{i} \ge 0,1 \le i \le n,n \in N^{*} } \right\}.$$

Then, the given discrete Z-number $Z = \left( {A,B} \right)$ will satisfy certain conditions as follows:

• (1) $\sum\limits_{i = 1}^{n} {p_{i} = 1}$, and $p_{i} \ge 0,\;\;\forall p_{i} \in P_{X}$;

• (2) $\sum\limits_{i = 1}^{n} {x_{i} p_{i} } = \sum\limits_{i = 1}^{n} {x_{i} \mu_{A} \left( {x_{i} } \right)} /\sum\limits_{i = 1}^{n} {\mu_{A} \left( {x_{i} } \right)}$ (where ‘/’ denotes division);

• (3) $\sum\limits_{i = 1}^{n} {\mu_{A} \left( {x_{i} } \right)p_{i} } = b_{j} ,b_{j} \in \text{supp}\left( B \right) = \left\{ {b_{i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\}$.

Two points exist with regard to Jaynes’s maximum entropy theory [34]. Firstly, only the probability distribution, which meets the constraint conditions and has the largest entropy value, should be selected when only partial constraint information is obtained. Secondly, any other choices about the probability distribution will constantly indicate that certain conditions or constraints have been added that we cannot derive on the basis of the information we have. For example, as stated in the Introduction, Yang and Wang’s study [33] subjectively added the constraint condition of minimum variance. Therefore, we select the underlying probability distribution of the Z-number with the largest entropy based on the preceding two conditions.

Definition 9

Let $Z = \left( {A,B} \right)$ be the given discrete Z-number about real-valued random variable $X$, and its membership functions of fuzzy and reliability restrictions are $\mu_{A} :\left\{ {x_{i} \in R|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{B} :\left\{ {b_{i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$, respectively. The underlying probability distribution on $X$ of the Z-number is $P_{X} = \left\{ {p_{i} |p_{i} \ge 0,1 \le i \le n,n \in N^{*} } \right\}$. Thus, the nonlinear programming model $M_{Z}$ is constructed as follows:

$$\begin{aligned} & {\text{m}}ax - \sum\limits_{i = 1}^{n} {p_{i} \ln p_{i} } \\ & \quad {\text{s}} . {\text{t}}.\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{n} {\mu_{A} \left( {x_{i} } \right)p_{i} } = b_{j} ,b_{j} \in \text{supp}\left( B \right) = \left\{ {b_{i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\}} \hfill \\ {\sum\limits_{i = 1}^{n} {x_{i} p_{i} } = \sum\limits_{i = 1}^{n} {x_{i} \mu_{A} \left( {x_{i} } \right)} /\sum\limits_{i = 1}^{n} {\mu_{A} \left( {x_{i} } \right)} } \hfill \\ {\sum\limits_{i = 1}^{n} {p_{i} = 1} } \hfill \\ {p_{i} \ge 0,\forall p_{i} \in P_{X} } \hfill \\ \end{array} } \right.. \\ \end{aligned}$$

(10)

Example 2

Given the discrete Z-number $Z = \left( {A,B} \right)$, its membership functions are as follows:

$$\mu_{A} = 0/1 + 0.5/2 + 1/3 + 0.5/4 + 0/5,$$

$$\mu_{B} = 0/0.2 + 0.5/0.35 + 1/0.5 + 0.5/0.65 + 0/0.8.$$

According to Definition 9,

$$\begin{aligned} & \hbox{max} \sum\limits_{i = 1}^{n} {p_{i} \ln p_{i} } \\ & \quad {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}l} {0 \times p_{1} + 0.5 \times p_{2} + 1 \times p_{3} + 0.5 \times p_{4} + 0 \times p_{5} = b_{j} ,b_{j} \in \left\{ {0.2,0.35,0.5,0.65,0.8} \right\}} \hfill \\ {0 \times p_{1} + 0.5 \times p_{2} + 1 \times p_{3} + 0.5 \times p_{4} + 0 \times p_{5} = 3} \hfill \\ {\sum\limits_{i = 1}^{n} {p_{i} = 1} } \hfill \\ {p_{i} \ge 0,\forall p_{i} \in P_{X} } \hfill \\ \end{array} } \right.. \\ \end{aligned}$$

By solving this mathematical model, the underlying probability distributions are shown in Table 1.

Table 1 Underlying probability distributions of $Z = \left( {A,B} \right)$

Table 1 indicates the following information.

Firstly, the different values of $b_{j}$ can result in different underlying probability distributions. Here, we use ‘result in’ instead of ‘generate’ because the value of $b_{j}$ yields inferential information on the basis of the principle of maximum entropy.

Secondly, the difference $\mu_{B} \left( {b_{j} } \right)$ on $b_{j}$ indicates the DM’s confidence level for the corresponding $P_{X}$. Thus, we should consider the underlying probability distributions and the corresponding membership values when calculating the cross entropy of the reliability restriction of Z-numbers.

Definition 10

Given two discrete Z-numbers $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$ whose membership functions are $\mu_{{A_{1} }} :\left\{ {x_{1k} \in R|1 \le k \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{A_{2} }} :\left\{ {x_{2k} \in R|1 \le k \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{B_{1} }} :\left\{ {b_{1i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{B_{2} }} :\left\{ {b_{2i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$, respectively, the cross-entropy core $E_{p}$ of $B_{1}$ and $B_{2}$ is defined as follows:

$$E_{p} = \left[ {{\text{e}}_{ij} } \right]_{n \times n} ,$$

(11)

which is an $n \times n$-dimensional matrix, of which each element is pure cross entropy independent of the content of information (i.e. the value of $X$), and ${\text{e}}_{ij}$ is equal to

$${\text{e}}_{ij} = H\left( {P_{1i} ,P_{2j} } \right) - H\left( {P_{1i} ,P_{1j} } \right) = \sum\limits_{k = 1}^{n} {p_{1ik} \ln \frac{{p_{1ik} }}{{p_{2jk} }}} ,$$

(12)

where $p_{1ik} = P_{1i} \left( {x_{k} } \right)$, $p_{2jk} = P_{2j} \left( {x_{k} } \right)$, $P_{1i}$ is the underlying probability distribution corresponding to the probability measure $b_{1i}$ of $Z_{1} = \left( {A_{1} ,B_{1} } \right)$, and $P_{2j}$ is the underlying probability distribution corresponding to probability measure $b_{2i}$ of $Z_{2} = \left( {A_{2} ,B_{2} } \right)$.

Definition 11

Let $Z = \left( {A,B} \right)$ be the given discrete Z-number, and the membership function of $B$ is $\mu_{B} :\left\{ {b_{i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$. The fuzzy strategy vector $M_{B}$ of $B$ is defined as follows:

$$M_{B} = \left[ {m_{i} } \right]_{1 \times n} ,$$

(13)

where $m_{i} = \mu_{B} \left( {b_{i} } \right)$($b_{i} \in {\text{supp}}\left( B \right) = \left\{ {b_{i} |1 \le i \le n,n \in N^{*} } \right\}$) is the fuzzy strategy of $B$.

Definition 12

Given two discrete Z-numbers $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$ whose membership functions are $\mu_{{A_{1} }} :\left\{ {x_{1k} \in R|1 \le k \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{A_{2} }} :\left\{ {x_{2k} \in R|1 \le k \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{B_{1} }} :\left\{ {b_{1i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$ and $\mu_{{B_{2} }} :\left\{ {b_{2i} \in \left[ {0,1} \right]|1 \le i \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$, respectively, the cross entropy of the reliability restriction of $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$ is defined as follows:

$$H^{r} \left( {Z_{1} ,Z_{2} } \right) = M_{1} E_{p} M_{2}^{T} ,$$

(14)

where $M_{1}$ and $M_{2}$ are the fuzzy strategy vectors of $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$, and $E_{p}$ is the cross-entropy core of the reliability restriction of $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$.

However, the aforementioned identity is not symmetric for $H^{r} \left( {Z_{1} ,Z_{2} } \right)$ in terms of its arguments. Thus, we develop a symmetric discrimination information measure as follows:

$$H^{R} \left( {Z_{1} ,Z_{2} } \right) = \left| {H^{r} \left( {Z_{1} ,Z_{2} } \right) - H^{r} \left( {Z_{1} ,Z_{1} } \right)} \right| + \left| {H^{r} \left( {Z_{2} ,Z_{1} } \right) - H^{r} \left( {Z_{2} ,Z_{2} } \right)} \right|.$$

(15)

Then, $H^{R} \left( {Z_{1} ,Z_{2} } \right) \ge 0$ and $H^{R} \left( {Z_{1} ,Z_{2} } \right) = 0$ exist if and only if $Z_{1} = Z_{2}$.

Example 3

Suppose that the human resource department of ABC Corporation evaluates the performance of two employees as ‘likely good’ and ‘certainly good’, and both of them are discrete Z-numbers whose membership functions are as follows:

$$\mu_{{A_{1} }} = 0/1 + 0.5/2 + 1/3 + 0.5/4 + 0/5,$$

$$\mu_{{B_{1} }} = 0/0.2 + 0.5/0.35 + 1/0.5 + 0.5/0.65 + 0/0.8,$$

$$\mu_{{A_{2} }} = 0/1 + 0.5/2 + 1/3 + 0.5/4 + 0/5,$$

$$\mu_{{B_{2} }} = 0/0.1 + 0.5/0.2 + 1/0.3 + 0.5/0.4 + 0/0.5.$$

The two employee’s fuzzy strategy vectors are

$$M_{1} = [0,0.5,1,0.5,0],$$

$$M_{2} = [0,0.5,1,0.5,0].$$

The two employee’s cross-entropy core of reliability restriction is:

$$E_{p} = \left[ {\begin{array}{lllll} {0.0813} \hfill & 0 \hfill & {0.0450} \hfill & {0.1584} \hfill & {0.3314} \hfill \\ {0.4097} \hfill & {0.1071} \hfill & {0.0100} \hfill & {0.0091} \hfill & {0.0781} \hfill \\ {0.9132} \hfill & {0.3894} \hfill & {0.1501} \hfill & {0.0349} \hfill & 0 \hfill \\ {1.5731} \hfill & {0.8279} \hfill & {0.4466} \hfill & {0.2170} \hfill & {0.0781} \hfill \\ {2.4081} \hfill & {1.4416} \hfill & {0.9181} \hfill & {0.5743} \hfill & {0.3314} \hfill \\ \end{array} } \right].$$

In view of Definition 12, the cross entropy of the reliability restriction of $Z_{1}$ and $Z_{2}$ can be calculated as follows:

$$H^{r} \left( {Z_{1} ,Z_{2} } \right) = M_{1} E_{p} M_{2}^{T} = 0.8808.$$

Furthermore, we have

$$H^{R} \left( {Z_{1} ,Z_{2} } \right) = 1.2012.$$

3.3 Comprehensive Weighted Cross Entropy of Z-numbers

We have separately discussed the cross entropy of the fuzzy and reliability restrictions of discrete Z-numbers according to Zadeh [16]. The cross entropy of fuzzy restriction considers the possibility distribution and the value limit interval of the associated random variable simultaneously; thus, Shang and Jiang’s fuzzy cross entropy [37] can be used for discrete Z-numbers. Furthermore, the cross-entropy definition of reliability restriction considers the influence of the possibility distribution of reliability restriction on the underlying probability distributions, which reflects the definition of $B$ component well. Furthermore, we combine the two cross-entropy methods into one comprehensive weighted cross entropy of Z-numbers, denoted as follows:

$$H^{\omega } \left( {Z_{1} ,Z_{2} } \right) = \omega H^{F} \left( {A_{1} ,A_{2} } \right) + \left( {1 - \omega } \right)H^{R} \left( {Z_{1} ,Z_{2} } \right),$$

(16)

where $\omega \in \left\{ {\omega |0 \le \omega \le 1,\omega \in R} \right\}$ reflects the DM’s preference about information fusion. The reliability restriction of Z-number will be considered increasingly important when $0 < \omega < 0.5$. However, the fuzzy restriction of Z-number may be remarkable for decision evaluation to pay substantial attention to the influence of fuzzy restriction when $0.5 < \omega < 1$. In addition, both of them will receive equal attention if $\omega = 0.5$. Particularly, when $\omega = 0$ or $\omega = 1$, the aforementioned formula will degenerate into a simpler form.

According to Definitions 8 and 12, Eq. (16) satisfies the following properties:

• (1)
  $$H^{\omega } \left( {Z_{1} ,Z_{2} } \right) \ge 0;$$

• (2) $H^{\omega } \left( {Z_{1} ,Z_{2} } \right) = 0$ if and only if $Z_{1} = Z_{2}$;

• (3)
  $$H^{\omega } \left( {Z_{1} ,Z_{2} } \right) = H^{\omega } \left( {Z_{2} ,Z_{1} } \right).$$

Example 4

Let $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$ be two discrete Z-numbers, and their membership functions are as follows:

$$\mu_{{A_{1} }} = 0/1 + 0.5/2 + 1/3 + 0.5/4 + 0/5,$$

$$\mu_{{B_{1} }} = 0/0.2 + 0.5/0.35 + 1/0.5 + 0.5/0.65 + 0/0.8,$$

$$\mu_{{A_{2} }} = 0/6 + 0.5/7 + 1/8 + 0.5/9 + 0/10,$$

$$\mu_{{B_{2} }} = 0/0.1 + 0.5/0.2 + 1/0.3 + 0.5/0.4 + 0/0.5.$$

Firstly, their cross entropy of fuzzy restriction is

$$H^{F} \left( {A_{1} ,A_{2} } \right) = 2.9484.$$

Secondly, their cross entropy of reliability restriction is

$$H^{R} \left( {Z_{1} ,Z_{2} } \right) = 1.2012.$$

Therefore, the comprehensive weighted cross entropy is

$$H^{0.5} \left( {Z_{1} ,Z_{2} } \right) = 0.5 \times H^{F} \left( {A_{1} ,A_{2} } \right) + \left( {1 - 0.5} \right) \times H^{R} \left( {Z_{1} ,Z_{2} } \right) = 2.0748.$$

4 TOPSIS Approach Based on Cross Entropy of Discrete Z-numbers

The TOPSIS method, produced by Hwang and Yoon [48], has become a classic MCDM approach [39, 49,50,51]. Similar to the VlseKriterijum-ska Optimizacija I Kompromisno Resenje (VIKOR) method [13], TOPSIS evaluates the priority of alternatives in view of the position of the alternative between the positive and negative ideal solutions. However, different from VIKOR, the TOPSIS method is effective and simpler. In this section, a type of extended TOPSIS method is used in the MCDM framework where the alternatives are evaluated by discrete Z-numbers.

For a MCDM problem, let $A = \left\{ {a_{i} |1 \le i \le m,i \in N^{ * } } \right\}$ be the set of all the provided alternatives and $C = \left\{ {c_{j} |1 \le j \le n,j \in N^{ * } } \right\}$ be the collection of criteria for evaluating the alternatives. The weight vector of criteria is $W = \left\{ {w_{j} |1 \le j \le n,j \in N^{ * } } \right\}$, where $w_{j} = W\left( {c_{j} } \right) = z_{j} = \left( {A_{j} ,B_{j} } \right)$ indicates the extent of the importance of the criterion. $D = \left[ {z_{ij} } \right]_{m \times n} = \left[ {\left( {A_{ij} ,B_{ij} } \right)} \right]_{m \times n}$ is the evaluation matrix of the DM, where $z_{ij} = \left( {A_{ij} ,B_{ij} } \right)$ is the discrete Z-number as the DM’s evaluation about alternative $a_{i}$ over criterion $c_{j}$.

Step 1 Normalise the evaluation matrix.

Two types of criterions, namely benefits and costs, are common. The information transformation regarding the fuzzy restriction of the Z-number is necessary. For example, the fuzzy restriction of $z_{ij} = \left( {A_{ij} ,B_{ij} } \right)$ with regard to the alternative $a_{i}$ under $c_{j}$ is one discrete fuzzy number with its membership $\mu_{{A_{ij} }} :\left\{ {x_{ijk} \in R|1 \le k \le n,n \in N^{*} } \right\} \to \left[ {0,1} \right]$. Thus, the following can exist:

$$x^{\prime}_{ijk} = \left\{ {\begin{array}{*{20}l} {\frac{{x_{ijk} - \mathop {\hbox{min} }\limits_{ijk} \left( {x_{ijk} } \right)}}{{\mathop {\hbox{max} }\limits_{ijk} \left( {x_{ijk} } \right) - \mathop {\hbox{min} }\limits_{ijk} \left( {x_{ijk} } \right)}}} \hfill & {j \in B} \hfill \\ {\frac{{\mathop {\hbox{max} }\limits_{ijk} \left( {x_{ijk} } \right) - x_{ijk} }}{{\mathop {\hbox{max} }\limits_{ijk} \left( {x_{ijk} } \right) - \mathop {\hbox{min} }\limits_{ijk} \left( {x_{ijk} } \right)}}} \hfill & {j \in C} \hfill \\ \end{array} } \right.,$$

(17)

where $B$ is the set of benefit criteria, and $C$ is the collection of cost criteria. Moreover, $\mu_{{A_{ij} }} \left( {x^{\prime}_{ijk} } \right) = \mu_{{A_{ij} }} \left( {x_{ijk} } \right)$ is satisfied. Therefore, the normalised evaluation information can be marked as $D^{N} = \left[ {z_{ij}^{N} } \right]_{m \times n} = \left[ {\left( {A_{ij}^{N} ,B_{ij} } \right)} \right]_{m \times n}$.

Step 2 Acquire the weight vector of criteria.

When the DM states the importance of criteria by combining Z-numbers and natural language terms, it is necessary to acquire the weight vector of criteria to complete the process of information fusion. In this step, a method based on the information entropy of Z-number is developed to solve the weight vector.

Definition 13

Let $Z = \left( {A,B} \right)$ be a Z-number. Then, the information entropy of $Z = \left( {A,B} \right)$ is defined as

$$H^{\omega } \left( Z \right) = \omega H^{f} \left( {A,A} \right) + \left( {1 - \omega } \right)H^{r} \left( {Z,Z} \right),$$

(18)

where $H^{\omega } \left( Z \right)$ is the comprehensive weighted cross entropy of $Z = \left( {A,B} \right)$, as depicted in Sect. 3.3.

Firstly, we calculate the information entropy for each criterion as follows.

The Z-entropy $H^{\omega } \left( {z_{j} } \right)$ of the criteria $c_{j}$ is calculated using Eq. (18).

Then, the criteria weights are calculated as follows:

$$\xi_{j} = \frac{{H^{\omega } \left( {z_{j} } \right)}}{{\sum\limits_{j = 1}^{n} {H^{\omega } \left( {z_{j} } \right)} }},$$

(19)

where $\xi_{j} \ge 0$, and $\sum\limits_{j = 1}^{n} {\xi_{j} } = 1$.

Therefore, the weight vector $\varXi = \left\{ {\xi_{j} |1 \le i \le n,i \in N^{*} } \right\}$ is completed.

Step 3 Obtain the positive and negative ideal solutions under each criterion.

$$z_{j}^{ + } = \mathop {\hbox{max} }\limits_{i} z_{ij}^{N} = \left( {A_{i\hbox{max} }^{N} ,B_{i\hbox{max} } } \right),$$

(20)

$$z_{j}^{ - } = \mathop {\hbox{min} }\limits_{i} z_{ij}^{N} = \left( {A_{i\hbox{min} }^{N} ,B_{i\hbox{min} } } \right),$$

(21)

where $z_{j}^{ + }$ and $z_{j}^{ - }$ are the positive and negative ideal solutions under criterion $c_{j}$, respectively.

Step 4 Calculate the cross entropy of each alternative and the positive and negative ideal solutions.

$$H\left( {a_{i} ,a^{ + } } \right) = \sum\limits_{j = 1}^{n} {\xi_{j} H^{\omega } \left( {z_{ij}^{N} ,z_{j}^{ + } } \right)} ,$$

(22)

$$H\left( {a_{i} ,a^{ - } } \right) = \sum\limits_{j = 1}^{n} {\xi_{j} H^{\omega } \left( {z_{ij}^{N} ,z_{j}^{ - } } \right)} ,$$

(23)

where $H\left( {a_{i} ,a^{ + } } \right)$ and $H\left( {a_{i} ,a^{ - } } \right)$ are the cross entropy of the alternative $a_{i}$ and the positive/negative ideal alternative, respectively.

Step 5 Calculate the comprehensive evaluation index of each alternative.

$$r_{i} = \frac{{H\left( {a_{i} ,a^{ - } } \right)}}{{H\left( {a_{i} ,a^{ - } } \right) + H\left( {a_{i} ,a^{ + } } \right)}},i = 1,2, \ldots ,m,$$

(24)

where $r_{i}$ is the comprehensive evaluation index of the alternative $a_{i}$.

Step 6 Rank the alternatives.

The larger the value of $r_{i}$, the higher the priority of the alternative $a_{i}$.

5 Illustrative Example

Intense market competition forces companies to strengthen their internal management, and HRM is an important part of modern corporate governance [52, 53]. As a key link in HRM, employee performance evaluation plays a considerable role in business management. In addition to certain quantitative assessment indicators, people are still accustomed to use certain qualitative indicators in HRM. In some cases, company managers prefer to use natural language to assess the performance of their subordinates in key areas. The process of performance appraisal can be regarded as a decision-making activity. According to Zadeh, the information from which the decision is based on must be reliable to a certain extent [16]. Therefore, when combined with natural language terms, a Z-number, which is related to the issue of reliability restriction of information, is appropriate as a tool for expressing assessment information in HRM. In this section, an illustrative example about the performance evaluation of HRM is presented with the aid of the algorithm in Sect. 4.

A vacancy exists in a middle management position at ABC Corporation. Therefore, the company’s top management needs to select one of the best candidates to serve in this position. The company’s HRM department has undertaken this task and is assisting the company’s top management to evaluate the performance of relevant candidates. The HRM department forms a temporary group, including psychologists, domain experts and sociologists, to determine the assessment indicators that need attention and to perform information fusion. The following criteria are considered: leadership $c_{1}$, planning and organisational skills $c_{2}$, judgment and decision ability $c_{3}$ and adaptability $c_{4}$. The company’s top management has identified several candidates ahead of time and has secretly determined the importance of each evaluation criterion in natural language terms. After interviews, questionnaires and certain small-scale panel discussions, the ad hoc panel fills out the assessment form for the candidates without any guidelines of weights information. Furthermore, the information on the importance of criteria will be made public to assist the panel in the final decision-making information fusion. The final evaluation information is presented in Table 5. The codebooks of linguistic terms $S$ and $S^{\prime}$ are illustrated as Figs. 2 and 3, respectively (Tables 2, 3, 4).

Table 2 Evaluation matrix for candidates

Table 3 Codebook of linguistic terms for fuzzy restriction

Table 4 Codebook of linguistic terms for reliability restriction

5.1 Application of the Proposed Approach

In this subsection, we use the proposed algorithm in Sect. 4 to aggregate information on decision evaluation texts.

Note The parameter $\omega$ in Eq. (16) represents the DM’s risk preference for information reliability. Therefore, we assume that $\omega$ is equal to 0.5 without loss of generality. That is to say, only the situation in which the DM is risk neutral is discussed in this section. $\omega$ can be set to any value in $\left[ {0,1} \right]$ if necessary.

Step 1 Normalise the evaluation matrix.

Firstly, the linguistic terms in Z-number contexts are converted into discrete fuzzy numbers on the basis of their codebooks. Then, converting the evaluation values according to Eq. (17) is unnecessary because all the criteria are benefit ones.

Step 2 Acquire the weight vector of criteria.

According to the method of (18) and (19) in Sect. 4, the Z-entropy of criteria and the weight vector are presented in Tables 5 and 6, respectively.

Table 5 Z-entropy of criteria

Table 6 Weight vector $\varXi$ of criteria

Step 3 Obtain the positive and negative ideal solutions under each criterion (Table 7).

Table 7 Linguistic term pairs of the positive/negative solutions

Step 4 Calculate the cross entropy of each alternative and the positive/negative ideal solution (Tables 8, 9, 10).

Table 8 Cross entropy of each candidate and the positive ideal solution

Table 9 Cross entropy of each candidate and the negative ideal solution

Table 10 Weighted cross entropy of each candidate and the positive/negative ideal solution

Step 5 Compute the comprehensive evaluation index of each candidate according to Eq. (24) (Table 11).

Table 11 Comprehensive evaluation index of each candidate

Step 6 Rank the candidates.

In view of the comprehensive evaluation indices, the priority of the candidates is as follows:

$$a_{2} \succ a_{4} \succ a_{1} \succ a_{3} .$$

(25)

Therefore, $a_{2}$ and $a_{3}$ are the highest and lowest rated candidates, respectively.

5.2 Sensitivity Analysis

This subsection aims to perform the sensitivity analysis of the proposed algorithm where the ranking result of alternatives may be affected by parameter $\omega$. As stated in Sect. 3.3, parameter $\omega$ reflects the DM’s distinct preference about fuzzy and reliability restrictions when information fusion occurs. Therefore, sensitivity analysis is necessary for the present study. The value of parameter $\omega$ will lie in the set of $\left\{ {\omega |\omega = 0.1k,0 \le k \le 10,k \in N} \right\}$. The different priorities of candidates under different values of $\omega$ are presented in Tables 12 and 13.

Table 12 Priority of candidates when $0 \le \omega < 0.5$

Table 13 Priority of candidates when $0.5 < \omega \le 1$

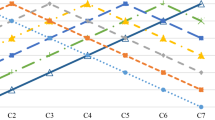
As shown in Tables 12 and 13, each candidate’s priority is different as parameter $\omega$ varies. Figure 1 shows a trend chart of the changes of priorities.

Fig. 1

Priority of candidates under different values of $\omega$

As shown in Fig. 1, the decision preference parameter $\omega$ has a remarkable impact on candidates’ ranking by affecting the relative importance of decision information with respect to fuzzy and reliability restrictions. The priorities of the candidates are consistent when $\omega$ lies in $\left[ {0.1,0.5} \right]$. Furthermore, the ordering of candidates is confusing when $\omega$ belongs to $\left[ {0.6,1} \right]$. Moreover, the regulation of $\omega$ is seemingly disordered. However, certain trends continue to be identifiable, such as the rise of the rankings of candidates $a_{1}$ and $a_{3}$ are and the decline of those of candidates $a_{2}$ and $a_{4}$.

To understand how the decision preference parameter $\omega$ affects the candidates’ ranking, every candidate’s closeness trend and the weight trend of criteria are shown in Figs. 2 and 3.

Fig. 2

Closeness trend of every candidate

Fig. 3

Weight trend of every criterion

As shown in Fig. 2, candidate $a_{3}$ becomes better than $a_{2}$ because their closeness has changed. Further details are explained in the discussion that follows. Firstly, the weight of $c_{3}$ rapidly increases (Fig. 3). Therefore, $z_{33} = \left( {s_{5} ,s^{\prime}_{3} } \right)$ being superior to $z_{23} = \left( {s_{4} ,s^{\prime}_{4} } \right)$ will have an ever-increasing contribution to $a_{3} \succ a_{2}$ (Table 2). Accordingly, $z_{32} = \left( {s_{3} ,s^{\prime}_{4} } \right) \prec z_{22} = \left( {s_{4} ,s^{\prime}_{3} } \right)$ will have a gradual reduction in the negative effect on $a_{3} \succ a_{2}$ as the weight of $c_{2}$ decreases. Thus, the priority of $a_{3}$ and $a_{2}$ changes.

The change of the priority of candidates in Fig. 1 seems chaotic. Here, such changes can be explained in conjunction with Figs. 2 and 3. Firstly, the weight of $c_{3}$ increases rapidly, whereas that of $c_{2}$ decreases. Therefore, the ranking of the candidates under criterion $c_{3}$ becomes increasingly important. Moreover, the priority of all the candidates under $c_{3}$ will be $a_{ 1} \succ a_{ 3} \succ a_{ 2} \succ a_{ 4}$ when $\omega$ is extremely close to one (Table 2). Consequently, the closeness of $a_{ 2}$ and $a_{ 4}$ will gradually decrease, and that of $a_{ 1}$ and $a_{ 3}$ will increase continuously (Fig. 2).

The preceding analysis reveals that the proposed algorithm has a good performance on its decision preference parameter. The result of the algorithm execution is consistent with our expectation. Different values of parameter can produce different rankings of candidates, which reflect the different DMs’ preferences about information reliability to a certain extent. Therefore, parameter $\omega$ plays the good role that we expect. Consequently, the preference parameter $\omega$ is necessary, and the comprehensive weighted cross-entropy measure (16) of Z-numbers is reasonable.

5.3 Comparative Analysis

Comparative analysis is an important tool, through which a decision-making approach can be examined in great depth. This section uses comparative analysis to discuss the feasibility and effectiveness of the proposed algorithm. Three methods are used simultaneously to rank the candidates for the middle management position presented in this study. This analysis aids in proving the effectiveness and applicability of our proposed method.

Aliyev [32] developed the distance measure of Z-number based on cut set as follows:

$$D\left( {Z_{1} ,Z_{2} } \right) = \frac{1}{n + 1}\sum\limits_{k = 1}^{n} {\left\{ {\left| {a_{{1a_{k} }}^{L} - a_{{2a_{k} }}^{L} } \right| + \left| {a_{{1a_{k} }}^{R} - a_{{2a_{k} }}^{R} } \right|} \right\}} + \frac{1}{m + 1}\sum\limits_{k = 1}^{m} {\left\{ {\left| {b_{{1a_{k} }}^{L} - b_{{2a_{k} }}^{L} } \right| + \left| {b_{{1a_{k} }}^{R} - b_{{2a_{k} }}^{R} } \right|} \right\}} .$$

(26)

Thereafter, Eq. (26) is used to calculate the distance between a certain alternative and the positive/negative ideal solutions. Moreover, the ranking of alternatives can be acquired on the basis of the priority indices.

Yaakob and Gegov [29] presented a new fuzzy TOPSIS group decision-making (GDM) method based on Z-number context. This approach is based on another method proposed by Kang [28] for Z-number conversion. Assuming one given Z-number $Z = \left( {A,B} \right)$, we have

$$\alpha = \frac{{\int {x\mu_{B} {\text{d}}x} }}{{\int {\mu {\text{d}}x} }},$$

(27)

where parameter $\alpha$ is the weight of the reliability restriction $B$ of $Z = \left( {A,B} \right)$. The middle parameter $\alpha$ is multiplied to the fuzzy restriction $A$ of $Z = \left( {A,B} \right)$. Therefore, the weighted Z-number can be acquired. Consequently, the decision-making problem where all the evaluation values of alternatives are Z-numbers is converted to an ordinary fuzzy MCDM where the evaluation values will be triangular or trapezoidal fuzzy numbers.

Shen and Wang [13] presented a novel fuzzy VIKOR decision-making method based on Z-number context. Their Z-VIKOR approach is based on the comprehensive weighted distance measure that they developed. Assuming two given Z-numbers $Z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $Z_{2} = \left( {A_{2} ,B_{2} } \right)$, the distance between them is

$$D_{\omega } \left( {Z_{1} ,Z_{2} } \right) = \omega {\text{ZRMD}}\left( {B_{1} ,B_{2} } \right) + \left( {1 - \omega } \right){\text{ZHD}}\left( {p_{{Z_{1} }} ,p_{{Z_{2} }} } \right),$$

(28)

where $\omega$ is the weight parameter, ${\text{ZRMD}}\left( {B_{1} ,B_{2} } \right)$ is the distance measure of reliability restriction, and ${\text{ZHD}}\left( {p_{{Z_{1} }} ,p_{{Z_{2} }} } \right)$ is the distance measure of underlying probability distributions. Therefore, the distance measure between any two Z-numbers can be acquired. Consequently, the decision-making problem where all the evaluation values of alternatives are Z-numbers can be solved by using the extended Z-VIKOR MCDM method proposed by Sheng and Wang.

Table 14 shows the priorities of the candidates produced by different ranking algorithms.

Table 14 Priorities produced by different methods

As shown in Table 14, the rankings of candidates produced by [29, 32] are consistent with that proposed in the present study when $\omega = 0. 8$. In addition, the optimal candidate generated by using Shen and Wang’s algorithm [13] is the same as the optimal one proposed here when $\omega = 0. 8$. Further details about the comparative analysis are presented as follows.

Firstly, Aliyev’s order is completely consistent with our proposed order when $\omega = 0. 8$ (Table 14). Therefore, Aliyev’s sorting result is only a special case of the sorting result of the algorithm presented in this study under a certain decision preference. However the method produced in [32] for calculating the distance between Z-numbers is problematic. In Eq. (26), the fuzzy and reliability restrictions of Z-number information are considered equally, which results in a serious misinterpretation of the original definition of Zadeh’s Z-number. Generally, $Z_{1} = \left( {A,B} \right)$ will not be equal to $Z_{2} = \left( {B,A} \right)$ in most situations. This method simply considers Z-number as a pair of values composed of two discrete fuzzy numbers. Therefore, the priority result recommended by this approach is not convincing.

Secondly, the ordering of candidates recommended by Yaakob’s sorting algorithm [29] is similar to the result of our proposed method when $\omega = 0. 8$. The best candidate is $a_{1}$, and the worst one is $a_{4}$. Furthermore, as shown in Figs. 1 and 2, the priority of $a_{2}$ is in a decreasing trend, whereas that of $a_{3}$ is in an increasing trend. The sorting method has reached a certain coincidence with our proposed approach ($\omega = 0. 8$). Yaakob’s approach places minimal emphasis on information reliability and objectively places more attention on the fuzzy restriction of Z-numbers. The authors’ algorithm is based on rigorous mathematical proofs and has good consistency with traditional fuzzy theory, which is meaningful for the exploratory study of Z-number. However, this method of processing Z-number does not consider Zadeh’s initial explanation of Z-number, which is unsatisfactory.

Thirdly, Shen and Wang [13] developed one comprehensive weighted Z-distance measure. On this basis, they proposed a Z-VIKOR MCDM framework. The optimal candidate generated by Z-VIKOR is consistent with our proposed approach, that is, $a_{1}$ ($\omega = 0. 8$; Table 14). Thus, the sorting results are generally consistent when parameter $\omega$ takes certain values. The optimal candidate recommended by the decision-making method in the present study is $a_{2}$ when $\omega$ takes certain smaller values (Sect. 5.2). This indicates that the weight of the fuzzy restriction of Z-number can affect the ranking result. Thus, $\left( {A_{ 1} ,B} \right) \ne \left( {A_{ 2} ,B} \right)$ may be different in many cases. However, the Z-distance measure developed by Shen and Wang is lacking at this point. Therefore, in comparison with their sorting method, the decision method in the present study is more flexible and effective.

The comparison of the proposed approach with other methods shows that the former is feasible and initially reveals certain additional advantages. Parameter $\omega$ reflects the DM’s preference for information reliability to a certain extent and can arrange the candidates’ ranking accordingly. From this analysis, the ordering of candidates, which cannot be produced by other methods, can be derived by adjusting the value of $\omega$. Nevertheless, these sorting sorts are reasonable because they are generated considering the different preferences of information reliability.

On the basis of the preceding comparative analysis, certain features of the proposed method can be obtained as follows.

• (1) The cross-entropy measure of discrete Z-numbers considers the fuzzy and reliability restrictions of Z-numbers simultaneously. The proposed method for comparing two discrete Z-numbers is consistent with Zadeh’s statement about Z-numbers. In comparison with other methods, ours pays more attention to the close relationship between the two components of Z-number.

• (2) The relative importance of ambiguity and reliability restrictions of information, which involves the DM’s preference during information fusion, should be considered. The parameter $\omega$ of cross entropy of two discrete Z-numbers can reflect the DM’s preference. The proposed approach can solve substantially complex decision problems by adjusting the value of $\omega$.

• (3) In view of the cross-entropy concept in this study, the extended TOPSIS under discrete Z-evaluation is constructed to solve the complex MCDM problem where the reliability of information must be considered. The extended TOPSIS method enhances the capability of the fuzzy TOPSIS method and expands its application scope.

Generally, the proposed method is an in-depth study of previous approaches and has practical feasibility and effectiveness.

6 Conclusions

Z-number considers the fuzzy and reliability restrictions of information. Since Zadeh produced Z-number, researchers have conducted extensive research on it. To minimise the loss of information during Z-information processing, this study discusses the cross entropy of discrete Z-numbers on the basis of the cross entropy of discrete fuzzy numbers and the cross entropy of probability distributions. Firstly, the cross entropy of fuzzy restriction between discrete Z-numbers is defined on the basis of the cross entropy of discrete fuzzy numbers. Secondly, the cross entropy of the reliability component of discrete Z-numbers is defined. Thirdly, this study constructs a comprehensive weighted cross entropy of discrete Z-numbers by adopting a risk preference parameter. Moreover, an extended TOPSIS method for the MCDM problem is developed. Finally, one illustrative example about the HRM issue is presented to illustrate the effectiveness of the proposed method.

Certain interesting paths worthy of further research are as follows.

• (1) The cross entropy of discrete Z-numbers is defined on the basis of the cross entropy of discrete fuzzy numbers. A good research path is possibly to discuss the cross entropy of continuous Z-numbers.

• (2) DMs are assumed honest in this study. However, certain DMs may be dishonest and use strategic weight manipulation in an attempt to obtain their desired ranking of alternatives [54, 55]. The weight information based on discrete Z-numbers is partially reliable information. In certain decision scenarios, DMs may implement strategic weight manipulation by changing the reliability restriction of weight information. Therefore, an interesting path is to study the weight setting of MCDM in the context of dishonesty.

• (3) GDM and consensus research are important research areas [56, 57]. In this study, DM’s risk preference parameter of the comprehensive weighted cross entropy is briefly discussed through sensitivity analysis. However, in the real-world consensus-reaching process, DMs often present different individual concerns on alternatives [58]. Therefore, how to determine DMs’ risk preference parameters in the GDM problem remains to be further studied.

Appendix: Proof of the properties of Eq. (16)

Proof

• (1) In accordance with Definitions 8 and 12, $H^{F} \left( {A_{1} ,A_{2} } \right) \ge 0$ and $H^{R} \left( {Z_{1} ,Z_{2} } \right) \ge 0$ exist.

Therefore, $H^{\omega } \left( {Z_{1} ,Z_{2} } \right) = \omega H^{F} \left( {A_{1} ,A_{2} } \right) + \left( {1 - \omega } \right)H^{R} \left( {Z_{1} ,Z_{2} } \right) \ge 0$ is satisfied.

• (2) On the basis of Definitions 8 and 12, if $Z_{1} = Z_{2}$, then $H^{F} \left( {A_{1} ,A_{2} } \right) = 0$ and $H^{R} \left( {Z_{1} ,Z_{2} } \right) = 0$ exist.

Therefore, $H^{\omega } \left( {Z_{1} ,Z_{2} } \right) = \omega H^{F} \left( {A_{1} ,A_{2} } \right) + \left( {1 - \omega } \right)H^{R} \left( {Z_{1} ,Z_{2} } \right) = 0$ is satisfied.

• (3) According to Definitions 4, 5, 8 and 12, if $Z_{1} = Z_{2}$, then $H^{F} \left( {A_{1} ,A_{2} } \right) = H^{F} \left( {A_{2} ,A_{1} } \right)$ and $H^{R} \left( {Z_{1} ,Z_{2} } \right) = H^{R} \left( {Z_{2} ,Z_{1} } \right)$ exist.

Therefore, $H^{\omega } \left( {Z_{1} ,Z_{2} } \right) = H^{\omega } \left( {Z_{2} ,Z_{1} } \right)$ is satisfied.$\hfill\square$